Competitive interaction of monovalent cations with DNA from 3D-RISM

Abstract

The composition of the ion atmosphere surrounding nucleic acids affects their folding, condensation and binding to other molecules. It is thus of fundamental importance to gain predictive insight into the formation of the ion atmosphere and thermodynamic consequences when varying ionic conditions. An early step toward this goal is to benchmark computational models against quantitative experimental measurements. Herein, we test the ability of the three dimensional reference interaction site model (3D-RISM) to reproduce preferential interaction parameters determined from ion counting (IC) experiments for mixed alkali chlorides and dsDNA. Calculations agree well with experiment with slight deviations for salt concentrations >200 mM and capture the observed trend where the extent of cation accumulation around the DNA varies inversely with its ionic size. Ion distributions indicate that the smaller, more competitive cations accumulate to a greater extent near the phosphoryl groups, penetrating deeper into the grooves. In accord with experiment, calculated IC profiles do not vary with sequence, although the predicted ion distributions in the grooves are sequence and ion size dependent. Calculations on other nucleic acid conformations predict that the variation in linear charge density has a minor effect on the extent of cation competition.

INTRODUCTION

The large negative charge inherent to nucleic acids requires stabilization by a neutralizing ion atmosphere that contains territorial and site-bound cations and excludes anions. Biological function of nucleic acids is highly sensitive to the content of the surrounding ion atmosphere which can affect secondary and tertiary structure, folding pathways, binding of proteins and small molecules, as well as condensation and packing in cells and viruses (1–3). The importance of the ion atmosphere surrounding the nucleic acids has motivated the development of a multitude of theoretical approaches aimed to advance our understanding of nucleic acid electrostatics (1,4–15 and the references therein). The first major step toward this goal was Manning's counter ion condensation theory that modeled DNA as an ideal uniformly charged cylinder (16). The next breakthrough came with the development of computational approaches to solve the non-linear Poisson–Boltzmann equation (NLPB) for atomistic macromolecular solutes providing predictions for the spatial distribution of ions around nucleic acids as well as solvation thermodynamics (12,17–22).

Although valuable for many applications, conventional NLPB is a mean field continuum theory that inherently does not take into account the effect of ion size and ion–ion correlation, which limits its predictive value in distinguishing ion-dependent binding and competition. Several extensions of NLPB have been made to include specific ion size effects (18,23–26) and more advanced models based on density-functional theory of liquids or Monte Carlo simulations were shown to effectively treat ion–ion correlations and have been applied to examine the ion environment around nucleic acids (27–34). These models demonstrate that explicit consideration of ion size effects and ion–ion correlations lead to significant deviations from the spatial distribution of ions relative to conventional NLPB calculations especially near a charged surface.

Molecular dynamics (MD) is one of the most powerful methods used for describing the spatial distribution of ions around nucleic acids at full atomic detail (35–37). MD simulations provide detailed dynamical information for water and ion distributions but are considerably computationally intensive due to the need to explicitly model a sufficiently large surrounding solvent environment such that bulk behavior is observed at the boundaries combined with a high degree of sampling over solvent configurations (35,36). Both of these issues are exacerbated at low bulk ion concentrations making practical calculations considerably more challenging in this regime.

The three dimensional interaction site model (3D-RISM) (38–40) is a molecular solvation theory method that treats ion size effects and ion–ion correlation but unlike MD simulation, can be practically applied for the prediction of solvation thermodynamics over a wide range of conditions (41,42). 3D-RISM calculations on nucleic acids are much less computationally intensive than MD simulations and calculations can be easily converged in the presence of micro-molar to molar salt concentrations (36). 3D-RISM and MD have been shown to yield similar layered solvent and ion distributions around nucleic acids and other biopolymers (36,38–40).

Quantitative experimental characterization of the ion atmosphere surrounding nucleic acids up until fairly recently has been limited since the territorial binding of ions cannot be captured by standard structural biology techniques or described alone by simple site binding models (4,43). Recently, departing from earlier ideas (44) experimental techniques that count the number of excess ions associated with nucleic acids have been developed (19,22,43,45). Such ‘ion counting’ (IC) measurements provide rich datasets for testing of existing and new models.

The goal of this work is to gain understanding of the strengths and limitations of existing methods to reproduce a wide range of quantitative IC experiment in order to guide the design of improved models for treating the ion atmosphere around nucleic acids. Ultimately a meaningful assessment of the predictive value of current models must come from a systematic comparison with experiments that provide quantitative information about the contents of the ion atmosphere. In a previous paper, we examined the ability of NLPB, 3D-RISM and MD simulation to reproduce IC results for single-component (NaCl) solutions, as well as compared the predicted ion distributions from the different methods (36). Overall a 3D-RISM protocol was identified that was able to reproduce IC profiles closely up to relatively high (0.7 M) bulk NaCl concentrations, while predicting structured spatial ion distributions close to those from MD simulations, with slightly stronger binding to phosphoryl groups on the backbone. Here, we extend our previous work to investigate the extent to which 3D-RISM can model ion size effects as manifested through ion competition for binding to dsDNA by comparing against a series of IC measurements using binary mixtures of alkali halides (22). The good agreement with these experiments affords an atomic-level interpretation of the data providing insight into the origin of the observed ion size effect on ion competition. This is an early important step toward gaining predictive insight into the formation of the ion atmosphere and thermodynamic consequences when varying ionic conditions.

MATERIALS AND METHODS

Three dimensional interaction site model (3D-RISM)

3D-RISM solves for the equilibrium 3D density distribution of aqueous salt solutions around a macromolecule (46–49) using molecular mechanical force fields to model the solute–solvent and solvent–solvent interactions. 3D-RISM is based on the Ornstein and Zernike integral equation theory (OZ equation) (50,51) which expresses the density distribution in terms of direct and indirect correlation functions. The OZ equation is inherently six-dimensional for polyatomic molecules due to the orientational dependence on the intermolecular interactions. The 3D-RISM formalism reduces this to 3D by orientationally averaging the solvent degrees of freedom such that the resulting solvent density distributions contain only a spatial dependence, 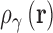. The distributions of atomic sites (γ) on water and ions are represented on 3D grids via the total correlation function (TCF), 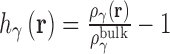and direct correlation function (DCF), 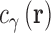, which are related as:

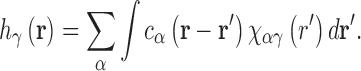(1)

χ_αγ(r) is the site–site solvent-susceptibility of solvent sites α and γ, and contains the orientationally averaged bulk properties of the solvent. We use the dielectrically consistent RISM (DRISM) integral equation (52,53) to pre-compute χ_αγ(r) using an analytic treatment of long-range electrostatics originally developed for the OZ equation (54–56) that has been applied to both 1D-RISM (57) and 3D-RISM (49,58,59).

As in all OZ-based theories a second, closure equation must be used to obtain a unique solution. Due to the complexity of the closure equation, an approximation must be used and the form of this approximation impacts the convergence of calculations as well as the resulting thermodynamic quantities and 3D densities. Many closure relations have been developed for integral equation theories, out of which the most popular are the hypernetted chain (HNC) (60) and partially-linearized Kovalenko–Hirata (KH) (47) equations. HNC produces good results for ionic (40,53,61,62) and polar systems (63–65) and has an exact closed form expression for the excess chemical potential when coupled with RISM theory (66). However HNC solutions are often difficult to converge. The KH closure (47) addresses this problem by linearizing regions of density greater than bulk 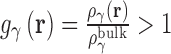. This closure is numerically robust and also has an exact, closed form expression for the excess chemical potential. The partial series expansion of order-n (PSE-n) (67) generalizes the linearization to a Taylor series:

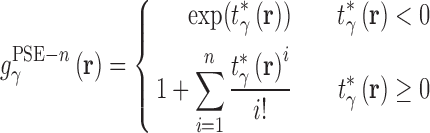(2)

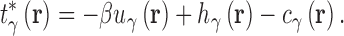where β is the reciprocal thermodynamic temperature and 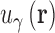is the pair potential between solvent site γ and the solute. For n = 1 the KH closure is recovered and HNC is the limiting case as n → ∞. Like HNC and KH, PSE-n has an exact, closed form expression for the chemical potential. A detailed description of 3D-RISM calculations for IC is given in (36).

DRISM calculations

DRISM calculations are used to determine the site–site solvent susceptibilities needed for 3D-RISM calculations. DRISM calculations were performed using the rism1d program in the AmberTools 13 and 14 molecular modeling package (68,69) and largely follow the procedure of (70). To obtain χ_αγ(r) of the bulk solvent the DRISM equation coupled with a closure relation was iteratively solved using a modified direct inversion of the iterative subspace approach (MDIIS) (71) to a residual tolerance of 10⁻¹² at a temperature of 298.15 K and a dielectric constant of 78.44 for bulk water. A grid spacing of 0.025 Å was used throughout (32 768 total grid points). To facilitate convergence solutions from lower order closures starting from KH, were used iteratively as initial guesses until the PSE-3 closure was converged.

DRISM calculations need the specification of bulk water and ion concentrations. As salt concentration is known, it is only the water concentration that has to be determined. Water concentration can be determined easily if the aqueous salt solution density is known (36,70). Since experimental data on all the salt mixtures used here is not available we will rely on an approximate approach based on a model for partial molar volumes of simple salts (72). The density of a solution is approximated as:

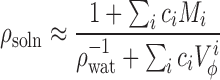(3)

where the sums go over all the salts found in solution and 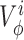is the partial molar volume of salt i that is a function of the salt molar concentration c_i. Equation 3 is exact for simple salts (72) and we found that it predicts available density measurements for these salts very well.

3D-RISM calculations

3D-RISM calculations were performed using the rism3d.snglpnt program in the AmberTools 14 molecular modeling package (68,69).

The Ornstein–Zernieke equation coupled with PSE-3 closure (67) was iteratively solved using MDIIS to a residual tolerance of 10⁻⁶ on a 300 x 300 x 300 Å grid with 0.5 Å grid spacing for all ion concentrations as in previous work (36).

Convergence was accelerated by sequentially performing several iterations with KH and PSE-2 closures (67) to provide an initial guess.

Nucleic acid sequences

The sequence for the 24 bp DNA duplex used to compare 3D-RISM estimated and experimental measurements was 5’-d(GGTGACGAGTGAGCTACTGGGCGG)-3’ and its complementary strand and henceforth this construct is referred to as 24L as in the original experimental work (22). The corresponding 24 bp RNA duplex (R24L) has the same sequence with T replaced by U and the 24 bp DNA/RNA hybrid (H24L) was formed as the 24 dGrC base pairs, and DNA triplex sequence (T24L) was formed from 24 d(TAT) triples. Two additional sequences were used to probe ion binding sequence dependence: 5’-d(GAGGTGTCCAGCGCTGGTCGAGTC)-3’ and its complementary strand (24La1), and 5’-d(GGAAAATTTTCGAATTCTGATGGC)-3’ and its complementary strand (24La2). The 3D structures of the RNA and DNA constructs were generated with Nucleic Acid Builder (NAB) (73) using helical parameters for B and A conformations. The 3D structures of the DNA/RNA hybrid and DNA triplex were generated using 3DNA (74).

Molecular mechanics force fields

The current implementation of 3D-RISM in AMBER (68,69) uses molecular mechanics force fields similar to those utilized for MD of biomolecules in explicit solvent. For the systems considered here that contain a nucleic acid molecule water and ions the force field is composed from the following parameter sets: (i) ff10 AMBER force field for nucleic acids (75,76) that specifies the partial charges, LJ parameters as well as bonded terms for nucleotides, (ii) SPC/E rigid water model (77) developed to describe the bulk properties of pure water that specifies the geometry partial charges and LJ parameters for water (iii) alkali halide parameters (78,79) developed to reproduce experimental ion solvation free energies and average contact distances; these parameters were optimized for several types of water models, including SPC/E. These alkali halides parameters do not display the previously observed unphysical salting-out effect when used in molecular simulations (80).

All the parameters presented above have been developed and optimized in the context of MD simulations and are commonly used together for simulations of nucleic acids. There is no a priori guarantee that force fields developed for MD simulation should perform comparably when used with 3D-RISM. However the similarity between particle distributions obtained from MD and 3D-RISM (36,38–40) suggest that current force fields can be used as a starting point for testing 3D-RISM against experimental data. Bulk properties of alkali halides determined using dielectrically consistent DRISM have been recently evaluated against a wide variety experimental measurements with the general conclusion that DRISM provides semi-quantitative agreement with experiment (70).

RESULTS AND DISCUSSION

Relating ion counting experiments and computed spatial ion distributions

IC experiments are run using an equilibrium dialysis setup. An aqueous salt solution containing the nucleic acid is dialyzed using a semipermeable membrane that allows only the passage of water and small ions (see Figure 1). The presence of the nucleic acid leads to an unequal distribution of ions and water across the membrane that can be expressed as a preferential interaction parameter (22):

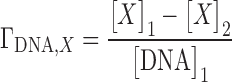(4)

In Equation 4 the indexes refer to the two sides of the membrane (see Figure 1). To simplify notation we will henceforth omit the subscripted ‘DNA’ index although it has to be kept in mind that preferential interaction parameters are measured for interacting species. Preferential interaction parameters are fundamental thermodynamic quantities in the theory of solutions and have been used to gain insight into the formation of the ionic atmosphere surrounding highly charged nucleic acids (1,16,81).

Figure 1.

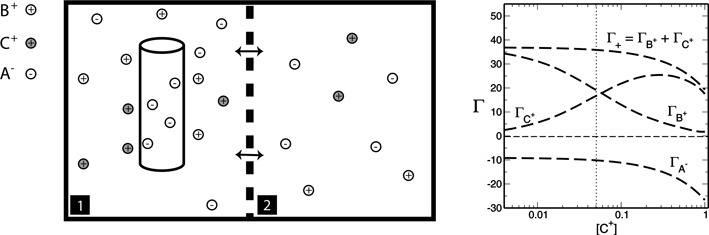
Ion counting (IC) competition experiments. (Left) Schematic of the IC competition experiments. Cell 1 containing an aqueous salt solution and the nucleic acid, is allowed to equilibrate with cell 2, containing only a salt solution, using a membrane (vertical dashed line) that permits the exchange of small ions and molecules. In the experiments presented herein, the concentration of the background cation (B⁺) is held constant (fixed), and the concentration of the competing cation (C⁺) is varied. (Right) Typical IC competition profile showing how the preferential interaction parameters (Equations 4 and 5) of the ionic species vary when changing the concentration of the competing cation. The vertical dotted line marks the point where the bulk concentration of both cations are equal.

There is a direct connection between preferential interaction parameters, Γ_X, of Equation 4 and the 3D distribution, or local concentration, of particles surrounding a solute, 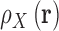. Preferential interaction parameters are defined as an integral measure of the perturbation of the local density of species in solution due the presence of a solute (41,82). When molar concentration units are used (83):

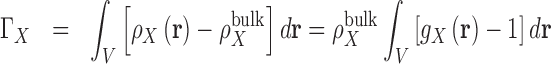(5)

where V is the system volume over which the integration is carried out. 3D distributions are commonly written as a product between a pair correlation function 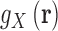, and the bulk particle density, 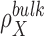, which is equivalent to a bulk concentration (41). In practice the region where the density is perturbed is localized around the solute and so the integrals can be carried out over a finite volume. To assure convergence, V has to be large enough to include the region in which the density is perturbed and a representative portion of the bulk (82). The choice of V is critical for nucleic acids systems where the range of correlation with the surrounding ion and solvent atmosphere can extend to distances of 20 to 30 Å from the nucleic acid surface. Using the analytic treatment of long-range electrostatics in 3D-RISM, this integral is performed over all-space.

The primary requirement for both theoretical and experimental IC measurements is to maintain the charge neutrality of the system. This is an indicator of having reached thermodynamic equilibrium and is equivalent to requiring that the entire excess charge brought by the ions is counterbalanced by the charge of the solute:

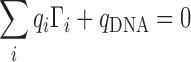(6)

where q_i is the charge of species i and the summation ranges over all species in the solution.

Comparison between ion counting (IC) competition profiles from 3D-RISM and experiment

The IC competition experiments used here as reference have been carried out in the presence of two alkali cations and a common anion. The background cation is maintained at constant concentration as the concentration of the competing cation is varied (22). An example of an IC competition profile is shown in Figure 1. The increase of the competing cation concentration leads to an increase of its preferential interaction parameter while the preferential interaction parameter of the background cation decreases.

Figure 2 shows a comparison between IC competition profiles derived from 3D-RISM calculations and several measurements (22) for Li⁺, K⁺ and Rb⁺ competition against a background of 50 mM Na⁺, and competition of Na⁺ against 50 mM of Li⁺. The agreement between theoretical estimates and experiment is excellent at low salt concentrations for all the ionic species in solution. The deviation from experiment becomes significant when the competing cation concentrations exceed ∼0.2 M with 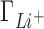being overestimated 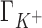and and 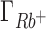being underestimated by 3D-RISM. 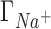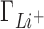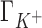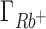remains closest to experiment over the entire range of concentrations and the deviations observed for , and are compensated by 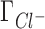. Preferential interaction parameter deviations from experiment for Li⁺, Rb⁺ and K⁺ competition against Na⁺ are concentration dependent, increasing with the concentration of the competing cation.

Figure 2.

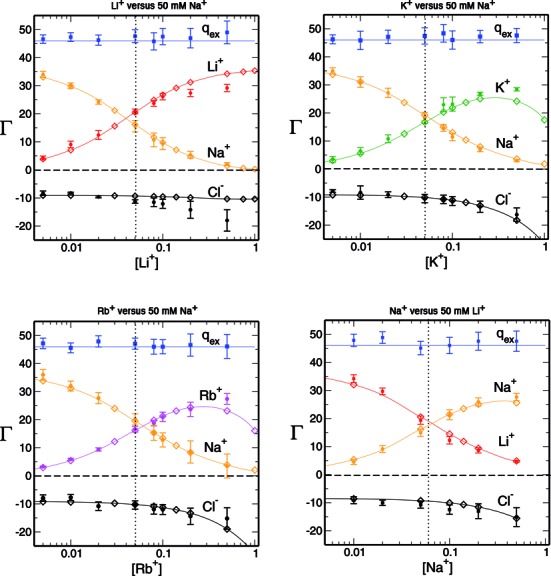
Comparison between IC competition profiles obtained from experiment (circles with error bars) and 3D-RISM (interpolated open diamonds). IC profiles shown in graphs at the top and lower left were determined in 50 mM Na⁺ background and the graph in the lower right was determined in 50 mM Li⁺ background. The vertical dotted line marks the point at which the bulk concentration of both cations are equal. q_ex is the total excess charge and has to counterbalance exactly the charge of the nucleic acid solute (−46e). The optimal value of q_ex is marked with a blue line and data from experiment is shown as solid squares. Preferential interaction parameters values are shown in Supplementary Table S1.

When Li⁺ concentration is maintained at 50 mM and Na⁺ concentration is varied, the deviations from experiment are not as large as in the previous cases. This suggests a subtle imbalance within the current model between the strength of interaction of Li⁺, K⁺ and Rb⁺ with the DNA relative to water.

Relative competitiveness of cations

The IC competition profiles presented in Figure 2 show that competing cations (C⁺) have different abilities to displace the background cation (B⁺) from the ion atmosphere. The competing cation bulk concentration required to equalize the number of accumulated background cations in the ion atmosphere depends on the relative size of the cations (Figure 2). A smaller competing cation will need a lower bulk concentration than that of the background cation to contribute an equivalence of the total condensed positive charge. To quantify the relative competitiveness of cations we will estimate a competition constant (c) from a single parameter model (discussed in detail in the Section B of the Supplementary Data) in which:

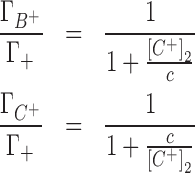(7)

where 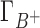and 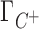are the preferential interaction parameters of the background and competing cation and Γ₊ is their sum, 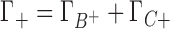; [C⁺]₂ is the bulk concentration of the competing cation. As shown throughout this work, 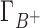, 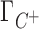and Γ₊ vary with bulk concentrations of competing and background cations. In short, the model assumes that the ratio of preferential interaction parameters of the background and competing cations is proportional to the ratio of the corresponding concentrations in the bulk. As shown in Supplementary Data (Section B, Figures 2 and 3), this assumption holds for concentration of up to 100–150 mM for both 3D-RISM and experimental data. The competition constant is related to the relative contribution of each cation to the total excess positive charge, Γ₊, and can be easily identified as the concentration of competing cation at which 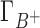equals 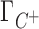, i.e. where the IC profiles of the two cations intersect. If c < [B⁺] then C⁺ is more competitive than B⁺; if c > [B⁺] then C⁺ is less competitive than B⁺.

Figure 3.

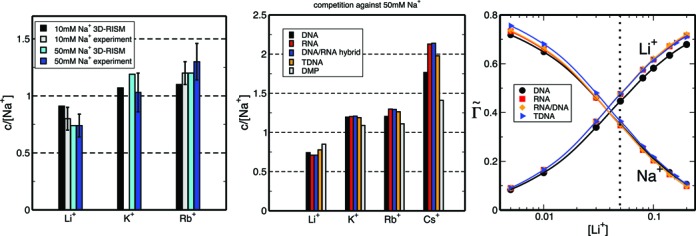
(Left) Comparison between competition constants obtained from experiment and 3D-RISM calculations. Experimentally derived estimates for the competition constant of K⁺ versus 10 mM Na⁺ do not exist. (Middle) Competition constants determined for a series of DNA (24L), RNA (R24L), DNA/RNA hybrid (H24L), triplex TDNA (T24L) constructs (see ‘Materials and Methods’ section for details) as well as dimethylphosphate (DMP). (Right) Overlay of charge-normalized ion competition profiles (Equation 9) for different nucleic acid constructs.

Figure 3 (left) compares competition constants estimated from existing experimental data and 3D-RISM calculations for competition against 50 mM as well as 10 mM Na⁺ background. For all the cases shown in Figure 3, competition constants follow the same trend where 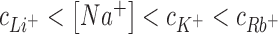. This is equivalent to having the cation affinity for DNA vary according to the following sequence Li⁺ < Na⁺ < K⁺ < Rb⁺. The competition constant of K⁺ derived from experimental data is marginally larger than unity, suggesting that Na⁺ and K⁺ have similar affinities. In the case of 3D-RISM calculation the competition constant of K⁺ is however closer to that of Rb⁺.

As noted earlier (22), and as shown in Section A of the Supplementary Data and Supplementary Figure S1, solving the conventional NLPB equation cannot distinguish between less and more competitive cations of the same charge. As such, competition constants resulting from conventional NLPB calculations will not depend on the ion size and within the model proposed here will be equal to the concentration of the background cation.

Spatial distributions of competing ions

A molecular level interpretation of ion competition can be drawn based on the direct connection between preferential interaction parameters and ion distributions around a solute (Equation 5). We will analyze the case in which the concentrations of the background and competing cations are equal (50 mM) to eliminate the effect of the mixing entropy. As shown in the previous section, in this case 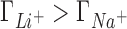, 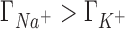and 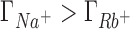(see Figure 2) which is equivalent to having a larger excess of positive charge density brought by the more competitive cation around the DNA solute. In what follows we aim to localize the excess positive charge brought by the more competitive cation.

In principle one could use for analysis the 3D distributions of ions around the DNA solute that are readily available from 3D-RISM. While such maps capture the full detail in all spatial dimensions, analysis and presentation are facilitated by creating distributions of lower dimensionality (36) in the following way.

Cylindrical radial distribution functions 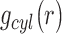, measure the average particle density in a direction perpendicular to the helical axis. The region corresponding to ions binding in the minor and major grooves of the DNA is located at r < 7.5 Å the region corresponding to ions binding to the phosphates is located for 7.5 < r < 15 Å (36).

Untwisted density maps capture the average particle distributions in planes perpendicular to the helical axis by rotating against the natural helical twist of the nucleic acid (36). Such maps isolate better than the cylindrical radial distribution functions the interactions with the grooves and phosphates and capture the layered distribution of ions or water specific to 3D-RISM and MD simulations.

To locate the regions that contribute to the excess of charge brought by the most competitive cation we will use a normalized running integral of the difference of two cations densities:

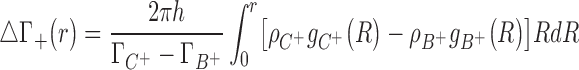(8)

where 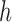corresponds to the distance on the z-axis over which the integration in cylindrical coordinates is carried out.

Figure 4 (left) compares the cylindrical radial distribution functions of the competing and background cations as well as their integrated difference. It can be observed that excess of charge brought by the more competitive cations is localized in the immediate vicinity of the solute. Specifically the cylindrical radial distribution functions locate the largest differences between the competing and background cations in the region usually associated with phosphate binding, which is located between 7.5 and 15 Å away from the helical axis. The integrated difference of the two cations densities shows that the largest contribution (∼80%) to the difference is located in the same region.

Figure 4.

The effect of cation size on spatial distribution functions. (Left) Cylindrical radial distribution functions of cations from 3D-RISM calculations where both the background (Na⁺) and competing (Li⁺, K⁺ and Rb⁺) cation have the same bulk concentration (50 mM). The normalized running integral of the difference between the background and competing cation densities,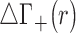 (Equation 8), is shown in black and its corresponding scale is shown on the right. The most competitive cations bring an excess of density located mainly in the vicinity of the DNA, particularly in the region of the phosphate binding, whereas for radii greater than ∼15 Å the densities of both cations are the same. (Right) Difference between 2D-untwisted ion densities (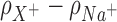) where X⁺ = Li⁺, K⁺ and Rb⁺. Untwisted densities for each cation are presented in Supplementary Figure S6.

Figure 4 presents the differences between the densities of each pair of competing cations using the untwisted mapping presented above (the separate density plots of each cation are provided in Supplementary Figure S6). It can be observed that the more competitive cation (Li⁺ in the first case, and Na⁺ in the next two cases) has a higher preferential occupancy near the phosphoryl groups and is able to penetrate deeper into the minor and major grooves. However, the excess charge due to closer contacts to the grooves have minor contribution to the extent of competition as shown by 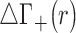. The larger cations are radially shifted away from the surface of the DNA solute, and due to the layered distribution are able to have higher densities in restricted areas than the smaller cations. To provide further support for the ability of smaller cations to approach closely to the phosphoryl groups, Supplementary Figures S4 and S5 present the spherical radial distribution functions of cations with respect to a phosphoryl group located on the nucleic acid backbone. The position of the first peak which corresponds to inner sphere contact increases from roughly 3 to 4 Å, as one traverses the series from Li⁺ to Cs⁺. The same trend is observed for the radial peaks corresponding to solvent separated contacts. Additionally, it is only Li⁺ that can approach the phosphoryl groups almost as close as water hydrogen atoms, which was also observed in a previous study (84).

Although the density corresponding to ions bound in the grooves makes fairly small contributions to the overall IC profiles it is still of great interest to examine this mode of binding due to its biological significance (2,3). Quantitative experimental measurements of the direct ratio of ions bound to the phosphates versus ions bound in the grooves are not yet available (85,86). Nonetheless an indirect experimental test related to groove binding is to examine whether change in sequence affects IC profiles. Such measurements have been reported in the context of ion competition (22) where it was observed that competition constants of Li⁺ and Rb⁺ against a Na⁺ background did not change when two alternative sequences were used. In the Supplementary Figure S7 we show that the IC competition profiles determined for the two alternative sequences are practically identical to those presented in Figure 2. However as shown in Supplementary Figures S6 the cation binding patterns in the grooves strongly depend on sequence being correlated to the placement of electronegative groups. Furthermore, using the GC/CG motif noted previously for chelating Na⁺ and K⁺ (36,87,88), Supplementary Figure S8 shows that ion binding patterns in the grooves and to phosphoryl groups strongly depend on the cation identity.

Prediction of ion counting competition profiles for A-RNA, RNA/DNA hybrid and triplex DNA

To further probe what features of the current model affects ion competition, we have expanded our calculations to a series of nucleic acid solutes adopting typical conformations, as well as to a dimethylphosphate ion as a mimic of the phosphoryl group of the nucleic acids backbone. The solutes series includes a 24mer A-RNA, RNA-DNA hybrid duplexes and a DNA (poly-ATT) triplex. All duplexes have a total charge of −46e as the B-DNA duplex studied in the previous sections; the DNA triplex has a total charge of −69e. There are no reported competition studies for the systems considered here. Previous ion competition measurements exist only for a DNA triplex containing a mixture of ATT and CGC⁺ base triplets, with a total charge of −65e (22) but a lower charge density (due to the protonated cytosines) than the poly ATT DNA triplex studied here.

When comparing preferential interaction parameters for nucleic acids of different charge it is useful to introduce the charge-normalized preferential interaction parameter:

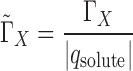(9)

Figure 3 (middle) compares competition constants when Li⁺, K⁺, Rb⁺ and Cs⁺ compete against a background of 50 mM Na⁺ in the presence of the aforementioned solutes. The values of the competition constants obtained in the presence of Cs⁺ (which are the highest in the series presented here) confirm the relation between ion size and the ability to compete. Estimated competition constants are very close to those determined for DNA, especially for Li⁺, K⁺ and Rb⁺, while for Cs⁺ there is a larger variation between the four nucleic acid conformations. Although the majority of competition constants do not change significantly, the total positive excess charge per phosphate at a specific concentration for the four nucleic acid conformations is slightly different and correlated to the variation in linear charge density. For example at low concentrations 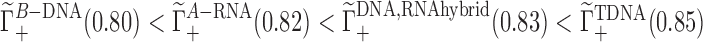. Within the current model, the independence between charge density and competition constants does not extend to the case of dimethylphosphate (Figure 3 middle). While competition constants determined for DMP follow the same trend as those for the nucleic acids studied here, they are much closer to the background cation concentration than those determined for their nucleic acid counterparts. Thus, the current model predicts that the polyelectrolyte nature of nucleic acids has a large impact on the competition constants and profiles, and that the change in nucleic acid conformation and linear charge density has minor effect.

Comparison with molecular dynamics

MD simulation with explicit water and ions is widely used to model the nucleic acid solvation environment at atomic level. There is a great interest to compare MD simulations and 3D-RISM since both methods can use molecular mechanics force fields and have been shown to yield similar layered distributions of ions and water (36,38–40).

MD simulations have been used extensively to study monovalent cation interactions with nucleic acids (35–37,84,87–100) driven in part by development of new force fields (37,78,80,90,93). These studies have provided insight at atomic level into the role of competitive binding of ions to phosphoryl groups (91,92) and the grooves (87–88,98,101,102). Ion and water distribution around DNA resulting from 3D-RISM and MD simulations have been recently compared (36) with a general observation that 3D-RISM using the same force field parameters, predicts a slightly stronger accumulation of cations near the phosphoryl groups. As shown here and previous work (36), this does not impede the ability of 3D-RISM to predict sequence and ion specific binding in the major and minor grooves of canonical nucleic acid structures.

Direct comparison between MD simulations and IC experiments can be made although with a significantly larger computational effort than usual simulation setups (35,36). Large simulation boxes are needed to include regions that represent both the heterogeneous ion atmosphere around the nucleic acid and the homogeneous bulk solution and long simulation times are required to establish a converged equilibrium between these regions such that statistically meaningful preferential ionteraction parameters can be determined. These issues become increasingly severe as the size of the nucleic acid increases and as the bulk salt concentrations decrease. Despite these challenges, recent MD simulations with newly developed force fields have shown great promise in reproducing quantitative IC profiles for ion competition (37,94).

CONCLUSION

Evaluation of competitive interaction of cations with nucleic acids is a crucial test for models attempting to describe the solvation environment around nucleic acids. Evaluation of models depends critically on the availability of accurate quantitative experimental measurements such as on counting competition experiments (19,22,43,45). These experiments have shown that the degree of competitiveness of monovalent cations is inversely correlated with their cationic radii (22).

In this paper we examined the ability of 3D-RISM to compute IC profiles for competition of a series of alkali cations (Li⁺, Na⁺, K⁺ and Rb⁺) with 24mer duplex DNA (22). Overall we found that 3D-RISM can capture the ion-size effect observed in IC competition experiments where a smaller ionic radius is associated with a larger competitive ability. 3D-RISM calculations perform well in reproducing IC competition profiles up to ∼0.2 M competing cation concentration. At larger concentrations, however, 3D-RISM predictions overestimate the number of condensed Li⁺ ions, and underestimate the number of condensed K⁺ and Rb⁺ ions. The molecular level picture that emerges from analyzing ion densities around the nucleic acid solute shows that the more competitive cations accumulate closer to the nucleic acid surface, especially near the phosphate groups. Varying the sequence does not significantly change the IC competition profiles determined using 3D-RISM, in accord with existing experimental data (22). However, the change in sequence does affect the ion binding patterns in both the minor and major grooves. Further, the relative binding of ions at the phosphates versus grooves is sensitive to ion size.

We expanded our calculations to make predictions for a series of other typical nucleic acid conformations such as A-RNA, DNA-RNA hybrid and triplex DNA. We found that while the total number of condensed cations varies with the linear charge density of the nucleic acid, the competition constants are largely invariant. Further, we show that cation competition is less pronounced for dimethylphosphate, suggesting that the polyelectrolyte nature of poly nucleic acids has a significant effect on the size dependent accumulation of ions near the nucleic acid surface. This work represents an important early step toward developing practical tools that predict the thermodynamic consequences of the ion environment around DNA and RNA.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

NIH [P01GM066275 to D.M.Y.; GM45811, GM103297 to D.A.C.]; National Science Foundation [OCI-1053575 to Extreme Science and Engineering Discovery Environment; ACI-1440031 to D.A.C and D.M.Y]. Funding for open access charge: NIH [P01GM066275 to D.M.Y.; GM45811, GM103297 to D.A.C.].

Conflict of interest statement. None declared.