Exploiting Linkage Disequilibrium for Ultrahigh-Dimensional Genome-Wide Data with an Integrated Statistical Approach

Abstract

Genome-wide data with millions of single-nucleotide polymorphisms (SNPs) can be highly correlated due to linkage disequilibrium (LD). The ultrahigh dimensionality of big data brings unprecedented challenges to statistical modeling such as noise accumulation, the curse of dimensionality, computational burden, spurious correlations, and a processing and storing bottleneck. The traditional statistical approaches lose their power due to $p\gg n$ (n is the number of observations and p is the number of SNPs) and the complex correlation structure among SNPs. In this article, we propose an integrated distance correlation ridge regression (DCRR) approach to accommodate the ultrahigh dimensionality, joint polygenic effects of multiple loci, and the complex LD structures. Initially, a distance correlation (DC) screening approach is used to extensively remove noise, after which LD structure is addressed using a ridge penalized multiple logistic regression (LRR) model. The false discovery rate, true positive discovery rate, and computational cost were simultaneously assessed through a large number of simulations. A binary trait of Arabidopsis thaliana, the hypersensitive response to the bacterial elicitor AvrRpm1, was analyzed in 84 inbred lines (28 susceptibilities and 56 resistances) with 216,130 SNPs. Compared to previous SNP discovery methods implemented on the same data set, the DCRR approach successfully detected the causative SNP while dramatically reducing spurious associations and computational time.

WITH recent developments in high-throughput genotyping technique, and dense maps of polymorphic loci within genomes, an ultrahigh dimension of single-nucleotide polymorphisms (SNPs) (typically >0.5 million) is increasingly common in contemporary genetics, computational biology, and other fields of research (Burton et al. 2007; Zeggini et al. 2007; Altshuler et al. 2008; 1000 Genomes Project Consortium 2010; Stein et al. 2010). Despite the fact that large-scale genome-wide association studies (GWAS) provide great power to unravel the genetic etiology of complex traits by taking advantage of extremely dense sets of genetic markers (Cohen et al. 2004; Visscher and Weissman 2011; Worthey et al. 2011; Chen et al. 2012), they bring concomitant challenges in computational cost, estimation accuracy, statistical inference, and algorithm stability (Fan et al. 2009, 2014). First, the number of SNPs p, in units of hundreds of thousands or millions, far exceeds the number of observations n, in units of hundreds or thousands. Referred to as “small n big p,” this situation disables the power of many traditional statistical models (Donoho et al. 2000; Fan and Li 2006). The unique problems that belong only to ultrahigh-dimensional big data, such as storage bottleneck, noise accumulation, spurious correlations, and incidental endogeneity, were pointed out by Fan et al. (2014). Computationally, the combinatorial search space grows exponentially with the number of predictors, called the “curse of dimensionality.” Second, most complex traits are mediated through multiple genetic variants, each conferring a small or moderate effect with low penetrance, which obscures the individual significance of each variant (Sun et al. 2009; Xu et al. 2010; Yoo et al. 2012; Mullin et al. 2013). Third, multicollinearity grows with dimensionality. As a result, the number and extent of spurious associations between genetic loci and phenotypes increase rapidly with increasing p due to noncausal SNPs highly correlated with causative ones (Fan and Lv 2008; Fan et al. 2012, 2014).

Linkage disequilibrium (LD), the nonrandom association of alleles at nearby loci, may be caused by frequent recombination, physically linked genetic variants, population admixture, or even genetic drift (Brown 1975; Devlin and Risch 1995; Patil et al. 2001; Dawson et al. 2002; Gabriel et al. 2002; Gibbs et al. 2003; McVean et al. 2004; Wang et al. 2005; Slatkin 2008; Grady et al. 2011). LD is one of the most important, extensive, and widespread features in genomes, with ∼70–80% of genomes showing regions of high LD (Dawson et al. 2002; Gabriel et al. 2002; Wall and Pritchard 2003; McVean et al. 2004; Wang et al. 2005). Additionally, LD patterns among a whole genome vary, with the average length of 60–200 kb in general populations (Jorde 2000; McVean et al. 2004; Wang et al. 2005). Excessive LD may hinder the ability to detect causative genetic variants truly influencing a phenotype. Strong LD existing among the loci of extremely dense panels provides correlated SNPs in the vicinity that share substantial amounts of information and introduce heterogeneity that can partially mask the effects of other SNPs. As a result, it is difficult to separate the individual variants that are truly causative from those confounding spurious variants that are irrelevant to the phenotype but highly correlated with the causative loci due to LD. Strong LD leads to inflated variance, incorrect statistical inferences, inaccurate tests of significance for the SNP, unstable parameter estimates, diminished significance for truly influential SNPs, and false scientific identifications (Cardon and Bell 2001; Daly et al. 2001; Reich et al. 2001; Crawford et al. 2004).

Many statistical models have been used to assess the association between genetic variants and phenotypes in GWAS. The prevailing GWAS strategies have focused on single-locus models (for example, the logistic regression with a single SNP as the predictor, the Cochran–Armitage test for trend (Armitage 1955), or Fisher’s exact test), which assess the potential association of each SNP in isolation from the others (Houlston and Peto 2004; Marchini et al. 2005; Balding 2006; Dong et al. 2008; Jo et al. 2008; He and Lin 2011; Hook et al. 2011; Molinaro et al. 2011; Sobrin et al. 2011; Xie et al. 2012). Although widely used for its simplicity, the single-locus model has limited power because it neglects the combined multiple joint effects of SNPs, inappropriately separates SNPs in LD, fails to differentiate potentially causative from noncausative variants, struggles with multiple correction due to an extremely large number of simultaneous tests, and yields both high false-positive and false-negative results (Burton et al. 2007; Malo et al. 2008; Manolio et al. 2009; Cule et al. 2011). The standard multiple-regression approaches, albeit accommodating joint effects of multiple SNPs and allowing for control of small LD, break down when moderate-to-strong LD exists among SNPs and are infeasible when the number of SNPs is larger than the number of observations (Gudmundsson et al. 2007; Haiman et al. 2007; Sun et al. 2009). In addition, multiple-regression models involve a large number of degrees of freedom and lack parsimony. The conditional logistic regression was proposed to accommodate the LD effects, but does not allow for the simultaneous quantification of each SNP individually along with the combined effects of other SNPs (Zavattari et al. 2001). Principal component analysis (PCA) or other clustering methods group SNPs according to their LD patterns. However, these approaches may miss the truly causative variants, undervalue the complexity of LD, and not allow the interpretation of the individual significance of each SNP. The partial least-squares (PLS) method has been used to address the correlation among predictors, but the theoretical properties of PLS (such as mean squared error) have not been established as thoroughly as in other approaches (Frank and Friedman 1993; Hawkins and Yin 2002).

Ridge regression (RR) (Hoerl and Kennard 1970), fitting a penalized likelihood with the penalty defined as the sum of the squares of each coefficient, has been used extensively to deal with the situation where the predictors are highly correlated and the number of predictors exceeds the number of subjects (Hoerl and Kennard 1970; Gruber 1998; Friedman et al. 2001; Hastie and Tibshirani 2004; Li et al. 2007; Zucknick et al. 2008; Malo et al. 2008; Sun et al. 2009; Cule et al. 2011). RR has been shown to be preferable to ordinary least squares (OLS), PCA, or other approaches in many contexts and achieves the smallest prediction error among a number of regression approaches after head-to-head comparisons (Frank and Friedman 1993). Through several simulations with varied LD strength, allele frequency, and effect size, Malo et al. (2008) compared the performance of RR, standard multiple regression, and single-locus regression for a continuous phenotype. They reported that RR performed best for each combination and the advantage of RR was more obvious when the LD was strong. They also reported that the single-locus regression was the worst among three approaches because it failed to differentiate causative SNPs from spurious SNPs that were merely in LD with the causative SNPs. Sun et al. (2009) identified a new genetic locus associated with a continuous trait by RR that was not detected by the single-locus model. Cule et al. (2011) extended the significance test of parameters proposed by Halawa and El Bassiouni (2000) and proposed an asymptotic test of significance for RR and demonstrated that the test was comparable to a permutation test but with much reduced computational cost for both continuous and binary phenotypes.

Although RR is powerful in addressing correlation and multiple joint effects, it is extremely time consuming and is designed only for a moderate number of predictors. Many approaches that are powerful for high dimension (i.e., $p>n$ but not $p\gg n$), such as Lasso or elastic net penalized regression (Austin et al. 2013; Waldmann et al. 2013), either are computationally infeasible or perform no better than random guessing, for ultrahigh-dimensional data due to noise accumulation; and RR is no exception (Fan and Fan 2008; Li et al. 2012b; Fan et al. 2014). As for GWAS, the signal-to-noise ratio is often very low, with only a small portion of SNPs contributing to a phenotype and the number of noncausative and causative SNPs showing great disparity. In light of these sparsity assumptions, feature screening has been proved to be highly effective and pivotal for its speed and accuracy to handle ultrahigh-dimensional data (Fan and Lv 2008; Hall and Miller 2009; Fan et al. 2011; Li et al. 2012a,b; Zhao and Li 2012). Feature screening forcefully filters a large amount of noise and decreases the original large scale to a moderate scale, overcomes noise accumulation difficulties, improves estimation accuracy, and reduces the computational burden. The distance correlation-based (DC) feature screening approach has an additional theoretical sure-screening property: all truly important predictors can be selected with the probability tending to one as the sample size goes to ∞ (Li et al. 2012b). Although a feature screening approach is powerful in handling ultrahigh-dimension data, it cannot provide any closer analysis such as parameter estimation and significance tests for each predictor. In sum, each approach has its own benefits and pitfalls.

In this article, we propose a novel integrated Distance Correlation Ridge Regression (DCRR) approach designed for case–control cohort whole-genome data, with a binary phenotype and 0.5–1 million SNPs. The DCRR first extensively filters noise with a loose threshold using DC and then intensively examines the significance of remaining informative SNPs by ridge penalized multiple logistic regression (LRR). DCRR integrates the benefits of both DC and RR while avoiding the drawbacks of both approaches. It is computationally efficient, reliable, and flexible, with a goal of accommodating LD between variants at different loci and hence differentiating the causative variants from the spurious variants that are in LD with the causative ones. It quantifies the significance of each SNP individually as well as accounts for the joint effects of all other SNPs in a multivariate sense and stabilizes the parameter estimates in the presence of strong LD and an ultrahigh dimension of SNPs in GWAS. The traditional RR involves a $O\left(n{p}^2+p^3\right)$ calculation (Hawkins and Yin 2002), which needs an intractable amount of time when p approaches 1 million. The DCRR approach that we propose dramatically decreases the calculation burden to $O\left(p+n^3\right),$ with a substantial saving for ultrahigh-dimension $p\gg n,$ and its computational speed mainly depends on the number of observations rather than the number of SNPs.

We demonstrate that our approach is uniformly and consistently powerful under a wide spectrum of different simulations of minor allele frequency (MAF), LD strength, and the number of SNPs, while controlling the false discovery rate (FDR) at <0.05. We compare our approaches with the popular single-locus Cochran–Armitage (CA) model and traditional LRR models and demonstrate that the stronger the LD or larger the dimension, the better performance of the DCRR approach, whose power persists even for low MAF. To further validate our approach, we reanalyze a published GWAS data set for a binary Arabidopsis thaliana trait.

Materials and Methods

Measurement of LD

Consider two biallelic loci in the same chromosome, with $A/a$ representing the alleles of the first loci and $B/b$ representing the alleles of the second loci. These two biallelic loci form four possible haplotypes: $AB,Ab,aB,$ and $ab.$ Let $f\left(A\right),f\left(a\right),f\left(B\right),$ and $f\left(b\right)$ denote the corresponding allele frequencies and $f\left(AB\right),f\left(Ab\right),f\left(aB\right),$ and $f\left(ab\right)$ denote the corresponding haplotype frequencies. LD, the nonindependence structure of the alleles for a pair of polymorphic loci at a population level, is generally measured as $D=f\left(AB\right)-f\left(A\right)f\left(B\right)=f\left(AB\right)f\left(ab\right)-f\left(Ab\right)f\left(aB\right)$ (Lewontin 1964). A D value close to zero corresponds to no LD. Although D quantifies how much haplotype frequencies deviate from the equilibrium state, it is highly dependent on allele frequencies and hence difficult to compare across different regions. Therefore, the normalized measure, $D^{\prime }=D/D_{\text{max}}$ is more widely used by removing the sensitiveness of allele frequencies (Lewontin 1964; González-Neira et al. 2004; Mueller 2004; Kulinskaya and Lewin 2009), where

$$D_{\max }=\{\begin{array}{ll}\max \left\{-f\left(A\right)f\left(B\right),-f\left(a\right)f\left(b\right)\right\},\hfill & \text{if}\hspace{0.17em}D<0\hfill \\ \min \left\{f\left(A\right)f\left(b\right),f\left(a\right)f\left(B\right)\right\},\hfill & \text{if}\hspace{0.17em}D\ge 0.\hfill \end{array}$$

The range of $D^{\prime }$ is between −1 and 1, with $\left|D^{\prime }\right|=1$ corresponding to complete LD and $D^{\prime }=0$ corresponding to no LD. Another widely used measure of LD is the statistical coefficient of determination, $r^2$ (Brown 1975; Pritchard and Przeworski 2001; González-Neira et al. 2004; Mueller 2004; Wang et al. 2005; Kulinskaya and Lewin 2009), defined as

$$r^2=\frac{D^2}{f\left(A\right)f\left(a\right)f\left(B\right)f\left(b\right)}.$$

Mueller (2004) reviewed the different properties and applications of these two measures of LD. The statistical significance test on D is performed by Pearson’s independence testing for the $2\times 2$ contingency table generated by the possible combinations of the alleles of a pair of loci, which is also equal to

$${\chi }^2=\frac{n{D}^2}{f\left(A\right)f\left(a\right)f\left(B\right)f\left(b\right)}=n{r}^2,$$ (1)

following a ${\chi }^2$ distribution with 1 d.f. (Weir et al. 1990; Zaykin et al. 2008; Kulinskaya and Lewin 2009).

Distance correlation-based feature screening

The main framework of the DCRR approach is to first extensively remove the noise via a distance correlation-based feature screening approach and then intensively address the correlation structure, using a ridge penalized multiple logistic regression model. Finally the significance test of each individual SNP is performed.

Let y be the binary phenotype with 1 representing case and 0 representing control. Let $X={\left(X_1,X_2,\dots ,X_p\right)}^T$ be the genotype vector of all SNPs, where p is the number of SNPs. For each biallelic locus, the three possible genotypes can be coded as 0 (for aa), 1 (for Aa), and 2 (for AA).

The dependence strength between two random vectors can be measured by the distance correlation (Dcorr) (Székely et al. 2007). Székely et al. showed that the Dcorr of two random vectors equals zero if and only if these two random vectors are independent. The distance covariance is defined as

$$\mathrm{dco}{\mathrm{v}}^2\left(y,X\right)={\displaystyle {\int }_{R^{1+p}}{\Vert {\phi }_{y,X}\left(t,s\right)-{\phi }_y\left(t\right){\phi }_X\left(s\right)\Vert }^{2}w\left(t,s\right)dtds,}$$ (2)

where ${\phi }_y\left(t\right)$ and ${\phi }_X\left(s\right)$ are the respective characteristic functions of y and X, ${\phi }_{y,X}\left(t,s\right)$ is the joint characteristic function of $\left(y,X\right),$ and

$$w\left(t,s\right)={\left\{c_1{c}_p{\Vert t\Vert }^2{\Vert s\Vert }_p^{1+p}\right\}}^{-1},$$

with $c_1=\pi ,$ $c_p={\pi }^{\left(1+p\right)/2}/\Gamma \left\{\left(1+p\right)/2\right\},$ and $\Vert \cdot \Vert$ stands for the Euclidean norm. Then the Dcorr is defined as

$$\mathrm{dcorr}\left(\mathbf{y},\mathbf{X}\right)=\frac{\mathrm{dcov}\left(\mathbf{y},\mathbf{X}\right)}{\sqrt{\mathrm{dcov}\left(\mathbf{y},\mathbf{y}\right)\hspace{0.17em}\mathrm{dcov}\left(\mathbf{X},\mathbf{X}\right)}}.$$ (3)

From Equations 2 and 3, we confirm that the DC approach does not assume any parametric model structure and works well for both linear and nonlinear associations. In addition, it works well for both categorical and continuous data without assuming which data type.

Székely et al. (2007) gave a numerically easier estimator of ${\widehat{\mathrm{dcov}}}^2\left(y,X\right)$ as

$${\widehat{\mathrm{dcov}}}^2\left(y,X\right)={\widehat{S}}_1+{\widehat{S}}_2-2{\widehat{S}}_3.$$ (4)

Let $y_i$ and $X_i$ denote the random sample of the populations y and X, respectively. Then

$$\begin{array}{c}{\widehat{S}}_1=\frac{1}{n^2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\Vert y_i-y_j\Vert {\Vert X_i-X_j\Vert }_p}}\\ {\widehat{S}}_2=\frac{1}{n^2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\Vert y_i-y_j\Vert }}\frac{1}{n^2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\Vert X_i-X_j\Vert }_p}},\\ {\widehat{S}}_3=\frac{1}{n^3}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\displaystyle \sum _{k=1}^n\Vert y_i-y_k\Vert {\Vert X_j-X_k\Vert }_p}}}.\end{array}$$ (5)

Finally, the point estimator $\widehat{\mathrm{dcorr}}\left(y,X\right)$ can be estimated by Equations 3–5.

Let $X_{\mathcal{C}}=\{X_j|X_j,j=1,\dots ,d,$ be the causative SNP, i.e., truly associated with the phenotype} and let $X_{\mathcal{N}}=\{X_k|X_k,k=1,\dots ,p-d,$ be the noise SNP, i.e., not relevant to the phenotype}. The idea of feature screening is to filter $X_{\mathcal{N}}$ and keep all true causative SNPs in the subset $X_{\mathcal{C}}.$ By decreasing the values of $\widehat{\mathrm{dcorr}}\left(y,X_i\right),$ $i=1,\dots ,p,$ we are able to rank the importance of SNPs from the highest to the lowest (Li et al. 2012b), with $X_{\mathcal{C}}$ located in front of $X_{\mathcal{N}}.$ Li et al. (2012b) theoretically proved that the DC feature screening has an additional agreeable theoretical sure-screening property, where all truly important predictors can be selected with the probability tending to one as the sample size goes to $\mathrm{\infty },$ if the tuning parameter d is sufficiently large. The watershed between importance and unimportance, i.e., the value of d, like other tuning parameters, is not trivial to determine. Li et al. (2012b) suggested to either set $d=\left[n/\log n\right]$ ($[\cdot ]$ is the integer part) or choose the top d SNPs such that $\widehat{\mathrm{dcorr}}\left(y,X_d\right)$ is greater than a prespecified constant.

Although the DC approach is very powerful at filtering noise and recognizing the truly important SNPs from millions of candidates, it may neglect some important SNPs that are individually uncorrelated yet jointly correlated with the phenotype, or it may highly rank some unimportant SNPs that are spuriously correlated with the phenotype due to their strong LD with other causative SNPs. To overcome these shortcomings, we use iterative distance correlation (IDC) to address possible complex situations of SNPs that can exist. The main difference between DC and IDC is that DC finalizes the first d members of $X_{\mathcal{C}}$ by only one step while IDC builds up $X_{\mathcal{C}}$ gradually with several steps; i.e., $X_{\mathcal{C}}=X_{\mathcal{C}1}\mathrm{\cup }{X}_{\mathcal{C}2}\mathrm{\cup }\dots \mathrm{\cup }{X}_{\mathcal{C}k},$ with $d=d_1+d_2+\dots +d_k,$ where $X_{\mathcal{C}i}$ stands for the members selected at the ith step and $d_i$ is the size of each set $X_{\mathcal{C}i},$ for $i=1,\dots ,k.$ The main idea of IDC is to iteratively adjust residuals obtained from regressing all remaining SNPs onto the selected members contained in $X_{\mathcal{C}}.$ Regressing unselected on selected, and adjusting residuals, effectively breaks down original complex correlation structure among SNPs. The iterative steps of IDC can be summarized as follows (Zhong and Zhu 2014):

• Step 1: Input the first $d_1$ members into $X_{\mathcal{C}}$ (i.e., $X_{\mathcal{C}}=X_{\mathcal{C}1}$), using DC to rank all candidates of X for y, where $d_1<d.$

• Step 2: Define $X_r=\left\{I_n-X_{\mathcal{C}}{\left(X_{\mathcal{C}}^T{X}_{\mathcal{C}}\right)}^{-1}{X}_{\mathcal{C}}^T\right\}{X}_{\mathcal{C}}^C,$ where $X_{\mathcal{C}}^C$ is the complement set of $X_{\mathcal{C}}.$ Then choose the second $d_2$ members into $X_{\mathcal{C}}$ (i.e., $X_{\mathcal{C}}=X_{\mathcal{C}1}\mathrm{\cup }{X}_{\mathcal{C}2}$), using DC to rank all candidates of $X_r$ for $y,$ where $d_1+d_2\le d.$

• Step 3: Repeat step 2 until the size of $X_{\mathcal{C}}$ reaches the prespecified number d.

Whether or not these $d_i$ at each step exhibit a negligible effect on the results, their magnitudes will appreciably affect results. Theoretically, smaller $d_i$ will yield better results, but also cause a dramatically lower computational speed. Therefore, we use a combination of DC and IDC to balance the computational cost and model performance simultaneously.

Ridge penalized multiple logistic regression

For LRR, y is still the binary phenotype and $X_{\mathcal{C}}$ the selected (important) SNPs with moderate dimension ($d=\left[n\right]$). For simplicity of notation, we use X to denote $X_{\mathcal{C}}.$ To address the correlation among SNPs, stabilize the model estimates, and test for significance of each individual SNP while accommodating the joint effects of others, we impose a ridge penalized logistic multiple-regression model (Le Cessie and Van Houwelingen 1992; Vago and Kemeny 2006). In traditional logistic regression, the probability of case is related to predictors by the inverse logit function

$$p\left(y_i=1|X\right)=\frac{e^{X_i\beta }}{1+e^{X_i\beta }}.$$

The parameter vector ${\beta }^{\lambda }$ of the ridge logistic regression can be estimated by maximizing the log likelihood subject to a size constraint on the $L_2$ norm of the coefficients via the Newton–Raphson algorithm

$$l\left(X,{\beta }^{\lambda }\right)={\displaystyle \sum _{i=1}^n{y}_i\log \left[p\left(y_i=1|X\right)\right]}+{\displaystyle \sum _{i=1}^n\left(1-y_i\right)\log \left[1-p\left(y_i=1|X\right)\right]-\lambda {\Vert \beta \Vert }^2}.$$

The first derivative of the penalized likelihood yields

$${\widehat{\beta }}^{\lambda }={\left(X^{T}WX+2\lambda I\right)}^{-1}{X}^{T}WZ,$$

where $W=\mathrm{diag}\left[\widehat{p}\left(y_i=1|X\right)\left(1-\widehat{p}\left(y_i=1|X\right)\right)\right],$ and Z is an $n\times 1$ vector with elements

$$z_i=\mathrm{logit}\left[\widehat{p}\left(y_i=1|X\right)\right]+\frac{y_i-\widehat{p}\left(y_i=1|X\right)}{\widehat{p}\left(y_i=1|X\right)\left(1-\widehat{p}\left(y_i=1|X\right)\right)}.$$

The tuning parameter λ controls the strength of shrinkage of the norm of β. A few methods have been proposed to choose the tuning parameter λ (Hoerl et al. 1975; Lawless and Wang 1976; Golub et al. 1979). One common approach is the ridge trace (Hoerl and Kennard 1970). The ridge trace is a plot of the parameter estimates over increasing λ values. The ideal λ is where all parameter estimates have stabilized. A suitable choice of $\lambda >0$ introduces a little bias but decreases the variance and hence minimizes the mean squared error (Le Cessie and Van Houwelingen 1992; Vago and Kemeny 2006),

$$\mathrm{MSE}\left(\widehat{\beta }\right)=Tr\left[\mathrm{Var}\left(\widehat{\beta }\right)\right]+{\left[\mathrm{bias}\left(\widehat{\beta }\right)\right]}^T\left[\mathrm{bias}\left(\widehat{\beta }\right)\right].$$

The asymptotic variance of ${\widehat{\beta }}^{\lambda }$ can be derived as

$$\mathrm{Var}\left(\widehat{{\beta }^{\lambda }}\right)={\left\{X^{T}WX+2\lambda I\right\}}^{-1}\left\{X^{T}WX\right\}{\left\{X^{T}WX+2\lambda I\right\}}^{-1}.$$

Hypothesis testing

The significance of each individual SNP, while accounting for the joint and correlated effects of other SNPs, is assessed via the hypothesis test

$${\mathrm{H}}_{0j}:{\beta }_j^{\lambda }=0\hspace{1em}\mathit{vs}.\hspace{1em}{\mathrm{H}}_{1j}:{\beta }_j^{\lambda }\ne 0,\hspace{1em}\text{for}\hspace{0.17em}j=1,\dots ,d.$$ (6)

The corresponding “nonexact” test statistic is

$$T^{\lambda }=\frac{{\widehat{\beta }}_j^{\lambda }}{se\left({\widehat{\beta }}_j^{\lambda }\right)}.$$

Halawa and El Bassiouni (2000) investigated this nonexact t-type test under two different λ’s via simulations of 84 different models and concluded that it has considerably larger powers in many cases or slightly less power in a few cases, compared to the test of traditional regression estimates via maximum likelihood. Cule et al. (2011) extended Halawa and EI Bassiouni’s test from a continuous to a binary response and claimed that the asymptotic standard normal distribution of the test statistic $T^{\lambda }$ under the null performs as well as that of a permutation test. Therefore, we also assume $T^{\lambda }\sim N\left(0,1\right)$ under the null and use standard normal distribution to perform the significance test of each SNP.

Since multiple SNPs are usually tested simultaneously, and the dimension of tests is small or moderate after the feature screening procedure ($d\ll p$), we use the simplest Bonferroni correction to control the family-wise error rate. Whereas the traditional single-locus model uses p for multiple correction, we use d instead because the actual number of tests involved is d. We set the SNPs that are filtered out by DC to have a P-value of 1 [i.e., $-\log \left(p\right)=0$] because they are not informative and are not considered for significance testing.

Simulation generating

To assess the performance of our approach, we conducted a large number of simulations to obtain the power and type I error rates under varied combinations of the number of SNPs (p), the correlation strength (ρ), and MAF. We compared our DCRR approach with the CA approach and the traditional LRR approach.

The correlated haplotype vector was simulated from a multivariate normal distribution with the mean vector randomly generated from Unif$\left(0,5\right)$ and the covariance structure designed as $\mathrm{AR}\left(1\right).$ The variance was fixed to be 1 and correlation parameter ρ was used to control the strength of LD among SNPs. Next, the individual allele of each haplotype was generated by dichotomizing the continuous haplotype values based on the MAF and the corresponding percentile obtained from the cumulative density function of the marginal normal distribution of each SNP. For each SNP, we generated two independent haplotypes and the sum of each pair of haplotypes was used to create the genotype, which yielded the $n\times p$-dimensional matrix X (Wang et al. 2007). To clearly describe all possible effects and roles of each SNP, we ascribed four definitions (Meng et al. 2009): risk SNP (rSNP), a truly causative SNP that is functionally associated with the phenotype; LD.rSNP, a noncausative SNP that is not associated with the phenotype but is in LD with rSNP; a noise SNP (nSNP) that is neither important for the phenotype nor in LD with any rSNP; and LD.nSNP, a nSNP that is not associated with the phenotype but is in LD with other nSNPs.

From the index set of the SNPs, $S=\left\{1,\dots ,p\right\},$ we randomly chose five rSNPs. Due to the property of AR(1), the SNP in the closest neighborhood of these rSNPs was the LD.rSNP with strongest correlations with rSNPs and hence substantially increased the difficulty in detecting the true rSNPs, which affected both type I error and power. Among the $S\backslash \mathrm{rSNP}$ set containing all $p-5$ nSNPs, those far away from these five rSNPs had negligible LD with the rSNP and acted as noise. The other nSNP located in close proximity to each nSNP was the LD.nSNP, and the correlation among noise SNPs also had the potential to act as confounders of the rSNPs.

The binary phenotype was generated based on the genotype matrix X and the effect size. Setting the β values of all five rSNPs at 1 and all other SNPs at 0, the probability of case was computed as

$$\mathrm{logit}\left[p\left(y_i=1|X\right)\right]=X\beta +\mathit{ϵ},$$

where $\mathit{ϵ}\sim N\left(0,1\right).$

The four criteria used to evaluate the performance of the models were defined as follows: strict power, the percentage of simultaneously rejecting all five rSNPs; power, the proportion of rejecting any of five rSNPs among all simulation replicates of rSNPs; type I error, the proportion of rejecting any of $p-5$ LD.rSNPs, nSNPs, and LD.nSNPs among all simulation replicates of these noncausative SNPs; and time, total time required to finish 100 replicates for each simulation setting and each approach.

Data availability

The Arabidopsis thaliana data is a public data set freely available at http://arabidopsis.gmi.oeaw.ac.at:5000/.

Results

Simulation design 1

We set $p=10\left(\text{signal}/\text{noise}=2\right),\hspace{0.5em}100\left(\text{signal}/\text{noise}=20\right),$ $1000 \left(\text{signal}/\text{noise}=200\right),$ and $10,000\left(\text{signal}/\text{noise}=2000\right)$ to consider small, medium, high, and ultrahigh dimensions of SNPs. We controlled the strength of LD from small to large as $\rho =0.2,\hspace{0.5em}0.4,\hspace{0.5em}0.6,\hspace{0.5em}\text{or}\hspace{0.5em}\mathrm{0.8.}$ A total of 48 combinations of MAF (MAF $=0.1,\hspace{0.5em}0.3,\hspace{0.5em}\text{or}\hspace{0.5em}0.5$), ρ, and p provided a comprehensive assessment on how our model performed under different conditions. We performed 100 replicates for 40 of the simulations, but only 10 replicates for the last 8 simulations where $p=10,000$ and MAF = 0.3 or 0.5, due to the extremely lengthy computational time of LRR. Different λ values were chosen according to different data requirements based on the ridge trace plots. After λ’s were determined, we used exactly the same λ values to compare both DCRR and LRR for the same data to ensure the comparisons were accurate. During the DC selection procedure, we chose $d=8$ for $p=10,$ $d=20$ for $p=100,$ and $d=n/ln\left(n\right)\simeq 80$ for $p=1000\hspace{0.5em}\text{and}\hspace{0.5em}10,000.$ To minimize other possible factors, equal numbers of case and control were generated and the sample size n was fixed at 500.

Simulation results of the 48 settings are summarized in Table 1 (MAF = 0.1), Table 2 (MAF = 0.3), and Table 3 (MAF = 0.5). When MAF = 0.3 or 0.5, all three approaches achieved satisfactorily high power and strict power for any dimension of SNPs and any LD strength (Figure 1). However, the high power of CA came at the cost of an extremely inflated type I error, which indicates that the single-SNP model neglected the correlations and joint effects among SNPs. Comparing Table 1, Table 2, and Table 3 simultaneously, we noted that the type I error of CA kept increasing as ρ increased from 0.2 to 0.8 for any MAF and p. In particular, when $p=10$ and $\rho =0.8,$ the false discovery rate of CA was as large as $100\text{\%}$ for all three different MAF values. Compared to CA, the type I errors of LRR and DCRR did not show an increasing trend as ρ increased, and almost all type I errors were $<\alpha =0.05.$

Table 1. Simulation results for MAF = 0.1.

LD Strength	Criteria	P = 10			P = 100
		CA	LRR	DCRR	CA	LRR	DCRR
$\rho =0.2$	Strict power	1	1	1	0.91	0.91	0.97
	Power	1	1	1	0.982	0.982	0.994
	Type 1	0.016	0.014	0.016	0.00032	0.00032	0.0026
	Time	16.34 sec	11.79 sec	78.89 sec	2.4 min	0.50 min	6.52 min
$\rho =0.4$	Strict power	1	1	1	0.93	0.93	0.98
	Power	1	1	1	0.984	0.984	0.996
	Type 1	0.05	0.036	0.04	0.0022	0.0022	0.0068
	Time	16.82 sec	24.20 sec	158.46 sec	2.44 min	0.54 min	6.54 min
$\rho =0.6$	Strict power	1	0.98	0.99	0.94	0.94	0.99
	Power	1	0.996	0.998	0.988	0.988	0.998
	Type 1	0.39	0.01	0.02	0.0088	0.0085	0.0195
	Time	15.96 sec	13.48 sec	80.45 sec	2.59 min	0.50 min	7.81 min
$\rho =0.8$	Strict power	1	0.94	0.98	0.94	0.96	0.99
	Power	1	0.988	0.996	0.988	0.992	0.998
	Type 1	0.99	0.018	0.044	0.0546	0.0287	0.0522
	Time	16.17 sec	14.58 sec	79.49 sec	2.6 min	0.59 min	7.12 min
		P = 1,000			P = 10,000
$\rho =0.2$	Strict power	0.74	0.72	0.92	0.37	0.57	0.99
	Power	0.944	0.94	0.984	0.832	0.896	0.998
	Type 1	0.00004	0.00005	0.0005	0.000007	0.000004	0.00049
	Time	48.48 min	35.96 min	73.91 min	95.71 hr	422.41 hr	107.08 hr
$\rho =0.4$	Strict power	0.68	0.67	0.91	0.40	0.48	0.91
	Power	0.93	0.93	0.982	0.836	0.846	0.982
	Type 1	0.00003	0.0003	0.0005	0.000004	0.000006	0.0005
	Time	47.34 min	33.68 min	69.86 min	97.87 hr	443.53 hr	111.42 hr
$\rho =0.6$	Strict power	0.77	0.78	0.96	0.39	0.42	0.93
	Power	0.95	0.952	0.992	0.834	0.874	0.986
	Type 1	0.00016	0.0002	0.001	0.000009	0.00001	0.00051
	Time	48.71 min	32.50 min	72.18 min	97.57 hr	420 hr	105 hr
$\rho =0.8$	Strict power	0.68	0.69	0.89	0.40	0.43	0.93
	Power	0.932	0.942	0.978	0.856	0.854	0.986
	Type 1	0.0012	0.0011	0.0037	0.00003	0.000036	0.00073
	Time	53.02 min	33.55 min	69.52 min	94.93 hr	379.62 hr	64.88 hr

Table 2. Simulation results for MAF = 0.3.

LD Strength	Criteria	P = 10			P = 100
		CA	LRR	DCRR	CA	LRR	DCRR
$\rho =0.2$	Strict power	1	1	1	1	1	1
	Power	1	1	1	1	1	1
	Type 1	0.046	0.028	0.034	0.00052	0.0053	0.0034
	Time	18.04 sec	12.41 sec	78.30 sec	2.43 min	0.58 min	7.56 min
$\rho =0.4$	Strict power	1	1	1	0.99	0.99	0.99
	Power	1	1	1	0.998	0.998	0.998
	Type 1	0.228	0	0.014	0.0086	0.0083	0.018
	Time	17.93 sec	13.14 sec	80.23 sec	2.40 min	0.59 min	7.55 min
$\rho =0.6$	Strict power	1	1	1	1	1	1
	Power	1	1	1	1	1	1
	Type 1	0.856	0.004	0.012	0.0354	0.0341	0.0508
	Time	18.43 sec	12.81 sec	77.97 sec	2.41 min	0.58 min	8.13 min
$\rho =0.8$	Strict power	1	1	0.87	1	1	1
	Power	1	1	0.974	1	1	1
	Type 1	1	0.006	0.028	0.1358	0.0107	0.0188
	Time	17.73 sec	13.23 sec	78.09 sec	2.44 min	0.657 min	7.16 min
		P = 1,000			P = 10,000
$\rho =0.2$	Strict power	0.96	0.96	0.97	0.9	0.9	1
	Power	0.992	0.992	0.994	0.98	0.98	1
	Type 1	0.00008	0.00008	0.0006	0	0	0.0005
	Time	57.32 min	36.59 min	49.36 min	9.33 hr	42.36 hr	11.21 hr
$\rho =0.4$	Strict power	0.98	0.98	0.99	1	1	1
	Power	0.996	0.996	0.998	1	1	1
	Type 1	0.00014	0.0001	0.0009	0.00001	0.00001	0.0005
	Time	50.78 min	34.13 min	73.3 min	10.35 hr	46.21 hr	10.22 hr
$\rho =0.6$	Strict power	0.98	0.98	1	1	1	1
	Power	0.996	0.998	1	1	1	1
	Type 1	0.00086	0.0008	0.0027	0.00005	0.00006	0.0006
	Time	49.02 min	35.33 min	71.10 min	10.94 hr	41.42 hr	10.99 hr
$\rho =0.8$	Strict power	0.97	0.97	1	1	1	1
	Power	0.994	0.994	1	1	1	1
	Type 1	0.0055	0.0051	0.0104	0.0004	0.0004	0.0016
	Time	50.55 min	32.55 min	69.95 min	10.65 hr	38.35 hr	10.20 hr

Table 3. Simulation results for MAF = 0.5.

LD Strength	Criteria	P = 10			P = 100
		CA	LRR	DCRR	CA	LRR	DCRR
$\rho =0.2$	Strict power	1	1	1	1	1	1
	Power	1	1	1	1	1	1
	Type 1	0.036	0.018	0.024	0.0015	0.0014	0.0043
	Time	18.82 sec	11.95 sec	78.62 sec	2.42 min	0.57 min	7.72 min
$\rho =0.4$	Strict power	1	1	1	1	1	1
	Power	1	1	1	1	1	1
	Type 1	0.296	0.0006	0.048	0.0105	0.0102	0.0189
	Time	17.55 sec	12.47 sec	79.92 sec	2.49 min	0.57 min	7.69 min
$\rho =0.6$	Strict power	1	1	1	1	1	1
	Power	1	1	1	1	1	1
	Type 1	0.908	0.008	0.036	0.0379	0.0259	0.0391
	Time	18.36 sec	13.64 sec	78.46 sec	2.42 min	0.60 min	7.51 min
$\rho =0.8$	Strict power	1	1	0.81	1	1	1
	Power	1	1	0.962	1	1	1
	Type 1	1	0.012	0.054	0.1581	0.0124	0.0215
	Time	17.91 sec	13.85 sec	78.31 sec	2.44 min	0.67 min	10.89 min
		P = 1000			P = 10,000
$\rho =0.2$	Strict power	1	1	1	0.9	0.9	1
	Power	1	1	1	0.98	0.98	1
	Type 1	0.00005	0.00005	0.0006	0.00001	0.00001	0.0004
	Time	54.31 min	35.62 min	73.38 min	10.65 hr	43.16 hr	10.68 hr
$\rho =0.4$	Strict power	1	1	1	0.9	0.9	1
	Power	1	1	1	0.98	0.98	1
	Type 1	0.00017	0.0002	0.0009	0.00001	0.00001	0.0006
	Time	48.07 min	33.62 min	71.57 min	11.12 hr	43.24 hr	11.47 hr
$\rho =0.6$	Strict power	0.99	1	1	1	1	1
	Power	0.998	1	1	1	1	1
	Type 1	0.0011	0.001	0.0036	0.00006	0.00007	0.00077
	Time	46.66 min	32.48 min	71.13 min	11.09 hr	39.40 hr	11.47 hr
$\rho =0.8$	Strict power	1	1	1	1	1	1
	Power	1	1	1	1	1	1
	Type 1	0.0011	0.001	0.0036	0.00047	0.00046	0.0020
	Time	47.85 min	34.67 min	72.65 min	10.87 hr	38.91 hr	10.48 hr

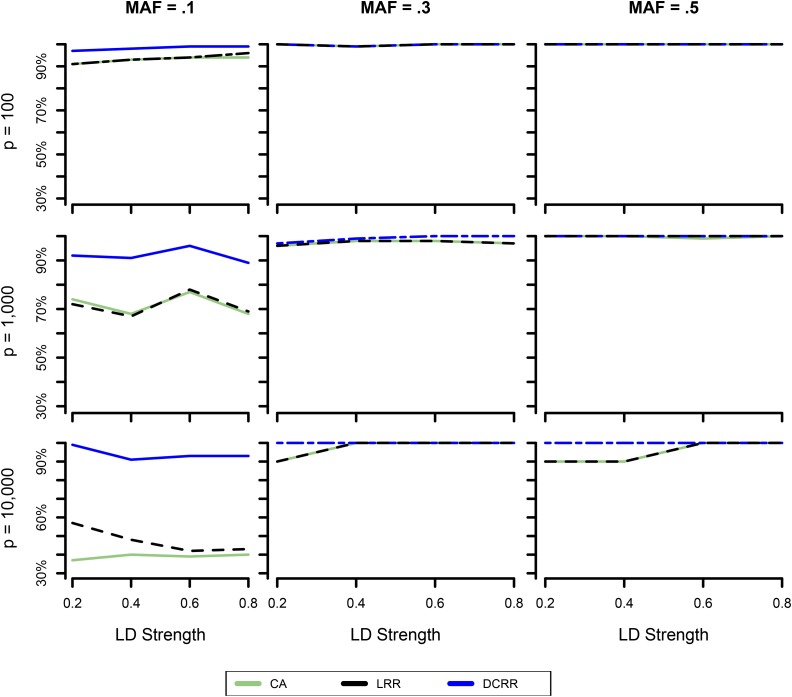
Figure 1.

Strict power with varied MAF and dimension. Shown is the changing pattern of strict power of three approaches as increasing ρ under combinations of varied MAF and dimension.

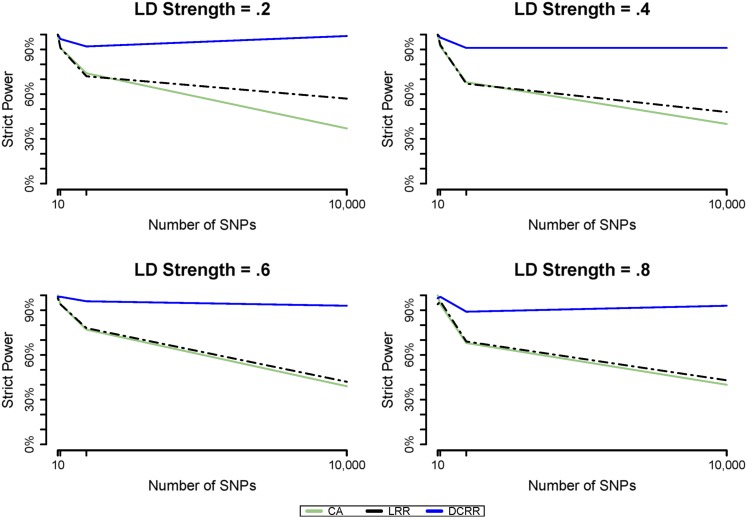
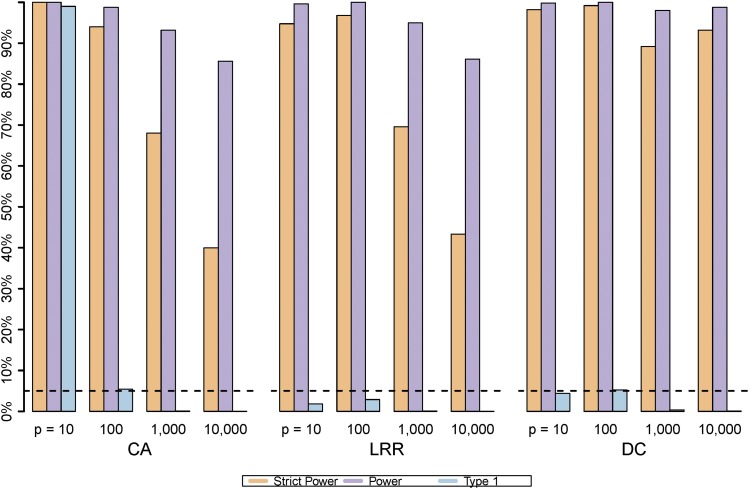
When MAF = 0.1, the possible range of D spanned from 0.01 to 0.81 and hence greatly increased the difficulty level of SNP being detected. As a result, when comparing the power and strict power of MAF = 0.1 with the other two MAF values, we noted that both power and strict power exhibited the smallest value in MAF = 0.1 for all three approaches (Figure 1). In particular, when the signal-to-noise ratio or dimension of SNPs increased dramatically, the strict power of MAF = 0.1 severely dropped for both CA and LRR for any given ρ (Figure 2). Indeed, the strict power of LRR and CA approximated $40\text{\%}$ for $p=10,000$ and $70\text{\%}$ for $p=1000.$ However, the strict power of DCRR more than doubled compared to that of CA and LRR for any ρ when MAF = 0.1 and $p=10,000$ (Figure 1 and Figure 2). Figure 3 shows the comparisons of strict power (in orange), power (in purple), and type I error (in light blue) simultaneously for three approaches and four dimensions when $\rho =\mathrm{0.8.}$ The strict power and power of CA and LRR decreased dramatically as p increased, but strict power and power of DCRR were relatively stable at a value $>90\text{\%}.$ Additionally, the type I error of CA was as high as $100\text{\%}$ for $p=10$ while all other approaches had type I error rates $<5\text{\%}.$ The type I error decreased as p increased for each approach because the ratio of n.SNP to LD.rSNP was increasing.

Figure 2.

Strict power as dimension increases. Shown is the changing pattern of strict power of three approaches as increasing p when MAF = 0.1 for each LD.

Figure 3.

Strict power, power, and type I error. Shown is the simultaneous changing pattern of strict power, power, and type I error rate of three approaches as increasing p when MAF = 0.1 and $\rho =\mathrm{0.8.}$

Of the 48 combinations of varied MAF, LD strength, and dimension, the DCRR method was consistently and uniformly more powerful than the other approaches, and the superiority of DCRR was striking under harsh conditions such as ultrahigh dimension or complex correlations. Among the 48 simulated comparisons, there were only two exceptions: when $p=10,$ $\rho =0.8,$ and MAF = 0.3 or 0.5, the power and strict power of DCRR were inferior to those of the other two approaches. This accidental drop was caused by one causative r.SNP that was not successfully selected from the top 8, but rather ranked 9th or 10th. By choosing the tuning parameter d sufficiently large, we were able to avoid this type of error. Since the DC feature screening approach is mainly designed for ultrahigh-dimensional cases, a dimension as low as 10 did not leave sufficient space for DC to select freely. We believe that the power of DCRR will be manifested for large-dimension problems, as occurred in the other 46 simulated comparisons.

Simulation design 2

To assess the advantages of IDC over the DC during the noise-filtering procedure and also judge the stability of the two tuning parameters (d and λ), we chose a more difficult but computationally faster setting, with $p=1000,$ MAF = 0.1, and $\rho =\mathrm{0.8.}$ A total of 100 simulation replications were performed for three values of $d=80,$ 250, and 500 and seven different values of λ varying from 0.5 to 10 (only three λ values are displayed in Table 4). We found that the tuning parameter λ selected by cross-validation (CV) provided very poor power and tended to choose λ values that were too small (Table 4). We concluded that IDC always showed uniformly higher or equal strict power and power than DC for all 21 combinations of d and λ values. Additionally, IDC was robust on the selection of λ values, which is an agreeable property because the tuning parameter is often difficult to determine in real data. For each given value of d, the strict power and power of IDC seldom changed when λ increased from 0.5 to 10. The strict power of IDC was always close to 0.89 and power was close to 0.98, no matter whether λ was 0.5, 5, or 10. For each λ, the strict power and power of $d=500$ were always the lowest among the three d values, which not only illustrated the destructive force of noise but also provided empirical experience for choosing d.

Table 4. Simulation comparisons for IDC and DC for varied combinations of λ and d.

Candidate Subset Size	Criteria	$\lambda =CV$		$\lambda =1$		$\lambda =10$
		DC	IDC	DC	IDC	DC	IDC
$d=80$	Strict power	0.28	0.64	0.88	0.89	0.89	0.90
	Power	0.77	0.91	0.98	0.98	0.98	0.98
	Type 1	0.00033	0.00163	0.00079	0.00183	0.00371	0.00372
$d=250$	Strict power	0.06	0.39	0.73	0.83	0.82	0.83
	Power	0.57	0.82	0.64	0.96	0.96	0.97
	Type 1	0.00013	0.00032	0.00063	0.00095	0.00211	0.00216
$d=500$	Strict power	0.17	0.66	0.62	0.77	0.77	0.78
	Power	0.67	0.92	0.91	0.95	0.95	0.95
	Type 1	0.00005	0.00040	0.00041	0.00072	0.00145	0.00150

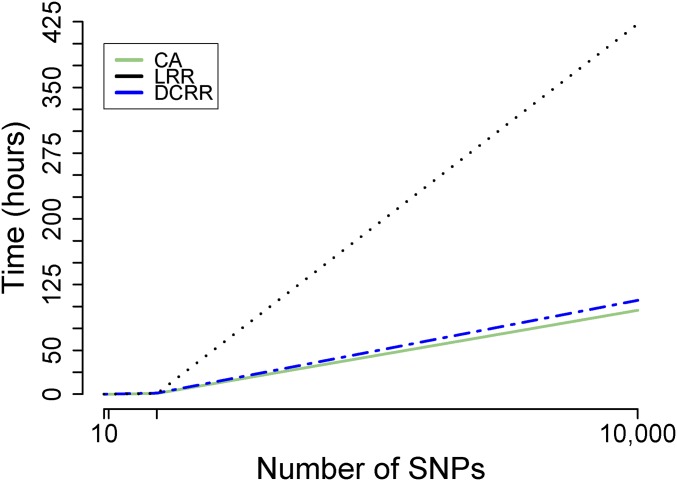
We recorded the total computational time of each approach, completing 100 simulation replicates for each fixed simulation setting. From Figure 4, we noted that the computational cost of DCRR dramatically decreased compared to LRR as dimension increased. The computational benefits of DCRR were manifested at $p=1000$ and became more remarkable for $p=10,000.$ The computational time of DCRR was similar to that of CA, which indicates that DCRR does not increase the computation cost despite considering multiple joint effects and correlation effects that were neglected by the single-SNP model.

Figure 4.

Time. Shown is the changing pattern of computational time (in minutes) of three approaches as increasing p.

Real data analysis

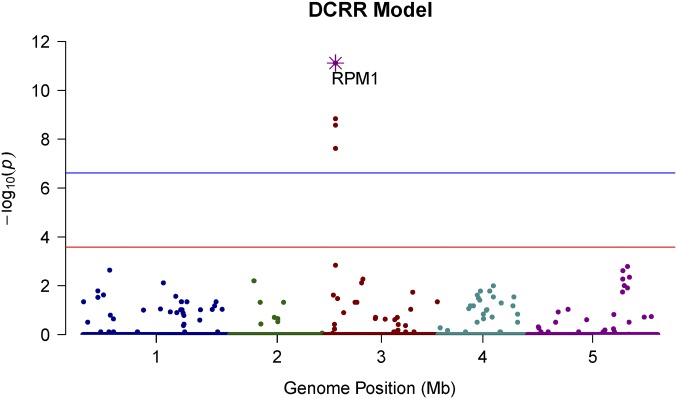
Our DCRR approach was applied to search for significant causative SNPs for a binary trait of the A. thaliana hypersensitive response to the bacterial elicitor AvrRpm1, with 84 inbred lines (28 susceptibilities and 56 resistances) and 216,130 SNPs. A. thaliana has a genome of ∼120 Mb and a SNP density of 1 SNP/500 bp (Atwell et al. 2010). Five statistical models have been tested on these same data and reported that this AvrRpm1 trait was monogenically regulated by the gene RPM1; i.e., the bacterial avirulence gene AvrRpm1 directly identified the corresponding resistance gene RESISTANCE TO P.SYRINGAW PV MACULICOLA 1 (PRM1) (Grant et al. 1995). Atwell et al. (2010) compared two single-SNP approaches: Fisher’s exact test without correcting for background confounding SNPs and a mixed model implemented in efficient mixed-model association (EMMA) to correct for confounding SNPs (supplementary figure 36 on p. 52 of Atwell et al. 2010). Shen et al. (2013) proposed a heteroscedastic effects model (HEM), determined $5\text{\%}$ genome-wide significance thresholds via a permutation test, and claimed that the HEM successfully eliminated many spurious associations and improved the traditional ridge regression (SNP-BLUP) approach (figure 2 of Shen et al. 2013). Our DCRR model effectively also identified the RPM1 gene in exactly the same position [chromosome (Chr) 3, 2,227,823 bp], with a significance level ${10}^{-12}$ on the highest peak. Figure 5 demonstrates the Manhattan plot of the AvrRpm1 trait along the whole genome, based on $-{\log }_{10}$ of genome-wide simultaneous P-values of 216,130 SNPs against its physical chromosomal position. The blue horizontal line corresponds to a $5\text{\%}$ genome-wide simultaneous significance threshold with Bonferroni correction for 250,000 tests. The red horizontal line represents the proposed multiple-correction threshold for the $5\text{\%}$ genome-wide simultaneous threshold with a Bonferroni correction for only $d=189$ tests.

Figure 5.

Manhattan plot of real data. Shown is the Manhattan plot of AvrRpm1 along the whole genome, based on $-{\log }_{10}$ of genome-wide simultaneous P-values of 216,130 SNPs against its physical chromosomal position. Chromosomes are shown in different colors. The current findings for the same data using five different approaches are compared.

The four significant causative polymorphisms that passed the DCRR threshold (Figure 5, in red) also passed the thresholds of other approaches (Figure 5, in blue) and are summarized in Table 5. Using the Arabidopsis Genome Initiative (AGI) genetic map and the Arabidopsis information resource (TAIR.org, verified on May 7, 2015) GBrowse database, we matched our significant findings with three genes. The rank 1 SNP lay within the single large exon of RPM1 (2,229,024–2,225,952). The rank 2 SNP lay ∼50 bp past the 3′ end of the RPM1 region. The rank 3 SNP lay within an intron in the neighboring alba DNA/RNA-binding protein (2,225,254–2,223,001), and the rank 22 SNP lay within exon 4 of the neighboring NSN1 gene (nucleostemin-like 1, 2,232,361–2,229,590). Additionally, the DCRR eliminated many nominally significant associations. Indeed, the shrinkage effect of the DCRR approach was much stronger than that of the other four approaches. We noted a reduction in number of moderate associations in the whole genome, and those with significance levels from ${10}^{-3}$ to ${10}^{-6}$ in EMMA and Fisher disappeared from DCRR. Additionally, one slightly significant SNP in Chr 5 in EMMA and some highly significant SNPs closely neighboring RPM1 in EMMA and Fisher were all eliminated in DCRR.

Table 5. Significant SNPs detected by DCRR based on AGI physical map (TAIR.org).

Rank	Chromosome	Base pair position (bp)	Gene	Dcorr	P-value
1	3	2,227,823	RPM1	0.5846	$7.64\times {10}^{-12}$
2	3	2,225,899		0.5075	$1.46\times {10}^{-9}$
3	3	2,225,040	alba DNA/RNA	0.5075	$2.67\times {10}^{-9}$
22	3	2,231,452	NSN1	0.3450	$2.39\times {10}^{-8}$

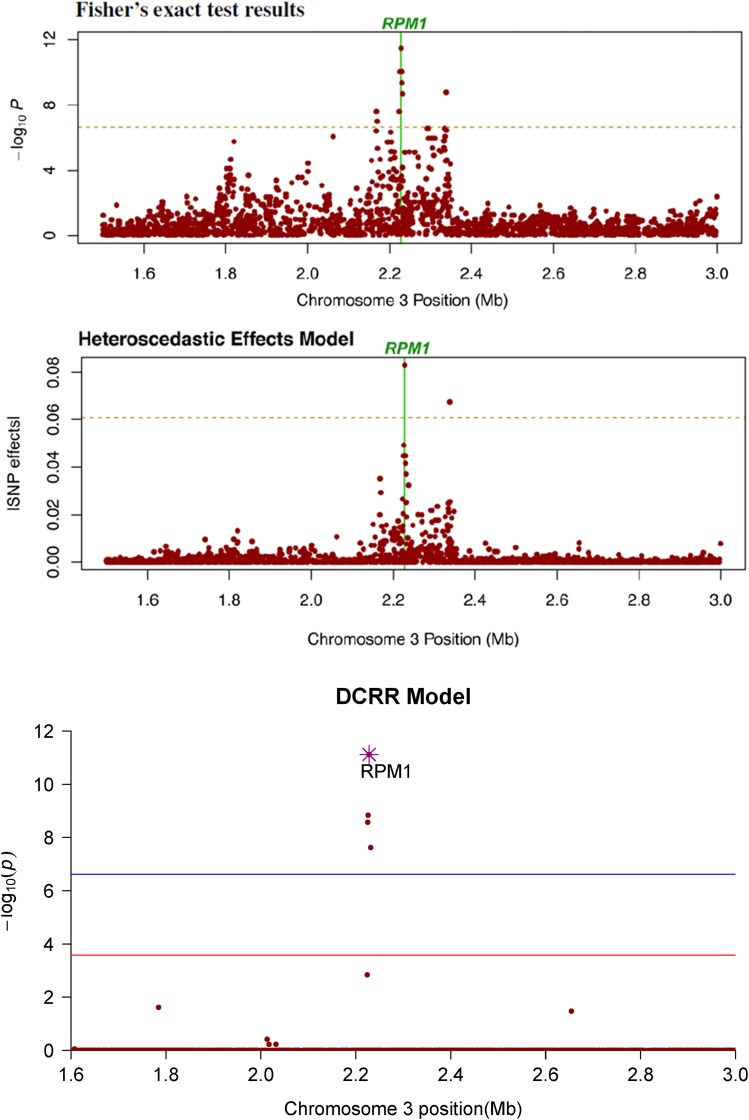
We noted a second peak (0.1 Mb away from RPM1) that was detected as highly significant by both the Fisher model and the HEM, judging from Figure 6 (Atwell et al. 2010; Shen et al. 2013). However, DCRR results indicated that it was a spurious signal confounded by strong background LD. If the process was limited to ranking by DC, that SNP indeed ranked high with a similar pattern to that of the Fisher model and HEM. However, the iterative DC that adjusted residuals to break down the original correlation structures reduced that SNP to an extremely low rank, $156,997\mathrm{th}$ among all candidates with a Dcorr value of just 0.0444. Therefore, it was highly unlikely that this SNP (Chr 3, 2,337,844 bp) was associated with the phenotype. To further verify this conclusion, we examined the LD of this SNP with several surrounding SNPs. After a ${\chi }^2$ test using Equation 1, we found that this SNP was in strong LD with >50 other polymorphisms (Table 6). As observed in Table 6, footnote a, it was highly correlated with all four significant SNPs reported in Table 5, especially having a P-value of ${10}^{-11}$ with RPM1. It was also highly correlated with many other noncausative SNPs; for example, it showed a P-value of ${10}^{-16}$ with position 2,334,985 and a P-value of ${10}^{-15}$ with position 2,335,305.

Figure 6.

Manhattan plot of critical region in real data analysis. Shown is a magnification of the genome region surrounding RPM1. The current findings for the same region using three different approaches are compared. The top and middle panels are reprinted from Shen et al. (2013) only for comparison purposes. Permission for it through Genetic Society of America. The bottom panel is constructed by us.

Table 6. The pairwise LD strength of the point located in Chr 3 with position number 2,337,844 bp with several surrounding SNPs.

Chromosome	Base pair position (bp)	${\chi }^2$	P-value
3	$2,227,823$a	41.9792	$9.22\times {10}^{-11}$
3	$2,225,899$a	29.9614	$4.41\times {10}^{-8}$
3	$2,231,452$a	24.9712	$5.81\times {10}^{-7}$
3	$2,225,040$a	18.9063	$1.37\times {10}^{-5}$
3	2,334,985	64.3782	$9.99\times {10}^{-16}$
3	2,335,305	60.2751	$8.21\times {10}^{-15}$
3	2,332,822	46.5432	$8.96\times {10}^{-12}$
3	2,333,137	49.6274	$1.85\times {10}^{-12}$
3	2,332,597	49.6274	$1.85\times {10}^{-12}$
3	2,334,723	38.4016	$5.75\times {10}^{-10}$
3	2,336,637	28.7376	$8.28\times {10}^{-8}$
3	2,336,926	31.2202	$2.30\times {10}^{-8}$
3	2,336,966	28.7376	$8.28\times {10}^{-8}$
3	2,334,909	31.7913	$1.71\times {10}^{-8}$
3	2,291,826	28.7225	$8.35\times {10}^{-8}$
3	2,295,084	28.7225	$8.35\times {10}^{-8}$
3	2,320,691	28.7225	$8.35\times {10}^{-8}$
3	2,294,447	26.2953	$2.92\times {10}^{-7}$
3	2,331,847	27.2956	$1.74\times {10}^{-7}$
3	2,336,077	27.2956	$1.74\times {10}^{-7}$
3	2,302,458	26.2953	$2.92\times {10}^{-7}$
3	2,302,750	26.2953	$2.92\times {10}^{-7}$
3	2,304,433	23.9354	$9.96\times {10}^{-7}$
3	2,304,563	26.2953	$2.92\times {10}^{-7}$
3	2,305,255	26.2953	$2.92\times {10}^{-7}$
3	2,306,492	26.2953	$2.92\times {10}^{-7}$
3	2,308,001	26.2953	$2.92\times {10}^{-7}$
3	2,310,061	26.2953	$2.92\times {10}^{-7}$
3	2,325,609	21.7285	$3.14\times {10}^{-6}$
3	2,261,331	20.7359	$5.27\times {10}^{-6}$
3	2,318,129	18.5587	$1.64\times {10}^{-5}$
3	2,326,014	17.2805	$3.22\times {10}^{-5}$
3	2,327,593	18.6292	$1.58\times {10}^{-5}$

^aThe P-value is obtained from a ${\chi }^2$ test with 1 d.f.

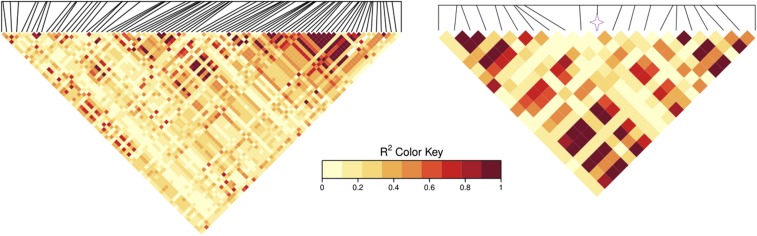
We further visually examined the genetic patterns for the region surrounding gene RPM1, using a haploview heatmap with a short range of 7.3 kb and a medium range of 28.1 kb (Figure 7). All pairwise $r^2$ among SNPs in the region were computed, with nine color schemes representing the varied levels of LD strengths (red denotes strong LD, yellow denotes medium LD, and white denotes negligible LD). The LD patterns among the closest SNPs to the right side of the causative SNP were very strong ($>0.9$), while the majority of SNPs were in medium LD ($r^2$ from 0.4 to 0.7). A close inspection of the 20 closest surrounding SNPs highlighted that the LD pattern in the neighborhood of RPM1 varied substantially, with 8 SNPs showing strong LD, 6 SNPs having medium LD, and 6 SNPs unlinked (i.e., $70\text{\%}$ closest SNPs had medium to strong LD with RPM1).

Figure 7.

Haploview heatmap. Shown is a plot of the surrounding SNPs in the RPM1 gene region. Left, medium range of 28.1 kb involving 100 neighboring SNPs; right, short range of 7.3 kb involving 20 neighboring SNPs.

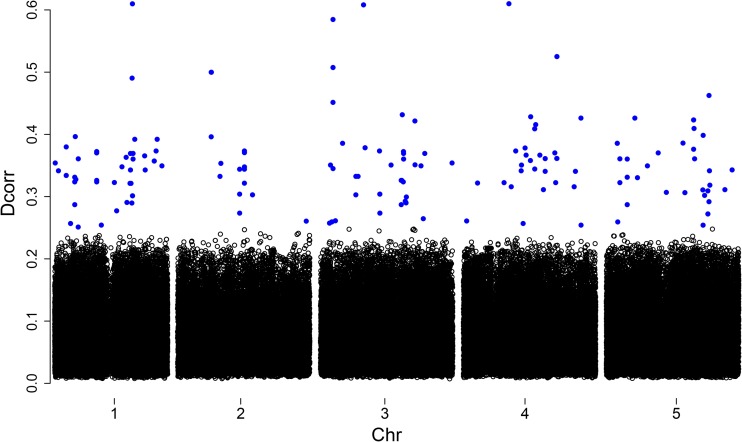
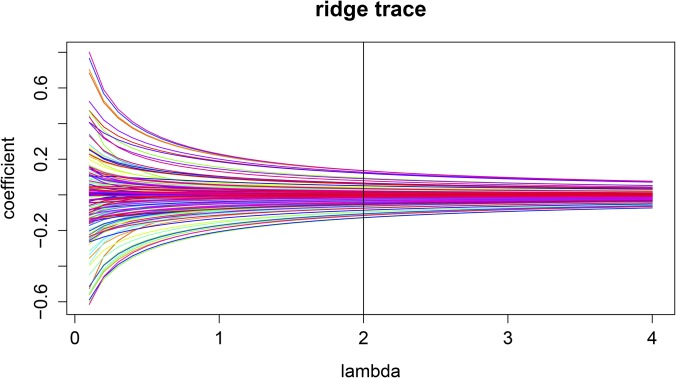
The total computation time for these data comprised 6 hr on a Windows operating system with a 2.10-Ghz Intel Xeon processor and 32 GB of RAM. The top $d=189$ important SNPs were selected by the iterative DC procedure, after which all noise SNPs whose Dcorr values were <0.25 were filtered (Figure 8). We choose $\lambda =2$ for our analysis (Figure 9). The results were relatively stable, and negligible differences were observed when we changed λ to any other number from 1 to 3.

Figure 8.

Dcorr value and location. Shown is a plot of the top $d=189$ important SNPs selected by the iterative DC procedure for AvrRpm1.

Figure 9.

Ridge trace. Shown is a plot of the 189 important SNPs using LRR for the AvrRpm1 data.

Discussion

High-throughput genotyping techniques and large data repositories of case–control sample consortia provide opportunities for GWAS to unravel the genetic etiology of complex traits. With the number of SNPs per DNA array growing from 10,000 to 1 million (Altshuler et al. 2008), the ultrahigh dimension of data sets is one of the grand challenges in GWAS.

We proposed a novel DCRR approach to address the complex LD, multiple joint genetic effects, and ultrahigh dimension problems inherent in whole-genome data. We considered an A. thaliana whole-genome data set that Atwell et al. (2010) reported as carrying several challenges: false-positive rates or spurious significant associations were present due to confounding effects of high population structure. The true-positive signal was difficult to identify because the a priori candidates were overrepresented by surrounding SNPs in the vicinity through complex diffuse “mountain range”-like peaks covering a broad and complex region without a clear center. Sometimes the true causal polymorphism did not have a stronger signal than the spurious ones, which could have occurred when r.SNPs were positively correlated with other r.SNPs or with genomic background SNPs. The sample size was relatively small ($n=84$), which may have limited the power of statistical significance. The natural selection on each locus may have been strong, such that the allele frequency distributions of the causative loci were very different from those of background noise loci. Those distributions may have further disabled many statistical approaches that address genome-wide associations. Finally, a single-SNP model may have caused model misspecification. As was stated by Atwell et al. (2010, p. 630), “At least for complex traits, the problem is better thought of as model misspecificaiton: when we carry out GWA analysis using a single SNP at a time (as was done here and in most other previous GWA studies), we are in effect modeling a multifactorial trait as if it were due to a single locus. The polygenic background of the trait is ignored, as are other unobserved variables.”

Our approach solved the challenges mentioned by Atwell et al. (2010). By breaking down the complex LDs among causative and noncausal SNPs, the causative effects were reinforced while the nominally spurious signals shrank toward zero. The shrinkage effect of the DCRR approach presented herein was more robust and accurate than that of previous approaches (Figure 5 and Figure 6), and the false-positive rates were decreased dramatically while the true-positive rates (power) increased. After filtering the majority of noise and reducing the SNPs from millions to hundreds, the problems caused by ultrahigh dimension were removed. After generating the MAF of all loci randomly from a $\mathrm{Unif}\left(0.05,0.95\right)$ distribution, which imitated strong natural selection effects and also considered the effects of rare alleles, the DCRR approach still successfully detected the causative SNPs. By considering multiple joint effects with complex correlation structures that were neglected by the single-SNP model, the power of DCRR is uniformly better than that of the other approaches in all simulations while the type I error of DCRR is higher than that of the other approaches but it is still controlled to be <0.05.

Malo et al. (2008) applied ridge regression to handle LD among genetic associations. Their work focused on continuous phenotypes and a moderate dimension ($p>n$ but not $p\gg n$) of SNP markers. Cule et al. (2011) proposed the asymptotic significance test approaches in ridge regression for both binary and continuous phenotypes, but their approach mainly focused on moderate dimensions as well. The advantages of DCRR were assessed extensively in a previous section and the DCRR approach can be easily extended to continuous phenotypes. Since a binary response tends to have fewer statistical properties, i.e., the prediction errors tend to be much higher for binary than for continuous outcomes, we expect that the performance of our DCRR approach for continuous traits will only improve.

Methods to increase the signal-to-noise ratio are critical for successful GWAS and the challenges of GWAS are not specific to the data set from Atwell et al. (2010). The monogenetic control with one causative locus in the AvrRpm1 data set may not fully highlight the power of the DCRR approach. In future work, we will apply the DCRR approach to polygenic traits such as human diseases or traits in organisms with agricultural importance. For organisms under artificial selection for trait improvement, such as agricultural crops, spurious or extraneous SNPs in a marker-assisted selection scheme could add cost and time in genotyping as well as possibly misdirect selection priorities. Therefore, the DCRR approach has the potential to provide improved efficiency and accuracy to researchers to design their experiments with applied outcomes wisely.