Imputing Genotypes in Biallelic Populations from Low-Coverage Sequence Data

Abstract

Low-coverage next-generation sequencing methodologies are routinely employed to genotype large populations. Missing data in these populations manifest both as missing markers and markers with incomplete allele recovery. False homozygous calls at heterozygous sites resulting from incomplete allele recovery confound many existing imputation algorithms. These types of systematic errors can be minimized by incorporating depth-of-sequencing read coverage into the imputation algorithm. Accordingly, we developed Low-Coverage Biallelic Impute (LB-Impute) to resolve missing data issues. LB-Impute uses a hidden Markov model that incorporates marker read coverage to determine variable emission probabilities. Robust, highly accurate imputation results were reliably obtained with LB-Impute, even at extremely low (<1×) average per-marker coverage. This finding will have implications for the design of genotype imputation algorithms in the future. LB-Impute is publicly available on GitHub at https://github.com/dellaporta-laboratory/LB-Impute.

THE imputation of missing genotype data has been a key research topic in statistical genetics since well before the advent of next-generation sequencing (NGS) technologies. The goal of many of these algorithms was to reconstruct haplotypes from Sanger or microarray-based genotyping, usually on human populations. Strategies employing the expectation-maximization algorithm (Hawley and Kidd 1995; Long et al. 1995; Qin et al. 2002; Scheet and Stephens 2006), Bayesian inference (Niu et al. 2002; Stephens and Donnelly 2003), or Markovian methodology (Stephens et al. 2001; Broman et al. 2003; Broman and Sen 2009), local ancestry and gametic phase, could be used to resolve missing markers within a population (Browning and Browning 2011). In these cases, missing genotypes were assigned based on the most likely proximal haplotypes. These computational methods greatly increased the informative content of genotyping information, especially for population studies (Spencer et al. 2009; Cleveland et al. 2011). While these programs were powerful and accurate, they also could be computationally expensive. Further, they assumed that available genotypes were largely correct, which could cause issues with sequencing data sets.

The development of programs that focused primarily on the imputation of missing data and haplotype phasing was likely motivated by several factors. Genome-wide association studies could be enhanced by the inference of additional markers using large multipopulation data sets such as the International HapMap Project (International HapMap Consortium et al. 2010). The emergence of the meta-analysis led to a need for algorithms that could merge disparate data sets (Browning and Browning 2007; Howie et al. 2009; Li et al. 2010; Liu et al. 2013; Fuchsberger et al. 2015). These algorithms often employed large haplotype reference panels to improve imputation (Marchini et al. 2007; Browning and Browning 2009; Howie et al. 2009). In biallelic recombinant plant populations, a parental reference panel is sufficient to explain the genetic structure of the offspring (Yu et al. 2008), but reference panels are often not available.

Genome resequencing has become a critical tool for characterizing genetic diversity in plant populations. Unlike genotyping and PCR-based assays, sequencing can characterize large numbers of useful markers without a priori knowledge of a given population’s genetic diversity. However, when applying genome resequencing to the study of large populations, both time and cost must be considered. Sequencing methods employing multiplexing, the simultaneous sequencing of multiple samples in a single pool, have been developed to enhance efficiency and reduce sample costs. These methods include multiplexed whole-genome sequencing (WGS), whole-exome sequencing (WES), restriction-site-associated DNA markers (RAD), and genotype by sequencing (GBS) (Miller et al. 2007; Broman and Sen 2009; Wu et al. 2010; Bamshad et al. 2011; Elshire et al. 2011; Li et al. 2011; Nielsen et al. 2011; 1000 Genomes Project Consortium et al. 2012; Heffelfinger et al. 2014). WES, RAD, and GBS, collectively called reduced-representation sequencing (RRS) methods, interrogate a small but consistent portion of a genome. The tradeoff occurs when large numbers of samples are pooled and sequenced together: individual-per-sample and per-site coverage can be highly variable.

Any low-coverage sequencing method will result in missing and erroneous genotypes. Missing data occur when sequencing coverage is insufficient to interrogate every available site and allele in each sample. Although a RRS experiment is restricted by design to a subset of the total number of alleles, it is highly unlikely that the entire set of available sites and alleles will be recovered in each sample. The proportion of unrecovered alleles increases with marker density and the level of multiplexing. Missing data manifest in two forms. The first form is seen when no alleles are recovered at a marker in a given sample, resulting in the absence of any genotype at that site. The second form occurs when one allele is not recovered at a given marker in a sample. In this case, if the site is monomorphic, no information is lost. If the marker is heterozygous in the sample, however, that site will be falsely identified as a homozygote (Swarts et al. 2014). Both missing sites and erroneous homozygote calls pose the greatest challenge to the imputation of missing data in low-coverage sequencing data sets.

Recently, several algorithms have emerged that impute RRS data, and GBS data sets in particular, generated from plant populations (Huang et al. 2014; Swarts et al. 2014; Rowan et al. 2015). Because GBS relies on both a high degree of multiplexing and reduced representation to maximize efficiency, it is emblematic of both the challenges and opportunities of processing low-coverage sequencing data. That is, it can efficiently produce population-scale data sets with calls on tens of thousands of markers, but within each individual sample there will be considerable missing data. The mpimpute algorithm provides the useful innovation of imputing missing parental data to improve the resolution of offspring data (Huang et al. 2014). Nevertheless, mpimpute is limited in the sense that it only imputes haploid (or homozygous) data and does not incorporate potentially useful read-depth information into the imputation method. A different approach used in Full-Sib Family Haplotype Imputation (FSFHap) (Bradbury et al. 2007; Swarts et al. 2014) is capable of imputing low-coverage sequencing data with high heterozygosity from biallelic populations. FSFHap works by first identifying parental haplotypes in the progeny. It then iterates over the progeny and identifies each site as being homozygous for one of the parents or heterozygous via a hidden Markov model (HMM). The key observation allowing resolution of heterozygosity is that a region that contains alleles from both parents is likely to be heterozygous, even if the recovered markers themselves are homozygous. Another recently published HMM-based approach, Trained Individual Genome Reconstruction (TIGER) (Rowan et al. 2015), translates genotypes into one of six observed states (AA, BB, AB, AU, BU, and UU, with U indicating an uncertain allele). This approach applies a cutoff of five reads of coverage, beneath which the possibility of a false homozygote is incorporated into the model in the form of the AU and BU observations. Finally, TIGER imputes genotypes using allele frequencies in a sliding-window method. While the TIGER algorithm is described in the paper by Rowan et al. (2015), software for the TIGER algorithm is not publically available.

Here we describe Low-Coverage Biallelic Impute (LB-Impute), an algorithm that has been designed to overcome the challenges of low-coverage sequencing in biallelic plant populations. Because low-sequencing coverage may result in false homozygosity, the probability of false homozygosity can be estimated by taking into account depth-of-coverage information at each marker. LB-Impute incorporates depth-of-coverage information into the emission probabilities of a HMM. Using this approach, LB-Impute is capable of correcting false homozygosity and imputing missing genotypes in biallelic sequencing data sets, even when per-marker coverage is extremely low (<1×).

Materials and Methods

LB-Impute is a HMM-based method. Emission and transition probabilities are calculated from allelic depth of coverage and the physical distance between markers. The Viterbi algorithm (Rabiner 1989) is used to determine the most likely sequence of parental ancestry (hidden states) for each offspring in a biallelic population. Choosing the most likely sequence of hidden states, instead of the best state for each marker, reduces the impact of individual erroneous markers in a data set. The assumption in the model is that markers are independent, in the sense that the emission and transition probabilities of a given marker will not influence the probabilities of surrounding markers. Therefore, LB-Impute uses a first-order Markov chain.

The steps of this algorithm can be broadly described as follows: (1) determination of parental haplotypes, (2) assignment of reference and nonreference alleles for each marker to parental states, (3) calculation of parental-state emission probabilities based on the depth-of-sequencing coverage of each allele in all markers, (4) determination of transition probabilities via the distance in base pairs between markers, (5) calculation of all possible paths through the hidden states (parental genotypes) from markers t to t + i via a Viterbi trellis, (6) selection of the parental genotype at marker t + 1 in the highest-probability path as the next genotype in the final path, (7) regeneration of the Viterbi trellis from markers t to t + i using the previous highest-probability path’s marker t + i genotype as the new marker M, (8) forward iteration of trellis markers across the entire chromosome, (9) reverse iteration of trellis windows across the entire chromosome, (10) comparison of the forward and reverse paths across the chromosome to determine a set of consensus genotypes for a given offspring, (11) setting of genotypes that conflict between paths to missing, (12) correcting of genotypes in the original data set that conflict with consensus calls to the consensus genotype, and (13) setting of missing genotypes between concordant consensus calls in the original data set to the consensus genotypes. A more detailed explanation of key steps in the algorithm follows.

The initial step of the algorithm is to assign emission probabilities to each marker. Parental ancestry is the hidden state. Each read is assigned to a parent based on its sequence, and a final emission probability is calculated based on the number of reads assigned to each parent and the probability of each read being erroneous. The emission probabilities for genetic contribution from a single parent, or homozygosity, at a given marker are calculated using the equation

$$E_{\text{N}} = {\left(1 - er{r}_{\text{r}}\right)}^{R_{\text{N}}}{\left(er{r}_{\text{r}}\right)}^{R_{\text{!N}}}$$ (1)

where E_N is the emission probability of a given hidden state, or parental ancestry, N for the given genotype, err_r is the probability of a sequencing error for each read at the position of a marker, R_N is the number of reads with sequence matching the sequence of parent N, and R_!N is the number of reads with sequence not matching the genotype of parent N. The raw emission probability for the heterozygous hidden state is calculated using the equation

$$E_{\text{H}}=\left({0.5}^{R_{\text{N}}}\right)\left({0.5}^{R_{\text{!N}}}\right)$$ (2)

where E_H is the emission probability of the third hidden state, heterozygosity, or genetic contribution from both parents at a given site.

While the raw emission probability takes into account the likelihood that any one read is erroneous, genotyping errors independent of coverage also may affect a data set. These genotyping errors include misalignment of reads to the reference genome, resulting in the incorrect placement of a genotype, and an unannotated paralogous artifact. It is therefore desirable to limit both the minimum and maximum emission probabilities to minimize the chance of an artifact overinfluencing the final imputed genotypes. To do this, each emission probability at a given position is divided by the maximum emission probability at said position. Then each probability is divided by 1 − 2 × err_g and finally has err_g added to it. The value err_g represents the probability of a genotyping error. The maximum and minimum possible emission probabilities for any given marker are (1 − err_g)/(1 + err_g) and err_g/(1 + err_g), respectively. Actual emission probabilities do not sum to 1 but instead will be constrained within these limits. The effect of emission probabilities on the model is determined by their ratios rather than their sum.

In LB-Impute, the transition probabilities depend on the probability of recombination between markers. This probability depends on the distance between markers. The probability of recombination is directly related to the distance in base pairs between markers. The equations used to calculate transition probabilities are

$$P_{\text{S}}=0.5 \left(1+e^{-\left({\text{Dist}}_{\text{M}}/{\text{Dist}}_{\text{R}}\right)} \right)$$ (3)

and

$$P_{\text{R}}=0.5\left(1-e^{-\left({\text{Dist}}_{\text{M}}/{\text{Dist}}_{\text{R}}\right)}\right)$$ (4)

where P_S is the probability of maintaining a given hidden state, and P_R is the probability of a recombination event causing a change of hidden states. Dist_M is the distance in base pairs between two markers, and Dist_R is the distance in base pairs for transition probabilities to equalize. By default, we assume that two recombinations are required to transition from one homozygous parental state to the other homozygous parental state, resulting in double recombination events between proximal markers being heavily penalized compared to single events. In a population with many recombination events (such as a recombinant inbred line), the user may choose to allow for double events to have the same transition probability as single recombination events.

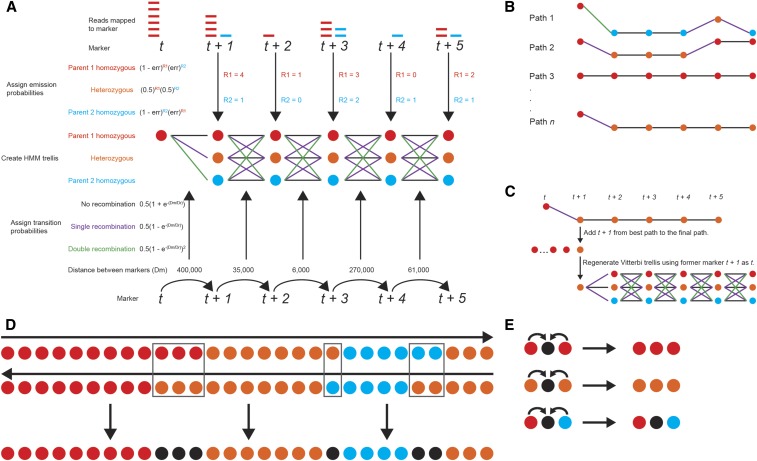
The final modification to the standard Viterbi algorithm (Rabiner 1989) is the use of a variable trellis window to identify recombination breakpoints. Because one of the assumptions in this program is that there may be a high rate of error for any one marker, the incorporation of information from multiple markers into a Markov chain may resolve this issue. While it would be ideal for this chain to stretch the entire length of the chromosome, it would be computationally inefficient to calculate the probability of every possible path through it, and therefore, an iterating-window approach is used. The user may select the number of markers to be incorporated into each trellis by changing the window size n. Within a window, the probabilities of every possible path between marker t and marker t + n (Figure 1A) are calculated using the emission and transition probabilities described earlier. After the probabilities of every possible path for a given window are calculated, the t + 1 hidden state of the path with the highest probability is selected (Figure 1B). Following this, the trellis is regenerated using the marker that was t + 1 as the new t (Figure 1C).

Figure 1.

Visual description of the LB-Impute algorithm. (A) Emission probabilities based on allelic depth of coverage and transition probabilities based on expected recombination rate and distance between markers are used to build a Viterbi trellis window from markers t to t + n. (B) The probabilities of every possible path through the Viterbi trellis window are calculated. (C) The path with the highest probability is selected, the state at t + 1 is added to the final path, and then a new trellis is regenerated with marker t + 1 as the new t. (D) Paths are calculated in forward and reverse directions. A final path is created from the consensus. At loci where the forward and reverse paths conflict (black boxes), a missing call is added to the final path. (E) Missing calls are resolved from the consensus of surrounding states. Where surrounding states conflict, the call is left missing.

LB-Impute first iterates these trellis windows across the entire chromosome in the forward direction, and then it iterates trellis windows across the entire chromosome in the reverse direction by inverting the order of the markers on the chromosome. This generates two complete paths of hidden parental states across the entire chromosome. This approach is taken because, while the emission and transition probabilities will be the same for the forward and reverse paths, the value of the starting marker t may differ. Hidden-state calls that are concordant between the forward and reverse paths are included in the final path. When the parental ancestry at a marker conflicts between the forward and reverse paths, the corresponding marker is set to missing in the final path for said offspring (Figure 1D). This is done even if the marker has a call in the original data set because the algorithm has determined the call to be unreliable. If the user prefers to obtain as many imputed calls as possible, he or she may choose to use the state with the higher probability from the forward and reverse paths to determine a genotype for the marker. Missing markers are inferred by the state of the flanking markers. When the states of the flanking marker are concordant, the missing marker is resolved to the genotype of the flanking markers. When they are discordant, the missing marker is not imputed (Figure 1E).

In addition to being able to impute both missing and falsely homozygous genotypes in the offspring, the LB-Impute algorithm allows imputation of missing parental alleles. Dense founder genotype maps are critical for interpreting markers and resolving recombination breakpoints with high resolution in many biallelic populations. Missing parental genotypes reduce the power of breakpoint resolution. To impute missing parental genotypes, parental haplotypes are recovered from observed markers in the offspring. The approach is similar to the one used to impute missing markers in the offspring. The difference is that the parental state of flanking markers is assigned to ambiguous rather than missing markers in each offspring. The consensus genotype, as determined across imputed offspring, for a missing parental marker is then assigned to the parent. Using this system of parental imputation followed by offspring imputation as described by Huang et al. (2014), a high-resolution map can be generated from low-coverage sequencing data.

Algorithm testing

To evaluate LB-Impute, it was tested on simulated F₁BC₁ and F₂ populations, two data sets generated from an actual maize F₂ population (Heffelfinger et al. 2014), and the IBM Maize Recombinant Inbred Line (RIL) population (Elshire et al. 2011). In the context of this study, an F₁BC₁ population is one in which an offspring (F₁) of inbred parents is backcrossed to one of the parents, producing a population in which only the recombination of the F₁ is observable, and homozygous alleles must come from the backcrossed parent. An F₂ population is the result of selfing an F₁ offspring to produce a biallelic population in which recombination can be observed on both chromosomes, and homozygous alleles from both parents are present. Performance comparisons were done with FSFHap.

Generation of simulated data:

Simulated F₁BC₁ and F₂ data sets were generated using a custom Java-implemented algorithm. The exact methodology for simulated data set construction is described in Supporting Information, File S1, Note 2. In total, 80 data sets, 40 F₁BC₁ and 40 F₂, were generated, with coverage values spaced evenly from 1000 reads per sample (0.1× coverage) up to 40,000 reads per sample (4.0× coverage). Twenty replicates were created for each data set.

The amount of missing or erroneous data was inversely proportional to read coverage. Missing data refers to sites within a sample where there are no aligned reads, resulting in an absent genotype call. Erroneous data occur when incomplete allele recovery results in false homozygosity at a given site. For instance, the simulated F₁BC₁ 4× coverage data sets had only 13.48% [±0.34% (SD)] missing or erroneous data, whereas the 0.1× coverage data sets had a missing or erroneous fraction of 95.16% [±0.20% (SD)] (Figure S1A). For the 4.0× and 0.1× F₂ data sets, the missing or erroneous fractions were 13.61% [±0.48% (SD)] and 95.12% [±0.34% (SD)], respectively (Figure S1B).

Preparation of real data:

GBS data sets from a previously described B73 × Country Gentleman (B73 × CG) F₂ maize population (Heffelfinger et al. 2014) and the IBM Maize RIL (Elshire et al. 2011) data set were prepared as described in File S1, Note 3. For the B73 × CG data sets, five validation sets were generated with half the calls with seven aligned reads randomly removed. At a depth of seven reads, the chance of a false homozygote is only 1.56% (Swarts et al. 2014). For the IBM Maize RIL population, five validation sets with half the markers with four aligned reads randomly removed were created. While it would have been preferable to use seven reads, the lower overall sequencing coverage resulted in most of the samples having zero markers with seven reads. While false homozygosity may have resulted in some of the markers being erroneous (12.5% of heterozygotes with four reads would be expected to be miscalled), the low levels of heterozygosity present in the data set owing to repeated selfing would be expected to minimize this effect.

Algorithm settings

For the analyses described, FSFHap (Swarts et al. 2014), Beagle (Browning and Browning 2007), and Mendel Impute (Chi et al. 2013) versions and settings are described in File S1, Note 1. LB-Impute was set to its default parameters. For emission probabilities, we assume a 5% resequencing error rate (err_r) and a 5% genotype error rate (err_g). To determine transition probabilities, a 10-Mbp recombination interval (Dist_R) was applied as described in Equations 3 and 4. We also used the default setting that transitions between homozygous parental states that are the product of two transition probabilities. The Markov trellis window was set to a length of 7. For the RIL data set, the double recombination events were treated as a single event.

Data availability

LB-Impute is publicly available at https://github.com/dellaporta-laboratory/LB-Impute. Test data files used in these analyses are also available on the Github site.

Results

Evaluation of LB-Impute was performed on five distinct data set categories: two simulated F₂ and F₁BC₁ populations, two maize B73 × CG F₂ populations, and one B73 × Mo17 RIL population. To evaluate the performance of LB-Impute, both the fraction of data imputed and the accuracy were measured. Results from the LB-Impute analyses were compared with those of FSFHap (Bradbury et al. 2007; Swarts et al. 2014), a widely used program designed to deal with false homozygosity resulting from incomplete coverage of heterozygous markers. Like LB-Impute, FSFHap is designed specifically to impute biallelic populations. The performance of both programs was tested on the set of simulated data sets and real data sets. Additionally, Beagle and Mendel Impute, which are not designed to account for false homozygosity, were tested on simulated data sets.

LB-Impute and FSFHap performance on simulated data

The first parameter considered was the fraction of data that was left missing in each imputed data set. LB-Impute left <1% of markers missing in the F₁BC₁ and F₂ data sets at ≥0.9× coverage. The lowest fraction of markers imputed was 94.54% [±0.36% (SD)]. FSFHap was unable to impute data sets in either the F₁BC₁ or F₂ data sets at <0.4× coverage but achieved >99% marker imputation in higher-coverage data sets (Figure S2).

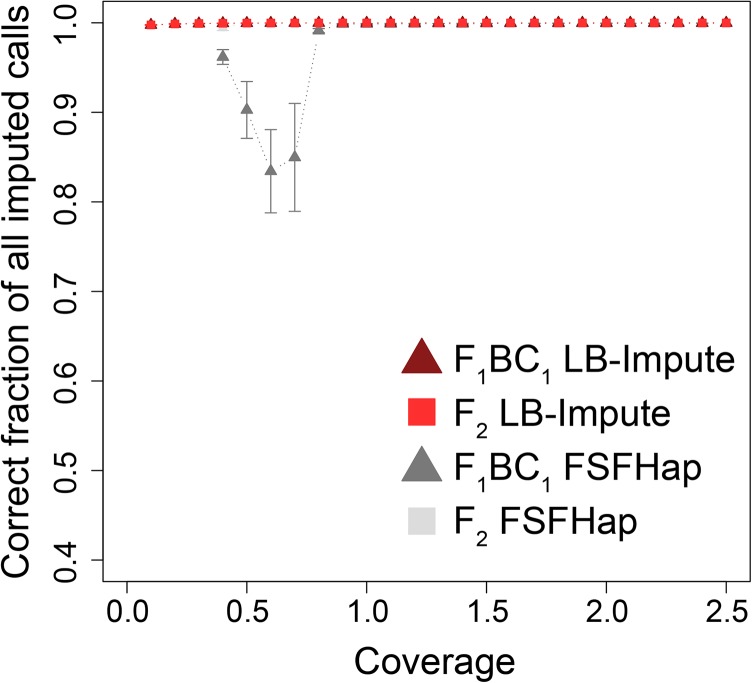
Both FSFHap and LB-Impute resolved all markers, not just those that were missing. Accordingly, absolute accuracy was measured as the fraction of nonmissing markers in the final imputed data sets that were correct (Figure 2). Importantly, LB-Impute achieved >99% accuracy in the F₁BC₁ and F₂ data sets at all tested levels (0.1–2.5×) of coverage. In contrast, for FSFHap, absolute accuracy ≥99% was achieved in most of the data sets, occurring with ≥0.8× coverage in F₁BC₁ and ≥0.4× coverage in F₂. The major exception to the trend of high absolute accuracy of FSFHap was its inability to impute data sets of either population at <0.4× coverage. The other exception to this trend was the 0.4–0.7× coverage data sets in F₁BC₁, inclusive, which reported a minimum absolute accuracy of 83.43% [±4.65% (SD)] at 0.6× coverage.

Figure 2.

Correct fraction of total imputed calls on simulated data sets. Error bars indicate SD of the mean.

Next, the fraction of recombination breakpoints imputed correctly (Figure S3A) and the mean number of missing markers around recombination breakpoints (Figure S3B) were evaluated. A recombination event was considered to be correctly imputed if the flanking imputed genotypes matched the true flanking genotypes of the recombination event. Missing markers were determined by the number of markers between the recombination event and the imputed genotypes. Again, LB-Impute was able to correctly impute recombination events with greater frequency in both the F₂ (minimum accuracy 77.16%, maximum accuracy 90.09%) and F₁BC₁ (minimum accuracy 76.87%, maximum accuracy 89.95%) populations than FSFHap (minimum accuracy 44.65%, maximum accuracy 80.71% for F₂; minimum accuracy 12.86%, maximum accuracy 63.07% for F₁BC₁). Most of the recombination events considered to be incorrectly imputed were the result of the imputed breakpoint being slightly offset from the true event rather than erroneous genotyping. The greater accuracy of LB-Impute was somewhat at the expense of the absolute number of markers imputed. LB-Impute left more missing markers (minimum of 2.35 markers per event, maximum of 150.57 markers per event) than FSFHap (minimum 0.15, maximum 3.30) in both the F₁BC₁ and F₂ data sets.

Finally, it was observed that FSFHap greatly outperformed LB-Impute in terms of run time, with run times ranging from 3.95 to 46.95 sec. As discussed next, these run times increased, however, when LB-Impute was set for greatest accuracy by extending the length of the trellis window.

Effect of LB-Impute window length on performance

The length of the Markov trellis window in LB-Impute affects how much information is used to predict genotype, the tradeoff being increased run times. To demonstrate this, window lengths of between 2 and 7 were tested on simulated F₂ (Figure S4A) and F₁BC₁ (Figure S4B) 0.1×, 0.5×, 1.0×, and 2.5× coverage data sets. Both accuracy and run time were evaluated. At window length 2, accuracy fell between 66.69 and 70.70%. At window length 7, accuracy was >99% in all simulations, and at window length 6, accuracy was greater than >98% in all simulations. The accuracy of other simulations varied with window length and coverage in a similar fashion.

Window length also had an effect on the fraction of markers imputed. A window length of 2 resulted in only 39.38–43.01% of the markers being imputed in F₂ populations, whereas longer window lengths saw greatly improved performance, with >94% of all markers being imputed by window length 7. Window size effect on run time was tested with a window size of 2, resulting in run times ranging from a minimum of 31.13 sec at 0.1× coverage to a maximum of 17,878.90 sec at 2.5× coverage with a window size of 7 (Figure S5, A and B).

Beagle and Mendel Impute performance

Beagle (Browning and Browning 2007) and Mendel Impute (Chi et al. 2013) were tested on all simulated F₂ and F₁BC₁ data sets, and the results were compared to those of LB-Impute. In F₁BC₁ data sets, Mendel Impute was able to impute at 98.76% [±1.51% (SD)] accuracy at 2.5× coverage and >90% accuracy at >1.5× coverage. Below 1.5× coverage, however, accuracy dropped off precipitously until reaching 50.10% [±1.74% (SD)] at 1.1× coverage. In F₂ data sets, it performed similarly at >1.5× coverage and better below, with a minimum accuracy of 72.61% [±1.50% (SD)] at 0.7× coverage (Figure S6A). Beagle had a maximum accuracy of 78.60% [±1.00% (SD)] at 2.5× coverage and a minimum of 50.69% [±1.97% (SD)] in the F₁BC₁ data sets. In the F₂ data sets, its maximum and minimum accuracies were 78.50% [±0.73% (SD)] and 37.07% [±0.19% (SD)] at 2.5× and 0.1× coverage, respectively (Figure S6B).

LB-Impute and FSFHap performance on real data

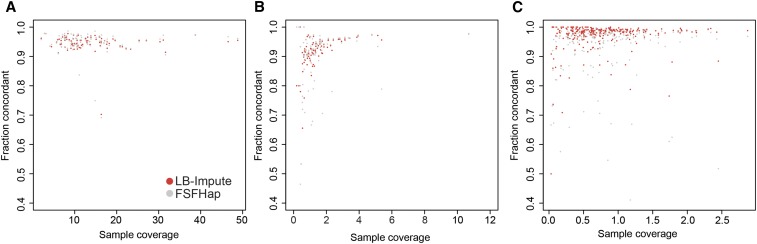
To determine the accuracy of LB-Impute on real sequencing data, it was tested on two GBS data sets generated from a maize B73 × CG F₂ population (Heffelfinger et al. 2014) and the IBM Maize RIL population (Elshire et al. 2011). One B73 × CG data set, containing 11,219 postfilter markers, was generated from a HincII digest of both parents plus 89 offspring (Figure 3A and Figure S7A). The other B73 × CG data set, produced by RsaI, had 127,144 postfilter markers identified in both parents and 90 offspring (Figure 3B and Figure S7B). Finally, the IBM Maize RIL data set consisted of 14,493 postfilter markers typed in 275 offspring (Figure 3C and Figure S7C). Of the 275 offspring, 255 had validation markers. The remaining 20 lacked sufficient sequencing coverage to contribute validation markers.

Figure 3.

Per-sample concordance of LB-Impute and FSFHap for (A) HincII B73 × CG, (B) RsaI B73 × CG, and (C) IBM Maize RIL population data sets.

Using default parameters (trellis window size of 7), LB-Impute was able to impute a mean of 99.87% [±0.01% (SD)] of all markers in HincII replicates and 99.18% [±0.01% (SD)] in RsaI replicates. FSFHap imputed 98.27% [±0.10% (SD)] of all markers in the HincII data set and 97.50% [±0.45% (SD)] in the RsaI data set. In the IBM Maize RIL data set, LB-Impute and FSFHap were able to impute 93.92% [±0.01% (SD)] and 99.15% [±0.01% (SD)] of the markers, respectively.

Concordance between imputed genotypes and the validation set was 94.62% [±3.02% (SD)] in HincII data sets and 91.44% [±6.73% (SD)] in RsaI data sets. For FSFHap, mean concordance was 94.71% [±4.05% (SD)] for HincII data sets and 89.70% [±9.76% (SD)] for RsaI data sets. In the IBM Maize RIL population, LB-Impute concordance was 96.98% [±5.14% (SD)], and FSFHap concordance was 93.27% [±11.24% (SD)]. LB-Impute performed significantly better than FSFHap for the RsaI (P = 0.045) and IBM Maize RIL data sets (P < 0.001), as evaluated by paired two-tailed t-test. LB-Impute and FSFHap produced comparable results for the HincII population (P = 0.70). LB-Impute mean run time was 5323.66 sec [±8.79 sec (SD)] for HincII replicates, 50,248.17 sec [±402.60 sec (SD)] for RsaI replicates, and 7092.82 sec [±380.97 sec (SD)] for the IBM Maize RIL data set. These run times are for the entire data set rather than each individual. Run times for FSFHap were not taken because multiple manual steps were required during the imputation process. As with the simulated data, the FSFHap algorithm itself was considerably faster than LB-Impute.

Discussion

Imputation algorithms have been critical for enhancing genotyping studies. While originally used to resolve calls missing in merged data sets and to increase the power of genome-wide association studies, new demands have been placed on this field of bioinformatics. One such demand has emerged from low-coverage genome resequencing of plant populations. LB-Impute resolves missing and erroneous data in these populations by incorporating allelic depth of coverage and physical distance between markers into a HMM.

Simulated data indicated that LB-Impute is highly suited for resolving missing and erroneous data, even at extremely low levels of coverage. Accuracy >99% was achieved at all tested levels of coverage (≥0.1×) in both F₂ and F₁BC₁ data sets. LB-Impute performed especially well compared to methods not designed for dealing with the issues associated with low-coverage sequencing (e.g., false homozygosity), such as Beagle (Browning and Browning 2007) and Mendel Impute (Chi et al. 2013). At 0.1× coverage, LB-Impute was able to maintain accuracy >99%, while both Beagle and Mendel Impute fell to as low as 37.07 and 49.51%, respectively. LB-Impute’s performance, however, was highly dependent on window size. With a window length of 6 or 7, the tradeoff for high accuracy was a dramatic increase in run time.

LB-Impute was tested on two maize GBS data sets (Heffelfinger et al. 2014) and the IBM Maize RIL population (Elshire et al. 2011) In the B73 × CG data sets, LB-Impute performed similarly to FSFHap with the HincII data set but slightly better with the RsaI and RIL data sets. Finally, it is worth noting that the true accuracy of the imputation results may be higher than the concordance because results corrected by imputation are likely to be more reliable than unimputed genotypes (Swarts et al. 2014).

A limitation to LB-Impute is that it is not designed to handle data from populations with more than two alleles. As the number of segregating haplotypes within the population increases, the number of hidden states expands according to the equation

$$\frac{n\left(n-1\right)}{2}+n$$ (5)

where n is the number of parental haplotypes. Given how the Viterbi trellis window is constructed, this results in an exponential increase in the number of possible paths through hidden states that must be solved. Going from a biallelic to a triallelic population results in an increase in the number of paths by a factor of 2^{(o + 1)}, where o is equal to the trellis window of the Viterbi algorithm. Compounding this problem is that as the number of parental haplotypes increases, the informative content of each individual marker decreases. To distinguish between haplotypes, the number of biallelic markers must be

$$n\le 2^m$$ (6)

where n is the number of haplotypes, and m is the number of biallelic markers. So, at minimum, two biallelic markers are required to distinguish between three haplotypes, three biallelic markers are required to distinguish between five haplotypes, and so on. Therefore, the trellis window described in this algorithm must increase with the number of segregating haplotypes to maintain the same level of power. Ultimately, the increase in computing time would cripple performance for even relatively simple multiallelic populations such as multiparent advanced generation intercross (MAGIC) lines (Cavanagh et al. 2008). One approach to resolving this issue with LB-Impute would be to eliminate the ability to compute the heterozygous state for highly homozygous populations. Homozygous populations, such as RILs, may contain residual heterozygosity owing to incomplete fixation of alleles or unintended outcrossing. The ability to identify lines with heterozygosity in populations that have undergone repeated selfing is a desirable objective.

As compared to FSFHap, LB-Impute should be used for imputing populations when parental genotypes are available. FSFHap’s ability to recover parental haplotypes without direct parental genotyping makes it useful for imputing large populations with no parental sequencing. Outside of these cases, such as large populations with parental sequencing, our results indicate the LB-Impute and FSFHap would perform similarly.

Conclusions

A critical goal in population genomics is to develop imputation methods suitable to detect heterozygosity and recombination in low-coverage data sets. We have successfully implemented a solution to this problem that allows for accurate parental and offspring imputation in low-coverage sequencing data sets in biallelic populations. The resulting algorithm, LB-Impute, is able to reliably resolve both missing data and false homozygosity even for samples with less than 1× coverage.

Challenges remain, however, especially in multiparental populations with more than two segregating alleles. Many populations used for agricultural breeding and research meet this description. Without reliable methods for resolving missing and erroneous data, the power of low-coverage multiplexed sequencing in these populations will be limited. While the method described in this paper is not suitable for populations with more than two alleles, it does identify read coverage as a key parameter for resolving this challenge.

The next generation of imputation algorithms for low-coverage sequencing data will benefit from using read coverage when identifying alleles present in a sample. By adjusting the probability of observed genotypes based on coverage combined with information about haplotype frequency gleaned from identical-by-descent (IBD) regions across samples, heterozygous regions will be more likely to be accurately phased. The need for considerable IBD homozygosity or phased parental haplotypes is unlikely to go away with improved algorithms and will instead most likely be remedied by long-read sequencing on all or part of a population.