A Robust Distribution-Free Test for Genetic Association Studies of Quantitative Traits

Abstract

In association studies of quantitative traits, the association of each genetic marker with the trait of interest is typically tested using the F-test assuming an additive genetic model. In practice, the true model is rarely known, and specifying an incorrect model can lead to a loss of power. For case-control studies, the maximum of test statistics optimal for additive, dominant, and recessive models has been shown to be robust to model mis-specification. The approach has later been extended to quantitative traits. However, the existing procedures assume that the trait is normally distributed and may not maintain correct type-I error rates and can also have reduced power when the assumption of normality is violated. Here, we introduce a maximum (MAX3) test that is based on ranks and is therefore distribution-free. We examine the behavior of the proposed method using a Monte-Carlo simulation with both normal and non-normal data and compare the results to the usual parametric procedures and other nonparametric alternatives. We show that the rank-based maximum test has favorable properties relative to other tests, especially in the case of symmetric distributions with heavy tails. We illustrate the method with data from a real association study of symmetric dimethylarginine (SDMA).

1 Introduction

Genetic association studies - which test for correlation between genetic markers, such as single nucleotide polymorphisms (SNPs), and a disease or a quantitative trait - have been a useful tool in identifying susceptibility loci for common diseases and traits (Hindorff et al. 2009). The analysis of such studies often requires specifying the genetic inheritance model, that is, the relationship between genotype and disease risk or mean value of the trait (Balding, 2006). Three of the models commonly used to describe genotype-trait relationship are additive, dominant, and recessive. When the true underlying model is known, powerful methods are available to detect the association (Sasieni, 1997; Zheng et al., 2003). In practice, the genetic model is rarely known a priori. For example, in genome-wide association studies (GWAS) that screen hundreds of thousands of genetic markers, different patterns of association could be observed at different loci. In the absence of knowledge of the true model, most GWA studies perform the analysis using the additive model, that is, assuming mean genotype effect is proportional to the number of copies of the variant allele (0, 1, or 2). Tests based on the additive model, however, can be inefficient for detecting dominant or recessive effects and could miss true-positive signals (Freidlin et al., 2002; Zheng et al., 2006). Thus, procedures that have high power for a wide range of genetic models are desirable.

To overcome model uncertainty, one simple approach is to compare mean genotype effects using standard statistical procedures such as the one-way analysis of variance. This method is robust in a sense that it does not assume any particular model (i.e., is model-free), but it is less powerful than tests tailored to a specific model (Balding, 2006). Further, it can give rise to spurious associations, detecting non-monotonic patterns that are not consistent with commonly observed inheritance modes. Several intermediate procedures that restrict the alternative space to a range of plausible genetic models have been developed for genetic studies, with early work focusing primarily on dichotomous outcomes (reviewed in Joo et al., 2010; Bagos, 2013). Freidlin et al. (2002) proposed two efficiency robust tests: one based on the linear combination (maximin efficiency robust test, MERT), the other on the maximum (MAX3) of Cochran-Armitage trend tests (Cochran, 1954; Armitage, 1955) optimal for different genetic models. They found that MAX3 was generally more powerful than the MERT. Several authors applied a similar approach to case-control studies, with significance of MAX3 assessed by permutation (Sladek et al., 2007), trivariate integration (González et al., 2008), or analytical approximation (Li et al., 2008). Zang et al. (2010) developed an efficient algorithm for computing the null distribution of MAX3 and implemented their methods in the R package Rassoc. Other authors considered the minimum of the p-values for the additive and the general 2-df (genotype-based) model as a test criterion (Wellcome Trust Case Control Consortium, 2007; Joo et al., 2009).

So and Sham (2011) extended the robust MAX3 approach to allow for quantitative traits and covariates. Their method is based on score tests in the framework of generalized linear models, and is implemented in the R package RobustSNP. Score tests are computationally faster than likelihood ratio tests; however, they do not provide the estimates of regression coefficients. Wang and Sheffield (2005) developed the constrained likelihood ratio test (CLRT) for both continuous and binary traits, in which the effect of the heterozygous genotype (1 variant allele) was restricted to be intermediate between the effects of the two homozygous genotypes (0 or 2 alleles). Lettre et al. (2007) used the maximum of F-tests optimal for different genetic models as a robust approach to quantitative trait association, but they relied on a computationally intensive permutation procedure to determine the significance of the test. Recently, Qu (2014) developed a robust combination approach based on an approximate joint distribution of several transformed F-tests, which avoided the computational burden of permutation testing and had the added advantage of allowing for covariates and the inclusion of tests with different degrees of freedom.

One limitation of the existing methods for quantitative trait association is the assumption that the within-genotype distributions of the trait are normal. In practice, many traits studied in genetics are markedly non-normal. Furthermore, modern genetic studies often examine hundreds of different traits simultaneously, so the exact distribution of each trait may be difficult to assess. For instance, in studies mapping expression quantitative trait loci (eQTL), the expression levels of thousands of genes, each treated as a quantitative trait, are tested for association with genetic markers. Given the large number of traits, robust screening tools that do not assume a particular shape of the distribution should be superior to normal theory tests. Many alternatives to the usual parametric procedures exist in statistical literature. For example, Kozlitina (2008) previously showed that a classic rank test for trend, Jonckheere-Terpstra (Jonckheere, 1954; Terpstra, 1952), had optimal properties for testing the association under an additive model. Similarly, the Fligner-Wolfe test (Fligner and Wolfe, 1982) was optimal for testing the association under dominant/recessive models. In the current paper, we consider the maximum of the above rank tests to create a robust distribution-free test for quantitative trait association. We derive the null correlations among the three rank tests and show that those are equivalent to correlations among model-based Cochran-Armitage and F-tests. Thus, previous results from the literature on efficiency robust tests can be applied to construct a rank-based MAX3 test.

An alternative approach to deal with non-normal data is to apply a transformation, such as a logarithm or a square root transformation, in order to achieve more normally distributed residuals. One method, in particular, that is increasingly being used in genetic studies, is to apply an inverse normal transformation (INT), or a normal scores transformation, to trait values before performing standard parametric tests of association (Scuteri et al., 2007; O’Donnell et al., 2011; Kettunen et al., 2012; Seppälä et al., 2014). Although this approach ensures that the marginal distribution of the trait is nearly normal, as noted by Beasley et al. (2009), the statistical properties of parametric tests based on INT have not been explored in the context of genetic studies, especially when compared to other nonparametric alternatives. As early as 1960, Hodges and Lehmann examined two-sample tests based on ranks and on normal scores and showed that while the normal scores tests might be preferable for distributions with a density that drops discontinuously to zero at one extreme, such as the exponential distribution, rank-based procedures could be more efficient for symmetric distributions with heavy tails, such as a normal distribution contaminated by gross outliers. Similar results were obtained by Knoke (1991) for the analysis of covariance. Other studies have found that the normal scores tests may not maintain correct type I error rate when the assumption of equal variance is violated (Pratt, 1964). Here, we compare the performance of the usual rank tests to those based on the inverse normal transformation under different distributions and in a situation typical of a genetic association study (i.e., unequal sample sizes for the three genotype classes).

In the next sections, we first examine the correlations among test statistics optimal for the three genetic models as a function of marker allele frequency and quantify the amount of efficiency lost due to model misspecification. We next investigate the size and power of rank tests and normal theory tests, applied to raw data and normal scores, through a simulation study under both normal and non-normal distributions. Finally, we demonstrate the method using the data from a real genetic association study of symmetric dimethylarginine (SDMA).

2 Methods

2.1 Notation and Hypothesis

Consider a genetic association study with N individuals and a biallelic marker (e.g., a SNP) having alleles A and B with population frequencies p_A = p and p_B = 1 − p, respectively. Assume, without loss of generality, that A is the less common allele. There are three possible genotypes at this marker locus: g₀ = BB, g₁ = BA, and g₂ = AA, indexed by i = 0, 1, 2, i.e., the number of copies of the less common allele. Denote the population frequencies of the three genotypes by p₀ = Pr(BB), p₁ = Pr(BA), and p₂ = Pr(AA). Assuming the population is in Hardy-Weinberg equilibrium (HWE), the genotype frequencies depend on the allele frequencies: p₀ = (1−p)², p₁ = 2p(1−p), p₂ = p². We note that the assumption of HWE is not required for the methods examined in this paper, but is used here to describe the expected relationship between genotype and allele frequencies in population-based genetic studies. Let n₀, n₁, n₂ be the observed numbers of individuals with each genotype (n₀ + n₁ + n₂ = N). In a random sample from the general population, the genotype counts (n₀, n₁, n₂) will follow a multinomial distribution, Mul(N; p₀, p₁, p₂).

Let Y_ij, i = 0, 1, 2, j = 1, 2,..., n_i be the measured outcome for individual j with genotype g_i, and assume that Y_ij have absolutely continuous distribution functions F_i(y) = F(y−μ_i), which differ at most in their location parameter, μ_i (mean or median). When there is no association between the genotype and the trait, the distributions, F_i, are equal; thus, the null hypothesis is H₀ : μ₀ = μ₁ = μ₂. Under the alternative, it is natural to expect a monotonic trend in the means (medians) against the number of copies of the A allele, that is, H₁ : μ₀ ≤ μ₁ ≤ μ₂ or μ₀ ≥ μ₁ ≥ μ₂ with at least one strict inequality. We note that the alternative H₁ is quite general and includes the commonly assumed genetic models: dominant (μ₀< μ₁ = μ₂), recessive (μ₀ = μ₁< μ₂), or additive (μ₁ = (μ₀ + μ₂)/2) as special cases.

2.2 Parametric Tests of Association

2.2.1 Model-Based Statistics

When Y_ij are normally and independently distributed about the means μ_i, with common, but unknown, variance σ², the most general method for testing the association is the one-way analysis of variance F-test on 2 and N−3 degrees of freedom (df), which compares H₀ to the alternative $H_1:{\mu }_i\ne {\mu }_i^{\prime }$ for some i ≠ i′. If the true mode of inheritance is known, however, a more powerful approach can be developed by viewing the problem as one of linear regression:

$$E[Y_{ij}]={\mu }_i=\alpha +\beta x_i,i=0,1,2,$$

where x_i are the scores assigned to genotypes g_i, and β is the allelic effect. The null and alternative hypotheses can be stated equivalently as H₀ : β = 0 versus H₁ : β ≠ 0, and the test, for a given set of scores, is based on the statistic:

$$T=\frac{\widehat{\beta }}{{\sigma }_{\widehat{\beta }}}=\frac{{\sum }_i{n}_i(x_i-\overline{x})({\overline{y}}_i-\overline{y})}{\sqrt{{\sum }_i{n}_i{(x_i-\overline{x})}^2}\widehat{\sigma }},$$ (1)

where ȳ_i = Σ_jy_ij/n_i, ȳ = Σ_i,jy_ij/Σ_i n_i, x̄ = Σ_i n_ix_i/Σ_in_i, and σ̂ is the within-group standard deviation. Under H₀, T follows a t-distribution with N−2 df, and is approximately standard normal in large samples. Equivalently, the test can be based on the criterion T², which follows an F-distribution with 1 and N−2 df.

The choice of the scores depends on the assumed genetic inheritance model. Intuitively, for a given model, the scores should have the same pattern as the means. In fact, the power of the regression test is a function of the Pearson’s correlation coefficient between the scores x_i and the means μ_i, and is maximized when the correlation is unity (Abelson and Tukey, 1963). Therefore, the optimal scores for the three commonly used models (dominant (DOM), recessive (REC), and additive (ADD)) are: x_DOM = (0, 1, 1), x_REC = (0, 0, 1), and x_ADD = (0, 1, 2). Note that the scores are invariant under linear transformations, i.e., the coding x_ADD = (0, 1/2, 1) is equivalent to x_ADD = (0, 1, 2). Under the dominant (recessive) models, the genotypes g₁ and g₂ (g₀ and g₁) are grouped together, so the regression test reduces to a two-sample t-test. When the scores are specified correctly, the 1-df (regression-based) test is more powerful than the 2-df (ANOVA) F-test.

2.2.2 Correlations and Relative Efficiency of Association Test Statistics

When the true inheritance pattern is unknown and the scores are misspecified, a loss in power can occur. To quantify the magnitude of the loss, we shall consider pairwise asymptotic relative efficiency (ARE) of model-based tests (defined as the limit of the reciprocal of the ratio of sample sizes required by a pair of tests to achieve the same power for the same alternative hypothesis) (Noether, 1955). It is well known that under certain regularity conditions the ARE of a test T₁ compared to a test T₂ when T₂ is optimal, e(T₁, T₂), is equal to the square of the correlation coefficient between their test statistics (van Eeden, 1963). In large samples, the correlation coefficient under H₀ between two statistics of the form (1) with model scores x_i and $x_i^{\prime }$, respectively, is equal to the correlation coefficient between the corresponding scores,

$$r=\frac{{\sum }_i{n}_i(x_i-\overline{x})(x_i^{\prime }-{\overline{x}}^{\prime })}{\sqrt{{\sum }_i{n}_i{(x_i-\overline{x})}^2}\sqrt{{\sum }_i{n}_i{(x_i^{\prime }-{\overline{x}}^{\prime })}^2}},$$ (2)

which for the three genetic models can be shown to be a function of sample sizes only (Appendix A):

$$\begin{array}{lll}\hfill \text{cor}(T_{\mathit{ADD}},T_{\mathit{DOM}})& =\hfill & \frac{n_0(n_1+2n_2)}{\sqrt{n_0(n_1+n_2)(n_0{n}_1+4n_0{n}_2+n_1{n}_2)}},\hfill \\ \hfill \text{cor}(T_{\mathit{ADD}},T_{\mathit{REC}})& =\hfill & \frac{n_2(n_1+2n_0)}{\sqrt{n_2(n_1+n_0)(n_0{n}_1+4n_0{n}_2+n_1{n}_2)}},\hfill \\ \hfill \text{cor}(T_{\mathit{DOM}},T_{\mathit{REC}})& =\hfill & \sqrt{\frac{n_0{n}_2}{(n_0+n_1)(n_1+n_2)}}.\hfill \end{array}$$ (3)

Perhaps, not surprisingly, these correlations are equivalent to those derived by Freidlin et al. (2002) in the context of a logistic regression model (with observed genotype frequencies n_i replaced by their expectations, Np_i). It is instructive to examine the size of these correlations and the relative efficiency of the three tests as a function of allele frequency. For the purposes of demonstration, we shall assume that for each p the genotype counts are in Hardy-Weinberg proportions, i.e., (n₀, n₁, n₂) = N{(1−p)²,2p(1−p), p²}.

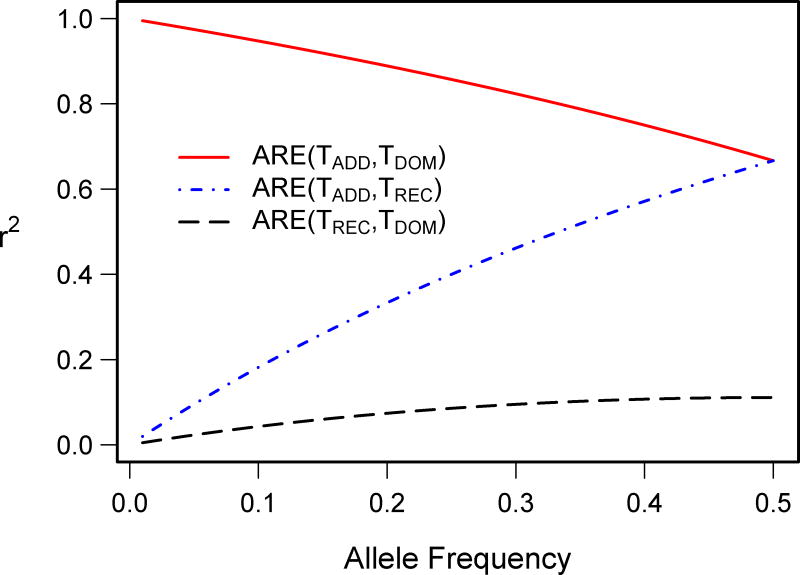
Figure 1 shows pairwise asymptotic relative efficiency of the test statistics for the three genetic models as a function of allele frequency, p. As the figure illustrates, the test statistics for the dominant and additive (DOM, ADD) models are strongly correlated over a wide range of allele frequencies (red solid curve). Hence, assuming an additive model, while the true effect is dominant, will not lead to a great loss in efficiency unless the allele is very common. For example, for p < 0.3, a regression test based on additive scores will be at least 80% as efficient as the test based on dominant scores when the true model is dominant (and vice versa). For very common alleles (p = 0.5), however, a test based on additive scores is only 67% as efficient as the optimal test when the true effect is dominant, meaning that one would need to increase the sample size by about 50% to achieve the same power as with an optimal test. On the other hand, as one can see from the blue dotted curve (ADD, REC), assuming an additive model when a recessive model is true, can lead to a substantial loss of efficiency. For example, the efficiency of a test based on additive scores to detect the recessive effects is at most 67% when p = 0.5 and substantially lower for less common alleles. Finally, examining the black dashed curve (REC, DOM) demonstrates that the efficiency of a test based on recessive scores while the dominant model is true, or vice versa, does not exceed 11%. These results suggest that compared to the common approach of assuming an additive model, we may expect robust tests to be especially useful for detecting the dominant effects of common alleles (p > 0.3) and, in particular, for detecting purely recessive effects at any allele frequency.

Figure 1.

Pairwise asymptotic relative efficiency of association statistics for the three genetic models as a function of allele frequency.

2.2.3 Robust Tests for Genetic Association

Since in most situations the true inheritance pattern is unknown, tests that have good power properties across a wider range of genetic models are needed. Such procedures are in general called efficiency robust (Gastwirth, 1985) and can often be constructed as a combination of the optimal test statistics for a family of plausible models generating the data. Here we briefly review two efficiency robust methods: the maximin efficiency robust test (MERT) and the maximum (MAX3) test (Freidlin et al., 2002).

For a family of M plausible data-generating models, with corresponding optimal (asymptotically most powerful) test statistics, T_k, k = 1,..., M, the test is called maximin efficiency robust (MERT) if it achieves higher minimum efficiency relative to the optimal test for each model in the family than any other test (Gastwirth, 1985; Freidlin et al., 1999). In other words, it maintains higher power than any other test, T_k, when the model is misspecified (within a specified family of M models). Assume that under the null hypothesis each T_k is asymptotically normally distributed - that is, Z_k = [T_k−E(T_k)]/Var^1/2(T_k) converges in law to N(0,1), where E(T_k) and Var(T_k) are the mean and variance of T_k - and that the set of statistics {Z_k} is asymptotically jointly normally distributed with an asymptotic correlation matrix {ρ_kl}, ρ_kl ≥ 0. The MERT can often be obtained as a linear combination of the tests for the two most divergent models in the family, i.e., models with the least correlation coefficient between their optimal test statistics, ρ^* = inf_k,l ρ_kl.

For the family of three genetic models (M = 3) with regression statistics {T_ADD, T_DOM, T_REC}, which are jointly asymptotically normally distributed with the null correlations given in (3), the dominant and recessive models are the most extreme pair, i.e., ρ^* = cor(T_DOM, T_REC) (Freidlin et al. 2002), and the MERT is given by:

$$Z_{\mathit{MERT}}=\frac{T_{\mathit{DOM}}+T_{\mathit{REC}}}{\sqrt{2(1+\text{cor}(T_{\mathit{DOM}},T_{\mathit{REC}}))}}.$$ (4)

A necessary and sufficient condition that Z_MERT is also the MERT for the entire family of models is that

$$1+\text{cor}(T_{\mathit{DOM}},T_{\mathit{REC}})\le \text{cor}(T_{\mathit{ADD}},T_{\mathit{DOM}})+\text{cor}(T_{\mathit{ADD}},T_{\mathit{REC}}).$$

This condition is satisfied for the family of genetic models (Freidlin et al. 2002). Since Z_MERT is a linear combination of two asymptotically normal statistics, it is asymptotically normally distributed with mean 0 and variance 1, and achieves maximin efficiency (1 +cor(T_DOM, T_REC))/2.

Perhaps a more intuitive approach is to calculate the test statistics for all three models and to use the maximum of three standardized statistics, Z_MAX = max{|Z_ADD|, |Z_DOM|, |Z_REC|}, as a test criterion. Since the direction of the association is not known a priori, the maximum is taken over the absolute values of the model-based statistics. The significance probabilities of the MAX3 statistic can be obtained by noting that

$$\begin{array}{l}Pr(Z_{\mathit{MAX}}>z)=1-Pr(\mid Z_{\mathit{ADD}}\mid \le z,\mid Z_{\mathit{DOM}}\mid \le z,\mid Z_{\mathit{REC}}\mid \le z)\\ =1-{\int }_{-z}^z{\int }_{-z}^z{\int }_{-z}^z\varphi (\mathbf{z};\mathbf{0},\mathrm{\sum })d\mathbf{z}\end{array}$$

where ϕ is a trivariate normal density with mean 0 and covariance matrix Σ. The integral can be evaluated numerically using computer routines for multivariate normal distribution implemented in mvtnorm package in R.

Since the maximum test relies on numerical integration, it is more computationally burdensome than the simpler MERT, however is often more powerful. Gastwirth (1985) noted that the relative performance of MERT depends on the correlation between the extreme pair of statistics, ρ^*, through its maximin efficiency (1 + ρ^*)/2. When the minimum correlation coefficient is low, MERT may perform poorly relative to other tests. Freidlin et al. (1999) showed that when ρ^*< 0.6, the MAX3 test is more powerful than MERT, but when ρ^*> 0.7 the two tests performed equivalently. Assuming Hardy-Weinberg equilibrium holds, and setting the observed genotype counts to their expectations,

$${\rho }^{\ast }=\text{cor}(T_{\mathit{DOM}},T_{\mathit{REC}})=\sqrt{\frac{n_0{n}_2}{(n_1+n_2)(n_1+n_0)}}=\sqrt{\frac{p(1-p)}{(2-p)(1+p)}}.$$

The quantity on the right-hand side is monotonically increasing in p on the interval (0,0.5], with a max_p ρ^* = ρ^* (0.5) = 0.33 (Figure 1). Even if HWE does not hold, however, one can show that as long as n₁ ≥ min{n₀, n₂} - that is, when there is no deficiency of heterozygotes - ρ^* will not exceed 0.7. Consequently, for the family of three genetic models, the MAX3 test should always be preferable to MERT, and we focus on the MAX3 approach in the remainder of the paper.

2.3 Distribution-Free Tests for Genetic Association

When the within-genotype distribution of the quantitative trait is non-normal, tests that do not assume normality can often achieve higher power than normal theory tests, while preserving the nominal type I error rate. Here, we review the available nonparametric procedures for testing the equality of k location parameters and then apply the principles of the previous section to develop a robust rank-based approach to quantitative trait association.

2.3.1 Jonckheere-Terpstra and Modified Jonckheere-Terpstra Tests for Trend

As in the case of normal data, the most general method for testing the equality of k means, is the rank-based analogue of the one-way analysis of variance, the Kruskal-Wallis (KW) test. A more powerful procedure can be obtained, though, when the ordering of the means is known. Perhaps the most well-known procedure for testing a monotonic trend in k means, is the distribution-free test proposed independently by Jonckheere (1954) and Terpstra (1952). The Jonckheere-Terpstra (JT) test criterion is the sum of the k(k−1)/2 pairwise Mann-Whitney U-statistics computed among the k samples,

$$J=\sum _{i=1}^{k-1}\sum _{j=i+1}^k{W}_{ij},$$ (5)

where

$$\begin{array}{c}{W}_{ij}=\sum _{r=1}^{n_i}\sum _{s=1}^{n_j}\varphi (Y_{ir},Y_{js})\\ \text{with}\varphi (Y_{ir},Y_{js})=\{\begin{array}{lll}1,\hfill & \text{if}{Y}_{ir}<Y_{js}\hfill & \hfill \\ 0,\hfill & \text{otherwise}\hfill & (i<j).\hfill \end{array}\end{array}$$

Neuhäuser et al. (1998) proposed a modification of the JT test (MJT), in which the pairwise comparisons were weighted by the “distance” between the two samples,

$$J^{\ast }=\sum _{i=1}^{k-1}\sum _{j=i+1}^k(j-i)W_{ij}.$$ (6)

The two methods perform similarly in large samples, but the modified test was shown to be more powerful than the original test in small samples and somewhat more sensitive to linear trends. Therefore, we shall use the modified test for testing the additive genetic effects.

The mean and variance of the modified statistic under the null hypothesis can be found from the moments of the corresponding two-sample Mann-Whitney counts (Appendix B). In the case of k = 3 samples, these take an especially simple form:

$$\begin{array}{c}\mathrm{E}(J^{\ast })=\frac{(n_0{n}_1+2n_0{n}_2+n_1{n}_2)}{2},\\ \text{Var}(J^{\ast })=\frac{(n_0{n}_1+4n_0{n}_2+n_1{n}_2)(N+1)}{12}.\end{array}$$

The significance probabilities of the modified test can be determined from the exact permutation distribution of the test statistic when the sample size is small. In large samples, J^* is approximately normally distributed, and the significance probabilities can be obtained by comparing Z_J* = [J^*−E(J^*)]/Var^1/2(J^*) to the standard normal distribution. To be more precise, a sufficient condition for the asymptotic normality of J (and hence J^*) is that at least two groups increase without limit as N → ∞ (Jonckheere, 1954). If, on the other hand, only one n_i tends to infinity as the total sample size increases, the limiting distribution of J will be platykurtic, and the procedure based on the normal approximation will tend to be conservative. For the case of three genotype classes in HWE, therefore, the asymptotic normality of the test should hold even for rare alleles, when the number of rare allele homozygotes is small (n₂≪ n₀).

2.3.2 Fligner-Wolfe Test for Simple Tree Alternatives

For comparing k treatments with a control, Fligner and Wolfe (1982) proposed a procedure that tests H₀ against a partially ordered (simple tree) alternative $H_1^{\prime }:{\mu }_0\le [{\mu }_1,\dots ,{\mu }_k]$. Their test criterion is a sum of k pairwise Mann-Whitney statistics comparing the control (i = 0) group to k treatment groups,

$$FW=\sum _{i=1}^k{W}_{0i}=W_{0(1,\dots ,k)}.$$ (7)

Note that FW is equivalent to a single Mann-Whitney-Wilcoxon test between the control group and the pooled data from k treatment groups. The Fligner and Wolfe test was shown to be more efficient than the linear trend tests for detecting concave and umbrella patterns, therefore it can be used for testing the association under dominant and recessive models, that is, FW_DOM = W₀₁ + W₀₂ = W_0(1,2) and FW_REC = W₀₂ + W₁₂ = W_(0,1)2. Under the null hypothesis, Z_FW = [FW − E(FW)]/Var^1/2(FW) is asymptotically normally distributed, with the mean and variance determined in the same way as for the corresponding Wilcoxon rank-sum test (see Appendix B).

2.3.3 Robust Rank-Based Tests for Quantitative Trait Association

Since all three statistics considered above are based on sums of pairwise Mann-Whitney counts, they are asymptotically normally distributed. Their correlations under the null hypothesis can be determined from the moments of the Mann-Whitney U-statistics. As shown in Appendix C, these correlations turn out to be exactly the same as those given in (3). Hence, provided all three sample sizes are sufficiently large, the results from the previous sections apply and we can obtain a distribution-free maximum (MAX3) test for quantitative trait association by using the maximum of the standardized rank ​tests {|Z_J*|, |Z_WDOM|, |Z_WREC|}.

2.3.4 Association Tests Based on Inverse Normal Transformation

As Beasley et al. (2009) finally concluded, one should thoroughly investigate the properties of parametric tests based on the inverse normal transformation in the context of genetic studies. This approach entails first transforming trait values (possibly adjusted for covariates) to ranks and then transforming the ranks to quantiles of a standard normal distribution using the formula:

$$Y_{ij}^{\prime }={\mathrm{\Phi }}^{-1}\left(\frac{r_{ij}-c}{N+1-2c}\right),$$ (8)

where r_ij is the rank of Y_ij among all N observations, Φ⁻¹ denotes the inverse of the cumulative distribution function of a standard normal variable, and c is an offset needed to avoid having the maximum observation transformed to infinity. Some commonly used values are c = 1/2, c = 3/8 (Blom, 1958) and c = 0 (van der Waerden, 1952); but a particular choice of c has little effect on the resulting scores for sufficiently large N, and is therefore unlikely to impact the final result. A value of c = 1/2 was used in the current study, and the transformed data $Y_{ij}^{\prime }$ were subsequently analyzed using parametric association tests of Section 2.2.

3 Simulation Experiment

We performed a simulation study to investigate the behavior of the usual parametric tests and their nonparametric counterparts based on ranks and the inverse normal transformation in the context of genetic association studies. Data were generated using the following model:

$$y_{ij}={\mu }_i+{\epsilon }_{ij},$$

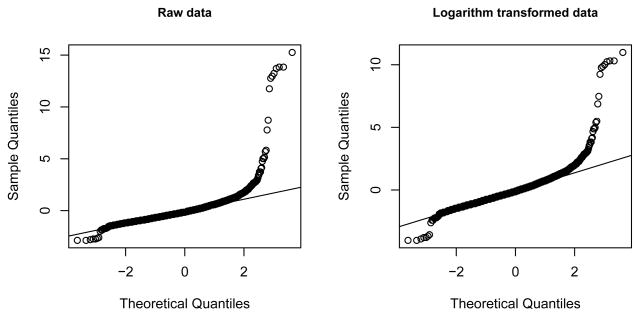
where μ_i is the mean trait value for genotype i and ε_ij, i = 0, 1, 2, j = 1,..., n_i are independently and identically distributed errors. The error term was sampled from the following distributions: (i) normal with mean 0 and variance 1; (ii) log-normal (μ = 0, σ = 1) as an example of a positively skewed distribution; (iii) Cauchy (median = 0, scale = 1) as an extreme example of a distribution with heavy tails; and (iv) empirical distribution of symmetric dimethylarginine (SDMA) - a marker of renal function measured in the Dallas Heart Study, a population-based cohort from Dallas, TX (see next section). The latter is a typical example of a quantitative trait that shows severe departures from normality and cannot be easily transformed to an approximate normal distribution by applying a simple transformation, such as a logarithm transformation (Figure 2). The characteristics of these distributions are summarized in Table 1. We generated the data under the null hypothesis, μ = (0,0,0), and under several alternatives: μ_ADD = (0, 0.5, 1)δ, μ_DOM = (0, 1, 1)δ, and μ_REC = (0, 0, 1) δ, corresponding to the additive, dominant, and recessive models, respectively. We also considered an “umbrella” alternative, μ_UMB = (0, 1, 0) δ. Such non-monotonic alternatives are not generally considered a plausible mode of association in studies of human disease traits, but could arise by chance in a GWAS. Thus a good association test should have high power under monotonic alternatives and low power under a non-monotonic alternative. The effect size, δ, and the parameters of the error-generating distributions were selected empirically to result in power estimates that were bound away from 100% because the differences in the behavior of different tests are more apparent when the power is moderate rather than close to 100%. We used a total sample of N = 2000, and generated individual genotype counts under the assumption of HWE for p = 0.03, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5. As explained above, the assumption of HWE is not required for our tests, but is used in our simulations to mimic the expected sample size proportions in a population-based genetic study. For large samples sizes (N > 200) fixing genotype counts at their expectation has a negligible effect on power estimates (Kozlitina et al., 2010). All tests were 2-sided with a nominal significance level of 0.05. Simulations were performed in R version 3.0.2 (http://cran.r-project.org) and included 100,000 replications. Empirical type-I error rates and power were estimated as the proportion of times a test rejected H₀ at α = 0.05.

Figure 2.

Normal quantile-quantile plots of symmetric dimethylarginine (SDMA) levels in the Dallas Heart Study. Left panel shows the distribution of the raw data; right panel shows the distribution of the data after a logarithm transformation. Both distributions were standardized to have mean 0 and variance of 1.

Table 1.

Distributions used for the error term in the simulation study

Distribution	Standard deviation	Skewness	Kurtosis
Normal	1	0	0
Log-normal	2.2	6.2	110.9
Cauchya	-	-	-
Empirical SDMA distributionb	1	6.4	78.3

^aThe variance and higher moments do not exist.

^bDistribution was standardized to have a mean 0 and variance 1.

The observed type I error rates of the proposed tests at the nominal α = 0.05 significance level are summarized in Table 2. We note that with 100,000 replications, the standard error of the estimates is 0.069%. As one might expect, all tests remained valid (that is, the true type I error rate did not exceed the nominal level of α = 0.05) under the normal error distribution.

Table 2.

Empirical type I error rates (%) of the normal theory and distribution-free tests at the nominal α = 5% significance level.

Error distribution	p	Test	Tested Model
			2 df	ADD	DOM	REC	MAX3
Normal	0.05	F-test (Y)	4.97	5.04	5.03	4.91	4.99
		Rank	4.69	5.00	5.00	4.70	4.62
		F-test (INT)	4.93	5.04	5.03	4.93	4.99
	0.1	F-test (Y)	5.10	4.95	5.02	4.99	5.04
		Rank	5.03	4.98	5.03	4.94	4.96
		F-test (INT)	5.10	4.94	5.03	4.98	5.03
	0.5	F-test (Y)	5.07	5.05	5.06	5.02	5.09
		Rank	5.09	5.05	5.06	5.03	5.09
		F-test (INT)	5.06	5.06	5.08	5.02	5.11
Log-normal	0.05	F-test (Y)	5.42	4.91	4.93	4.53	5.60
		Rank	4.84	5.01	5.06	4.77	4.68
		F-test (INT)	5.05	5.04	5.04	5.01	5.07
	0.1	F-test (Y)	5.12	5.04	5.02	4.69	5.18
		Rank	4.94	4.93	4.99	4.97	4.96
		F-test (INT)	5.08	4.98	4.98	5.05	5.11
	0.5	F-test (Y)	4.96	4.98	5.04	4.97	4.99
		Rank	5.07	5.03	5.03	4.96	5.06
		F-test (INT)	5.16	4.97	5.03	4.98	5.05
Cauchy	0.05	F-test (Y)	6.92	8.21	8.38	1.63	7.78
		Rank	4.74	5.00	4.95	4.77	4.67
		F-test (INT)	5.03	5.02	5.00	4.96	5.01
	0.1	F-test (Y)	4.43	5.22	7.69	3.18	5.06
		Rank	4.89	4.91	4.97	4.91	4.88
		F-test (INT)	4.93	4.95	4.97	4.98	4.95
	0.5	F-test (Y)	2.41	3.37	4.12	4.06	3.23
		Rank	5.04	5.00	5.15	4.90	5.08
		F-test (INT)	5.10	5.03	5.15	4.98	5.12
Empirical SDMA distribution	0.05	F-test (Y)	4.24	4.77	4.80	2.87	4.58
		Rank	4.71	4.93	4.90	4.72	4.61
		F-test (INT)	4.99	4.90	4.93	4.97	4.97
	0.1	F-test (Y)	6.16	4.91	4.94	5.27	6.38
		Rank	4.83	4.92	4.88	4.93	4.83
		F-test (INT)	4.91	4.93	4.95	4.92	4.92
	0.5	F-test (Y)	4.83	5.06	4.83	5.04	4.89
		Rank	4.97	5.05	4.96	5.08	5.09
		F-test (INT)	5.01	5.12	5.03	5.09	5.11

Note: The estimates are based on 100,000 replications. Standard error (SE) = 0.069%. Bolded entries indicate empirical type I error rates that are significantly greater than the nominal α level at the 95% confidence level. Italicized numbers indicate empirical type I error rates that are significantly smaller than the nominal α level at the 95% confidence level. The expected sample sizes under p = 0.05, 0.1, and 0.5, are (n₀, n₁, n₂) = (1805, 190, 5), (1620, 360, 20), and (500, 1000, 500), respectively.

In contrast, when the parent distribution was non-normal, the significance level of the usual parametric tests could be either inflated or deflated, and the differences appeared to be greatest in the case of heavy-tailed distributions, such as Cauchy and empirical SDMA distribution, as well as for low allele frequencies. For the lowest allele frequency setting (p = 0.05), some rank tests (Kruskal-Wallis, Mann-Witney-Wilcoxon for the recessive model, and rank-based MAX3) tended to have a smaller actual significance level than the nominal value of 0.05, as the saymptotic approximation to the distribution of the test statistic may not be very accurate when one of the samples is small (n₂ = 5). While such a conservative procedure maintains its validity, it may also be less powerful than other tests. Remarkably, tests based on INT seemed to maintain their nominal significance level in all situations: of the 60 estimates presented in Table 2, only 2 fell outside the approximate 95% two-sided confidence interval, which is in agreement with what would be expected by chance.

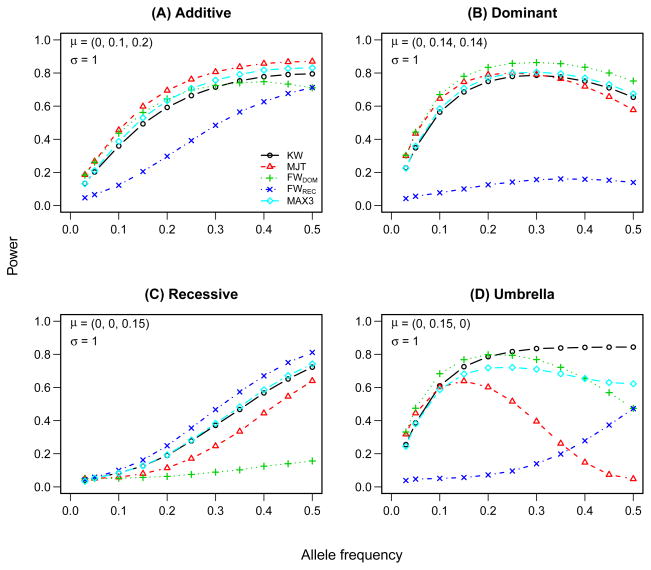
Figure 3 illustrates the empirical power of the model-based and model-free rank tests under different genetic models. (The results for parametric tests and tests based on the inverse normal transformation are similar and are provided in Supplementary tables.) One should bear in mind that a Monte-Carlo simulation with 100,000 replications implies that the maximum standard error of each power estimate is 0.16%. As we would expect, for each genetic model, a test designed for that model achieves the highest power. A test designed for an additive model (MJT) has relatively high power to detect dominant effects for low to medium-frequency alleles (p < 0.3), but can perform poorly for more common alleles. On the other hand, when the true model is recessive, a test assuming an additive model has very low efficiency relative to robust tests (MAX3 and KW), unless the allele frequency is close to 0.5. The robust MAX3 test has intermediate performance between the model-free test (KW) and model-specific tests (MJT, FW_DOM, and FW_REC). At the same time, MAX3 has substantially lower power than the general 2 df test (KW) under a non-monotonic (umbrella) alternative.

Figure 3.

Power of rank-based association tests under normal error distribution and different genetic models. The parameters of data generating model are shown in the upper left corner. KW - Kruskal-Wallis test; MJT - modified Jonckheere-Terpstra test; FW - Fligner-Wolfe test for the dominant (DOM) and recessive (REC) models; MAX3 - rank-based maximum test.

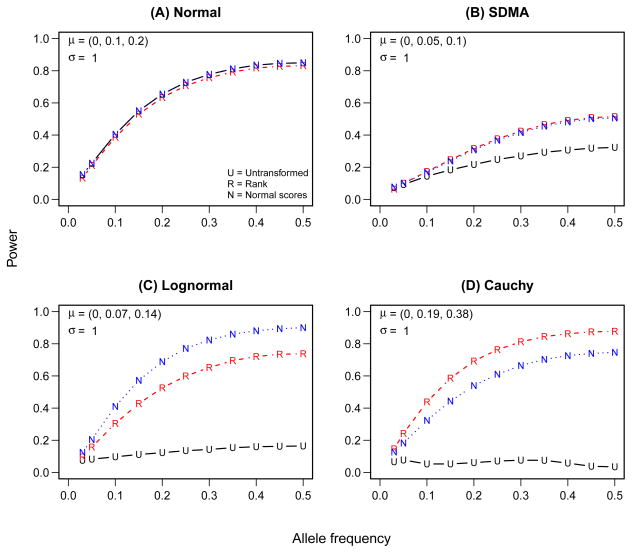
Finally, Figure 4 displays the power of the MAX3 test based on untransformed data (U), usual ranks (R), and a rank-based inverse-normal transformation (N) under different error distributions. We focus here on the performance of the MAX3 test because it was shown to have relatively high power regardless of the genetic model. The results for model-based and 2 df tests are similar (see Supplementary table 2). Not surprisingly, MAX3 based on the usual parametric F-tests and on the inverse normal transformation (normal scores) have almost identical power, when the error distribution is normal (Figure 4A). Notably, rank-based MAX3 is only slightly less powerful than the parametric MAX3 under normality - a consequence of the well-known asymptotic performance results for the Mann-Whitney-Wilcoxon test relative to the two-samlpe t-test (Lehmann, 1975). Under empirical SDMA distribution, both nonparametric approaches (based on ranks and the normal scores) have higher power than parametric MAX3. The performance of tests based on ranks and INT is almost indistinguishable, with the rank test having a slight advantage over the normal scores test (see Supplementary table 2 for numerical estimates).

Figure 4.

Power of the maximum (MAX3) test under the additive genetic model and different error distributions. The alternative hypotheses are indicated in the upper left corner of each panel.

Nonparametric tests exhibit an even larger increase in power over the normal theory test under the two distributions with the greatest departures from normality, the log-normal and the Cauchy. The test based on INT is preferable to the rank test under the log-normal distribution (which is positively skewed and has zero density for observations less than zero), while the rank test is more efficient under Cauchy distribution (which has extremely heavy tails and gross errors). These observations are consistent with the theoretical result of Hodges and Lehmann (1960).

4 Application to an Association Study of Symmetrical Dimethylarginine (SDMA)

To illustrate the utility of the proposed method we applied the tests discussed in this paper to an association study of SDMA levels in African American participants of the Dallas Heart Study (DHS) - a multiethnic population-based sample of Dallas County (Victor et al., 2004). Symmetrical dimethylarginine is a marker of renal function and has been shown to be an independent risk factor for adverse cardiovascular events (Bode-Böger et al., 2006; Wang et al., 2009). We focus on African Americans in this paper - the largest ethnic group represented in the DHS that has the highest prevalence of both chronic kidney and cardiovascular disease. Genotypes for more than 9000 SNPs across the genome and plasma levels of SDMA were obtained for 1,760 African American subjects. After removing SNPs that were monomorphic in the study population, a total of 8,994 SNPs were tested for association with SDMA, including 7,141 SNPs for which all three genotypes were observed. We used age and gender adjusted SDMA levels as a quantitative trait. Even after applying a logarithm or a Box-Cox transformation (Box and Cox, 1964), the residual SDMA distribution had longer tails and showed other deviations from normality (Figure 2). The analysis was performed using 4 different approaches: (1) raw (i.e., untransformed) trait values were adjusted for gender and age and the residuals tested for association with SNPs using parametric tests; (2) trait values were adjusted for gender and age after first applying a Box-Cox transformation (λ = 0.1) and the residuals were analyzed using parametric association tests; (3) the residuals from (2) were further transformed using an inverse normal transformation before applying parametric association tests; (4) the residuals from (2) were analyzed using rank tests.

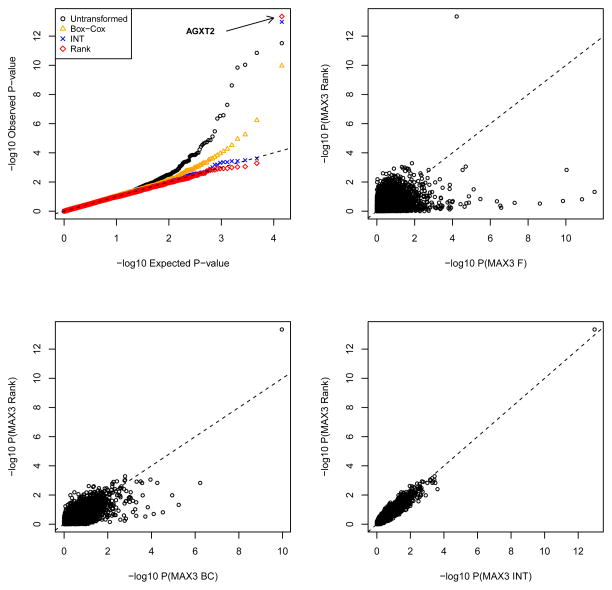
Figure 5 summarizes the p-values from the association analysis using rank-based MAX3 test and parametric MAX3 applied to residual SDMA values after no transformation (untransformed), Box-Cox transformation and an inverse-normal transformation. The strongest association with SDMA was observed for a SNP in the gene AGXT2 (rs37369), recently shown to be associated with SDMA in a genome-wide association study of the methylarginine traits that included 5,110 individuals of European descent (Seppälä et al., 2014). Notably, this SNP was not ranked as the top association by the usual parametric analysis applied to raw data, as illustrated in the top right panel of Figure 5. Although the remaining three methods identified this SNP at a genome-wide significance level (p < 10 ⁻⁸), the p-values for the two nonparametric tests (MAX3 Rank and MAX3 INT) were several orders of magnitude lower than the p-value for the MAX3 test based on Box-Cox transformed data. Finally, MAX3 based on ranks was slightly more significant than the test based on INT (Figure 5 and Table 3).

Figure 5.

Summary of significance results from association analysis of symmetric dimethylarginine (SDMA) levels in the Dallas Heart Study. Top left panel: quantile-quantile plot of -log10 p-values. The strongest association result refers to the rs37369 SNP in AGXT2. Top right - bottom right panels: scatters plot of p-values for the MAX3 test based on ranks against parametric MAX3 applied to raw data (MAX3 F, top right), to Box-Cox transformed data (bottom left, MAX3 BC), and to inverse-normal transformed data (bottom right, MAX3 INT).

Table 3.

Comparison of significance levels for AGXT2 rs37369 by the examined tests

Test	Tested Model
	ADD	DOM	REC	MAX3
F-test (Y)	2.1 × 10−5	5.7 × 10−4	4.4 × 10−4	5.9 × 10−5
F-test (Box-Cox)	7.6 × 10−11	1.5 × 10−7	7.2 × 10−8	1.1 × 10−10
F-test (INT)	9.2 × 10−14	2.6 × 10−9	5.3 × 10−10	1.1 × 10−13
Rank	2.0 × 10−14	1.1 × 10−9	1.4 × 10−10	4.5 × 10−14

Bold face indicates the most significant result across all tests. Italicized P-values do not meet the Bonferroni-corrected significance threshold based on the number of tests performed.

At the same time, parametric MAX3 test applied to raw data - and to a lesser degree Box-Cox transformed data - produced several other results with p < 0.0001 that did not reach the same level of significance using nonparametric methods (Figure 5). Table 4 reports the proportion of tests reaching the nominal significance levels of 0.01 and 0.05, and demonstrates that parametric tests applied to raw and Box-Cox transformed data (especially the test optimal for the recessive model and MAX3) generated an excess of p-values below these levels of significance compared to what would be expected under the complete null hypothesis. Given that most SNPs tested in a genetic association study are expected to have no effect on the trait, these results likely represent false positive associations. A closer inspection of the data revealed that most of the SNPs with discordant p-values for the parametric and rank-based MAX3 tests were low-frequency alleles (p < 0.05) with the smallest p-value under a recessive model (data not shown). When the number of variant allele homozygotes is small (n₂< 5) and the assumption of normally distributed residuals is violated, asymptotic results may not apply and the F-test comparing the means may be sensitive to the effect of outliers. Nonparametric tests are robust to outliers and produce more conservative results in this situation.

Table 4.

Proportions (%) of tests that meet specified significance levels

α	Test	Tested Model
		ADD	DOM	REC	MAX3
0.01	F-test (Y)	1.12	0.92	2.30	1.92
	F-test (Box-Cox)	1.05	0.92	1.39	1.22
	F-test (INT)	0.92	0.85	1.08	0.94
	Rank	0.98	0.97	1.01	0.91
0.05	F-test (Y)	5.10	4.97	5.48	5.88
	F-test (Box-Cox)	5.43	5.13	5.42	5.55
	F-test (INT)	4.83	4.89	5.15	4.89
	Rank	4.79	4.69	5.10	4.57

Bolded entries indicate proportions that are significantly greater than expected under the complete null hypothesis at the 95% confidence level.

5 Discussion

In this paper we have described a robust distribution-free method for quantitative trait association. The proposed method uses the maximum of three rank tests (MAX3) optimal for different genetic models as its test criterion and adjusts the significance level to account for the correlation among the corresponding tests. We find that the rank-based MAX3 test maintains good power and validity (correct type I error rate) across a wide range of distributions and genetic models. Specifically, the test is only slightly less powerful than its parametric counterpart when the data are normally distributed, but is far superior to the parametric test when there are outliers or other deviations from normality. The proposed method is computationally efficient and is easy to implement. Therefore, it can serve as a fast screening tool for large-scale (e.g., genome-wide) association studies of complex traits with non-normal distributions.

The method described here is based on the principles of efficiency robustness, used by Freidlin et al. (2002) to develop robust tests for case-control studies. By showing that the null correlations among rank tests optimal for different genetic models are identical to those derived for binary and normal data, we were able to apply the results from previous studies to develop a robust test for quantitative traits with non-normal distributions. In addition, we have examined the null correlations among test statistics optimal for different genetic models as a function of minor allele frequency and quantified the loss of efficiency due to model misspecification. Although previous studies provided some examples of the relative performance of different tests under selected allele frequencies, our analysis generalizes these results and provides an additional insight about the behavior of robust and model-based tests. Both our simulations and analytical results (Figure 1) suggest that, compared to the conventional approach of using an additive model, robust tests offer the greatest gain in power for detecting dominant effects of common alleles (p > 0.3) and recessive effects at any allele frequency.

Many traits examined in genetic studies have distinctly non-normal distributions. Consequently, the assumption of normally distributed residuals is often violated and standard statistical tests that rely on normal theory may not maintain any good properties. The most common approach to deal with non-normal data is to perform a transformation, such as a logarithm transformation, prior to analysis to achieve more normally distributed residuals. Many genetic studies have used this approach, however few report whether the assumption of normally distributed residuals is satisfied after the transformation. Here we show that even a modest residual departure from normality can lead to reduced power and an inflated type I error rate, especially for low-frequency alleles. The MAX3 approach described in this paper is based on ranks and is not sensitive to outliers or other departures from normality. The method could be especially useful for large-scale association studies that look at multiple traits, such as eQTL mapping or metabolomic studies (Illig et al. 2010; Suhre et al., 2011). In such situations, it may be difficult to assess the distribution of each trait and find a suitable transformation, therefore tests that do not rely on a particular shape of a distribution are desirable.

An alternative approach to analyze non-normal traits, that has recently gained acceptance in genetic research, is to perform an inverse normal transformation of the data before applying standard parametric tests of association (Scuteri et al., 2007; O’Donnell et al., 2011; Kettunen et al., 2012; Seppälä et al., 2014). This approach ensures that the data resemble the normal distribution as closely as possible, and has the desirable property of being at least as efficient as the normal theory tests (ARE ≥ 1) for all distributions (Chernoff and Savage, 1958). Despite the widespread use of INTs and their desirable theoretical properties, no large simulation study has investigated the performance of parametric tests based on the INT in the context of genetic studies, as Beasley et al. (2009) point out. Here we have examined the performance of the tests based on INT relative to the usual parametric tests and rank tests using a simulation study with different distributions, genetic models, and minor allele frequencies. We demonstrate that the method maintains its favorable properties in a variety of situations and therefore presents an attractive alternative for quantitative trait association. One additional advantage of the method is that existing software packages, such as PLINK (Purcell et al., 2007), can be readily applied to calculate model-based statistics once the transformation of the data has been performed. Relative to the rank tests, the method may have an advantage when the underlying distribution is skewed or has a density that drops discontinuously to zero at one extreme, such as the log-normal or exponential distribution (Hodges and Lehmann, 1960). On the other hand, rank tests may be preferable in the case of approximately symmetric heavy-tailed distributions, with outliers at both extremes of the distribution.

Instead of taking a maximum over three specified genetic models, a more general approach is to maximize the trend test over all possible monotonic alternatives consistent with a genotype-trait relationship. Wang and Sheffield (2005) considered such an approach and developed a constrained likelihood ratio test (CLRT) under non-overdominance constraint. They mentioned that CLRT could be viewed as a two-sided version of a test for order-restricted alternatives (Barlow et al., 1972). A rank-based analogue of the order-restricted test has been described in statistical literature (Chacko, 1963; Shorack, 1964) and could be applied to genetic association studies. Based on the results of Wang and Sheffield (2005) and Zheng and Chen (2005), however, we expect that CLRT and MAX3 would have similar performance. At the same time, MAX3 is conceptually simpler and does not require special software to implement. Therefore, we focus on the maximum of three rank-based association tests in the current study.

GWAS have successfully identified hundreds of loci that contribute to common disease traits, yet all of the variants discovered to date explain only a small proportion of interindividual variation in these traits (Maher, 2008; Manolio et al., 2009). The remaining “missing heritability” has been attributed in part to the effects of rare genetic variants that were not screened by the typical GWAS. Yet, it is also possible that genetic variants with non-additive effects account for part of the unexplained variability. While there are a few examples of studies that have used a robust combination approach similar to the one described in this paper (WTCCC, 2007; Sladek et al., 2007), the vast majority of GWAS rely on the conventional approach or testing the association under an additive genetic model, and thus could miss variants with non-additive effects. Adopting robust association tests as part of the routine analysis of GWAS could help uncover additional variants that influence complex traits non-additively.

Another possible explanation for missing heritability lies in the existence of genetic interactions (epistasis) among loci (Maher, 2008; Manolio et al., 2009; Zuk et al., 2012). One limitation of the rank tests described in this paper is that they are restricted to a one-way layout and do not lend themselves to multi-locus analysis. However, generalizations of rank tests for multi-way layouts have been developed in statistical literature (for example, in Akritas et al., 1997) and these could potentially be used to extend the present methods to multi-locus analysis allowing for gene-gene interactions. At the same time, we note that tests based on normal scores (INTs) rely on standard parametric models, and could, therefore, be incorporated into existing methods (reviewed in Cordell, 2009) to investigate the role of gene-gene interactions, after the initial GWAS analysis has been performed. This question deserves further investigation.

In summary, we have described a robust method for quantitative trait association that is not affected by deviations from both an assumed genetic model and an assumed distribution. The proposed method could be a useful screening tool for large-scale association studies when neither the inheritance mode, nor the distribution of the trait is known in advance.

Appendix A

We note that the unstandardized association statistics are in the form $T={\sum }_{i=0}^2{n}_i{c}_i{\overline{y}}_i$, where c_i = (x_i−x̄), ${\sum }_{i=0}^2{n}_i{c}_i=0$, are known constants. Hence, under H₀, E(T) = 0, Var(T) = σ² Σ_i n_i(x_i−x̄)², and $\text{Cov}(T,T^{\prime })={\sigma }^2{\sum }_i{n}_i(x_i-\overline{x})(x_i^{\prime }-{\overline{x}}^{\prime })$. Therefore, the correlation coefficient under H₀ of two test statistics with scores x_i and $x_i^{\prime }$ is given by (2). Further, since ${\hat{\sigma }}^2$ is a consistent estimator of σ², the correlation coefficient between two regression statistics of the form (1) is asymptotically equivalent to (2). For the three test statistics based on scores x_ADD = (0, 1, 2), x_DOM = (0, 1, 1), and x_REC = (0, 0, 1), the correlation coefficients are derived as follows.

$${\overline{x}}_{\mathit{ADD}}=\frac{n_1+2n_2}{N};{\overline{x}}_{\mathit{DOM}}=\frac{n_1+n_2}{N};{\overline{x}}_{\mathit{REC}}=\frac{n_2}{N}.$$

Using the shortcut formulas for the variance, $\text{Var}(T)={\sigma }^2({\sum }_i{n}_i{x}_i^2-N{\overline{x}}^2)$, and covariance, $\text{Cov}(T,T^{\prime })={\sigma }^2({\sum }_i{n}_i{x}_i{x}_i^{\prime }-N\overline{x}{\overline{x}}^{\prime })$, we calculate:

$$\begin{array}{lll}\text{Var}(T_{\mathit{ADD}})\hfill & =\hfill & {\sigma }^2\left[n_1·1^2+n_2·2^2-N{\left(\frac{n_1+2n_2}{N}\right)}^2\right]={\sigma }^2\left[n_1+4n_2-\frac{{(n_1+2n_2)}^2}{N}\right]=\hfill \\ \hfill & =\hfill & \frac{{\sigma }^2}{N}\left[n_1(N-n_1)+4n_2(N-n_1-n_2)\right]=\frac{(n_0{n}_1+n_1{n}_2+4n_0{n}_2){\sigma }^2}{N},\hfill \\ \text{Var}(T_{\mathit{DOM}})\hfill & =\hfill & {\sigma }^2\left[(n_1+n_2)·1^2-N{\left(\frac{n_1+n_2}{N}\right)}^2\right]={\sigma }^2(n_1+n_2)\left(1-\frac{n_1+n_2}{N}\right)=\hfill \\ \hfill & =\hfill & \frac{n_0(n_1+n_2){\sigma }^2}{N},\hfill \\ \text{Var}(T_{\mathit{REC}})\hfill & =\hfill & {\sigma }^2\left[n_2·1^2-N{\left(\frac{n_2}{N}\right)}^2\right]={\sigma }^2(n_2)\left(1-\frac{n_2}{N}\right)=\frac{n_2(n_0+n_1){\sigma }^2}{N},\hfill \end{array}$$

and

$$\begin{array}{lll}\text{Cov}(T_{\mathit{ADD}},T_{\mathit{DOM}})\hfill & =\hfill & {\sigma }^2\left[n_0·0·0+n_1·1·1+n_2·1·2-N\left(\frac{n_1+2n_2}{N}\right)\left(\frac{n_1+n_2}{N}\right)\right]=\hfill \\ \hfill & =\hfill & {\sigma }^2(n_1+2n_2)\left(1-\frac{n_1+n_2}{N}\right)=\frac{n_0(n_1+2n_2){\sigma }^2}{N},\hfill \\ \text{Cov}(T_{\mathit{ADD}},T_{\mathit{REC}})\hfill & =\hfill & {\sigma }^2\left[n_0·0·0+n_1·1·0+n_2·2·1-N\left(\frac{n_1+2n_2}{N}\right)\left(\frac{n_2}{N}\right)\right]=\hfill \\ \hfill & =\hfill & {\sigma }^2(n_2)\left(2-\frac{n_1+2n_2}{N}\right)=\frac{n_2(n_1+2n_0){\sigma }^2}{N},\hfill \\ \text{Cov}(T_{\mathit{DOM}},T_{\mathit{REC}})\hfill & =\hfill & {\sigma }^2\left[n_0·0·0+n_1·1·0+n_2·1·1-N\left(\frac{n_1+n_2}{N}\right)\left(\frac{n_2}{N}\right)\right]=\hfill \\ \hfill & =\hfill & {\sigma }^2(n_2)\left(2-\frac{n_1+n_2}{N}\right)=\frac{n_0{n}_2{\sigma }^2}{N}.\hfill \end{array}$$

Finally, dividing covariances by the variance terms, we obtain the correlations:

$$\begin{array}{lll}\hfill \text{cor}(T_{\mathit{ADD}},T_{\mathit{DOM}})& =\hfill & \frac{n_0(n_1+2n_2)}{\sqrt{n_0(n_1+n_2)(n_0{n}_1+4n_0{n}_2+n_1{n}_2)}},\hfill \\ \hfill \text{cor}(T_{\mathit{ADD}},T_{\mathit{REC}})& =\hfill & \frac{n_2(n_1+2n_0)}{\sqrt{n_2(n_1+n_0)(n_0{n}_1+4n_0{n}_2+n_1{n}_2)}},\hfill \\ \hfill \text{cor}(T_{\mathit{DOM}},T_{\mathit{REC}})& =\hfill & \frac{n_0{n}_2}{\sqrt{n_2(n_0+n_1)n_0(n_1+n_2)}}=\sqrt{\frac{n_0{n}_2}{(n_0+n_1)(n_1+n_2)}}.\hfill \end{array}$$

Appendix B

The means and (co-)variances of the rank-based k-sample trend tests under the null hypothesis can be calculated from the moments of two-sample Mann-Whitney statistics (see Tryon, 1972):

$$\begin{array}{lll}\hfill \mathrm{E}(W_{ij})& =\hfill & \frac{n_i{n}_j}{2},i\ne j,\hfill \\ \hfill \text{Var}(W_{ij})& =\hfill & \frac{n_i{n}_j(n_i+n_j+1)}{12},i\ne j,\hfill \\ \hfill \text{Cov}(W_{ij},W_{il})& =\hfill & \text{Cov}(W_{ji},W_{li})=\frac{n_i{n}_j{n}_l}{12},\text{if}\mathit{ijl}\text{are}\text{all}\text{different},\hfill \\ \hfill \text{Cov}(W_{ij},W_{li})& =\hfill & \text{Cov}(W_{ji},W_{il})=-\frac{n_i{n}_j{n}_l}{12},\text{if}\mathit{ijl}\text{are}\text{all}\text{different},\hfill \\ \hfill \text{Cov}(W_{ij},W_{lm})& =\hfill & 0,\text{if}\mathit{ijlm}\text{are}\text{all}\text{different.}\hfill \end{array}$$

Also, recalling that W_ij is the number of times an observation from the j^th sample exceeds one from the i^th sample, it follows that W_ij +W_il = W_i(j+l), where W_i(j+l) is the Mann-Whitney statistic comparing the combined data from the j^th and l^th samples to the i^th sample.

The mean and variance of the modified Jonckheere statistic $J^{\ast }={\sum }_{i=1}^{k-1}{\sum }_{j=i+1}^k(j-i)W_{ij}$ are given by:

$$\mathrm{E}(J^{\ast })=\sum _{i<j}(j-i)\mathrm{E}(W_{ij})=\sum _{i<j}\frac{(j-i)n_i{n}_j}{2},$$

and

$$\begin{array}{l}\text{Var}(J^{\ast })=\text{Var}\left(\sum _{i<j}(j-i)W_{ij}\right)\\ =\sum _{i<j}{(j-i)}^2\text{Var}(W_{ij})+\sum _{i<j}\sum _{i^{\prime }<j^{\prime }}(j-i)(j^{\prime }-i^{\prime })\text{Cov}(W_{ij}{W}_{i^{\prime }{j}^{\prime }}).\end{array}$$

In the case of k = 3, the above expressions reduce to:

$$\begin{array}{c}{J}^{\ast }=\sum _{i=0}^{k-2}\sum _{j=i+1}^{k-1}(j-i)W_{ij}=W_{01}+2W_{02}+W_{12},\\ \mathrm{E}(J^{\ast })=\frac{n_{01}+2n_{02}+n_{12}}{2},\end{array}$$

$$\begin{array}{l}\text{Var}(J^{\ast })=\text{Var}(W_{01}+2W_{02}+W_{12})=\\ =\text{Var}(W_{01})+4\text{Var}(W_{02})+\text{Var}(W_{12})+2(2^2-1(1))\text{Cov}(W_{01},W_{02})=\\ =\frac{n_0{n}_1(n_0+n_1+1)}{12}+4\frac{n_0{n}_2(n_0+n_2+1)}{12}+\frac{n_1{n}_2(n_1+n_2+1)}{12}+6\frac{n_0{n}_1{n}_2}{12}=\\ =\frac{n_0{n}_1(N+1)}{12}+4\frac{n_0{n}_2(N+1)}{12}+\frac{n_1{n}_2(N+1)}{12}\\ =\frac{(n_0{n}_1+4n_0{n}_2+n_1{n}_2)(N+1)}{12}.\end{array}$$

Appendix C

The robust association test is based on the standardized versions of

$$\begin{array}{c}{J}^{\ast }=W_{01}+2W_{02}+W_{12},\\ F{W}_{\mathit{DOM}}=W_{0(1+2)},\\ F{W}_{\mathit{REC}}=W_{(0+1)2}.\end{array}$$

Note that MJT can be alternatively expressed as

$$J^{\ast }=W_{0(1+2)}+W_{(0+1)2}=F{W}_{\mathit{DOM}}+F{W}_{\mathit{REC}}.$$

Hence,

$$\begin{array}{l}\text{Cov}(T_{\mathit{MJT}},F{W}_{\mathit{DOM}})=\text{Cov}(F{W}_{\mathit{DOM}}+F{W}_{\mathit{REC}},F{W}_{\mathit{DOM}})=\\ =\text{Var}(F{W}_{\mathit{DOM}})+\text{Cov}(F{W}_{\mathit{DOM}},F{W}_{\mathit{REC}})=\\ =\frac{n_0(n_1+n_2)(N+1)}{12}+\frac{n_0{n}_2(N+1)}{12}=\frac{n_0(n_1+2n_2)(N+1)}{12}.\end{array}$$

Similarly

$$\text{Cov}(J^{\ast },F{W}_{\mathit{REC}})=\frac{n_2(n_1+2n_0)(N+1)}{12},$$

and

$$\begin{array}{l}\text{Cov}(F{W}_{\mathit{DOM}},F{W}_{\mathit{REC}})=\text{Cov}(W_{0(1+2)},W_{(0+1)2})=\\ =\text{Cov}(W_{01}+W_{02},W_{02}+W_{12})=\\ =\text{Cov}(W_{01},W_{02})+\text{Cov}(W_{01},W_{12})+\text{Cov}(W_{02},W_{12})+\text{Var}(W_{02})=\\ =\frac{n_0{n}_1{n}_2}{12}+\frac{n_0{n}_2(n_0+n_2+1)}{12}=\frac{n_0{n}_2(N+1)}{12}.\end{array}$$

Now, we can obtain the correlations,

$$\begin{array}{lll}\hfill \text{cor}(J^{\ast },F{W}_{\mathit{DOM}})& =\hfill & \frac{n_0(n_1+2n_2)}{\sqrt{(n_0{n}_1+4n_0{n}_2+n_1{n}_2)n_0(n_1+n_2)}},\hfill \\ \hfill \text{cor}(J^{\ast },F{W}_{\mathit{REC}})& =\hfill & \frac{n_2(n_1+2n_0)}{\sqrt{(n_0{n}_1+4n_0{n}_2+n_1{n}_2)n_2(n_1+n_0)}},\hfill \\ \hfill \text{cor}(F{W}_{\mathit{DOM}},F{W}_{\mathit{REC}})& =\hfill & \sqrt{\frac{n_0{n}_2}{(n_1+n_2)(n_1+n_0)}}.\hfill \end{array}$$

The above correlation coefficients are equivalent to those derived for regression based statistics.