Anderson localization of electrons in single crystals: Li_xFe₇Se₈

The Anderson localization, which was predicted more than half a century ago, is realized for electron system in a 3D single crystal.

Abstract

Anderson (disorder-induced) localization, proposed more than half a century ago, has inspired numerous efforts to explore the absence of wave diffusions in disordered media. However, the proposed disorder-induced metal-insulator transition (MIT), associated with the nonpropagative electron waves, has hardly been observed in three-dimensional (3D) crystalline materials, let alone single crystals. We report the observation of an MIT in centimeter-size single crystals of Li_xFe₇Se₈ induced by lattice disorder. Both specific heat and infrared reflectance measurements reveal the presence of considerable electronic states in the vicinity of the Fermi level when the MIT occurs, suggesting that the transition is not due to Coulomb repulsion mechanism. The 3D variable range hopping regime evidenced by electrical transport measurements at low temperatures indicates the localized nature of the electronic states on the Fermi level. Quantitative analyses of carrier concentration, carrier mobility, and simulated density of states (DOS) fully support that Li_xFe₇Se₈ is an Anderson insulator. On the basis of these results, we provide a unified DOS picture to explain all the experimental results, and a schematic diagram for finding other potential Anderson insulators. This material will thus serve as a rich playground for both theoretical and experimental investigations on MITs and disorder-induced phenomena.

INTRODUCTION

Electrical conduction in crystalline solids is attributable to the fact of nonscattering propagation of electron waves. Such electrons are in extended states, and their wave characters are described as Bloch waves. However, this mechanism could not be valid when disorder gets involved. In certain cases, the electronic states in a metal could go from extended states to localized states; thus, a metal-insulator transition (MIT) will ensue. Anderson (1) first suggested that an ordered lattice with uncorrelated random potentials would eventually trap itinerant electrons, that is, Anderson localization, leading to a disorder-driven MIT. It is essentially a phenomenon of interference of electron waves, relying on degree of disorder in potential. MITs driven by Anderson localization differ in mechanism from ones by Mott transition and Peierls transition. Mott transition (2) arises from Coulomb interactions controlled by screening, where the degree of disorder is considerably less important, whereas Peierls transition is induced by change in crystal structure.

Originally proposed in electron systems, Anderson localization is highly relevant to wave phenomena and has been observed for photons (3–5), classical waves (6–8), matter waves (9), and cold atoms (10, 11). For electrons, Anderson localization has been confirmed in one dimension (1D) (12–14) and 2D (15, 16), both experimentally (17, 18) and theoretically (19–24). For 3D materials, although numerous publications are dedicated to doped semiconductors (25, 26), the MITs in these materials are now reckoned to result from the combined effects of Mott transition and Anderson localization (2). Recently, an MIT solely governed by disorder was observed in polycrystalline semiconducting GeTe-Sb₂Te₃ system (27–29). However, the small grain sizes (~10 to 20 nm) in GeSb₂Te₄ compounds complicate the understanding of transport properties, and to synthesize disordered GeSb₂Te₄ single crystals has not been yet feasible. Thus, to unambiguously determine the effect of lattice disorder on electron localization experimentally is still being pursued. Additionally, a recent study indicated the MIT observed in polycrystalline FeSe:Cu (30, 31) might be related to disorder. The progress has motivated us to find a 3D single crystalline Anderson insulator, which might serve as a paradigm to study disordered electronic systems.

Here, we report the occurrence of Anderson localization in 3D single crystals of Li_xFe₇Se₈. The driving force behind its MIT stems from the randomness associated with Li doping to clean crystal Fe₇Se₈, resulting in a strong disordered potential. This randomness does not only destroy the superstructure of Fe₇Se₈ but also suppresses its spin ordering. We show that a large amount of electronic states at the Fermi level are still present; the electrical conduction exhibits a variable range hopping (VRH) behavior after the transition from metal to insulator. Additionally, localization length (ξ) is estimated to be about 12.3 Å, indicating that the electrons are localized within their next nearest neighboring unit cells. Quantitative analyses based on carrier concentration, density of states (DOS), and carrier mobility all support the occurrence of Anderson localization in Li_xFe₇Se₈. All these phenomena could be fully explained by a phenomenological picture of electron localization.

RESULTS

The structure of Fe₇Se₈, reported by various authors (32, 33), adopts the “NiAs” structure, consisting of the stacking of FeSe layer along the c axis with space group P6₃/mmc and lattice constant a = 3.63 Å and c = 5.89 Å (see Fig. 1). Fe vacancies usually appear in one layer among every three or four layers, resulting in a 3c or 4c superstructure. Additional diffraction peaks can be observed because of superstructure. The ordered vacancies are the origin of ferrimagnetism and are responsible for the spin reorientation when the temperature decreases down to about 150 K (33). Electrical measurements also show that both “3c” and “4c” Fe₇Se₈ are metals [see fig. S1 or the work of Kamimura (34)].

Fig. 1. Crystal structure of Fe₇Se₈, Li_xFe₇Se₈, and optical photograph of single crystals.

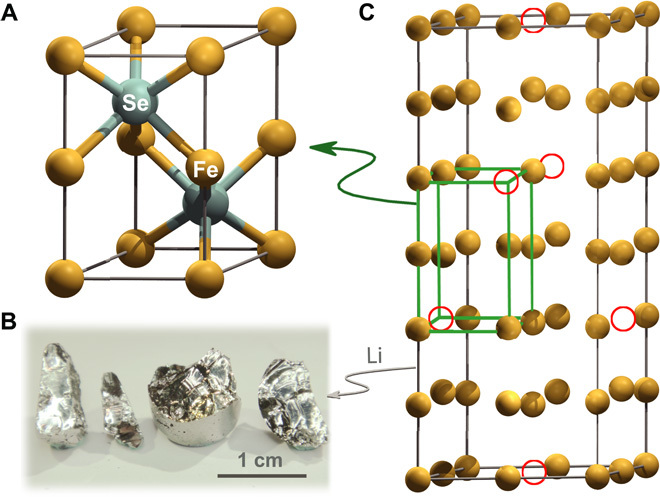
(A) Fundamental NiAs structure of Li_xFe₇Se₈ with space group P6₃/mmc. (B) Optical photograph of Li_xFe₇Se₈ crystals. The acquired single crystals have metallic luster, and they are very robust against air and water and can be used in a variety of fields. (C) Crystal structure of parent compound Fe₇Se₈ (only 3c-Fe₇Se₈ is presented). Open circles denote vacancies, and Se atoms are omitted for clarity.

We tried to dope Li, Na, Mg, and Co into Fe₇Se₈ but found that only Li could enter the lattice to form single-crystal Li_xFe₇Se₈. This solid solution at 0.5 < x ≤ 0.89 can be easily grown into single crystals up to a centimeter in size with metallic luster (Fig. 1B). Below x = 0.5, a double-phase region exists. Fully occupied LiFe₇Se₈ powder can be grown by using Li₂FeSe₂ flux as described in Materials and Methods. The structure determinations are performed by single-crystal diffraction and powder diffraction, respectively, which are shown in table S1 and fig. S2. A striking feature of the diffraction patterns is the gradual decrease in intensity for the superstructure peaks. With Li doping at about x = 0.53, the superstructure peaks totally disappear (Fig. 2A) and the structure is reduced to the fundamental NiAs structure with a = 3.6648(5) Å and c = 5.9708(7) Å. This result manifests that the disorder most likely originates from Fe sites. We also conducted transmission electron microscopy (TEM) experiments on Li_xFe₇Se₈ and Fe₇Se₈ (fig. S3) because TEM is much more sensitive to superstructures than x-ray. Electron diffraction spots corresponding to superstructure gradually become vague and finally disappear in Li_0.89Fe₇Se₈. Because the ferrimagnetism of Fe₇Se₈ comes from the long-range order of local magnetic moment of Fe atoms with an intralayer ferromagnetism and interlayer antiferromagnetism picture (34), it is reasonable to speculate the suppression of ferrimagnetism when the Fe ions are in chaos. As shown in Fig. 2B, the ferrimagnetism of Li_xFe₇Se₈ (x ≥ 0.53) almost vanishes (x = 0.53 is multiplied by 30 and offset for clarity). Detailed investigations of magnetic properties together with the evolution of superstructures in TEM will be published elsewhere because they are not directly related to the present theme. Thus, disorder is verified to exist on Li_xFe₇Se₈ lattices, which is a prerequisite for Anderson localization (1).

Fig. 2. Superstructure and magnetization of Li_xFe₇Se₈.

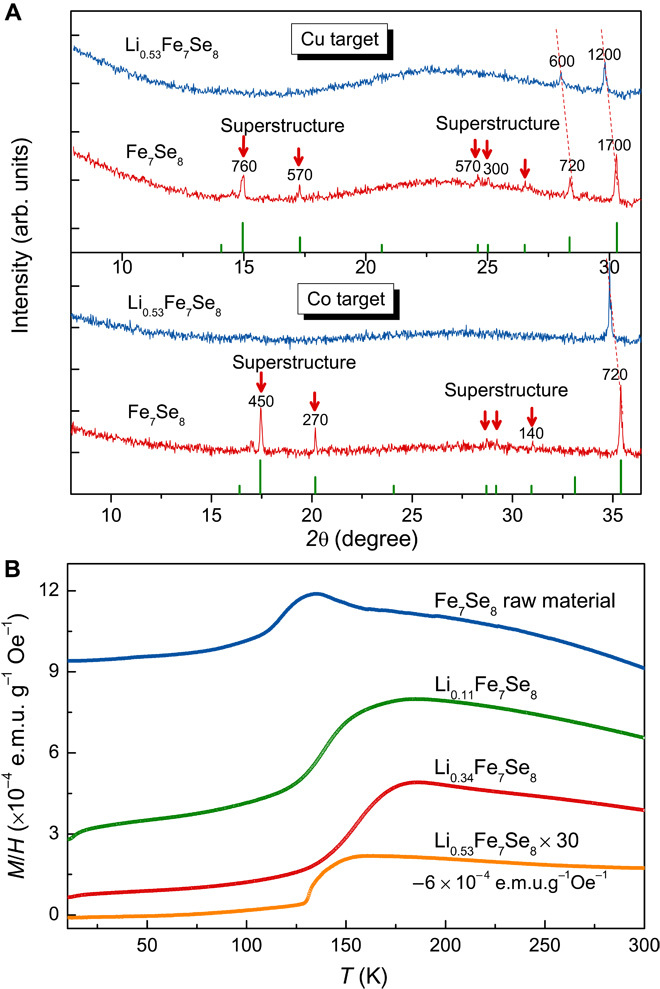
(A) Powder x-ray diffraction (XRD) of Li_0.53Fe₇Se₈ and Fe₇Se₈ with both Cu and Co Kα radiations. To see the superstructure peaks clearly, low-angle parts are shown exclusively. They are 8° to 31° and 8° to 36° for Cu and Co targets, respectively. These patterns are collected for long and same time duration. Peaks corresponding to superstructure are marked by red arrows. The number on each peak is its intensity counts (background is subtracted). These superstructure peaks of Fe₇Se₈ can be seen clearly with both Cu and Co Kα radiations, but systematically disappear in Li_0.53Fe₇Se₈. Red dot lines show the shifts of the peaks of fundamental NiAs structure, indicating the enlargement of lattice parameters after doping. (B) Suppression of magnetism of Li_xFe₇Se₈ with the increment of lithium content. Inflections at around 130 to 150 K are caused by residual Fe₇Se₈, which experiences spin reorientation at this temperature (33). The magnetization of Li_0.53Fe₇Se₈ is multiplied by 30 for clarity.

The effect of such disorder, if strong enough to destroy the periodic potential, should be first reflected in electrical transport measurements. As shown in Fig. 3A, when 6.6% of the 2a Wyckoff position is occupied by Li atoms, Li_0.53Fe₇Se₈ shows an insulating behavior (dρ/dt < 0); thus, an MIT occurs. It is worth noting that this MIT is opposite to that in doped semiconductors, where an insulating-to-metallic transition takes place (25). Another distinct feature of Li_xFe₇Se₈ from doped semiconductors is that they have relatively small resistivity. Note that the highest value is about 1 ohm·cm at 2 K for x = 0.89. To estimate the carrier concentration (n) before and after Li doping, we performed Hall measurements at room temperature and found that n values of Li_xFe₇Se₈ and Fe₇Se₈ lie above 10²¹ cm⁻³, supporting the observed small resistivity. We are yet to determine the accurate values of n because the Hall coefficients of 3D materials with high carrier concentration are quite small. Furthermore, we measured the resistivity of Li_0.89Fe₇Se₈ and Li_0.53Fe₇Se₈ at a magnetic field of 8 T. The result shows no difference at 0- and 8-T field (see fig. S4), indicating that the possible charge ordering is not significant (35, 36).

Fig. 3. Resistivity and lnρ versus T^{−1/ν + 1} plots of Li_xFe₇Se₈.

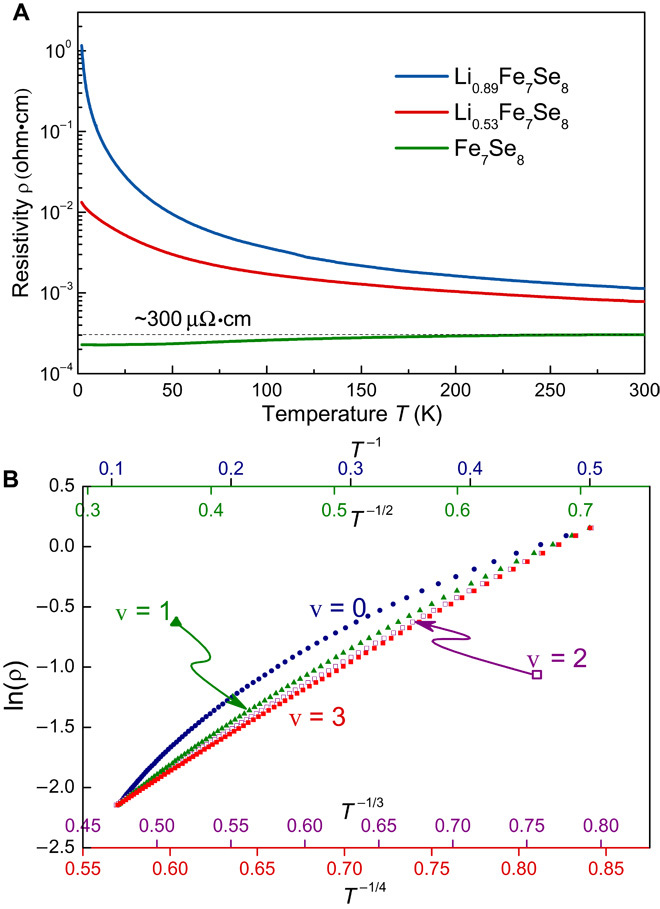
(A) The resistivities for two different Li doping samples (0.53 and 0.89) and parent compound (Fe₇Se₈) are shown from 2 to 300 K. Overall, the metallic Fe₇Se₈ is turned into insulators by doping electrons. The measurements are performed roughly on ab plane. Above x = 0.53, the slope of resistivity is negative (dρ/dt < 0), indicating an insulating behavior. This nonmetal behavior is enhanced with increasing the Li doping. (B) Plots of lnρ versus T^−1/ν+1 of Li_0.89Fe₇Se₈ from 2 to 10 K. We fit the same resistivity data of Li_0.89Fe₇Se₈ by using VRH formulas ρ = ρ₀·exp(T₀/T)^1/(ν+1), where ν = 1, 2, and 3 corresponding to 1D, 2D, and 3D material, respectively. ν = 0, which denotes the traditional insulator with band gap, is also included for comparison. ν = 3 fits best among all the fittings.

For an Anderson insulator, the hopping of electrons to their nearest neighboring sites is prohibited at low temperatures, because electrons need to overcome a high-energy barrier induced by disorder. Instead, these electrons have to find other sites to hop where energies between initial and final sites are close (37). This results in ρ = ρ₀·exp(T₀/T)^{1/ν + 1}, where ν = 1, 2, and 3 for 1D, 2D, and 3D, respectively. In Fig. 3B, we plot lnρ versus T^{−1/(ν + 1)} for Li_0.89Fe₇Se₈ from 2 to 10 K (that of Li_0.53Fe₇Se₈ is shown in fig. S5). Clearly, ν = 3 gives the most straight line, which means that the experimental conductivity obeys a 3D VRH region. This suggests that there are electronic states trapped in the vicinity of the Fermi surface, indicating the occurrence of Anderson localization. We note that a Coulomb gap in crystalline GeSb₂Te₄ has been reported recently (38), where the temperature-dependent resistivity changes from T^−1/4 to T^−1/2 below 5 K. ν = 1 (T^−1/2 law) does not only mean 1D VRH but also corresponds to a dimension-independent Efros-Shklovskii hopping (39), namely, a soft gap opening at low temperature, when Coulomb repulsion is involved. However, our data fit better against T^−1/4 rather than against T^−1/2 even down to 2 K. If there is a soft gap at E_F, the slope of lnρ ~ T^−1/4 should increase at the low-temperature region. Apparently, this is not the case of Li_0.89Fe₇Se₈.

Another useful approach to distinguish Anderson transition from other possible mechanisms for MIT is to confirm that the E_F is located within the localized states region (40). It is known that Sommerfeld coefficient γ is directly related with the DOS, N(E_F), on the Fermi surface through the equation

$$N(E_{\mathrm{F}})=(3/{\mathrm{\pi }}^2{k_{\text{B}}}^2)\cdot \mathrm{\gamma }\cdot (m/m^{*})$$ (1)

where k_B, m, and m* are Boltzmann constant and true and effective mass of electron, respectively. We have measured the heat capacity at low temperatures, 2 to 4 K, to extract γ. Figure 4A shows the variation of γ with respect to Li doping in Li_xFe₇Se₈.

Fig. 4. Sommerfeld coefficients γ with different Li dopings and applied magnetic fields.

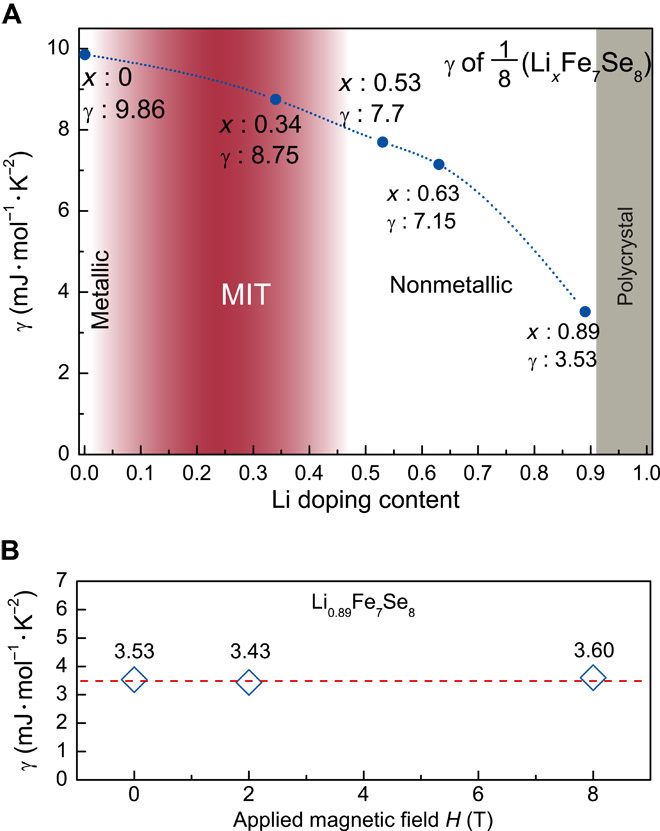
(A) Each point is acquired by fitting the data with the formula C_p/T = γ + βT² between 2 and 4 K (C_p is the specific heat and βT² is the lattice contribution part). The raw data are shown in fig. S7. All the γ is normalized into fundamental NiAs structure, namely, 1/8(Li_xFe₇Se₈). The γ of metallic Fe₇Se₈ is 9.86 mJ/mol-K², lying in the typical value range of transitional metals (5 to 10 mJ/mol-K²) and agreeing with the data from the literature (45). Then, an MIT will ensue in the double-phase region. The γ values at x = 0.53 and 0.63 decrease slightly compared with those of Fe₇Se₈. The Sommerfeld coefficient continuously declines to 3.53 mJ/mol-K² at x = 0.89. Single crystal at x > 0.89 has not yet been obtained. (B) Sommerfeld coefficient γ of Li_0.89Fe₇Se₈ with applied magnetic field of 0, 2, and 8 T, respectively. All the fields are applied at room temperature. The purpose is to exclude the possible linear specific heat contribution of spin glass. As the figure shows, the Sommerfeld coefficient remains around 3.5 mJ/mol-K² under external fields.

We have found that the γ of Li_0.53Fe₇Se₈ on the insulating side of MIT is quite large (up to 7.7 mJ/mol-K²). The observation could be interpreted from the following two aspects. First, the γ on the insulator side of the MIT region is not far away from that of the metallic Fe₇Se₈ (γ = 9.86 mJ/mol-K²). If we ignore the difference of effective mass before and after Li doping, the number of electrons on the E_F in Li_0.53Fe₇Se₈ is comparable to that of Fe₇Se₈. Moderate variation of m*/m does not influence the conclusion. Second, the effective mass in Fe-based materials is found to be about 2 to 3. We tentatively use m* = 3 m_e here (41), giving a N(E_F) = 9.7 × 10⁴⁶ m⁻³ J⁻¹ for 1/8(Li_0.53Fe₇Se₈) by Eq. 1. “1/8” is introduced to normalize Li_0.53Fe₇Se₈ into a fundamental NiAs structure. The γ changes gradually from 9.86 to 3.53 mJ/mol-K² at the highest doping level (x = 0.89) among single crystals L_xFe₇Se₈. This decline is mainly caused by carrier localization and will be discussed in detail later. The N(E_F) of x = 0.89 sample is 4.5 × 10⁴⁶ m⁻³ J⁻¹, which is comparable to that of Li_0.53Fe₇Se₈. In short, there exists a high amount of electronic states near the E_F, and it does not change much during the MIT.

It is known that spin glass could also contribute to a linear term in specific heat, which has been well described in a two-level tunneling model (42). We would rule out the possibility of spin glass by measuring γ under different magnetic fields. As shown in Fig. 4B, we see no difference in γ at 2 and 8 T as compared to zero field. So, we could conclude that the measured γ is totally contributed by the electrons at the E_F.

Optical spectroscopy is a powerful technique to investigate charge dynamics of materials. We applied this method to Li_0.89Fe₇Se₈. As shown in Fig. 5, the room temperature reflectance and real part of optical conductivity spectrum versus photon energy curve manifest a typical metallic behavior (see fig. S6 for Li_0.53Fe₇Se₈). In light of the Drude-Lorentz fit of the optical conductivity, the plasma frequency ω_p of about 10,700 cm⁻¹ could be obtained. The carrier concentration is estimated by

$$n=(0.724\times {10}^{21}{\text{cm}}^{-3})\cdot (m*/m_{\mathrm{e}})\cdot {({\mathrm{\omega }}_{\mathrm{p}}/8066)}^2$$ (2)

Thus, the obtained n is 3.8 × 10²¹ cm⁻³, compatible with the Hall measurements. That is, the infrared reflectance data reveal an intriguing metallic response in the Anderson insulating state at room temperature.

Fig. 5. The room temperature reflectance and the real part of optical conductivity spectrum for Li_0.89Fe₇Se₈.

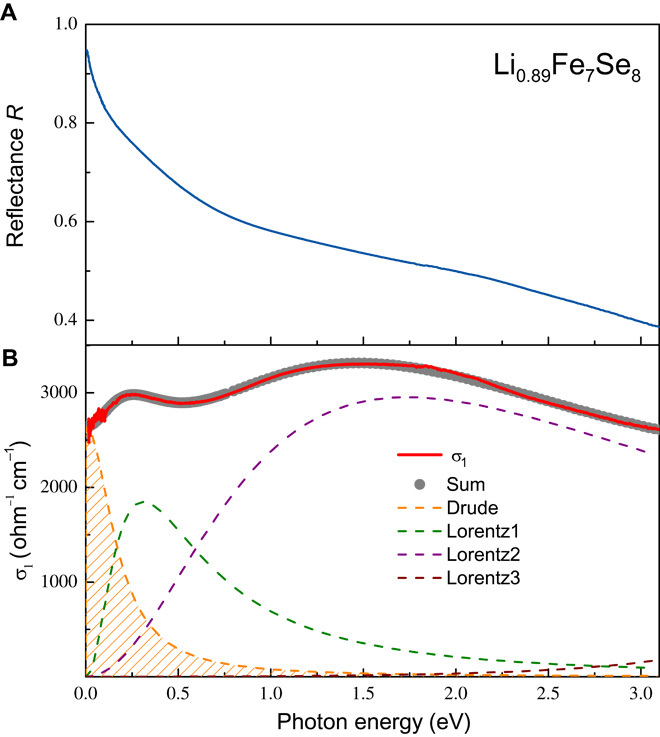
The measurement was performed on a combination of Bruker IFS 80v and 113v at room temperature in the frequency range from 100 to 25,000 cm⁻¹ (12 meV to 3.1 eV). (A) The reflectance of Li_0.89Fe₇Se₈ approaches unity at zero frequency, resembling a typical metal response. (B) The optical conductivity was acquired by the Kramers-Kronig transformation of the reflectance spectrum. The Drude-Lorentz model was used to decompose the optical conductivity spectra into Drude component (orange dashed area) and Lorentz component (other broken lines), where the former describes the contribution from conduction electrons and the latter represents the interband transitions. Apparently, a Drude-like feature is observed at low frequencies, and we obtain the plasma frequency of conduction carriers ω_p ~10,700 cm⁻¹. ω_p values for Fe₇Se₈ and Li_0.53Fe₇Se₈ are listed in Table 1.

With the obtained carrier concentration, we can further calculate the localization length (ξ) by

$$T_0=16(1/k_{\text{B}}\cdot N(E_{\mathrm{F}})\cdot {\mathrm{\xi }}^3)$$ (3)

where T₀ is the fitting parameter for VRH transport. By substituting N(E_F)_IR and T₀ for Li_0.89Fe₇Se₈ (see Table 1) into Eq. 3, we get ξ = 12.3 Å. This suggests that the wave functions of electrons only extend to their next nearest neighboring unit cells. We could estimate the critical carrier concentration (n_c) of MIT by the Mott criterion, n_c^1/3a_H* = 0.26 (a_H* denotes effective Bohr radius). Here, ξ is regarded as a better choice over a_H*. As in strongly disorder systems, the extension of the electron wave function is confined within the localization length (43). The calculated n_c values are shown in Table 1. The carrier concentration for the sample with x = 0.53, if viewed as an MIT point, is seven orders of magnitude larger than its n_c, apparently deviating from the criterion. Even for the x = 0.89 sample, n_IR is two orders of magnitude larger than n_c. All these facts demonstrate that Li_xFe₇Se₈ compounds do not obey the Mott law.

Table 1. Summary of the physical parameters derived from electrical, specific heat, and optical measurements for Li_xFe₇Se₈.

IR and Cp are the data extracted from infrared spectra and specific heat measurements, respectively.

LixFe7Se8	x = 0 (Fe7Se8)	x = 0.53	x = 0.89
σ300K (Ω−1 cm−1)	3,300	1,277	877
σ2K (Ω−1 cm−1)	4,386	77	0.86
ωp (cm−1)	11,300	11,000	10,700
nIR (cm−3)	4.3 × 1021	4.0 × 1021	3.8 × 1021
nCp (cm−3)	4.6 × 1021	2.2 × 1021	2.1 × 1020
N(EF)IR (m−3 J−1)	1.2 × 1047	1.18 × 1047	1.16 × 1047
N(EF)Cp (m−3 J−1)	1.3 × 1047	9.7 × 1046	4.5 × 1046
nIR(x)/nIR(Fe7Se8)	100%	93%	88%
nCp(x)/nCp(Fe7Se8)	100%	48%	5%
nc	—	4 × 1014	9.5 × 1018
nIR/nc	—	1 × 107	4 × 102
μ300K (cm3/V s)	4.8	2	1.4
μ2K (cm3/V s)	6.0	0.2	2.6 × 10−2
T0 (K)	—	~0.2	5,373
ξ (Å)	Inf	~360	12.3

DISCUSSION

The combination of electrical, optical, and specific heat measurements allows us to extract other physical parameters as summarized in Table 1 (see Statistical analysis in Materials and Methods for more details). A preliminary density functional theory calculation without considering disorder is shown in fig. S8, in which the Li doping does not change the rigid band of Fe₇Se₈ significantly and N(E_F) remains substantially unchanged. This result is consistent with the values of N(E_F)_IR and n_IR(Li_xFe₇Se₈)/n_IR(Fe₇Se₈) acquired from optical measurements at room temperature. In strongly disordered samples, although the number of total electronic states at E_F remains the same, the measurable effective states will decrease upon temperature reduction, as evidenced by our low-temperature specific heat measurements: the derived n_Cp(Li_xFe₇Se₈)/n_Cp(Fe₇Se₈) values at 2 K drop by 52% (for x = 0.53) and 95% (for x = 0.89) as compared to the values obtained at room temperature, suggesting that most of the localized electrons at low temperatures get delocalized by thermal activation at room temperature. Similar behavior has also been reported by Siegrist et al. (27) and Jost et al. (29). The carrier mobility μ could reflect the degree of disorder. A decline of μ could be seen with the increasing Li doping at 2 or 300 K. For x = 0.89 sample, μ drops two orders of magnitude down to 2 K, where Anderson localization prevails. However, for Fe₇Se₈, its carrier mobility slightly increases because at low temperature phonon scattering decreases.

On the basis of the current results, a physical scenario in the present MIT is proposed in Fig. 6A. The dopant Li has dual functions. First, it slightly shifts the Fermi level. Second, disorder is introduced by Li doping, as indicated by the disappearance of superstructure. As a result, some electronic states near the band tail begin to be localized to form a mobility edge E_M. When the localized region increases beyond E_F, it triggers the MIT (Fig. 6A, middle). With increased Li content, E_M will move far away from band tails, enhancing the VRH behavior in conduction (Fig. 6A, right). This strengthening disorder can explain the decrease of γ in specific heat.

Fig. 6. DOS evolution and carrier concentration versus disorder diagram.

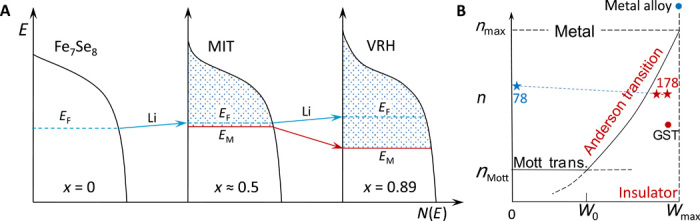
(A) On the basis of the shape of DOS (see fig. S8), N(E) is shaped qualitatively as downward parabolas. Disorder herein will cause exponential tails. In Fe₇Se₈ (left), E_F cuts in the middle of the band; electrons stay itinerant near the E_F. The doping of Li does not only slightly raise E_F but also introduces disorder and leads to the appearance of a mobility edge E_M, which separates localized areas (shaded region) and itinerant area part. When the E_M shifts below E_F (middle), MIT occurs. At higher lithium contents (right), VRH will become more prominent with the enhancement of disorder as described in the text. (B) This figure is adapted from Gantmakher and Man (44). Horizontal axis represents disorder strength (W), vertical axis represents carrier concentration (n), and solid lines represent the boundaries of MIT (explained by Anderson localization or Mott transition mechanism). Asterisks and dots represent Li_xFe₇Se₈, GeSb₂Te₄, and metal alloy.

The occurrence of MIT in a disordered system could be seen as the competition between disorder and carrier concentration. In Fig. 6B, we present a sketch diagram with respect to carrier concentration n and disorder strength W, proposed by Gantmakher and Man (44). In the region with moderate n and high W, the probability to find Anderson localization is high. In Li_xFe₇Se₈, n equals to 10²¹ cm⁻³, which is a moderate value; therefore, it is possible to obtain an insulator by Li doping. Given this, we can also understand why metal alloys with very high n ~10²³ cm⁻³ can hardly be turned into insulators, even in amorphous forms.

Here, a new 3D single crystal, Li_xFe₇Se₈, with disorder-induced MIT is reported. It is the doping of Li that destroys the ordered arrangement of Fe vacancies in Fe₇Se₈, produces large amount of disorder, and finally results in electron localization at the E_F. The nature of Anderson localization is confirmed by the results of electrical transport, heat capacity, optical measurements, and the analyses of localization length, carrier concentration, DOS, and carrier mobility. By using this same approach, that is, doping metals to obtain insulators, more disorder-induced MITs are anticipated. This discovery opens a new avenue to explore diverse aspects regarding disorder and MIT and could enhance our understanding of electronic structure of materials.

MATERIALS AND METHODS

Synthesis

We first synthesized Fe₇Se₈ following the method described by Okazaki (32). The acquired Fe₇Se₈, together with certain amount of Li, was loaded into Al₂O₃ crucibles in glove box. Then, the alumina crucibles were sealed within evacuated quartz tubes backfilled with 0.4 atm argon. Single crystals were synthesized by heating the tubes to 1323 K, holding for several hours, and cooling to 1173 K in 3 to 5 days. Li_xFe₇Se₈ crystals are quite stable and can be manipulated conveniently in air. Fully occupied LiFe₇Se₈ powder was prepared by mixing Li_xFe₇Se₈ with Li₂FeSe₂ by 1:1 in weight and reacting at 1173 K for several hours. (Li₂FeSe₂, isostructural with Li₂FeS₂, is another new Li-Fe-Se rhombohedral compound discovered by us and can easily be washed away by water.)

Structure

Single phases are acquired for ~0.5 < x ≤ 0.89. With increasing Li doping, lattice constants a gradually increases from 3.65 to 3.69 Å and c from 5.97 to 6.008 Å. Structure refinements on two typical single-phase samples are shown in fig. S2.

X-ray diffraction

Powder XRDs were carried out at room temperature using a PANalytical X’Pert PRO diffractometer with Cu and Co Kα radiation. Indexing and Rietveld refinements of the diffraction data were performed with DICVOL06 and FULLPROF package, respectively. Single-crystal diffraction of Li_0.89Fe₇Se₈ was collected at 100 K on a Bruker three-circle platform diffractometer equipped with SMART APEX CCD detector. The SHELXTL package was used for the structure determination and refinement.

Transmission electron microscope

Thin samples for TEM observations were prepared by crushing the crystals in an agate mortar filled with alcohol and then dispersing the resulting fine fragments suspended in alcohol on holey carbon films supported by copper grids. The TEM observations were carried out on a Philips CM200 electron microscope with field emission gun operated at 200 keV.

Magnetization

Magnetic susceptibility was characterized at H = 1 T, using a vibrating sample magnetometer (Quantum Design).

Electrical transport

Samples for electrical measurements were oriented by a goniometer and carefully cut and polished into rectangular shape. A standard four-probe method was used by using silver paste.

Specific heat

Specific heat measurements were carried out by a heat capacity option of Physical Property Measurement System (Quantum Design). We first performed the addenda measurements and then mounted 20 to 30 mg of samples on the platform to measure their specific heat at low temperatures.

Infrared experiments

See figure caption of Fig. 5.

Statistical analysis

(i) Fermi wave vector k_F = (3π²n)^1/3

(ii) Fermi energy E_F = ħ²k_F²/2m^*

(iii) DOS at Fermi surface N(E_F) = 3n/2E_F

(iv) Mobility μ = σ/en

For the derivation of N(E_F), n_IR, and localization length ξ, see the main text.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/2/e1501283/DC1

Fig. S1. In-plane and out-of-plane resistivity of 3c-Fe₇Se₈.

Fig. S2. Rietveld refinements of Li_xFe₇Se₈.

Fig. S3. Electron diffraction patterns of 3c-Fe₇Se₈ and Li_0.89Fe₇Se₈ taken along [100] direction.

Fig. S4. The plots of lnρ versus T^−1/ν+1 of Li_0.53Fe₇Se₈ from 2 to 10 K.

Fig. S5. Resistivity of Li_0.53Fe₇Se₈ and Li_0.89Fe₇Se₈ at magnetic field of 0 and 8 T.

Fig. S6. The room temperature reflectance and the real part of optical conductivity spectrum for Li_0.53Fe₇Se₈.

Fig. S7. C_p/T versus T² plots of Li_xFe₇Se₈.

Fig. S8. DOS of Li_xFe₇Se₈ for x = 0, 1/3, 2/3, and 1, respectively.

Table S1. Summary of data collection and refinement parameters for Li_0.89Fe₇Se₈.