Differentially Private Frequent Sequence Mining via Sampling-based Candidate Pruning

Abstract

In this paper, we study the problem of mining frequent sequences under the rigorous differential privacy model. We explore the possibility of designing a differentially private frequent sequence mining (FSM) algorithm which can achieve both high data utility and a high degree of privacy. We found, in differentially private FSM, the amount of required noise is proportionate to the number of candidate sequences. If we could effectively reduce the number of unpromising candidate sequences, the utility and privacy tradeoff can be significantly improved. To this end, by leveraging a sampling-based candidate pruning technique, we propose a novel differentially private FSM algorithm, which is referred to as PFS². The core of our algorithm is to utilize sample databases to further prune the candidate sequences generated based on the downward closure property. In particular, we use the noisy local support of candidate sequences in the sample databases to estimate which sequences are potentially frequent. To improve the accuracy of such private estimations, a sequence shrinking method is proposed to enforce the length constraint on the sample databases. Moreover, to decrease the probability of misestimating frequent sequences as infrequent, a threshold relaxation method is proposed to relax the user-specified threshold for the sample databases. Through formal privacy analysis, we show that our PFS² algorithm is ε-differentially private. Extensive experiments on real datasets illustrate that our PFS² algorithm can privately find frequent sequences with high accuracy.

I. Introduction

Frequent sequence mining (FSM) is a fundamental component in a number of important data mining tasks with broad applications, ranging from Web usage analysis to location-based recommendation system. Despite valuable insights the discovery of frequent sequences could potentially provide, if the data is sensitive (e.g., DNA sequences, mobility traces and web browsing histories), releasing frequent sequences might pose considerable threats to individual's privacy.

Differential privacy [1] has been proposed as a way to address such problem. Unlike the anonymization-based privacy models (e.g., k-anonymity [2] and l-diversity [3]), differential privacy provides strongly theoretical guarantees on the privacy of released data without making assumptions about the adversary's prior knowledge. By adding a carefully chosen amount of noise, differential privacy assures that the output of a computation is insensitive to the change in any individual's record. Thus, it restricts privacy leaks through the results.

In this paper, we focus on the design of differentially private FSM algorithms. Given a collection of input sequences, FSM is to find all sequences that occur in the input sequences more frequently than a given threshold. Although differentially private algorithms exist for mining special cases of frequent sequences (e.g., frequent consecutive item sequences [4]), we are not aware of any existing study that can support general FSM under differential privacy.

To make FSM satisfy differential privacy, a straightforward approach is to leverage the downward closure property [5] to generate the candidate sequences (i.e., all possible frequent sequences), and add perturbation noise to the support of each candidate sequence. However, this approach suffers poor performance. The root cause is the large number of generated candidate sequences, which leads to a large amount of perturbation noise. We observe, in practice, the number of real frequent sequences is much smaller than the number of candidate sequences generated based on the downward closure property. In addition, in frequent pattern mining, the frequency of a pattern can be considered as the probability of a record containing this pattern. For most patterns, their frequencies in a small part of the database are approximately equal to their frequencies in the original database. Thus, it is sufficient to estimate which patterns are potentially frequent based on a small part of the database [6], [7]. These observations motivate us to design a differentially private FSM algorithm which utilizes a small part of the database to further prune candidate sequences generated based on the downward closure property, such that the amount of noise required by differential privacy is significantly reduced and the utility of the results can be considerably improved.

To this end, we propose a novel differentially private FSM algorithm, called PFS² (i.e., differentially Private Frequent Sequence mining via Sampling-based Candidate Pruning). In PFS², we privately discover frequent sequences in order of increasing length. In particular, we first generate multiple disjoint sample databases. Then, to discover frequent k-sequences (i.e., the frequent sequences containing k items), we utilize frequent (k-1)-sequences to generate candidate k-sequences based on the downward closure property. Next, the k-th sample database is utilized to further prune the candidate k-sequences. Finally, we compute the noisy support of remaining candidate k-sequences in the original database and output the candidate k-sequences whose noisy supports exceed the user-specified threshold as frequent k-sequences.

The core of our PFS² algorithm is to effectively prune the candidate sequences. The local supports of candidate sequences in the sample database are used to estimate which sequences are potentially frequent. Due to the privacy requirement, we have to add noise to the local support of each candidate sequence to avoid privacy breach. To estimate which sequences are potentially frequent accurately, it is necessary to reduce the amount of added noise. In differentially private frequent itemset mining, enforcing the length constraint on itemsets has been proven as an effective method for reducing the amount of added noise [8]. However, due to the inherent sequentiality of sequential data, this method cannot be used in differentially private FSM. In addition, the sequences in the sample database are randomly drawn from the original database. It causes many frequent sequences to become infrequent in the sample database. If we simply use the user-specified threshold to estimate which sequences are potentially frequent, many frequent sequences will be misestimated as infrequent. Thus, how to accurately estimate which candidate sequences are potentially frequent while satisfying differential privacy is a challenging task. To address these challenges, we propose two effective methods, namely, sequence shrinking and threshold relaxation.

For the sequence shrinking method, it consists of three schemes: irrelevant item deletion, consecutive patterns compression and sequence reconstruction. In particular, the irrelevant item deletion and consecutive patterns compression schemes can effectively shorten sequences without losing frequency information. After shortened by these two schemes, if some sequences still violate the length constraint, we use the sequence reconstruction scheme to construct new sequences which can satisfy the length constraint and preserve frequency information as much as possible. By using the sequence shrinking method in the sample database, we can effectively reduce the amount of noise added to the support of sequences.

In the threshold relaxation method, we theoretically quantify the relationship between the decrement of the threshold and the probability of misestimating frequent sequences as infrequent. Based on the theoretical results, we relax the threshold for the sample database to estimate which candidate sequences are potentially frequent. In doing so, the probability of misestimating frequent sequences as infrequent is effectively decreased.

Through formal privacy analysis, we prove our PFS² algorithm guarantees ε-differential privacy. Extensive experimental results on real datasets show that our PFS² algorithm achieves high data utility. Besides, to demonstrate the generality of the sampling-based candidate pruning technique, we also extend this technique to frequent itemset mining. Preliminary experimental results show the performance of existing algorithm [8] is significantly improved by adopting this technique. To summarize, our key contributions are:

1. We introduce the sampling-based candidate pruning technique as an effective means of achieving high data utility in the context of differentially private FSM. This technique is not only suitable for mining frequent sequences under differential privacy, but also can be extended to design other differentially private frequent pattern mining algorithms.

2. We develop a novel differentially private FSM algorithm PFS² by leveraging our sampling-based candidate pruning technique. To privately estimate which candidate sequences are potentially frequent accurately, we propose two methods, namely sequence shrinking and threshold relaxation.

3. Through formal privacy analysis, we prove our proposed PFS² algorithm satisfies ε-differential privacy. We conduct an extensive experimental study over real datasets. The experimental results demonstrate that our PFS² algorithm can privately find frequent sequences with high accuracy.

II. Related Work

Differentially Private Frequent Pattern Mining

We coarsely categorize previous differentially private frequent pattern mining studies into three groups according to the type of pattern being mined.

Sequence

Xiong et al. [4] propose a two-phase differentially private algorithm for mining frequent consecutive item sequences. They first utilize a prefix tree to find candidate sequences, and then leverage a database transformation technique to refine the support of candidate sequences. Compared with this work, we focus on a more general case of FSM, which aims to find all combinations of items that frequently appear in input sequences but not necessarily consecutively.

Several studies have been proposed to address the issue of publishing sequence databases under differential privacy [9], [10]. In particular, Chen et al. [9] propose a differentially private sequence database publishing algorithm based on a prefix tree. In [10], the authors employ a variable-length n-gram model to extract the necessary information of the sequence databases, and utilize an exploration tree to reduce the amount of added noise. These two studies differ from ours in the following aspects. First, they focus on the publication of sequence databases, while our work aims at the release of frequent sequences. Moreover, these two studies utilize the tree structure to group input sequences (grams) to mitigate the impact of added noise. In contrast, we leverage the tree structure to group candidate sequences, so that we can efficiently find the candidate sequences contained in a sequence.

Itemset

Several algorithms have been proposed to tackle the problem of differentially private frequent itemset mining (FIM) [11], [12], [8]. In particular, Bhaskar et al. [11] propose two differentially private FIM algorithms, which adapt the Laplace mechanism [13] and the exponential mechanism [14] respectively. To meet the challenge of high dimensionality of transaction database, Li et al. [12] introduce the PrivBasis algorithm which projects the input high dimensional database onto lower dimensions. In [8], Zeng et al. improve the utility-privacy tradeoff by limiting the length of transactions. They propose a differentially private FIM algorithm which truncates transactions in the original database to improve the quality of the results. Different from [8], to improve the utility-privacy tradeoff, we prune candidate sequences by leveraging the sampling-based candidate pruning technique. Moreover, we shrink sequences in the sample databases, such that we can prune the unpromising candidate sequences more accurately. For the above differentially private FIM algorithms, they are shown to be effective in some scenarios. However, differences between the itemset and the sequence make these algorithms not applicable for differentially private FSM.

Two studies [15], [16] have been proposed to tackle the problem of publishing transaction databases under differential privacy. Chen et al. [15] propose a probabilistic top-down partitioning algorithm which employs context free taxonomy trees. Zhang et al. [16] present an algorithm which uses an item-free taxonomy tree and an update bounded mechanism to privately publish databases on an incremental scenario.

Graph

Shen et al. [17] address the problem of frequent graph mining under differential privacy. They integrate the process of frequent graph mining and the privacy protection into a Markov Chain Monte Carlo framework.

Other Studies

There is a series of studies on publishing aggregate statistics about data streams under differential privacy. In particular, Fan et al. [18] propose a framework to release real-time aggregate statistics by using adaptive sampling and filtering. Cao et al. [19] present two solutions to answer a set of sliding window count queries. Very recently, Kellaris et al. [20] propose ω-event privacy to protect the event sequences occurring within any window of ω timestamps.

Differential privacy has also been investigated in the context of machine learning. Zhang et al. [21] present a functional mechanism to enforce differential privacy in regression analysis. In [22], the authors propose a differentially private model fitting solution based on genetic algorithms. Very recently, Zhang et al. [23] utilize Bayesian networks to effectively publish high-dimensional data.

III. Preliminaries

A. Differential Privacy

Differential privacy [1] has become a de-facto standard privacy notion in private data analysis. Differential privacy requires the outputs of algorithms to be approximately same even if any individual's record in the database is arbitrarily changed. Thus, the presence or absence of any individual's record has a statistically negligible effect on the outputs. Formally, differential privacy is defined as follows.

Definition 1: (ε-differential privacy). A private algorithm 𝒜 satisfies ε-differential privacy iff for any databases D and D′ which differ by at most one record, and for any subset of outputs S ⊆ Range(𝒜),

$$Pr[\mathcal{A}(D)\in S]\le e^{\epsilon }\times Pr[\mathcal{A}(D^{\prime })\in S],$$

where the probability is taken over the randomness of 𝒜.

A fundamental concept for guaranteeing differential privacy is the sensitivity. It is used to measure the maximum change in the outputs of a function when any individual's record in the database is changed.

Definition 2: (Sensitivity). Given any function f: D → ℝⁿ, for any database D₁, D₂ which differ by at most one record, the sensitivity of function f is:

$$\mathrm{\Delta }f=\underset{D_1,D_2}{max}\Vert f(D_1)-f(D_2)\Vert .$$

Dwork et al. [13] propose the Laplace mechanism to achieve differential privacy. For a function whose outputs are real, they prove that differential privacy can be achieved by adding noise drawn randomly from Laplace distribution. The Laplace distribution with magnitude λ, i.e., Lap(λ), follows probability density function $Pr[x|\lambda ]=\frac{1}{2\lambda }exp(-\frac{|x|}{\lambda })$, where $\lambda =\frac{\mathrm{\Delta }f}{\epsilon }$ is determined by the desired privacy budget ε and the sensitivity Δf of the function.

Theorem 1: For any function f : D → ℝⁿ with sensitivity Δf, the algorithm

$$\mathcal{A}(D)=f(D)+<{\mathit{\text{Lap}}}_1(\lambda ),\dots ,{\mathit{\text{Lap}}}_n(\lambda )>$$

satisfies ε-differential privacy, where Lap_i(λ) is drawn i.i.d from a Laplace distribution with scale Δf/ε.

For a function whose outputs are integer, Ghosh et al. [24] propose the Geometric mechanism. The magnitude of the added noise conforms to a two-sided geometric distribution G(α) with the probability mass function $Pr[x|\alpha ]=\frac{exp(\alpha )-1}{exp(\alpha )+1}\times exp{(\alpha )}^{-|x|}$, where α > 0.

Theorem 2: Let f : D → ℝⁿ be a function which outputs integer values, and its sensitivity is Δf. The algorithm

$$\mathcal{A}(D)=f(D)+<G_1(\lambda ),\dots ,G_n(\lambda )>$$

guarantees ε-differential privacy, where G_i(λ) i.i.d samples from a geometric distribution G(ε/Δf).

To support multiple differentially private computations, the composability [13] theorems guarantee the overall privacy.

Theorem 3: (Sequential Composition [13]) Let 𝒜₁, …, 𝒜_k be k algorithms, each provides ε_i-differential privacy. A sequence of algorithms 𝒜_i(D) over database D provides (Σε_i)-differential privacy.

Theorem 4: (Parallel Composition [13]) Let 𝒜₁, …, 𝒜_k be k algorithms, each provides ε_i-differential privacy. A sequence of algorithms 𝒜_i(D_i) over disjoint databases D_i provides max(ε_i)-differential privacy.

B. Frequent Sequence Mining

Suppose the alphabet is I = {i₁, …, i_|I|}. A sequence S is an ordered list of items. We use S = s₁s₂…s_|S| to denote a sequence of length |S|. A sequence S is called a k-sequence if it contains k items. Sequence S = s₁s₂…s_|S| is contained in another sequence T = t₁t₂…t_|T| if there exist integers w₁ < w₂ < … < w_|S| such that s₁ = T_w1, s₂ = T_w2, …, s_|S| = T_w|S|. If S is contained in T, we say that S is a subsequence of T and T is a supersequence of S, denoted S ⊆ T. For example, if S = acd and T = abcdeg, then S ⊆ T.

A sequence database D is a multiset of input sequences, where each input sequence represents an individual's record. The support (frequency) of sequence S is the number (percentage) of input sequences containing S. Our measure of support corresponds to the concept of document frequency in text mining. The minimum support threshold is a number of input sequences, while the relative threshold is a percentage of input sequences. Given the user-specified minimum support (relative) threshold, a sequence is called frequent if its support (frequency) is no less than this threshold. In the rest of this paper, we use “threshold” as shorthand for “minimum support threshold”. The FSM problem considered in the paper is as follows: Given a sequence database and a threshold, find the set of all frequent sequences in the sequence database and also compute the support of each frequent sequence.

IV. A Straightforward Approach

In this section, we present a straightforward approach to find frequent sequences under differential privacy. The main idea is to add noise to the support of all possible frequent sequences and determine which sequences are frequent based on their noisy supports. In particular, we find frequent sequences in order of increasing length. During the mining process, the downward closure property [5] is utilized. The downward closure property states that a sequence is frequent iff all of its subsequences are frequent. Thus, for mining frequent k-sequences, we only need to compute the noisy support of the k-sequences whose (k-1)-subsequences are all frequent. We call such k-sequences candidate k-sequences. For the candidate k-sequences whose noisy supports exceed the user-specified threshold, we output them as frequent k-sequences.

Privacy Analysis

Let Q_k denote the support computations of the candidate k-sequences. The magnitude of noise added to the support of candidate k-sequences depends on the allocated privacy budget and the sensitivity of Q_k. Suppose the maximal length of frequent sequences is L_f. We uniformly assign Q_k a privacy budget ε/L_f. Moreover, since adding (removing) an input sequence can, in the worst case, affect the support of all candidate sequences by one, the sensitivity of Q_k (i.e., Δk) is the number of candidate k-sequences. Thus, adding geometric noise $G(\frac{\epsilon }{L_f\times \mathrm{\Delta }k})$ in Q_k satisfies $\frac{\epsilon }{L_f}$-differential privacy. The process of mining frequent sequences can be considered as a series of computations Q = 〈Q₁, …, Q_Lf〉. Based on the sequential composition property [13], this approach as a whole maintains ε-differential privacy.

Limitations

The approach discussed above, however, produces poor results. The root cause of the poor performance is the large number of candidate sequences. It results in the sensitivity of the support computations being prohibitively high. For example, if there are 10³ candidate 2-sequences, the sensitivity of computing the support of candidate 2-sequences is Δ = 10³. It indicates, even if the privacy level is low (e.g. ε = 5), the support of candidate 2-sequences has to be perturbed by very large amounts of noise, which drastically reduces the utility of the results.

V. Sampling-based Candidate Pruning

As discussed in Sec. IV, the amount of noise required by differential privacy in FSM is proportionate to the number of candidate sequences. In practice, we found the number of real frequent sequences is much smaller than the number of candidate sequences which are generated based on the downward closure property. For example, in database MSNBC, given the relative threshold θ = 0.02, the number of frequent 2-sequences is 32 while the number of generated candidate 2-sequences is 225. As another example, in database BIBLE, given the relative threshold θ = 0.15, the number of frequent 2-sequences is 21 while the number of generated candidate 2-sequences is 254. Thus, if we could further prune the candidate sequences generated based on the downward closure property, the amount of noise required by differential privacy can be significantly reduced, which considerably improves the utility of the results.

In FSM, for most sequences, it is sufficient to estimate if they are frequent based on a small part of the database. This is because, the frequency of a sequence can be considered as the probability of an input sequence containing it, such that the frequency of a sequence in a small part of the database is approximately equal to its frequency in the original database. Therefore, by utilizing a small part of the database, we can further prune the candidate sequences generated based on the downward closure property.

To this end, we propose a sampling-based candidate sequences pruning approach. Given the candidate k-sequences and a small sample database randomly drawn from the original database, we use the local support of candidate sequences in the sample database to estimate which candidate k-sequences are potentially frequent. Due to the privacy requirement, we have to add noise to the local support of candidate sequences. To estimate which candidate sequences are potentially frequent accurately, we propose a sequence shrinking method to effectively reduce the amount of added noise. The sequence shrinking method consists of three novel schemes, which can enforce the length constraint on sequences while preserving frequency information as much as possible (See Sec. V-A). Moreover, to decrease the probability of misestimating frequent sequences as infrequent, we propose a threshold relaxation method. We theoretically quantify the relationship between the decrement of the threshold and the probability of misestimating frequent sequences as infrequent. By using the threshold relaxation method, we relax the user-specified threshold for the sample database to estimate which candidate sequences are potentially frequent (See Sec. V-B).

Algorithm 1 Sampling-based Candidate Pruning
Input:
	Candidate k-Sequences Ck; Sample Database dbk; Privacy Budget ε4;
	Threshold θ; Maximal Length Constraint lmax;
Output:
	Potentially Frequent k-Sequences PF;
1:	${\mathit{\text{db}}}_k^{\prime }$ ← Transform sample database dbk; \\ see Sec. V-A
2:	θ′ ←- Relax threshold θ; \\ see Sec. V-B
3:	PF ← discover_potentially_frequent_sequences (Ck, ${\mathit{\text{db}}}_k^{\prime }$, ε4, θ′);
4:	return PF;

Algorithm 1 shows the steps of our sampling-based candidate pruning approach. Specifically, given a sample database, we first transform the sample database to enforce the length constraint (line 1). For the sequences whose lengths violate the length constraint, we shrink them by using our sequence shrinking method. Then, we relax the threshold for the sample database to estimate which candidate sequences are potentially frequent (line 2). For each candidate sequence, if its noisy support on the transformed database exceeds the new threshold, we regard it as a potentially frequent sequence (line 3).

A. Sequence Shrinking

In the sample database, we use the local support of sequences to estimate which sequences are potentially frequent. Due to the privacy requirement, we have to add noise to the local support of each sequence to guarantee differential privacy. To make the estimation more accurate, the added noise should be as little as possible.

In differentially private frequent itemset mining, enforcing the length constraint on transactions has been proposed as an effective way for reducing the amount of added noise. By limiting the length of transactions, even if a transaction is arbitrarily changed, the number of affected itemsets is restricted, and thus the sensitivity of computing the support of itemsets can be reduced. However, existing method for limiting the length of transactions [8] is designed for itemsets. It cannot be applied to limit the length of sequences.

To this end, we introduce our sequence shrinking method. For the estimation of frequent k-sequences, the candidate k-sequences contained in each sequence S can be considered as the frequency information in S. Ideally, when we shrink S, we want to get a new sequence which meets the length constraint and preserves as much frequency information as possible. To get some insight into potential approaches, consider the following example.

Example 5.1: For a sequence A = abcbbce and candidate 2-sequences ab, be, bb and ae, we can see sequences A₁ = abbbe and A₂ = abbe contain the same candidate sequences as A. Obviously, A₂ appears to be preferable to A and A₁ as it contains fewer items.

Based on the observation of above example, we propose two schemes that are useful in shrinking sequences: irrelevant item deletion and consecutive patterns compression. These two schemes can effectively shorten the sequences without causing any frequency information loss.

Irrelevant Item Deletion

Given a sequence, it is clear that the items not contained in any candidate sequence do not contribute to the frequencies of the candidate sequences. We call such items irrelevant items. Deleting irrelevant items from sequences does not incur frequency information loss. For instance, in Example 5.1, item c is irrelevant. We can see that A = abcbbce contains the same candidate sequences as A₁ = abbbe, which is obtained by removing item c from A. The following lemma asserts that we can simply delete all irrelevant items at once to obtain a new sequence.

Lemma 1: (Irrelevant Item Deletion) Let S = s₁…s_|S| and I be the set of items which are not contained in any candidate k-sequence. Sequence S_−I is obtained by deleting the items in I from S. Then,

$${\mathit{\text{contain}}}_k(S)={\mathit{\text{contain}}}_k(S_{-I}),$$

where Contain_k(T) is the set of candidate k-sequences in T.

Based on the downward closure property, if an item is irrelevant for candidate k-sequences, it will be also irrelevant for candidate sequences of length larger than k. Thus, irrelevant item deletion is very effective in shrinking sequences when we estimate the support of long candidate sequences.

Consecutive Patterns Compression

A sequence might contain a certain pattern which appears consecutively. The pattern ab, for example, appears consecutively in sequence ababab. Lemma 2 ensures that, for the estimation of potentially frequent k-sequences, we can compress consecutive j patterns into consecutive k patterns without causing any frequency information loss (j > k).

Lemma 2: (Consecutive Patterns Compression) Let p^k denote pattern p appearing consecutively k times, and T₁|T₂|T₃ denote a sequence which is the concatenation of sequences T₁, T₂ and T₃. Let Contain_k(T) be the set of candidate k-sequences contained in sequence T. Then, for sequences T₁|p^j|T₂ and T₁|p^k|T₂, where j > k, we have:

$${\mathit{\text{contain}}}_k(T_1|p^j|T_2)={\mathit{\text{contain}}}_k(T_1|p^k|T_2).$$

Clearly, the k items in a candidate k-sequence come from at most k patterns. Thus, for consecutive j patterns (j>k), we can safely compress them into consecutive k patterns. Continuing from Example 5.1, sequence A₁=abbbe contains the same candidate 2-sequences as A₂=abbe, which is generated by using two consecutive patterns b to replace bbb.

In consecutive patterns compression, when estimating potentially short frequent sequences, we can use a small number of patterns to replace the original consecutive patterns. Thus, consecutive patterns compression is particularly effective in shrinking sequences when we estimate short frequent sequences. Besides, since it is computationally expensive to discover consecutive patterns of all possible lengths, we only compress the consecutive patterns where each pattern contains no more than 3 items. In our experiments, we found such setting has already lead to a good compression for the sequences.

Sequence Reconstruction

The irrelevant item deletion and consecutive patterns compression can effectively shrink sequences without incurring any frequency information loss. However, after applying these two schemes, some sequences might still violate the length constraint. We have to delete some items from the sequences until they meet the constraint. Clearly, if we randomly delete items, much frequency information in the sequences will be lost, which leads to inaccurate estimations of potentially frequent sequences.

Intuitively, when shrinking a sequence, we want to preserve as many candidate sequences as possible. Formally, suppose the maximal length constraint is l_max. Given the candidate k-sequences and a sequence S (|S| > l_max), we aim to construct a new sequence Ŝ(|Ŝ| = l_max), such that the number of common candidate k-sequences contained in both S and Ŝ is maximized. A naive approach is to enumerate all possible sequences whose length is l_max and find the sequence which contains the maximum number of common candidate sequences with S. However, this approach suffers from exponential time complexity. If there are |I| items, for example, we have to enumerate |I|^lmax sequences, which is computationally infeasible in practice.

To this end, we put forward our sequence reconstruction scheme. Given an input sequence, to efficiently find its contained candidate sequences, we propose a candidate sequence tree, called CS-tree. It groups candidate sequences with identical prefix into the same branch. The height of the CS-tree is equal to the length of candidate sequences. Each node in the CS-tree is labeled by an item and associated with a sequence of items from the root to it. Figure 1 illustrates the CS-tree of the candidate 3-sequence set {abc, bcd, bda, bdb}.

Fig. 1. A Simple Candidate Sequence Tree.

For a CS-tree constructed based on candidate k-sequences, the nodes at level k are associated with candidate k-sequences. We call the nodes at level k c-nodes, In addition, every node at level k-1 is associated with a (k-1)-sequence which can generate a candidate k-sequence by appending an item to its end. We call the nodes at level k-1 g-nodes, and call their associated sequences generating sequences.

The details of our sequence reconstruction scheme are shown in Algorithm 2, which has a time complexity of O(l_max · k · |C_k|²). Given a sequence S and the CS-tree CT constructed based on candidate k-sequences C_k, we first find the candidate k-sequences C̃_k contained in S and then use C̃_k to build a new CS-tree denoted by subCT (line 1). Tree subCT is a subtree of CT. In the following, we show how to construct a new sequence Ŝ by using tree subCT. The main idea is to iteratively append items which can introduce the maximum number of candidate sequences in C̃_k into Ŝ until Ŝ reaches the length constraint.

In particular, we first append a candidate sequence in C̃_k to Ŝ. We show how to select such candidate sequence as follows. For each candidate sequence cs in C̃_k, the set of (k-1)-subsequences of cs might contain several generating sequences of other candidate sequences in C̃_k. These generating sequences correspond to a set of g-nodes in subCT. For each child node of these g-nodes, its associated candidate sequence can be introduced into cs by appending its labeled item to cs. The more child nodes these g-nodes have, the more candidate k-sequences can utilize the (k-1)-subsequences of cs as their prefixes. Thus, for each candidate sequence in C̃_k, we find the g-nodes whose associated generating sequences are (k-1)-subsequences of this candidate sequence, and use the number of the child nodes of these g-nodes as its score (line 4). We refer to such score as c-score. We select the candidate sequence with highest c-score and append it to Ŝ (line 6). If multiple candidate sequences have the same c-score, the one containing more different items will be appended. This is because such sequence can produce more different subsequences, and thus has chances to generate more candidate sequences. Moreover, to differentiate the candidate sequences not contained in Ŝ, we remove the c-node corresponding to the appended candidate sequence from subCT (line 7).

Algorithm 2 Sequence Reconstruction
Input:
	Sequence S; CS-tree CT constructed based on candidate k-sequences Ck;
	Maximal Length Constraint lmax;
Output:
	Sequence Ŝ;
1:	subCT ← build_CSTree (CT, S);
2:	for each candidate sequence cs in S do
3:	cs.GN ← find_GNodes (cs, subCT);
4:	cs.score ← sum_childNodes (cs.GN);
5:	end for
6:	s ← Select a candidate sequence;
7:	insert (Ŝ, s); update_tree(subCT, s);
8:	while |Ŝ| < lmax do
9:	GN ← find_GNodes (Ŝ, subCT);
10:	if GN.childNodeNum() ≠ 0 then
11:	for each g-node gn in GN do
12:	Item_GNode_Map ← map_item_g-node (gn);
13:	end for
14:	item i ← find_item (Item_GNode_Map);
15:	insert (Ŝ, i); update_Tree (subCT, i, Item_GNode_Map);
16:	else
17:	for each c-node cn in subCT do
18:	cs ← cn's associated sequence;
19:	cs.GN ← find_GNodes (cs, subCT);
20:	cs.score ← sum_childNodes (cs.GN);
21:	end for
22:	s ← Select a candidate sequence;
23:	insert (Ŝ, s); update_Tree(subCT, s);
24:	end if
25:	end while
26:	return Ŝ;

Next, we use subCT to find the generating sequences which are (k-1)-subsequences of Ŝ. Let GN denote the set of g-nodes corresponding to these generating sequences (line 9). Depending on whether the g-nodes in GN have child nodes, we append items to Ŝ in the following manners.

On the one hand, if the g-nodes in GN have child nodes, we will append an item to Ŝ. For each child node of the g-nodes in GN, its associated candidate sequence can be introduced into Ŝ by appending its labeled item. If multiple child nodes are labeled by the same item, by appending this item, their associated candidate sequences can be introduced into Ŝ simultaneously. Therefore, to introduce the maximum number of candidate sequences into Ŝ, we append the item, which appears in the most child nodes, to Ŝ (line 14). After that, we also remove the child nodes labeled by this item from subCT (line 15).

On the other hand, if the g-nodes in GN do not have any child node, no candidate sequence can be introduced into Ŝ by appending only one item. Instead, we will select and append a candidate k-sequence which is in C̃_k but not contained in Ŝ. Recall that, when a candidate sequence is introduced into Ŝ, its corresponding c-node is removed from subCT. Hence, the candidate sequences not contained in Ŝ are the associated sequences of the c-nodes remaining in subCT. For each candidate sequence in C̃_k but not contained in Ŝ, we compute its c-score (line 20). We select the candidate sequence with highest c-score and append this candidate sequence to Ŝ (line 22). If multiple candidate sequences have the same c-score, we append the candidate sequence containing more different items. After that, we remove the c-node corresponding to the appended candidate sequence from subCT (line 23).

Sequence Shrinking Method

To summarize, given the candidate k-sequences and a sequence S whose length exceeds the length constraint, we shrink S by the following steps. We first delete the irrelevant items from S. Then, we iteratively compress consecutive patterns in S in order of increasing pattern length. The irrelevant items deletion and consecutive patterns compression schemes do not cause the decrease of the support of candidate k-sequences. At last, if the length of S still violates the length constraint, we use the sequence reconstruction scheme to construct a new sequence, which might cause some frequency information loss.

B. Threshold Relaxation

In the sample database, the noisy local supports of candidate sequences are used to estimate which candidate sequences are potentially frequent. However, the sample database is drawn randomly from the original database, which might cause many frequent sequences to become infrequent in the sample database. Moreover, the local supports of sequences are also affected by the noise added to guarantee differential privacy and the information loss caused by limiting the length of sequences. Therefore, if we simply use the user-specified threshold to estimate which candidate sequences are potentially frequent, it might lead to many misestimations.

Due to the downward closure property, if a frequent sequence is misestimated as infrequent, its supersequences are all regarded as infrequent sequences without even computing their supports. It drastically reduces the utility of the results. Thus, the threshold should be relaxed to avoid this problem. However, it is hard to quantify how much the threshold should be decreased. In particular, if the threshold is decreased too little, many frequent sequences might still be misestimated as infrequent; if the threshold is decreased too much, only a few candidate sequences can be pruned.

To this end, we theoretically quantify the relationship between the decrement of the threshold and the probability of misestimating frequent sequences as infrequent. To quantify such relationship, we start from the following problem: given a candidate k-sequence t, what is the relationship between its noisy support in the sample database db and its actual support in the original database D?

Let sup_t, ${\mathit{\text{sup}}}_t^{\prime }$ be the actual support of t in D, db respectively. Suppose D contains |D| input sequences. If we randomly choose an input sequence from D, the probability of this input sequence containing t can be regarded as f_t = sup_t/|D|. Since the sequences in db are drawn randomly and independently from D, we can approximately think the probability of each sequence in db containing t is essentially constant and equal to f_t. Then, ${\mathit{\text{sup}}}_t^{\prime }$ follows a binomial distribution:

$${\mathit{\text{sup}}}_t^{\prime }~B(|db|,f_t).$$

It is known that, if the number of trials is large, the binomial distribution is approximately equal to the normal distribution. We assume the number of sequences in db is large enough, and ${\mathit{\text{sup}}}_t^{\prime }$ can be approximated by a normal distribution:

$${\mathit{\text{sup}}}_t^{\prime }~\mathit{\text{Normal}}(f_t·|db|,f_t·(1-f_t)·|db|).$$

Due to the privacy requirement, in the sample database, we add noise to the local support of candidate sequences to avoid privacy breach. As discussed in Sec. V-A, we enforce the length constraint on the sample database to reduce such noise. It might lead to a decrease in the support of some candidate sequences. In our experiments, however, we found our irrelevant item deletion and consecutive patterns compression schemes can effectively shorten the length of sequences, and only a few sequences need to be transformed by our sequence reconstruction scheme. It means our sequence shrinking method does not introduce many errors. Thus, in the analysis of the relationship between t's actual support in D and t's noisy support in db, we assume our sequence shrinking method does not incur frequency information loss.

In our PFS² algorithm, we employ the Laplace mechanism to perturb the support of sequences. Suppose the sensitivity of computing the local support of candidate k-sequences in db is Δ and the privacy budget assigned to this computation is ε. Then, the noise added to the local support of each candidate k-sequence in db is chosen independently at random from a Laplace distribution with scaling parameter ω = Δ/ε. Let ξ denote the amount of noise added to ${\mathit{\text{sup}}}_t^{\prime }$. Then, ξ follows a Laplace distribution:

$$\xi ~\mathit{\text{Laplace}}(0,\omega ).$$

The noisy support of t in db, n-sup_t, can be regarded as the linear combination ${\mathit{\text{sup}}}_t^{\prime }+\xi$. Since the support of a candidate sequence is irrelevant to the amount of added noise, ${\mathit{\text{sup}}}_t^{\prime }$ and ξ are two random variables distributed independently of each other. In [25], it proves that, if X and Y are independent random variables having Normal(μ, σ²) and Laplace(λ, φ) distributions respectively, the cumulative distribution function (i.e., cdf) of Z = X + Y can be expressed as:

$$\begin{array}{l}F(z)=\frac{1}{2}\text{erfc}(\frac{\lambda +\mu -z}{\sqrt{2}\sigma })\\ -\frac{1}{4}exp(\frac{\lambda +\mu -z}{\phi }+\frac{{\sigma }^2}{2{\phi }^2})\text{erfc}(\frac{\lambda +\mu -z}{\sqrt{2}\sigma }+\frac{\sigma }{\sqrt{2}\phi })\\ +\frac{1}{4}exp(-\frac{\lambda +\mu -z}{\phi }+\frac{{\sigma }^2}{2{\phi }^2})\text{erfc}(-\frac{\lambda +\mu -z}{\sqrt{2}\sigma }+\frac{\sigma }{\sqrt{2}\phi }),\end{array}$$

where erfc is the complementary error function:

$$\text{erfc}(x)={\int }_x^{\infty }exp(-t^2)dt.$$

Therefore, given the actual support of t in D, by setting its corresponding parameters μ, σ, λ and φ, we can obtain the cdf of t's noisy support in db.

After deriving the relationship between the noisy support of a sequence in the sample database and its actual support in the original database, we compare the probabilities of estimating candidate sequences with different supports as infrequent.

Theorem 5: Let t₁ and t₂ be two candidate k-sequences. Suppose, in the original database D, t₁'s actual support sup₁ is smaller than t₂'s actual support sup₂. Then, in the sample database db, the probability of estimating t₁ as infrequent is larger than the probability of estimating t₂ as infrequent.

Proof: Since sup₁ is smaller than sup₂, t₁'s frequency f₁ = sup₁/|D| is smaller than t₂'s frequency f₂ = sup₂/|D|. Let n-sup₁ and n-sup₂ denote the noisy support of t₁ and t₂ in the sample database db, respectively. By setting parameters μ₁, σ₁, λ₁ and φ₁ based on f₁, we can get the cdf F₁ of n-sup₁. Similarly, by setting parameters μ₂, σ₂, λ₂ and φ₂ based on f₂, we can get the cdf F₂ of n-sup₂.

To compare probabilities of estimating t₁ as infrequent and estimating t₂ as infrequent, we utilize the characters of the distribution curve of the sum of independent normal and Laplace random variables. As shown in [25], for independent random normal variable X∼N(μ, σ²) and Laplace variable Y∼Laplace(λ, φ), the curve of the probability density function of Z=X+Y is a characteristic symmetric shape that has equal sized tails and quickly falls off towards zero. The distribution curve is very similar to the normal distribution. In particular, the location of the curve is mainly determined by μ/σ and λ/φ. When μ/σ or λ/φ increases, the curve is shifted right. In addition, the spread of the curve is primarily controlled by φ/σ. When φ/σ increases, the curve becomes narrower.

In the sample database db, for sequences t₁ and t₂, the amount of noise added to their supports is chosen independently from the same Laplace distribution. Thus, we have φ₁ = φ₂ and λ₁ = λ₂. Moreover, since μ₁ = f₁|db|, ${\sigma }_1^2=f_1(1-f_1)|db|$ and μ₂ = f₂|db|, ${\sigma }_2^2=f_2(1-f_2)|db|$, we have:

$$\frac{{\mu }_2}{{\sigma }_2}=\sqrt{\frac{f_2|db|}{(1-f_2)|db|}}>\sqrt{\frac{f_1|db|}{(1-f_1)|db|}}=\frac{{\mu }_1}{{\sigma }_1}.$$

As λ₁/φ₁ = λ₂/φ₂ and μ₁/σ₁ < μ₂/σ₂, the distribution curve of n-sup₂ is shifted right compared with that of n-sup₁.

For $\sigma =\sqrt{f(1-f)|db|}$, its value is increasing in the f interval of [0, 0.5] while decreasing in the f interval of [0.5, 1]. Thus, we cannot determine whether φ₁/σ₁ is larger or smaller than φ₂/σ₂, or theoretically analyze if the distribution curve of n-sup₂ is narrower or wider compared with that of n-sup₁. In our experiments, however, we found, when the support of a sequence in the original database increases, the distribution curve is shifted right significantly while the spread of the distribution curve does not obviously change. Thus, we approximately think the spreads of the distribution curves of n-sup₁ and n-sup₂ are the same. Suppose the threshold used in the sample database is θ′. Since sup₂ is larger than sup₁, the distribution curve of n-sup₂ is shifted right compared with that of n-sup₁. Thus, F₂(θ′) should be smaller than F₁(θ′). It indicates, the probability of estimating t₂ as infrequent is smaller than the probability of estimating t₁ as infrequent.

Based on the above analysis, we can derive the relationship between the decrement of the threshold in the sample database and the probability of misestimating frequent sequences as infrequent. Let t_θ be a k-sequence whose actual support in the original database is equal to the user-specified threshold θ. We first compute the cdf F_tθ of the noisy support of t_θ in the sample database db. Suppose, after relaxation, the threshold used in db is θ′. Then, the probability of estimating t_θ as infrequent (i.e., the probability of t_θ's noisy support in db smaller than θ′) is F_tθ(θ′). Since the actual support of any frequent k-sequence is not smaller than θ, based on the analysis above, we can see the probability of misestimating a frequent k-sequence as infrequent is not larger than F_tθ(θ′).

Threshold Relaxation Method

Given the sample database db_k and the candidate k-sequences C_k, we first assume there is a k-sequence t_k whose actual support in the original database is the user-specified threshold. Then, we compute the cdf F_tk of the noisy support of t_k in db_k. We set F_tk(θ′) = ζ and compute the corresponding θ′. In the sample database db_k, we use θ′ to estimate which candidate sequences are potentially frequent. We refer to ζ as relaxation parameter. In our experiments, we find, when ζ is set to be 0.3, it typically obtains good results (see Sec. VII-E).

VI. PFS² Algorithm

A. PFS² Algorithm Description

Our PFS² algorithm is shown in Algorithm 3. It consists of two phases. In particular, in the pre-mining phase, we extract some statistical information from the database. Then, in the mining phase, we privately find frequent sequences in order of increasing length. The sampling-based candidate pruning technique (i.e., sequence shrinking and threshold relaxation methods) is used in this phase. Besides, we divide the total privacy budget ε into five portions ε₁, …, ε₅. Specifically, ε₁, ε₂ and ε₃ are used in the pre-mining phase, ε₄ is used in the sample databases to prune candidate sequences and ε₅ is used for the support computations in the original database. In the rest of this subsection, we present the details of our algorithm.

Algorithm 3 PFS2 Algorithm
Input:
	Original database D; Threshold θ; Maximal length constraint upper bound l1;
	Percentage η; Privacy budgets ε1, …, ε5.
Output:
	Frequent Sequences FS;
1:	/**** Pre-Mining Phase ****/
2:	|D| ← get the noisy number of total input sequences using ε1;
3:	for l2 = 1; p < η; l2 ++ do
4:	αl2 = get the noisy number of input sequences with length l2 using ε2;
5:	$p=({\sum }_{j=1}^{l_2}{\alpha }_j)/|D|$;
6:	end for
7:	lmax ← min{l1, l2};
8:	β ← get noisy maximal support of sequences of length from 1 to lmax using ε3;
9:	Lf ← estimate_max_frequent_sequence_length (θ, β);
10:	/**** Mining Phase ****/
11:	FS ← ø;
12:	dbSet ← randomly_partition_database (D, Lf);
13:	ε′ ← ε5/Lf;
14:	for k from 1 to Lf do
15:	if k == 1 then
16:	Candidate Set Ck ← all items in the alphabet;
17:	else
18:	Candidate Set Ck ← generate_candidates (FSk—1);
19:	end if
20:	$C_k^{\prime }$ ← Sampling_based_Candidate_Pruning(Ck, dbk, ε4, θ, lmax); /**** See Algorithm 1 ****/
21:	FSk ← discover_frequent_sequences ( $C_k^{\prime }$, D, ε′, θ);
22:	FS += FSk;
23:	end for
24:	return FS;

Pre-Mining Phase

In the pre-mining phase, we first compute the maximal length constraint l_max in the sample databases. Like [8], [4], we determine l_max in a heuristic way by setting l_max=min{l₁, l₂}. In particular, the parameter l₁ represents an upper bound on the length of input sequences. It determines a maximum value of the error introduced by the noise in support computations. Instead, the parameter l₂ is computed from the database. Let |D| be the number of total input sequences and α_i be the number of input sequences with length i. Starting from l₂=1, we incrementally compute the percentage $p=({\sum }_{j=1}^{l_2}{\alpha }_j)/|D|$ until p is at least η (line 3-6). Due to the privacy requirement, we add geometric noise G(ε₁) to |D| and add noise G(ε₂) to each α_i (1 ≤ i ≤ l₂).

To better utilize the privacy budget, we also estimate the maximal length of frequent sequences L_f. Since we enforce the length constraint l_max on the sample databases, L_f should not be larger than l_max. To estimate L_f, we first compute β = {β₁, …, β_lmax}, where β_i is the maximal support of i-sequences. Then we add noise G(ε₂/ ⎾logl_max⏋) to each β_i (line 8). We set L_f to be the integer y such that β_y is the smallest value exceeding threshold θ (line 9).

Mining Phase

In the mining phase, we first randomly partition the original database D into L_f disjoint databases dbSet, each of which contains approximately |D|/L_f sequences (line 12). We use these generated disjoint databases as the sample databases to prune candidate sequences.

In the following, we privately find frequent sequences in order of increasing length. In particular, for mining frequent k-sequences, we first generate the candidate k-sequences C_k. If k=1, the candidate sequences are all items. If k>1, the candidate sequences are generated based on the frequent (k-1)-sequences by using the downward closure property. Then, given the k-th sample database db_k, we utilize algorithm Sampling-based_Candidate_Pruning (i.e., Algorithm 1) to prune unpromising candidate k-sequences (See Sec. V). After that, we compute the noisy support of remaining candidate k-sequences $C_k^{\prime }$ on the original database D. Notice that, we do not limit the length of input sequences in the original database. For each candidate k-sequence in $C_k^{\prime }$ we add Laplace noise $\mathit{\text{Lap}}(|C_k^{\prime }|/{\epsilon }^{\prime })$ to its support in D, where ε′=ε₅/L_f. The candidate k-sequences whose noisy supports on D exceed threshold θ are output as frequent k-sequences. This process continues until all frequent sequences of lengths from 1 to L_f are found.

B. Privacy Analysis of PFS² Algorithm

In this subsection, we give the privacy analysis of our PFS² algorithm. Since the key step in our algorithm is pruning the candidate sequences based on the sample databases, we first prove our pruning technique satisfies ε₄-differential privacy.

Theorem 6: The sampling-based candidate pruning technique (i.e., Algorithm 1) guarantees ε₄-differential privacy.

Proof: Given the candidate k-sequences C_k and the k-th generated sample database db_k, we use the noisy local support of C_k in db_k to estimate which candidate k-sequences are potentially frequent. To reduce the amount of added noise, we use our sequence shrinking method to enforce the length constraint l_max on db_k. Since a sequence of length l_max can contain at most ${(}_k^{l_{\mathit{max}}})$ different k-sequences, adding (removing) a sequence in the transformed sample database ${\mathit{\text{db}}}_k^{\prime }$ can increase (decrease) the support of at most $\mathit{min}\left\{{(}_k^{l_{\mathit{max}}}\right),|C_k|\}$ candidate k-sequences by 1. It means the sensitivity of computing the support of C_k in ${\mathit{\text{db}}}_k^{\prime }$ is $\mathrm{\Delta }k=\mathit{min}\left\{{(}_k^{l_{\mathit{max}}}\right),|C_k|\}$. Thus, adding Laplace noise Lap(Δ_k/ε₄) to the local support of C_k satisfies ε₄-differential privacy in ${\mathit{\text{db}}}_k^{\prime }$.

In our sequence shrinking method, to shrink a sequence, our three schemes do not use any other sequences but only relying on C_k and l_max (see Sec. V-A). As shown in Theorem 7, l_max is differentially private. C_k also does not breach the privacy because it is generated based on frequent (k-1)-sequences, and frequent (k-1)-sequences are determined by the noisy supports. Thus, our sequence shrinking method is a local transformation (see Def. 7 in [8]). Based on Theorem 7 in [8] and Theorem 5 in [4], as long as the transformation is local, applying an ε₄-differentially private algorithm on ${\mathit{\text{db}}}_k^{\prime }$ also guarantees ε₄-differential privacy for db_k.

For our threshold relaxation method, only using the number of sequences in the sample database has privacy implications (see Sec. V-B). We approximately think each sample database contains |D|/L_f sequences, where |D| is the number of total input sequences and L_f is the number of sample databases (i.e., the maximal length of frequent sequences). As shown in Theorem 7, |D| and L_f are differentially private. Thus, our threshold relaxation method does not breach the privacy. In summary, our sampling-based candidate pruning technique (i.e., Algorithm 1) satisfies ε₄-differential privacy.

In the following, we prove that the PFS² algorithm overall guarantees ε-differential privacy.

Theorem 7: The PFS² algorithm (i.e., Algorithm 3) satisfies ε-differential privacy.

Proof: In the pre-mining phase of our algorithm, for the computation of |D| (i.e., the number of total input sequences), as adding (removing) an input sequence only affects |D| by 1, the sensitivity of this computation is 1. Thus, adding geometric noise G(ε₁) in computing |D| satisfies ε₁-differential privacy. Similarly, the sensitivity of computing α_i (i.e., the number of i-sequences) is 1. We add noise G(ε₂) in computing α_i, which satisfies ε₂-differential privacy. In the pre-mining phase, we compute α₁, …, α_l2, such that $\left({\sum }_{j=1}^{l_2}{\alpha }_j\right)/|D|$ is larger than the input parameter η. Since a single input sequence can affect only one element among α₁, …, α_l2 (i.e., the sets of input sequences with different lengths are disjoint), based on the parallel composition property [13], the privacy budgets used in computing α₁, …, α_l2 do not need to accumulate. In addition, for the maximal length constraint l_max, as it is estimated based on |D| and α₁, …, α_l2, we can safely use l_max. Besides, in the pre-mining phase, we also compute β = {β₁, …, β_lmax}, where β_i is the maximal support of i-sequences. Since the elements in β are non-increasing, as shown in [8], adding noise G(ε₃/⎾logl_max⏋) in computing β is ε₃-differentially private. For the maximal length of frequent sequences L_f, since it is estimated based on β, we can safely use L_f.

In the mining phase, we first randomly partition the original database into L_f disjoint sample databases. Then, given the candidate k-sequences, we use the k-th sample database to prune them. Theorem 6 proves our pruning technique is ε₄-differentially private. After pruning, we compute the noisy support of remaining candidate k-sequences $C_k^{\prime }$ in the original database D. Notice that, we do not limit the length of input sequences in the original database. Since adding (removing) one sequence without length constraint can at most affect the support of all $C_k^{\prime }$ by 1, the sensitivity of computing the support of $C_k^{\prime }$ in D is $|C_k^{\prime }|$. In addition, we uniformly divide ε₅ into L_f portions and allocate ε′ = ε₅/L_f to the support computations of $C_k^{\prime }$ in D. Thus, adding Laplace noisy $\mathit{\text{Lap}}(|C_k^{\prime }|/{\in }^{\prime })$ to the support of $C_k^{\prime }$ in D satisfies ε′-differential privacy.

Since all sample databases are disjoint, due to the parallel composition property [13], the privacy budget used in sample databases can be summed separately. In summary, based on the sequential composition property [13], we can conclude that our PFS² algorithm satisfies (ε₁ + ε₂ + ε₃ + ε₄ + L_f × ε′) = ε-differential privacy.

VII. Experiments

A. Experiment Setup

As the PFS² algorithm is the first algorithm that supports general FSM under differential privacy, we compare the PFS² algorithm with two differentially private sequence database publishing algorithms. The first is the algorithm proposed in [10] which utilizes variable length n-grams (referred to as n-gram). The second is the algorithm proposed in [9] which utilizes a prefix tree structure (referred to as Prefix). For algorithms n-gram and Prefix, to privately find frequent sequences, we first run them on the original sequence databases to generate anonymized databases, and then run the non-private FSM algorithm GSP [26] over the anonymized databases.

We implement all algorithms in JAVA. The code of n-gram is provided by its authors and Prefix is implemented as described in [9]. We conduct all experiments on a PC with Intel Core2 Duo E8400 CPU (3.0GHz) and 4GB RAM. Because the algorithms involve randomization, we run each algorithm ten times and report its average results. In the experiments, we use the relative threshold. Since n-gram and Prefix generate new sequence datasets, the number of sequences in the original dataset might be different from the number of sequences in the new datasets. For n-gram and Prefix, we use the relative threshold with respect to the original dataset.

In PFS², we allocate the privacy budget ε as follows: ε₁ = 0.025ε, ε₂ = 0.025ε, ε₃ = 0.05ε, ε₄ = 0.45ε and ε₅ = 0.45ε. Like [8], [4], the parameter η used in the pre-mining phase of PFS² is set to be 0.85. We set the privacy budget ε to be 1.0 and the relaxation parameter ζ to be 0.3. We also show the experiment results under varying ε in Sec. VII-C and illustrate the experiment results under varying ζ in Sec. VII-E.

Datasets

In the experiments, we use three publicly available real sequence datasets. Since the original data in dataset House_Power appears as time-series, like [4], we discretize these values and successively construct a sequence from every 50 samples. A summary of the characteristics of these three datasets is shown in Table I.

Table I. Sequence Dataset Characteristics.

Dataset	#Sequences	#Items	Max.length	Avg.length
MSNBC	989818	17	14795	4.75
BIBLE	36369	13905	100	21.64
House Power	40986	21	50	50

Utility Measures

To evaluate the performance of the three algorithms, we follow the widely used standard metrics: F-score [8], [4] and Relative Error (RE) [12]. In particular, we employ the F-score to measure the utility of generated frequent sequences. Moreover, we employ the RE to measure the error with respect to the actual supports of sequences.

B. Frequent Sequence Mining

We first compare the performance of algorithms PFS², n-gram and Prefix with different values of threshold on three datasets. We do not show the performance of Prefix in BIBLE as Prefix does not scale to handle datasets with large number of items. In BIBLE, it contains 13905 items. It is hard for Prefix to construct a prefix tree for BIBLE. For PFS², the statistical information (i.e., the maximal length constraint l_max enforced on the sample databases and the estimated maximal length of frequent sequences L_f under different values of threshold θ) is shown in Tab. II.

From Fig. 2, we can see PFS² substantially outperforms n-gram and Prefix. In particular, n-gram and Prefix also limit the length of input sequences. However, they directly delete items exceeding the limit. which loses much information. In contrast, we utilize sample databases to prune candidate sequences. We enforce the length constraint on the sample databases by using our sequence shrinking method, which can effectively preserve the frequency information and significantly improve the utility of the results. Another interesting phenomenon is Prefix obtains good performance in MSNBC while not producing reasonable results in House_Power. One reason for that phenomenon is Prefix uses the prefixes of input sequences, usually less than 20 items, to construct a prefix tree. If the average length of input sequences is long (e.g., in House_Power), the prefix tree cannot preserve enough frequency information, which inevitably leads to poor performance.

Fig. 2. Frequent Sequence Mining.

From Fig. 2, we can also see PFS² obtains good performance in term of RE (usually less than 5%). The reasons are explained as follows. For metric RE, it focuses on the supports of released sequences. In PFS², thanks to the sampling-based candidate pruning technique, the number of candidate sequences computed in the original database is significantly reduced. It means the amount of noise added to the support of each released frequent sequence is small. Moreover, we do not enforce the length constraint on the original database, and thus the support of released frequent sequences is not affected by the transformation of the database. Hence, PFS² is able to achieve a surprisingly good performance in term of RE.

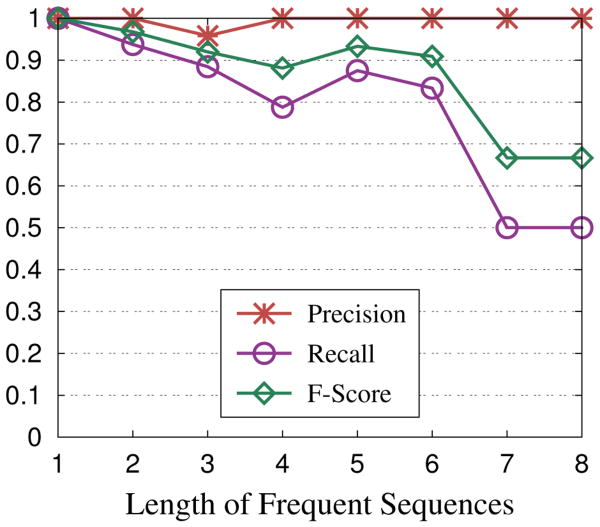
We also show the precision and recall on House_Power in Fig. 2(g)-2(h). We observe the precision of PFS² is very good but the recall decreases a little. This is mainly because, in the sample databases, although our irrelevant item deletion and consecutive patterns compression schemes can effectively shorten sequences, some long sequences still need to be transformed by the sequence reconstruction scheme. It leads to frequency information loss. As a result, some frequent sequences are not identified from the sample databases and the recall is decreased. In Fig. 5, we show the precision, recall and F-score of PFS² for frequent sequences with different lengths on House_Power. We set the relative threshold to be 0.36. We can see PFS² achieves good performance in term of precision, but recall drops for frequent sequences of length 7 and 8. This is mainly due to the small number of frequent sequences of length 7 and 8. Even though only a few frequent sequences are missed, the recall will be significantly decreased.

Fig. 5. Frequent Sequences in House_Power.

C. Effect of Privacy Budget

Fig. 3 shows the performance of PFS², n-gram and Prefix under varying privacy budget on MSNBC (for relative threshold θ=0.015) and on House_Power (for relative threshold θ=0.34). Obviously, PFS² constantly achieves better performance at the same level of privacy. We observe all algorithms behave in a similar way: the quality of the results is improved as ε increases. This is because, as ε increases, a lower degree of privacy is guaranteed and a lower magnitude of noise is added. We also observe the quality of the results is more stable on MSNBC. This can be explained by the high supports of sequences in MSNBC, which are more resistant to the noise.

Fig. 3. Effect of Privacy Budget.

D. Effect of Sequence Shrinking and Threshold Relaxation

Fig. 4 shows how the sequence shrinking and threshold relaxation methods affect the performance of PFS² on datasets BIBLE and House Power. Let RR denote the algorithm which randomly deletes items to enforce the length constraint on the sample datasets and does not relax the user-specified threshold. Let SR denote the algorithm which uses our sequence shrinking method to limit the length of sequences in the sample datasets but does not relax the user-specified threshold.

Fig. 4. Effect of Sequence Shrinking and Threshold Relaxation Methods.

Form Fig. 4, we can see, without using sequence shrinking and threshold relaxation methods, RR does not produce reasonable results. We also observe both the sequence shrinking and threshold relaxation methods are very effective at improving the performance of PFS² in term of F-score. For metric RE, all these algorithms achieve good performance, although it slightly decreases after we use the two methods. This is because, by using these two methods, we identify more real frequent sequences from the sample datasets. The increase of remaining candidate sequences slightly raises the amount of noise added to the support of released frequent sequences.

E. Effect of Relaxation Parameter

In Fig. 6, we show the performance of PFS² by varying the relaxation parameter ζ (used in our threshold relaxation method). We set relative threshold θ=0.05 on MSNBC, θ=0.1 on BIBLE, and θ=0.3 on House_Power. We can see, when ζ is set to be 0.3, PFS² typically obtains good results.

Fig. 6. Effect of Relaxation Parameter.

F. Benefit of Sampling-based Candidate Pruning

In this subsection, we study the benefit of our sampling-based candidate pruning technique. We compare PFS² to a differentially private FSM algorithm via enforcing the length constraint on the original database. Let PL denote this algorithm. In particular, given the candidate k-sequences, PL utilizes our sequence shrinking method to transform the original dataset and determines which sequences are frequent based on their noisy supports on the transformed dataset.

From Fig. 7, we can see PFS² achieves better performance. This is because, compared with PL, PFS² uses sample datasets to prune candidate sequences, which effectively reduces the sensitivity of computing the support of candidate sequences. In contrast, PL limits the length of sequences in the original database to reduce such sensitivity. However, it introduces a new source of error by discarding items from sequences. Due to the privacy requirement, it is hard to precisely compensate such information loss. Thus, PL introduces more errors.

Fig. 7. Effect of Sampling on Frequent Sequence Mining.

To better understand the benefit of the sampling-based candidate pruning technique, we apply it to frequent itemset mining by extending the algorithm proposed in [8] (which is referred to as TT). Specifically, for mining frequent k-itemsets, given a sample dataset, we use TT's smart truncating method to transform it and use our threshold relaxation method to relax the user-specified threshold. Then, we utilize the transformed sample dataset to prune candidate k-itemsets generated based on the downward closure property. For the remaining candidate k-itemsets, we compute their noisy supports on the original dataset. The candidate k-itemsets whose noisy supports in the original database exceed the user-specified threshold are output as frequent. We use two transaction datasets in this experiment: POS and Pumsb-star. Their characteristics are illustrated in Tab. III. We show the experiment results in Fig. 8. It is not surprising that the performance of TT is significantly improved by utilizing our sampling-based candidate pruning technique.

Fig. 8. Effect of Sampling on Frequent Itemset Mining.

VIII. Conclusion

In this paper, we investigate the problem of designing a differentially private FSM algorithm. We observe the amount of required noise in differentially private FSM is proportionate to the number of candidate sequences. We introduce a sampling-based candidate pruning technique as an effective means of reducing the number of candidate sequences, which can significantly improve the utility and privacy tradeoff. By leveraging the sampling-based candidate pruning technique, we design our differentially private FSM algorithm PFS². In particular, given the candidate sequences, we use their noisy local supports in a sample database to estimate which sequences are potentially frequent. To improve the accuracy of such private estimations, we propose a sequence shrinking method which can enforce the length constraint on the sample database while effectively preserving the frequency information. Moreover, we propose a threshold relaxation method, which relaxes the user-specified threshold for the sample database to estimate which candidate sequences are potentially frequent. Formal privacy analysis and the results of extensive experiments on real datasets show that our PFS² algorithm can achieve a high degree of privacy and high data utility.

Table II. Statistic Information in PFS².

Dataset	lmax	Lf/θ	Lf/θ	Lf/θ	Lf/θ	Lf/θ
MSNBC	8	8/0.005	8/0.01	8/0.015	8/0.02	7/0.025
BIBLE	32	5/0.1	5/0.12	4/0.14	4/0.16	4/0.18
House_Power	30	10/0.3	9/0.32	9/0.34	8/0.36	7/0.38

Table III. Transaction Dataset Characteristics.

Dataset	#Transactions	#Items	Max.length	Avg.length
POS	515597	1657	164	6.5
Pumsb-star	49046	2088	63	50.5