Abstract
Electrorotation is widely used for characterization of biological cells and materials using a rotating electric field. Generally, multiphase AC electric fields and quadrupolar electrode configuration are needed to create a rotating electric field for electrorotation. In this study, we demonstrate a simple method to rotate dielectrophoretically trapped microparticles using a stationary AC electric field. Coplanar interdigitated electrodes are used to create a linearly polarized nonuniform AC electric field. This nonuniform electric field is employed for dielectrophoretic trapping of microparticles as well as for generating electroosmotic flow in the vicinity of the electrodes resulting in rotation of microparticles in a microfluidic device. The rotation of barium titanate microparticles is observed in 2-propanol and methanol solvent at a frequency below 1 kHz. A particle rotation rate as high as 240 revolutions per minute is observed. It is demonstrated that precise manipulation (both rotation rate and equilibrium position) of the particles is possible by controlling the frequency of the applied electric field. At low frequency range, the equilibrium positions of the microparticles are observed between the electrode edge and electrode center. This method of particle manipulation is different from electrorotation as it uses induced AC electroosmosis instead of electric torque as in the case of electrorotation. Moreover, it has been shown that a microparticle can be rotated along its own axis without any translational motion.
I. INTRODUCTION
With recent advances in low cost lithographic microfabrication techniques, lab-on-a-chip devices find increasing uses in various disciplines including biomedical research and analytical chemistry. These chips can handle ultra-low sample volume, which makes them a popular tool for biological cell manipulation, sorting, extraction, transportation, and characterization. In these small chips, it is possible to take advantage of several electrokinetic phenomena such as electrorotation,1 dielectrophoresis,2 electroosmosis,3 etc., due to the fact that high electric field can be generated in a micron/sub-micron test space by applying relatively low electric potential. These phenomena are often utilized independently or in combination to achieve the desired manipulation of microparticles. Electrorotation is typically used to characterize biological cells,4 whereas dielectrophoresis is used for characterization, manipulation, and separation of biological particles.5–7 Electroosmosis is generally required to transport biological cells in small microfluidic chips.8–10
Electric field induced microparticle rotation has become a powerful technique to evaluate cell membrane dielectric properties.11–13 The advantage of this technique is that it allows noninvasive study of individual cells in vitro. Apart from the measurement of dielectric properties, cell rotation can be useful in studying cell morphology. Rotational motion of microparticles is typically induced by applying a rotating electric field. A rotating electric field can be created by arranging four electrodes and by exciting alternate electrodes with an AC signal having phase difference.14,15 When a particle is placed in such an electric field, dipole moment is induced in the particle. If the electric field is rotated, there will be an electric torque due to interaction of new orientation of the electric field and remnant dipole of the particle resulting from previous orientation of the electric field. This electric torque is responsible for cell/microparticle rotation as demonstrated by Huang et al.16 Through a comprehensive theoretical work, Pickard17 reported that a rotating electric field is indeed required for observing particle rotation due to the Born-Lertes effect. Despite that, Pohl and Crane18 have reported rotation of yeast cells in a stationary electric field which met with skepticism by researchers in the field of electrorotation. The purpose of that work was to study the yield of yeast collection on electrodes by dielectrophoresis where cell rotation was observed as a secondary effect. However, cell rotation was not observed for all cells as some random cells chose to rotate whereas others were stationary. It was hypothesized that a charge transfer process at the cell-fluid interface may be responsible for electro-hydrodynamic effects, which resulted in rotation of cells. No reasonable explanations existed at that time, though it was the first work that demonstrated cell rotation in a stationary electric field. Later, Hou and Chang19 demonstrated the rotation of small latex particles in a cylindrical path. In their study, latex particles were rotated along an axis parallel to electrodes by applying a DC bias to an AC electric field in a planar microelectrode configuration. Although rotation of particles as well as band formation is shown, it is not clear whether the particles rotated on their own axis, which is known as self-rotation.
In a recent study, self-rotation of biological cells is reported in an opto-electrokinetic chip using high frequency stationary electric field,20 but the reasons for self-rotation remain unclear. Lately, Vaillier et al.21 presented a comprehensive study of biological cell behavior in a stationary AC electric field, and demonstrated human cell rotation close to the electrode edge at moderate frequencies (30–65 KHz). They have argued that fluid vortices formed due to Joule heating combined with the dielectrophoretic force caused the cells to rotate within a very narrow frequency range. However, they did not observe any self-rotation of cells at low applied electric frequency where the AC electroosmotic flow might be dominant.
The AC electroosmotic flow is induced due to ionic cloud migration in response to tangential applied electric field on electrode surface, and only occurs when applied frequency is far below charge relaxation frequency of the fluid.22 Fluid flow in this low frequency regime is demonstrated as a useful tool for trapping microparticles on the electrode surface using coplanar electrodes.23–25 For example, Wu et al.24 used the AC electroosmotic flow to bring bacteria to a trapping area or a stagnation zone for faster detection by an electric impedance spectroscopy. Though trapping of particles is achieved in those studies, none of them demonstrated the controlled rotation of particles. The competition of hydrodynamic drag and electrostatic force is also employed for cell separation. Zhou et al.26 demonstrated that interplay of AC electroosmosis and dielectrophoresis can be used for cell separation in this low frequency regime. Tathireddy et al.27 used the AC electroosmotic flow induced on electrode at low frequencies to analyze nanoparticle dynamics. Even though coupling of hydrodynamic and electric forces on the particle at low frequency exhibits interesting particle dynamics and separation trends, controlled particle rotation, where the particle rotation axis remains stationary, has not been addressed in the literature.
In this work, we present a controlled particle rotation in a stationary electric field (Fig. 1) due to AC electroosmotic flow on the dielectrophoretically trapped microparticles. It has been demonstrated that particle equilibrium position and rotation rates are the direct result of the interplay of hydrodynamic and electric forces active on the particle. We specifically stay at the low frequency regime to take advantage of the AC electroosmotic perturbation to create hydrodynamic torque on the dielectrophoretically trapped microparticles. To our knowledge, controlled self-rotation of the dielectrophoretically trapped microparticles using AC electroosmosis has not been reported before. The rest of the paper has been organized in following manner. First, particle dynamics in the presence of dielectrophoresis and AC electroosmosis is briefly discussed. Next, the fabrication technique for the microfluidic chip used in our experiments is explained. Then, experimental setup and methods used for this study are discussed. Finally, particle equilibrium positions and rotation rates are analyzed due to the combined effect of dielectrophoresis and AC electroosmosis.
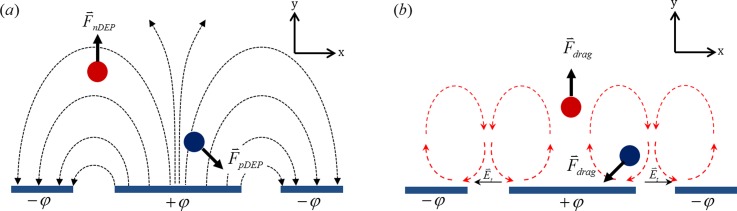
FIG. 1.
(a) Schematic of electric field lines on coplanar electrodes. Particle influenced by negative dielectrophoresis (red) will move away from electrodes. Particle under positive dielectrophoretic (blue) force will move towards closest electrode edge. (b) Schematic of AC electroosmotic flow circulating on coplanar electrodes. If a particle is placed above electrode, viscous drag will push it away from electrode (red). When placed between electrodes (blue), viscous drag will bring it closer to electrode.
II. PARTICLE DYNAMICS
Electrokinetic motion of particles in a microfluidic chip depends heavily on the geometry of the chip and the electrode layout among many other parameters. Like the experimental work of Tathireddy et al.,27 we have used coplanar electrode strips arranged in an array laid out at the bottom of the test chamber (Fig. 2). This layout can create non-uniformity in the electric field required for dielectrophoretic manipulation. Even though we have multiple electrodes in the test chamber, particle dynamics above each electrode is exactly the same. Hence, it will suffice to analyze particle motion above one electrode. Figure 1 represents a segment of the test chamber showing one electrode at the center and half width of two other adjacent electrodes on each side.
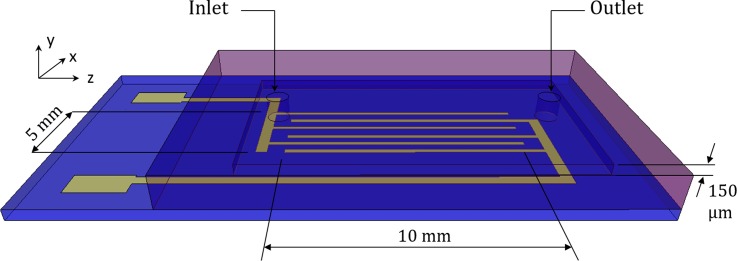
FIG. 2.
Schematic of the microchip. Coplanar electrodes lie at the bottom surface of test chamber on a glass substrate. Particle movement is observed using a microscope positioned right above the chip (figure not drawn to scale).
A. Influence of dielectrophoretic force on particle
Dielectrophoresis is a nonlinear electrokinetic phenomenon and it can be used to manipulate particles. Unlike other electrokinetic phenomena, dielectrophoretic force is only active at the regions of non-uniform electric fields.28 In the case of coplanar electrodes, non-uniform electric field lines have roughly semicircular shape as shown in Fig. 1(a). Electric field strength is highest at the electrode edges, and its magnitude decreases away from the electrode edge. As a matter of fact, the magnitude of the electric field decays exponentially in the vertical direction as we move further away from the electrode surface.29 Depending on the relative polarizability of the particle with respect to the suspending media, a particle might go towards the higher (positive DEP) or lower (negative DEP) electric field regions. The relative polarizability can be determined by the Clausius-Mossotti factor as
| (1a) |
where subscripts “p” and “m” denote particle and media, respectively, and is the complex permittivity given as
| (1b) |
Here, and are permittivity and conductivity, respectively. Thus, the Clausius-Mossotti factor is a complex number, which depends on the fluid and particle dielectric properties as well as on the driving frequency . The real part of , , determines the direction of dielectrophoretic force on a particle. For instance, if , the particle will be subjected to positive dielectrophoresis and it will go towards the higher electric field region, and vice versa. Figure 1(a) shows the direction of the particle during the positive (pDEP) and negative (nDEP) dielectrophoresis.
The time averaged dielectrophoretic force on a particle can be found as
| (2) |
where is the particle radius and is the root mean squared electric field.
B. Influence of AC electroosmotic flow
At the polarizable surfaces, i.e., metal electrodes, the electric double layer (EDL) is induced due to the excitation of electrodes.22,30,31 Excess accumulated charge in this EDL interacts with the tangential component of the external electric field. This gives rise to the electroosmotic flow over the electrode surface and can be modeled by the Helmholtz-Smoluchowski equation30
| (3) |
where , , , and are time averaged electroosmotic slip velocity, viscosity of medium, complex potential drop across electric double layer, and complex conjugate of tangential electric field, respectively. Electroosmotic flow in AC electric field over bar electrodes has been demonstrated by Ramos et al.22,31 Typically, for coplanar electrodes, the direction of this velocity is from the edge of the electrode to the center as shown in Fig. 1(b). Maximum velocity occurs at the electrode edge and diminishes towards the center of the electrode. This creates two counter rotating circulating fluid vortices above the electrode. A microparticle placed in this flow field will experience the hydrodynamic force and will migrate away from electrode edges where the flow velocity is highest, as can be seen from Fig. 1(b). At large frequencies (above ∼100 kHz), ion migration cannot keep up with rapidly changing electrode polarity and an electric double layer cannot form over the electrode. This means electroosmotic flow at large frequencies will subside to the point that particle motion will not be affected by the fluid flow. Hence, at high frequencies, AC electroosmotic flow can be suppressed and particle motion can be controlled by means of dielectrophoresis. However, at low frequencies, the motion of the particle will be the result of net force due to both dielectrophoretic and hydrodynamic forces on the particle as well as the weight of the particle. The combined electric and hydrodynamic forces coupled with particle weight create a unique window to observe rotational effect on the particle.
III. MICROFLUIDIC CHIP DESIGN AND FABRICATION
A. Microfluidic chip specifications
A microfluidic chip is designed and fabricated in the cleanroom facility, located at Washington State University. The test compartment is 10 mm long, 5 mm wide, and 150 μm deep as shown in Fig. 2(a). Titanium (Ti) electrodes are patterned on top of a glass substrate using photolithographic techniques. A recess is molded onto a polydimethylsiloxane (PDMS) slab, which is used as the main test chamber. This PDMS slab is then bonded to the glass substrate. PDMS is optically transparent which facilitates observation of particle motion using a microscope objective placed vertically above the chip. The top PDMS surface contains two access holes for injection and removal of particle suspension. The bottom glass substrate has an array of 60 μm wide coplanar interdigitated bar electrodes as shown in Figure 3. Gaps between adjacent electrodes are kept at 40 μm.
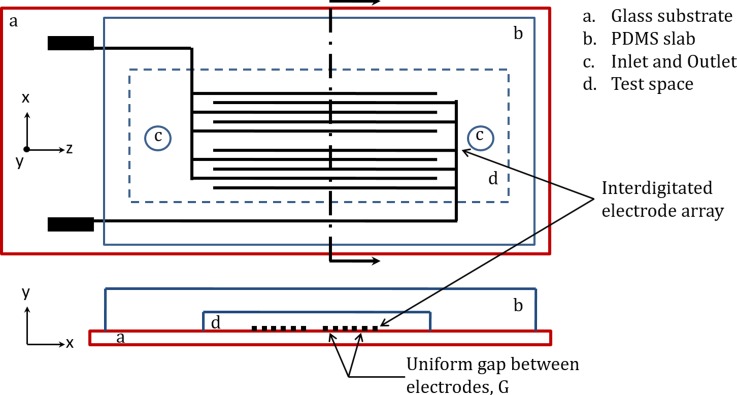
FIG. 3.
Schematic of the experimental chamber. Top frame (top view) shows the layout of bar interdigitated electrodes. The test compartment has insulating walls and ceiling, made of polydimethylsiloxane (PDMS). Two access holes for suspension loading/unloading are shown. Bottom frame (cross sectional view) shows test chamber formed by bottom glass substrate and top PDMS slab. Electrodes are located at the bottom of test chamber, patterned on the glass substrate (figure not drawn to scale).
B. Microfabrication technique
A 3″ × 2″ glass substrate (Alexis Scientific™, NY, USA) is cleaned with acetone, 2-propanol, and deionized water, and blow dried with nitrogen to remove all foreign particles (Fig. 4(a)). SU-8 2010 negative photoresist (MicroChem, MA, USA) is spin coated at 3000 rpm for 30 s on the glass substrate (Fig. 4(b)). The photoresist coated substrate is then soft baked on a hotplate (Series 04664, Cole Parmer, IL, USA) at 95 °C for 5 min. The prebaked photoresist is left for 10 min at room temperature to allow it to cool down. A printed plastic mask containing the electrode's image is then placed on top of the hardened photoresist. The substrate with the mask is exposed to near ultraviolet light of 360 nm wavelength at 150 mJ/cm2 for 40 s using a mask aligner (Hybralign, Series 500, Optical Associates Inc., CA, USA) (Fig. 4(c)). Post baking of photoresist is performed at 110 °C on a hotplate for 3 min. After cooling down at room temperature for 5 min, the film is developed in SU-8 developer (MicroChem, MA, USA) for 1 min (Figure 4(d)). While submerged in developer solution, an ultrasonicator is used for fast and clean removal of photoresist from the surface where electrodes are to be printed. After development is completed, we obtain a patterned photoresist layer on glass substrate. This photoresist layer is used as a sacrificial layer in a subsequent electrode patterning step. A titanium target is used to deposit a layer of titanium having thickness of 300 nm on the substrate in a sputtering chamber (Auto 306, Edwards, NY, USA). Titanium is first uniformly deposited on photoresist coating and on the glass exposed in between the patterned photoresist layer (Fig. 4(e)). Metalized substrate is then submerged in the photoresist remover (PG, MicroChem, MA, USA) bath at 40 °C for 30 min to remove the titanium coated sacrificial photoresist layer (Fig. 4(f)). Glass slide with the patterned electrode is then cleaned with acetone, 2-propanol, and deionized water to ensure all residues are removed.
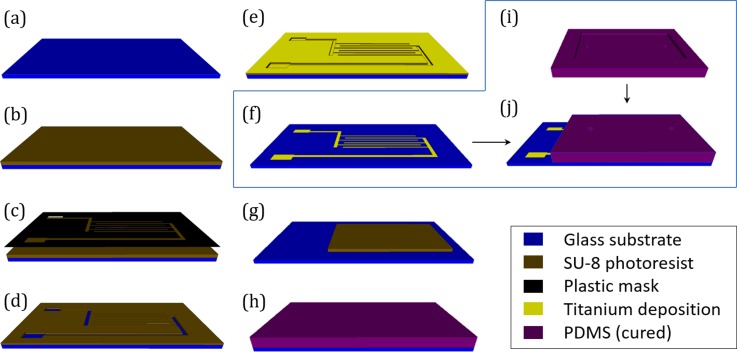
FIG. 4.
Illustration of microchip fabrication sequence. (a) Clean (5 step cleaning) glass substrate. (b) Spin coated, pre baked SU-8 2010 photoresist on glass substrate. (c) Patterning of SU-8 photoresist by plastic mask containing electrode pattern. (d) Developed photoresist exposing part of glass substrate where electrode material will be deposited. (e) Deposition of 300 nm thick titanium on the substrate. (f) Patterned electrodes on glass substrate after removal of sacrificial SU-8 with excess metal deposition. (g) Steps (a) to (d) are followed to create a replica of the test compartment using SU-8 2035 thick photoresist on a separate glass substrate. (h) Liquid polydimethylsiloxane is poured onto the mold and cured. (i) Cured polydimethylsiloxane slab containing emboss of test compartment is stripped from the glass substrate (flip side view). Two holes are punched out to act as inlet and outlet. (j) Glass substrate with electrodes (step f) and polydimethylsiloxane slab (step i) are exposed to oxygen plasma and contact bonded to complete the fabrication process.
Next, another SU-8 2035 mold on a glass slide (Fig. 4(g)) is created for the PDMS molding following the steps of Figs. 4(a)–4(d). This SU-8 mold will be used as the master for creating the test chamber later; hence, the height of this mold is kept at 150 μm. The increased thickness of the mold requires changes in baking time, duration, and UV exposure time. We have used similar process parameters, as described by Jubery et al.32 for fabrication of the thick mold. The flexible and transparent channel, which caps the electrode and forms the test space, is made out of PDMS (184 Sylgard Elastomer, MI, USA) by soft lithography. Briefly, the two components of PDMS are mixed at 10:1 (v/v) and poured on the prepared mold (Fig. 4(h)). The PDMS slab is cured at 60 °C for 4 h on a hotplate and stripped from the mold (Fig. 4(i)). The stripped PDMS slab now is conformed to the shape of the test chamber. After pattern transfer is completed, two 500 μm diameter holes are punched out at both ends of the test chamber impression to allow fluid and particles to be injected into the chamber.
The PDMS slab with chamber impression and electrode integrated glass substrate are exposed to oxygen plasma (PE 200, South Bay Tech, CA, USA) at 21 W and 170 mTorr pressure for 30 s. Oxidized PDMS and glass surfaces are brought into contact immediately following the exposure to form an irreversible covalent siloxane bond33 (Fig. 4(j)). The fabricated test chamber is leak proof and can be accessed through two holes punched out earlier.
IV. MATERIALS AND EXPERIMENTAL SETUP
A. Microparticle and solvent
In this study, rotation of barium titanate microparticles is observed in nonaqueous media. Barium titanate ceramics find many uses in resistors, capacitors, gas sensors, and other electronic devices. Because of their large dielectric constant, barium titanate particles are very suitable for observing positive dielectrophoresis in most commonly used solvents. Also, their relatively large density makes it possible for them to stay close to the electrode surface at the bottom of the chip, where one can investigate particle dynamics under the influence of AC electroosmotic flow.
Barium titanate glass microspheres are purchased from Coshperic (Santa Barbara, CA, USA). Microparticles are obtained in powder form and the mean diameter of these particles is 30 μm. The density of these particles is 4.5 gm/cc. The electrical conductivity of these barium titanate particles is negligible at ∼10−13 S/m, while the dielectric constant of those particles is roughly 3000.34 Non-aqueous solvents, 2-propanol (PrOH) and methanol (MeOH), are chosen as media for our experiments. They are ideal for large electrical potential applications without the fear of hydrolysis, which is relatively common in the case of water. The solvents are obtained from Capitol Scientific, Austin, TX, USA. The dielectric constant of 2-propanol and methanol is 18.9 and 33.7, respectively.35 The viscosity of 2-propanol and methanol is 2.044 mPa s and 0.545 mPa s, respectively,36 while the density of 2-propanol and methanol is 0.786 gm/cc and 0.7914 gm/cc, respectively.37 Ionic conductivity is calculated roughly to be 1.1 × 10−6 S/m and 8.5 × 10−6 S/m for 2-propanol and methanol, respectively, from the electroosmotic mobility values.38
B. Method
Dilute suspension of microparticles is prepared by adding 1 mg of microparticle powder in 500 μl of solvent. Prepared suspension is then loaded into the test chamber via polystyrene tubing and syringe. The inlet diameter of access holes to test chamber is slightly smaller than tubing diameter (∼700 μm) which allows for a tight fit and leak proof loading of suspension in the chip. The syringe and loading tube are detached from the test chamber after loading the particle suspension to ensure no pressure build-up. This measure is taken to suppress any pressure driven fluid flow in the test chamber. After ensuring no fluid movement in the test chamber, the chip is placed under a standard microscope objective (Leitz Ergolux, Buffalo Grove, IL, USA) and wired up to the power supply, as shown in Fig. 5. A function generator (Tektronix TM504, Beaverton, OR, USA) is used to apply single phase AC electric potentials at the electrodes. The amplitude of the electric potential is kept fixed at 7.5 V at all times, while the frequency is varied between 40 Hz and 700 Hz to observe the effect on particle dynamics. An oscilloscope (Tektronix TDS 2002, Beaverton, OR, USA) is used to measure the driving frequency and potential.
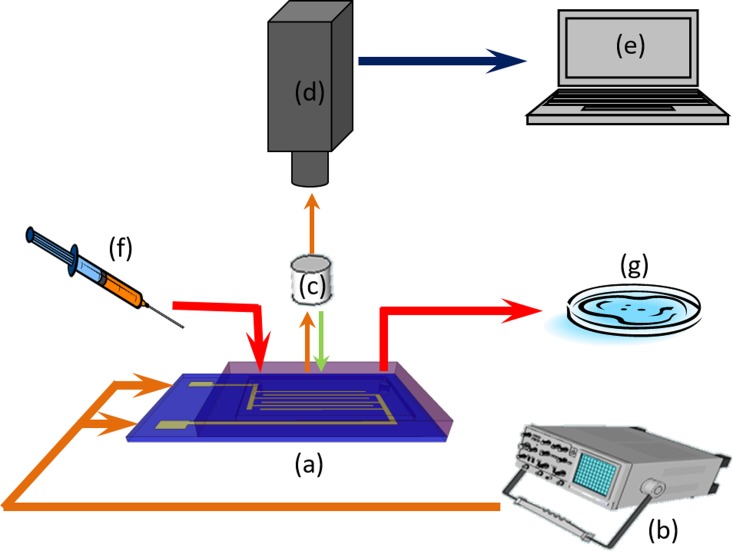
FIG. 5.
Schematic of the setup: (a) Microfluidic chip, (b) function generator, (c) microscope objective, (d) digital camera, (e) image processor, (f) syringe pump, and (g) waste pool.
Owing to the transparency of the PDMS slab, it is easy to visualize particle motion through the top thick PDMS layer of the channel during the experiment. A Canon powershot camera with 30 fps rate (A2850, Melville, NY, USA) is fitted to the microscope to capture particle movement. These movie files are transferred to a computer and particle spin rate is measured during post processing steps. An open source video editing software (OpenShot Video Editor) is used to measure the spin rate by calculating the number of frames elapsed between each rotation.
It would be ideal if individual particles could be loaded in the test space for investigation. However, the simple chip design adopted for this study does not have a provision for letting one microparticle at a time into the test space. Rather, the test space is filled with numerous particles. Particles in close proximity can give rise to “particle-particle interaction” and can influence particle dynamics under the applied electric field.39 To avoid such interactions, a zone has been selected by thorough inspection of the entire test space, where a lone particle is available and whose vicinity (radius of 100 μm) is clear of any other particle. Dynamics of that lone particle is observed, recorded, and measured.
V. RESULTS AND DISCUSSION
A. Particle equilibrium under AC electric field
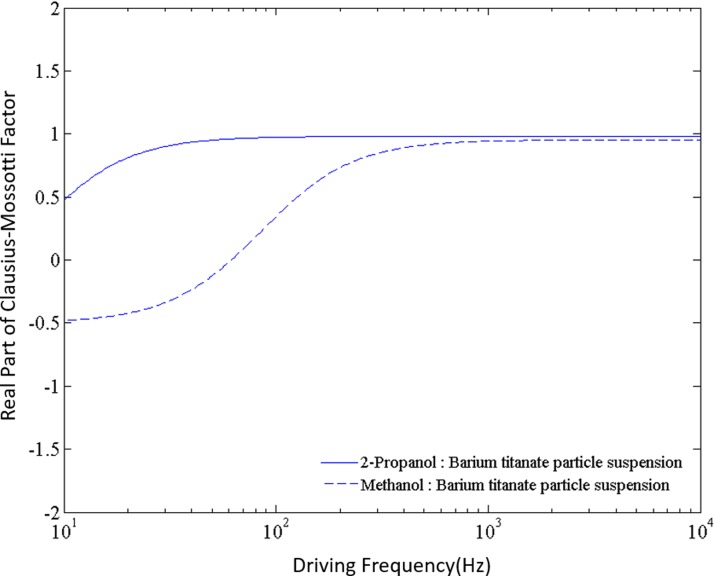
In this section, we present the equilibrium position of particles in 2-propanol and methanol at different applied frequencies of the electric field. In our experiments, the applied frequency range for 2-propanol is from 40 to 90 Hz, while for methanol the range is from 200 to 700 Hz. For both solvents, the barium titanate particle will be subjected to positive dielectrophoresis for the applied frequency range since the real part of the Clausius-Mossotti factor is positive (Fig. 6) within their respective working frequencies. In other words, under the action of a non-uniform electric field, a suspended barium titanate particle will try to go towards the electrode edge where the electric field strength is the maximum. However, instead of reaching the electrode edge, we have observed the barium titanate microparticle to attain different equilibrium positions depending on the applied frequency. This observation is significantly different from others reported in the literature.
FIG. 6.
Real part of Clausius-Mossotti factor for barium titanate particles suspended in 2-propanol and methanol media. It can be seen that within the range of 40–100 Hz in 2-propanol, real part of Clausius-Mossotti factor is positive. This factor is also positive within the range of 200–700 Hz in case of methanol.
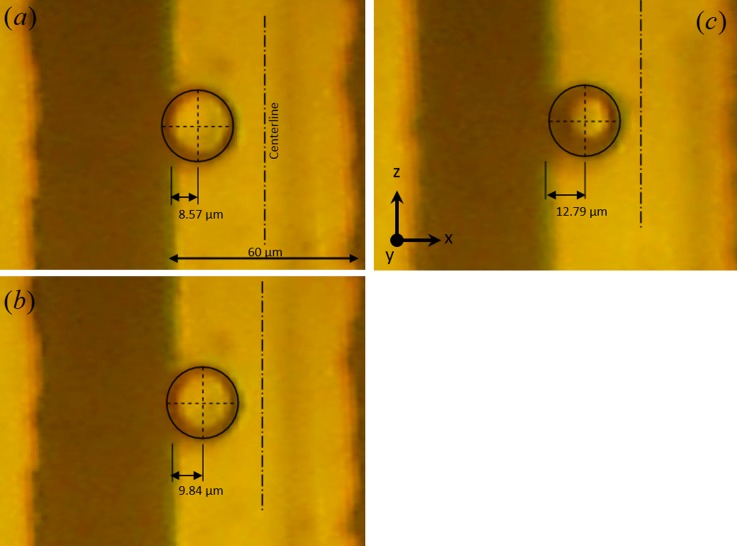
Figure 7 shows the equilibrium position of barium titanate microparticles in 2-propanol solution. It can be seen that at lowest applied frequency (40 Hz), the particle is positioned closer to the electrode edge. The equilibrium position of the particle shifts when applied frequency is changed while the magnitude of the applied potential is kept fixed at 7.5 V. The distance between the particle center and the electrode edge increases from 8.57 μm to 12.79 μm when driving frequency is increased from 40 Hz to 50 Hz. A shift in particle position takes place within the range of 40–90 Hz in the case of 2-propanol in barium titanate suspension. At 90 Hz, the particle reaches the centerline and stays there for any frequency greater than 90 Hz. In other words, our experimental study shows that the equilibrium position of the particle moves from the center of the electrode to the edge as the frequency is decreased. The particle shows similar behavior above every electrode, and these experiments are quite reversible.
FIG. 7.
Barium titanate particle of roughly 25 μm diameter is shown above a 60 μm wide electrode. Particle equilibrium position varies with driving frequency for a constant applied potential (7.5 V). Particle's center location is displayed with respect to the edge of the electrode in all cases. Electrode center is shown as a vertical dashed-dotted line. Particle positions observed in 2-propanol at (a) 40 Hz, (b) 45 Hz, and (c) 50 Hz.
Similar motion of barium titanate particle is observed in methanol as shown in Fig. 8. In this case, the particle motion is observed within the range of 200–700 Hz which is an order of magnitude higher than in the case of 2-propanol. In this case as well, at higher frequencies, the particle is seen to reach the electrode centerline. The frequency dependent equilibrium position of particles suggests that other electric field driven mechanisms are involved in our experimental observation. If only positive dielectrophoresis is active, particles should stay at the electrode edge at all applied frequencies. Yet, we observe from Figs. 7 and 8 that there is a distinct particle motion from electrode edge towards the center as applied frequency is increased. The shift in the particle's equilibrium position with changing frequency cannot be fully explained by dielectrophoretic force alone. We hypothesize that AC electroosmotic fluid flow is responsible for this frequency dependent behavior of barium titanate particles.
FIG. 8.
Barium titanate particle of roughly 25 μm diameter is shown above a 60 μm wide electrode. Particle equilibrium position varies with driving frequency for a constant applied potential (7.5 V). In all cases, particle's center location is displayed with respect to the edge of the electrode. Electrode center is shown as a vertical dashed-dotted line. Particle positions observed in methanol at (a) 300 Hz, (b) 400 Hz, and (c) 500 Hz.
Seminal work of Ramos et al.22,31 demonstrated that in the case of coplanar electrodes, electroosmotic flow is induced on the electrode surface at low frequencies resulting from the interaction of tangential components of nonlinear electric field and ions accumulated in an electric double layer. It is established that typically the direction of this AC electroosmotic flow is from the electrode edge towards the center. When a particle resides close to the electrode surface, the hydrodynamic force felt by the particle due to AC electroosmotic flow counteracts the dielectrophoretic force and prohibits the particle from reaching the electrode edge. As a matter of fact, the electroosmotic flow velocity is a strong function of driving frequency. Hence, increase in frequency causes the rise in flow velocity and hydrodynamic force on the particle. This in turn shifts the force balance and the particle moves towards the electrode center. To prove this hypothesis, a numerical model is employed which takes into account both electric field driven force and viscous force on the particle. In our numerical model, owing to the low Reynolds number in the microfluidic device, the fluid flow velocity is obtained from the Stokes equation as
| (4) |
Here, is the viscosity of fluid, is the fluid velocity, is the pressure, and is an identity tensor. It is important to note that the electric double layer next to the electrode surface was not estimated explicitly. The contribution of electric double layer and resulting AC electroosmotic flow is accounted for using a slip velocity (Eq. (3)) at the electrode surface, while no penetration and no slip velocity are used at the insulating surfaces. In our experimental work, no external pressure is applied during particle electrorotation experiments. Thus, the pressure is set to zero at all boundary points.
In our numerical scheme, momentum conservation equations (Eq. (4)) are solved along with the incompressible continuity equation () to determine the resultant flow field in an applied electric field. The computation of electroosmotic flow velocity requires a complex electric field, . In this study, the complex electric potential, , is obtained from Eq. (5)40
| (5) |
In this simplified model, the estimation of potential distribution in the electric double layer is not required. Rather, a mixed boundary condition is used on the electrode surface to take into account the potential drop in the electric double layer as41
| (6) |
Here, is applied potential at the electrode, is the unit normal, is the applied angular frequency, and is total capacitance of the electric double layer. The electric potential is set to zero at the insulating surface, while time periodic electric potential is used on the active electrode surfaces. For electroosmotic slip velocity (Eq. (3)), the potential drop across the electric double layer () can be calculated from the difference of electrode potential () and the potential at the bulk electrolyte (). All required material properties for numerical simulations are presented in Section IV A.
Next, viscous and time averaged dielectrophoretic forces acting on a particle are calculated from the flow field () and the electric field () as
| (7) |
| (8) |
where is the real part of the particle's complex permittivity, is the conjugate of the electric field , and is the surface area.
Under quasi-equilibrium condition, the location of the particle's equilibrium position can be obtained from
| (9) |
| (10) |
We used an iterative scheme to obtain the equilibrium location of the particle. At equilibrium condition, the velocity of particle approaches zero.
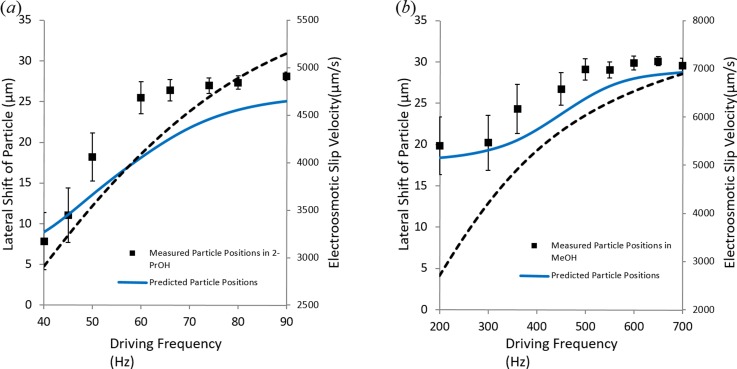
The predicted lateral (x) equilibrium positions of the particle qualitatively match with the experimental observations for both 2-propanol (Fig. 9(a)) and methanol (Fig. 9(b)). The reason for relatively large error bars in experimental measurements is primarily due to the large variance in particle size ( μm) from the mean particle size, which is 30 μm.
FIG. 9.
Predicted and measured barium titanate particle position in (a) 2-propanol and (b) methanol in a domain having 60 μm wide electrode and 40 μm gap between electrodes. Here, the lateral shift is the distance between the electrode edge and the particle center. Applied potential is 7.5 V. The numerically predicted slip velocity at the tip (edge) of the electrode is presented with the dotted line as a function of frequency. The vertical (y) equilibrium positions of particle are also calculated from the force balance in the y-direction by considering particle's weight, dielectrophoretic force, and viscous drag from the AC electroosmotic flow, but they are not presented here due to lack of reliable experimental data in the vertical direction.
Our numerical work confirms that particle's equilibrium position shifts towards the center with an increase in the frequency and this is due to the AC electroosmotic flow dependence on frequency as shown in Fig. 9. The AC electroosmotic flow is sensitive to applied frequency for both 2-propanol and methanol. Our model predicts that there is a gradual rise of velocity until peak velocity is achieved in both cases. In the case of 2-propanol, it can be seen from Fig. 9(a) that within the operating frequency range the electroosmotic velocity keeps rising on the electrode surface. The electroosmotic velocity plotted in Fig. 9(a) is calculated at the tip of the electrode where its magnitude is the highest. This gradual rise in velocity causes increased hydrodynamic force on the particle, which shifts the equilibrium position further towards the electrode center. At 90 Hz, the particle reaches close to the electrode center (located at x = 30 μm) and stays there with further increase in frequency. Though estimated electroosmotic slip velocity keeps rising after 90 Hz, particle position remains unchanged as it reaches the electrode centerline. The reason for that is, close to the electrode center, a counter flow originating from the other electrode edge gets prominent on the particle. Hence, increase in the AC electroosmotic velocity does not necessarily mean change in particle position since the net force on the particle will be zero when it reaches the electrode center.
Barium titanate particles exhibit similar behavior in methanol but the frequency range in this case is 200–700 Hz as can be seen from Fig. 9(b). The difference in the frequency range in case of two media arises from different charging time of the double layer in respective medium. Double layer charging time and the resulting electroosmotic flow over the electrode surface depend on the fluid properties such as electrical conductivity, permittivity, and Debye length.41 Difference in these properties of the two media used is responsible for the observed difference in the experimental frequency range.
B. Particle rotation
We have observed barium titanate particle rotation in both suspensions, i.e., in 2-propanol and in methanol. Figure 10 shows stable rotation of an irregular barium titanate particle in methanol for an applied potential of 7.5 V. We intentionally selected a particle with an irregular shape, as the irregularity of the particle, in this case, is useful to observe a different particle orientation as a function of time. The particle spin is recorded to be 131 revolutions per minute for an applied frequency of 450 Hz. The particle equilibrium position observed is stable and measured to be ∼18.58 μm while it is going through rotational motion. The particle rotation is due to the hydrodynamic torque generated around the particle. The origin of hydrodynamic torque lies on non-uniform flow distribution around the particle. At the region in between the particle and electrode surface, there exists high horizontal flow velocity compared to far above from the electrode. This non-uniformity of flow creates hydrodynamic torque on the particle. Uniform spheroids also exhibit similar rotational motion (see movies in the supplementary materials42). Particle rotation has been observed within the range of frequencies used during our experiments at their respected equilibrium positions.
FIG. 10.
A barium titanate particle rotating at 131 rpm about an axis parallel to electrode edge at 450 Hz and 7.5 V in methanol. Particle orientation is shown at (a) 0 s, (b) 0.554 s, (c) 1.09 s. Particle position displayed here is roughly 18.58 μm away from the electrode edge and is stable. Controlled and stable particle rotations are obtained for uniform microsphere, although a particle with defects is shown in this figure for vivid demonstration of particle rotation. See movies in the supplementary materials.42
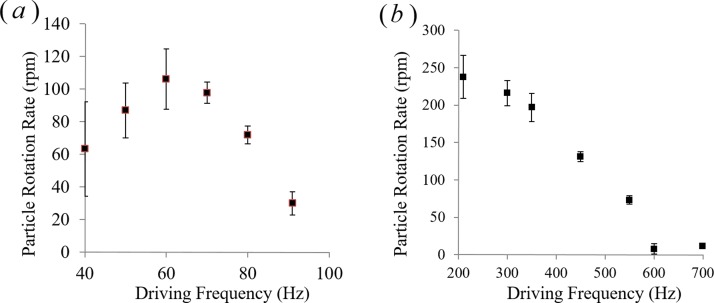
The rotation rate of barium titanate particles is shown in Fig. 11 for both 2-propanol and in methanol. In the case of 2-propanol (Fig. 11(a)), the observed rotation rate has a peak around 60 Hz and gradually decays when frequency is increased. The initial rise of the particle rotation rates from 40 to 60 Hz is due to the increased AC electroosmotic flow rates. However, at the same time the particle gets pushed further towards the electrode center. With the further increase in frequency (above 60 Hz), the particle shifts significantly towards the electrode center and particle rotation rate decays with it. A detailed investigation of the flow velocity profile over the electrode is needed to explain the decrease in the rotation rate.
FIG. 11.
Rotation rates of regular barium titanate particle in (a) 2-propanol and (b) methanol are plotted as a function of driving frequency for an applied electric potential amplitude of 7.5 V. At all frequencies, particle position is found stable while it undergoes rotational motion due to the combined positive dielectrophoresis and electroosmosis.
Green et al.30 have studied AC electroosmotic flow created by coplanar electrodes, and they found that electroosmotic velocity is the maximum at the electrode edge and it decreases toward the center of the electrode. This sharp decrease in flow velocity is responsible for the decay in the rotation rate with the increase in the frequency. Thus, it can be concluded that electroosmotic flow created over the electrode is able to push the particle equilibrium towards the electrode center, but at the same time, flow non-uniformity around the particle goes down at higher frequencies. Also, as the particle approaches the electrode centerline, a counter flow is experienced by the particle originating from the other edge of the electrode. A combination of these two effects experiences dwindling particle rotation rates at positions near the electrode center. A similar trend is seen for barium titanate particles immersed in methanol (Fig. 11(b)). The only discrepancy in this case is we have not seen a rise to the peak rotation rate as is visible in the case of 2-propanol. This happens because in case of methanol instability in flow has been detected at lower frequencies (100–200 Hz). Most probably, Faradic reaction takes place, which alters the flow field and particle rotation rates in this low frequency regime. However, at frequencies greater than 200 Hz, in the case of methanol, a similar trend of particle equilibrium positions and rotation rates is observed.
VI. CONCLUDING REMARKS
A simple experimental technique is presented to rotate microparticles in a microfluidic device using a stationary AC electric field. A microfluidic chip is fabricated out of glass and PDMS. The glass substrate has an array of interdigitated coplanar titanium electrodes. Particle dynamics is observed via the top clear PDMS surface of the channel. Two different fluid media, 2-propanol and methanol, are used to rotate barium titanate microparticles using a stationary electric field. It has been shown that the combination of positive dielectrophoresis and AC electroosmotic flow can be used to control particle equilibrium position and rotation rate by changing the frequency of the applied electric field. In 2-propanol, the equilibrium position shifts within the frequency range of 40–90 Hz and a total lateral shift of 17 μm across electrode width is recorded. In methanol, a shift in particle position is recorded within the frequency range of 200–700 Hz and the total lateral shift is 12 μm. It is also observed that the movement of the particle is always symmetric with respect to the centerline of bar electrodes. In other words, the lateral movement of the particle is observed between one of the electrode edges and the electrode centerline. It has been demonstrated that barium titanate particles go through stable rotation at their equilibrium position. These rotation rates are a function of equilibrium positions and frequency. We have observed a maximum rotation rate of 105 revolutions per minute in 2-propanol at 60 Hz and 205 revolutions per minute in methanol at 200 Hz. Hydrodynamic torque induced on the particle due to non-uniform flow field in the channel is probably responsible for particle rotation. This novel microparticle rotation method will be helpful for visualization of biological cell morphology with the inexpensive standard laboratory tools.
ACKNOWLEDGMENTS
This work was supported in part by the National Science Foundation under Grant No. CBET 1250107.
References
- 1. Huang J., Yu K., Gu G., and Karttunen M., Phys. Rev. E 67(5), 051405 (2003). 10.1103/PhysRevE.67.051405 [DOI] [PubMed] [Google Scholar]
- 2. Pohl H. A. and Pohl H., Dielectrophoresis: The Behavior of Neutral Matter in Nonuniform Electric Fields ( Cambridge University Press, Cambridge, 1978). [Google Scholar]
- 3. Salgado J. D., Horiuchi K., and Dutta P., J. Micromech. Microeng. 16, 920–928 (2006). 10.1088/0960-1317/16/5/007 [DOI] [Google Scholar]
- 4. Foster K. R., Sauer F. A., and Schwan H. P., Biophys. J. 63(1), 180 (1992). 10.1016/S0006-3495(92)81588-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Pethig R., Biomicrofluidics 4(2), 022811 (2010). 10.1063/1.3456626 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Jones T. B., IEEE Eng. Med. Biol. Mag. 22(6), 33–42 (2003). 10.1109/MEMB.2003.1304999 [DOI] [PubMed] [Google Scholar]
- 7. Jubery T. Z., Srivastava S. K., and Dutta P., Electrophoresis 35, 691–713 (2014). 10.1002/elps.201300424 [DOI] [PubMed] [Google Scholar]
- 8. Takamura Y., Onoda H., Inokuchi H., Adachi S., Oki A., and Horiike Y., Electrophoresis 24(1–2), 185–192 (2003). 10.1002/elps.200390012 [DOI] [PubMed] [Google Scholar]
- 9. Roman G. T., Hlaus T., Bass K. J., Seelhammer T. G., and Culbertson C. T., Anal. Chem. 77(5), 1414–1422 (2005). 10.1021/ac048811z [DOI] [PubMed] [Google Scholar]
- 10. Lazar I. M. and Karger B. L., Anal. Chem. 74(24), 6259–6268 (2002). 10.1021/ac0203950 [DOI] [PubMed] [Google Scholar]
- 11. Washizu M. and Jones T., J. Electrost. 38(3), 199–211 (1996). 10.1016/S0304-3886(96)00025-3 [DOI] [Google Scholar]
- 12. Huang Y., Holzel R., Pethig R., and Wang X.-B., Phys. Med. Biol. 37(7), 1499 (1992). 10.1088/0031-9155/37/7/003 [DOI] [PubMed] [Google Scholar]
- 13. Wang X.-B., Huang Y., Gascoyne P. R., Becker F. F., Hölzel R., and Pethig R., Biochim. Biophys. Acta 1193(2), 330–344 (1994). 10.1016/0005-2736(94)90170-8 [DOI] [PubMed] [Google Scholar]
- 14. Goater A. and Pethig R., Parasitology 117(07), 177–189 (1999). 10.1017/S0031182099004114 [DOI] [Google Scholar]
- 15. Arnold W. and Zimmermann U., J. Electrost. 21(2), 151–191 (1988). 10.1016/0304-3886(88)90027-7 [DOI] [Google Scholar]
- 16. Huang C., Chen A., Guo M., and Yu J., Biotechnol. Lett. 29(9), 1307–1313 (2007). 10.1007/s10529-007-9414-6 [DOI] [PubMed] [Google Scholar]
- 17. Pickard W. F., Il Nuovo Cimento 21(2), 316–332 (1961). 10.1007/BF02832557 [DOI] [Google Scholar]
- 18. Pohl H. A. and Crane J. S., Biophys. J. 11(9), 711–727 (1971). 10.1016/S0006-3495(71)86249-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Hou D. and Chang H.-C., Phys. Fluids 18(7), 071702 (2006). 10.1063/1.2221348 [DOI] [Google Scholar]
- 20. Chau L. H., Liang W. F., Cheung F. W. K., Liu W. K., Li W. J., Chen S. C., and Lee G. B., PloS One 8(1), e51577 (2013). 10.1371/journal.pone.0051577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Vaillier C., Honegger T., Kermarrec F., Gidrol X., and Peyrade D., PloS One 9(4), e95231 (2014). 10.1371/journal.pone.0095231 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Gonzalez A., Ramos A., Green N., Castellanos A., and Morgan H., Phys. Rev. E 61(4), 4019 (2000). 10.1103/PhysRevE.61.4019 [DOI] [PubMed] [Google Scholar]
- 23. Liu S.-J., Wei H.-H., Hwang S.-H., and Chang H.-C., Phys. Rev. E 82(2), 026308 (2010). 10.1103/PhysRevE.82.026308 [DOI] [PubMed] [Google Scholar]
- 24. Wu J., Ben Y., Battigelli D., and Chang H.-C., Ind. Eng. Chem. Res. 44(8), 2815–2822 (2005). 10.1021/ie049417u [DOI] [Google Scholar]
- 25. Wu J., Ben Y., and Chang H.-C., Microfluid. Nanofluid. 1(2), 161–167 (2005). 10.1007/s10404-004-0024-5 [DOI] [Google Scholar]
- 26. Zhou H., White L. R., and Tilton R. D., J. Colloid Interface Sci. 285(1), 179–191 (2005). 10.1016/j.jcis.2004.11.040 [DOI] [PubMed] [Google Scholar]
- 27. Tathireddy P., Choi Y.-H., and Skliar M., J. Electrost. 66(11), 609–619 (2008). 10.1016/j.elstat.2008.09.002 [DOI] [Google Scholar]
- 28. Jubery T. Z. and Dutta P., Numerical Heat Transfer, Part A 64, 107–131 (2013). 10.1080/10407782.2013.773780 [DOI] [Google Scholar]
- 29. Morgan H. and Green N. G., AC Electrokinetics: Colloids and Nanoparticles ( Research Studies Press, 2003). [Google Scholar]
- 30. Green N. G., Ramos A., Gonzalez A., Morgan H., and Castellanos A., Phys. Rev. E 66(2), 026305 (2002). 10.1103/PhysRevE.66.026305 [DOI] [PubMed] [Google Scholar]
- 31. Ramos A., Morgan H., Green N., and Castellanos A., J. Phys. D: Appl. Phys. 31(18), 2338 (1998). 10.1088/0022-3727/31/18/021 [DOI] [Google Scholar]
- 32. Jubery T. Z., Hossan M. R., Bottenus D. R., Ivory C. F., Dong W., and Dutta P., Biomicrofluidics 6, 016503 (2012). 10.1063/1.3683163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Duffy D. C., McDonald J. C., Schueller O. J. A., and Whitesides G. M., Anal. Chem. 70(23), 4974–4984 (1998). 10.1021/ac980656z [DOI] [PubMed] [Google Scholar]
- 34. Yao K., Zhang L., Yao X., and Zhu W., J. Mater. Sci. 32(14), 3659–3665 (1997). 10.1023/A:1018638631777 [DOI] [Google Scholar]
- 35. Scriba G. K., J. Chromatogr. A 1159(1), 28–41 (2007). 10.1016/j.chroma.2007.02.005 [DOI] [PubMed] [Google Scholar]
- 36. Porras S. P., Riekkola M. L., and Kenndler E., Electrophoresis 24(10), 1485–1498 (2003). 10.1002/elps.200305373 [DOI] [PubMed] [Google Scholar]
- 37. Monick J. A., Alcohols: Their Chemistry, Properties, and Manufacture ( Reinhold Book Corporation, New York, 1968). [Google Scholar]
- 38. Valkó I. E., Sirén H., and Riekkola M. L., J. Microcolumn Sep. 11(3), 199–208 (1999). [DOI] [Google Scholar]
- 39. Hossan M. R., Dillon R., Roy A. K., and Dutta P., J. Colloid Interface Sci. 394, 619–629 (2013). 10.1016/j.jcis.2012.12.039 [DOI] [PubMed] [Google Scholar]
- 40. Hossan M. R., Dillon R., and Dutta P., J. Comput. Phys. 270, 640–659 (2014). 10.1016/j.jcp.2014.04.012 [DOI] [Google Scholar]
- 41. Bazant M. Z., Thornton K., and Ajdari A., Phys. Rev. E 70(2), 021506 (2004). 10.1103/PhysRevE.70.021506 [DOI] [PubMed] [Google Scholar]
- 42.See supplementary material at http://dx.doi.org/10.1063/1.4943032E-BIOMGB-10-007602 for rotation of barium titanate microparticles in 2-propanol and methanol at different electric field frequency.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1063/1.4943032E-BIOMGB-10-007602 for rotation of barium titanate microparticles in 2-propanol and methanol at different electric field frequency.