Molecular Basis of S100A1 Activation at Saturating and Subsaturating Calcium Concentrations

Abstract

The S100A1 protein mediates a wide variety of physiological processes through its binding of calcium (Ca²⁺) and endogenous target proteins. S100A1 presents two Ca²⁺-binding domains: a high-affinity “canonical” EF (cEF) hand and a low-affinity “pseudo” EF (pEF) hand. Accumulating evidence suggests that both Ca²⁺-binding sites must be saturated to stabilize an open state conducive to peptide recognition, yet the pEF hand’s low affinity limits Ca²⁺ binding at normal physiological concentrations. To understand the molecular basis of Ca²⁺ binding and open-state stabilization, we performed 100 ns molecular dynamics simulations of S100A1 in the apo/holo (Ca²⁺-free/bound) states and a half-saturated state, for which only the cEF sites are Ca²⁺-bound. Our simulations indicate that the pattern of oxygen coordination about Ca²⁺ in the cEF relative to the pEF site contributes to the former’s higher affinity, whereas Ca²⁺ binding strongly reshapes the protein’s conformational dynamics by disrupting β-sheet coupling between EF hands. Moreover, modeling of the half-saturated configuration suggests that the open state is unstable and reverts toward a closed state in the absence of the pEF Ca²⁺ ion. These findings indicate that Ca²⁺ binding at the cEF site alone is insufficient to stabilize opening; thus, posttranslational modification of the protein may be required for target peptide binding at subsaturating intracellular Ca²⁺ levels.

Introduction

S100A1 is a Ca²⁺-binding protein commonly found in neuronal, renal (1), and cardiac (2, 3) tissue, in the latter of which it is implicated in cardiomyopathy (for reviews, see (4, 5)). S100A1 contributes to a variety of protein-protein interaction (PPI) events after Ca²⁺-dependent activation, including those of the sarcoplasmic reticulum (ryanodine receptor (6, 7), SERCA2a and phospholamban (8, 9), and a cationic channel (TRPM3 (3)) to regulate Ca²⁺ homeostasis (10). The S100A1 protein forms a globular homodimer that contains two Ca²⁺-binding sites per monomer, as shown in Fig. 1. Each S100A1 monomer presents two Ca²⁺-binding sites consisting of a helix-loop-helix secondary-structure motif that is commonly called the “EF hand” (11). The canonical form of the EF hand, which we refer to as the cEF hand, consists of 12 residues and is highly conserved in many Ca²⁺-binding proteins, such as calmodulin (CaM) and troponin C (TnC) (12, 13).

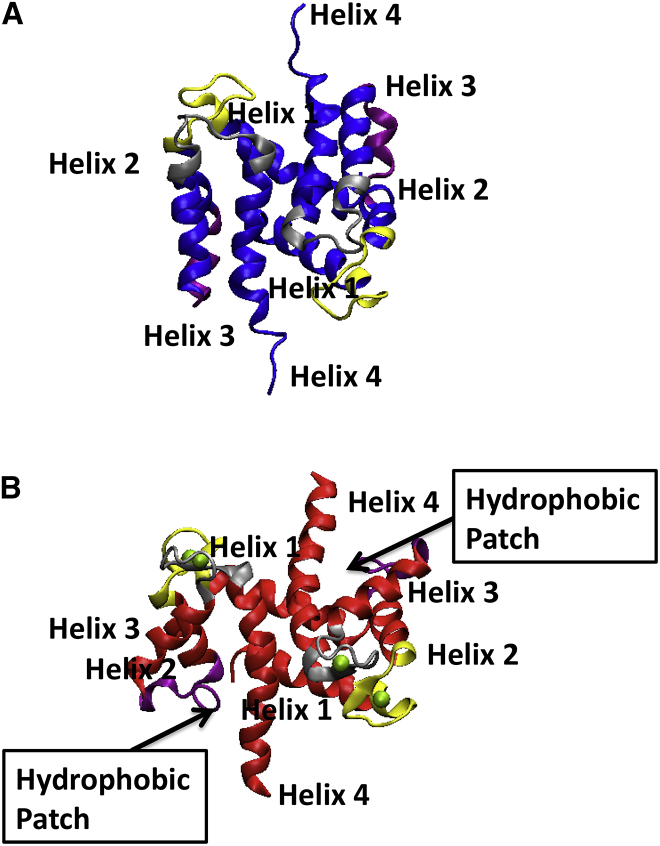
Figure 1.

NMR structures of the human apo (PDB: 2L0P) (A) and holo (PDB: 2LP3) S100A1 (B) states (26, 29). The pEF (yellow), linker (purple), cEF (gray), and helical bundle (red) are represented in the structures, and the Ca²⁺ ions (green) are shown for the holo form. The binding of Ca²⁺ ions reveals a hydrophobic protein recognition patch near H3. To see this figure in color, go online.

The S100A1 cEF region spans 12 residues between D62 and E73, whereas the second, “pseudo” EF hand (pEF), is unique to the S100 family and related proteins, with 14 residues bridging S19 to E32 (11, 14). Experiments show that the first Ca²⁺ ion binds to the cEF with a dissociation constant, K_d, of 27–250 μM compared to a K_d of 250–16,700 μM for the pEF domain (15, 16)). It is further believed that Ca²⁺ binding to pEF proceeds in a noncooperative fashion (15), but the structural basis of consecutive binding remains unclear.

Upon saturation of the S100A1 monomer with two Ca²⁺ ions, the protein undergoes a conformational change from a closed to an open state that is characterized by the exposure of hydrophobic residues between helices 3 (H3) and 4 (H4) (15, 16) (see Fig. 1). It is the presentation of this open hydrophobic patch that promotes PPIs (17, 18), in a fashion similar to PPI formation by the TnC (19, 20, 21, 22) and CaM proteins (23, 24, 25). Nuclear magnetic resonance (NMR) studies have revealed atomic-resolution details of the S100A1 conformations in the apo (Ca²⁺-free) (26, 27, 28), holo (Ca²⁺-saturated) (16, 29) (Fig. 1, A and B), and target-protein-bound states (6, 17, 18). An open question, however, is how S100A1 participates in peptide-binding events given that saturation of the cEF and pEF hands requires Ca²⁺ ion concentrations of 100–10,000 μM, whereas physiological intracellular Ca²⁺ rarely exceeds tens of micromolar Ca²⁺ in localized regions (30, 31).

To answer this question, we characterized key physiochemical drivers of high-affinity Ca²⁺ binding and the stabilization of the open state in the apo and holo states using molecular simulations. We complemented these analyses with simulations of the “half-saturated” configuration, for which only the cEF site is Ca²⁺ bound, to investigate the relative stability of the open and closed states when the pEF hand is devoid of Ca²⁺ ions. To this end, we performed 100 ns molecular dynamics (MD) simulations of the apo and holo states, as well as extended (>120 ns) runs on the half-saturated holo states to model the S100A1 structure and dynamics under physiological binding configurations. We relate the protein’s Ca²⁺ and target-protein-binding mechanisms to structural dynamics local to the binding domains as well as to allosterically driven global conformational motions. First, we analyzed the binding site by estimating NMR amide order parameters as indicators of protein flexibility, for Ca²⁺-binding domains in the apo and holo states. Second, we compared the relative positioning and coordination of EF-hand oxygens in the presence and absence of Ca²⁺ ion in the pEF and cEF hands. Third, we examined the impact of Ca²⁺-ion binding on the global conformation of the protein through cross correlation, principal-component analysis (PCA), and measuring bundle helix displacements. Our results support prior experimental studies (15) suggesting that full EF-hand saturation is required for open-state stabilization. Hence, posttranslational modification of the protein may be required to form the open state for peptide recognition at physiological Ca²⁺ concentration levels. Moreover, our simulations provide, to our knowledge, new insight into 1) how chelating oxygen distributions and charges within the EF hands may tune Ca²⁺ binding affinities, and 2) the allosteric control of open-state stabilization via correlative motions and disruption of β-sheet formation between the cEF and pEF domains.

Materials and Methods

MD simulations

NMR-derived homodimeric structures were used as starting conformations for the apo state (PDB: 2L0P (26) and 2LLU (28)), and holo state (PDB: 2LP3) (29). Using TLeap (32, 33), all systems were neutralized, explicitly solvated in a 20.0-Å-margin TIP3P water box in 0.15 M KCl solution and parameterized with the AMBER-12SB force field (FF) (34). The protein consists of 186 residues in a system of ∼20,000 water molecules and 130 neutralizing ions, for a total of ∼60,000 atoms. Ca²⁺ parameters were based on a recent formulation for divalent ions (Li-Merz (35)) shown to reproduce experimental coordination numbers and hydration free energies through optimizing the cations’ 12-6 Lennard Jones interactions (35). In the Results and Discussion section, we verify that the Li-Merz cation reasonably reproduces experimentally estimated coordination distances and EF-hand amide order parameters. Generally speaking, we have found that standard Ca²⁺ parameters, such as those from Marchand et al. (36), perform reasonably well for recapitulating coordinating structures and order parameters in EF-hand-based Ca²⁺-binding proteins, including TnC (37, 38). The PMEMD module within the AMBER 14 package (32, 33) was used for minimization and equilibration, whereas the pmemd.cuda engines were used for the initial 100 ns production MD runs performed in quadruplicate. MD simulations in part utilized resources provided by the XSEDE high performance computing facilities (39). Our model of the half-saturated S100A1 was based on removing Ca²⁺ ions from the pEF hand of the holo structure (PDB: 2LP3); attempts to add Ca²⁺ ions to the apo state did not lead to an adequately coordinated structure. We recognize that the unresolved equilibrium conformations of the half-saturated state may entail localized reorganization of the protein; we approached this challenge by first performing normal equilibration routines to relax the EF-hand regions, followed by long-timescale MD simulations performed in succession. As discussed in the Results and Discussion section, significant relaxation of the protein toward an apo-like state was observed within 60 ns. We also performed four additional runs for snapshots from two of the half-saturated trajectories (see Section S1.3.6 in the Supporting Material). Further details of the MD simulation configurations are summarized in Section S1.1.1 in the Supporting Material).

Simulation trajectory analysis

Order parameters

Backbone N-H order parameters were calculated using the isotropic reorientational eigenmode dynamics approach (40) via the ptraj and mat2s2.py programs. Twenty scans consisting of window sizes of 5 ns (2500 frames) from the 100 ns (50,000 frames) saved for each simulation were used, which is comparable to the window sizes suggested by Genheden et al. (40).

Helix angles

Interhlx (K. Yap, University of Toronto, Toronto, Ontario, Canada) was used to calculate the interhelical angles. Helical lengths matched those from the respective NMR references and are outlined in Table S1. The helical angles were calculated for 500 snapshots saved every 0.2 ns during the 100 ns simulations.

Trajectory analysis and Ca²⁺/oxygen radial distributions

Standard trajectory analyses including root mean square fluctuations (RMSFs), hydrogen-bonding patterns, and oxygen/Ca²⁺ distances were computed using the Lightweight Object-Oriented Structure library (LOOS) ((41) and T. D. Romo and A. Grossfield, 2013, Biophys. J., abstract). Common reference positions were obtained by aligning the α-carbon atoms to the holo-state configuration (PDB: 2LP3 (29)). For Ca²⁺ coordination comparisons with the apo cases, the Ca²⁺ ion position was approximated by the corresponding location in the aligned holo state. Except where noted, all custom analyses were written in python and are available at https://bitbucket.org/pkhlab/pkh-lab-analyses/.

Electrostatic score

Two-dimensional histograms of the number of Ca²⁺-oxygen contacts with respect to time and distance were computed for all side-chain oxygens and backbone oxygens to illustrate interactions between the Ca²⁺ ion and its oxygen ligands. We defined an electrostatic score (Eq. 1) to assess the interactions indicated in these histograms:

$$E_{\text{elec}}=q_{{\text{Ca}}^{2+}}\sum _{r_i}\sum _{j=\text{bb},\text{sc}}\left(q_j{\rho }_j\left(r_i\right)r_i^{-1}\right),$$ (1)

where $E_{\text{elec}}$ is the electrostatic score, $q_{{\text{Ca}}^{2+}}$ is the charge on the Ca²⁺ ion (+2), $q_{\text{bb}}$ and $q_{\text{sc}}$ are based on CHARMM partial charges for the backbone and side-chain oxygen atoms (−0.51 and −0.76, respectively) (42, 43, 44), and ρ is the density of oxygen atoms at distance $r_i$ (Å). Although this formula resembles the Poisson model of electrostatic energy for a cloud of point charges, we opted for a simplified score given the difficulty of estimating a position-dependent dielectric constant in the neighborhood of the bound ion. The advantage of this approach is that we can qualitatively assess how the electrostatic field in the EF-hand domain changes between the apo and holo states. Conventional procedures for assessing interaction energies, such as molecular mechanics/Poisson Boltzmann surface area analysis (MM/PBSA) (45, 46, 47, 48), are facilitated when an explicit Ca²⁺ ion is included in all simulations, which is unfeasible for the apo state. Nevertheless, to ensure that our electrostatic score was consistent with conventional interaction energy methods, we determined the MM electrostatic energies from the MM/PBSA program for the holo and half-saturated cases, as discussed in Section S1.2 in the Supporting Material.

PCA

The Bio3D package (49) was used to quantify the large-scale protein conformational changes shared by proteins homologous to S100A1, according to procedures we outlined for two related Ca²⁺-binding proteins (see Kekenes-Huskey et al. (37) and Lindert et al. (38)). A BLAST search (50) on the human S100A1 sequence was performed with the NMR structure (PDB: 2L0P) (26) as input. Seven hundred and seventy-eight sequences were found, and the top 56 chains from 28 homodimer proteins with sequence identities ranging above 92.5% were used for subsequent sequence alignment and PCA. From these homologous sequences, Bio3D identified an invariant core of atoms with the least positional variation across all available protein structures. The invariant core most strongly consisted of those atoms buried within the S100A1 helical bundle. All structural sequences were aligned to this core, after which PCA was performed to identify bases presenting the largest modes of structural variation. The largest principal components (PCs) represent the most significant conformational differences between the apo and holo proteins; PCs 1 and 2 accounted for 74.4% of the variance, with PC1 making up 57.2% of the variance.

Residue cross correlation analysis

The four trajectories for each case were aligned using LOOS to both chains in the first frame of the respective NMR conformations. In Bio3D, residue cross correlation analysis was conducted with the dynamical cross correlation map (49, 51, 52) on the α-carbons of chain A (residues 1–93) for each protein.

Results and Discussion

Predicted Ca²⁺-coordination and N-H order parameters are consistent with NMR data

We first verified that our predicted coordination distances in the holo state are consistent with NMR-derived NOESY inter-proton distance constraints (29) (Table S2). The coordination distances in the simulations were measured between the specified atoms for every time step (2 fs) over the course of 100 ns, from which means and standard deviations were reported based on the averages for each independent simulation. The simulated data were compared against coordinating distances reflected in the ensemble of holo NMR structures (PDB: 2LP3 (29)). Nearly all average coordinating distances shown for the NMR structures were within 2.91 Å, compared to 2.77 Å in our simulations. One exception was the Ca²⁺-N64 O_δ1 distance, for which we report an average distance of 4.26 ± 2.28 Å versus the NMR measured distances of 2.55 ± 0.04 Å. The larger standard deviation in our data reflects that the Ca²⁺/N64 O_δ1 atoms were bound for a significant fraction of the simulation, although the Ca²⁺ ion would frequently exchange binding partners with water in the EF-hand domain. These data confirm that the Li-Merz Ca²⁺ parameter set reasonably reproduce experimentally determined coordination numbers and distances, despite their optimization for reproducing solvation structure and energies (35).

We next compared protein conformational dynamics reflected in our simulations with appropriate experimentally derived observables. Specifically, amide nitrogen/hydrogen order parameters have been widely used to probe backbone mobility in EF-hand-based proteins, particularly in the presence and absence of Ca²⁺ (29, 53). By definition, order parameters approaching 1.0 signify greater protein rigidity, whereas order parameters approaching 0.0 imply greater flexibility. Order-parameter calculations thereby enable assessment of the Ca²⁺-binding site and linker region stability, which can further be validated against experimental data. Specifically, prior NMR studies (29) of S100A1 in its apo and holo states indicated significant changes in backbone mobility, especially near the Ca²⁺-binding region, where the presence of Ca²⁺ suppressed EF-hand fluctuations (leading to larger order parameters) relative to the apo state.

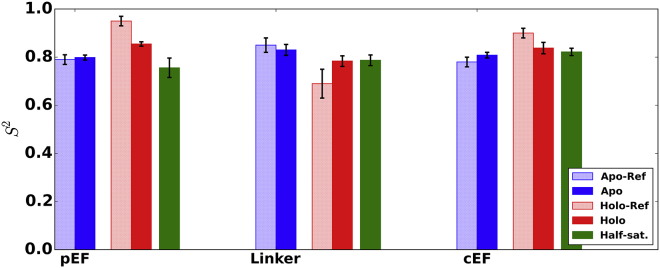
In Fig. 2, we compare prior NMR-derived order parameters with computed estimates averaged from four 100 ns simulations. In the three regions presented, the pEF hand (residues S19–E32; see Table S1), the linker (residues L41–D50), and the cEF hand (residues D62–E73), the estimates for the apo state are in good agreement with experiment (0.80 ± 0.01 theoretical versus 0.79 ± 0.02 experimental for pEF, 0.81 ± 0.01 versus 0.78 ± 0.02 for cEF, and 0.83 ± 0.02 versus 0.85 ± 0.03 for the linker). For the holo state, we note that the calculated order parameters were greater for the Ca²⁺-binding sites relative to those calculated for the the apo state (0.85 ± 0.01 calculated holo versus 0.80 ± 0.01 calculated apo for the pEF and 0.84 ± 0.02 calculated holo versus 0.81 ± 0.01 calculated apo for the cEF), which signifies more rigid EF hands in the Ca²⁺-bound state. The decreased mobility in the EF holo state undoubtedly arises in part because the backbone and side-chain oxygens involved in coordinating Ca²⁺ are strongly bound and thus restrict backbone movement. We note, however, that our computed order parameters for the holo cases were similar to, but somewhat smaller than, the experimental holo measurements. This modest difference may suggest that our simulations moderately overestimated the lability of Ca²⁺-binding regions. If this is the case, further refined Ca²⁺/oxygen parameters (54) or use of polarizable force fields (55) may better stabilize coordination and recapitulate the order parameters derived from NMR studies. We nevertheless find agreement with the experimental trends for the linker region, residues 41–50, which suggest smaller order parameters for the holo state (calculated 0.78 ± 0.02) than for the apo state (calculated 0.83 ± 0.02). The holo state’s smaller order parameters indicate greater linker mobility compared to the apo state, although the underlying mechanism is unclear.

Figure 2.

Experimental order parameters (29), S², for the apo (light blue) and holo (light red) cases versus the respective calculated order parameters (dark blue and dark red, respectively) and the calculated half-saturated cEF states (green). Vertical error bars represent standard deviations of the four averages of the two chains in each simulation. Predictions for the apo and holo states were consistent with experiment. To see this figure in color, go online.

The concurrence of our predicted order parameters and coordination distances with experiment suggest that the Li-Merz parameters are sufficiently reliable for predicting conformational and dynamic properties of small Ca²⁺-binding proteins. These findings are also consistent with those of prior studies of similar globular Ca²⁺-binding proteins, including TnC (37, 38, 56, 57), CaM (58, 59), and calbindin (36, 60), which demonstrated good agreement with experimental measurements such as chelation distances, order parameters, and global conformational dynamics, using conventional MD protocols without polarization effects. Also remarkable were the results from Jiang et al. for Ca²⁺ binding to calbindin (60), for which the free energy of binding was within 2.1 kcal/mol of the experimental measurements. We note, however, that explicit consideration of polarization and charge transfer effects via ab initio methods (61) or polarizable models (45, 55, 62) are likely required for obtaining further refined estimates of protein/cation affinity. Validation of such methodologies and parameters may consider excellent experimental protein/cation affinity data such as those reported for CaM (63), for which site-specific affinity data were precisely measured. We nevertheless anticipate that subtle variation in chelation energetics due to these nonclassical phenomena would have limited impact on the chelation shell structure and global protein conformational dynamics, given the consistency of classical force-field MD simulations of Ca²⁺-binding proteins with experimental probes of protein dynamics.

It has been reported (15) that at physiological Ca²⁺ concentrations, the pEF hand is not Ca²⁺ bound, and thus, the S100A1 open state is inaccessible. To provide insight into the backbone dynamics of the most probable binding configuration in physiological systems, we present order parameters for the half-saturated (cEF-only) S100A1 protein (see Fig. 2). Our calculated results indicate similar order parameters in the cEF region for the fully saturated holo and half-saturated systems (0.84 ± 0.02 and 0.82 ± 0.02, respectively), with modestly smaller order parameters for the latter configuration. Order parameters for the pEF region of the half-saturated state (0.76 ± 0.04) were comparable to and somewhat smaller than those reported for the unsaturated (apo) state (calculated as 0.80 ± 0.01) as opposed to the fully saturated holo state (calculated as 0.85 ± 0.01). The similarity of the pEF dynamics in the apo and half-saturated cases suggests that the presence of cEF-hand Ca²⁺ has little impact on the structure and mobility of the pEF region, which may support experimental observations of minimal Ca²⁺-binding cooperativity (15). We find that the linker region is equally mobile in the half- and fully saturated configurations, which may indicate that the cEF-bound Ca²⁺ ion is sufficient to induce linker mobility.

In Section S1.3.2 in the Supporting Material, we present backbone amide nitrogen root mean-square fluctuations (RMSFs) for the apo, holo, and half-saturated states that quantify the relative lability of the EF-hand domains in a manner similar, but not equivalent, to the amide order parameters (Fig. S1). We find that in the pEF hand, the reported RMSFs were significantly greater for the apo and half-saturated proteins than for the holo states. This behavior was not unexpected, given that strong Ca²⁺/oxygen interactions in the holo state should be expected to dampen pEF hand mobility. In the cEF hand, we note that the holo and half-saturated RMSFs were statistically comparable. Since the RMSF values merely indicate the relative fluctuations of the residues and not their positional decorrelation implied in order parameter analysis (64), these data indicate that the amides continued to fluctuate, although they were strongly constrained by the complexed Ca²⁺.

Oxygen radial distribution about the bound Ca²⁺ ion

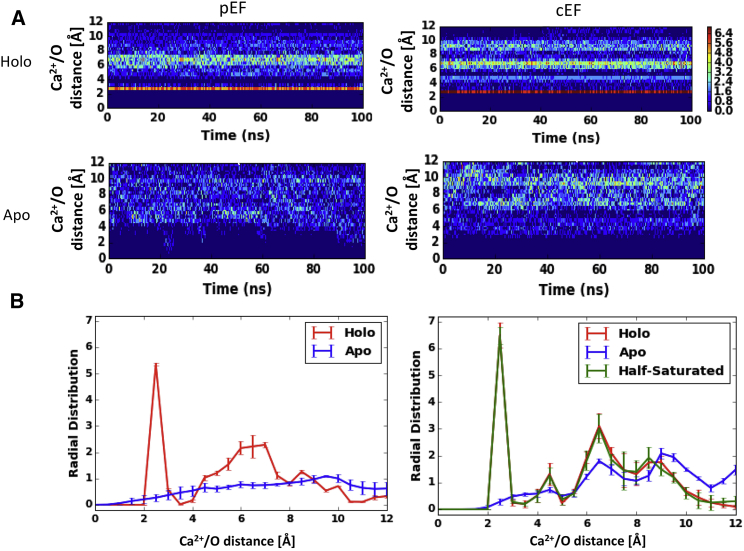
We further investigated the Ca²⁺ coordination to understand the molecular basis for higher Ca²⁺ affinity at the cEF relative to the pEF hand (15). Canonical high-affinity EF-hand Ca²⁺ binding is typically afforded by short Ca²⁺/oxygen distances (1.8–3.5 Å) stemming from seven oxygens arranged in a pentagonal bipyramidal fashion (12, 13, 65). In the cEF hand (D62–E73), the Ca²⁺ ion coordinated with seven oxygens, six of which were side-chain carboxylate oxygens and one backbone amide oxygen. The pEF hand (S19–E32) presented two additional residues relative to the cEF hand, which still promoted seven coordinate oxygens, although in this case, four arose from backbone oxygens, two from side-chain oxygens, and one from a bound water molecule (14). In Fig. 3, we report radial distributions of EF-hand oxygens within 12 Å of the coordinated Ca²⁺ position for the half-saturated and fully saturated holo states. For comparison, we also present data for the oxygen radial distribution in the apo state to demonstrate the substantial reorganization of coordinating ligands upon presentation of the Ca²⁺ ion. Fig. 3 A shows the oxygen population with respect to distance and time for the pEF and cEF hands, for which 7.0 is the optimal coordination number (11, 14). For both pEF and cEF hands in the holo case, nearly optimal coordination at 2.5 Å is evidenced by a distinct red line that persists throughout the simulations. However, the cEF hand presents a higher degree of coordination, 6.45 ± 0.47, relative to the pEF hand, 5.32 ± 0.06. The nonintegral coordination number reflects the transient nature of Ca²⁺/S100A1 oxygen binding owing to the rotation of side-chain carboxylate groups and exchange with bound solvent waters (not shown). Overall, the higher radial probability of coordinating oxygens for the cEF hand relative to pEF is consistent with the former’s greater Ca²⁺ affinity.

Figure 3.

Time-dependent Ca²⁺/oxygen distances (A) and averaged radial distribution of oxygen/Ca²⁺ (B) for the pEF (left) and cEF (right) hands. Vertical error bars indicate the mean ± SD of all four runs. Ca²⁺ binding localizes chelating oxygens to an ∼2.5-Å-radius coordination shell. To see this figure in color, go online.

The extent of EF-hand reorganization upon binding Ca²⁺ ions can be inferred from our apo-state data, for which the absence of Ca²⁺ ions permitted broadly and sparsely distributed chelating oxygens (see Fig. 3, A and B). Although this point of reference is biased toward the Ca²⁺-bound configuration, it nevertheless illuminates the considerable mobility of the ligating oxygens. This behavior is consistent with the small order parameters reported in the EF-hand regions by Nowakowski et al. (29). For the half-saturated states, the reported cEF distribution is nearly coincident with the statistics observed in the holo configuration. In other words, the loss of the pEF Ca²⁺ ions has no apparent effect on the cEF coordinating oxygens, which may support prior experimental evidence suggesting that pEF and cEF bind Ca²⁺ noncooperatively (15). We note, however, that the half-saturated pEF-hand conformation significantly differed from that of the Ca²⁺-free and fully saturated states, so we are unable to unambiguously define an approximate Ca²⁺ ion position for computing oxygen radial distributions. In the next section, we assess the approximate energetic stabilization due to these chelation patterns.

Calculated electrostatic scores based on chelating oxygens

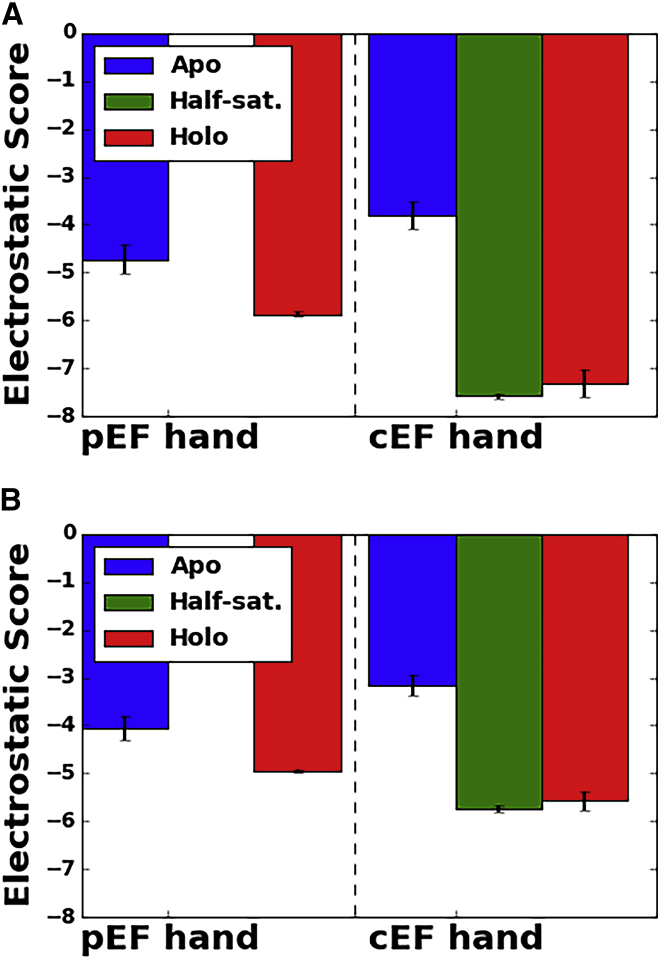
The Ca²⁺ cation is anchored in the EF-hand binding site via electrostatic interactions with negatively charged oxygens, the resulting enthalpy of which likely dominates the binding free energy (66). To relate our simulated coordination geometries to an approximate electrostatic contribution to binding enthalpies, we introduce an “electrostatic score” that resembles Coulomb’s law (Eq. 1). Similar to techniques applied to Ca²⁺-binding channels, this score provides a simple metric for assessing the electrostatic potential from the chelating ions for both the Ca²⁺-free- and Ca²⁺-bound-state protein/cation interactions (67). We note that the higher negative partial charge in the coordinating side-chain carboxylic acid oxygens relative to backbone amide oxygens should lead to more favorable scores for the cEF versus pEF coordination. Indeed, the holo state cEF hand reports a more favorable average electrostatic score than the pEF hand by 1.46 units (pEF, −5.87 ± 0.04; cEF: −7.33 ± 0.29), as shown in Fig. 4 A, which is consistent with experimental binding trends. In Fig. 4 B and Section S1.3.3 in the Supporting Material, we show that the difference in electrostatic scores narrowed when all oxygens were assumed to share the same partial charge, as is assumed in some models (68). Hence, although it is understood that the positions of coordinating ligands are important determinants of Ca²⁺ affinity (12, 13, 65), these data indicate that oxygen partial charges and potentially mobilities further tune affinity. Although this electrostatic score assessment is simplistic, it captures the predominant electrostatic enthalpic contribution to the binding free energy and has a consistent trend with MM electrostatic interaction energies determined directly from AMBER MM/PBSA analysis (see Section S1.3.4 in the Supporting Material).

Figure 4.

Electrostatic scores for the apo (blue), half-saturated (green), and fully saturated holo (red) states averaged over quadruplicate simulations. Results are given assuming partial charges of −0.51 and −0.76 on side-chain and backbone oxygens (A) versus uniform charges of −0.51 for both oxygen types (B). Vertical error bars indicate the mean ± SD of the eight electrostatic scores for two protein chains and four simulation runs. The higher density of coordinating oxygens and more negative partial charges in the cEF hand yield more stabilizing scores than for the pEF hand. To see this figure in color, go online.

We additionally computed the electrostatic score based on the apo state conformation to assess the gain in favorable enthalpic interactions as the protein relaxes in the presence of Ca²⁺ ions to form optimal binding interactions. As in the previous section, we present data for the apo state centered about the approximate position the Ca²⁺ ion would assume upon binding, to demonstrate the considerable change in the electrostatic environment upon chelating Ca²⁺. Given comparable electrostatic scores for the apo states of the pEF and cEF hands (−4.72 ± 0.32 and −3.80 ± 0.30, respectively), Ca²⁺ ion binding yields greater reorganization energy for the latter, as holo state scores were 1.15 and 3.53 units more negative, respectively. Similar to our analysis of oxygen radial distributions in the previous section, we find that the electrostatic score for the Ca²⁺-bound cEF hand in the half-saturated state (−7.58 ± 0.07) is nearly indistinguishable from that in the fully saturated holo state and further supports lack of cooperativity in pEF Ca²⁺ binding (15). However, there remains the possibility that the Ca²⁺-bound cEF site preorganizes the pEF hand to facilitate rapid Ca²⁺ ion association rates, as we speculated previously for the EF hand in TnC mutants (37). Moreover, significant entropic contributions from coordinating oxygen desolvation and conformational reorganization will understandably contribute to the overall observed affinity (14). Although it is beyond the scope of this study, rigorous approaches for deriving binding free energies, such as free-energy perturbation or thermodynamic integration, could potentially help quantify these effects (47, 69, 70, 71).

Stability of hydrogen bonds within the EF-hand β-sheets

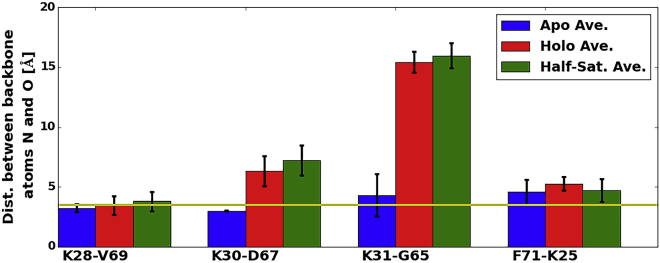
To examine stabilizing contributions to the EF-hand regions, we calculated the average distance between the backbone amide nitrogen and oxygen atoms comprising β-sheets linking the pEF and cEF hands (Fig. 5). We observe that four hydrogen bonds, including K25-F71, K28-V69, K30-D67, and K31-G65 (polar heavy atom distances <3.5 Å), form within the β-sheets of the apo case, compared with only one in the holo case between K28 and V69. The larger degree of hydrogen bonding in the apo configuration likely helps stabilize the EF hand, which may help preorganize the binding site for Ca²⁺-ion recognition (14). Meanwhile, the half-saturated case presents an intermediate degree of hydrogen bonding (two bonds, L28-V69 and K25-F71), which correlates with its order parameters. Notably, the largest change in the distance between two potential hydrogen-bond partners occurred between K31 and G65. In the apo state, they are separated by 4.33 ± 1.77 Å in the intact β-sheet secondary structure, but in the holo and half-saturated states, that distance increases to 15.43 ± 0.85 Å and 15.98 ± 1.04 Å, respectively, and thereby disrupt the β-sheet. As discussed further in Section S1.3.5 in the Supporting Material, we attribute this deviation to Ca²⁺ ion binding at the cEF hand. Specifically, N64 and D66 reorient to directly coordinate the Ca²⁺ ion, thereby pulling G65 away from active hydrogen bonding with residue K31 and compromising the β-sheet interaction. We will later present evidence that the disrupted β-sheet coupling upon Ca²⁺ binding directly correlates with increased mobility of helix 4 (H4), which together suggests that β-sheet hydrogen-bond breaking may trigger open-state formation.

Figure 5.

Average distances (Å) between backbone amide nitrogen and oxygen atoms of the residues in the EF hands forming the β-sheets in the apo case (blue), holo case (red), and half-saturated case (green). Standard deviations are shown. The yellow line indicates the 3.5 Å mark, which we define as the hydrogen-bond cutoff. Ca²⁺ ion binding disrupts the β-sheet hydrogen-bond network in both the half-saturated and holo states. To see this figure in color, go online.

Configuration and variability of the helix 3 and helix 4 angles

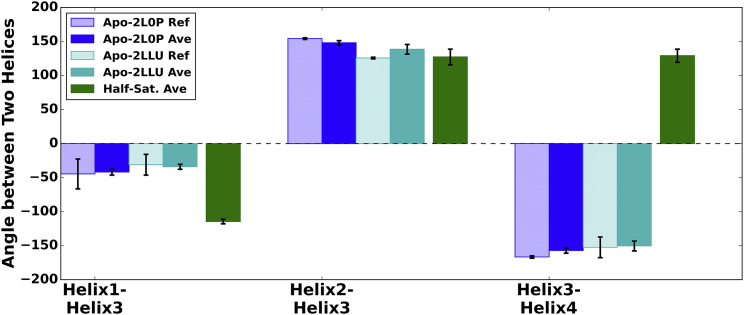
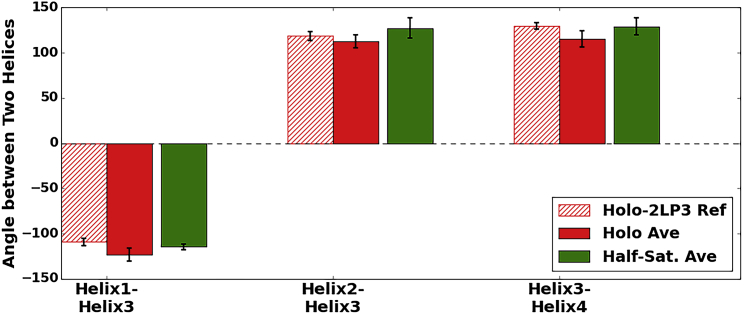
Ca²⁺ ion binding at the cEF and pEF hands is known to expose a hydrophobic PPI site between H3 and H4 (6, 15, 16, 17, 18). Interhelical angles have thus been commonly used (6, 16, 17, 28, 29, 72) to assess the transition between open and closed states. Experimental studies (26, 28, 29) of the apo versus holo conformations have indicated significant interhelical angle changes between H1 and H3 (−44.6 ± 21.9° versus −109.1 ± 4.1° for the 2L0P apo and 2LP3 holo cases, respectively) and between H3 and H4 (−166.6 ± 1.7° versus 129.9 ± 3.6° for the 2L0P apo and 2LP3 holo cases, respectively), culminating from the progression of H3 from closed to open states. Our helical angle measurements for the apo (Fig. 6) and holo states (Fig. 7) show excellent agreement between the simulation and the experiment. Namely, we observe for H3 and H4 that average values for the apo simulations are −157.2 ± 3.9° and −150.4 ± 7.3° versus 115.3 ± 8.9° in the holo state. For the half-saturated case, the H3 and H4 angle approached 129.1 ± 9.7°, which is consistent with the holo state configuration. We will note in the subsequent section, however, that the half-saturated state fleetingly progresses toward an apo-like configuration characterized by closing of the H3/H4 angle. The comparatively sparse numbers and short durations of these excursions are apparently insufficient to significantly shift the interhelical angle average.

Figure 6.

Computed versus experimental mean interhelical angles between H1 and H3, H2 and H3, and H3 and H4 for two apo NMR cases (PDB: 2L0P (blue) (26), 2LLU (cyan) (28)), and the half-saturated state (green). On average, the H1/H3 and H3/H4 angles in the half-saturated state are inconsistent with those in the apo state. To see this figure in color, go online.

Figure 7.

Computed (solid) versus experimental (hatched) mean interhelical angles between H1 and H3, H2 and H3, and H3 and H4 for one holo NMR case (PDB: 2LP3 (red) (29)) and the half-saturated state (green). On average, H1/H3 and H3/H4 angles in the half-saturated state are consistent with those in the holo state. To see this figure in color, go online.

PCA of protein-recognition-site exposure

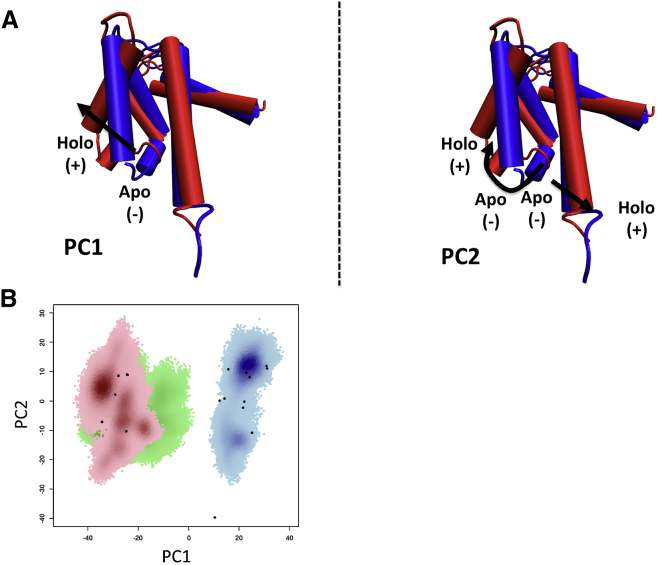
Ca²⁺ ion binding is known to expose the hydrophobic PPI site via migration of H3 toward an open-state configuration (17, 18), which is accompanied by significant structural reorganization of the protein. To simplify interpretation of our simulations, we used PCA to project the protein’s predominant conformational changes into a basis that clearly distinguished the apo from the holo states. The first two (largest eigenvalue) PCs for all S100A1 homologous structures available in the Protein Data Bank are shown in Fig. 8. In Fig. 8 A, we relate the PC bases to the conformational motions of the protein. PC1 is characterized by the swinging movement of H3 as it tilts outward from the apo state (26) toward the holo state (29) to allow room for binding peptides (6, 18). PC2 is characterized by the unwinding of the H4 C-terminus (data not shown), though it is not clear whether this loss of helical secondary structure plays a role in tuning Ca²⁺ affinity in S100A1 variants. In Fig. 8 B, we demonstrate that the apo and holo structures are clearly separated by the first PC (PC1); specifically, the holo structures are localized to PC1 = −10 to −45 and the apo structures to PC1 = 5–40. We further find that S100A1 variants with higher Ca²⁺ ion affinity (for example, the holo rat S100A1 bound to the TRTK12 peptide) tend to have more positive PC2 values than those with weaker affinity. Similarly, two peptide-bound S100A1 rat protein structures with high Ca²⁺ ion affinity exhibit more positive PC2 values than the human holo state examined in this study.

Figure 8.

(A) PC1 (left) and PC2 (right) compared against the NMR structures of the human apo protein (blue; PDB: 2L0P) (26) and the human holo protein (red; PDB: 2LP3) (29). Movement of the respective PCs is in the direction from apo, indicated by (−), to holo, indicated by (+), as shown by the black arrows. PC1 is characterized by the swinging of the third helix away from the helical bundle. PC2 is characterized by the rotation of the third helix and the tilting of the fourth helix, both away from the helical bundle. (B) PCA for the four MD trajectories of the apo (blue), holo (red), and half-saturated (green) proteins, with NMR structures indicated as black dots. The half-saturated system samples intermediate regions along PC1 between the apo and holo states. To see this figure in color, go online.

Using these PCs, we show in Fig. 8 B the projections of the four MD trajectories of the apo, fully saturated holo, and half-saturated cases. For the apo case, the protein conformation samples PC2 extensively −27 to 27), but not PC1 (5–40), which suggests that the apo state remained in the closed configuration. Similarly, for the holo case, the trajectory is restricted to more negative PC1 values, indicating that the protein remains open. In contrast, the half-saturated state trajectories span a larger range of PC1 values, suggesting occasional excursions toward an apo-like closed state.

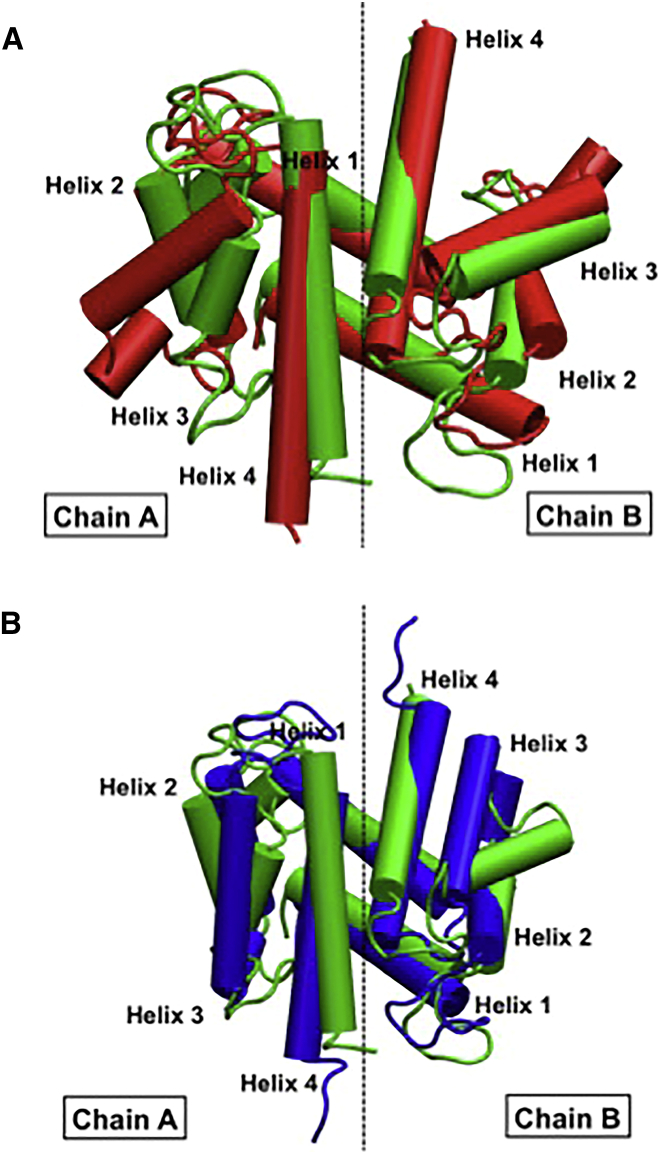
To investigate the hypothesis that the removal of the pEF Ca²⁺ ions may prompt relaxation from the open toward the closed state, we selected four snapshots from intermediate PC1 values for extended MD simulations. In Fig. 9, we compare a snapshot from one 100 ns extended simulation with apo and holo S100A1 NMR structures (26, 29). The snapshot indicates that the chain A H3 unwinds by several turns and tilts inward to closely resemble the apo NMR structure, whereas the chain B H3 maintains its original open position. Thus, it is apparent that in the absence of pEF Ca²⁺ions, the open state may relax back to the closed state. Similar trends are reported in the other extended trajectories in Fig. S4. These results agree with data from Goch et al. (15) indicating that the hydrophobic patch was less solvent-exposed in subsaturating levels of Ca²⁺. Overall, our data imply that the Ca²⁺ ion-bound pEF plays a critical role in stabilizing the holo-like state, despite its lesser affinity for Ca²⁺ ions relative to the cEF hand. Nevertheless, longer-duration MD simulations are likely required to fully repack H3 into the S100A1 helical bundle to more closely resemble the apo state. It is interesting to note that thiolation, glutathionylation, and nitrosylation of C85 on H4 has been suggested to increase Ca²⁺ binding affinity and induce significant conformational changes in the protein (15, 28, 72). Although few chemically modified C85 structures have been resolved, an attractive hypothesis is that covalently modified C85 could prevent H3 and H4 from fully closing, thereby producing a semiopen state that facilitates target peptide binding in the absence of pEF Ca²⁺ ions.

Figure 9.

Comparison of a half-saturated S100A1 snapshot (green) extended for 100 ns beyond the initial 60 ns MD run against holo (A, red) and apo (B, blue) S100A1 structures (26, 29). These half-saturated snapshots show a closer resemblance to the closed apo state; similar trends are reported for three other extended half-saturated simulations. To see this figure in color, go online.

Cross-correlation analysis of interresidue coupling

Ca²⁺ ion binding at the pEF site (formed from H1 and H2) appears to modulate the H3 position, despite the fact that H3 and H4 are bridged by the cEF hand. This behavior is a hallmark of allostery, for which substrate binding induces protein conformational changes distal to the recognition region. A prominent hypothesis for allostery evokes the notion that long-range correlations between a binding site and distal regions of the protein (73) are involved in transferring the binding signal. We therefore report in Fig. 10 the cross correlation of Cα atom positions to uncover potential trends in this allosteric mechanism.

Figure 10.

Residue cross correlation analysis for the human S100A1 protein in the apo (A), half-saturated (B), and holo (C) states. Cyan regions represent positive correlation, and magenta regions represent negative or anticorrelation. The half-saturated case presents correlation structure intermediate to the apo and holo cases. To see this figure in color, go online.

For the apo state (Fig. 10 A), we observe a small number of anticorrelated residues arising from breathing (opening) motions of H4 with H1 and H2, as well as with the EF hands. We note, however, a distinct positive correlation approximately between residues K25–K30 and E68–F71. This region corresponds to the β-sheet that tightly couples the EF hands in the apo state (14). Beyond these correlations, minimal coupling between distal regions is apparent. In contrast, the holo state (Fig. 10 C) presents a rich variety of off-diagonal (distal) correlations that evidence strong coupling between distal regions of the protein. We observe strong positive correlations, for instance, between H2, the linker region, and H3, as well as between H1, the pEF, the linker, and H3. Moreover, the negative correlations involving cEF and H4 appear to be intensified in the holo state relative to the apo site, which is suggestive of a breathing motion near the hydrophobic patch. Our earlier observations of EF-hand β-sheet decoupling upon Ca²⁺ binding appear to abolish the positive correlation in the K25–K30/E68–F71 region reported in the apo state with anticorrelative motions. Since these negative correlations extend from the β-sheet over the entirety of H4, we speculate that the β-sheet decoupling is the allosteric driver of the open-state formation. We additionally note in Fig. 10 C that C85 was anticorrelated with H3 residues 55–60 in the holo state, which may serve as additional evidence that C85 functionalization could enhance decoupling of H3 from H4. Hence, the barrier to exposing the hydrophobic region may be reduced and thus obviate the binding of Ca²⁺ ions at the pEF site, in support of findings from Zhukov et al (72). Similar analysis applied to the half-saturated state (Fig. 10 B) yields correlations intermediate between those of the apo and holo states that are suggestive of partial progression toward those configurations. More sophisticated methodologies for analyzing allostery in proteins, such as the mutual-information (74) or transmission-pathway (75) approach, could potentially provide greater insight into the Ca²⁺-driven allostery of open-state formation.

Conclusions

Our MD simulations of the human S100A1 protein reveal structural and dynamic details of Ca²⁺ binding at the EF hands and its influence in forming the protein’s functionally active open state. Using a primitive electrostatic scoring function, we find that the higher density and more negative partial charges of the coordinating oxygens in the cEF hand relative to the pEF region correlate with the former’s stronger affinity for Ca²⁺ ions. In a separate manuscript, we are extending our primitive electrostatic score to include enthalpic and entropic terms to better quantify these affinities. We further find that in the absence of Ca²⁺ ion binding at the pEF hand, S100A1 appears to revert to an apo-like closed configuration whereby anticorrelation between H4 and the helical bundle in the holo state is diminished. We believe this transition is afforded by decoupling β-sheets linking the EF hands upon Ca²⁺ ion binding. Finally, the evident role of H4 in the transition between the apo and holo states appears consistent with reports of enhanced signaling propensity for chemically modified H4 C85 variants at subsaturating levels of Ca²⁺. This insight into the molecular basis of high-affinity Ca²⁺ binding and its impact on allostery in S100A1 will be invaluable for understanding the function of the broad family of S100A-class proteins.

Author Contributions

C.E.S. designed the research, performed the research, analyzed the data, and wrote the article. P.K.H. designed the research, analyzed the data, and wrote the article.

Editor: Michael Feig.

Supporting Citations

References (76, 77, 78, 79, 80) appear in the Supporting Material.