MreB-Dependent Organization of the E. coli Cytoplasmic Membrane Controls Membrane Protein Diffusion

Abstract

The functional organization of prokaryotic cell membranes, which is essential for many cellular processes, has been challenging to analyze due to the small size and nonflat geometry of bacterial cells. Here, we use single-molecule fluorescence microscopy and three-dimensional quantitative analyses in live Escherichia coli to demonstrate that its cytoplasmic membrane contains microdomains with distinct physical properties. We show that the stability of these microdomains depends on the integrity of the MreB cytoskeletal network underneath the membrane. We explore how the interplay between cytoskeleton and membrane affects trans-membrane protein (TMP) diffusion and reveal that the mobility of the TMPs tested is subdiffusive, most likely caused by confinement of TMP mobility by the submembranous MreB network. Our findings demonstrate that the dynamic architecture of prokaryotic cell membranes is controlled by the MreB cytoskeleton and regulates the mobility of TMPs.

Introduction

Life requires cellular organization in time and space, a principle that applies to all branches of the evolutionary tree, including bacteria. Bacteria rely on temporal and spatial organization for processes as diverse as cell division (1), morphogenesis (2), and chemotaxis (3). These processes in particular are dependent on the functional organization of the membrane. Because bacterial cells lack membrane-bounded organelles, most of the membrane-dependent processes ranging from signaling and nutrient uptake to respiration and trans-membrane protein (TMP) folding are contained in a single membrane, the bacterial cytoplasmic membrane. This multitude of processes is brought about by a variety of proteins, including TMPs. Some TMPs function as discrete units, while others work in teams and assemble in homo- and heteromeric complexes. TMPs mostly rely on lateral diffusion to encounter an interaction partner or a binding site within the plane of the membrane. While initially conceived as a homogeneous lipid bilayer serving as a reaction platform for freely diffusing membrane proteins, membranes are increasingly perceived to be crowded, inhomogeneous, and subdivided into domains (4).

Over the past decades, the cortical actin cytoskeleton in eukaryotic cells has emerged as a key modulator of plasma-membrane organization (5, 6, 7). The viscoelastic network of F-actin attached to the inner leaflet of the plasma membrane can alter membrane component mobility. It has been shown to act as a network of physical barriers to lipid and protein diffusion that effectively subdivides the plasma membrane into compartments (8, 9, 10), but has also been involved in the formation of membrane domains with distinct composition and function, such as lipid rafts (11, 12, 13, 14). As a result, the lateral diffusion of lipids and TMPs in eukaryotic plasma membranes is often complex, characterized by anomalous diffusion (also referred to as “subdiffusion”). Anomalously diffusing lipids and TMPs show rapid and random (Brownian) diffusion at short length scales (often up to ∼100 nm, i.e., the mesh size of the actin network) and substantially slower diffusion at larger length scales (8, 15, 16).

For a long time, the bacterial membrane was believed to not contain functionally distinct lipid domains. In the past years it has, however, become evident that organization does occur in bacterial membranes. For example, cardiolipin was reported to be enriched in the polar regions of the Gram-negative bacterium Escherichia coli (17), and small regions of high order, with similar properties as lipid rafts in animal cells, have been reported in the Gram-positive Bacillus subtilis and various other bacteria (18). Recently, liquid-disordered lipid domains, called regions of increased fluidity (RIFs), have been visualized in B. subtilis using specific fluorescent membrane probes (19). Interestingly, the formation of these RIFs was shown to be dependent on the bacterial actin homolog MreB, suggesting that the interplay between the submembranous cytoskeleton and the plasma membrane could be an evolutionarily conserved mechanism controlling the plasma membrane organization in both prokaryotic and eukaryotic cells.

The prokaryotic MreB builds a cytoskeleton that is quite distinct from its eukaryotic homolog actin. Rather than forming a network that is persistent over long distances, MreB polymerizes along the cytoplasmic membrane into short, uncoordinated filaments (2, 20). MreB does not control morphogenesis by directly imposing cellular geometry but by locally coordinating peptidoglycan cell-wall synthesis, resulting in a persistent movement of individual MreB filaments around the membrane driven by the cell-wall synthesis machinery (21, 22). Although several reports have described TMP and lipid diffusion in living E. coli (23, 24, 25, 26, 27, 28, 29), a systematic investigation of these processes and the involvement of the MreB cytoskeleton is lacking.

Here, by combining single-molecule fluorescence microscopy, three-dimensional (3D) quantitative image analyses, and small-molecule inhibitors of MreB function, we investigate the influence of the bacterial MreB cytoskeleton on the diffusion of lipid probes and TMPs within the cytoplasmic membrane of live E. coli. We demonstrate the existence of microdomains in the membrane with distinct physical properties, which become destabilized upon inhibition of MreB polymerization. Although TMP diffusion is homogeneous, the MreB-dependent membrane organization appears to cause subdiffusion. Inhibition of MreB polymerization results in increased and normal Brownian TMP mobility. Furthermore, we find that the diffusion coefficients of GFP-labeled TMPs decrease with increased protein radius, essentially as described by the Saffman-Delbrück theory (30). This is surprising considering that the membrane is highly crowded and compartmentalized by the MreB cytoskeleton. Our data suggest that, similar to eukaryotic cells, the submembranous cytoskeleton in bacteria exerts control over the spatiotemporal organization of the cytoplasmic membrane and modulates the dynamics of lipids and TMPs.

Materials and Methods

Bacterial strains and plasmids

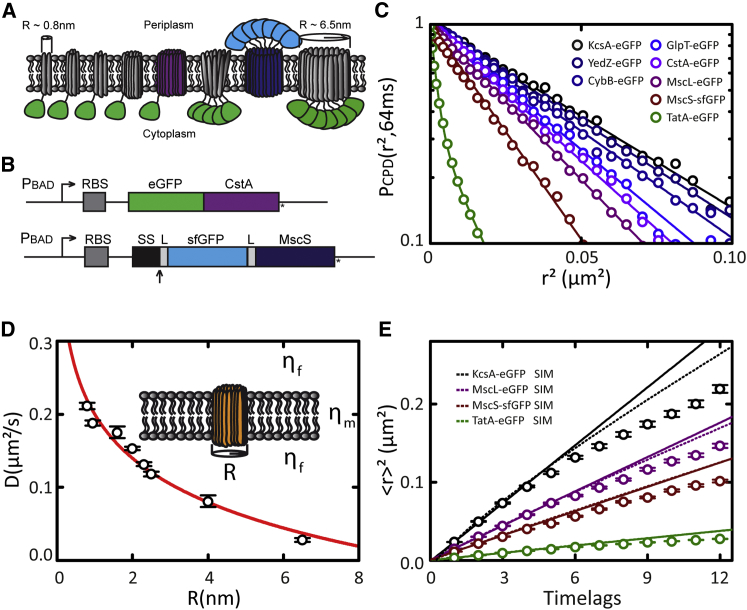
The following E. coli TMPs (see Table 1) were selected based on their lack of known specific protein-protein interactions and radius in the plane of the membrane: monomeric peptide transporter CstA, monomeric synthetic membrane protein WALP-KcsA, monomeric electron transporters YedZ and CybB, monomeric Glycerol-3-phosphate transporter GlpT, pentameric mechanosensitive channel protein of large conductance MscL, heptameric mechanosensitive channel protein of small conductance MscS, and oligomeric twin arginine translocation pore protein TatA. Fusion genes with enhanced green fluorescent protein (eGFP) were cloned into plasmids pBad24 or pBad33 that allowed tight regulation of protein expression (31). Membrane inclusion radii were estimated from the following 3D structures available in the Protein Data Bank (PDB): KcsA (PDB: 2KB1), MscL (PDB: 2OAR), MscS (PDB: 2OAU), GlpT (PDB: 1PW4), and CybB (PDB: 4GD3; complex with hydrogenase 1). For YedZ, a homology model was built using the automated service (32) (www.proteinmodelportal.org). The TMP radius in the plane of the membrane was measured from the PDB model using PyMol (DeLano Scientific, http://www.pymol.org). Some proteins had a rather elliptically shaped membrane inclusion. In that case, the average of the long and the short radius was used. The radius of large TatA-eGFP complexes was estimated based on the 3D architecture obtained via electron microscopy (33).

Table 1.

Mobility of TMPs and Lipid Dyes in the Presence and Absence of A22

TM-Protein/Lipid Dye	Radius (nm)	DMSD (μm2/s)
WALP-KcsA-eGFP	0.9	0.211 ± 0.004
YedZ-eGFP	1.3	0.188 ± 0.004
CybB-eGFP	1.7	0.175 ± 0.008
GlpT-eGFP	2.0	0.153 ± 0.003
CstA-eGFP	2.3	0.131 ± 0.003
CstA-eGFP +A22	2.3	0.207 ± 0.052
MscL-eGFP	2.5	0.118 ± 0.003
MscS-sfGFP	4.0	0.081 ± 0.008
TatA-eGFP	6.5	0.026 ± 0.003
Bodipy FL-C12	—	1.502 ± 0.078
Bodipy FL-C12+A22	—	1.463 ± 0.089
DiI-C12	—	0.365 ± 0.012
DiI-C12+A22	—	0.561 ± 0.021

For the first five proteins, eGFP was fused to the cytoplasmic amino-terminus. The open reading frames coding for YedZ, CybB, GlpT, and CstA TMPs were amplified from the chromosome of E. coli strain MC4100 by polymerase chain reaction (PCR). For WALP-KcsA, the open reading frame was amplified from a plasmid (a kind gift from Peter van Ulsen, Vrije Universiteit Amsterdam and Antoinette Killian, University of Utrecht). PCR products were restricted with SpeI and SalI restriction enzymes and transferred to a pBAD24 (31) expression plasmid containing an in-frame eGFP gene upstream from the multiple cloning site.

For MscL and TatA, eGFP was fused to the cytoplasmic carboxy-terminus. For MscL, first, the open reading frame of MscL was amplified from the E. coli genome (strain MC4100) by PCR using (5′GGGAATTCATGAGCATTATTAAAGAATTTCGCGAATTTGCGATGCGCGGGAAC-3′) as forward primer and (5′-TTCTCCTTTACCCATGCCGCTGCCGCTGCCGCTAGAGCGGTTATTCTG-3′) as reverse primer. Then, the open reading frame of eGFP was amplified from a plasmid by PCR using (5′-CAGAATAACCGCTCTAGCGGCAGCGGCAGCGGCATGGGTAAAGGAGAA-3′) as forward primer and (5′GTGTCGACTCATTTGTATAGTTCATCCATGCCATGTGTAATCCCAGCAGCTGT-3′) as reverse primer. Finally, these two fragments were fused by Gibson assembly and ligated into pBAD24, as described above. For TatA-eGFP, an existing plasmid was used (34).

In the case of MscS, the cytoplasmic carboxy-terminus is essential for heptamerization and is therefore not accessible for fusion with eGFP. The amino-terminus is located at the periplasmic side of the membrane, which hampers folding of eGFP. Instead, an amino-terminal fusion with superfolder GFP (sfGFP) (35) was generated, which was able to fold and become fluorescent. The signal sequence of DsbA was used to achieve cotranslational translocation of sfGFP into the periplasm. The open reading frame of the DsbA N-terminal signal peptide was amplified from the E. coli genome (strain MC4100) using (5′-GGGAATTCATGAAAAAGATTTGGCTGGCGCTGGCTGGTTTA-3′) as forward primer and (5′-AGCCGGATCCGCGCCACCCTCGAGATCTTCATACTGCGCCGCCGATGC-3′) as reverse primer. The gene encoding sfGFP was amplified from a plasmid (35) (a kind gift from Thomas G. Bernhardt, Harvard Medical School, Boston, MA) using (5′-GCATCGGCGGCGCAGTATGAAGATCTCGAGGGTGGCGCGGATCCGGCT-3′) as forward primer and (5′-AACATTCAAATCTTCGCCGCTGCCGCTGCCGCTTTTGTAGAGCTCATC-3′) as reverse primer. The MscS open reading frame was amplified from the E. coli genome (strain MC4100) using (5′GATGAGCTCTACAAAAGCGGCAGCGGCAGCGGCGAAGATTTGAATGTT-3′) as forward primer and (5′GTGTCGACTTACGCAGCTTTGTCTTCTTTCACCCGCTTAAAGTTCACATC-3′) as reverse primer. Finally, the three amplified DNA fragments were fused together in a Gibson assembly reaction (60 min at 50°C) using 1.33X Gibson master mix (New England Biolabs, Ipswich, MA), restricted with EcoRI and SalI restriction enzymes, and ligated into the pBAD24 expression plasmid.

Sample preparation and wide-field fluorescence microscopy

E. coli strain MC4100 was transformed using a pBAD24 plasmid containing the gene of interest and plated on YT agar plates containing ampicillin (100 μg/mL). Single colonies that grew on ampicillin plates were inoculated in YT media containing 100 μg/mL ampicillin and grown overnight at 220 rpm and at 37°C. From the overnight culture, 50 μL was added to 4950 μL fresh YT media containing the appropriate antibiotics. Cells were grown for 90 min to reach mid-log phase at 220 rpm and 37°C. Cells were collected by centrifugation for 2 min and suspended in minimal medium M9 (0.6% w/v Na₂HPO₄⋅2H₂O, 0.3% w/v KH₂PO₄, 0.1% w/v NH₄Cl, 0.1% w/v NaCl, 0.002 M MgSO₄, 0.4% w/v glucose, and 0.0001 M CaCl₂). For imaging, resuspended cells in minimal medium were immobilized on a thin agarose pad (1.5% (w/v) agarose in M9 medium) between a microscope slide and a coverslip (both plasma-cleaned). Finally, the sample chambers were sealed with VALAP (10 g Paraffin, 10 g Lanolin, 10 g Vaseline). Before imaging, samples were incubated on the microscope for 30 min to allow the cells to adjust to the imaging temperature (23 ± 1°C). Bacteria were then imaged at a constant temperature of 23°C using a custom-built, epi-illuminated wide-field fluorescence microscope built around an inverted microscope body (Eclipse Ti; Nikon, Tokyo, Japan) equipped with an apochromatic 100× 1.49 NA total internal reflection (TIRF) oil-immersion objective and a stage top incubator system (TOKAI HIT, Shizuoka, Japan). Excitation light (wavelength 491 and 561 nm, intensity ∼200 W/cm² in image plane) was provided by diode-pumped solid-state lasers (Cobolt, Solna, Sweden). Fluorescence images were taken continuously with an electron-multiplying charge-coupled device camera (model No. iXon3 type 897; Andor Technology, Belfast, Ireland), with an integration time of 32 ms per image, unless indicated otherwise. The total magnification was 200x, corresponding to 80 × 80 nm per pixel.

Each protein was measured in three independent experiments (>80 trajectories per experiment, trajectory length ≥ 4, average length ∼15 time lags of 32 ms). A comparison of the single-particle intensities tracked in live E. coli with those of surface-immobilized, purified eGFP, shows that the intensities were as expected on basis of the number of GFPs per protein (i.e., the monomeric proteins showed a similar intensity distribution as eGFP, MscL gave a distribution of 1.4 ± 0.4 eGFP molecules, and MscS gave a distribution of 1.8 ± 0.6; note that they were expressed in the presence of unlabeled protein at wild-type levels; see Fig. S4 and Table S1 in the Supporting Material). In case of TatA-eGFP, which was expressed in a TatA knock-out strain (36), single-particle intensities were used to select large complexes consisting of at least 30 monomers yielding a distribution of 38.4 ± 6.6 eGFP molecules.

For DiI-C12 or Bodipy FL-C12 staining experiments, YT was supplemented with DiI-C12 (5 μg/mL) (19) or Bodipy FL-C12 (0.4 μg/mL) (37) during regrowth. Before immobilization on the microscope slides, cells were washed three times with M9 to remove unbound dye.

Plasmolysis was performed as described in Fishov and Woldringh (38). In short, cells grown to mid-log phase were resuspended in M9 that was supplemented with 15% sucrose. After 2 min, cells were fixed using 2.5% glutaraldehyde (39) and imaged subsequently (Fig. S1).

To minimize the effect of A22 on the shape of E. coli cells, A22 (10 μg/mL) (40) was only supplemented into M9 that was used for cell resuspension and immobilization on the microscope slides.

Single-particle tracking

Images were analyzed using custom-written routines in MATLAB (The MathWorks, Natick, MA). For automated single-particle tracking in bacteria, a modified version of the tracking algorithm utrack (41) was used. To account for changes in the point-spread function due to axial movement of particles along the highly curved bacterial surface (in or out of focus), the location and intensity of the particles was obtained by a Gaussian fit with variable width. In addition, background subtraction was performed using a local approach allowing multiparticle localization (29). Subsequently, the particle localizations were linked to obtain single-particle trajectories using the utrack linking algorithm. For further analysis, trajectories with a total length less than four subsequent time points were discarded.

Determination of single eGFP fluorescence intensity

Single eGFP intensities were measured in vitro using E. coli expressed and purified eGFP in imaging buffer (50 mM Tris, pH 8.0, 100 mM NaCl, 2 mM MgCl₂) immobilized on a 22 × 22 mm cover glass (High Precision No. 1.5H, Cat. No. 0107052; Marienfeld, Lauda-Königshofen, Germany).

3D coordinate transformation

On basis of the sum of fluorescence images acquired for single-particle tracking, the outline of the cell's perimeter was fit by a cylinder of length L and radius r, capped on both ends with half-spheres of radius r and confirmed by overlaying the single-particle localization, which was rendered with a two-dimensional (2D) Gaussian of width σ = 30 nm, the approximate localization precision. Based on their localization, single-molecule trajectories were assigned to their respective bacterium. For each bacterium, the 2D coordinates of its assigned trajectories were transformed according to a local Cartesian coordinate system with its origin at the junction of the short and long axis of the cell and y axis parallel to the long axis,

$$x_{\text{loc}}=\left(x-x_O\right)\text{cos}\left(\theta \right)-\left(y-y_O\right)\text{sin}\left(\theta \right),$$

and

$$y_{\text{loc}}=\left(x-x_O\right)\text{sin}\left(\theta \right)+\left(y-y_O\right)\text{cos}\left(\theta \right).$$ (1)

For localizations occurring in the cylindrical region of the bacterium (−L/2 < y_loc < L/2), the z coordinate was calculated using the cylindrical coordinate transformation,

$$x_{\text{loc}}=r\text{cos}\left({\theta }_{\text{loc}}\right)$$

and

$$z_{\text{loc}}=r\text{sin}\left({\theta }_{\text{loc}}\right)=r\text{sin}\left(a\text{cos}\left(\frac{x_{\text{loc}}}{r}\right)\right).$$ (2)

For localizations occurring in the upper cap (L/2 < y_loc < L/2+r), the coordinates were calculated using

$$x_{\text{loc}}=r\text{sin}\left({\theta }_{\text{loc}}\right)\text{cos}\left({\phi }_{\text{loc}}\right),$$

$$y_{\text{loc}}-L/2=r\text{sin}\left({\theta }_{\text{loc}}\right)\text{sin}\left({\phi }_{\text{loc}}\right),$$

and

$$z_{\text{loc}}=r\text{cos}\left({\theta }_{\text{loc}}\right)=r\text{cos}\left(a\text{sin}\left(\frac{x_{\text{loc}}}{r}\times \frac{1}{\text{sin}(a\text{tan}\left(\frac{x_{\text{loc}}}{\left(y_{\text{loc}}-L/2\right)}\right))}\right)\right).$$ (3)

Coordinates of locations in the lower cap (−L/2−r < y_loc < −L/2) were transformed accordingly. Based on their localization within the bacteria, trajectory segments were assigned to either the cylindrical or one of the cap regions when longer than four time points, and discarded otherwise.

Inverse projection of displacement distribution

For generating a matrix of projected displacement distributions (PDDs) as previously described in Oswald et al. (42), a 3D bacterial surface model was generated, consisting of a cylinder with 1 μm diameter and 1 μm length, capped on both ends with half-spheres with 0.5 μm radius. Triangulation of this model was achieved using 3D modeling software (Google Sketchup). The cylindrical part of the model consists of 38 triangles forming 24 flat patches, while each of the half-sphere end caps is composed of 264 triangles forming 144 flat patches. The average angle between each flat patch is 15°.

PDDs were generated by sampling displacement vectors of a given length by randomly distributing individual displacements over the model surface and determining their projected length in the 2D plane. By limiting the sampling area, different depths of field can be simulated. To simulate epi wide-field elimination, a depth of field (DOF) of 500 nm was chosen, effectively probing the lower side of the bacterium. To simulate TIRF microscopy data, the effective depth of field was limited to the lower 150 nm of the bacterium. The normalized PDD represents the probability distribution for finding a 2D-projected length given a 3D displacement with particular length on the probed surface of the bacterial model. For 3D displacements ranging from 0 to 1000 nm, in 5 nm increments, PDDs were generated sampling 10⁵ displacements per given length, yielding a transformation matrix that can convert any distribution of 3D displacements (with 5 nm bin size) over the surface of the spatial model in a 2D-projected displacement distribution (with 5 nm bin size) by simple multiplication of an input distribution vector with the transformation matrix (42). For inverse projection of displacement distribution (IPODD), the projection matrix was inverted using Gaussian elimination. The inverted projection matrix was used to convert measured 2D-projected displacement distributions into the most probable 3D displacement distribution over the probed model surface.

Mean-squared displacement analysis

For each single-molecule trajectory of N consecutive images, the displacement distribution r_i,nΔt at a time interval τ = nΔt was determined as follows:

$$\begin{array}{l}{r}_{i,n\Delta \text{t}}=\sqrt[2]{{\left(x\left(i\Delta t+n\Delta t\right)-x\left(i\Delta t\right)\right)}^2+{\left(y\left(i\Delta t+n\Delta t\right)-y\left(i\Delta t\right)\right)}^2}\\ \text{for}i=1\dots N\text{and}n=1\dots 4.\end{array}$$ (4)

Values for r_i,nΔt from all detected single-molecule trajectories were pooled into a discrete 2D displacement probability distribution PD_2D(mΔr,τ) for time intervals τ ≤ 4Δt and bin sizes ranging from 0 to 1000 nm, in Δr = 5 nm increments. IPODD was performed by multiplying the PD_2D(mΔr,τ) with the appropriate inverted projection matrix, yielding the most probable global 3D displacement probability distribution PD_3D(τ). The average diffusion constant was determined by means of mean-squared displacement (MSD) analysis (43) including the experimental localization accuracy:

$$\langle R_{3D}{\left(\tau \right)}^2\rangle =\frac{{\sum }_i\left(PD\left(i\Delta r,\tau \right)\times i\Delta r^2\right)}{{\sum }_{j}PD\left(j\Delta r,\tau \right)}=4D\tau +4{\sigma }^2.$$ (5)

Fits yielded localization accuracies σ ranging from 26 nm (CybB-eGFP) to 43 nm (KcsA-eGFP) with a mean of 32 nm and standard deviation of 3 nm.

Cumulative probability distribution analysis

Heterogeneity in diffusion was probed by analyzing the cumulative probability distribution (CPD). To this end, the discrete 3D-corrected displacement distribution PD(τ) for a given time-lag was integrated:

$$CPD\left(m\Delta r^2,\tau \right)=1-CP{D}^{\prime }\left(m\Delta r^2,\tau \right)=1-\frac{{\sum }_{i=1}^{m}PD\left(i\Delta r,\tau \right)}{{\sum }_{j}PD\left(j\Delta r,\tau \right)}.$$ (6)

Assuming two populations simultaneously exhibiting Brownian motion, the corresponding cumulative probability function (CPF) is expected to resemble the sum of two exponentials (44):

$$CPF\left(m\Delta r^2,\tau \right)=1-CP{F}^{\prime }\left(m\Delta r^2,\tau \right)=\gamma \times e^{\frac{-m\Delta r^2}{4D_1\tau +4{\sigma }^2}}+\left(1-\gamma \right)\times e^{\frac{-m\Delta r^2}{4D_2\tau +4{\sigma }^2}}.$$ (7)

The experimental CPD was fitted with the CPF excluding data points <10⁻¹ to minimize the contribution of noise at low probability values. The localization accuracy σ was set to 30 nm, consistent with the results obtained from the MSD analysis.

Estimation of DiI-C12 domain sizes

Long low-mobility single-molecule trajectories of DiI-C12 molecules as well as long low-mobility stretches of trajectories displaying obvious switching in mobility were considered to estimate DiI-domain sizes (Fig. S3 a). As a measure for the space explored by low-mobility DiI-molecules, the standard deviation σ of single-molecule localization from their mean localization was calculated (Fig. S3 b):

$$\sigma =\sqrt{\frac{{\sum }_i^N({\left(x_i-\overline{x}\right)}^2+{\left(y_i-\overline{y}\right)}^2)}{N}}.$$ (8)

Brownian motion simulation and long time-lag MSD analysis

The 3D bacterial surface model was used to assess the effect of a limited depth of field on the MSD analysis of normal Brownian motion. Per time lag, 200 trajectories of a length of 100 displacements were simulated with their origins randomly placed on the bacterial model. For each diffusion-step, a displacement r was drawn from a Rayleigh distribution corresponding to the time-lag and diffusion constant simulated. The direction of the displacement vector $\overrightarrow{r}$ with respect to the latter location was determined by a randomly chosen lateral angle α. Displacements with their start- and/or end-position occurring outside of the considered depth of field were discarded. In accordance with experimental conditions, the DOF for the epifluorescence microscopy simulations (single-particle tracking on TMPs) was set to the lower-half of the bacterial model (0 nm ≤ z ≤ 500 nm) and for the TIRF simulations (single-molecule tracking on DiI-C12 and Bodipy FL-C12) to 0 nm ≤ z ≤ 150 nm with respect to the bottom of the bacterial model. The remaining displacements were analyzed in terms of MSD analysis (Fig. S6).

For all lipid dyes and TMPs investigated, the experimentally obtained diffusion constants were used for DOF simulations. MSD values of DOF-filtered simulation data increasingly deviate from the unfiltered simulation data with increasing time-lag, resulting in a subdiffusive MSD curve (Fig. S7).

For DiI-C12 and Bodipy FL-C12, the experimental and DOF-simulated MSD curves are in good agreement, suggesting that the apparent subdiffusive behavior can solely be accounted for by the limited depth of field under experimental conditions (Fig. S7). In contrast, experimental MSD curves for all TMPs show an additional subdiffusive deviation compared to the DOF-simulated data (Fig. S8).

Results

MreB organizes lipid microdomains

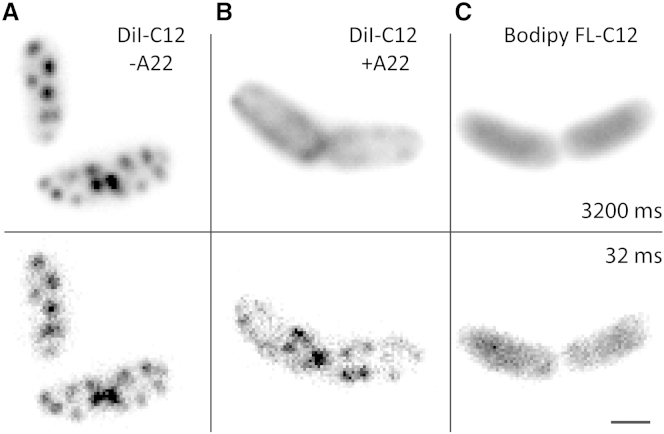
We first investigated whether the cytoplasmic membrane of E. coli contains RIFs, as reported before for B. subtilis (19). These RIFs can be specifically stained with the fluorescent dye DiI-C12, which has a preference for liquid-disordered regions of membranes due to its short hydrophobic tail (45). We grew E. coli in the presence of DiI-C12 and observed a stable, punctuated fluorescence pattern (Fig. 1 a). DiI-C12 specifically localized to the cytoplasmic membrane, as demonstrated by performing plasmolysis (Fig. S1). The size of the fluorescence spots was limited by the optical resolution of our microscope (∼300 nm), which implies that the DiI-C12-containing membrane patches are smaller than a few hundred nanometers. We then grew E. coli in the presence of the membrane dye Bodipy FL-C12, which has no preference for ordered or disordered regions (37), resulting in homogenous staining of the whole cytoplasmic membrane (Fig. 1 c). To rule out that DiI-C12 domains are formed due to a phase separation in the lipids at room temperature, as might be expected from the phase transition of the E. coli membrane around 28°C described by Nenninger et al. (37), we repeated the DiI-C12 staining experiment at 37°C and did observe the same punctuated fluorescence pattern (Fig. S2). Together, these experiments indicate that, both at room temperature and 37°C, the cytoplasmic membrane of E. coli contains domains with distinct properties, most likely of more fluidic nature compared to the rest of the membrane (19).

Figure 1.

MreB-dependent microdomains in the cytoplasmic membrane of E. coli bacteria. (A–C) Live E. coli cells stained with lipid dyes. (Top panels) Time-averaged images (100 frames). (Bottom panels) Single frames of 32 ms. (A) DiI-C12; (B) DiI-C12 in the presence of MreB-polymerization inhibitor A22; and (C) Bodipy FL-C12.

We next tested whether the bacterial cytoskeleton plays a role in organizing DiI-C12-containing domains in the E. coli membrane, as it does in B. subtilis (19). When treating bacteria with A22, a small-molecule inhibitor of MreB polymerization (40), the cytoplasmic membrane appeared homogeneously stained with DiI-C12 (Fig. 1 b). Upon closer inspection with shorter exposure times (32 ms), however, the fluorescence pattern looked far more intriguing: DiI-C12-stained patches were observed, but these patches were much more mobile and instable compared to cells not treated with A22 (Fig. 1, a and b; Movies S1 and S2).

Microdomains form via MreB-induced lipid confinement

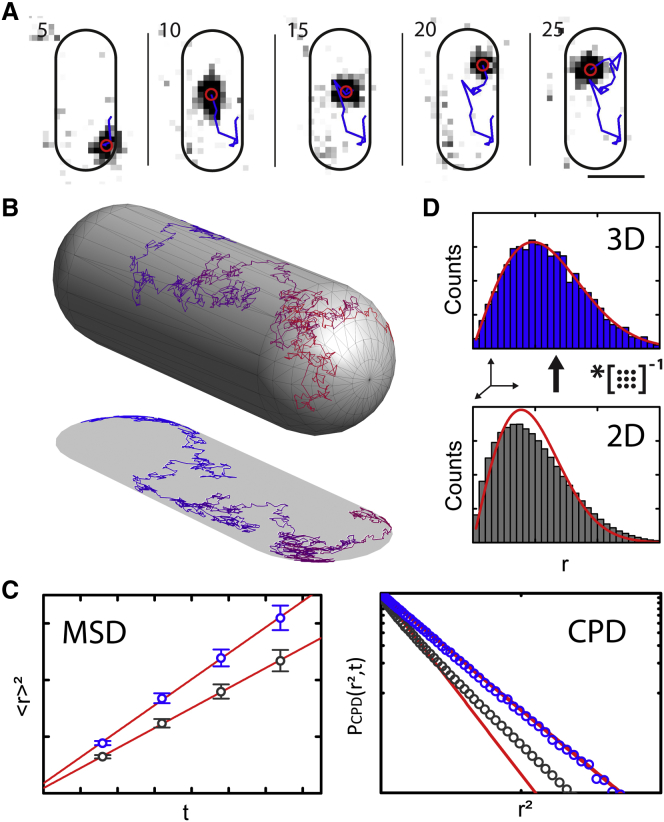
To obtain more insight into the mechanisms leading to lipid-domain formation, we tracked the fate of individual DiI-C12 molecules, either in the absence or in the presence of A22, using short exposure times of 12 ms with laser excitation in TIRF mode. Stacks of images were analyzed with automated single-particle tracking analysis (Fig. 2 a), allowing reconstruction of the single-molecule trajectories. Because trajectories obtained in this way are 2D projections of the actual 3D paths along the highly curved cytoplasmic membrane (Fig. 2 b), straightforward analysis of raw 2D data would yield erroneous results (Fig. 2 c) (28, 29, 34, 42). To avoid this, we here apply IPODD (42) to obtain quantitative 3D insights in the diffusion process (Fig. 2 d).

Figure 2.

Single-particle tracking of individual lipid dye molecules and diffusion analysis. (A) Time-lapse images of a DiI-C12 molecule tracked in the cytoplasmic membrane of a live E. coli cell (horizontal scale bar, 1 μm). Indicated are frame numbers; time interval between two consecutive frames = 12 ms. (B) Illustration of a simulated 3D diffusion trajectory in the curved membrane of an E. coli cell. (C) Simulated MSD (left) and CPD (right) curves in 3D (blue) and projected in 2D (gray). As illustrated, 2D projection yields a 30% reduced diffusion coefficient using MSD analysis and distorts the monoexponentially decaying CPD of 3D displacements. (D) Schematic of IPODD: 2D displacement distribution (gray) can be processed via IPODD to find the most likely 3D displacement distribution (blue). Fits to Rayleigh distributions (red) indicate that the distortion introduced by 2D projection is restored in the resulting 3D displacement distribution (42).

From 3D-corrected distributions of step sizes, diffusion coefficients were determined using MSD analysis. For a normally diffusing molecule, the MSD increases linearly with the time interval Δt:

$$\langle r{\left(\Delta t\right)}^2\rangle =4D\Delta t+4{\sigma }^2.$$ (9)

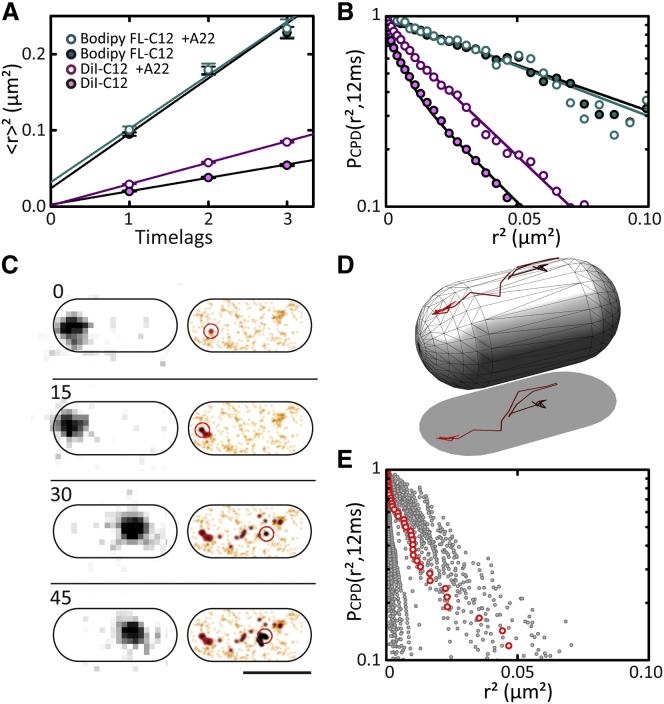
The diffusion coefficient D and the localization error σ can thus be readily obtained from a straight-line fit to the MSDs plotted as a function of time interval (Fig. 3 a). We found that the diffusion coefficient of Bodipy Fl-C12 is rather high, and independent of MreB polymerization (D = 1.502 ± 0.078 μm² s⁻¹ without A22; 1.463 ± 0.089 μm² s⁻¹ with A22). In contrast, diffusion of DiI-C12 is significantly faster when MreB polymerization is inhibited (D = 0.365 ± 0.012 μm² s⁻¹ without A22; 0.561 ± 0.021 μm² s⁻¹ with A22; Fig. 3 a and Table 1).

Figure 3.

MreB depolymerization increases DiI-C12 mobility by reducing the capture probability of DiI-C12 molecules. (A) MSD and (B) CPD analysis of Bodipy FL-C12 (cyan) and DiI-C12 (magenta) diffusion in the absence (solid symbols) and presence (open symbols) of A22. (Solid lines) linear (A) or exponential (B) fits (see text and Tables 1 and S2). (C) Individual, long single-molecule trajectory of DiI-C12. (Left panel) Sequence of raw images; (right panel) 2D-Gaussian-rendered single-molecule positions of the trajectory, color-coded according to their occurrence in time from red to black. (Orange) Pre- and succeeding single-molecule events recorded within the observed bacterium. The DiI-C12 molecule diffuses between two capture sites where it essentially remains immobile for 15 frames. Frame numbers are indicated on the left; time interval between two consecutive frames = 12 ms. Scale bar (bottom right), 1 μm. (D) 3D-coordinate transformation of the trajectory of (C) allows for recovering the 3D trajectory plotted on a 3D bacterial model. (E) CPD analysis of the long single-molecule DiI-C12 trajectories using the actual 3D displacements. CPD calculated from trajectory visualized in (C) highlighted in red.

Visual inspection of the image sequences gave the impression that the mobility behavior of individual DiI-C12 molecules is rather heterogeneous. To find out if individual DiI-C12 molecules diffuse uniformly, we determined the cumulative probability distribution (CPD) of the IPODD-corrected displacement distributions. In contrast to MSD analysis, which is an averaging technique, CPD analysis can reveal heterogeneity (46). The CPD is defined as the probability that a particle steps out of a circle of radius r after a time-lag t. Plotting the CPD against r² yields an exponentially decaying function for a single species diffusing with diffusion coefficient D (46):

$$CPD\left(r^2,t\right)=e^{-\frac{r^2}{4D\Delta t+4{\sigma }^2}}.$$ (10)

Diffusion of Bodipy Fl-C12 was found to be homogeneous and independent of treatment with A22 (Fig. 3 b; Table 1). Remarkably, the CPD of DiI-C12 displacements did not follow a single exponential decay (Fig. 3 b). The CPD could, however, be well fitted with the sum of two exponentials (Fig. 3 b), reflecting heterogeneous diffusion, i.e., the presence of at least two populations with distinct diffusion coefficients (D₁ and D₂), with relative occurrences γ and 1-γ, respectively. In cells with a functional MreB cytoskeleton, DiI-C12 diffuses within the membrane in two equal populations (D₁ = 0.029 ± 0.008 μm² s⁻¹, D₂ = 0.584 ± 0.007 μm² s⁻¹, γ = 0.49 ± 0.01) (Fig. 3 b). The diffusion coefficient of the slow component indicates that this fraction is almost immobile. In contrast, in cells treated with A22, the CPD of DiI-C12 appeared less heterogeneous and less steep, indicating a higher overall mobility of individual DiI-C12 molecules. While a two-exponential fit yielded similar diffusion coefficients as for cells with unperturbed MreB, their relative occurrence was substantially different, with the fast-diffusing component dominating (D₁ = 0.006 ± 0.090 μm² s⁻¹, D₂ = 0.617 ± 0.020 μm² s⁻¹, γ = 0.17 ± 0.06), consistent with the increased mobility obtained with MSD analysis.

We next tested whether individual DiI-C12 molecules diffuse either in the slow- or in the fast-diffusive mode all the time, or if individual molecules switch between the two modes. In Fig. 3 c and Movie S3, an example trajectory is shown of an individual DiI-C12 molecule. First, it is nearly immobile for 15 frames, and then diffuses for an equivalent time, until it gets trapped at a different location. Because 3D correction using IPODD only works well for large data sets, another approach was taken to obtain insight in 3D displacements from individual trajectories using coordinate transformation (Fig. 3 d). In Fig. 3 e, CPD plots of a number of long, coordinate-transformed trajectories are shown. Two groups of trajectories can be discriminated. For many trajectories, the CPD decays rapidly, representing DiI-C12 molecules that remain trapped for most of the observation time. For a second group of trajectories, the CPDs are less steep, suggesting that they correspond to freely diffusing DiI-C12 molecules. As in the case of the molecule displayed in Fig. 3 c, the CPDs of some trajectories are bimodal (Fig. 3 e), indicating switching between the trapped and the mobile mode.

Together these observations suggest that DiI-C12-containing lipid domains form via a diffusion-capture mechanism: individual DiI-C12 molecules appear to diffuse freely between MreB-stabilized capture sites where they are transiently confined. To obtain better insight into the size of these domains, we determined, for 40 long trajectories where DiI-C12 molecules appeared trapped, the spread (standard deviation) of individual DiI-C12 localizations within the trajectories. This yielded a distribution of standard deviations with a mean of ∼40 nm (Fig. S3; Movie S4), comparable with size estimates of lipid rafts in eukaryotic cells (14). This value is, however, close to the localization error under our experimental conditions (∼30 nm), which occludes discerning between the possibilities that DiI-C12 molecule are truly immobilized or diffuse freely within domains of ∼40 nm diameter.

TMP diffusion is homogeneous yet confined by MreB

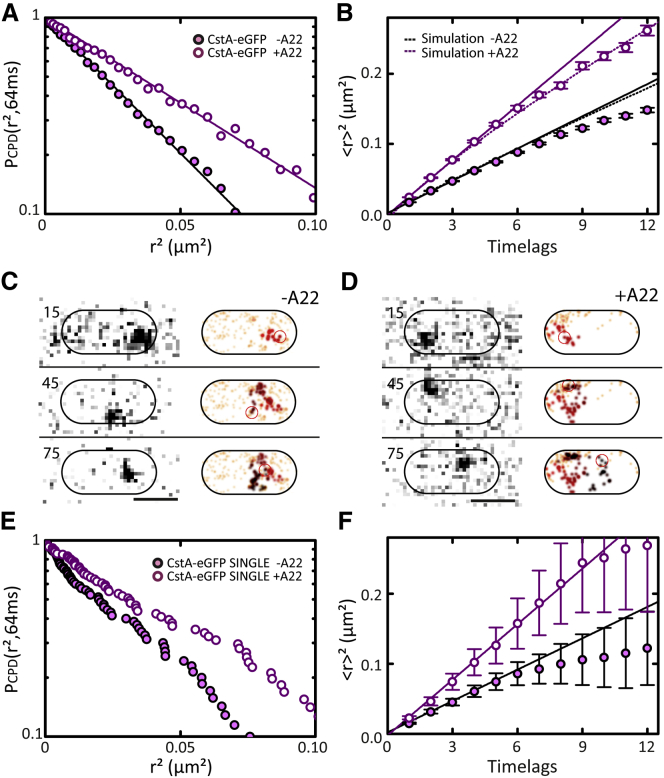
Having established that MreB organizes lipid domains within the E. coli cytoplasmic membrane, we wondered whether this domain structure results in TMPs experiencing different environments, leading to heterogeneous TMP diffusion. To test this, we expressed the monomeric peptide transporter CstA, a protein consisting of 18 trans-membrane helices, fused to eGFP in E. coli (see Materials and Methods), and visualized and analyzed its diffusion as described above for DiI-C12 using epi laser-excitation. Remarkably, CPD analysis revealed that CstA-eGFP diffusion is homogeneous (Fig. 4 a). Also, long trajectories of individual CstA-eGFP molecules did not show signs of heterogeneity (Figs. 4 c and S5 a; Movie S5). These results indicate that CstA-eGFP is not confined or immobilized by MreB, in the way we observed for the membrane probe DiI-C12. To investigate whether the MreB cytoskeleton has an effect on TMP diffusion at all, we measured CstA-eGFP diffusion in the presence of A22 and observed that diffusion was still homogeneous but that the diffusion coefficient substantially increased (from 0.13 to 0.21 μm² s⁻¹; Fig. 4, a, d, and e; Table 1; Movie S6).

Figure 4.

TMP diffusion in the presence and absence of polymerized MreB. (A) CPD analysis of CstA-eGFP diffusion in the absence (solid symbols) and presence (open symbols) of MreB-polymerization inhibitor A22. (Solid lines) Fits with single-exponential functions (Table S2). (B) MSD plots of experimental data shown in (A). (Solid lines) Linear fits on the first four time lags (Table 1). (Dotted lines) Nonlinear fits on MSD values simulated by a random walk with the same diffusion coefficient over the part of a bacterial cell that is observable by wide-field epifluorescence microscopy. (C and D) Individual, long single-molecule trajectory of CstA-eGFP in absence (C) and presence (D) of A22. (Left panel) Sequence of raw images; (right panel) 2D-Gaussian-rendered single-molecule positions of the trajectory, color-coded according to their occurrence in time from red to black. (Orange) Pre- and succeeding single-molecule events recorded within the observed bacterium. Frame numbers are indicated on the left; time interval between two consecutive frames = 32 ms. (E and F) CPD and MSD analysis, respectively, on the individual single-molecule trajectories of CstA-eGFP from (C) and (D). (F) Fits were performed as in (B). Color-coding as in (A).

How could the inhibition of MreB polymerization result in faster TMP diffusion? The simplest explanation would be that depolymerization of membrane-bound MreB relieves spatial confinement of the TMPs. Confinement typically quenches displacements at longer timescales, resulting in a nonlinear dependence of the MSD on time lag that is referred to as subdiffusion:

$$\langle r{\left(\Delta t\right)}^2\rangle =4D\Delta t^{\alpha }+4{\sigma }^2,$$ (11)

with α < 1 (47). To test whether CstA-eGFP displays subdiffusive behavior, we calculated MSDs and observed linear scaling of MSD with time for the first four time lags. Notably, at longer timescales the MSD curve showed clear nonlinear scaling (Fig. 4 b). Nonlinear scaling, however, can also be caused by the observable membrane area being limited (by the size of the bacterium and the DOF of our microscope). To assess these effects, we simulated Brownian motion along a 3D bacterial surface model and excluded diffusion steps that reached outside the observable membrane area (see Materials and Methods and Fig. S6). We first compared experimental data from the lipid dyes Bodipy FL-C12 and DiI-C12 to simulations. For the lipid dyes, the nonlinear scaling of the MSDs at longer time lags was fully consistent with normal Brownian motion limited by the observable membrane area (Fig. S7). In contrast, the MSD values of CstA-eGFP at longer time lags substantially deviated from the simulated ones (Fig. 4 b), indicating that this protein moves in a subdiffusive manner. The subdiffusive behavior was also observed in long individual CstA-eGFP trajectories (Fig. 4 f). To find out whether the subdiffusion was caused by the MreB cytoskeleton, we analyzed CstA-eGFP diffusion in the presence of A22. Strikingly, the MSD curve of CstA-eGFP did not deviate from the simulations, indicating that the TMPs diffused in a normal, Brownian way when MreB polymerization was inhibited (Fig. 4 b). The same could be observed in MSD curves obtained from long individual trajectories of CstA-eGFP in the presence of A22 (Fig. 4 f).

To rule out that the MreB-dependent subdiffusion is specific for CstA-eGFP, we generated seven more TMP-eGFP fusion proteins (Fig. 5, a and b; Table 1; see Materials and Methods). Apart from the TatA translocation pore, which exists in various oligomeric states and interacts with accessory proteins TatB and TatC (27, 29), these proteins were chosen for their apparent lack of specific protein-protein interactions. We recorded diffusion data for all seven TMPs and applied CPD analysis as described above (Fig. 5 c). For large oligomeric TatA-eGFP complexes, CPD analysis revealed two populations with distinct diffusion coefficients differing by approximately one order of magnitude (D₁ = 0.016 ± 0.001 μm² s⁻¹, D₂ = 0.176 ± 0.004 μm² s⁻¹, γ = 0.90 ± 0.01). Also for individual TatA-eGFP complexes, heterogeneous diffusion could be observed (Fig. S5 b; Movie S7). We speculate that this is connected to its function—the translocation of folded proteins over the membrane—which might involve substantial conformational changes of the Tat translocation pores (48). All other CPDs, however, could be well described with a single exponential function, showing that TatA-eGFP is an exception and that TMPs in general diffuse homogeneously.

Figure 5.

Size-dependent TMP diffusion in the cytoplasmic membrane of E. coli bacteria. (A) Illustration of the library of the eight GFP-tagged TMPs used in this study (see Table 1 for names and radii). (B) Schematic of GFP fusion constructs: (top) eGFP (green) fused to the amino-terminus of CstA. (Bottom) sfGFP (light blue) fused to the periplasmic amino-terminus of MscS, preceded by the signal sequence (SS) of DsbA, to achieve cotranslational translocation of sfGFP. (Arrow) Site of leader peptidase processing; L indicates a short flexible linker. (C) CPD analysis of TMP diffusion within time lag of 64 ms. (Straight, solid lines) Single-exponential fits to the CPD data. In the case of TatA-eGFP, a double-exponential function was fitted. Fit results are presented in Table S2. (D) Diffusion coefficients obtained using MSD analysis (Table 1) plotted against radius R of corresponding TMP. Fitting the Saffman-Delbrück model yields a membrane viscosity μ_m of 1.2 ± 0.1 Pa·s and bulk viscosity μ_f of 0.24 ± 0.02 Pa∙s. (E) MSD analysis of KcsA-eGFP, MscL-eGFP, MscS-sfGFP, and TatA-eGFP. Time lag = 32 ms. (Solid lines) Linear fits on the first four time lags (Table 1). (Dotted lines) Nonlinear fits on MSD values simulated by a random walk with the same diffusion coefficient over the part of a bacterial cell that is observable by wide-field epifluorescence microscopy. Color-coding as in (C).

We then analyzed whether subdiffusion at longer timescales is a general feature as well. Indeed, MSDs of all TMPs consistently displayed substantial deviations at longer timescales compared to simulated ones, confirming that confinement effects at relatively long timescales are a general feature of TMPs in the E. coli cytoplasmic membrane (Fig. 5 e; Fig. S8).

TMP diffusion is weakly size-dependent

Our set of eight TMPs with differently sized membrane inclusions allowed us to assess the size-dependence of diffusion, which might contain additional information about the diffusion mechanism. The well-known Saffman-Delbrück model (30) considers the membrane as a thin, 2D layer of viscous fluid (with height h, and membrane viscosity μ_m) that is surrounded by a less viscous bulk fluid (with bulk viscosity μ_f), representing the cytoplasmic and the extracellular space. It predicts a weak logarithmic dependence of the diffusion coefficient on the radius of the protein:

$$D=\frac{k_{\text{B}}T}{4\pi {\mu }_{m}h}\left(\text{ln}\left(\frac{{\mu }_{m}h}{{\mu }_{f}R}\right)-\gamma \right),$$ (12)

with k_B as Boltzmann’s constant, T as the temperature, and γ ≈ 0.5772 as Euler’s constant. The model has been experimentally confirmed for TMPs in artificial lipid bilayers (49, 50). In eukaryotic membranes however, much stronger size-dependencies have been observed (51). This is believed to be a direct effect of the cortical actin mesh subdividing the membrane into compartments: smaller proteins have a much larger propensity to escape from one compartment to another than larger ones. To reveal the size-dependence of TMP diffusion in the E. coli cytoplasmic membrane, we plotted the diffusion coefficients against the radius of the trans-membrane part of the protein and observed a decrease of the diffusion coefficient with increased size (Fig. 5 d). Remarkably, the size dependence of the TMP diffusion coefficients can be well described by the Saffman-Delbrück model, with μ_m = 1.0 ± 0.1 Pa·s and μ_f = 0.21 ± 0.01 Pa·s (Fig. 5 d), despite the MreB-controlled heterogeneity of the E. coli cytoplasmic membrane.

Discussion

We have shown, using the membrane probe DiI-C12, which has a preference for disordered regions, that the E. coli cytoplasmic membrane contains domains of distinct physical properties. Those domains were rather static and appeared to be randomly distributed over the membrane. Tracking individual DiI-C12 molecules revealed that they switch between mobile and immobile states rather frequently. In their immobile state, DiI-C12 molecules appear to remain localized within ∼40 nm. These observations indicate that DiI-C12 lipid dyes might be contained by a diffusion-capture mechanism. The stability of the lipid domains requires polymerized MreB: inhibition of MreB polymerization resulted in mobile, less stable domains and less restricted diffusion of single DiI-C12 molecules. A similar effect of MreB on membrane organization has been observed before for B. subtilis (19). The mechanism by which MreB controls lipid microdomains remains elusive. For eukaryotic membranes, a picket-fence model has been proposed, in which the dense cortical actin cytoskeleton forms nanometer-sized compartments physically restricting lipid diffusion (8). Because the prokaryotic MreB cytoskeleton is less dense and spatially uncoordinated (2, 20), it is not likely that MreB can compartmentalize the prokaryotic membrane in the same way. The tendency we observed for the formation of transient DiI-C12-contained lipid domains in the absence of polymerized MreB indicates that lipid self-organization plays an important role in microdomain formation, similar to what has been proposed for the formation of eukaryotic lipid rafts (52), and that MreB stabilizes them.

One might expect that protein diffusion would be affected by the heterogeneity in membrane composition, for example resulting in distinct diffusion coefficients in different regions of the membrane. Remarkably, the diffusion of almost all proteins investigated could be well described by a single population. This apparent homogeneity in diffusion properties might be the result of the limited temporal and spatial resolution of our measurements. Within the 32 ms exposure time, the proteins move tens to hundreds of nanometers, which could result in an effective averaging out of membrane heterogeneity on this length scale. Yet, the possibility that, in addition, the TMPs are excluded from certain regions in the membrane cannot be ruled out. This latter possibility is supported by our experimental results on TMP diffusion in the presence and absence of polymerized MreB. On the one hand, polymerized MreB has a confining effect on TMPs, which is reflected by the subdiffusive nature of TMP diffusion, resulting in shorter displacements at longer timescales than expected for normal Brownian diffusion. On the other hand, at short timescales TMP diffusion is substantially faster (∼50%) upon inhibition of MreB polymerization. This might be the effect of mixing of the destabilized lipid microdomains with bulk membrane, resulting in a less viscous membrane environment sensed by the TMPs.

We have furthermore demonstrated that size-dependent TMP diffusion in E. coli can be well described by the Saffman-Delbrück model (30). This is a surprising result, because the high degree of crowding in the E. coli membrane as well as the MreB-regulated membrane heterogeneity appear to be in contradiction with the assumptions underlying the model, which describes the membrane as a continuous, thin viscous fluid. As discussed above, the discontinuity and granularity of the TMP-crowded membrane (with crowder size and distance on the order of a few nanometers) are most likely averaged out in our experiments. A fit with the Saffman-Delbrück model to our data results in a membrane viscosity that is 16–40 times higher than found in vitro (49, 50). Also the bulk viscosity is substantially higher (∼200–300 times) than reported in in vitro studies on giant unilaminar vesicles (49, 50). These values should not be interpreted as the actual viscosities of the membrane and the cytosolic/periplasmic fluid in E. coli. They rather represent effective viscosities accounting for the effect of collisions with other macromolecules in this highly crowded space.

In conclusion, our findings show that MreB plays a crucial role in the spatiotemporal organization of the cytoplasmic membrane of E. coli: it stabilizes physically distinct lipid microdomains and modulates the dynamics of lipids and TMPs. The weak size-dependence of TMP diffusion as well as the confinement at larger time- and length scales compared to eukaryotes (53) most likely reflects the uncoordinated nature of the MreB cytoskeleton opposed to the dense and regular mesh of cortical actin. Our findings thus indicate that the interplay between the submembranous cytoskeleton and the cytoplasmic membrane is an evolutionarily conserved mechanism controlling the cytoplasmic membrane organization in both prokaryotic and eukaryotic cells.

Author Contributions

E.J.G.P. and Y.J.M.B. initiated research; F.O., A.V., E.J.G.P., and Y.J.M.B. designed experiments; A.V. constructed plasmids; F.O. and A.V. performed experiments; F.O. performed data analysis; all authors contributed to data interpretation; and F.O., A.V., E.J.G.P., and Y.J.M.B. wrote the article.

Editor: Amitabha Chattopadhyay.

Supporting Material

Movie S1. Movie of E. coli Stained with DiI-C12 Observed with Continuous Epifluorescence Illumination and 32-ms Exposure Time per Frame

Scale bar, 1 μm.

Movie S2. Movie of E. coli Stained with DiI-C12 in Presence of A22 Observed with Continuous Epifluorescence Illumination and 32-ms Exposure Time per Frame

Scale bar, 1 μm.

Movie S3. Movie of a DiI-C12 Single-Molecule Trajectory—Depicted in Fig. 3 c—Observed with Continuous TIRF-Fluorescence Illumination and 12-ms Exposure Time per Frame

(Top) Raw images. (Bottom) 2D-Gaussian-rendered single-molecule positions of the trajectory. Scale bar, 1 μm.

Movie S4. Movie of a DiI-C12 Mobility Switching Single-Molecule Trajectory Observed with Continuous TIRF-Fluorescence Illumination and 12-ms Exposure Time per Frame

(Bottom) Raw images. (Top) 2D-Gaussian-rendered single-molecule positions of the trajectory with its mobile stretch in red and immobile stretch in blue. Scale bar, 1 μm.

Movie S5. Movie of a CstA-eGFP Single-Molecule Trajectory—Depicted in Fig. 4 c—Observed with Continuous Epi-Fluorescence Illumination and 32-ms Exposure Time per Frame

(Top) Raw images. (Bottom) 2D-Gaussian-rendered single-molecule positions of the trajectory. Scale bar, 1 μm.

Movie S6. Movie of a CstA-eGFP Single-Molecule Trajectory in Presence of A22—Depicted in Fig. 4 d—Observed with Continuous Epifluorescence Illumination and 32-ms Exposure Time per Frame

(Top) Raw images. (Bottom) 2D-Gaussian-rendered single-molecule positions of the trajectory. Scale bar, 1 μm.

Movie S7. Movie of a TatA-eGFP Single-Molecule Trajectory Observed with Continuous Epifluorescence Illumination and 32-ms Exposure Time per Frame

(Top) Raw images. (Bottom) 2D-Gaussian-rendered single-molecule positions of the trajectory. Scale bar, 1 μm.