Untangling the Influence of a Protein Knot on Folding

Abstract

Entanglement and knots occur across all aspects of the physical world. Despite the common belief that knots are too complicated for incorporation into proteins, knots have been identified in the native fold of a growing number of proteins. The discovery of proteins with this unique backbone characteristic has challenged the preconceptions about the complexity of biological structures, as well as current folding theories. Given the intricacies of the knotted geometry, the interplay between a protein’s fold, structure, and function is of particular interest. Interestingly, for most of these proteins, the knotted region appears critical both in folding and function, although full understanding of these contributions is still incomplete. Here, we experimentally reveal the impact of the knot on the landscape, the origin of the bistable nature of the knotted protein, and broaden the view of knot formation as uniquely decoupled from folding.

Introduction

From our daily life we know that knots provide stability and security in physical systems. Our shoelaces remain tied; for example, because it takes a substantial amount of directed energy to free the laces. Protein knots, while unique, may be advantageous for protein stability and function. In fact, some studies have demonstrated the protein stabilizing potential of knots (1, 2). However, this area has not been systematically explored. A problematic factor with understanding and characterizing knot formation in proteins is that current experimental studies have been hampered by the extreme difficulty in untying deeply knotted proteins, even after secondary and tertiary structure has been disrupted (3, 4). Although experimental systems are limited in the study of backbone-knot formation in proteins, it has been successfully explored on the computational level (1, 2, 5, 6, 7, 8, 9, 10, 11, 12, 13). Computational modeling and limited experimental data together suggest that folding experiments on knotted proteins have been performed, thus far, largely under conditions probing the reversibility of unfolding/refolding of a polypeptide chain that remains knotted (1, 2, 14), because the knot persists even when all other folded elements have been denatured (4).Consequently, the mechanism of tangling, and thus knot formation, is still beyond experimental resolution. Moreover, many of the ideas generated from theoretical models have yet to be compared to experimental data on the same proteins, although recent translational experiments of homologous knotted proteins indicate that knot tying is a rate-limiting step en route to native (15, 16), consistent with the abundance of modeling data (12, 13, 17, 18, 19, 20). Interestingly, these experimental results suggest that the plasticity of the knot-folding landscape is more constricted than computationally observed for these constructs (15, 16, 21). Here, we have chosen to experimentally explore the persistence of the knot through analysis of the folding of the hypothetical MTase protein from Thermotoga maritima, which is one of the smallest members of the structurally homologous SPOUT MTase 3₁ trefoil knot proteins that have been experimentally studied so far, thus we term it a minimal tied trefoil (MTT_Tm) (14, 22).

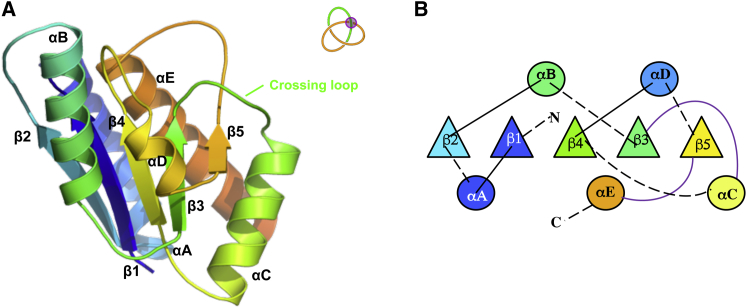
MTT_Tm displays all the structural elements characteristic of the α /β-knot MTases (Fig. 1, A and B), with five parallel β-strands sandwiched between five α-helices, and the 3₁ knot appearing toward the C-terminus of the protein. Most modeling representations of this class of protein, to date, describe the folding landscape of these proteins as principally driven via threading the C-terminus of the protein through the knotting loop until the knot is formed, as the overall fold develops (10, 12, 19, 23, 24, 25, 26). Translational experiments further implicate this as the dominant route in knot-folding (15, 21). Interestingly, a handful of computational observations have also captured the possibility of knotting through an alternate mechanism of loop-flipping, where a knot forms in a single, jump rope-like move (10, 12, 23, 24). This is important as it suggests diversity in the folding pathways for knotting, consisting of steps that are not limited by an entropic penalty, such as that resulting from threading a loop to form a knot. As the folding landscape may include both tied and untied versions of a knot-protein, detection of these varying folding species are (and thus far have been) experimentally challenging to observe. Interestingly, near-native-like species have been regularly observed computationally as intermediate states during knotting (13, 20, 27, 28, 29). These native-like species are relatively stable, thus contributing to observable trapped kinetic states and slow folding (17, 30). In unique circumstances, this trapping can lead to bistability and hysteresis, an apparent equilibrium state resulting from the heterogeneous population of these multistable species (3, 31, 32). As potentially significant entropic barriers during knot-folding have been alluded to previously (10, 12, 13, 20, 23, 24, 25), there is the implication that there are energetic benefits to knot formation. This is of particular interest when probing the folding mechanism for proteins with novel geometric folds, such as the knotted α /β fold. A key question that remains is what is the impact of the knot on the overall landscape of a protein? Here, we probe that question via exploring the landscape of the MTT_Tm with experimental thermodynamic and kinetic analyses.

Figure 1.

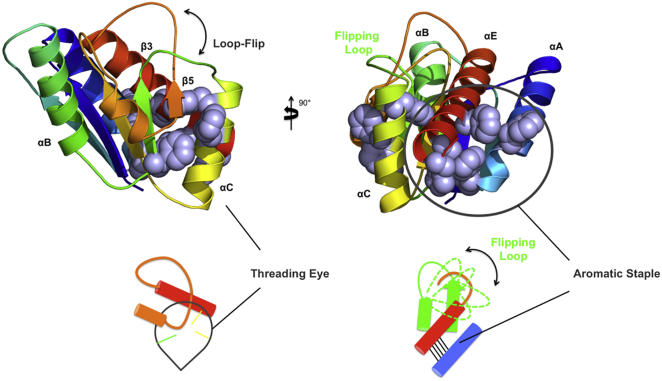
Structural and mechanistic overview of MTT_Tm. (A) Molecular representation of MTT_Tm, indicating the secondary structure and key features in the structure, as well as the 3₁ knot topology. Overall, MTT_Tm displays the structural elements characteristic of all α /β-knot MTases. (B) Cartoon representation of the protein structure, following the same color scheme. Purple highlights the knot crossing loops. To see this figure in color, go online.

Materials and MethodsCloning, expression, and purification of MTT_TM

The DNA corresponding to MTT_Tm was amplified by polymerase chain reaction, restriction digested and ligated into the pET-24a expression vector (Novagen, Madison, WI), generating a construct with a 6× His-tag fused to the N-terminus of the protein. The ligated DNA was transformed into Escherichia coli (E. coli) DH5α competent cells (Novagen) and insert-containing DNA purified from isolated colonies verified by sequencing (Eton Bioscience, San Diego, CA). The insert-containing vector was transformed into E. coli BL21 (DE3) competent cells (Invitrogen, Carlsbad, CA). A lysogeny broth culture was inoculated with these cells and grown at 37°C until an OD₆₀₀ of 0.6 was obtained. Protein expression was induced by the addition of 1 mM isopropyl-β-D-thiogalactoside (final concentration) and the temperature was subsequently reduced to 25°C during protein expression. The cells were harvested after 12 h by centrifugation (6,300 × g) for 10 min. The media was carefully decanted, and the resulting pellets were resuspended in buffer containing 50 mM sodium phosphate, 300 mM NaCl, 5 mM β-mercaptoethanol (βME), pH 8.0. The cells were lysed using an EmusiFlex-C5 (Avestin, Ottawa, Ontario, Canada). After clarification of the crude extract by high-speed centrifugation (15,000 × g), the lysate was loaded onto an inner membrane anion channel column on the Profinia Affinity Purification System (Bio-Rad, Irvine, CA). The inner membrane anion channel column was extensively washed with buffer containing 100 mM sodium phosphate buffer, 600 mM NaCl, 10 mM βME, at pH 8.0. The protein was eluted with buffer containing 100 mM sodium phosphate, 600 mM NaCl, 10 mM βME, 500 mM imidazole at pH 8.0. The protein was clarified by filtration and then loaded onto a HiPrep 26/60 Sephacryl S-200 HR column (GE Healthcare Life Sciences, Pittsburgh, PA), equilibrated in buffer containing 75 mM sodium acetate buffer, pH 5.6, and 1% glycerol. The protein was collected by fractionation and protein was assessed by sodium dodecyl sulfate-polyacrylamide gel electrophoresis and judged to be >95%.

Equilibrium stability measurements

Equilibrium unfolding and refolding studies were collected on a 60 DS Spectropolarimeter (Aviv Instruments, Lakewood, NJ). Protein samples were prepared in buffer containing 75 mM sodium acetate, pH 6.2, and varying concentrations of denaturant, ranging from 0 to 6 M guanidinium hydrochloride (Gdn-HCl). The protein solutions were allowed to equilibrate for varying time frames (1 week, unfolding; 2 weeks, 6 months refolding) at 25°C before data acquisition. A wavelength spectrum from 250 to 205 nm was collected for each sample dilution at 25°C. The change in ellipticity at 222 nm was monitored for the change in native helical signal as a function of denaturant concentration and time of exposure. The longer incubation measurements were completed on the identical samples at the given timeframe (6 months). Protein samples were assessed for chemical integrity. Equilibrium unfolding and refolding circular dichroism (CD) data were fit with GraphPad Prism version 6.0 software as described previously (33).

Kinetic measurements

Manual mixing folding kinetics were collected as described previously (33) and monitored with a 60 DS Spectropolarimeter (Aviv Instruments). Protein concentrations were typically 1 mM. Samples were prepared in buffer containing 75 mM sodium acetate, pH 6.2, with varying concentrations of denaturant, ranging from 1.6 to 6 M Gdn-HCl as indicted in the respective plots. The change in ellipticity at 222 nm as a function of time upon rapid dilution of protein into a given final Gdn-HCl concentration was followed to monitor changes in the state of the protein. The acquired data curves were fit to mono- and biexponential equations as well as stretched exponential functions as described in the text, similar to previous reports (33).

Theoretical denaturation profile

Modeling of the denaturation profiles of the tangling versus the global fold of the protein using the parameters obtained from the fits of the experimental data were obtained as described previously (34).

Molecular representations

All molecular representations were prepared with MacPyMol (35) using Protein Data Bank (PDB): 1O6D.

Results and Discussion

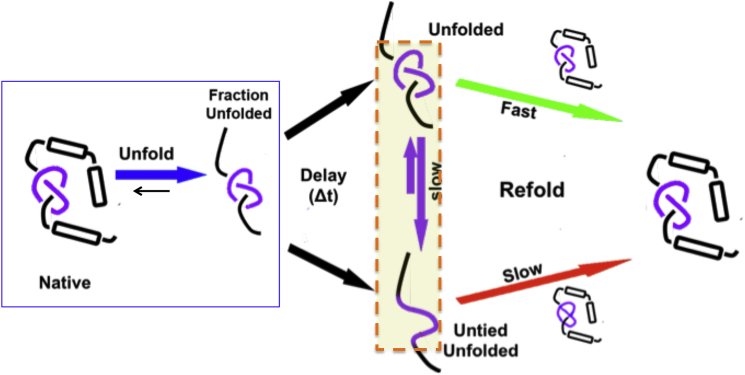
Equilibrium stability experiments describe the sequence-structure-energy relationship for a given protein, and help detail the complexity of the unfolded basin. For the vast majority of proteins, the unfolding and refolding equilibrium curves superimpose when collected on chemically denatured proteins, indicating full reversibility in folding and similarities in both the folding and unfolding landscapes. Thermal unfolding studies oftentimes do not superimpose because of irreversibility introduced as a result of chemical modification and aggregation events. To assess reversibility of the reactions, traditionally, equilibrium unfolding and refolding curves are collected only after waiting much greater than times equivalent to greater than five half-lives of the slowest folding reaction, as assessed by denaturant-induced kinetic unfolding studies and following probes of the native structure as a function of time. Typically, optical signals provide robust tools for protein folding studies (36, 37). Disruption in secondary and tertiary structure can be followed as a function of time and denaturant concentration via a signature signal change, and the time needed to equilibrate samples before collecting data for assessing the thermodynamic stability of a given protein can be ensured for typical proteins (Normally incubation times of all samples for times greater than five half-lives of the slowest time point observed in kinetic chevron studies is sufficient for the vast majority of proteins as that leads to ≫97% equilibration of all samples. Recall folding rates typically increase at high and low denaturant concentrations.) (34). Here, as in the case of the unusual geometry of the green fluorescent protein (GFP), we have an atypical system where bistability and unusual geometric constraints leads to atypical behavior on the folding landscape of these proteins in the transition region (3). In addition, the tied state in the unfolded ensemble does not have a characteristic optical signal that is readily monitored (4). Thus, highly extended periods in denaturing conditions, beyond that normally needed to unfold the helices and strands are needed to untie the knot.

Typical experimental unfolding studies of a knotted protein that equilibrates samples for five half-lives, as judged by disruption of secondary and tertiary structures, will be judged fully reversible and give the thermodynamic stability of the protein and the knot as the protein will have never untied and the two-states populated will be folded-tied and unfolded-tied (Fig. 2, blue box region left), consistent with the few reports available (4). Of importance, a much more extended time is needed for the conversion of unfolded-tied to unfolded-untied (Fig. 2, middle orange highlighted region) relative to folding (unfolding). Consistent with simulations, unfolding (but still tied) and untying (and fully unfolded) are distinct reactions from one another and an extended time delay allows for a shift in these two populations (3) (Fig. 2). Acquiring an equilibrium refolding curve after much delayed time will result in a shift in the apparent equilibrium curve as the unfolded basin will be heterogeneous with respect to the extent of entanglement. As even more time is spent in denaturant, the population of untied protein is expected to increase, thus further shifts in the apparent refolding curves, most notably in the transition region. In addition, as the unfolded basin is shifting over time, kinetic refolding studies are expected to show a change from a major population of fast folding tied species to a heterogeneous population of species as the unfolded protein becomes untangled over time (Fig. 2, right).

Figure 2.

Schematic of the proposed origin of heterogeneity in the mechanism of folding for the knotted protein, MTT_Tm. Proposed folding mechanism where the orange boxed region highlights the suggested slow interconversion to a fully unfolded, untied species. To see this figure in color, go online.

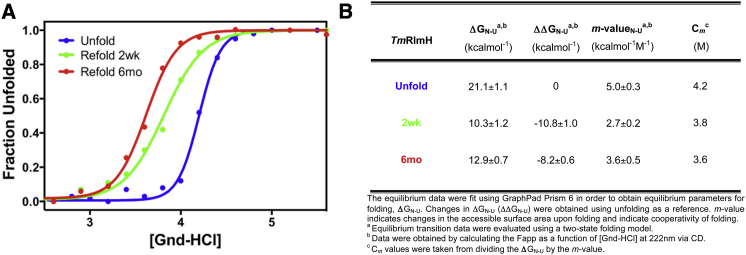
Consistent with the model presented in Fig. 2, our experimental unfolding and refolding curves (Fig. 3 A) clearly show an unconventional folding landscape, as they do not superimpose. This unusual experimental behavior is termed hysteresis, a pathway dependent, bistable property in a given system that is most evident during the evaluation of thermodynamic equilibrium experiments (3). These observations are consistent with the distinctly separate timescales (decoupling) needed for unfolding and side chain mediated untying for the knotted native state (17). The unfolding transition for MTT_Tm fits well to a simple two-state model as previously described (3), and allows for the calculation of the apparent thermodynamic parameters. This transition gives an upper limit on the stability and likely reflects the transition between the folded-tied and unfolded-tied ensemble of states as discussed previously. The fits for the 2-week and 6-month incubation times are given for comparison (Fig. 3 B). These values indicate a highly stable protein, consistent with homologous knot-proteins (4), with a highly cooperative transition to the unfolded (Fig. 3 B). Varying the equilibration time in denaturant has a striking effect on the midpoint and slope, or cooperativity, of the observed refolding transitions. The longer the time allowed for protein incubation in denaturant, the greater the contrast in cooperativity (Fig. 3), signifying changes in the exposed surface area of the available ensemble of species upon refolding. We propose that an increase in the unfolded-untied species is populated over longer time periods of denaturation (Fig. 2), consistent with the observed hysteretic behavior. The best fit to a two-state (Fig. 3) equation suggests that while a small population of an intermediate or alternative native state is present in the ensemble (Fig. 2), the population is not distinct enough in signal nor denaturant dependence under our current conditions to warrant higher order fitting as described previously (38).

Figure 3.

Unfolding and refolding transitions of MTT_Tm. (A) Denaturant-induced unfolding (blue) and refolding (red and green) measured by CD spectroscopy. The red and green refolding curves represent incubation timescales, 2 weeks and 6 months, respectively. The unfolding (blue) and refolding (red and green) transitions show hysteresis, as the curves do not overlay. This is consistent with a shift in the folded ensemble, related to the uncoupling of unfolding and untying. (B) The calculated thermodynamic parameters for the respective curves are presented. The fit of the data was to a two-state model, to determine the free energy of stabilization (ΔG) and the denaturant concentration-dependence of the transition, m-value, for the respective states. To see this figure in color, go online.

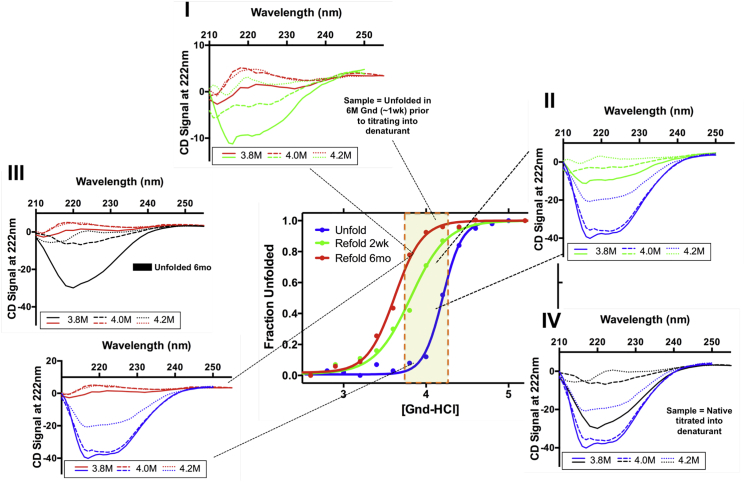
For proteins with significant thermal stabilities, as observed with GFP (32), differences in the folding landscape are additionally complicated both by protein stability, unusual modifications of the protein backbone coupled with additional isomerization events (proline, chromophore, rotational), and full unfolding/refolding curves appear with a gap in thermodynamic superimposability. This hysteretic behavior observed on a complex folding landscape is linked to a slow entropic search toward an active conformation (3). The challenges in identifying hysteresis and the resulting thermodynamic implications are oftentimes captured through a deeper examination of the optical data attributed to this phenomenon, where subtle differences in optical signals are revealed (Fig. 4). For this α /β knot fold, a strong helical signal is the signature observation for the native fold by CD (Fig. 4). The overall helical signature does not change, that is, the protein does not shift between a left- and a right-handed helical signature. In addition, under strongly unfolding conditions, all helical signal is lost, and under strongly refolding conditions all helical signal is regained. However, in the intermediate regime of the transition curve, where there is a weighted population of folded and unfolded protein depending on protein stability (39), we also observe a time-dependent change in helical content over extremely long time frames (Fig. 4, IV), consistent with a progressive loss of more helical signal within the hysteresis zone (40). The proportion of the population that can maintain key secondary structure interactions diminishes, because the relevant equilibrium is between native-tied and unfolded-tied protein (Fig. 2), eventually diminishes with extended time as the knot becomes untangled from its optimal crossings in the unfolded state. This is magnified in the transition zone as also described for the unrelated, high contact order protein GFP (31, 32, 40). Unlike what is observed when diluting to high denaturant concentrations where secondary structure is disrupted or when refolding to strongly native conditions (where secondary structure is fully recovered) the transition region affords conditions for decoupling of folding from intricate geometric effects in highly stable systems.

Figure 4.

Hysteresis in MTT_Tm. The gap in superimposability of the respective folding curves is a result of distinct differences in the helical signal of the acquired data. (I) Dilution points (3.8, 4.0, and 4.2 M) are represented by solid, dashed, and dotted lines, respectively. Black lines represent the unfolded protein after 6 months equilibration (identical samples). (IV, bottom right) The unfolding data (blue) shows the presence of a strong helical signal, despite the equilibration time, that does not change after prolonged incubation (black). (II, upper right) Comparison of the unfolded and shorter refolded incubation (green) reveals a loss in helical signal, suggesting a shift in the population ensemble toward more unfolded. (III, left) As the incubation period is prolonged (red), a change in the observed helical trend is observed, compared to the unfolded (blue, black). The overall signal is consistent with random coil, a state generally accepted as unfolded. (IV, center) Comparison of the refolding incubation times (green, red), indicate the eventual loss of the helical signal over time. The comparative analysis of the denaturant-induced unfolding at two incubation times is from identical samples. To see this figure in color, go online.

The change in the content of helical secondary structure content in the hysteresis zone (40) over significant incubation times observed here may be correlated to the presence of two stabilizing features in MTT_Tm: 1) the long flipped-loop that helps create the knot in this protein and 2) a stabilizing network of aromatic side-chain interactions between the threaded C-terminal helix and the initial long N-terminal helix, an aromatic staple, where contacts between the helices related to knotting can help preserve the knotted region (Fig. 5). Here, it may be that an aromatic staple (Fig. 5, gray) between αA and αE (Fig. 5, the threaded helix in red), contribute to the energy barrier to fully unfolded (and untying the protein) as the loop can flip back before the N- and C-terminal helices dissociate. That is, flipping the crossing loop allows for efficient untying in the absence of the stabilizing helical staple as the helices dissociate and αE unplugs (through) from the threading loop (Fig. 5). However, with the aromatic staple in place, reflipping of the crossing loop stabilizes against both helix-helix unpacking and untying, preventing full unfolding (Fig. 5). Consistent with this hypothesis, experimental folding data for proteins with fewer packing interactions, in similar regions, exhibit far less hysteretic behavior (14). Furthermore, experimental conditions may further slow this transition (38) implicating irreversible tied-denatured states (4). Contrastingly, strong denaturing conditions for extended incubation times destabilizes these effects, consistent with the observed CD wavelength traces at equivalent dilutions (identical samples over time, see Materials and Methods) show reduced helical signal during refolding (Fig. 4, II). This more random coil-like signal (Figs. 4, I and III) implicates an increase in the population of unstructured species where the helix-helix interaction is disrupted. Thus, the high-entropy barrier related to unknotting and the aromatic staple is overcome in denaturant over a longer equilibration time, and refolding may progress from a basin where an untied-unfolded population is more prevalent, consistent with the proposed mechanism (Fig. 2) and previous simulated work (3). This comparative analysis of hysteresis highlights the added complexity of the knot-folding landscape. Our proposal suggests a competition between loop-flipping and the strength of the aromatic staple that favors the threaded element (Fig. 5). We propose strong interactions between aromatic residues, as uniquely revealed here with the π-stacking between helices in MTT_Tm, the uncrossed state will more often recross before the threaded helix can unfold, and not allow complete untying (Fig. 5). Thus, the tied (or tangled) state will be recaptured. Given enough time, though, the untangled state will prevail. This proposed mechanism can dominate the landscape over one where the C-terminus of helix αE must plug through the knotting loop as folding elements form (8, 23).

Figure 5.

Schematic of the proposed aromatic staple. A molecular representation and schematic of the aromatic staple side-chain interactions associated with stabilizing the helices implicated in knot-tying. The aromatic region is highlighted in gray. To see this figure in color, go online.

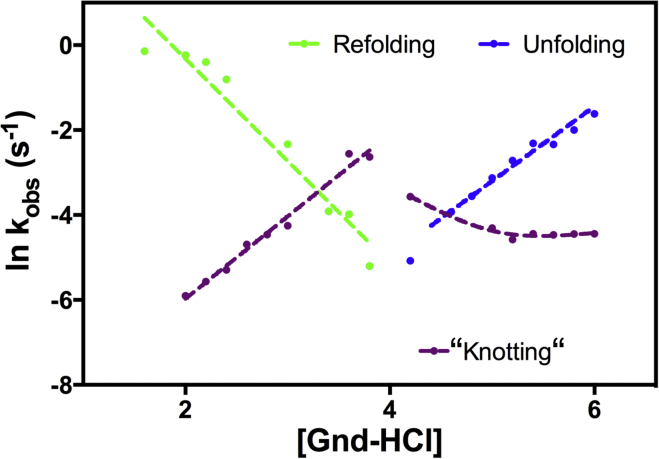
The observed shift in the unfolded-untied population experimentally observed here (Fig. 4), indicates the rates associated with folding and knotting (tying/untying) are kinetically uncoupled. Thus, an independent signal related to the coupling/decoupling of folding and tying/untying, in a manner analogous to the classical observations of proline-isomerization-limited folding, may be experimentally observed (41). We probe this question here, through folding kinetic experiments. The CD-detected data exhibit single-exponential kinetics when a fast unfold/refold reaction is carried out, as is expected for a protein that remains in the tied state with the knot region intact (Fig. 2). As the protein is allowed to incubate longer in nonnative conditions, the observed kinetics begin to exhibit more complex kinetic transitions to both the native and unfolded states, as indicated (Fig. S1 in the Supporting Material). We fit the resulting data to compressed, stretched, and multiexponential models. With the stretched exponential fits to the data, the exponential parameter, β, must be used in a range that is rare for describing protein folding kinetics; thus, we chose to use multiexponential fits for simplicity (23). The denaturant-dependent folding data was best fit to a biexponential rate equation, similar to previous knot kinetic reports (23) because the double exponential is simplest in describing the kinetic data. A plot of the natural log of the rate constants (k_obs) as a function of final denaturant concentration is given in Fig. 6. Under conditions strongly favoring folding (Fig. 6, green) or unfolding (Fig. 6, blue), the observed denaturant dependence of the major phase is as expected for denaturant-dependent kinetic behavior. The observed rates at intermediate denaturant concentrations are slowest, as expected for a protein folding reactions. Remarkably, the second kinetic phase displays a unique inverted trend as a function of final denaturant concentration to that observed for the principle folding reaction (Fig. 6, purple). This phase is noticeably slower than the folding rate at both strongly unfolding and refolding conditions, but is comparable to the observed folding rate at intermediate denaturant concentrations (Fig. 6). We attribute this kinetic phase to knot-related loop-flipping and knot-associated changes, as illustrated in Fig. 5. The unconventional folding kinetics observed here demonstrate that given conditions favoring strongly folded species, the barrier for knotting and knot-associated changes are indeed limiting, and kinetically observed as distinct from folding, consistent with computational models (3, 23). Furthermore, at high denaturant, where unfolding progresses faster than untying, a rollover is observed. We attribute this to the population of the trapped tied-unfolded (tangled) species. This is consistent with observations of multiple routes and kinetic traps in knot folding/unfolding (Fig. 7), including those that also help mitigate off-pathway kinetic traps, such as backtracking and slipknotting (8, 9, 23).

Figure 6.

Chevron plot of the calculated folding kinetic rates from the two-exponential fit for MTT_Tm as a function of Gdn-HCl concentration. The refolding (green), unfolding (blue), and knotting (purple) rates are plotted as points, with dashed lines added to aid the eye. Both refolding and unfolding of the initial rate constant follow a trend consistent with general observations for folding. The knot rate constants (purple) deviate from the normal trend, where (un)tied is slower than folding/unfolding, and limiting as the folding midpoint is reached. The roll in untying (right) is attributed to trapping, where folded-untied species are more prevalent. To see this figure in color, go online.

Figure 7.

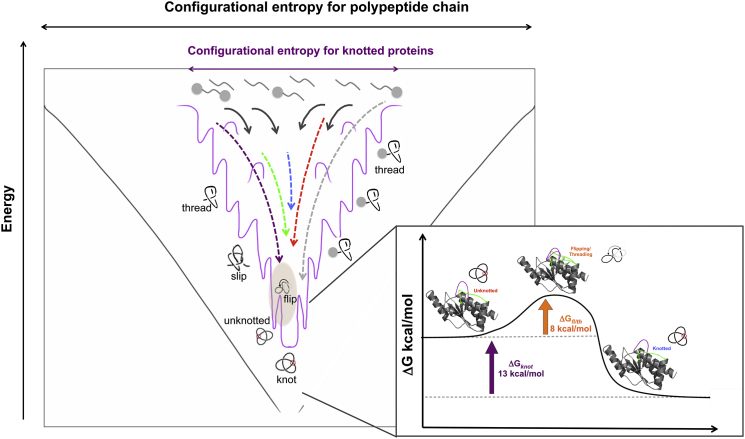
An energy landscape diagram showing the limited configurational entropy for the knot topology. Arrows highlight folding pathways, with the colors representing the experimental data presented in this study. Gray represents the route highlighted in translational experiments with fused proteins (15, 21). An activation energy diagram for the proposed functional folding-knotting pathway highlights a transition point where flipping of the knot-forming loops forms the knot. The unknotted-folding construct is on the reaction coordinate as a near-native species, contributing to the observed hysteretic gap at equilibrium. To see this figure in color, go online.

Decoupling of tying and folding/unfolding in theoretical observations of knot-folding for this protein reveal disparate timescales for their occurrence (3, 8). The current experimental kinetic observations reported here are consistent with these principle findings. Of importance, given the complexity of the kinetic fits (Fig. 5) and the apparent hysteric behavior of the protein revealed through equilibrium analysis (Figs. 3 and 4), it is highly probable that the knot dominates the folding landscape as a high activation energy barrier, as initially suggested in the knot-folding analysis of an engineered knot-protein (2) and revealed through fitting the folding kinetic data to the simplest available model (Fig. S2). The limited experimental data for knot proteins, in general, indicate that the folding-knotting landscape is modulated by the time spent in denaturant, thus, the time allowed to untangle the protein (2, 3, 4). This is particularly evident in recent studies where refolding jumps were performed from different denaturant starting points, yielding different folding rates (2). The less stringent conditions folded faster, demonstrating a shift in the population of the unfolded basin to a tied-unfolded species (2). Similar to our proposed folding-knotting mechanism (Fig. 2), the transition between untied-unfolded versus unfolded-tied is slow, and the timescale for observing thermodynamic shifts are dependent on the sample conditions and incubation time (38).

Using the kinetic folding rates attributed to knot-limited folding, an apparent free energy associated with the formation of the knot can be estimated (12.7 kcal•mol-1) (Fig. S3). This is significant as it suggests that the stability of the knot-region is substantial compared to the native fold and may be a significant contributing factor to the observed complexity at equilibrium, as the system does not immediately respond to the forces that are applied (hysteresis). Furthermore, as knotting has been experimentally observed to be rate limiting, thus occurring late in folding (15, 21), we suggest a near-native-untied species occurs as a result of the bifurcation in the energy landscape (Fig. 7). Simulations suggest the transition state of knot-proteins correlate to threading the C-terminus (23). In a folding landscape of diverse routes, the limiting configurational entropy for this distinct fold slows folding as the geometric constraints introduce a variety of other complex structural consequences. Here, an activation energy diagram illustrates the potential compensation necessary to reach the native state from a folded-untied species (Fig. 7). The bistability and plasticity in the experimental landscape required to overcome the costs of folding, in this case, tying the knot, is highlighted. Interestingly, the current identification of the stabilizing aromatic staple interactions that join the threading elements further facilitating loop-flipping (Fig. 5) captures the unique foldin event on this otherwise diverse landscape.

Conclusions

Here, we experimentally demonstrate the complex nature of knotting and folding through the identification of a slow transition to untangling events, previously unrevealed. This observed hysteresis highlights the heterogeneity of the landscape, including multistable species. Additionally, through thermodynamic and kinetic analyses, we demonstrate the significance of tangling to the overall stability of the protein. We speculate that a novel subset of side-chain interactions, related to the formation of the knot through loop-flipping, further broadens the view of knot-folding as uniquely decoupled from folding. Taken together, the availability of the flipping route, where a flip of a knot-crossing loop leads to untying/tying (10, 12, 17), and determination of the energy necessary to overcome the topological barrier(s) related to flipping (Fig. 7), suggest that the route monitored here may be consistent with translational events, as nascent-chain folding off the ribosome would further bias the conformational search of the protein fold (16).

Author Contributions

D.T.C. and P.A.J. designed experiments. P.A.J. contributed reagents; D.T.C. performed biochemical experiments; D.T.C and P.A.J. analyzed data; D.T.C. and P.A.J. wrote and edited the article.

Editor: James Cole.