Scavenging dissolved oxygen via acoustic droplet vaporization

Abstract

Acoustic droplet vaporization (ADV) of perfluorocarbon emulsions has been explored for diagnostic and therapeutic applications. Previous studies have demonstrated that vaporization of a liquid droplet results in a gas microbubble with a diameter 5 to 6 times larger than the initial droplet diameter. The expansion factor can increase to a factor of 10 in gassy fluids as a result of air diffusing from the surrounding fluid into the microbubble. This study investigates the potential of this process to serve as an ultrasound-mediated gas scavenging technology. Perfluoropentane droplets diluted in phosphate-buffered saline (PBS) were insonified by a 2 MHz transducer at peak rarefactional pressures lower than and greater than the ADV pressure amplitude threshold in an in vitro flow phantom. The change in dissolved oxygen (DO) of the PBS before and after ADV was measured. A numerical model of gas scavenging, based on conservation of mass and equal partial pressures of gases at equilibrium, was developed. At insonation pressures exceeding the ADV threshold, the DO of air-saturated PBS decreased with increasing insonation pressures, dropping as low as 25% of air saturation within 20 s. The decrease in DO of the PBS during ADV was dependent on the volumetric size distribution of the droplets and the fraction of droplets transitioned during ultrasound exposure. Numerically predicted changes in DO from the model agreed with the experimentally measured DO, indicating that concentration gradients can explain this phenomenon. Using computationally modified droplet size distributions that would be suitable for in vivo applications, the DO of the PBS was found to decrease with increasing concentrations. This study demonstrates that ADV can significantly decrease the DO in an aqueous fluid, which may have direct therapeutic applications and should be considered for ADV-based diagnostic or therapeutic applications.

1. Introduction

The phenomenon of acoustic droplet vaporization (ADV), the acoustically mediated phase transition of liquid perfluorocarbon droplets into gas bubbles, is under investigation for several biomedical applications. Submicron-sized perfluorocarbon droplets extravasate from leaky tumor vessels, undergo ADV, and provide contrast on ultrasound images of cancerous tissue [1,2]. ADV-induced microbubbles generated from micron-sized droplets have also been investigated as point targets for phase aberration correction [3-5]. Further, contrast-enhanced photoacoustic images have been created using ADV to trigger the localized release of cardiogreen dye from a perfluoropentane (PFP) double emulsion [6].

ADV is also being explored for various direct and adjuvant therapeutic applications. Micron-sized perfluorocarbon microbubbles created via ADV have been shown to occlude capillary beds and arterioles, which can facilitate embolotherapy in cancer treatment [3,7,8]. Previous studies have also demonstrated ADV-mediated delivery of chemotherapeutic drugs such as paclitaxel [9], chlorambucil [10], and doxorubicin [11] loaded in perfluorocarbon droplets. Thermal ablation of cancerous lesions has been enhanced using perfluorocarbon droplets as cavitation nuclei during high intensity focused ultrasound (HIFU) exposure [12-14]. Further, ADV microbubbles can provide contrast-enhanced image guidance during treatment [12]. More recently, perfluorocarbon droplets have been shown to lower the acoustic power needed for HIFU-mediated lysis of blood clots relative to HIFU exposure without droplets [15]. Spatiotemporally-controlled ADV-mediated drug release from perfluorocarbon double emulsions has also been shown to regulate the mechanical properties of tissue-engineered scaffolds [16].

ADV results in a significant volumetric expansion of the perfluorocarbon. The ideal gas law was used to predict a volumetric expansion of a factor of 125 (i.e., a radial expansion of 5) [3], and the measured volumetric expansion of evaporating perfluoropentane was a factor of 151 (i.e., a radial expansion factor of 5.3) [3]. Kripfgans et al. [3] also computed a radial expansion factor of 5.9 which accounts for the diffusion of gases into and out of the microbubbles. Kang et al. [17] optically characterized the growth of the ADV-induced PFP microbubbles under various insonation parameters and measured the expansion factor due to ingassing to be between 2 and 3. Sheeran et al. [1] reported that the radial expansion factor of decafluorobutane droplets was 6 ± 1 in a degassed fluid (1.5 ppm of oxygen) and 10 ± 2 in an air-saturated fluid (6 ppm of oxygen). From these results, the amount of ingassing and thus the expansion factor appear to depend on the experimental conditions, potentially including the gas saturation of the fluid, formulation of the droplet, and concentration of the droplets. The diffusion of gases into perfluorocarbon-based ultrasound contrast agents has also been discussed in other studies [18-21]. Further, the high solubility of oxygen in perfluorochemicals [22,23] and the use of perfluorochemicals as blood substitute agents have been demonstrated in previous studies [24,25]. Johnson et al. [26] demonstrated that liquid PFP droplets alone can scavenge dissolved oxygen from the surrounding fluid. Culp et al. [27] subsequently demonstrated that a PFP emulsion can transport sufficient oxygen to ischemic tissue to decrease infarct volume in a rabbit stroke model.

Although these studies demonstrate that dissolved gases in a fluid can diffuse in and out of perfluorocarbon droplets, the change in dissolved gas in the surrounding fluid as a result of ADV has not been quantified. The current study reports on experimental measurements and numerical computations of the change in dissolved oxygen (DO) of a fluid containing PFP droplets before and after ultrasound exposure. PFP droplets diluted in saline were injected in a flow phantom containing inline dissolved oxygen (DO) sensors. The droplets were insonified using a single-element focused transducer at peak rarefactional pressures lower than and greater than the ADV acoustic pressure threshold amplitude. The effect of altering the size distribution and concentration of the droplets were investigated numerically. The phenomenon of ultrasound-mediated gas diffusion concomitant with the cavitation nucleation associated with ADV can have implications on current biomedical applications of ADV as well as serve as a potential strategy to scavenge gases in situ.

2. Materials and Methods

2.1 Preparation of Albumin-coated Perfluoropentane (PFP) Droplets

Albumin-coated PFP droplets were prepared based on a previously established protocol [3]. Briefly, 0.25 ml of dodecafluoropentane (Strem Chemicals, Newburyport, MA, USA) was added gravimetrically to 2 ml vials followed by the addition of 0.75 ml of 4 mg/ml bovine serum albumin (Sigma Aldrich, St. Louis, MO, USA) in phosphate buffered saline (PBS) (Sigma Aldrich). The vials were sealed with a rubber stopper, crimped, and placed on ice prior to amalgamation at 4800 rpm for 30 s in an amalgamator (WIG-L-BUG, Dentsply Rinn, Elgin, IL, USA) at 5 °C to obtain albumin-coated PFP droplets. The vials were refrigerated for at least 24 h before use. Vials were used within 2 days of being manufactured. The size distribution of the droplets was measured with a Coulter counter (Multisizer 4, Beckman Coulter Inc., Brea, CA, USA).

2.2 Experimental setup

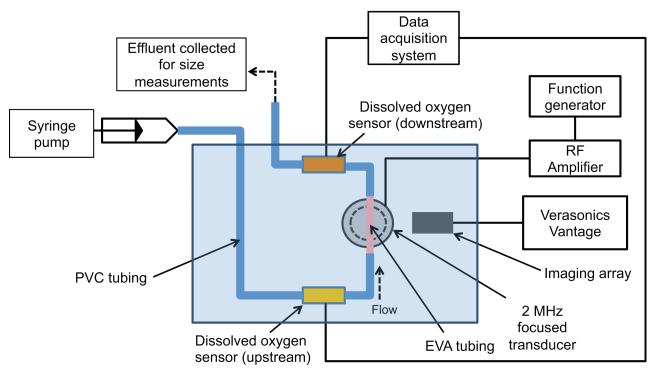
The albumin-coated PFP emulsion was diluted in air-saturated PBS (1:30 v/v) and slowly drawn into a 60 ml syringe through an 18 G needle. Using a syringe pump, the droplets in PBS were pumped through an in vitro flow phantom (Figure 1) at 5 ml/min. The flow phantom consisted of polyvinyl chloride tubing (McMaster-Carr, Aurora, OH, USA), in-line dissolved oxygen (DO) sensors (OXFTC, Pyroscience, Aachen, Germany) and ethyl vinyl alcohol (EVA) tubing (McMaster) immersed in a tank of degassed water maintained at 37 °C. ADV was induced by a single-element 2 MHz focused transducer (H106, Sonic concepts, Bothell, WA, USA) as the droplets flowed through the EVA tubing. Based on a previous study [28] the EVA tubing was used because it had an inner diameter of 1 mm which was comparable to the −6 dB elevational beamwidth of the 2 MHz focused transducer (1.1 mm), thin walls (0.38 mm), and high acoustic transmission coefficient (94%) to ensure uniform insonation of the droplets. The 2 MHz focused transducer had an aperture diameter of 6.3 cm and a focal distance of 6.4 cm.

Figure 1. Experimental setup.

In vitro flow system to measure changes in dissolved oxygen (DO) in a fluid during ADV. PFP droplets diluted in air-saturated PBS were infused into the flow system and insonified by the 2 MHz transducer with an aperture of 6.3 cm and a focal distance of 6.4 cm. DO sensors placed upstream and downstream of the insonation were used to quantify changes in DO of the fluid during ADV. The imaging array was used to confirm the formation of microbubbles during ADV. The effluent collected from the flow system was used to quantify the size distribution of droplets in the absence and presence of ultrasound exposure.

B-mode images of the insonified droplets were acquired using an ultrasound research scanner (Vantage 256, Verasonics, Kirkland, WA, USA) equipped with a linear array transducer (L7-4, center frequency 5 MHz, Philips, Bothell, WA, USA), to monitor the formation of microbubbles [3]. DO in the fluid was measured over 120 s using in-line DO sensors located upstream and downstream of the insonation region. Based on a flow rate of 5 mL/min, fluid took approximately 20 s to travel from the ultrasound focus to the downstream DO sensor. The in-line DO sensors consisted of a luer lock flow-through cell and a fiber optic spot fiber (SPFIB-Bare, Pyro Science GmbH, Aachen, Germany) connected to an optical oxygen meter (FireStingO2, Pyro Science). The DO sensors were calibrated according to the manufacturer’s instructions to measure 100% DO in air-saturated PBS at 37 °C. The effluent from the flow system was collected and diluted in PBS to obtain a final concentration of 1:8000 (v/v). The surviving droplets in the diluted effluent were measured in a Coulter counter (Multisizer 4, Beckman Coulter, Brea, CA, USA) equipped with a 30 μm aperture.

2.3 Ultrasound parameters

The acoustic output and the spatial beam profile of the 2 MHz transducer were calibrated up to 2 MPa peak rarefactional pressure using a 0.4 mm membrane hydrophone (Precision Acoustics, Dorchester, UK) mounted on a three-dimensional stepper-motor controlled system (Velmex NF90 Series, Velmex Inc., 291 Bloomfield, NY). A linear relationship between the voltage applied to the transducer and the peak rarefactional pressures below 2 MPa was obtained. A linear extrapolation of this relationship was used to estimate peak rarefactional pressures above 2 MPa [29,30]. The −3 dB focal volume of the 2 MHz transducer was 0.7 mm × 0.7 mm × 5.4 mm (azimuth × elevation × range), thus allowing a relatively uniform pressure field inside the EVA tubing (inner diameter 1 mm).

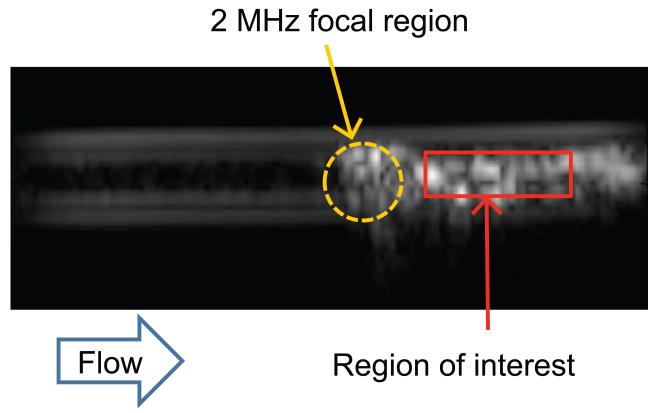
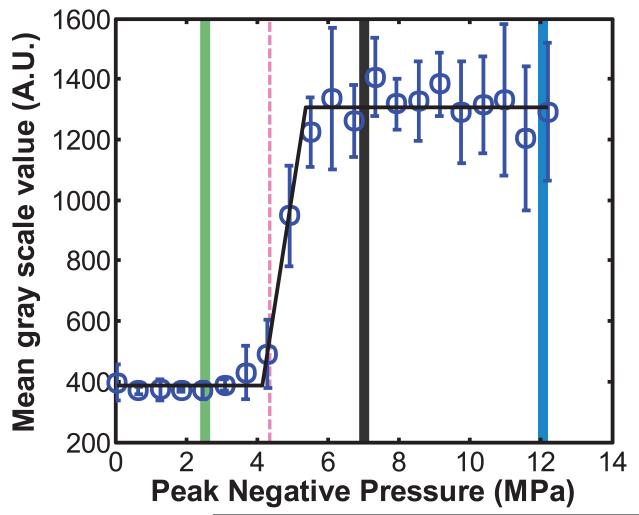
The acoustic droplet vaporization threshold was determined using established methods based on changes in echogenicity [3]. The peak rarefactional pressure of the 2 MHz transducer was ramped from 0 MPa to 12.2 MPa in steps of 0.6 MPa. The pulse repetition frequency was 100 Hz and the pulse duration was 5 μs. At each peak rarefactional pressure setting, a B-mode image of the droplets was acquired. The mean grayscale value was ascertained within a region of interest defined in the lumen downstream of the 2 MHz insonation location (Figure 2a). A piecewise linear fit of the mean grayscale value as a function of the peak rarefactional pressure was used to define the acoustic droplet vaporization threshold. The threshold was defined as the rarefactional pressure amplitude corresponding to the intersection between the first two lines of the piece-wise linear fit based on previous studies [3,31] (Figure 2b). The threshold was determined for four vials of the PFP droplets (one measurement per vial) and the mean and standard deviation of the thresholds were computed after confirming the normality of the data using the Jarque Bera test in MATLAB^® (Mathworks, Natick, MA, USA). Based on this ADV threshold, the PFP droplets were subsequently insonified at peak rarefactional pressures greater than and less than the ADV threshold to quantify changes in DO in the fluid.

Figure 2. Determination of the acoustic droplet vaporization threshold.

(a) B-mode image of EVA tubing containing PFP droplets exposed to 4.9 MPa peak rarefactional pressure ultrasound pulses. The mean gray scale value within the region of interest demarcated in red was quantified as the downstream echogenicity after ADV. (b) A linear piece-wise function (black line) was fit to the mean gray scale values. The ADV threshold was defined as the pressure where the first two lines of the piece-wise function intersected. The threshold pressure is indicated by the dotted line. The pressures indicated by the green, gray, and blue bars at 2.5 MPa, 7.3 MPa, and 12.2 MPa were used in subsequent experiments to measure changes in DO in the fluid induced by ADV.

2.4 Mathematical model

Prior to exposure to ultrasound, the fluid system consisted of two components, namely the PFP droplets and the surrounding PBS liquid. Upon exposure to ultrasound a fraction of the droplets underwent ADV and were converted into microbubbles. Therefore the fluid system after ultrasound exposure consisted of three components, PFP microbubbles, the surviving PFP droplets, and the surrounding fluid (PBS). At equilibrium, the partial pressure of oxygen in the PFP microbubbles, the surviving PFP droplets, and the surrounding PBS liquid are equal as shown in equation 1.

$$\frac{\mathit{RT}{n}_b}{V_b}=\frac{{\mathit{kn}}_d}{{\mathit{SV}}_d}=\frac{{\mathit{kn}}_l}{V_l},$$ (1)

where the first term is the partial pressure of oxygen in the PFP microbubbles given by the ideal gas law, R is the ideal gas constant, T is the temperature, V_b is the total volume of the PFP microbubbles, and n_b is the number of moles of oxygen in the microbubbles. The second term is the partial pressure of oxygen in the droplet according to Henry’s law, where S is the ratio of solubility of oxygen in liquid PFP (80% v/v) [32] to that in water (3% v/v) [33], k is Henry’s constant for oxygen in water (759 L·atm/mol) [34], n_d is the number of moles of oxygen in the droplets surviving ultrasound exposure, and V_d is the total volume of the PFP liquid droplets surviving ultrasound exposure. The third term is the partial pressure of oxygen in the surrounding liquid using Henry’s law where n_l is the number of moles of oxygen in the surrounding liquid, and V_l is the volume of the surrounding liquid.

Further, based on the law of conservation of mass in a closed system, the total number of moles of oxygen in the fluid system should remain constant before and after ultrasound exposure as shown in equation 2.

$$\frac{P_{d0}{V}_{d0}S+P_{l0}{V}_l}{k}=n_b+n_d+n_l$$ (2)

The left hand side of the equation is the number of moles of oxygen in the fluid system before ultrasound exposure and the right hand side of the equation is the number of moles of oxygen in the fluid system after ultrasound exposure. P_l0 is the initial partial pressure of oxygen in the liquid surrounding the droplets which is measured by the upstream DO sensor. P_d0 is the initial partial pressure of oxygen in the PFP droplets without ultrasound exposure and is assumed to be in equilibrium with P_l0. V_d0 is the total volume of all of the PFP droplets in the effluent without being exposed to ultrasound.

The total volume of droplets in the effluent before exposure to ultrasound (V_d0 ), as well as the total volume of droplets in the effluent after ultrasound exposure (V_d), were measured using a Coulter counter 10 min after collecting a sample of the effluent. The sample was allowed to sit 10 min at room temperature to allow any microbubbles to either dissolve or float out of solution. To assess whether any microbubbles were present in the sample after 10 min, the acoustic attenuation spectra of the sample containing droplets with and without ultrasound exposure were measured from two vials of droplets [35]. A Kolmogorov-Smirnov test resulted in a p-value greater than 0.05, indicating that the attenuation spectra of the droplets with and without ultrasound exposure were not significantly different. From this it was inferred that the effluent only contained droplets.

The fraction of surviving droplets at each diameter was defined as the ratio of the number density of droplets after ultrasound exposure to the number density of droplets without ultrasound exposure. Based on calculations made by Kripfgans et al. [3], the microbubbles formed upon ADV undergo a volumetric expansion by a factor of 125 at 37 °C. Additionally, as reported in several studies [1,3,17,36], the microbubble grows due to ingassing. At equilibrium, the microbubble volume based on the ideal gas law will be:

$$V_b=\frac{\mathit{RT}}{P_{\mathit{atmosphere}}}\left(n_{\mathit{PFP}}+n_{O_2}+n_{N_2}+n_{\mathit{Ar}}+n_{{\mathit{CO}}_2}+n_{\mathit{Ne}}+n_{\mathit{He}}\right),$$ (3)

where n denotes the number of moles of gas and the subscripts denote the different gases that will be present in the microbubble after ingassing. The proportions of each non-PFP gas in the microbubble will be the same as the proportions of each non-PFP gas dissolved in the fluid, which in turn was equilibrated with air. Therefore the proportions of each non-PFP gas in the microbubble will be the same as the proportions of the gases in standard air (i.e., nitrogen composing approximately 78%, oxygen composing approximately 21%, et cetera). Equation 3 can be rewritten as:

$$V_b=\frac{{\mathit{RTn}}_{\mathit{PFP}}}{P_{\mathit{atmosphere}}}+\frac{\mathit{RT}}{P_{\mathit{atmosphere}}}\cdot (n_{O_2}\cdot \frac{n_{\mathit{air}}}{n_{O_2}}),$$ (4)

where n_air is the number of gas molecules that compose a unit volume of standard air. The total number of air molecules to oxygen molecules is 4.7733. Further, n_O2 in equation 4 is equal to n_b as defined in equation 2. The total volume of the microbubbles (V_b) can therefore be rewritten by expressing the first term in equation 4 in terms of the total volume of droplets that were vaporized during ADV and the expansion factor of 125, as:

$$V_b=\left(V_{d0}-V_d\right)\times 125\frac{4.7733\cdot n_b\mathit{RT}}{P_{\mathit{atmosphere}}}$$ (5)

By solving equations 1, 2, and 5, simultaneously, the number of moles of oxygen in the liquid per unit volume n_l/V_l can be calculated. The percent dissolved oxygen in the surrounding fluid after ultrasound exposure is predicted to be:

$${\mathit{DO}}_l=\frac{{\mathit{kn}}_l}{V_l{P}_{l0}}\times {\mathit{DO}}_{l0},$$ (6)

where DO_l0 is the initial dissolved oxygen in the liquid surrounding the PFP droplets and DO_l is the predicted dissolved oxygen in the surrounding liquid in equilibrium with phase-transitioned PFP droplets after ultrasound exposure.

2.5 Centrifugation of droplets

Transitioning droplets in the arterial system after intravenous injection requires the droplets to flow through the pulmonary capillaries. De Jong et al. [37], estimated the size distribution of ultrasound contrast agents that pass through the lungs based on the size distribution of the pulmonary capillaries [38]. The same technique was applied to estimate the size distribution of droplets that would pass through the lung. Briefly, the size distribution of human lung capillaries was used to compute a cumulative probability density function for passage of particles through the pulmonary capillary bed. It was assumed that each droplet was likely to pass through the lungs if it had a smaller diameter than the pulmonary capillary. The cumulative probability density function was multiplied by the number density size distribution of the droplets.

The size distribution of the droplets was subsequently modified using centrifugation to remove a large fraction of the droplets that would not be predicted to survive lung filtration. Centrifugation techniques have been previously used for size separation of ultrasound contrast agent microbubbles [39,40]. The PFP emulsion was diluted in PBS (1:4.8 v/v) and centrifuged at a relative centrifugal force of 9 g for 5 min at 21 °C (Allegra, Beckman Coulter). After centrifugation, 2.88 ml of the supernatant was collected. The centrifugation speed and time were selected so that only droplets that were approximately 6 μm or less remained in the supernatant. These droplets, which will be referred to as centrifuged droplets, were used in the subsequent ultrasound experiments.

2.6 Computed droplet size distributions and concentrations

In order to determine an optimal droplet size distribution and concentration for in vivo applications, the trade-off between maximum gas scavenging and the potential for droplets to occlude lung capillaries after intravenous injection were considered. Larger droplets undergo a phase-transition more efficiently [10], but also have a higher probability of occluding pulmonary capillaries. Another limitation is the maximum concentration of droplets within the blood stream that can be tolerated by the body. Previous studies of perfluoropentane droplets in animals (rabbits and canines) have not reported adverse events when the estimated in vivo concentrations are approximately 10⁵ to 10⁶ droplets/ml [4,7,8,13]. This concentration range is similar to the FDA approved concentration of perfluorocarbon-based ultrasound contrast agents in humans, based on the calculation of a bolus injection diluted by the total blood volume in humans (5 × 10⁶ microbubbles/ml) [41].

A set of computations were performed to determine a size distribution of PFP droplets with an in situ concentration of no more than 5 × 10⁶ droplets/ml that would cause at least a 50% decrease in DO in the fluid surrounding the droplets. Gaussian probability density functions with a range of standard deviations from 0.1 μm to 4 μm in steps of 0.1 μm were used to represent size-isolation filters. Experimentally obtained size distributions of centrifuged droplets without and with ultrasound exposure were multiplied by these size isolation filters to obtain a family of curves that represented computationally modified size distributions. The computed droplet-size distribution with the smallest mean diameter that was predicted to lower the DO in the fluid to 50% at a concentration of 5 × 10⁶ droplets/ml was selected. This computationally modified size distribution was subsequently scaled to vary the concentration of droplets from 10³ to 10⁹ droplets/ml. The predicted dissolved oxygen concentration in the fluid surrounding the computationally modified size distributions were calculated as described in section 2.4.

2.7 Statistical analysis

Measured and predicted DO values were compared using the Student’s t-test in QuickCalcs (GraphPad, La Jolla, CA, USA). Differences in volume-weighted number density size distributions were assessed using the Kolmogorov-Smirnov test in MATLAB^®. For all statistical tests, a p-values less than 0.05 used to denote a statistically different result.

3. Results

3.1 Ultrasound-mediated phase-transition response

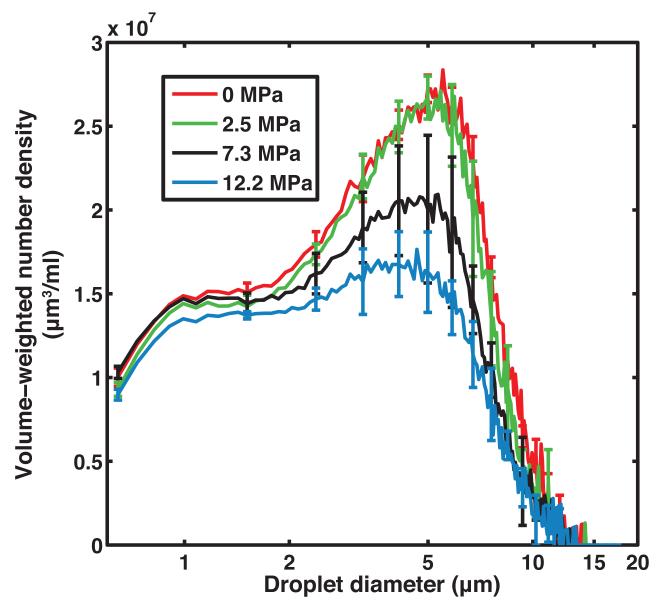
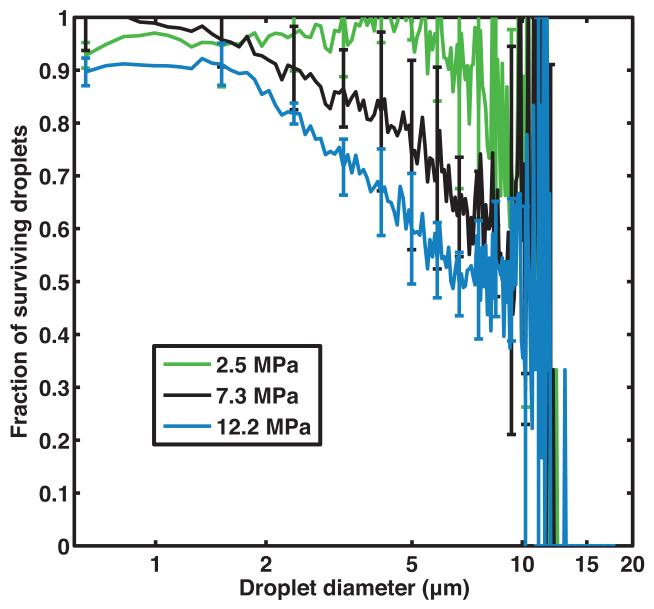
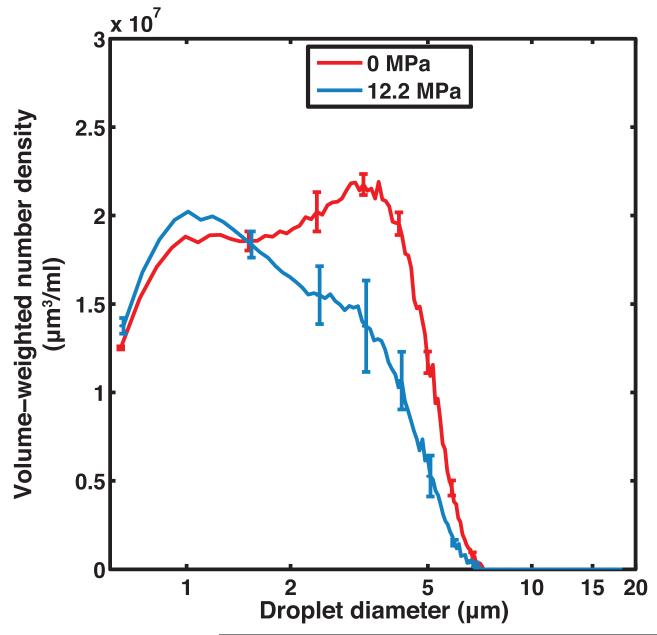
Figure 2b shows that the ADV threshold of non-centrifuged PFP droplets insonified by pulses with a 2 MHz center frequency, 5 μs pulse duration, and 100 Hz PRF was 4.2 ± 0.7 MPa (peak rarefactional). It was noted that at larger insonation pressure amplitudes, the B-mode image was saturated and shadowing was observed due to the higher concentration of ADV-induced PFP microbubbles in the downstream ROI. Based on the ADV threshold, subsequent insonations of the droplets were carried out at peak rarefactional pressures of 2.5 MPa, 7.3 MPa, and 12.2 MPa. The volume-weighted number-density size distribution of PFP droplets without ultrasound exposure and with ultrasound exposure are shown in Figure 3a. Figure 3b shows the surviving fraction of droplets after ultrasound exposure (i.e. the ratio of the number of surviving PFP droplets to the number of PFP droplets in the effluent with no ultrasound exposure). Droplets smaller than 2 μm did not transition appreciably using this particular ultrasound exposure scheme. Above 2 μm, the fraction of surviving droplets decreased approximately linearly.

Figure 3. Size distribution of effluent droplets from flow system.

(a) Volume-weighted number-density size distribution of non-centrifuged PFP droplets in the effluent without ultrasound exposure (0 MPa) and after ultrasound exposure at 2.5 MPa, 7.3 MPa, and 12.2 MPa (peak rarefactional). Error bars indicate the standard deviation of three measurements. (b) The fraction of surviving PFP droplets was calculated as the ratio of number of droplets surviving ultrasound exposure (2.5 MPa, 7.3 MPa, and 12.2 MPa) to the number of droplets measured without ultrasound exposure (0 MPa). Error bars indicate the propagated error based on the standard deviations from Fig 3a.

The net radial expansion of the droplets into microbubbles due to ADV and subsequent ingassing was calculated for the total volume of microbubbles using equation 7 to provide an average expansion across all droplet sizes:

$$\text{radial expansion}={\left(\frac{V_b}{V_{d0}-V_d}\right)}^{1∕3}.$$ (7)

The radial expansion factor was 6.8, 5.6, and 5.4 for droplets exposed to 2.5 MPa, 7.3 MPa, and 12.2 MPa respectively.

3.2 Effect of acoustic peak rarefactional pressure on DO in fluid containing PFP droplets

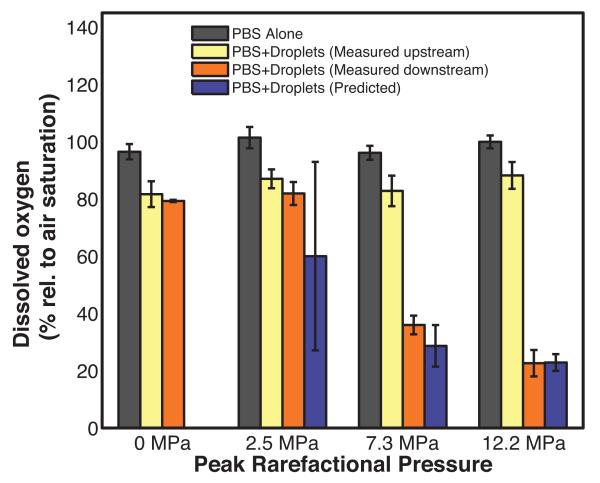
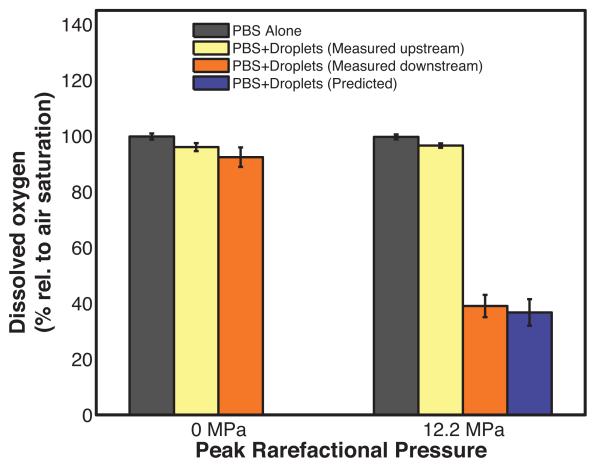
The non-centrifuged droplets were insonified by peak rarefactional pressure amplitudes lower than (2.5 MPa) and greater than (7.3 MPa and 12.2 MPa) the ADV threshold pressure amplitude (4.2 ± 0.7 MPa) to ascertain changes in dissolved oxygen in the surrounding fluid due to ADV. Figure 4 shows the DO measured for air-saturated PBS alone (average value from both sensors), for the PBS surrounding the droplets as a function of insonation pressure, and the numerically predicted DO. The DO of the air-saturated PBS alone was 97 ± 3% both upstream and downstream of the insonation region. The addition of PFP droplets resulted in a decrease in the DO to 84 ± 3% without ultrasound exposure (0 MPa).

Figure 4. Dissolved oxygen of fluids exposed to different insonation pressures.

Percent dissolved oxygen (DO) relative to air-saturated phosphate buffered saline (PBS) measured in the absence of droplets (black bars), measured upstream of the insonation region in the presence of non-centrifuged droplets (yellow bars), and measured downstream of the insonation in the presence of non-centrifuged droplets (orange bars) as a function of the ultrasound peak rarefactional pressure. Error bars indicate the standard deviation of three measurements. The violet bars indicate the predicted DO after ultrasound exposure of non-centrifuged droplets. The predicted DO values are not statistically different from the DO measured downstream of the insonation region. Error bars indicate the propagated error based on the standard deviations from Fig 3a and equation 6.

The DO in the surrounding fluid after insonifying the PFP droplets with ultrasound at 2.5 MPa peak rarefactional pressure was not statistically significantly different from the DO of the fluid surrounding the droplets upstream of the 2.5 MPa ultrasound insonation. The downstream DO measurement at 2.5 MPa was also not statistically significantly different from the DO with no ultrasound exposure (0 MPa) (Figure 4). At acoustic pressure amplitudes exceeding the ADV threshold, the downstream DO in the surrounding fluid decreased to 36 ± 3% and 27 ± 5% after ultrasound exposure at 7.3 MPa and 12.2 MPa, respectively (Figure 4). The predicted DO values were not statistically different from the measured downstream values of the DO.

3.3 Effect of size distribution of droplets on DO in fluid

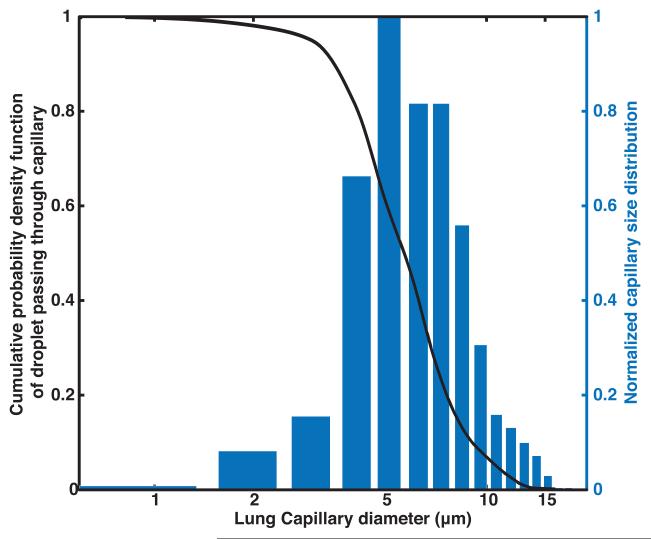
Figure 5a shows the number density of the capillaries in a human lung as measured by Hogg et al. [38]. This number density was used to compute the cumulative probability density function of droplets passing through the lung capillaries. The calculated volume-weighted number-density size distribution of PFP droplets after passing through the lung capillaries is shown in Figure 5b. Only 54% of the PFP volume is predicted to pass through the lungs for non-centrifuged droplets while 86% of the PFP volume is predicted to pass through the lungs for centrifuged droplets.

Figure 5. Calculated size distribution of droplets surviving one pass through the lung.

a) The number density of capillaries in human lung (Hogg et al 1987) is shown as a bar plot and cumulative probability density function of a droplet passing through lung capillaries shown as a black curve. b) Measured volume-weighted number-density size distribution of non-centrifuged PFP droplets (solid black) and calculated volume-weighted number-density size distribution of non-centrifuged PFP droplets that survive one pass through pulmonary capillaries (dashed black). Measured volume-weighted number-density size distribution of PFP droplets centrifuged at 9 g for 5 min (solid red) and calculated volume-weighted number-density size distribution of centrifuged PFP droplets that survive one pass through pulmonary capillaries (dashed red).

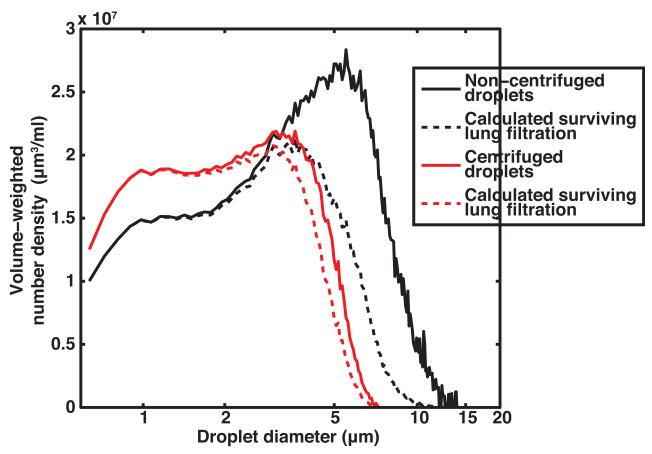
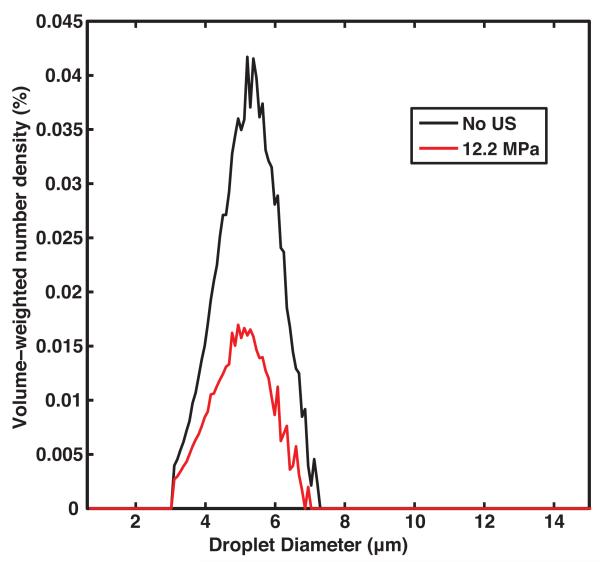
Figure 6a shows the volume-weighted number-density size distribution of the centrifuged droplets in the effluent without ultrasound insonation and after 12.2 MPa peak rarefactional pressure insonation. The droplets were insonified at 12.2 MPa to minimize the number of surviving droplets and maximize the decrease in dissolved oxygen. Figure 6b shows the corresponding measured and predicted DO in the surrounding fluid. The DO in the fluid surrounding the centrifuged droplets upstream of the ultrasound insonation was 93 ± 3 %. The downstream DO in the fluid surrounding the centrifuged droplets after exposure to ultrasound with a 12.2 MPa peak rarefactional pressure was 39 ± 4% (Figure 6b). The measured and predicted DO values were not statistically significantly different.

Figure 6. Size distribution of centrifuged droplets and their oxygen scavenging effect.

(a) Measured volume-weighted number-density size distribution of centrifuged PFP droplets in flow alone and after 12.2 MPa peak rarefactional ultrasound exposure. Error bars indicate the standard deviation of three measurements. b) Percent dissolved oxygen measured with air-saturated PBS alone (black bars), measured upstream of the insonation region with centrifuged droplets (yellow bars), and measured downstream of the insonation region with centrifuged droplets (orange bars) in the absence (0 MPa) and presence (12.2 MPa) of ultrasound exposure. Error bars indicate the standard deviation of three measurements. The predicted dissolved oxygen (violet bar) was not statistically different than the dissolved oxygen measured downstream of the insonation region. Error bars indicate the propagated error based on the standard deviations from Fig 6a and equation 6.

3.4 Effect of concentration of droplets on DO in fluid

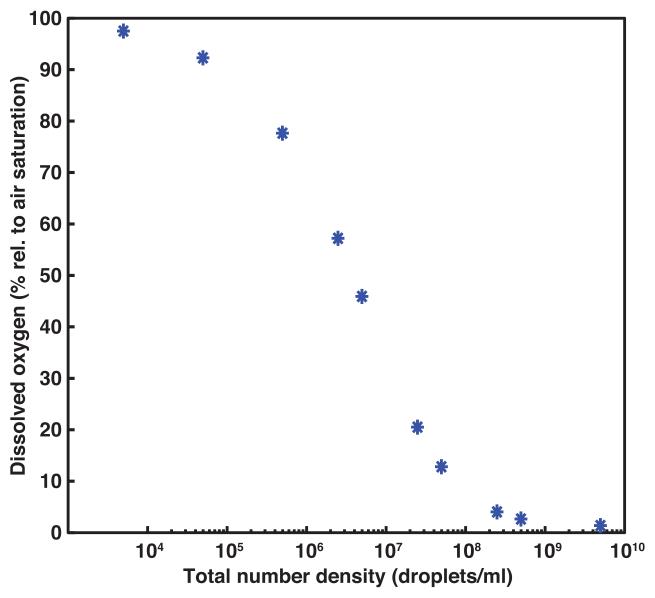
Figure 7a shows the computationally modified size distributions that were obtained after applying a Gaussian probability density function with a mean and standard deviation of 5.16 ± 2 μm to the centrifuged droplet distributions without ultrasound exposure and after 12.2 MPa peak rarefactional ultrasound exposure (Figure 6a). These size distributions were normalized by the total volume of PFP without ultrasound exposure. These volume-weighted size distributions were multiplied by a range of total number densities of droplets and used to compute the change in dissolved oxygen in the surrounding fluid as a function of droplet density (Figure 7b). Using a total number density of 4.9 × 10⁶ droplets/ml, the predicted DO was 46%. The predicted DO after ultrasound exposure decreases with an increasing number of droplets as shown in Figure 7b.

Figure 7. Dissolved oxygen change as a function of concentration for a monodisperse droplet distribution.

(a) The computed volume-weighted size distribution is shown without ultrasound exposure (black line) and after exposure to 12.2 MPa peak rarefactional pressure (red line). The size distributions (measured and computed) are normalized by the total volume of the PFP droplets without ultrasound exposure. The size distributions were obtained by applying a Gaussian probability density function with a mean and standard deviation of 5.16 ± 2 μm to the centrifuged droplet distributions shown in Figure 6a. (b) The predicted dissolved oxygen is shown as a function of the concentration of the computed size distribution. Using this computed size distribution, the mathematical model (equation 6) yielded a predicted decrease in dissolved oxygen of 46% with an initial concentration of 4.9 × 10⁶ droplets/ml.

4. Discussion

4.1 Ultrasound-mediated phase-transition response

The ADV pressure threshold ascertained in the current study was 4.2 ± 0.7 MPa (peak rarefactional) using pulses with a center frequency of 2 MHz, a pulse duration of 5 μs, and a PRF of 100 Hz (Figure 2b). An ADV threshold of 3.1 MPa peak rarefactional pressure is predicted at 2 MHz using the inverse square relationship between insonation frequency and ADV thresholds ascertained by Kripfgans et al. [3,4]. The higher ADV threshold measured using our system could be due to the difference in transducer geometries, focal volume sizes, and consequent nonlinear propagation, as well as the amount of albumin used to make the droplets.

The surviving fraction of droplets after ultrasound exposure shown in Figure 3b can be used to calculate the ADV efficiency as defined by Fabiilli et al. [10], which is the fraction of droplets that vaporize. The relationship between the surviving fraction of droplets after ultrasound exposure and the droplet diameter (Figure 3b) was qualitatively similar to observations on transition efficiency made by Fabiilli et al. [10] who used a 6.3 MHz insonation. Fabiilli et al. [10] also observed that droplets smaller than 2 μm did not transition efficiently and the ADV efficiency increased linearly with droplet diameters between 2 μm and 12 μm. The reduced transition efficiency below 2 μm is also consistent with the superharmonic focusing theory of ADV that was proposed by Shpak et al.[43]. Shpak et al. [43] demonstrated that the spherical shape of the droplet and the acoustic impedance mismatch between the perfluorocarbon and the surrounding medium resulted in the focusing of superharmonics inside the droplet causing a gain in the rarefactional pressure amplitude. Based on this study, as the droplet diameter decreases the focal gain also decreases. Therefore it is less likely that a small droplet will phase transition during ultrasound insonation.

For insonation pressures above the ADV pressure threshold, the net radial expansion factor was 5.6 and 5.4 for 7.3 MPa and 12.2 MPa insonations, respectively. This radial expansion is slightly greater than the radial expansion predicted by the ideal gas law (5.0×, [3]), similar to the experimentally measured radial expansion reported by Kripfgans et al. [3] (5.3×) and smaller than the expansion measured by Sheeran et al. [1] (10×) and Reznik et al. [36] (50×). Based on the model developed in this study, the amount of ingassing depends on the concentration of microbubbles formed as well as the concentration of dissolved gases in the vicinity of these bubbles. For very dilute suspensions of microbubbles, more gas will flow into the microbubbles to reach equilibrium. For more concentrated suspensions less gas will flow into each microbubble to reach equilibrium in a closed system. It is possible that differences in droplet concentration between Kripfgans et al. [3], Sheeran et al. [1], Reznik et al. [36], and the current study could explain the differences in observed radial expansion. The observed trend of a lower radial expansion for higher insonation pressures, which corresponded with more droplets converted into microbubbles per unit volume, is consistent with this hypothesis.

4.2 Effect of acoustic peak rarefactional pressure on DO in fluid containing PFP droplets

Figure 4 shows that the DO of the PBS alone was 97 ± 3% and that the addition of non-centrifuged droplets with no ultrasound exposure (0 MPa peak rarefactional pressure amplitude) caused the DO to drop to 84 ± 3% at 37 °C. The DO of the fluid surrounding the non-centrifuged droplets measured at the outlet of the infusion syringe was 90 ± 1%. It was also noted that spontaneous vaporization of PFP droplets occurred on the surface of the syringe plunger. These bubbles from spontaneous vaporization also scavenged oxygen resulting in a drop in the DO from 97 ± 3% to 90 ± 1%. The DO in the fluid surrounding the non-centrifuged droplets with the upstream and downstream sensors was 91 ± 1% at 22 °C. Few if any microbubbles from spontaneous vaporization were visually observed in the flow phantom at 22 °C. However, when the droplets were injected, gas bubbles from spontaneous vaporization were observed in the flow system at 37 °C. Thus spontaneous vaporization in the tubing also accounts for the DO drop from 90 ± 1% to 84 ± 3%. Furthermore, spontaneous vaporization would be expected to occur more readily as the droplet diameter increases due to a lower Laplace pressure. This assumption is consistent with the observation that the DO in the fluid surrounding centrifuged droplets at 37°C was higher (93 ± 3%) than non-centrifuged droplets (84 ± 3%), even though the number densities of centrifuged and non-centrifuged droplets were similar.

Figure 4 also shows that the DO in the fluid decreased with increasing insonation pressure. This observation is likely due to a larger fraction of droplets undergoing ADV (Figure 3) resulting in a greater amount of oxygen being scavenged after a 12.2 MPa insonation compared to a 7.3 MPa insonation. This explanation is supported by the numerical predictions. No statistically significant differences were observed between the measured and predicted DO in the fluid after ADV. The peak rarefactional pressure amplitude exposure dictates the fraction of droplets transitioned into PFP microbubbles and therefore also dictates the amount of DO scavenged from the surrounding fluid based on conservation of mass and equal partial pressures at equilibrium.

Note that the mathematical model is simplistic and accounts for the DO in the fluid at equilibrium, neglecting microbubble dissolution. This model does not take into consideration the temporal kinetics of diffusion of gases into and out of the PFP microbubbles. We note that Kripfgans et al. [3] predicted that ingassing would occur within hundreds of milliseconds, which is consistent with the experimentally measured growth of microbubbles reported by Kang et al. [17]. The microbubbles (including perfluoropentane, nitrogen, oxygen, etc.) would subsequently dissolve over tens of seconds. Kripfgans et al.[3] predicted that the microbubble diameter would be within 90% of its maximum diameter 20 s after ultrasound exposure. Our dissolved oxygen measurements were made within 20 s of ultrasound exposure, likely before significant dissolution occurred.

The numerical model also does not account for changes in the microbubbles due to continued acoustic insonation. Based on the volumetric flow rate and pulse repetition frequency used in this study, it was estimated that the droplets would be exposed to 7-8 ultrasound pulses, each approximately 10 cycles in duration, in the focal volume. Previous studies have described the effects of rectified diffusion [44] and acoustically driven diffusion [45] on the gas content within a microbubble. These phenomena could increase or decrease the dissolved oxygen in the fluid. Fragmentation of the microbubbles may also occur at these insonation pressures. However as long as the PFP gas does not dissolve rapidly, the total volume of PFP gas available to scavenge dissolved oxygen does not change and therefore the total volume of scavenged oxygen would not change. Future revisions to the model can be developed to incorporate these microbubble dynamics.

An additional limitation of the model is that it does not take into account surface tension, which could cause size dependent effects on the expansion. However, Sheeran et al. [1] showed that the expansion factor does not depend on droplet diameter for droplets greater than approximately 3 μm in diameter. In this study and the study by Fabiilli et al. [10], few droplets less than 3 μm in diameter were phase-transitioned, which, as described above, is consistent with the superharmonic focusing theory of acoustic droplet vaporization [43]. Therefore the effects of surface tension were not included in the model. However other studies have used nanodroplets [1,12] to nucleate ADV. In order to provide an accurate estimate of the amount of dissolved oxygen scavenged by bubbles produced from nanodroplets, the radius-dependent Laplace pressure must be considered. The inclusion of the Laplace pressure in the model would likely result in a decreased amount of dissolved oxygen being scavenged.

Despite these limitations, the DO predictions from the mathematical model agreed with the measured values (p-values were equal to 0.32, 0.18, and 0.95 for 2.5 MPa, 7.3 MPa, and 12.2 MPa insonations, respectively).

The numerical model and experiments were limited to scavenging dissolved oxygen, which may have applications in treating reperfusion injury [46]. Further, the effect should be applicable to other dissolved gases because the mechanism is based on diffusion gradients. This effect might have potential use in scavenging carbon dioxide and nitrogen for treating localized acidosis and decompression sickness, respectively. The effect has already been explored using spontaneous vaporization (i.e. no ultrasound) of a perfluoropentane emulsion for nitrogen scavenging [47].

4.3 Effect of centrifugation on the droplet size distribution and DO in the fluid

Centrifugation of the droplets removed all but 14% of the PFP volume that would not be expected to pass through the pulmonary capillaries [36]. This PFP volume corresponded to 8.4 × 10⁶ centrifuged droplets. If each of these large droplets were to occlude the blood flow to a single alveoli, approximately 3% of the alveoli would be affected [38]. However, each alveolus is fed by a network of capillary segments and it is unlikely that a single droplet would occlude a single alveolus. The largest sized droplets within a centrifuged emulsion depends on the centrifugation speed and duration [39,40]. An optimal size distribution of centrifuged droplets could be found which would enable a higher percentage of droplets to pass through the pulmonary capillaries [37].

Shown in Figure 6b, the centrifuged droplets without ultrasound exposure did not cause a significant decrease in the DO of the surrounding fluid, whereas non-centrifuged droplets without ultrasound exposure did cause a significant decrease in the DO of the surrounding fluid (Figure 4). Droplets with diameters greater than 5 μm, which have a greater tendency to undergo spontaneous vaporization due to lower Laplace pressures, were filtered out through the centrifugation process (Figure 5b).

The DO after 12.2 MPa peak rarefactional pressure insonation of centrifuged droplets was 39 ± 4% which was higher than the DO after insonation of non-centrifuged droplets at the same pressure amplitude (22 ± 4%). By keeping the total number density of droplets injected in the flow phantom approximately the same (4 × 10⁸ droplets/ml) for centrifuged and non-centrifuged droplets, the total volume of PFP in the injection and thus the total volume of PFP converted to a gas was not the same. The total volume of PFP converted to gas microbubbles dictates the change in dissolved oxygen (Equation 6). Despite the absence of these large droplets and microbubbles in the centrifuged emulsion, which scavenge significant amounts of oxygen, a greater than 40% decrease in DO in the surrounding fluid was observed. The size distribution of the droplets plays an important role in the amount of DO scavenged from the fluid during ADV.

4.4 Concentration and size distribution optimization

Note that in this study the total number density of centrifuged and non-centrifuged droplets used in the flow system was 4.95 ± 0.04 × 10⁸ droplets/ml and 4.09 ± 0.06 × 10⁸ droplets/ml. Previous in vitro studies used droplets formulated employing the same methods as the current study with concentrations ranging from 3 × 10⁵ droplets/ml [13] to 7 × 10⁷ droplets/ml [10]. The concentration of droplets in previous ADV in vivo studies ranged from 6.5 × 10⁵ droplets/ml [7] to 1.4 ×10⁶ droplets/ml, based on dividing the total number of droplets injected by the total blood volume of the animal [13]. The FDA-approved in vivo concentrations of the perfluorocarbon-based ultrasound contrast agents Definity^® and Optison^® are 5 × 10⁶ microbubbles/ml [41] and 1.4 × 10⁶ microbubbles/ml [48] respectively. We note that the size distribution of Definity^® is similar but not the same as the size distribution of the droplets used in this study [35]. These concentrations are based on the total bolus injection of microbubbles divided by the total blood pool volume. Thus the concentration of PFP droplets used in the current study is two orders of magnitude higher than previous in vitro and in vivo studies. A significant fraction of the total number of droplets used in this study did not contribute to a change in the DO of the surrounding fluid because they did not vaporize. Less than 10% of droplets smaller than 2 μm were converted into microbubbles with a 12.2 MPa peak rarefaction pressure insonation, yet these droplets contributed to more than 85% of the total number density of droplets. These non-activated droplets (< 2 μm) could be removed from the emulsion to reduce the total number of droplets that would be injected in vivo. Either microfluidic techniques [49] or differential centrifugation [39,40] could be employed to achieve such an optimal size distribution.

Because such size isolation techniques have not yet been fully developed for PFP droplets, a numerical approach was used to identify an appropriate size distribution of the droplets which, when used at a concentration of at most 5 × 10⁶ droplets/ml, would induce at least a 50% reduction in DO during ADV. Based on these constraints, the size distribution curve shown in Figure 7a would be suitable for scavenging DO from the surrounding fluid via ADV in intravascular applications. To emphasize the importance of size isolation, a droplet concentration of 4 × 10⁸ droplets/ml for the size distribution shown in Figure 7a would yield a predicted DO of 3%. In comparison, the DO predicted using the size distribution of the centrifuged droplets (Figure 6a) with a concentration of 4 × 10⁸ droplets/ml was 39%.

Additionally, the DO after ADV was estimated for previous in vitro studies as 95% and 50% based on droplet concentrations of 3 × 10⁵ droplets/ml [13] and 7 × 10⁷ droplets/ml [10] respectively. The estimated DO decrease in previous in vivo studies was 91% and 80% based on droplet concentrations of 6.5 × 10⁵ droplets/ml [7] and 1.4 ×10⁶ droplets/ml [13] respectively. The droplet size distribution in these previous studies was assumed to be similar to that in the current study because the same droplet manufacturing protocol was used. The DO estimation also assumes that the ADV transition efficiency in these studies was similar to that in the current study. However, the transition efficiency, and thus the amount of scavenged oxygen, is dependent on ultrasound insonation parameters such as pressure amplitude, frequency, and pulse duration. Therefore the actual changes in DO in those experiments may be different.

4.5 Role of ultrasound parameters in droplet conversion

The ultrasound parameters used in this study were not particularly effective at transitioning the phase of the droplets. Only approximately 40% of the 5 μm droplets were transitioned with a 12.2 MPa peak rarefactional pressure amplitude (Figure 3b). It was observed that increasing the ultrasound insonation pressure amplitude increased the fraction of droplets transitioned (Figure 3b). To scavenge additional oxygen, the ultrasound insonation parameters could be modified. Larger pressure amplitudes are required for lower frequency ultrasound exposure to convert the droplets to microbubbles [4,43]. Additionally, smaller droplets require larger pressure amplitudes to transition [1,43,50] and a lower percentage of the droplets undergo a phase transition [10]. Increasing the pulse duration or simultaneously administering a perfluorocarbon-based ultrasound contrast agent has also been shown to lower the transition threshold and likely would increase the transition efficiency [42].

4.6 Potential fate of scavenged oxygen in vivo

Eventually the microbubbles with scavenged oxygen will dissolve, releasing the oxygen back into the blood where it would likely either bind to hemoglobin, increase the dissolved oxygen content of plasma, or both. This dissolution is anticipated to happen on a time scale of tens of seconds [3]. Blood circulates through the adult human body approximately once per minute [51]. As the blood circulates through the pulmonary capillary bed, the dissolved oxygen in the blood would return to normal oxygen levels and the perfluoropentane microbubbles would be exhaled similar to the excretion of other perfluorocarbon-based ultrasound contrast agent gases [52,53].

5. Conclusions

Local scavenging of dissolved oxygen from a fluid via acoustic droplet vaporization of a perfluoropentane emulsion was quantified in an in vitro flow phantom. The predicted change in dissolved oxygen using a simple numerical model based on conservation of mass and isobaric partial pressures agreed with the dissolved oxygen measurements (p-values were equal to 0.32, 0.18, and 0.95 for 2.5 MPa, 7.3 MPa, and 12.2 MPa insonations, respectively). The data suggest that the mechanism of gas manipulation is based on dissolved gas concentration gradients, which would likely occur for other important dissolved gases, such as nitrogen and carbon dioxide. The volume of perfluoropentane phase transitioned dictates the amount of dissolved oxygen scavenged from a fluid. The acoustic peak rarefaction pressure, the volumetric size distribution of the droplets, and the concentration of the droplets all affect the volume of perfluoropentane undergoing phase transition. The scavenging effect was rapid with dissolved oxygen decreasing from 100% air saturation to approximately 22% of air saturation in less than 20 seconds in a 5 ml/min flow.

Highlights.

• The phenomenon of acoustic droplet vaporization scavenging dissolved oxygen from air-saturated fluid has been demonstrated.

• A numerical model indicates that the mechanism is based on dissolved gas concentration gradients following the volumetric expansion associated with acoustic droplet vaporization.

• The decrease in dissolved oxygen is dependent on the insonation pressure, the size distribution of the droplets, and the concentration of the droplets.

Abbreviations

ADV

Acoustic droplet vaporization

PFP

Perfluoropentane

DO

Dissolved oxygen

PBS

Phosphate buffered saline

EVA

Ethyl vinyl acetate