Validation of a T₁ and T₂* leakage correction method based on multi-echo DSC-MRI using MION as a reference standard

Abstract

Purpose

A combined biophysical- and pharmacokinetic-based method is proposed to separate, quantify, and correct for both T₁ and T₂* leakage effects using dual-echo DSC acquisitions to provide more accurate hemodynamic measures, as validated by a reference intravascular contrast agent (CA).

Methods

Dual-echo DSC-MRI data were acquired in two rodent glioma models. The T₁ leakage effects were removed and also quantified in order to subsequently correct for the remaining T₂* leakage effects. Pharmacokinetic, biophysical, and combined biophysical and pharmacokinetic models were used to obtain corrected cerebral blood volume (CBV) and cerebral blood flow (CBF), and these were compared with CBV and CBF from an intravascular CA.

Results

T₁-corrected CBV was significantly overestimated compared to MION CBV, while T₁+T₂*-correction yielded CBV values closer to the reference values. The pharmacokinetic and simplified biophysical methods showed similar results and underestimated CBV in tumors exhibiting strong T₂* leakage effects. The combined method was effective for correcting T₁ and T₂* leakage effects across tumor types.

Conclusions

Correcting for both T₁ and T₂* leakage effects yielded more accurate measures of CBV. The combined correction method yields more reliable CBV measures than either correction method alone, but for certain brain tumor types (e.g., gliomas) the simplified biophysical method may provide a robust and computationally efficient alternative.

Introduction

Dynamic susceptibility contrast (DSC) MRI in stroke and tumor has the potential to report on clinically useful diagnostic and therapeutic outcomes (1-7). In various pathologies, however, a compromised blood-brain barrier (BBB) leads to extravasation of gadolinium-based contrast agents (CA) and can severely alter the derived perfusion measures cerebral blood volume (CBV) and flow (CBF) and mean transit time (MTT) (7,8). Of the derived parameters, CBV is both the most reported and the most affected by CA extravasation (8), although CBF may also be affected to a smaller degree (9,10). There are three main sources of error that occur as a result of CA extravasation. First, as CA leaks out of the vasculature, it shortens the extravascular extracellular water T₁, leading to increased post-bolus signals and thus decreased post-bolus ΔR₂*. This results in underestimations of CBV. Second, leakage of CA also leads to T₂* effects due to changes in the susceptibility differences between the various compartments (e.g., intravascular to extravascular-extracellular or intracellular to extracellular) (11,12). As these effects depend on the CA compartmentalization, the resulting signals can be either increased or decreased but typically manifest as decreased signals (11,13). This leads to increased post-bolus ΔR₂* and thus overestimations of CBV. Finally, the central volume theorem underpinning DSC-MRI states that CBV is proportional to the flow-scaled integral of the capillary residue function, under the explicit assumption that the CA remains intravascular (14). In cases of CA extravasation, this is clearly violated, and uncorrected CBV values reflect the altered (larger) CA distribution volume (7,10).

Several methods have been proposed to reduce or remove leakage effects. The focus historically has been on T₁ leakage effects, where signal- and sequence-based methods (including pre-load bolus, low flip angle, gamma-variate fitting) have reduced T₁ sensitivity (8). Pharmacokinetic model-based correction methods have also been proposed (7,15,16). The most widely-used Weisskoff method estimates the leakage effects by comparing tumor ΔR₂* curves to those in a reference non-enhancing tissue, and the estimated leakage effects are then subtracted (2,7,16-18). Using this method, Boxerman et al. (7) showed that relative CBV (rCBV) correlates with glioma grade only when corrected for CA leakage. While this method is easy to implement, it assumes an identical MTT between the tumor and reference tissue, leading to potentially incorrect hemodynamic measures (19). An alternative approach later proposed by Bjornerud et al. (15) is based on a modified dynamic-contrast-enhanced (DCE) pharmacokinetic model that combines perfusion and permeability (20), resulting in a MTT-insensitive CBV correction method. This method is performed following deconvolution of the tissue residue function with the arterial input function (AIF), and existing challenges for this method include both accurate determination of the AIF and improved deconvolution stability in regions of low SNR. Moreover, CBF is not corrected for leakage effects as the model assumes the CA remains intravascular during the initial capillary transit phase (10,15). The corrections originally proposed by Weisskoff and Bjornerud are both potentially problematic because they simultaneously correct for both T₁ and T₂* leakage effects by relying on single echo data. Such data may exhibit competing T₁ and T₂* leakage effects whose biophysical bases are inherently dissimilar and require unique correction strategies that are not accounted for in pharmacokinetic models.

Dual- or multi-echo sequences (9,21,22) separate the T₁ leakage effects to provide both T₁-insensitive ΔR₂* time series and T₁-weighted signals extrapolated to TE=0. These dual-echo sequences are now recommended for DSC-MRI to obtain T₁-insensitive gradient-echo hemodynamic measures (8). As the dual-echo acquisition removes T₁ leakage effect, it also isolates (and enhances sensitivity to) the T₂* leakage effects, which can then be corrected by subsequent leakage correction methods. Previously, Schmiedeskamp et al. (10) utilized dual-echo-derived T₁-weighted signals to correct for T₂* leakage effects by combining the biophysical method proposed by Quarles (11) and the pharmacokinetic method proposed by Bjornerud (15). As with the original Bjornerud correction, this CBV correction method relies on sophisticated pharmacokinetic modeling and multistep fitting algorithms and does not correct CBF for leakage effects (10,15).

The primary focus of this study is to establish a MTT-insensitive leakage correction method for CBV and CBF that accounts for the biophysical basis of T₂* leakage effects. The biophysical model (11) underlying this method treats the observed ΔR₂* as a sum of the intra- and extravascular ΔR₂* components. Using a dual-echo acquisition to estimate the extravascular ΔR₂* component, the T₁-insensitive dual-echo ΔR₂* can be corrected for T₂* leakage effects. Corrections are performed using both a simplified biophysical model and a combined biophysical-pharmacokinetic model, and these corrections are compared to a purely pharmacokinetic model based on the Weisskoff method. Corrected CBF and CBV are shown in two rat brain tumor models exhibiting different combined T₁ and T₂* leakage effects. The resulting CBF and CBV are compared to reference standard CBF and CBV from injection of an intravascular iron oxide contrast agent in the same animals during the same imaging session.

Theory

As CA flows through blood vessels during bolus passage, it induces strong T₂* effects due to susceptibility gradients between the contrast-containing intravascular space and contrast-free extravascular space. However, in areas of BBB breakdown, leakage of CA out of the intravascular space and into the extravascular space leads to additional T₁ and T₂* relaxation effects. Due to the increased sensitivity to T₂* effects using dual-echo sequences, it is well known that CA leakage leads to increased ΔR₂* as a result of mesoscopic effects of CA compartmentalization around cells (12), resulting in overestimations of CBV. One approach to correct for these effects is to apply a pharmacokinetic model to the acquired ΔR₂* data to estimate the vascular and extravascular contributions simultaneously (10,13,23) and derive corrected estimates of CBV. As an alternative strategy, we propose an approach that provides leakage-corrected ΔR₂* time courses that may be subsequently analyzed using existing deconvolution analysis software or algorithms. Similar to previous studies (11,13,23), an empirical linear model is used to describe the measured ΔR₂* data as the sum of the vascular and extravascular contributions:

$$\mathrm{\Delta }{R}_{2,\mathit{\text{meas}}}^{\ast }(t)=r_{2,p}^{\ast }{v}_p{C}_p(t)+r_{2,e}^{\ast }{v}_e{C}_e(t)$$ [1]

where $r_{2,p}^{\ast }$ and $r_{2,e}^{\ast }$ are the T₂* relaxivities for plasma and extravascular-extracellular space (EES), respectively, and v_p, C_p, v_e, and C_e are the volume fractions and CA concentrations of the EES and blood plasma, respectively. (A full list of relevant parameters can be found in Table S1 in the Supporting Material.) The first term represents the intravascular ΔR₂* contribution while the second term represents the extravascular ΔR₂* contribution that presents as a result of CA leakage. The T₂* relaxivities are related to the geometric features of the vascular ( $r_{2,p}^{\ast }$) and extravascular extracellular ( $r_{2,e}^{\ast }$) compartments. Of particular interest, $r_{2,e}^{\ast }$ predominantly reflects the underlying cellular features that define the spatial boundaries or geometry of the CA distribution volume. This is in contrast to T₁ leakage effects, which reflect the direct interaction of the CA with water in the EES and can be characterized by the CA's T₁ relaxivity and traditional pharmacokinetic models. Because cellular features (e.g., density, spacing, size, shape) vary within and across tumors, a simple pharmacokinetic treatment of T₂* leakage effects may be unable to accurately characterize and remove their confounding influence on DSC-MRI data. This implies that efforts to correct T₂* leakage effects should include voxel-wise estimates of $r_{2,e}^{\ast }$.

To isolate the intravascular ΔR₂* term, the extravascular ΔR₂* contribution ( $r_{2,e}^{\ast }{v}_e{C}_e(t)$) can be calculated and then subtracted from the measured ΔR₂*. This requires estimation of both $r_{2,e}^{\ast }$ and v_eC_e(t) as follows. From dual-echo DSC-MRI, a T₁-weighted signal can be combined with a pre-contrast T₁ map to obtain the tissue CA concentration (C_t = ΔR₁/r₁), where r₁ is the CA T₁ relaxivity. The extended Tofts model (24,25) can be applied to isolate the contribution of v_eC_e(t) to the total tissue CA concentration (C_t(t)). As Sourbron et al. (23) has previously shown, the effective extravascular T₂* relaxivity $r_{2,e}^{\ast }$ can be obtained by fitting the dual-echo ΔR₂* to the appropriate model (given here by Eq. 1), where v_eC_e(t) and v_pC_p(t) are inputs from the extended Tofts model and the only unknowns are $r_{2,e}^{\ast }$ and $r_{2,p}^{\ast }$. The corrected ΔR₂* can be thus computed using

$$\mathrm{\Delta }{R}_{2,\mathit{\text{corr}}}^{\ast }(t)=\mathrm{\Delta }{R}_{2,\mathit{\text{meas}}}^{\ast }(t)-r_{2,e}^{\ast }{v}_e{C}_e(t)$$ [2]

The equations shown in [1] and [2] are similar in form to the Weisskoff leakage correction strategy (2,7,16-18), where the corrected ΔR₂* is computed as the difference between the measured time series and an estimate of the dynamic leakage effects. These leakage effects are estimated using a scaled version of the time integral of ΔR₂*(t) taken from non-enhancing tissue, which implies that the extravascular contrast agent concentration time courses across tumor voxels are scaled versions of the same underlying profile. By leveraging the ΔR₁ information provided by dual-echo DSC-MRI signals, a similar heuristic leakage correction approach can be derived that quantifies the voxel-wise contrast agent concentration profiles, thereby accounting for local heterogeneity in the underlying contrast agent kinetics.

For this simplified approach, the extravascular ΔR₂* contribution is approximated as $r_{2,t}^{\ast }{C}_t(t)$. In this case, C_t is taken directly from ΔR₁/r₁ under the assumption that C_t(t) predominantly reflects the extravascular CA concentration, similar to the conventional Tofts model (25,26) used for DCE-MRI that assumes negligible intravascular contribution. The dynamic C_t(t) is scaled by $r_{2,t}^{\ast }$, which is the effective tissue transverse CA relaxivity. As previously shown, when computed at CA equilibrium, $r_{2,t}^{\ast }$ is insensitive to the vasculature because there is no susceptibility difference between the intra- and extravascular space (12); thus as for $r_{2,e}^{\ast },r_{2,t}^{\ast }$ predominantly reflects cellular features. The $r_{2,t}^{\ast }$ can be calculated voxel-wise from simultaneously acquired dual-echo ΔR₂* and ΔR₁ data. Using the ΔR₁ information to calculate the tissue CA concentration (C_t = ΔR₁/r₁), $r_{2,t}^{\ast }$ can be computed as:

$$r_{2,t}^{\ast }=\frac{\mathrm{\Delta }{R}_{2,\mathit{\text{meas}}}^{\ast }}{C_t}=\frac{r_1\cdot \mathrm{\Delta }{R}_{2,\mathit{\text{meas}}}^{\ast }}{\mathrm{\Delta }{R}_1}$$ [3]

Similar in form to the correction provided by Eq. [2] and the Weisskoff approach, the corrected ΔR₂* can be computed using:

$$\mathrm{\Delta }{R}_{2,\mathit{\text{corr}}}^{\ast }(t)=\mathrm{\Delta }{R}_{2,\mathit{\text{meas}}}^{\ast }(t)-r_{2,t}^{\ast }{C}_t(t)$$ [4]

Note that the proposed correction strategies described in Eqs. [2] and [4] do not rely upon estimates of a given voxel's CA concentration time course or the effective contrast agent relaxivity, such as that used in the Weisskoff correction of single-echo DSC-MRI data (7,16,18). Rather, these methods leverage the dual-echo based ΔR₂* and ΔR₁ data in order to measure these parameters.

Methods

Simulations

To demonstrate the validity of the proposed simplified T₂* leakage correction technique, a computational study was conducted based on simulated 3D tissue structures composed of randomly packed ellipsoids around fractal tree based vascular networks using the finite perturber finite difference method (FPFDM) (27). First, a pharmacokinetic two-compartmental model described in (28) was used to compute the vascular and EES CA concentration (C_p and C_e) time-courses using physiologically relevant CBV, CBF, K^trans and v_e values along with the AIF as an input. The resulting C_p and C_e curves, the simulated tissue structures, the water diffusion coefficient, and relevant pulse sequence parameters were then used to compute simulated ΔR₂* time curves using the FPFDM. The effective tissue relaxivity $r_{2,t}^{\ast }$ was calculated using time points at CA concentration equilibrium, allowing computation of the corrected ΔR₂* time-courses according to Eqs. [2] and [4].

Animals Methods

All animal studies were performed in accordance with National Institutes of Health (NIH) Institutional Animal Care and Use Committee (IACUC) protocols. For all procedures and imaging, the animals were immobilized in a stereotactic head holder. Anesthesia was induced using 3-5% isoflurane in air and maintained with 1-2.5% isoflurane in air. Body temperature was maintained at 38°C using forced warm air. Male Fischer (n=12) and Wistar (n=9) rats (Harlan Laboratories, Indianapolis, IN) were inoculated with 1×10⁵ 9L and C6 glioma cells (American Type Culture Collection, Manassas VA), respectively, at 1 mm anterior and 3 mm lateral to the bregma and 4 mm depth from the dural surface. Imaging was performed after 16 days.

MRI Methods

MRI was performed at 4.7T (Agilent, Santa Clara, CA). Pre-contrast T₁ maps were acquired using an inversion recovery (IR) snapshot FLASH GE sequence (8 inversion times exponentially spaced from 250 ms to 6 s, TR = 8 s, TE = 2.9 ms, and α = 15°). A spin- and gradient-echo (SAGE) EPI sequence was used to obtain five echoes (10,29,30), including two gradient echoes (dual-echo). Standard slice-selective sinc pulses were used. A 64×64 acquisition matrix within a 36×36 mm² FOV was acquired with 8 1-mm thick slices. Partial Fourier encoding (48 of 64 lines acquired) was used to obtain acceptable gradient echo times (TE₁ and TE₂ = 8.6 and 35 ms). The partially sampled k-space data were reconstructed to full Fourier space using an iterative homodyne reconstruction algorithm (31,32) in Matlab (Mathworks, Inc.). To obtain adequate temporal resolution for dynamic studies, a TR of 1 s was used for 10 minutes. After 80 s of baseline images, 0.4 mmol/kg gadolinium-diethylenetriamine pentaacetic acid (Gd-DTPA) was injected via jugular catheter. After 30 minutes to allow partial Gd-DTPA clearance, 3 mg/kg MION was injected via a second jugular catheter. The MION was diluted with sterile saline to provide an equal injection volume to the Gd-DTPA injection.

Post-processing and Analysis

To increase the SNR, the DSC data was first reconstructed to 2-mm slice thickness by averaging the signal of two consecutive slices. The first two (gradient) echoes were used to calculate the T₁-insensitive dual-echo ΔR₂*. All leakage correction methods were applied to dual-echo data, which is inherently corrected for T₁ leakage. Thus, the ability of the corrections methods to correct for T₂* leakage effects was determined. Three methods of leakage correction were compared: a pharmacokinetic model based on the Weisskoff method (Method 1) and two variations of the biophysical model proposed herein (Methods 2 and 3). Method 2 utilizes the simplified biophysical model in Eq. 4, while Method 3 combines biophysical and pharmacokinetic methods (Eq. 2).

In Method 1, the corrected ΔR₂* curve is obtained by fitting the measured ΔR₂* curve to a reference, whole brain non-enhancing curve to determine the leakage-relevant parameter. As in the original implementations for single echo data, the whole brain non-enhancing mask was created by comparing the signal from TE₂ during the post-bolus phase (90 s post-injection) to the pre-bolus signal. Voxels with post-bolus signal that was greater than or less than one standard deviation from the prebolus mean signal were excluded from the whole-brain non-enhancing mask. The mask was applied to the dual-echo data to create the reference curve $\overline{\mathrm{\Delta }{R}_2^{\ast }(t)}$ and its time integral ${\int }_0^t\overline{\mathrm{\Delta }{R}_2^{\ast }(t\prime )}dt\prime$. The measured dual-echo ΔR₂* was fit to Equation 5 to obtain the leakage parameter K₂:

$$\mathrm{\Delta }{R}_2^{\ast }(t)\approx K_1\cdot \overline{\mathrm{\Delta }{R}_2^{\ast }(t)}-K_2{\int }_0^t\overline{\mathrm{\Delta }{R}_2^{\ast }(t\prime )}dt\prime$$ [5]

Consistent with correction of both T₁ and T₂* leakage effects (7,17), K₂ was permitted to have positive or negative values. In contrast to prior implementations, Method 1 did not utilize a pre-load bolus to reduce T₁ leakage effects, as this would preclude analysis using Method 2, but rather the correction was applied to T₁-insensitive dual-echo data.

In Method 2, the corrected ΔR₂* curve was obtained by subtracting a voxel-wise estimate of $r_{2,t}^{\ast }{C}_t(t)$ (Eq. [4]). To approximate C_t, the dual-echo T₁–weighted signals were combined with a pre-contrast T₁ map to obtain a ΔR₁ curve, as previously described (30,33). To convert ΔR₁ to C_t, a r₁ relaxivity of 3.9 mM^-1s^-1 for Gd-DTPA was used (34). The effective tissue transverse relaxivity ( $r_{2,t}^{\ast }$) in the EES at CA equilibrium was determined from the mean voxel-wise dual-echo ΔR₂* and ΔR₁ at 1 minute intervals from 2 to 8 minutes post-injection to determine the optimal range of scan times for calculation of $r_{2,t}^{\ast }$ (Supporting Material, Figure S1). Subsequently, $r_{2,t}^{\ast }$ was calculated from 5 to 6 minutes post-injection. The voxel-wise extravasation term $r_{2,t}^{\ast }{C}_t(t)$ was subtracted from the corresponding dual-echo ΔR₂* to determine the T₁- and T₂*-leakage corrected ΔR₂*.

In Method 3, the corrected ΔR₂* curve was obtained by subtracting a voxel-wise estimate of $r_{2,e}^{\ast }{v}_e{C}_e(t)$ (Eq. [2]). The tissue CA concentration C_t(t) was estimated as in Method 2. Using the extended Tofts model (24), v_eC_e(t) was obtained by fitting C_t(t):

$$C_t(t)=v_p{C}_p(t)+v_e{C}_e(t)=v_p{C}_p(t)+K^{\mathit{\text{trans}}}\underset{0}{\overset{t}{\int }}{C}_p(\tau )\cdot e^{-K^{\mathit{\text{trans}}}\cdot (t-\tau )/v_e}d\tau$$ [6]

The vascular input function C_p(t) was determined from the ΔR₁ data (35) and was scaled until C_t(t) in muscle yielded a v_e of 0.11 (36). Voxels with non-physiological volume fractions (v_p,e < 0 or v_p,e > 1) were set to zero and were not used for subsequent analysis. The extravascular CA T₂* relaxivity $r_{2,e}^{\ast }$ was obtained by fitting the dual-echo ΔR₂* to Equation 1, where v_eC_e and v_pC_p are inputs from the extended Tofts model and the only unknowns are $r_{2,e}^{\ast }$ and $r_{2,p}^{\ast }$. The voxel-wise extravasation term $r_{2,e}^{\ast }{v}_e{C}_e(t)$ was subtracted from the corresponding dual-echo ΔR₂* to determine the T₁- and T₂*-leakage corrected ΔR₂*.

The dual-echo (T₁-corrected) ΔR₂* was used for determination of the arterial input function (AIF), which was selected using an automated method (37) specifically adapted for use with multi-echo acquisitions (38). An adaptive threshold based on image SNR (39) was used for deconvolution. CBF was taken as the maximum of the impulse response function determined from the circular singular value decomposition (SVD) of the AIF and tissue ΔR₂* (40). CBV was determined from the ratio of the scaled integrals of the tissue ΔR₂* curve and the arterial input function curve. For display purposes in Figure 3, CBV and CBF were normalized to 4% and 60 ml/100g/min in gray matter. For subsequent figures, CBV and CBF are given relative to contralateral normal tissue, as indicated using rCBV and rCBF.

Figure 3.

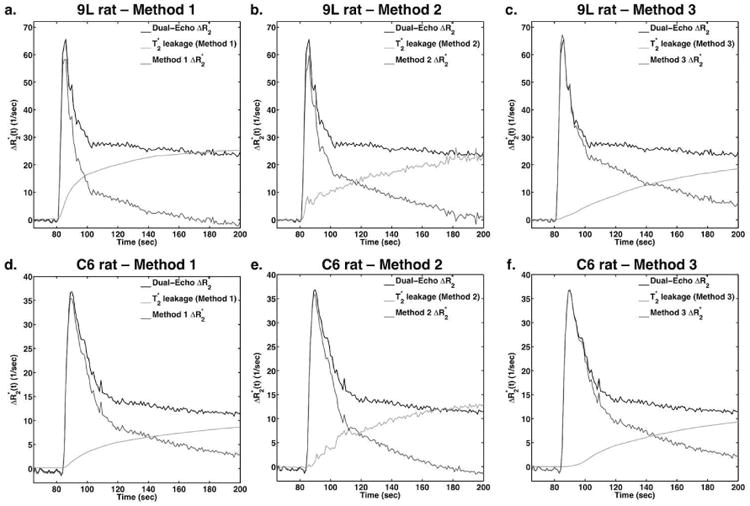
Comparison of T₁- and T₂* leakage correction using Methods 1 (a,d), 2 (b,e), and 3 (c,f) in 9L (a-c) and C6 (d-f) tumor ROIs. For each panel, the T₁-corrected dual-echo ΔR₂* is shown, along with the T₂* leakage term derived from the leakage correction methods and the resulting corrected ΔR₂*.

The Gd-DTPA DSC measures were obtained using 120 points (= 120s) of data, with 60s before and 60s after injection. To match the number of points included following bolus passage to the Gd-DTPA analysis, the MION DSC measures were obtained using 110 points (= 110s) of data, with 60s before and 50s after injection. The T₁-corrected (dual-echo) and T₁- and T₂*-corrected (Method 1 based on the Weisskoff correction and Methods 2 and 3 proposed herein) Gd-DTPA-based DSC parameters were compared to the MION-based DSC parameters. To match the Gd-DTPA analysis, the MION DSC parameters were obtained from the dual-echo signals.

Mean transit time sensitivity

To determine how sensitive Method 1 is to MTT variations, percent error in rCBV was determined as a function of MTT. To this end, MTT bins were created for low, mid, and high MTT using the mean and standard deviation (std) of the normal tissue MTT. More specifically, voxels with MTT less than 1 std from the normal tissue MTT were binned into the low MTT bin; voxels with MTT within 1 std of the normal tissue MTT were binned into the mid MTT bin; voxels with MTT greater than 1 std higher than the normal tissue MTT were binned into the high MTT bin. These bins were then used to determine the rCBV percent error for dual-echo and Methods 1, 2, and 3.

Statistical Analysis

Data analysis was performed on regions of interest (ROIs) that were initially drawn from T₂-weighted fast spin echo (FSE) images at a long TE (80ms), with the tumor ROIs further refined using a 15% enhancement threshold compared to the normal tissue ROIs. Voxels with non-physiological volume fractions were excluded from the ROI analysis. The perfusion parameters are reported as group mean ± std for the 9L and C6 tumor types. Concordance correlation coefficient (CCC) and Pearson's correlation coefficient (R) were used to assess linear agreement, with the former used as a measure of accuracy and the latter as a measure of precision. Significance was tested using a paired t-test between the MION DSC parameters and the dual-echo (T₁-corrected only) and T₁- and T₂*-corrected DSC parameters. Results were considered significant at p<0.05.

Results

Figure 1 demonstrates the simulated time-courses (a-c) for a given vascular volume fraction of 8% and cell volume fraction of 60%. The CA concentration in the plasma and EES are shown in Figure 1a, along with the corresponding ΔR₂* time-courses for no leakage, uncorrected, C_t corrected, and v_eC_e corrected simulations (Figures 1b-c). CA leakage leads to elevated ΔR₂*, while correction with C_t overcorrects the leakage effects and leads to underestimated ΔR₂*. Note that the inclusion of the v_pC_p term in C_t causes a large underestimation in the peak amplitude. Correction with v_eC_e yields ΔR₂* time-courses that most closely resembles the ΔR₂* observed for the CA contained within the vessels, with only slight effects on the peak amplitude. Figure 1d compares the CBV percent difference between no leakage and the uncorrected CBV, C_t corrected CBV, and v_eC_e corrected CBV. The uncorrected CBV strongly overestimates the true CBV for all v_p values, while both corrections come closer to the true CBV. Corrections using C_t tend to underestimate CBV, with increasing error for increasing vascular volume contributions. Corrections using v_eC_e yield CBV measurements that are within 15% of the true CBV for all v_p values.

Figure 1.

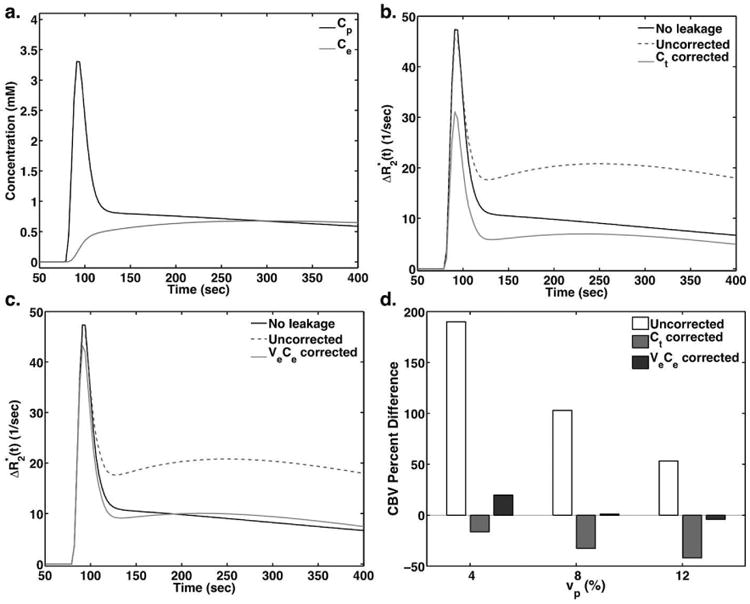
(a) Simulated C_p and C_e curves for an 8% vascular volume fraction and 60% cell volume fraction using a two-compartment model and PFM. (b-c) Simulated ΔR₂* curves for no leakage, uncorrected, and corrected using $r_{2,t}^{\ast }{\mathrm{C}}_{\mathrm{t}}$ (b, Method 2) and $r_{2,e}^{\ast }{\mathrm{v}}_{\mathrm{e}}{\mathrm{C}}_{\mathrm{e}}$ (c, Method 3). (d) Bar plots showing the CBV percent difference between the true CBV and the uncorrected and corrected CBV.

Figure 2 shows example time-courses in a 9L tumor (top) and C6 tumor (bottom) using Gd-DTPA (left) and MION (right) CA. The AIF in each case is also shown, which tends to be higher and narrower, peaking earlier, than the time-courses in normal and tumor tissue. The dual-echo ΔR₂* in the 9L tumor showed clear T₂* leakage effects, manifesting as extremely elevated post-bolus ΔR₂*. On the other hand, the dual-echo ΔR₂* in the C6 tumor exhibited minimal T₂* leakage effects. The Gd-DTPA exhibited a wider FWHM than MION despite having identical injection volumes and speeds, which can be attributed to the higher viscosity of the Gd-DTPA. The DSC analysis limits of 60 s post-bolus for Gd-DTPA and 50 s post-bolus for MION are also shown, where these limits were chosen to match the number of points included following bolus passage.

Figure 2.

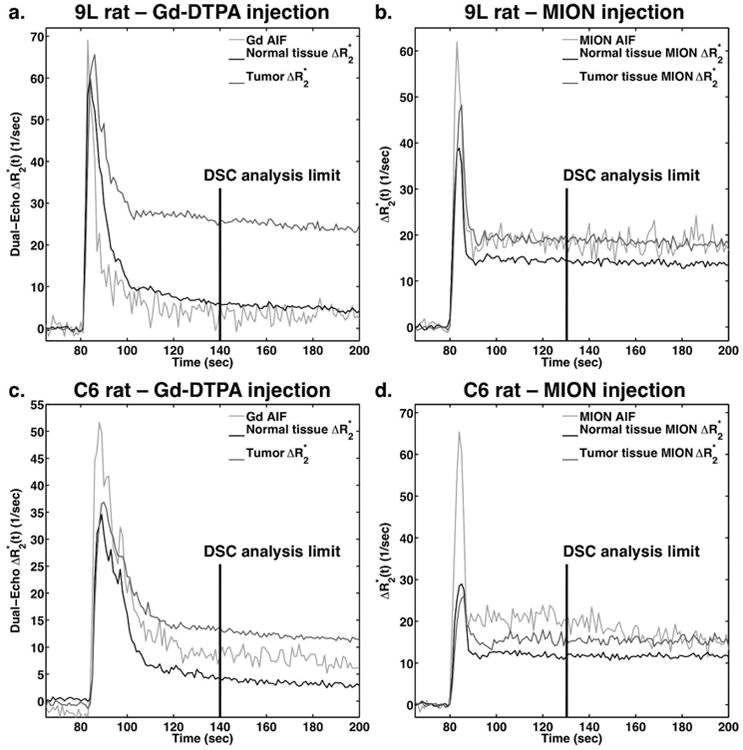
Dynamic dual-echo ΔR₂* curves following bolus injection of Gd-DTPA (a,c) and MION (b,d) in 9L (a,b) and C6 (c,d) tumor ROIs. Normal tissue ROIs and AIFs are also shown for each tumor and contrast agent. DSC analysis was limited to 60 seconds post-injection for Gd-DTPA and 50 seconds post-injection for MION.

Figure 3 compares the effects of each leakage correction method on 9L (top) and C6 (bottom) tumor time-courses. The 9L tumor showed strong T₂* leakage effects in the dual-echo ΔR₂*, and these were corrected differently with each method (Methods 1-3, left to right). The shapes of the leakage terms in each method are dissimilar, leading to different corrected ΔR₂* time-courses. In particular, the corrections given by Methods 1 and 2 reduce the ΔR₂* more substantially than that provided by Method 3 during the initial bolus passage. Although the dual-echo ΔR₂* in the C6 tumors appeared relatively normal, all correction methods changed the ΔR₂* time courses indicating the presence of T₂* leakage effects. Note that because Methods 1 and 3 involve data fitting to obtain the leakage term, this term is artificially smoother than the voxel-based leakage term in Method 2. Fitting the C_t curve to the standard Tofts model would yield smoothed curves similar to Methods 1 and 3.

The CBV and CBF maps in 9L (top rows) and C6 (bottom rows) tumors are shown in Figure 4 for T₁-corrected dual-echo, Methods 1, 2, and 3, and MION. The dual-echo CBV was overestimated compared to the MION CBV for the 9L due to strong T₂* leakage effects, while the dual-echo CBV was fairly close to the MION CBV in the T₁-dominant C6 tumors. In the 9L tumors, the T₁- and T₂*-corrected CBV maps using Methods 1-3 much more closely matched that of MION. All three methods performed comparably in the C6 tumor. CBF was fairly consistent across dual-echo and methods 1 and 2, indicating only minor effects of leakage of CBF. In general, CBF was slightly underestimated using Gd-DTPA compared to MION.

Figure 4.

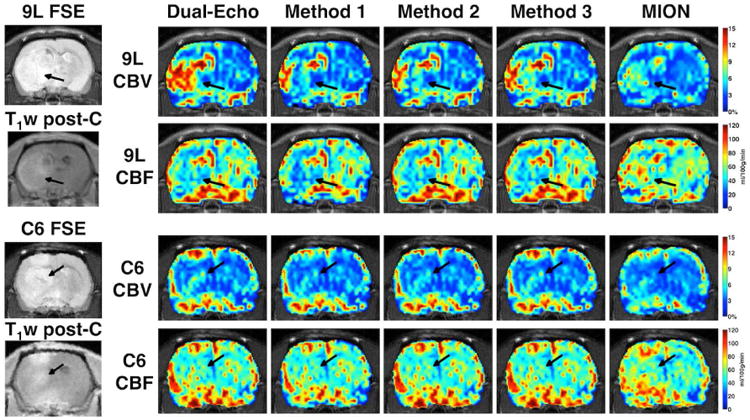
T₁-corrected dual-echo, T₁- and T₂*-corrected (Methods 1, 2, and 3), and MION-based CBV and CBF in 9L (top) and C6 (bottom) tumor-bearing rats. Fast spin echo (FSE) and T₁-weighted post-contrast images show tumor location.

Figure 5 shows plots of rCBV from T₁-corrected dual-echo and Methods 1-3 versus MION rCBV in both tumor types. Dual-echo rCBV is highly overestimated for both 9L and C6 tumors, while the corrected rCBVs with Methods 1-3 generally provided linear fits closer to the line of unity. Table 1 summarizes the Gd-DTPA and MION mean (std) rCBV and rCBF for all 9L and C6 tumors. The parameters (slope, CCC, R, and p-value) from the linear fits of each correction method versus MION are also summarized in Table 1. Leakage correction substantially improved the Gd-DTPA rCBV compared to MION. Leakage correction did not significantly change rCBF, which was underestimated for all measures relative to MION.

Figure 5.

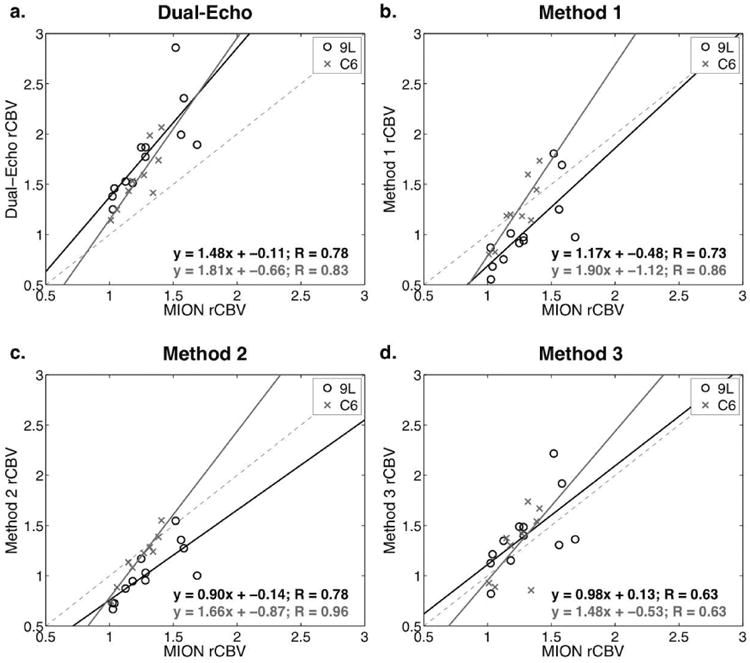
Scatter plots showing rCBV from T₁-corrected dual-echo and Methods 1-3 (T₁- and T₂*-corrected) versus MION rCBV in 9L and C6 tumors. The 9L tumor values and linear regressions are shown in black, and the C6 tumor values and linear regressions are shown in gray.

Table 1.

Relative CBV and CBF parameters in 9L and C6 tumors for dual-echo, correction methods 1-3, and MION. Slope, CCC, R, and p-values are obtained from each method versus MION.

		9L					C6
	Method	Mean (std)	slopea	CCCa	Ra	P-valuea	Mean (std)	slopea	CCCa	Ra	P-valuea
rCBV	Dual-Echo	1.81 (0.45)	1.48	0.30	0.78	0.003	1.57 (0.31)	1.81	0.30	0.83	0.006
	Method 1	1.04 (0.38)	1.17	0.48	0.73	0.007	1.24 (0.32)	1.90	0.65	0.86	0.003
	Method 2	1.02 (0.27)	0.90	0.47	0.78	0.003	1.17 (0.25)	1.66	0.79	0.96	<0.001
	Method 3	1.40 (0.37)	0.98	0.54	0.63	0.027	1.30 (0.34)	1.48	0.43	0.63	0.07
	MION	1.30 (0.24)	--	--	--	--	1.23 (0.14)	--	--	--	--
rCBF	Dual-Echo	0.88 (0.20)	0.51	0.40	0.54	0.07	1.13 (0.18)	0.37	0.34	0.43	0.25
	Method 1	0.83 (0.20)	0.49	0.32	0.51	0.09	1.08 (0.19)	0.44	0.33	0.47	0.20
	Method 2	0.81 (0.18)	0.49	0.31	0.57	0.05	1.07 (0.17)	0.36	0.27	0.44	0.24
	Method 3	0.87 (0.19)	0.48	0.37	0.52	0.08	1.10 (0.20)	0.31	0.23	0.32	0.40
	MION	1.04 (0.21)	--	--	--	--	1.26 (0.20)	--	--	--	--

std: standard deviation; CCC: concordance correlation coefficient; R: Pearson's correlation coefficient;

^abetween each method and MION

The bar plots in Figure 6 show rCBV and rCBV percent error in 9L and C6 tumors using dual-echo, Methods 1, 2, and 3, and reference MION measurements. With MION, the 9L and C6 tumors were both characterized by elevated rCBV and rCBF (Table 1). The 9L tumors typically had higher rMTT, while the C6 tumors were characterized by rMTTs similar to normal tissue. The Gd-DTPA rCBV in 9L tumors was significantly different from MION using dual-echo (p < 0.01), while Methods 1 and 2 significantly underestimated rCBV (p < 0.01). Method 3 provided a more reliable estimate of rCBV in 9L tumors and was not significantly different from MION (p = 0.22). Methods 1 and 2 were not significantly different, while both were significantly different from Method 3 (p < 0.01). In C6 tumors, the dual-echo rCBV was significantly overestimated (p < 0.01), while Methods 1-3 provided more reliable estimates of rCBV compared to MION (p = 0.99, 0.13, and 0.48, respectively). None of the correction methods (Method 1, 2, and 3) were significantly different from each other.

Figure 6.

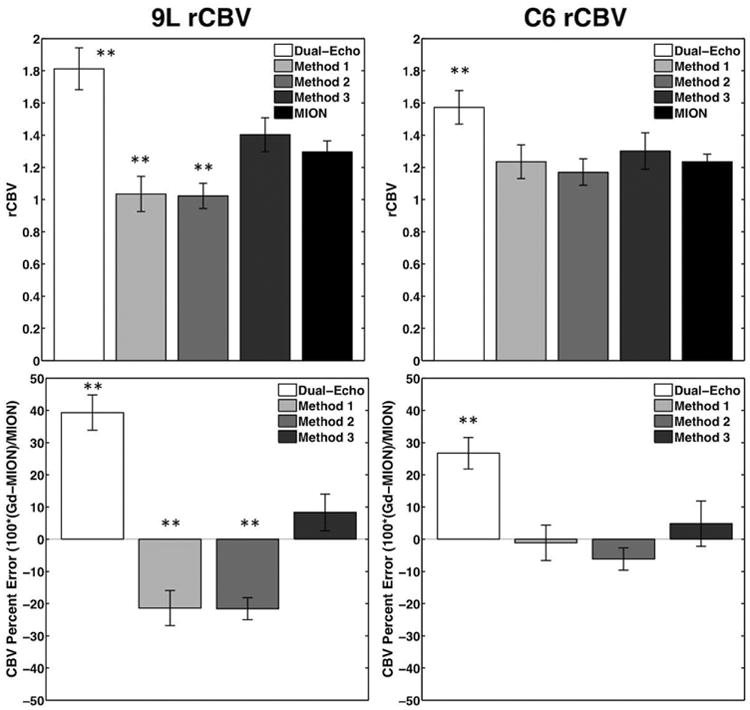
Bar plots showing mean rCBV and CBV percent error in 9L (n=12) and C6 (n=9) tumors for T₁-corrected dual-echo, Methods 1, 2 and 3 (T₁- and T₂*-corrected), and MION reference. **p<0.01 and *p<0.05.

Bland-Altman plots (Figure 7) revealed a positive bias for dual-echo rCBV for both tumor types, and a general trend appeared as rCBV increased for dual-echo to overestimate the MION CBV. In 9L tumors, Methods 1 and 2 had a slight negative bias for rCBV, while Method 3 showed little to no bias. Methods 1-3 showed little to no bias for the C6 tumors.

Figure 7.

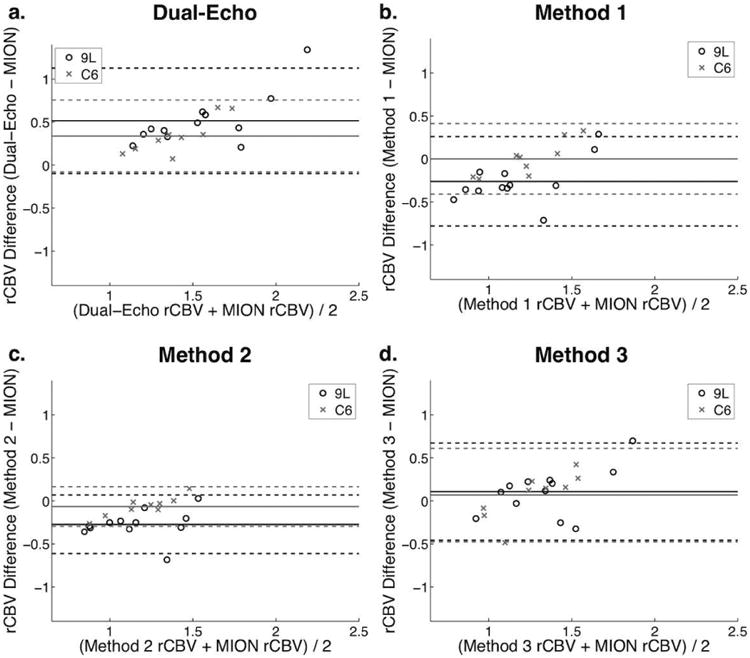
Bland-Altman plots comparing dual-echo, Method 1, Method 2, and Method 3 rCBV with MION rCBV for 9L (open circles) and C6 tumors (x marks).

Figure 8 shows the rCBV percent error as a function of MION MTT for MTT bins with low, mid, and high MTT relative to normal tissue MTT. In the 9L tumors, the low MTT bin comprised 3% of the tumor voxels, while the mid and high MTT bins comprised 68% and 29% of the tumor voxels, respectively. The dual-echo rCBV was significantly overestimated for all MTT bins (p < 0.01). All corrections methods (1-3) significantly overestimated rCBV for the low MTT bin. Methods 1 and 2 significantly underestimated rCBV for the mid and high MTT bins (p < 0.05), while Method 3 rCBV was not significantly different from MION rCBV (p > 0.05). For the C6 tumors, the low and mid MTT bins comprised 10% and 78% of the tumor voxels, respectively, while the high MTT bins comprised 12% of tumor voxels. Once again, dual-echo rCBV was overestimated for all MTT bins. In this tumor model, Methods 1 and 3 were not significantly different from MION rCBV for any MTT, while Method 2 was significantly different from MION in the high MTT bin.

Figure 8.

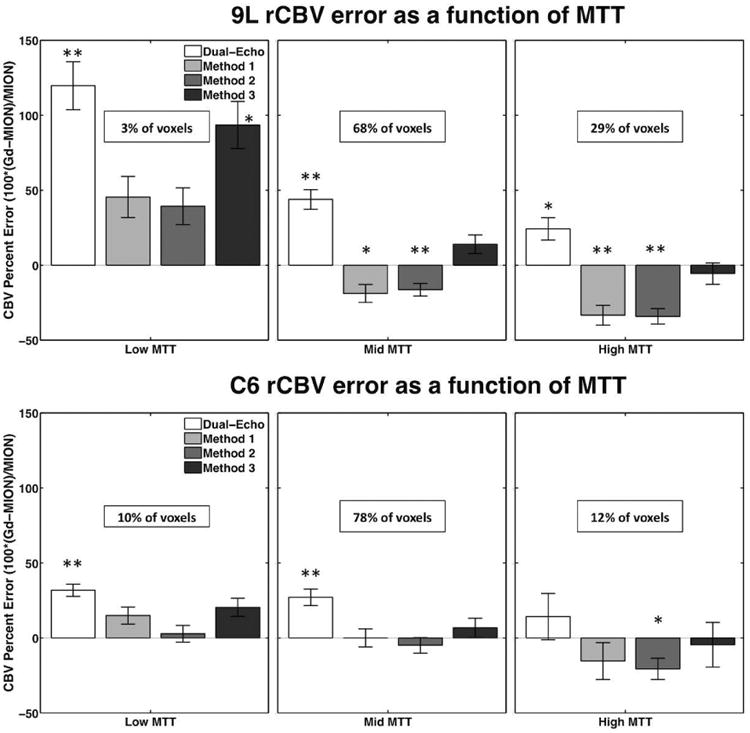
Bar plots showing rCBV percent error (relative to MION rCBV) in 9L and C6 tumors as a function of MTT for dual-echo and Methods 1, 2, and 3. The percents of all voxels described by each bin (low, mid, and high MTT) are shown in each panel. **p<0.01 and *p<0.05.

Discussion

Previous reports have shown that single-echo DSC-MRI data, uncorrected for leakage effects, have complex combinations of T₁ and T₂* leakage effects (8,41) that can lead to unreliable measures of CBV and CBF. In this study, we have proposed a combined biophysical and pharmacokinetic approach for correcting both T₁ and T₂* leakage effects using multi-echo DSC data, as well as a further simplification of the proposed model that does not require pharmacokinetic modeling. Using this combined method, we have shown that T₁ and T₂* correction provides reliable perfusion parameters that are comparable to MION, while further simplifying this model may provide reasonable rCBV values without data fitting. In addition to comparisons with MION DSC-MRI, the methods proposed herein (Methods 2 and 3) were compared to the pharmacokinetic correction method established by Weisskoff (Method 1). The Weisskoff method for correcting single-echo rCBV data with a pre-load was previously validated using steady-state MION CBV as the reference standard in 9L tumors (16).

In the present study, dynamic MION data permitted measurement of both CBF and CBV using similar perfusion analysis methods for both types of CA. Further, the correction reliability of each method was compared in two tumor models that exhibit dissimilar leakage effects. The 9L gliosarcoma tumors have substantial T₁ and T₂* leakage effects, while the C6 glioblastoma tumors have T₁-dominant leakage effects. In the 9L tumors, Method 3 provided the most reliable rCBV results, whereas Methods 1-3 provided similar rCBV values in the C6 tumors. The 9L tumors were also characterized by a high tumor MTT. MTT sensitivity is a known drawback of the Weisskoff method (19), and MTT heterogeneity has been previously noted in human tumors (10,15). Method 3 did not exhibit MTT dependence and may be applicable to a wider range of hemodynamic conditions. Despite its sensitivity to MTT, Method 1 provided similar perfusion parameters to Method 2, which tended to underestimate MION rCBV in the 9L tumors and agreed with MION rCBV in the C6 tumors. Gd-DTPA CBF was underestimated compared to MION CBF, and this was not altered by leakage correction, consistent with previous reports showing minor (9) or negligible (10,15) effects of CA leakage on CBF.

In contrast to prior implementations, Method 1 did not include a pre-load bolus to reduce T₁ leakage effects (7,16), as all three Methods were applied to T₁-insensitive dual-echo data to correct isolated T₂* leakage effects. As noted above, T₁ leakage effects can be effectively described by traditional pharmacokinetic models, as they derive from the direct interaction of tissue water with the CA, which has a known (or assumed) relaxivity. In contrast, T₂* effects are more complex, originating from increased magnetic field heterogeneity due to the compartmentalization of CA around cells (12,27). In the limiting cases of data only sensitive to either T₁ or T₂* leakage effects, this implies that the parameters K₂ and K_a from the Weisskoff and Bjornerud methods reflect, in the case of T₁ leakage effects, the degree of CA extravasation (e.g., a mixed measure of permeability and the volume fraction of the EES) or, in the case of T₂* leakage effects, a tissue's cellular properties (e.g., cell density, size, orientation, shape) and the local CA concentration. In practice, all single-echo based DSC-MRI data is a complex combination of competing T₁ and T₂* leakage effects and their presence depends on CA pharmacokinetics, tissue microstructure, and pulse sequence parameters. These potential confounds motivated the development of the leakage correction technique proposed herein, which has the advantages of eliminating T₁ leakage effects, quantifying voxel-wise CA concentration time curves, and using this information to estimate and remove T₂* leakage effects that depend upon the underlying tissue cytoarchitecture.

Several assumptions were made in our correction methods. The first assumption is that the empirical biophysical model (Equation 1) accurately describes the underlying biophysical basis of CA-induced T₂* leakage effects. This model itself is a simplification of the models proposed in Refs (10,13,23), where we assume that the gradient term is negligible relative to v_pC_p and v_eC_e, similar to Ref (10). In contrast, Soubron et al. (13,23) includes the gradient correction term in their biophysical model, which may be more accurate in describing the underlying relaxivity contributions. The strong agreement between Method 3 and the MION CBV data indicate, at least in the context of these animal tumor models, that the gradient term has negligible influence on the measured leakage effects. In Method 2, we further assume that the measured ΔR₁ (= r₁ · C_t) primarily reflects the CA in the EES. This assumption is tested in Method 3, where the tissue CA concentration is taken as a weighted sum of the plasma and EES concentrations (C_t = v_pC_p + v_eC_e), assuming again that the intracellular concentration is zero. The 9L tumors tend to be more vascular than the C6 tumors, which could explain why Method 2 tends to underestimate rCBV in the 9L tumors, while providing reasonable rCBV values in the C6 tumors. Another major assumption in Method 2 is that $r_{2,t}^{\ast }$ is a reasonable approximation for $r_{2,e}^{\ast }$. As previously shown (12), $r_{2,t}^{\ast }$ is highly sensitive to cellular properties, such as cell size and density. Although $r_{2,t}^{\ast }$ was found to be approximately 25-30% higher than $r_{2,e}^{\ast }$, this may be an acceptable assumption given the agreement with MION data. A final assumption is that the equilibrium relaxivity $r_{2,t}^{\ast }$ remains constant over the dynamic time course. This is unlikely to be a significant source of error as choosing different equilibrium points did not significantly alter our resulting CBF and CBV measures.

A potential limitation of our method is that reliable extraction of DCE-MRI based pharmacokinetic parameters requires acquisition times that are greater than traditional DSC-MRI scans (at least 5 minutes of post-contrast data) (42,43). However, the additional scan time has the advantage of enabling the simultaneous assessment of DSC- and DCE-MRI data (22). It should also be noted that the proposed technique assumes unidirectional CA transport out of the vasculature and may not be valid in highly permeable tissues, where CA from the EES re-enters the intravascular space. A final limitation of this study is that, as is typical in most DSC-MRI studies, literature values of arterial and vascular CA relaxivity were not used to convert ΔR₂* to CA concentration. As a result, quantitative absolute values for CBV and CBF could not be obtained.

Unlike these relative homogeneous animal models, human tumors exhibit a range of T₁ and T₂* leakage effects. From single-echo DSC-MRI studies (using moderate to high flip angles (60-90°) and typical echo times (> 40 ms), primary central nervous system lymphomas (PCNSL) predominantly exhibit T₁ leakage effects, gliomas mostly exhibit T₁ effects (approx. 60-70% of voxels), and brain metastasis primarily show T₂* effects (15,44). Accordingly, the results herein would suggest that for dual-echo DSC-MRI data acquired in PCNSL and gliomas, Methods 1-3 would yield similar rCBV results, but in brain metastases, Method 3 would provide the most reliable rCBV data. These observations, however, need to be validated in clinical studies.

Conclusions

In conclusion, we have demonstrated that dual-echo based CBV maps that are not corrected for T₂* leakage effects are unreliable. Correcting dual-echo DSC-MRI data using the only pharmacokinetic or biophysical models (Methods 1 and 2, respectively) yields underestimated rCBV in tumors with strong T₂* leakage effects and more reliable perfusion parameters in tumors with moderate T₂* leakage effects. By leveraging the dual-echo data to compute the voxel-wise CA concentration time series and taking into account the biophysical basis of T₂* leakage effects, the combined pharmacokinetic and biophysical approach yields more reliable perfusion parameters. The simplified biophysical method (Method 2) is computationally efficient, as it requires no model fitting, which could ease its clinical translation for the assessment of brain tumor hemodynamic characterization and treatment response, particularly in the context of gliomas that show limited to moderate T₂* leakage effects.

Supplementary Material

Supp FigureS1 & TableS1

Figure S1 – Top left: Plot showing average percent change in $r_{2,t}^{\ast }$ as a function of the time point of determination (that is, the x-label 2:3 represents the percent $r_{2,t}^{\ast }$ change between the 2-3 minute interval and the 3-4 minute interval). Bottom right: Bar plots showing mean corrected rCBV using Methods 2 (C_t) in 9L (n=12) and C6 (n=9) tumors, where the effective tissue relaxivity $r_{2,t}^{\ast }$ was determined at 1-minute intervals from 2 to 8 minutes post-injection. The arrowheads indicate the interval chosen for subsequent analyses (5 to 6 minutes post-injection). Left: Percent error between estimates of $r_{2,t}^{\ast }$ and fits of $r_{2,e}^{\ast }$, showing overestimations between 25 and 30% for $r_{2,t}^{\ast }$.

Table S1 – List of relevant parameters for Methods 2 and 3.