Data-driven optimized flip angle selection for T₁ estimation from spoiled gradient echo acquisitions

Abstract

Purpose

Define criteria for selection of optimal flip angle sets for T₁ estimation and evaluate effects on T₁ mapping.

Theory and Methods

Flip angle sets for SPGR-based T₁ mapping were selected by minimizing T₁ estimate variance weighted by the joint density of M₀ and T₁ in an initial acquisition. The effect of optimized flip angle selection on T₁ estimate error was measured using simulations and experimental data in the human and rat brain.

Results

For 2-point acquisitions, optimized angle sets were similar to those proposed by other groups, and therefore performed similarly. For multi-point acquisitions, optimal angle sets for T₁ mapping in the brain consisted of a repetition of two angles. Implementation of optimal angles reduced T₁ estimate variance by 30–40% compared to a multi-point acquisition using a range of angles. Performance of the optimal angle set was equivalent to that of a repetition of the two-angle set selected using criteria proposed by other researchers.

Conclusion

Repetition of two carefully selected flip angles notably improves the precision of resulting T₁ estimates compared with acquisitions using a range of flip angles. This work provides a flexible and widely applicable optimization method of particular use for those who repeatedly perform T₁ estimation.

Introduction

T₁ estimation is a quantitative MRI tool with a variety of applications, including monitoring myelin-related disease, diagnosing Parkinson’s disease, and studying tissue perfusion (1–3). The gold standard for T₁ estimation is an inversion recovery sequence with multiple inversion times (4). However, inversion recovery scans require repetition times (TRs) much longer than the longest T₁ of interest, rendering them impractical for use in clinical scans or in vivo research settings. For this reason, a multiple flip angle spoiled gradient echo (SPGR) approach is commonly employed to reduce scan time for T₁ mapping (5). More recently, several researchers have proposed supplemental methods to correct for common sources of error in resulting SPGR-based T₁ estimates, such as incomplete spoiling and imperfect RF pulses (6–8).

For SPGR-based T₁ mapping, a minimum number of flip angles must be carefully selected to maximize the accuracy and precision of the T₁ estimate and minimize scan time. Several works addressing angle selection criteria settle on the same optimal flip angles in a 2-point acquisition despite differences in selection approach. These approaches include variance minimization (9), definition of an efficiency function related to both the T₁ estimate variance and the scan time (10), and maximizing the product of the regression line dynamic range and the fractional signal with respect to the Ernst angle (11). Another approach uses criteria of T₁-to-noise ratio maximization to select larger flip angle sets (12). However, these approaches address T₁ estimation in the simplified setting of a single or average T₁ value. Tissues and pathologies of interest contain a continuous distribution of T₁ values, which can complicate the task of selecting optimal flip angles. Furthermore, most of these approaches address the optimized selection of just two flip angles and therefore do not develop approaches that can be generalized to the selection of larger angle sets.

The selection of flip angles for more realistic imaging tasks has also been addressed in several studies. Cheng and Wright propose selection of 3-point angle sets based on the minimum and maximum of the range of T₁ values to be estimated (13). T₁ variance minimization has also been used to select 2-point sets for several different ranges of T₁ values to be estimated (14). In another study, researchers selected 3-point angle sets to maximize T₁ mapping efficiency over a realistic range of T₁ values (15). Although useful, these approaches lack flexibility to select any number of flip angles, and they do not take into account the full shape and range of the T₁ and M₀ distributions of the anatomy being imaged.

In this study, we aim to address these missing components of flip angle selection schemes with the goal of providing a robust flip angle selection method that can be applied in almost any setting. To do so, we develop a data-driven approach based on T₁ variance minimization to determine the optimal set of any number of flip angles for T₁ estimation. The T₁ distribution in the imaging subject of interest is taken into account using an initial acquisition. We describe and apply a novel set of flip angle selection criteria, based on minimization of the variance in the T₁ estimates weighted by the joint density of M₀ and T₁. Using experimental data and simulations, we evaluate the effects of this optimized acquisition design on the precision and accuracy of T₁ estimates. The concepts behind the proposed method were previously described in abstract form (16).

Theory

In the general setting of nonlinear least squares-based (NLS) parameter estimation, as is used for T₁ and M₀ estimation in this work, the objective function can be represented by

$$f_{NLS}(\gamma )=\frac{1}{2}\sum _{i=1}^n{r}_i{(\gamma )}^2$$ [1]

where γ is the parameter vector to be estimated and r_i(γ) are the error terms or the residual terms if r_i are evaluated at the NLS estimate. Defining r = [r₁ r₂ … r_n]^T, the gradient vector and the Hessian matrix of f_NLS(γ) can be expressed respectively as

$${\nabla }_{\gamma }{f}_{NLS}(\gamma )={\mathit{J}}_{\gamma }^T(\mathit{r})·\mathit{r}$$ [2]

and

$${\nabla }_{\gamma }^2{f}_{NLS}(\gamma )={\mathit{J}}_{\gamma }^T(\mathit{r})·{\mathit{J}}_{\gamma }(\mathit{r})+\sum _{i=1}^n{r}_i{\mathit{T}}_{\mathit{i}}$$ [3]

where [T_i]_kl = ∂²r_i/∂γ_k∂γ_l is the second order derivative of the residual term, and the Jacobian matrix is defined as [J_γ(r)]_ij ≡ ∂r_i/∂γ_j. According to the framework of error propagation (17), the covariance matrix of the estimated parameter can be written as

$${\mathbf{\Sigma }}_{\gamma }={\sigma }^2{[{\nabla }_{\gamma }^2{f}_{NLS}(\gamma )]}^{-1}$$ [4]

where σ² is the unknown noise variance. However, in a computational experimental design setting, the covariance matrix takes a much simpler form:

$${\mathbf{\Sigma }}_{\gamma }={\sigma }^2{[{\mathit{J}}_{\gamma }^T(\mathit{r}){\mathit{J}}_{\gamma }(\mathit{r})]}^{-1}$$ [5]

because the residual terms are assumed to be zero on the average. This assumption is based on that of Gaussian-distributed noise contributing to residuals that average to zero and are independent of the parameters of interest.

In the setting of T₁ estimation, the appropriate term of this covariance matrix can be used to define an objective function for minimization of variance in the NLS-based T₁ estimate. The NLS objective function for T₁ estimation from variable flip angle SPGR acquisitions can be written as

$$f_{NLS}(\gamma )=\frac{1}{2}\sum _{i=1}^n{(s_i-M_0\text{sin}({\alpha }_i)\frac{1-e^{\raisebox{1ex}{$-TR$}\!\left/ \!\raisebox{-1ex}{$T_1$}\right.}}{1-\text{cos}({\alpha }_i)e^{\raisebox{1ex}{$-TR$}\!\left/ \!\raisebox{-1ex}{$T_1$}\right.}})}^2$$ [6]

where s_i are the observed signals, α_i are the flip angles, M₀ is the unknown equilibrium longitudinal magnetization, TR is the repetition time, and T₁ is the unknown longitudinal relaxation time. Therefore, γ=[M₀ T₁]^T. We note here that repetition time is held constant and held close to the minimum allowable by the MR system, echo time (TE) is similarly held close to the practical minimum, and therefore differences in T₂* decay are assumed negligible for this specific setting.

Taking the derivative of the error with respect to both M₀ and T₁, we arrive at the expressions for the terms in the Jacobian matrix:

$$\frac{\partial r_i}{\partial {\gamma }_1}\equiv \frac{\partial r_i}{\partial M_0}=-\text{sin}({\alpha }_i)\frac{1-e^{\raisebox{1ex}{$-TR$}\!\left/ \!\raisebox{-1ex}{$T_1$}\right.}}{1-\text{cos}({\alpha }_i)e^{\raisebox{1ex}{$-TR$}\!\left/ \!\raisebox{-1ex}{$T_1$}\right.}}$$ [7]

and

$$\frac{\partial r_i}{\partial {\gamma }_2}\equiv \frac{\partial r_i}{\partial T_1}=\frac{M_{0}TR}{T_1^2}\frac{(1-\text{cos}({\alpha }_i))\text{sin}({\alpha }_i)e^{\raisebox{1ex}{$-TR$}\!\left/ \!\raisebox{-1ex}{$T_1$}\right.}}{{(1-\text{cos}({\alpha }_i)e^{\raisebox{1ex}{$-TR$}\!\left/ \!\raisebox{-1ex}{$T_1$}\right.})}^2}$$ [8]

With some algebraic manipulation, as shown in Appendix A, the determinant of J_γ^T(r)J_γ(r) and the components of the covariance matrix Σ_γ can be expressed as

$$\text{det}({\mathit{J}}_{\gamma }^T(\mathit{r}){\mathit{J}}_{\gamma }(\mathit{r}))=\frac{E^2{(E-1)}^{3}T{R}^2{M}_0^2}{T_1^4}\sum _{i=1}^n\sum _{j=1}^n{A}_{ij}$$ [9]

$${[{\mathbf{\Sigma }}_{\gamma }]}_{11}=\frac{{\sigma }^2}{{(E-1)}^3}\frac{{\sum }_{i=1}^n\frac{{\text{sin}}^2({\alpha }_i){(1-\text{cos}({\alpha }_i))}^2}{{(E-\text{cos}({\alpha }_i))}^4}}{{\sum }_{i=1}^n{\sum }_{j=1}^n{A}_{ij}}$$ [10]

$${[{\mathbf{\Sigma }}_{\gamma }]}_{22}=\frac{{\sigma }^2{T}_1^4}{E^2(E-1)T{R}^2{M}_0^2}\frac{{\sum }_{i=1}^n\frac{{\text{sin}}^2({\alpha }_i)}{{(E-\text{cos}({\alpha }_i))}^2}}{{\sum }_{i=1}^n{\sum }_{j=1}^n{A}_{ij}}$$ [11]

$${[{\mathbf{\Sigma }}_{\gamma }]}_{12}={[{\mathbf{\Sigma }}_{\gamma }]}_{21}=\frac{{\sigma }^2{T}_1^2}{E{(E-1)}^{2}TR{M}_0}\frac{{\sum }_{i=1}^n\frac{{\text{sin}}^2({\alpha }_i)(1-\text{cos}({\alpha }_i))}{{(E-\text{cos}({\alpha }_i))}^3}}{{\sum }_{i=1}^n{\sum }_{j=1}^n{A}_{ij}}$$ [12]

where $A_{ij}=\frac{{\text{sin}}^2({\alpha }_i){\text{sin}}^2({\alpha }_j)(1-\text{cos}({\alpha }_j))(\text{cos}({\alpha }_i)-\text{cos}({\alpha }_j))}{{(E-\text{cos}({\alpha }_i))}^3{(E-\text{cos}({\alpha }_j))}^4}$ and E = exp(TR/T₁). Note that [Σ_γ]₁₁, [Σ_γ]₂₂, and [Σ_γ]₂₁ are the variance of M₀, the variance of T₁, and the covariance of M₀ and T₁, respectively. A similar derivation for the T₁ estimate variance, along with the analytical result for the two-angle T₁ estimate, has previously been published by Wood (18).

Methods

Study design

In order to test the described T₁ variance minimization criteria for SPGR flip angle selection, we pursued following approach. First, an objective function for flip angle selection was defined based on minimizing T₁ variance in the imaging volume of interest. Second, optimal flip angle sets and control flip angle sets were defined based on T₁ and M₀ maps calculated from an open-source IR data set in the human brain. Using these T₁ and M₀ maps as ground truth, simulations were performed to compare the relative performance of several flip angle sets for SPGR-based T₁ estimation. Third, the proposed flip angle selection technique was tested in the ex vivo rat brain both with simulations and experimentally. Using an initial IR acquisition and resulting T₁ and M₀ maps, optimal flip angle sets and alternate flip angle sets were defined. To compare the performance of these flip angle sets, simulations were performed using IR-based T₁ and M₀ maps as ground truth. Last, experimental data was again acquired in the ex vivo rat brain using data-driven flip angle sets in order to compare the inter-scan variance when different angle sets were used.

Flip angle selection

In an NLS fitting problem, the covariance matrix of the parameters for estimation (in this case, M₀ and T₁) is given by the inverse of the Hessian matrix multiplied by the unknown noise variance, as described above. Therefore, assuming a constant noise variance σ² in the voxels of interest (i.e., those representing the tissue in which T₁ will be estimated), a single term from the inverse of the Hessian can be used to estimate the variance in the T₁ estimate at each voxel, given by ${\sigma }_{T_1}^2\propto {[{\mathbf{\Sigma }}_{\gamma }]}_{22}$.

The selection of the two optimal flip angles for T₁ estimation was guided by the goal to minimize the variance in the T₁ estimate. Therefore, an objective function for flip angle selection, Ω, was defined according to the equation

$$\mathrm{\Omega }=\sum _{\mathit{\text{All}}{M}_0,T_1}{\sigma }_{T_1}^{2}P(M_0,T_1)$$ [13]

where P(M₀, T₁) is the smoothed joint probability density estimate of M₀ and T₁ over the imaging volume or region of interest. To select optimal flip angles for any imaging setting, this objective function was minimized using the user inputs of TR, number of desired flip angles (N_α), and P(M₀, T₁). While TR and N_α can be selected based on the constraints of the imaging setting and time available, P(M₀, T₁) is more complicated to provide. In this work, we pursue a data-driven approach in which P(M₀, T₁) is estimated from an initial set of T₁ and M₀ maps based on a non-optimized SPGR acquisition. For all optimized flip angle sets in this work, P(M₀, T₁) was specified using the subset of image voxels in the brain tissue.

T₁ estimation

In both simulations and analysis of experimental data, an estimate for T₁ and M₀ in each voxel was obtained using the Levenberg-Marquardt approach for non-linear least squares fitting (19) with the goal of minimizing the objective function in Eq. 6. It should be noted that the above nonlinear least squares fitting problem can also be reformulated as a simple iterative linear fitting problem (20). For experimental data, a calculated B₁ map was taken into account in the parameter estimation procedure (6). This correction was used due to the variability of the relationship between nominal and actual flip angle and the potentially significant effect thereof on T₁ estimation. Iterations were continued until the step size between successive estimates was extremely small (<10⁻¹⁵), the objective function was appropriately small (<10⁻⁶), or after 500 iterations. All image processing, simulations, and computational work was performed in MATLAB R2014b (The MathWorks, Natick, MA).

Simulations

Simulations were performed to evaluate the precision and accuracy of T₁ mapping with the flip angles selected as described above. They were also used to compare these results with those obtained using previously proposed flip angle sets and selection techniques (11, 12). Using inversion recovery data from the Quantitative MRI Analysis Package (QMAP, http://www.medphysics.wisc.edu/~samsonov/qmap/), FSL’s Brain Extraction Tool (21), and FMRIB’s Linear Image Registration Tool (22, 23), T₁ and M₀ maps in the human brain were calculated and used as ground truth. From these maps, optimal flip angles were determined as described above. For comparison of the 2-point angle set, flip angle sets were selected using Deoni and colleagues’ 2-point selection criteria based on the mean T₁ in the segmented human brain (11). For comparison of the 10-point angle set, two other flip angle sets were selected. One of these sets was based on repetition of the 2-point set described above (referred to as “10-point repeat”). The other set of angles, referred to as “10-point range,” is based on a previously proposed optimal 10-angle set for T₁ mapping in the human brain that covers a range of angles, which is a common approach to T₁ mapping with VFA SPGR (12, 24, 25). The “10-point range” set was selected in order to determine the impact of using a repetition of two carefully selected flip angles compared to a range of flip angles. The flip angle sets used in simulations are shown in Table 1.

Table 1.

Flip angle sets used in simulations and experiments of SPGR-based T₁ estimation

Optimal angle set	Human Simulation	Rat Simulation	Rat Experimental
Nα = 2	4.7°, 27.2°	3.6°, 21.7°	Not tested
Nα = 10	5×4.7°, 5×27.2°	5×3.6°, 5×21.7°	5×3.2°, 5×18.6°
Control angle set
Nα = 2	5.1°, 30.0°	4.8°, 27.1°	Not tested
Nα = 10 repeat	5×5.1°, 5×30.0°	5×4.8°, 5×27.1°	5×3.5°, 5×19.8°
Nα = 10 range	2°, 3°, 4°, 5°, 7°, 9°, 12°, 14°, 16°, 18°	2°, 3°, 4°, 5°, 7°, 9°, 12°, 14°, 16°, 18°	2°, 3°, 4°, 5°, 7°, 9°, 12°, 14°, 16°, 18°

In simulations of SPGR acquisition, the signal in each voxel was calculated according to the SPGR signal equation included in Eq. 6. Noisy MR signals were modeled to follow a Rician distribution. Noise was added according to the model $S_N=\sqrt{{(S+{\epsilon }_1)}^2+{{\epsilon }_2}^2}$, where S is the signal magnitude and ε₁ and ε₂ are random values from a normal distribution of mean zero and standard deviation dependent upon S and user-defined signal-to-noise ratio (SNR). Noisy signals were calculated in 500 realizations, and T₁ and M₀ were estimated as described above. Results were used to calculate the bias and variance of the SPGR-based T₁ estimates. The relative performance of optimal flip angles compared to other flip angle sets was measuring at 6 SNR values ranging from 5 to 40. Simulations were similarly performed using IR-based T₁ and M₀ maps in the ex vivo rat brain as the ground truth, using the flip angle sets shown in Table 1.

MR imaging

Imaging experiments were performed on a 4.7T small animal scanner (MRBR 4.7T/310, Agilent Technologies, Santa Clara, CA) with a quadrature volume RF coil for signal transmission and reception. An ex vivo rat brain was scanned because it has a continuous distribution of T₁ and M₀ values, as would be expected in a human subject. A 3D SPGR pulse sequence was performed using three individual flip angle sets, shown in Table 1. Each flip angle set was repeated three times to measure experimental variance in T₁ estimates. To minimize scan time and maximize the MR signal collected, the TR and TE were minimized and had values of 9.08 ms and 3.81 ms, respectively. Other scan parameters were as follows: matrix size = 128 × 128 × 128, slab size = 30 mm × 20 mm × 20 mm, total scan time = 2 min 31 s per FA. (For clarity, in experiments with more than one acquisition at each FA, each acquisition is referred to as an individual FA rather than an additional average.) A flip angle map was acquired using an actual flip-angle imaging SPGR scan with scan parameters as follows: TR1/TR2 = 5.9/29.5 ms, TE = 2.22 ms, α = 55°, matrix size = 64 × 64 × 64 (6).

To calculate a T₁ map in the ex vivo rat brain for simulations, an IR acquisition was used. A set of 2D spin-echo scans was acquired at a range of 8 inversion times between 8 and 4000 ms. Other scan parameters were held constant and were as follows: TR = 6 s, TE = 13.82 ms, NEX = 4, matrix size = 128 × 128, in-plane FOV = 20 × 20 mm, with 50 slices of 0.5 mm thickness.

Results

Selection of optimal flip angles

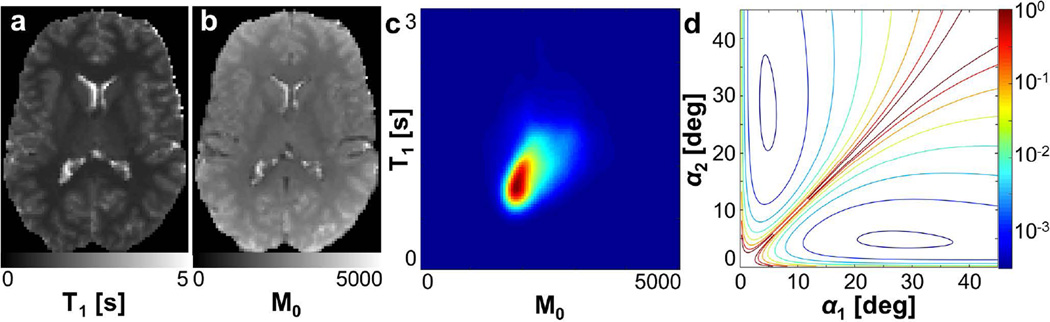
It was found that the optimal flip angles for minimizing T₁ variance were, as expected, dependent upon the joint T₁ and M₀ distribution in the region of interest. Using the proposed flip angle selection approach, any number of optimal flip angles specific to reducing T₁ variance in the ROI used to define P(M₀, T₁) could be determined. A representative set of parameter maps used for input to the flip angle selection algorithm is shown in Figure 1a–b. These maps were estimated from an open-source inversion recovery data set (QMAP). The resulting smoothed joint density function of T₁ and M₀ in the human brain is shown in Figure 1c. Finally, the objective function for selection of two flip angles is plotted in Figure 1d, and agrees well with the expected shape shown in previous works addressing selection of 2-angle sets (9–11, 14). In the limit of a single T₁ value in the region used to define P(M₀, T₁), the proposed flip angle selection approach resulted in the same two recommended angles as the approach proposed by Deoni and colleagues (11).

FIG. 1.

Representative input to flip angle selection algorithm. Initial estimates of (a) T₁ map and (b) M₀ map in the human brain based on an inversion recovery data set. (c) Joint density distribution of T₁ and M₀ based on the maps in (a) and (b). (d) Flip angle minimization objective function, shown here for 2 flip angle selection for the purposes of visualization.

For even-numbered flip angle sets greater than two, it was found that the optimal flip angle sets were repetitions of the pair of two optimal flip angles. For odd-numbered flip angle sets greater than two, it was found that the optimal flip angle sets were repetitions of two angles. Interestingly, the specific angles varied based on the number of flip angles. Table 2 shows the specific flip angle sets selected for different set sizes using the human brain to define the smoothed joint density of T₁ and M₀ as algorithm input. It is important to note that, particularly for selection of an odd number of flip angles, local minima were present in the objective function landscape. In these cases, optimal angles were selected based on inputting several different initial points for the minimum search and selecting optimal angles that corresponded to the minimum of the objective function that was found. For odd-numbered angle sets, two local minima with the same objective function values were found (see Table 2). Generally, the angle selection algorithm selected erroneous local minima in the case of an unreasonable search input.

Table 2.

Representative optimal flip angle sets with varying flip angle set sizes. From this list, even-numbered sets were used in human simulations. Odd-numbered sets are included to illustrate typical results of the flip angle selection algorithm.

Flip angle set size	α1	α2	α3	α4	α5	α6	α7	α8	α9	α10
2	4.7°	27.2°
3	4.9°	28.9°	28.9°
3	4.0°	4.0°	24.1°
4	4.7°	4.7°	27.2°	27.2°
5	4.7°	4.7°	27.7°	27.7°	27.7°
5	4.2°	4.2°	4.2°	24.9°	24.9°
6	4.7°	4.7°	4.7°	27.2°	27.2°	27.2°
8	4.7°	4.7°	4.7°	4.7°	27.2°	27.2°	27.2°	27.2°
10	4.7°	4.7°	4.7°	4.7°	4.7°	27.2°	27.2°	27.2°	27.2°	27.2°

Simulations

To test the effect of using the proposed angle sets on the variance and bias in T₁ estimates, simulations were performed using IR-based T₁ and M₀ maps of a human brain and an ex vivo rat brain as digital phantoms. These parameter maps were also used as input to the angle selection algorithm for definition of P(M₀, T₁). Simulation results were used to calculate the bias, variance, and root mean squared error (RMSE) of the SPGR-based T₁ estimate.

In human simulations using 2-angle estimates, it was found that optimized angles had very slightly improved performance compared to Deoni angles and greatly improved performance compared to arbitrarily selected angles. The improvement in performance at all SNR values, with the exception of SNR = 30, was measured by a RMSE reduction of 0.40 – 3.10%. The percent reduction in RMSE was greater at lower SNR values, indicating that the proposed method resulted in improved performance particularly for low SNR settings. In simulations using 10-angle acquisitions for T₁ estimation, it was found that optimized angles had improved performance compared to the 10-point range set (Fig. 2). This improvement was measured by a reduction in T₁ estimate RMSE of 42% at all SNR values. However, optimal angles had nearly identical performance to the 10-point repeat set, again with relative performance independent of SNR. The RMSE in human brain T₁ estimates calculated for all SNR values and angle sets are shown in Table 3.

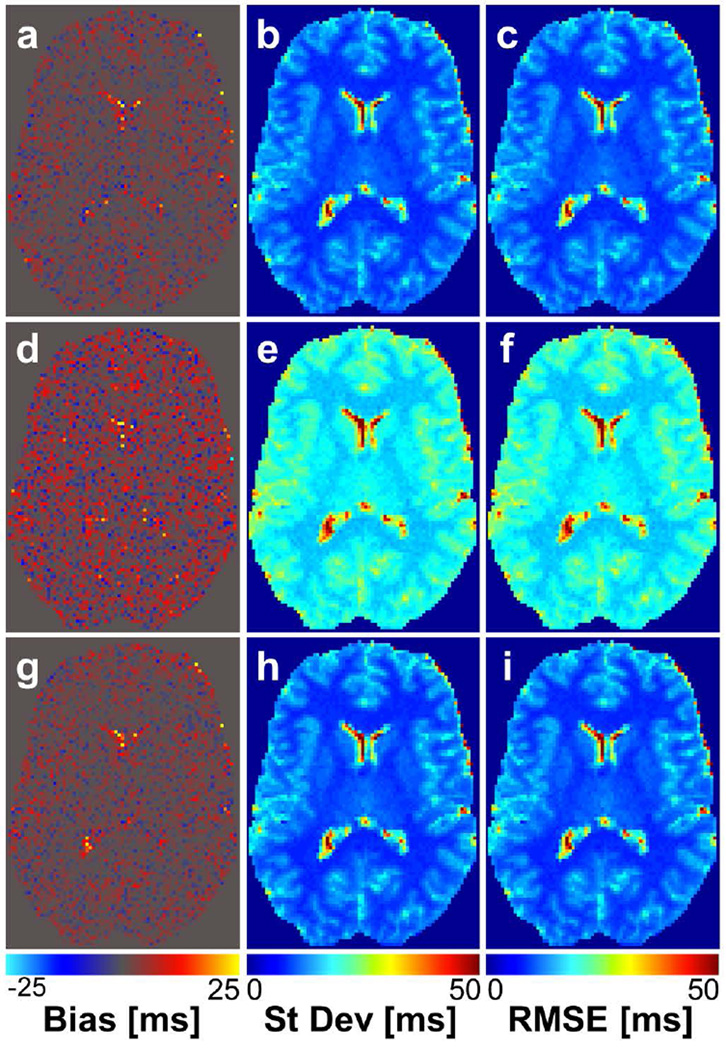
FIG. 2.

T₁ bias (a, d, g), standard deviation (b, e, h), and RMSE (c, f, i) maps based on simulations of T₁ mapping in the human brain using 10-angle acquisitions at SNR = 20. a–c correspond to simulation results using the 10 angles selected with our proposed method; d–f correspond to results using the 10-point range angle set; g–i correspond to results using a the 10-point repeat set. All measurements are in units of ms.

Table 3.

Results of simulations in the human brain. The RMSE in T₁ estimates (units of s) are given for each angle set and SNR. RMSE % change is in comparison to optimal angle set for that same number of flip angles.

	Nα = 2			Nα = 10
SNR	Optimal angle set	Control angle set		Optimal angle set	10-point repeat		10-point range
	RMSE	RMSE	% change	RMSE	RMSE	% change	RMSE	% change
5	5.94E-1	6.13E-1	+3.20	2.15E-1	2.17E-1	+0.93	3.74E-1	+74.0
10	2.50E-1	2.51E-1	+0.40	1.07E-1	1.07E-1	--	1.87E-1	+74.8
15	1.62E-1	1.63E-1	+0.62	7.13E-2	7.13E-2	--	1.24E-1	+73.9
20	1.21E-1	1.21E-1	--	5.36E-2	5.36E-2	--	9.33E-2	+74.1
30	8.02E-2	8.00E-2	−0.25	3.57E-2	3.57E-2	--	6.21E-2	+73.9
40	6.00E-2	6.00E-2	--	2.68E-2	2.68E-2	--	4.66E-2	+73.9

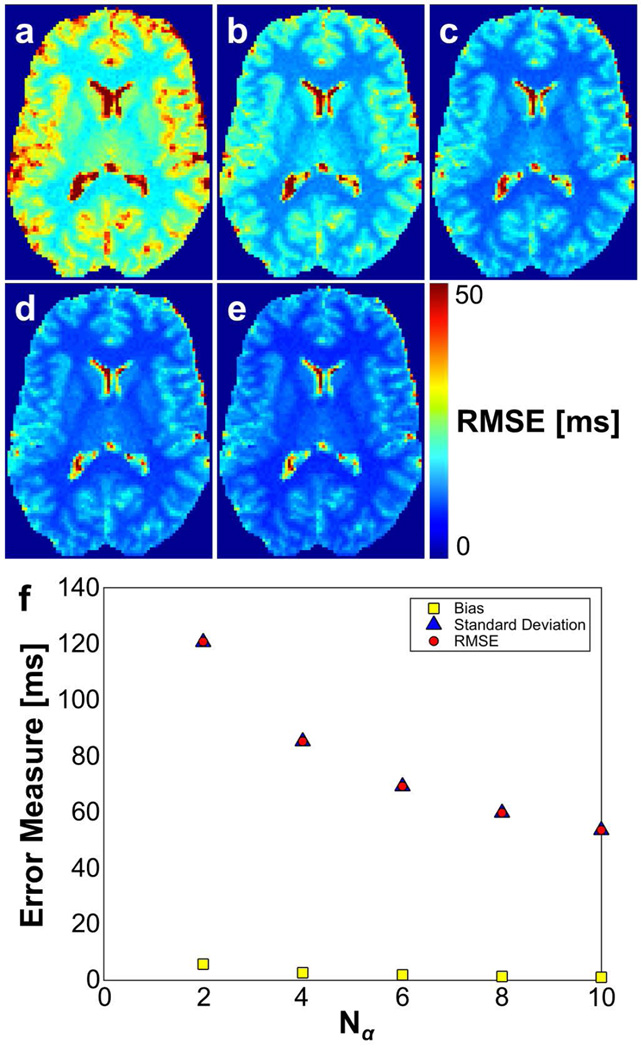
Simulations were also used to compare the relative performance of 2-, 4-, 6-, 8-, and 10-point optimal angle acquisitions for T₁ estimation (angle sets listed in Table 2). As shown in Figure 3, increasing the number of flip angles used for acquisition reduces the RMSE in the T₁ estimate primarily by reducing variance. It should be noted that this is equivalent to increasing the number of averages at 2 optimal flip angles. Variance was the primary contributor to RMSE, as evidenced by estimate standard deviation ranging from 20–50 times greater than estimate bias at the range of SNR used in these simulations (Table 4).

FIG. 3.

(a–e) RMSE in T₁ estimates from simulations of 2, 4, 6, 8, and 10-angle SPGR acquisitions, respectively. (f) Bias, standard deviation, and RMSE in T₁ estimates plotted versus number of acquisition flip angles. The estimate variance is the primary contributor to error in the T₁ estimate. All measurements are in units of ms.

Table 4.

Effect of number of flip angles on bias, standard deviation, and RMSE of resulting T₁ estimates (all measures in units of s). Results are based on simulations in the human brain with an SNR of 20 and using flip angle sets listed in Table 2. Percent change in RMSE is compared to that of the N_α = 2 estimate.

	Nα = 2	Nα = 4	Nα = 6	Nα = 8	Nα = 10
Bias	5.77E-3	2.75E-3	1.92E-3	1.39E-3	1.13E-3
Standard Deviation	1.21E-1	8.52E-2	6.92E-2	5.98E-2	5.36E-2
RMSE	1.21E-1	8.52E-2	6.92E-2	5.98E-2	5.36E-2
RMSE % change		−29.4	−42.7	−50.5	−55.6

In 2-point ex vivo rat brain simulations, it was found that optimized angles only slightly improved performance (RMSE reduction of 2.37%) at the lowest SNR value. At higher SNR values, Deoni angles out-performed optimized angles, with an RMSE reduction of 2.22 – 3.05%. These results confirm the finding in human simulations that our angle selection method performs most strongly in low-SNR scenarios. For 10-angle estimates, it was found that optimized angles had improved performance compared to the 10-point range angle set, reflected in an RMSE reduction of approximately 38% at all SNR values. Compared to the 10-point repeat angle set, optimized angles had slightly worse performance, independent of SNR. Simulation results in the ex vivo rat brain are shown in Table 5.

Table 5.

Results of simulations in the rat brain. The RMSE in T₁ estimates (units of s) are given for each angle set and SNR. RMSE % change is in comparison to optimal angle set for that same number of flip angles.

	Nα = 2			Nα = 10
SNR	Optimal angle set	Control angle set		Optimal angle set	10-point repeat		10-point range
	RMSE	RMSE	% change	RMSE	RMSE	% change	RMSE	% change
5	1.93E-1	1.98E-1	+2.59	7.31E-2	7.16E-2	−2.05	1.20E-1	+64.2
10	8.47E-2	8.29E-2	−2.13	3.66E-2	3.56E-2	−2.73	5.94E-2	+62.3
15	5.54E-2	5.40E-2	−2.53	2.44E-2	2.37E-2	−2.87	3.96E-2	+62.3
20	4.13E-2	4.01E-2	−2.91	1.83E-2	1.77E-2	−3.28	2.97E-2	+62.3
30	2.74E-2	2.66E-2	−2.92	1.22E-2	1.18E-2	−3.28	1.99E-2	+63.1
40	2.05E-2	1.99E-2	−2.93	9.14E-3	8.87E-3	−2.95	1.49E-2	+63.0

Experimental T₁ mapping

To test the impact of implementing optimal angles in an experimental scanning scenario, an ex vivo rat brain was scanned first using the 10-point range angle set. The resulting estimated T₁ and M₀ maps were used to define P(M₀, T₁) in the rat brain, and from this, optimal angle sets and control angle sets were selected (Table 1). The rat brain was then scanned again using these data-driven angle sets. To observe the effect of acquisition flip angles on the variance of T₁ estimates, scan protocols for T₁ mapping were repeated three times in order to calculate the experimental variance in the T₁ estimate. T₁ standard deviation maps for the three angle sets used 10-point range, optimal 10-point, and 10-point repeat) are shown in Fig. 4a–c.

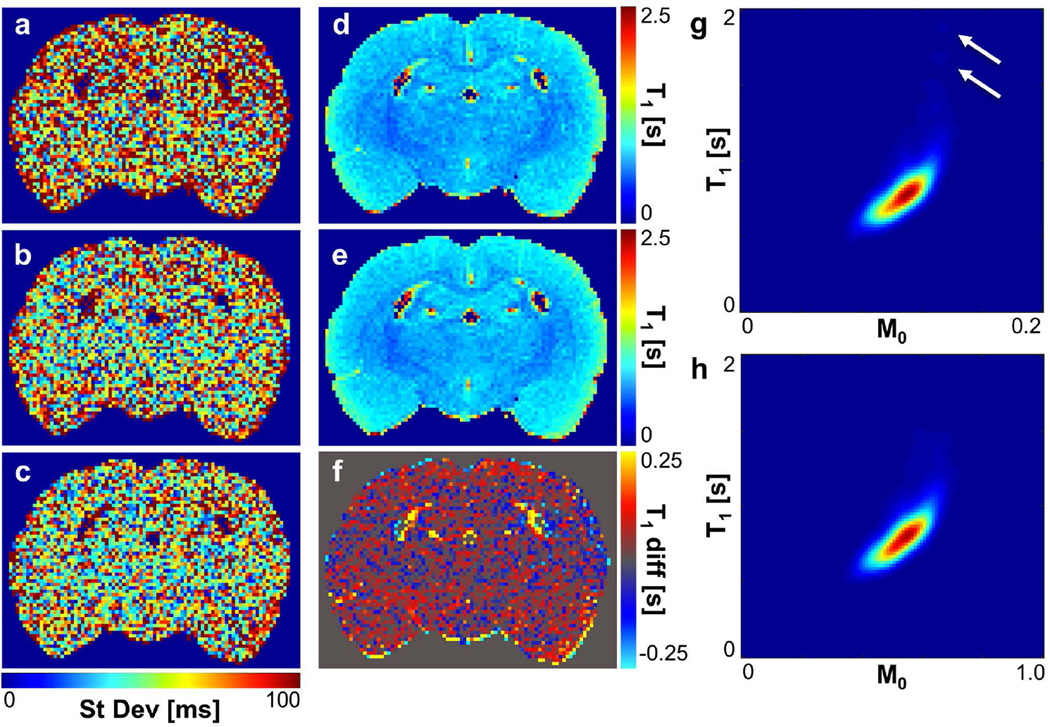
FIG. 4.

Maps of inter-scan standard deviation in T₁ show reduced variation when the 10-point optimal angle set (b) or 10-point repeat angle set (c) is used compared to the 10-point range angle set (a). See Table 1 for specific angle sets used for acquisition. T₁ maps of the rat brain (c) prior to flip angle optimization and (d) after flip angle optimization 10-point optimal angle set) show an increase in the average T₁ estimate in the rat brain by 15.8 ms, more easily observable in (e) the T₁ difference map (difference = optimal – 10-point range). Smoothed joint density functions of T₁ and M₀ (f) prior to and (g) following flip angle optimization also show this slight shift, along with the elimination of a small population of voxels with high initial T₁ estimates (T₁ > 1.5 s, white arrows). (T₁ map, difference map, and P(T₁, M₀) are not shown for the 10-point repeat angle set because results are nearly identical to those for the 10-point optimal angle set under visual inspection.)

The mean inter-scan standard deviation in the T₁ estimate was measured to be 73.3 ms when data were acquired using the 10-point range angle set. This standard deviation decreased to 61.2 ms when using the optimal flip angle set (N_α = 10). Interestingly, a slight additional decrease in inter-scan standard deviation, to 59.0 ms, was observed when data were acquired with the 10-point repeat angle set based on Deoni and colleagues’ criteria for selection of two flip angles (11). Therefore, use of flip angle sets in which two carefully selected flip angles were each repeated 5 times reduced inter-scan T₁ estimate standard deviation in the rat brain by 16–20% when compared with the 10-point range angle set (variance reduction of 30–35%). Notably, the angle sets composed of a repeat of two angles selected using Deoni and colleagues’ criteria out-performed those selected using our variance minimization objective function in terms of inter-scan variance reduction.

T₁ mapping results showed that T₁ estimates in the rat brain were, on average, 15.8 ms higher when estimated using the optimized flip angles rather than the range of flip angles (P < 0.0001). When estimated using the 10-angle repeat set, T₁ estimates were, on average, 24.3 ms higher than the range of flip angles (P < 0.0001). The difference of 8.5 ms between the 10 optimal angles and 10 angle repeat set was also found to be significant (P < 0.0001). Estimation of the smoothed joint density function of T₁ and M₀ from pre- and post-optimization acquisitions (Fig. 4d–e) also showed a slight shift of the mean T₁ estimate in the rat brain toward higher T₁ values when optimized angles were used. Elimination of a small population of voxels with high, outlying T₁ estimates (T₁ > 1.5 s) was also observed.

Discussion and Conclusions

In this work, we have proposed and evaluated a new data-driven method for selection of SPGR flip angles for T₁ estimation. In the proposed angle selection method, we aimed to provide increased flexibility compared to previously developed approaches. This flexibility is particularly designed (1) to select any number of acquisition flip angles based on available scan time and (2) to select flip angles when the T₁ distribution of interest is non-Gaussian and is therefore not well-described by the mean of the distribution.

In selecting multi-point optimal flip angle sets in two settings, the human brain and the rat brain, we found that the optimal flip angle set consisted of the repetition of two optimal angles. This is in disagreement with the common practice of acquiring data at a range of flip angles to cover a wide range of the SPGR signal curve (12, 24, 25). Instead, it more strongly agrees with Deoni and colleagues’ 2-point angle selection method, which maximizes the product of the dynamic range and the fractional signal of the acquired data (11, 18). It is also in agreement with a previous study confirming improved T₁ mapping performance when using a small set of carefully selected flip angles over a larger set covering a range of angles (13).

Simulations testing these optimized angle sets showed very similar RMSE performance when comparing two optimized angles to two angles selected with Deoni and colleagues’ criteria. For greater than two angles, simulations also show that a repetition of two carefully selected flip angles has significantly improved performance compared to using a range of angles. However, our simulations assumed perfect RF coil performance in which nominal and actual flip angle match exactly. In a true scanning scenario, the relationship between of nominal and actual flip angle can vary greatly, and system-specific RF performance should be considered when optimizing scan protocol (13). This could be achieved by scaling the optimal flip angles according to the expected RF performance or by adjusting flip angle sets to cover a small range close to the optimal angles within the expected range of flip angle variation.

Simulations further elucidated the relative performance of different flip angle sets with respect to both bias and variance. As shown in Figure 3f, variance contributed relatively much more (20–50×) than bias to the RMSE of the T₁ estimate. This supports the work in our group and others in which flip angle selection is guided by an objective of T₁ variance minimization. When studying the effect of using optimal flip angles experimentally, we indeed found that T₁ variance was reduced by 30% when compared to T₁ estimated from SPGR acquisitions at a range of angles. These simulations also agreed with previous work showing that T₁ estimates from VFA SPGR acquisitions tend to have positive bias when compared with the gold standard IR-based estimation approach (4).

Experimental measurement of inter-scan variance using three different 10-point acquisition angle sets showed that the use of a repetition of two thoughtfully selected flip angles indeed reduced estimate variability when compared to an acquisition using a more broad range of angles. The out-performance of our proposed optimal flip angle set in comparison to the 10-point repeat angle set could be due to imperfect RF performance, which in our scans caused actual flip angles to be approximately 80% of the nominal prescribed flip angles. This reduction would cause the two angles in the 10-point repeat set to be closer in magnitude to the intended optimal angles. The effects of this imperfect RF performance on the variability in T₁ estimates further emphasizes that it is an important consideration in the design of SPGR-based T₁ mapping experiments.

Based on these simulation and experimental results, the application of this flip angle selection technique to T₁ mapping in research and clinical settings could notably reduce variance in T₁ estimates if used in place of a set consisting of a range of flip angles. However, in many situations, the implementation of such an algorithm may be excessively complicated to incorporate into experimental design. In the imaging settings similar to those presented in this paper, in which T₁ distributions approach a Gaussian shape, we suggest that it would be as effective and much simpler to use Deoni and colleagues’ criteria for selection of two flip angles based on the mean T₁ in the volume of interest. If time allows for additional data collection or increased SNR is desired, these two angles should be repeated (multiple averages collected at each flip angle) as necessary. It should be noted, however, that the use of just two repeated flip angles might not be appropriate in some scenarios. When more than one T₁ component is present in a voxel, deviation from the SPGR signal equation cannot be identified unless a flip angle set containing more than two unique points is used. Researchers interested in detecting the presence of multiple T₁ times in individual voxels may find it useful and necessary to incorporate additional acquisition angles in addition to the two optimal angles for T₁ variance minimization.

Future extensions of this work will evaluate the performance of our proposed angle selection in situations with more distinctly non-Gaussian T₁ distributions. In this way, we hope to determine whether there are situations in which this more simplified angle selection approach using Deoni and colleagues’ set of criteria is not appropriate. Furthermore, more specific definition of P(M₀, T₁) based on the tissue of interest may be appropriate in some research and clinical settings. For example, specific flip angles could be selected for T₁ mapping in the white matter in the study of myelin-related disease by using only segmented white matter voxels to define P(M₀, T₁).

In conclusion, this work demonstrates that the precision of T₁ estimates from SPGR acquisitions can be improved by using flip angles selected based on minimization of the T₁ variance weighted by the smoothed joint density of T₁ and M₀. Specifically, our proposed approach significantly out-performed T₁ estimation using a range of flip angles when the same total number of flip angles were used. Interestingly, when comparing the proposed angle selection method with previously proposed selection criteria, we found that Deoni and colleagues’ 2-angle selection criteria can also be effectively used to determine the two angles to be repeated for a multi-point acquisition with nearly identically improved performance (11). The proposed flip angle selection approach resulted in either equivalent or up to 42% reduced RMSE compared to other flip angle selection criteria in simulations. Experimentally, implementation of optimal angles reduced inter-scan variability in T₁ estimates by 30%. The application of this data-driven technique for optimal flip angle selection has applications in clinical and research settings where scans are performed repeatedly in the same anatomical region (e.g., the human brain) or on the same equipment (consistent scanner and coil).

Appendix A

From Eq. 7–8, the Jacobian matrix can be written as

$${\mathit{J}}_{\gamma }(\mathit{r})=\left[\begin{array}{cc}\hfill \raisebox{1ex}{$\partial r_1$}\!\left/ \!\raisebox{-1ex}{$\partial {\gamma }_1$}\right.\hfill & \hfill \raisebox{1ex}{$\partial r_1$}\!\left/ \!\raisebox{-1ex}{$\partial {\gamma }_2$}\right.\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \raisebox{1ex}{$\partial r_n$}\!\left/ \!\raisebox{-1ex}{$\partial {\gamma }_1$}\right.\hfill & \hfill \raisebox{1ex}{$\partial r_n$}\!\left/ \!\raisebox{-1ex}{$\partial {\gamma }_2$}\right.\hfill \end{array}\right]$$

where $\raisebox{1ex}{$\partial r_i$}\!\left/ \!\raisebox{-1ex}{$\partial {\gamma }_1$}\right.\equiv \raisebox{1ex}{$\partial r_i$}\!\left/ \!\raisebox{-1ex}{$\partial M_0$}\right.$ and $\raisebox{1ex}{$\partial r_i$}\!\left/ \!\raisebox{-1ex}{$\partial {\gamma }_2$}\right.\equiv \raisebox{1ex}{$\partial r_i$}\!\left/ \!\raisebox{-1ex}{$\partial T_1$}\right.$. Therefore,

$${\mathit{J}}_{\gamma }^T(\mathit{r}){\mathit{J}}_{\gamma }(\mathit{r})=\left[\begin{array}{cc}\hfill \sum _{i=1}^n{(\partial r_i/\partial {\gamma }_1)}^2\hfill & \hfill \sum _{i=1}^n(\partial r_i/\partial {\gamma }_1)(\partial r_i/\partial {\gamma }_2)\hfill \\ \hfill \sum _{i=1}^n(\partial r_i/\partial {\gamma }_1)(\partial r_i/\partial {\gamma }_2)\hfill & \hfill \sum _{i=1}^n{(\partial r_i/\partial {\gamma }_2)}^2\hfill \end{array}\right]$$

By defining E = exp(TR/T₁), Eq. 7–8 can be rewritten as follows:

$$\frac{\partial r_i}{\partial {\gamma }_1}=\frac{(1-E)\text{sin}({\alpha }_i)}{E-\text{cos}({\alpha }_i)}$$

and

$$\frac{\partial r_i}{\partial {\gamma }_2}=\frac{M_0·TR·E(1-\text{cos}({\alpha }_i))\text{sin}({\alpha }_i)}{T_1^2{(E-\text{cos}({\alpha }_i))}^2}$$

so that

$${\left(\frac{\partial r_i}{\partial {\gamma }_1}\right)}^2=\frac{{(1-E)}^2{\text{sin}}^2({\alpha }_i)}{{(E-\text{cos}({\alpha }_i))}^2}$$

$${\left(\frac{\partial r_i}{\partial {\gamma }_2}\right)}^2=\frac{M_0^{2}T{R}^2{E}^2{(1-\text{cos}({\alpha }_i))}^2{\text{sin}}^2({\alpha }_i)}{T_1^4{(E-\text{cos}({\alpha }_i))}^4}$$

and

$$\left(\frac{\partial r_i}{\partial {\gamma }_1}\right)\left(\frac{\partial r_i}{\partial {\gamma }_2}\right)=\frac{M_0·TR·E(1-E)(1-\text{cos}({\alpha }_i)){\text{sin}}^2({\alpha }_i)}{T_1^2{(E-\text{cos}({\alpha }_i))}^3}$$

The determinant of ${\mathit{J}}_{\gamma }^{\mathit{T}}(\mathit{r}){\mathit{J}}_{\gamma }(\mathit{r})$ can then be written as a double summation:

$$\text{det}({\mathit{J}}_{\gamma }^{\mathit{T}}(\mathit{r}){\mathit{J}}_{\gamma }(\mathit{r}))=\left(\sum _{i=1}^n{(\partial r_i/\partial {\gamma }_1)}^2\right)\left(\sum _{i=1}^n{(\partial r_i/\partial {\gamma }_2)}^2\right)-(\sum _{i=1}^n(\partial r_i/\partial {\gamma }_1)(\partial r_i/\partial {\gamma }_2))(\sum _{i=1}^n(\partial r_i/\partial {\gamma }_1)(\partial r_i/\partial {\gamma }_2))=\sum _{i=1}^n\sum _{j=1}^n{(\partial r_i/\partial {\gamma }_1)}^2{(\partial r_j/\partial {\gamma }_2)}^2-(\partial r_i/\partial {\gamma }_1)(\partial r_i/\partial {\gamma }_2)(\partial r_j/\partial {\gamma }_1)(\partial r_j/\partial {\gamma }_2)=\frac{M_0^{2}T{R}^2{E}^2{(1-E)}^2}{T_1^4}\sum _{i=1}^n\sum _{j=1}^n(\frac{{\text{sin}}^2({\alpha }_i){\text{sin}}^2({\alpha }_j){(1-\text{cos}({\alpha }_j))}^2}{{(E-\text{cos}({\alpha }_j))}^4{(E-\text{cos}({\alpha }_i))}^2}-\frac{{\text{sin}}^2({\alpha }_i){\text{sin}}^2({\alpha }_j)(1-\text{cos}({\alpha }_i))(1-\text{cos}({\alpha }_j))}{{(E-\text{cos}({\alpha }_j))}^3{(E-\text{cos}({\alpha }_i))}^3})=\frac{M_0^{2}T{R}^2{E}^2{(1-E)}^2}{T_1^4}\sum _{i=1}^n\sum _{j=1}^n\frac{{\text{sin}}^2({\alpha }_i){\text{sin}}^2({\alpha }_j)(1-\text{cos}({\alpha }_j))}{{(E-\text{cos}({\alpha }_j))}^4{(E-\text{cos}({\alpha }_i))}^3}\{(1-\text{cos}({\alpha }_j))(E-\text{cos}({\alpha }_i))-(E-\text{cos}({\alpha }_j))(1-\text{cos}({\alpha }_i))\}=\frac{M_0^{2}T{R}^2{E}^2{(1-E)}^2}{T_1^4}\sum _{i=1}^n\sum _{j=1}^n\frac{{\text{sin}}^2({\alpha }_i){\text{sin}}^2({\alpha }_j)(1-\text{cos}({\alpha }_j))}{{(E-\text{cos}({\alpha }_j))}^4{(E-\text{cos}({\alpha }_i))}^3}\{(1-E)(\text{cos}({\alpha }_j)-\text{cos}({\alpha }_i))\}=\frac{M_0^{2}T{R}^2{E}^2{(1-E)}^3}{T_1^4}\sum _{i=1}^n\sum _{j=1}^n\frac{{\text{sin}}^2({\alpha }_i){\text{sin}}^2({\alpha }_j)(1-\text{cos}({\alpha }_j))(\text{cos}({\alpha }_j)-\text{cos}({\alpha }_i))}{{(E-\text{cos}({\alpha }_j))}^4{(E-\text{cos}({\alpha }_i))}^3}$$

Once the determinant of ${\mathit{J}}_{\gamma }^{\mathit{T}}(\mathit{r}){\mathit{J}}_{\gamma }(\mathit{r})$ is obtained, the covariance matrix can be computed quite easily; therefore, the derivation will not be shown here.