Abstract
Statistical shape analysis has been an important area of research with applications in biology, anatomy, neuroscience, agriculture, paleontology, etc. Unfortunately, the proposed methods are rarely quantitatively evaluated, and as shown in recent studies, when they are evaluated, significant discrepancies exist in their outputs. In this work, we concentrate on the problem of finding the consistent location of deformation between two population of shapes. We propose a new shape analysis algorithm along with a framework to perform a quantitative evaluation of its performance. Specifically, the algorithm constructs a Signed Poisson Map (SPoM) by solving two Poisson equations on the volumetric shapes of arbitrary topology, and statistical analysis is then carried out on the SPoMs. The method is quantitatively evaluated on synthetic shapes and applied on real shape data sets in brain structures.
Keywords: Statistical shape analysis, Quantitative evaluation, Poisson equation, Reproducibility
1. Introduction
Statistical shape analysis is an actively studied topic with several proposed algorithms, see [32, 58, 20, 6, 1, 53, 35, 42, 41, 23, 25, 29] and references therein. They find wide application areas including biology [62], neuroscience [44], agriculture [9], and paleontology [49]. However, to the best of our knowledge, there have been few quantitative evaluations of these methods, and when they are evaluated significant discrepancies exist between the state-of-the-art techniques [19]. This poses an urgent need for not only new, but also validated algorithms.
In this paper, we concentrate on the problem of finding local shape differences (e.g. local thinning) between two populations of shapes that are hypothesized to have subtle differences (e.g. shape differences of the hippocampus between the brain of schizophrenics and their normal controls). Before presenting the proposed framework, we briefly review several existing shape analysis methods representative of the current state of the art.
1.1. Related work
Group analysis of shapes relies primarily on two components. First, an appropriate representation and correspondence between shapes need to be established so that they can be compared. Equivalently, this step converts all the geometric objects to a common domain. Second, statistical tests can be performed between shapes or groups of shapes within this common domain, leading to the potential detection of local shape differences. A few different strategies have been explored to solve these two steps, which we briefly review below.
1.1.1. Surface parametrization based methods
In the first group of methods, the shapes are analyzed through an explicit surface parametrization process. Specifically, the original shapes are represented as functions on simple domains such as the two-sphere 𝕊2. Then, functional analysis techniques are employed to process the functions into various basis functions and the coefficients are studied. For instance, the spherical harmonics (SPHARM) were used in [20, 54, 49], and a weighted-SPHARM scheme is used in [7] to alleviate the ringing effects. Moreover, the spherical wavelets are used in [37, 36, 18]. Because of the requirement that the shapes are parametrized on spherical domain, often times a topology correction step is carried out to ensure spherical topology. After that, an area-preserving, distortion-minimizing spherical mapping is computed to spherically parametrize the surfaces. Once the surface is defined as functions on the sphere, the surface correspondences are established as functions defined on the sphere, and the spherical harmonics coefficients can be computed. As a result, statistical tests are carried out at each point on the surface, resulting in a p-values map defined on the sphere, illustrating the difference between the two groups of shapes.
1.1.2. Dense mapping based methods
In this group of methods, the correspondence between surfaces is constructed by a spatial mapping. In [27, 55, 56, 14], the Large Deformation Diffeomorphic Metric Mapping (LDDMM) scheme is used for matching surfaces in which the flow field is a geodesic in a Riemannian structure of diffeomorphism. After the correspondences have been established, the discrepancies in the corresponding points on the surfaces are captured using statistical analysis tools. In addition to the mapping defined on surfaces, the LD-DMM can also be applied to Euclidean grid and volumetric representation of shapes.
Under the discrete setting, shapes have been modeled as points (particles) sets where the particles are distributed on the surfaces. In order to create the correspondence among all the shapes, authors in [8, 10] adopted several methods based on manual assignment, curve length based re-parametrization, and the minimization of the description length. An entropy based energy functional is optimized [6, 48]. The resulting particles are corresponding across the population.
In most analysis pipelines, establishing correspondence between shape is the central task. In contrast to finding the finding correspondences between surfaces, some methods register volumetric representations of shapes and analyze the resulting deformation fields [2, 1, 21, 60].
1.1.3. Other analysis methods
In all of the above methods, a common approach is that a scalar valued map is displayed on a reference shape to indicate the location of shape changes. Another group of methods does not compute such scalar field. In contrast, they provide a single value, or a low dimensional vector to describe the shapes, or the “distances” among shapes. For instance, the eigenvalues of the Laplace-Beltrami operator on the surfaces are computed to measure the shape distances [38, 46, 29, 13]. Researchers in [45] use the Gromov-Hausdorff distance for non-rigid almost isometric shapes. In addition, the mass transport distance and the LDDMM metric have also been used [39, 40, 3]. Researchers in [33] constructed a Riemannian structure for shapes and derived a distance between shapes that is invariant to rigid motion, global scaling, and reparametrization. The medial representation has also been used to describe shapes and to provide local statistics on a medial model [5, 22, 50, 43, 59, 26].
For planner shapes, other types of curve reparameterization are used in order to mitigate the difficulty in registration and correspondence construction [30]. For the purpose of shape classification and identification, authors in [30] proposed a Riemannian manifold for the space of curves and extract the geodesics on the manifold that represent the smooth deformation between curves. In 3D, however, such a reparameterization approach would have to consider the 3D invariance as well as the choice of different surface curvatures.
Another related area is the learning of shapes. Essentially, a low dimensional space is constructed from a group of shapes for the purpose of capturing different modes of variations of the shape [8, 10, 34]. The main purpose if to build a model for the shapes and measure the representation capability of the model for new and possible unseen shapes in the same category. Though related, the purpose of these algorithms are different from the present study in that they do not detect the localized/regional shape different between two groups of shapes. On the other hand, the relationship between this area of study and the present one is that the shape correspondence plays important roles in both areas, and authors in [10] used a set of simple shapes where the landmarks are easily identifiable, and use them to test the shape learning capability. Three global measurements are proposed to characterize the representation power of the learned more. In 3D, however, no such evaluation is performed. Indeed, in 3D, manual marking of landmarks are not simply tedious but in fact not feasible when large set of testing is performed. Secondly and possibly more importantly, when handling the real anatomical shapes, the determination of the “ground-truth landmarks” are not as straightforward as in 2D synthetic shapes. Addressing those two problems in a coherent framework are the two main contributions of the present study.
Moreover, in order to learn the shape model, the principal component analysis (PCA) is used in [8, 12, 10]. The number of variations is picked so that the cumulative energy exceeds a fraction of total variance. Such criteria work quite well when the shape variation contributes significantly in the L2 sense. On the other hand, when the shape variance is only a localized change, which does not have significant L2 type energy contribution, the measurement is not sensitive to capture such shape changes. The present paper is focusing on the localized shape changes. For some of the testing cases, the area that has a slight deformation only occupies less than 1% of total shape surface. In such a case, measured by fraction of total variation, such localized deformation is easy to be captured. If we set the threshold too high to capture those, then we will include statistically not significant variations, or those artifacts caused by correspondence construction.
1.2. Our contributions
Establishing correspondence between shapes lies at the core of shape analysis; unfortunately it is an ill-posed problem. As we briefly discussed above, various methods impose different constraints and/or regularizations in order to handle such a problem. In this paper we use Poisson’s equation to generate a point wise one-to-one mapping between shapes that is bijective and smoothly invertible. This property is beneficial especially for convoluted anatomical structures.
Perhaps more important than inventing yet another shape analysis algorithm, is designing a quantitative evaluation framework and validating the SPoM algorithm in a wide range of shape variation scenarios. Although existing shape analysis algorithms have found many applications, they are rarely validated with ground truth data and compared to each other in a standardized fashion. In [19], we have shown that large discrepancies exist among some of the most widely adopted shape analysis algorithms. Indeed, when faced with the task of detecting regions of shape differences between two groups, the methods tested rarely agreed on the location and extent of the differences. One limitation of [19] is that while it provides a qualitative evaluation framework, the quantitative evaluation is incomplete. As a result, a novel quantitative morphometry evaluation framework is the second contribution of the present study. We believe the objective and quantitative evaluation framework would benefit all the application areas in providing accurate and reliable results.
Following this order, first, we present a novel shape analysis method based on solving the Poisson equation in Section 2.1. We then design a quantitative evaluation framework (Section 2.2) by which the proposed and previous algorithms are quantitatively evaluated (Section 3).
2. Method
2.1. Shape analysis using signed Poisson map
In the proposed algorithm, we start with the shapes defined as binary volumes. Specifically, denote the two groups of shapes as and where ; i ∈ {A, B}, j ∈ {1, …, Ni}, and Ω ⊂ ℝ3 is a compact set. Moreover for the rigor of the subsequent discussions, we assume where Ω̊ is the interior of Ω.
Following [51, 12], we define “shape” as the quotient group of the geometric features of an object modulo the similarity transformation group. In particular, similarly to LDDMM and TBM/DBM methods, we will be focusing on detecting the localized nonlinear deformation of a shape, when compared to a “reference shape”. Therefore, in order to remove the differences among the shapes caused by their position, pose, and size differences, a joint registration is performed. In particular, we opt to use an alternating two-step un-biased registration scheme:
| (1) |
| (2) |
where F is the similarity transformation in the homogeneous representation. In the M-step, the mean shape χ is computed based on the current pose of all the shapes. Then in the R-step, all the shapes are registered to the current mean shape χ by minimizing the L2 norm between each shape and χ. After registration, the M-step is computed again, and the R-step repeats. In our experiments, the convergence of such a scheme can be achieved within less than 5 iterations and the resulting registered shapes are denoted as and and the final mean shape is denoted as χ(x).
In order to compare different geometric objects, we propose to embed them to functions defined on a common domain. To that end, for each shape , j ∈ {1, …, Ni}, a function is built by solving the Poisson equation:
| (3) |
Because of the requirement that , the image boundary and the Dirichlet boundary condition on ∂Ω has been included in the boundary condition in Equation (3). Then, another function is constructed by solving the following equation with mixed Dirichlet and Neumann boundary conditions:
| (4) |
where n is the outward normal direction of the image domain Ω. Numerically, the second order implicit scheme is used for solving both Poisson equations (3) and (4). Once solved, by combining them together we define the SPoM as
| (5) |
Poisson’s equation is an elliptic partial differential equation (PDE) that is used in a wide range of applications including chemical reaction, electrostatics, mechanical engineering and theoretical physics. For example, in electrostatics, it can describe the potential energy field induced by a charge density distribution [16]. The solution to this equation is a smooth function (at least C2). One of the reason that the second order Poisson equation is adopted, over the commonly used Signed Distance Map (SDM) in the level set fields, is that there are no singularities or crossings of its characteristics. This is an important feature for constructing a point-wise one-to-one correspondence between shapes without ambiguity. In a broader sense, it has been widely accepted that in general shapes live on a curved high dimensional manifold. As a consequence, when constructing the correspondence between two shapes, such a curved structure has to be respected. Then, depending on the different metric defined, different geodesic and geometric flows can be derived that morph one shape to the other, determining the correspondence between different shapes. Indeed, different metrics have been defined in various scenarios such as in [52, 24, 28, 3, 50]. In this work, due to the nature of the solution of the Poisson equation, it is guaranteed that such a trajectory is smooth and does not have crossing singularities. As a result, the trajectory between two shapes will remain in the Lie group of diffeomorphic deformation. Moreover, the computation of such a Poisson map and thus the correspondence can be solved by efficient numerical solver with great numerical stability, comparing to the methods that explicitly and iteratively compute the flow.
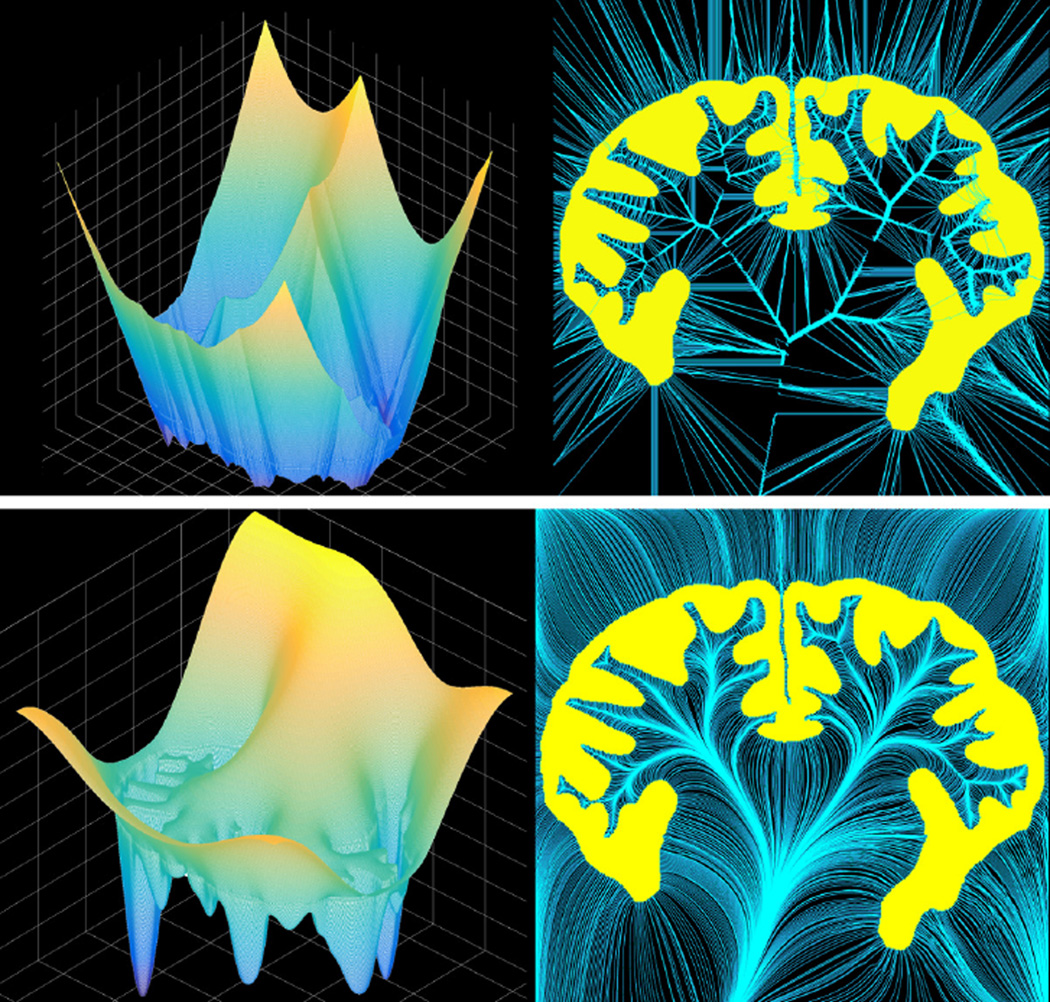
In Figure 1, a two-dimensional shape of the brain cortex (yellow region in the two right panels) is used for illustration. The top left panel shows the surface plot of the SDM and the top right panel shows its characteristic curves, in which many crossings/singularities can be observed. Since the crossings of the characteristic curves indicate ambiguity in point-wise correspondence, the morphological analysis thereafter is hampered. In contrast, as shown in the bottom row, the SPoM of the same shape is much smoother and more importantly, the characteristic curves do not cross [15]. As a result, this will induce a smooth bijection between the shapes. Indeed, the main difference lies in the utilization of second and/or higher order derivatives. The SDF only uses the first order information and generates the rough landscape which causes the non-uniqueness of the correspondence. The proposed SPoM is in fact a special case of level set method using second order PDE. Such higher order information guarantees the smoothness and bijective property, as shown in Figure 1.
Figure 1.
The SDM (top row) and the SPoM (bottom row) of the same 2D shape.
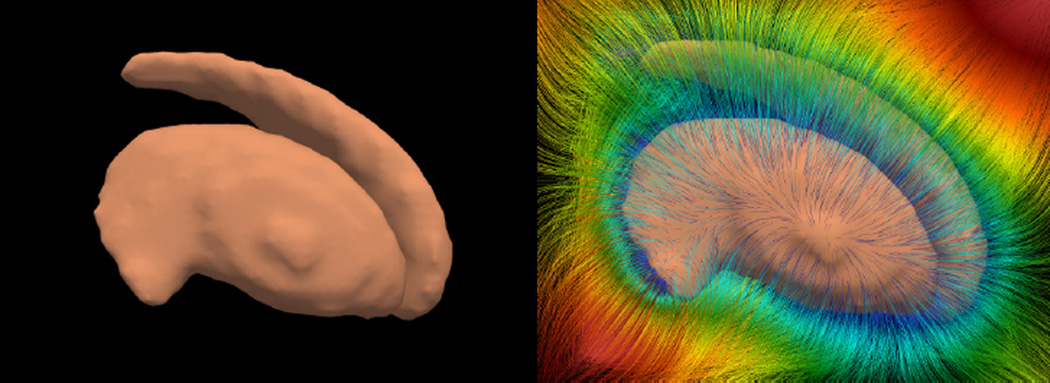
In 3D, the SPoM of the striatum (a sub-cortical structure in the left panel of Figure 2) is computed and its characteristic curves are traced out in 3D and are shown on the right. The colors on the characteristic curves render the values of the SPoM. It can be observed that with such a large number of curves, there is not crossing between them.
Figure 2.
The 3D striatum shape (left) and the characteristic curves of its SPoM. The colors on the curves indicate the SPoM values.
After such a shape-to-function embedding, one needs to find a common domain where the shape differences are going to be extracted. A natural choice would be the surface of the mean shape M = {x ∈ Ω̊ : χ(x) = 0.5}, i.e., the 0.5-isosurface of χ(x). Once such common domain is identified, a bundle is then constructed with M being the base surface for each shape . Such a bundle of curves connect the corresponding points between the mean shape surface and each of the shape being compared. Specifically, at each point x, the curve segment is defined by the differential equation as
| (6) |
| (7) |
As noted above, such a curve segment connects the point x on the mean shape to the corresponding point on the shape . As shown in Figure 1 and 2, since the characteristic curves do not cross each other, the correspondences between points are bijective [15].
The bundles having been computed, the “Poisson-distance”, , is computed by integrating along such curves segments as
| (8) |
| (9) |
Numerically, the fourth-order Runge-Kutta method is used for computing the integration. Starting from the point q̃, the numerical integration traces out the gradient flow of the Poisson field and obtains the Poisson-distance . At this point, all the shapes have been converted to scalar functions defined on the same domain M, which enables subsequent statistical analysis.
In the scenario of comparing two populations of shapes group A and group B, we can extract for each point m on M, two groups of numbers and . The sign of indicates the direction of deviation of at this point relative to the mean shape (positive means it is locally inside the mean shape and negative means outside). The absolute value of represents the magnitude of the deviation. The permutation test is then used to test the null hypothesis that the means of the groups 𝒢A (m) and 𝒢B (m) are the same at each point m. The resulting p-values gives us a p-value map defined on the mean shape surface, which is further refined by correcting the multiple comparison effect using the false discovery rate algorithm [4].
2.2. Quantitative evaluation framework
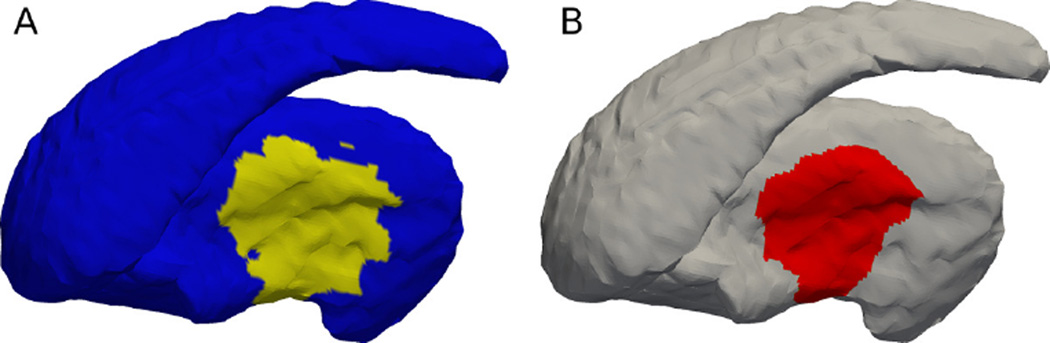
Quantitative evaluation of algorithm performance should be a de facto component of any image analysis endeavour. Unfortunately, the field of statistical shape analysis, especially the method that aims at detecting the localized significant deformed regions, is lacking thorough evaluation. Part of the problem is due to the lack of a reference standard. In addition, most methods represent their results as a p-value map displayed on a template shape (often a median/mean shape). Unfortunately, different algorithms produce different template shapes, as shown in Figure 3. The three shapes of caudate nucleus are the template (average) shapes generated by three different shape analysis methods from the same two sets of shapes. The red regions on them are respectively the detected region by three algorithms. As a result, the difficulty here is to compare two functions defined on different (though similar) domains.
Figure 3.
Different shape analysis algorithms gives different surface/domain on which the group-wise significantly different regions are shown in red. How to compare regions on different domains is one difficulty for evaluating shape analysis algorithms
Our method is inspired by a common image segmentation evaluation procedure, which measures the amount of overlap between a method’s output and a gold standard using the Dice coefficient [11]. Unfortunately, as illustrated in Figure 3, different shape analysis algorithms output their results as significant regions defined on different 3D surfaces, or even on 3D point set without topological information. The difficulty therefore lies in how to compare the “overlapping” between two regions on two different surfaces (or even point set). Towards addressing this issue, our contribution is a procedure to connect the outputs of different shape analysis methods into a common domain where an overlap measure of p-value maps can be computed.
The first problem, creating a gold standard, can be solved using synthetic shapes with known deformations as outlined in [17, 19]. In short, an arbitrary number of shapes are generated, using a manifold learning procedure based on manually traced structures. A joint labeling of the resulting shapes into consistently located sub-regions allows us to apply a known smooth deformation to a specific location in all shapes. The final output is a set of structures with an abnormality of known magnitude and location.
In order to solve the second issue, essentially, one needs to have the point-wise correspondence between average shapes. Then, the characteristic functions defined on them can be linked together and be compared. Contrasting to the original shape analysis task where the shape correspondences are constructed and then the shapes compared, here the functions defined on the shapes also have to be pulled back and compared. Indeed, this is another shape analysis problem. Consequently, one needs to evaluate an un-evaluated shape analysis algorithm with another one, and this brings the situation into a chicken-egg cycle.
To solve such a problem, the key observation lies in the fact that the mean shapes (and the functions defined on them) generated by different algorithms are derived from the same set of synthesized shapes, where the notion of deformations are available. Based on this, we leverage the consistency of the labeling of the deformed region across the entire population of shapes and pass the label of the deformed region onto the mean shape. The ground truth location of the deformed region on the template shape is therefore known and can be compared with the region outlined as statistically significant by the algorithm.
In order to facilitate the following discussion, we briefly review the basic steps of shape and deformation generation in [17, 19]. First, a set of training shapes, represented as binary images Ti : Ω → {0, 1}; i = 1, …, NT, are given. We assume these shapes have been aligned so that the differences in the rigid transformation and isotropic scaling have been removed. Second, a local linear embedding based manifold learning algorithm is adopted to model the shape manifold Ti’s reside in [47]. The manifold can then be sampled and an arbitrary number of new shapes can be generated. We denote them as Ui : Ω → [0, 1]; i ∈ ℕ and correspondingly Si ≔ {x ∈ Ω : Ui(x) = 0.5} is the surface representation of the i-th shape.
After that, a deformation can be induced at a location and magnitude that are consistent across all shapes. Intuitively, bumps/dimples with similar location, extent and magnitude are added to all the shapes. To that end, a joint clustering algorithm decomposes all the shapes (Si’s) into the same number of labeled patches where the patch with the same label occupies similar region on different shapes. Formally, each shape Si has a label map Li : Si → {1, …, NL} defined on it. NL is the total number of regions and effectively controls the scale of synthesized deformation. Larger NL corresponds to smaller area for each labeled region and smaller NL means each region is relatively large. Using such a parameter we are able to evaluate the shape analysis algorithms’ performance on the deformations at multi-scales.
Among the labels, one ld is picked (by the user) and the region having that label, ϒi ⊂ Si, will later be deformed by a user given vector γ which governs the direction and magnitude of the deformation. Since this region ϒi has a known label ld and occupies similar locations on each Ui, it is tempting to consider comparing the final significant region (defined as p-value being smaller than pc), to this region ϒi, and use the overlapping ratio as a measurement of shape analysis performance. However, it is noticed that ϒi is only a subset of the actual deformed region. The reason is explained below.
If all and only the points in ϒi move with the same constant vector γ, a sharp step will appear at the region’s boundary, between fully moved points and their static neighbors. In order to avoid such a situation and make the deformation smooth and realistic, the deformation is modulated by a smoothing field. Specifically, a spatial weighting function ωi : ℝ3 → ℝ3 is constructed as
| (10) |
After that, the ωi-modulated deformation field defined as γωi(x) is applied to the surfaces Si. The function ωi has a unit response in the region ϒi. Outside it, depending on the parameter σ, ωi gradually vanishes. (Theoretically, the Gaussian function has unbounded support. However, practically, it quickly drops below certain small threshold ε such as 10−6.)
Such a smoothing inevitably spreads the deformation into regions surrounding ϒi. In fact, the region ϒ̃i defined as ϒ̃i ≔ {x : ω(x) ≥ ε} is the final region that got deformed and apparently, ϒi ⊂ ϒ̃i. A binary function bi : Si → {0, 1} is defined as the characteristic function of ϒi. This provides the ground truth for the deformed region on each shape.
Such information (ϒi and bi) can be passed through the statistical shape analysis algorithms. Specifically, when the mean shape is generated, the bi map will be inherited onto the mean shape. Formally, this can be achieved using a distance modulated voting scheme. For a point x on the mean shape M, define the map b : M → {0, 1} as
| (11) |
| (12) |
| (13) |
| (14) |
The Euclidean distance in Equation (11) can be replaced by other more sophisticated distance such as the Poisson distance as in Equation (8). However, due to the fact that different mean shapes have smaller variances than different individual shapes, the Euclidean distance is found sufficient for such a purpose. This is also consistent with the comparison between SDM and SPoM in the experiment Section 3.
This map b indicates the location of the induced deformation on the mean shape compared to the p-value map computed by the shape analysis algorithm. Similarly to the Dice coefficient, we evaluate the the Dice-coefficient-on-surface, DCS:
| (15) |
where
| (16) |
| (17) |
This DCs is the final quantity that can be used to compare the performance of different shape analysis algorithms.
2.2.1. On the retrospective evaluation
As can be observed, this evaluation method requires the ability to project the labeling of each input shape into the template space. It is usually not an issue when evaluating one’s method, but is more difficult for retrospective evaluation of different methods where the internals of each algorithm is not necessarily available and all that is given is a template shape and a p-value map.
On the other hand, given the rich resources available of various shape analysis algorithms, it is desirable to be able to evaluate them for the purposes of, e.g., uncertainty estimation and/or serving as another opinion. To that end, facing the difficulty that it is not straightforward to modify the their source codes to add the component of passing the label as discussed above, one possibility is to use certain algorithm that has been quantitatively evaluated as above, and use its result to evaluate a retrospective algorithm/ software. Indeed, once a certain shape analysis algorithm has been evaluated in such a way and achieved the desired accuracy, one can revive the “chicken-egg cycle” and evaluate other algorithms using the validated one.
Mathematically, we assume that two different shape analysis algorithms provide two average shapes Mi, Mj ⊂ Ω, respectively. On them, the detected group-wise different regions are depicted as functions pi : Mi → [0, 1] where the region on Mi with pi < pc = 0.05 indicates that this region is statistically different between the two shape groups.
Following the above discussion, we assume that the algorithm-i has been validated and we have certain confidence in its results. However, editing algorithm-j’s source code to enable the quantitative evaluation is not straightforward. As a result, the purpose of the retrospective evaluation is to use algorithm-i to evaluate another algorithm-j. To that end, the key component is to establish the correspondence between Mi and Mj, denoted as a mapping .
In order to compute , one can use, for example, the scheme in Section 2.1 to build a Poisson map from Mi and following the characteristics of the field to map to Mj. Specifically, one can solve the equations:
| (18) |
and
| (19) |
and finally let
| (20) |
Once the SPoM of Mi is build, the correspondence between Mi and Mj can be constructed. Specifically, for any point u on Mj, the corresponding point is computed by tracing the negative gradient field of as
| (21) |
| (22) |
| (23) |
Having been constructed, the p-value map on Mj, pj can be pulled back onto Mi as . Since now the maps pi and p̃j are defined on the same surface Mi, the significant regions dictated by them can now be compared. Formally, denote the significant regions as Ri ≔ {x ∈ Mi : pi(x) < 0.05} and Rj ≔ {x ∈ Mi : p̃j(x) < 0.05}, and their overlapping can be computed similar to the regular Dice-coefficient as
| (24) |
Such a quantity can be regarded as a performance measurement of algorithm-j relative to the algorithm-i.
While such a evaluation process provide insight on the relative-performance among different shape analysis algorithms, there are some aspects that we would like to address: First, evidently, the key step is the construction of the correspondence . Above the scheme in Section 2.1 is used to build a Poisson map from Mi and the correspondence with Mj is constructed. Another simpler approach can adopt the closest distance as the criteria. That is, where y is the closest point on Mj to x ∈ Mi. Apparently, there are numerous choice for building such a and this leaves the arbitrariness for the system. Second, for new algorithm, the prospective evaluation scheme detailed in Section 2.2 directly compares the algorithm outputs with the “ground truth” generated from the shape synthesis step and therefore seems a more straightforward metric. As a result, in the experiment section below, such a “black box” approach is not used.
3. Experiments and Results
In this section, we first demonstrate the pipeline of the proposed shape analysis method and the evaluation framework in two groups of synthetic shapes (Sections 3.1 and 3.2). Then, the robustness and accuracy of the proposed SPoM based method are statistically tested against different underlying landscapes such as scales, locations, and curvatures (Sections 3.3 and 3.4). After thorough evaluations on the synthetic data sets with ground truth, the method is applied on real shape data sets in the static and longitudinal evolution of the schizophrenia patients (Sections 3.5 and 3.6).
3.1. Synthetic Caudate nucleus
In this experiment, the shape synthesizing algorithm in [19] is adopted and a total of 100 caudate shapes are generated. At the caudate head region, we generate a hypertrophy towards the ventral (downward direction in this figure) direction similar to that in [19]. Figure 4 shows six synthetic caudate shapes with their respective deformed versions. One can observe that the synthetic shapes all have realistic but different shapes. The deformations are subtle and challenging to be captured even by eye. Moreover, although their shapes differ, the deformed regions all occupy similar locations on the body.
Figure 4.
Example of benchmark caudate shapes with known deformation. Top row: examples of the synthetic left caudates. Bottom row: Corresponding deformed caudate shapes. Arrow at the bottom-left corner points to the region of synthetic hypertrophy at the caudate head. Dots in the top-right corner indicate the shapes that are used for morphometry study. That is, only one in the corresponding shape pairs is used.
The consistency in deformation locations are guaranteed by the joint clustering, which effectively associates a label with each point on the shape. Then, one label, in this case the green region at the caudate head (arrow pointed) in Figure 5(A), is chosen to deform towards the ventral direction (downward direction in this figure). This green region corresponds to the ϒi on this shape. However, in order to keep the deformation smooth and realistic, the actual deformation region is shown as the highlighted region in Figure 5(B), which corresponds to the ϒ̃i. Such a region will then be compared with the significant region detected by the shape analysis algorithm by computing the Dice-coefficient-on-surface DCS.
Figure 5.
The caudate depicts; (A). The regions generated by the clustering. The green region at the bottom side of the caudate head (arrow pointed) is the region picked to be deformed. (B). The highlighted region shows the actual deformed region ϒ̃i. This is significantly larger than the green region in (A) due to the procedure in order to keep the deformation smooth and realistic.
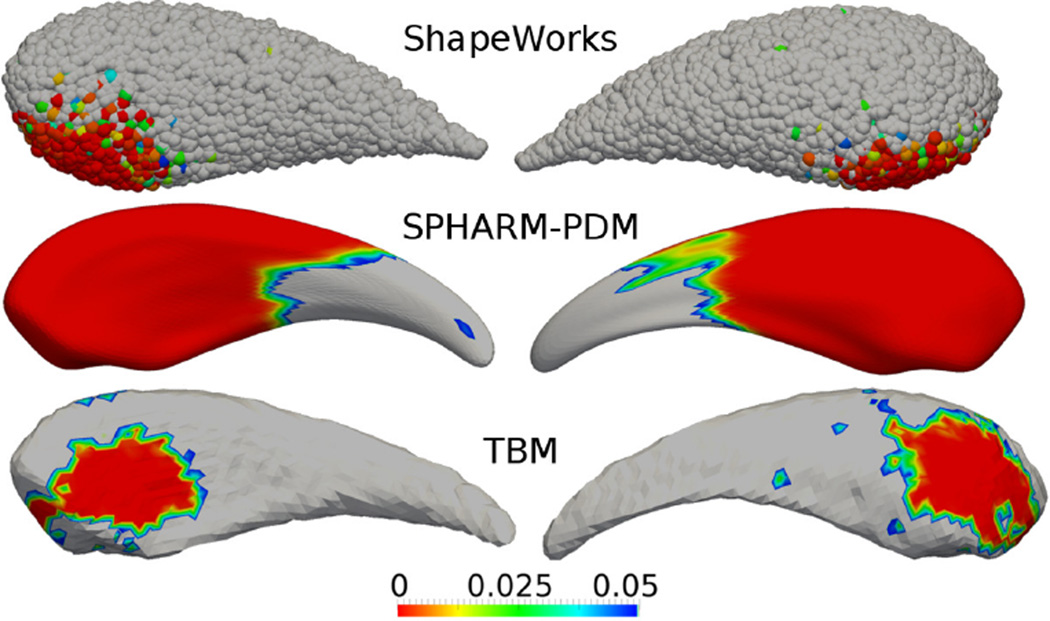
The proposed SPoM shape analysis method detects the statistically significant regions as shown in Figure 7(B). Comparing to the ground truth region in Figure 7(A) (same as 5(B) putting here for easy comparison), The matching between the two can be visually observed. As comparison, the same tests are also performed on three other methods: the point distribution method based on spherical harmonics (SPHARM-PDM) [20, 54, 49], the entropy based particle correspondence method (ShapeWorks) [6, 48], and a variant of the Tensor Based Morphometry (TBM) [2, 1, 21, 60, 19]. The results are shown in Figure 6, visual inspection is able to determine the accuracy of the proposed algorithm.
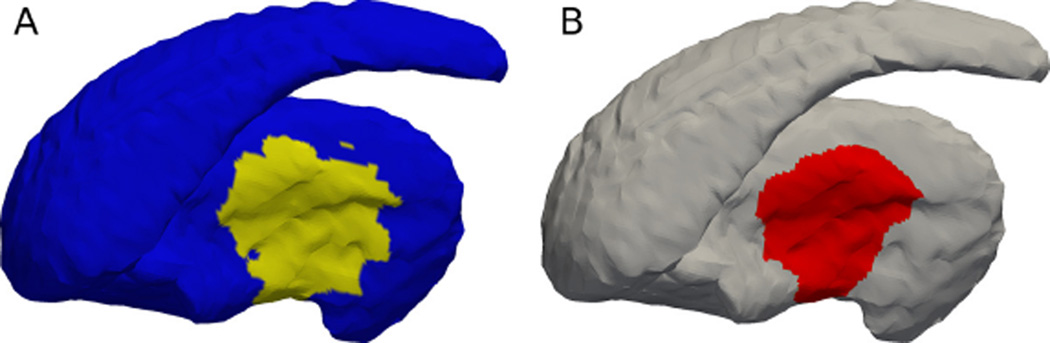
Figure 7.
(A) The ground truth deformed region is shown in yellow. (Same as Figure 5(B) putting here for easy comparison.) (B) The detected significant different region (p-value less than 5%) between the two groups. The matching between the two can be visually observed. Dice is 0.92.
Figure 6.
Results of several state-of-the-art methods on the caudate. The P-value maps are rendered on the mean shapes computed by different algorithms. P-values greater than 0.05 are shown in gray.
In addition to the visual assessment, the Dice-coefficient-on-surface DCS = 0.92.
3.2. Synthetic Striatum
Similar to [19], 100 striatum shapes are generated. Among them, a region of deformation on the medial side of the left putamen is generated, which is highlighted in Figure 8(A). Applying the proposed SPoM algorithm on this synthetic data set we obtain the resulting FDR corrected p-value map displayed on the mean shape shown in Figure 8(B). The non-gray region are determined as the significantly different between the two groups. As can be seen, the detected regions correspond well with the deformation region synthesized. In this case, the Dice-coefficient-on-surface DCS = 0.85.
Figure 8.
Result on striatum shapes. (A) The ground truth deformed region is shown in yellow. (B) The detected significant different region (p-value less than 5%) between the two groups. Dice is 0.85.
The results of other widely used algorithms are shown in Figure 11 of [19]. It is apparent that many results are quite off the ground truth. This poses rather serious risk on the fields utilizing the statistical morphometry techniques. On the other hand, it demonstrates again the necessity and importance of providing a new shape analysis algorithm with careful and quantitative evaluation.
After these two experiments that demonstrate the proposed pipeline and qualitatively compare with those in [19], we systematically and quantitatively evaluate the proposed method in the following sections.
3.3. Location experiments on synthetic Striatum
If the deformation is located at the sharp tip of the structure, would the underlying landscape affect the difficulty and accuracy of detecting it? In this experiment, the location of the deformation is varied after which the proposed algorithm is applied on. The resulting DCs values are recorded and analyzed against the underlying shape landscape.
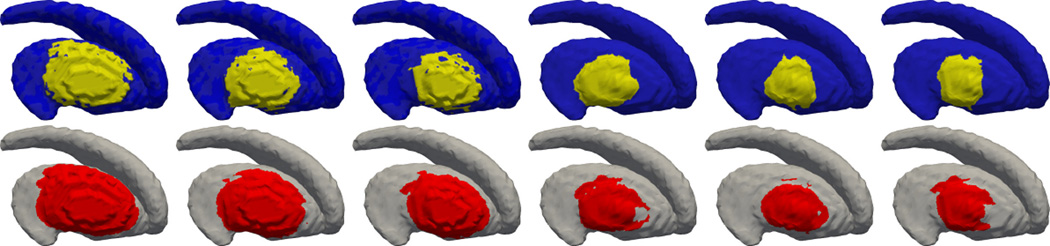
To this end, 100 different regions are selected and deformed on the testing shapes. The striatum is chosen as the “base” testing shape due to the fact that it has rich geometric features such as both positive and negative curvature regions. Six of the results are shown in Figure 9. As can be visually observed, when the deformation is at the tail of the caudate, the detection accuracy as measured by the DCS, is the lowest. The DCS of all the 100 tests are computed and their mean is 0.83 with standard deviation of 0.07.
Figure 9.
Each of the six columns contains the ground truth deformation region at top and the detected deformation region. The DCS’s are, from left to right, 0.77, 0.72, 0.85, 0.70, 0.85, 0.88.
As comparison, the same tests are also performed on two other methods. The first method is a variant of the Tensor Based Morphometry (TBM) [2, 1, 21, 60, 19] which achieves the overall best performance in [19]. The performance of TBM is shown in Table 2.
Table 2.
The Dice-on-surface coefficients of same tests using TBM.
| DCS | 67 | 52 | 54 | 65 | 68 | 65 | 51 | 73 | 59 | 60 | 66 | 60 | 52 | 67 | 74 | 72 | 56 | 62 | 71 | 74 |
| DCS | 71 | 66 | 62 | 67 | 57 | 67 | 53 | 68 | 62 | 74 | 57 | 57 | 64 | 59 | 73 | 65 | 58 | 56 | 55 | 65 |
| DCS | 69 | 55 | 73 | 60 | 69 | 59 | 71 | 74 | 64 | 56 | 63 | 73 | 53 | 68 | 55 | 67 | 61 | 57 | 59 | 54 |
| DCS | 55 | 56 | 59 | 71 | 53 | 68 | 60 | 55 | 74 | 66 | 50 | 61 | 51 | 71 | 69 | 68 | 66 | 66 | 72 | 70 |
| DCS | 74 | 58 | 64 | 73 | 62 | 72 | 60 | 52 | 62 | 74 | 72 | 57 | 64 | 58 | 65 | 59 | 56 | 72 | 56 | 66 |
Under single sided t-test, the proposed algorithm performs significantly better than TBM. Furthermore, in order to demonstrate the benefit of using the SPoM instead of other correspondence such as the signed distance map (SDM), the proposed method is modified by replacing SPoM by SDM while keeping everything else the same. The results of the tests are shown in Table 3. The proposed algorithm is significantly better under single sided t-test with p-value threshold at 0.01.
Table 3.
The Dice-on-surface coefficients of same tests using SDM.
| DCS | 73 | 72 | 71 | 91 | 80 | 76 | 88 | 76 | 85 | 79 | 90 | 70 | 79 | 72 | 83 | 83 | 72 | 64 | 89 | 84 |
| DCS | 80 | 79 | 80 | 80 | 80 | 92 | 86 | 88 | 91 | 83 | 82 | 81 | 93 | 88 | 82 | 74 | 74 | 66 | 68 | 63 |
| DCS | 85 | 76 | 82 | 87 | 91 | 82 | 92 | 72 | 88 | 73 | 73 | 72 | 71 | 80 | 82 | 70 | 70 | 77 | 71 | 70 |
| DCS | 80 | 88 | 82 | 92 | 93 | 83 | 86 | 72 | 81 | 82 | 84 | 77 | 81 | 67 | 68 | 75 | 68 | 71 | 70 | 79 |
| DCS | 89 | 95 | 72 | 80 | 83 | 81 | 71 | 86 | 78 | 74 | 84 | 68 | 78 | 91 | 85 | 68 | 82 | 81 | 80 | 83 |
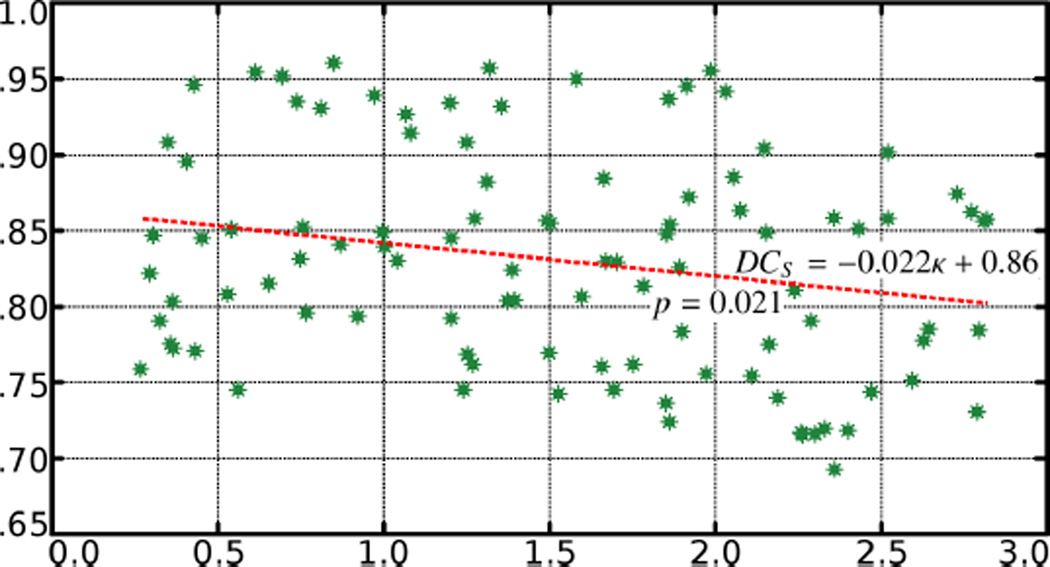
It is observed that the Dice coefficients are lower in the tip regions on the shape. In order to quantitatively investigate such effect of the underlying landscape on the DCS, the mean curvature κ of the surface is computed at each point x. Then, the average absolute mean curvature κ̄ is computed under the ground truth region. That is,
| (25) |
The κ̄ of the ground truth region in each of the 100 tests is computed and plotted against the resulting DCS and the results are shown in Table 1 and Figure 10.
Table 1.
The Dice-on-surface coefficients at different locations. This shows the effect of the underlying shape curvature on the accuracy of detecting the deformed regions. DCS values have been multiplied by 100 to reduce table width.
| κ̄ DCS |
.27 76 |
.36 78 |
.43 77 |
.61 95 |
.76 85 |
.92 79 |
1.1 93 |
1.2 75 |
1.3 88 |
1.4 80 |
1.6 95 |
1.7 75 |
1.9 85 |
1.9 78 |
2.0 94 |
2.2 85 |
2.3 72 |
2.4 69 |
2.5 90 |
2.8 86 |
| κ̄ DCS |
.29 82 |
.36 80 |
.45 85 |
.65 82 |
.77 80 |
.97 94 |
1.1 91 |
1.3 91 |
1.3 96 |
1.5 86 |
1.6 81 |
1.7 83 |
1.9 94 |
1.9 95 |
2.1 89 |
2.2 78 |
2.3 79 |
2.4 72 |
2.6 75 |
2.8 73 |
| κ̄ DCS |
.30 85 |
.37 77 |
.53 81 |
.70 95 |
.81 93 |
1.0 85 |
1.2 93 |
1.3 77 |
1.4 93 |
1.5 77 |
1.7 76 |
1.8 76 |
1.9 72 |
1.9 87 |
2.1 86 |
2.2 74 |
2.3 72 |
2.4 85 |
2.6 78 |
2.8 78 |
| κ̄ DCS |
.33 79 |
.41 90 |
.54 85 |
.74 93 |
.85 96 |
1.0 84 |
1.2 85 |
1.3 76 |
1.4 80 |
1.5 85 |
1.7 88 |
1.8 81 |
1.9 85 |
2 76 |
2.1 75 |
2.2 81 |
2.3 72 |
2.5 74 |
2.6 79 |
2.8 86 |
| κ̄ DCS |
.35 91 |
.43 95 |
.56 75 |
.75 83 |
.87 84 |
1.0 83 |
1.2 79 |
1.3 86 |
1.4 82 |
1.5 74 |
1.7 83 |
1.9 74 |
1.9 83 |
2 96 |
2.1 90 |
2.3 72 |
2.4 86 |
2.5 86 |
2.7 87 |
2.8 86 |
Figure 10.
The DCS values plotted with respect to average absolute mean curvature in the deformed region. The DCS value decrease as curvature goes up. The p-value is 0.021.
From the figure and the regression analysis one can observe that as a general trend the DCS value decrease as curvature goes up. The p-value is 0.021.
3.4. Scale experiments on synthetic Striatum
Another factor that may affect the shape analysis is the scale of the deformation. In order to test the influence of the deformation scale on the resulting accuracy, the deformation is induced at the similar location. The lateral side of putamen, as highlighted in Figure 11, is picked due to the fact that it has relative flat landscape. As a result, the underlying curvature distribution of deformation at different scale does not vary much.
Figure 11.
Each of the six columns contains the ground truth deformation region at top and the detected deformation region. The DCS’s are, from left to right, 0.85, 0.86, 0.87, 0.84, 0.82, 0.83
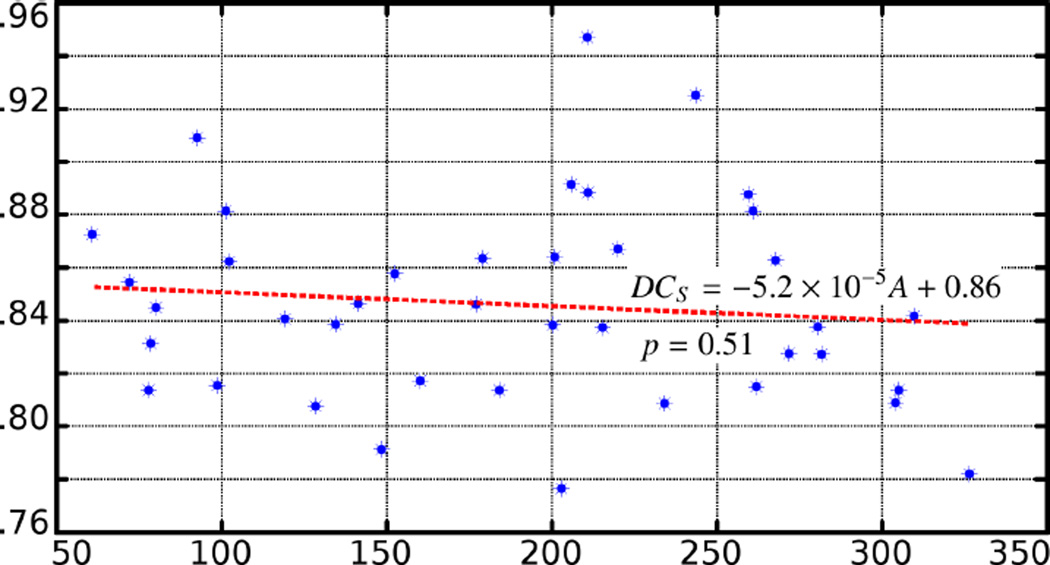
Six examples are shown in Figure 11. In addition, all the statistics as well as the linear regression are given in Table 4 and Figure 12. From the figure and regression analysis one can observe that as a general trend the DCS value is robust with respect to the area of the deformation.
Table 4.
The Dice-on-surface coefficients at different deformation scales. The area of deformation is measured in mm2. DCS values have been multiplied by 100 to reduce table width.
| area DCS |
60.7 87 |
78 81 |
80.1 85 |
98.6 82 |
102 86 |
129 81 |
142 85 |
152 86 |
177 85 |
184 81 |
201 86 |
206 89 |
211 89 |
220 87 |
244 93 |
261 88 |
268 86 |
280 84 |
304 81 |
310 84 |
| area DCS |
72.1 85 |
78.6 83 |
92.6 91 |
101 88 |
119 84 |
135 84 |
149 79 |
160 82 |
179 86 |
200 84 |
203 78 |
211 95 |
216 84 |
234 81 |
260 89 |
262 81 |
272 83 |
282 83 |
305 81 |
326 78 |
Figure 12.
The DCS values plotted with respect to area of the deformed region. The DCS value is not statistically significantly correlated with the area. The p-value is 0.51.
Similar to the previous section, the scale test is also performed on the TBM and SDM; their respective results are shown in Table 5 and 6.
Table 5.
The Dice-on-surface coefficients at different deformation scales for TBM.
| DCS | 72 | 71 | 73 | 74 | 73 | 74 | 74 | 73 | 73 | 74 | 77 | 71 | 74 | 75 | 76 | 74 | 72 | 75 | 74 | 75 |
| DCS | 66 | 72 | 70 | 72 | 76 | 73 | 77 | 69 | 70 | 70 | 75 | 74 | 76 | 73 | 77 | 72 | 73 | 74 | 74 | 75 |
Table 6.
The Dice-on-surface coefficients at different deformation scales for SDM.
| DCS | 86 | 80 | 86 | 81 | 84 | 82 | 84 | 85 | 86 | 82 | 86 | 88 | 88 | 88 | 92 | 89 | 87 | 85 | 81 | 83 |
| DCS | 84 | 82 | 90 | 86 | 84 | 85 | 79 | 83 | 83 | 83 | 79 | 90 | 83 | 79 | 85 | 82 | 85 | 82 | 82 | 77 |
It is interesting to observe that when the deformation occurs at such a relatively flat region, the capability and accuracy of detecting it is similar (not significantly different) between SPoM and SDM. This is consistent with the property of the characteristic curves of SPoM and SDM.
3.5. Striatum in schizophrenia vs healthy control
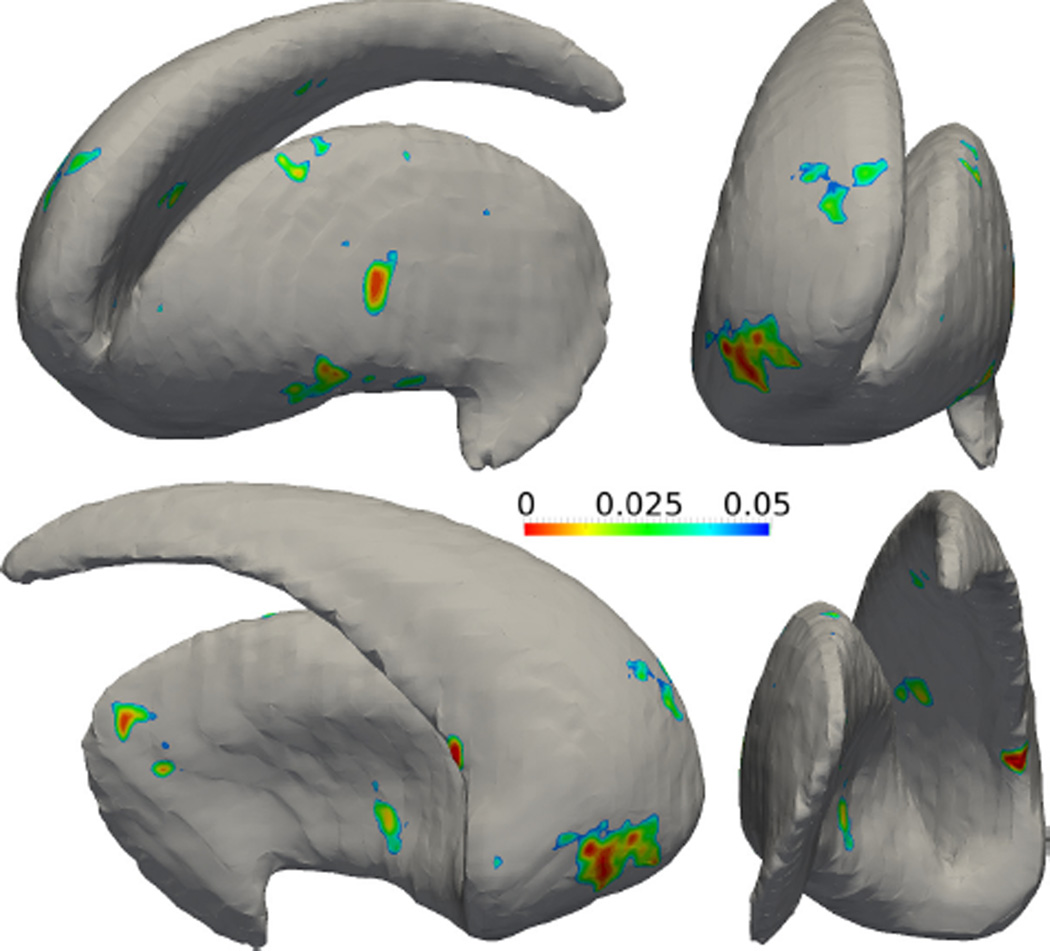
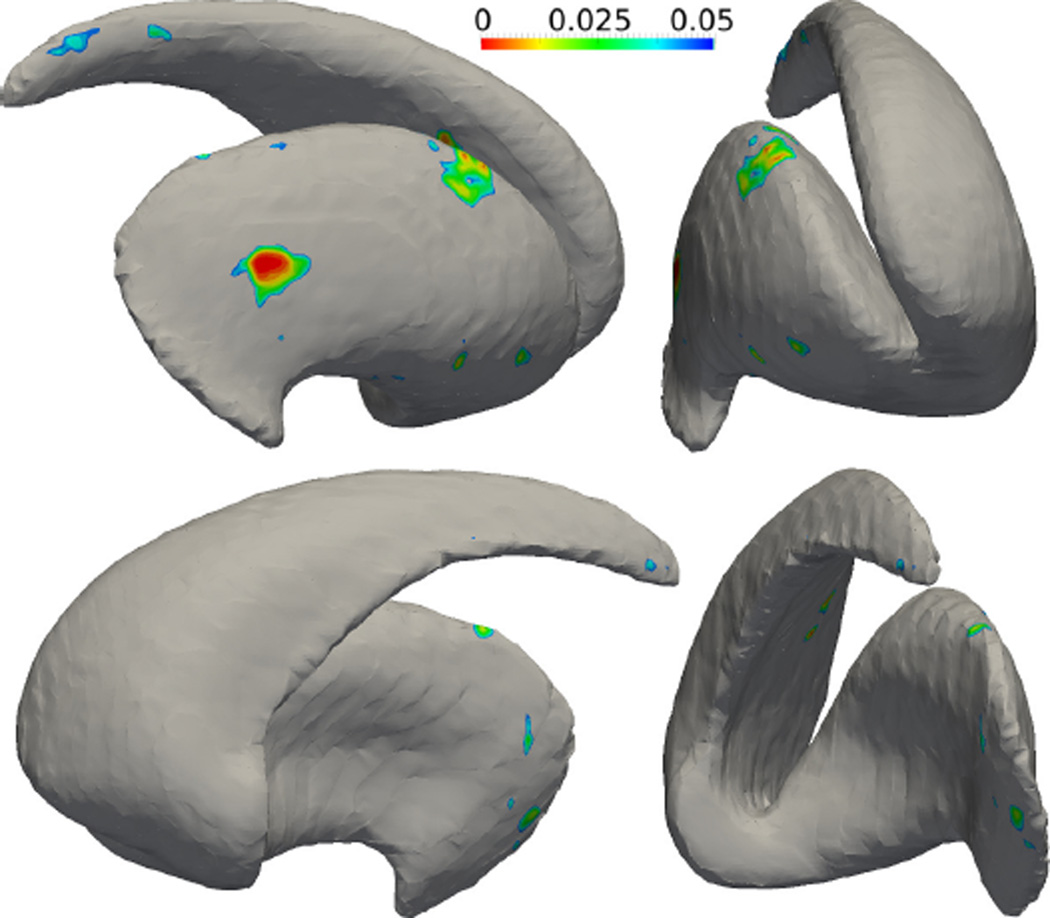
After the SPoM algorithm has been quantitatively evaluated on the synthetic data sets and gained good performance, in this experiment, the algorithm is applied on two sets of real subjects’ striatum shapes. Specifically, 27 schizophrenia patients and 27 matched healthy subjects were scanned. Their striatum shapes were extracted manually by experts in the Brigham and Women’s hospital, Harvard Medical School. The two groups of shapes are analyzed using the proposed SPoM algorithm. The colored regions in Figure 13 indicate the significantly different areas between the healthy and schizophrenia group on the left striatum, viewed from different directions. In a similar fashion, the colored regions in Figure 14 indicate the significantly different areas between the two groups on the right striatum. Unfortunately, such significant regions did not pass the FDR correction: after FDR correction, no significant region is detected.
Figure 13.
The analysis results of the left striatum between a group of healthy subjects and schizophrenia patients. Color indicates the statistically different regions between the two groups.
Figure 14.
The analysis results of the right striatum between a group of healthy subjects and schizophrenia patients. Color indicates the statistically different regions between the two groups.
3.6. Amygdala hippocampus complex in schizophrenia vs healthy control
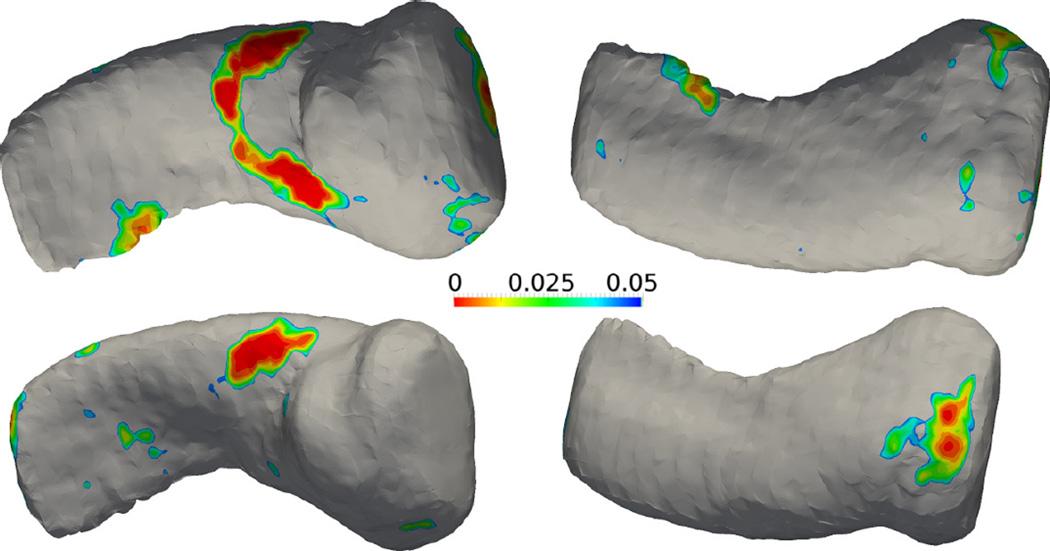
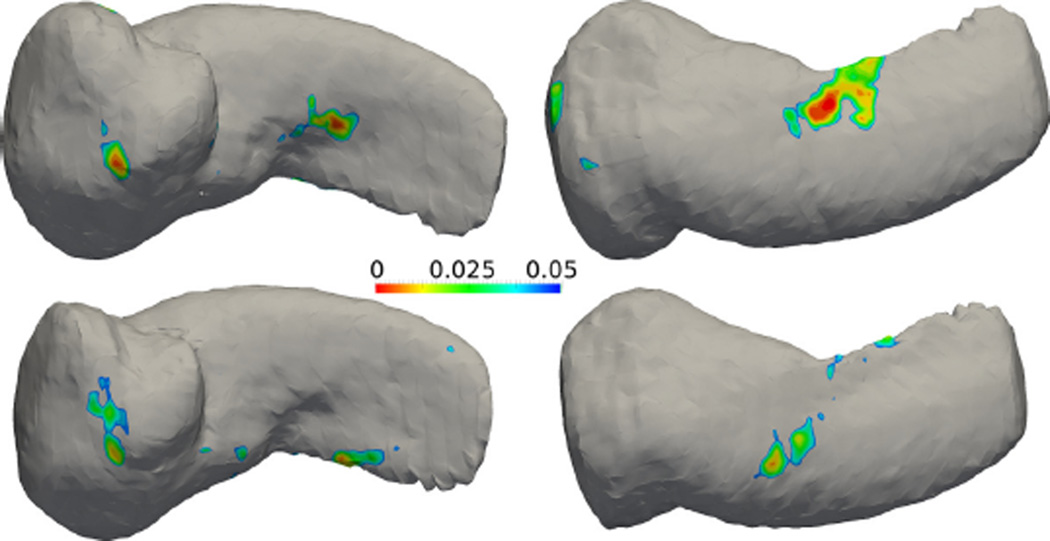
In this experiment, the SPoM algorithm is applied on two sets of longitudinal patient data. Specifically, 19 schizophrenia patients were scanned twice separated by one year. In the control group, 20 matched healthy subjects were scanned twice with the same interval. Their Amygdala-hippocampus-complex (AHC) shapes were extracted manually by experts in the Brigham and Women’s hospital, Harvard Medical School. The AHC shapes are analyzed using the proposed algorithm. In the top row of Figure 15 and Figure 16, the colorful regions indicate the significantly different areas between the healthy and schizophrenia group at time 1. In the bottom row, similar results are shown for time 2. As can be seen, the areas of difference are consistent with slight migration. This may provide insight on the longitudinal evolution of the disease. However, such significant regions again did not pass the FDR correction: after FDR correction, no significant region is detected.
Figure 15.
Results of the left amygdala-hippocampus complex. Top row: mean shape at time 1 with raw p-value map. Bottom row: mean shape at time 2 with raw p-value map.
Figure 16.
Results of the right amygdala-hippocampus complex. Top row: mean shape at time 1 with raw p-value map. Bottom row: mean shape at time 2 with raw p-value map.
4. Conclusion and Future Research Directions
The contribution of this study is twofold. First, we proposed a new statistical shape analysis/morphometry technique based on the Signed Poisson Map. In addition, a quantitatively evaluation framework is proposed to systematically evaluate the proposed algorithm. Future studies would benefit from such a framework in providing more robust and quantitatively evaluated techniques.
The proposed algorithm also has certain limitations in discriminating very thin structures, such as the thin tail of the caudate. This is partially due to the input data which has a rather coarse resolution (1mm3), but from the construction of the mean shape which smoothes out some of the finer shape details. Group based atlas construction methods, such as [57], would be very useful in constructing sharper mean shapes.
Moreover, the proposed algorithm analyzes the entire shape in a uniform fashion. However, weighting functions could be added to highlight the importance of certain area on the shape [31, 61], which may provide more biologically meaningful results.
The analysis results on the schizophrenia patients with the healthy subjects, did not detect statistically significant difference between the two groups after correcting the multiple comparison effect. This, however, is not consistent with some of the previous studies. Equipped with the quantitative evaluation technique, future research will study these cases to identify the reason for such inconsistencies.
Highlights.
The contribution of this study is two folds. First, we proposed a new statistical shape analysis/morphometry technique based on the Signed Poisson Map (SPoM). In addition, a quantitatively evaluation framework is proposed to systematically evaluate the proposed algorithm.
To the best of our knowledge, this is the first quantitative morphometry evaluation framework and the proposed SPoM method is the first shape analysis method that has been systematically and quantitatively validated and evaluated.
We believe the objective and quantitative evaluation framework would benefit later development of new statistical shape analysis algorithms as we as the application areas in providing accurate and reliable results.
Acknowledgments
This project was supported by in part by grants from NIH R01 MH82918.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Ashburner J, Friston K. Voxel-based morphometry–the methods. Neuroimage. 2000;11:805–821. doi: 10.1006/nimg.2000.0582. [DOI] [PubMed] [Google Scholar]
- 2.Ashburner J, Hutton C, Frackowiak R, Johnsrude I, Price C, Friston K. Identifying global anatomical differences: deformation-based morphometry. Human Brain Mapping. 1998;6:348–357. doi: 10.1002/(SICI)1097-0193(1998)6:5/6<348::AID-HBM4>3.0.CO;2-P. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Beg MF, Miller MI, Trouvé A, Younes L. Computing large deformation metric mappings via geodesic flows of diffeomorphisms. International journal of computer vision. 2005;61:139–157. [Google Scholar]
- 4.Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B. 1995:289–300. [Google Scholar]
- 5.Bouix S, Siddiqi K, Tannenbaum A. Flux driven automatic centerline extraction. Medical Image Analysis. 2005;9:209–221. doi: 10.1016/j.media.2004.06.026. [DOI] [PubMed] [Google Scholar]
- 6.Cates J, Fletcher P, Styner M, Hazlett H, Whitaker R. Particle-based shape analysis of multi-object complexes. MICCAI. 2008:477–485. doi: 10.1007/978-3-540-85988-8_57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chung MK, Dalton KM, Davidson RJ. Tensor-based cortical surface morphometry via weighted spherical harmonic representation. IEEE Transactions on Medical Imaging. 2008;27:1143–1151. doi: 10.1109/TMI.2008.918338. [DOI] [PubMed] [Google Scholar]
- 8.Cootes TF, Taylor CJ, Cooper DH, Graham J. Active shape models-their training and application. Computer vision and image understanding. 1995;61:38–59. [Google Scholar]
- 9.Costa C, Antonucci F, Pallottino F, Aguzzi J, Sun DW, Menesatti P. Shape analysis of agricultural products: a review of recent research advances and potential application to computer vision. Food and Bioprocess Technology. 2011;4:673–692. [Google Scholar]
- 10.Davies RH. Learning shape: optimal models for analysing natural variability [Google Scholar]
- 11.Dice L. Measures of the amount of ecologic association between species. Ecology. 1945;26:297–302. [Google Scholar]
- 12.Dryden I, Mardia K. Statistical shape analysis. John Wiley & Sons; 1998. [Google Scholar]
- 13.Dubrovina A, Kimmel R. Matching shapes by eigende-composition of the laplace-beltrami operator. Proc. 3DPVT. 2010 [Google Scholar]
- 14.Durrleman S, Pennec X, Trouvé A, Thompson P, Ayache N. Inferring brain variability from diffeomorphic deformations of currents: an integrative approach. Medical image analysis. 2008;12:626–637. doi: 10.1016/j.media.2008.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Evans LC. Partial differential equations. 1998 [Google Scholar]
- 16.Evans LC. Partial differential equations. American Mathematical Society; 1999. [Google Scholar]
- 17.Gao Y, Bouix S. Mesh Processing in Medical Image Analysis 2012. Springer; 2012. Synthesis of realistic subcortical anatomy with known surface deformations; pp. 80–88. [Google Scholar]
- 18.Gao Y, Nain D, LeFaucheur X, Tannenbaum A. MICCAI Workshop on Open Source. Brisbane, Australia: Insight Journal; 2007. Spherical wavelet ITK filter. [Google Scholar]
- 19.Gao Y, Riklin-Raviv T, Bouix S. Shape analysis, a field in need of careful validation. Human Brain Mapping. 2014;35:4965–4978. doi: 10.1002/hbm.22525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gerig G, Styner M, Jones D, Weinberger D, Lieberman J. IEEE MMBIA. IEEE; 2001. Shape analysis of brain ventricles using spharm; pp. 171–178. [Google Scholar]
- 21.Good CD, Johnsrude IS, Ashburner J, Henson RN, Fristen K, Frackowiak RS. A voxel-based morphometric study of ageing in 465 normal adult human brains, in: Biomedical Imaging, 2002; 5th IEEE EMBS International Summer School on IEEE; 2002. p. 16. [Google Scholar]
- 22.Gorczowski K, Styner M, Jeong JY, Marron J, Piven J, Hazlett HC, Pizer SM, Gerig G. Statistical shape analysis of multi-object complexes, in: Computer Vision and Pattern Recognition, 2007. CVPR’07; IEEE Conference on, IEEE; 2007. pp. 1–8. [Google Scholar]
- 23.Haidar H, Bouix S, Levitt JJ, McCarley RW, Shenton ME, Soul JS. Characterizing the shape of anatomical structures with poisson’s equation. Medical Imaging, IEEE Transactions on. 2006;25:1249–1257. doi: 10.1109/tmi.2006.881378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Huckemann S, Hotz T, Munk A. Intrinsic shape analysis: Geodesic pca for riemannian manifolds modulo isometric lie group actions. 2010 doi: 10.1109/TPAMI.2009.117. [DOI] [PubMed] [Google Scholar]
- 25.Hufnagel H, Pennec X, Ehrhardt J, Handels H, Ayache N. Shape analysis using a point-based statistical shape model built on correspondence probabilities. MICCAI. 2007:959–967. doi: 10.1007/978-3-540-75757-3_116. [DOI] [PubMed] [Google Scholar]
- 26.Joshi S, Pizer S, Fletcher PT, Yushkevich P, Thall A, Marron J. Multiscale deformable model segmentation and statistical shape analysis using medial descriptions. Medical Imaging, IEEE Transactions on. 2002;21:538–550. doi: 10.1109/TMI.2002.1009389. [DOI] [PubMed] [Google Scholar]
- 27.Joshi SC, Miller MI, Grenander U. On the geometry and shape of brain sub-manifolds. International Journal of Pattern Recognition and Artificial Intelligence. 1997;11:1317–1343. [Google Scholar]
- 28.Kendall DG. Shape manifolds, procrustean metrics, and complex projective spaces. Bulletin of the London Mathematical Society. 1984;16:81–121. [Google Scholar]
- 29.Kim SG, Chung MK, Schaefer SM, van Reekum C, Davidson RJ. Sparse shape representation using the laplace-beltrami eigenfunctions and its application to modeling subcortical structures. Mathematical Methods in Biomedical Image Analysis (MMBIA), 2012 IEEE Workshop on, IEEE. 2012:25–32. doi: 10.1109/MMBIA.2012.6164736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Klassen E, Srivastava A, Mio W, Joshi SH. Analysis of planar shapes using geodesic paths on shape spaces. Pattern Analysis and Machine Intelligence. IEEE Transactions on. 2004;26:372–383. doi: 10.1109/TPAMI.2004.1262333. [DOI] [PubMed] [Google Scholar]
- 31.Kong L, et al. Ph.D. thesis. University of Alberta; 2009. On multivariate quantile regression: directional approach and application with growth charts. [Google Scholar]
- 32.Krim H, Yezzi A., Jr Statistics and analysis of shape. Control and Cybernetics. 2007;36 [Google Scholar]
- 33.Kurtek S, Klassen E, Ding Z, Srivastava A. A novel riemannian framework for shape analysis of 3d objects; Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on, IEEE; 2010. pp. 1625–1632. [Google Scholar]
- 34.Leventon ME, Grimson WEL, Faugeras O. Statistical shape influence in geodesic active contours; Computer Vision and Pattern Recognition, 2000. Proceedings. IEEE Conference on, IEEE; 2000. pp. 316–323. [Google Scholar]
- 35.Miller M. Computational anatomy: shape, growth, and atrophy comparison via diffeomorphisms. NeuroImage. 2004;23:S19–S33. doi: 10.1016/j.neuroimage.2004.07.021. [DOI] [PubMed] [Google Scholar]
- 36.Nain D, Haker S, Bobick A, Tannenbaum A. Multiscale 3-d shape representation and segmentation using spherical wavelets. IEEE Transactions on Medical Imaging. 2007;26:598–618. doi: 10.1109/TMI.2007.893284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nain D, Haker S, Bobick A, Tannenbaum AR. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2005. Springer; 2005. Multiscale 3D shape analysis using spherical wavelets; pp. 459–467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Niethammer M, Reuter M, Wolter FE, Bouix S, Peinecke N, Koo MS, Shenton ME. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2007. Springer; 2007. Global medical shape analysis using the laplace-beltrami spectrum; pp. 850–857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Osada R, Funkhouser T, Chazelle B, Dobkin D. Matching 3d models with shape distributions; Shape Modeling and Applications, SMI 2001 International Conference on., IEEE; 2001. pp. 154–166. [Google Scholar]
- 40.Osada R, Funkhouser T, Chazelle B, Dobkin D. Shape distributions. ACM Transactions on Graphics (TOG) 2002;21:807–832. [Google Scholar]
- 41.Peter A, Rangarajan A. Shape analysis using the fisherrao riemannian metric: Unifying shape representation and deformation. IEEE ISBI, IEEE. 2006:1164–1167. [Google Scholar]
- 42.Pichon E, Nain D, Niethammer M. A laplace equation approach for shape comparison. Proceedings of SPIE. 2006:614119–614110. [Google Scholar]
- 43.Pizer SM, Jung S, Goswami D, Vicory J, Zhao X, Chaudhuri R, Damon JN, Huckemann S, Marron J. Innovations for Shape Analysis. Springer; 2013. Nested sphere statistics of skeletal models; pp. 93–115. [Google Scholar]
- 44.Qiu A, Crocetti D, Adler M, Mahone EM, Denckla MB, Miller MI, Mostofsky SH. Basal ganglia volume and shape in children with attention deficit hyperactivity disorder. The American journal of psychiatry. 2009;166:74. doi: 10.1176/appi.ajp.2008.08030426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Raviv D, Dubrovina A, Kimmel R. Scale Space and Variational Methods in Computer Vision. Springer; 2012. Hierarchical matching of non-rigid shapes; pp. 604–615. [Google Scholar]
- 46.Reuter M, Wolter FE, Shenton M, Niethammer M. Laplace-beltrami eigenvalues and topological features of eigen-functions for statistical shape analysis. Computer-Aided Design. 2009;41:739–755. doi: 10.1016/j.cad.2009.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Roweis S, Saul L. Nonlinear dimensionality reduction by locally linear embedding. Science. 2000;290:2323. doi: 10.1126/science.290.5500.2323. [DOI] [PubMed] [Google Scholar]
- 48.Scientific Computing and Imaging Institute (SCI) shapeWorks: An open-source tool for constructing compact statistical point-based models of ensembles of similar shapes that does not rely on specific surface parameterization. 2008 URL: http://www.sci.utah.edu/software.html. [Google Scholar]
- 49.Shen L, Farid H, McPeek M. Modeling three-dimensional morphological structures using spherical harmonics. Evolution. 2009;63:1003–1016. doi: 10.1111/j.1558-5646.2008.00557.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Siddiqi K, Pizer SM. Medial representations: mathematics, algorithms and applications. Vol. 37. Springer; 2008. [Google Scholar]
- 51.Small C. The statistical theory of shape. Springer Verlag; 1996. [Google Scholar]
- 52.Sommer S, Lauze F, Hauberg S, Nielsen M. Computer Vision–ECCV 2010. Springer; 2010. Manifold valued statistics, exact principal geodesic analysis and the effect of linear approximations; pp. 43–56. [Google Scholar]
- 53.Styner M, Gerig G, Lieberman J, Jones D, Weinberger D. Statistical shape analysis of neuroanatomical structures based on medial models. Medical Image Analysis. 2003;7:207–220. doi: 10.1016/s1361-8415(02)00110-x. [DOI] [PubMed] [Google Scholar]
- 54.Styner M, Oguz I, Xu S, Brechbühler C, Pantazis D, Levitt J, Shenton M, Gerig G. Framework for the statistical shape analysis of brain structures using spharm-pdm. The insight journal. 2006:242. [PMC free article] [PubMed] [Google Scholar]
- 55.Vaillant M, Glaunes J. Information Processing in Medical Imaging. Springer; 2005. Surface matching via currents; pp. 381–392. [DOI] [PubMed] [Google Scholar]
- 56.Vaillant M, Qiu A, Glaunès J, Miller MI. Diffeomorphic metric surface mapping in subregion of the superior temporal gyrus. NeuroImage. 2007;34:1149–1159. doi: 10.1016/j.neuroimage.2006.08.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Wu G, Jia H, Wang Q, Shen D. Sharpmean: group-wise registration guided by sharp mean image and tree-based registration. NeuroImage. 2011;56:1968–1981. doi: 10.1016/j.neuroimage.2011.03.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Younes L. Shapes and diffeomorphisms. Vol. 171. Springer; 2010. [Google Scholar]
- 59.Yushkevich P, Zhang H, Gee JC, et al. Continuous medial representation for anatomical structures. Medical Imaging, IEEE Transactions on. 2006;25:1547–1564. doi: 10.1109/tmi.2006.884634. [DOI] [PubMed] [Google Scholar]
- 60.Zarei M, Mataix-Cols D, Heyman I, Hough M, Doherty J, Burge L, Winmill L, Nijhawan S, Matthews PM, James A. Changes in gray matter volume and white matter microstructure in adolescents with obsessive-compulsive disorder. Biological psychiatry. 2011;70:1083–1090. doi: 10.1016/j.biopsych.2011.06.032. [DOI] [PubMed] [Google Scholar]
- 61.Zhu H, Styner M, Li Y, Kong L, Shi Y, Lin W, Coe C, Gilmore JH. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2010. Springer; 2010. Multivariate varying coefficient models for dti tract statistics; pp. 690–697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Ziezold H. Mean figures and mean shapes applied to biological figure and shape distributions in the plane. Biometrical journal. 1994;36:491–510. [Google Scholar]