Abstract
Mediation analysis is a popular framework for identifying underlying mechanisms in social psychology. In the context of simple mediation, we review and discuss the implications of three facets of mediation analysis: (a) conceptualization of the relations between the variables, (b) statistical approaches, and (c) relevant elements of design. We also highlight the issue of equivalent models that are inherent in simple mediation. The extent to which results are meaningful stem directly from choices regarding these three facets of mediation analysis. We conclude by discussing how mediation analysis can be better applied to examine causal processes, highlight the limits of simple mediation, and make recommendations for better practice.
Keywords: mediation, concepts, model assumptions, equivalent models, research design
Mediation analysis is an exceedingly popular framework for testing hypotheses about causal mechanisms. Research in social psychology accounts for 34% of studies published using mediation analysis in psychology (MacKinnon, Fairchild & Fritz, 2007). Over 6 months in 2007, 41% of articles published in Personality and Social Psychology Bulletin (PSPB) reported at least one mediation analysis (Kashy, Donnellan, Ackerman, & Russell, 2009). From 2005 to 2009, 59% of articles in Journal of Personality and Social Psychology and 65% of articles in PSPB involved mediation analyses (Rucker, Preacher, Tormala, & Petty, 2011).
The popularity of mediation lies in its promise of identifying the underlying mechanism driving the causal effect of an independent variable (X) on a dependent variable (Y). The statement “X causes Y” is a black-box view of causality and does not inform of the how or why behind the effect. The mediator (M) is theorized to transmit the effect of X on Y (Baron & Kenny, 1986; Judd & Kenny, 1981); a change in X results in a change in M that translates in turn to an effect on Y (diagram D in Figure 1). Here, the causal chain embeds the idea of a sequence in that the process unfolds over time (Kenny, Korchmaros & Bolger, 2003).
Figure 1.
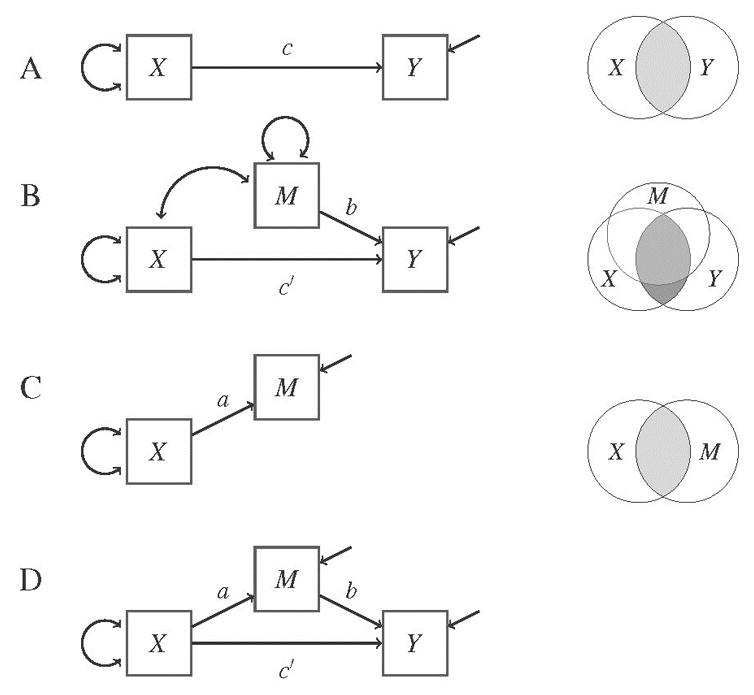
Four sets of diagrams depicting concepts in mediation. Diagrams on the left are path diagrams with letters a, b, c and c′ representing standardized coefficients. Diagrams on the right are Venn diagrams where the shaded areas between circles relate to shared variances among the variables. Endogenous variables with arrows pointing towards them are dependent variables and exogenous variables with arrow emerging from them are independent variables.
In this article, we address three questions about mediation analysis as typically implemented and interpreted by social psychologists. First, which concept of mediation is being used? Second, what statistical approach is being applied to the data? Third, what type of design is used to generate the data? Answers to these questions, in combination, determine the specifics of how results from a study using mediation analysis can be accurately interpreted. The use of multiple linear regression (MLR) is first detailed followed by the structural equation model (SEM) given recent recommendations (e.g., Iacobucci, Saldanha & Deng, 2007; Rucker et al., 2011) and certain cautions regarding these models are described. We focus on models with one independent variable, one dependent variable, and one mediator (i.e., simple mediation) because of their simplicity and frequency of use, and our review highlights the many weaknesses of this model. Our conclusions present several recommendations for better research using mediation analysis that suggest abandoning simple mediation models for models that better represent a process that unfolds over time.
Concepts of Mediation
Concept 1: Explaining a Causal Effect
Mediation was first conceived as an approach to answer the question: given a causal effect X→Y, could a third variable M be identified such that M explains X→Y (Baron & Kenny, 1986; Judd & Kenny, 1981)? Figure 1 depicts four conditions that are purportedly required to establish M as the explanatory variable of X→Y (Baron & Kenny, 1986). Path diagrams and their commensurate Venn diagrams are shown in the left and right of Figure 1, respectively. The four conditions are:
There is a causal effect X→Y to explain (path c, diagram A).
Adding M to the regression of Y onto X leads to a substantial reduction from the total effect c to the direct effect c′(path diagram B); this statement is mathematically expressed as c–c′ ≠ 0.
There is a causal effect X→M (path a, diagram C).
There is a causal effect M→Y (path b, diagram B), controlling for X. Conditions 3 and 4 situate M temporally between X and Y.
The indirect or mediated effect is quantified by c–c′, or ab, and M is called the intervening variable. Mediation requires these three variables to be operationally defined within a single study (Kenny et al., 2003) because interest is in X →Y unfolding over time, where M is an explanation of this causal effect.
Venn diagrams can also depict mediation; X→Y (path c) is mathematically analogous to the variance in Y accounted for by X (shaded area in Venn diagram A). Adding M to the regression of Y on X is represented by the third circle in Venn diagram B and the extent to which M accounts for the effect of X on Y is represented by the lighter shaded area where all three circles overlap. The unique variance in Y due to X is the darker shaded area in Venn diagram B (c.f., path cprime;) and the unique variance in Y due to M is represented by the unshaded area that M overlaps with Y (c.f., path b). Finally, the variance in M accounted for by X is depicted as the shaded area in Venn diagram C (c.f., path a).
When these four conditions are met, M is taken to explain X→Y. The main focus of these steps is to identify a variable (i.e., a mediator) that drives the causal effect as the mechanism underlying the X→Y relation. This concept of mediation rests on the highly restrictive assumption that all the linear effects are consistent (i.e., a, b, and c are all positive, c is positive with a and b negative, or c is negative with a and b having opposite signs; Davis, 1985). Only in the presence of consistent mediation are the phrases “complete mediation” and “partial mediation” meaningful. This first concept of mediation was subsequently refined because consistent mediation is not typically observed in practice; consistent mediation occurs in half of the eight possible combinations of directions that a, b, and c can take. The refinement of the concept of mediation shifted emphasis from identifying a mediator that explains the causal effect X→Y to the indirect effect of X→M→Y that is carried by the mediator.
Concept 2: Intervening Variable Effect
A newer concept of mediation focuses on the indirect effect X→M→Y (MacKinnon, Lockwood, Hoffman, West & Sheets, 2002), where mediation is composed of X→M (path a) and M→Y (path b). The mediated effect X→M→Y is a change in X that brings about a change in M, resulting in a change in Y. Under this concept, the mediator no longer retains the status of an underlying mechanism that accounts for the effect of X→Y because establishing X→Y is no longer necessary. Recall that the first concept of mediation is an amalgamation of three ideas: (a) there is a total causal effect, c, (b) there is mediation, c–c′ or ab, and (c) M accounts for some or most of the causal effect. The second concept is reduced to the mediated effect that is carried by paths a and b, requiring two of the four conditions of the first concept, rendering the total and direct effects (c and c′) irrelevant. Here, mediation is no longer about identifying an explanatory variable, because there is no requirement for X→Y to be explained, but about the effect carried by the intervening variable M.
Implications
Conclusions drawn from the two concepts of mediation are different. Under both concepts, the mediated effect (ab or c–c′) is the change in Y due to a one unit increase in X through M. The first concept of mediation, however, goes one step further by establishing M as the explanatory variable of X→Y. This addition comes with the hefty price of more assumptions in consistent mediation, resulting in low power (MacKinnon et al., 2002).
The conceptual and statistical models used to evaluate mediation could both be communicated using various diagrams, and clarity in what those diagrams represent reduces potential confusion. For instance, when the mediator is examined as an explanatory variable to X→Y using SEM, diagrams A and D in Figure 1 should be presented. Conversely, when the mediator is couched as an intervening variable and statistically evaluated using SEM, only diagram D in Figure 1 should be presented. When diagrams unequivocally communicate both the concept of and the statistical model used to evaluate mediation, hypothesis validity (Wampold, Davis & Good, 1990) is ensured. When this validity is present, studies on mediation could reasonably evaluate causal mechanisms or intervening variable effects.
Statistical Approaches
The epistemological basis of statistics in psychology has evolved from applying a set of mechanistic procedures to formulating and evaluating statistical models (Rodgers, 2010; Tukey, 1969). Mediation analysis is slowly adopting this shift, reflected in using SEM over MLR. Here, we highlight disadvantages of using MLR instead of SEM and focus on the SEM framework and its assumptions. We also make use of a published empirical example to illustrate certain disadvantages of the simple mediation model. Implications of these disadvantages are then discussed.
Modeling Frameworks
Multiple Linear Regression
The MLR equations for simple mediation are:
| (1) |
| (2) |
| (3) |
where Y, X and M are standardized such that the intercepts for the equations are 0 and not represented. The caret symbol “^” distinguishes estimated paths from their population parameters (c.f., Figure 1). Equation 1 maps onto panel A; ĉ is the change in Y due to a standard unit increase in X. Equation 2 maps onto panel B; b̂ is the change in Y due to a standard unit increase in M, controlling for X and ĉ′ is the change in Y due to a standard unit increase in X controlling for M. Finally, Equation 3 maps onto panel C; âis the change in M due to a standard unit increase in X. These three equations are consistent with the dated idea that statistics is a set of mechanistic procedures (e.g., causal steps procedure for Concept 1).
When interest is in the mediated effect (Concept 2 and part of Concept 1), either ab or c–c′ is tested for significance. Significance can be evaluated with many procedures such as the joint test (Kenny, Kashy & Bolger, 1998), the Sobel (1982, 1986) test, resampling methods (Bollen & Stine, 1990), the distribution of product method (MacKinnon, Fritz, Williams & Lockwood, 2007), and Bayesian methods (Beisanz, Falk & Savalei, 2010). Under desirable data conditions (i.e., large sample size, normality of variables, measurement reliability, and large effect sizes), these approaches would have identical results. Under less desirable data conditions, care should be taken in choosing among these approaches because they diverge in performance. Unfortunately, such methodological developments shift focus away from the crux of mediation analysis, which is about thoughtfully studying causal mechanisms. We now highlight the SEM approach, which promotes modeling phenomena over applying procedures.
Structural equation model
The univariate MLR can only be applied to a single dependent variable (e.g., Y or M) whereas the multivariate SEM can be applied to one or more dependent variables (e.g., Y and M simultaneously). The SEM approach to mediation specifies one model for X, M, and Y (Concept 2), which offers several conceptual advantages. The joint modeling of outcomes M and Y in SEM (Equations 1 and 2) mirrors the idea that mediation concerns a single causal process that unfolds over time, requiring the three variables to be operationally defined within a single study. Although applying a piecemeal MLR approach to modeling mediation would produce the same results as SEM, using the multivariate SEM to simultaneously estimate a, b, and c′ is consistent with the idea that mediation is a single process. Mediation is distinct from a causal chain of effects, which treats X→M and M→Y as separate processes (Spencer, Zanna & Fong, 2004). This paradigm cannot be estimated with SEM, and could be confused with mediation (e.g., Maier, Elliot, & Lichtenfeld, 2008) because it is usually estimated with separate MLR models.
Additionally, when the mediator is evaluated as a variable that explains X→Y (Concept 1), SEM embodies the epistemological idea of modeling phenomena. First, the model in diagram A of Figure 1 is fit to the data. Next, the model represented by diagram A is modified to the model represented by diagram D by including M as a second outcome. Our next sections raise serious issues with simple mediation that are more clearly elucidated from the SEM.
Model Assumptions
All parametric models, including mediation, require assumptions to insure that the expected value of estimates are equal to their true parameter value (i.e., unbiased), estimates approach their true parameter values as sample size increases (i.e., consistent), and the standard errors of parameter estimates are as small as possible (i.e., efficient) which translates to most powerful tests. Assumptions are also required for estimated standard errors to be unbiased for accurate p-values and confidence levels. In practice, model assumptions are violated to some extent and we state the well-documented but often overlooked conditions that are required for drawing unambiguous conclusions in tests of mediation.
Normality
In MLR, estimates are obtained via the ordinary least squares (OLS) estimator and normality of the residuals of M and Y is assumed to allow for inference. In SEM, the default estimator is maximum likelihood (ML) which requires X, M, and Y to be multivariate normal; this assumption could be relaxed to accommodate fixed levels of X (e.g., experimental conditions). Multivariate normality implies linearity of the parameters and models with linear parameters include forms where variables could be nonlinearly related to one another (e.g., interactions). In simple mediation, the relationships among X, M, and Y are assumed to be linear and straightforward extensions to this model could include nonlinear effects with linear parameters such as moderated mediation (Muller, Judd & Yzerbyt, 2007; Preacher, Rucker & Hayes, 2007) that can be seamlessly incorporated into the SEM (Preacher, Zyphur & Zhang, 2010).
Given linearity of parameters together with non-normally distributed X, M, and Y, parameter estimates (â, b̂, ĉ, and ĉ′) remain unbiased but their standard errors are incorrect. Here, the direction and strength of estimated effects could be interpreted without consequence although inferences about them are improper. Biased estimated standard errors are readily addressed by using alternative estimators that generate heteroscedastic-consistent standard errors in MLR (e.g., Long & Ervin, 2000) or robust corrections in SEM (see Savalei, 2014 for a review).
With nonlinear relationships among X, M, and Y that manifest in non-normal distributions (e.g., binary outcomes), statistical extensions of linear models that properly account for nonlinearity are alternatives (e.g., logistic and probit models, MacKinnon, Lockwood, Brown, Wang & Hoffman, 2007, or extended SEM, Muthén & Muthén, 2012, Neale et al., 2015). When the relationships among X, M, and Y are non-linear and misspecified, erroneous conclusions ensue; a trivial example is applying a linear model to proportion data. The problem of misspecification is related to the more general but often ignored and unachievable assumption of the model being exactly correct.
Model is exactly correct
Unbiased estimates are attained when the specified model perfectly represents reality (or relations in the population). The model in diagram D of Figure 1 states that only three variables are involved in mediation and that the paths linking them are linear. Any deviation from diagram D constitutes misspecification which could be: (a) incorrect functional form between variables (e.g., unmodeled nonlinearity), (b) omission of key variables, or (c) imperfect measurement. The first concept was briefly discussed and the latter two concepts are described below.
Omitted variables
When a model omits key variables, estimated parameters are biased. Consider Equations 1 and 2 (diagrams A and B in Figure 1). Equation 2 includes M and X as predictors of Y whereas Equation 1 omits M. Given that there is an indirect effect of M in the population (i.e., Equation 2 is correct), the omission of M results in a biased estimate of X→Y, quantified by the difference between ĉ and ĉ′. Stated differently, ĉ′ is a biased estimate of c assuming that Equation 2 is correct in the population. The omission of M results in the biased estimate ĉ, accompanied by improper standard errors and inference.
Omitted variables are often called confounders that suppress or enhance marginal effects (e.g., c), resulting in smaller or larger conditional effects (e.g., c′), respectively. Mediation involves the causal chain X→M→Y and experiments are the gold standard in establishing causality. Typically, levels of X undergo random assignment such that causality in X→M and X→Y could be inferred because randomization reduces the possibility of confounding in these pathways (c.f., Pearl, 2014). Yet, M cannot and logically should not be manipulated because theory dictates that changes in X cause changes in M. The mere observation of M raises the question of whether a causal statement M→Y is viable (Winship & Morgan, 1999). Randomization in X does not resolve potential confounding in M→Y; levels of M that are observed could be due to X, omitted variables that influence both X and M, or omitted variables that lie in between X and M in a causal chain. Additionally, randomization of X does not address the possibility that X has effects on other confounders that could subsequently affect Y; omitted variables could still influence both X and Y or lie between X and Y in a causal chain (i.e., another variable akin to M).
When manipulation of the predictor (e.g., M) is unfeasible, researchers could make use of alternative statistical methods such as instrumental variables (Angrist, Imbens & Rubin, 1996; Shadish, Cook & Campbell, 2002), principal stratification (Jo, 2008), inverse probability weighting (Coffman, 2011; Coffman & Zhong, 2012), sensitivity analysis (Imai, Keele, and Tingley, 2010), and SEM to enhance the causal interpretation of X→M (MacKinnon & Pirlott, 2015). Although MLR can also be used to incorporate omitted variables and obtain identical estimates as the SEM, the SEM has the advantage of being simpler to implement (i.e., specify a single modified SEM versus fit several modified MLR equations) and encourages researchers to conceive of mediation as a system of effects. Yet, elements of research design (e.g., randomization), are superior to methodological workarounds by directly imbuing properties to the data that allow for unequivocal causal interpretations.
Measurement error
The simple mediation model (diagram D, Figure 1) presupposes that X, M, and Y are perfectly measured, but unreliability of M results in downward-biased estimates of the indirect effect, ab (Hoyle & Kenny, 1999). Latent variables of X, M, and Y are relatively free of measurement error and their inclusion in models of simple mediation reduces bias in â, b̂, ĉ, and ĉ′ (Bollen, 1989, pp. 151–176; MacKinnon, 2008, pp. 151–176).
There is a bias-efficiency trade-off when latent versus observed variables are specified in simple mediation (Ledgerwood & Shrout, 2011). When measurement error is accounted for with latent variables to reduce bias, more parameters (e.g., factor loadings) are estimated and poorer estimate efficiency or larger standard errors result. Conversely, assuming perfect measurement of X, M, and Y with observed variables leads to more efficient estimates at the cost of estimate bias. Despite this conundrum of prioritizing between unbiasedness versus efficiency, non-significant but minimally biased estimates can be more meaningfully interpreted compared to significant but largely biased estimates.
Implications
Accurate conclusions about mediation based on OLS estimates in MLR or ML estimates in SEM require assumptions of normality and the model being exactly correct to be met, but both assumptions are violated in practice. As described above, non-normality can be addressed by using robust estimators or nonlinear models. The imperfection of models is a reality to be acknowledged and addressed by thoughtfully modeling a network of variables instead of perfunctorily conducting statistical procedures. The highly restrictive simple mediation model is not the only model available for studying intervening variable effects or causal mechanisms (Imai, Keele & Tingley, 2010) and SEM can more easily accommodate a larger network of variables to include omitted variables, account for nonlinear effects, and quantify measurement error compared to MLR. Generating multiple competing models, evaluating their fit to the data via SEM, selecting a final model, and eventually validating it in an independent sample effectively addresses issues of working with imperfect models (MacCallum, 2003). Such a process generates new knowledge on what are plausible representations of reality. Another challenge to modeling simple mediation is the existence of equivalent models.
Equivalent Models
Equivalent models are mathematically indistinguishable from one another in terms of goodness-of-fit, even though they have different parameterizations (MacCallum, Wegener, Uchino, & Fabrigar, 1993). The issue of equivalent models is relatively unknown in MLR, but has received much attention in SEM (e.g., Bentler & Satorra, 2010; Hershberger, 2006; Raykov & Marcoulides, 2001) and is highly relevant to simple mediation (c.f., Thoemmes, 2015).
Consider a simple linear regression where Y is regressed onto X (diagram A, Figure 1). The standardized regression coefficient is the Pearson correlation between X and Y, ĉ = rYX, and the variance in Y accounted for by X is the squared correlation . When X is instead regressed onto Y, the standardized regression coefficient is exactly the same, rYX = rXY and . These two models are equivalent and model equations do not reflect directionality between variables (c.f., Venn diagrams). Equivalent models can only be distinguished in terms of their substantive meaning. In this example, one model would be more meaningful than the other if there is a strong reason for designating one variable as predictor and the other as outcome.
The simple mediation model and all MLR models are untestable or saturated models, which have perfect goodness-of-fit. Saturated models perfectly reproduce the means, variances, and correlations of the observed variables and are the basis of the existence of equivalent models (Lee & Hershberger, 1990). Below we illustrate the problem of equivalent models that cannot be tested or compared in simple mediation with a published example.
Empirical demonstration
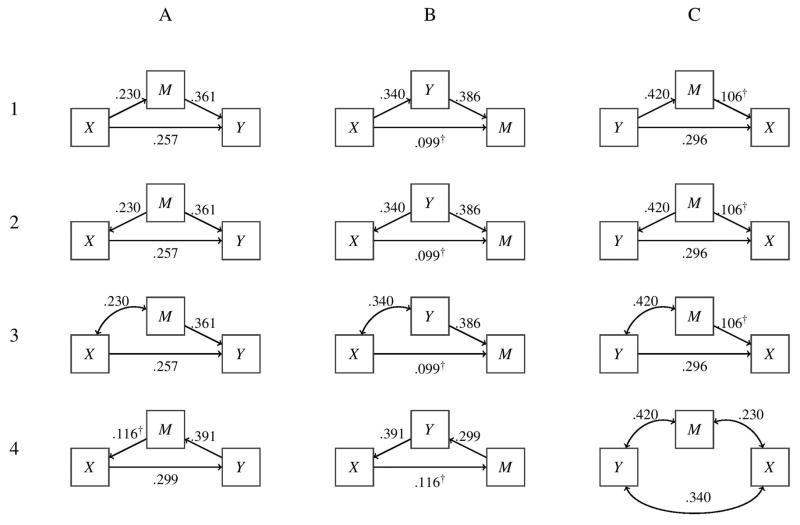
In a cross-sectional study of N = 304 adolescents, Garcia et al. (2012) examined whether positive emotions (Y) were due to persistence (X) through self-directedness or the aptitude in developing good habits for behaving according to long-term values and goals (M). Individual differences in persistence were posited to increase self-directedness, which in turn promotes positive emotions. The diagram A1 of Figure 2 depicts the mediation model reported; the indirect effect was significant, âb̂ = 0.027, Sobel z = 3.55, p < .0001. The researchers concluded that persistent adolescents experience more positive emotions because they are self-directed.
Figure 2.
The set of 12 plausible equivalent models associated with the simple mediation model reported in Garcia et al. (2012). X = persistence, M = self-directedness, and Y = positive affect. All standardized path coefficients and Person correlation coefficients, situated above nondirectional pathways, are significant at α =.05 unless indicated by
Beyond this model, there are 11 equivalent models (see Figure 2). The models depicted in the 12 path diagrams equally account for the data (i.e., they all have perfect goodness-of-fit) and are therefore mathematically indistinguishable from one another. The path diagrams are mainly organized according to the distal outcome of the network of variables by columns; Y is the distal outcome in column A, M is the distal outcome in column B, and X is the distal outcome in column C. The diagrams in the first three rows of Figure 2 preserve the same directional and non-directional paths among the variables and the diagrams in the last row include less conventional equivalent models.
Consider the models in column A. Model A2 is obtained by changing X→M in A1 to M→X, reversing the roles of predictor and outcome. Model A2 states that persistence mediates the relationship between self-directedness and positive affect. Model A2 alternatively supports the interpretation that self-directedness confounds the relationship between persistence and positive affect (c.f., MacKinnon & Pirlott, 2015). Model A3 is obtained from A2 by changing X→M to a non-directional path or correlation; this model is an MLR model where persistence and self-directedness are predictors of positive affect. Path diagram B of Figure 1 is the same model as A3 in Figure 2, where the correlational path is not explicitly depicted.
Model A4 posits a feedback loop where persistence influences positive affect, positive affect influences self-directedness, and self-directedness influences persistence. Model B4 is obtained from A4 where all the directional pathways are reversed. The estimates in A4 and B4 are comparable; the effect of self-directedness on persistence is not significant, suggesting a causal chain with no feedback loop. Finally, model C4 presupposes no directional pathways among the three correlated variables; rXY =.34, rXM = .23, and rMY = .42.
The remaining six equivalent models in columns B and C are different from the models in column A in terms of their distal outcome. Model B1 hypothesizes that persistence influences self-directedness through positive affect. Similarly, model C1 theorizes that self-directedness affects persistence through positive affect. However, mediation is not present as the effect of self-directedness to persistence is not significant. It is conceivable for one to expound on all 12 equivalent models and find existing theories or devise new arguments in support of the purported relationships among X, M, and Y.
MacKinnon, Krull and Lockwood (2000) recognize that mediation, confounding and suppression effects are mathematically equivalent (e.g., models A1 and A2). M could be a mediator, confounder, or suppressor. Reducing these three plausible roles of M and reducing the number of equivalent models that can represent the three variables of X, M, and Y, rests solely on conceptual grounds when no variables are manipulated or assessed at different points in time (MacCallum et al., 1993).
Implications
Absent of random assignment to levels of X, the simple mediation model is equivalent to 11 alternatives and the originally conceived model is not more compelling or meaningful because of its a priori status; this argument assumes that alternative and statistically equivalent models not initially considered are inferior to the a priori model (MacCallum et al., 1993). Such a position is inconsistent with open-mindedness that accompanies radical advancements in science. Equivalent models provide opportunities to consider novel theoretical possibilities that could result in significant breakthroughs. All equivalent models should be generated, considered, and eliminated by evaluating each model in terms of its meaningfulness. Elements of research design are highly useful in reducing the set of equivalent models. Experimental manipulation of X renders directional pathways from M, or Y, to X invalid. Additionally, the ordered measurement of X, M, and Y in a carefully timed longitudinal sequence reduces the number of plausible models to A1, A3 and C4 because M and Y cannot influence X and M, respectively, against the passage of time. With repeated measures of X, Y, and M, the simple mediation model cannot adequately model these data because the stability of and changes in these variables over time as well as their autocorrelation should be taken into account.
Research Design
Experiments
X causes Y when (a) the cause preceded the effect, (b) the cause is related to the effect, and (c) there are no plausible alternative explanations for the effect other than the cause (Shadish et al., 2002). Random assignment of X situates X in time before relevant changes in M and Y occur. Additionally, randomization of X is an external manipulation of the putative cause and reduces potential bias by equalizing the effect of omitted variables across the experimental levels of X. Thus, random assignment in experiments bestows properties to the collected data that allows for causal inferences about X→Y and X→M.
Applications of simple mediation do not typically use experiments. Only 24% of a random sample of 50 out of 410 articles on mediation involved randomized experiments (Gelfand, Mensinger & Tenhave, 2009). This observation possibly reflects the difficulty in randomizing X due to ethical and practical concerns. When randomization is not viable, other methods that eliminate alternative plausible explanations of the effect should be pursued (see MacKinnon & Pirlott, 2015; Murnane & Willett, 2011).
Longitudinal Designs
Any causal effect, say M→Y, cannot occur instantaneously as M is logically placed in time before Y. The superficial use of a longitudinal design does not necessarily address weaknesses of the cross-sectional design (i.e., all variables are measured in the same instance); to properly model and assess mediation, measures of M and Y should be precisely timed such that the anticipated effects of X→M and M→Y have occurred as the process unfolds over time (Cole & Maxwell. 2003; Gollob & Reichardt, 1991). Despite the relevance of longitudinal designs in mediation, cross-sectional studies are the modal design in mediation; 54% were cross-sectional and 21% involved longitudinal measurement (Gelfand et al., 2009). Across five APA journals most likely to have published studies on mediation in 2005, 53% were cross-sectional and 38% were half-longitudinal (Cole & Maxwell, 2003) in that time elapsed either between X and M or M and Y but not both (Maxwell & Cole, 2007). Such trends are alarming because the estimates from cross-sectional designs are highly biased and tend not to be replicated in longitudinal studies (Maxwell & Cole, 2007; Maxwell, Cole & Mitchell, 2011).
Fitting the simple mediation model to repeated measures data is inappropriate and pertinent extensions have been developed for modeling mediation in longitudinal data (see Preacher, 2015). Example modeling frameworks related to SEM are multilevel models (Bauer, Preacher & Gil, 2006; Kenny et al., 2003), latent curve models (Selig & Preacher, 2009), and autoregressive models (Maxwell & Cole, 2007; Maxwell et al., 2011).
Implications
Research design is essential for drawing unequivocal conclusions about causality. Statistical methods cannot atone for shortcomings in research design (e.g., improperly timed measures of X and M; Cole & Maxwell, 2003) and the strongest claims regarding causal mediation are based on studies that utilize elements of experimental manipulation and repeated measures. Although Gelfand et al. (2009) did not identify any study that used experimental manipulation with repeated measures, researchers have started employing these design elements successfully (e.g., Fuemmeler et al., 2006; Tein, Sandler, MacKinnon & Wolchik, 2004).
Discussion and Recommendations
The careful study of causal mechanisms is a challenging but important endeavor (Bullock, Green & Ha, 2010). We reviewed concepts, statistical approaches, and elements of design in studies of simple mediation. The hope is that researchers employing mediation analyses would have an appreciation of these related considerations, promoting informed choices from study conception to completion. Below, we provide recommendations in relation to each aspect of mediation to enhance current practice.
Researchers should explicitly state which concept of mediation is being investigated in order to promote hypothesis validity (Wampold et al., 1990). Hypothesis validity guarantees that researchers are accurately operationalizing their research questions into testable hypotheses, leading to results that address pertinent research questions.
Conducting mediation analyses in a procedural fashion via MLR discourages researchers from thoughtfully puzzling over relations between the variables, leaving them less open to plausible, informative modifications of their initial model. We recommend using SEM over MLR for investigating mediation because the simultaneous and multivariate nature of SEM encourages theorizing about the processes involving X, M, and Y in a plausibly larger network of variables, subtly shifting the statistical focus from applying procedures to modeling phenomena (Rodgers, 2010; Tukey, 1969). The flexibility of SEM also allows for straightforward model modifications to readily address potential problems of model misspecification (e.g., omitted variables, measurement error and nonlinear relationships that are linear in their parameters).
Shifting from MLR to SEM also highlights the issue of equivalent models. When randomization to levels of X and the measurement of X, M, and Y at appropriately spaced time points are not features of the research design, there are 11 models that are mathematically identical to a given arrangement of variables in the simple mediation model. Such equivalent models may suggest plausible relationships among the variables and aid in theory development. All equivalent models should be considered and discussed as part of the process of arriving at the final model.
The study of causal relationships necessitates the use of experimental manipulation with randomization. In simple mediation, X is manipulated whereas M is not because M has to take on values caused by X. Studies designed to examine mediation have the unavoidable weakness of being unable to form strong causal inferences about M→Y. One solution is to establish the causal path M→Y in a separate study and plan to replicate the effect in a study designed to evaluate the full causal chain posited in mediation models (MacKinnon & Pirlott, 2015).
The use of cross-sectional designs for studying mediation is strongly discouraged because the results they produce can be biased and misleading. Instead, longitudinal designs rightly recognize that mediation is about processes that unfold over time. Multiple measures of X, M, and Y should be collected such that the nature of how the process unfolds could be closely modeled, especially when the timing of the full effect of X on M and M on Y are unknown. Ultimately, the simple mediation model is ineffective in evaluating causal processes and mechanisms.
Methodological approaches for more complex models of mediation are an active field of inquiry and mediation as a framework is one of the most mature and well-developed approaches for understanding causal processes. Researchers should abandon simple mediation models for more complex models, especially longitudinal models, which better answer questions about causal mechanisms. The careful consideration of the issues we have raised and implementation of the recommendations we have offered would further advance the discovery and explication of causal mechanisms.
Acknowledgments
This work was supported by the Social Sciences and Humanities Research Council of Canada Insight Development Grant awarded to Jolynn Pek. During preparation of this manuscript, the second author was supported by National Institute on Drug Abuse (NIDA) Grant P30 DA023026. The contents of this manuscript are solely the responsibility of the authors and do not necessarily represent the official views of NIDA. We thank R. Philip Chalmers for his assistance with Figure 2.
Contributor Information
Jolynn Pek, York University.
Rick H. Hoyle, Duke University
References
- Angrist JD, Imbens GW, Rubin DB. Identification of causal effects using instrumental variables. Journal of the American Statistical Association. 1996;91:444–455. doi: 10.1080/01621459.1996.10476902. [DOI] [Google Scholar]
- Baron RM, Kenny DA. The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037/0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Bauer DJ, Preacher KJ, Gil KM. Conceptualizing and testing random indirect effects and moderated mediation in multilevel models: New procedures and recommendations. Psychological Methods. 2006;11:142–163. doi: 10.1037/1082-989X.11.2.142. [DOI] [PubMed] [Google Scholar]
- Bentler PM, Satorra A. Testing model nesting and equivalence. Psychological Methods. 2010;15:111–123. doi: 10.1037/a0019625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biesanz JC, Falk CF, Savalei V. Assessing mediational models: Testing and interval estimation for indirect effects. Multivariate Behavioral Research. 2010;45:661–701. doi: 10.1080/00273171.2010.498292. [DOI] [PubMed] [Google Scholar]
- Bollen KA. Structural equation models with latent variables. New York: Wiley; 1989. [Google Scholar]
- Bollen KA, Stine R. Direct and indirect effects: Classical and bootstrap estimates of variability. Sociological Methodology. 1990;20:15–140. doi: 10.1177/0049124192021002004. [DOI] [Google Scholar]
- Bullock JG, Green DP, Ha SE. Yes, but what’s the mechanism? (Don’t expect an easy answer) Journal of Personality and Social Psychology. 2010;98:550–558. doi: 10.1037/a0018933. [DOI] [PubMed] [Google Scholar]
- Coffman DL. Estimating causal effects in mediation analysis using propensity scores. Structural Equation Modeling. 2011;18:357–369. doi: 10.1080/10705511.2011.582001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coffman DL, Zhong W. Assessing mediation using marginal structural models in the presence of confounding and moderation. Psychological Methods. 2012;17:642–664. doi: 10.1037/a0029311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole DA, Maxwell SE. Testing mediational models with longitudinal data: questions and tips in the use of structural equation modeling. Journal of Abnormal Psychology. 2003;112:558–577. doi: 10.1037/0021-843X.112.4.558. [DOI] [PubMed] [Google Scholar]
- Davis MD. The logic of causal order. Beverly Hills, CA: Sage; 1985. [Google Scholar]
- Fuemmeler BF, Mâsse LC, Yaroch AL, Resnicow K, Campbell MK, Carr C, Williams A. Psychosocial mediation of fruit and vegetable consumption in the body and soul effectiveness trial. Health Psychology. 2006;25:474–483. doi: 10.1037/0278-6133.25.4.474. [DOI] [PubMed] [Google Scholar]
- Garcia D, Kerekes N, Archer T. A will and a proper way leading to happiness: Self-directedness mediates the effect of persistence on positive affectivity. Personality and Individual Differences. 2012;53:1034–1038. doi: 10.1016/j.paid.2012.07.025. [DOI] [Google Scholar]
- Gelfand LA, Mensinger JL, Tenhave T. Mediation analysis: A retrospective snapshot of practice and more recent directions. The Journal of General Psychology. 2009;136:153–178. doi: 10.3200/GENP.136.2.153-178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gollob HF, Reichardt CS. Interpreting and estimating indirect effects assuming time lags really matter. In: Collins LM, Horn JL, editors. Best methods for the analysis of change: Recent advances, unanswered questions, future directions. Washington, DC: American Psychological Association; 1991. pp. 243–259. [Google Scholar]
- Hershberger SL. The problem of equivalent structural models. In: Hancock GR, Mueller RO, editors. Structural equation modeling: A second course. Charlotte, NC: Information Age; 2006. pp. 13–41. [Google Scholar]
- Hoyle RH, Kenny DA. Sample size, reliability, and tests of statistical mediation. In: Hoyle RH, editor. Statistical strategies for small sample research. Thousand Oaks, CA: Sage; 1999. pp. 195–222. [Google Scholar]
- Iacobucci D, Saldanha N, Deng X. A meditation on mediation: Evidence that structural equations models perform better than regressions. Journal of Consumer Psychology. 2007;17:139–153. doi: 10.1016/S1057-7408(07)70020-7. [DOI] [Google Scholar]
- Imai K, Keele L, Tingley D. A general approach to causal mediation analysis. Psychological Methods. 2010;15:309–334. doi: 10.1037/a0020761. [DOI] [PubMed] [Google Scholar]
- Jo B. Causal inference in randomized experiments with mediational processes. Psychological Methods. 2008;13:314–336. doi: 10.1037/a0014207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Judd CM, Kenny DA. Process analysis estimating mediation in treatment evaluations. Evaluation Review. 1981;5:602–619. doi: 10.1177/0193841X8100500502. [DOI] [Google Scholar]
- Kashy DA, Donnellan MB, Ackerman RA, Russell DW. Reporting and interpreting research in PSPB: Practices, principles, and pragmatics. Personality and Social Psychology Bulletin. 2009;35:1131–1142. doi: 10.1177/0146167208331253. [DOI] [PubMed] [Google Scholar]
- Kenny DA, Kashy DD, Bolger N. Data analysis in social psychology. In: Gilbert D, Fiske S, Lindzey G, editors. Handbook of social psychology. 4. New York, NY: McGraw-Hill; 1998. pp. 233–265. [Google Scholar]
- Kenny DA, Korchmaros JD, Bolger N. Lower level mediation in multilevel models. Psychological Methods. 2003;8:115–128. doi: 10.1037/1082-989X.8.2.115. [DOI] [PubMed] [Google Scholar]
- Ledgerwood A, Shrout PE. The trade-off between accuracy and precision in latent variable models of mediation processes. Journal of Personality and Social Psychology. 2011;101:1174–1188. doi: 10.1037/a0024776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S, Hershberger S. A simple rule for generating equivalent models in covariance structure modeling. Multivariate Behavioral Research. 1990;25:313–334. doi: 10.1207/s15327906mbr25034. [DOI] [PubMed] [Google Scholar]
- Long JS, Ervin LH. Using heteroscedasticity consistent standard errors in the linear regression model. The American Statistician. 2000;54:217–224. doi: 10.1080/00031305.2000.10474549. [DOI] [Google Scholar]
- MacCallum RC. 2001 presidential address: Working with imperfect models. Multivariate Behavioral Research. 2003;38:113–139. doi: 10.1207/S15327906MBR3801_5. [DOI] [PubMed] [Google Scholar]
- MacCallum RC, Wegener DT, Uchino BN, Fabrigar LR. The problem of equivalent models in applications of covariance structure analysis. Psychological Bulletin. 1993;114:185–199. doi: 10.1037/0033-2909.114.1.185. [DOI] [PubMed] [Google Scholar]
- MacKinnon DP. Introduction to statistical mediation analysis. New York, NY: Lawrence Erlbaum Associates; 2008. [Google Scholar]
- MacKinnon DP, Fairchild AJ, Fritz MS. Mediation analysis. Annual Review of Psychology. 2007;58:593–614. doi: 10.1146/annurev.psych.58.110405.085542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Fritz MS, Williams J, Lockwood CM. Distribution of the product confidence limits for the indirect effect: Program PRODCLIN. Behavior Research Methods. 2007;39:384–389. doi: 10.3758/BF03193007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Krull JL, Lockwood CM. Equivalence of the mediation, confounding and suppression effect. Prevention Science. 2000;1:173–181. doi: 10.1023/A:1026595011371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Brown CH, Wang W, Hoffman JM. The intermediate endpoint effect in logistic and probit regression. Clinical Trials. 2007;4:499–513. doi: 10.1177/1740774507083434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychological Methods. 2002;7:83–104. doi: 10.1037/1082-989X.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Pirlott AG. Statistical approaches for enhancing causal interpretation of the M to Y relation in mediation analysis. Personality and Social Psychology Review. 2015;19:30–43. doi: 10.1177/1088868314542878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maier MA, Elliot AJ, Lichtenfeld S. Mediation of the negative effect of red on intellectual performance. Personality and Social Psychology Bulletin. 2008;34:1530–1540. doi: 10.1177/0146167208323104. [DOI] [PubMed] [Google Scholar]
- Maxwell SE, Cole DA. Bias in cross-sectional analyses of longitudinal mediation. Psychological Methods. 2007;12:23–44. doi: 10.1037/1082-989X.12.1.23. [DOI] [PubMed] [Google Scholar]
- Maxwell SE, Cole DA, Mitchell MA. Bias in cross-sectional analyses of longitudinal mediation: Partial and complete mediation under an autoregressive model. Multivariate Behavioral Research. 2011;46:816–841. doi: 10.1080/00273171.2011.606716. [DOI] [PubMed] [Google Scholar]
- Muller D, Judd CM, Yzerbyt VY. When moderation is mediated and mediation is moderated. Journal of Personality and Social Psychology. 2005;89:852–863. doi: 10.1037/0022-3514.89.6.852. [DOI] [PubMed] [Google Scholar]
- Murnane RJ, Willett JB. Methods matter: Improving causal inference in educational and social science research. New York, NY: Oxford University Press; 2011. [Google Scholar]
- Muthén LK, Muthén BO. Mplus user’s guide. 7. Los Angeles, CA: Muthén & Muthén; 2012. Computer software manual. [Google Scholar]
- Neale MC, Hunter MD, Pritkin J, Zahery M, Brick TR, Kirkpatrick RM, Boker SM. OpenMx 2.0: Extended structural equation and statistical modeling. Psychometrika. 2015 doi: 10.1007/s11336-014-9435-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearl J. Interpretation and identification of causal mediation. Psychological Methods. 2014;19:459–481. doi: 10.1037/a0036434. [DOI] [PubMed] [Google Scholar]
- Preacher KJ. Advances in mediation analysis: A survey and synthesis of new developments. Annual Review of Psychology. 2015;66:825–852. doi: 10.1146/annurev-psych-010814-015258. [DOI] [PubMed] [Google Scholar]
- Preacher KJ, Rucker DD, Hayes AF. Addressing moderated mediation hypotheses: Theory, methods, and prescriptions. Multivariate Behavioral Research. 2007;42:185–227. doi: 10.1080/00273170701341316. [DOI] [PubMed] [Google Scholar]
- Preacher KJ, Zyphur MJ, Zhang Z. A general multilevel SEM framework for assessing multilevel mediation. Psychological Methods. 2010;15:209–233. doi: 10.1037/a0020141. [DOI] [PubMed] [Google Scholar]
- Raykov T, Marcoulides GA. Can there be infinitely many models equivalent to a given covariance structure model? Structural Equation Modeling. 2001;8:142–149. doi: 10.1207/S15328007SEM08018. [DOI] [Google Scholar]
- Rodgers JL. The epistemology of mathematical and statistical modeling: A quiet methodological revolution. American Psychologist. 2010;65:1–12. doi: 10.1037/a0018326. [DOI] [PubMed] [Google Scholar]
- Rucker DD, Preacher KJ, Tormala ZL, Petty RE. Mediation analysis in social psychology: Current practices and new recommendations. Social and Personality Psychology Compass. 2011;5:359–371. doi: 10.1111/j.1751-9004.2011.00355.x. [DOI] [Google Scholar]
- Savalei V. Understanding robust corrections in structural equation modeling. Structural Equation Modeling. 2014;21:149–160. doi: 10.1080/10705511.2013.824793. [DOI] [Google Scholar]
- Selig JP, Preacher KJ. Mediation models for longitudinal data in developmental research. Research in Human Development. 2009;6:144–164. doi: 10.1080/15427600902911247. [DOI] [Google Scholar]
- Shadish WR, Cook TD, Campbell DT. Experimental and quasi-experimental designs for generalized causal inference. Boston, MA: Houghton Mifflin; 2002. [Google Scholar]
- Sobel ME. Asymptotic confidence intervals for indirect effects in structural equation models. Sociological Methodology. 1982;13:290–312. doi: 10.2307/270723. [DOI] [Google Scholar]
- Sobel ME. Some new results on indirect effects and their standard errors in covariance structure models. Sociological Methodology. 1986;16:159–186. Retrieved from http://www.jstor.org/stable/270922. [Google Scholar]
- Spencer SJ, Zanna MP, Fong GT. Establishing a causal chain: Why experiments are often more effective than mediational analyses in examining psychological processes. Journal of Personality and Social Psychology. 2005;89:845–851. doi: 10.1037/0022-3514.89.6.845. [DOI] [PubMed] [Google Scholar]
- Tein JY, Sandler IN, MacKinnon DP, Wolchik SA. How did it work? Who did it work for? Mediation in the context of a moderated prevention effect for children of divorce. Journal of Consulting and Clinical Psychology. 2004;72:617–624. doi: 10.1037/0022-006X.72.4.617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thoemmes F. Reversing arrows in mediation models does not distinguish plausible models. Basic and Applied Social Psychology. 2015;37:226–234. doi: 10.1080/01973533.2015.1049351. [DOI] [Google Scholar]
- Tukey JW. Analyzing data: Sanctification or detective work? American Psychologist. 1969;24:83–91. [Google Scholar]
- Wampold BE, Davis B, Good RH. Hypothesis validity of clinical research. Journal of Consulting and Clinical Psychology. 1990;58:360–367. doi: 10.1037/0022-006X.58.3.360. [DOI] [PubMed] [Google Scholar]
- Winship C, Morgan SL. The estimation of causal effects from observational data. Annual Review of Sociology. 1999;25:659–706. Retrieved from http://www.jstor.org/stable/22352. [Google Scholar]