Comparing Smoothing Techniques for Fitting the Nonlinear Effect of Covariate in Cox Models

Abstract

Background and Objective:

Cox model is a popular model in survival analysis, which assumes linearity of the covariate on the log hazard function, While continuous covariates can affect the hazard through more complicated nonlinear functional forms and therefore, Cox models with continuous covariates are prone to misspecification due to not fitting the correct functional form for continuous covariates. In this study, a smooth nonlinear covariate effect would be approximated by different spline functions.

Material and Methods:

We applied three flexible nonparametric smoothing techniques for nonlinear covariate effect in the Cox models: penalized splines, restricted cubic splines and natural splines. Akaike information criterion (AIC) and degrees of freedom were used to smoothing parameter selection in penalized splines model. The ability of nonparametric methods was evaluated to recover the true functional form of linear, quadratic and nonlinear functions, using different simulated sample sizes. Data analysis was carried out using R 2.11.0 software and significant levels were considered 0.05.

Results:

Based on AIC, the penalized spline method had consistently lower mean square error compared to others to selection of smoothed parameter. The same result was obtained with real data.

Conclusion:

Penalized spline smoothing method, with AIC to smoothing parameter selection, was more accurate in evaluate of relation between covariate and log hazard function than other methods.

1. INTRODUCTION

The Cox Proportional Hazard model is a popular model in survival analysis for detecting the effect of some set of variables on the Hazard. This model is popular largely because there is no need to consider specific distribution function to the hazard function. In Cox proportional hazard model

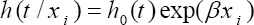
Is Unspecified and non-negative function of time that called a baseline hazard function and is a matrices of covariates related to the i_th person (1). One of the important assumptions in Cox model is that the covariate has a linear effect on the log hazard function. However, Continuous variables can be an influence on the risk with non-linear forms and ignoring this can alter the results (2).

Adding a nonlinear function to a variable in the Cox model needs to rewrite the model as follows:

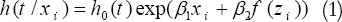
In this case, the effect of the z is done on a baseline hazard function through f function. Nature Conservation of survival data makes that non linear form of variables be more than linear form. Fitting bad functional form to the data is a state of a curse of dimensionality and lead to bias and reduce the power of relation statistical tests (3).

LeBlanc and Crowley showed that mean error of the Cox model with inappropriate functional form three times higher than the model that includes the nonlinear functional effect form (4). Functional form of the covariate can be added to the model directly and then decision making about Stay nonlinear effects in the model with Wald’s statistic (1).

Smoothing methods include techniques such as kernel smoothing, polynomials and splines. Kernel smoothing uses a set of local weights to generate a smoothed estimate. However, in certain applications, this can be mathematically difficult.

Polynomials are the simplest functional smoothed form, where you can easily add the term to the right of the model. But the use of polynomials is a crude method for estimation, which may be a complex function (5). An alternative approach would be splines, which they used to fit nonlinear relationships. Splines are pieced of polynomial functions that limited to certain control points, which called knots (6).

Splines are sensitive to the number and position of knots. Unlike polynomials, allow for a more local fit to the data and fitting after the knots can be limited to the linear (7). Generally, there are three methods to estimate splines: smoothing splines, polynomial splines and penalized splines. Better performance of polynomial splines depends on the number and location of knots. To overcome this problem, smoothing splines uses all of points as knots. But when you have a large number of discrete time points, the number of parameters that must be estimated to be high and this is will be complicated calculations (8). Smoothing splines like polynomial splines use a large number of knots, while reduce the influence of knots with a penalized term. Penalized spline is very similar to smoothing splines, but use a fewer knot significantly (3).

The model restrictions are incorporated in the splines; this leads to a better fit. For example, restricted cubic spline, which is also known as natural cubic splines, is the limited cubic spline that the tails are limited to linear. In this method, the number of knots previously known and their positions are based on data quantile (9). In this paper, three smoothing methods that have been used in the last decade in medicine and epidemiology studies have examined: Penalize spline, restricted cubic spline and natural spline. All these methods can easily include to the Cox and linear models.

2. METHODS

In this analytical study to determine the nonlinear effects of covariate three non-parametric methods Penalize spline, restricted cubic spline and natural spline in Cox model were used. The ability of nonparametric methods was evaluated to recover the true functional form of linear, quadratic and nonlinear functions, using different simulated sample sizes. Data analysis was carried out using R 3.1.0 software and significant levels were considered 0.05.

2.1. Spline

The most common method of estimating function of f function in equation (1) is the use of splines. The Spline linear estimator is as follows:

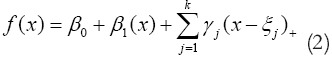
That 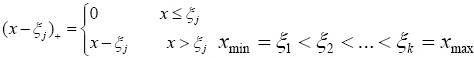are the knots. Linear estimator of spline can be a sequence of linear pieces which knots are continuous functions. More generally a piece of polynomials of degree p can be written as follows:

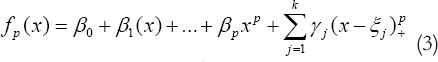
That are the basic functions and any spline with p 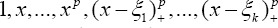degree is the Linear combination of these functions. However, the number and location of knots in the spline functions play an important role to estimate link function. For a specified number of knots can place them position in equal proportions between the minimum and maximum of continuous variable. Usually, can put number of knots between 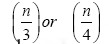. Ruppert presented a study on selection of in detail. And noted that the best interval for the number of nodes can be (10).

2.2. Penalized spline

Using high knots caused overestimation and use of knots with a small number, it is estimated to be low. This method is based on reducing the number of knots so that the number of knots greater than the number of knots required for spline regression method but is less than the number of knots in smoothing spline method. For this purpose, penalize smoothing can be used. In penalized spline:

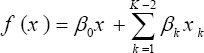
That’s is the Non-linear basis functions proportional with the knots. At this stage, the piece of cubic polynomial or other types of this polynomials such as B-spline or truncated power bases may be used. In restricted cubic spline, coefficient of knots are estimated by maximizing the partial likelihood function but this coefficients are estimated with added λ the at The second derivative of f as follows:

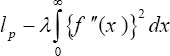
That’s is the log of partial likelihood. Spline function with two different implementation in R software for Cox model was considered. In the standard implementation df = 4 are used as a criterion for smoothing whereas in the other method the minimizing of AIC criteria is used for determining the degree of freedom.

2.3. Restricted cubic spline

Restricted cubic spline are the cubic spline regression that first and second derivatives are continuous in knots. This method is limited to after the last knot and before the first knot to be linear. Although linear sequence of the model may be causes the inadequacy. To use this method, at first determined the number of knots on a covariate. In standard statistical software, this amount is pre-determined on quantiles of covariate. In this way, we can write f as equation:

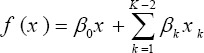
Spline variable that provided by restricted cubic spline function are placed in the Cox proportional hazard regression model. The predetermined number of knots in a standard software including R in order rcspline.eval, 4 knots are equal to the distance that uses truncated power basis.

2.4. Natural spline:

Natural spline basically is restricted cubic spline that used B-spline functions instead of a piece of polynomial to estimate. Function ns in R software uses a df=4.

2.5. Simulation:

Smoothing methods in Cox proportional hazard models were compared through simulation. Focusing on the estimated ability to detect coverage of functional relationship between independent variables and survival time. Comparisons are based on simulated data of these functions:

For each function, three different sample sizes were generated with 500 replicated for one hundred equally spaced design points between 0.05 to 5. Such as Bender (11) and Strasak (12) for generated outcome data in cox proportional hazard model hazard rate where the baseline hazard is given by 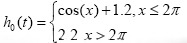was considered. Independent censoring times was generated from. The goodness of fit was measured by the empirical mean squared error (MSE), 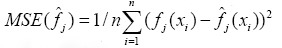. The results of MSE are shown in Table 1.

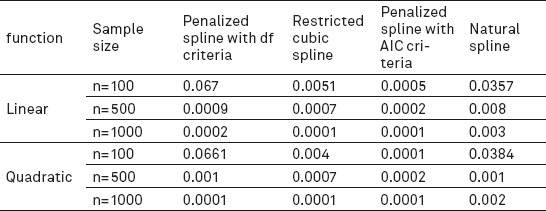
Table 1.

The mean square error of experiments with three different sample size for the above-mentioned methods

3. RESULTS

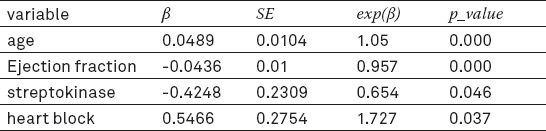
To compare methods of smoothing, patients with acute myocardial infarction information was used. Information including gender, age, diabetes, block, taking A streptokinase, ejection fraction, blood pressure, cholesterol, arrhythmia and so on are collected for 650 patients with acute myocardial infarction. Esamail Nasab and et al. primary examined data on the Cox model (13). The results of Cox model for two factors, streptokinase and heart blocks and two continuous variables, age and ejection fraction are listed in Table 2.

Table 2.

Results of Cox model for coronary artery disease.

As expected, With the change parameter of exponential distribution data with different levels of censoring were generated and, no change in mean square.

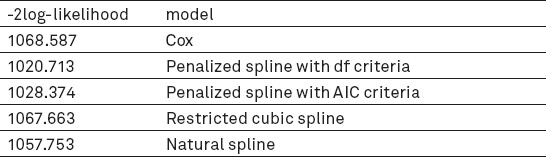
For each of the methods of smoothing 2 log-likelihood for the model on continuous variables age and ejection fraction are shown in Table 3.

Table 3.

2 log-likelihood scores for the models used to estimate the survival rate of patients with coronary artery disease.

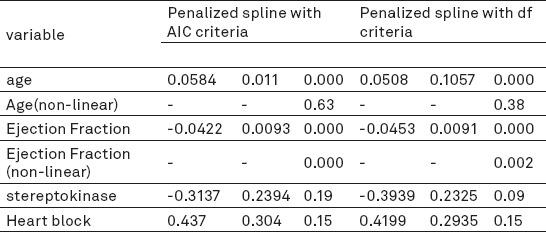
The log of hazard versus two continuously variable based on the smoothing methods have been shown in Figure 1. Akaike information criterion (AIC) and degrees of freedom were used to smoothing parameter selection in penalized splines model. This criteria was different from standard criteria to determine the number of knots in the penalized splines. The results of fitting the penalized splines model in two different situation are shown in Table 4.

Graph 1.

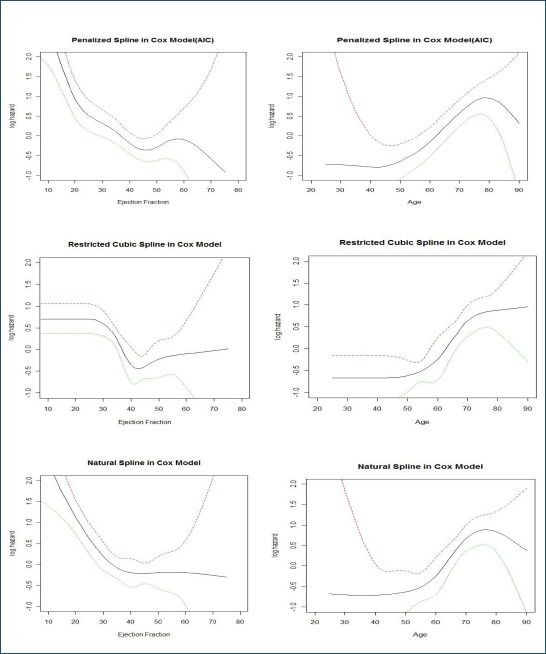
The log of hazard versus age and ejection fraction with 95% CI.

Table 4.

The results of penalized splines with the AIC and the degree of freedom in determining the smoothing parameter

4. DISCUSSION

Cox regression model using three methods of smoothing the nonlinear effects on cardiovascular disease data that leads to determine the relationship between death and cardiovascular disease risk factors and also in simulated data to be considered.

The results of mean square error showed that the penalized splines has the lowest AIC criteria in all cases the non-linear relationship between the hazard logarithm and the risk factors was considered. This decline continued with increasing sample size. The mean square error for other methods decreased By increasing the sample size and it can be said that this value except for natural spline smoothing technique was the same as other models with a sample size of 1000.

In Table 1, by increasing the sample size from 100 to 500 and higher reduce of mean square error for penalized splines with degrees of freedom is more intuitive than other methods. But in general it can be said that the performance of penalized splines with AIC criteria used for all functions is better than the other methods.

Given the significant difference between penalized splines with two different criteria for determining the smoothness parameter, it seems that AIC criteria is more accurate than other measures. Malloy and et al. (14) compares the methods of smoothing parameter with penalized splines in the Cox model. In The simulation study presented, any of the measures had no preferences. However, AIC and adjusted AIC criteria have the lowest mean square error.

Sleeper and Harrington (1) were used the spline regression with close ties to estimate the effects of covariates in the Cox proportional hazard model. They suggest that 5 or less than 5 knots it is necessary to do so.

Le Blanc and Crowley (4) were used the adjusted method for selecting the location of other knots in the spline regression for Cox proportional hazard model. Although their methods used the piecewise linear functions to fit the model.

Gray (7) was offered the cubic spline with certain changes, which are calculated by using a smaller set of knot. He used 10 knots and cubic splines between knots. In this study, the more knots and B-spline are used.

In the actual data that the relationship between death and other cardiovascular risk factors were unknown, instead of the mean square error criteria, the log-likelihood criterion was used. The results of the log-likelihood shows that the penalized splines with AIC criterion in determining the number of knots have the best fit. Although the log-likelihood values are not a lot of difference and it is not clear which of the methods are preferable.

Eliers and Marx (15) suggested that the degree of freedom in the penalized splines method selecting by AIC criteria, although these measures may lead to less smooth in data with high dispersion.

Fractional polynomials also another kind of smoothing methods, which are distributed between splines and polynomials. Strasak et al. (12) were deficit that penalized splines in certain cases are superior than the fractional functions.

Due to Figure 1, natural spline and restricted cubic spline not have an ability to fit any relationship between age and ejection fraction with the log hazard function as penalized splines. Based on estimated regression coefficients in smoothing methods, significant variables were changed. Non-linear effect of age in Table 4 according to the method of penalized splines in the two cases considered, was not significant. All three methods have an improper fit that it is specified particularly from the primary point of lower confidence interval in Figure 1. Yao and Lee (16) offered a new algorithm to locate the knots in a variable range for the smoothing method of penalized splines to linear models, which can be continued using them in future studies for Cox model and can be continued study with different types of censorship.

5. CONCLUSION

Penalize spline smoothing method with AIC criteria to determining the smoothing parameter provides more accurate than other methods of smoothing in determining the relationship between the logarithm of hazard and covariates in the Cox regression model.