Ngram time series model to predict activity type and energy cost from wrist, hip and ankle accelerometers: implications of age

Abstract

To develop and test time series single site and multi-site placement models, we used wrist, hip and ankle processed accelerometer data to estimate energy cost and type of physical activity in adults. Ninety-nine subjects in three age groups (18–39, 40–64, 65 + years) performed 11 activities while wearing three triaxial accelereometers: one each on the non-dominant wrist, hip, and ankle. During each activity net oxygen cost (METs) was assessed. The time series of accelerometer signals were represented in terms of uniformly discretized values called bins. Support Vector Machine was used for activity classification with bins and every pair of bins used as features. Bagged decision tree regression was used for net metabolic cost prediction. To evaluate model performance we employed the jackknife leave-one-out cross validation method. Single accelerometer and multi-accelerometer site model estimates across and within age group revealed similar accuracy, with a bias range of −0.03 to 0.01 METs, bias percent of −0.8 to 0.3%, and a rMSE range of 0.81–1.04 METs. Multi-site accelerometer location models improved activity type classification over single site location models from a low of 69.3% to a maximum of 92.8% accuracy. For each accelerometer site location model, or combined site location model, percent accuracy classification decreased as a function of age group, or when young age groups models were generalized to older age groups. Specific age group models on average performed better than when all age groups were combined. A time series computation show promising results for predicting energy cost and activity type. Differences in prediction across age group, a lack of generalizability across age groups, and that age group specific models perform better than when all ages are combined needs to be considered as analytic calibration procedures to detect energy cost and type are further developed.

Introduction

Accurate and precise measurement of free-living physical activity (PA) is essential to elucidate determinants of PA behavior, discern the role PA has in the etiology and prevention/rehabilitation of chronic disease, conduct national PA surveillance, and evaluate efficacy of activity enhancing interventions. The current quandary faced is that free-living PA is a complex behavior to assess. There is a need for assessment methodologies to be able to assess free-living activities that can be short and sporadic in nature, of varying PA intensities (PAI) and resulting energy cost, and those that can span many different activity domains (e.g. occupation, transportation, household, and leisure-time). In an effort to answer this need, the last 10–15 years has seen a tremendous growth in the use of portable motion sensors, notably accelerometer sensor technology, and accelerometer data processing methods.

In the past, accelerometer output was largely reported as summations of accelerometer scores, typically as counts per minute. Such counts per minute units were generally arbitrary and device specific, and summation intervals were largely based upon memory and battery life capacity. From accelerometer data, regression approaches were used to estimate energy cost of PA, or time spent in different PAI level (Freedson et al 1998, Hendelman et al 2000, Swartz et al 2000, Matthews 2005, Crouter et al 2006, Heil 2006, Crouter and Bassett 2008, Crouter et al 2010). These regression formulas were developed from laboratory walking and running activities (Freedson et al 1998), or walking and running activities combined with simulated activities of daily living (Freedson et al 1998, Hendelman et al 2000, Swartz et al 2000, Crouter et al 2006, Heil 2006, Crouter and Bassett 2008, Crouter et al 2010). These regression estimates have been noted as being problematic because of the large individual error associated with PA prediction (Strath et al 2003, Lyden et al 2011) and an inability to accurately assess PAI across different activity domains (Ward 2005). Advancement in accelerometer sensor technology now allows for large quantities of acceleration data to be captured and stored for long periods of time, allowing for more sophisticated computation methods, such as machine learning, a branch of artificial intelligence, in an attempt to increase accuracy and precision of accelerometer estimates of free-living PA.

Machine learning approaches applied to PA assessment utilize accelerometer sensor signals derived from activities and ‘learn’ how they relate to the energy cost of movement and the type of movement. There are a number of different machine learning approaches, some currently employed ones using accelerometer data include hidden Markov models (Pober et al 2006), decision trees (Bao and Intille 2004, Ermes et al 2008), and artificial neural networks (Zhang et al 2003, 2012, Rothney et al 2007, Staudenmayer et al 2009). Current machine learning approaches offer more accuracy and precision over traditional regression approaches to estimate energy cost (Staudenmayer et al 2009). This has been shown with methods employing multiple accelerometers (Rothney et al 2007, Zhang et al 2012, Mannini et al 2013), wrist worn accelerometers (Zhang et al 2012) and more commonly a single accelerometer placed on either the hip or low back (Bonomi et al 2009a, 2009b, 2010, Staudenmayer et al 2009, Freedson et al 2011). Furthermore, a major advancement to this data processing method is the ability to accurately predict activity domain and type (Bonomi et al 2009a, 2009b, Staudenmayer et al 2009, Freedson et al 2011). These results show promise for advanced computational approaches as an accurate and precise method to assess both PA energy cost and activity type.

Machine learning methods require data to be represented in terms of features and their values. Since the data for PA assessment task is in the form of time series of accelerometer signals, it does not lend itself to an obvious feature representation. The previous machine learning approaches applied to PA assessment task used carefully engineered and often complex statistical features which were thought to be a good representation for the accelerometer time series. The approach presented in this paper does not require any feature engineering and uses very simple features which are discretized values straight from the accelerometer time series. The idea of this simple feature representation for time series is borrowed from the ngram model used to represent text documents for document classification and other tasks in natural language processing (Jurafsky and Martin 2008) and information retrieval (Manning et al 2008). This method of representing time series in terms of ngrams has been recently used for other classification tasks (Lin and Li 2009, Ordonez et al 2011 December 18–21), however, to our knowledge it has not been used for predicting numerical values, and it has not been applied to accelerometer sensor data in an effort to evaluate predictive capabilities for both energy cost and activity type.

To date there has been limited attention given to how developed computational methods using single site accelerometer placement, or multi-site accelerometer placement perform across different age-groups. Advancement in age is accompanied with greater inter- and intra-variability in movement, including variability in gait (Callisaya et al 2010b), and greater upper body movement variability during designated tasks (Darling et al 1989). Because of known movement pattern differences that occur with age, machine learning approaches may not be able to generalize particularly well to older subjects when trained on data from younger individuals. Hence there is a strong scientific need to evaluate machine learning data processing approaches across the aging spectrum. Accordingly, the purpose of this study was two-fold: first to examine an ngram machine learning computational approach applied to portable accelerometer sensor data and evaluate whether multi-limb monitoring would improve upon single site accelerometer PA cost and activity type classification; and second, to examine generalizability of model predictions developed on the young across identified age group classifications compared with age group specific model predictions.

Methods

Participants

Ninety-nine adults were recruited by local advertisement to participate in this study. Participants were block recruited by both age and gender. Thirty-three adults were within a 18–39 years (17 male, 16 female), 40–64 years (16 male, 17 female), and 65+ years age group classification (15 male, 18 female), respectively. All procedures were approved by the local institutional ethics review board, and all participants provided written informed consent prior to starting the study.

Study overview

Participants reported to the Clinical and Translational Science Institutes Adult Translational Research Unit (CTSI TRU) at the Medical College of Wisconsin early in the morning on day number 1. On this day participants were consented, underwent a measure for resting metabolic rate (RMR), and had general anthropometrics assessed. Following this visit, all participants reported to the Physical Activity and Health Research Laboratory at the University of Wisconsin-Milwaukee. During this visit, each participant underwent a measure of body composition via a dual energy x-ray absorptiometry (DEXA) scan and completed a total of 11 different activities comprised of general walking activities and typical activities of daily living. During these activities participants wore a portable metabolic measurement system to assess energy cost of each activity, while also wearing three accelerometers, one each placed on the non-dominant side for hip, wrist, and ankle.

Anthropometrics and body composition

Anthropometrics were taken in the morning following an overnight fast. Body mass (kg), measured to the nearest 0.01 kg, and height (cm), measured to the nearest 0.1 cm, with minimal clothing and no shoes were taken using a calibrated physician’s scale and stadiometer (Detecto, Kansas City, MS). Body mass index (BMI) was calculated by dividing body mass (kg) by height squared (m²). Body composition was assessed using three-compartmental total body fat using DXA (GE Lunar Prodigy, Madison, WI).

Resting metabolic rate

RMR was assessed following recommended measurement conditions (Compher et al 2006). All participants refrained from engagement in intense PA the day prior to reporting to the CTSI TRU early in the morning after a 12 h fast. All measurements were taken in a quiet and constant temperature (~24 °C, ~50% humidity) condition. All participants were awake in a supine position for 30 min. Respiratory exchange measurements were determined by an open-circuit computerized indirect calorimeter method (ParvoMedics 2400 TrueOne, Sandy UT) utilizing a flow-through transparent canopy-hood. The system was calibrated each morning prior to use with a reference gas mixture of 1.00% for carbon dioxide and 19.51% for oxygen. The first 10 min of each person’s data were disregarded following rest. A minimum of 10 min of steady-state conditions (<5% coefficient of variation) were used for the calculated of RMR.

Physical activity battery

Each participant completed six treadmill walking activities, 7 min each, 40.2–107.2 m·min⁻¹ in 13.4 m·min⁻¹ increments. Following a rest period of 15 min each participant was then asked to complete the following activities of daily living, computer work, vacuuming, mopping/sweeping, carrying/lifting boxes of three different weights (4.5, 6.8, and 9.1 kg), and walking/intermittent stair climbing, for 7 min each. During this time each person was fitted with a portable computerized indirect calorimeter metabolic measurement system (Cosmed K4b², Cosmed, S.r.l., Italy). This portable system has been shown to be valid (McLaughlin et al 2001) across a wide range of physiological intensity.

Physical activity accelerometer monitoring

During each treadmill walking and lifestyle activity participants wore three ActiGraph GT3x Accelerometers (ActiGraph LLC, Fort Walton Beach, FL). This device is a small (3.8 × 3.7 × 1.8 cm), lightweight (28 g), triaxial accelerometer. Each accelerometer was initialized to record data in 1 s epochs. Participants wore one accelerometer secured via a belt on the superior iliac spine along the anterior axillary line on non-dominant hip, one positioned over the posterior dorsal aspect of the non-dominant wrist midway between the radial and ulnar styloid processes secured by a Velcro strap, and one secured at the ankle, just proximal to the lateral malleolus by a Velcro strap. All monitors were labeled by site, and the same three accelerometers were used throughout the duration of the study.

Data processing: energy cost

Breath-by-breath data from the portable metabolic measurement system were averaged over 1 min-periods to derive VO₂ values in mL O₂·kg⁻¹·min⁻¹ with min 3–6 averaged and used for data analysis purposes. Given that factors of sex, age and body composition can affect measures of RMR (Katch et al 2011), thus limiting the generalizability of using the common definition of 1 MET = 3.5 mL O₂·kg⁻¹·min⁻¹, each activity oxygen consumption value obtained per participant was divided by their measured RMR value in mL O₂·kg⁻¹·min⁻¹ to derive measured METs per activity.

Data processing: physical activity accelerometer—Ngram-based feature representation

For every activity, the acceleration magnitudes recorded per second formed a numerical time series. Accelerometer data for mins 3–6 was used for each activity to coincide with data utilized for energy cost analysis. For applying machine learning methods, these time series were represented in terms of ngrams, borrowing a technique from natural language processing. An ngram is defined as a contiguous sequence of one or more words found in natural language text (Jurafsky and Martin 2008). Given that a text document is a series of words and a time series is a series of numbers, the same idea can be also applied to time series classification (Lin et al 2012). However, unlike words which come from a finite vocabulary, there are infinite possible numbers; hence it is necessary to first fix a ‘vocabulary’ size for numbers which is a parameter. There are multiple ways to do this (Lin et al 2012), in this work we do it as follows. If the chosen vocabulary size is, b, then the interval from minimum to maximum numbers (determined from of all the time series data) is uniformly divided into b bins. Each numerical value in the time series is then replaced by the bin number it fell into, thus effectively discretizing the time series. The entire original time series is thus transformed into a series of binnumbers. This transformed time series is then treated in the same way as a document of words, and each individual bin number (unigram), each pair of adjacent bin numbers (bigrams) etc., are used as ngram features. There will be as many number of unigram features as the value of b, and there will be as many number of bigram features as the value of b*b. The value of a feature is the frequency with which an ngram occurs in a time series.

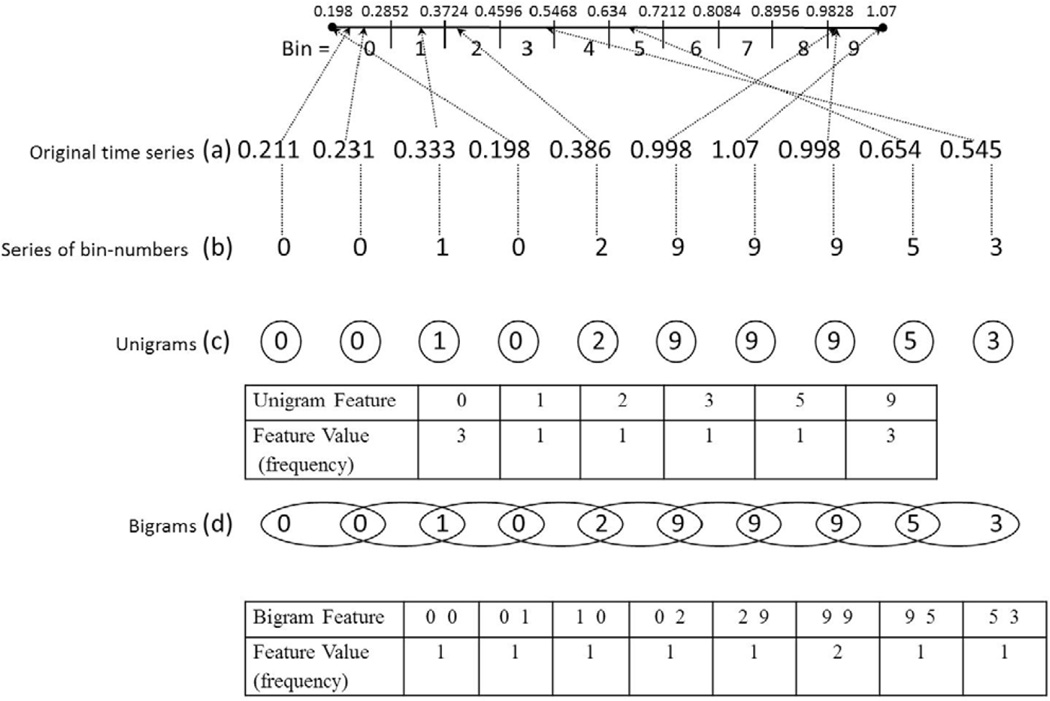
Figure 1 illustrates an example of ngram features. The chosen vocabulary size is 10, hence each number in the original series (a) is mapped to one of the 10 uniform bins between the minimum and maximum values resulting in a series of bin-numbers (b). The unigram features are shown as circles in (c) and the bigram features are shown as ellipses in (d) along with their feature values (frequencies). The unigrams and bigrams with zero feature values are not shown. In this example, a unigram feature ‘0’ captures how many times the accelerometer recorded a value between 0.198 and 0.2852 (first bin). Similarly, a bigram feature ‘0 1’ captures how many times the accelerometer recorded a jump from a value between 0.198 and 0.2852 (first bin) to a value between 0.2852 and 0.3724 (second bin). These ngram features are similar to the ‘bag-of-patterns’ features (named after ‘bag-of-words’ term used in text classification) used by Lin et al (2012) for time series classification. The machine learning technique will thus use this information to learn to distinguish between different physical activities or to estimate their energy costs.

Figure 1.

An illustration of time series ngram features. (a) A given original time series, i.e. a series of numbers. The interval from minimum (0.198) to maximum (1.07) is uniformly divided into 10 (chosen parameter) bins shown on the top. (b) The bin numbers in which the points of the time series fell into. (c) Unigram features (circles) and their values (frequencies) in the series of bin-numbers. (d) Bigram features (ellipses) and their feature values (frequencies).

Modeling and statistical methods

We used two different ngram modeling approaches applied to the accelerometer data: One to predict PA type, the second to predict METs and energy cost. For PA type classification, unigrams (acceleration magnitude during an activity) and bigrams (occurrence of changing acceleration from one magnitude to another) were used as features and their frequencies in the sequence normalized by the duration of the activity were used as feature values. The activities performed by the participants during the physical activity battery protocol were grouped into the following walking categories: (1) ‘Slow Walk’ = less than 67 m·min⁻¹, (2) ‘Moderate Walk’ = 67–80.4 m·min⁻¹, (3) ‘Fast Walk’ = 80.4 m·min⁻¹. As such, each ambulatory category was collapsed from 2 other categories, resulting in an n = 66 for sample size for activity classification. All simulated activities of daily living were analyzed by actual activity; (1) computer work, (2) vacuuming, (3) sweeping/mopping, (4) carrying boxes, and (5) walking with intermittent stair climbing. A total of eight activity types were therefore used in activity type detection. Support Vector Machines (SVM) were used for activity type classification because they are known to work well with thousands of features which is very common for ngram models to contain (Cristianini and Shawe-Taylor 2000). A linear kernel was found to work well and a higher degree kernel did not improve the performance.

For PA energy cost estimation, unigrams were found to be sufficient as features, and unlike PA type classification, adding bigrams did not improve estimates. Instead of using normalized frequencies of the unigrams as feature values, the product of the unigram’s value (bin-number) and its normalized frequency were used as feature values. Bagged decision tree models (Breiman 1996) were used for energy cost estimation.

Models were developed for the hip worn, wrist worn, ankle worn accelerometer only, and then combinations of Hip + Ankle, Hip + Wrist, Ankle + Wrist, and Hip + Wrist + Ankle. The aforementioned models were run for all ages combined and then further separated by age category, 18–39 years, 40–64 years, and 65 + years, for a total of 28 different models. Furthermore, models developed on the 18–39 years were evaluated on age groups 40–64 years, and 65 + years to evaluate generalizability. For models of all ages we selected a stratified random sample of 11 individuals from each age range (total 33), so as not to increase the sample size and model fit. Covariates of gender, height, weight, body fat percentage and gait speed were also used as features for both activity type classification and energy cost estimation, but did not improve prediction (data not shown). The performance of each model was tested using the leave-one-subject-out cross-validation method (Hastie et al 2001). Biases (mean difference between accelerometer model prediction and measured energy cost, and percent bias) and root mean squared error (rMSE, square root of the mean of the squared differences between the accelerometer model prediction and measured energy cost) were calculated, and difference analyzed by independent t-tests. Classification accuracy was computed across all models as the percentage of activities correctly classified out of all the activities completed during testing. Confusion matrices were generated for error analysis to determine how well a particular type of activity was misclassified as an activity of another type. The freely available machine learning and data mining software Weka was used for these machine learning methods with their default parameter settings.

Results

Descriptive results

Physical characteristics of study participants are presented in table 1. By design, age was significantly different across all three groups. Percent body fat (P < 0.05) was significantly higher in the 65 + year age group compared with the 18–39 year age group. Average gait speed was significantly slower in the 65 + year age group compared to both the 18–39 year (P < 0.05) and the 40–64 year (P < 0.05) age groups.

Table 1.

Participant demographics, data are presented as mean ± SD.

Variable	18–39 years (n = 33)	40–64 yearrs (n = 33)	≥65 years (n = 33)	All (n = 33)
Age (years)	28.0 ± 6.4	53.9 ± 6.3	71.1 ± 4.1a	49.3 ± 17.4
Mass (kg)	76.5 ± 17.5	75.8 ± 17.8	73.2 ± 12.9	75.5 ± 16.6
Body fat (%)	23.3 ± 9.1	28.0 ± 10.1	32.1 ± 8.9b	27.4 ± 10.0
Gait (m s−2)	1.41 ± 0.17	1.39 ± 0.21	1.29 ± 0.17c	1.38 ± 0.19
RMR (mL O2·kg−1 min−1)	3.11 ± 0.36	2.87 ± 0.47	2.72 ± 0.32b	3.01 ± 0.39

^aSignificantly different across all ages (p < 0.05).

^bSignificantly different than 18–39 years (p < 0.05).

^cSignificantly different than 40–64 years (p < 0.05).

Predicting energy cost

Tables 2(A)–(C) show validation results for each single-site and multi-site accelerometer site model broken down by each age group, combined for all age groups, for both age specific and age generalized models (18–39 years models evaluated on older age groups). For all subjects combined, all model predictions resulted in similar small levels of bias (−.001 to .013 METs), percent bias (−.375 to .297 percent) and rMSE (1.03–1.07 METs). When examining within age group, there was a notable decrement in accuracy within the ≥65 year age group when compared to both 18–39 year and 40–64 year age groups. This trend is apparent across all models, with increasing bias and rMSE were significantly different between ≥65years and 40–64 years for Hip (1.02 versus 0.81 METs, p< 0.05, respectively) and between ≥65years and 40–64 years for Hip + Wrist (1.04 versus 0.84, p< 0.05, respectively).

Table 2.

(A) Age specific and generalizability ngram-MET bias and their 95% confidence intervals for all accelerometer sites by age. (B) Age specific and generalizability ngram-MET percent bias for all accelerometer sites by age. (C) Age specific and generalizability ngram-MET rMSE for all accelerometer sites by age.

(A)
	Age Specifica bias				Generalizabilityb bias
Accelerometer site	18–39 years (n = 33)	40–64 years (n = 33)	≥65 years (n = 33)	All (n = 33)	40–64 years (n = 33)	≥ 65 years (n = 33)
Ankle	0.010 (−0.078, 0.098)	−0.023 (−0.11, 0.069)	−0.021 (−0.13, 0.084)	−0.016 (−0.13, 0.095)	−0.088 (−0.18, 0.002)	−0.057 (−0.18, 0.062)
Hip	0.005 (−0.083, 0.094)	−0.002 (−0.087, 0.084)	−0.022 (−0.13, 0.087)	0.013 (−0.099, 0.13)	−0.065 (−0.16, 0.028)	−0.058 (−0.18, 0.062)
Wrist	0.002 (−0.087, 0.09)	−0.010 (−0.1, 0.084)	−0.014 (−0.12, 0.095)	−0.001 (−0.11, 0.11)	−0.009 (−0.099, 0.082)	−0.077 (−0.19, 0.041)
Hip + Wrist	0.004 (−0.084, 0.092)	−0.008 (−0.097, 0.081)	−0.022 (−0.13, 0.09)	−0.001 (−0.11, 0.11)	−0.130c,d (−0.22,−0.033)	−0.079 (−0.2, 0.04)
Ankle + Wrist	0.009 (−0.079, 0.097)	−0.009 (−0.1, 0.084)	−0.030 (−0.14, 0.077)	−0.015 (−0.13, 0.096)	−0.120 (−0.2,−0.028)	−0.055 (−0.17, 0.063)
Ankle + Hip	0.012 (−0.077, 0.1)	0.011 (−0.077, 0.099)	−0.033 (−0.14, 0.074)	−0.008 (−0.12, 0.1)	−0.160c,d (−0.25,−0.064)	−0.079 (−0.2, 0.041)
Ankle + Hip + Wrist	0.014 (−0.074, 0.1)	0.004 (−0.086, 0.094)	−0.034 (−0.14, 0.075)	−0.011 (−0.12, 0.1)	−0.190c,d (−0.28,−0.095)	−0.066 (−0.18, 0.053)
(B)
	Age Specifica percent bias				Generalizabilityb percent bias
Accelerometer site	18–39 years (n = 33)	40–64 years (n = 33)	≥65 years (n = 33)	All (n = 99)	40–64 years (n = 33)	≥65 years (n = 33)
Ankle	0.239	−0.529	−0.477	−0.375	−1.930	−1.290
Hip	0.123	−0.036	−0.506	0.297	−1.420	−1.320
Wrist	0.037	−0.220	−0.313	−0.012	−0.191	−1.740
Hip + Wrist	0.093	−0.187	−0.489	−0.027	−2.830d	−1.790
Ankle + Wrist	0.203	−0.195	−0.688	−0.333	−2.550d	−1.240
Ankle + Hip	0.272	0.250	−0.760	−0.183	−3.440d	−1.800
Ankle + Hip + Wrist	0.327	0.096	−0.777	−0.256	−4.120d	−1.500
(C)
	Age Specifica rMSE				Generalizabilityb rMSE
Accelerometer site	18–39 years (n = 33)	40–64 years (n = 33)	≥65 years (n = 33)	All (n = 33)	40–64 years (n = 33)	≥ 65 years (n = 33)
Ankle	0.85	0.87	0.98	1.05d	0.87	1.11d
Hip	0.86	0.81	1.02e	1.06d,e	0.89	1.12d
Wrist	0.86	0.89	1.02	1.03	0.87	1.10d
Hip + Wrist	0.85	0.84	1.04e	1.05d,e	0.93	1.11d
Ankle + Wrist	0.85	0.87	1.00	1.05d	0.85	1.10d
Ankle + Hip	0.86	0.83	1.00	1.07d,e	0.90	1.13d
Ankle + Hip + Wrist	0.86	0.85	1.02	1.06d,e	0.91	1.11d

^aAge Specific—model estimates developed and tested within age group classification.

^bGeneralizability—model developed on the young age group (18–39 years) and tested on the other age group classifications (40–64, ≥65 years).

^cSignificantly different from zero (p < 0.05).

^dSignificantly different than 18–39 years (p < 0.05).

^eSignificantly different than 40–64 years (p < 0.05).

Specific to generalizability, when models developed on the young are evaluated on other age group classifications, results reveal that each model has higher error associated with prediction. For instance, single site estimates for Hip for 40–64 years had a bias, bias percent, and rMSE of 0.002 METs,−0.036%, and 0.81 METs associated with age specific models, and 0.065 METs, −1.42%, and 0.89 METs associated with age generalized models. Similarly for the ≥65 years, Hip estimates had a bias, bias percent, and rMSE of 0.022 METs,−0.506%, and 1.02 METs associated with age specific models, and 0.058 METs, −1.32%, and 1.12 METs associated with age generalized models. Similar results are apparent across all site model estimates.

We provide supplemental data (supplemental tables 1(A)–(C) and 2(A)–(C) (stacks.iop.org/PM/36/2335/mmedia)) that break down bias, bias percent, and rMSE into ambulatory walking and ADL activities separately. Of note, results on the whole for ambulatory walking were better with smaller error when compared with ADLs, for all ages combined and for age group specific accelerometer site models. For generalizability models, ADL activities had more error compared with the ambulatory activities for the 18–39 year model tested on the 40–64 year olds, however this was reversed when the 18–39 year model was tested on the ≥65 year olds—ambulatory activities had higher error compared with ADLs across all accelerometer site models.

Predicting physical activity type classification

For all participants combined single accelerometer classification models for the ankle (83.0%) and hip (81.6%) gave similar results, with weaker estimates from wrist alone (68.6%) (table 3). Two-accelerometer (Hip + Wrist, Ankle + Wrist, Ankle + Hip) and 3-accelerometer models (Ankle + Hip + Wrist) performed marginally better than single-site models, with the highest percent classification being 89.2% from the three-site placement model. When analyzing by individual age group, subtle differences were noted. Within the 18–39 year age group two-site (Hip + Wrist, Ankle + Wrist, Ankle + Hip) and three-site (Ankle +Hip + Wrist) models performed similarly with correctly classifying the ADL and walking activities 88.4 to 92.8% of the time. A similar trend was noted across other age groups, with two-site and three-site models correctly classifying activities with the 40–64 year age group and 65+ year age group, 83.2 to 92.6%, and 76.4 to 86.0%, of the time, respectively. There was an overall decrement in classification accuracy for all single site and multi-site models with advancing age group. When evaluating the generalizability of models developed on the younger age group and tested across age group classifications, there were decrements in accuracy. For instance, when examining the Ankle + Hip + Wrist model, 40–64 years age specific percent classification was 92.61%, decreasing to 77.59% when the younger 18–39 years model was generalized to this age group. Similarly, for the ≥65 years group, age specific models were more accurate than generalized models, 85.97% to 81.48%, respectively (see table 3). Collectively, decrements in accuracy were fairly consistent across all models.

Table 3.

Age specific and generalizability classification accuracy across all activities^c.

	Age specifica				Generalizabilityb
Accelerometer site	18–39 years (n= 33)	40–64 years (n= 33)	≥65 years (n = 33)	All (n= 33)	40–64 years (n= 33)	≥65 years (n = 33)
Ankle	87.57	85.51	72.54	83.00	78.99	77.61
Hip	80.11	76.42	71.94	81.59	37.25	68.36
Wrist	77.62	69.89	69.25	68.56	64.71	67.46
Hip + Wrist	88.40	83.24	76.42	86.69	61.34	77.91
Ankle + Wrist	92.81	88.35	82.09	86.40	82.07	84.18
Ankle + Hip	88.40	90.34	78.21	82.72	68.35	77.41
Ankle + Hip + Wrist	92.82	92.61	85.97	89.24	77.59	82.48

^aAge Specific—model estimates developed and tested within age group classification.

^bGeneralizability—model developed on the young age group and tested on the other age group classifications.

^cWalking activities 1.5 mph and 2.0 mph. 2.5 mph and 3.0 mph, 3.5 mph and 4.0 mph were collapsed into single categories of slow walk, moderate walk and fast walk, respectively for purposes of activity classification only.

Note: values are presented as a percentage.

Tables 4(A)–(D) show example confusion matrices for all age groups combined for accelerometer site placement models Hip, Wrist, Hip + Wrist and Ankle + Hip + Wrist. Hip placement models performed well for ambulatory activities, but generally had greater confusion for ADL like-kind movement activities (i.e. vacuuming and mop/sweeping. Wrist models generally had confusion distinguishing ambulatory activities of different intensity, and ADL like-kind activities. Combination accelerometer site-placement models performed better, with less confusion for within ambulatory activities and ADL kind-like activities. All confusion matrices for all specific age groups and generalizability models are provide in supplemental data table 3 (stacks.iop.org/PM/36/2335/mmedia).

Table 4.

Confusion matrix for activity type estimation from selected accelerometer models. Data presented as cases. (A) Hip model accelerometer estimate: all age group. (B) Wrist model accelerometer estimate: all age group. (C) Hip + Wrist model accelerometer estimate: all age group. (D) Ankle + Hip + Wrist model accelerometer estimate: all age group.

(A)
Classified as:	a	b	c	d	e	f	g	h
a = 1.5–2.0 mph	57	5	0	0	1	0	2	1
b = 2.5–3.0 mph	5	54	2	1	0	0	0	3
c = 3.5–4.0 mph	2	2	52	1	0	0	0	0
d = Computer	0	0	0	32	0	1	0	0
e = Vacuuming	1	0	0	0	21	11	0	0
f = Mop/Sweep	0	0	0	0	8	24	1	0
g = Boxes	1	0	0	0	1	3	28	0
h = Walk/Stairs	1	6	0	1	0	0	0	25
(B)
Classified as:	a	b	c	d	e	f	g	h
a = 1.5–2.0 mph	50	10	0	0	5	0	0	1
b = 2.5–3.0 mph	11	39	10	1	0	1	0	3
c = 3.5–4.0 mph	2	21	28	1	0	1	0	4
d = Computer	0	0	0	32	1	0	0	0
e = Vacuuming	2	0	0	0	21	10	0	0
f = Mop/Sweep	0	0	0	0	7	21	5	0
g = Boxes	1	0	0	0	1	4	27	0
h = Walk/Stairs	1	6	0	1	0	1	0	24
(C)
Classified as:	a	b	c	d	e	f	g	h
a = 1.5–2.0 mph	59	4	1	0	1	0	0	1
b = 2.5–3.0 mph	4	54	4	1	0	0	0	2
c = 3.5–4.0 mph	0	5	49	1	0	1	0	1
d = Computer	0	0	0	32	1	0	0	0
e = Vacuuming	1	0	0	0	21	11	0	0
f = Mop/Sweep	0	0	0	0	8	24	1	0
g = Boxes	1	0	0	0	1	3	28	0
h = Walk/Stairs	1	6	0	1	0	0	0	25
(D)
Classified as:	a	b	c	d	e	f	g	h
a = 1.5–2.0 mph	61	4	0	0	0	0	1	0
b = 2.5–3.0 mph	4	57	2	1	0	0	0	1
c = 3.5–4.0 mph	1	2	52	1	1	0	0	0
d = Computer	0	0	0	32	1	0	0	0
e = Vacuuming	0	0	0	0	26	7	0	0
f = Mop/Sweep	0	0	0	0	1	31	1	0
g = Boxes	1	0	0	0	2	0	30	0
h = Walk/Stairs	3	3	0	1	0	0	0	26

Discussion

In this study, we evaluated a novel method of machine learning, an ngram natural language processing approach, applied to accelerometer data obtained from hip, wrist and ankle placement to evaluate the validity of single site and multi-site models for predicting energy cost of activities and to identify activity type in a sample of adults stratified by young (18–39 years), middle (40–64 years), and old age (≥65 years). A secondary aim was to evaluate the generalizability of accelerometer site model predictions developed on the young age group applied to other age groups. Main findings revealed the ngram approach produced valid estimates of energy cost, with a bias of −0.034 to 0.014 METs, bias percent −0.777 to 0.327 percent, and a rMSE of 0.84–1.04 METs across single-site, multi-site, and all age group accelerometer models. The ngram method also produced a high level of accuracy in predicting PA type 69.3–92.8% of the time using single-site and multi-site accelerometer models across all age groups. Generalizability of models across age groups collectively resulted in less accurate predictions for energy cost and activity type, irrespective of the single-site or multi-site model employed, compared with age group specific models. Furthermore, of note is that when models are developed on all participants, they perform on average worse than age specific models. The present results are unique in that they show an overall decrement in accuracy for estimating energy cost and PA type with advancing age group classifications, an improvement in PA estimates with increasing site placements evaluated, a diminished accuracy with employment of age-generalized accelerometer model estimates, and overall improvement for energy cost and activity type estimations when developing models on age specific groups, rather than all participants combined.

Previous studies have explored machine learning approaches to estimate energy cost, with successful results, providing evidence that advanced computational approaches to estimate energy cost is a plausible and effective option. Staudenmayer et al (2009) developed an artificial neural network (ANN) using the single-site hip worn ActiGraph GT1M accelerometer assessing activity within domains of sedentary, household, locomotion, and sport activities. Results indicated an average MET bias of 0.05 and a rMSE of 1.22 METs (Staudenmayer et al 2009). Upon further work from this group, still employing single-site hip worn placement in a larger sample across more ADLs, ANN cross-validation prediction accuracy of 0.00 MET biases, and 1.43 MET rMSE were reported (Freedson et al 2011). In this same paper, prediction models were then cross-validated in a small independent sample from a separate institution, revealing 0.32 MET biases, and 1.99 MET rMSE across all activities. In the current study, average MET bias for the ngram approach revealed a small bias for all subjects at the site of the Hip, 0.01 METs, and a smaller rMSE of 1.02 METs. Extending this work to investigate multi-site accelerometer placement prediction models, our results revealed that for energy cost prediction across all activities, model predictions (biases, rMSE) were similar across Ankle (−0.016, 1.05 METs), Hip (0.013, 1.06 METs), Wrist (−0.001, 1.03 METs), Hip + Wrist (−0.001, 1.05 METs), Ankle + Wrist (−0.015, 1.05 METs), Ankle + Hip (−0.008, 1.07 METs), and Ankle + Hip + Wrist (−0.011, 1.06 METs). These new results reveal that multi-site accelerometer models did not substantially improve upon single-site accelerometer model estimates for energy cost for all ages combined.

An advantage to employing advanced analytical approaches to analyze body-worn motion sensor data is the ability to identify PA type. Common to most studies is to engage in a series of different activities and then classify activities into groupings by domain, for instance 20 different activities may be engaged in, but all activities will be grouped into domains such as household, locomotion, sport, and occupation categories. During the current study 11 different activities were performed by all participants. Walking activities were broken into three different classes, slow, moderate, and fast and five ADLs were also performed. We elected to evaluate individual activities due to smaller number of activities undertaken, rather than breaking into classes of activity such as household, inactivity, sport, locomotion, as other research groups have done. Pertaining to activity classification, Bonomi et al (2009a) reported a 93% classification accuracy using a DT approach across 7 different classes of activity type, condensed from 20 different activities, in a sample of 20 young men and women using a single accelerometer position on the lowback. Staudenmayer et al (2009) using an ANN analytical approach applied to a hip-worn accelerometer reported a 88.8% correct activity classification type across different routines encompassing locomotion, sport and activities of daily living. Similarly, Freedson et al (2011) also using a single hip-worn accelerometer reported activity classifications by activity type, with correct classifications for household, locomotion and sport activities 98.1%, 89.5% and 23.7%, respectively. Mannini et al (2013) using SVM reported activity classification results for body-worn accelerometers across two sites, wrist and ankle. Site placement was only considered separately in this study, with the ankle showing a higher overall classification accuracy at 95.0%, with the wrist providing an 84.7% accuracy rate. The results of Mannini et al (2013) are consistent with the current study results that showed that when monitor placements were considered individually the wrist performed the weakest of all three sites, at only 68.6% accurate for all ages combined, with the ankle performing the best eliciting an 87.6% accuracy.

Of additional interest to the field of physical activity monitoring is the added benefit of wearing multiple body-worn sensors across different site placements. De Vries et al (2011) tested different ANN models to predict activity type using the ActiGraph GT1M placed on the right hip and right ankle. Results revealed that the combination of the hip and ankle monitors yielded the highest accuracy at 83.0%, compared with single site estimates from the hip (80.4%) and ankle (77.7%). In the current study, we elected to assess prediction capabilities across single-site and multi-site models, focusing on hip, wrist and ankle. Estimates using all three monitors, placed on the ankle, hip, and wrist, provided the most accurate classification accuracy for all activities (89.2%), across all age groups. When only two monitors were combined, the hip and wrist combination and the ankle and wrist combination elicited similar accuracy for all ages in activity classification revealing an 86.7% and 86.4% accuracy, respectively.

As one ages it has been well established that movement patterns alter, with notable gait fluctuations plausibly resulting from motor and postural control alterations associated with advancing years and/or disease related conditions resulting in central and peripheral nervous system changes (Hausdorff 2007, Callisaya et al 2010a). Movement variability has also been noted to change with advancing age across upper body tasks, revealing large intra- and inter-individual variability (Darling et al 1989). These differences in movement dynamics are therefore likely to influence body-worn motion sensor predictions of energy cost and activity type recognition. To evaluate this we elected to recruit a sample stratified by age, and develop analytical models to predict energy cost and activity type by age group, young (18–39 years), middle (40–64 years) and old (≥65 years). Previous studies have relied upon narrow age group calibrations (Bonomi et al 2009b), or have recruited a large age range of participants, for instance 18–75 years to develop both energy cost and activity type/classification, however, none have discretized these groups (Freedson et al 1998, Staudenmayer et al 2009, De Vries et al 2011, Mannini et al 2013). In the current study results reveal that all model estimates for energy cost are weaker for the older group (≥65 years) when compared to younger age groups (18–39 and 40–64 years). This decrement in accuracy is evident when examining activity type classification, with the old age group revealing a lower percent classification across single-site and multi-site model estimates. To further extend this work, in the current study we also elected to examine the generalizability of model estimates, and specifically test young age group models evaluated on middle and old age groups. Pertaining to energy cost estimates, when comparing age specific models for the 40–64 years and ≥65 years groups to the generalized models, for every model tested biases and rMSE were higher. Similarly, when generalized models were compared to age specific for the 40–64 years and ≥65 years groups for the purpose of activity classification, results were collectively less accurate. These new results, specific to this ngram machine learning method, would signify age impacts model performance even when models are age standardized, and that age generalized models are less precise than age specific models. Future algorithm calibration work should consider these findings.

Studies tend to recruit a wide age range of participants for purposes of calibration with the desire to develop prediction models that can be generalized to all age groups (Freedson et al 1998, Staudenmayer et al 2009, De Vries et al 2011, Mannini et al 2013). Of particular relevance in the current study, models developed on all ages combined performed worse on average across all accelerometer site placement models than when models were developed on specific age groups. Future physical activity assessment calibration studies would benefit from stratified age group prediction model development, and/or developing correction factors when applying models to different age groups.

This study had several important strengths to note. Resting metabolic rate was measured and used to calculate the actual metabolic equivalent for each participant, providing a more accurate depiction of energy cost than using typical denominations of 3.5 ml kg⁻¹ min⁻¹. A new novel, simplistic ngram time-series machine learning analytical approach was applied to energy cost and activity type prediction. A large age range was examined, permitting whole group, age specific, and age generalized models to be evaluated. Limitations to the current study include a limited number of activities evaluated and only unilateral monitoring sites employed. Further studies would benefit from examining more activities, permitting individual activities and activity domain examination. Furthermore, bi-lateral monitor placement, for instance, left and right sided wrist, hip and ankle assessment would be advantageous to examine. Future studies would also benefit from comparing a multitude of different machine learning techniques to fully discern logistics of: (a) which analytical technique performs better for energy cost and activity type estimations; (b) which analytical time has the fastest processing time, which will become important when evaluating real-time data acquisition and estimation; (c) incorporating structured activity estimations, as in the current study, in combination with semi-structured activities that incorporate activity transitions; and (d) how well different analytical techniques perform in real world settings over extended days of monitoring.

In conclusion, the current study showed a novel ngram time-series machine learning analytical approach applied to body worn accelerometer data to be an accurate method for energy cost prediction and activity type recognition. Multi-site motion sensor model predictions do not substantially improve upon energy cost estimates, but can improve activity classification across and within age groups. Model accuracy varies across age group classifications, with a decrement in accuracy of energy cost and activity type classification within older age groups. Age generalized models do not perform as well as age specific energy cost and activity type recognition model estimates when using this approach. In the current study models developed on specific age groups on average perform better for energy cost prediction and activity type estimation than when all age groups are combined. As further calibration studies are examined researchers would benefit from considering age as a discrete category for all model development.