Abstract
Objectives
Mycobacterium tuberculosis can exist in different states in vitro, which can be denoted as fast multiplying, slow multiplying and non-multiplying. Characterizing the natural growth of M. tuberculosis could provide a framework for accurate characterization of drug effects on the different bacterial states.
Methods
The natural growth data of M. tuberculosis H37Rv used in this study consisted of viability defined as cfu versus time based on data from an in vitro hypoxia system. External validation of the natural growth model was conducted using data representing the rate of incorporation of radiolabelled methionine into proteins by the bacteria. Rifampicin time–kill curves from log-phase (0.25–16 mg/L) and stationary-phase (0.5–64 mg/L) cultures were used to assess the model's ability to describe drug effects by evaluating different linear and non-linear exposure–response relationships.
Results
The final pharmacometric model consisted of a three-compartment differential equation system representing fast-, slow- and non-multiplying bacteria. Model predictions correlated well with the external data (R2 = 0.98). The rifampicin effects on log-phase and stationary-phase cultures were separately and simultaneously described by including the drug effect on the different bacterial states. The predicted reduction in log10 cfu after 14 days and at 0.5 mg/L was 2.2 and 0.8 in the log-phase and stationary-phase systems, respectively.
Conclusions
The model provides predictions of the change in bacterial numbers for the different bacterial states with and without drug effect and could thus be used as a framework for studying anti-tubercular drug effects in vitro.
Introduction
Tuberculosis, caused by Mycobacterium tuberculosis, is ranked as the second leading cause of death worldwide due to an infectious disease.1 One of the underlying problems with efforts to enhance control of the disease is the persistence of bacteria that cannot be eradicated by antimicrobial agents or the immune system. Therefore, new drugs and optimization of the current standard treatment with the aim of shortening the current treatment duration are highly important. New tools and strategies are needed to establish effective predictive model systems to smooth the transition of laboratory-based data to clinical studies. Since the development of new drugs requires large investments, any tool or strategy that could decrease the risk of failure during late-phase drug development is naturally interesting. Pharmacometrics has been promoted as a methodology to rationalize and inform drug development through the application of mathematical and statistical methods for the characterization and prediction of pharmacokinetics and pharmacodynamics. In contrast to the use of summary endpoints to describe pharmacokinetic–pharmacodynamic relationships of antibiotics, pharmacometric models provide integration of the time course of the relationships between exposure, effect and the underlying disease-specific mechanisms. Thereby, they provide valuable information for evaluation of the rational use of existing drug regimens and in the development of new drugs.
Pharmacometric models have been successfully applied to in vitro data, e.g. describing antibacterial effects on Streptococcus pyogenes2–4 and Pseudomonas aeruginosa.5–8 In vitro studies, offering greater flexibility with regard to study design and being less expensive to perform, are an attractive complement to in vivo studies. In order to provide an accurate characterization of the in vitro antibacterial effect on M. tuberculosis, characterization of in vitro natural growth without drug exposure is needed.
In a tuberculosis infection, multiplying bacteria (defined as bacteria exhibiting genomic growth and the ability to segregate into a new self-propagating unit9) and non-multiplying bacteria can exist side by side.9 Although antibiotics are able to kill multiplying bacteria, most are very ineffective at killing non-multiplying bacteria.10 Targeting both multiplying and non-multiplying populations is regarded as an essential way of shortening treatment duration and slowing emergence of drug resistance.11 Quantification of drug effects on non-multiplying bacteria is hence essential when targeting a translational modelling framework.
Characterization of antibacterial activity has historically been performed using bacterial cultures displaying exponential growth, i.e. cultures that are in log phase. However, regulatory guidelines have suggested that targeting bacteria from stationary-phase cultures, or cultures displaying no net growth or death, is important in the development of new agents as data from these cultures may indicate sterilizing activity against M. tuberculosis in vivo.12 From the use of hypoxia-driven in vitro systems, stationary-phase M. tuberculosis has been suggested to be able to exist in what have been referred to as dormant or non-replicating forms.13,14 Evidence has since shown that M. tuberculosis can exist, both in vitro and in vivo, in transient bacterial states in which the organisms, while being able to multiply in liquid media, are not able to form colonies on solid media.15–19 This has also been shown to be the case in sputum.20,21 The existence of such a bacterial state is in line with what has been shown when utilizing a modelling approach to describe the relationship between cfu and Mycobacterial Growth Indicator Tube (MGIT) time to positivity using matched liquid culture and colony count data.22
The dormant bacteria are one part of a simplified classification comprising three bacterial states—fast-multiplying, slow-multiplying and non-multiplying—that have been suggested to describe the cycle of M. tuberculosis growth.11 This simplification represents a continuum of growth states ranging from fast- to non-multiplying that most likely exists in humans. Within this context it is important to address the fact that measurement of cfu counts only enables quantification of bacilli that can multiply on solid media.
We therefore aimed to develop a population pharmacometric template model that would allow the study of anti-tubercular drug effects on the different bacterial states of M. tuberculosis. External validation of the model predictions using data on the rate of incorporation of radiolabelled amino acid into proteins by the bacteria was performed. The model's ability to act as a framework for studying anti-tubercular drug effects was exemplified and evaluated by characterizing the effect of rifampicin on both log-phase and stationary-phase bacterial cultures.
Materials and methods
In vitro assays and bacteria
Three types of in vitro assays were used in the viability assessed by cfu: a natural growth assay without drug effect; a time–kill assay utilizing log-phase bacterial cultures exposed to rifampicin; and a time–kill assay utilizing stationary-phase bacterial cultures exposed to rifampicin. An additional in vitro assay assessing the incorporation of [35S]methionine into M. tuberculosis cells was included as an external validation of the pharmacometric model. M. tuberculosis strain H37Rv was used in all in vitro assays.
Natural growth assay
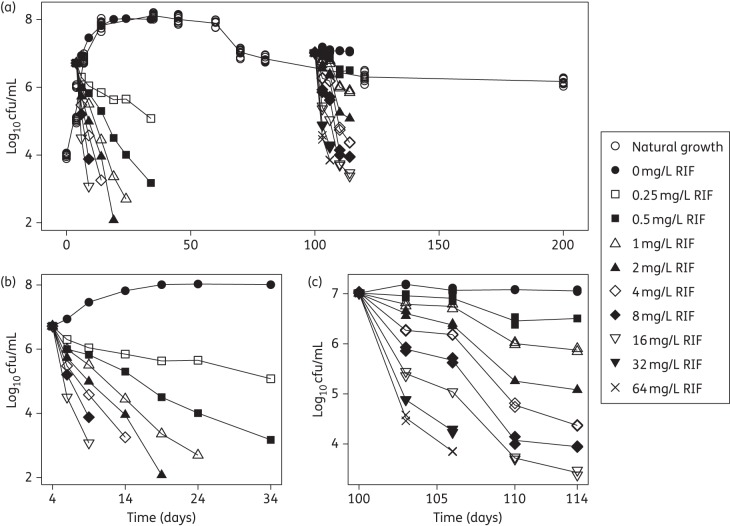
M. tuberculosis strain H37Rv was grown in 7H9 medium supplemented with 10% albumin dextrose complex (ADC, Becton, Dickinson, UK) and containing 0.05% Tween 80 at 37°C without disturbance for up to 200 days; 12 replicates were included. At different timepoints, the clumps of bacilli in each of a set of 10 mL cultures were broken up by vortexing with 2 mm diameter glass beads for 5 min, followed by sonication in a water bath sonicator (Branson Ultrasonic, USA) for 5 min to obtain an evenly dispersed suspension of bacilli. Viability was estimated by plating a series of 10-fold dilutions of the cultures on 7H11 agar medium supplemented with oleic albumin dextrose complex (OADC, Becton, Dickinson, UK) and defined as cfu/mL (Figure 1).
Figure 1.
Mean observed log10 cfu versus time. (a) Combination plot of all the data from the three in vitro systems: the 200 day natural growth system; the log-phase system with and without rifampicin (RIF); and the stationary-phase system with and without RIF. (b) The log-phase system with and without rifampicin, pre-grown for 4 days and studied for 30 days. (c) The stationary-phase system with and without rifampicin, pre-grown for 100 days and studied for 14 days.
Time–kill assays
Log-phase M. tuberculosis H37Rv (grown to 4 days) was incubated with 0, 0.25, 0.5, 1, 2, 4, 8 and 16 mg/L rifampicin at 37°C with no replicates. Stationary-phase cultures (grown to 100 days) were incubated with 0, 0.5, 1, 2, 4, 8, 16, 32 and 64 mg/L rifampicin at 37°C with two replicates. Viability of the cultures was determined by cfu counting at days 0, 2, 5, 10, 15, 20 and 30 after drug exposure for the log-phase cultures and at days 0, 3, 6, 10 and 14 after drug exposure for the stationary-phase cultures (Figure 1).
Pharmacometric model building
To enable a semi-mechanistic description of the in vitro antibacterial effect on the different states of M. tuberculosis H37Rv, characterization of the in vitro natural growth of the bacteria without drug effect as quantified by cfu counting was initially performed. The rifampicin concentration–effect relationship for the log- and stationary-phase cultures was then investigated using different linear and non-linear functions.
The natural growth of M. tuberculosis H37Rv was characterized using a model with three bacterial states (Figure 2). The basis of the model development was a system with three differential equations (equations 1–3), representing fast-, slow- and non-multiplying bacteria, for which different growth functions and transfer rates were evaluated.
| (1) |
| (2) |
| (3) |
Figure 2.
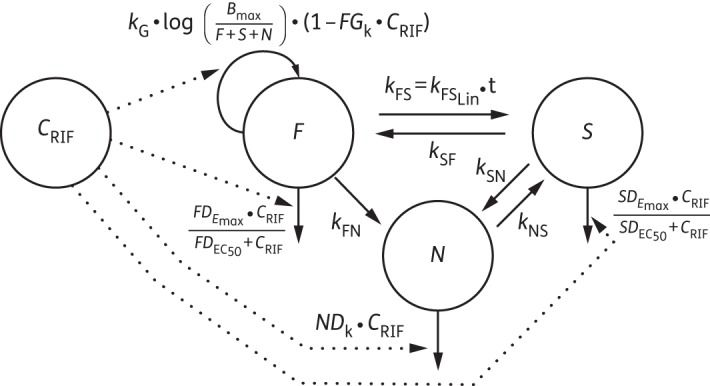
Schematic illustration of the multistate tuberculosis pharmacometric model with inclusion of rifampicin pharmacokinetics (drug model). CRIF, rifampicin (RIF) concentration; F, fast-multiplying state; S, slow-multiplying state; N, non-multiplying state; kG, growth rate of the fast-multiplying state bacteria; kFS, time-dependent linear rate parameter describing transfer from fast- to slow-multiplying state; kSF, first-order transfer rate between slow- and fast-multiplying states; kFN, first-order transfer rate between fast- and non-multiplying states; kSN, first-order transfer rate between slow- and non-multiplying states; kNS, first-order transfer rate between non-multiplying and slow-multiplying states; FGk, linear drug-induced inhibition of fast-multiplying state growth; , maximum achievable drug-induced fast-multiplying state kill rate; , concentration at 50% of ; , maximum achievable drug-induced slow-multiplying state kill rate; , concentration at 50% of ; NDk, non-multiplying state kill rate.
A reduced form of the model without the non-multiplying state (equation 3) was also evaluated. As the cfu count reflects only the bacteria that are able to multiply on solid media, only the numbers in the fast- and slow-multiplying states, as a sum, were part of the model prediction of the data. Further, as the cfu count is a summary measure of total viable bacteria, the inoculum is the sum of the initial bacterial numbers in the fast-multiplying (F0) and the slow-multiplying (S0) states. A model with estimation of both F0 and S0 was compared with models with either F0 or S0 fixed to 0, representing a situation where all bacteria would be in the fast-multiplying or slow-multiplying state at the time of inoculum. The growth rates of the fast-multiplying and slow-multiplying bacteria were evaluated, as exemplified for the fast-multiplying bacterial state, using exponential (equation 4), Gompertz (equation 5) and logistic (equation 6) growth functions
| (4) |
| (5) |
| (6) |
in which kG is the growth rate and Bmax is the system-specific carrying capacity. F, S and N are the bacterial numbers predicted by the model in the fast-, slow- and non-multiplying states, respectively. As discussed above, the cfu count reflects only the bacteria that are able to multiply on solid media (fast and slow). The non-multiplying state was, however, allowed to influence the predictions as described in equations (5 and 6). Equations (5 and 6) were also evaluated without including N. In the simplest model structure, still involving the three bacterial states, bacterial movement between the different states can be described via first-order linear rate constants relating to the transfer from one state to another. The transfer rate of fast-multiplying to slow-multiplying bacteria (kFS) was evaluated as a constant transfer rate and as a transfer rate that incorporated stimulation of transfer by the total number of bacteria in the fast-, slow- and non-multiplying states (equation 7). Further, time dependency in the fast-to-slow transfer was evaluated using a linear (equation 8) and an Emax (equation 9) and an exponential (equation 10) function. For equations 8–10 kFS will be 0 at the start of the experiment (time = 0).
| (7) |
| (8) |
| (9) |
| (10) |
Here, t is time, tmax is the maximum time and t50 is the time when the transfer rate has reached 50% of tmax. Initial runs revealed that the rate of transfer from N to F (kNF) was close to zero and was therefore assumed to be negligible and thus fixed to 0 in further model development.
The effects of rifampicin on cultures in log phase and stationary phase were evaluated separately using rifampicin data, natural growth data and fixed parameter estimates from the natural growth model. The parameters kG, Bmax, F0 and S0 were evaluated for significant differences between the natural growth and the log and stationary natural growth control experiments.
The effects of rifampicin were evaluated, where applicable, as inhibition of growth and kill rates on each of the three bacterial states using linear functions (equation 11), ordinary Emax functions (equation 12) and sigmoidal Emax functions (equation 13):
| (11) |
| (12) |
| (13) |
where CRIF is rifampicin concentration in the system.
Inhibition of growth by the drug effect (E) was implemented in the differential equation system as a fractional inhibition, as exemplified for the fast-multiplying bacterial state (equation 14),23 whereas the drug effect, as a kill rate, of the fast-, slow- and non-multiplying states was implemented as an additive bacterial killing-rate constant imposed by the drug as exemplified for the slow-multiplying bacterial state (equation 15):24
| (14) |
| (15) |
Evaluation of drug effect was conducted by evaluating all possible combinations of effects on the three different bacterial states, where applicable, as either inhibition of growth or as a kill rate, as well as for the different exposure–response functions described in equations (11–13). The best model from this step, judged by criteria outlined below, was evaluated in a last step by reducing each of the different exposure–response functions to their simpler form in order to confirm the appropriateness of the final model.
In addition to separately describing the effect of rifampicin on the log-phase and stationary-phase cultures, an evaluation of the effect of rifampicin using data combined from both the log phase and the stationary phase was performed.
External validation
External validation of the model describing the in vitro natural growth without drug effect was performed using a dataset consisting of the rate of incorporation of radiolabelled methionine ([35S]methionine) into proteins by the bacteria. For incorporation of radioactive methionine into proteins of M. tuberculosis, 3 mL of 4, 10, 20, 30, 40 and 50 day cultures with 1–2 × 108 cfu/mL of bacilli were incubated with 30 μCi of [35S]methionine at 37°C for 1 h. Also, 30 μCi of [35S]methionine was added to heat-killed cultures. Radioactive labelling was terminated after a chase with 10 mM l-methionine. The bacterial cells were harvested by centrifugation at 12 000 g for 15 min and washed three times with PBS containing 1 mM l-methionine. Bacterial cells were lysed by vortexing for 5 min with an equal amount of glass beads (75–150 µm, Sigma) in distilled water. The incorporation of [35S]methionine into total proteins was determined by scintillation counting of radioactivity and calculated as cpm of trichloroacetic acid-precipitated proteins.
This was correlated to, as a percentage, the mean of the natural growth model predicted typical fast-multiplying bacterial number out of the predicted typical fast- plus slow-multiplying bacterial number, i.e. 100×(F / F + S).
Data analysis and software
All data analysis was performed in the software NONMEM (version 7.3; Icon Development Solutions, http://www.iconplc.com/technology/products/nonmem) using the first-order conditional estimation method with interaction (FOCE INTER).25 R (version 3.2; R Foundation for Statistical Computing, http://www.R-project.org) was used for data management and Xpose (version 4.5.0; Department of Pharmaceutical Biosciences, Uppsala University, http://xpose.sourceforge.net) was used for graphical assessment of results.26 PsN (version 4.4.5; Department of Pharmaceutical Biosciences, Uppsala University, http://psn.sourceforge.net) was used for running models,26 generating visual predictive checks (VPCs)26 and prediction-corrected visual predictive checks (pcVPCs).27 Numerical model comparison and a run record were utilized and maintained with the software Pirana (version 2.9.2; Pirana Software & Consulting, http://www.pirana-software.com).26 Model evaluation was done by evaluation of goodness-of-fit plots, precision in parameters, objective function values (OFVs), scientific plausibility, VPCs and pcVPCs. The OFV given by NONMEM, which approximates −2 log(likelihood) of the data given the model, was utilized in likelihood ratio testing (LRT) to compare nested models. The difference in OFV (ΔOFV) is approximately χ2 distributed and dependent on the significance level and degrees of freedom. For this analysis a significance level of 0.05 was used, which hence corresponds to a critical ΔOFV of 3.84 for 1 degree of freedom.
Data below the limit of quantification (LOQ, 25%), was handled using the M3 method,28 with LOQ set to 10 cfu. The LOQ was defined as the lowest number of bacteria that need to be present in the growth tube to be able to detect 1 cfu, taking into account the dilution of the plated sample. Inclusion of variability was evaluated on the parameters F0, S0 and kG using a log normal variability distribution model.
Results
A schematic representation of the final pharmacometric model describing the natural growth and the concentration–effect relationship of rifampicin from the simultaneous fit of the log- and stationary-phase data is shown in Figure 2 and parameter estimates are given in Table 1.
Table 1.
Parameter estimates of the final multistate tuberculosis pharmacometric model applied to cfu data from rifampicin log- and stationary-phase M. tuberculosis H37Rv cultures
| Parameter | Estimate | RSE (%) |
|---|---|---|
| a (days−1) | 0.897 × 10−6 | 1.2 |
| a (days−1) | 0.186 | 4.3 |
| a (days−1) | 0.0145 | 4.9 |
| a (days−1) | 0.123 × 10−2 | 2.7 |
| a,b (days−2) | 0.166 × 10−2 | 1.6 |
| a (mL−1) | 9770 | 2.4 |
| a,c (days−1) | 0.206 | 1 |
| a (days−1) | 0.102 | 12.5 |
| a (mL−1) | 4.1 | 2.9 |
| a (mL−1) | 674 × 103 | 39.2 |
| a (mL−1) | 242 × 106 | 4.5 |
| a (mL−1) | 1410 × 106 | 0.8 |
| (L·mg−1) | 0.017 | 11.1 |
| (days−1) | 2.15 | 4.5 |
| (mg·L−1) | 0.52 | 9.8 |
| (days−1) | 1.56 | 4.7 |
| (mg·L−1) | 13.4 | 10.4 |
| (L·mg−1·days−1) | 0.24 | 12.6 |
| ωFa (%) | 473.3 | 5.9 |
| Proportional residual error (%) | 63.8 | 7.8 |
kFN, first-order transfer rate between fast- and non-multiplying state; kSN, first-order transfer rate between slow- and non-multiplying state; kSF first-order transfer rate between slow- and fast-multiplying state; kNS, first-order transfer rate between non- and slow-multiplying state, S0 initial slow-multiplying state bacterial number; kG, growth rate of the fast multiplying state bacteria; growth rate of the fast-multiplying state bacteria in experiments with rifampicin log phase cultures; F0 initial fast-multiplying state bacterial number; initial fast-multiplying state bacterial number in experiments with rifampicin log phase cultures; Bmax, system carrying capacity; , system carrying capacity in experiments with rifampicin stationary phase cultures; FGk, linear drug-induced inhibition of fast-multiplying state growth; , maximum achievable drug-induced fast-multiplying state kill rate; , concentration at 50% of ; , maximum achievable drug-induced slow-multiplying state kill rate; , concentration at 50% of ; NDk, non-multiplying state kill rate; ωF, variability in F0 expressed as coefficient of variation; RSE, relative standard error reported on the approximate standard deviation scale.
aFixed during drug evaluation.
b.
c.
Natural growth model
The final multistate tuberculosis pharmacometric model describes the in vitro growth of M. tuberculosis utilizing a fast-, a slow- and a non-multiplying state. Estimation of the initial bacterial numbers in the fast-multiplying (F0) and the slow-multiplying (S0) bacterial states resulted in a significant decrease in OFV when compared with fixing either F0 or S0 to 0. Inclusion of variability in F0 (ωF) resulted in a better fit and a significant drop in OFV (ΔOFV = −67.5). Growth of the fast-multiplying bacteria, kG, was best described by a Gompertz function (OFV = −41.5) compared with the exponential (OFV = 325) and the logistic growth function (OFV = 10.7). Addition of any of the growth functions to the slow-multiplying state did not result in any significant improvement in the OFV. The rate of transfer between the fast- and the slow-multiplying states, kFS, was best described with a time-dependent linear function (equation 8), which described the data better than any of the other functions evaluated.
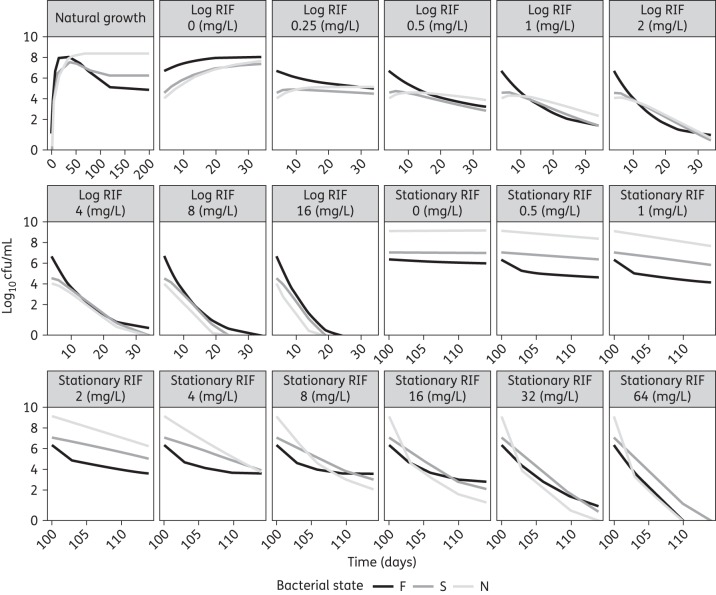
In Figure 3, in the panel entitled natural growth, the predicted bacterial numbers in the different states over time are shown as a mean of the 12 replicates. Figure 4 shows a VPC of the final multistate tuberculosis pharmacometric model without drug effect (natural growth).
Figure 3.
Model-predicted typical M. tuberculosis bacterial numbers in the fast-, slow- and non-multiplying states without drug (natural growth) and after different static rifampicin (RIF) concentrations in log- and stationary-phase cultures.
Figure 4.
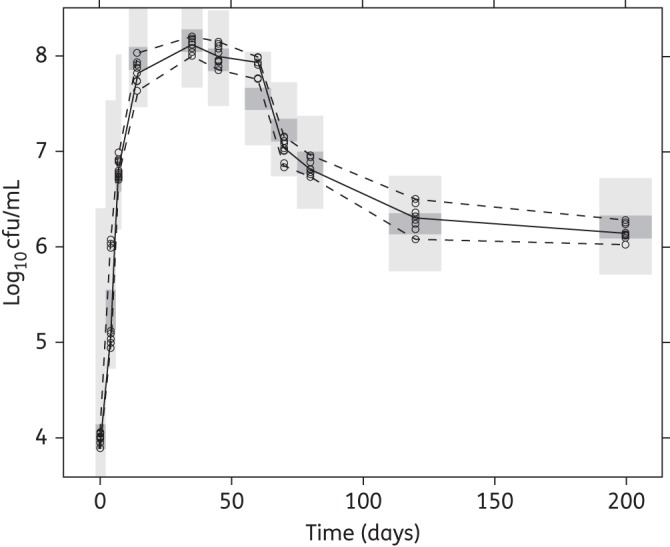
VPC of the final multistate tuberculosis pharmacometric model using H37Rv M. tuberculosis in vitro without drug (natural growth). Open circles are observed log10 cfu data, the solid line is the median of the observed data and the dashed lines are the 5th and 95th percentiles of the observed data. The top and bottom shaded areas are the 95% CIs for the 5th and 95th percentiles of simulated data. The middle shaded area is the 95% CI for the median of the simulated data.
External validation
The external validation of the final model describing the natural growth showed a strong correlation (R2 = 0.98, Figure 5) between the rate of incorporation of radiolabelled methionine into proteins by the bacteria and, as a percentage, the mean of the natural growth model predicted typical fast-multiplying bacterial number out of the predicted typical fast- plus slow-multiplying bacterial number, i.e. 100×(F / F + S).
Figure 5.
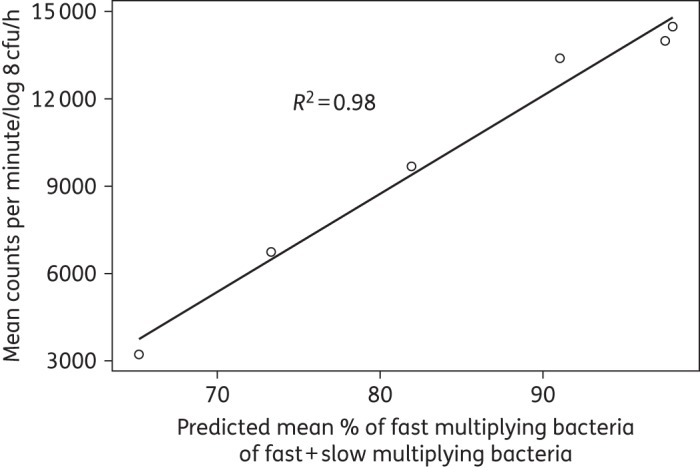
Correlation between the rate of incorporation of radiolabelled methionine ([35S]methionine) into proteins by the bacteria and, as a percentage, the mean of the natural growth model predicted typical fast-multiplying bacterial number out of the predicted typical fast- plus slow-multiplying bacterial number.
Rifampicin exposure–response models
The rifampicin effect on the bacterial system was linked to the bacterial system description, the multistate tuberculosis pharmacometric model, by including a rifampicin pharmacokinetic model. The rifampicin pharmacokinetic model consisted of one compartment accounting for rifampicin in vitro pharmacokinetics (Figure 2). The in vitro system was a static system where the exposure remained constant over time. As such, no elimination from the drug compartment in the model was included. Drugs can further bind to laboratory material,29 i.e. adherence, resulting in less available effective drug in the in vitro system. However, no information about adherence of rifampicin in these systems was known.
The evaluation of differences between the natural growth control data from the log-phase cultures and the natural growth data, due to experimental specific differences, resulted in the inclusion in the final model of separate and significant (decrease in OFV of 99 points) kG and F0 values for the log-phase natural growth control data ( and ) (Table 1). Evaluation in the same manner using the stationary-phase and natural growth data resulted in the inclusion in the final model of a separate and significant (decrease in OFV of 401 points) Bmax for the stationary natural growth control data () (Table 1). Addition of these parameters thus resulted in decreased OFV and allowed a better prediction of the natural growth control data (Figure S1, available as Supplementary data at JAC Online).
The effect of rifampicin on the different bacterial states was evaluated separately for the log-phase and stationary-phase cultures, where applicable, as either an inhibition of growth or a kill rate. A simultaneous evaluation using the log-phase and the stationary-phase data was also performed and the final simultaneous fit model included inhibition of fast-multiplying bacterial growth, kill rate of the fast-multiplying bacteria, kill rate of the slow-multiplying bacilli and kill rate of the non-multiplying bacilli. The final effect parameterization differed from the model describing only the log-phase culture data, which did not support inclusion of a kill rate in the non-multiplying state. The predicted reduction in log10 cfu after 14 days and at 0.5 mg/L was 2.2 and 0.8 in the log-phase and stationary-phase system, respectively. A schematic illustration of where the drug effect was implemented in the multistate tuberculosis pharmacometric model is shown in Figure 2 and parameter estimates are given in Table 1. The final differential equation system of the multistate tuberculosis pharmacometric model was as follows:
The residual error from the estimation of the natural growth data was 40% and the standard errors (RSEs) for all natural growth-associated parameters were ≤5%. Simultaneous estimation of all parameters resulted in a decrease in OFV (ΔOFV = −28). However, the simultaneous estimation resulted in a lower number of significant digits (1.3) and was not selected as the final model.
As indicated by the pcVPC (Figures 6 and 7) and the individual fits (Figure S2) the final multistate tuberculosis pharmacometric model well described the rifampicin effect for a wide range of concentrations for both log- and stationary-phase cultures. Figure 3 shows the model-predicted change in bacterial numbers over time for natural growth and after rifampicin exposure in both the log- and stationary-phase cultures.
Figure 6.
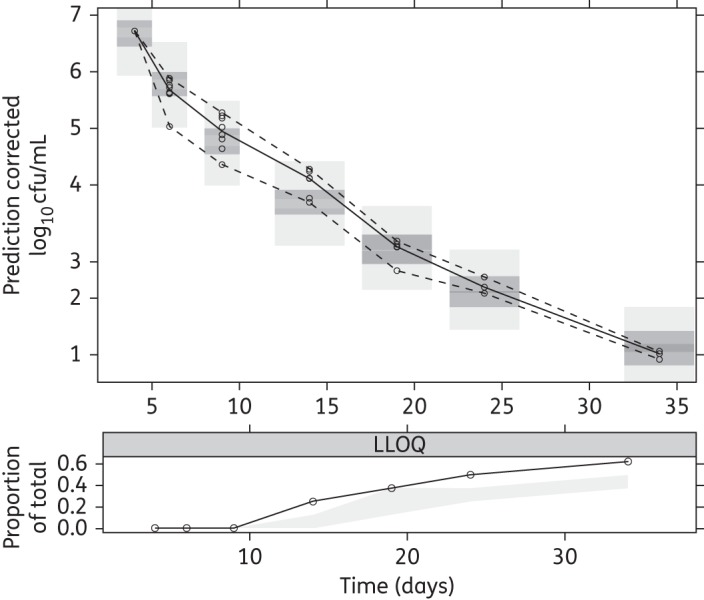
pcVPC for log-phase data of the final multistate tuberculosis pharmacometric model using log- and stationary-phase H37Rv M. tuberculosis in vitro and different static rifampicin concentrations. Open circles are prediction-corrected observed log-phase log10 cfu data after different static rifampicin concentrations, the solid line is the median of the observed data and the dashed lines are the 5th and 95th percentiles of the observed data. The top and bottom shaded areas are the 95% CIs for the 5th and 95th percentiles of simulated data. The middle shaded area is the 95% CI for the median of the simulated data. The black solid line in the lower plot is the median of data below the LOQ. The shaded area in the lower plot is the 95% CI for the simulated LOQ data.
Figure 7.
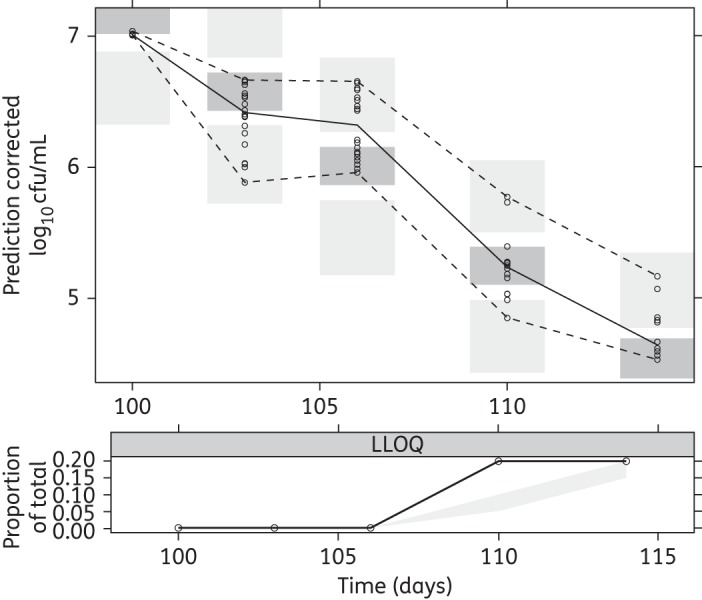
pcVPC for stationary-phase data of the final multistate tuberculosis pharmacometric model using log- and stationary-phase H37Rv M. tuberculosis in vitro and different static rifampicin concentrations. Open circles are prediction-corrected observed stationary-phase log10 cfu data after different static rifampicin concentrations, the solid line is the median of the observed data and the dashed lines are the 5th and 95th percentiles of the observed data. The top and bottom shaded areas are the 95% CIs for the 5th and 95th percentiles of simulated data. The middle shaded area is the 95% CI for the median of the simulated data. The black solid line in the lower plot is the median of data below the LOQ. The shaded area in the lower plot is the 95% CI for the simulated LOQ data.
Discussion
In this work we have developed a multistate tuberculosis pharmacometric model consisting of three different bacterial states. Previous work describing the effect of anti-tubercular drugs have used exponential30 or bi-exponential31,32 models relating to one or two types of visible bacterial states. A two sub-state model without the non-growing state resulted in a much poorer fit (ΔOFV = +300) compared with the final multistate tuberculosis pharmacometric model. In Figure 2, the final model structure of the multistate tuberculosis pharmacometric model together with the drug effect model for describing the effect of rifampicin on log- and stationary-phase cultures is shown. The multistate tuberculosis pharmacometric model constitutes a semi-mechanistic pharmacokinetic pharmacodynamics template model for studying anti-tubercular drug effects.
The model was developed using cfu counts from natural growth data of M. tuberculosis H37Rv in an in vitro hypoxia system together with the decline in cfu counts after different concentrations of rifampicin in log- and stationary-phase cultures. In in vitro systems, slow- or non-multiplying states of M. tuberculosis are thought to be induced by hypoxia.14 In the in vitro hypoxic system, the bacilli initially grow in the top layer of an unagitated culture. They slowly adapt to microaerophilic and eventually to anaerobic conditions while sinking and finally settling on the bottom of the container. At 30–40 days, replication can no longer be detected and at this point the organisms are in stationary phase.33 In late stationary-phase cultures after 60 days of incubation, protein synthesis is switched off.34 However, the dormant stationary-phase bacteria are able to reinitiate protein synthesis as a response to favourable changes in the environment.34 Furthermore, the ability of M. tuberculosis to remain dormant in stationary phase whilst retaining the ability to reinitiate multiplication has been shown in vitro,15–17 in vivo19 and in sputum20,21,35 using methods involving resuscitation-promoting factors (RPFs). It remains to be shown whether the hypoxia-driven in vitro system reflects the same bacterial behaviour that is present in clinical infections, but the system represents a powerful method of studying antibacterial drug effect not only during exponential growth, but also during the stationary phase.36,37
In the model presented in this work, culture-positive bacteria are represented by the fast- and slow-multiplying state and the culture-negative, but still responsive, bacterial state is represented by the non-multiplying state (Figure 2). From the cfu assay it is not possible to directly distinguish between bacteria in the fast- and slow-multiplying states, as the cfu count is a sum of the total number of bacteria that are able to multiply on solid media. It is hence not possible to assign a specific number of cfu that is associated with either the fast- or the slow-multiplying state. Instead the model was allowed to estimate the number of bacteria associated with the fast-multiplying and the slow-multiplying bacterial states. A similar approach of performing multiple state predictions based on one observation has previously been utilized to describe the life cycles of Plasmodium falciparum38 and S. pyogenes.2 As the cfu count reflects only the bacteria that are able to multiply on solid media, the numbers in the fast- and slow- multiplying states, as a sum, were part of the model prediction of the data. However, the non-multiplying state influences the predictions as described in equation 5. This resulted in a significantly better description of the data as judged by OFV (ΔOFV = −159). Inclusion of non-culturable, non-multiplying, bacteria in the model structure but outside the predictions of the visible (culture positive) bacteria has previously been conducted with the same biomarker (cfu) for Escherichia coli.39 It has also been utilized in describing the life cycle and drug effect on P. falciparum.40 As the clinical relevance of these non-culturable bacteria is undoubtedly large, it is naturally of great interest to be able to quantify drug effect on this type of bacteria.
In the pharmacometric model the growth of the fast-multiplying bacteria was best captured by a Gompertz growth function. This growth function involves a cap on growth, i.e. the total carrying capacity of the system, Bmax. This growth function is more mechanistic than an exponential function that allows the bacterial population to grow to an infinite number. However, in a system where natural growth is observed during a shorter time period, the growth is equivalent to an exponential function and can replace the Gompertz function. Previous research has shown that M. tuberculosis switches off RNA and protein synthesis when entering stationary phase.34,41,42 This suggests that bacteria in the slow-multiplying state would have a lower multiplication rate compared with those in the fast-multiplying state. However, some multiplication by bacteria in the slow-multiplying state is still theoretically possible. The decision not to include growth in the slow-multiplying state was based on lack of a significant drop in OFV; however, the authors recognize that growth of the slow-state bacteria is possible but not supported by the data and the model parameterization presented.
The rate parameter characterizing movement of bacteria from the non-multiplying state to the fast-multiplying state, kNF, was fixed to zero. This transfer is naturally possible in a true mechanistic setting and is also seen in vitro when bacteria from stationary-phase cultures are placed in fresh growth conditions, exhibiting reinitiation of increased growth. If a culture is reinitiated from a stationary phase by diluting and placing it in more favourable conditions, it is bound to contain non-growing bacteria as it originated from stationary conditions. These non-growing bacteria will then change into fast-growing bacteria. It was, however, impossible with the data used in this analysis to quantify the initial number of non-multiplying bacteria and hence the transfer from the non-growing to the fast-growing state. The decision not to include a natural death rate in the natural growth system was based on results from a recent study43 that demonstrated that when M. tuberculosis was grown in vitro, the majority of bacilli entered a viable but non-culturable stage on solid media, bacilli were however detectable when using 7H9 liquid medium. However, a subpopulation of persistent bacilli was only resuscitated using RPFs, proteins secreted by M. tuberculosis.44 These RPF-dependent persisters were also present in sputum.21 It was clearly demonstrated that the decline in cfu counts after 60 days of incubation was not due to bacterial death. Instead it was due to the entry of bacilli into a persistent stage, which can only be ended by RPFs.43 Further, the prediction of the total number of bacteria in the system was uninfluenced by the number of dead bacteria, and hence the introduction of a fixed value for the rate of death will not change the ratio between the other states. Description of the natural growth of M. tuberculosis H37Rv when subjected to an in vitro hypoxia system is crucial for obtaining growth and transfer rates for the bacteria when no drugs are present. The final multistate tuberculosis pharmacometric model was very well able to capture, as judged based on the VPC (Figure 4), the observed changes in cfu over time. The strong correlation in the external validation (R2 = 0.98) speaks highly in favour of the prediction provided by the model of both the fast- and the slow-multiplying bacterial numbers over time, as the incorporation should be driven mainly by the fast-multiplying bacteria,34 which are predicted by the model to make up the majority of bacteria in log-phase cultures (Figure 3).
To describe the effect of rifampicin exposure, a compartment accounting for rifampicin pharmacokinetics was linked to the multistate tuberculosis pharmacometric model. However, a static concentration of rifampicin, i.e. no change in concentration over time, was assumed since there was no information about degradation of rifampicin in the systems. Furthermore, no change in media was made over time that could have mimicked in vivo elimination. Degradation of rifampicin has been shown to occur in vitro, but the conclusions with regard to loss of activity are not clear as it is possible that active degradation products exist.45 Evaluation of the use of a fixed rifampicin degradation rate with a half-life of ∼8 days45 with the final log-phase, stationary-phase or combined model indicated that this might not be the case as this led to increased OFVs and no improvement in pcVPCs. In the case of existing degradation, the assumption of a static concentration could, of course, lead to a skewed exposure–response relationship and consequently it is highly advisable to quantify concentrations over time or in cases where appropriate, biological activity over time.
The evaluation of differences between the natural growth data and the log- and stationary-phase natural growth control data in parameter estimates due to experiment-specific properties revealed that there were significant differences in the growth (kG) and initial number of fast-multiplying bacteria (F0) between the experimental settings of the log and natural growth systems. A significant difference between the stationary phase and natural growth was similarly found in maximum system carrying capacity (Bmax). Differences in these parameters between the three experiments are visible when plotting the data from all three datasets used for model development together (Figure 1). There is a clear difference between the natural growth data and the log-phase natural growth control data at day 4. Similarly, there is a difference between the natural growth data and the stationary-phase natural growth control data at day 100. These differences in parameter estimates are thought to reflect differences relating to e.g. the start inoculum and other differences in how the experiments were carried out or, to some extent, differences in experimental conditions. The improvement in describing the log- and stationary-phase natural growth controls when using separate kG and F0 for the log-phase data and Bmax for the stationary phase data compared with using the estimates from natural growth is shown in Figure S1.
In the final model, using the log- and stationary-phase rifampicin treatment data, the rifampicin effect was included as inhibition of the growth function of the fast-multiplying state and as a kill rate of the fast-, slow- and non-multiplying states. Differentiation between the drug effect as inhibition of growth or as a kill rate of the fast-multiplying bacterial state was possible, possibly due to the inclusion of the maximum and the present bacterial number in the fast-multiplying state growth function. It is important to realize that the effect parameterization of any drug will be heavily dependent on the data, i.e. whether the bacterial culture is in log or stationary phase. A drug effect that is studied with bacteria from a log-phase culture will naturally not have the same ratio between the different growth states as when comparison is made with a stationary-phase growth culture. The multistate tuberculosis pharmacometric model was developed on natural growth, emanating from a hypoxia-driven in vitro system studied over 200 days, thus capturing both the log and the stationary phase. As shown, the multistate tuberculosis pharmacometric model can be used for quantifying the drug effect on cultures in either log or stationary phase by taking into account the duration of pre-growth of the bacteria before subjecting them to the drug effect and evaluating differences in experiment-specific settings.
All observed data from the natural growth experiments were above the LOQ. Rifampicin drug effect data below the LOQ (cfu = 10, 25% for the log-phase and 10% for the stationary-phase data) were handled by using the M3 method in NONMEM.28 The final model handles the LOQ data in an adequate way, as indicated by the pcVPC lower limit of quantification (LLOQ) plots (Figures 6 and 7); a slight under-prediction is present in the log-phase LLOQ plot (Figure 6) from 24 days and in the stationary-phase LLOQ plot (Figure 7) at 110 days. This method allows incorporation of the observations that are under the LOQ by treating them as categorical data. Non-inclusion of LOQ data has been shown to introduce substantial bias in parameter estimates46,47 and substitution of LOQ/2 data for LOQ has been reported as inferior to using the M3 method.48
In summary, the multistate tuberculosis pharmacometric model provides predictions over time for a fast-, slow-, non-multiplying bacterial state with and without drug effect. The model constitutes the groundwork for the possibility of a model-based drug development approach for novel anti-tuberculosis compounds, and the application of the model using in vivo data (animal and clinical) should thus be investigated.
Funding
The research leading to these results has received funding from the Swedish Research Council (grant number 521-2011-3442) and the Innovative Medicines Initiative Joint Undertaking (www.imi.europe.eu) under grant agreement no. 115337, resources of which are composed of financial contribution from the European Union's Seventh Framework Programme (FP7/2007-2013) and EFPIA companies' in-kind contribution.
Transparency declarations
None to declare.
Supplementary data
Figures S1 and S2 are available as Supplementary data at JAC Online (http://jac.oxfordjournals.org/).
Acknowledgements
Some of the results presented here have been presented at the Interscience Conference of Antimicrobial Agents and Chemotherapy (ICAAC) 2014 and 2015 (abstracts A026 and A1706, respectively) and at the International Workshop on Clinical Pharmacology of Tuberculosis Drugs 2014 and 2015 (abstracts 9 and 24, respectively).
References
- 1.World Health Organization. Global Tuberculosis Report 2014. http://apps.who.int/iris/bitstream/10665/137094/1/9789241564809_eng.pdf.
- 2.Nielsen EI, Viberg A, Löwdin E et al. . Semimechanistic pharmacokinetic/pharmacodynamic model for assessment of activity of antibacterial agents from time–kill curve experiments. Antimicrob Agents Chemother 2007; 51: 128–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nielsen EI, Cars O, Friberg LE. Pharmacokinetic/pharmacodynamic (PK/PD) indices of antibiotics predicted by a semimechanistic PKPD model: a step toward model-based dose optimization. Antimicrob Agents Chemother 2011; 55: 4619–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Okusanya OO, Tsuji BT, Bülitta JB et al. . Evaluation of the pharmacokinetics-pharmacodynamics of fusidic acid against Staphylococcus aureus and Streptococcus pyogenes using in vitro infection models: implications for dose selection. Diagn Microbiol Infect Dis 2011; 70: 101–11. [DOI] [PubMed] [Google Scholar]
- 5.Bulitta JB, Ly NS, Yang JC et al. . Development and qualification of a pharmacodynamic model for the pronounced inoculum effect of ceftazidime against Pseudomonas aeruginosa. Antimicrob Agents Chemother 2009; 53: 46–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mouton JW, Vinks AA. Pharmacokinetic/pharmacodynamic modelling of antibacterials in vitro and in vivo using bacterial growth and kill kinetics: the minimum inhibitory concentration versus stationary concentration. Clin Pharmacokinet 2005; 44: 201–10. [DOI] [PubMed] [Google Scholar]
- 7.Mohamed AF, Cars O, Friberg LE. A pharmacokinetic/pharmacodynamic model developed for the effect of colistin on Pseudomonas aeruginosa in vitro with evaluation of population pharmacokinetic variability on simulated bacterial killing. J Antimicrob Chemother 2014; 69: 1350–61. [DOI] [PubMed] [Google Scholar]
- 8.Tam VH, Schilling AN, Nikolaou M. Modelling time–kill studies to discern the pharmacodynamics of meropenem. J Antimicrob Chemother 2005; 55: 699–706. [DOI] [PubMed] [Google Scholar]
- 9.Coates A, Hu Y, Bax R et al. . The future challenges facing the development of new antimicrobial drugs. Nat Rev Drug Discov 2002; 1: 895–910. [DOI] [PubMed] [Google Scholar]
- 10.Coates ARM, Hu Y. New strategies for antibacterial drug design: targeting non-multiplying latent bacteria. Drugs R D 2006; 7: 133–51. [DOI] [PubMed] [Google Scholar]
- 11.Coates ARM, Hu Y. Targeting non-multiplying organisms as a way to develop novel antimicrobials. Trends Pharmacol Sci 2008; 29: 143–50. [DOI] [PubMed] [Google Scholar]
- 12.Committee for Medicinal Products for Human Use. Addendum to the Note for Guidance on Evaluation of Medicinal Product Indicated for Treatment of Bacterial Infections - To Specifically Address the Clinical Development of New Agents to Treat Disease due to Mycobacterium tuberculosis. London: European Medicinal Agency, 2010. http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2010/01/WC500070049.pdf. [Google Scholar]
- 13.Wayne LG. Dynamics of submerged growth of Mycobacterium tuberculosis under aerobic and microaerophilic conditions. Am Rev Respir Dis 1976; 114: 807–11. [DOI] [PubMed] [Google Scholar]
- 14.Wayne LG. Dormancy of Mycobacterium tuberculosis and latency of disease. Eur J Clin Microbiol Infect Dis 1994; 13: 908–14. [DOI] [PubMed] [Google Scholar]
- 15.Downing KJ, Mischenko VV, Shleeva MO et al. . Mutants of Mycobacterium tuberculosis lacking three of the five rpf-like genes are defective for growth in vivo and for resuscitation in vitro. Infect Immun 2005; 73: 3038–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kana BD, Gordhan BG, Downing KJ et al. . The resuscitation-promoting factors of Mycobacterium tuberculosis are required for virulence and resuscitation from dormancy but are collectively dispensable for growth in vitro. Mol Microbiol 2008; 67: 672–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shleeva MO, Bagramyan K, Telkov MV et al. . Formation and resuscitation of ‘non-culturable’ cells of Rhodococcus rhodochrous and Mycobacterium tuberculosis in prolonged stationary phase. Microbiology 2002; 148: 1581–91. [DOI] [PubMed] [Google Scholar]
- 18.Shleeva MO, Kudykina YK, Vostroknutova GN et al. . Dormant ovoid cells of Mycobacterium tuberculosis are formed in response to gradual external acidification. Tuberculosis (Edinb) 2011; 91: 146–54. [DOI] [PubMed] [Google Scholar]
- 19.Turapov O, Glenn S, Kana B et al. . The in vivo environment accelerates generation of resuscitation-promoting factor-dependent mycobacteria. Am J Respir Crit Care Med 2014; 190: 1455–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dhillon J, Fourie PB, Mitchison DA. Persister populations of Mycobacterium tuberculosis in sputum that grow in liquid but not on solid culture media. J Antimicrob Chemother 2014; 69: 437–40. [DOI] [PubMed] [Google Scholar]
- 21.Mukamolova GV, Turapov O, Malkin J et al. . Resuscitation-promoting factors reveal an occult population of tubercle bacilli in sputum. Am J Respir Crit Care Med 2010; 181: 174–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bowness R, Boeree MJ, Aarnoutse R et al. . The relationship between Mycobacterium tuberculosis MGIT time to positivity and cfu in sputum samples demonstrates changing bacterial phenotypes potentially reflecting the impact of chemotherapy on critical sub-populations. J Antimicrob Chemother 2015; 70: 448–55. [DOI] [PubMed] [Google Scholar]
- 23.Harigaya Y, Bulitta JB, Forrest A et al. . Pharmacodynamics of vancomycin at simulated epithelial lining fluid concentrations against methicillin-resistant Staphylococcus aureus (MRSA): implications for dosing in MRSA pneumonia. Antimicrob Agents Chemother 2009; 53: 3894–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mouton JW, Vinks AA, Punt NC. Pharmacokinetic-pharmacodynamic modeling of activity of ceftazidime during continuous and intermittent infusion. Antimicrob Agents Chemother 1997; 41: 733–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Beal S, Sheiner LB, Boeckmann A et al. . NONMEM User's Guides (1989-2013). Ellicott City, MD: ICON Development Solutions, 2013. [Google Scholar]
- 26.Keizer RJ, Karlsson MO, Hooker A. Modeling and Simulation Workbench for NONMEM: tutorial on Pirana, PsN, and Xpose. CPT Pharmacomet Syst Pharmacol 2013; 2: e50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bergstrand M, Hooker AC, Wallin JE et al. . Prediction-corrected visual predictive checks for diagnosing nonlinear mixed-effects models. AAPS J 2011; 13: 143–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Beal SL. Ways to fit a PK model with some data below the quantification limit. J Pharmacokinet Pharmacodyn 2001; 28: 481–504. [DOI] [PubMed] [Google Scholar]
- 29.Karvanen M, Malmberg C, Mohamed A et al. . Colistin is extensively lost during normal experimental conditions. In: Abstracts of the Fifty-first Interscience Conference on Antimicrobial Agents and Chemotherapy, Chicago, IL, 2011. Abstract D-690. American Society for Microbiology, Washington, DC, USA. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gillespie SH, Gosling RD, Charalambous BM. A reiterative method for calculating the early bactericidal activity of antituberculosis drugs. Am J Respir Crit Care Med 2002; 166: 31–5. [DOI] [PubMed] [Google Scholar]
- 31.Davies GR, Brindle R, Khoo SH et al. . Use of nonlinear mixed-effects analysis for improved precision of early pharmacodynamic measures in tuberculosis treatment. Antimicrob Agents Chemother 2006; 50: 3154–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chigutsa E, Patel K, Denti P et al. . A time-to-event pharmacodynamic model describing treatment response in patients with pulmonary tuberculosis using days to positivity in automated liquid mycobacterial culture. Antimicrob Agents Chemother 2013; 57: 789–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wayne LG. Synchronized replication of Mycobacterium tuberculosis. Infect Immun 1977; 17: 528–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hu YM, Butcher PD, Sole K et al. . Protein synthesis is shutdown in dormant Mycobacterium tuberculosis and is reversed by oxygen or heat shock. FEMS Microbiol Lett 1998; 158: 139–45. [DOI] [PubMed] [Google Scholar]
- 35.Garton NJ, Waddell SJ, Sherratt AL et al. . Cytological and transcript analyses reveal fat and lazy persister-like bacilli in tuberculous sputum. PLoS Med 2008; 5: e75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hu Y, Coates AR, Mitchison DA. Sterilising action of pyrazinamide in models of dormant and rifampicin-tolerant Mycobacterium tuberculosis. Int J Tuberc Lung Dis 2006; 10: 317–22. [PubMed] [Google Scholar]
- 37.Hu Y, Coates ARM, Mitchison DA. Sterilizing activities of fluoroquinolones against rifampin-tolerant populations of Mycobacterium tuberculosis. Antimicrob Agents Chemother 2003; 47: 653–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Svensson USH, Alin H, Karlsson MO et al. . Population pharmacokinetic and pharmacodynamic modelling of artemisinin and mefloquine enantiomers in patients with falciparum malaria. Eur J Clin Pharmacol 2002; 58: 339–51. [DOI] [PubMed] [Google Scholar]
- 39.Khan DD, Lagerbäck P, Cao S et al. . A mechanism-based pharmacokinetic/pharmacodynamic model allows prediction of antibiotic killing from MIC values for WT and mutants. J Antimicrob Chemother 2015. [DOI] [PubMed] [Google Scholar]
- 40.Hietala SF, Mårtensson A, Ngasala B et al. . Population pharmacokinetics and pharmacodynamics of artemether and lumefantrine during combination treatment in children with uncomplicated falciparum malaria in Tanzania. Antimicrob Agents Chemother 2010; 54: 4780–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hu Y, Butcher PD, Mangan JA et al. . Regulation of hmp gene transcription in Mycobacterium tuberculosis: effects of oxygen limitation and nitrosative and oxidative stress. J Bacteriol 1999; 181: 3486–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hu Y, Mangan JA, Dhillon J et al. . Detection of mRNA transcripts and active transcription in persistent Mycobacterium tuberculosis induced by exposure to rifampin or pyrazinamide. J Bacteriol 2000; 182: 6358–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hu Y, Liu A, Ortega-Muro F et al. . High dose rifampicin kills persisters, shortens treatment duration and reduces relapse rate in vitro and in vivo. Antimicrob Resist Chemother 2015; 6: 641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mukamolova GV, Kaprelyants AS, Young DI et al. . A bacterial cytokine. Proc Natl Acad Sci USA 1998; 95: 8916–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Yu X, Jiang G, Li H et al. . Rifampin stability in 7H9 broth and Löwenstein-Jensen medium. J Clin Microbiol 2011; 49: 784–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Duval V, Karlsson MO. Impact of omission or replacement of data below the limit of quantification on parameter estimates in a two-compartment model. Pharm Res 2002; 19: 1835–40. [DOI] [PubMed] [Google Scholar]
- 47.Hing JP, Woolfrey SG, Greenslade D et al. . Analysis of toxicokinetic data using NONMEM: impact of quantification limit and replacement strategies for censored data. J Pharmacokinet Pharmacodyn 2001; 28: 465–79. [DOI] [PubMed] [Google Scholar]
- 48.Bergstrand M, Karlsson MO. Handling data below the limit of quantification in mixed effect models. AAPS J 2009; 11: 371–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.