Gene Duplicability of Core Genes Is Highly Consistent across All Angiosperms

Large-scale analysis of a set of core gene families shows that gene duplicability is surprisingly similar across 37 angiosperm genomes and independent whole-genome duplication events.

Abstract

Gene duplication is an important mechanism for adding to genomic novelty. Hence, which genes undergo duplication and are preserved following duplication is an important question. It has been observed that gene duplicability, or the ability of genes to be retained following duplication, is a nonrandom process, with certain genes being more amenable to survive duplication events than others. Primarily, gene essentiality and the type of duplication (small-scale versus large-scale) have been shown in different species to influence the (long-term) survival of novel genes. However, an overarching view of “gene duplicability” is lacking, mainly due to the fact that previous studies usually focused on individual species and did not account for the influence of genomic context and the time of duplication. Here, we present a large-scale study in which we investigated duplicate retention for 9178 gene families shared between 37 flowering plant species, referred to as angiosperm core gene families. For most gene families, we observe a strikingly consistent pattern of gene duplicability across species, with gene families being either primarily single-copy or multicopy in all species. An intermediate class contains gene families that are often retained in duplicate for periods extending to tens of millions of years after whole-genome duplication, but ultimately appear to be largely restored to singleton status, suggesting that these genes may be dosage balance sensitive. The distinction between single-copy and multicopy gene families is reflected in their functional annotation, with single-copy genes being mainly involved in the maintenance of genome stability and organelle function and multicopy genes in signaling, transport, and metabolism. The intermediate class was overrepresented in regulatory genes, further suggesting that these represent putative dosage-balance-sensitive genes.

INTRODUCTION

Since the seminal work of Susumu Ohno (Ohno, 1970), the importance of gene and genome duplication for evolution and adaptation has been well appreciated. Indeed, ample examples of gene diversification following duplication have been described and “gene duplicability,” by which we mean the ability of genes to be preserved in a population following duplication, has been extensively studied (Davis and Petrov, 2004; Koonin et al., 2004; He and Zhang, 2006; Liang et al., 2008; Rambaldi et al., 2008; Makino et al., 2009; Woods et al., 2013). Studies published on a large array of species seem to converge on the idea that some duplicated genes are more likely to be preserved in a population, and as such to potentially contribute to functional innovation, than other genes. One factor that seems to influence gene duplicability is the mode of duplication, as in several organisms that have undergone ancient whole-genome duplications (WGDs) it has been shown that different sets of genes were retained following WGD and small-scale duplication (SSD) events (Papp et al., 2003; Blanc and Wolfe, 2004a; Seoighe and Gehring, 2004; Maere et al., 2005a; Aury et al., 2006; Freeling, 2009).

Both SSDs and WGDs have occurred frequently in the flowering plant lineage, and in particular WGDs have happened at a much higher rate than in, for instance, fungi or animals (Van de Peer et al., 2009a; Vanneste et al., 2014a). Studying the Arabidopsis thaliana genome, it has been observed that certain sets of genes have almost exclusively duplicated through WGDs (Blanc and Wolfe, 2004a; Seoighe and Gehring, 2004; Maere et al., 2005a). These genes have distinctive functional features, as they primarily encode transcription factors and components of multiprotein complexes and are involved in development and in signaling pathways (Blanc and Wolfe, 2004a; Seoighe and Gehring, 2004; Maere et al., 2005a; Freeling, 2009). A potential explanation for this phenomenon is given by the gene dosage balance theory, which states that for many genes that participate in essential complex cellular networks or protein complexes, it is crucial that the stoichiometry between the gene products is maintained (Papp et al., 2003; Birchler et al., 2005; Aury et al., 2006; Birchler and Veitia, 2007, 2012; Edger and Pires, 2009). While WGD preserves the relative dosage between genes, the stoichiometry is disrupted when only one or few interaction partners are duplicated. In other plant species, vertebrate and unicellular organisms that have also undergone ancient WGDs, similar observations were made (Aury et al., 2006; Brunet et al., 2006; Huminiecki and Heldin, 2010; Makino and McLysaght, 2010; Rodgers-Melnick et al., 2012). Hence, while gene loss following SSD is generally a relatively fast process, with average duplicate half-life estimates being in the range of a few million years (Lynch and Conery, 2000), after WGD, a substantial set of genes is often retained in duplicate for a much longer time (Maere et al., 2005a). For instance, it is estimated that ∼16% of the genes for Arabidopsis are still present in duplicate following the most recent WGD that occurred ∼49 million years ago (mya; Vanneste et al., 2014a), while 75% of the genes are still present in duplicate in soybean (Glycine max), which underwent a WGD ∼13 mya (Schmutz et al., 2010). Whether these genes will be retained indefinitely is still an unresolved question (Buggs et al., 2012; McGrath and Lynch, 2012; Douglas et al., 2015), although the lower numbers of retained genes reported for more ancient WGD events seems to suggest that, at least for a subset of genes, dosage constraints eventually get relaxed, leading to functional diversification or loss of these genes.

In stark contrast to observations of prolonged retention of a set of dosage-sensitive genes are recent observations that a substantial fraction of core angiosperm genes, i.e., genes that are present in all angiosperm genomes, occur as singletons throughout, suggesting that their duplication might be detrimental (Paterson et al., 2006; Armisén et al., 2008; Edger and Pires, 2009; Duarte et al., 2010; De Smet et al., 2013; Han et al., 2014). While these observations are not necessarily in contradiction with each other, as they likely concern different gene sets, an overarching picture that unifies the different observations regarding gene duplicability is currently still missing. Specifically, the fact that most studies concerning gene duplicability report species-specific patterns adds to the confusion, as genetic context, species biology, ecological requirements at the time of duplication, and the timing of the WGD event might greatly influence the observed duplicate retention patterns (Barker et al., 2008; Soltis et al., 2010; Carretero-Paulet and Fares, 2012; Conant, 2014).

Here, we undertake a large-scale comparative approach to determine whether patterns of gene duplicability can be generalized across diverse lineages. In particular, we investigate the duplicability of 9178 core angiosperm genes identified across 37 different angiosperm genomes and covering 20 putative WGD events. For most gene families, our analyses reveal a striking nonrandom picture of gene duplicability, with the majority of the core genes occurring as single copies in almost all of the angiosperm genomes and a more restricted set of genes occurring in duplicate throughout. This pattern is supported by a strong functional dichotomy between both classes of gene families, with single-copy genes being involved in the maintenance of genome integrity and organelle function and multicopy genes being biased toward signaling, transport, and metabolism. Next to these two extremes, we also identified an intermediate class of gene families that show a pattern of prolonged duplicate retention spanning several tens of millions of years following WGD but appear to eventually also mostly return to singleton status. We hypothesize that dosage balance constraints prolong duplicate retention in these particular gene families. Overall, we advocate that, at least for genes present in all angiosperms, the so-called core genes, selection plays an important role in the long-term preservation or nonpreservation of duplicated genes, considering the highly nonrandom pattern that arises in this cross-species and cross-duplication event analysis.

RESULTS

Core Angiosperm Gene Families Show a Strong Preference toward the Single-Copy State

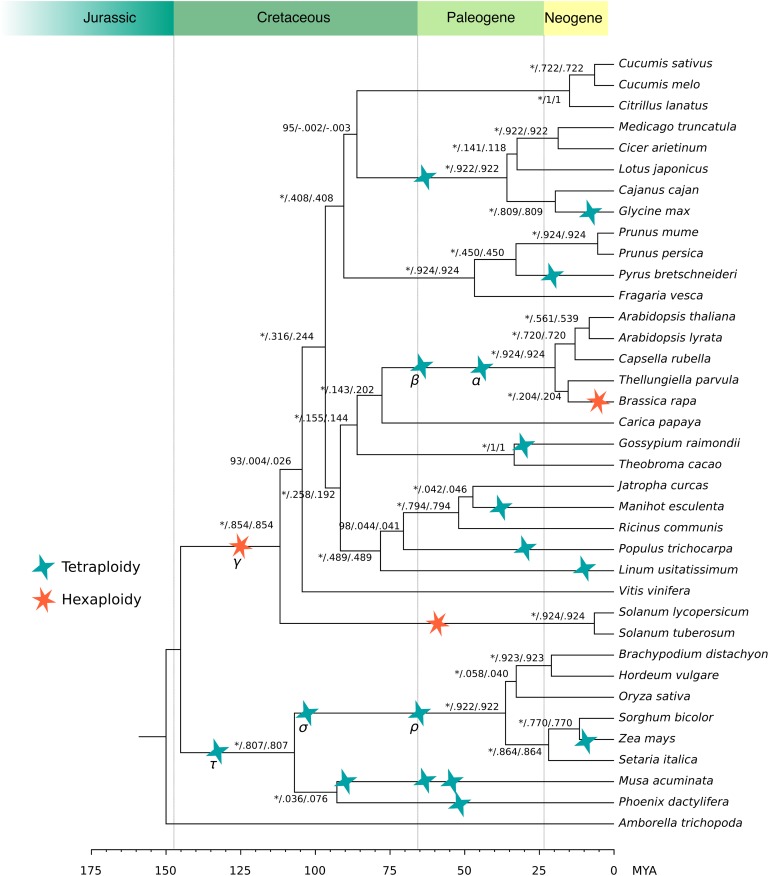
We collected the protein coding sequences for 37 sequenced angiosperm genomes (Figure 1) and constructed gene families using OrthoMCL (see Methods). To ensure that each of these gene families traced back to a single angiosperm ancestral gene, we further processed these gene families using phylogenetic tree construction followed by reconciliation of the gene trees and the species tree (see Methods). Of the 69,133 gene families that were obtained using OrthoMCL and verified by phylogenetic analysis, 9178 belong to the angiosperm core genome, defined as that part of the genome containing genes present in all angiosperms, including the angiosperm ancestor. To accommodate for errors in genome annotation, the presence of partial genome sequences and errors in gene family construction and/or phylogenetic analysis, we allowed for gene families in this core set to be missing in up to five genomes (see Supplemental Figure 1 for a justification of this threshold). This set of genes was used in this study for all subsequent analyses. For each gene family, we calculated the fraction of species for which the gene family contains exactly one copy, further referred to as single-copy percentage (SCP). For instance, a value of 0.7 means that for that particular gene family, 70% of the species examined have exactly one copy, while 30% of the species have more than one copy. The distribution of the SCPs for all core gene families is depicted in Figure 2. As can be observed, the distribution is highly skewed toward high SCPs, with the mean of the distribution lying at 66.8% and the mode of the distribution at 87.5%. Furthermore, if we remove genomes that still have a high number of retained duplicates due to a recent (<20 mya) WGD event (such as soybean [G. max], flax [Linum usitatissimum], maize [Zea mays], and Brassica rapa; Figure 1), we observe an even stronger shift toward the single-copy state with the mode of the distribution being at 92.5% (Supplemental Figure 2).

Figure 1.

Angiosperm Species Tree.

Phylogenetic tree depicting the relationships among the 37 angiosperm genomes used in this article. The tree topology was inferred from a concatenated alignment based on 107 almost single-copy gene families (see Methods). Numbers on the branches represent bootstrap supports (* for 100%), internode certainty (IC), and internode certainty all (ICA), respectively. WGD events were inferred from literature (Jiao et al., 2014; Vanneste et al., 2014a) and are depicted by stars. Only WGD duplications were considered that are more recent than the angiosperm common ancestor.

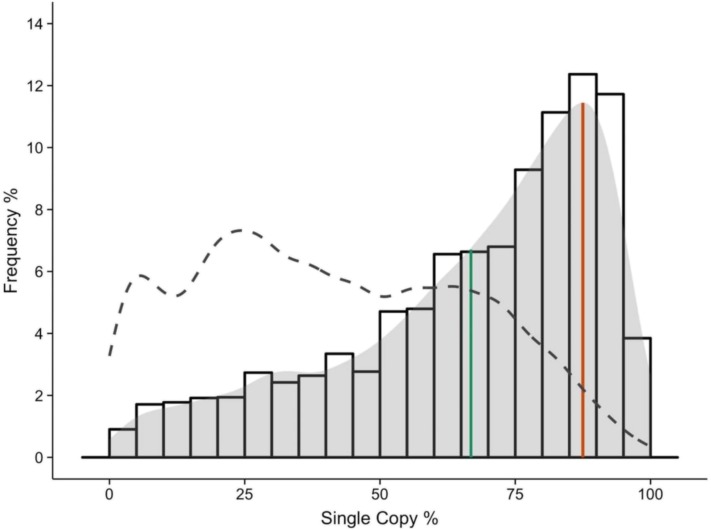
Figure 2.

Overall Distribution of Single-Copy Percentage for All Angiosperm Core Gene Families.

The distribution depicts the degree to which the 9178 core gene families are single copy in the 37 angiosperm species investigated. The x axis represents, for each gene family, the percentage of species with exactly one gene copy with respect to the total number of species in the family. The distribution illustrates a very strong tendency of angiosperm core gene families toward the single-copy state. The mode (87.5%) and the mean (66.8%) of the distribution are indicated by red and green lines, respectively. The observed distribution strongly deviates from the expected distribution under a stochastic duplicate BD model (depicted by dashed lines).

Since the most likely outcome following gene duplication is duplicate loss, with average duplicate half-lives estimated at a few million years for SSDs (Lynch and Conery, 2000), we assessed whether our observations could be explained by simple stochastic gene duplication and loss dynamics. Therefore, we simulated gene family copy number evolution along the 37 species tree, using a probabilistic model in which SSD is modeled as a random birth-death (BD) process (Bailey, 1964) and that takes into account known WGD events by assuming an instantaneous doubling (or triplication) of all genes, as by Rabier et al. (2014) (see Methods). Using this model as a null hypothesis and using realistic rates of small-scale gene duplication and loss, λ, sampled from a normal distribution with mean μ = 0.53 and sd σ = 0.156 duplications/losses per evolutionary time unit (see Methods), we generated gene counts at the leaves of the species tree for 9178 × 1000 = 9,178,000 simulated gene families. We observe that the SCP distribution under the null model has a mode of 22.5% on average, compared with 87.5% for the core angiosperm gene families and that both distributions are significantly different (P < 2.2e-16, Wilcoxon rank-sum test) (Figure 2). Hence, under the neutral scenario of stochastic gene birth and death, there is no bias toward the single-copy state. We repeated this analysis for different sampling distributions of λ-values and observed that the general trend of the distribution of SCPs for the simulated families remains similar, indicating that rejection of the null hypothesis is robust with respect to changes in the distribution of λ-values. Therefore, our observations suggest that gene families belonging to the so-called angiosperm core genome (i.e., gene families present in all angiosperm genomes) are skewed toward the single-copy state more strongly than expected under a random gene duplication loss process and hence appear to be under (strong) selection to be single copy.

Homoeologs Are Quickly Lost Following WGD

The observation that many core gene families are single copy, in spite of the large number of both recent and ancient genome duplication events, seems to suggest that gene loss occurs relatively fast following WGD. The large number of WGD events in this study and their different ages (Figure 1) provide an excellent case to study duplicate retention following WGD (Lloyd et al., 2014).

To study the dynamics of duplicate gene retention in the core gene families, we first assessed the contribution of WGDs compared with SSDs to duplicate retention in the core gene families. Specifically, we applied gene tree–species tree reconciliation to obtain predictions of duplication events and their associated timing for all gene families (see Methods). To this end, we classified each node in the species tree (Figure 1) as either being associated with WGD or SSD, based on whether WGD events have been predicted on the branch leading to the specific node (Supplemental Figure 3). We then compared the predicted numbers of duplication events at WGD nodes versus SSD nodes for both core and noncore gene families, the latter referring to gene families that arose more recently than the angiosperm common ancestor or that underwent massive gene loss in some species since speciation from the angiosperm common ancestor. For the core gene families, we estimated that in total 69.8% (65,531 out of 93,942 predicted duplication events) of the duplications could be attributed to WGDs, whereas for the noncore gene families, this was only 34.6% (48,778 out of 140,786 predicted duplication events) (Supplemental Figure 4). Hence, for core families, compared with noncore gene families, the presence of duplicates seems to be biased toward WGD-associated gene duplication (P < 2.2e-16, Fisher’s exact test) (also see Supplemental Figure 5). In further support of the hypothesis that core gene families were more heavily impacted by WGD than noncore gene families, we observed that K_s-based (number of synonymous substitutions per synonymous site) age distributions of duplicated gene pairs in the different species show clear peaks for the predicted WGD events if only duplicates from the core gene families are considered, while these peaks seemed to be absent for age distributions constructed for duplicates of noncore gene families (Supplemental Figure 6). Hence, core gene families appear to be particularly suited to study duplicate preservation patterns following WGD.

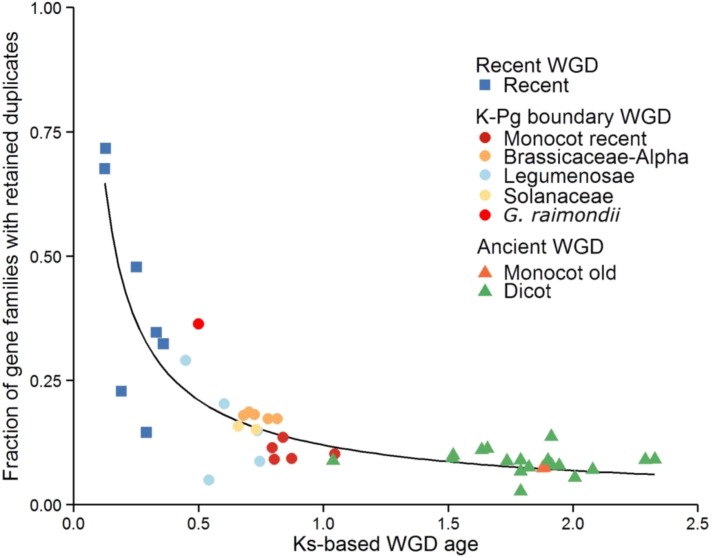
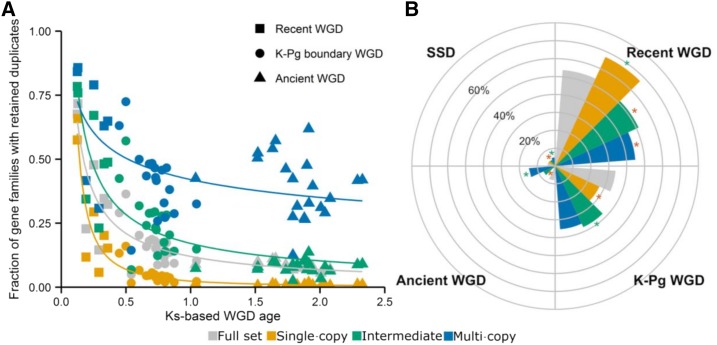
We took advantage of the large number of WGD events and their different ages to study the dynamics of gene duplicate loss following WGDs. To this end, we assigned retained duplicates in the core gene families to the different WGD events or as being created by SSD based on a Gaussian Mixture Modeling (GMM) approach (see Methods). This way, for each species, we obtained predictions of the timing (expressed in K_s values) of the WGD events they experienced and the number of gene families with retained duplicates for each of the WGD events (Lynch and Conery, 2003; Blanc and Wolfe, 2004b; Vanneste et al., 2013) (see Methods). We used these data to assess the relationship between the number of gene families with retained duplicates and the estimated timing of the WGD events. As can be seen in Figure 3, duplicate retention subsequent to WGD follows an L-shaped curve that can be approximated by a power-law function (see Methods), confirming common expectations that gene loss subsequent to WGD is initially fast and then slows down. A similar power-law pattern was recently also observed in a genome-wide analysis of duplicate retention following WGD for a more restricted set of genomes (Lloyd et al., 2014). For ease of interpretation, we grouped the WGD events into three different sets according to the overall time frame during which the WGD event occurred. “Ancient” refers to the WGD events that have been predicted to have occurred at least 75 mya (Figure 1). This includes the ancient γ WGD event that is shared by all dicots and the σ WGD event that is shared by the Poaceae. Using the mixture modeling approach, we could not find support for the predicted ancient τ event that is shared by all monocots (Jiao et al., 2014). “K-Pg boundary” refers to WGD events situated at approximately the K-Pg (Cretaceous-Paleogene) boundary, which reflects a clustering of WGD events at ∼50 to 70 mya (Vanneste et al., 2014a). Finally, the “recent WGD” set includes the duplication events that are more recent than the K-Pg boundary (<50 mya). In Figure 3, duplicate retention patterns associated with the “recent WGD” events show a steep decline as a function of WGD age. Whereas on average 41.64% (sd 21.74%) of the core gene families retain duplicates for the recent WGD events, for the “K-Pg boundary” WGDs, the number of core gene families with retained duplicates has dropped to on average 16.04% (sd 7.48%), and for the “Ancient set,” this number further reduces to 8.37% on average (sd 2.24%).

Figure 3.

Duplicate Gene Retention in Function of Time Since WGD.

Each dot represents the fraction of core gene families with retained duplicates following a specific WGD (y axis), as a function of WGD age, expressed in K_s units (x axis). The timing of the WGD events and the particular gene families that retained duplicates following a specific WGD event were inferred by fitting Gaussian mixture models to K_s age distributions for all 37 species separately (see Methods). As such, each point represents a species-specific estimate for a WGD and WGD events shared by multiple descendant species will be represented by multiple data points that cannot be regarded as being independent. SSD-related peaks and dubious WGD peak callings were omitted. Additional information on all the peaks can be found in Supplemental Table 2 and Supplemental Figure 7. A power-law function was fitted to the data (χ² goodness-of-fit = 0.77, P = 1).

The distinction between SSD and WGD duplicates in this article are approximate, and SSD numbers are likely underestimated by both strategies (GMM and reconciliation method) because some SSDs might be located on a WGD branch (gene tree–species tree reconciliation) or might be hidden under a WGD peak (GMM analysis). However, we do not expect this to have a large influence on the observations that core gene families in contrast to noncore gene families are mainly duplicated by WGD nor on observed differences in gene duplicability patterns for different gene family groups (see further), as this underestimation likely affects all gene families equally.

Core Gene Families Belong to Different Groups That Reflect Major Differences in Gene Duplicability

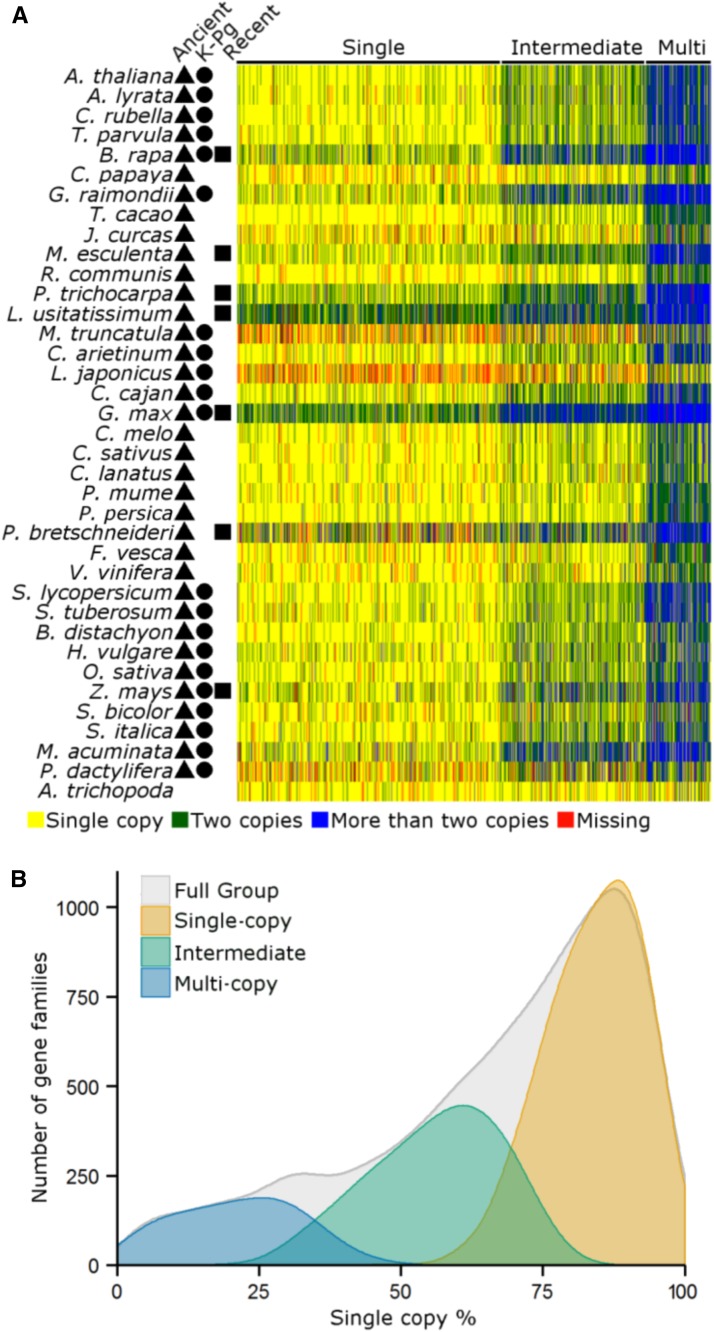
Our global analyses on duplicate retention following WGD show that the majority of the angiosperm core gene families revert quickly to the single-copy state following WGD. Yet, the distribution in Figure 2 suggests that certain gene families revert faster to single-copy status than others. Therefore, we explored gene family specific differences in duplicate retention by constructing a copy number profile matrix, which for each gene family lists the number of genes for a given species. We classified gene families into different groups based on an unbiased clustering of their copy number profiles. Using a subsampling strategy in combination with clustering (Monti et al., 2003) (see Methods), we found that the data are best described by three stable clusters (Figure 4A; Supplemental Figures 8 and 9): Group 1 contains 5097 gene families and covers 5473 Arabidopsis genes, Group 2 contains 2832 gene families and covers 4312 Arabidopsis genes, and Group 3 contains 1249 gene families and covers 3255 Arabidopsis genes. The heat map in Figure 4A clearly shows the overall tendency of gene families in Group 1 to occur as single copies. If duplicates are present, these are mainly biased toward species with recent WGDs. Gene families within Group 2 show mainly duplicate retention for species that are associated with “recent” and “K-Pg Boundary” WGDs, while being largely single copy for species that only underwent “Ancient” WGDs. The latter suggests that while duplicates for these gene families are in general preserved for prolonged times, they eventually largely return to single-copy status. Finally, gene families in Group 3 have retained duplicates for all species, also for the ones that only underwent “ancient” WGDs. We also observe that the outgroup species Amborella trichopoda, which has no evidence of WGDs postdating angiosperm diversification (Amborella Genome Project, 2013), seems to be singleton for most of the core gene families, further substantiating the above observations that core gene families mainly duplicate through WGDs. Investigating the SCPs for the gene families in the three groups confirms that gene families in the first group show a strong preference toward the single-copy state, whereas gene families in the third group represent gene families with a strong tendency to be multicopy in the majority of the species. The SCP distributions for each of the three groups are significantly different (P < 2.2e-16 for all comparisons, Kruskal-Wallis test followed by Dunn’s test with Benjamini-Hochberg multiple testing correction), and there is almost no overlap in SCPs for Groups 1 and 3 (Figure 4B). We will further refer to the gene families in Group 1 as single-copy, those in Group 2 as intermediate, and those in Group 3 as multicopy.

Figure 4.

Core Gene Families Partition into Three Groups Based on Clustering of the Copy-Number Profile Data.

(A) Heat map of the clustered copy number profile matrix. Rows represent species and columns represent the core gene families. Gene families (columns) are sorted according to the three different groups obtained by k-means clustering. Symbols indicate for each species whether WGD events that might have contributed to duplicates in the species fall into the “recent” (rectangle), “K-Pg boundary” (circle), or “ancient” (triangle) category.

(B) SCP distributions for the gene families in each of the three different groups. The distribution of the Full Group shows the SCP distribution of all core gene families together (cf. Figure 2).

Whereas the analyses described above clearly show differences in duplicate retention patterns for the different gene families, it does not provide direct information on the origin of the retained duplicates: For example, are duplicates in the multicopy group also more ancient than those in the other two groups or is the increased number of species with duplicates in the multicopy group mainly due to recent lineage-specific expansions? Therefore, we investigated whether the copy number patterns observed in Figure 4 are related to different ages of retained duplicates in the three groups using duplication age predictions obtained by GMM of K_s-based age distributions and gene tree–species tree reconciliation (see Methods). The former approach (GMM modeling) provides us with species-specific estimates of duplication ages expressed on continuous time scales (K_s values), whereas the latter approach (reconciliation) gives estimates of the absolute counts of duplication events on a gene family base. Hence, the GMM approach provides multiple estimates of duplicate retention per WGD for events with multiple descendant species, since the modeling is performed in a species-specific manner and as such predictions for the same event are obtained for the species separately. These predictions are not necessarily independent since gene losses following duplication might have predated speciation. However, since K_s values and their distributions are not always comparable between species (Smith and Donoghue, 2008), the multiple estimates obtained for the same event in different species could not be collapsed. We used the GMM approach to study duplicate retention dynamics over time for gene families in the three different groups similarly as we did above for the full set of core gene families (Figure 3). Overall, when comparing numbers of retained duplicates for the core gene families in function of the WGD ages, we observed that gene families in the three different groups differ markedly in their duplicate retention dynamics over time (P < 9.2e-06 for all comparisons, Kruskall-Wallis test followed by Dunn’s test with Benjamini-Hochberg multiple testing correction) (Figure 5A). In particular, we observed higher duplicate retention for all WGD event classes (i.e., for “recent,” “K-Pg boundary,” and “ancient” WGD events) for the core gene families in the multicopy group, whereas the proportion of core gene families in the single-copy group with retained duplicates is consistently lower (Figure 5A). Next, we used the gene tree–species tree reconciliation approach to obtain absolute counts of predicted duplications and their corresponding ages for all core gene families and used these data to identify group-specific differences in duplicate retention for specific duplication age classes compared with the full set of core gene families (Figure 5B). This shows that gene families in the single-copy group seem to be specifically biased toward duplicates from the “recent” WGDs (P = 3.55e-137, Fisher’s exact test with Bonferroni multiple-testing correction), while duplicates from the “K-Pg boundary” (P = 5.79e-83, Fisher’s exact test with Bonferroni multiple-testing correction) and “ancient” (P = 6.36e-98, Fisher’s exact test with Bonferroni multiple-testing correction) events are underrepresented. Duplicate retention for gene families in the intermediate group is biased toward the “K-Pg boundary” events (P = 5.05e-45, Fisher’s exact test with Bonferroni multiple-testing correction). Multicopy gene families are enriched for duplicates from the “ancient” events (P = 2.09e-50, Fisher’s exact test with Bonferroni multiple-testing correction), while showing a deficit in duplications from the “recent” events (P = 1.81e-73, Fisher’s exact test with Bonferroni multiple-testing correction). SSDs are underrepresented in the intermediate group (P = 1.65e-23, Fisher’s exact test with Bonferroni multiple-testing correction), while being overrepresented in the multicopy group (P = 1.50e-22, Fisher’s exact test with Bonferroni multiple-testing correction). A comparison of the relative number of duplications obtained for each duplication age class based on gene tree–species tree reconciliation and GMM of K_s-based age distributions provide consistent results (Supplemental Figure 10). Despite these differences in duplicate retention for the three groups, all groups have retained more duplicates from the “recent” events, followed by the “K-Pg boundary” and the “ancient” events (Figures 5A and 5B).

Figure 5.

Analyses of Duplication Events of the Three Groups.

(A) For each of the clusters in Figure 4, power-law functions were fitted to the corresponding data points representing the fraction of core gene families with retained duplicates following a particular WGD (y axis) as a function of WGD age (x axis), as in Figure 3 (χ² goodness-of-fit single-copy group = 0.52, P = 1; χ² goodness-of-fit intermediate group = 1.38, P = 1; χ² goodness-of-fit multicopy group = 1.83, P = 1). The “full set” curve corresponds to the curve represented in Figure 3.

(B) Polar diagram depicting the fraction of duplication events in each gene family group belonging to either “recent,” “K-Pg boundary,” “ancient” WGDs, or “SSD” events. Here, predicted duplication events were inferred based on gene tree–species tree reconciliation. Green and red asterisks denote statistically significant over- and underrepresentation, respectively, of duplicates of a certain class for a specific group, comparing each time the number of associated duplications for each group with that of the full set (gray bar) by Fisher’s exact test. Similar results were obtained using predicted duplication events inferred using Gaussian mixture modeling of K_s distributions (Supplemental Figure 10).

The Partitioning in Different Groups Is Mirrored by Gene Function

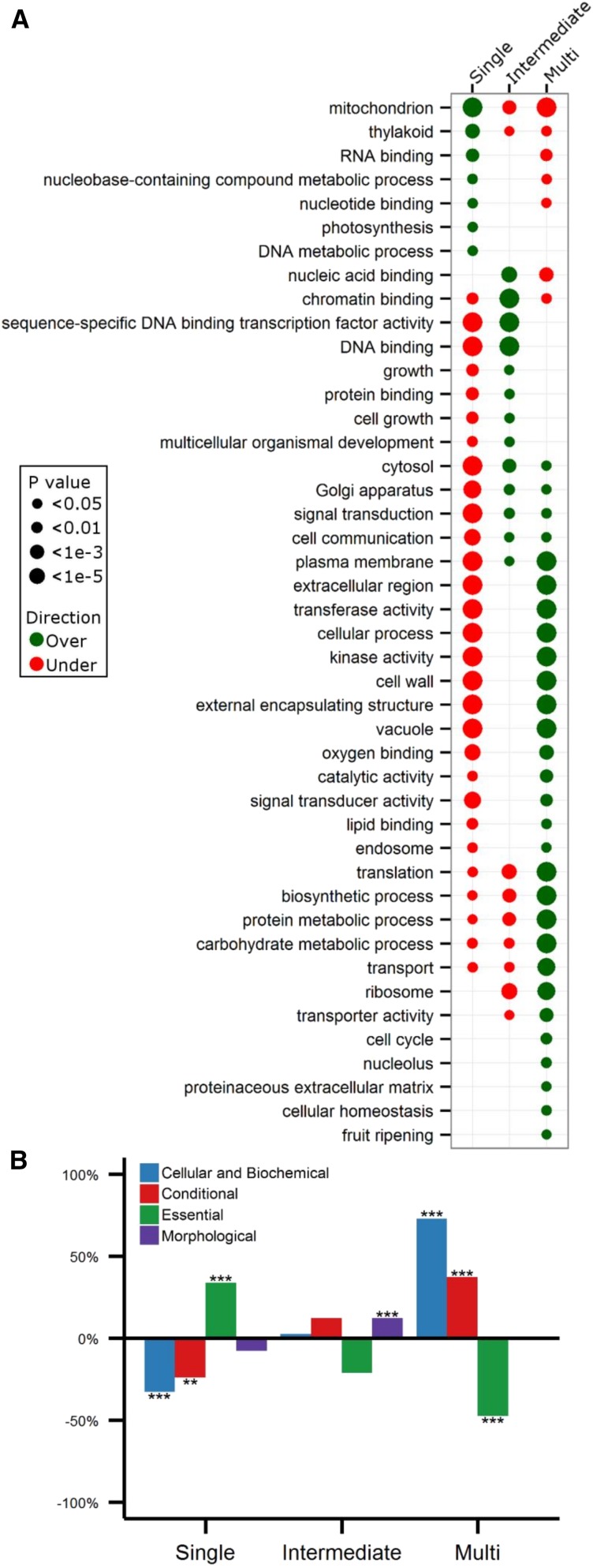
We conducted a GOSlim enrichment analysis of the Arabidopsis genes in the three different groups, revealing that the three different groups have a remarkably different functional composition (Figure 6A). The “single-copy” group is enriched for genes that function in organelles (e.g., “mitochondrion,” “thylakoid,” and “photosynthesis”) and that have to do with the maintenance of DNA repair and integrity (e.g., “DNA metabolic process” and “nucleobase-containing compound metabolic process”). An independent analysis of 2090 nuclear-encoded chloroplast-targeted genes taken from The Chloroplast Function Database (Myouga et al., 2013) supported the overrepresentation of genes with chloroplast-associated functions in this particular group (P = 1.1e-59, Fisher’s exact test with Bonferroni multiple-testing correction). No such overrepresentation was found for the “intermediate” and “multicopy” groups (Supplemental Figure 11). The “intermediate” group is enriched for genes that are involved in development (“multicellular organism development”) and growth and regulation of transcription (“transcription factor activity” and “chromatin binding”). This last observation was confirmed by an independent analysis of 1795 putative transcription factors in Arabidopsis (Pérez-Rodríguez et al., 2010), which showed that these genes were clearly overrepresented in the “intermediate” group (P = 4.8e-17, Fisher’s exact test with Bonferroni multiple testing correction) while not being enriched for the “multicopy” group and being underrepresented in the “single-copy” group (Supplemental Figure 12). The overrepresentation of regulatory genes in this group, together with the longer retention times for these gene families, suggests that this group mainly consists of dosage-balance-sensitive genes (Birchler et al., 2005; Maere et al., 2005a; Freeling and Thomas, 2006; Edger and Pires, 2009). We further investigated this hypothesis by assessing the extent to which genes within this group are involved in protein interactions (Papp et al., 2003) and the contribution of WGD to duplicate retention for this specific group (Papp et al., 2003; Blanc and Wolfe, 2004a; Maere et al., 2005a), which represent two characteristics, other than functional overrepresentation, associated with dosage balance constraints. First, we observed that Arabidopsis interacting protein pairs (see Methods) are indeed most overrepresented in the “intermediate” group, yet these results are only borderline significant following multiple testing correction (P = 0.01, randomization test with Bonferroni multiple-testing corrections) (Supplemental Table 1). Second, while all core gene families duplicate preferentially by WGD, the “intermediate” group has a higher fraction of WGD-associated duplicates versus SSD-associated duplicates compared with the “single-copy” group (P = 2.96e-17, Fisher’s exact test with Bonferroni multiple-testing correction) or “multicopy” group (P = 2.76e-61, Fisher’s exact test with Bonferroni multiple-testing correction), as derived from the gene tree–species tree reconciliation predictions, strengthening our belief that the “intermediate” group contains dosage-balance-sensitive gene families. Finally, “multicopy” gene families are enriched for genes that appear to be involved in the interaction with the environment (“signal transduction,” “transport,” and “cell wall”), translation, and different metabolic processes (“carbohydrate and protein metabolic process,” “biosynthetic process,” and “catalytic activity”).

Figure 6.

Functional Analyses of the Three Different Groups.

(A) GOSlim enrichments and underrepresentations calculated for the Arabidopsis genes in each of the three gene family groups in Figure 4. Dot sizes are representative for the statistical significance of over- (green) or underrepresentation (red).

(B) Enrichment analysis of the three gene family groups for knockout mutant phenotype annotations (Lloyd and Meinke, 2012). Bars represent overrepresentation (positive values) or underrepresentation (negative values) of knockout phenotypes belonging to any of four functional categories (bar colors). Asterisks denote significance levels as calculated by Fisher’s exact test (***P < 0.001 and **P < 0.05).

We also analyzed a data set that describes loss-of-function (LOF) phenotypes for 2400 Arabidopsis genes (Lloyd and Meinke, 2012) of which 1521 are present in the core gene set. Genes within this data set are placed in four different groups according to their knockout phenotype. We find that the three core angiosperm groups show markedly different signatures with regards to their classification into LOF phenotype groups (Figure 6B). In particular, genes in the “single-copy” group are enriched for the “essential” category (P = 1.44e-39, Fisher’s exact test with Bonferroni multiple-testing correction), consisting of genes that are essential for early development and survival. On the other hand, essential genes are underrepresented in the “multicopy” group. This is agreement with recent observations that lethal genes in Arabidopsis usually lack duplicates in this particular genome (Lloyd et al., 2015). It is noteworthy that overrepresentation of essential genes in the “single-copy” group is not specifically due to the genes involved in DNA integrity within the single-copy set, but also organelle genes are associated with essentiality (Lloyd and Meinke, 2012). The “intermediate” set is enriched for genes of the “morphological” class (P = 6.96e-05, Fisher’s exact test with Bonferroni multiple-testing correction), which contains genes associated with clear morphological phenotypes, involved in reproduction and timing (e.g., flowering time and senescence), in agreement with the strong overrepresentation of developmental genes in this particular group. Finally, the “multicopy” class is overrepresented for genes in the “cellular and biochemical” group (i.e., genes functioning in metabolism or other biochemical pathways or showing phenotypic effects at the cellular level) (P = 1.14e-06, Fisher’s exact test with Bonferroni multiple-testing correction) and “conditional” class (P = 6.84e-04, Fisher’s exact test with Bonferroni multiple-testing correction) (i.e., genes that respond to biotic and abiotic stress), consistent with GOSlim enrichment results. In summary, both the GOSlim enrichment analysis and the analysis of LOF phenotype data indicate that the separation of core gene families into three different groups according to gene duplicability is mirrored by a separation of the gene families in the space of gene functions.

DISCUSSION

We assessed duplicate retention patterns for 9178 core angiosperm gene families (i.e., gene families shared by all angiosperm species) in 37 angiosperm genomes, covering 20 putative WGD events. Assessing the retention of duplicated genes across such a large number of genomes and duplication events allows for replicated tests of gene duplicability, mitigating potential biases due to differences between individual species and WGDs (Barker et al., 2008; Soltis et al., 2010; Carretero-Paulet and Fares, 2012; Conant et al., 2014). In addition, because of the varied age range of the WGD events in our data set and the observed large contribution of WGD to the expansion of core gene families, we were able to compare duplicate retention patterns across WGD events of different ages.

We observe that gene duplicability is highly consistent across angiosperm genomes, with over 50% of the core angiosperm genes reverting quickly to single-copy status following duplication, whereas a much smaller set seems to occur in multiple copies throughout. An intermediate group is formed by putative dosage-balance-sensitive genes that are maintained in duplicate for prolonged periods of time, but eventually mostly return to single-copy status. By showing that there is a clear distinction between genes that generally occur as a single-copy throughout and genes that show prolonged duplicate retention in the genome or that are retained “indefinitely” following WGD, we reconcile previous observations on high numbers of single-copy genes shared across multiple angiosperm genomes, despite the many, often nested, WGD events they experienced (Paterson et al., 2006; Duarte et al., 2010; De Smet et al., 2013; Han et al., 2014), with observations that duplicates can be retained for long periods following WGD (Blanc and Wolfe, 2004a; Maere et al., 2005a). Previous, smaller-scale comparisons of duplicate retention following WGD in multiple plant species have observed strong differences between species (Barker et al., 2008; Carretero-Paulet and Fares, 2012). These differences do most probably exist, yet, by focusing on a large number of species and a large number of WGD events, we were able to retrieve dominant and striking patterns of gene duplicability that have remained concealed in smaller-scale comparisons. As our study only focused on core gene families, it is possible that important differences between species result from duplicate retention patterns in gene families that were not considered in this analysis. In addition, while here we showed that the overall duplicate retention tendency seems to be highly consistent across a large number of species and duplication events for the angiosperm core gene families, further detailed cross-species exploration of duplications in both core and noncore angiosperm gene families might reveal other parallelisms in duplicate retention that have remained concealed in this work. For instance, other works have shown that the mode of SSD (primarily tandem versus transposition duplication) is also preserved cross-taxon for certain gene families (Freeling et al., 2008; Wang et al., 2011; Woodhouse et al., 2011).

We found that gene duplicability is highly associated with gene function, with single-copy genes being biased toward essential genes, functioning in genome integrity pathways and organelles and multicopy genes being biased toward functions involved in interactions with the environment. An evaluation of duplicate gene loss and retention patterns following the three successive WGDs in Arabidopsis uncovered similar correlations between duplicate retention pattern and gene function as the ones observed here (Maere et al., 2005a). Here, we show that these function retention patterns can be generalized across a large number of angiosperm genomes and WGD events. In addition, these patterns appear not to be limited to the plant kingdom: In a study focusing on the duplication history of genes across 17 ascomycete genomes, a similar functional separation was observed between genes that generally occur in duplicate and those that are single copy in most ascomycetes (Wapinski et al., 2007). Likewise, a large-scale analysis of prokaryotic genomes suggested that the number of genes functioning in DNA repair and replication remains relatively constant irrespective of genome size, whereas the number of transcription factors, genes involved in signaling, and transporter genes seems to increase with increasing genome size (van Nimwegen, 2003; Molina and van Nimwegen, 2009). Consequently, patterns of duplicate retention and loss for core genes in angiosperms and other organisms appear to abide by general function-based rules.

The question remains what causes these specific duplication patterns to occur. Given the overall short half-lives of duplicate genes (Lynch and Conery, 2000), one could speculate that the observed high fraction of single-copy gene families and a more limited number of multicopy gene families are caused by a stochastic gene duplication and loss process. We tested this hypothesis and found that stochastic BD processes cannot reproduce the observed duplicability distribution, which is heavily skewed toward single-copy gene families. In addition, the observed overall consistency of patterns across genomes and across large-scale duplication events and the functional enrichments observed for the various duplicability classes of gene families argue against such a random scenario. Considering the strong association with gene function, a possibility is that gene function directly or indirectly constrains gene duplicability. The observed patterns of gene duplicability are indeed consistent with the idea of the existence of a conserved core that needs to remain untouched (“single-copy” group) and the existence of processes that are more amenable to modifications and that might be responsible for adaptations to new environments and the evolution of distinct morphological features (“multicopy” group) (Kitano, 2004). Gene duplication in itself can indeed modulate gene function in a negative way and as such impact core gene function by, for instance, increasing absolute gene dosage of genes with strict gene expression constraints (Siegel and Amon, 2012) through the accumulation of mutations in duplicate copies with potential pleiotropic negative effects on wild-type fitness (Bridgham et al., 2008; Dean et al., 2008; De Smet et al., 2013; Kaltenegger and Ober, 2015) or potential cytotoxic effects (e.g., protein misfolding) (Zhang and Yang, 2015). As a result, duplicates of genes sensitive to these processes might be eradicated quickly, also after WGD. On the other hand, repeated biased retention of certain duplicates for long periods of time (“intermediate” group) or indefinitely (“multicopy” group) suggests a mechanism of duplicate retention other than sub-/neofunctionalization, which are in general assumed to be slow processes (Lynch and Katju, 2004) and would not be expected to lead to repeated biased retention. Considering the primary role of WGD in duplicate retention of the core genes and the specific association of gene functions enriched in the “intermediate” and “multicopy” groups with previously defined putative dosage-balance-sensitive genes (Blanc and Wolfe, 2004b; Maere et al., 2005a), we hypothesize that dosage balance constraints may have contributed to the prolonged retention of duplicate genes in these sets. Prolonged retention of duplicate genes, accompanied by gradual circumvention of dosage balance constraints, may increase the possibility that duplicate genes diversify and get permanently preserved (Birchler and Veitia, 2012; Conant et al., 2014). Alternatively, duplicate genes could also be permanently retained through absolute dosage constraints replacing over time the relative dosage balance constraints responsible for initial duplicate retention (Bekaert et al., 2011; Conant, 2014). In our results, the “intermediate” group of gene families exhibits the hallmarks of dosage balance constraints that wear off over time, leading to prolonged preservation and ultimately loss of duplicates. A subset of genes in the “multicopy” group may also have been retained initially because of dosage balance constraints and, in this instance, preserved indefinitely through other mechanisms; in particular, transporters, signaling transducers, and cell communication genes have been reported earlier as potentially dosage balance sensitive (Blanc and Wolfe, 2004a; Maere et al., 2005a). On the other hand, the “multicopy” set of gene families is also enriched in “environmentally responsive” genes. Consequently, their repeated and biased retention following WGD might be a consequence of an increased adaptive advantage of polyploidy under environmental stress. Indeed, increasing evidence suggests that polyploids show wider environmental tolerance and higher levels of phenotypic plasticity than diploids (Van de Peer et al., 2009b; Hahn et al., 2012; te Beest et al., 2012; Yona et al., 2012; Chao et al., 2013; Vanneste et al., 2014b; Selmecki et al., 2015; Sunshine et al., 2015). In particular, transporters and metabolic genes, enriched in the “multicopy” class, have been identified before as putative driver genes explaining the increased tolerance of polyploids for environmental stress (Dunham et al., 2002; Selmecki et al., 2006, 2015; Gresham et al., 2008; Yang et al., 2014; Sunshine et al., 2015). Despite the strong correlation between gene duplicability and gene function observed here, it remains to be further investigated which evolutionary mechanisms are responsible for the observed strong bias in duplicate retention patterns, and it remains to be established whether gene function directly influences gene duplicability or whether biased gene retention could be a by-product of other evolutionary phenomena instead, such as for instance the preservation of intermolecular interactions (dosage balance) or sequence constraints related to high levels of gene expression (Davis and Petrov, 2004; Drummond and Wilke, 2008). In particular, since network structure is often believed to constrain protein evolution and to underlie complex phenotypic traits, future work into this direction might benefit from investigating gene duplicability in a network context (Bekaert et al., 2011; D’Antonio and Ciccarelli, 2011; Alvarez-Ponce and Fares, 2012; Chae et al., 2012; Conant, 2014).

METHODS

Genome Data

We employed protein-coding genes from 37 fully sequenced angiosperm genomes, 35 of which were used by Vanneste et al. (2014a). Protein-coding sequences for Amborella trichopoda (Amborella Genome Project, 2013) and Capsella rubella (Slotte et al., 2013) were retrieved from the Amborella Genome Database (http://www.amborella.org/) and Phytozome V10, respectively.

Gene Family Prediction

OrthoMCL

We identified gene families based on protein sequence similarities by OrthoMCL (Li et al., 2003). After all-against-all BLASTP searches, OrthoMCL was used to group proteins with high sequence similarity into gene families. An important parameter of OrthoMCL is the inflation parameter, which controls cluster tightness. We calculated gene families for different inflation parameter values (i.e., 1.5, 2.0, 2.5, and 3.0) to assess its influence and observed large variations in the number of gene families detected and their overall size. We decided to use the inflation parameter that gives on average the largest gene families (i.e., 1.5), since the gene families are further processed by phylogenetic tree construction (and split up if necessary; see below). As such, we obtained 69,133 multigene families.

Species Tree Construction

A species tree was constructed from a concatenated multiple sequence alignment inferred from 107 gene families that are present in all of the 37 angiosperm species and contain no more than 40 genes in total. The genes within these 107 gene families are on average longer than 150 amino acid residues. If a species had paralogs in a gene family, we only kept the paralog with the most orthologous hits in the gene family in the intermediate OrthoMCL results file. We used Muscle (3.8.31) (Edgar, 2004) with default parameters to perform multiple sequence alignments for each gene family based on the amino acid sequences. We then used trimal (1.4) to remove low quality regions of the alignments based on an automatically selected threshold (-strictplus), which depends on a distribution of residue similarity inferred from multiple sequence alignment for each gene family (Capella-Gutiérrez et al., 2009). Multiple sequence alignments of amino acid sequences were back-translated into alignments of codon sequences and were concatenated one by one into an integrated alignment. In the end, we obtained an alignment of 36,631 codons with 109,893 nucleotide sites (see Supplemental Data Set 1 for the alignment and Supplemental Data Set 2 for data source and accession numbers of genes in the alignment).

To construct the species tree, we used CodonPhyML (1.0) (Gil et al., 2013) under three different codon models that differ in their instantaneous substitution rates between codons, being the Muse and Gaut (MG) model (Muse and Gaut, 1994), the Goldman and Yang (GY) model (Goldman and Yang, 1994), and the YAP model (Yap et al., 2010). The stationary frequency of codons and the transition-transversion ratio were estimated by maximum likelihood. The different ratios of nonsynonymous to synonymous substitution rate (ω) over the sequence alignment were drawn from a discrete gamma distribution with three, four, or five classes. The parameters α and β of the gamma distribution were optimized by maximum likelihood. An initial tree was built using the BioNJ algorithm, based on the empirical model ECMK07. CodonPhyML then employs Nearest Neighbor Interchange and Subtree Pruning and Regrafting to optimize the tree topology. Branch lengths and model parameters are also fully optimized during this process.

Based on the different codon models and parameters described above, we obtained nine phylogenetic trees with identical topology but with slightly different branch lengths. The branch lengths of the different trees have no effects on the phylogenetic placement of WGDs (see “Evolution of Gene Families under a Stochastic BD Null Model” and Supplemental Figure 13). We used the Akaike Information Criterion (AIC) to compare likelihoods for the different trees and selected the tree with the lowest AIC tree as the species tree in this study. This tree corresponds to the tree inferred under the MG model with five classes for ω.

We calculated bootstrap support values for all branches of the species tree by obtaining 100 bootstrap samples for the concatenated multiple sequence alignment and running CodonPhyML on each bootstrapped alignment using the same model and parameter settings as chosen for the species tree. The bootstrap values were added on each branch of the species tree by RAxML (Stamatakis, 2014). As an alternative support measure to the bootstrap, we assessed the degree of congruence between the species tree topology and the topology of the 107 gene trees, also obtained using codonPhyML with the same parameter settings, for the gene families used for species tree construction. Specifically, using RAxML, we calculated two measures: (1) internode certainty (IC) and (2) IC All (ICA), which evaluate the support for an internode in the species tree by considering its frequency in the set of 107 gene trees (Salichos and Rokas, 2013; Salichos et al., 2014). An IC value of one means that none of the gene tree topologies conflict with the species tree topology, whereas a value close to zero for internodes suggests that there is another possible bipartition that occurs with almost equal frequency to the inferred one. In the end, the species tree was rooted on the branch of the basal angiosperm species A. trichopoda and was visualized by FigTree (http://tree.bio.ed.ac.uk/software/figtree/). This obtained species tree is largely consistent with the APGIII tree (Bremer et al., 2009) (see Supplemental Figure 14 for a comparison).

Gene Tree Construction and Reconciliation

Next, we implemented a pipeline to automatically construct phylogenetic trees for all 69,133 gene families and to test whether these trees could be traced back to a single angiosperm ancestral gene. We first removed 253 gene families with more than 200 genes because of the enormous computational resources required by large gene families. We then built maximum likelihood phylogenetic trees for each of the remaining gene families with more than two genes. Multiple sequence alignments based on protein sequences were produced using Muscle with default settings (Edgar, 2004) and were further trimmed by trimal in a heuristic automated approach (-automated1) (Capella-Gutiérrez et al., 2009). The processed multiple sequence alignments were fed into PhyML 3.0 (Guindon et al., 2010) using the LG model with the equilibrium frequencies defined in the substitution model. The best trees produced from either Nearest Neighbor Interchange or Subtree Pruning and Regrafting were retained as maximum likelihood gene trees. To obtain branch support values for the gene trees, we used the SH-like approximate likelihood-ratio test (Anisimova and Gascuel, 2006) instead of traditional bootstrap values because of its speed.

For 28,946 gene families with at least four genes from at least two different species, we used gene tree–species tree reconciliation (Stolzer et al., 2012) to root the gene trees and to obtain estimates of duplication and speciation events along the gene tree. For the remaining 39,934 gene trees, prediction of duplication and speciation events is trivial (see below). Since the reconciliation process is error prone (Hahn, 2007; Nguyen et al., 2013; Wu et al., 2013) and depends on the quality of the gene tree, species tree, and the parameter settings of the reconciliation method, we implemented a pipeline to mitigate these problems as much as possible: (1) Since PhyML does not explore the entire search space of possible tree topologies, we investigated whether alternative tree topologies with improved reconciliation duplication/loss costs, obtained by branch rearrangements of the original gene trees in the reconciliation strep (see below), had an increased likelihood under the multiple sequence alignment than the gene tree produced by PhyML. As such, we obtained a reconciled gene tree that is maximally supported by both the reconciliation criterion (in this instance duplication/loss cost) and the multiple sequence alignment as described by Wu et al. (2013). (2) To deal with the problem of reconciliation solutions being dependent on the parameter settings, we performed the reconciliation with a range of different parameter settings and also considered multiple possible optimal reconciliations under the same parameter settings, if available. Since duplication/speciation events that were predicted for multiple parameter settings are assumed to be more reliable (Nguyen et al., 2013), we built a majority-rule consensus reconciliation in which we only retained duplication/speciation events supported by at least 50% of the reconciliations (see “Gene Tree–Species Tree Reconciliation Pipeline”).

If a duplication event was predicted at the Angiosperm-associated node, we split the phylogenetic tree into two subtrees (and, hence, also two associated gene families), ensuring that each subtree traced back to a single ancestral Angiosperm gene. With this procedure, we obtained 11,131 gene families with gene trees tracing back to an angiosperm ancestral gene. From this set we removed the gene families that did not have gene copies for at least 32 out of 37 species (Supplemental Figure 1), ending up with a final set of 9178 core gene families.

For the remaining 39,934 gene families (i.e., gene families with at least two species but no more than three genes or gene families that are only present in one species), we inferred duplication events by simply applying the following rules (Supplemental Figure 15). For gene families with only one species, after mid-point rerooting of the gene tree, each node in the tree represents a duplication node. For gene families with two genes, nodes were annotated as duplication nodes if the two genes were from the same species. For gene families with three genes, we used the topology of the gene tree to infer the duplication events.

Gene Tree–Species Tree Reconciliation Pipeline

We used NOTUNG version 8 (Stolzer et al., 2012) for reconciliation. NOTUNG is based on the maximal parsimony criterion and outputs the reconciled tree that minimizes the overall duplication/loss cost. We first ran NOTUNG in the “rooting” mode, saving different trees with different optimal rootings under the given duplication/loss cost scheme. We then ran NOTUNG in the “reconcile” mode, again retaining different optimal reconciliation solutions. We also ran NOTUNG in the “rearrange” mode, which allows for weakly supported branches (provided by aLRT scores) to be rearranged. We used two different thresholds, a more stringent one in which only branches with an aLRT ≤ 0.5 could be rearranged and a more relaxed one in which rearrangements were not restricted by aLRT scores. Since running NOTUNG in the rearrange mode essentially modifies the unrooted tree topology, we used the CONSEL program (Shimodaira, 2002) to select the tree topology that has the highest likelihood for the multiple sequence alignment. The motivation behind this whole procedure is to obtain the tree topology that both minimizes duplication-loss cost and has the highest likelihood for the multiple sequence alignment, as was proposed by Nguyen et al. (2013). We also performed tree reconciliation for different values for the duplication and loss cost parameters: {(1,1),(1,2),(2,1),(2,2)}. Finally, we combined all “optimal” reconciliations according to the parsimony criterion and corresponding to the most optimal unrooted tree topology according to the multiple sequence alignment into one consensus reconciliation. NOTUNG predicts for each node in the gene tree whether it arose through duplication or speciation. We calculated two confidence scores for the predicted duplication events since these are further used for downstream analyses: (1) the duplication consistency score (Vilella et al., 2009), which assesses the imbalance of the predicted duplication event by comparing the overlap in species on the daughter branches with their union; and (2) the annotation support score, which assesses the reliability of the duplication event based on the annotation or age given by NOTUNG to the duplication event. We noticed that there are duplication events with a high duplication consistency that seem to date back to the angiosperm common ancestor but that only encompass one monocot and one dicot species. Hence, we calculated the annotation support as the ratio of the total number of species associated with a duplication node in the gene tree to the expected number of species associated with that node in the species tree and deemed duplication events with low annotation support scores as being unreliable. In this article, we only considered duplication events exceeding a duplication consistency score of 0.2 and with an annotation support of at least 0.5. We found that the number of predicted duplication events stays relatively stable for duplication consistency scores up until 0.4 (Supplemental Figure 16).

K_s-Based Age Distributions

K_s-Based Estimation of Timing of Duplication

Estimates of K_s values were obtained for all paralogous pairs associated with the predicted duplication events inferred by the gene tree–species tree reconciliation process. For cases where there are multiple possible pairs for a predicted duplication event, we calculated K_s values for all possible gene pairs and selected the gene pair with the smallest K_s value to represent the timing of the duplication event. For each paralogous gene pair, we aligned the protein coding sequences using ClustalW (Oliver et al., 2005) using parameter recommendations from Hall (2004). PAL2NAL (Suyama et al., 2006) was used to back-translate the aligned amino acids into corresponding codons without gaps. Then, codeml (Goldman and Yang, 1994) from PAML (Yang, 1997, 2007) was used to obtain K_s values for each gene pair using the GY model with stationary codon frequencies empirically estimated by the F3x4 model.

Gaussian Mixture Modeling of K_s-Based Age Distributions

For each species in our data set, we fitted Gaussian mixtures to age distributions inferred from K_s values (Lynch and Conery, 2003; Blanc and Wolfe, 2004b; Vanneste et al., 2013) using the R package “mixtools.” We ignored K_s values that exceeded 5.0. First, we determined for each age distribution the number of components (k) using the “boot.comp” function. Specifically, we performed parametric bootstraps with 1000 bootstrap realizations of the likelihood ratio statistic for testing the null hypothesis of a k-component fit versus the alternative hypothesis of a (k+1)-component fit. For this test, a significance level of 0.01 was used. For each age distribution, we tested the presence of one to six components. The number of components determined in this first step was used to fit a mixture of Gaussian models to the K_s distribution, using the “normalmixEM” function with the following parameters: k = k, maxit = 1e30, maxrestarts = 1e3, epsilon = 1e-50. We manually curated the obtained peaks, only further focusing on solid WGD peaks (Supplemental Figure 17). Dispersed background peaks with mean μ > 3 and model peaks with obvious misfits to the data were ignored for the purpose of duplication assignment. We assume that each remaining peak corresponds to a WGD event, except for the first peak, which likely consists of recent small-scale duplications (Maere et al., 2005a). A duplication was assigned to the peak that showed the highest probability density at the K_s value obtained for its representative paralog pair (Maere et al., 2005a). For each WGD, we obtain an associated estimate of the number of gene families with retained duplicates as the ratio of the number of core gene families with duplicates for that event to the total number of core gene families. Each peak was characterized by an age (expressed in K_s values) that corresponded to the mean (μ) of the Gaussian mixture component (see Supplemental Table 2 for detailed peak information). To assess duplicate retention in function of time since duplication, we plotted duplicate retention associated with a certain WGD (y) in function of the predicted age of that event (x). We then fitted exponential and power-law functions to these data. Both functions have previously been used to describe the relationship between duplicate retention and time since duplication (Lynch and Conery, 2000; Maere et al., 2005a). In all instances, the power-law fit was preferred over the exponential fit based on the χ² goodness-of-fit measure (Supplemental Figure 18 and Supplemental Table 3).

Evolution of Gene Families under a Stochastic BD Null Model

The Null Model

The null hypothesis describes the evolution of gene families along the phylogeny as a random BD process with equal rates of SSD gene duplication and loss per evolutionary time unit (unit branch length), λ, as proposed by Bailey (1964). Since WGDs violate the assumption of independency of duplication events in Bailey's BD model (Bailey, 1964), we placed these events as separate nodes on the branches of the species tree, similar to the strategy employed by Rabier et al. (2014). At WGD nodes, all gene family members are instantaneously duplicated (or triplicated, depending on the nature of the polyploidy event). As in the model of Rabier et al. (2014), we assume that a given fraction of duplicates is lost very quickly after WGD, represented by an immediate loss rate parameter q in our model. The remaining WGD duplicates are lost over time at a loss rate λ, the same as for SSD duplicates. A full description of the model will be published elsewhere.

Our purpose is to use this BD model to generate gene counts at the leaves of the species tree for a number of simulated gene families and compare the SCP distribution of these simulated families to the SCP distribution observed for the core gene families. In each run, we simulated gene counts under the random BD model for 9178 gene families, corresponding to the number of families in the core set. We performed 1000 such runs and estimated the SCP null distribution as a kernel density function over the 9178 × 1000 simulations.

For each simulated gene family, we sample a value for λ and q from predefined distributions (see below), and we assume that the root size (the gene count at the root of the species tree) is equal to 1. We start at the root and generate a gene count for each of the child nodes of the root through an MCMC process that samples a child node size from the node size probability distribution function described in the BD model (Bailey, 1964); 5000 MCMC steps were used as burn-in to guarantee MCMC convergence to the stationary BD probability distribution. The same procedure is used for any further progeny node up to the leaf nodes, each time starting from the previously generated gene count at its parent node. At WGD nodes, the node size is multiplied after node size sampling with 1+ d.(1−q) to mimic the WGD effect, with d = 1 for duplications and d = 2 for triplications. In our simulations, we imposed the limitation of generating at least 32 non-zero gene counts at the leaves of the species tree, to be consistent with the fact that the core gene families studied were required to be present in at least 32 out of 37 species.

The q value to be used for a given duplicate BD simulation is uniformly sampled from the range [0-1], with 0 being complete retention and 1 complete loss of duplicates immediately after WGD (q is assumed to be the same for all WGDs across the tree; i.e., it is assumed to be a property of the gene family). The λ-value to be used for a given simulation is sampled from a normal distribution with mean λ_av = 0.53 and sd σ = 0.156. The rationale for sampling birth rates from this specific distribution is the following. We assume that the average duplication rate per gene, λ_av, is approximately equal to the average synonymous substitution rate per synonymous site (Lynch and Conery, 2003):

(1)

where “t time unit” stands for the evolutionary time unit used in the species tree (where branch lengths are expressed in terms of the number of substitutions per codon t), i.e., the evolutionary time needed to obtain one substitution per codon on average (unit branch length t = 1). To assess approximately how many synonymous substitutions per synonymous site (K_s) are expected to occur per t time unit in an average plant DNA sequence, we inferred an average relationship between t and K_s from the following formula for the number of substitutions per codon t in a given sequence (Yang and Nielsen, 2000):

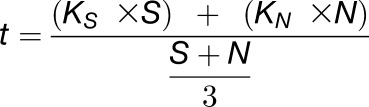(2)

with S and N the number of synonymous and nonsynonymous sites in the sequence and K_s and K_N the number of synonymous and nonsynonymous substitutions per (non)synonymous site, respectively. Equation 2 can be rewritten as:

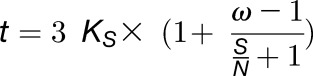(3)

with ω = K_N/K_s the ratio of nonsynonymous substitutions per nonsynonymous site to synonymous substitutions per synonymous site and S/N the ratio of synonymous sites to nonsynonymous sites in a sequence. For both ω and S/N, we substitute genome-wide average estimates to obtain an approximate relationship between t and K_s for an average sequence evolving under average selective pressure. Taking S/N = 0.345 for the average codon (Nei and Gojobori, 1986), and taking an ω value of 0.5 on average (as observed for Arabidopsis duplicates in the K_s range [0,1]; Vanneste et al., 2013), the following estimate of t as a function of K_s is obtained for the average plant DNA sequence:

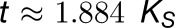(4)

In other words, in one t time unit, 1/1.884∼0.53 synonymous substitutions are estimated to have accumulated per synonymous site on average. We use this estimate in Equation 1 to obtain an estimate of the average duplication rate per gene λ_av = 0.53/gene/(t time unit). To assess how this λ_av estimate compares to literature estimates of duplication rates expressed per gene per million years, we used the average duplicate K_s and absolute age estimates for fairly recent WGDs (0 < K_s < 1, in the range where K_s estimates are reliable) reported by Vanneste et al. (2014a) to convert the resulting estimate λ_av = 0.53/gene/(t time unit) = 1/gene/(K_s time unit) to an estimate of the duplication rate expressed per million years (here, one K_s time unit is the evolutionary time it takes to obtain K_s = 1 on average, which corresponds to 1/0.53∼1.884 t time units according to Equation 4). By dividing the average WGD duplicate pair K_s estimates by twice the absolute WGD age estimates reported by Vanneste et al. (2014a) (note that the evolutionary time elapsed between WGD duplicates in million years (My) is twice the age of the WGD) and averaging over all WGDs, we get a K_s/My conversion factor of 0.00585, giving λ_av = 0.00585/gene/My, which is reasonably comparable to earlier estimates of duplications/gene/My across species (Lynch and Conery, 2003; Hahn et al., 2005). With the average duplication rate λ_av in our tree estimated at 0.53/gene/(t time unit), we defined a λ-distribution around this value with sd 0.156, so that more than 99% of the probability mass lies within the λ interval [0-1]. Qualitatively similar results were obtained with other λ_av values and λ-distribution shapes (results not shown).

Dating WGDs

To run the simulations described above, WGD events need to be added to the phylogenetic tree as new nodes with known branch lengths in terms of t, the number of substitutions per codon. To this end, for each of the WGDs, we averaged the t estimates for all (predicted) homoeologs for which the K_s estimates fall within the WGD K_s range described by Vanneste et al. (2014a). t and K_s estimates for all homoeolog pairs were obtained using codeml (Goldman and Yang, 1994) as described by Vanneste et al. (2014a). As we repeated this procedure for each species separately (except for C. rubella and A. trichopoda, which were not analyzed by Vanneste et al. [2014a]), multiple t estimates were obtained for shared WGDs. In this case, we used the average species-specific t-estimates to position a given shared WGD on the tree.

All of the resulting WGD estimates were positioned on the species phylogeny in a manner consistent with their taxonomic positioning reported earlier (Jiao et al., 2014; Vanneste et al., 2014a), except for the most recent WGDs in Gossypium raimondii and maize (Zea mays), which were inferred by our t-estimation protocol to be positioned on older branches than the accepted ones, likely because of t and K_s estimation and averaging inaccuracies. In these cases, we positioned the WGD in the beginning of the branch reported in literature. See Supplemental Figure 13 for the tree that was obtained using this approach.

Clustering of the Copy Number Profile Matrix

To determine gene family-specific differences in duplicate retention, the gene family data were transformed into a count matrix, in which elements represent the number of gene copies for a certain gene family (columns) in a certain species (rows). To reduce the influence of outliers (families with lots of genes), we only used gene families with maximum three gene copies per species. We clustered this matrix in the direction of the gene families using ConsensusClusterPlus, which incorporates a subsampling approach to infer cluster number and cluster confidence (Monti et al., 2003; Wilkerson and Hayes, 2010). This R implemented package was run using the following options: maxK = 8, reps=100, pItem=0.8, pFeature=1, k-means, inner linkage=average, final linkage=average, distance=pearson. A solution with three clusters was found to be optimal according to the built-in cluster stability criterion (Supplemental Figure 8) (Monti et al., 2003)

Functional Data

PPI Data in Arabidopsis

A compendium of protein-protein interactions in Arabidopsis was constructed combining the following sources: BioGRID 3.2.110 (Chatr-Aryamontri et al., 2013), CORNET (only experimentally validated interactions) (De Bodt et al., 2012), STRINGv9.1 (only category Binding) (Franceschini et al., 2013), EVEX (only category binding) (Van Landeghem et al., 2013), and a TAP data set assembled from literature (Takahashi et al., 2008; Pauwels et al., 2010; Van Leene et al., 2010; Bassard et al., 2012; Domenichini et al., 2012; Eloy et al., 2012; Antoni et al., 2013; Cromer et al., 2013; Di Rubbo et al., 2013; Heijde et al., 2013; Spinner et al., 2013; Fonseca et al., 2014; Gadeyne et al., 2014; Perez et al., 2014; Vercruyssen et al., 2014). After removing redundancy and self-interactions, this lead to a set with a total of 46,113 interactions between 9813 proteins.

Enrichment of PPI, LOF, Chloroplast Genes, and Transcription Factors

The Fisher's exact test was used to calculate if a class is overrepresented in a given set of genes. In order to test whether there are more protein interactions within a group than between a group, 1000 randomized interaction networks with the same degree distribution were constructed. For each group of genes a z-score was obtained by comparing the number of protein interactions within the group based on the extant PPI network with the distribution of within-group interaction counts observed in the randomized networks. Z-scores were then converted into one-tailed P values.

Functional Enrichment Analysis

The BINGO 2.44 Cytoscape plug-in (Maere et al., 2005b) was used to calculate functional enrichment values for the set of Arabidopsis genes. We used a P value threshold of 0.05, and P values were corrected for multiple testing using the Benjamini and Hochberg method (Benjamini and Hochberg, 1995).

Accession Numbers

Sequence data from this article can be found in the Arabidopsis Genome Initiative or GenBank/EMBL databases under the accession numbers listed in Supplemental Data Set 2.

Supplemental Data

• Supplemental Figure 1. Motivation for the 32 out of 37 species cut-off to define core gene families.

• Supplemental Figure 2. The distribution of single-copy percentages (SCPs) for all core gene families, with SCPs calculated upon removing the highly duplicated genomes of Glycine max, Linum usitatissimum, Brassica rapa, and Zea mays.

• Supplemental Figure 3. Classification of species tree nodes as SSD or WGD.

• Supplemental Figure 4. Core gene families mainly duplicate through WGD.

• Supplemental Figure 5. Comparison of the number of duplications for core and noncore gene families at WGD and SSD nodes on a gene family base.

• Supplemental Figure 6. K_s distributions of duplicated pairs from core and noncore gene families in 12 species.

• Supplemental Figure 7. Duplicate gene retention in function of time since WGD.

• Supplemental Figure 8. Criteria that we used to choose the optimal number of clusters for k-means clustering of the copy-number matrix.

• Supplemental Figure 9. Consensus matrices obtained for different number of clusters k.

• Supplemental Figure 10. Polar diagrams depicting the fraction of duplication events in each gene family group belonging to either the “recent,” “K-Pg boundary,” “ancient,” or “SSD” duplication classes.

• Supplemental Figure 11. Over- and underrepresentation of an independent set of 2090 nuclear-encoded chloroplast-targeted genes obtained from The Chloroplast Function Database.

• Supplemental Figure 12. Over- and underrepresentation of an independent set of 1795 putative transcription factors.

• Supplemental Figure 13. Mapping of the whole-genome duplications and triplications on the species tree.

• Supplemental Figure 14. Conflicting clades between the species tree used in this paper and which we inferred from 107 core gene families and the APGIII tree.

• Supplemental Figure 15. Explanation of how duplications were inferred for gene families with at least two species but no more than three genes or gene families that are only present in one species.

• Supplemental Figure 16. The change in the total number of predicted duplication events in core gene families in function of the threshold on the duplication consistency score.

• Supplemental Figure 17. Gaussian mixture models were fit to the K_s distribution of each species.

• Supplemental Figure 18. Comparison of power-law fit and exponential fit to the data obtained from the Gaussian Mixture Modeling of K_s-based age distributions.

• Supplemental Table 1. Comparison of the numbers of interacting protein pairs in each group to those obtained from randomized networks.

• Supplemental Table 2. Description of all identified peaks inferred from the K_s-based age distributions.

• Supplemental Table 3. Comparison of the power-law and the exponential fit.

• Supplemental Data Set 1. Concatenated multiple sequence alignment for 107 genes to reconstruct the species tree.

• Supplemental Data Set 2. Data source and accession numbers of 107 genes used for reconstruction of the species tree.

Glossary

WGD

whole-genome duplication

SSD

small-scale duplication

mya

million years ago

SCP

single-copy percentage

BD

birth-death

GMM

Gaussian Mixture Modeling