Atoms of recognition in human and computer vision

Significance

Discovering the visual features and representations used by the brain to recognize objects is a central problem in the study of vision. Recent successes in computational models of visual recognition naturally raise the question: Do computer systems and the human brain use similar or different computations? We show by combining a novel method (minimal images) and simulations that the human recognition system uses features and learning processes, which are critical for recognition, but are not used by current models. The study uses a “phase transition” phenomenon in minimal images, in which minor changes to the image have a drastic effect on its recognition. The results show fundamental limitations of current approaches and suggest directions to produce more realistic and better-performing models.

Abstract

Discovering the visual features and representations used by the brain to recognize objects is a central problem in the study of vision. Recently, neural network models of visual object recognition, including biological and deep network models, have shown remarkable progress and have begun to rival human performance in some challenging tasks. These models are trained on image examples and learn to extract features and representations and to use them for categorization. It remains unclear, however, whether the representations and learning processes discovered by current models are similar to those used by the human visual system. Here we show, by introducing and using minimal recognizable images, that the human visual system uses features and processes that are not used by current models and that are critical for recognition. We found by psychophysical studies that at the level of minimal recognizable images a minute change in the image can have a drastic effect on recognition, thus identifying features that are critical for the task. Simulations then showed that current models cannot explain this sensitivity to precise feature configurations and, more generally, do not learn to recognize minimal images at a human level. The role of the features shown here is revealed uniquely at the minimal level, where the contribution of each feature is essential. A full understanding of the learning and use of such features will extend our understanding of visual recognition and its cortical mechanisms and will enhance the capacity of computational models to learn from visual experience and to deal with recognition and detailed image interpretation.

The human visual system makes highly effective use of limited information (1, 2). As shown below (Fig. 1 and Figs. S1 and S2), it can recognize consistently subconfigurations that are severely reduced in size or resolution. Effective recognition of reduced configurations is desirable for dealing with image variability: Images of a given category are highly variable, making recognition difficult, but this variability is reduced at the level of recognizable but minimal subconfigurations (Fig. 1B). Minimal recognizable configurations (MIRCs) are useful for effective recognition, but, as shown below, they also are computationally challenging because each MIRC is nonredundant and therefore requires the effective use of all available information. We use them here as sensitive tools to identify fundamental limitations of existing models of visual recognition and directions for essential extensions.

Fig. 1.

Reduced configurations. (A) Configurations that are reduced in size (Left) or resolution (Right) can often be recognized on their own. (B) The full images (Upper Row) are highly variable. Recognition of the common action can be obtained from local configurations (Lower Row), in which variability is reduced.

Fig. S1.

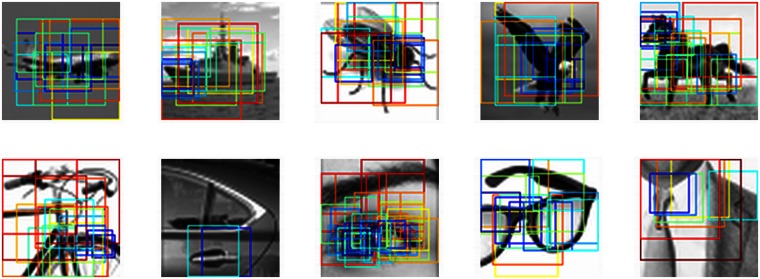
MIRCs. Discovered MIRCs for each of the 10 original images (10 object classes) are ordered from large to small image coverage within each class. Below each MIRC are the recognition rate (Left) and size in image samples (Right).

Fig. S2.

MIRCs coverage. Each colored frame outlines a MIRC (which may be at a reduced resolution). Together, they provide a redundant representation because recognition can be obtained from a single MIRC. Warmer colors of the MIRC frame outline areas of larger coverage.

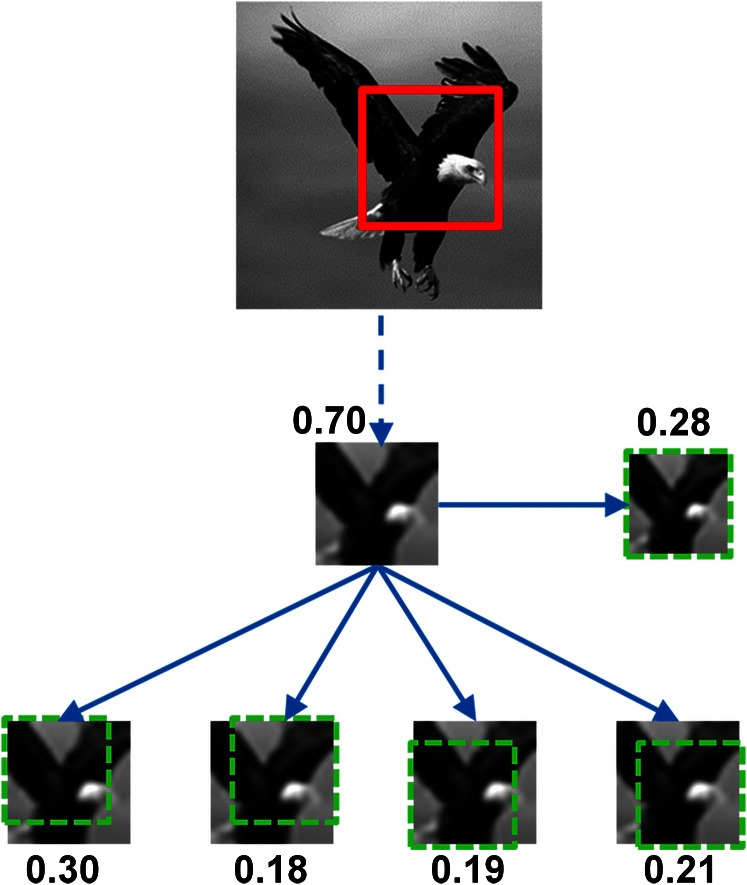
A MIRC is defined as an image patch that can be reliably recognized by human observers and which is minimal in that further reduction in either size or resolution makes the patch unrecognizable (below criterion) (Methods). To discover MIRCs, we conducted a large-scale psychophysical experiment for classification. We started from 10 greyscale images, each showing an object from a different class (Fig. S3), and tested a large hierarchy of patches at different positions and decreasing size and resolution. Each patch in this hierarchy has five descendants, obtained by either cropping the image or reducing its resolution (Fig. 2). If an image patch was recognizable, we continued to test the recognition of its descendants by additional observers. A recognizable patch in this hierarchy is identified as a MIRC if none of its five descendants reaches a recognition criterion (50% recognition; results are insensitive to criterion) (Methods and Fig. S4). Each human subject viewed a single patch from each image with unlimited viewing time and was not tested again. Testing was conducted online using the Amazon Mechanical Turk (MTurk) (3, 4) with about 14,000 subjects viewing 3,553 different patches combined with controls for consistency and presentation size (Methods). The size of the patches was measured in image samples, i.e., the number of samples required to represent the image without redundancy [twice the image frequency cutoff (5)]. For presentation to subjects, all patches were scaled to 100 × 100 pixels by standard interpolation; this scaling increases the size of the presented image smoothly without adding or losing information.

Fig. S3.

Original images used in the human study. The image stimuli in the human study were extracted from these 10 original images (10 object categories). In the experiment, the size of each original image was 50 × 50 image samples, or a cutoff spatial frequency of 25 cycles per image.

Fig. 2.

MIRCs discovery. If an image patch was recognized by human subjects, five descendants were presented to additional observers: Four were obtained by cropping 20% of the image (Bottom Row) and one by 20% reduced resolution (Middle Row, Right). The process was repeated on all descendants until none of the descendants reached recognition criterion (50%). Detailed examples are shown in Fig. S4. The numbers next to each image indicate the fraction of subjects that correctly recognized the image.

Fig. S4.

MIRC hierarchical trees. Examples of MIRCs (in red boxes) and their hierarchical trees, including subimage descendants (sub-MIRCs) and superimage ancestors (super-MIRCs). At the top of each tree is a depiction of the MIRC’s position in the original image marked in a red-bordered box. The human recognition rate is shown below the image patches.

Results

Discovered MIRCs.

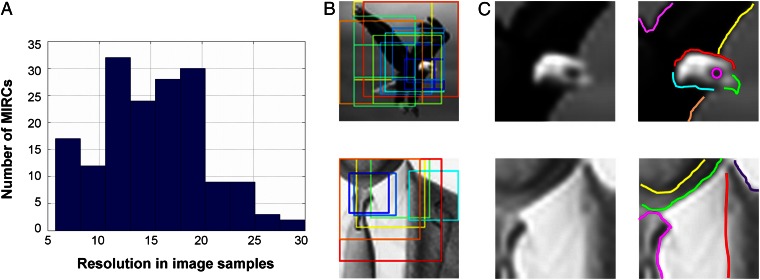
Each of the 10 original images was covered by multiple MIRCs (15.1 ± 7.6 per image, excluding highly overlapping MIRCs) (Methods) at different positions and sizes (Fig. 3 and Figs. S1 and S2). The resolution (measured in image samples) was small (14.92 ± 5.2 samples) (Fig. 3A), with some correlation (0.46) between resolution and size (the fraction of the object covered). Because each MIRC is recognizable on its own, this coverage provides robustness to occlusion and distortions at the object level, because some MIRCs may be occluded and the overall object may distort and still be recognized by a subset of recognizable MIRCs.

Fig. 3.

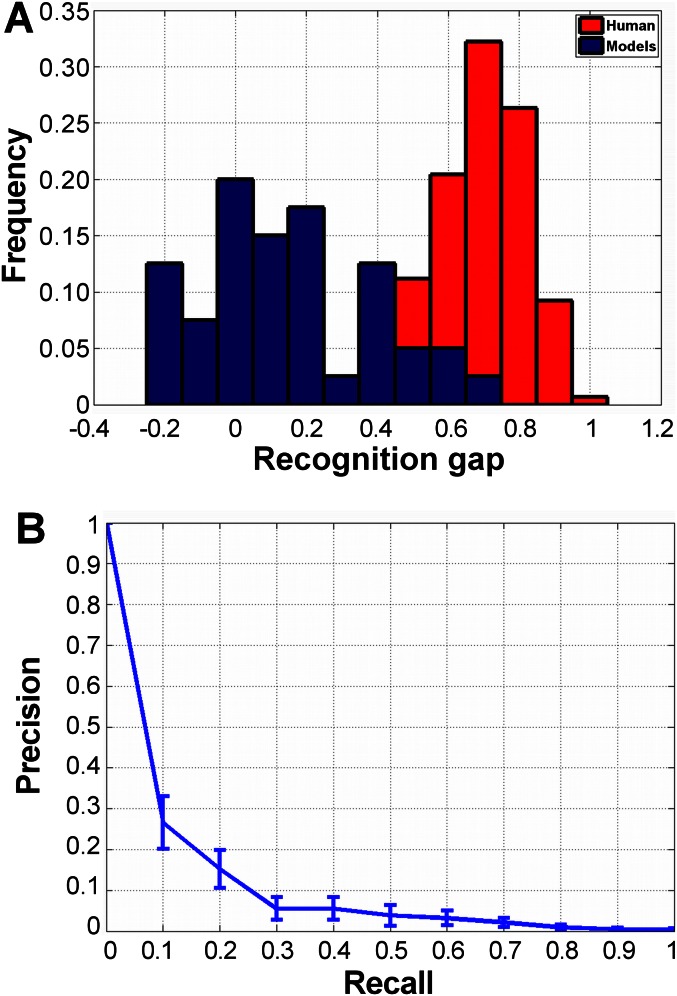
(A) Distribution of MIRCs’ resolution (measured in image samples), average 14.92 ± 5.2 samples. (B) MIRCs’ coverage. The original images are covered by multiple MIRCs at different positions, sizes, and resolutions. Each colored frame outlines a MIRC (which may be at a reduced resolution). Because each MIRC is recognizable on its own, this coverage provides robustness to occlusion and transformations. (C) Detailed internal interpretation labeled by subjects (n = 30) (Methods). Suit image parts: tie, shirt, jacket, chin, neck. Eagle image parts: eye, beak, head, wing, body, sky.

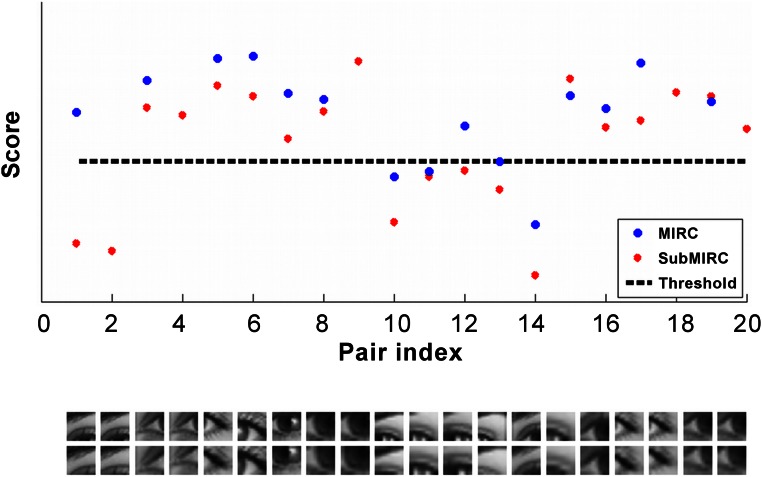
The transition in recognition rate from a MIRC image to a nonrecognizable descendant (termed a “sub-MIRC”) is typically sharp: A surprisingly small change at the MIRC level can make it unrecognizable (Fig. 4). The drop in recognition rate was quantified by measuring a recognition gradient, defined as the maximal difference in recognition rate between the MIRC and its five descendants. The average gradient was 0.57 ± 0.11, indicating that much of the drop from full to no recognition occurs for a small change at the MIRC level (the MIRC itself or one level above, where the gradient also was found to be high). The examples in Fig. 4 illustrate how small changes at the MIRC level can have a dramatic effect on recognition rates. These changes disrupt visual features to which the recognition system is sensitive (6–9); these features are present in the MIRCs but not in the sub-MIRCs. Crucially, the role of these features is revealed uniquely at the MIRC level, because information is more redundant in the full-object image, and a similar loss of features will have a small effect. By comparing recognition rates of models at the MIRC and sub-MIRC levels, we were able to test computationally whether current models of human and computer vision extract and use similar visual features and to test the ability of recognition models to recognize minimal images at a human level. The models in our testing included HMAX (10), a high-performing biological model of the primate ventral stream, along with four state-of-the-art computer vision models: (i) the Deformable Part Model (DPM) (11); (ii) support vector machines (SVM) applied to histograms of gradients (HOG) representations (12); (iii) extended Bag-of-Words (BOW) (13, 14); and (iv) deep convolutional networks (Methods) (15). All are among the top-performing schemes in standard evaluations (16).

Fig. 4.

Recognition gradient. A small change in images at the MIRC level can cause a large drop in the human recognition rate. Shown are examples of MIRCs (A and B) and corresponding sub-MIRCs (A* and B*). The numbers under each image indicate the human recognition rate. The average drop in recognition for these pairs is 0.67.

Training Models on Full-Object Images.

We first tested the models after training with full-object images. Each of the classification schemes was trained by a set of class and nonclass images to produce a classifier that then could be applied to novel test images. For each of the 10 objects in the original images we used 60 class images and an average of 727,000 nonclass images (Methods). Results did not change by increasing the number of training class images to 472 (Methods and SI Methods). The class examples showed full-object images similar in shape and viewing direction to the stimuli in the psychophysical test (Fig. S5).

Fig. S5.

Full-object image siblings. Sixty class images (airplane in this example) were obtained from the web (Google images, Flickr) by selecting images similar (using HOG similarity) to the corresponding original image of the same class that was used in the human psychophysics experiment.

After training, all classifiers showed good classification results when applied to novel full-object images, as is consistent with the reported results for these classifiers [average precision (AP) = 0.84 ± 0.19 across classes]. The trained classifiers then were tested on MIRC and sub-MIRC images from the human testing, with the image patch shown in its original location and size and surrounded by an average gray image. The first objective was to test whether the sharp transition shown in human recognition between images at the MIRC level and their descendant sub-MIRCs is reproduced by any of the models (the accuracy of MIRC detection is discussed separately below). An average of 10 MIRC level patches per class and 16 of their similar sub-MIRCs were selected for testing, together with 246,000 nonclass patches. These MIRCs represent about 62% of the total number of MIRCs and were selected to have human recognition rates above 65% for MIRCs and below 20% for sub-MIRCs (Methods). To test the recognition gap, we set the acceptance threshold of the classifier to match the average human recognition rate for the class (e.g., 81% for the MIRC-level patches from the original image of an eye) (Methods and Fig. S6) and then compared the percentage of MIRCs vs. sub-MIRCs that exceeded the classifier's acceptance threshold (results were insensitive to threshold setting over the range of recognition rates 0.5–0.9).

Fig. S6.

Acceptance thresholds for models. (Upper) A visualization of the procedure for determining the models’ acceptance thresholds [in this example the RCNN model (15) applied to the eye class]. The human recognition rate for the MIRCs was 0.81. The threshold is set so that the model recognition rate will match the human recognition rate (0.80; 12 of 15 MIRCs exceed the threshold). For this threshold, the model recognition rate for the sub-MIRCs is 0.65, a gap of 0.15. (Lower) Columns show MIRC/sub-MIRC pairs; several pairs have the same MIRC, because a single MIRC has more than one sub-MIRC. To test the sensitivity of the models’ recognition gap to the threshold setting, we first set the threshold to produce a recognition rate for MIRCs of 0.50 (instead of 0.80). This recognition rate yields a recognition gap of 0.23. When the recognition rate is set to 0.90, the recognition gap is 0.18. On average, across classes and models, the mean recognition gap for this range of threshold setting is 0.13, indicating that the models’ recognition gap was insensitive to threshold setting.

We computed the gap between MIRC and sub-MIRC recognition rates for the 10 classes and the different models and compared the gaps in the models’ and human recognition rates. None of the models came close to replicating the large drop shown in human recognition (average gap 0.14 ± 0.24 for models vs. 0.71 ± 0.05 for humans) (Fig. S7A). The difference between the models’ and human gaps was highly significant for all computer-version models (P < 1.64 × 10⁻⁴ for all classifiers, n = 10 classes, df = 9, average 16 pairs per class, one-tailed paired t test). HMAX (10) showed similar results (gap 0.21 ± 0.23). The gap is small because, for the models, the representations of MIRCs and sub-MIRCs are closely similar, and consequently the recognition scores of MIRCs and sub-MIRCs are not well separated.

Fig. S7.

Models’ recognition gap and performance. (A) Distributions of the recognition gap (between MIRCs and their similar but unrecognized sub-MIRCs) by humans and by computational models (average gap over all MIRC and sub-MIRC pairs of the same class). (B) Models performance: Precision recall curve of the computational models’ training of full-object images (average of four classifiers). The error bars show the SD for each recall rate.

It should be noted that recognition rates by themselves do not directly reflect the accuracy of the learned classifier: A classifier can recognize a large fraction of MIRC and sub-MIRC examples by setting a low acceptance threshold, but doing so will result in the erroneous acceptance of nonclass images. In all models, the accuracy of MIRC recognition (AP 0.07 ± 0.10) (Fig. S7B) was low compared with the recognition of full objects (AP 0.84 ± 0.19) and was still lower for sub-MIRCs (0.02 ± 0.05). At these low MIRC recognition rates the system will be hampered by a large number of false detections.

A conceivable possibility is that the performance of model networks applied to minimal images could be improved to the human level by increasing the size of the model network or the number of explicitly or implicitly labeled training data. Our tests suggest that although these possibilities cannot be ruled out, they appear unlikely to be sufficient. In terms of network size, doubling the number of levels (see ref. 17 vs. ref. 18) did not improve MIRC recognition performance. Regarding training examples, our testing included two network models (17, 18) that were trained previously on 1.2 million examples from 1,000 categories, including 7 of our 10 classes, but the recognition gap and accuracy of these models applied to MIRC images were similar to those in the other models.

We considered the possibility that the models are trained for a binary decision, class vs. nonclass, whereas humans recognize multiple classes simultaneously, but we found that the gap is similar and somewhat smaller for multiclass recognition (Methods and SI Methods). We also examined responses of intermediate units in the network models and found that results for the best-performing intermediate layers were similar to the results of the network's standard top-level output (Methods).

Training Models on Image Patches.

In a further test we simplified the learning task by training the models directly with images at the MIRC level rather than with full-object images. Class examples were taken from the same class images used in full-object learning but using local regions at the true MIRC locations and approximate scale (average 46 examples per class) that had been verified empirically to be recognizable on their own (Methods and Fig. S8). After training, the models’ accuracy in recognizing MIRC images was significantly higher than in learning from full-object images but still was low in absolute terms and in comparison with human recognition (AP 0.74 ± 0.21 for training on patches vs. 0.07 ± 0.10 for training on full-object images) (SI Methods, Training Object on Image Patches and SI Methods, Human Binary Classification Test). The gap in recognition between MIRC and sub-MIRC images remained low (0.20 ± 0.15 averaged over pairs and classifiers) and was significantly lower than the human gap for all classifiers (P < 1.87 × 10⁻⁴ for all classifiers, n = 10 classes, df = 9, one-tailed paired t test) (Methods and SI Methods).

Fig. S8.

MIRC siblings. (A) Discovered MIRCs, one from each of the 10 original images. (B–F) Five examples of extracted image patches from the full-object image siblings (Fig. S5) at a position and size similar to the discovered MIRCs in A. Below each image is its human recognition rate.

Detailed Internal Interpretation.

An additional limitation of current modeling compared with human vision is the ability to perform a detailed internal interpretation of MIRC images. Although MIRCs are “atomic” in the sense that their partial images become unrecognizable, our tests showed that humans can consistently recognize multiple components internal to the MIRC (Methods and Fig. 3C). Such internal interpretation is beyond the capacities of current neural network models, and it can contribute to accurate recognition, because a false detection could be rejected if it does not have the expected internal interpretation.

Discussion

The results indicate that the human visual system uses features and processes that current models do not. As a result, humans are better at recognizing minimal images, and they exhibit a sharp drop in recognition at the MIRC level, which is not replicated in models. The sharp drop at the MIRC level also suggests that different human observers share similar visual representations, because the transitions occur for the same images, regardless of individual visual experience. An interesting open question is whether the additional features and processes are used in the visual system as a part of the cortical feed-forward process (19) or by a top-down process (20–23), which currently is missing from the purely feed-forward computational models.

We hypothesize based on initial computational modeling that top-down processes are likely to be involved. The reason is that detailed interpretation appears to require features and interrelations that are relatively complex and are class-specific, in the sense that their presence depends on a specific class and location (24). This application of top-down processes naturally divides the recognition process into two main stages: The first leads to the initial activation of class candidates, which is incomplete and with limited accuracy. The activated representations then trigger the application of class-specific interpretation and validation processes, which recover richer and more accurate interpretation of the visible scene.

A further study of the extraction and use of such features by the brain, combining physiological recordings and modeling, will extend our understanding of visual recognition and improve the capacity of computational models to deal with recognition and detailed image interpretation.

Methods

Data for MIRC Discovery.

A set of 10 images was used to discover MIRCs in the psychophysics experiment. These images of objects and object parts (one image from each of 10 classes) were used to generate the stimuli for the human tests (Fig. S3). Each image was of size 50 × 50 image samples (cutoff frequency of 25 cycles per image).

Data for Training and Testing on Full-Object Images.

A set of 600 images was used for training models on full-object images. For each of the 10 images in the psychophysical experiment, 60 training class images were obtained (from Google images, Flickr) by selecting similar images as measured by their HOG (12) representations; examples are given in Fig. S5. The images were of full objects (e.g., the side view of a car rather than the door only). These images provided positive class examples on which the classifiers were trained, using 30–50 images for training; the rest of the images were used for testing. (Different training/testing splits yielded similar results.) We also tested the effect of increasing the number of positive examples to 472 (split into 342 training and 130 testing) on three classes (horse, bicycle, and airplane) for which large datasets are available in PASCAL (16) and ImageNet (25). For the convolutional neural network (CNN) multiclass model used (15), the number of training images was 1.2 million from 1,000 categories, including 7 of the 10 classes used in our experiment.

To introduce some size variations, two sizes differing by 20% were used for each image. The size of the full-object images was scaled so that the part used in the human experiment (e.g., the car door) was 50 × 50 image samples (with 20% variation). For use in the different classifiers, the images were interpolated to match the format used by the specific implementations [e.g., 227 × 227 for regions with CNN (RCNN)] (15). The negative images were taken from PASCAL VOC 2011 (host.robots.ox.ac.uk/pascal/VOC/voc2011/index.html), an average of 727,440 nonclass image regions per class extracted from 2,260 images used in training and 246,000 image regions extracted from a different set of 2,260 images used for testing. The number of nonclass images is larger than the class images used in training and testing, because this difference is also common under natural viewing conditions of class and nonclass images.

Data for Training and Testing on Image Patches.

The image patches used for training and testing were taken from the same 600 images used in full-object image training, but local regions at the true location and size of MIRCs and sub-MIRCs (called the “siblings dataset”) (Fig. S8) were used. Patches were scaled to a common size for each of the classifiers. An average of 46 image patches from each class (23 MIRCs and 23 sub-MIRC siblings) were used as positive class examples, together with a pool of 1,734,000 random nonclass patches of similar sizes taken from 2,260 nonclass images. Negative nonclass images during testing were 225,000 random patches from another set of 2,260 images.

Model Versions and Parameters.

The versions and parameters of the four classification models used were as follows. The HOG (12) model used the implementation of VLFeat version 0.9.17 (www.vlfeat.org/), an open and portable library of computer vision algorithms, using cell size 8. For BOW we used the selective search method (26) using the implementation of VLFeat with an encoding of VLAD (vector of locally aggregated descriptors) (14, 27), a dictionary of size 20, a 3 × 3 grid division, and dense SIFT (28) descriptor. DPM (11) used latest version (release 5, www.cs.berkeley.edu/∼rbg/latent/) with a single mode. For RCNN we used a pretrained network (15), which uses the last feature layer of the deep network trained on ImageNet (17) as a descriptor. Additional deep-network models tested were a model developed for recognizing small (32 × 32) images (29), and Very Deep Convolutional Network (18), which was adapted for recognizing small images. HMAX (10) used the implementation of Cortical Network Simulator (CNS) (30) with six scales, a buffer size of 640 × 640, and a base size of 384 × 384.

MIRCs Discovery Experiment.

This psychophysics experiment identified MIRCs within the original 10 images at different sizes and resolutions (by steps of 20%). At each trial, a single image patch from each of the 10 images, starting with the full-object image, was presented to observers. If a patch was recognizable, five descendants were presented to additional observers; four of the descendants were obtained by cropping (by 20%) at one corner, and one was a reduced resolution of the full patch. For instance, the 50 × 50 original image produced four cropped images of size 40 × 40 samples, together with a 40 × 40 reduced-resolution copy of the original (Fig. 2). For presentation, all patches were rescaled to 100 × 100 pixels by image interpolation so that the size of the presented image was increased without the addition or loss of information. A search algorithm was used to accelerate the search, based on the following monotonicity assumption: If a patch P is recognizable, then larger patches or P at a higher resolution will also be recognized; similarly, if P is not recognized, then a cropped or reduced resolution version also will be unrecognized.

A recognizable patch was identified as a MIRC (Fig. 2 and Fig. S4) if none of its five descendants reached a recognition criterion of 50%. (The acceptance threshold has only a small effect on the final MIRCs because of the sharp gradient in recognition rate at the MIRC level.) Each subject viewed a single patch from each image and was not tested again. The full procedure required a large number of subjects (a total of 14,008 different subjects; average age 31.5 y; 52% males). Testing was conducted online using the Amazon MTurk platform (3, 4). Each subject viewed a single patch from each of the 10 original images (i.e., class images) and one “catch” image (a highly recognizable image for control purposes, as explained below). Subjects were given the following instructions: “Below are 11 images of objects and object parts. For each image type the name of the object or part in the image. If you do not recognize anything type ‘none’.” Presentation time was not limited, and the subject responded by typing the labels. All experiments and procedures were approved by the institutional review boards of the Weizmann Institute of Science, Rehovot, Israel. All participants gave informed consent before starting the experiments.

In comparative studies MTurk has been shown to produce reliable repeatable behavior data, and many classic findings in cognitive psychology have been replicated using data collected online (4). The testing was accompanied by the following controls. To verify comprehension (4), each test included a highly recognizable image; responses were rejected if this catch image was not correctly recognized (rejection rate <1%). We tested the consistency of the responses by dividing the responses of 30 subjects for each of 1,419 image patches into two groups of 15 workers per group and compared responses across groups. Correlation was 0.91, and the difference was not significant (n = 1,419, P = 0.29, two-tailed paired t test), showing that the procedure yields consistent recognition rates. A laboratory test under controlled conditions replicated the recognition results obtained in the online study: Recognition rates for 20 MIRCs/sub-MIRCs in the online and laboratory studies had correlation of 0.84, and all MIRC/sub-MIRC pairs that were statistically different in the online study were also statistically different in the laboratory study. Because viewing size cannot be accurately controlled in the online trials, we verified in a laboratory experiment that recognition rates do not change significantly over 1–4° of visual angle.

Subjects were excluded from the analysis if they failed to label all 10 class image patches or failed to label the catch image correctly (failure rate, 2.2%). The average number of valid responses was 23.7 per patch tested. A response was scored as 1 if it gave the correct object name and as 0 otherwise. Some answers required decisions regarding the use of related terms, e.g., whether “bee” instead of “fly” would be accepted. The decision was based on the WordNet hierarchy (31): We allowed sister terms that have the same direct parent (hypernym) or two levels up. For instance, “'cow” was accepted as a label for “horse,” but “dog” or “bear” was not. Part-names were accepted if they correctly labeled the visible object in the partial image (e.g., “wheel” in bicycle, “tie” in suit image, “jet engine” for the airplane part); descriptions that did not name specific objects (e.g., “cloth,” “an animal part,” “wire”) were not accepted.

Training Models on Full-Object Images.

Training was done for each of the classifiers using the training data, except for the multiclass CNN classifier (15), which was pretrained on 1,000 object categories based on ImageNet (27). Classifiers then were tested on novel full images using standard procedures, followed by testing on MIRC and sub-MIRC test images.

Detection of MIRCs and sub-MIRCs.

An average of 10 MIRC level patches and 16 of their sub-MIRCs were selected for testing per class. These MIRCs, which represent about 62% of the total number of MIRCs, were selected based on their recognition gap (human recognition rate above 65% for MIRC level patches and below 20% for their sub-MIRCs) and image similarity between MIRCs and sub-MIRCs (as measured by overlap of image contours); the same MIRC could have several sub-MIRCs. The tested patches were placed in their original size and location on a gray background; for example, an eye MIRC with a size of 20 × 20 samples (obtained in the human experiment) was placed on gray background image at the original eye location.

Computing the recognition gap.

To obtain the classification results of a model, the model’s classification score was compared against an acceptance threshold (32), and scores above threshold were considered detections. After training a model classifier, we set its acceptance threshold to produce the same recognition rate of MIRC patches as the human recognition rate for the same class. For example, for the eye class, the average human recognition rate of MIRCs was 0.81; the model threshold was set so that the model’s recognition rate of MIRCs was 0.8. We then found the recognition rate of the sub-MIRCs using this threshold. The difference between the recognition rates of MIRCs and sub-MIRCs is the classifier's recognition gap. (Fig. S6). In an additional test we tested the gap while varying the threshold to produce recognition rates in the range 0.5–0.9 and found that the results were insensitive to the setting of the models’ threshold. For the computational models, the scores of sub-MIRCs were intermixed with the scores of MIRCs, limiting the recognition gap between the two, as compared with human vision.

Multiclass estimation.

The computational models are trained for a binary decision, class vs. nonclass, whereas humans recognize multiple classes simultaneously. This multiclass task can lead to cases in which classification results of the correct class may be overridden by a competing class. The multiclass effect was evaluated in two ways. The first was by simulations, using statistics from the human test, and the second was by direct multiclass classification, using the CNN multiclass classifier (15). The mean rate of giving a wrong-class response (rather than producing the ‘none’ label) in the human experiments ranged from 37% for the lowest recognition rates to 4% at highest recognition rates. The effect of multiclass decision on the binary classifier was simulated by allowing each tested MIRC or sub-MIRC to be overridden by a class other than the tested category, with a probability that varied linearly between 4% for the highest-scoring results and 37% for the lowest-scoring results in each class. The gap between MIRC and sub-MIRC recognition was computed as before, but with the additional misclassifications produced by the simulated multiclass effect. The average recognition gap between MIRCs and sub-MIRCS was 0.11 ± 0.16 for multiclass vs. 0.14 ± 0.24 for binary classification. The multiclass effect was expected to be small because the scores in the models for the MIRCs and sub-MIRCs were highly intermixed. Multiclass classification also was tested directly using the CNN model that was trained previously on 1,000 categories (15), including 7 of our 10 classes. Given a test image, the model produces the probability that this image belongs to each of the network categories. The score for each MIRC and sub-MIRC is the probability of the tested class given the test image (e.g., the probability of the airplane class given an airplane MIRC or sub-MIRC). The average gap for the seven classes was small (0.14 ± 0.35) with no significant difference between MIRCs and sub-MIRCs.

Classification accuracy was computed by the AP of the classifier, the standard evaluation measure for classifiers (16). To compare the AP in the full object, the MIRC, and the sub-MIRC classification tasks, we normalize the results to the same number of positive and negative examples across the three test sets.

Intermediate units.

In training and testing the HMAX model (10), we examined whether any intermediate units in the network developed a specific response to a MIRC image during training. Following full-object image training, we tested the responses of all units at all layers of the network to MIRC patches and nonclass patches. We identified the best-performing unit at each of the network's layers (denoted S1, C1, S2, C2, S3, and C3) in terms of its precision in recognizing a particular MIRC type. On this set, the AP at the network output was 94 ± 9% for full-object images and 19 ± 19% for MIRCs. For units with best AP across the network, results were low, but still were higher than the single C3 output unit: AP = 40 ± 24% at the S2 level, 44 ± 27% at the C2 level, and 39 ± 21% at the S3 level.

Training Models on Image Patches.

The classifiers used in the full-object image experiment were trained and tested for image patches. For the RCNN model (15), the test patch was either in its original size or was scaled up to the network size of 227 × 227. In addition, the deep network model (29) and Very Deep Convolutional Network model (18), adapted for recognizing small images, were tested also. Training and testing procedures were the same as for the full-object image test, repeating in five-folds, each using 37 patches for training and nine for testing. Before the computational testing, we measured in psychophysical testing the recognition rates of all the patches from all class images to compare human and model recognition rates directly on the same image (see examples in Fig. S8). After training, we compared the recognition rates of MIRCs and sub-MIRCs by the different models and their recognition accuracy, as in the full-object image test.

We also tested intermediate units in a deep convolutional network (18) by selecting a layer (the eighth of 19) in which units’ receptive field sizes best approximated the size of MIRC patches. The activation levels of all units in this layer were used as an input layer to an SVM classifier, replacing the usual top-level layer. The gap and accuracy of MIRC classification based on the intermediate units were not significantly changed compared with the results of the networks’ tested top-level output.

Internal Interpretation Labeling.

Subjects (n = 30) were presented with a MIRC image in which a red arrow pointed to a location in an image (e.g., the beak of the eagle) and were asked to name the indicated location. Alternatively, one side of a contour was colored red, and subjects produced two labels for the two sides of the contour (e.g., ship and sea). In both alternatives the subjects also were asked to name the object they saw in the image (without the markings).

SI Methods

Training Models on Full-Object Images.

The human average MIRC recall was 0.81, and the sub-MIRC recall was 0.10. The models' average MIRC and sub-MIRC recall were 0.84 and 0.70, respectively. The HMAX model showed similar results, with MIRC and sub-MIRC recognition rates of 0.84 and 0.63, respectively, and a recognition gap of 0.21 ± 0.23.

The differences between the human and model recognition gaps were highly significant for all the models tested (n = 10 classes, df = 9, one-tailed paired t test): DPM: P < 1.05 × 10⁻⁵; BOW: P < 1.64 × 10⁻⁴; HOG: P < 4.2 × 10⁻⁵; RCNN: P < 3.88 × 10⁻⁶; and HMAX: P < 6.89 × 10⁻⁵.

In terms of accuracy, we computed the equal error rate (EER) in the receiver operating characteristic (ROC) curve of the computational models. The error (average across models) was 0.02 for full-object images but was high for the MIRCs (0.23) and sub-MIRCs (0.23). Similarly for HMAX, the EER was 0.03, 0.33, and 0.39 for the full object, MIRC, and sub-MIRC images, respectively.

When training with more class images, the MIRC vs. sub-MIRC recognition gap remained small compared with human recognition (models gap of 0.01 ± 0.18 vs. human gap of 0.7 ± 0.06: BOW: P < 0.046; HOG: P < 0.002; RCNN: P < 0.006; n = 3 classes, df = 2, one-tailed paired t test). The CNN multiclass model has been trained on 1.2 million images from 1,000 categories (including the seven categories we use). For this model, too, the recognition gap was small (0.14 ± 0.35), and recognition accuracy was low. The AP was 0.36, 0.01, and 0.01 for a full-object image, MIRC, and sub-MIRC, respectively, and the EER in the ROC curve was 0.03, 0.31, and 0.35, respectively.

Training Models on Image Patches.

None of the models produced a recognition gap that was comparable to the human gap: The human gap was higher, and the differences between each of the models and human results were all highly significant (n = 10 classes, df = 9, one-tailed paired t test; DPM: P < 1.87 × 10⁻⁴; BOW: P < 3.75 × 10⁻⁵; HOG: P < 1.3 × 10⁻⁶; RCNN: P < 1.71 × 10⁻⁷; HMAX: P < 4.62 × 10⁻⁸). The AP of MIRC recognition across classifiers was 0.74 ± 0.21 and lower (0.38) for the HMAX model. All additional deep-network models we tested [Very Deep Convolutional Network (18) and the net model for small images (29)] gave similar results.

Human Binary Classification Test.

We noted that models often produced false MIRC detections that appear unacceptable to humans. We therefore compared the distribution of errors made by humans and the HMAX model in recognizing minimal images. Humans (n = 30) were tested in 12 trials, each using 60 image patches, 30 positive class examples, and 30 nonclass images. The positive set included MIRC patches from the siblings’ dataset above (Fig. S8). These images were similar to one of the discovered MIRCs depicting the same object part (e.g., horse torso) at the same image resolution and were recognizable when tested on human subjects in a free classification task. The 30 negative image patches were automatically selected by the following procedure: A DPM classifier (11) was trained on separate positive examples together with a large number of randomly selected patches, as described above in the sections on training models on image patches. We then used the 30 top-scoring nonclass patches as hard negatives for testing.

All 60 image patches were presented on the screen in five randomly ordered rows (12 patches per row). Subjects were asked to tag each image patch as a positive or negative example of the object category (e.g., ship). The experiment consisted of 12 trials in total, one trial per each of the 10 object categories, except for the eye (two patches), the horse (three patches) with different object parts, and the car (not tested). Of the 360 subjects, we discarded responses that failed to label one or more images, leaving 275 complete responses.

To compare human results with a biological model applied to the same images, the HMAX model (10) was trained on image patches as described above and was applied to the same 60 image patches that were presented to the human subjects in each of the 12 trials.

We tested whether the HMAX model response vector to the 60 images was a likely response, given the distribution of human responses, or an outlier. We measured the Euclidean distance between the response vectors of human subjects to the ground truth and found that the distance of the response vector of the model to the ground truth is unlikely to come from the same distribution. The test was a two-sample, tailed t test with the null hypothesis that the distance between the HMAX response vector and the ground-truth vector in each class (X), and the distance between human response vectors and the ground-truth response in each class (Y) are independent random samples from normal distributions with equal means and unequal, unknown variances (Welch's t test using MathWorks MATLAB ttest2 function). The null hypothesis was rejected (P = 9.41 × 10⁻⁵, n1 = 12, n2 = 275, df = 12.19).

Humans also were significantly better than the model at MIRC recognition. We compared the classification accuracy of the test images by humans vs. the HMAX model. For humans, we calculated the classification score for each test image as the fraction of positive responses out of the total number of responses for the image. We computed the ROC graphs for humans and the HMAX model for each of the 12 classes and used the EER for the comparison. The average human EER was significantly lower (humans: 0.75% error ± 13.6 × 10⁻³, model: 15.9% error ± 8.27 × 10⁻²; P = 1.30 × 10⁻⁶, df = 22, one-tailed paired t test).