Cognitive fatigue influences students’ performance on standardized tests

Significance

We identify one potential source of bias that influences children’s performance on standardized tests and that is predictable based on psychological theory: the time at which students take the test. Using test data for all children attending Danish public schools between school years 2009/10 and 2012/13, we find that, for every hour later in the day, test scores decrease by 0.9% of an SD. In addition, a 20- to 30-minute break improves average test scores. Time of day affects students’ test performance because, over the course of a regular day, students’ mental resources get taxed. Thus, as the day wears on, students become increasingly fatigued and consequently more likely to underperform on a standardized test.

Abstract

Using test data for all children attending Danish public schools between school years 2009/10 and 2012/13, we examine how the time of the test affects performance. Test time is determined by the weekly class schedule and computer availability at the school. We find that, for every hour later in the day, test performance decreases by 0.9% of an SD (95% CI, 0.7–1.0%). However, a 20- to 30-minute break improves average test performance by 1.7% of an SD (95% CI, 1.2–2.2%). These findings have two important policy implications: First, cognitive fatigue should be taken into consideration when deciding on the length of the school day and the frequency and duration of breaks throughout the day. Second, school accountability systems should control for the influence of external factors on test scores.

Education plays an important role in societies across the globe. The knowledge and skills children acquire as they progress through school often constitute the basis of their success later in life. To evaluate the effectiveness of schooling on children and to provide data to better manage school systems and develop education curriculum, legislators and administrators across societies have used standardized tests as their primary tool as they commonly believe test data are a reliable indicator of student ability (1, 2). In fact, these tests have become an integral part of the education process and are often used in drafting education policy, such as the No Child Left Behind Act and Race to the Top in the United States. As a result, students, teachers, principals, and superintendents are increasingly being evaluated (and compensated) based on test results (2).

A typical standardized test assesses a student’s knowledge base in an academic domain, such as science, reading, or mathematics. When taking a standardized test, the substance of the test, its administration, and scoring procedures are the same for all takers (3). Identical tests, with identical degrees of difficulty and identical grading methods, are propagated as the most fair, objective, and unbiased means of assessing how a student is progressing in her learning.

The widespread use of standardized testing is based on two fundamental assumptions (3): that standardized tests are designed objectively, without bias, and that they accurately assess a student’s academic knowledge. Despite these goals in the creation of standardized tests, in this paper we identify one potential source of bias that drives test results and that is predictable based on psychological theory: the time at which students take the test. We use data from a context in which the timing of the test depends on the weekly class schedule and computer availability at the school and thus is random to the individual. These factors are common conditions of standardized testing. We suggest, and find, that the time at which students take tests affects their performance. Specifically, we argue that time of day influences students’ test performance because, over the course of a regular day, students’ mental resources get taxed. Thus, as the day wears on, students become increasingly fatigued and consequently more likely to underperform on a standardized test. We also suggest, and find, that breaks allow students to recharge their mental resources, with benefits for their test scores.

We base these predictions on psychological research on cognitive fatigue, an increasingly common human condition that results from sustained cognitive engagement that taxes people’s mental resources (4). Persistent cognitive fatigue has been shown to lead to burnout at work, lower motivation, increased distractibility, and poor information processing (5–12). In addition, cognitive fatigue is detrimental to individuals’ judgments and decisions, even those of experts. For instance, in the context of repeated judicial judgments, judges are more likely to deny a prisoner’s request and accept the status quo outcome as they advance through the sequence of cases without breaks on a given day (13). Evidence for the same type of decision fatigue has been found in other contexts, including consumers making choices among various alternatives (14) and physicians prescribing unnecessary antibiotics (15). Across these contexts, the overall demand of multiple decisions people face throughout the day on their cognitive resources erodes their ability to resist making easier and potentially inappropriate or bad decisions.

At the same time, research has highlighted the beneficial effects of breaks. Breaks help people recover physiologically from fatigue and thus serve a rejuvenating function (16, 17). For instance, workers who stretch physically during short breaks from data entry tasks have been found to perform better than those who do not take breaks (16). Breaks can also create the slack time necessary to identify new ideas or simply reflect (18–20), with benefit for performance.

In this paper, we build on this work by examining how cognitive fatigue influences students’ performance on standardized tests. We use data on the full population of children in Danish public schools from school years between 2009/10 and 2012/13 (i.e., children aged 8–15) and focus on the effects of both time of the test and breaks—factors that directly relate to students’ cognitive fatigue.

The Study

In Denmark, compulsory schooling begins in August of the calendar year the child turns 6 and ends after 10 years of schooling. Approximately 80% of children attend public school (14% attend private schools and 6% attend boarding schools and other types of schools). With the purpose of contributing to the continuous evaluation and improvement of the public school system, in 2010, the Danish Government introduced a yearly national testing program called The National Tests. This program consists of 10 mandatory tests: a reading test every second year (grades 2, 4, 6, and 8), a math test in grades 3 and 6, and other tests on different topics (geography, physics, chemistry, and biology) in grades 7 and 8. Each test consists of three parts, presented in random order. (Importantly, there is no ordering of the subtests. The subareas are not tested after each other; rather, a student might first get a question to subarea 1, then to subarea 2, then to subarea 1 again, then to subarea 3, and so on.) For instance, the math test is divided into Numbers and Algebra, Geometry, and Applied Math. In our analyses, we take the simple average across these three parts and standardize the score by subject, test year, and grade (with mean 0 and SD 1). This approach enables us to interpret effects in terms of SD.

These tests are adaptive: the test system chooses the questions based on the student’s level of proficiency as displayed during the test and calculates the test results automatically.

Our dataset comprises all two million tests taken in Denmark between school years 2009/2010 and 2012/2013. Data are provided by the Ministry for Education and linked to administrative registers from Statistics Denmark, a government agency. The administrative data give us information about sex, age, parental background (education and income), and birth weight. The parental characteristics are measured in the calendar year prior to the test year. Our sample consists of 2,034,964 observations from 2,105 schools and 570,376 students. We excluded 17,863 observations (0.9% of the initial sample) to ensure that only normal tests (i.e., tests that were not taken under special circumstances) were included (see SI Text for details). We made no other sample selection.

Two characteristics of these tests should be noted. First, the main purpose of these tests is for teachers covering specific topics (e.g., geography) to gain insight into each student’s achievements for the creation of individually targeted teaching plans. Teachers have no obvious incentive to manipulate students’ performance, and parents are presented with the test results on a simple five-point scale.

Second, these tests are computer based: to test the students, the teacher covering a specific topic has to prebook a test session within the test period (January–April of each year). Therefore, the test time is an exogenous variable because it depends on the availability of a computer room and students’ class schedules. Our analysis confirms that students are allocated to different times randomly. In fact, covariates are balanced across test time, and our results are robust to using within-student variation (i.e., variation in test time across years within the same subject for the same student, as shown in SI Text). In short, our data represent a natural experiment and thus a unique opportunity to test the effects of time of day and breaks on test scores.

During the school day, students have two larger breaks during which they can eat, play, and chat. Usually these breaks are scheduled around 10:00 AM and 12:00 PM and last about 20–30 minutes. As we use a large sample of 2,105 schools, and each school can organize its schedule independently, we contacted 10% of the schools by phone and asked them about their breaks schedule. We received responses from 95 schools (a 45% response rate). Our interviews revealed that 83% of the schools’ first break starts between 9:20 AM and 10:00 AM and that 68% have a second break starting between 11:20 AM and 12:00 PM. Finally, we asked if test days follow a different schedule. Eighty-four percent of the schools we interviewed confirmed they follow the usual break schedule on test days. (Results using only the schools that we contacted confirm those reported below and are shown in SI Text.)

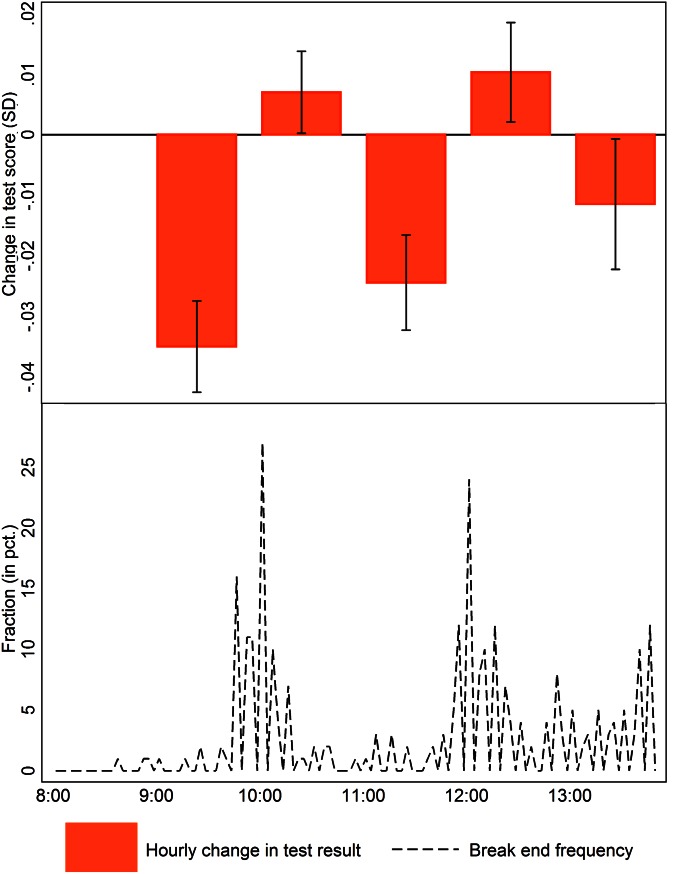
To test our main predictions, we first focus on the effect of test time. The upper panel of Fig. 1 shows the hour-to-hour difference in the average test score by test time. We created this graph by estimating a linear model of test score on indicators for test hour using ordinary least squares (OLS). In the model, we control for school, grade, subject, day of the week, and test-year fixed effects, as well as for parental education, parental income, birth weight, sex, spring child, and origin. As the graph shows, time of day influences test performance in a nonlinear way: although the average test score deteriorates from 8:00 to 9:00 AM, it improves from 9:00 to 10:00 AM. This alternating pattern of improvements and deterioration continues during the day (see SI Text for details).

Fig. 1.

Hour-to-hour effect on test scores and break patterns. Effects are estimated based on administrative data from Statistics Denmark. (Upper) How the average test score changes from hour to hour. (Lower) Distribution of when breaks end, based on a survey conducted on 10% of the schools. The hourly effect is estimated in a linear model controlling for unobserved time invariant fixed effects on grade, day of the week, and school level. We also control for test year fixed effects, as well as parental income, parental education, nonwestern origin, sex, spring child, and birth weight. The details on the model and estimation procedure are shown in SI Text, along with a table with regression results.

Next, we focus on the effect of having the test after a typical break. By typical break, we mean a break that commonly occurs at the same time throughout the week, across schools. The dashed line in the lower part of Fig. 1 shows the breaks time. Breaks typically end just before 10:00 AM and 12:00 PM. Together, the hour-to-hour changes and the break pattern show that test performance declines during the day but improves at test hours just after a break. Breaks, it appears, recharge students’ cognitive energy, thus leading to better test scores.

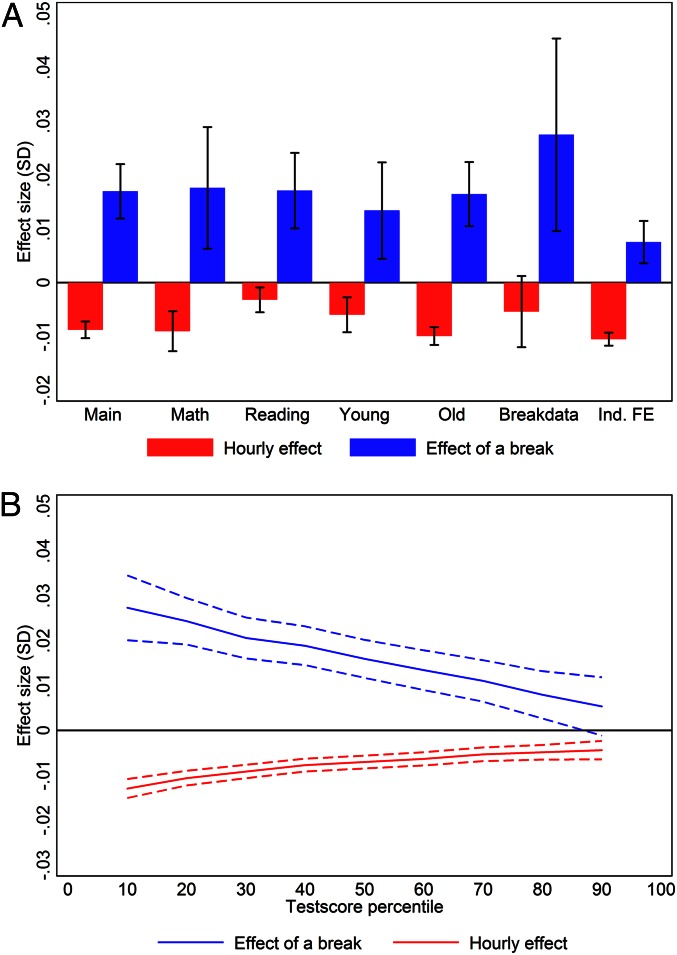
Next, to provide further support for our hypotheses, we explicitly model the effects of time of day and breaks by estimating the linear relationship between test score, test hour, and breaks. The model is estimated by OLS and also includes the individual characteristics and the fixed effects described above. The point estimates on break and test hour are shown in Fig. 2. Fig. 2A shows these point estimates for various specifications and subsamples. The first two bars show that for the full sample, the test score is reduced by 0.9% (95% CI, 0.7–1.0%) of an SD for every hour (the red bar), but a break improves the test score by 1.7% (95% CI, 1.2–2.2%) of an SD (the blue bar). We then conduct the same analyses for various subsamples but find limited evidence of heterogeneous effect of breaks across subject (i.e., mathematics vs. reading) and age (i.e., young vs. old). For hour of the day, the effect is more pronounced for tests in mathematics and older children. The last four bars show that the results are robust to two important robustness checks: using only data on the subsample of schools we included in the break survey and using only within students’ variation in test hour (i.e., including individual fixed effects). In this individual fixed effects specification, we remove any individual time-and-subject-invariant unobserved effect, but still find the same pattern of improvements during breaks and deterioration for every hour later in the day the test is taken. These effects, therefore, are not driven by selection of students into specific times of the day.

Fig. 2.

Effect of time of day and breaks. Effects are estimated based on administrative data from Statistics Denmark. The figures show the parameter estimates for break and test hour from estimating a linear model of test score on test hour and break and controlling for test year fixed effects, as well as parental income, parental education, nonwestern origin, sex, spring child, and birth weight. We also control for school, grade, subject, and day of the week fixed effects. The details on the model and estimation procedure are shown in SI Text, along with a table with regression results. (A) Main effect and the effect by subgroups. (B) Results from quantile regression at the 10th, 20th, 30th, 40th,…,90th percentiles using Canay’s plugin fixed effect estimator (21). The graph shows the effect of breaks and test hour over the test score distribution.

Fig. 2B shows the heterogeneous effects of test hour and breaks on different percentiles of the test score distributions. The graph was created based on quantile regressions and shows the effect of breaks and test hour for different percentiles of the test score distribution. This analysis shows that both breaks and time of day affect the lower end of the distribution, i.e., the low performing students, significantly more than the upper end of the test score distribution, i.e., the high performing students. For the 10th percentile, a break causes 2.7% (95% CI, 2.0–3.5%) of an SD improvement in test score, and for every hour later in the day, the test performance worsens by 1.3% (95% CI, 1.0–1.5%) of an SD. At the upper end of the distribution, there is no effect of breaks on performance, and for every hour, the test score declines by only 0.4% (95% CI, 0.2–0.6%) of an SD.

Overall, the results of our analyses provide support for our hypotheses that taking tests later in the day worsens performance and taking tests after a break improves performance.

Conclusion

Standardized testing is commonly used to assess student knowledge across countries and often drives education policy. Despite its implications for students’ development and future, it is not without bias. In this paper, we examined the influence of the time at which students take tests and of breaks on test performance. In Denmark, as in many other places across the globe, test time is determined by the weekly class schedule and computer availability at schools. We find that, for every hour later in the day, test scores decrease by 0.9% SDs. In addition, a 20- to 30-minute break improves average test scores. Importantly, a break causes an improvement in test scores that is larger than the hourly deterioration. Therefore, if there was a break after every hour, test scores would actually improve over the day. However, if, like in the Danish system, there is only a break every other hour, the total effect is negative. Our results also show that low-performing students are those who suffer more from fatigue and benefit more from breaks. Thus, having breaks before testing is especially important in schools with students who are struggling and performing at low levels.

To understand effect sizes, we computed the simple correlations between test score and parent income, parental education, and school days (see SI Text for details). We find that an hour later in the day causes a deterioration in test score that corresponds to 1,000 USD lower household income, a month less parental education, or 10 school days. A break causes an improvement in test score that corresponds to about 1,900 USD higher household income, almost 2 months of parental education, or 19 school days. The effect sizes are small but nonnegligible compared to the unconditional influence of individual characteristics.

Importantly, the students in our sample are young children and early adolescents, and older adolescents may fare differently. We hope future research will investigate this possibility. Future work could also examine other forms of potential variation in students’ performance on standardized tests, including circadian rhythms (22). In fact, research has shown individuals’ cognitive functioning (e.g., memory and attention) is at its peak at their optimal time of day and decreases substantially at their nonoptimal times (23–25).

Our results should not be interpreted as evidence that that the start time of the school day should change to later (thus allowing students to sleep in, as currently debated in the United States) or that schools tests should be administered earlier in the day. Rather, we believe these results to have two important policy implications: first, cognitive fatigue should be taken into consideration when deciding on the length of the school day and the frequency and duration of breaks. Our results show that longer school days can be justified, if they include an appropriate number of breaks. Second, school accountability systems should control for the influence of external factors on test scores. How can school systems handle such potential biases? One approach would be to adjust the test scores based on the parameters identified in this paper. Based on our results, policy makers should adjust upward test scores by 0.9% of an SD for every hour later in the day the test is taken, and adjust downward tests after breaks with 1.7% of an SD. We recognize that this approach may not always be feasible to implement in practice given that it would require continuous monitoring and adjustments. A more straightforward approach would be to plan tests as closely after breaks as possible. Moreover, as breaks and time of day clearly affect students’ test performance, we also expect other external factors like hunger, light conditions, and noise to play a role. These external factors should be accounted for when comparing test scores across children and schools.

Data and Methods

Here we describe how to obtain access to the data analyzed in our paper. For additional methodological detail, full results, and tables, please refer to SI Text. The project was carried out under Agreement 2015-57-0083 between The Danish Data Protection Agency and the Danish National Centre for Social Research. Specifically, this study was approved by the research board of the Danish National Centre for Social Research under Project US2280 and approved by the Danish protection agency under Agreement 2015-57-0083. We note that there is no Danish institutional review board for studies that are not randomized controlled trials.

The analyses are based on data from administrative registers on the Danish population provided by Statistics Denmark and the Danish Ministry for Education. All analyses have been conducted on a server hosted by Statistics Denmark and owned by The Danish National Centre for Social Research (SFI server project number 704335). All calculations were done with the software STATA (version 13.0). Given that these data contain personal identifiers and sensitive information for residents, they are confidential under the Danish Administrative Procedures (§27) and the Danish Criminal Code (§152). Therefore, we cannot make the data publicly available. However, independent researchers can apply to Statistics Denmark for access, and we will assist in this process in any way we can. If interested researchers request and obtain access to the data, they can use the stata code included in SI Appendix to reproduce the results of the analyses reported in the paper and in the SI Text.

Statistics Denmark requires that researchers who access the confidential information receive approval by a Danish Research Institute. The Danish National Centre for Social Research is willing to grant researchers access to this project, given that they satisfy the existing requirements. As of today, the formal requirements involve a test in data policies and a signed agreement. More information on the Danish National Centre for Social Research can be found at www.sfi.dk.

The Danish Ministry for Education granted us access to all test results from the mandatory National Tests in Danish Public Schools between school years 2009/2010 and 2012/2013. The data were sent from the Ministry to Statistics Denmark. Statistics Denmark anonymized the personal identifiers and provided information on each student’s birth weight, parental income rank, parental education (years), and sex. Before analyzing the data, we excluded 14,945 tests that were taken at 2:00 PM and 2,918 tests that were taken in grades and subject combinations that are out of schedule. The pattern of results for tests occurring at 2:00 PM is in line with the overall conclusions we draw in our research, but this test time was so uncommon that we excluded it from the sample. In total we excluded 17,863 of 2,052,827 observations (0.9% of the raw sample). All conclusions remain unchanged if we conduct the analyses on the raw sample. The sample selection is done to ensure that the analysis is based on normal tests and not tests that were taken under special circumstances.

SI Text

Data.

The analyses are based on data from administrative registers on the Danish population provided by Statistics Denmark and the Danish Ministry for Education. The Danish Ministry for Education granted us access to all test results from the mandatory National Tests in Danish Public Schools between school years 2009/2010 and 2012/2013. The data were sent from the Ministry to Statistics Denmark. Statistics Denmark anonymized the personal identifiers and provided information on each student’s birth weight, parental income, parental education (years), and sex. Before analyzing the data, we excluded 14,945 tests that were taken at 2:00 PM and 2,918 tests that were taken in grades and subject combinations that are out of schedule. The pattern of results for tests occurring at 2:00 PM is in line with the overall conclusions we draw in our research, but this test time was so uncommon that we excluded it from the sample. In total we excluded 17,863 of 2,052,827 observations (0.9% of the raw sample). All conclusions remain unchanged if we conduct the analyses on the raw sample. The sample selection is done to ensure that the analysis is based on normal tests and not tests that were taken under special circumstances.

Methodology.

The test data contain information on each individual’s test time and test performance. The main analysis is based on a comparison of mean test scores over test times. This mean comparison provides an estimate of the causal effect of test time on test performance given that the test time is not correlated with any observed or unobserved individual characteristics. In the Danish setting, variation in test time is created by the way the tests are planned. Specifically, a test time is selected based on three criteria: (i) the teacher has to plan the test in the weekly schedule of the given subject; (ii) the computer facilities must be available; and (iii) the test must be taken in the Spring term. The test time is then determined according to these criteria, and often the availability of computer facilities is the binding constraint. We claim that this creates variation in test time that is as good as random to the individual. We provide support for this claim later in SI Text.

To test our hypothesis regarding the effect of time of the test on test score, we first estimate a linear relationship between test score and test hour

$$testscor{e}_{ti}={\alpha }_0+{\alpha }_{1}testhou{r}_{ti}+{\mathit{ϵ}}_{ti}.$$ [S1]

Model S1 is estimated using OLS. It estimates the correlation between the time of the day when the test is taken and the test score. However, as breaks are likely to influence students’ fatigue, we relax the linear assumption and allow each test hour to have a separate effect. In our preferred specification, we exploit variation within schools (i.e., school fixed effects), within grades (i.e., grade fixed effects), within days of the week (i.e., day of the week fixed effects), within test years (i.e., test year fixed effects), and within subjects (i.e., subject fixed effect). The estimation equation for Fig. 1 is thus given by

$${\mathit{testscore}}_{ti}={\alpha }_0+{\alpha }_1{9}_{ti}+{\alpha }_2{10}_{ti}+{\alpha }_3{11}_{ti}+{\alpha }_4{12}_{ti}+{\alpha }_5{13}_{ti}+{\mathit{\tau DOW}}_{ti}++{\mathit{\beta Year}}_{ti}+{\mathit{\gamma Subject}}_{ti}+{\mathit{\theta }G\mathit{rade}}_{ti}+{\mathit{\delta School}}_{ti}+\mathit{\mu }{\mathit{X}}_{it}+{\mathit{ϵ}}_{ti},$$ [S2]

where 9–13 are indicators for the hour the test t of individual i started. Year, Subject, DOW, Grade, and School are vectors of indicators for the test year, subject, day of the week, grade, and school, and they thus capture the fixed effects. X is a vector of individual control variables: parental education, household income, household income rank, birth weight, spring birth, sex, and nonwestern origin. Covariates are measured in the calendar year before the test is taken. Model S2 is estimated using OLS.

Distributional assumptions.

As the dataset we use in our analyses includes more than two million observations, we can rely on the asymptotic properties (see chapter 2 in ref. 26). However, we assess the distribution of the dependent variable in the following sections to fully understand the nature of our outcome variable of interest.

SEs.

As both observed and unobserved factors might be correlated within schools, we allow arbitrary correlation within these units when computing the SEs, according to the recommendations in ref. 27.

Missing values.

For a small fraction of the sample, we are not able to match individual background characteristics to the test score data. This attrition is balanced across test hours. In the regressions, we include indicators for missing values and replace the missing value with a zero. This strategy is only valid if the values are missing at random. Missing values most likely occur because the student was not living in Denmark the year before the test. Results only change slightly when covariates are excluded, which suggests that covariates are not systematically correlated with test hour and missing values are not systematically correlated with test hour. Despite the minimal change in results we obtain when we exclude covariates, the significance of the results is not affected.

Discussion of main results.

The upper part of Fig. 1 shows the hour-to-hour change in test scores. The point-estimate for coefficient ${\alpha }_1$ gives the estimate for the change in test score when the test is at 9:00 AM instead of 8:00 AM. The coefficient ${\alpha }_2$ gives the point-estimate for the change in test score when the test is at 10:00 AM instead of 8:00 AM. We obtain the point estimate for the change in test score from 9:00 AM to 10:00 AM from ${\alpha }_2-{\alpha }_1$, which gives the height of the bar for 10:00 AM in Fig. 1. The SE for this difference is calculated using the estimated covariance matrix: $se\left({\widehat{\alpha }}_2-{\widehat{\alpha }}_1\right)=\sqrt{var\left({\widehat{\alpha }}_1\right)+var\left({\widehat{\alpha }}_2\right)-2\text{cov}\left({\widehat{\alpha }}_1,{\widehat{\alpha }}_2\right)}$. The error bars in Fig. 1 are calculated by $\left({\widehat{\alpha }}_2-{\widehat{\alpha }}_1\right)\pm 1.96*se\left({\widehat{\alpha }}_2-{\widehat{\alpha }}_1\right)$.

We used this specification because it allows every test hour to have its own effect. As the upper part of Fig. 1 shows, a test taken at 9:00 AM instead of 8:00 AM causes a test score reduction of 0.35% of an SD. Likewise, the bar at 10:00 AM, with a height of 0.07% of an SD, shows that test scores improve by 0.07% of an SD from 9:00 AM to 10:00 AM (the height of this bar is computed by 0.35 − 0.28, based on the estimates at 9 and 10, in column 4 in Table S1).

Table S1.

Main regression results

Variable	1	2	3	4	5	6	7
testhour	−0.006***				−0.005***	−0.008***	−0.009***
	(0.001)				(0.001)	(0.001)	(0.001)
break					0.025***	0.019***	0.017***
					(0.006)	(0.003)	(0.003)
9		−0.050***	−0.038***	−0.035***
		(0.009)	(0.004)	(0.004)
10		−0.038***	−0.029***	−0.028***
		(0.005)	(0.003)	(0.003)
11		−0.060***	−0.055***	−0.052***
		(0.009)	(0.004)	(0.004)
12		−0.033***	−0.042***	−0.042***
		(0.007)	(0.004)	(0.004)
13		−0.039***	−0.052***	−0.054***
		(0.011)	(0.006)	(0.006)
Fixed effects included	No	No	Yes	Yes	No	Yes	Yes
Individual controls	No	No	No	Yes	No	No	Yes
Number of schools			2,028	2,028		2,028	2,028
Smallest group			2	2		2	2
Largest group			3,984	3,984		3,984	3,984
F-value th9 = th10..= th13 = 0		14.84	38.61	39.59
P value th9 = th10..= th13 = 0		0.00	0.00	0.00
Model degrees of freedom		5	20	30	2	17	27
Adjusted R2		0.00	0.00	0.08	0.00	0.00	0.08
AIC	5,774,756	5,774,188	5,626,905	5,462,886	5,774,577	5,627,291	5,463,303
Observations	2,034,964	2,034,964	2,034,887	2,034,887	2,034,964	2,034,887	2,034,887

The dependent variable in each model is standardized test score. All estimates are obtained using ordinary least squares (OLS). Column 1 shows the point estimate for ${\alpha }_1$ from estimating model S1. Columns 2–4 show results from estimating model S2. Columns 5–7 show results from estimating model S3. The table only shows the point estimates for the coefficients ${\alpha }_1-{\alpha }_5$ in model S2 and coefficients ${\alpha }_1$ and ${\alpha }_2$ for model S3. Columns 2 and 5 show results from estimating models without any control variables. Columns 3 and 6 show results from estimating simple models with only school, year, day of the week, grade, and subject fixed effects. Columns 4 and 7 show results from estimating the full models without individual fixed effects. SEs clustered at the school level are shown in parentheses. Number of schools show the number of schools included and thus also the level of fixed effects and clustering. Smallest/largest group shows the smallest/largest number of observations from one school. F-value gives the F-statistic for a test of joint significance for the hourly indicators in columns 2–5, and P value gives the corresponding P values. This P value is for the null hypothesis that all hourly indicators are zero. Model degrees of freedom specifies the number the degrees of freedom used by the model. AIC gives the Akaike information criteria. Smaller AICs are generally preferred. The term observations refers to the number of observations included in the regressions. The dependent variable is standardized within the test year, grade, and subject cell. As fixed effects on the school level implies comparisons within schools, we only include schools with at least two tests. Regressions are based on administrative data from Statistics Denmark and the Danish Ministry for Education, for all mandatory tests 2009/10–2012/13.

^***P < 0.01; **P < 0.05; *P < 0.1.

Next, we focus on the effect of having the test after a typical break. By typical break, we mean a break that commonly occurs at the same time throughout the week, across schools. The lower part of Fig. 1 shows the distribution of breaks across schools. Specifically, it plots the time when the breaks commonly end. We focus on the time when the breaks end because breaks vary in their length. We contacted 10% of the 2,105 schools in our dataset and asked about the break schedule. We received responses from 95 schools, corresponding to a 45% response rate. Eighty-four percent of the schools we interviewed confirmed they follow the usual break schedule on test days. As the lower part of Fig. 1 shows, almost all schools have breaks before the 10:00 AM test and again before the 12:00 PM test.

Because we hypothesized that breaks cause test improvements, we also estimate a more restricted version of the relationship between test hour and test performance, where we include a variable for test hour (as in model S1) and an indicator for whether the test was taken after a typical break. This approach is used for Fig. 2. The estimation equation for Fig. 2 is thus given by

$$testscor{e}_{ti}={\alpha }_0+{\alpha }_{1}brea{k}_{ti}+{\alpha }_{2}testhou{r}_{ti}+\mathit{\mu }{\mathit{X}}_{it}+\mathit{\tau DO}{\mathit{W}}_{ti}+\mathit{\beta Yea}{\mathit{r}}_{ti}+\mathit{\gamma Subjec}{\mathit{t}}_{ti}+\mathit{\theta Grad}{\mathit{e}}_{ti}+\mathit{\delta Schoo}{\mathit{l}}_{ti}+{\mathit{ϵ}}_{ti},$$ [S3]

where break is an indicator for the test being taken at a time that is usually after a break (8:00 AM, 10:00 AM, 12:00 PM). Fig. 2A shows the point estimates and error bars for the coefficients ${\alpha }_1$ and ${\alpha }_2$. The bar “Main” is for the full sample. The bar “Math” only includes tests in Mathematics. The bar “Reading” only includes tests in Reading/Danish. The bar “Young” only includes tests taken in grades 2–4. The bar “Old” only includes tests taken in grades 6–8. The bar “Break data” only includes tests taken in the schools with information on the break schedule. The bar “Individual FE” is for a version where we include individual fixed effects and thus only exploit variation in test time from year to year or subject to subject, within the same student. As the upper part of Fig. 2A shows, test scores worsen for every hour later in the day the test is taken (the red bars), but improve after a break (the blue bars). This pattern holds across subsamples and specifications.

Fig. 2B shows the results from a quantile regression of model S3 on the 10th, 20th,…,90th percentiles using the Canay plug-in fixed effects approach (22). The OLS estimation above estimates the effect on the mean. With a quantile regression we can estimate the effect on specific quantiles (or percentiles) of the test distribution. Although the estimation used above shows how average test scores change after breaks and during the day, this regression shows how the median (or for example the 10th percentile) test scores are affected by time of the day. In a linear regression using OLS, is it straightforward to control for the school fixed effects, as the linear specification allows us to cancel these effects out. The same approach cannot be used with quantile regressions, as the estimation is nonlinear. Canay (22) introduced an estimator where we first clean the dependent variable for the fixed effects (i.e., the unobserved school fixed effects), and then use this cleaned dependent variable in the quantile regression framework, which is the methodology we apply here.

Table S1 shows the results from estimating the main models. Column 1 shows the estimates from estimating model S1. The first row shows that for every hour later in the day, the test score is reduced by 0.6% of an SD. In column 2, we relax the assumption of linearity and allow each test hour to have its own effect. The point estimate in row 9 shows that tests at 9:00 AM on average are 5% of an SD worse than tests at 8:00 AM. The point estimate in row 10 shows that tests at 10:00 AM on average are 3.8% of an SD worse than tests at 8:00 AM, and thus 1.2% points better than tests at 9:00 AM. Tests at 11:00 AM are 6% of an SD worse than at 8:00 AM and 2.2% points worse than at 10:00 AM. The point estimates in column 2 of row 12 show that at 12:00 PM test scores are on average 3.3% of an SD lower than at 8:00 AM, and finally row 13 shows that tests at 1:00 PM are 3.9% of an SD worse than tests at 8:00 AM. Together, these results show that taking the test earlier in the day is advantageous to students as it is related to higher test scores. This pattern of results is likely the result of increased cognitive fatigue as the day wears on, consistent with our theorizing based on existing work in psychology.

In column 3 of Table S1, we further added school, test year, grade, subject, and day of the week fixed effects. In this specification, we only include schools with at least two tests (which forces us to drop 77 schools/observations out of 2,034,965 observations). Although in column 2 we show how average test scores change from hour to hour, overall, in column 3 we show how test scores change from hour to hour, holding the school, day of the week, test year, subject, and grade constant. Controlling for these factors reduces the magnitude of the estimates somewhat, but the overall pattern remains unchanged. In column 4, we further added individual controls, namely child birth weight, parental education, parental income, sex, and origin. Adding these covariates only has a minor effect on the point estimates, and the conclusion remains unchanged.

In column 5 of Table S1, we show point estimates from estimating model S3. The first row shows that for every hour later in the day, test scores worsen by 0.5% of an SD, but the estimates for break in the next row shows that, after breaks, test scores improve by 2.5% of an SD. Although column 5, like column 2, is a simple comparison across all schools and subjects, column 6, just like column 3, also controls for fixed effects and thus shows the effect of breaks and test hour while holding other factors fixed. This change increases the effect of time of day on test scores slightly, from 0.5% to 0.8% of an SD, and reduces the effect of breaks from 2.5% to 1.9% of an SD. In column 7, we further added individual controls, which only causes a negligible effect on the point estimates. Once we keep both fixed effects and individual characteristics constant, we find that the test scores worsen by 0.9% of an SD for every hour later in the day the test is taken, and breaks cause an improvement of 1.7% of an SD.

The lower part of Table S1 shows various model characteristics and diagnostics. We include 2,028 schools in the sample. For the smallest school, we only have two tests, whereas for the largest school, we have 3,984 observations. Next we conduct an F-test of the joint significance for the hourly indicators in columns 2–4. They all clearly show that we reject the null hypotheses that these coefficients are zero. The adjusted R² is very low across specifications, which is not uncommon in microeconometrics. In columns 4 and 7, which are the preferred specifications used to create Figs. 1 and 2, the adjusted R² is 0.08.

Distribution of Test Scores.

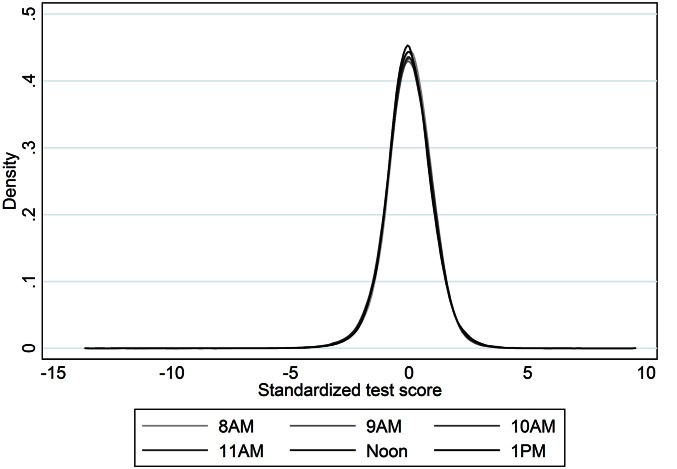
As mentioned above, we rely on asymptotic characteristics of the estimator for both the estimation of the point-estimates and the inference. However, to better understand the data and the results, it is useful to consider the distribution of the test score (our main dependent measure). Fig. S1 shows kernel density estimates for the raw test scores, by test hour. The distributions seem normal, but with somewhat long tails. The graph shows that there are no systematic differences in the overall distribution of tests across test times, with the exception of slight shifts of the distributions along the x axis. In other words, tests at 9:00 AM are shifted slightly to the right compared with tests at 8:00 AM, indicating worse test performance at 9:00 AM than at 8:00 AM, but the overall shape of the test score distribution does not differ across the distribution (e.g., the shape of the distribution at 9:00 AM looks similar to the distribution at 11:00 AM). The results of this analysis give us confidence that our results are not driven by obscure properties of the distribution of test scores. In addition, this gives us confidence that the regression analyses we conducted to examine the effects of time of day and breaks on test scores are valid, and are not subject to bias.

Fig. S1.

Test score distribution. The plots were created using a triangular kernel with a bandwidth of 0.25, separately for each test hour.

As Good as Random Variation in Test Time.

As mentioned earlier, the results we obtained in the main analyses we conducted can be interpreted as causal effects of test hour/breaks on test performance if, and only if, the test time is as good as random. We assess this assumption in three ways:

• i)We regress the covariates (birth weight, parental income, parental education) on test hour and compare the z-scores (t-values) across sample sizes with the z-scores from the main analyses. The intuition is that, although for specifications with test scores as dependent variables the hourly indicators are expected to be precisely estimated, the specifications using covariates as dependent variables should not give very precise estimates of the hourly indicators, as this would indicate that the hourly indicators are closely correlated with individual characteristics. The plotted z-scores are used to compute P values, and larger z-scores will result in lower P values.
• ii)We compare means of covariates (birth weight, parental income, parental education) across test hours. The motivation for this test is that we expect variable means to be fairly constant across test hour and only show minor differences. Although test i shows the statistical test (in terms of z-scores) and the statistical significance, this assessment allows for a means comparison of the size of the differences across test hours.
• iii)We conduct a very conservative estimation with individual fixed effects, where we only exploit within individual variation across years and/or subjects. Importantly, in this specification, we remove any time-and-subject-invariant unobserved effect, and we can thus rule out the possibility that the effects we observe in the data are driven by specific students attending tests at specific times.

A comparison of z-scores.

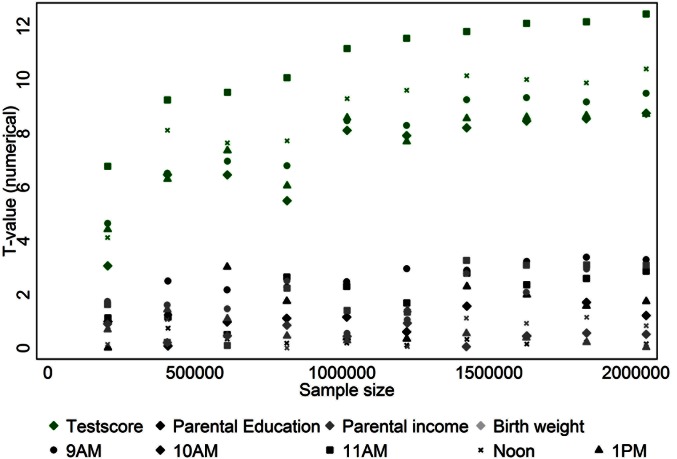
Fig. S2 shows the z-scores (t-values) for the hourly indicators from estimating model S2 with OLS (without controls, but with fixed effects). The dependent values are the test hour (the green scatters), parental education, parental income, and birth weight (the gray scatters). If test hour is as good as random, we would not expect test hour indicators to be precisely estimated when the covariates are used as dependent variables. To give an idea of the importance of the sample size, we draw nine random subsamples of the data used for the main analysis and show the precision in each of these samples. As Fig. S2 shows, most indicators for the covariates are estimated with low precision with t-values between 0 and 2. For the main regression (i.e., the regression using test scores as the dependent variable), all indicators are estimated with a high level of precision, for all sample sizes.

Fig. S2.

z-Scores for different specification of model S1 and varying sample size. The t-values are calculated by estimating model S2 with fixed effects, but without any individual controls, using OLS. The t-values are then obtained by $t={\widehat{\alpha }}_1/\widehat{se}\left({\widehat{\alpha }}_1\right)$. The green scatters are obtained from models using the test scores as dependent variables. The gray scatters are obtained from estimating the model using the corresponding covariate as the dependent variable.

The first column of scatters, for a sample size of 200,000 observations, show that all z-scores for the covariates are between 0 and 2, whereas z-scores for test score are between 3 and 7. For this sample size, a 5% significance level corresponds to a z-score cutoff of ∼2, so that all estimates <2 are nonsignificant, and all estimates >2 are significant. The scatters thus show that, although our main result regarding the effect of time of day the test is taken is also present in a sample of 200,000 results, none of the covariates is significantly correlated with test hour in that sample.

The column of scatters to the far right shows z-scores for the main estimation with more than 2,000,000 observations. For test score (the green scatters), all z-scores are >8 and very precisely estimated, whereas z-scores for covariates are between 3 and 0 (the gray scatters). Some of the z-scores for covariates thus indicate significance at a 5% level, which is as expected, given that we conduct 20 tests. However, convincingly, these analyses show that the specifications using covariates as dependent variables do not provide very precise estimates of the hourly indicators. This result suggests that the hourly indicators are not correlated with individual characteristics.

Variable means across test time for covariates.

Next, we examine the average values for the characteristics of the children, at each test hour, and report the results in Table S2. Column 8 shows the average characteristics for the test takers at 8:00 AM. These test takers had an average birth weight of 3,307 g. Their parents had completed 14.26 y of schooling (chosen as the highest value of either the father or the mother), and their annual household income (adjusted for size of the family) is on average 385,000 DKK (56,000 USD). The next column shows that test takers at 9:00 AM had a birth weight that, on average, was 3 g lower, their parents had completed 0.08 y less education, and their household income was 5,000 DKK lower (730 USD). The table shows that variable means differ slightly from hour to hour, but not in a systematic pattern: the parents’ years of schooling is highest at 1:00 PM, which is the time with lowest child birth weight and the highest share of children with nonwestern origin.

Table S2.

Variable means across test time

Variable	All	Test hour
		8	9	10	11	12	13
Full sample
Test uncertainty	0.26	0.26	0.27	0.26	0.28	0.26	0.26
School day	179.89	180.10	180.02	178.81	180.49	180.83	179.80
Child birth weight (g)	3,298	3,307	3,304	3,300	3,303	3,282	3,272
Parents’ years of schooling	14.24	14.26	14.18	14.21	14.25	14.30	14.33
Household income, 1,000 DKK	386.17	384.64	379.79	386.07	382.60	396.16	396.96
Household income percentile	57.05	57.14	56.32	56.98	56.77	57.91	58.16
Nonwestern origin	0.09	0.08	0.09	0.09	0.08	0.09	0.10
Female	0.49	0.49	0.48	0.49	0.49	0.49	0.49
Spring child	0.50	0.50	0.49	0.49	0.50	0.50	0.50
Missing birth weight data	0.06	0.06	0.06	0.06	0.06	0.06	0.06
Missing education data	0.03	0.03	0.03	0.03	0.02	0.02	0.01
Observations	2,034,964	400,139	424,868	528,764	259,649	295,032	126,512
Subsample of schools included in the break data sample
Test uncertainty	0.24	0.24	0.22	0.25	0.27	0.24	0.25
School day	179.65	179.18	179.57	180.18	179.61	179.86	178.93
Child birth weight (g)	3,305	3,302	3,303	3,303	3,321	3,295	3,323
Parents’ years of schooling	14.29	14.26	14.17	14.30	14.35	14.38	14.40
Household income, 1,000 DKK	389.37	392.55	376.89	393.87	385.21	397.78	390.23
Household income percentile	57.25	57.43	56.11	57.42	57.06	58.10	58.18
Nonwestern origin	0.08	0.08	0.08	0.09	0.06	0.08	0.08
Female	0.49	0.50	0.49	0.49	0.49	0.49	0.48
Spring child	0.50	0.49	0.50	0.49	0.49	0.50	0.51
Missing birth weight data	0.06	0.06	0.06	0.06	0.05	0.06	0.05
Missing education data	0.03	0.03	0.03	0.03	0.02	0.02	0.01
Observations	121,709	25,561	24,025	31,198	17,039	16,995	6,891

The table shows simple averages for subsamples across test hours. Test uncertainty is the estimated uncertainty for the test result (only available for years 2011–2013). This variable measures how precisely the individual test score was estimated by the computer. (The uncertainty comes from the fact that the test can be more or less accurate to measure the student performance. Each question contributes to the precision of the test, reducing uncertainty. That is, the test is adaptive, and the computer tries to calculate the individuals level. For instance, if the student reaches a level where every time he/she gets a harder question, he/she answers wrong, but every time he/she gets an easier question, he/she answers right, there will be very low uncertainty on test score.) Income is adjusted to the 2010 price level and adjusted for household size using the square root approach. Spring child is a child born in the period January–June of the year being considered. Because the school starting age cutoff is January 1, these children have the highest expected school starting age. The variable called school days refers to the number of days from the start of the school year to the test day, not counting weekends. Parents’ years of schooling is the years of schooling completed by the mother or father (the highest value).

There is thus no clear pattern indicating that individual characteristics are better at test times that are associated with better test scores. In other words, differences in individual characteristics across the students in our sample cannot explain the effects of time of day and breaks on test performance.

Within-individual fixed effects.

Fig. 2 shows the point estimate for the coefficients on breaks and test hour in model S3 for various specifications. Table S3 shows the corresponding point estimates, where row testhour provides the height of the red bars in Fig. 2, and row break provides the estimates used for the height of the blue bars in Fig. 2. The row testhour thus gives the estimate of the change in average test score (measured in SDs) that an hour later in the day causes. The row break provides the estimates on the average improvements in test scores caused by breaks. As these analyses show, the overall pattern of results is very consistent across subsamples and specifications. However, it is worth noting that the effect of test hour varies more across subsamples than breaks.

Table S3.

Regression results

Variable	Main (1)	Math (2)	Reading (3)	Young (4)	Old (5)	Break data (6)	Individual FE (7)
testhour	−0.009***	−0.009***	−0.003**	−0.006***	−0.010***	−0.005	−0.011***
	(0.001)	(0.002)	(0.001)	(0.002)	(0.001)	(0.003)	(0.001)
break	0.017***	0.018**	0.017***	0.013**	0.016***	0.027**	0.008***
	(0.003)	(0.006)	(0.004)	(0.005)	(0.003)	(0.009)	(0.002)
Number of schools/individuals	2,028	1,901	2,015	1,868	1,987	84	492,020
Smallest group	2	1	1	1	1	95	2
Largest group	3,984	835	1,552	1,285	3,130	3,196	11
Model degrees of freedom	27	19	21	20	24	27	26
Adjusted R2	0.078	0.081	0.097	0.083	0.077	0.081	0.002
AIC	5,462,809	1,135,288	2,220,067	1,704,095	3,742,861	323,208	3,139,887
Observations	2,034,887	426,615	836,115	637,974	1,396,913	121,709	1,956,608

Dependent variable: standardized test scores. The row break shows the point estimate for the coefficients on break and test hour in model S3. All models are estimated with the full set of covariates and fixed effects. Column 1 is for the full sample. In column 2, only tests in mathematics are included. In column 3, only tests in reading are included. In column 4, only tests for grades 2–4 are included. In column 5, only tests for grades 6–8 are included. In column 6, we only included the schools included in the break survey. In column 7, we estimated a modified version of model S2, using individual fixed effects. SEs clustered at the school level are shown in parentheses. Number of schools show the number of schools included (individuals for column 7, and thus also the level of fixed effects and clustering (Individual FE in column 7 is also clustered at the school level). Smallest/largest group shows the smallest/largest number of observations from one school/one individual. Model degrees of freedom specifies the number the degrees of freedom used by the model. AIC gives the Akaike information criteria. Smaller AICs are generally preferred. Observations refers to the number of observations included in the regressions. The dependent variable is standardized within the test year, grade, and subject cell. As fixed effects on the school level implies comparisons within schools, we only include schools with at least two tests. Regressions are based on administrative data from Statistics Denmark and the Danish Ministry for Education, for all mandatory tests 2009/10–2012/13.

^***P < 0.01; **P < 0.05; *P < 0.1.

Column 7 shows the point estimate from a model with individual fixed effects, where we only exploit variation in test time within the same individual. An example for this within-individual variation is that the test in Reading is at 8:00 AM in 1 y and at 11:00 AM in another year, or when the test is at 10:00 AM in Mathematics but at 12:00 PM in Reading. Thus, these analyses suggest, our conclusion regarding both the effect of time at which the test is taken, and the effect of breaks holds even if we remove all individual time and subject invariant unobserved fixed effects.

Percentiles.

To assess the sensitivity of the results with respect to the measurement of the test scores (i.e., our dependent variable), we estimated all main specifications using percentile scores instead of standardized test scores. For each subject, test year, and grade combination, we sorted the test results according to test score and sorted these observations into 100 equally sized bins. The first bin, bin 1, includes the 1% lowest scores. The last bin, bin 100, includes the 1% highest test scores. We then use these bins (or percentiles) as dependent variables in the main regressions, instead of standardized test scores. Table S4 corresponds to Table S1, but using these percentile scores as dependent variables.

Table S4.

Regression results

Variable	1	2	3	4	5	6	7
testhour	−0.159***				−0.127***	−0.226***	−0.236***
	(0.038)				(0.036)	(0.023)	(0.022)
break					0.691***	0.534***	0.487***
					(0.188)	(0.075)	(0.071)
9		−1.353***	−1.069***	−0.978***
		(0.247)	(0.111)	(0.106)
10		−0.983***	−0.788***	−0.749***
		(0.149)	(0.094)	(0.090)
11		−1.556***	−1.470***	−1.392***
		(0.250)	(0.123)	(0.118)
12		−0.844***	−1.130***	−1.124***
		(0.190)	(0.114)	(0.110)
13		−1.077***	−1.463***	−1.524***
		(0.305)	(0.165)	(0.157)
Fixed effects included	No	No	Yes	Yes	No	Yes	Yes
Individual controls	No	No	No	Yes	No	No	Yes
Number of schools			2,028	2,028		2,028	2,028
Smallest group			2	2		2	2
Largest group			3,984	3,984		3,984	3,984
F-value th9 = th10..= th13 = 0		11.711	36.617	37.727
P value th9 = th10..= th13 = 0		0.000	0.000	0.000
Model degrees of freedom		5	20	30	2	17	27
Adjusted R2		0.00	0.00	0.08	0.00	0.00	0.08
AIC	19,460,401	19,459,913	19,320,488	19,149,059	194,601,29	19,3205,44	19,149,447
Observations	2,034,964	2,034,964	2,034,887	2,034,887	2,034,964	2,034,887	2,034,887

Dependent variable: test score percentiles. All estimates are obtained using OLS. Column 1 shows the point estimate for ${\alpha }_1$ from estimating model S1. Columns 2–4 show results from estimating model S2 using ordinary least squares. Columns 5–7 show results from estimating model S3 using ordinary least squares. The table only shows the point estimates for the coefficients ${\alpha }_1-{\alpha }_5$ in model S2 and coefficient ${\alpha }_1$ and ${\alpha }_2$ for model S3. Columns 2 and 5 show results from estimating models without any control variables. Columns 3 and 6 show results from estimating simple models with only school, year, day of the week, grade, and subject fixed effects. Columns 4 and 7 show results from estimating the full models without individual fixed effects. SEs clustered at the school level are shown in parentheses. Number of schools show the number of schools included and thus also the level of fixed effects and clustering. Smallest/largest group shows the smallest/largest number of observations from one school. F-value gives the F-statistic for a test of joint significance for the hourly indicators, and P value gives the corresponding P values. Model degrees of freedom specifies the number the degrees of freedom used by the model. AIC gives the Akaike information criteria. Smaller AICs are generally preferred. Observations refers to the number of observations included in the regressions. The dependent variable is test score percentile rank (1–100) within the test year, grade, and subject cell. As fixed effects on the school level implies comparisons within schools, we only include schools with at least two tests. Regressions are based on administrative data from Statistics Denmark and the Danish Ministry for Education, for all mandatory tests 2009/10–2012/13.

^***P < 0.01; **P < 0.05; *P < 0.1.

The point estimate in column 1 shows that for every hour later in the day, the average test score is reduced by 0.159 percentiles. Column 2 shows that tests at 9:00 AM on average have a 1.353 lower percentile score than tests at 8:00 AM, whereas tests at 10:00 AM and tests at 1:00 PM have a 1.077 percentile score lower average than tests at 8:00 AM. As for Table S1, also in Table S4, columns 3 and 4 are like column 2, but with more controls and fixed effects. Finally, columns 5–7 show the effect of time of the day, controlling for breaks. The coefficients reported in column 7 show that taking the test an hour later causes the average test score to decrease by 0.236 percentiles, whereas a break causes an improvement of 0.487 percentile scores. Overall, these results are consistent with those presented in Table S1 and provide support for our hypotheses that taking tests later in the day worsens performance and taking tests after a break improves performance.

Effect Sizes.

To understand effect sizes of our observed effects, we compare the size of the point estimates with the point estimates for correlations between background characteristics and test scores. We therefore estimate a simple model for the linear relationship between standardized test score and individual birth weight, parental income, parental education, and the number of school days before the test. We conduct four separate regressions, one for each of these covariates.

Table S5 show point estimates for the coefficient ${\alpha }_1$, from estimating the following model using OLS:

$$testscor{e}_{ti}={\alpha }_0+{\alpha }_1{x}_{ti}+{\mathit{ϵ}}_{ti},$$ [S4]

where the dependent variable is the standardized test score and the variable x is the household income (column 1), birth weight (column 2), parents’ years of schooling (column 3), or number of school days before the test (column 4). These regression results are used to evaluate the effect sizes of our observed effects that we discuss in the conclusion section of the paper.

Table S5.

Regression results

Variable	1	2	3	4
Household income	0.0013***
	(0.0000)
Birth weight		0.0001***
		(0.0000)
Years of schooling			0.1195***
			(0.0010)
School days				0.0009***
				(0.0001)
Adjusted R2	0.06	0.00	0.10	0.00
AIC	5,554,828	5,361,776	5,404,795	5,773,793
N	2,002,033	1,899,159	1,981,671	2,034,964

Dependent variable: standardized test score. SEs clustered at the school level are shown in parentheses. AIC gives the Akaike information criteria. Observations shows number of observations included in the regressions. The dependent variable is standardized within the test year, grade, and subject cell. We removed outliers in income and birth weight (first and last percentile). This is done because, in this linear regression, measurement errors (e.g., birth weight of 10 kg) would have a huge impact on the point estimates. However, overall the conclusions are not very sensitive to this change.

^***P < 0.01; **P < 0.05; *P < 0.1.

For example, Table S5 shows that for every 1,000 DKK higher in household income, test scores increase by 0.13% of an SD. Recall that for every hour later during the day, test scores worsens by 0.9% of an SD. This hourly effect thus corresponds to 0.9/0.13 = 7,000 DKK (∼1,000 USD) difference in household income.

Likewise, for birth weight: 1 g higher birth weight corresponds to 0.01% of an SD higher test scores according to the estimates in Table S5, such that the hourly effect of 0.9% of an SD corresponds to 0.9/0.01 = 90 g higher birth weight. The coefficient in column 3 shows that 1 y higher in parental education corresponds to 11.95% of an SD higher test score. The hourly effect is thus 0.9/11.95 = 0.075 y of education.

Finally, column 4 shows the correlation between the number of school days before the test (not adjusting for holidays, i.e., including them) and test score. One additional school day corresponds to 0.09% of an SD better test score. The hour-to-hour effect therefore corresponds to 0.9/0.09 = 10 school days.

Overall, these analyses suggest that the effects of time of the test and breaks on test score observed in our main analyses are meaningful, despite that the coefficients per se may seem rather small given the large sample of observations in our dataset.

Stata Do-Files.

Four Stata do-files were used for the analyses we conducted (SI Appendix). They are as follows:

• i)preamble.do specifies the paths and global variables.
• ii)createdata.do creates the analyses data based on the raw data from Statistics Denmark and the Danish Ministry for Education.
• iii)analysis_main_doc.do conducts all of the analyses used for the main document.
• iv)analysis_appendix.do conducts all of the analyses used for SI Text.