Invisible metallic mesh

Significance

We introduce and demonstrate an invisible material––a solid composite possessing identical electromagnetic properties as air so that its arbitrarily shaped object neither reflects nor refracts light at any angle of incidence in free space. Such a material is self-invisible, unlike the cloaks for minimizing the scattering of other items. Invisible materials could provide improved mechanical stability, electrical conduction, and heat dissipation to a system, without disturbing the original electromagnetic design. One immediate application would be toward perfect antenna radomes.

Abstract

A solid material possessing identical electromagnetic properties as air has yet to be found in nature. Such a medium of arbitrary shape would neither reflect nor refract light at any angle of incidence in free space. Here, we introduce nonscattering corrugated metallic wires to construct such a medium. This was accomplished by aligning the dark-state frequencies in multiple scattering channels of a single wire. Analytical solutions, full-wave simulations, and microwave measurement results on 3D printed samples show omnidirectional invisibility in any configuration. This invisible metallic mesh can improve mechanical stability, electrical conduction, and heat dissipation of a system, without disturbing the electromagnetic design. Our approach is simple, robust, and scalable to higher frequencies.

We introduce a solid material that is itself omnidirectionally invisible, possessing identical electromagnetic properties as air (i.e., not a cloak) at a desired frequency. Such a material could provide improved mechanical stability, electrical conduction, and heat dissipation to a system without disturbing incident electromagnetic radiation. One immediate application would be toward perfect antenna radomes. Unlike cloaks (1, 2), such a transparent and self-invisible material has yet to be demonstrated. Previous research (3–18) has shown that a single sphere or cylinder coated with plasmonic or dielectric layers can have a dark state with considerably suppressed scattering cross-section, due to the destructive interference between two resonances in one of its scattering channels. Nevertheless, a massive collection of these objects will have an accumulated and detectable disturbance to the original field distribution. Here we overcome this bottleneck by lining up the dark-state frequencies in different channels. Specifically, we derive analytically, verify numerically, and demonstrate experimentally that deliberately designed corrugated metallic wires can have record-low scattering amplitudes, achieved by aligning the nodal frequencies of the first two scattering channels. This enables an arbitrary assembly of these wires to be omnidirectionally invisible and the effective constitutive parameters nearly identical to air. Measured transmission spectra at microwave frequencies reveal indistinguishable results for all of the arrangements of the 3D-printed samples studied.

Although artificial dielectrics comprising conducting elements, now known as metamaterials, have been researched since the 1950s (19), such an air-like material simultaneously having unity permittivity and unity permeability has not been achieved. Our result is also fundamentally different from reflectionless materials such as perfect absorbers (20, 21) or Huygens metasurfaces (22–24). In contrast to these, our nonscattering material is both reflectionless and refractionless in arbitrary shapes under any incident angle.

This paper is organized as follows. First, we present the analytical solution of an ideal infinite corrugated thin conducting wire having an extremely low scattering width at a particular frequency. Materials made of such wires, having identical permittivity and permeability as air, would be invisible. Second, we design such an invisible medium using realistic materials modeled by full-wave simulations. Lastly, we describe the fabrication of a sample using this design and demonstrate its omnidirectional invisibility using microwave measurements.

Results

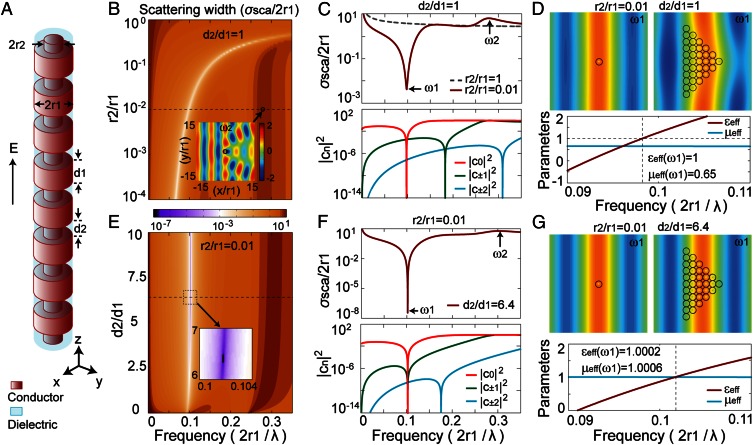
We begin by considering the plane wave scattering by an infinite cylindrical conducting wire with a radius r₁, as shown in Fig. 1A (when r₂ = r₁). When the incident electric field is parallel to the wire, the normalized scattering width σ_sca/2r₁ can be derived as σ_sca/2r₁ = (2/k₀r₁)${{\displaystyle \sum }}_{n=-\infty }^{+\infty }\left|J_n\left(k_0{r}_1\right)/H_n^{\left(2\right)}\left(k_0{r}_1\right)\right|$² by the Mie solution (25) (Derivation of the Scattering Width of the Infinite Corrugated Conducting Wire), where J_n and H_n⁽²⁾ denote a Bessel function and a Hankel function of the second kind, respectively. The normalized scattering width is plotted as the dashed gray line in Fig. 1C. At high frequencies, the scattering width σ_sca approaches a value equal to twice the wire diameter. There is only one resonance occurring at zero (dc) frequency, where the scattering width diverges. This can be explained using the resonance frequency [ω₀ = 1/(2π$\sqrt{LC}$)] of inductance L and capacitance C of circuit elements. A thin long wire has an effective infinite inductance and capacitance (L, C→∞) (26, 27), leading to a zero resonance frequency (ω₀→0).

Fig. 1.

Analytical solutions to wave scattering off corrugated conducting wires. (A) Geometry of a corrugated cylindrical conducting wire, whose open volumes are filled with a dielectric ε_r = 6ε₀. (B) The normalized total scattering widths for varying r₂/r₁ with subwavelength features d₁, d₂, set to d₂/d₁ = 1. (Inset) Total electric field around the wire under a unit-amplitude plane-wave incidence at normalized frequency ω₂ $\approx$ 0.28 for r₂/r₁ = 0.01. (C, Top) Total scattering widths for r₂/r₁ = 0.01 (red line) and r₂/r₁ =1 (dashed gray line); the minimum scattering width is 4.8$\times$ 10⁻³ at ω₁. (C, Bottom) Corresponding magnitudes of scattering coefficients (|c_n|²) of different orders. The dips for zeroth-, first-, and second orders appear at different frequencies. (D, Top Left) Total electric field scattering off a single wire. (D, Top Right) Total electric field scattering off multiple closely arranged wires. The incident fields are unit-amplitude plane waves at frequency ω₁. (D, Bottom) Retrieved effective constitutive parameters of the closely arranged wires, ε_eff(ω₁) = 1 and μ_eff(ω₁) = 0.65. (E) Normalized total scattering width as a function of d₂/d₁ with r₂/r₁ = 0.01. (F, Top) Total scattering width with r₂/r₁ = 0.01 and d₂/d₁ = 6.4; the minimum normalized scattering width is 3.5 $\times$ 10⁻⁸ at ω₁ = 0.1017. (F, Bottom) Scattering coefficients, where the nodal frequencies of the zeroth- and first orders coincide at ω₁. (G, Top Left) Total electric field for a single wire. (G, Top Right) Total electric fields for multiple closely arranged wires. (G, Bottom) Retrieved effective constitutive parameters of the closely arranged wires, ε_eff(ω₁) = 1.0002 and μ_eff(ω₁) = 1.0006.

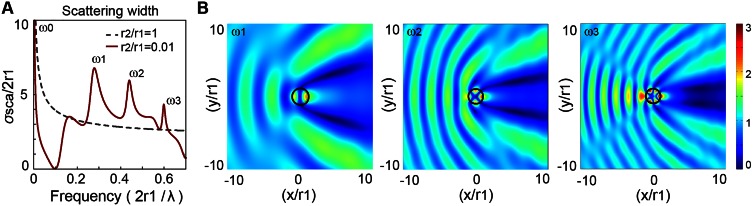
It is known that a scattering dark state (scattering dip in frequency) universally exists between two resonances (scattering peaks), where the two resonances destructively interfere with equal amplitude but opposite phase in the same scattering and polarization channel (18). We can thus create such a scattering dark state by introducing a second resonance in the wire other than the one at dc. To introduce more resonances, we corrugate the wire by shrinking it periodically along the wire as shown in Fig. 1A. This corrugated wire consists of coaxial cylinders with different radii (r₁ and r₂) and heights (d₁ and d₂), where d₁ and d₂ are both far smaller than the free-space wavelength. Similar corrugated conducting wires have been proposed for guiding surface plasmon polaritons (28). The open volume can be filled with a low-loss material (dielectric constant ε_r) to improve the mechanical strength and increase the working wavelength, so the corrugations are more subwavelength and can be well described by the effective medium theory (29). Each open cylindrical space inside the wire forms a whispering gallery (WG) resonator; its spectrum and mode profiles are plotted in Fig. S1.

Fig. S1.

WG resonances of the corrugated wires. (A) Analytically calculated normalized scattering widths (red line) for d₂/d₁ = 1 and r₂/r₁ = 0.01. The dashed gray line represents the scattering width for an infinite conducting cylinder, where r₂/r₁ = 1. (B) Analytically calculated amplitudes of the total electric fields under the incidence of a unit-amplitude plane wave at resonance frequencies ω₁, ω₂, and ω₃, respectively. We can see obvious various WG modes.

For such an infinite corrugated wire, its normalized scattering width can also be analytically derived, under the effective medium approximation, as (see Derivation of the Scattering Width of the Infinite Corrugated Conducting Wire for detailed derivation)

$${\sigma }_{sca}/2r_1=\frac{2}{k_0{r}_1}{\displaystyle \sum _{n=-\infty }^{+\infty }{\left|c_n\right|}^2},$$ [1]

where $c_n=\left(J_n\left(k_0{r}_1\right)[J_n\left(k_{eff}{r}_2\right)Y_n\prime \left(k_{eff}{r}_1\right)-J_n\prime \left(k_{eff}{r}_1\right)Y_n\left(k_{eff}{r}_2\right)]-{\eta }_{eff}{J}_n\prime \left(k_0{r}_1\right)[J_n\left(k_{eff}{r}_2\right)Y_n\left(k_{eff}{r}_1\right)-J_n\left(k_{eff}{r}_1\right)Y_n\left(k_{eff}{r}_2\right)]\right)/{\eta }_{eff}{H}_n^2\prime \left(k_0{r}_1\right)[J_n\left(k_{eff}{r}_2\right)Y_n\left(k_{eff}{r}_1\right)-J_n\left(k_{eff}{r}_1\right)Y_n\left(k_{eff}{r}_2\right)]-H_n^2\left(k_0{r}_1\right)[J_n\left(k_{eff}{r}_2\right)Y_n\prime \left(k_{eff}{r}_1\right)-J_n\prime \left(k_{eff}{r}_1\right)Y_n\left(k_{eff}{r}_2\right)]$, denotes the expanded nth-order scattering coefficient in Bessel (J_n and Y_n), Hankel functions (H_n⁽²⁾), and their derivatives. Here $k_{eff}=\omega n_{eff}=\omega \sqrt{u_{\left|\right|}^{eff}\times {\epsilon }_z^{eff}}=\omega \sqrt{{\epsilon }_r{u}_0}$, ${\eta }_{eff}=\sqrt{u_{\left|\right|}^{eff}/{\epsilon }_z^{eff}}=[d_2/(d_1+d_2)]\sqrt{u_0/{\epsilon }_r}$, where ε_z^eff = ε_r(d₁+d₂)/d₂ and μ_||^eff = μ₀d₂/(d₁+d₂) are the effective permittivity and permeability of the corrugated volume (r₂ ≤ ρ ≤ r₁) derived in Derivation of the Scattering Width of the Infinite Corrugated Conducting Wire. We note that J₀′(k₀r₁) approaches zero when k₀r₁ is a small number for a thin wire. So, the nodal frequency of c₀ has almost no dependence on η_eff, consequently independent of d₁ and d₂. Although the total scattering width σ_sca/2r₁ is the sum of all of the scattering coefficients |c_n|², |c_n|² is negligibly small when n is larger than k₀r₁ (∼0.3 in our case) (30). As shown in Fig. 1F, |c₂|² is as small as 10⁻⁸. So, the electromagnetic properties can mostly be determined by the first two scattering coefficients c₀ and c₁.

Shown as a white stripe in Fig. 1B, there will always exist a scattering dark state whose frequency ω₁ lies between those of the dc resonance and the first WG resonance (ω₂ $\approx$ 0.28) of the corrugated wire. In this plot, we vary the ratio of r₂/r₁ while fixing d₁/d₂ = 1 and ε_r = 6. In Fig. 1C, we decompose the total scattering width into individual orders and find that each order has its own zero-scattering frequency. Because the zeroth order is dominant, the dip in the total scattering corresponds to the nodal frequency of the zeroth scattering order c₀. The same mechanism enabled previous studies on transparent (cloaking) wires (3–9), invisible particles (10–18), or scattering dark states (31–34).

However, the vanishing of c₀ = 0 is not enough to make a collection of these wires invisible; the total scattering amplitude is not small enough when c₁ ≠ 0. In Fig. 1D, we show the obvious distortion of a scattered wave by a set of these wires packed closely. For a better understanding, we also show the effective constitutive parameters of an array of such wires at the bottom of Fig. 1D, using a homogenization approach (35). At ω₁, ε_eff = 1 and μ_eff $=$ 0.65. Although the effective permittivity of the material ε_eff is 1 (the same as that of free space), μ_eff ≠ 1. By solving the Mie scattering solutions for a homogeneous dielectric thin wire (Scattering of a Homogeneous Infinite Dielectric Cylinder with Radius r), we show that c₀ = 0 requires ε = 1 and c₁ = 0 requires μ = 1. Because the nodal frequencies of c₀ and c₁ in general occur at different frequencies for a single element, ε = μ = 1 cannot be satisfied simultaneously for an assembly of them. This is why no transparently invisible metamaterial has been reported to date.

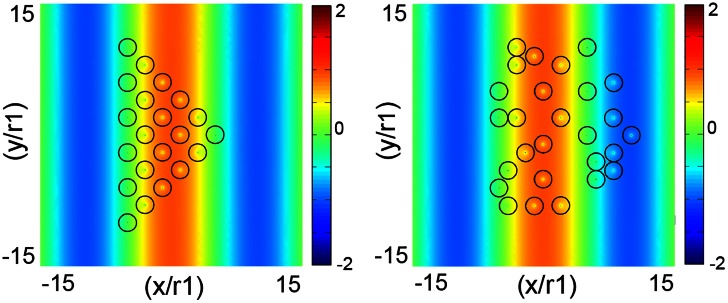
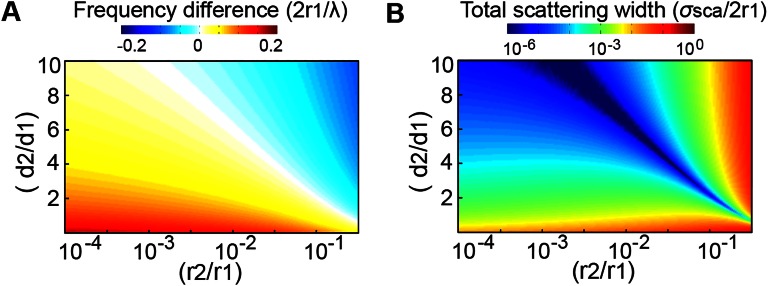
Now, we tune the nodal frequency of c₁ to coincide with that of c₀ for an individual wire (i.e., c₀ = c₁ = 0 at the same frequency), which results in a further decrease of the total scattering amplitude by 5 orders of magnitude to a negligible value. Consequently, ε_eff ≈ μ_eff ≈ 1 for an arbitrary assembly of such wires. We achieve this by tuning the geometry of the corrugation. We have seen that c₀ is almost independent of d₂/d₁, whereas the c_i (i > 0) have a strong dependence on d₂/d₁. For example, the white line (nodal frequency of c₀) in Fig. 1E is almost a straight vertical line that does not change with d₂/d₁. So, by varying d₂/d₁, we can freely tune the nodal frequency of c₁ toward that of c₀. Starting with the configuration in Fig. 1B where r₂/r₁ is fixed at 0.01, we tune the ratio of d₂/d₁ from 1 to ∼6.4 in Fig. 1E. The nodal frequencies of c₀ and c₁ coincide and the total scattering width decreases by 5 orders of magnitude to a record-low scattering width of 3.5$\times$ 10⁻⁸ (which eventually will be limited by material losses in experiments). At the same time, μ_eff increases from 0.65 to 1.0006. Consequently, the wave experiences no distortion after impinging on closely arranged wires in Fig. 1G, compared with Fig. 1D. (More results are provided in Fig. S2 for different arrangements of the wires.) This means arbitrary composites of such wires should be practically invisible. We emphasize that such an alignment of nodal frequencies can robustly occur at any frequency by tuning r₂/r₁ and d₂/d₁ (Fig. S3).

Fig. S2.

Total electric field scattering off loose arrangements of the wires.

Fig. S3.

Robust invisibility of the corrugated wires. (A) Separation between the nodal frequencies of the zeroth- and first-order scattering coefficients with respect to the scans of r₂/r₁ and d₂/d₁. (B) Calculated total scattering widths with respect to the scans of r₂/r₁ and d₂/d₁. We conclude that the nodal frequencies of the zeroth- and first-order scattering coefficients can always be tuned to coincide. Consequently, the total scattering width at this frequency would be very much compressed.

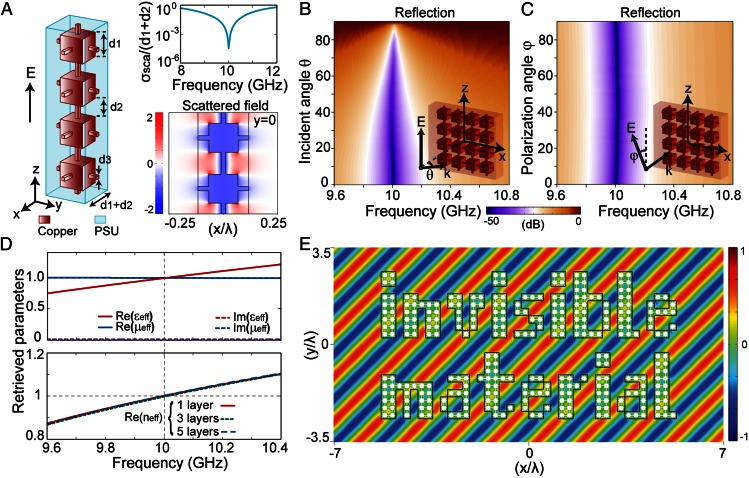
For ease of fabrication, we modify the cylinders in the wire into cubes in Fig. 2A. We connect the cubes with thin square-shaped rods symmetrical in the x-, y-, and z directions. This makes the original wire structure cubic symmetric, which removes the previous constraint that the field polarization has to be vertical. This conducting skeleton is embedded in a low-loss dielectric. Such a modified construction, still being subwavelength, has no qualitative change in its scattering properties from the corrugated wires studied analytically in Fig. 1. We performed full-wave simulations on this rectangular wire structure using CST Microwave Studio. The dimensions are d₁ = 4 mm, d₂ = 3 mm, and d₃= 0.6 mm. The conductor is copper with a conductance of 5.986 × 10⁷ S/m, and the dielectric is polysulfone (PSU) with dielectric constant of 3 and loss tangent of 0.0013. Shown in Fig. 2A, the invisible frequency occurs at around 10 GHz with a normalized scattering width as low as 5 × 10⁻⁵. The scattered electric field (difference between fields with and without the wire) is almost all localized inside the wire, consistent with the near-zero scattering width. The opposite phase at different sections along the wire leads to the cancellation of the outgoing waves in the far field. We note that this structure has a low loss at the invisible frequency that is spectrally far away from the resonances.

Fig. 2.

Numerical results of the invisible material made of corrugated metallic wires. (A, Left) Geometry of a modified wire, composed of corrugated conducting square wire embedded in a dielectric with ε_r = 3 and a loss tangent of 0.0013. (A, Top Right) Normalized scattering width (5$\times$ 10⁻⁵ at 10 GHz) under a normal plane-wave incidence along the x axis with the unit-amplitude electric field polarized along the z axis. (A, Bottom Right) Scattered electric field around the corrugated wire at 10 GHz. (B) Simulated reflectance spectra (S₁₁) for one layer of wires with respect to the angle of incidence. (C) Simulated reflectance spectra with respect to the polarization angle. (D) Retrieved effective parameters of the solid slab composed of closely arranged corrugated wires with different layer thickness. For the one-layer slab, ε_eff = 0.9999 + 0.006i, μ_eff = 1, and the refractive index n_eff ∼ 1 + 0.003i at 10 GHz. (E) Steady-state electric field distribution under an oblique plane-wave incidence at 10 GHz upon an invisible material-shaped structure composed of the designed wires. The electric field is polarized along the z axis.

When the wires are packed into a single 2D plane as in Fig. 2B (Inset), the reflection spectra off the mesh sheet show hardly any dispersion in either the polarization direction or incident angle, as long as the incident electric field is parallel to the sample plane (S-polarized). The reflection is lower than −45 dB for normal incidence and remains below −30 dB for the incident angle of 80°. The performance is also independent of the polarization angle as shown in Fig. 2C, a result of its in-plane geometry. Again, we show the effective constitutive parameters of this layer of wires in Fig. 2D (Top). At 10 GHz, ε_eff = 0.9999 + 0.006i and μ_eff = 1. Accordingly, the real part of its effective refractive index is almost unity and it is nearly independent of the number of layers as shown in Fig. 2D (Bottom). So, we can conclude that arbitrary arrangements of this mesh will be invisible as long as the electric field is parallel to the metallic wire within the beam width. To further illustrate this unique air-like material, we performed full-wave simulations on a network of wires with selected wires to represent the words “invisible material” shown in Fig. 2E. Under an oblique incidence of plane wave at 10 GHz, the steady-state total electric fields in air stay undisturbed, showing a perfect invisibility. Animation of the electric field propagation can be found in Movies S1–S4.

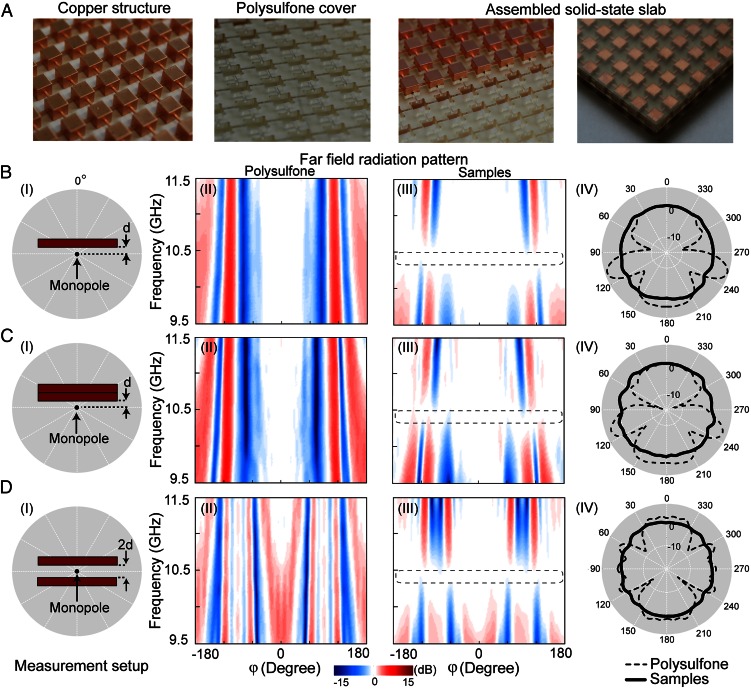
As shown in Fig. 3A, the sample was fabricated by sandwiching the copper-connected cubes between two pieces of PSU covers. The dimensions of the samples are 217 × 252 × 7 mm³ (31 × 36 × 1 in periods). To make the copper structure, we first 3D-print a plastic array of the connected cubes using stereolithography (material: Accura 60). Then, a metal sputtering process was used to coat the surfaces of the plastic array with 50 μm of copper film that is well above the skin depth (0.64 μm) at 10 GHz. The two PSU cover layers were machined with grooves and square openings so the copper structure could be embedded tightly inside.

Fig. 3.

Experimental measurements of the fabricated samples. (A) Slab samples composed of closely arranged corrugated wires. (B) Experimental far-field radiation pattern measured for a single layer of slab. (B, I) Experimental setup; (B, II and III) measured field amplitude for an identical PSU slab and the sample slab; and (B, IV) radiation pattern. (C) Measurement for two stacked layers. (D) Measurement for two spaced slabs. d is 20 mm. The radiation patterns in polar coordinates are plotted with data at 10.4 GHz.

In the measurements, three sets of sample configurations were studied. In the first configuration (Fig. 3B), one layer of the assembled slab was placed on a rotation stage spinning around a small monopole antenna with a separation distance of d (20 mm) from the slab, shown in Fig. 3 B, I. We choose this subwavelength separation to observe a strong redistribution of fields due to the sample. A wideband signal was fed into the monopole, and a wideband receiving lens antenna was placed at the other side to detect the far-field radiation patterns by measuring transmission amplitudes S₂₁ (S parameter) using an Agilent E8361A network analyzer. All transmission amplitudes are normalized by the reference transmission signal when the sample is removed. For comparison, a reference measurement was performed by replacing the sample with a PSU slab of the same size. Shown in Fig. 3 B, II, the radiation pattern of the PSU sample is strongly directional for all frequencies. But, for the designed sample shown in Fig. 3 B, III, there exists a frequency range around 10.4 GHz where the radiation pattern is almost a circle within a 7.2% relative bandwidth where the scattering amplitudes are less than ±1 dB. For a direct comparison in Fig. 3 B, IV, we plot the transmission amplitudes in angular polar coordinates for both the sample and the reference at 10.4 GHz, validating the omnidirectional invisibility of the sample. Although fabrication imperfections inevitably degrade the performance and shift the operating frequency from 10 to 10.4 GHz, the measurement results agree with our analytic and numerical results.

In the second configuration (Fig. 3C), two slab samples were stacked together as a thicker one. Equivalent sets of measurements were performed as those for the first configuration. In the third configuration (Fig. 3D), the two slab samples were separated on the two sides of the source antenna. In both configurations, similar results were obtained as those of the first configuration. The above results confirm that the fabricated sample is omnidirectionally invisible regardless of its geometry.

Derivation of the Scattering Width of the Infinite Corrugated Conducting Wire

For the infinite corrugated conducting wire shown in Fig. 1A in the main text, when d₁ + d₂ is far smaller than the free-space wavelength, the corrugated volume (r₂ ≤ ρ ≤ r₁) can be represented as a homogeneous but anisotropic effective medium with diagonal permittivity and permeability tensors given by ref. 37, i.e.,

$${\epsilon }_{\mathrm{cover}}=diag\left({\epsilon }_{\left|\right|}^{eff},{\epsilon }_{\left|\right|}^{eff},{\epsilon }_z^{eff}\right)=diag\left(\frac{\sigma d_1}{j\omega \left(d_1+d_2\right)},\frac{\sigma d_1}{j\omega \left(d_1+d_2\right)},\frac{{\epsilon }_r\left(d_1+d_2\right)}{d_2}\right),$$ [S1]

$${\mu }_{\mathrm{cover}}=diag\left({\mu }_{\left|\right|}^{eff},{\mu }_{\left|\right|}^{eff},{\mu }_z^{eff}\right)=diag\left(\frac{{\mu }_0{d}_2}{\left(d_1+d_2\right)},\frac{{\mu }_0{d}_2}{\left(d_1+d_2\right)},{\mu }_0\right).$$ [S2]

Here, σ is the conductivity of the wire and ε_r is the permittivity of the dielectric filling. Consequently, such a corrugated conducting wire can be considered as a cylindrical conductor coated with one layer of the effective medium with constitutive parameters given in [S1] and [S2].

When the incident wave is polarized along the z direction and propagates alone the x axis (Fig. 1A, main text), the electric field in the corrugated region (r₂ ≤ ρ ≤ r₁) and the total electric field in the air region (ρ ≥ r₁) can be described as

$$\begin{array}{l}\mathbf{E}=E_0{\displaystyle \sum _{n=-\infty }^{+\infty }{\left(-i\right)}^{-n}\left[a_n{J}_n\left(k_{eff}\rho \right)+b_n{Y}_n\left(k_{eff}\rho \right)\right]e^{-in\phi }\widehat{z}}\hspace{0.17em}\left(r_2\le \rho \le r_1\right)\\ {\mathbf{E}}_{total}={\mathbf{E}}_{inc}+{\mathbf{E}}_{sca}=E_0{\displaystyle \sum _{n=-\infty }^{+\infty }{\left(-i\right)}^{-n}{J}_n\left(k_0\rho \right)e^{-in\phi }\widehat{z}}+E_0{\displaystyle \sum _{n=-\infty }^{+\infty }{\left(-i\right)}^{-n}{c}_n{H}_n^{\left(2\right)}\left(k_0\rho \right)e^{-in\phi }\widehat{z}}\hspace{1em}\left(r_1\le \rho \right),\end{array}$$ [S3]

where E₀ is the amplitude of incident electric field E_inc, E_sca is the scattered electric field in the air region, J_n and Y_n are the Bessel functions, and H_n⁽²⁾ is the Hankel function of the second kind (25). The c_n is the scattering coefficient of the scattered wave in the nth angular momentum channel. c_n can be determined from the boundary conditions following the same procedures in ref. 3. Then, the normalized scattering width σ_sca /2r₁ is the sum of |c_n|². That is,

$$\begin{array}{c}{\sigma }_{sca}/2r_1=\frac{2}{k_0{r}_1}{\displaystyle \sum _{n=-\infty }^{+\infty }{\left|c_n\right|}^2}\\ c_n=\frac{J_n\left(k_0{r}_1\right)\left[J_n\left(k_{eff}{r}_2\right)Y_n^{\prime }\left(k_{eff}{r}_1\right)-J_n^{\prime }\left(k_{eff}{r}_1\right)Y_n\left(k_{eff}{r}_2\right)\right]-{\eta }_{eff}{J}_n^{\prime }\left(k_0{r}_1\right)\left[J_n\left(k_{eff}{r}_2\right)Y_n\left(k_{eff}{r}_1\right)-J_n\left(k_{eff}{r}_1\right)Y_n\left(k_{eff}{r}_2\right)\right]}{{\eta }_{eff}{H}_n^{2\prime }\left(k_0{r}_1\right)\left[J_n\left(k_{eff}{r}_2\right)Y_n\left(k_{eff}{r}_1\right)-J_n\left(k_{eff}{r}_1\right)Y_n\left(k_{eff}{r}_2\right)\right]-H_n^2\left(k_0{r}_1\right)\left[J_n\left(k_{eff}{r}_2\right)Y_n^{\prime }\left(k_{eff}{r}_1\right)-J_n^{\prime }\left(k_{eff}{r}_1\right)Y_n\left(k_{eff}{r}_2\right)\right]}.\\ k_{eff}=\omega \sqrt{u_{\left|\right|}^{eff}\cdot {\epsilon }_z^{eff}}\\ {\eta }_{eff}=\sqrt{u_{\left|\right|}^{eff}/{\epsilon }_z^{eff}}.\end{array}$$ [S4]

Note that when r₂ = r₁, such a corrugated wire is reduced to a cylindrical conducting wire. Then, c_n in Eq. S4 is turned to be J_n(k₀r₁)/H_n⁽²⁾(k₀r₁). Meanwhile, the normalized scattering width for a cylindrical conducting wire with radius r₁ is${\sigma }_{sca}/2r_1=2/k_0{r}_1{\displaystyle {\sum }_{n=-\mathrm{\infty }}^{+\mathrm{\infty }}{\left|J_n\left(k_0{r}_1\right)/H_n^{\left(2\right)}\left(k_0{r}_1\right)\right|}^2}$.

When the incident wave has a magnetic field polarized along the z axis, the involved effective constitutive parameters of the corrugated volume (r₂ ≤ ρ ≤ r₁) are ε_||^eff = σd₁/[jω[d₁+d₂]] and μ_z^eff = μ₀, meaning that the corrugated volume can be represented as the conductor. So, the corresponding scattering width is the same as that for an infinite cylindrical conducting cylinder with radius r₁, taking the form of ${\sigma }_{sca}/2r_1=2/k_0{r}_1{\displaystyle {\sum }_{n=-\mathrm{\infty }}^{+\mathrm{\infty }}{\left|J_n^{\prime }\left(k_0{r}_1\right)/H_n^{\left(2\right)\prime }\left(k_0{r}_1\right)\right|}^2}$. It is 0 at 0 (dc) frequency and approaches 2 toward high frequencies.

Scattering of a Homogeneous Infinite Dielectric Cylinder with Radius r

For the plane-wave incidence with the electric field polarized along the axis of the dielectric cylinder, the normalized scattering width for such a cylinder can be derived based on the Mie solution as (38)

$${\sigma }_{sca}/2r=\frac{2}{k_{0}r}{\displaystyle \sum _{n=-\infty }^{+\infty }{\left|a_n\right|}^2}=\frac{2}{k_{0}r}{\displaystyle \sum _{n=-\infty }^{+\infty }{\left|\frac{J_n\left(k_{0}r\right)J_n\prime \left(kr\right)-\eta J_n\left(kr\right)J_n\prime \left(k_{0}r\right)}{\eta H_n^2\prime \left(k_{0}r\right)J_n\left(kr\right)-J_n\prime \left(kr\right)H_n^2\left(k_{0}r\right)}\right|}^2},$$ [S5]

where k₀ = $\omega \sqrt{{\mu }_0{\epsilon }_0}$ is the wave vector in free space, k = $k_0\sqrt{\mu \epsilon }$ and η = ${\eta }_0\sqrt{\mu /\epsilon }$ are the wave vector and wave impedance in the cylinder, respectively. ε and μ are the relative permittivity and permeability of the cylinder, respectively. In the subwavelength limit, assuming |kr| << 1 and |k₀r| << 1, the higher-order a_n (n > 1) are all negligible. Using the small argument forms of Bessel and Hankel functions, the two leading scattering amplitudes vanish (a₀ = a₁ = 0) when

$$\sqrt{\mu /\epsilon }\left(\epsilon -1\right)=0\hspace{0.5em}\text{for}\hspace{0.5em}{a}_0=0,$$ [S6]

$$1-\mu =0\hspace{0.5em}\text{for}\hspace{0.5em}{a}_1=1.$$

It is seen that ε = 1 sets a₀ = 0 and μ = 1 sets a₁ = 0.

Similarly, under the plane-wave incidence with the magnetic field polarized along the axis of the cylinder, the normalized scattering is described as

$${\sigma }_{sca}/2r=\frac{2}{k_{0}r}{\displaystyle \sum _{n=-\infty }^{+\infty }{\left|a_n\right|}^2}=\frac{2}{k_{0}r}{\displaystyle \sum _{n=-\infty }^{+\infty }{\left|\frac{J_n\left(kr\right)J_n\prime \left(k_{0}r\right)-\eta J_n\left(k_{0}r\right)J_n\prime \left(kr\right)}{\eta H_n^2\left(k_{0}r\right)J_n\prime \left(kr\right)-J_n\left(kr\right)H_n^2\prime \left(k_{0}r\right)}\right|}^2}.$$ [S7]

Under the subwavelength limit, the conditions for a₀ = 0 and a₁ = 0 are

$$1‐\mu =0\hspace{0.5em}\text{for}\hspace{0.5em}{a}_0=0,$$ [S8]

$$\sqrt{\mu /\epsilon }\left(\epsilon -1\right)=0\hspace{0.5em}\text{for}\hspace{0.5em}{a}_1=0.$$

Discussion

In conclusion, we have demonstrated the ability to construct invisible microwave materials out of corrugated wires with record-low scattering width. Our analytical analyses, numerical simulations, and experimental measurements are all consistent. We hope this work will inspire new technological applications, one important example being the construction of perfect antenna radomes. Objects can also be cloaked inside the metallic cubes. The proposed approach is simple, robust, and scalable to higher frequencies using low-loss metals. Based on the general ability to control the frequency dispersions by multiple resonant structures (36), it should be possible to design wider-bandwidth materials invisible to both polarizations using our approach.