Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Jul 1.
Published in final edited form as: Neuroimage. 2015 Aug 18;124(Pt A):300–309. doi: 10.1016/j.neuroimage.2015.08.027

Identifying functional subdivisions in the human brain using meta-analytic activation modeling-based parcellation

Yong Yang a,b,#, Lingzhong Fan a,#, Congying Chu a,b, Junjie Zhuo d, Jiaojian Wang d, Peter T Fox f, Simon B Eickhoff g,h, Tianzi Jiang a,b,c,d,e,*
PMCID: PMC4791060  NIHMSID: NIHMS764400  PMID: 26296500

Abstract

Parcellation of the human brain into fine-grained units by grouping voxels into distinct clusters has been an effective approach for delineating specific brain regions and their subregions. Published neuroimaging studies employing coordinate-based meta-analyses have shown that the activation foci and their corresponding behavioral categories may contain useful information about the anatomical–functional organization of brain regions. Inspired by these developments, we proposed a new parcellation scheme called meta-analytic activation modeling-based parcellation (MAMP) that uses meta-analytically obtained information. The raw meta data, including the experiments and the reported activation coordinates related to a brain region of interest, were acquired from the Brainmap database. Using this data, we first obtained the “modeled activation” pattern by modeling the voxel-wise activation probability given spatial uncertainty for each experiment that featured at least one focus within the region of interest. Then, we processed these “modeled activation” patterns across the experiments with a K-means clustering algorithm to group the voxels into different subregions. In order to verify the reliability of the method, we employed our method to parcellate the amygdala and the left Brodmann area 44 (BA44). The parcellation results were quite consistent with previous cytoarchitectonic and in vivo neuroimaging findings. Therefore, the MAMP proposed in the current study could be a useful complement to other methods for uncovering the functional organization of the human brain.

Keywords: Meta-analysis, Activation modeling, Parcellation, Neuroimaging, Behavior domain

Introduction

Neuroimaging techniques have been used to find the relationships between function and structure in the human brain (for an overview see Eickhoff & Grefkes, 2011). From one perspective, researchers want to know which brain region is activated by the task at hand (Fox and Lancaster, 2002). Additionally, they want to know which tasks a brain region will participate in and how brain regions interact and cooperate with each other to accomplish a task. The relationship between tasks and brain activations is, however, complex. Because of the complexity of the mechanisms of brain function, a single task will commonly activate several brain regions simultaneously. In fact, different brain regions need to cooperate to accomplish almost any task (Bullmore and Sporns, 2009; Fox and Friston, 2012). On the other hand, considerable evidence suggests that one brain region may be involved in different functional networks (Bressler, 1995; Bullmore and Sporns, 2009) and activated in many different tasks (e.g., Dosenbach et al., 2006). The best way to simultaneously characterize the structural and functional properties of the human brain currently seems to be to use functional neuroimaging techniques such as functional magnetic resonance imaging (fMRI) or positron emission tomography (PET). In functional neuroimaging studies, researchers use such techniques to localize the brain regions that participate in certain tasks. The statistical map related to a particular task encodes the information about the two aspects of the relationships. In this paper, we will refer to the way a region activates in different tasks as its activation pattern. Regions that have similar activation patterns across different tasks may thus belong to the same functional community and work together to accomplish common mental processes (Smith et al., 2009). Based on this, we assumed that if the activation level of two voxels covaries across experiments, meaning that they both have a high level of activation in the same group of tasks and a low level of activation in other tasks, they should form a distinct module or functionally homogenous region. Thus, it is possible to design some elaborate task fMRI experiments and use such task-dependent activation patterns to study the functional topology of the human brain. However, the major problem is that the information needed to predict which tasks will cover the function of a brain region is not really known. Another problem is that it would be very costly to collect so many task fMRI images in a single study.

Due to the development of various neuroimaging study databases and tools such as Brainmap (Fox et al., 2005) and Neurosynth (Yarkoni et al., 2011), researchers have been able to begin to focus on the coordinate-based meta-analysis of neuroimaging studies. Rather than collecting the raw task fMRI images or the statistical parametric maps, these databases store the peak coordinates of the statistical maps related to a particular task, reported in standard space. The advantage of meta-analysis is that researchers can recruit published statistics to perform higher-level statistical analyses without having to collect the actual image data. The key in such coordinate-based meta-analyses has been to model the whole brain activation using the sparse peak coordinates; this modeling procedure has been implemented in several algorithms such as the activation likelihood estimation algorithm (ALE) (Laird et al., 2005; Turkeltaub et al., 2002) and multi-level kernel density analysis (MKDA) (Wager et al., 2009). This type of coordinate-based meta-analysis has been used to study the functional connectivity of brain regions and further used to perform task-dependent parcellations. Toro et al. (2008) mapped the functional connectivity between regions by estimating the co-occurrence of the voxel activity across several neuroimaging studies. This approach was later formalized as meta-analytic connectivity modeling (MACM) (Robinson et al., 2010), which used the ALE algorithm to identify regions showing statistically significant co-activation patterns, i.e., the task-dependent functional connectivity of the seed region. Later such meta-analytic co-activation maps were used as voxel-wise features to identify the subregions in a given area (Eickhoff et al., 2011). Moreover, the behavioral metadata in the Brainmap database, specifically the paradigm and behavioral domain descriptions of the experiments, enable researchers to infer the functional properties of the subregions. Recently, the method was successfully used to parcellate various brain regions, including the amygdala, BA44, and the posterior superior temporal gyrus (Bzdok et al., 2013; Clos et al., 2013; Wang et al., 2015).

Co-activation-based parcellation is quite similar to connectivity-based parcellation (Anwander et al., 2007; Beckmann et al., 2009; Mars et al., 2011; Wang et al., 2012). Although the covariance of resting state signal fluctuations is conceptually different from these methods, some researchers have directly used covariance to parcellate brain areas (Zhang et al., 2014). Similarly, another study used the Brainmap database to investigate the covariance within the activation pattern rather than focusing on co-activations (Smith et al., 2009). In this latter study, an independent component analysis (ICA)-based analysis of spatial activation maps from Brainmap discovered some major explicit activation networks that are very similar to the majority of networks that can be identified by measuring spontaneous covariations in the resting fMRI brain. By an extension of this to parcellation, it is possible to measure the voxel-wise similarity directly rather than doing this through identifying the co-activation pattern. For this reason, we proposed a new meta-analysis-based parcellation method called meta-analytic activation modeling-based parcellation (MAMP) by modeling of the voxel-wise activation followed by the K-means clustering algorithm. To test the accuracy of this method, we used it to parcellate the amygdala and the left side BA44 that had previously been parcellated using the MACM method (Bzdok et al., 2013; Clos et al., 2013).

Materials and methods

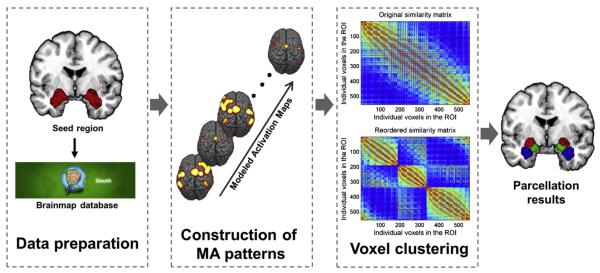
In our method we assumed that, in contrast to two voxels in different regions, foci located in a functionally homogeneous region or subregion should tend to be reported in experiments that share the same paradigm and should have similar activation patterns that co-vary across experiments from different paradigms. To estimate the activation of a voxel in an experiment, we applied the modeled activation value (MA value) from the ALE algorithm. The modeled activation value estimates the likelihood of a particular voxel's being activated during a given experiment. Such MA value images across experiments were combined to form MA value image sequences. This sequence of MA values was treated as a feature profile for each voxel. Then we applied the K-means clustering algorithm to the MA value sequences. This method can divide the region of interest (ROI) into functionally homogenous subregions, and also can help us to interpret the relationship between the functions of the subregions and the specific tasks to which they respond. The basic steps of our method included data preparation to obtain ROI related experiments from the Brainmap database followed by construction of voxel-wise MA patterns based on meta-analytic activation modeling and voxel clustering, as shown in Fig. 1.

Fig. 1.

Fig. 1

Open in a new tab

Pipeline of MAMP. Schematic of MAMP pipeline. The raw meta data related to a ROI were acquired form the Brainmap database; molded activation patterns were constructed using the ALE algorithm; voxels were grouped into subregions by applying K-means clustering to the MA patterns.

Data preparation

The image files for the two ROIs, i.e., the amygdala and the BA44, were created with the Anatomy Toolbox in SPM8 (Eickhoff et al., 2005). Specially, the left and right amygdala ROIs were composed of three micro-anatomically-defined cyto-architectonic subregions of the amygdala (Amunts et al., 2005), namely the laterobasal nuclei group (LB), centromedial nuclei group (CM), and the superficial nuclei group (SF) in the Jülich amygdala atlas. All the ROIs were down sampled to a 2 mm × 2 mm × 2 mm resolution space.

We then searched the Brainmap database (Fox et al., 2005; Fox and Lancaster, 2002) to get the ROI-related functional experiments. Brainmap archives over 10,000 neuroimaging experiments with the coordinates of reported activations and labels each experiment with its experimental paradigms and behavior domains, a practice which makes it feasible to perform a task-based analysis. We constrained our analysis to fMRI (functional magnetic resonance imaging) and PET (positron emission tomography) experiments with conventional mapping (no interventions, no group comparisons) which used healthy participants and reported the results as coordinates in stereotaxic space. These inclusion criteria yielded ~7300 eligible experiments at the time of the analysis. From these experiments, we then filtered out those that reported activation foci located in and surrounding the ROIs we had selected with a 2 mm tolerance margin outside the ROIs.

Meta-analytic activation modeling

First, we constructed the meta-analytic modeled activation profiles. For each experiment obtained from the database, we used the modeled activation value obtained from the ALE algorithm (Eickhoff et al., 2009) to estimate the probability of activation for each seed voxel in the ROI. Each reported focus was modeled by a 3D Gaussian distribution with adaptive full-width at half-maximum (FWHM), which depends on the sample size in the experiment, to evaluate the spatial uncertainty of the real position of the focus and the inter-subject localization uncertainty. Let Xi denote the situation in which the i th focus is located in a given voxel. The probability of Xi occurring at a seed voxel is

Pr(Xi)=exp(−di2∕2σ2)((2π)3∕2σ3).ΔV

where di is the Euclidean distance from the center of the seed voxel to the i th focus and σ is the standard deviation of the Gaussian distribution. To obtain the probability estimate for the entire voxel volume instead of just its central point, the Gaussian probability density was multiplied by the voxel size, ΔV. The voxel-wise MA value takes the maximum probability associated with any one focus, as reported from the experiment (Turkeltaub et al., 2012).

MA(x,y,z)=max(Pr(Xi))

After calculating MA values for each voxel in each experiment, the values were rearranged into a N × M matrix (1173 × 1307,556 × 413, 584 × 386 for the left BA44, the left amygdala, and the right amygdala, respectively), where N was the number of seed voxels and M was the number of experiments that activated a particular ROI. The row vector of M elements is called the modeled activation pattern. Each element in the sequence measures the activation level of the voxel in the corresponding experiment. The activation pattern series varies across experiments. The features of a particular voxel (the activation likelihoods in different experiments) are independent of each other. The features of different voxels will be correlated given that activation likelihoods are spatially smooth. We normalized each row of the MA patterns to unit vectors to ensure that the features were scale invariant.

Similarity matrix calculating

We computed the similarity between every pair of meta-analytically-modeled activation patterns and got an N × N similarity matrix. Different metrics, such as correlation (the sample linear correlation between observations), Euclidean similarity (one minus the normalized Euclidean distance), and cosine similarity (one minus the cosine distance), can be used to compute the similarity matrix. We tested our method on all of these most widely used similarity measures.

Voxel clustering and experiment clustering

Once we produced the MA patterns, we used clustering algorithms to cluster the voxels. We could have used any of several clustering algorithms, such as K-means or N-cut. For the convenience of allowing a comparison between the MAMP and MACM, we used the K-means clustering algorithm, which was implemented in Matlab 2012a, because that algorithm was used in the MACM. K-means clustering is a non-hierarchical clustering method that uses an iterative algorithm to separate the seed region into a previously selected number of K non-overlapping clusters (Hartigan and Wong, 1979). Clustering using the K-means algorithm consists of minimizing the variance within clusters and maximizing the variance between clusters by first computing the centroid of each cluster and subsequently reassigning voxels to the clusters such that their difference from the nearest centroid is minimal. We needed to choose K, the number of clusters, and the distance metric. All three distances used to compute a similarity matrix, for which correlation, Euclidean similarity, and cosine similarity could be used here. The input of the clustering algorithm was an N × M MA value sequence and K (the number of the clusters); the output was the index vector of the cluster label. For the amygdala, both left and right, we set K to 3, expecting to get parcellation results which were similar to those in the cytoarchitecture map from the Anatomy Toolbox. For the left BA44, we set K to 5 based on the MACM parcellation results (Clos et al., 2013). To measure the overlap of the corresponding subregions between different parcellation methods (cytoarchitecture, MACM, and MAMP), we computed the dice index for each pair of subregions. The dice coefficient is a statistic used for comparing the similarity of two sets:

s=2∣X∩Y∣∣X∣+∣Y∣.

As we assumed, voxels in the same subregion tended to be activated under the same functional paradigms. In other words, it is likely that different groups of voxels may be activated by different groups of experiments. Or even further, these groups of experiments may belong to different behavior domains. To find the relationship between activation and tasks, we used the K-means clustering algorithm to group the experiments into K subsets. After that, both the N × M MA value matrix and the N × N similarity matrix were reordered to find whether the K subsets of the experiments corresponded to each individual voxel cluster. This is possible because each voxel cluster will have a high activation in its corresponding experiments but a low activation in other experiments.

Function decoding

Furthermore, we employed behavior analysis to characterize the function of each subregion. The functional profile of a subregion quantitatively describes the statistical association between the activation of the region and the behavior domains. The behavioral domains comprise the main categories of cognition, action, perception, emotion, and interoception, as well as their related subcategories. These categories denote the mental processes that have been isolated by contrasts between different conditions. We filtered the Brainmap database for those experiments that featured at least one focus of activation within the ROI that we were currently researching. We then determined the individual functional profile of the MAMP-derived clusters using both forward and reverse inference (Clos et al., 2013). Forward inference refers to the probability of observing activity in a brain region given knowledge of the psychological process, represented as P(activation ∣ domain), whereas reverse inference refers to the probability of a psychological process's being present given knowledge of the activation in a particular brain region, represented as P(domain ∣ activation). Using forward inference, a cluster's functional profile was determined by identifying taxonomic labels for which the probability of finding activation in the respective cluster was significantly higher than the a priori chance (across the entire database) of finding activation in that particular cluster. Significance was established using a binomial test (p < 0.05; Eickhoff et al., 2011; Nickl-Jockschat et al., 2012). That is, we tested whether the conditional probability of activation given a particular label [P(activation ∣ domain)] was higher than the baseline probability of activating the brain region in question per se [P(activation)]. Using reverse inference, a cluster's functional profile was determined by identifying the most likely behavioral domains given activation in a particular cluster. This likelihood P(domain ∣ activation) can be derived from P(activation ∣ domain) as well as P(domain) and P(activation) using Bayes' rule. Significance was then assessed by means of a chi-square test (p < 0.05).

Results

Parcellation of the amygdala

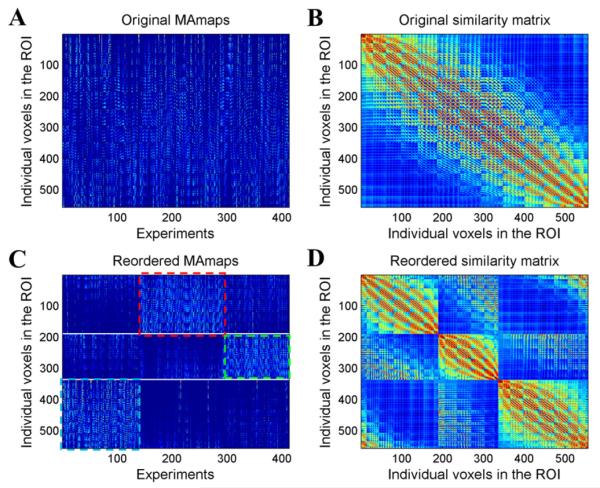
In the cytoarchitecture results as well as in the previous MACM-based parcellation results, the human amygdala was divided into three subregions, the laterobasal nuclei group (LB), centromedial nuclei group (CM), and superficial nuclei group (SF). In order to maintain consistency, the cluster number K in our experiment was also set to three. Fig. 2 displays the computational procedure of the MAMP process performed on the MA value patterns of the left amygdala. Figs. 2A and B show the original MA maps and the original similarity matrix. We filtered out 413 experiments that featured at least one focus that fell within the area of the left amygdala. Each column in the MA map matrix represents the MA map for each experiment within the ROI. Each row (the modeled activation pattern), reflects the likelihood of the voxel to activate in the experiment. The similarity matrix was computed as the cosine similarity between two MA value sequences, as shown in Fig. 2B. After clustering the voxels, we were able to reorder the MA maps to clearly reveal the different activation patterns of distinct groups of voxels (Fig. 2C). In the reordered MA maps, the rows were arranged in the order of cluster 1 (CM), cluster 2 (SF) and cluster 3 (LB). The experiments were also grouped into three subsets using clustering based on the similarity of the spatial activation map for each pair of experiments. From this we saw that the three subsets of the experiments and the three subregions corresponded very well. The red, green and blue rectangles in Fig. 2 mark three different groups of experiments with a relatively higher activation for each cluster. The CM subregion had a relatively higher activation for the second group of experiments, marked with red rectangles. The SF had a higher activation in the third group of experiments, marked with green rectangles. The LB had a higher activation in the first group of experiments, marked with blue rectangles. The reordered similarity matrix (Fig. 2D) shows the separation between the three groups of voxels. It shows a high similarity inside a group but a low similarity between groups, leading to higher value blocks along the diagonal line.

Fig. 2.

Fig. 2

Open in a new tab

Original and reordered MA maps and similarity matrix for the left amygdala. (A) Original MA maps. (B) Original similarity matrix. (C) Reordered MA maps. From top to bottom, each row represents a voxel in the ROI in the order of cluster 1, cluster 2, and cluster 3. From left to right, each column represents an experiment in the order of the grouped three subsets of the experiments. (D) Reordered similarity matrix.

Fig. 3A shows the results of parcellating the amygdala using cytoarchitecture, MACM, and MAMP. Both the MAMP and MACM results demonstrated inter-hemisphere symmetry in the shape and topology of the subregions. As shown in Fig. S3, the parcellation results were robust to the choice of different similarity measures. We computed the dice coefficients of the volumes from the three different parcellations to see whether the dice coefficients would be consistent between the methods. The topology of the three subregions derived from all three methods was highly similar between the different methods, as showed in the bar chart of the dice coefficient computed for each pair of corresponding subregions (Fig. 3B). In particular, the MACM and MAMP methods yielded very similar results. The lowest dice coefficient between these two meta-analytic methods was 0.89 for the left SF. The comparison between the two data-driven methods and the histological maximum probability map provided strong support for the biological meaningfulness of the data driven methods, that is, for either MACM or MAMP.

Fig. 3.

Fig. 3

Open in a new tab

Parcellation of the amygdala. (A) Three subregions (red: CM, green: SF, blue: LB) of the parcellation of the left amygdala using different methods (cytoarchitecture, MACM-CBP and MAMP). (B) Overlap (Dice coefficient) of the voxels in the subregions between different methods.

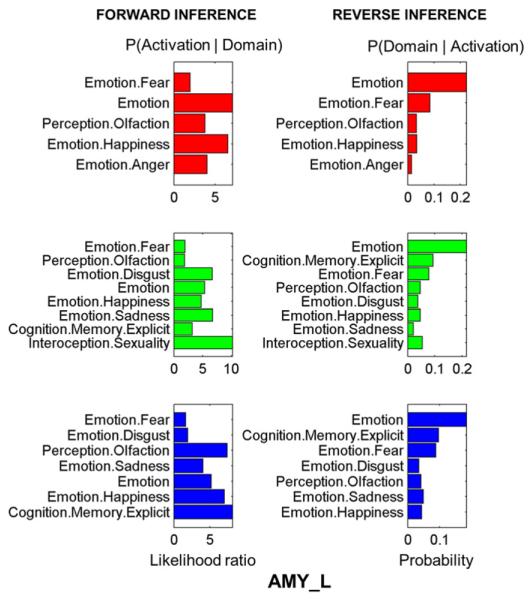
Fig. 4 shows the function decoding results for the left amygdala. Only the results that remained significant (p < 0.05) after a false discovery rate (FDR) correction are displayed. For the left amygdala, all three sub-regions were highly activated by tasks involved with domains such as those involved with emotion (e.g. fear or happiness) or with olfactory perception. The CM was specifically related with the emotion of anger, whereas the SF was related with the emotion of disgust. Sexuality interoception was strongly present in the SF. The right amygdala also showed a close relationship with emotion but had slightly different functional profiles between the three subregions (see Supplementary Fig. S2).

Fig. 4.

Fig. 4

Open in a new tab

Behavior domains of the subregions in the left amygdala. Forward inference on the final clusters: significant activation probability of the cluster given a certain domain (left column). Reverse inference on the final clusters: significant probability of domain (left column) occurrence given activation in a cluster. Color code: Red = CM, green = SF, blue = LB.

Parcellation of the left BA44

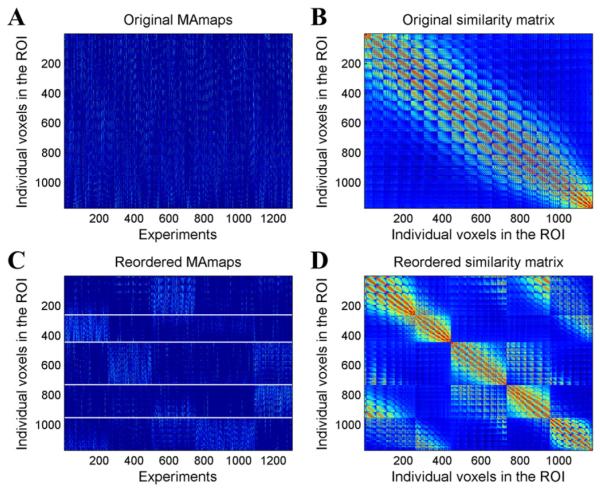
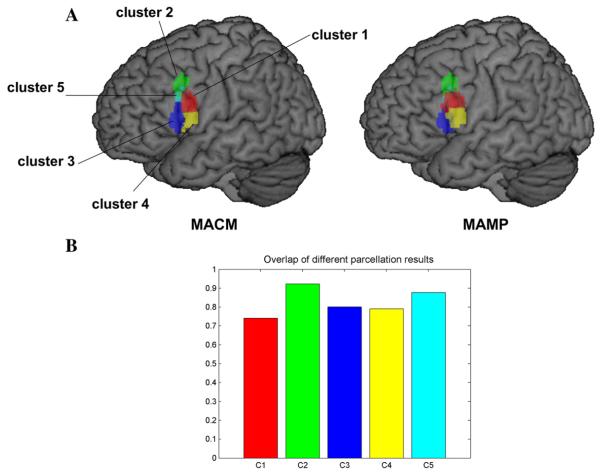
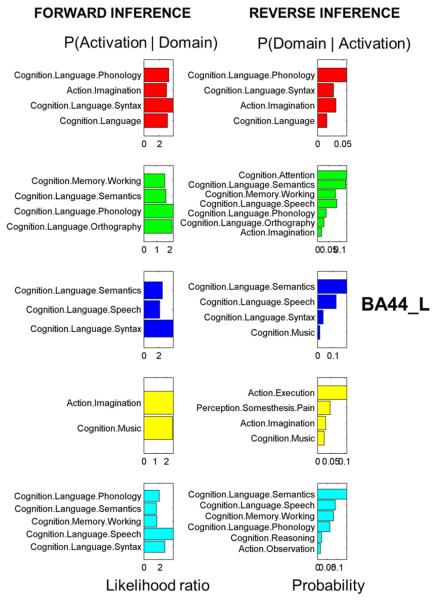
Common brain region parcellation methods depend on choosing the most optimal and reasonable cluster number. In order to focus on a comparison with previous results, we chose a cluster number of five, as previous MACM parcellation results yielded this number (Clos et al., 2013). We filtered 1307 experiments that featured at least one focus falling within the left BA44. After calculating the MA maps we got a 1173 × 1307 MA value pattern matrix (Fig. 5A). The original cosine similarity matrix before clustering is displayed in Fig. 5B. After the K-means clustering, the voxels in the ROI were grouped into five isolated sets. Again, we used the K-means clustering algorithms to detect the subgroup structure of the experiments by clustering the MA maps within the ROI (columns in the MA value sequence matrix). As shown in the reordered MA map matrix (Fig. 5C), the apparent blocks in the matrix indicate that each subgroup of voxels corresponded with certain sets of experiments. The rows of the matrix indicate that voxels from different subregions had different activation patterns. The columns of the matrix indicate that different sets of experiments activated distinct brain regions within the ROI. Fig. 5D shows the reordered similarity matrix with higher value blocks along the diagonal line. The correspondence between the results of the two methods was high (Fig. 6). The dice coefficients between the two methods were on average above 0.74 for the five subregions (Fig. 6), indicating that the location of the five clusters corresponded well in the two methods. Cluster 1 showed the greatest difference between the two results. The differences may be attributable to uncertainty about the location of the borders between the subregions. The function profiles of the five subregions showed that all five subregions were highly associated with language related functions (Fig. 7). Four subregions, not including cluster 3, were involved with action. Cluster 4 was involved with music. Cluster 2 and cluster 5 were involved with working memory.

Fig. 5.

Fig. 5

Open in a new tab

Original and reordered MA maps and similarity matrix for the left BA44. (A) Original MA maps. (B) Original similarity matrix. (C) Reordered MA maps. From top to bottom, each row represents a voxel in the ROI in the order of cluster 1, cluster 2, and cluster 3. From left to right, each column represents an experiment in the order of the grouped three subsets of the experiments. (D) Reordered similarity matrix.

Fig. 6.

Fig. 6

Open in a new tab

Parcellation of the left BA44. (A) Five subregions labeled cluster 1 (red), cluster 2 (green), cluster 3 (blue), cluster 4 (yellow) and cluster 5 (cyan). (B) Overlap (Dice coefficient) of the voxels in the subregions between the results using MACM and MAMP.

Fig. 7.

Fig. 7

Open in a new tab

Behavior domains of the subregions in the left BA44. Forward inference on the final clusters: significant activation probability of the cluster given a certain domain (left column). Reverse inference on the final clusters: significant probability of domain (left column) occurrence given activation in a cluster. Color code: Red = cluster 1, green = cluster 2, blue = cluster 3, yellow = cluster 4, cyan = cluster 5.

Voxel-wise density map

According to our assumption, different subregions should express different activation patterns. This can be confirmed by checking the reordered MA maps in Figs. 2C or 5C. We see that the subsets of the experiments and those of the subregions corresponded very closely. The subset of the experiments showed spatially varied density within the ROI. Different sets of experiments divided up the ROI. We call this the voxel-wise density map of the experiments.

Supplementary experiments showed that the MAMP algorithm is invariant to the choice of the similarity measure. The K-means obtained using different similarity measures provided almost identical results for both the amygdala and the BA44 (Figs. S1, S2).

Discussion

In this study, we proposed a new method called meta-analytic activation modeling-based parcellation in which we utilized the information in the Brainmap database to identify subregions in the left and right amygdala and the left area 44. The experiments on these areas showed subregional structures that were consistent with previous cytoarchitecture and MACM-based parcellation studies. Furthermore, we applied behavioral domain analysis for each subregion to make inferences about the functions of the subregions. We verified that each subregion was activated in different sets of experiments.

Method comparisons

Brain parcellation currently uses several different approaches, which can be categorized based on the data modality and the similarity measure strategy that they use. One strategy for measuring voxel-wise similarity is to first compute the voxel-wise connectivity profiles, such as those derived from anatomical, resting-state functional, and task-dependent co-activation-based connectivity data. Then these connectivity profiles are used to measure the similarity between voxels indirectly. The other is a local strategy, which is often used in fMRI-based parcellations. In this type of study, the local covariance of the voxel-wise fMRI time series is computed as the voxel-wise similarity. Different modalities can also provide different information about brain structure and function. Anatomical connectivity estimates the fiber tracts between individual brain regions, but such structural connectivity cannot fully encode the functional network structure of the brain (Honey et al., 2009). Therefore, we cannot guarantee that identifying differences in structure will yield accurate information about functionally distinct subregions. In resting state functional connectivity studies, the dynamics of the resting fMRI can lead to unstable results. Compared with task fMRI data, resting state signals tend to yield an insignificant amount of information about functional relationships and thus are not likely to provide much information about the function of a brain region. This defect restricts the use of this technique. Both a whole brain connectivity strategy and the local covariance have been used in resting state fMRI-based parcellations (Yeo et al., 2011; Zhang et al., 2014). Since our goal was to obtain brain function-structure mapping, we were obliged to dig deeply into the task-fMRI data. MACM-based connectivity took advantage of the rich information encoded in task-dependent neuroimaging studies and used global information by computing the connectivity with the rest of the brain. In fact, we can envision the available data as being processed according to a 2 (resting state fMRI data, coordinate-based meta data) × 2 (whole brain connectivity-based strategy, local covariance-based strategy) matrix of methods. Since 3/4 of this information was previously available (various studies have combined resting state data with either local or whole brain data and MACM supplied the third by combining whole brain connectivity with meta data), MAMP fills the last cell by combining resting state fMRI data with the local covariance. Our covariance-based strategy is conceptually different from that used in MACM in that our scheme directly measured the task-dependent functional relationship between two voxels within each ROI rather than across the entire brain. The advantage of a local strategy is that the measurement of voxel-wise similarity is direct and efficient. Our method recruits only the local activation information, whereas MACM must compute the whole brain MA map for each voxel. Thus, our MAMP method avoids error propagation arising from an indirect relationship, making the results more direct and interpretable. Interestingly, the MACM-based parcellation and that obtained by MAMP provided almost identical results in our experiments. This reflects the intrinsic relationship between these two methods. To some degree, our similarity measure of the MA value pattern can be expected to be close to the MACM-based similarity measure of the co-activation pattern. If one voxel is coactive with another, these two voxels should always either be simultaneously present or absent in any given experiment. In this situation, their MA value patterns will be similar as well. In spite of both our observed similarity between our MACM method and the MAMP as well as a reasonable explanation of why these should be similar, future studies should investigate to see whether these two methods produce greater differences in other regions. In either case, this may help to elucidate the underlying mechanisms.

Modeled activation value pattern

The most pivotal aspect of our method is the modeled activation value pattern. Some peak coordinate-based meta-analytical neuroimaging studies used the MA value to estimate the activation of a voxel in each experiment. This is the basis of the ALE algorithm (Laird et al., 2005; Turkeltaub et al., 2002) and of MACM-based parcellation. Another study used the MA value pattern as a voxel-wise feature to identify specific major activation networks in the Brainmap database (Smith et al., 2009).

An MA value pattern models the spatial uncertainty of a peak that has been identified using contrasting conditions and resembles the statistical activation map from the experiment. The peaks reported in a neuroimaging study constitute a rather discrete and sparse representation of the activation map obtained from an experiment. The activation level of the voxels other than those that are reported as peaks is unknown. Using 3D Gaussian kernel smoothing, we transformed the discrete activation map into a ‘continuous activation map’, a new statistical parametric map that represents the likelihood of the location of the peaks. After the transformation, every voxel in the ROI had an MA value for each experiment. If we had a sufficient number and variety of kinds of experiments archived in the database, almost every gray matter voxel in the brain image would be activated in some of the experiments. Under such an ideal condition, the MA pattern of any voxel would not be zero or meaningless but would have meaningful values that would fluctuate across the experiments. However, in practice, some voxels, particularly in larger ROIs, will always be near zero. This thorny problem however, exists in almost all coordinate-based meta-analysis tools. In fMRI or PET studies, activation usually appears in a cluster of several voxels that have statistically surpassed a certain threshold rather than in an isolated voxel. This is especially true because spatial smoothing is a common preprocessing step in these studies. Therefore, the neighboring voxels will share similar activation patterns with the peak voxel. By modeling peaks with a Gaussian kernel center at the peak, we were similarly able to estimate the activation level of the neighboring voxels of the peaks. This model also thereby takes into account uncertainties about the coordinates of the focus in a group analysis.

Density map of experiments

The density map for the experiments indicated that different subregions were specifically activated by different sets of experiments. This finding may be explained by results from Laird et al. (2011), which furthered the work of Smith et al. (2009) by exploring the relationship between the ICA maps derived from the Brainmap database and the behavioral metadata associated with these components. They found corresponding relationships between the network architecture and the Brainmap taxonomy, a finding that indicated each independent component corresponded with specific tasks. Another study constructed a meta-analytic network that revealed community structure (Crossley et al., 2013). That study found that many aspects of the co-activation network converged with a connectivity network derived from resting state fMRI data. These studies indicate that, as with resting fMRI, the task functional networks are organized into modules, and the role of a module is explicitly characterized by the related task behavior domain. In our method, the subregions in a ROI may belong to different networks or communities and respond to different tasks, as shown by the behavior profiles for each subregion. This can also be confirmed by previous MACM based parcellation studies because the subregions differentiate between the co-activation patterns. Therefore, their MA value patterns show differences between the subregions. The networks that the subregions involve may overlap. Nevertheless, wherever Brainmap has enough experiments to cover a sufficient number of task configurations for the subregions, we should be able to differentiate the subregions.

Parcellation results

Amygdala

Our results showed a subregion configuration that was similar to previous cytoarchitecture studies (Amunts et al., 2005; Eickhoff et al., 2005) and to MACM-based parcellation (Bzdok et al., 2013; Robinson et al., 2010). The correspondence between microstructure and task-based meta-analytic parcellation indicates that functional topology may have an underlying structural basis, though this may not be true for all brain regions. Although the two different meta-analytic methods deal with the data in different ways, in that MACM uses the whole brain gray matter to get the co-activation pattern for each voxel while MAMP uses only local information to compute the activation pattern, they provided almost identical results. This may be because voxels in the same region have both the same co-activation pattern and the same activation pattern across the experiments. The two approaches are similar in that they both use a task-based activation to represent a region functionally.

Area 44

The left BA44 is known as part of the Broca's area, a region involved in semantic tasks. Some recent findings have indicated that the BA44 is activated in tasks such as music perception and hand movements (Brown et al., 2006; Rizzolatti et al., 2002). Postmortem, receptor-based parcellation of Broca's area has suggested that this area is organized into the anterior–dorsal area 44d and the posterior–ventral area 44v (Amunts et al., 2010; Amunts et al., 1999; Amunts and Zilles, 2012). A recent MACM-based study revealed that this area can be separated into five functionally heterogeneous regions (Clos et al., 2013). The region was first divided into anterior and posterior clusters. Then the anterior portion was hierarchically separated into clusters 2, 3, and 5 and the ventral portion was separated into clusters 1 and 4 (Fig. 4A). The MAMP method provided similar results to the MACM parcellation with a high overlap between each pair of subregions (Fig. 4B).

Based on the behavior analysis, the three anterior clusters are engaged in language-related task domains, such as semantics, phonology, syntax, speech, and working memory, while the functional profiles of the two posterior clusters indicate that the BA44 is also involved in functions such as music perception and action (Fig. 5).

Methodological considerations

Our method is based on published neuroimaging studies. That means that all the information our method retrieved was from existing experiments. We cannot guarantee that the whole brain and all its subregions were completely covered by these studies. The number of available experiments would not have been sufficient for a less studied brain region, which could have led to unreliable results. There is currently no way to judge whether the database contained enough experiments involving a particular region to allow us to perform an adequate parcellation. However, this does not mean that the results are meaningless. Our study indicated that the results were very consistent with a cytoarchitecture-based parcellation, indicating that the results are biologically meaningful. Nevertheless, we must take care in interpreting the results, so making further comparisons with results from other modalities, such as microstructure (Amunts et al., 2007), resting-state fMRI (Cohen et al., 2008), and diffusion tensor imaging (DTI) (Fan et al., 2014) will be necessary.

Conclusion

In this study, we proposed a new brain parcellation scheme that modeled activation patterns for each voxel across the experiments in the Brainmap database. Reconstructing the peaks in neuroimaging studies into MA values and mapping their activation patterns enabled us to retrieve task-related information in the neuroimaging study databases. Because we were able to verify its identification of subregions in both cortical and subcortical areas, MAMP seems to be able to provide a fresh method for mining the Brainmap data and can complement other brain parcellation schemes with different neuroimaging modalities.

Supplementary Material

Fig. S1
Fig. S2
Fig. S3
Fig. S4

Acknowledgments

This work was partially supported by the National Key Basic Research and Development Program (973) (Grant Nos. 2011CB707801 and 2012CB720702), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB02030300), and the National Natural Science Foundation of China (Grant Nos. 91132301 and 91432302), the Deutsche Forschungsgemeinschaft (DFG, EI 816/4-1; EI 816/6-1) and the National Institute of Mental Health (R01-MH0 74457). We appreciate the editing assistance of Rhoda E. and Edmund F. Perozzi.

Footnotes

Conflict of interest

The authors have declared no conflict of interest.

References

  1. Amunts K, Zilles K. Architecture and organizational principles of Broca's region. Trends Cogn. Sci. 2012;16:418–426. doi: 10.1016/j.tics.2012.06.005. [DOI] [PubMed] [Google Scholar]
  2. Amunts K, Schleicher A, Burgel U, Mohlberg H, Uylings HB, Zilles K. Broca's region revisited: cytoarchitecture and intersubject variability. J. Comp. Neurol. 1999;412:319–341. doi: 10.1002/(sici)1096-9861(19990920)412:2<319::aid-cne10>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
  3. Amunts K, Kedo O, Kindler M, Pieperhoff P, Mohlberg H, Shah NJ, Habel U, Schneider F, Zilles K. Cytoarchitectonic mapping of the human amygdala, hippocampal region and entorhinal cortex: intersubject variability and probability maps. Anat. Embryol. (Berl.) 2005;210:343–352. doi: 10.1007/s00429-005-0025-5. [DOI] [PubMed] [Google Scholar]
  4. Amunts K, Schleicher A, Zilles K. Cytoarchitecture of the cerebral cortex — more than localization. Neuroimage. 2007;37:1061–1065. doi: 10.1016/j.neuroimage.2007.02.037. (discussion 1066–1068) [DOI] [PubMed] [Google Scholar]
  5. Amunts K, Lenzen M, Friederici AD, Schleicher A, Morosan P, Palomero-Gallagher N, Zilles K. Broca's region: novel organizational principles and multiple receptor mapping. PLoS Biol. 2010;8 doi: 10.1371/journal.pbio.1000489. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Anwander A, Tittgemeyer M, von Cramon DY, Friederici AD, Knosche TR. Connectivity-Based Parcellation of Broca's Area. Cereb. Cortex. 2007;17:816–825. doi: 10.1093/cercor/bhk034. [DOI] [PubMed] [Google Scholar]
  7. Beckmann M, Johansen-Berg H, Rushworth MF. Connectivity-based parcellation of human cingulate cortex and its relation to functional specialization. J. Neurosci. 2009;29:1175–1190. doi: 10.1523/JNEUROSCI.3328-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bressler SL. Large-scale cortical networks and cognition. Brain Res. Brain Res. Rev. 1995;20:288–304. doi: 10.1016/0165-0173(94)00016-i. [DOI] [PubMed] [Google Scholar]
  9. Brown S, Martinez MJ, Parsons LM. Music and language side by side in the brain: a PET study of the generation of melodies and sentences. Eur. J. Neurosci. 2006;23:2791–2803. doi: 10.1111/j.1460-9568.2006.04785.x. [DOI] [PubMed] [Google Scholar]
  10. Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009;10:186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
  11. Bzdok D, Laird AR, Zilles K, Fox PT, Eickhoff SB. An investigation of the structural, connectional, and functional subspecialization in the human amygdala. Hum. Brain Mapp. 2013;34:3247–3266. doi: 10.1002/hbm.22138. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Clos M, Amunts K, Laird AR, Fox PT, Eickhoff SB. Tackling the multifunctional nature of Broca's region meta-analytically: co-activation-based parcellation of area 44. Neuroimage. 2013;83:174–188. doi: 10.1016/j.neuroimage.2013.06.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Cohen AL, Fair DA, Dosenbach NU, Miezin FM, Dierker D, Van Essen DC, Schlaggar BL, Petersen SE. Defining functional areas in individual human brains using resting functional connectivity MRI. Neuroimage. 2008;41:45–57. doi: 10.1016/j.neuroimage.2008.01.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Crossley NA, Mechelli A, Vértes PE, Winton-Brown TT, Patel AX, Ginestet CE, McGuire P, Bullmore ET. Cognitive relevance of the community structure of the human brain functional coactivation network. Proc. Natl. Acad. Sci. 2013;110:11583–11588. doi: 10.1073/pnas.1220826110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Dosenbach NUF, Visscher KM, Palmer ED, Miezin FM, Wenger KK, Kang HSC, Burgund ED, Grimes AL, Schlaggar BL, Petersen SE. A core system for the implementation of task sets. Neuron. 2006;50:799–812. doi: 10.1016/j.neuron.2006.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Eickhoff SB, Grefkes C. Approaches for the integrated analysis of structure, function and connectivity of the human brain. Clin. EEG Neurosci. 2011;42:107–121. doi: 10.1177/155005941104200211. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Eickhoff SB, Stephan KE, Mohlberg H, Grefkes C, Fink GR, Amunts K, Zilles K. A new SPM toolbox for combining probabilistic cytoarchitectonic maps and functional imaging data. Neuroimage. 2005;25:1325–1335. doi: 10.1016/j.neuroimage.2004.12.034. [DOI] [PubMed] [Google Scholar]
  18. Eickhoff SB, Laird AR, Grefkes C, Wang LE, Zilles K, Fox PT. Coordinate-based activation likelihood estimation meta-analysis of neuroimaging data: a random-effects approach based on empirical estimates of spatial uncertainty. Hum. Brain Mapp. 2009;30:2907–2926. doi: 10.1002/hbm.20718. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Eickhoff SB, Bzdok D, Laird AR, Roski C, Caspers S, Zilles K, Fox PT. Co-activation patterns distinguish cortical modules, their connectivity and functional differentiation. Neuroimage. 2011;57:938–949. doi: 10.1016/j.neuroimage.2011.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Fan L, Wang J, Zhang Y, Han W, Yu C, Jiang T. Connectivity-based parcellation of the human temporal pole using diffusion tensor imaging. Cereb. Cortex. 2014;24:3365–3378. doi: 10.1093/cercor/bht196. [DOI] [PubMed] [Google Scholar]
  21. Fox PT, Friston KJ. Distributed processing; distributed functions? Neuroimage. 2012;61:407–426. doi: 10.1016/j.neuroimage.2011.12.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Fox PT, Lancaster JL. Opinion: mapping context and content: the BrainMap model. Nat. Rev. Neurosci. 2002;3:319–321. doi: 10.1038/nrn789. [DOI] [PubMed] [Google Scholar]
  23. Fox PT, Laird AR, Fox SP, Fox PM, Uecker AM, Crank M, Koenig SF, Lancaster JL. BrainMap taxonomy of experimental design: description and evaluation. Hum. Brain Mapp. 2005;25:185–198. doi: 10.1002/hbm.20141. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hartigan JA, Wong MA. Algorithm AS 136: a k-means clustering algorithm. Appl. Stat. 1979:100–108. [Google Scholar]
  25. Honey CJ, Sporns O, Cammoun L, Gigandet X, Thiran JP, Meuli R, Hagmann P. Predicting human resting-state functional connectivity from structural connectivity. Proc. Natl. Acad. Sci. U. S. A. 2009;106:2035–2040. doi: 10.1073/pnas.0811168106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Laird AR, Fox PM, Price CJ, Glahn DC, Uecker AM, Lancaster JL, Turkeltaub PE, Kochunov P, Fox PT. ALE meta-analysis: controlling the false discovery rate and performing statistical contrasts. Hum. Brain Mapp. 2005;25:155–164. doi: 10.1002/hbm.20136. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Laird AR, Fox PM, Eickhoff SB, Turner JA, Ray KL, McKay DR, Glahn DC, Beckmann CF, Smith SM, Fox PT. Behavioral interpretations of intrinsic connectivity networks. J. Cogn. Neurosci. 2011;23:4022–4037. doi: 10.1162/jocn_a_00077. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Mars RB, Jbabdi S, Sallet J, O'Reilly JX, Croxson PL, Olivier E, Noonan MP, Bergmann C, Mitchell AS, Baxter MG, Behrens TE, Johansen-Berg H, Tomassini V, Miller KL, Rushworth MF. Diffusion-weighted imaging tractography-based parcellation of the human parietal cortex and comparison with human and macaque resting-state functional connectivity. J. Neurosci. 2011;31:4087–4100. doi: 10.1523/JNEUROSCI.5102-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Nickl-Jockschat T, Habel U, Maria Michel T, Manning J, Laird AR, Fox PT, Schneider F, Eickhoff SB. Brain structure anomalies in autism spectrum disorder — a meta-analysis of VBM studies using anatomic likelihood estimation. Hum. Brain Mapp. 2012;33:1470–1489. doi: 10.1002/hbm.21299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Rizzolatti G, Fogassi L, Gallese V. Motor and cognitive functions of the ventral premotor cortex. Curr. Opin. Neurobiol. 2002;12:149–154. doi: 10.1016/s0959-4388(02)00308-2. [DOI] [PubMed] [Google Scholar]
  31. Robinson JL, Laird AR, Glahn DC, Lovallo WR, Fox PT. Metaanalytic connectivity modeling: delineating the functional connectivity of the human amygdala. Hum. Brain Mapp. 2010;31:173–184. doi: 10.1002/hbm.20854. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Filippini N, Watkins KE, Toro R, Laird AR, Beckmann CF. Correspondence of the brain's functional architecture during activation and rest. Proc. Natl. Acad. Sci. U. S. A. 2009;106:13040–13045. doi: 10.1073/pnas.0905267106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Toro R, Fox PT, Paus T. Functional coactivation map of the human brain. Cereb. Cortex. 2008;18:2553–2559. doi: 10.1093/cercor/bhn014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Turkeltaub PE, Eden GF, Jones KM, Zeffiro TA. Meta-analysis of the functional neuroanatomy of single-word reading: method and validation. Neuroimage. 2002;16:765–780. doi: 10.1006/nimg.2002.1131. [DOI] [PubMed] [Google Scholar]
  35. Turkeltaub PE, Eickhoff SB, Laird AR, Fox M, Wiener M, Fox P. Minimizing within-experiment and within-group effects in Activation Likelihood Estimation meta-analyses. Hum. Brain Mapp. 2012;33:1–13. doi: 10.1002/hbm.21186. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Wager TD, Lindquist MA, Nichols TE, Kober H, Van Snellenberg JX. Evaluating the consistency and specificity of neuroimaging data using meta-analysis. Neuroimage. 2009;45:S210–S221. doi: 10.1016/j.neuroimage.2008.10.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Wang J, Fan L, Zhang Y, Liu Y, Jiang D, Zhang Y, Yu C, Jiang T. Tractography-based parcellation of the human left inferior parietal lobule. Neuroimage. 2012;63:641–652. doi: 10.1016/j.neuroimage.2012.07.045. [DOI] [PubMed] [Google Scholar]
  38. Wang J, Fan L, Wang Y, Xu W, Jiang T, Fox PT, Eickhoff SB, Yu C, Jiang T. Determination of the posterior boundary of Wernicke's area based on multimodal connectivity profiles. Hum. Brain Mapp. 2015;36:1908–1924. doi: 10.1002/hbm.22745. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Yarkoni T, Poldrack RA, Nichols TE, Van Essen DC, Wager TD. Large-scale automated synthesis of human functional neuroimaging data. Nat. Methods. 2011;8:665–670. doi: 10.1038/nmeth.1635. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Yeo BT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Roffman JL, Smoller JW, Zollei L, Polimeni JR, Fischl B, Liu H, Buckner RL. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol. 2011;106:1125–1165. doi: 10.1152/jn.00338.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Zhang Y, Caspers S, Fan L, Fan Y, Song M, Liu C, Mo Y, Roski C, Eickhoff S, Amunts K, Jiang T. Robust brain parcellation using sparse representation on resting-state fMRI. Brain Struct. Funct. 2014 doi: 10.1007/s00429-014-0874-x. http://dx.doi.org/10.1007/s00429-014-0874-x. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Fig. S1
NIHMS764400-supplement-Fig__S1.jpeg (1.4MB, jpeg)
Fig. S2
NIHMS764400-supplement-Fig__S2.jpeg (334.7KB, jpeg)
Fig. S3
NIHMS764400-supplement-Fig__S3.jpeg (275.5KB, jpeg)
Fig. S4
NIHMS764400-supplement-Fig__S4.jpeg (536.9KB, jpeg)

RESOURCES