Abstract
Activation Likelihood Estimation (ALE) is an objective, quantitative technique for coordinate‐based meta‐analysis (CBMA) of neuroimaging results that has been validated for a variety of uses. Stepwise modifications have improved ALE's theoretical and statistical rigor since its introduction. Here, we evaluate two avenues to further optimize ALE. First, we demonstrate that the maximum contribution of an experiment makes to an ALE map is related to the number of foci it reports and their proximity. We present a modified ALE algorithm that eliminates these within‐experiment effects. However, we show that these effects only account for 2–3% of cumulative ALE values, and removing them has little impact on thresholded ALE maps. Next, we present an alternate organizational approach to datasets that prevents subject groups with multiple experiments in a dataset from influencing ALE values more than others. This modification decreases cumulative ALE values by 7–9%, changes the relative magnitude of some clusters, and reduces cluster extents. Overall, differences between results of the standard approach and these new methods were small. This finding validates previous ALE reports against concerns that they were driven by within‐experiment or within‐group effects. We suggest that the modified ALE algorithm is theoretically advantageous compared with the current algorithm, and that the alternate organization of datasets is the most conservative approach for typical ALE analyses and other CBMA methods. Combining the two modifications minimizes both within‐experiment and within‐group effects, optimizing the degree to which ALE values represent concordance of findings across independent reports. Hum Brain Mapp, 2012. © 2011 Wiley Periodicals, Inc.
Keywords: fMRI, magnetic resonance imaging, PET, meta‐analysis, neuroimaging, functional neuroimaging, activation likelihood estimation
INTRODUCTION
Reliable meta‐analytic techniques become increasingly important as the volume of neuroimaging literature rapidly expands. Coordinate‐based meta‐analysis (CBMA) approaches use published activation peaks reported in standardized coordinate spaces, termed activation foci, rather than raw images as their input [Laird et al.,2009a,b; Turkeltaub et al.,2002; Wager et al.,2004,2007]. Activation Likelihood Estimation (ALE), a commonly used CBMA method, is typically used to identify concordance across functional imaging studies of a cognitive process [Binder et al.,2009; Turkeltaub and Coslett,2010], or to compare activity between processes or populations [Caspers et al.,2010; Chouinard and Goodale,2010; Maisog et al.,2008; Minzenberg et al.,2009; Spreng et al.,2010; Vytal and Hamann,2009]. It has also been used to synthesize voxel‐based morphometry results [Di et al.,2009; Ferreira et al.,2009; Glahn et al.,2008], to define regions of interest for new imaging experiments [Karlsgodt et al.,2010; Laird et al.,2008; Zevin et al.,2010], or for functional connectivity mapping [Eickhoff et al.,2010; Laird et al.,2009a,b; Robinson et al.,2010].
ALE models the uncertainty in localization of activation foci using Gaussian probability density distributions. The voxelwise union of these distributions yields the ALE value, an estimate of the likelihood that at least one of the foci in a dataset was truly located at a given voxel. Stepwise modifications to the original technique have improved its theoretical and statistical rigor [Eickhoff et al.,2009; Laird et al.,2005], but further optimization is possible.
Here, we present two new modifications to ALE that limit the influence of within‐experiment and within‐group effects on ALE maps. The term experiment in this context refers to a single analysis reported in a neuroimaging paper. Within‐experiment effects occur because multiple foci reported close together in a single experiment may influence ALE values using the current method. Methodological factors such as the smoothing kernel and statistical threshold largely determine the number and proximity of activation foci reported. These differences between studies cannot be modified retrospectively in CBMA, but a small change to the ALE algorithm presented here addresses this issue by considering the spatial distribution of foci reported by an experiment while preventing within‐experiment coherence of foci from influencing ALE values.
Within‐group effects impact the results of ALE and other CBMA methods because groups of subjects with multiple experiments in a dataset may influence results more than groups with only one experiment. While this may be appropriate if the cognitive operations recruited by the various experiments are different (as in meta‐analytic connectivity mapping), most meta‐analyses select experiments based on their common cognitive demands. Activation patterns produced by the same group of subjects performing multiple similar tasks, usually in the same scanning session, however, do not represent independent observations. To address this issue, some have stipulated that datasets include only one experiment per subject group [e.g., Turkeltaub and Coslett,2010], but this approach excludes potentially informative results from analysis. Using the modified ALE algorithm presented here, this issue can be addressed by organizing datasets according to subject group rather than by experiment (the standard organizational approach used by ALE and other CBMA techniques).
In this article, we first evaluate the impact of limiting within‐experiment effects on ALE results by comparing the modified algorithm with the standard algorithm. We then evaluate the impact of limiting within‐group effects in ALE by comparing the results with the modified algorithm when foci are organized either by subject group or experiment.
MATERIALS AND METHODS
Standard ALE
The standard ALE algorithm is illustrated in Figure 1. In ALE, users organize the activation foci in their dataset based on their source in the literature. Typically, foci are organized by the experiment that reported them. Gaussian widths are calculated based on empirical quantification of the uncertainty inherent in spatial normalization, and the relationship between sample size and inter‐subject localization uncertainty [Eickhoff et al.,2009]. An individual map of activation likelihood, called a Modeled Activation map (MA map), is then calculated for each experiment by taking the voxelwise union of the Gaussians for all of the foci derived from that experiment. The ALE map is then calculated as the voxelwise union of the MA maps from a dataset. Null distributions account for the increased likelihood of identifying activation foci in gray matter, and a random‐effects significance test uses the null hypothesis that neuroimaging experiments produce patterns of activation that are spatially independent from one another [Eickhoff et al.,2009]. Analyses were performed using GingerALE 2.0 (http://brainmap.org), and also implemented in C++ for further calculations on MA values. Standard ALE and modified ALE analyses were conducted using two different critical thresholds (FDR of 0.05 and 0.01), and a minimum cluster size of 100 mm3.
Figure 1.
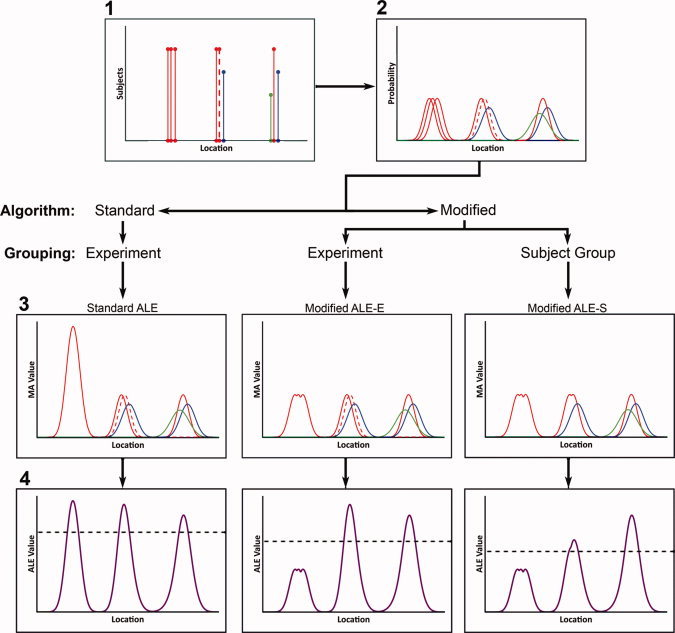
Illustration of ALE methods in 1‐dimensional space. In Step 1 (top left), foci are collected and converted to the same standardized coordinate space. Foci here were drawn from three unique subject groups (shown in red, blue, and green), each with different Ns. Two experiments were included from the red group (solid and dotted red lines). In Step 2, individual foci are modeled as Gaussians with an area under the curve of 1, and widths calculated from the Ns (Eickhoff et al.,2009). In Step 3, MA maps are calculated. Standard ALE (left) takes the union of all Gaussians, resulting in high MA values for experiments reporting foci close together. Using the modified ALE algorithm, foci are organized either by experiment (modified ALE‐E, middle) or subject group (modified ALE‐S, right). Modified ALE‐E determines the voxelwise MA value as the maximum probability associated with any one Gaussian from an experiment. Modified ALE‐S takes the maximum probability of any one Gaussian from a subject group. In Step 4, the ALE value is calculated for each method as the union of MA maps. The critical threshold (dotted black line) is determined based on random samples of MA values, and will be lower for the modified ALE methods at a given FDR because MA values are lower.
Modified ALE Algorithm With Foci Organized By Experiment (Modified ALE‐E)
Instead of taking the union of probabilities associated with all the foci reported by an experiment to determine the voxelwise MA value, the modified algorithm takes the maximum probability associated with any one focus reported by the experiment (see Fig. 1). This always corresponds to the probability of the focus with the shortest Euclidean distance to the voxel in question. In this way, MA maps reflect the spatial distribution of activation likelihoods associated with reported foci, without allowing multiple foci from a single experiment to jointly influence the individual MA value of a single voxel. The ALE value is then calculated as the voxelwise union of the probabilities in all the MA maps, just as in the standard algorithm. This modified ALE‐E value represents the likelihood that at least one experiment activated a given voxel. GingerALE 2.0 Java code and C++ code were modified to implement the new algorithm.
Modified ALE Algorithm With Foci Organized By Subject Group (Modified ALE‐S)
The modified algorithm was also implemented with foci organized by subject group. By organizing foci in this way, one MA map is generated for each unique subject group instead of each experiment (see Fig. 1). Again, the union of MA maps is taken to calculate the ALE map, just as in the standard ALE and modified ALE‐E analyses. This approach prevents multiple foci from a single experiment from cumulatively influencing MA values, and prevents multiple experiments performed by one subject group from cumulatively influencing ALE values. This modified ALE‐S value represents the likelihood that activity was found for at least one subject group at a given voxel.
Datasets Used for the Analyses
The algorithms were tested using two previously published datasets including both PET and fMRI papers on normal subjects. The cumulative dataset included 52 papers, 52 subject groups, 65 experiments, and 618 foci. Each will be discussed briefly below:
Temporal Processing (41 papers, 41 subject groups, 49 experiments, 446 foci): This dataset included fMRI and PET papers on time perception and production using a variety of tasks on healthy adult subjects. Each paper only used one subject group, but six papers included two experiments, and one included three. Details of the dataset are reported in Table I of Wiener et al. [2010].
Table I.
Results of analyses on the timing dataset
| Extent at FDR 0.05 (mm3) | Extent at FDR 0.01 (mm3) | Peak location | Peak ALE value (×10−3) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cluster | Standard | Modified ALE‐E | Modified ALE‐S | Cluster | Standard | Modified ALE‐E | Modified ALE‐S | Standard | Modified ALE‐E | Modified ALE‐S | Standard | Modified ALE‐E | Modified ALE‐S |
| 1 | 13,208 | 12,752 | 11,760 | 1 | 5,336 | 5,016 | 4,376 | (46, 8, 16) | (46, 8, 16) | (46, 10, 16) | 46.3 | 38.7 | 27.0 |
| (32, 18, 4) | (32, 18, 4) | (32, 18, 4) | 29.1 | 29.0 | 29.0 | ||||||||
| x | x | (46, 12, 4) | x | x | 21.0 | ||||||||
| 1/2 | ,192 | ,216 | (44, 14, 32) | (46, 16, 32) | (46, 16, 32) | 17.3 | 16.4 | 16.4 | |||||
| 3 | 2,288 | 2,336 | 1,808 | (14, 8, 8) | (14, 8, 8) | (14, 8, 6) | 35.1 | 33.8 | 23.6 | ||||
| 4 | ,344 | ,368 | ,128 | (42, 0, 36) | (42, 0, 36) | (44, 2, 38) | 20.7 | 20.7 | 15.7 | ||||
| 5 | ,296 | ,112 | ,144 | (34, 26, 30) | (36, 24, 30) | (36, 24, 30) | 17.9 | 15.7 | 15.7 | ||||
| x | (32, 30, 30) | (32, 30, 30) | x | 12.3 | 12.3 | ||||||||
| x | x | (52, 18, 14) | x | x | 12.5 | ||||||||
| 6 | 9,312 | 9,752 | 7,848 | 6 | 6,184 | 6,464 | 4,392 | (−18, 4, 10) | (−18, 4, 10) | (−16, 6, 10) | 34.0 | 34.0 | 26.0 |
| (−48, 8, 12) | (−50, 6, 14) | (−48, 8, 12) | 25.5 | 25.0 | 16.9 | ||||||||
| x | x | (−52, 10, 24) | x | x | 13.1 | ||||||||
| (−34, 12, 4) | (−32, 14, 4) | (−34, 14, 2) | 23.3 | 21.6 | 20.1 | ||||||||
| x | (−38, 16, 0) | x | x | 22.4 | x | ||||||||
| (−48, 12, 2) | (−48, 12, 2) | (−50, 12, 2) | 23.0 | 22.0 | 15.1 | ||||||||
| (−26, 10, 2) | (−26, 10, 2) | (−22, 12, 2) | 22.0 | 21.8 | 17.9 | ||||||||
| (−28, 24, 4) | (−28, 24, 4) | (−28, 24, 4) | 16.7 | 16.7 | 16.7 | ||||||||
| 3 | 9,152 | 9,304 | 8,912 | 7 | 7,424 | 7,528 | 7,208 | (0, −2, 54) | (−2, −2, 54) | (0, 0, 54) | 44.6 | 43.3 | 37.7 |
| (0, 6, 48) | (2, 8, 46) | x | 40.6 | 38.3 | x | ||||||||
| 4 | 4,200 | 4,328 | 4,200 | 8 | 2,456 | 2,640 | 2,248 | (40, −42, 42) | (40, −42, 42) | (40, −42, 42) | 31.8 | 30.6 | 25.0 |
| (48, −32, 46) | (48, −32, 46) | (48, −32, 46) | 17.1 | 17.1 | 17.0 | ||||||||
| x | x | (46, −48, 32) | x | x | 14.6 | ||||||||
| 5 | 2,552 | 2,592 | 1,920 | 9 | 1,624 | 1,584 | ,880 | (−26, −4, 52) | (−28, −6, 50) | (−24, −4, 52) | 29.3 | 25.9 | 22.2 |
| x | x | (−32, −18, 56) | x | x | 14.9 | ||||||||
| 6 | 2,376 | 2,512 | 2,232 | 10 | 1,592 | 1,648 | 1,392 | (−48, −6, 44) | (−48, −6, 44) | (−48, −6, 44) | 25.3 | 25.3 | 24.8 |
| 7 | 1,832 | 1,688 | ,880 | 11 | 1,184 | 1,080 | ,352 | (26, −6, 50) | (24, −8, 50) | (24, −8, 50) | 25.7 | 22.7 | 16.1 |
| 8 | 1,568 | 1,640 | 1,272 | 12 | ,920 | 1,064 | ,688 | (−14, −12, 4) | (−14, −12, 4) | (−14, −12, 4) | 22.7 | 22.7 | 20.9 |
| 9 | 1,520 | 1,624 | 1,288 | 13 | ,792 | ,928 | ,584 | (−28, −60, −36) | (−28, −60, −36) | (−28, −60, −36) | 24.6 | 24.6 | 18.6 |
| 10 | 1,432 | 1,208 | ,600 | 14 | ,568 | ,440 | ,200 | (10, −16, 8) | (10, −16, 6) | (10, −16, 6) | 20.9 | 19.6 | 17.0 |
| (10, −20, −6) | (10, −20, −6) | x | 16.4 | 15.9 | x | ||||||||
| x | x | (10, −14, 12) | x | x | 11.8 | ||||||||
| 11 | 1,016 | 1,048 | ,320 | 15 | ,648 | ,712 | x | (−38, −44, 46) | (−38, −44, 48) | (−36, −46, 48) | 27.5 | 27.0 | 15.6 |
| 12 | 936 | 1,016 | ,688 | 16 | ,448 | ,496 | ,336 | (38, −54, −32) | (38, −54, −32) | (38, −54, −32) | 20.8 | 20.8 | 19.6 |
| 13 | ,936 | 1,088 | 1,240 | 17 | ,344 | ,424 | ,464 | (−30, 40, 24) | (−30, 40, 24) | (−30, 40, 24) | 19.8 | 19.8 | 19.8 |
| (−32, 32, 30) | (−32, 32, 30) | (−32, 32, 30) | 13.3 | 13.3 | 13.3 | ||||||||
| 14 | ,896 | ,896 | ,552 | 18 | ,432 | ,464 | ,208 | (26, −58, −18) | (26, −58, −18) | (28, −60, −20) | 21.5 | 21.2 | 15.8 |
| 15 | ,544 | ,592 | ,656 | 19 | ,264 | ,296 | ,344 | (60, −36, 4) | (60, −36, 4) | (60, −36, 4) | 21.3 | 21.3 | 21.3 |
| 16 | ,448 | ,488 | ,128 | 20 | ,176 | ,232 | x | (22, −66, 40) | (22, −66, 40) | (22, −64, 40) | 18.7 | 18.7 | 12.9 |
| 17 | ,440 | ,624 | ,728 | 21 | ,120 | ,200 | ,216 | (6, 20, 34) | (6, 20, 34) | (6, 22, 34) | 16.6 | 16.5 | 16.5 |
| x | (−6, 24, 34) | (−6, 24, 34) | x | 13.0 | 13.0 | ||||||||
| 18 | ,408 | ,456 | x | x | x | x | (−12, −66, 50) | (−12, −66, 50) | x | 15.1 | 15.1 | x | |
| (−18, −70, 44) | (−18, −70, 44) | x | 14.3 | 14.3 | x | ||||||||
| 19 | ,392 | ,488 | ,552 | 22 | x | ,112 | ,176 | (44, 42, 10) | (44, 42, 10) | (44, 42, 10) | 15.8 | 15.8 | 15.8 |
| 20 | ,224 | x | x | x | x | x | (−22, −56, −22) | x | x | 14.6 | x | x | |
| 21 | ,208 | ,280 | ,320 | x | x | x | (30, 38, 20) | (30, 38, 20) | (30, 38, 20) | 14.3 | 14.3 | 14.3 | |
| 22 | x | ,136 | x | x | x | x | x | (−32, −66, −16) | x | x | 14.2 | x | |
| 23 | x | ,128 | x | x | x | x | x | (40, −20, −4) | x | x | 14.2 | x | |
| 24 | x | x | ,128 | x | x | x | x | x | (48, 18, −10) | x | x | 12.6 | |
Clusters significant at FDR of .05 are shown. Bolded peaks are also significant at FDR of 0.01.
Reading (11 papers, 11 subject groups, 16 experiments, 172 foci): This dataset included PET papers on aloud single word reading in healthy adult subjects. Each paper again only used one subject group, but two experiments were included from one paper, and four from another. Details of the dataset are reported in Figure 1 of Turkeltaub et al. [2002].
RESULTS
Comparison of Algorithms: Standard ALE Versus Modified ALE‐E
The comparison between standard ALE and modified ALE‐E analyses was used to evaluate whether within‐experiment coherence of foci impacts standard ALE analyses, and whether the modified algorithm addresses this issue.
First, we evaluated whether experiments reporting many foci drive peak MA values higher than other experiments in standard ALE analyses. We analyzed the cumulative dataset using the standard ALE algorithm and extracted the single maximum value from each MA map. The maximum voxel in each MA map is most likely to be influenced by within‐experiment effects, and is most likely to produce erroneously significant results in overall ALE maps. Peak MA value was directly related to the number of foci the experiment reported (Fig. 2A; R 2 = 0.22, P = 0.0001). This relationship was not significant for peak MA values calculated using the modified ALE‐E approach (Fig. 2B, R 2 = 0.05, P = 0.09), and the slope of the regression line decreased fivefold.
Figure 2.

Relationship between maximal MA value and number of foci. The maximum MA value derived from each experiment in the cumulative dataset is plotted against the number of foci reported by the experiment. MA values were calculated using the standard algorithm (A), and modified ALE‐E (B).
The relationship between number of foci and peak MA value should mainly be related to the proximity of foci, since foci close together will cumulatively impact MA values more than foci farther apart. To examine this, we evaluated whether experiments reporting foci close together drive peak MA values higher than other experiments in standard ALE analyses. Peak MA value for each experiment was inversely related to the minimum distance between foci reported by the experiment (Fig. 3A; R 2 = 0.13, P = 0.004). MA values were greatest when minimum distances were less than 10 mm. This relationship was negated by the modified algorithm (Fig. 3B, R 2 = 0.01, P = 0.38).
Figure 3.
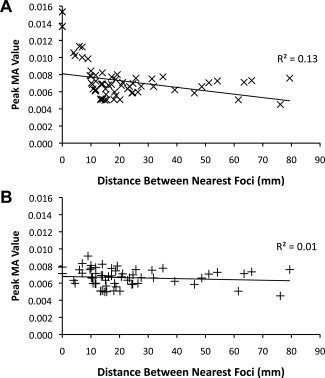
Relationship between maximal MA value and proximity of foci. The maximum MA value derived from each experiment in the cumulative dataset is plotted against the smallest distance between any two foci reported by the experiment. MA values were calculated using the standard algorithm (A), and modified ALE‐E (B).
In standard ALE, maximum MA values are related to the number of subjects in an experiment because the width of Gaussian probability models is inversely related to N, and a narrow Gaussian has a higher peak value (see Fig. 1). However, the relationship between maximum MA value and N should be weakened in standard ALE if spatial overlap of multiple Gaussians in some experiments drives the maximum MA value beyond the peak value of a single Gaussian. Maximal MA values in the cumulative dataset did relate to N using the standard ALE algorithm (Fig. 4A; R 2 = 0.29, P < 0.0001). In the modified ALE‐E analysis, this relationship was essentially direct (Fig. 4B, R 2 = 0.86, P < 0.0001) because the maximum MA value is simply the peak value of a single Gaussian probability distribution.
Figure 4.
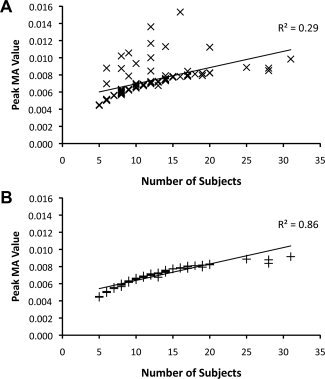
Relationship between maximal MA value and number of subjects. The maximum MA value derived from each experiment in the cumulative dataset is plotted against the N of the experiment. MA values were calculated using the standard algorithm (A), and modified ALE‐E (B).
Next we evaluated ALE maps calculated using the two algorithms to determine the impact of removing within‐experiment effects on ALE results. First, we evaluated the overall magnitude of the difference between the two algorithms by calculating cumulative unthresholded ALE values throughout standardized space using each algorithm. The difference between these values provides a measure of the impact that within‐experiment effects have on standard ALE maps before critical thresholding. The cumulative reduction in ALE values by the modified ALE‐E analysis was 3.1% for the timing dataset, and 2.3% for the reading dataset.
Next, we evaluated the thresholded ALE maps. Overall, the two algorithms produced very similar results for both datasets in terms of patterns of significant findings (Figs. 5 and 6; Tables I and II), extent of overlapping voxels, and number of common clusters (Table III). For both datasets, the modified ALE algorithm resulted in a slightly greater number of significant voxels than standard ALE at both critical thresholds (Table III). The modified algorithm removed clusters that were driven solely by within‐experiment effects. For example, only one cluster in the timing analysis was significant using the standard ALE algorithm but not the modified algorithm (peak at −22, −56, 22). In this case, a single experiment reported two foci 4.5 mm apart surrounding the ALE peak. Across both datasets, clusters that were significant using only one algorithm or the other were small (200 to 456 mm3 in extent; 27 to 57 voxels).
Figure 5.
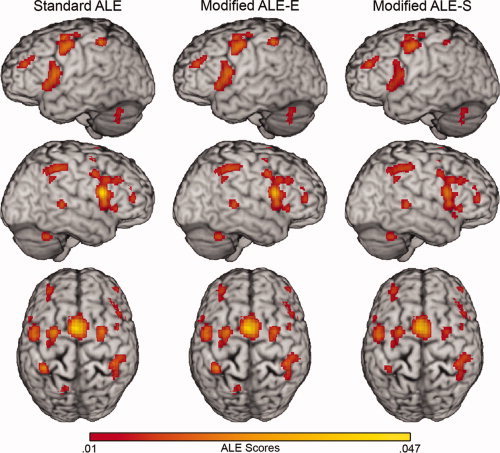
ALE analyses of the timing dataset. Rendered hemispheres of the standard ALE, modified ALE‐E, and modified ALE‐S analyses of the timing dataset with an FDR of 0.05 and a minimum cluster extent of 100 mm3. Renderings are maximum intensity projections with a search depth of 16 mm rendered on the Colin brain in Talairach space.
Figure 6.
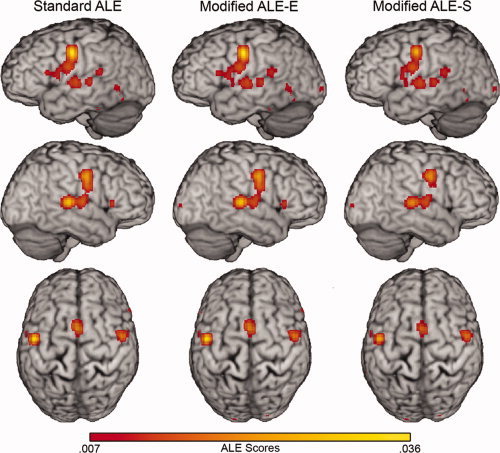
ALE analyses of the reading dataset. Rendered hemispheres of the standard ALE, modified ALE‐E, and modified ALE‐S analyses of the reading dataset with an FDR of 0.05 and a minimum cluster extent of 100 mm3. Renderings are maximum intensity projections with a search depth of 16 mm rendered on the Colin brain in Talairach space.
Table II.
Results of analyses on the reading dataset
| Extent at FDR 0.05 (mm3) | Extent at FDR 0.01 (mm3) | Peak location | Peak ALE value (×10− 3) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cluster | Standard | Modified ALE‐E | Modified ALE‐S | Cluster | Standard | Modified ALE‐E | Modified ALE‐S | Standard | Modified ALE‐E | Modified ALE‐S | Standard | Modified ALE‐E | Modified ALE‐S |
| 1 | 8,832 | 9,040 | 3,744 | 1 | 2,384 | 2,632 | 2,232 | (54, −28, 6) | (54, −28, 6) | (56, −28, 6) | 29.9 | 29.8 | 21.9 |
| (54, −12, 8) | (54, −12, 10) | (54, −12, 10) | 16.6 | 14.5 | 14.4 | ||||||||
| x | (52, −14, 6) | (52, −14, 6) | x | 14.3 | 14.3 | ||||||||
| 1/2 | Clust 1 | Clust 1 | 3,448 | 2 | 3,400 | 3,656 | 2,312 | (44, −10, 34) | (44, −10, 34) | (48, −8, 36) | 26.6 | 26.3 | 22.1 |
| 3 | 5,080 | 5,416 | 4,512 | 3 | 2,896 | 3,168 | 2,448 | (−48, −12, 36) | (−48, −12, 36) | (−46, −12, 38) | 35.8 | 35.7 | 27.6 |
| (−48, −8, 20) | (−48, −8, 20) | (−48, −8, 20) | 14.9 | 14.7 | 14.7 | ||||||||
| (−50, 14, 14) | (−50, 14, 14) | x | 9.7 | 9.7 | x | ||||||||
| x | (−50, 6, 12) | (−52, 4, 10) | x | 9.5 | 9.1 | ||||||||
| x | (−52, 0, 2) | (−52, 0, 2) | x | 8.3 | 8.3 | ||||||||
| 4 | 4,888 | 5,192 | 2,480 | 4 | 2,736 | 3,064 | ,144 | (−14, −66, −16) | (−14, −66, −16) | (−12, −64, −16) | 21.4 | 21.4 | 11.2 |
| 4/5 | Clust 4 | Clust 4 | Clust 4 | 4/5 | Clust 4 | Clust 4 | ,944 | (0, −68, −16) | (0, −68, −16) | (0, −68, −16) | 18.1 | 18.1 | 14.1 |
| (18, −68, −14) | (18, −68, −14) | x | 16.2 | 16.1 | x | ||||||||
| x | (10, −62, −16) | (10, −62, −16) | x | 14.7 | 13.8 | ||||||||
| x | (20, −64, −24) | x | x | 9.4 | x | ||||||||
| 6 | 2,784 | 2,896 | 2,528 | 6 | 1,744 | 2,016 | 1,576 | (0, 2, 52) | (0, 2, 52) | (0, 0, 50) | 24.4 | 23.5 | 18.9 |
| x | x | (2, 0, 54) | x | x | 18.5 | ||||||||
| 7 | 1,552 | 1,680 | 1,200 | 7 | ,480 | ,704 | ,376 | (−34, −60, −10) | (−34, −60, −10) | (−34, −60, −10) | 15.0 | 15.0 | 13.7 |
| 8 | 1,240 | 1,248 | 1,352 | 8 | ,448 | ,592 | ,672 | (−56, −16, 2) | (−56, −16, 2) | (−56, −16, 2) | 14.7 | 14.6 | 14.6 |
| 9 | ,456 | x | x | 9 | ,216 | x | x | (−12, 28, 0) | x | x | 15.8 | x | x |
| 10 | ,440 | ,512 | ,568 | 10 | x | ,200 | ,224 | (−54, −32, 4) | (−54, −32, 4) | (−54, −32, 4) | 12.7 | 12.7 | 12.7 |
| 11 | ,272 | ,336 | x | 11 | x | ,104 | x | (56, 20, 4) | (56, 20, 4) | x | 11.9 | 11.9 | x |
| 12 | ,256 | ,360 | ,440 | x | x | x | (−58, −44, 16) | (−58, −44, 16) | (−58, −44, 16) | 10.2 | 10.2 | 10.2 | |
| 13 | ,240 | x | x | x | x | x | (−28, −56, −24) | x | x | 11.3 | x | x | |
| 14 | ,240 | ,296 | x | x | x | x | (−36, −40, −24) | (−36, −40, −24) | x | 11.5 | 11.5 | x | |
| 15 | ,192 | ,232 | ,272 | x | x | x | (6, −24, 0) | (6, −24, 0) | (6, −24, 0) | 10.5 | 10.4 | 10.4 | |
| 16 | ,152 | ,176 | ,256 | x | x | x | (−16, −14, 4) | (−16, −14, 4) | (−16, −14, 4) | 9.8 | 9.7 | 9.7 | |
| 17 | ,104 | ,184 | ,216 | x | x | x | (−30, 20, 10) | (−30, 20, 10) | (−30, 20, 10) | 9.6 | 9.6 | 9.6 | |
| 18 | x | ,144 | ,176 | x | x | x | x | (28, 10, 10) | (28, 10, 10) | x | 8.8 | 8.8 | |
| x | (32, 6, 4) | (32, 6, 4) | x | 8.6 | 8.6 | ||||||||
| 19 | x | ,120 | ,152 | x | x | x | x | (−24, −18, 14) | (−24, −18, 14) | x | 9.2 | 9.2 | |
| 20 | x | ,112 | ,144 | x | x | x | x | (−18, −98, −4) | (−18, −98, −4) | x | 8.6 | 8.6 | |
| 21 | x | ,112 | ,152 | x | x | x | x | (20, −92, 0) | (20, −92, 0) | x | 9.2 | 9.2 | |
| 22 | x | x | ,240 | x | x | x | x | x | (22, −68, −14) | x | x | 9.8 | |
| 23 | x | x | ,216 | x | x | x | x | x | (24, −60, −24) | x | x | 9.1 | |
| 24 | x | x | ,160 | x | x | x | x | x | (12, −30, 8) | x | x | 8.6 | |
| x | x | (8, −32, 16) | x | x | 8.6 | ||||||||
Clusters significant at FDR of 0.05 are shown. Bolded peaks are also significant at FDR of 0.01.
Table III.
Comparison of significant extent using different algorithms
| Analysis | Total significant ALE extent (mm3) | Common significant extent (mm3) | Extent significant only with one algorithm (mm3) | Clusters significant with both algorithms | Clusters in standard ALE split by modified ALE‐E | Clusters significant only with one algorithm | |||
|---|---|---|---|---|---|---|---|---|---|
| Standard | Modified ALE‐E | Standard | Modified ALE‐E | Standard | Modified ALE‐E | ||||
| Timing | |||||||||
| FDR .05 | 53,600 | 54,640 | 51,936 | 1,664 | 2,704 | 20 | 0 | 1 | 2 |
| FDR .01 | 33,440 | 34,336 | 32,360 | 1,080 | 1,976 | 20 | 1 | 0 | 1 |
| Reading | |||||||||
| FDR .05 | 26,728 | 28,056 | 25,760 | ,968 | 2,296 | 13 | 0 | 2 | 4 |
| FDR .01 | 14,304 | 16,136 | 14,000 | ,304 | 2,136 | 7 | 0 | 1 | 2 |
Within common clusters, the locations of local maxima were similar using the two algorithms. Across the two datasets, 45 local maxima were identical in the two analyses, 11 were in adjacent voxels, and 8 were only peaks using the modified algorithm (these voxels were typically also significant using the standard algorithm, but were not local maxima).
The two algorithms also produced similar results in terms of the magnitude of significant peaks, although some ALE scores were reduced by the modified algorithm. The largest reduction occurred at the overall peak in the standard ALE timing analysis (at 46, 8, 16), where the ALE value was reduced from 0.0463 to 0.0387 using the modified algorithm. In this case, a duplicate focus in this previously published dataset accounted for the high standard ALE value. The modified algorithm reduced other standard ALE peaks because experiments reported foci in close proximity. For example, one peak in the timing analyses (−26, −4, 52) was reduced from an ALE value of 0.0293 to 0.0259. One experiment reported two foci 7 mm apart surrounding the location of this ALE peak.
Comparison of Organizational Strategies: Modified ALE‐E Versus Modified ALE‐S
We compared the results of the modified ALE‐E and modified ALE‐S analyses to evaluate the impact of within‐group effects on ALE results. In comparison to modified ALE‐E values, the modified ALE‐S analysis reduced cumulative brain‐wide ALE values by 7.6% for the timing dataset, and 8.6% for the reading dataset.
Next we evaluated the thresholded ALE maps. The two grouping strategies produced similar results in terms of pattern of significant findings (Figs. 5 and 6, Tables I and II), but the modified ALE‐S approach was more conservative in terms of the total extent of significant ALE values regardless of the dataset or critical threshold (Table IV). Although the majority of significant voxels were significant regardless of grouping strategy, 18 to 34% of modified ALE‐E voxels were not significant using the modified ALE‐S approach, depending on the dataset and critical threshold. In comparison, only 2 to 5% of modified ALE‐S significant voxels were not significant using the modified ALE‐E approach (due to a reduced critical threshold with ALE‐S at the same FDR, as illustrated in Fig. 1).
Table IV.
Comparison of significant extent using different grouping strategies
| Total significant ALE extent (mm3) | Common significant extent (mm3) | Extent significant only with one grouping strategy (mm3) | Clusters significant with both grouping strategies | Clusters in modified ALE‐E split by modified ALE‐S | Clusters significant only with one grouping strategy | ||||
|---|---|---|---|---|---|---|---|---|---|
| Modified ALE‐E | Modified ALE‐S | Modified ALE‐E | Modified ALE‐S | Modified ALE‐E | Modified ALE‐S | ||||
| Timing | |||||||||
| FDR .05 | 54,640 | 46,224 | 44,864 | 9,776 | 1,360 | 19 | 0 | 3 | 1 |
| FDR .01 | 34,336 | 26,360 | 25,720 | 8,616 | ,640 | 20 | 0 | 2 | 0 |
| Reading | |||||||||
| FDR .05 | 28,056 | 22,256 | 21,200 | 6,856 | 1,056 | 15 | 1 | 2 | 3 |
| FDR .01 | 16,136 | 10,928 | 10,688 | 5,448 | ,240 | 8 | 1 | 1 | 0 |
Despite these differences in extent, most clusters were significant regardless of grouping strategy (Table IV). Clusters that were removed by the modified ALE‐S approach were influenced by within‐group effects. For example, three small timing clusters were significant using modified ALE‐E, but not ALE‐S at an FDR of 0.05 (peaks at −12, −66, 50; −32, −66, −16; 40, −20, −4). In each case, two foci were reported near the peak voxel by different experiments from a single subject group (1 mm and 2 mm; 1 mm and 1 mm; 1 mm and 2.2 mm), and the closest focus from another subject group was farther from the peak (8.3 mm; 11 mm; 12.9 mm). Only one timing cluster was significant in the modified ALE‐S analysis, but not the modified ALE‐E analysis (peak at 48, 18, −10). Here, two unique subject groups reported foci immediately near the peak (1.7 mm and 1.8 mm). Notably, all of these clusters were small (456, 136, 128, and 128 mm3) and none were significant at an FDR of 0.01.
At this stricter threshold, clusters that were significant using modified ALE‐E but not ALE‐S derived from minimal between‐group agreement with added within‐group effects. For example, a timing cluster removed by modified ALE‐S (peak at −38, −44, 48), derived from two experiments from one subject group that reported foci within 1 mm of the peak, two experiments from another subject group that reported foci within 3 mm of the peak, and a third experiment that reported two foci within 10 mm of the peak. In contrast, for the smallest timing cluster in the modified ALE‐S analysis at an FDR of 0.01 (peak at 44, 42, 10), four independent subject groups reported foci within 10 mm of the peak.
Within clusters identified by both approaches, the locations of local maxima were similar using the two grouping strategies. Across the two datasets, 40 local maxima were identical using either of the two grouping strategies. Among other maxima, 16 were in adjacent voxels, 3 were nearby (4.5 mm, 4.9 mm, and 4.9 mm), and 12 were only peaks using one of the grouping strategies (these voxels were typically significant using either approach, but were only local maxima using one).
Organizing foci by subject group reduced the magnitude of some significant ALE peaks substantially. In one case, a peak in the modified ALE‐E timing analysis (46, 8, 16, which was the one for which the duplicate focus was detected) was reduced from 0.0387 to 0.0270. Nine experiments from seven unique subject groups reported foci within 10 mm of this peak. In contrast, the ALE value of another local peak in the same cluster (at 32, 18, 4) was identical in the two analyses (.0290). Nine experiments reported foci within 10 mm of this peak, each from a unique subject group.
DISCUSSION
Within‐Experiment Effects and the Modified ALE Algorithm
ALE has proven a valuable meta‐analytic tool, but one theoretical shortcoming has been that the ALE statistic reflects spatial coherence across activation foci regardless of their source in the literature [Wager et al.,2007]. The recent development of a random‐effects significance test for ALE has alleviated these concerns considerably. Still, we demonstrated here that the number of foci an experiment reports, and the proximity of those foci, can potentially impact the maximum contribution a particular experiment makes to an ALE map. The modified ALE algorithm presented here eliminates these effects.
When the two algorithms were directly compared, however, we found only minor difference between the resultant ALE maps in terms of the cumulative effect on unthresholded ALE values, and the significance of major clusters. There were some differences in significance of small clusters, but these were minimal using a relatively strict threshold (FDR of 0.01). In line with our theoretical considerations, clusters that the modified algorithm eliminated were small and derived mainly from single experiments reporting two foci in close proximity. Reducing high MA values that derived from within‐experiment coherence removed a subtle rightward skew in random‐effects null distributions, allowing ALE values reflecting moderate coherence across experiments to reach significance using the modified algorithm.
The overall similarity between the results of the two algorithms indicates that coherence of foci within individual experiments has contributed relatively little to previously published ALE results. The modified algorithm is theoretically advantageous though, given that the number and proximity of foci reported by experiments did impact standard MA peak values. Further, the modified algorithm prevents single experiments from biasing results under extreme circumstances, like duplication errors in lists of foci, or meta‐analyses in which a single experiment reports far more foci than all others.
The difference between the modified and standard ALE algorithms is somewhat analogous to the difference between two other CBMA techniques, kernel density analysis (KDA) and multilevel kernel density analysis (MKDA) [Wager et al.,2004,2007]. KDA represents each activation focus as a sphere, and counts the number of overlapping spheres at each voxel to evaluate for spatial coherence between foci. In MKDA, overlapping spheres from the same experiment are not additive, such that the count at each voxel represents the number of overlapping experiments. In MKDA, the user sets the size of the spheres, and arbitrary weights can be given based on the N of experiments and whether fixed‐ or random‐effects statistics were used by the experiment. The main theoretical difference between ALE and MKDA is that ALE evaluates probabilities of activity localization, where MKDA uses experiment counts [Wager et al.,2009]. The main practical difference (especially using the modified ALE algorithm) is that ALE models foci as 3‐D Gaussians, where MKDA uses spheres. We prefer Gaussians because they are sensible in the context of random field theory [Worsley et al.,1996], can be used to empirically model the influence of methodological factors on localization uncertainty, and give continuous probability estimates that optimize precision. Still, the differences between ALE and MKDA are small compared with the similarities between them, and the choice of technique matters less than the initial choice to perform a quantitative CBMA rather than an informal review.
Within‐Group Effects and the Modified Organizational Approach
In ALE and MKDA, one implicit assumption is that each experiment represents an independent source of activation foci, regardless of whether the experiments were reported in different papers or were performed by different subjects. This assumption is likely valid if multiple experiments reported by a single paper recruit different cognitive processes, but may become problematic when they are similar in terms of the cognitive constructs they engage. If different subjects performed the experiments, they could be considered independent, but more often papers use a single group of subjects and either report multiple task contrasts, or report multiple analyses of a single task (e.g., subtraction versus correlation with an external variable). This issue is exemplified by the original ALE dataset (the reading dataset reanalyzed here) [Turkeltaub et al.,2002]. One paper reported four similar reading tasks for the same subjects. Many of the foci were colocalized between tasks, representing redundant activations due to repeated recruitment of the same cognitive operations. To include as many tasks as possible in the analysis, all of the experiments (tasks) were included in the dataset, allowing this group of subjects to influence ALE values to a greater degree than others. Using the current ALE algorithm, the only way to address this problem is to stipulate that only one experiment from a given group of subjects can be included in a dataset, but this approach excludes potentially informative results.
The modified ALE algorithm and organizational approach outlined here address this concern, and allow the entire spatial distribution of activations in a paper to be represented because individual experiments need not be excluded. When we evaluated the impact of this alternate grouping strategy, we found that cumulative ALE values were reduced by 7–9%. This demonstrates that within‐group effects in ALE analyses may be greater than within‐experiment effects, but still account for a relatively small proportion of ALE values. The cumulative impact of both within‐experiment and within‐group effects on previously published ALE values was approximately 10% by this measure.
Reflecting the small impact of within‐group effects on ALE results, the overall ALE maps were quite similar between the two grouping strategies, and all of the large clusters were significant regardless of the approach used. Organizing by subject group was more conservative in terms of the extent of clusters, and small clusters that derived mainly from concordance within subject groups were eliminated. The relative ALE values of significant clusters also changed in some cases, such that ALE values better reflected concordance of foci across independent reports. Removing within‐group effects reduced MA values in the null distributions, and unmasked small clusters derived from multiple unique subject groups. On the basis of these results, we feel that for most standard meta‐analyses, organizing datasets by subject group is more conservative than organizing by experiment, and optimizes the degree to which ALE values quantify concordance across the literature. Although we were specifically interested in ALE here, the same principles apply to MKDA, and we suggest that organizing foci by subject group in most MKDA analyses would be optimal as well.
Grouping foci by subject group may not be appropriate for all types of meta‐analyses however. Above, we considered “typical” meta‐analyses that aim to quantify consistency in localization of cognitive constructs or neural processing units. In contrast to these analyses, grouping foci by experiment is appropriate for meta‐analytic connectivity mapping (MACM) studies that examine patterns of coactivation across a variety of tasks [Eickhoff et al.,2010; Robinson et al.,2010; Smith et al.,2009]. In these cases, organizing foci by subject group could result in apparent coactivation of areas that actually occurred during different experiments. In a hypothetical example, one paper may report a finger‐tapping task that activated primary motor cortex only, and a separate visual task that activated primary visual cortex only. If these foci were grouped together, both the motor and visual activity would be represented in the same MA map, resulting in apparent functional connectivity even though none was present in the original data. Thus, to preserve the co‐occurrence structure of foci, they must be organized by experiment rather than subject group.
CONCLUSIONS
We confirmed that within‐experiment concordance can impact MA values using the standard algorithm, but found that removing these effects using the modified algorithm produced negligible differences in ALE maps. Within‐group effects had a small impact on ALE values; removing them by organizing foci according to subject group improved the degree to which ALE values represent colocalization across the literature, and made ALE maps more conservative. Overall, differences between ALE results using these approaches were small relative to the similarities between them. This finding validates previously published ALE analyses against concerns that they were driven largely by within‐experiment or within‐group effects. Still, we suggest that the modified ALE algorithm presented here is theoretically advantageous compared with the current algorithm, and that organizing foci by subject group rather than experiment is the more conservative and appropriate approach for most analyses using ALE or MKDA.
REFERENCES
- Binder JR, Desai RH, Graves WW, Conant LL ( 2009): Where is the semantic system? A critical review and meta‐analysis of 120 functional neuroimaging studies. Cereb Cortex 19: 2767–2796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caspers S, Zilles K, Laird AR, Eickhoff SB ( 2010): ALE meta‐analysis of action observation and imitation in the human brain. NeuroImage 50: 1148–1167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chouinard PA, Goodale MA ( 2010): Category‐specific neural processing for naming pictures of animals and naming pictures of tools: An ALE meta‐analysis. Neuropsychologia 48: 409–418. [DOI] [PubMed] [Google Scholar]
- Di X, Chan RC, Gong QY ( 2009): White matter reduction in patients with schizophrenia as revealed by voxel‐based morphometry: An activation likelihood estimation meta‐analysis. Progress in neuro‐psychopharmacology and biological psychiatry 33: 1390–1394. [DOI] [PubMed] [Google Scholar]
- Eickhoff SB, Laird AR, Grefkes C, Wang LE, Zilles K, Fox PT ( 2009): Coordinate‐based activation likelihood estimation meta‐analysis of neuroimaging data: A random‐effects approach based on empirical estimates of spatial uncertainty. Hum brain Mapp. 30:2907–2926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff SB, Jbabdi S, Caspers S, Laird AR, Fox PT, Zilles K, Behrens TE ( 2010): Anatomical and functional connectivity of cytoarchitectonic areas within the human parietal operculum. J Neurosci 30: 6409–6421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferreira LK, Diniz BS, Forlenza OV, Busatto GF, Zanetti MV ( 2009): Neurostructural predictors of Alzheimer's disease: A meta‐analysis of VBM studies. Neurobiol Aging. DOI: 10.1016/j.neurobiolaging.2009.11.008. [DOI] [PubMed] [Google Scholar]
- Glahn DC, Laird AR, Ellison‐Wright I, Thelen SM, Robinson JL, Lancaster JL, Bullmore E, Fox PT ( 2008): Meta‐analysis of gray matter anomalies in schizophrenia: Application of anatomic likelihood estimation and network analysis. Biol Psychiatry 64: 774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlsgodt KH, Kochunov P, Winkler AM, Laird AR, Almasy L, Duggirala R, Olvera RL, Fox PT, Blangero J, Glahn DC ( 2010): A multimodal assessment of the genetic control over working memory. J Neurosci 30: 8197–8202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird AR, Fox PM, Price CJ, Glahn DC, Uecker AM, Lancaster JL, Turkeltaub PE, Kochunov P, Fox PT ( 2005): ALE meta‐analysis: controlling the false discovery rate and performing statistical contrasts. Hum Brain Mapp 25: 155–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird AR, Robbins JM, Li K, Price LR, Cykowski MD, Narayana S, Laird RW, Franklin C, Fox PT ( 2008): Modeling motor connectivity using TMS/PET and structural equation modeling. NeuroImage 41: 424–436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird AR, Eickhoff SB, Li K, Robin DA, Glahn DC, Fox PT ( 2009a): Investigating the functional heterogeneity of the default mode network using coordinate‐based meta‐analytic modeling. J Neurosci 29: 14496–14505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird AR, Lancaster JL, Fox PT ( 2009b): Lost in localization? The focus is meta‐analysis. NeuroImage 48: 18–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maisog JM, Einbinder ER, Flowers DL, Turkeltaub PE, Eden GF ( 2008): A meta‐analysis of functional neuroimaging studies of dyslexia. Ann N Y Acad Sci 1145: 237–259. [DOI] [PubMed] [Google Scholar]
- Minzenberg MJ, Laird AR, Thelen S, Carter CS, Glahn DC ( 2009): Meta‐analysis of 41 functional neuroimaging studies of executive function in schizophrenia. Arch Gen Psychiatry 66: 811–822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson JL, Laird AR, Glahn DC, Lovallo WR, Fox PT ( 2010): Metaanalytic connectivity modeling: Delineating the functional connectivity of the human amygdala. Hum Brain Mapp 31: 173–184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Filippini N, Watkins KE, Toro R, Laird AR, Beckmann CF ( 2009): Correspondence of the brain's functional architecture during activation and rest. Proc Natl Acad Sci USA 106: 13040–13045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spreng RN, Wojtowicz M, Grady CL ( 2010): Reliable differences in brain activity between young and old adults: A quantitative meta‐analysis across multiple cognitive domains. Neurosci Biobehav Rev 34: 1178–1194. [DOI] [PubMed] [Google Scholar]
- Turkeltaub P, Eden G, Jones K, Zeffiro T ( 2002): Meta‐analysis of the functional neuroanatomy of single‐word reading: Method and validation. Neuroimage 16( 3 Part 1): 765–780. [DOI] [PubMed] [Google Scholar]
- Turkeltaub PE, Coslett HB ( 2010): Localization of sublexical speech perception components. Brain Lang 114: 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vytal K, Hamann S ( 2010): Neuroimaging support for discrete neural correlates of basic emotions: A voxel‐based meta‐analysis. J Cogn Neurosci 22:2864–2885. [DOI] [PubMed] [Google Scholar]
- Wager TD, Jonides J, Reading S ( 2004): Neuroimaging studies of shifting attention: A meta‐analysis. NeuroImage 22: 1679–1693. [DOI] [PubMed] [Google Scholar]
- Wager TD, Lindquist M, Kaplan L ( 2007): Meta‐analysis of functional neuroimaging data: Current and future directions. Social Cogn Affect Neurosci 2: 150–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wager TD, Lindquist MA, Nichols TE, Kober H, Van Snellenberg JX ( 2009): Evaluating the consistency and specificity of neuroimaging data using meta‐analysis. NeuroImage 45( 1 Suppl): S210–S221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiener M, Turkeltaub P, Coslett HB ( 2010): The image of time: A voxel‐wise meta‐analysis. NeuroImage 49:1728–1740. [DOI] [PubMed] [Google Scholar]
- Worsley KJ, Marrett S, Neelin P, Vandal AC, Friston KJ, Evans AC ( 1996): A unified statistical approach for determining significant signals in images of cerebral activation. Hum Brain Mapp 4: 58–73. [DOI] [PubMed] [Google Scholar]
- Zevin JD, Yang J, Skipper JI, McCandliss BD ( 2010): Domain general change detection accounts for "dishabituation" effects in temporal‐parietal regions in functional magnetic resonance imaging studies of speech perception. J Neurosci 30: 1110–1117. [DOI] [PMC free article] [PubMed] [Google Scholar]


