Abstract
Recent studies have revealed that linkage disequilibrium (LD) patterns vary across the human genome with some regions of high LD interspersed by regions of low LD. A small fraction of SNPs (tag SNPs) is sufficient to capture most of the haplotype structure of the human genome. In this paper, we develop a method to partition haplotypes into blocks and to identify tag SNPs based on genotype data by combining a dynamic programming algorithm for haplotype block partitioning and tag SNP selection based on haplotype data with a variation of the expectation maximization (EM) algorithm for haplotype inference. We assess the effects of using either haplotype or genotype data in haplotype block identification and tag SNP selection as a function of several factors, including sample size, density or number of SNPs studied, allele frequencies, fraction of missing data, and genotyping error rate, using extensive simulations. We find that a modest number of haplotype or genotype samples will result in consistent block partitions and tag SNP selection. The power of association studies based on tag SNPs using genotype data is similar to that using haplotype data.
Linkage disequilibrium (LD), which refers to the nonrandom association of alleles at different loci (Lewontin 1964) in haplotypes, plays a central role in genome-wide association studies for identifying genetic variation responsible for common diseases (Risch and Merikangas 1996; Kruglyak 1999; Nordborg and Tavaré 2002; Weiss and Clark 2002). Compared with traditional linkage studies, association studies based on LD have two major advantages. First, only unrelated individuals need to be genotyped, which makes it possible to study a large number of individuals. Second, because LD reflects a large number of historical recombination events, rather than just those in a pedigree, it is possible to fine-map disease-causing mutations. Single nucleotide polymorphisms (SNPs) are preferred to other genetic markers, such as microsatellites, because of their high abundance, relatively low mutation rate, and easy adaptability to automatic genotyping.
The number of SNPs required for a genome-wide association study depends on the pattern of LD. The more rapid the decay of LD, the more SNPs that are needed. Previous studies have shown substantial variation in LD pattern across the human genome (Dunning et al. 2000; Taillon-Miller et al. 2000; Eisenbarth et al. 2001; Reich et al. 2002). The number of SNPs needed for a genome-wide association study has been greatly debated in recent years. The estimations by either simulations (Kruglyak 1999) or empirical studies (e.g., Reich et al. 2002) based on LD showed substantial variations. Recent studies showed that LD pattern varies greatly across the human genome with some regions of high LD interspersed by regions of low LD (Daly et al. 2001; Johnson et al. 2001; Patil et al. 2001; Dawson et al. 2002; Gabriel et al. 2002). These high LD regions are referred to as blocks in the literature. Only a small number of characteristic (“tag”) SNPs is sufficient to capture most of haplotype structure of the human genome in high LD regions (Johnson et al. 2001; Patil et al. 2001). Thus, genotyping effort could be greatly reduced without much loss of power for association studies (Zhang et al. 2002a).
Many methods have been developed to identify haplotype blocks and corresponding tag SNPs (Patil et al. 2001; Gabriel et al. 2002; Wang et al. 2002; Zhang et al. 2002b; Anderson and Novembre 2003; Koivisto et al. 2003). Some of these methods assume that the individual haplotype phase has already been resolved in advance. Although laboratory techniques, such as allele-specific long-range PCR (MichlataosBeloin et al. 1996) or diploid-to-haploid conversion (Papadopolous et al. 1995; Yan et al. 2000; Douglas et al. 2001), have been used to determine haplotypes in diploid individuals, these approaches are technologically demanding and cost-prohibitive, which makes it extremely difficult to carry out a large-scale study across the whole genome such as the one reported by Patil et al. (2001). As a consequence, in large-scale projects such as the HapMap project, only genotype data will be generated in many projects. It is thus necessary to develop methods to directly extract LD patterns from genotype data. In this paper, we combine the dynamic programming algorithms for haplotype block partitioning and tag SNP selection (Zhang et al. 2002b) and a partition-ligation–expectation-maximization (PL-EM) algorithm for haplotype inference (Qin et al. 2002) to infer the haplotype block structure from genotype data.
The accuracy of haplotype inference using the expectation-maximization (EM) algorithm depends on several factors including sample size, number of SNPs, allele frequency, fraction of missing data, genotyping error rate, and LD between these SNPs, which have been extensively studied both in simulation studies (Fallin and Schork 2000; Kirk and Cardon 2002) and with molecular haplotype data (Tishkoff et al. 2000). When statistically inferred haplotypes from genotype data are used in haplotype block determination and tag SNP selection, these factors will certainly affect the results of the block partitioning and tag SNP selection. More importantly, these factors themselves also affect the usage of the identified tag SNPs in association studies. In this paper, we conduct extensive simulations to study the effects of factors such as the sample size, the allele frequency, the number or density of SNPs, the fraction of missing data, and the genotyping error rate on haplotype block partitioning and tag SNP selection based on both haplotype and genotype data.
METHODS
Haplotype Block Partitioning and Tag SNP Selection Based on Genotype Data
Several methods have been developed for haplotype block partitioning and tag SNP selection based on haplotype data or genotype data (Daly et al. 2001; Patil et al. 2001; Gabriel et al. 2002; Wang et al. 2002; Zhang et al. 2002b). Available methods can be classified into two categories. In the first category, haplotype blocks are first obtained based on a pairwise LD pattern (Gabriel et al. 2002) or a four-gamete test (Wang et al. 2002). Tag SNPs are then selected as a followup study in each resulting block. In the second group, the objective is to minimize the total number of tag SNPs over a region of interest or the whole genome (Patil et al. 2001; Zhang et al. 2002b). Haplotype blocks are used as a tool to achieve this objective. The algorithms developed in Patil et al. (2001) and Zhang et al. (2002b) can only be applied to haplotype data. In this paper, we follow the second group of methods and extend the algorithms to genotype data.
In the dynamic programming algorithm for haplotype block partitioning and tag SNP selection based on haplotype data, Zhang et al. (2002b) used the following recursive formula:
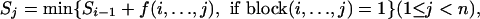 |
where f(i,..., j) is the number of tag SNPs in this block, block(i,..., j) is a Boolean function, and block(i,..., j) = 1 if and only if SNP (i,..., j) can form a block, Sj is the minimum number of tag SNPs for the optimal haplotype block partition of the first j SNPs, and S0 = 0. Any criteria for defining blocks and tag SNPs can be incorporated in this algorithm. For simplicity of presentation, the definitions of blocks and tag SNPs in Patil et al. (2001) were used. As in Patil et al. (2001), we define a consecutive set of SNPs of size one or larger as a block if the common haplotypes account for at least α percent of all the observed haplotypes, where the common haplotypes refer to those with frequency no less than β. Tag SNPs in a block are selected to minimize the number of SNPs that can distinguish at least α percent of all the observed haplotypes. The block partition with the minimum total number of tag SNPs can be obtained by backtracking.
The basic idea for haplotype block partitioning using genotype data can be described as follows. For each consecutive set of SNPs, the frequencies of haplotypes are inferred using an EM algorithm and are used in block identification and tag SNP selection. It is worth noting that we infer haplotypes and their frequencies for each consecutive set of SNPs that can form a potential block, rather than for the entire set of SNPs.
Many methods have been developed to infer haplotypes based on genotypes of unrelated individuals. These methods can be divided into those based on combinatorics (Clark 1990; Gusfield 2001, 2002) and those based on statistics (Excoffier and Slatkin 1995; Hawley and Kidd 1995; Long et al. 1995; Stephens et al. 2001; Lin et al. 2002; Niu et al. 2002; Qin et al. 2002). For methods based on combinatorics, the two haplotypes of an individual are directly assigned and the frequencies of haplotypes are estimated based on assigned haplotypes. For statistics-based methods, the haplotype frequencies are first estimated, and then two haplotypes are assigned to each individual genotype according to the likelihood function based on an underlying model. There are still debates about the optimal methods for inferring haplotype frequencies and reconstructing haplotypes of individuals, but some evidence suggests that statistics-based methods tend to be more robust (Niu et al. 2002). Here we combine the haplotype-based dynamic programming algorithm for haplotype block partition with the partition-ligation–expectation-maximization (PL-EM) algorithm for haplotype inference (Qin et al. 2002). In the PL-EM algorithm, all of the SNP loci are broken down into “atomistic” units that only contain several SNPs (usually five to eight SNPs) and have one or two common SNPs with adjacent units. The standard EM algorithm is first used within each unit to infer the haplotype frequencies and haplotype pairs forming a genotype, then two adjacent partial haplotypes are “ligated” using the EM algorithm again. In general, the EM algorithm is time- and space-efficient only for a small number of SNP markers. Thus, this strategy could solve the speed and memory constraint of canonical EM algorithms and makes it suitable for large-scale recovery of haplotypes from genotype data.
For clarity, the algorithm combining the dynamic programming algorithm and the PL-EM algorithm for haplotype block partitioning based on genotype data is outlined below:
Let S0 = 0 and start from j = 1 and i = j.
Use the PL-EM algorithm to infer the haplotype frequencies and the haplotypes carried by each individual for the consecutive set of SNPs (i,..., j).
Determine if the SNPs (i,..., j) can form a block based on the estimated haplotypes carried by each individual in step 2. Calculate the Boolean function block(i,..., j).
If block(i,..., j) = 1, calculate f(i,..., j) and let Sj = Si - 1 + f(i,..., j) if i = j or Sj = min{Sj, Si - 1 + f(i,..., j)} if i < j.
If block(i,..., j) = 1 and i > 1, let i = i - 1 and go to step 2.
If block(i,..., j) = 0 or i = 1, let j = j + 1 and i = j. If j ≤ n (the total number of SNPs), go to step 2; otherwise, stop and use the recursion to find the blocks and the corresponding tag SNPs.
To infer the haplotype phase from large-scale genotype data, Eskin et al. (2003) combined a local haplotype prediction algorithm and a dynamic programming algorithm to determine the block boundaries directly from the genotype data. In their local haplotype prediction algorithm, they determined a set of possible haplotypes that appear in samples based on imperfect phylogeny (Gusfield 2002), in which the number of distinct haplotypes is much less than the number of distinct haplotypes that are compatible with genotypes of samples. This makes it possible to estimate the frequency of these haplotypes using the EM algorithm for a relative large number of SNPs. When applying their method to a real data set of Daly et al. (2001), they searched all possible blocks consisting of up to 30 SNPs using their haplotype prediction algorithm and obtained blocks by minimizing the total number of tag SNPs using a dynamic programming algorithm. However, it is not clear if their local haplotype prediction algorithm could be extended to predict haplotypes for a large number of SNPs, especially for more than 100 SNPs. In this situation, the decreased number of haplotypes that are compatible with imperfect phylogeny could be too large to be handled by the canonical EM algorithm. Our current implementation of the PL-EM algorithm can predict haplotypes of ∼100 individuals for up to 250 SNPs, and it can be further scaled up with more efficient coding and parallel computers. This scale should be large enough for most studies.
The Coalescent Process With Recombination
We simulate a large number of haplotypes consisting of many consecutive SNPs across a genomic region, using the coalescent process with recombination based on the neutral Wright-Fisher model of genetic variation (Hudson 1983; Kaplan and Hudson 1985; Griffiths and Marjoram 1997). In each simulation, the genealogies of 2000 haplotypes are generated with a population recombination rate r over the region of interest. It is known that recombination hot and cold spots can give rise to discrete block-like patterns (Jeffreys et al. 2001; Schneider et al. 2002). However, empirical studies and simulations indicate that haplotype blocks can also arise in the absence of recombination hot spots (Wang et al. 2002; Philips et al. 2003). Thus, we first assume that recombination occurs uniformly over the region. For simplicity of exposition, we denote the region of interest by the interval [0, 1]. Once the ancestral relationship among haplotypes is generated, SNPs are added using an infinite-many-sites model with a population mutation rate θ. The infinite-many-sites model assumes that mutations occur uniformly in [0,1], and a new mutation creates a new SNP that does not exist in the population yet; recurrent mutations are not allowed. In our simulations, we set both r and θ equal to 200. These parameters correspond roughly to 200 kb in the human genome (Nordborg and Tavaré 2002). We simulate a total of 20 data sets for our study.
The above simulations are based on a constant population size model with uniform recombination rate and may not accommodate all features of human evolution. To assess the consequences of departure from these assumptions for our method, we use a modified program of Hudson to simulate two additional data sets. First, we simulate 20 populations with recombination hot spots. In each population, we randomly select five regions with recombination rates 10–15 times higher than the background recombination rate. Each region spans 2% of the region of the interest. Second, we simulate 20 populations with recent population expansion. We assume that the population was constant at size 10,000 for a very long period of time and began exponentially growing until the present population size of 107 from 1500 generations ago. In the rest of this paper, we simply refer to the population without recombination hot spots and constant population size, the population with recombination hot spots only and the population with expansion only as P0, P1, and P2, respectively.
Setting of Factors
We study how factors, including the number of haplotypes, the density and minor allele frequency of SNPs, the fraction of missing data, and the genotyping error rate, affect the block partitioning, tag SNP selection, and power of association studies based on both haplotype and genotype data. These factors are set as follows. The number of haplotypes is fixed at 20, 50, 80, and 100 (corresponding to 10, 25, 40, and 50 individuals when using genotype data), respectively. The minimum distance between two adjacent SNPs varies from 0.0025, 0.005, 0.01, to 0.025, which is equivalent to ∼1 SNP per 0.5 kb, 1 kb, 2 kb, and 5 kb, respectively. We also constrain the lower bound of the minor allele frequency of SNPs used in block partitioning to be at least 0.01, 0.05, 0.10, 0.15, and 0.20. We first choose a set of SNPs such that any two adjacent SNPs are separated by at least a given distance. Then each SNP is kept in the set based on its minor allele frequency in the simulated populations (estimated from 2000 haplotypes) rather than its minor allele frequency in each selected sample set. Therefore, for a given density of SNPs, the set containing only common SNPs is the subset of the one that also contains rare SNPs. This design allows us to investigate the effect of allele frequency in block identification and tag SNP selection. However, many rare SNPs will not be polymorphic if the sample size is relatively small. The missing rate is set at 1%, 2%, 5%, and 10%, respectively. The genotyping error rate varies from 0.5%, 1%, 2%, to 5%, comparable with assessment of genotyping error in different technologies and experimental designs.
Power Analysis
It is important to define an appropriate metric or statistic to measure the success of the algorithm as well as the effects of the variables we adjust. Because the primary reason for the current interest in block partitioning is to reduce the genotyping expense in association studies, we quantify our comparison results through power analysis (Zhang et al. 2002a). Specifically, we follow the procedures in Zhang et al. (2002a) to compare the power in association studies for five different sets of SNPs: (1) the SNPs that are used in block partitioning and tag SNP selection; (2) the tag SNPs obtained by the haplotype data with our method; (3) the same number of randomly selected SNPs as in set 2; (4) the tag SNPs identified by the genotype data; and (5) the same number of randomly selected SNPs as in set 4.
In this paper, we choose a marker locus as the disease locus in simulated haplotype data if it satisfies two conditions: (1) the frequency of the minor allele is between 0.125 and 0.175; and (2) the position of the marker is between 0.45 and 0.55. The first condition restricts the disease allele frequency, and the second condition constrains that the disease locus is approximately in the middle of the region of interest. This marker will not be used in the mapping and the haplotype block partitioning. In the second step, we generate case-control and case-parent samples according to a multiplicative disease model. The penetrance for genotypes dd, dD, and DD is c, cγ, and cγ2, respectively, where c is the phenocopy rate and γ is the genotype relative risk. D and d are the high- and low-risk alleles, respectively, at the disease locus. We simply set γ = 4 and c = 0.024 here, which can be computed with a disease prevalence of 0.05 and a disease allele frequency of 0.15. For case-control design, we generate 100 cases and 100 controls. For family design, we generate 100 affected individuals with their parents. In the third step, we identify the haplotype blocks and the tag SNPs based on the subsamples and analyze the data using the five sets of SNPs as discussed in the previous paragraph. In our statistical analysis, we use both individual SNPs and two-locus haplotypes and use the Bonferroni correction to adjust the p-value. For individual SNP analysis, the standard χ2 statistic for the case-control design (Olson and Wijsman 1994) and the TDT method for family data (Spielman et al. 1993) are used, respectively. For two-locus haplotype analysis, the methods proposed by Zaykin et al. (2002) and Zhao et al. (2000) are implemented for case-control samples and family samples, respectively. At last, we repeat the above procedures 50 times for each haplotype data set to obtain a total of 1000 replicates to compare the power using different sets of SNPs. We only report the results based on two-locus haplotype analysis. The results based on individual SNP analysis are similar to the results based on haplotype analysis except that the power is lower in all the scenarios we studied here (data not shown). As noted before (Zhang et al. 2002a), the lower power of individual SNP analysis compared with haplotype analysis is due to our simulation model. If the disease locus is one of the tag SNPs, individual SNP analysis can be more powerful than haplotype analysis.
Other statistics, including the total number of tag SNPs, the total number of SNPs used in block partitioning and tag SNP selection, and the number of blocks, are recorded as additional measures for the detailed study.
RESULTS
Application to a 5q31 Data Set
Daly et al. (2001) studied a 500-kb region on human Chromosome 5q31 that may contain a genetic variant responsible for Crohn disease, by genotyping 103 SNPs with minor allele frequency at least 5% for 129 triads. A total of 258 transmitted and 258 untransmitted haplotypes were determined. Based on these haplotypes, they found that the region could be divided into 11 blocks. In each block, at most four common haplotypes account for >90% of the observed haplotypes.
To test our algorithm, only the genotypes of the offspring are used. Here, we require that the tag SNPs in a block are the minimal set of SNPs that can distinguish at least α percent of all the haplotypes. The common haplotypes in this application are those with frequency at least β percent. We vary α as 80% or 90% and β as 5% or 10%, respectively. The number of tag SNPs, the number of blocks, and the number of SNPs in the largest block for different α and β are given in Table 1. As expected, the number of tag SNPs and the number of blocks increase with the increase of α and β. However, the effect of α is much greater than the effect of β in block partitioning and tag SNP selection. When α is raised from 80% to 90%, the number of tag SNPs increases from 13 to 26 (100%) and from 16 to 28 (75%) based on β = 5% and β = 10%, respectively. When β is raised from 5% to 10%, the number of tag SNPs only increases by 3 (23%) and 2 (8%) for α = 80% and α = 90%, respectively.
Table 1.
The Block Partitioning Results Using Different α and βa
| α | β | Number of tag SNPs | Number of blocks | Number of SNPs in the largest blocks |
|---|---|---|---|---|
| 80% | 5% | 13 | 10 | 36 |
| 10% | 16 | 13 | 28 | |
| 90% | 5% | 26 | 12 | 23 |
| 10% | 28 | 19 | 21 |
Based on the genotypes of the offspring in Daly et al (2001)
It is important to compare the block partition results using haplotype data and those using genotype data. We infer the transmitted haplotypes and untransmitted haplotypes from genotypes of the parents–offspring trios at each SNP independently. When the genotypes of the father, mother, and offspring at a locus are all available, we can uniquely infer the transmitted allele and untransmitted allele except when they have the same heterozygous genotype. If we cannot infer the transmitted allele at an SNP locus, we treat it as missing data. The number of tag SNPs and the number of blocks are 13 and 14 based on haplotype data using α = 80% and β = 10%, respectively. These numbers are very close to those obtained using genotype data.
Figure 1 shows the positions of boundary SNPs in blocks obtained by our dynamic programming algorithm for different α and β, using either the genotype data or the haplotype data. The block boundaries reported by Daly et al. (2001) are also given, in which we include several single SNPs that were dropped out from their original blocks and connect them to the adjacent SNPs by lines. From Figure 1, we can see that most of the blocks produced by the dynamic programming algorithm are consistent with those produced by Daly et al. (2001). Comparing with the D′ patterns displayed by GOLD (Abecasis and Cookson, 2002; figure not shown), most of the block boundaries fall into regions with low D′. Here we do not use a rigorous statistical measure to compare the block partitions. We point out that different haplotype block partition algorithms do not give the same results as they use different criteria to create the block partitions.
Figure 1.
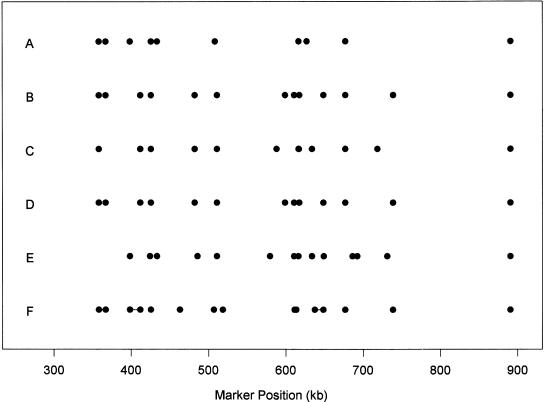
The positions of the ending SNPs in blocks. (A–D) Genotype data are used. (A) α = 80%, β = 5%; (B) α = 80%, β = 10%; (C) α = 90%, β = 5%; (D) α = 90%, β = 10%; (E) α = 80%, β = 10% with the haplotype data. (F) The blocks reported in Daly et al. (2001), where lines indicate regions not in their blocks.
The Effects of Sample Size, Minor Allele Frequency, SNP Density, Missing Data, and Genotyping Error on Block Partition and Tag SNP Selection
In this section, we assess how factors, including the number of haplotypes, SNP density, minor allele frequency of SNPs, the fraction of missing data, and the genotyping error rate, affect the block partition results using haplotype data as well as genotype data. The two parameters α and β used in the dynamic programming algorithm are set at 80% and 10%, respectively.
Sample Size
Table 2 shows the total number of SNPs used in the study and the number of tag SNPs based on different sample sizes and different SNP density on the basis of population P0. The minor allele frequency of the SNPs included in the study is at least 5%. For the same SNP density, by varying the number of haplotypes (20, 50, 80, and 100), Table 2 shows that the number of tag SNPs increases with the sample size, because many rare SNPs are not polymorphic in the small samples. The number of tag SNPs increases from 24 to 31 as the sample size increases from 20 to 80 using 103 SNPs and the haplotype data. Thus, sample size is an important factor for block detection and tag SNP selection. When the number of haplotypes is at least 50 (25 individuals), the number of tag SNPs is close to that obtained from 100 haplotypes. The number of tag SNPs and the number of blocks are almost identical for sample sizes 80 and 100. The number of tag SNPs identified using the genotype data is almost the same as that identified by using the haplotype data for the same sample size. Thus, we use at least 80 haplotypes (40 individuals) for the rest of study. This sample size is consistent with observations in Wang et al. (2002) and Thompson et al. (2003), in which they studied the effect of sample size based on other tag SNP selection methods.
Table 2.
The Results of Block Partitioning for Different Sample Sizes Based on Population P0 With α = 80% and β = 10%
| Number of haplotypes | Distance (kb) | No. of SNPs | Average no. of tag SNPs using haplotype | Average no. of tag SNPs using genotype |
|---|---|---|---|---|
| 20 | 1 | 103 | 23.7 | 23.9 |
| 50 | 29.5 | 29.5 | ||
| 80 | 30.8 | 30.7 | ||
| 100 | 31.1 | 31.0 | ||
| 20 | 2 | 56 | 15.1 | 15.2 |
| 50 | 18.1 | 18.0 | ||
| 80 | 18.7 | 18.6 | ||
| 100 | 18.9 | 18.9 |
SNPs with minor allele frequency >5% are used. The SNP density varies from one SNP per kilobase to 2 kb.
The Minor Allele Frequency
Figure 2 shows the power using SNPs with different minor allele frequencies for different tests and populations. The density is set as one SNP per kilobase. Several conclusions emerge from this figure. First, for family-based design, the power using tag SNPs is generally less than the power using all SNPs, but greater than the power using the same number of randomly selected SNPs. This is true for all three populations. For case-control design, the power using tag SNPs can be higher than the power using all SNPs. This is probably caused by the relative large number of degrees of freedom when all the SNPs are used. This result is consistent with the results in Thompson et al. (2003). Second, the power using tag SNPs decreases as the threshold for minor allele frequency increases because fewer and fewer tag SNPs are being used. However, we note that the decrease of power is small. Third, the power using tag SNPs identified by the haplotype data is almost the same as the power using tag SNPs identified using the genotype data.
Figure 2.
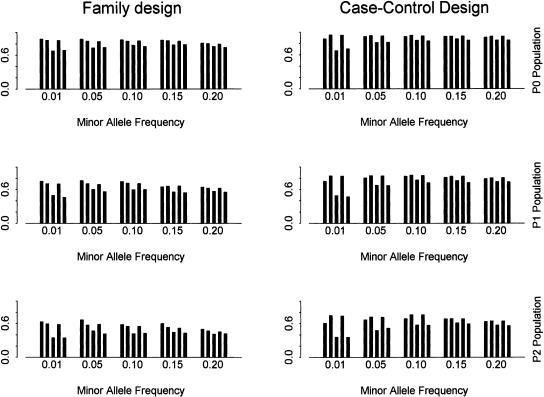
The power using SNPs with different minor allele frequencies with α = 80% and β = 10%. The SNP density is set as one SNP per kilobase. The power is obtained using two-locus haplotype data. In each bin (i.e., for each minor allele frequency), it shows the power using (from left to right): (1) all SNPs for block partitioning and tag SNP selection; (2) tag SNPs identified by the haplotype data; (3) the same number of random SNPs as in set 2; (4) tag SNPs identified by the genotype data; (5) the same number of random SNPs as in set 4.
Figure 3 shows the total number of SNPs, the number of tag SNPs identified by the haplotype data, and the number of tag SNPs identified by the genotype data for different populations. We notice that the number of tag SNPs identified decreases as the threshold for minor allele frequency increases because fewer and fewer SNPs are used. However, the difference between them is very small compared with that of the number of SNPs included in the study. For example, when the threshold for minor allele frequency is changed from 0.01 to 0.05, then to 0.15, with the approximate density of one SNP per kilobase, the total number of SNPs decreases from 162 to 100, then to 61, whereas the number of tag SNPs only decreases from 34 to 33, then to 31 for population P0. This result suggests that the blocks and tag SNPs could be reliably identified by common SNPs. The number of tag SNPs identified by the genotype data is slightly less than the number of tag SNPs identified by the haplotype data, and such a difference is within two SNPs. At last, we note that the power and the number of tag SNPs are different for different populations. More tag SNPs are needed, and the power of association study drops moderately with the inclusion of the recombination hot spots and the population expansion in our simulations. As an example, the number of tag SNPs is 29, 31, and 32 for populations P0, P1, and P2 with minor allele frequency >5% and a density of 1 kb per SNP. The power using the two-locus haplotype TDT method for the tag SNPs is 0.86, 0.76, and 0.60 for the three populations. Both recombination hot spots and population growth decrease LD in the region with a high recombination rate. Therefore, more tag SNPs are needed, and the power of an association study decreases as more recombination hot spots are introduced and the effective population size increases.
Figure 3.
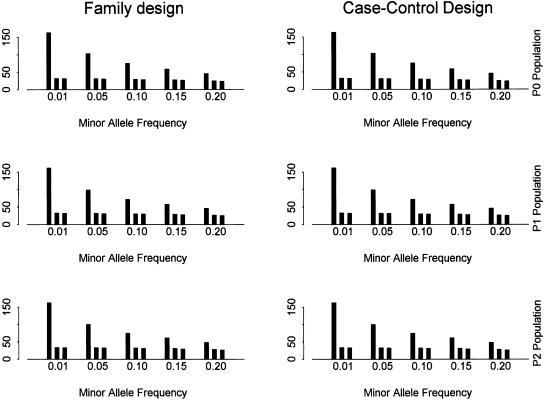
The number of SNPs and tag SNPs for different minor allele frequencies with α = 80% and β = 10%. The SNP density is set as one SNP per kilobase. In each bin (i.e., for each minor allele frequency), it shows the number of (from left to right) (1) all SNPs for block partitioning and tag SNP selection; (2) tag SNPs identified by the haplotype data; (3) tag SNPs identified by the genotype data.
The SNP Density and the Genotype Missing Rate
Figure 4 shows the power using SNPs with different SNP density for different tests and populations. The lower bound of minor allele frequency is set as 0.05. Correspondingly, Figure 5 shows the total number of SNPs, the number of tag SNPs identified by the haplotype data, and the number of tag SNPs identified by the genotype data. Similar patterns as in the above subsection are observed. In addition, the power and the number of tag SNPs drop quickly when the SNP density decreases as fewer and fewer SNPs are included. This observation has important implications for the HapMap project. The tag SNPs identified by this approach only explain the variation in other already typed SNPs, and may not explain the other (common) SNPs in the population. The decrease in the power of association studies is still substantial when the SNP density is decreased from one SNP per 0.5 kb to one SNP per 1 kb. The significant effect of SNP density on haplotype block partition and tag SNP selection has also been observed in real SNP data sets (Cardon et al. 2003; Wall and Pritchard 2003).
Figure 4.
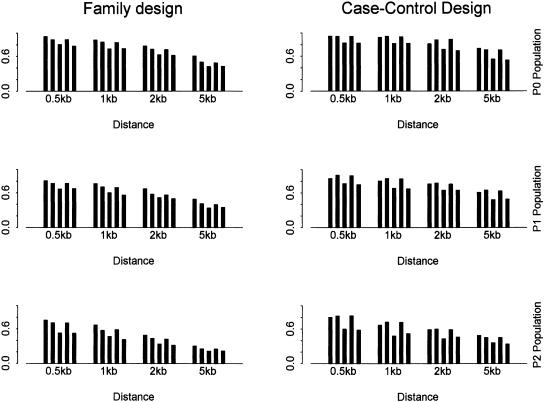
The power using SNPs with different density with α = 80% and β = 10%. SNPs with minor allele frequency >0.05 are used. The power is obtained using two-locus haplotype data. In each bin (i.e., distance between adjacent markers), it shows the power using (from left to right): (1) all SNPs for block partitioning and tag SNP selection; (2) tag SNPs identified by the haplotype data; (3) the same number of random SNPs as in set 2; (4) tag SNPs identified by the genotype data; (5) the same number of random SNPs as in set 4.
Figure 5.
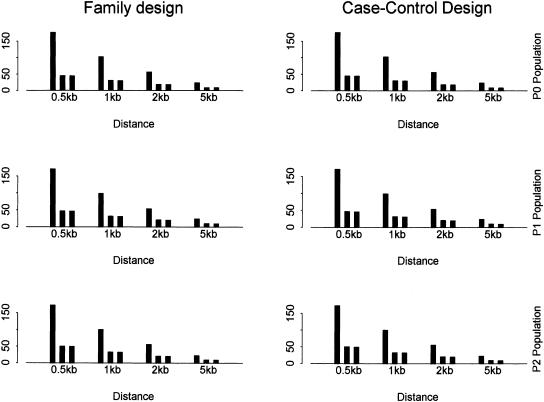
The number of SNPs and tag SNPs for different SNP density with α = 80% and β = 10%. SNPs with minor allele frequency >0.05 are used. In each bin (i.e., distance between adjacent markers), it shows the number of (from left to right) (1) all SNPs for block partitioning and tag SNP selection; (2) tag SNPs identified by the haplotype data; (3) tag SNPs identified by the genotype data.
To assess the effect of missing data on block partitioning and tag SNP selection, we use the following scheme to describe the single genotype reads being randomly missing in a sample. That is, an allele at each locus in a sample is randomly set as missing with a small probability. Figure 6 shows the power using SNPs with different missing rates for different tests and populations. The threshold of minor allele frequency is set as 0.05. The SNP density is set as one SNP per kilobase. Correspondingly, Figure 7 shows the total number of SNPs, the number of tag SNPs identified by the haplotype data, and the number of tag SNPs identified by the genotype data. The results with other minor allele frequencies and SNP density show similar patterns (data not shown). The power and the number of tag SNPs with and without moderate missing data are roughly the same, even at a missing rate of 10%.
Figure 6.
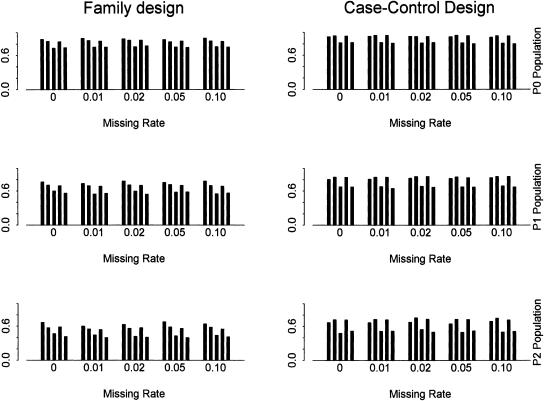
The power for different missing rates with α = 80% and β = 10%. SNPs with minor allele frequency >0.05 are used. The SNP density is set as one SNP per kilobase. The power is obtained using two-locus haplotype data. In each bin (i.e., genotype missing rate), it shows the power using (from left to right): (1) all SNPs for block partitioning and tag SNP selection; (2) tag SNPs identified by the haplotype data; (3) the same number of random SNPs as in set 2; (4) tag SNPs identified by the genotype data; (5) the same number of random SNPs as in set 4.
Figure 7.
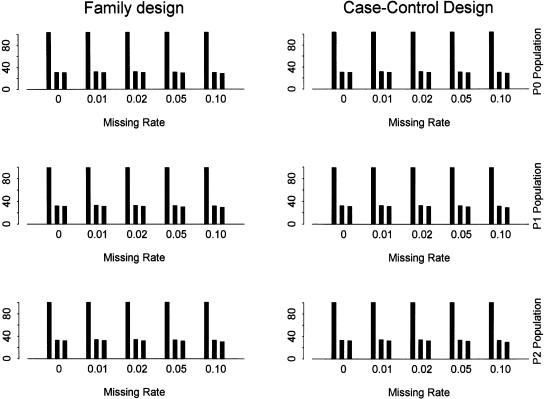
The number of SNPs and tag SNPs for different genotype missing rates with α = 80% and β = 10%. The SNPs with minor allele frequency >0.05 are used. The SNP density is set as one SNP per kilobase. In each bin (i.e., genotype missing rate), it shows the number of (from left to right) (1) all SNPs for block partitioning and tag SNP selection; (2) tag SNPs identified by the haplotype data; (3) tag SNPs identified by the genotype data.
Genotyping Errors
We next study the effects of genotyping errors on block partitioning and tag SNP selection. For each allele at a locus in a sample, we flip it to its complementary allele with a small probability equal to the genotyping error rate. The genotyping error rate varies from 0.5%, 1%, 2%, to 5%. The results for SNPs with minor allele frequency >5% and SNP density of one SNP per kilobase are reported in Table 3. When the genotyping error rate is <0.5%, the number of tag SNPs is very close to that without genotyping errors. The number of tag SNPs increases rapidly with the genotyping error rate. One possible reason is that genotyping errors can greatly reduce observed LD between SNPs.
Table 3.
The Results of Block Partitioning for Different Genotyping Error Rates Based on Population P0 With α = 80% and β = 10%
|
Family design
|
Population design
|
||||
|---|---|---|---|---|---|
| Genotyping error rate | No. of SNPs | Average no. of tag SNPs using haplotype | Average no. of tag SNPs using genotype | Average no. of tag SNPs using haplotype | Average no. of tag SNPs using genotype |
| 0% | 103 | 31 | 30 | 31 | 30 |
| 0.5% | 103 | 32 | 31 | 32 | 31 |
| 1% | 103 | 33 | 32 | 33 | 33 |
| 2% | 103 | 36 | 35 | 36 | 36 |
| 5% | 103 | 43 | 43 | 43 | 43 |
The SNPs with minor allele frequency >5% are used. The density of SNPs is set as one SNP per kilobase.
DISCUSSION
The observation of inhomogeneous LD patterns across the human genome suggests one possible way to reduce genotyping efforts in association studies. Zhang et al. (2002b) developed a dynamic program to minimize the total number of tag SNPs based on haplotype data. In general, haplotype data are difficult to obtain from experiments, especially in large-scale studies. Various algorithms have been developed to infer haplotypes from genotype data. By applying a novel partition-ligation scheme developed by Niu et al. (2002), Qin et al. (2002) deployed an EM-based approach, namely PL-EM, to enable efficient and accurate haplotype inference with a large number of SNP markers. We combine the dynamic programming algorithm and the PL-EM algorithm together for haplotype block partitioning and tag SNP selection based on genotype data. The method has been successfully tested using a real data set. We also show that our program for haplotype block partitioning and tag SNP selection based on genotype data gives similar results compared with those obtained based on haplotype data. Actually, the difference for the number of SNPs using haplotype data and genotype data is negligible under a wide range of scenarios for a moderate sample size even with missing data.
One naïve way to perform haplotype block partition and tag SNP selection based on genotype data is to estimate haplotype frequency and assign haplotypes to each individual from genotype data first, and then apply the block and tag SNP finding algorithm for haplotypes. However, for large regions with low LD, the EM algorithm is not accurate. It is desirable to use the strategy used in our algorithm. That is, to estimate the haplotype frequency and to assign haplotypes to each individual in each potential block. First, it has been shown that the accuracy can be improved when the block boundaries are incorporated in the PL-EM algorithm (Qin et al. 2002). Because we do not know the blocks in advance, a good strategy is to apply the PL-EM algorithm to each potential block. Second, the strategy used in our algorithm allows us to partition haplotype blocks and select tag SNPS in a genome-wide scale, whereas the EM algorithm will become infeasible to estimate the haplotype frequency for such a large number of SNPs involved.
In our algorithm to identify haplotype block and tag SNPs using genotype data, we estimate the frequency of haplotypes and assign haplotypes to each individual within all potential blocks rather than in the whole region. This idea can be applied to other algorithms for haplotype block partitioning, such as the dynamic programming algorithms for haplotype block partitioning with limited resources (Zhang et al. 2003). With minor modification of the PL-EM algorithm, it can also be extended to data obtained by pooling experiments that are developed for further reduction of genotyping expense in large-scale association studies (Sham et al. 2002). In DNA pooling, several individuals are genotyped in a single pool rather than a single individual. Then frequencies of alleles and haplotypes are estimated from a set of pooled genotypes. Comparing the overall cost of the different designs, Wang et al. (2003) found that that pooling of two individuals can be more cost-effective than individual genotyping, especially when a large number of SNPs are studied. It would further reduce the genotyping burden in association studies to combine tag SNPs with DNA pooling technology.
We investigate the influence of several factors on haplotype block partitioning and tag SNP selection. Our studies suggest that ∼80 haplotypes or 40 individuals are roughly enough to identify tag SNPs and blocks. Given the density of SNPs, the information loss of using only common SNPs is minor. The number of tag SNPs is essentially the same when more rare SNPs are included in the analysis. We also find that the most severe factors on haplotype block partitioning and tag SNPs' selection are the density of SNPs and the genotyping error rate. Although a relatively high fraction of missing data will result in loss of some rare haplotypes in the PL-EM algorithm, the effect is mild in haplotype block partitioning and tag SNP selection when the missing rate is <10%.
In this study, we use the coalescent theory to simulate the haplotypes. We first simulate populations with constant population size and homogeneous mutation and recombination rates. We also simulate two additional populations, one with recombination hot spots and the other with population expansion. Although the power and the number of tag SNPs are different across populations, their trends are the same. Our simulation still may not capture some features of human evolution, and therefore further studies of the influence of these factors on haplotype block partition and tag SNP selection using more complex simulations as well as real data sets are needed.
Acknowledgments
This work is partially supported by NSF DMS-0104129 and NIH HG02518 (Z.S.Q., J.S.L.) and NIH P50 HG 002790, NIH DK53392, NIH RR16522, NSF EIA-0112934, and the University of Southern California (K.Z., M.S.W., T.C., F.S.). We thank Peter Calabrese for providing his program to simulate the haplotype data with recombination hot spots. We also thank three anonymous reviewers for their thoughtful comments.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.1837404. Article published online before print in April 2004.
References
- Abecasis, G.R. and Cookson, W.O. 2000. GOLD—Graphical overview of linkage disequilibrium. Bioinformatics 16: 182-183. [DOI] [PubMed] [Google Scholar]
- Anderson, E.C. and Novembre, J. 2003. Finding haplotype block boundaries by using the minimum-description-length principle. Am. J. Hum. Genet. 73: 336-354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardon, L.R., Ke, X., Lawrence, R., Carter, N., Rogers, J., Stavrides, G., Willey, D., Mullikin, J., Hunt, S., Bentley, D.R., et al. 2003. Towards a fine-scale linkage disequilibrium map of human chromosome 20. Am. J. Hum. Genet. 73 (Suppl): 271.12844283 [Google Scholar]
- Clark, A.G. 1990. Inference of haplotypes from PCR-amplified samples of diploid populations. Mol. Biol. Evol. 7: 111-122. [DOI] [PubMed] [Google Scholar]
- Daly, M.J., Rioux, J.D., Schaffner, S.F., Hudson, T.J., and Lander, E.S. 2001. High-resolution haplotype structure in the human genome. Nat. Genet. 29: 229-232. [DOI] [PubMed] [Google Scholar]
- Dawson, E., Abecasis, G.R., Bumpstead, S., Chen, Y., Hunt, S., Beare, D.M., Pabial, J., Dibling, T., Tinsley, E., Kirby, S., et al. 2002. A first-generation linkage disequilibrium map of chromosome 22. Nature 418: 544-548. [DOI] [PubMed] [Google Scholar]
- Douglas, J.A., Boehnke, M., Gillanders, E., Trent, J.M., and Gruber, S.B. 2001. Experimentally-derived haplotypes substantially increase the efficiency of linkage disequilibrium studies. Nat. Genet. 28: 361-364. [DOI] [PubMed] [Google Scholar]
- Dunning, A.M., Durocher, F., Healey, C.S., Teare, M.D., McBride, S.E., Carlomoahno, F., Xu, C.F., Dawnson, E., Rhodes, S., Ueda, S., et al. 2000. The extent of linkage disequilibrium in four populations with distinct demographic histories. Am. J. Hum. Genet. 67: 1544-1554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisenbarth, I., Striedel, A.M., Moschgath, E., Vodel, W., and Assum, G. 2001. Long-range sequence composition mirrors linkage disequilibrium pattern in 1 1.13 MB region of human chromosome 22. Hum. Mol. Genet. 24: 2833-2839. [DOI] [PubMed] [Google Scholar]
- Eskin, E., Halperin, E., and Eskin, E. 2003. Large scale recovery of haplotypes from genotype data using imperfect phylogeny. In Proceedings of the Seventh Annual International Conference on Research in Computational Molecular Biology (RECOMB 2003) (eds. W. Miller et al.), pp. 104-113. ACM, New York.
- Excoffier, L. and Slatkin, M. 1995. Maximum-likelihood estimation of molecular haplotype frequencies in a diploid population. Mol. Biol. Evol. 12: 921-927. [DOI] [PubMed] [Google Scholar]
- Fallin, D. and Schork, N. 2000. Accuracy of haplotype frequency estimation for biallelic loci, via the expectation-maximization algorithm for unphased diploid genotype data. Am. J. Hum. Genet. 67: 947-959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabriel, S.B., Schaffner, S.F., Nguyen, H., Moore, J.M., Roy, J., Blumenstiel, B., Higgins, J., DeFelice, M., Lochner, A., Faggart, M., et al. 2002. The structure of haplotype blocks in the human genome. Science 296: 2225-2229. [DOI] [PubMed] [Google Scholar]
- Griffiths, R.C. and Marjoram, P. 1997. An ancestral recombination graph. In Progress in population genetics and human evolution (eds. P. Donnelly and S. Tavaré), pp. 257-270. Springer-Verlag, New York.
- Gusfield, D. 2001. Inference of haplotypes from samples of diploid populations: Complexity and algorithms. J. Comp. Biol. 8: 305-323. [DOI] [PubMed] [Google Scholar]
- ———. 2002. Haplotyping as perfect phylogeny: Conceptual framework and efficient solutions. In Proceedings of the Sixth Annual International Conference on Research in Computational Molecular Biology (RECOMB 2002) (eds. G. Myers et al.), pp. 166-175. ACM, New York.
- Hawley, M.E. and Kidd, K.K. 1995. HAPLO: A program using the EM algorithm to estimate the frequencies of multi-site haplotypes. J. Hered. 86: 409-411. [DOI] [PubMed] [Google Scholar]
- Hudson, R.R. 1983. Properties of a neutral-allele model with intragenic recombination. Theor. Popul. Genet. 23: 183-201. [DOI] [PubMed] [Google Scholar]
- Jeffreys, A.J., Kauppi, L., and Neumann, R. 2001. Intensely punctate meiotic recombination in the class II region of the major histocompatibility complex. Nat. Genet. 29: 217-222. [DOI] [PubMed] [Google Scholar]
- Johnson, G.C.L., Esposito, L., Barratt, B.J., Smith, A.N., Heward, J., Di Genova, G., Ueda, H., Cordell, H.J., Eaves, I.A., Dudbridge, F., et al. 2001. Haplotype tagging for the identification of common disease genes. Nat. Genet. 29: 233-237. [DOI] [PubMed] [Google Scholar]
- Kaplan, N.L. and Hudson, R.R. 1985. The use of sample genealogies for studying a selectively neutral m-loci model with recombination. Theor. Popul. Biol. 28: 382-396. [DOI] [PubMed] [Google Scholar]
- Kirk, K.M. and Cardon, L.R. 2002. The impact of genotyping error on haplotype reconstruction and frequency estimation. Eur. J. Hum. Genet. 10: 616-622. [DOI] [PubMed] [Google Scholar]
- Koivisto, M., Perola, M., Varilo, T., Hennah, W., Ekelund J., Lukk, M., Peltonen, L., Ukkonen, E., and Mannila H. 2003. An MDL method for finding haplotype blocks and for estimating the strength of haplotype block boundaries. Pac. Sym. Biocomput. 8: 502-513. [DOI] [PubMed] [Google Scholar]
- Kruglyak, L. 1999. Prospects for whole-genome linkage disequilibrium mapping of common disease genes. Nat. Genet. 22: 139-144. [DOI] [PubMed] [Google Scholar]
- Lewontin, R.C. 1964. The interaction of selection and linkage I. General considerations; heterotic models. Genetics 49: 49-67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin, S., Cutler, D.J., Zwick, M.E., and Chakravarti, A. 2002. Haplotype inference in random population samples. Am. J. Hum. Genet. 71: 1129-1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long, J.C., Williams, R.C., and Urbanek, M. 1995. An E-M algorithm and testing strategy for multiple-locus haplotypes. Am. J. Hum. Genet. 56: 799-810. [PMC free article] [PubMed] [Google Scholar]
- MichlataosBeloin, S., Tishkoff, S.A., Bentley, K.L., Kidd, K.K., and Ruano, G. 1996. Molecular haplotyping of genetic markers 10 kb apart by allelic-specific long-range PCR. Nucleic Acids Res. 24: 4841-4843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu, T., Qin, Z., Xu, X., and Liu, J.S. 2002. Bayesian haplotype inference for multiple linked single-nucleotide polymorphisms. Am. J. Hum. Genet. 70: 157-159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordborg, M. and Tavaré, S. 2002. Linkage disequilibrium: What history has to tell us. Trends Genet. 18: 83-90. [DOI] [PubMed] [Google Scholar]
- Olson, J.M. and Wijsman, E.M. 1994. Design and sample size considerations in the detection of linkage disequilibrium with a disease locus. Am. J. Hum. Genet. 55: 574-580. [PMC free article] [PubMed] [Google Scholar]
- Papadopolous, N., Leach, F.S., Kinzler, K.W., and Vogelstein, B. 1995. Monoallelic mutation analysis (MAMA) for identifying germline mutations. Nat. Genet. 11: 99-102. [DOI] [PubMed] [Google Scholar]
- Patil, N., Berno, A.J., Hinds, D.A., Barrett, W.A., Doshi, J.M., Hacker, C.R., Kautzer, C.R., Lee, D.H., Marjoribanks, C., McDonough, D.P., et al. 2001. Blocks of limited haplotype diversity revealed by high-resolution scanning of human chromosome 21. Science 294: 1719-1723. [DOI] [PubMed] [Google Scholar]
- Philips, M.S., Lawrence, R., Sachidanandam, R., Morris, A.P., Balding, D.J., Donaldson, M.A., Studebaker, J.F., Ankener, W.M., Alfisi, S.V., Kuo, F.S., et al. 2003. Chromosome-wide distribution of haplotype blocks and the role of recombination hot spots. Nat. Genet. 33: 382-387. [DOI] [PubMed] [Google Scholar]
- Qin, Z., Niu, T., and Liu, J. 2002. Partitioning-Ligation-Expectation-Maximization algorithm for haplotype inference with single-nucleotide polymorphisms. Am. J. Hum. Genet. 71: 1242-1247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich, D.E., Schaffner, S.F., Daly, M.J., McVean, G., Mullikin, J.C., Higgins, J.M., Richter, D.J., Lander, E.S., and Altshuler, D. 2002. Human genome sequence variation and the influence of gene history, mutation and recombination. Nat. Genet. 32: 135-142. [DOI] [PubMed] [Google Scholar]
- Risch, N. and Merikangas, K. 1996. The future of genetic studies of complex human diseases. Science 273: 1516-1517. [DOI] [PubMed] [Google Scholar]
- Schneider, J.A., Peto, T.E., Boone, R.A., Boyce, A.J., and Clegg, J.B. 2002. Direct measurement of the male recombination fraction in the human β-globin hot spot. Hum. Mol. Genet. 11: 207-215. [DOI] [PubMed] [Google Scholar]
- Sham, P., Bader, J.S., Craig, I., O'Donovan, M., and Owen, M. 2002. DNA pooling: A tool for larger-scale association studies. Nat. Rev. Genet. 3: 862-871. [DOI] [PubMed] [Google Scholar]
- Spielman, R.S., McGinnis, R.E., and Ewens, W.J. 1993. Transmission test for linkage disequilibrium: The insulin gene region and insulin-dependent diabetes mellitus (IDDM). Am. J. Hum. Genet. 52: 506-516. [PMC free article] [PubMed] [Google Scholar]
- Stephens, M., Smith, N.J., and Donnelly, P. 2001. A new statistical method for haplotype reconstruction from population data. Am. J. Hum. Genet. 68: 978-989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taillon-Miller, P., Bauer-Sardina, I., Saccone, N.L., Putzel, J., Laitinen, T., Cao, A., Kere, J., Pilia, G., Rice, J.P., and Kwork, P.Y. 2000. Juxtaposed regions of extensive and minimal linkage disequilibrium in human Xq25 and Xq28. Nat. Genet. 25: 324-328. [DOI] [PubMed] [Google Scholar]
- Thompson, D., Stram, D., Goldgar, D., and Witte, J.S. 2003. Haplotype tagging single nucleotide polymorphisms and association studies. Hum. Hered. 56: 48-55. [DOI] [PubMed] [Google Scholar]
- Tishkoff, S.A., Pakstis, A.J., Ruano, G., and Kidd, K.K. 2000. The accuracy of statistical methods for estimation of haplotype frequencies: An example from the CD4 locus. Am. J. Hum. Genet. 67: 518-522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wall, J.D. and Pritchard, J.K. 2003. Haplotype blocks and linkage disequilibrium in the human genome. Nat. Rev. Genet. 4: 587-597. [DOI] [PubMed] [Google Scholar]
- Wang, N., Akey, J.M., Zhang, K., Chakraborty, K., and Jin, L. 2002. Distribution of recombination crossovers and the origin of haplotype blocks: The interplay of population history, recombination, and mutation. Am. J. Hum. Genet. 71: 1227-1234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, S., Kidd, K.K., and Zhao, H. 2003. On the use of DNA pooling to estimate haplotype frequencies. Genet. Epidemiol. 24: 74-82. [DOI] [PubMed] [Google Scholar]
- Weiss, K.M. and Clark, A.G. 2002. Linkage disequilibrium and the mapping of complex human traits. Trends Genet. 18: 19-24. [DOI] [PubMed] [Google Scholar]
- Yan, H., Papadopoulos, N., Marra, G., Perrera, C., Jiricny, J., Boland, C.R., Lynch, H.T., Chadwick, R.B., de la Chapelle, A., Berg, K., et al. 2000. Conversion of diploidy to haploidy. Nature. 403: 723-724. [DOI] [PubMed] [Google Scholar]
- Zaykin, D.V., Westfall, P.H., Young, S.S., Karnoub, M.A., Wagner, M.J., and Ehm, M.G. 2002. Testing association of statistically inferred haplotypes with discrete and continuous traits in samples of unrelated individuals. Hum. Hered. 53: 79-91. [DOI] [PubMed] [Google Scholar]
- Zhang, K., Calabrese, P., Nordborg, M., and Sun, F. 2002a. Haplotype block structure and its applications in association studies: Power and study design. Am. J. Hum. Genet. 71: 1386-1394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, K., Deng, M., Chen, T., Waterman, M.S., and Sun, F. 2002b. A dynamic programming algorithm for haplotype block partitioning. Proc. Natl. Acad. Sci. 99: 7335-7339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, K., Sun, F., Waterman, M.S., and Chen, T. 2003. Haplotype block partition with limited resources and applications to human chromosome 21 haplotype data. Am. J. Hum. Genet. 73: 63-73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao, H., Zhang, S., Kathleen, R., Merinkangas, K.R., Trixler, M., Wildenauer, D.B., Sun, F., and Kidd, K.K. 2000. Transmission/disequilibrium tests using multiple tightly linked markers. Am. J. Hum. Genet. 67: 936-946. [DOI] [PMC free article] [PubMed] [Google Scholar]


