Abstract
Rebound spiking properties of medial entorhinal cortex (mEC) stellate cells induced by inhibition may underlie their functional properties in awake behaving rats, including the temporal phase separation of distinct grid cells and differences in grid cell firing properties. We investigated rebound spiking properties using whole cell patch recording in entorhinal slices, holding cells near spiking threshold and delivering sinusoidal inputs, superimposed with realistic inhibitory synaptic inputs to test the capacity of cells to selectively respond to specific phases of inhibitory input. Stellate cells showed a specific phase range of hyperpolarizing inputs that elicited spiking, but non-stellate cells did not show phase specificity. In both cell types, the phase range of spiking output occurred between the peak and subsequent descending zero crossing of the sinusoid. The phases of inhibitory inputs that induced spikes shifted earlier as the baseline sinusoid frequency increased, while spiking output shifted to later phases. Increases in magnitude of the inhibitory inputs shifted the spiking output to earlier phases. Pharmacological blockade of h-current abolished the phase selectivity of hyperpolarizing inputs eliciting spikes. A network computational model using cells possessing similar rebound properties as found in vitro produces spatially periodic firing properties resembling grid cell firing when a simulated animal moves along a linear track. These results suggest that the ability of mEC stellate cells to fire rebound spikes in response to a specific range of phases of inhibition could support complex attractor dynamics that provide completion and separation to maintain spiking activity of specific grid cell populations.
Keywords: h-current, Inhibition, Oscillations, Resonance, Whole-cell
1. Introduction
Layer II stellate cells of the medial entorhinal cortex (mEC) display a number of well-studied cellular properties, including subthreshold membrane potential oscillations (Alonso & Llinás, 1989; Klink & Alonso, 1993), membrane potential resonance (Erchova, Kreck, Heinemann, & Herz, 2004; Giocomo, Zilli, Fransén, & Hasselmo, 2007; Haas & White, 2002) and periodic spatial firing in vivo (Domnisoru, Kinkhabwala, & Tank, 2013; Schmidt-Hieber & Häusser, 2013) that could contribute to the firing of entorhinal neurons in a grid cell pattern (Hafting, Fyhn, Molden, Moser, & Moser, 2005). The intrinsic properties of stellate cells show increases in membrane potential oscillation period along the dorsal-to-ventral (D/V) axis of the mEC (Boehlen, Heinemann, & Erchova, 2010; Giocomo & Hasselmo, 2008a,b; Giocomo et al., 2007) that resemble the increasing gradient of grid cell firing field size and spacing (Hafting et al., 2005; Sargolini et al., 2006). Similarly, the intrinsic spiking frequency of grid cells measured by autocorrelograms differs along the D/V axis and shows changes with running speed (Jeewajee, Barry, O'Keefe, & Burgess, 2008). These experimental data have encouraged the use of oscillatory dynamics to model grid cell properties in a class of models termed oscillatory interference models (Blair, Welday, & Zhang, 2007; Burgess, Barry, Jeffery, & O'Keefe, 2005; Burgess, Barry, & O'Keefe, 2007; Hasselmo, Giocomo, & Zilli, 2007; Blair, Gupta, & Zhang, 2008; Burgess, 2008) that could link intrinsic cellular properties to grid cell properties.
Another class of grid cell models, termed continuous attractor dynamic models, focuses on synaptic interactions between neurons that could interact with intrinsic properties. Attractor dynamic models use symmetric recurrent network connections to generate grid cell firing patterns, and use differences in asymmetric synaptic interactions regulated by running velocity to create differences in grid cell firing field size and spacing (Burak & Fiete, 2009; Couey et al., 2013; Fuhs & Touretzky, 2006; Guanella, Kiper, & Verschure, 2007; Pastoll, Solanka, Van Rossum, & Nolan, 2013). Recent in vivo data support elements of the network activity demonstrated by attractor models including shared features of spacing and orientation within individual modules (Stensola et al., 2012) that shift together during environmental manipulations (Barry, Hayman, Burgess, & Jeffery, 2007; Yoon et al., 2013). Attractor dynamic models have properties of both pattern separation, to avoid having neural activity spread throughout the network, and pattern completion to maintain firing in the set of neurons within a population coding a specific representation.
Stellate cells of the mEC are embedded in an inhibitory network. They share little to no direct synaptic connections with one another, but instead interact indirectly through inhibitory interneurons (Couey et al., 2013; Pastoll et al., 2013). The strong inhibitory innervation of stellate cells coupled with their intrinsic properties suggests a functional role for rebound spiking. Rebound spikes occur in response to release from hyperpolarizing current pulses and are dependent on the presence of the h-current (Ih, Alonso & Llinás, 1989; Klink & Alonso, 1993; Shay, Boardman, James, & Hasselmo, 2012). Recent models have simulated grid cell firing behaviors using phase interactions between theta oscillations and stellate cell rebound spikes (Hasselmo, 2013; Hasselmo & Shay, 2014). These rebound spiking models are similar to ‘hybrid’ grid cell models (Bush & Burgess, 2014; Navratilova et al., 2012; Schmidt-Hieber & Häusser, 2013) in that the generation of grid cells relies on the combination of recurrent network connectivity and intrinsic cellular properties. The main goals of this study were to gain a better experimental understanding of rebound spiking in mEC and to test the viability of rebound spiking as a mechanism of grid cell function within the framework of the rebound spiking models. The rebound spiking found in these models represents a type of attractor dynamics dependent on feedback inhibition, in that the activity is maintained within a subpopulation of neurons without external input. Correspondingly, these models show temporal dynamics that allow pattern separation to prevent activity from spreading throughout the network, and that allow pattern completion to reactivate any neuron that happens to stop firing.
We performed experiments to test how the interaction of rebound spiking properties with network oscillations could allow temporal selection of a discrete population of neurons. Hyperpolarizing inputs mimicking synaptic input were superimposed on a baseline sinusoidal current injection and delivered to layer II mEC stellate cells. We analyzed the phases of hyperpolarizing inputs (relative to the baseline oscillation) that caused spikes as well as the output phases of spikes. Our results indicate that inhibitory inputs have a particular phase range that can induce spiking, allowing feedback from a single inhibitory interneuron to selectively trigger network activity in a discrete population of active neurons, while performing completion by recruiting inactive neurons that should be active. In addition, output spiking occurs at a narrow phase range. The input phase preference was dependent on the presence of the h-current and both input and output phases changed with oscillation frequency and magnitude of inhibitory input. Simulation of a network of stellate cells with rebound spiking properties (Izhikevich, 2007) that also includes inhibitory feedback and oscillatory input regulated by the medial septum, showed that spatial periodicity resembling grid cell firing can be produced with rebound spiking (Hasselmo, 2013; Hasselmo & Shay, 2014). These results support the hypothesis that rebound spiking could contribute to the generation of grid cells.
2. Methods
2.1. Slice preparation
All experimental protocols were approved by the Institutional Animal Care and Use Committee of Boston University. Slice preparation and recording techniques were similar to those in Shay et al., 2012. Briefly, male and female Long-Evans rat pups (postnatal days 17–21, Charles River, Wilmington, MA) were deeply anesthetized with 1–2 ml of isoflurane (Abbot Laboratories). After absence of tail and pedal reflex, brains were rapidly removed, submerged in ice-cold artificial cerebrospinal fluid (aCSF) containing (in mM) 125 NaCl, 2.0 CaCl, 2.5 KCl, 1.25 NaH2PO4, 25 NaHCO3, 25 d-glucose, and 1.0 MgCl2 (pH adjusted to 7.4 with 95% O2–5% CO2). Horizontal slices, 400-μm thick, were made with a vibroslicer (Leica VT1000). Slices were immediately transferred to a holding chamber containing aCSF and incubated at 32 °C for 30 min and were left at room temperature for 30 min before recordings began.
2.2. Electrophysiological recordings
Slices were placed in a recording chamber perfused with aCSF, constantly bubbled with 95% O2–5% CO2. In a subset of recordings (n = 17), 2 mM kynurenic acid and 100 μM picrotoxin were added to the recording solution to block glutamatergic and GABAergic synaptic transmission, respectively. All recordings were made between 35 and 37 °C. Whole-cell pipettes were fabricated with borosilicate glass capillaries by means of a P-90 horizontal puller (Sutter Instruments). Pipettes were filled with an internal solution containing (in mM) 120 K-gluconate, 10 HEPES, 0.2 EGTA, 20 KCl, 2.0 MgCl2, 4.0 Na2ATP, 0.3 Na3GTP, and 7 phosphocreatine-diTris (pH adjusted to 7.3 with KOH). In addition, 0.1% biocytin was included in the internal solution for the purpose of labeling. Filled pipettes had resistances between 3 and 5 MΩ. Cells were visualized under an upright microscope (Olympus BX51I or Zeiss Axioskop 2) using a CMOS (complementary metal–oxide semiconductor) digital Rolera Bolt camera (QImaging, Surrey, BC, Canada) or a near infrared charge-coupled device camera (JAI CV-M50IR). Tight seals (>1 GΩ) were formed and whole-cell access was achieved by brief negative pressure. Current clamp recordings were made with a Multi Clamp 700B amplifier (Axon Instruments). Built-in capacitance compensation and bridge balance circuitry was used to correct for and monitor series resistance throughout experiments. Recordings were sampled between 5 and 20 kHz using Clampex 10.0 (Axon Instruments).
Upon whole-cell access, cells were allowed to equilibrate for 2–5 min. Basic cellular properties were qualitatively measured in real time to test the presence of stellate cell electrophysiological signatures (Alonso & Klink, 1993; Alonso & Llinás, 1989; Dickson et al., 2000). Inclusion criteria included resting membrane potentials negative to −55 mV, input resistances below 120 MΩ, a strong sag potential (sag ratio range = 0.22–0.43, median sag ratio = 0.37), calculated as in Heys et al. (2013) using the following equation:
| (1) |
sMPOs, overshooting action potentials (above zero mV), cluster spiking, and series resistances ≤30 MΩ. Cells displaying these properties were then used to investigate rebound spiking. In some cases, cells lacking these properties were investigated as a control (n = 7). At resting membrane potential, 0.5 s square step currents ranging from −500 to 500 pA (25 pA increments) were delivered to cells in order to qualitatively visualize sag potentials and spiking behavior. All remaining in vitro stimuli were generated in MATLAB and exported for delivery by Clampex 10.0. To identify each cell's preferred input frequency, the MATLAB chirp function was used to create a 20 s sinusoidal input increasing linearly from 0 to 20 Hz, sampled at 20 kHz. The amplitude of the input current chirp function ranged between 10 and 100 pA in different cells to ensure subthreshold responses at different holding potentials. The response to the input current chirp function was measured at different holding potentials (−70 mV to −55 mV), and the value of resonance frequency was obtained as the frequency of the peak amplitude of response (rounded to the nearest Hz) at −55 mV and was used as the primary frequency (see below for use of additional frequencies) of the sinusoid used to test rebound spiking. Rebound spiking protocols were run at depolarized membrane potentials (mean = −55.24 mV; standard deviation = 3.37 mV) near the value at which the primary resonance frequency was measured. These membrane potentials were substantially depolarized relative to the resting potential of the neurons (mean = 62.91 mV; standard deviation = 3.23 mV). Running protocols near −55 mV ensured that spiking did not occur at the peaks of the sinusoidal oscillation, making it easier to measure the effects of hyperpolarizing inputs. In addition, at this depolarized membrane potential rebound spiking is more robust.
The following sinusoidal inputs were all sampled at 5 kHz. First we measured spiking in the absence of rebound dynamics by delivering control “empty sinusoids” consisting of sinusoidal inputs with amplitudes of 50 pA and fixed frequencies ranging from 1 to 12 Hz (1 Hz increments). For all other remaining protocols, simulated synaptic inputs (hyperpolarizing for tests of rebound spiking, depolarizing for control tests of spike induction) were superimposed on 50 pA sinusoids. Synaptic inputs (Isyn) were simulated using a double exponential of the form:
| (2) |
where τ1 and τ2 are the fast and slow time constants, respectively. For all protocols, τ1 = 0.001 s and τ2 = 0.005 s. Recording trials were 200 s long, containing seven 20 s epochs of sinusoidal oscillations separated by 5 s of baseline current (DC) between each epoch, and 12.5 s of baseline DC current at the beginning and end of each trial. In standard protocols, the magnitude of the input pulse was scaled to be twice the peak to peak amplitude of the sinusoidal input (100 pA) and input pulses were placed such that each subsequent peak was (17/16) * 2 * pi radians after the previous input (resulting in cycling through a full range of possible phases with steps of 2 * pi/16). The standard protocol was run at the resonance frequency of a given cell as well as frequencies ±2 Hz from the resonance frequency. For normalized input protocols, we took the largest magnitude of current in the standard protocol (i.e. when hyperpolarizing input occurred at the trough of the sinusoid) and scaled each hyperpolarizing input to that value. Therefore, regardless of phase, each input reached the same absolute current value in our normalized protocol. “Randomized” input protocols were generated by placing the input pulse of each baseline cycle on a random phase. Possible phases were limited to increments of (2 * pi/16), and were sampled such that there were an equal number of inputs at each phase. “Sparse” inputs were generated by placing simulated synaptic inputs on every other cycle of the baseline sinusoid. The input pulse on every other sinusoid cycle was (2 * pi/16) radians later in phase than the previous input. “Magnitude” protocols used input pulses with amplitudes that were 1/2, 1/4, or 1/8 that of the standard input.
In a subset of cells (n = 6), baseline recordings were performed, followed by continuous bath perfusion of 10 μM ZD7288 (Tocris, Sigma). After ten minutes of drug wash, experiments were then repeated in order to assess the role of the h-current in rebound spiking behavior. For all drug wash conditions, synaptic blockers (2 mM kynurenic acid, 100 μM picrotoxin) were used in both baseline and drug wash conditions.
2.3. Data analysis
Data for each run were exported from Clampex to MATLAB for analyses. Cells responded to input current chirp functions with the envelope of the amplitude of their membrane potential response reaching a peak when the input approached their resonant frequency. Resonant frequency was determined using techniques previously described (Erchova et al., 2004; Shay et al., 2012) using MATLAB curve fitting routines. The impedance [Z(f)] was taken as the ratio of the magnitude of the Fourier transform of the output (membrane voltage) to the magnitude of the Fourier transform of the input (chirp and DC injection). The peak of the impedance curve, determined by MATLAB lsqcurvefit routine, was then taken as the resonance frequency. The reported voltage for each chirp response was determined as the average value before the chirp stimulus began.
Cell spiking responses to sinusoidal inputs were detected by sampling for periods of depolarized membrane potential with a peak height that reached positive values above 0 mV. The phase of a spike in reference to the baseline oscillation was determined based on the timing of the peak voltage of the spike. For all input signals except the empty sinusoid, preceding input phase was determined as the phase of hyperpolarizing current injection input directly preceding the spike. In instances where more than one spike was elicited from a given input (i.e. in drug wash condition), only the first spike was included for analyses. The holding voltage for each epoch of a trial was determined as the mean voltage during the dead-space directly preceding the epoch, accounting for any drift in membrane potential between different sinusoid segments but not within segments. In order to determine the statistical properties of phase of spiking responses across the full data set, the mean resultant angle (MRA) and the mean resultant length (MRL) for hyperpolarizing/depolarizing current inputs and spiking output were determined for each cell and the population. The following equations were used to compute MRA and MRL respectively:
| (3) |
| (4) |
where i is the imaginary constant, θ is an angular variable, arctan2 is the four-quadrant arc tangent function, and imag() and real() represent the real and imaginary components of the complex exponential. All circular analyses and statistics were done using the CircStat toolbox (Berens, 2009) for MATLAB. Circular statistical tests included the parametric Watson Williams test for determining whether the mean directions of two or more groups are identical or not, and paired t-tests to determine significant differences between the MRL distributions of two groups.
2.4. Biophysical simulation methods
To demonstrate the role of rebound spiking in network dynamics, we tested single cell models of rebound spiking and incorporated these into network simulations. Single neuron models used the framework developed by Izhikevich (2007) with the following equations:
| (5) |
| (6) |
where v is the membrane potential, u is the current, Ib is the baseline holding current, I is the injected current, C is the membrane capacitance (pF), vr is the resting membrane potential (mV), vt is the threshold voltage, k is the fast activation current with a, the fast current and b, the slow current, vpeak is the maximum voltage of a spike, c is the reset voltage, and d is the reset current. Parameters were chosen to match previously published values (Izhikevich, 2007) used to replicate properties of stellate cell recordings in mEC (Burton, Economo, Lee, & White, 2008). For all simulations we used the following parameter values: Ib = 130, C = 200, vr = −60, vt = −45, k = 0.75, a = 0.007 for low frequency resonance, a = 0.015 for high frequency resonance, b = 14.2, c = −50, d = 100, and vpeak = 100. For single cell properties such as resonance frequency and sag potential, we injected (I, Eq. (5)) the same chirp function and hyperpolarizing step currents as used in slice experiments. We also injected the same inhibitory synaptic inputs (I, Eq. (5)) used in slice experiments to investigate rebound spiking in the modeled cell. Data analyses of the output from single cell simulations were performed in the same manner as the analyses of in vitro recording data.
Finally, to analyze the potential role of the rebound spiking properties demonstrated in these experiments, we incorporated these rebound spiking properties into network simulations. Izhikevich neurons with the parameter values above were placed in a feedback inhibitory network and also received theta rhythmic sinusoidal input to model medial septal input. These network simulations demonstrate that rebound spiking could maintain network spiking activity and could allow systematic shifts in network spiking activity between different neurons that receive oscillatory input with different phases caused by regulation of local inhibition by the medial septum (Hasselmo, 2013).
In this simulation of network properties, we simulated two independent populations of Izhikevich stellate cells with membrane potentials labeled with different subscripts vT1 and vT2 because they end up firing on opposite cycles of theta rhythm oscillations (T1 and T2). This firing on opposite cycles is consistent with data on theta cycle skipping in medial entorhinal cortex in which neurons fire on alternating cycles of network theta rhythm (Brandon, Bogaard, Schultheiss, & Hasselmo, 2013; Deshmukh, Yoganarasimha, Voicu, & Knierim, 2010; Jeffery, Donnett, & O'Keefe, 1995). Mechanisms of theta cycle skipping were simulated previously with populations of stellate cells, pyramidal cells and interneurons (Brandon et al., 2013). The stellate cells each have their own internal dynamical variables uT1 and uT2 that mediate rebound spiking. In addition, they interact with two sets of inhibitory interneurons iT1 and iT2. In the model, the synaptic interaction with inhibitory interneurons is mediated by uniform connectivity strengths Wis for stellate input to interneurons and Wsi for interneuron input to stellate cells. There are no direct excitatory synaptic connections between stellate cells in the model, consistent with physiological data from entorhinal cortex (Couey et al., 2013; Dhillon & Jones, 2000).
The network dynamics are described by the following equations:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
The membrane potential of each stellate cell is represented by vT1 for individual stellate cells in population T1, and vT2 in stellate population T2. The internal activation of the h-current in each stellate cell is simulated using the recovery variable uT1 in stellate cells in population T1 and uT1 in population T2. The stellate cells generate spiking output to interneurons at specific time steps (shown in square brackets), when v > vpeak, v is reset to the value of parameter c, and u is reset to u + d. In some network simulations, we tested a Gaussian distribution of the parameter a with different standard deviations.
The variable i represents the membrane potentials of interneurons, which also display discrete spiking output when they cross a threshold h. Spikes in the interneurons cause hyperpolarizing inhibitory feedback potentials in the same population of interneurons immediately after the spike. In addition, spikes in the interneurons cause inhibitory synaptic potentials in the population of stellate cells with the opposite population index (e.g. iT1 inhibits vT2 and iT2 inhibits vT1). The same uniform connection matrix Wsi connects the inhibitory cells iT1 to all stellate cells in population vT2, and connect the inhibitory cells iT2 to all stellate cells in population vT1. All stellate cells in population vT1 send output to two interneurons iT21–2 via matrix Wis that connects to the entire stellate cell population vT2 via the matrix Wsi, and all stellate cells in population vT2 send output to two interneurons iT11–2 via matrix Wis that connects to the entire stellate cell population vT1 via matrix Wsi.
Each stellate cell also receives oscillatory input representing the modulation of inhibitory input regulated by input from the medial septum with a range of different temporal phases according to the equation:
| (12) |
where f is the medial septal frequency, vT1 is the stellate cell index and “n” is the total number of stellate cells in the population. The same range of phases influence the stellate cells in population T2 as well. The initial activity in each simulation was activated by giving an initial hyperpolarizing input to specific stellate cells, causing a depolarizing rebound that generated a rebound spike that activated inhibitory interneurons and initiated further rebound spiking activity in the simulation.
3. Results
3.1. Confirmation of stellate cell type
The focus of this study was to analyze near threshold rebound spiking behavior elicited by sinusoidal inputs superimposed with inhibitory post-synaptic currents. The phases of hyperpolarizing input pulses that induced spikes and the output phases of these spikes, relative to sinusoidal oscillations, were analyzed in 72 layer II stellate cells and 7 layer III non-stellate cells of the mEC.
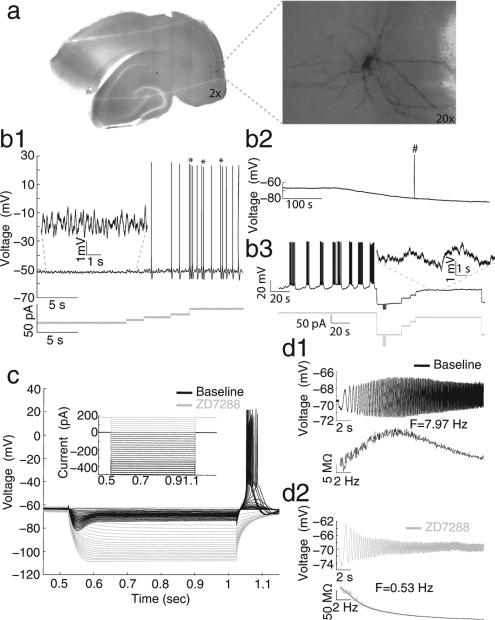
Micrographs of a horizontal brain slice (Fig. 1) with two magnifications show the cell's location within the mEC superficial layers as well as morphological detail, revealing a large soma and dendrites radiating in all directions. These morphological characteristics are indicative of stellate cells (Alonso & Klink, 1993). Cells displayed a number of electrophysiological properties that are typical of stellate cells including subthreshold membrane potential oscillations (sMPOs) with amplitudes between 2 and 5 mV (Fig. 1b1, inset), cluster spiking, defined by epochs of two or three successive spikes separated by sMPOs (Fig. 1b1, asterisks), subthreshold resonance frequencies in the theta range (3–8 Hz, Fig. 1d1), and a prominent sag potential in response to hyperpolarizing step currents coupled with rebound spiking upon release of the hyperpolarizing current (Fig. 1c, black trace). Upon application of 10 μM ZD7288, a selective h-current blocker, the resting membrane potential gradually became hyperpolarized (Fig. 1b2), and the cell ceased to show sMPOs (panels b3, inset), sag potential, rebound spiking (panel c, gray trace) and resonance (panel d2). Additionally, cluster spiking was replaced by a behavior described as cyclical transitions between low frequency firing and periods of inactivity (Fig. 1b3, note the scale of the time axis). In addition to the consistent observation of these basic electrophysiological properties, all 14 recovered cell fills (out of 72 recorded cells) had similar stellate-like morphologies. Furthermore we recorded 7 cells that lacked stellate-like electrophysiological properties and were able to recover cell fills in three of these cells. All three cells lacked stellate-like morphologies (data not shown). Similar to previous articles (Alonso & Klink, 1993; Klink & Alonso, 1997), this supported the standard use of electrophysiological characteristics to classify cell types.
Fig. 1.
Intrinsic electrophysiological properties of stellate cells and loss of these properties with the h-current blocker ZD7288. (a) Photomicrographs display a representative cell's anatomical location within the slice (left) as well as the typical stellate cell morphology (right). All data shown in b–d were recorded from this cell. (b1) This panel shows representative examples of electrophysiological properties of stellate cells including sMPOs (left) and spike clustering behavior (marked by asterisks on right). (b2) Bath application of ZD7288 consistently causes a gradual hyperpolarization in membrane potential (note holding potential is at 0 pA; #, spontaneous spike truncated). (b3) In ZD7288, spiking behavior shows cyclical transitions of low frequency spiking and inactivity after drug wash. The inset in b3 shows that sMPOs are lost compared to inset in b1. (c) Voltage sag and rebound spiking are abolished by drug wash (compare black and gray responses). (d) Following drug application, resonant frequency changes, in this particular cell, from 7.97 Hz (d1, black) to 0.53 Hz (d2, gray).
3.2. Phase specificity of rebound spiking
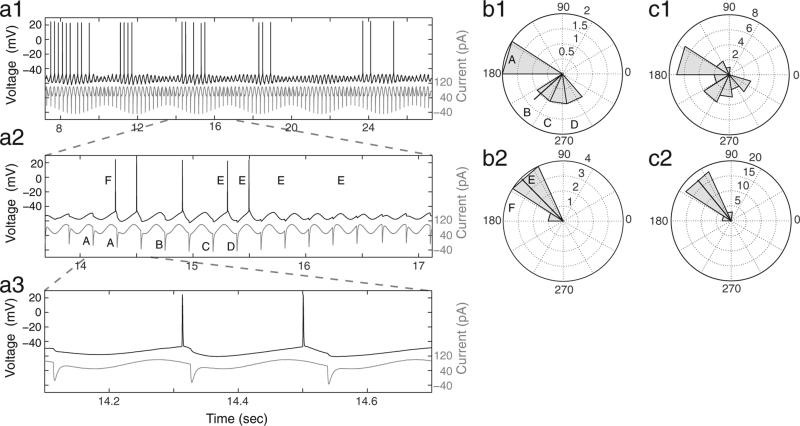
We next characterized the response of mEC stellate cells to the standard hyperpolarizing input by performing quantitative analyses of the phases of hyperpolarizing input pulses inducing spikes and the output phases of spiking (Fig. 2). There are a number of important findings from these analyses. First, there was a limited range of input phases of hyperpolarizing current pulses that caused spiking. Second, the phases of output spiking covered a narrow range, despite the larger phase range of inhibitory synaptic inputs. Lastly, a comparison between phase histograms from a single epoch (b) and all epochs of this particular cell (c) demonstrates the consistency of the observed rebound spiking responses.
Fig. 2.
Stellate cells display rebound spiking in response to a limited range of phases of hyperpolarizing input pulses and with a limited range of output spiking phases. (a) An example stellate cell response (top, black) to the standard input (bottom, gray) is shown at three time scales (a1, a2 and a3) to demonstrate rebound spiking behavior. (b) Rose plots correspond to the data in a2 and show the phases, relative to the baseline oscillation, of hyperpolarizing input pulses that induce spiking (b1) and the phases of output spiking (b2). The black line in each rose plot is the MRA, and the length of the line is indicative of the MRL of the phase distribution. Uppercase letters in b1 and b2 correspond to those in a2 and show what phase bin each hyperpolarizing input pulse (A–D) or output spike (E and F) falls into for each corresponding rose plot. (c) Rose plots show the same input and output phase analyses as in b1–b2 but correspond to all data collected in response to the standard input for this representative cell.
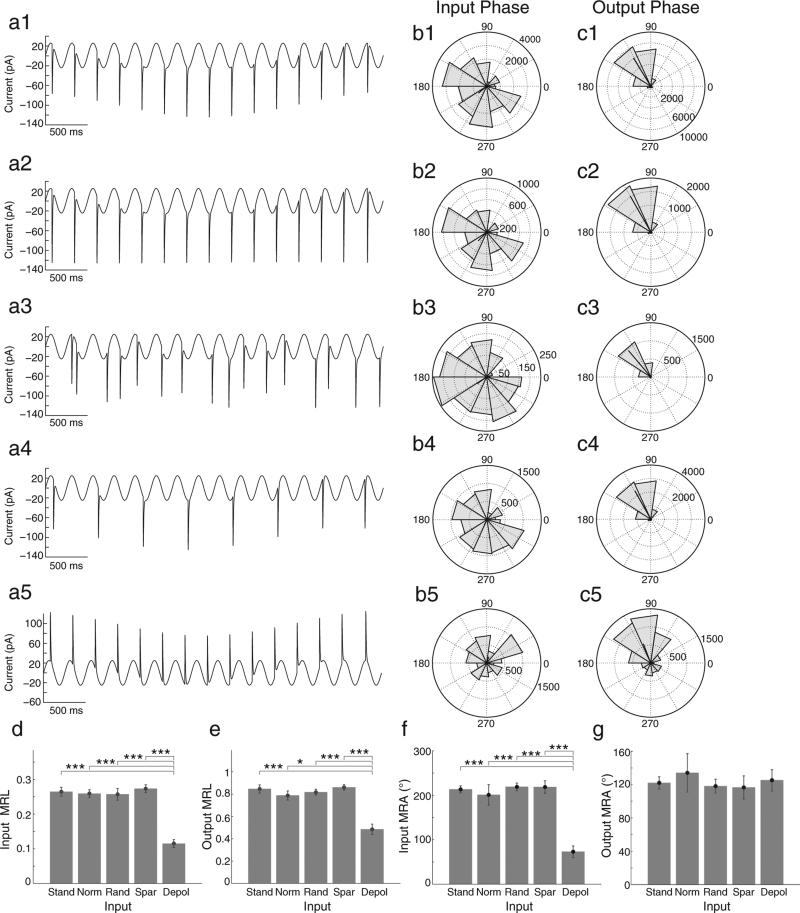
Our population data further demonstrate the consistency of phase effects and verify that these effects are due to intrinsic rebound spiking properties. We compared standard input, with different types of control inputs consisting of the normalized, random, sparse, and excitatory synaptic inputs (Fig. 3a1–a5). Our results indicate that stellate cells showed similar phase specific spiking after hyperpolarizing input pulses at different phases in different conditions (Fig. 3d–g). These similar responses to hyperpolarizing input pulses indicate that rebound spiking behaviors were similar when hyperpolarizing inputs were constructed to have equal local minima at all input phases (a2), that the output spiking phases were not determined by the order of previous hyperpolarizing inputs (a3), nor were output spiking phases determined by the timing of hyperpolarizing inputs on the preceding cycle (a4). However, in response to depolarizing inputs, the population of stellate cells had significantly lower input MRL (d), output MRL (e), and input MRA (f) compared to hyperpolarizing inputs (paired t-test, *p < 0.05; ***p < 0.001). These data suggest that stellate cells respond much differently to the phase of depolarizing inputs than to the phase of hyperpolarizing inputs. For excitatory inputs, the average input phase eliciting spikes occurs significantly earlier than for hyperpolarizing inputs (f, paired t-test, ***p < 0.001), and the distribution of input phases that cause spiking is significantly wider compared to hyperpolarizing inputs (d, paired t-test, ***p < 0.001). Furthermore, although the average spiking phase is similar (g), excitatory driven spiking occurs with a significantly broader output phase distribution compared to inhibitory driven rebound spiking (e, paired t-test, *p < 0.05 ***p < 0.001). Overall, our data suggest that rebound spiking was elicited within a smaller input phase window and that rebound spiking is produced in a more precise manner relative to oscillations than spikes produced by depolarizing input.
Fig. 3.
Hyperpolarizing and depolarizing input pulses have differential preferred input phases that induce spiking. (a) Control current inputs used are shown in the first column. These include (a1) standard, (a2) normalized, (a3) random, (a4) sparse, and (a5) depolarizing current inputs, respectively. (b–d) Rose plots show phase histograms for hyperpolarizing (a1–a4) or depolarizing (a5) input pulses that induce subsequent spiking (b1–b5) and for the phase of output spiking (c1–c5) for the entire population (n = 72) of cells. Rose plots correspond to a given input with matching numerical labels in each row. (d and e) Bar graphs show input (d) and output (e) MRLs do not differ between hyperpolarizing inputs, but are significantly larger than the response to depolarizing inputs in terms of both input and output MRLs (paired t-test, *p < 0.05; ***p < 0.001). (f and g) Bar graphs show input MRAs (f) do not differ between different patterns of hyperpolarizing input pulses, but are significantly larger than depolarizing inputs (paired t-test, ***p < 0.001), while all output MRAs are similar (g). Abbreviations in d–g are as follow: Stand = standard input, Norm = normalized input, Rand = random input, Spar = Sparse input, and Depol = depolarizing input.
3.3. The effects of oscillation frequency on input and output phase
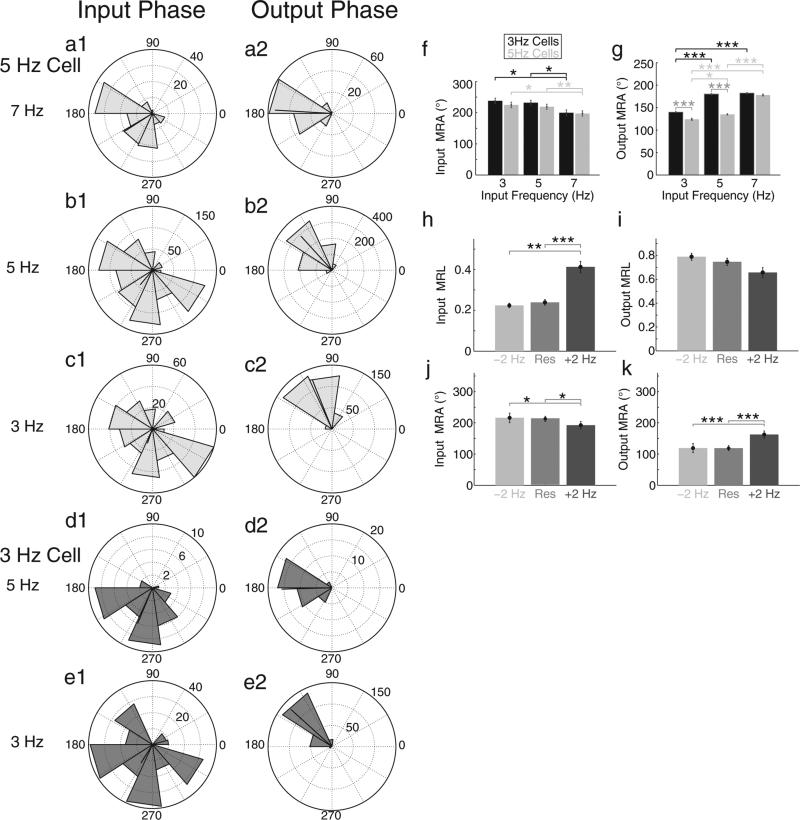
Whereas data presented thus far have been shown for inputs containing sinusoidal oscillations with a frequency close to the cell's depolarized resonance frequency, analyses from inputs with oscillations at +2 Hz and −2 Hz from cells’ depolarized resonance frequencies are presented in Fig. 4. Both within cell and across cell analyses were done. Cells with a resonance frequency near 3 Hz or 5 Hz behaved similarly when inputs were delivered at their respective depolarized resonance frequency (compare b1–b2 with e1–e2) as well as when inputs were delivered at +2 Hz from their resonance frequency (compare a1–a2 with d1–d2). However, cells with resonance near 3 Hz receiving input oscillations at either 3 Hz or 5 Hz fired at later phases (higher MRA) compared to cells with a resonant frequency of 5 Hz (f, parametric Watson Williams test, ***p < 0.001). This suggests that with a fixed frequency background oscillation, cells with lower resonant frequencies tend to fire at later phases compared to cells with higher resonant frequencies. However, preferred spiking phases for both cell populations converged at 7 Hz. Interestingly, our previous study (Shay et al., 2012) showed that as a stellate cell's membrane potential was hyperpolarized, its resonance frequency asymptotically approached a maximum frequency of approximately 7 Hz. That both cell properties have a saturation point suggests a similar cellular mechanism. It is likely that Ih regulates the integration of the sinusoid and hyperpolarizing input, and that at a critical frequency Ih is no longer able to keep pace with the oscillation, and therefore the resonance frequency and average spiking phase reach a maximum value.
Fig. 4.
Preferred hyperpolarizing input and spiking phases correlate with increased relative input frequency. (a–e) Rose plots display data from cells with a depolarized resonant frequency of 5 Hz (a–c, light gray) and 3 Hz (d, e, dark gray). Hyperpolarizing input pulse phase (a1, b1, c1, d1, e1) and output spiking phase (a2, b2, c2, d2, e2) analyses from standard inputs of 7 Hz (a1–a3), 5 Hz (b1–b3, d1–d3), and 3 Hz (c1–c3, e1–e3) are shown in each row. Note that cells behave similarly at their depolarized resonant frequencies (compare b1–b3 with e1–e3, respectively), as well as at +2 Hz from their depolarized resonant frequency (compare a1–a3 with d1–d3, respectively). (f and g) Summary bar graphs compare input MRA (f) and output MRA (g) for populations of cells with 3 Hz (black) and 5 Hz (gray) resonant frequencies. (f) There were no significant differences between the two populations of cells at all tested input frequencies. However within each population, significant decreases (parametric Watson Williams test, *p < 0.05; **p < 0.01) in input MRA occurred between 3 Hz and 7 Hz as well as 5 Hz and 7 Hz input oscillations. (g) At 3 and 5 Hz baseline oscillation frequencies the 3 Hz resonant frequency cell population had significantly higher output MRA (parametric Watson Williams test, ***p < 0.001), indicating a later average spiking phase, compared to the 5 Hz cell population. However, At 7 Hz there was no significant difference in output MRA. Within population analyses show significant increases in output MRA as oscillation frequency was increased for the 3 Hz (parametric Watson Williams test, 3 Hz vs. 5 Hz and 5 Hz vs. 7 Hz, ***p < 0.001) and the 5 Hz population (parametric Watson Williams test, 3 Hz vs. 5 Hz, *p < 0.05; 3 Hz vs. 7 Hz and 5 Hz vs. 7 Hz, ***p < 0.001). (h and i) Population data of MRLs of hyperpolarizing inputs and outputs. There are significant increases in MRL of spike inducing inputs (h) between inputs at a cell's resonant frequency and at +2 Hz the resonant frequency (paired, ***p < 0.001), as well as −2 Hz the resonant frequency (paired t-test, **p < 0.01). (i) The mean resultant length of output spiking displays an inverse trend with frequency but fails to reach statistical significance. (j and k) Population MRAs of hyperpolarizing inputs causing spikes and output spiking as a function of relative input frequency. As the input frequency was increased beyond a cell's resonance frequency significantly earlier input phases were preferred (j, parametric Watson Williams test, *p < 0.05) and cells spiked at significantly later phases (k, parametric Watson Williams test, ***p < 0.001).
We also reported the frequency dependence of rebound spiking phase for our population data (Fig. 4 panels h–k). As the baseline oscillation frequency was increased beyond a cell's resonant frequency, the distribution of preferred inputs became significantly narrower (h, paired t-test, **p < 0.01; ***p < 0.001) and shifted to significantly earlier phases (j, parametric Watson Williams test, *p < 0.05), while spiking phase shifted to significantly later phases (k, parametric Watson Williams test, ***p < 0.001). These data suggest that as the sinusoidal oscillation frequency increases relative to resonance frequency, the input phase window to produce a spike decreases in width and shifts to earlier phases, while the average output phase shifts to later phases. In addition, a higher intrinsic resonance frequency of a cell causes it to fire in response to earlier phases of input and generates output spikes at earlier phases. Earlier input phases for inducing spiking and output phases of spiking could influence the spacing of grid cell firing fields by causing more rapid transitions between firing fields.
3.4. The effects of the magnitude of hyperpolarizing inputs on input and output phase
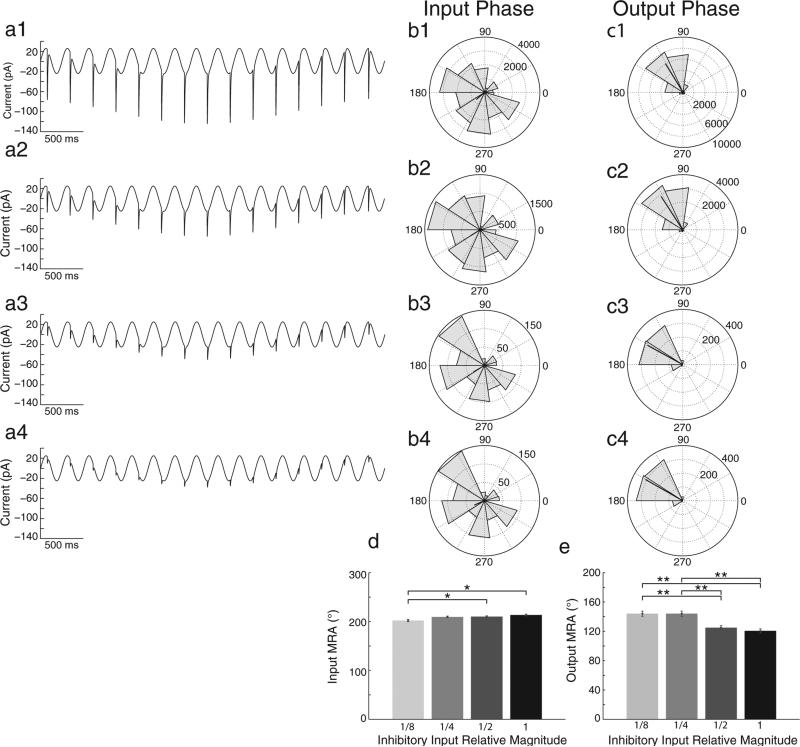
We tested how changes in the magnitude of inhibitory synaptic inputs would affect rebound spiking, with hyperpolarizing inputs of full magnitude, half magnitude, quarter magnitude, and eighth magnitude, respectively (Fig. 5, Panels a1–a4). As the magnitude of hyperpolarizing inputs was decreased, the input MRA slightly decreased (d, parametric Watson Williams test, 1/8 vs.1/2 and 1/8 vs. 1, *p < 0.05) while the MRA of spiking increased (e). In fact 1/8 and 1/4 magnitudes gave significantly larger output MRAs than 1/2 and full magnitude hyperpolarizing inputs (e, parametric Watson Williams test, p < 0.001). These data suggest that the strength of inhibition can change the rebound spiking phase in stellate cells, with stronger inhibition causing earlier spiking phase. This could allow larger inhibition magnitudes to cause faster transitions between firing fields of the sort shown below.
Fig. 5.
Decreasing magnitude of inhibitory synaptic input correlates with later spiking output phase. (a) Standard input currents are shown with decreases in the magnitude of hyperpolarizing synaptic input pulses from full magnitude (a1), to half magnitude (a2), quarter magnitude (a3), and eighth magnitude (a4). (b and c) Rose plots show population (n = 15 cells) phase histograms for hyperpolarizing input pulses that induce spiking (b1–b4) and for output spiking phase (c1–c4). Rose plots correspond to a given magnitude input with matching numerical labels in each row. (d and e) Population bar graphs show that as the magnitude of hyperpolarizing input decreases there is a small but significant decrease in input MRA between 1/8 and 1/2 as well as 1/8 and full magnitude inputs (d, parametric Watson Williams test, *p < 0.05), while the output (spiking) MRA is significantly larger (later phase) for 1/8 and 1/4, than for 1/2 and full magnitudes (e, parametric Watson Williams test, **p < 0.01).
3.5. The effect of pharmacological blockade of HCN channels on the phase specificity of hyperpolarizing inputs causing spikes
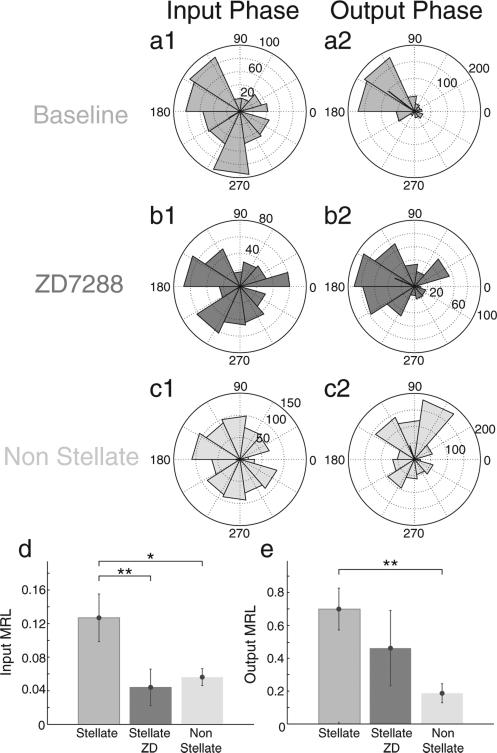
We have shown that pharmacological blockade of the h-current abolished rebound spiking to hyperpolarizing square current pulses (Fig. 1c). This finding prompted us to test whether blockade of the h-current with 10 μM ZD7288 would alter the phase specificity of rebound spiking in stellate cells in response to our standard sinusoidal input. We also tested rebound spiking properties in layer III mEC non stellate cells (n = 7), which possess much weaker h-current compared to stellate cells. The MRL of hyperpolarizing inputs significantly decreased in stellate cells (n = 6) following drug application (Fig. 6d, paired t-test, **p < 0.01). Stellate cells in the baseline condition had significantly higher MRLs for hyperpolarizing inputs compared to non-stellates (paired t-test, *p < 0.05) but following the drug condition, stellate cells did not significantly differ from non-stellate cells in the response to input phase. The phase specificity of spiking output (MRL) in stellate cells under baseline conditions were significantly larger than non-stellates (Fig. 6e, paired t-test, **p < 0.01), and was smaller, but did not reach statistical significance after blocking the h-current. That is, blockade of h-current reduced phase specificity of spiking output. Together these data suggest that the h-current shapes the phase specificity in which hyperpolarizing inputs can elicit rebound spiking, but is likely to be only partially involved in regulating spiking output phase.
Fig. 6.
Ih is necessary for phase specificity of hyperpolarization induced rebound spiking. (a–c) Rose plots for standard inputs in stellate cells (n = 6) before (a) and after (b) application of ZD7288 as well as in non-stellate cells (n = 7, c). Rose plots display phase histograms for hyperpolarizing input pulses that induce spiking (a1, b1, c1) and for output spiking phase (a2, b2, c2). (d) Summary bar graph demonstrates that following h-current blockade, stellate cells lose the phase specificity for hyperpolarizing input, as indicated by a significant decrease in hyperpolarizing input MRL (paired t-test, **p < 0.01). Furthermore, this significant lack of input specificity is also present in non-stellate cells compared to baseline stellate cells (paired t-test, *p < 0.05). (e) Summary bar graph demonstrates that blocking the h-current in stellate cells decreases the specificity of output spiking phase, shown by a decrease in the MRL of output spiking phase, but this does not reach statistical significance. However compared to stellate cells, non-stellate cells display a significantly smaller MRL (paired t-test, **p < 0.01), and therefore, less phase specificity of output spiking.
3.6. Single cell simulations of rebound spiking
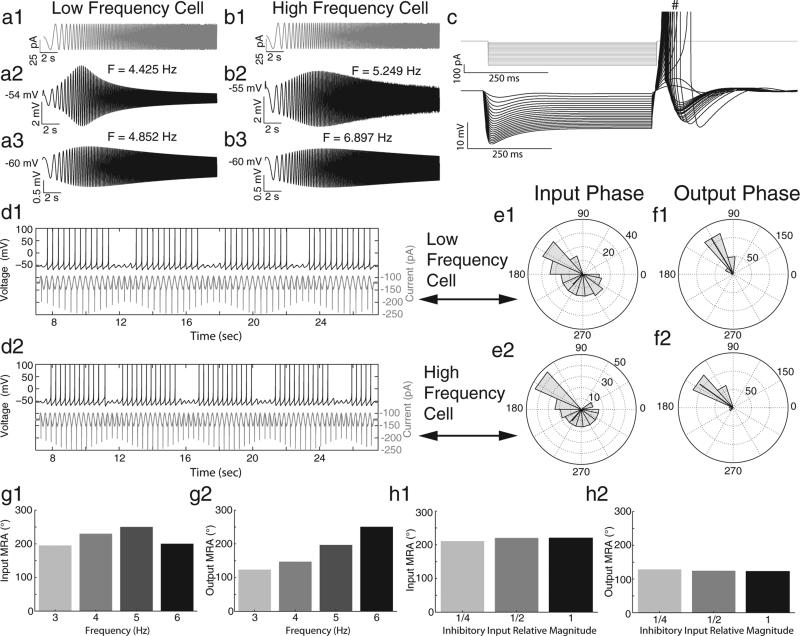
Next we simulated data from Izhikevich (2007) neurons in which parameters were selected to produce behaviors similar to what we recorded in vitro (Fig. 7). By tuning the a parameter in Eq. (6), we were able to produce cells with differential resonance frequencies at both depolarized membrane potentials (a2, b2) and near a cell's resting membrane potential (a3, b3). Similar to previous data (Erchova et al., 2004; Shay et al., 2012), model cells showed decreased resonance frequencies with depolarization. In addition, Izhikevich neurons responded to square wave hyperpolarizing currents with a prominent sag potential, and fired rebound spikes upon release from the step current (c). Similar to our experimental data, our simulated cells showed phase specificity to hyperpolarizing inputs and similar output spiking phases in response to the same sinusoidal inputs used in vitro (d–f). In response to changes in baseline oscillation frequency, simulated cells shifted their spiking MRAs to later phases, similar to what we observed in vitro (g2). However, the MRAs of the phase of hyperpolarizing inputs that caused spikes also shifted to later phases (d1), which was contrary to what was observed in vitro, where hyperpolarizing input phases that caused spiking moved to earlier phases. The reason for these differences is most likely due to the simplified parameter space of the Izhikevich cell model. Using a more detailed biophysical cell model may help to fully replicate the results observed in vitro. In response to decreases in the magnitude of hyperpolarizing inputs, the model cells behaved similarly to stellate cells; the MRA of spikes induced by hyperpolarizing inputs decreased (earlier phases elicited spikes, h1), while the MRA of spiking output increased (spiking output occurred at later phases, h2).
Fig. 7.
Izhikevich neurons possess similar intrinsic and rebound spiking properties as stellate cells. (a and b) In response to a chirp function stimulus (a1, b1) a low frequency Izhikevich neuron displays a lower depolarized resonance frequency (a2, 4.425 Hz) and a lower resonance frequency near its resting membrane potential (a3, 4.852 Hz) compared to a high frequency Izhikevich neuron (b2, 5.249 Hz; b3, 6.897 Hz). Differential frequency preferences were achieved by tuning the a parameter in Eq. (6) (low frequency cell, a = 0.007; high frequency cell, a = 0.015). (c) In response to hyperpolarizing square current steps, Izhikevich neurons display a prominent sag potential and upon release of the current step, fire rebound spikes (# denotes truncated spikes, data shown from low frequency cell in a). (d) When the low (d1) and high (d2) frequency Izhikevich neurons receive hyperpolarizing synaptic input pulses superimposed on a sinusoid, the cells spike to a subset of phases of hyperpolarizing input pulses. (e and f) Rose plots show the phases of hyperpolarizing input pulses inducing spikes for the low (e1) and high (e2) frequency Izhikevich neuron, as well as each cell's respective phase range of output spiking (f1, f2). (g and h) Summary bar graphs show how increasing the baseline oscillation frequency (g) and the magnitude of hyperpolarizing inputs (h) affect the input MRA (g1, h1) and output MRA (g2, h2) of the low frequency cell.
3.7. Network simulations of rebound spiking
The resonance and rebound spiking dynamics of simulated stellate cells shown above in Fig. 7 are able to generate grid cell firing properties during one dimensional movement in a network model. The crucial network connectivity is shown in Fig. 8a, and depicts stellate cells receiving oscillatory inhibitory inputs regulated by input from the medial septum, and feedback inhibition from local interneurons. As described in the equations, the oscillatory input regulated by the medial septum has different phases for different stellate cells, resulting in differential responses due to phase sensitivity to the timing of inhibitory synaptic input that influences the full population of stellate cells simultaneously. The result of the different oscillation phases regulated by medial septal input is that specific subsets of neurons will spike in response to the same phase of hyperpolarizing synaptic input to the entire population. These properties allow separation of a specific population of neuronal activity because only a subset of neurons will spike due to the timing of the hyperpolarizing input relative to the phase regulated by medial septal input.
Fig. 8.
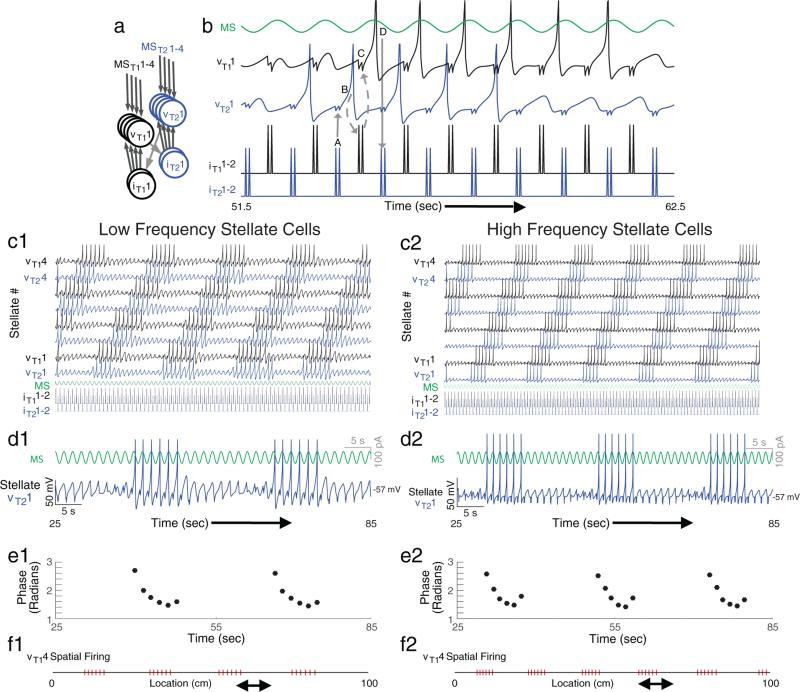
A model with stellate cells, possessing resonance and rebound spiking properties, embedded in an inhibitory network creates theta skipping and grid cell firing patterns on a linear track. (a) Our model uses stellate cells (v) that receive oscillatory input regulated by the medial septum (MS) and feedback inhibition from interneurons (i). (b) Inhibition causes rebound spiking (A) in a stellate cell (vT11) on the first cycle of theta cycle skipping that activates an interneuron (B) which inhibits (C) another stellate cell (vT21) causing a rebound spike (D) that activates another interneuron that activates the first stellate cell (vT11). This process is repeated, resulting in cyclical activity of stellate cells on alternating cycles. (c) In this model, stellate cells receive oscillatory input with different phases regulated by the medial septum and receive feedback inhibition from two interneurons. Each cell's membrane potential is shown with a thick line, and if rebound spiking (e.g. vT11) is faster than the period of oscillatory input, then feedback inhibition (iT21) slowly shifts spiking to cells with earlier phases (e.g. vT22). (d and f) Looking at a portion of a single cell's activity in relation to its oscillatory input (d) shows that spiking shifts to earlier phases over time. This theta phase precession is depicted quantitatively in (e). Plotting spiking in relation to the animal's location as it runs the linear track shows periodic spatial firing resembling grid cell activity (f).
Note that this network lacks excitatory monosynaptic connections between stellate cells, and therefore stellate cells interact only via interneurons. Despite the presence of only inhibitory feedback between stellate cells, the network can maintain spiking activity in stellate cells as shown in Fig. 8b, which shows a detailed view of a selection of neurons from the larger simulation of 8 stellate cells and 4 interneurons shown in Fig. 8c. The arrows in Fig. 8b show how inhibitory potentials cause a rebound spike in the second stellate cell (vT21), which activates the first interneuron (iT11) causing a rebound spike in the first stellate cell (vT11). This rebound spike then generates a spike in the second interneuron (iT21) and the cycle repeats itself. As shown here, the model generates spiking activity that occurs on alternate theta cycles in different stellate cells, accounting for theta cycle skipping observed in vivo (Brandon et al., 2013). This same phenomenon was shown with large numbers of neurons in previous models (Fig. 7C in Brandon et al., 2013). In addition, we tested simulations with random selection of stellate-interneuron connections and interneuron-stellate connections. These randomly connected networks still demonstrated theta cycle skipping in stellate cells about 80% of the time due to the phase specificity for inducing rebound spikes in stellate cells. Analysis of the development of these types of circuits is a topic for future studies beyond the scope of this paper.
Constructing a network model consisting of multiple cell pairs and providing each with oscillatory input of different phase regulated by medial septal inputs, results in spiking output dependent on the difference between the time of the oscillation period and the speed of rebound spiking. This network behavior can be seen in Fig. 8c. Periodic firing of individual stellate cells occurs at different times throughout the run due to the timing of the feedback inhibitory input from interneurons going to all stellate cells in a population that only generates spiking when it interacts with a specific range of phases of oscillatory input to individual stellate cells. Thus, the nonspecific feedback signal can separately activate a subset of the stellate cell population.
For example, consider the stellate cell in the bottom row (vT11). This cell starts out inactive because the hyperpolarizing input, due to spiking of the inhibitory interneuron, arrives at a time that does not cause a rebound spike. However, the input of this same interneuron to other stellate cells (e.g. vT14) arrives at the correct phase relative to oscillatory input and causes rebound spiking. Note that the time between the interneuron spike and a stellate cell rebound spike is slightly shorter than the wavelength of the oscillatory input regulated by the medial septum. As each rebound spike occurs earlier in phase relative to the oscillatory input, it causes interneuron spiking at an earlier phase. Eventually, the phase of interneuron spiking comes early enough to fall within the range of input phases that evoke rebound spiking in vT11, causing it to start spiking. The rebound of this cell is slightly faster than the period of the oscillatory input, so each spike comes at a slightly earlier phase on each cycle of the oscillatory input, causing slightly earlier spiking of the interneuron until eventually the interneuron input comes too early in phase and falls out of the range of phases that induce rebound spiking in vT11. This demonstrates how the rebound spiking properties of the cell could allow spiking in a delimited period of time due to both the limited range of input phases inducing rebound spikes and the timing of output spikes relative to the wavelength of oscillatory input regulated by the medial septum. These basic properties are robust to the use of a Gaussian distribution of the rebound spiking parameter a across stellate cells within the same network. We consistently saw the same functional properties as in Fig. 8 after adding Gaussian noise to the parameter a with standard deviation (σ) of 30% of the magnitude of parameter a, and commonly saw effective function with even higher standard deviation.
Looking at a portion of a single stellate cell's spiking output (Fig. 8d), one can see how spiking phase precesses (Fig. 8e) relative to network theta rhythm as the animal moves through a firing field. Plotting spiking output along the spatial domain, periodic firing fields along the linear track are observed (Fig. 8f), similar to grid cell firing as a rat runs on a linear track. The physiological differences in resonance and rebound properties between different neurons shown in Fig. 7a3 versus Fig. 7b3 can generate substantial differences in the size and spacing of firing fields as shown in Fig. 8f1 versus Fig. 8f2. This model has the property of all oscillatory interference models (e.g. Burgess, 2008; Burgess et al., 2007) that the spacing depends on the differences in frequency or period between two rhythms. In this model, the size and spacing arises from the difference between the temporal period of the rebound spiking and the period of the oscillations regulated by medial septum.
As shown in Fig. 5, the amplitude of inhibitory input determines the speed of rebound spiking. For weak inhibitory input, the speed of rebound spiking could match the period of oscillatory input, allowing the firing to remain in one cell, whereas stronger inhibitory input could cause faster rebound spiking and a more rapid shift between cells in the population as shown in previous modeling (Hasselmo, 2013). Simulations in the previous paper (Hasselmo, 2013; Hasselmo & Shay, 2014) show that if the running speed of the rat determines the magnitude of feedback inhibition, the velocity of the running can determine the rate of transition between neurons firing in different firing fields. This was shown with progressive changes in the magnitude of inhibition that caused progressive shortening of the time between firing fields in simulations (Hasselmo, 2013; Hasselmo & Shay, 2014). The influence of running speed on transitions between neurons corresponds to a mechanism for the integration of velocity to determine the individual neurons that fire. This would allow firing of grid cells that is driven by the running velocity of the rat, as shown in many models of grid cells (Blair et al., 2008; Burgess, 2008; Burgess et al., 2007; Hasselmo, 2008) that can simulate grid cells on complex two-dimensional trajectories with continuous changes in the frequency of interacting cosine function oscillations. The rebound spiking mechanism described here has been shown to function over short two-dimensional trajectories (Hasselmo & Shay, 2014), but shows a build-up of trajectory error due to the limited number of neurons and the discrete nature of spiking.
4. Discussion
4.1. Phase specificity of rebound spiking
The physiological results presented here show a characterization of rebound spiking in response to hyperpolarizing current injection representing inhibitory post synaptic currents in stellate cells of the mEC. Hyperpolarizing inputs were superimposed on fixed frequency sinusoidal inputs in order to simulate an idealized theta rhythm observed in vivo. Our method reveals a specific range of phases of hyperpolarizing inputs that cause spiking. This demonstrates that the phase of oscillatory input to stellate cells can determine which subpopulation of neurons will be active in response to global inhibitory feedback pulses. This provides a potential mechanism by which network dynamics can interact with feedback inhibition to separate activity into a discrete population of neurons. This same mechanism can also complete the activity of the subpopulation by activating any inactive neurons that should be active.
The phase specificity of hyperpolarizing inputs that elicit spikes is dependent on the presence of Ih, as blocking the Ih with 10 μM ZD7288 abolished the phase specificity in response to hyperpolarizing input pulses. The ability of Ih to limit the input phases causing spikes is important, as this allows the periodic firing fields in the model presented here. The narrow temporal phase range of output spiking is consistent with in vivo data in which spiking in layer II EC is limited to a narrow temporal phase range of the theta oscillation (Quilichini, Sirota, & Buzsaki, 2010). However, in contrast to the dependence of input phase on Ih, the consistent output spiking phase range we observed does not appear to be dependent on Ih as spiking phases of cells were consistent in non-stellate cells as well as in stellate cells before and after drug application. This similarity is likely due to the output phase of spiking activity in both types of cells being regulated by the interaction of currents activated by depolarization with the peak of the sinusoidal oscillation.
4.2. Linking resonance and rebound spiking to grid cell spatial periodicity
In the computational model, the periodic firing behavior of stellate cells relies on the difference between the period of the theta oscillation and the timing of the induction of rebound spiking, which is dependent on a cell's resonant frequency. The resulting constraint on neural activity due to this interaction is analogous to the beat pattern in oscillatory interference models (Burgess, 2008; Burgess et al., 2007), in that it determines the grid cell firing field size and spacing, and determines the slope of theta phase precession observed in vivo (Climer, Newman, & Hasselmo, 2013; Hafting, Fyhn, Bonnevie, Moser, & Moser, 2008; Hasselmo, 2013; Kjelstrup et al., 2008). Our data support the link between resonance and rebound spiking as cells with different resonant frequencies preferentially responded with rebound spikes to different input phases for a given sinusoidal input frequency. This difference in rebound spiking phase for different resonance frequencies could contribute to the difference in spacing of grid cell firing observed for neurons recorded at different D/V positions of mEC (Hafting et al., 2005; Stensola et al., 2012) as the resonance frequency of layer II mEC stellate cells decreases along the D/V axis (Boehlen et al., 2010; Giocomo & Hasselmo, 2009; Giocomo et al., 2007). In this theoretical framework, stellate cells in dorsal mEC with higher resonance frequencies and possessing faster rebound spiking compared to ventral stellates would have smaller spatial firing fields and smaller spacing between fields. The simulations in Fig. 8f1 and f2 show how this difference in size and spacing could arise from the physiological differences in resonance frequency.
Consistent with our results, Giocomo et al. (2011) have shown that grid cell firing fields in HCN1 knockout mice become larger and less sharp across all D/V locations. The absence of the HCN1 subunit doesn't completely abolish Ih in stellate cells, as other HCN subunits (e.g. HCN2) are still present; however, the Ih fast time constants, sag potentials, and resonance frequencies are decreased (Giocomo & Hasselmo, 2009). Taken with our data, these results suggest that the speed of rebound spiking would be decreased with HCN1 knockout, leading to expanding grid fields and spacing. Although stellate cell rebound spiking properties in HCN1 knockout mice have not been characterized, it is possible that they behave similar to our non stellate cells (or as our pharmacological blockade of Ih), and respond to hyperpolarizing inputs with decreased phase specificity.
Similarly, cells that do not express a lot of Ih, and lack theta frequency resonance, such as pyramidal cells in layer II (Domnisoru et al., 2013; Ray et al., 2014; Tang et al., 2014) and non-stellate cells in deeper layers of mEC (Sargolini et al., 2006; Boccara et al., 2010) still produce grid cell firing patterns. These cells may inherit their grid cell spiking pattern from other cells, or perhaps rely on other mechanisms for grid cell generation such as attractor dynamics. Therefore, rebound spiking may be just one of many mechanisms contributing to the generation of grids.
4.3. Significance of magnitudes of hyperpolarization
We found that the phase of rebound spiking can also change systematically with magnitude of hyperpolarizing input pulses (Fig. 3g). This provides a potential mechanism for representation of velocity, as shortening the interval to rebound spiking corresponds to a higher frequency of a velocity-controlled oscillator in an oscillatory interference model of grid cells (Blair et al., 2008; Burgess, 2008; Burgess et al., 2007; Bush & Burgess, 2014; Hasselmo, 2008). This property is required to allow trajectories with different running speeds to generate firing in spatially consistent locations. If the rat runs more rapidly through firing fields, then larger feedback inhibition could allow faster rebound spikes that would result in a faster transition of spiking between different firing fields. This inhibitory velocity signal is reasonable as medial EC PV interneurons show increased firing rates with increased running speed (Buetfering, Allen, & Monyer, 2014; Hinman, Brandon, Chapman, & Hasselmo, 2013).
Our in vitro and modeling data show that as the magnitude of hyperpolarizing input pulses increases, output spiking phase becomes earlier, suggesting that the number and or strength of inhibitory synapses onto a stellate cell can contribute to its spiking phase. In addition to allowing regulation dependent on velocity, this could also contribute to the D/V difference in spacing of grid cell firing fields. PV interneurons differentially target stellate cells along the D/V axis of mEC. Dorsal stellate cells receive a greater number of and more widespread PV inhibitory synaptic contacts compared to ventral stellate cells (Beed et al., 2013). The stronger inhibition in dorsal stellates could lead to faster rebound spiking and smaller spacing between grid cell firing fields compared to ventral stellate cells. This indicates another way that the interaction between PV interneurons and stellate cells could contribute to the spacing of grid cell firing fields through rebound spiking properties.
4.4. Relationship of model to MSDB-medial EC anatomical connectivity
GABAergic neurons of the MSDB have been proposed to be largely responsible for generating theta (Stewart & Fox, 1990). The majority of MSDB inhibitory neurons express PV and selectively project to interneurons of the hippocampus (Freund, 1989; Freund & Antal, 1988). Anterograde and retrograde tracing studies (Alonso & Köhler, 1984) have shown the EC receives anatomically specific inputs from the MSDB; inputs to medial EC tend to come from the most medial portions of the MSDB, where the most dense MSDB PV cell population is located (Alonso, Coveñas, Lara, & Aijón, 1990; Kiss, Patel, Baimbridge, & Freund, 1990). Recently it has been shown that optogenetic stimulation of axons of GABAergic medial septal cells causes monosynaptic IPSPs in over 60% of medial EC interneurons (Gonzalez-Sulser et al., 2014). The study distinguished mEC interneuron subtypes in terms of fast spiking and low-threshold spiking behaviors. However it is unclear how many different interneuron subtypes were targeted by medial septal GABAergic projections, and the connectivity of these interneurons with other medial EC cells is not known. Our model uses direct oscillatory inputs to stellate cells as a simplification, but this oscillatory input is not intended to represent a direct influence of medial septum. Instead, this oscillatory input is meant to represent the effect of septal input synapsing on and regulating rhythmic activity of a population(s) of interneurons distinct from those receiving input from stellate cells shown in Fig. 8. As an alternative, our model is able to work with the medial septal theta input synapsing directly onto the medial EC interneurons mediating feedback inhibition in Fig. 8 (these simulations are not shown). The mechanism of this alternate model has been published elsewhere (Hasselmo & Shay, 2014).
We have simulated theta skipping and grid cell firing behavior by selecting parameters of the Izhikevich neuron that match cellular properties found in vitro. Our model consists of stellate cells possessing resonance and rebound spiking properties that are embedded in an inhibitory network. When medial septal theta rhythmic input is delivered to stellate cells they generate grid cell firing activity. Loss of this medial septal subthreshold oscillatory input in the model results in the loss of spatially specific firing (Hasselmo, 2013). The network architecture used in this model therefore accounts for the loss of grid cell spatial periodicity shown experimentally with inactivation of the medial septum (Brandon et al., 2011; Koenig, Linder, Leutgeb, & Leutgeb, 2011).
4.5. Significance to other grid cell models
The interaction of hyperpolarizing input pulses and sinusoidal input in our experimental data is analogous to the interaction of feedback inhibition and oscillatory input used in our model in which rebound spiking causes periodic firing of different entorhinal neurons. This interaction of the speed of rebound spiking with the period of oscillatory input regulated by medial septum is analogous to the interaction of different oscillations used in the oscillatory interference model of grid cells (Blair et al., 2008; Burgess, 2008; Burgess et al., 2007; Bush & Burgess, 2014; Hasselmo, 2008). The oscillatory input at different phases arising from the medial septum could be generated by a mechanism such as the ring attractor network (Blair et al., 2007) that was proposed to involve neurons in a ring that sequentially activate each other at different phases. The ring attractor could provide a stable baseline frequency as in the simulation presented here. Alternatively, the ring attractor could provide medial septal regulation of oscillatory input that changes frequency relative to a stable period of rebound spiking, allowing differential phase interactions dependent upon running speed. Cells of the medial septum show firing rates dependent on the animal's running speed (King, Reece, & O'Keefe, 1998; Zhou, Tamura, Kuriwaki, & Ono, 1999) as well as cosine directional tuning of theta burst frequencies (Welday, Shlifer, Bloom, Zhang, & Blair, 2011), suggesting that both running speed and direction coding are present in the medial septum. Previous data show changes in frequency of theta rhythm associated with running speed (Hinman, Penley, Long, Escabi, & Chrobak, 2010; Jeewajee et al., 2008; Maurer, Vanrhoads, Sutherland, Lipa, & McNaughton, 2005; Rivas, Gaztelu, & Garcia-Austt, 1996), that might arise from changes in the rhythmic activity of septal theta cells (Welday et al., 2011; Hinman et al., 2013). Changes in medial septal theta frequency could provide an alternate mechanism for velocity-dependent changes in the inhibition-induced period of membrane potential oscillations in stellate cells relative to the timing of rebound spikes. This provides another possible way of representing running velocity in a network model, in contrast to the use of changes in magnitude of feedback inhibition.
Kropff and Treves (2008) have suggested that Hebbian plasticity in feed-forward synapses could enable the emergence of grid cell firing from slowly changing sensory inputs coupled with neuronal firing adaptation, rather than from self-representations of velocity. This mechanism differs from our mechanism as it focuses on the influence of adaptation on neural activity during initial formation of grid cell representations. However, we believe this mechanism during initial learning could be complementary with our rebound spiking model by providing initial learning of sensory influence on grid cells could complement and correct the updating of grid cells based on self-motion.
4.6. Relationship to previous in vitro data
A previous slice physiology study has shown that depending on the phase an inhibitory synaptic input is delivered during a 5 Hz oscillation, it is able to delay or advance the timing of repetitive spiking activity in CA1 pyramidal cells (Kwag & Paulsen, 2009). This spike time advancement is dependent on the Ih as it is abolished by ZD7288. While this study was not studying rebound spiking per se, there are important similarities to our study. Kwag and Paulsen were recording from cells containing Ih, they were holding these cells close to threshold, and they were delivering theta oscillations, as well as hyperpolarizing inputs. Both studies found that Ih interacted with both the oscillations and inhibition to dynamically change, in our case the hyperpolarizing input phase causing spiking, and in their case the phase of repetitive spiking output induced by the sinusoidal input. Whether a similar phenomenon to the Kwag and Paulsen effect exists in medial EC stellate cells was outside of the scope of our project, but is an intriguing question.
4.7. Relationship to previous in vivo data
In vivo intracellular recordings in the mEC have shown ramp depolarizations and sMPOs in stellate cells during traversals through grid cell firing fields (Domnisoru et al., 2013; Schmidt-Hieber & Häusser, 2013). Although ramp depolarizations drive spiking (Domnisoru et al., 2013; Schmidt-Hieber & Häusser, 2013), spikes occur preferentially at the peaks of theta oscillations (Domnisoru et al., 2013). These data are generally consistent with our data. In our experiments, stellate cells had to be sufficiently depolarized above resting potential with current injection in order to display rebound spiking, and rebound spikes occurred near the peak of the theta oscillation. Note that in Fig. 2 the lowest hyperpolarization of membrane potential between spikes is −60.24 mV, which is well above that neuron's resting potential of −62.43 mV. When a stellate cell's membrane potential is shifted closer to threshold via depolarizing ramps, a cell could integrate inhibitory inputs that cause rebound spikes. As we have shown in our model, this rebound spiking mechanism can account for phase precession and can therefore support temporal codes similar to oscillatory interference models. However, as shown in Figs. 7 and 8, the simulations of rebound spiking used here require neurons to go below their resting potential to generate rebound spikes, in contrast to our experimental data and the previous data showing that membrane potential does not always return to rest during field crossings (Domnisoru et al., 2013). This might reflect the fact that the simplified Izhikevich neurons used here do not have different compartments for different portions of the neuron. In multi-compartment models (Ferrante, Shay, Tsuno, Chapman, & Hasselmo, 2014), hyperpolarizing inputs can activate h-current in dendritic compartments of the neuron without causing a substantial hyperpolarizing deflection below resting potential in the membrane potential recorded at the soma. Future in vivo work will be crucial to identifying what cell type(s) contribute to ramp depolarizations as well as to whether or not interneurons can cause rebound spiking in mEC stellate cells.
Recent in vivo optogenetic experiments (Buetfering et al., 2014) explored the role of recurrent inhibition in generation of grid cells, showing that PV cells fire across a wide range of spatial locations, and a single interneuron can interact with grid cells coding very different spatial locations. This is consistent with our simulations (Fig. 8) in which single interneurons fire at a wide range of different spatial locations and provide input to grid cells coding multiple different spatial locations. They also showed that grid cells did not change during stimulation of interneurons at specific temporal phase relative to theta rhythm oscillation. Our experimental and computational results suggest that despite the variable incoming phase of the inhibitory synaptic inputs, only a subset of these inputs would cause spiking in grid cells, and the restricted spatial location of stellate spikes would be preserved. This might prevent an effect of optogenetic stimulation of interneurons on location coding by grid cells. Furthermore, the pairing of inhibition with an excitatory drive would be more effective in generating rebound spikes. Therefore when inhibitory inputs coincide with ramp depolarizations rebound spiking could contribute to grid cell spiking activity. However without this depolarization, i.e. at locations out of a grid cell's firing field, inhibitory inputs would be less likely to occur. This might also contribute to the lack of effect of theta phase specific activation of inhibitory interneurons.
Stark et al. (2013) have demonstrated that optogenetic chirp (0–40 Hz) activation of PV interneurons causes rebound spiking at theta-band frequencies in CA1 and neocortical pyramidal cells. Similar to the shifts in output spiking phase observed in our rebound spiking data, the frequency of theta-band spiking resonance was modulated by the magnitude of inhibition and was dependent on the h-current. It is an open question whether stellate cells would display similar spiking resonance properties. However, it seems possible as stellate cells possess even stronger Ih and subthreshold resonance properties compared to CA1 and neocortical pyramidal cells (Alonso & Llinás, 1989; Erchova et al., 2004). These data offer an alternative function for PV driven rebound spikes, where instead of the delay of a single rebound spike determining spatial firing, the frequency of rebound spiking could determine grid cell activity. Future investigations of spiking resonance and rebound spiking properties in mEC of navigating animals could help answer these questions.
4.8. Concluding remarks
In conclusion, our experimental and modeling results suggest that the ability of mEC stellate cells to fire rebound spikes in response to a particular range of inhibitory input phases could underlie an ability to perform temporal pattern separation. The rebound spiking provides a dynamical mechanism in which feedback inhibition at specific phases results in self-sustained activity with complex attractor dynamics. The phase specificity of rebound spiking allows temporal pattern separation to reduce the rebound spiking of neurons with a different phase of medial septal input. The phase specificity also allows pattern completion to cause rebound spiking in previously inactive neurons with the correct phase of medial septal input. This rebound spiking mechanism for temporal pattern separation may also allow separation of grid cells into different module populations with different size and spacing of firing fields. The size and spacing of grid fields is determined by the resonance frequency that determines the delay of rebound spiking of the stellate cell relative to the period of medial septal GABA input to the stellate cell. Because of this, both the resonance properties and the frequency of medial septal GABAergic input will determine the size of different firing fields, whereas the spatial phase of the firing field is dictated by the temporal phase of the medial septal GABA input onto that stellate cell.
Acknowledgments
This work was supported by the National Institute of Mental Health (R01 MH61492, R01 MH60013); and the Office of Naval Research (MURI N00014-10-1-0936).
Abbreviations
- mEC
medial entorhinal cortex
- sMPOs
subthreshold membrane potential oscillations
- MRA
mean resultant angle
- MRL
mean resultant length
- D/V
dorsal-to-ventral
- PV
parvalbumin
- MSDB
medial septum/diagonal band of Broca
Footnotes
The authors declare no competing financial interests.
References
- Alonso JR, Coveñas R, Lara J, Aijón J. Distribution of parvalbumin immunoreactivity in the rat septal area. Brain Research Bulletin. 1990;24:41–48. doi: 10.1016/0361-9230(90)90287-a. [DOI] [PubMed] [Google Scholar]
- Alonso A, Klink R. Differential electroresponsiveness of stellate and pyramidal-like cells of medial entorhinal cortex layer II. Journal of Neurophysiology. 1993;70:128–143. doi: 10.1152/jn.1993.70.1.128. [DOI] [PubMed] [Google Scholar]
- Alonso A, Köhler C. A study of the reciprocal connections between the septum and the entorhinal area using anterograde and retrograde axonal transport methods in the rat brain. Journal of Comparative Neurology. 1984;225:327–343. doi: 10.1002/cne.902250303. [DOI] [PubMed] [Google Scholar]
- Alonso A, Llinás RR. Subthreshold Na+-dependent theta-like rhythmicity in stellate cells of entorhinal cortex layer II. Nature. 1989;342:175–177. doi: 10.1038/342175a0. [DOI] [PubMed] [Google Scholar]
- Barry C, Hayman R, Burgess N, Jeffery KJ. Experience-dependent rescaling of entorhinal grids. Nature Neuroscience. 2007;10:682–684. doi: 10.1038/nn1905. [DOI] [PubMed] [Google Scholar]
- Beed P, Gundlfinger A, Schneiderbauer S, Song J, Böhm C, Burgalossi A, et al. Inhibitory gradient along the dorsoventral axis in the medial entorhinal cortex. Neuron. 2013;79:1197–1207. doi: 10.1016/j.neuron.2013.06.038. [DOI] [PubMed] [Google Scholar]
- Berens P. CircStat: A MATLAB toolbox for circular statistics. Journal of Statistical Software. 2009;31:1–21. [Google Scholar]
- Blair HT, Gupta K, Zhang K. Conversion of a phase- to a rate-coded position signal by a three-stage model of theta cells, grid cells, and place cells. Hippocampus. 2008;18:1239–1255. doi: 10.1002/hipo.20509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blair HT, Welday AC, Zhang K. Scale-invariant memory representations emerge from moiré interference between grid fields that produce theta oscillations: A computational model. Journal of Neuroscience. 2007;27:3211–3229. doi: 10.1523/JNEUROSCI.4724-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boccara CN, Sargolini F, Thoresen VH, Solstad T, Witter MP, Moser EI, Moser M-B. Grid cells in pre- and parasubiculum. Nature Neuroscience. 2010;13:987–994. doi: 10.1038/nn.2602. [DOI] [PubMed] [Google Scholar]
- Boehlen A, Heinemann U, Erchova I. The range of intrinsic frequencies represented by medial entorhinal cortex stellate cells extends with age. Journal of Neuroscience. 2010;30:4585–4589. doi: 10.1523/JNEUROSCI.4939-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandon MP, Bogaard AR, Libby CP, Connerney MA, Gupta K, Hasselmo ME. Reduction of theta rhythm dissociates grid cell spatial periodicity from directional tuning. Science. 2011;332:595–599. doi: 10.1126/science.1201652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandon MP, Bogaard AR, Schultheiss NW, Hasselmo ME. Segregation of cortical head direction cell assemblies on alternating theta cycles. Nature Neuroscience. 2013;16:739–748. doi: 10.1038/nn.3383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buetfering C, Allen K, Monyer H. Parvalbumin interneurons provide grid cell-driven recurrent inhibition in the medial entorhinal cortex. Nature Neuroscience. 2014;17:710–718. doi: 10.1038/nn.3696. [DOI] [PubMed] [Google Scholar]
- Burak Y, Fiete IR. Accurate path integration in continuous attractor network models of grid cells. Public Library of Science Computational Biology. 2009;5:e1000291. doi: 10.1371/journal.pcbi.1000291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess N. Grid cells and theta as oscillatory interference: Theory and predictions. Hippocampus. 2008;18(12):1157–1174. doi: 10.1002/hipo.20518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess N, Barry C, O'Keefe J. An oscillatory interference model of grid cell firing. Hippocampus. 2007;812:801–812. doi: 10.1002/hipo.20327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess N, Barry C, Jeffery KJ, O'Keefe J. A grid and place cell model of path integration utilizing phase precession versus theta.. Computational cognitive neuroscience meeting; Washington, D.C.. 2005. [Google Scholar]
- Burton BG, Economo MN, Lee GJ, White JA. Development of theta rhythmicity in entorhinal stellate cells of the juvenile rat. Journal of Neurophysiology. 2008;100:3144–3157. doi: 10.1152/jn.90424.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bush D, Burgess N. A hybrid oscillatory interference/continuous attractor network model of grid cell firing. Journal of Neuroscience. 2014;34:5065–5079. doi: 10.1523/JNEUROSCI.4017-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Climer JR, Newman EL, Hasselmo ME. Phase coding by grid cells in unconstrained environments: Two-dimensional phase precession. European Journal of Neuroscience. 2013;38(4):2526–2541. doi: 10.1111/ejn.12256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Couey JJ, Witoelar A, Zhang S-J, Zheng K, Ye J, Dunn B, et al. Recurrent inhibitory circuitry as a mechanism for grid formation. Nature Neuroscience. 2013;16:318–334. doi: 10.1038/nn.3310. [DOI] [PubMed] [Google Scholar]
- Deshmukh SS, Yoganarasimha D, Voicu H, Knierim JJ. Theta modulation in the medial and the lateral entorhinal cortices. Journal of Neurophysiology. 2010;104:994–1006. doi: 10.1152/jn.01141.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhillon A, Jones RS. Laminar differences in recurrent excitatory transmission in the rat entorhinal cortex in vitro. Neuroscience. 2000;99:413–422. doi: 10.1016/s0306-4522(00)00225-6. [DOI] [PubMed] [Google Scholar]
- Dickson, Clayton T, Magistretti J, Shalinsky MH, Fransén E, Hasselmo ME, Alonso A. Properties and role of I(h) in the pacing of subthreshold oscillations in entorhinal cortex layer II neurons. Journal of Neurophysiology. 2000;83:2562–2579. doi: 10.1152/jn.2000.83.5.2562. [DOI] [PubMed] [Google Scholar]
- Domnisoru C, Kinkhabwala AA, Tank DW. Membrane potential dynamics of grid cells. Nature. 2013;495:199–204. doi: 10.1038/nature11973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erchova I, Kreck G, Heinemann U, Herz AVM. Dynamics of rat entorhinal cortex layer II and III cells: Characteristics of membrane potential resonance at rest predict oscillation properties near threshold. Journal of Physiology. 2004;560:89–110. doi: 10.1113/jphysiol.2004.069930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrante M, Shay CF, Tsuno Y, Chapman GW, Hasselmo ME. Post-inhibitory rebound spikes in rat MEC layer II/III principal cells: In-vivo, in-vitro, and in-silico evidence and characterization. Society for Neuroscience Abstract. 2014;40(297):11. [Google Scholar]
- Freund TF. GABAergic septohippocampal neurons contain parvalbumin. Brain Research. 1989;478:375–381. doi: 10.1016/0006-8993(89)91520-5. [DOI] [PubMed] [Google Scholar]
- Freund TF, Antal M. GABA-containing neurons in the septum control inhibitory interneurons in the hippocampus. Nature. 1988;336:170–173. doi: 10.1038/336170a0. [DOI] [PubMed] [Google Scholar]
- Fuhs MC, Touretzky DS. A spin glass model of path integration in rat medial entorhinal cortex. Journal of Neuroscience. 2006;26(16):4266–4276. doi: 10.1523/JNEUROSCI.4353-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giocomo LM, Hasselmo ME. Computation by oscillations: Implications of experimental data for theoretical models of grid cells. Hippocampus. 2008a;18:1186–1199. doi: 10.1002/hipo.20501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giocomo LM, Hasselmo ME. Time constants of h current in layer II stellate cells differ along the dorsal to ventral axis of medial entorhinal cortex. Journal of Neuroscience. 2008b;28:9414–9425. doi: 10.1523/JNEUROSCI.3196-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giocomo LM, Hasselmo ME. Knock-out of HCN1 subunit flattens dorsal–ventral frequency gradient of medial entorhinal neurons in adult mice. Journal of Neuroscience. 2009;29:7625–7630. doi: 10.1523/JNEUROSCI.0609-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giocomo LM, Hussaini SA, Zheng F, Kandel ER, Moser M-B, Moser EI. Grid cells use HCN1 channels for spatial scaling. Cell. 2011;147:1159–1170. doi: 10.1016/j.cell.2011.08.051. [DOI] [PubMed] [Google Scholar]
- Giocomo LM, Zilli EA, Fransén E, Hasselmo ME. Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science. 2007;315:1719–1722. doi: 10.1126/science.1139207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez-Sulser A, Parthier D, Candela A, McClure C, Pastoll H, Garden D, et al. GABAergic projections from the medial septum selectively inhibit interneurons in the medial entorhinal cortex. Journal of Neuroscience. 2014;34:16739–16743. doi: 10.1523/JNEUROSCI.1612-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guanella A, Kiper D, Verschure P. A model of grid cells based on a twisted torus topology. International Journal of Neural Systems. 2007;17:231–240. doi: 10.1142/S0129065707001093. [DOI] [PubMed] [Google Scholar]
- Haas JS, White JA. Frequency selectivity of layer II stellate cells in the medial entorhinal cortex. Journal of Neurophysiology. 2002;88:2422–2429. doi: 10.1152/jn.00598.2002. [DOI] [PubMed] [Google Scholar]
- Hafting T, Fyhn M, Bonnevie T, Moser M-B, Moser EI. Hippocampus-independent phase precession in entorhinal grid cells. Nature. 2008;453:1248–1252. doi: 10.1038/nature06957. [DOI] [PubMed] [Google Scholar]
- Hafting T, Fyhn M, Molden S, Moser M-B, Moser EI. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
- Hasselmo ME. Grid cell mechanisms and function: Contributions of entorhinal persistent spiking and phase resetting. Hippocampus. 2008;18:1213–1229. doi: 10.1002/hipo.20512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo ME. Neuronal rebound spiking, resonance frequency and theta cycle skipping may contribute to grid cell firing in medial entorhinal cortex. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences. 2013;369:20120523. doi: 10.1098/rstb.2012.0523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo ME, Giocomo LM, Zilli EA. Grid cell firing may arise from interference of theta frequency membrane potential oscillations in single neurons. Hippocampus. 2007;1271:1252–1271. doi: 10.1002/hipo.20374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo ME, Shay CF. Grid cell firing patterns may arise from feedback interaction between intrinsic rebound spiking and transverse traveling waves with multiple heading angles. Frontiers in Systems Neuroscience. 2014;8:201. doi: 10.3389/fnsys.2014.00201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinman JR, Brandon MP, Chapman GW, Hasselmo ME. Speed modulation of medial entorhinal cortical neurons during medial septal inactivation. Society for Neuroscience Abstract. 2013;39:769.01. [Google Scholar]
- Hinman JR, Penley SC, Long LL, Escabi MA, Chrobak JJ. Septotemporal variation in dynamics of theta: Speed and habituation. Journal of Neurophysiology. 2010;105:2675–2686. doi: 10.1152/jn.00837.2010. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM. Dynamical systems in neuroscience: The geometry of excitability and bursting. MIT Press; Cambridge, MA: 2007. [Google Scholar]
- Jeewajee A, Barry C, O'Keefe J, Burgess N. Grid cells and theta as oscillatory interference: Electrophysiological data from freely moving rats. Hippocampus. 2008;18:1175–1185. doi: 10.1002/hipo.20510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffery KJ, Donnett JG, O'Keefe J. Medial septal control of theta-correlated unit firing in the entorhinal cortex of awake rats. Neuroreport. 1995;6:2166–2170. doi: 10.1097/00001756-199511000-00017. [DOI] [PubMed] [Google Scholar]
- King C, Reece M, O'Keefe J. The rhythmicity of cells of the medial septum/diagonal band of Broca in the awake freely moving rat: Relationships with behaviour and hippocampal theta. European Journal of Neuroscience. 1998;10:464–477. doi: 10.1046/j.1460-9568.1998.00026.x. [DOI] [PubMed] [Google Scholar]
- Kiss J, Patel AJ, Baimbridge KG, Freund TF. Topographical localization of neurons containing parvalbumin and choline acetyltransferase in the medial septum-diagonal band region of the rat. Neuroscience. 1990;36:61–72. doi: 10.1016/0306-4522(90)90351-4. [DOI] [PubMed] [Google Scholar]
- Kjelstrup KB, Solstad T, Brun VH, Hafting T, Leutgeb S, Witter MP, et al. Finite scale of spatial representation in the hippocampus. Science. 2008;321:140–143. doi: 10.1126/science.1157086. [DOI] [PubMed] [Google Scholar]
- Klink R, Alonso A. Ionic mechanisms for the subthreshold oscillations and differential electroresponsiveness of medial entorhinal cortex layer II neurons. Journal of Neurophysiology. 1993;70:144–157. doi: 10.1152/jn.1993.70.1.144. [DOI] [PubMed] [Google Scholar]
- Klink R, Alonso A. Ionic mechanisms of muscarinic depolarization in entorhinal cortex layer II neurons. Journal of Neurophysiology. 1997;77:1829–1843. doi: 10.1152/jn.1997.77.4.1829. [DOI] [PubMed] [Google Scholar]
- Koenig J, Linder AN, Leutgeb JK, Leutgeb S. The spatial periodicity of grid cells is not sustained during reduced theta oscillations. Science. 2011;332:592–595. doi: 10.1126/science.1201685. [DOI] [PubMed] [Google Scholar]
- Kropff E, Treves A. The emergence of grid cells: Intelligent design or just adaptation? Hippocampus. 2008;18(12):1256–1269. doi: 10.1002/hipo.20520. [DOI] [PubMed] [Google Scholar]
- Kwag J, Paulsen O. Bidirectional control of spike timing by GABA(A) receptor-mediated inhibition during theta oscillation in CA1 pyramidal neurons. Neuroreport. 2009;20:1209–1213. doi: 10.1097/WNR.0b013e32832f5cc7. [DOI] [PubMed] [Google Scholar]
- Maurer AP, Vanrhoads SR, Sutherland GR, Lipa P, McNaughton BL. Self-motion and the origin of differential spatial scaling along the septo-temporal axis of the hippocampus. Hippocampus. 2005;15:841–852. doi: 10.1002/hipo.20114. [DOI] [PubMed] [Google Scholar]
- Navratilova Z, Giocomo LM, Fellous J-M, Hasselmo ME, McNaughton BL. Phase precession and variable spatial scaling in a periodic attractor map model of medial entorhinal grid cells with realistic after-spike dynamics. Hippocampus. 2011;22:772–789. doi: 10.1002/hipo.20939. [DOI] [PubMed] [Google Scholar]
- Pastoll H, Solanka L, Van Rossum MCW, Nolan MF. Feedback inhibition enables theta-nested gamma oscillations and grid firing fields. Neuron. 2013;77:141–154. doi: 10.1016/j.neuron.2012.11.032. [DOI] [PubMed] [Google Scholar]
- Quilichini P, Sirota A, Buzsaki G. Intrinsic circuit organization and theta-gamma oscillation dynamics in the entorhinal cortex of the rat. Journal of Neuroscience. 2010;30:11128–11142. doi: 10.1523/JNEUROSCI.1327-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray S, Naumann R, Burgalossi A, Tang Q, Schmidt H, Brecht M. Grid-layout and theta-modulation of layer 2 pyramidal neurons in medial entorhinal cortex. Science. 2014;343:891–896. doi: 10.1126/science.1243028. [DOI] [PubMed] [Google Scholar]
- Rivas J, Gaztelu JM, Garcia-Austt E. Changes in hippocampal cell discharge patterns and theta rhythm spectral properties as a function of walking velocity in the guinea pig. Experimental Brain Research. 1996;108:113–118. doi: 10.1007/BF00242908. [DOI] [PubMed] [Google Scholar]
- Sargolini F, Fyhn M, Hafting T, McNaughton BL, Witter MP, Moser MB, Moser EI. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science. 2006;312(5774):758–762. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]
- Schmidt-Hieber C, Häusser M. Cellular mechanisms of spatial navigation in the medial entorhinal cortex. Nature Neuroscience. 2013;16:325–331. doi: 10.1038/nn.3340. [DOI] [PubMed] [Google Scholar]
- Shay CF, Boardman IS, James NM, Hasselmo ME. Voltage dependence of subthreshold resonance frequency in layer II of medial entorhinal cortex. Hippocampus. 2012;22:1733–1749. doi: 10.1002/hipo.22008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stark E, Eichler R, Roux L, Fujisawa S, Rotstein HG, Buzsáki G. Inhibition-induced theta resonance in cortical circuits. Neuron. 2013;80:1263–1276. doi: 10.1016/j.neuron.2013.09.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stensola H, Stensola T, Solstad T, Frøland K, Moser M-B, Moser EI. The entorhinal grid map is discretized. Nature. 2012;492:72–78. doi: 10.1038/nature11649. [DOI] [PubMed] [Google Scholar]
- Stewart M, Fox SE. Do septal neurons pace the hippocampal theta rhythm? Trends in Neuroscience. 1990;13:163–168. doi: 10.1016/0166-2236(90)90040-h. [DOI] [PubMed] [Google Scholar]
- Tang Q, Burgalossi A, Ebbesen CL, Ray S, Naumann R, Schmidt H, Brecht M. Pyramidal and stellate cell specificity of grid and border representations in layer 2 of medial entorhinal cortex. Neuron. 2014;84:1191–1197. doi: 10.1016/j.neuron.2014.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welday AC, Shlifer IG, Bloom ML, Zhang K, Blair HT. Cosine directional tuning of theta cell burst frequencies: Evidence for spatial coding by oscillatory interference. Journal of Neuroscience. 2011;31:16157–16176. doi: 10.1523/JNEUROSCI.0712-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoon K, Buice MA, Barry C, Hayman R, Burgess N, Fiete IR. Specific evidence of low-dimensional continuous attractor dynamics in grid cells. Nature Neuroscience. 2013;16:1077–1084. doi: 10.1038/nn.3450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou TL, Tamura R, Kuriwaki J, Ono T. Comparison of medial and lateral septal neuron activity during performance of spatial tasks in rats. Hippocampus. 1999;9:220–234. doi: 10.1002/(SICI)1098-1063(1999)9:3<220::AID-HIPO3>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]