Abstract
Many neurons fire spontaneously, and the rate of this firing is subject to neuromodulation. How this firing affects functional connectivity within a neural network remains largely unexplored. Here we show that changes in spontaneous firing of cartwheel interneurons in the mouse dorsal cochlear nucleus (DCN) alter the effective convergence ratio of interneurons onto their postsynaptic targets through short-term synaptic plasticity. Spontaneous firing of cartwheel cells led to activity-dependent synaptic depression of individual cartwheel synapses. Depression was rapid and profound at stimulation frequencies between 10 and 200 Hz, suggesting the presence of high release probability (Pr) vesicles at these inhibitory synapses. Weak, transient synaptic facilitation could be induced after synapses were predepressed, indicating that low-Pr vesicles are also recruited, and may thus support steady-state transmission. A two-pool vesicle depletion model with 10-fold differences in Pr could account for the synaptic depression over a wide range of stimulus conditions. As a result of depression during high spontaneous activity, more cartwheel interneurons were required for effective inhibition. Convergence of four interneurons was sufficient to compensate for the effects of depression during physiologically expected rates of activity. By simulating synaptic release during spontaneous firing, we found that recruitment of low-Pr vesicles at the synapse plays a critical role in maintaining effective inhibition within a small population of interneurons. The interplay between spontaneous spiking, short-term synaptic plasticity, and vesicle recruitment thus determines the effective size of a convergent neural network.
SIGNIFICANCE STATEMENT We examined the relationship between the structure of a small neural circuit and the properties of its individual synapses. Successful synaptic inhibition of a target cell firing requires a critical inhibitory synaptic strength. Synapses often become depressed during spontaneous presynaptic activity, and this increases the number of presynaptic neurons needed to mediate inhibition. We show that depression is limited by the presence of a pool of vesicles that resist depletion. Thus, the size of this vesicle pool determines the size of the circuit needed to mediate inhibition during different patterns of activity.
Keywords: auditory, depression, glycine, plasticity, vesicle
Introduction
Many neurons fire action potentials even without afferent stimuli (Do and Bean, 2003; Häusser et al., 2004; Hermann et al., 2007; Person and Raman, 2012a). At synapses with relatively high vesicular release probability (Pr), such ongoing activity would deplete the available pool of vesicles, leading to sustained synaptic depression (Zucker and Regehr, 2002; Hermann et al., 2007; Yang and Xu-Friedman, 2015). Consequently, spontaneously active neurons may fail to relay the information from afferent stimuli. Indeed, studies have shown that synaptic depression induced by spontaneous spiking in presynaptic cells significantly reduces stimulus-driven responses in the postsynaptic cell (Hermann et al., 2007; Groh et al., 2008). Importantly, spontaneous spiking rate can be modified, for example, by neuromodulators, thus regulating synaptic depression and the efficacy of afferent signals (Kuo and Trussell, 2011; Owen et al., 2013).
However, neural circuits do not only relay afferent signals but also integrate multiple sources of information carried by different sets of afferent inputs. Accordingly, depressed synapses, which individually may not drive a postsynaptic cell to spike, may still be effective when different inputs are active simultaneously. Such coincident detection of afferent stimuli can be important for sensory integration in the nervous system (Kuba et al., 2002; Cook et al., 2003; Groh et al., 2008). Hence, at synapses with activity-dependent depression, presynaptic spontaneous spiking not only reduces the strength of individual afferents but also determines the needs for integration from multiple afferents converging onto the postsynaptic cell. Thus, we distinguish between an anatomical convergence ratio onto a postsynaptic neuron and an effective convergence ratio that accounts for dynamic changes in synaptic strength at individual synapses.
The interplay between spontaneous spiking, synaptic depression, and integration of multiple afferent inputs to define the effective convergence ratio is studied here in a circuit formed by cartwheel inhibitory interneurons onto fusiform principal cells in the mouse dorsal cochlear nucleus (DCN). The DCN is an initial station in the ascending auditory pathway that integrates multisensory modalities with auditory information (Oertel and Young, 2004). Multisensory inputs are relayed by excitatory parallel fibers and influence sound-evoked responses in the fusiform cells (Koehler et al., 2011) (see Fig. 1A). This modulation involves not only direct excitation from parallel fibers but also feedforward inhibition from cartwheel interneurons (Roberts and Trussell, 2010; Kuo and Trussell, 2011). Indeed, in vivo stimulation of parallel fiber/multisensory pathway often cause a long-lasting inhibition of fusiform cell firing, highlighting the potency of cartwheel cell activity (Young et al., 1995; Davis et al., 1996; Shore, 2005; Kanold et al., 2011). However, cartwheel cells fire spontaneously in vivo (Davis and Young, 1997; Portfors and Roberts, 2007; Ma and Brenowitz, 2012), leading to sustained synaptic depression and weaker feedforward inhibition driven by parallel fibers (Kuo and Trussell, 2011). This phenomenon raises the question of how chronically depressed cartwheel synapses can provide effective inhibition under physiological conditions.
Figure 1.
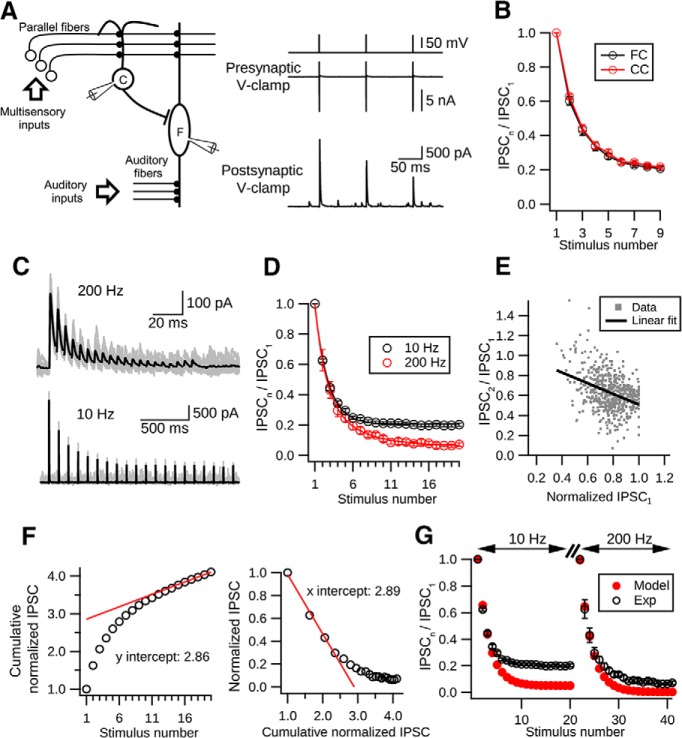
Short-term depression at cartwheel cell synapses. A, Left, Simplified DCN circuit and paired recording diagram. Right, Example traces from a connected pair. Presynaptic cartwheel cell (C) was voltage-clamped at −60 mV and escaping spikes evoked by 0.2 ms voltage pulses of (80 mV). Corresponding IPSCs were recorded in the postsynaptic cell, in this case a fusiform cell (F). B, Kinetics of short-term synaptic depression in cartwheel-cartwheel connections (CC, red) and cartwheel-fusiform cell connection (FC, black) are not significantly different (p > 0.05, t test). Data collected from these two connections were therefore pooled (n = 10, CC; n = 5, FC). C, Example traces showing that synaptic depression occurs at low and high frequencies. Top, IPSCs evoked by 20 pulses of 200 Hz stimulation. Bottom, IPSCs evoked by 20 pulses at 10 Hz. Black traces represent the averages of at least 15 individual sweeps (gray). D, Summary of short-term depression at low and high frequencies. Black represents synaptic depression kinetics at 10 Hz. N = 15 connections. A single exponential function can be fit with a decay constant of 1.70 ± 0.04 stimuli. Red represents synaptic depression at 200 Hz. N = 6 connections. A double exponential function can be fit with 1.37 ± 0.18 stimuli and 4.57 ± 1.05 stimuli for fast and slow decay constants, respectively. Fast component is 59 ± 11% of fit. E, Negative correlation between the paired-pulse ratio (IPSC2/IPSC1) and peak amplitudes of IPSC1. N = 15 connections. Each gray dot represents the paired-pulse ratio with its corresponding IPSC1 amplitude in a single trial during 10 Hz stimulation. At least 20 trials were repeated for each connection. The peak IPSC1 amplitudes in each connection were normalized to the biggest IPSC1 amplitude in the same connection. Black line indicates a linear regression fit to all the dots. p < 0.001, R2 = 0.14, 581 points. F, Two approaches to estimating the size of the readily releasable pool and initial vesicular Pr. Left, Plot cumulative-normalized IPSCs against the stimulation number (open circles). The relative size of the pool is the y-intercept (2.86) of a linear regression line (red) back-extrapolated from the last 5 points. Right, Plot-normalized IPSC amplitude against the cumulative-normalized IPSC amplitude. The relative size of the pool is the x-intercept (2.89) of the linear regression line (red) extrapolated from the first 4 points. Both approaches give similar estimates for the Pr (left, 1/2.86 = 0.349; right, 1/2.89 = 0.346). G, Single-pool depletion model (Pr = 0.35, recovery time constant: 5.5 s) cannot account for cartwheel synaptic depression. Black represents experimental data. Red represents model predictions. The model matches the first 4 data points during depression but greatly overestimates the degree of depression in both 10 Hz and 200 Hz evoked responses.
We hypothesize that the number of presynaptic neurons required for inhibition (i.e., the effective convergence ratio) is a function of the state of depression of individual synapses. Thus, the spontaneous firing rate of neurons and the microphysiology of their synapses together may impact the ratio. To quantify the depression level of synaptic transmission at different spontaneous firing frequencies, we made recordings between connected cartwheel-fusiform cell pairs and analyzed the kinetics of synaptic depression under diverse stimulus paradigms. We described the process of depression quantitatively using a model featuring two pools of vesicles with distinct Pr. The depletion of these two populations of vesicles at different proportions leads to rate-dependent depression at cartwheel synapse. Despite prominent synaptic depression, the effective cartwheel-fusiform convergence ratio at high spontaneous spiking rates was surprisingly small (<4). The synaptic depression model suggests that low-Pr vesicles sustain the release during high-frequency spiking and thus ensure effective inhibition performed in a small circuit. Hence, the properties of synaptic vesicles that control the degree of synaptic depression provide a foundation for defining effective circuit convergence as spike rates of neurons are varied by neuromodulators. This work may be generalized to other brain regions that use convergent circuits and depressing synapses.
Materials and Methods
Animals.
Wild-type C57BL/6 mice (P16-P27) were used for paired recording experiments. For photostimulation experiments, GlyT2-Cre;Ai32 transgenic mice were used, generated by crossing male ChR2(H134R)-EYFP reporter line (Ai32) with a female GlyT2-Cre line. Use and handling of animals in this study were approved by Oregon Health and Science University Institutional Animal Care and Use Committee.
Brain slice preparation.
Animals were anesthetized by isoflurane and then decapitated. After removing the skull, a coronal cut at the midbrain was made to dissect out the brainstem. The front side of the brainstem was then glued on a stage. The lateral side of the brainstem was turned to face the vibratome (Leica VT1200S) blade and tilted downwards at an angle of ∼10°. Coronal brainstem slices containing DCN (220 μm thick) were collected in warm (34°C) artificial CSF (ACSF) solutions containing the following (in mm): 130 NaCl, 2.1 KCl, 1.2 KH2PO4, 3 Na-HEPES, 11 glucose, 20 NaHCO3, 1 MgSO4, and 1.7 CaCl2, saturated with 5% CO2-95% O2, ∼305 mOsm. After cutting, the slices were stored in ACSF at 34°C for ∼30 min for recovery and then kept at room temperature (∼22°C) until use.
Electrophysiology.
During recording, slices were transferred to a recording chamber constantly perfused with warm ACSF (∼34°C) controlled by a peristaltic tubing pump (Ismatec CP78016-30). Cells were visualized with a 40 × magnification objective on the stage of an upright microscope (Olympus BX51W) equipped with an infrared Dodt contrast mask and fluorescence optics. Typically, round cells with diameter ∼15 μm in the DCN molecular layer were usually cartwheel cells and were confirmed by complex spiking in response to a current step. Elliptoid cells with transverse diameter ∼20 μm in the DCN fusiform cell layer were usually fusiform cells and were confirmed by their large membrane capacitance (>35 pF) and their regular spiking pattern. Recording electrodes (4–7 mΩ) were pulled from borosilicate glass (WPI 1B150F-4) by a vertical puller (Narishige P-10). Series resistances were usually <12 mΩ, compensated by 80%, and monitored throughout the course of the recording. Data were discarded if the series resistance changed by >25%. In paired recording experiments, we used a pipette solution containing the following (in mm): 113 K-gluconate, 1.75 MgCl2, 2.75 MgSO4, 9 HEPES, 0.1 EGTA, 14 Tris2-phosphocreatine, 0.3 Tris-GTP, and 4 Na2-ATP, with pH adjusted to ∼7.3 with KOH and osmolarity adjusted to ∼295 mOsm with sucrose. The calculated chloride reversal potential (ECl) using this solution was ∼−97 mV. To establish paired recordings from synaptically connected cartwheel-cartwheel or cartwheel-fusiform cells, whole-cell voltage-clamp recordings from both cells were performed; each cell received a burst of voltage pulses (from −60 to 20 mV, 0.2 ms/pulse, 3 pulses at 200 Hz) to test whether that cell could evoke IPSCs in the other cell. The latency for the unitary IPSC after the presynaptic escaping spike was usually <0.5 ms (Roberts et al., 2008). Cartwheel-to-fusiform cell IPSCs have submillisecond rise times (Roberts and Trussell, 2010), suggesting somatic and proximal dendritic sites of contact, consistent with morphological analyses (Rubio and Juiz, 2004). In each paired recording, the membrane potential of the presynaptic cell was held at −60 mV, whereas the postsynaptic cell was held between −50 mV and −60 mV. For current-clamp recordings during channelrhodopsin stimulation, the pipette solution contained 2.75 MgCl2 and 1.75 MgSO4 instead of 1.75 MgCl2 and 2.75 MgSO4 to mimic the ECl of fusiform cell measured by perforated-patch recording (−84 mV) (Kim and Trussell, 2009). The membrane potential of fusiform cells was kept ∼−60 mV by bias current injection (from −100 to −250 pA). Corrections to holding potential were only made to estimate synaptic conductance, based on a 13 mV junction potential (see Fig. 6). In some experiments, the chloride reversal was shifted to −44 mV (Vhold = −70 mV) using a pipette fill containing (in mm) as follows: K-gluconate 105, KCl 15.5, MgCl2 4.8, HEPES, 10, EGTA 0.1, Tris2-phosphocreatine 14, Tris-GTP 0.5, Na2-ATP 4, to achieve inward IPSCs.
Figure 6.
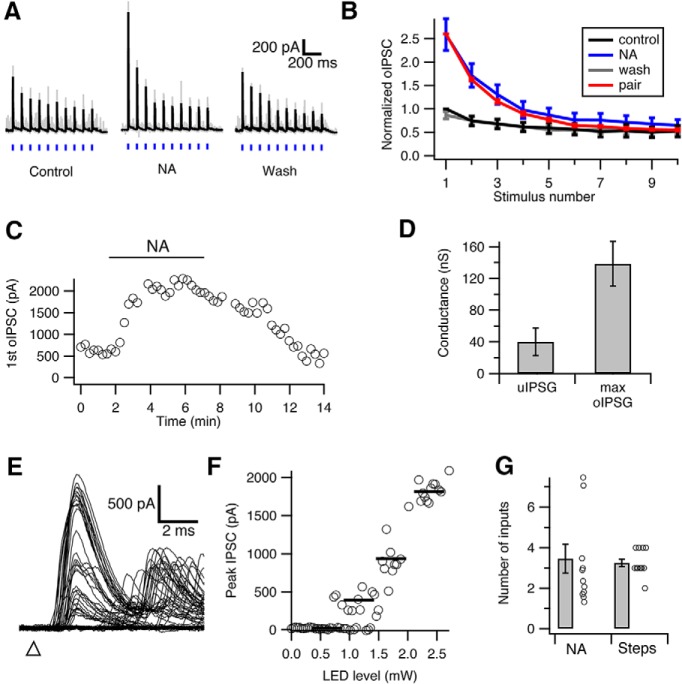
Low convergence ratio in the cartwheel-fusiform circuit. A, Optically evoked IPSCs (oIPSC) in fusiform cells during 3.5 mW blue light stimulation (blue vertical bars). The amplitude of oIPSC and its degree of depression is enhanced by 10 μm noradrenaline (NA) (Kuo and Trussell, 2011), as NA relieves sustained cartwheel cell synaptic depression by blocking spontaneous spiking. Black represents average traces from 10 individual traces (gray). B, Summary of peak oIPSC during repetitive light stimulation. Peaks are normalized to the first oIPSC in control. NA not only increased peak oIPSC amplitudes but also revealed a stronger degree of synaptic depression. Also shown is data from paired recordings in Figure 1B (red, scaled to the first response in NA), showing that depression of oIPSC or electrically evoked IPSCs is similar. C, Time course of change in peak amplitude change in the first oIPSC of a train during application of NA. D, Comparison between the unitary conductance of cartwheel-fusiform synapse from paired recordings (uIPSG, 40.0 ± 17.3 nS, n = 6) and the maximum optically evoked synaptic conductance in the presence of NA (max oIPSG, 138.5 ± 23.3 nS, n = 11). E, Example traces of oIPSC in a fusiform cell evoked by increasing light intensities. Triangle represents start time of flash. F, Plot of the peak oIPSC amplitudes of the traces shown in E against LED stimulation intensity (gray circles). Black bars represent the steps resolved by K-means cluster analysis. Three jumps are evident, indicating that 3 cartwheel cells converged onto this fusiform cell. G, Summary of the number of cartwheel cell inputs converging onto a fusiform cell estimated by the two methods (A–D vs E, F). Number estimated by the maximum conductance method (NA) is 3.7 ± 0.9 (n = 11), and the number estimated by the steps method (step) is 3.3 ± 0.2 (n = 12). No significant difference is observed between the two methods (p = 0.34, Mann–Whitney test).
Data acquisition.
Electrophysiological data were acquired with a Multiclamp 700B amplifier and pClamp 10.3 software.
Photostimulation.
To activate ChR2 in the brain slices, we used a 470 nm LED (Sutter Instruments TLEDPLUS-Y) coupled through the epi-illumination port of the microscope. Pulses of blue light (0.5 ms/pulse) were delivered through pClamp control, and cells were illuminated at the focal plane under the 40 × 0.8 NA objective. The illumination area at the focal plane had a diameter ∼1 mm. The maximum power of the incident light provided by the LED under the objective was ∼3.4 mW (Newport 1815-C power meter with 818-ST sensor), corresponding to an irradiance of ∼4.3 mW/mm2. The irradiance used during photostimulation experiments was usually much weaker and ranged from 3.8 μW/mm2 to 1.8 mW/mm2 (see Fig. 7).
Figure 7.
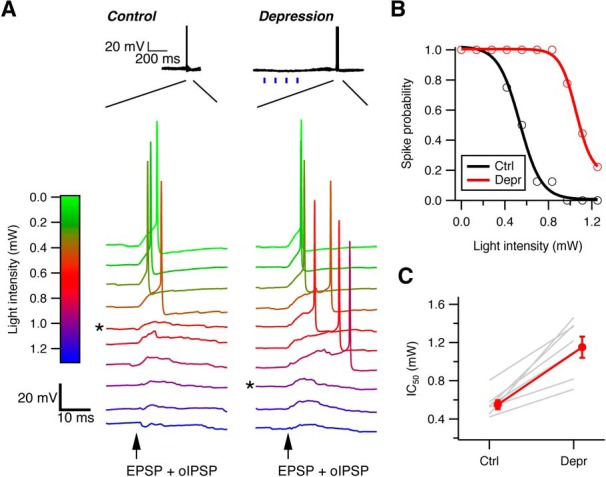
Effective size of cartwheel-fusiform circuit increases with spontaneous spiking in cartwheel cells. A, Example traces of action potentials in a fusiform cell evoked by current injection of an EPSC waveform plus optically evoked IPSPs (oIPSP) by different intensities of blue light under control (left) and enhanced-synaptic depression (right) conditions. Top, Under enhanced-depression conditions, four repetitive light-stimulation pulses (blue vertical bars) were applied before action potential generation to increase spiking and synaptic depression in the entire cartwheel cell population. * Minimal light intensity to inhibit spike. B, Plot of fusiform cell spike probability against the light intensities that evoke oIPSP after repeating the protocol in A 10–20 times. A sigmoidal fit to the points yields a light-inhibition curve and an IC50 of the light intensity that inhibits 50% of spike generation for each condition. C, Summary of IC50 changes in 7 fusiform cells recorded. In every cell, the IC50 shifts toward more positive under the enhance depression state, indicating the number of cartwheel cells required to effectively inhibit fusiform cell firing increases as their spontaneous spiking rate increases. IC50 for control: 0.55 ± 0.05 mW; depression: 1.15 ± 0.11 mW. p = 0.001 (paired t test).
Data analysis.
Electrophysiology data were analyzed in IGOR Pro 6.34 using Neuromatic package (http://www.neuromatic.thinkrandom.com/) and custom-written procedures. Peak IPSC amplitudes from each cell were measured from traces averaged from at least 15 trials. Statistical comparisons were done in IGOR or R (http://www.R-project.org/). Averages are represented as mean ± SEM. Group comparison was done by t test if the data were distributed normally (data normality was tested using Shapiro–Wilk test in R); otherwise, a Mann–Whitney U test was used. Optimal number of ChR2-evoked synaptic inputs to each cell was determined using K-means cluster analysis and elbow method (Ferragamo et al., 1998; Cao and Oertel, 2010; Chabrol et al., 2015) with custom-written scripts in R.
Modeling synaptic depression.
A computational model for synaptic depression was devised in IGOR using custom-written procedures. Single- and two-pool vesicle depletion models for synaptic depression were adopted from a release site model as described in previous studies (Weis et al., 1999; Brenowitz and Trussell, 2001; Trommershäuser et al., 2003). For the single-pool model, the synapse had nini available release sites at rest and each site released a vesicle with probability p in response to stimulation. Hence, upon stimulation, there were on average N vesicles released, where
After stimulation, the number of emptied sites recovered (so that they can be releasable again) following a rate constant (1/τ). The number of available release sites ni just before the ith stimulus is given by the following:
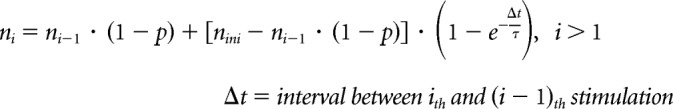 |
Assuming that p does not change during stimulation, the ith stimulus causes Ni vesicles to be released:
For the two-pool model, the number of total release sites at rest nini was divided among each pool according to fractions r1 and r2 (r1 + r2 = 1) so that pool 1 contained (nini · r1) release sites and pool 2 contained (nini · r2) release sites. Upon stimulation, each pool depletes and replenishes vesicles independently according to its own p and τ. The total number of vesicles released at the ith stimulation during train stimulation (Ni) is the sum of release from each pool. The evoked responses can therefore be presented as the total number of released vesicles multiplied by quantal size. We assumed that the quantal size is the same for each pool and does not change during stimulation because glycine receptors do not desensitize quickly (Harty and Manis, 1998). Therefore, the normalized IPSC predicted by the model is exactly the normalized number of vesicles released during train stimulation. The normalized release was then compared with experimental data using a curve fitting procedure GenCurvefit (Andrew Nelson and Australian Nuclear Science and Technology Organisation) to obtain best-fit parameters for the two-pool model.
Immunostaining for ChR2-(H134R)-EYFP.
One GlyT2-Cre; Ai32 mouse was transcardially perfused with 4% PFA, and the brainstem part containing DCN was dissected out for postfixation. After postfixation, the tissue was sectioned at 30 μm thickness, washed in PBS for several times, blocked in BSA, and incubated in a rabbit polyclonal anti-GFP AlexaFluor-488 conjugate (1:200; A21311, Invitrogen) overnight. The sections were then examined under a confocal microscope (Olympus Fluoview1000).
Reagents and chemicals.
All reagents, except for SR-95531 (Tocris Bioscience), were purchased from Sigma.
Results
Rapid short-term depression at cartwheel cell synapse
Synaptic depression at cartwheel cell glycinergic terminals has been previously reported (Roberts et al., 2008; Mancilla and Manis, 2009; Kuo and Trussell, 2011); however, a detailed description of its kinetics is still lacking. We therefore measured short-term plasticity in paired recordings from synaptically coupled cartwheel cells (n = 10, amplitude of IPSC1: from 124.1 to 532.1 pA, median 261.6 pA, mean ± SD: 301.6 ± 151.8 pA) or coupled cartwheel and fusiform cells (n = 5, amplitude of IPSC1: from 264.0 to 2883.0 pA, median: 480.2 pA, mean ± SD: 958.8 ± 1099.7 pA) (Fig. 1A,B). There was one particularly strong cartwheel-fusiform connection in our dataset (2883.0 pA), whereas the others ranged from 124.1 to 850.0 pA. Apart from this outlier, the range is consistent with previous studies (Roberts and Trussell, 2010). The range of strengths may reflect the variable distances between cells and the effects of tissue slicing. Statistical analysis showed no differences in the kinetics of synaptic depression between the types of connections (cartwheel-cartwheel vs cartwheel-fusiform); therefore, these data were pooled together (Fig. 1B; t test). Cartwheel cells fire bursts of high-frequency complex spikes (3–5 spikes at >200 Hz) and regular simple spikes (∼0.1–20 Hz) spontaneously or in response to current injection (Kim and Trussell, 2007; Bender et al., 2012). To measure synaptic responses to a fixed number of presynaptic action potentials in the absence of background firing, we voltage-clamped presynaptic cartwheel cells at −60 mV and induced escaping simple spikes by delivering a train of 0.2 ms, 80 mV voltage steps (Fig. 1B) (Roberts et al., 2008). We found that the synapse exhibited a fast and pronounced synaptic depression in response to 10 Hz train stimulation, reaching steady state (∼20% of the initial response) rapidly after ∼5–6 stimuli (Fig. 1D; decay constant: 1.70 ± 0.04 stimuli when fit to a single exponential function).
We next tested whether high-frequency stimulation of the synapse could also lead to such strong synaptic depression because high-frequency activity can in principle lead to calcium accumulation at terminals and trigger facilitation (Zucker and Regehr, 2002). However, cartwheel synaptic responses to a 20 pulse, 200 Hz train still showed strong synaptic depression (Fig. 1C). The profile of this decay could be fit with a double exponential function with 1.39 ± 0.18 stimuli and 4.58 ± 1.05 stimuli for fast and slow decay time constants (fast component 59 ± 11% of fit), respectively. Together with the 10 Hz responses, these results suggested that cartwheel synapses always exhibit synaptic depression when activated from a quiescent state.
It has been suggested that release probability is low in vivo due to low [Ca2+]e in the CSF, resulting a reduction in the degree of short-term synaptic depression compared with in vitro conditions (Borst, 2010). However, at cartwheel synapses, we still observed a ∼70% decrease in peak IPSC amplitude during a 20 pulse 10 Hz stimulation when we reduced [Ca2+]e to 1.2 mm (IPSC16–20/IPSC1: 0.28 ± 0.07; data not shown). This suggests that, in vivo, continuous low-frequency activity would still depress cartwheel synapse by a large degree.
Single-pool vesicle depletion model is unable to explain synaptic depression
We next explored the mechanism of such fast and pronounced short-term depression. We excluded postsynaptic receptor desensitization because cartwheel cell synapses are mostly glycinergic (Apostolides and Trussell, 2013) and glycine receptors desensitize slowly (Harty and Manis, 1998). Moreover, desensitization as a causative factor in depression is inconsistent with the observation that the depression decay rate, in terms of stimulus number, for 10 Hz was similar to the fast decay rate at 200 Hz (1.7 vs 1.37, respectively). Depression is also unlikely to be caused by receptor saturation because depression occurs even at low frequency (10 Hz) and glycine should unbind the receptor completely during the 100 ms interstimulus interval. We also repeated the experiments using high [Cl−] internal (ECl: −44 mV) and found that there was no significant difference in steady-state response (mean ± SD of IPSC16 to IPSC20: low [Cl−]i: 0.20 ± 0.03, n = 15; high [Cl−]i: 0.19 ± 0.04, n = 6; p = 0.67, unpaired t test), excluding the possibility that [Cl−]i accumulation during repetitive stimulation would lead to a decrease in chloride driving force and cause synaptic depression (Thompson and Gähwiler, 1989). Therefore, depression is most likely to have a presynaptic mechanism. Indeed, as predicted from a vesicle depletion model, the paired-pulse ratio of the second versus the first IPSC peak amplitude during 10 Hz stimulation tends to be smaller when the first IPSC was larger (Fig. 1E; 581 points, pooled data from 15 cells, >20 trials per cell, linear regression fit, R2 = 0.14, p < 0.001) (Debanne et al., 1996; Regehr, 2012).
To explore the hypothesis of vesicle depletion quantitatively, we began with its simplest form, which assumes that every release site in the pool has the same vesicle Pr and replenishment rate, with replenishment rate proportional to the number of emptied release sites (Brenowitz and Trussell, 2001; Thanawala and Regehr, 2013). To estimate the Pr, we first calculated the size of the readily releasable pool. Two methods were used: (1) by back-extrapolating from the last 5 points of cumulative normalized IPSC amplitude during 200 Hz stimulation to the y-axis (Schneggenburger et al., 1999); and (2) by extrapolating the first 4 points of the normalized IPSC amplitude versus cumulative normalized IPSC amplitude plot to the x-axis (Elmqvist and Quastel, 1965; Lu and Trussell, 2000). Although each method emphasizes different features of the data, they gave similar estimates of the relative size of readily releasable pool compared with the first release in the 200 Hz train (2.86 from Method 1 and 2.89 from Method 2; Fig. 1F). Hence, we obtained a rather high-Pr of ∼0.35 by calculating the released fraction in the first response (1/2.86 = 0.349, Method 1; 1/2.89 = 0.346, Method 2). Combined with the previously measured recovery time constant (5.5 s) from synaptic depression (Kuo and Trussell, 2011), a single-pool depletion model for the cartwheel synapse was built. However, although the model predicted well the rate of decay of the first four responses to the 10 or 200 Hz train stimulation, it greatly overestimated the degree of depression at steady state, similar to the observations of Weis et al. (1999) (Fig. 1G). Because the pool size and Pr estimation methods mentioned above are only valid when the vesicle population is homogeneous (e.g., vesicles have the same Pr and recovery time constant) (Neher, 2015), this result suggests that there might be different distributions in the vesicle properties at cartwheel synapse. The overestimation of the degree of depression suggested that the depletion rate of vesicle pool was slower during steady-state depression, and this could be explained by recruitment of low-Pr vesicles (Sakaba and Neher, 2001a; Trommershäuser et al., 2003).
Two-pool vesicle depletion model accounts for synaptic depression
If low-Pr vesicles are recruited during synaptic stimulation, one would expect to see short-term synaptic facilitation after depression is complete because low-Pr vesicles are often subject to facilitation (Müller et al., 2010). Indeed, when high-frequency stimulation was applied after the synapse was predepressed by low-frequency stimulation, we observed a modest (∼20% compared with the first response to high-frequency stimulation) synaptic facilitation in the second and third responses (Fig. 2A,B [asterisk in B]). Further high-frequency stimuli continued to depress the synapse. Interestingly, the decay rate of the responses to this high-frequency stimulation is similar to the slow component of the decay seen upon high-frequency stimulation evoked from a nondepressed state (5.87 ± 0.583 stimuli vs 4.57 ± 1.05 stimuli), and no fast phase was present. This result suggests that the initial 10 Hz train fully depleted a population of high-Pr vesicles and that sustained transmission was mediated by a population of low-Pr vesicles, which are subject to facilitation and followed by further depression when the stimulation rate is sharply increased.
Figure 2.
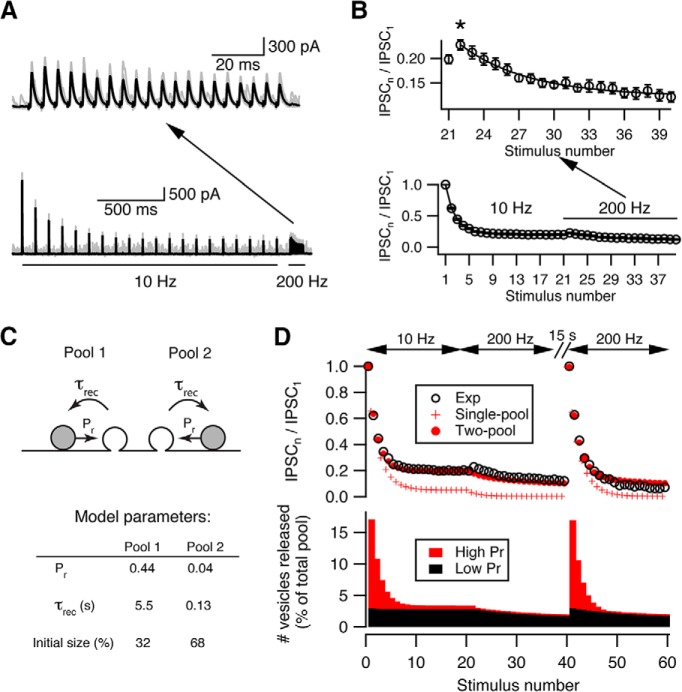
Two-pool depletion model accounts for synaptic depression at cartwheel synapses. A, Example traces showing that short-term facilitation was revealed by high-frequency (200 Hz) stimulation after the synapse is predepressed by low-frequency (10 Hz) stimulation. Top, Zoom-in of the traces evoked by 200 Hz stimulation shown below. Black represents average trace from 20 individual traces (gray). B, Summary of synaptic facilitation kinetics from 15 connections. Top, Zoom-in of the 200 Hz evoked responses shown below. The decay of the 200 Hz responses can be fit by a single exponential with a decay constant of 4.57 ± 1.05 stimuli, which is similar to the slow decay time constant (5.87 ± 0.58 stimuli) of the 200 Hz responses evoked from a resting state. This indicates that the depletion of a low-Pr pool can only be revealed by high-frequency stimulation. N = 15 connections. * indicates onset of facilitation. C, Top, Diagram of a two-pool depletion model. Each pool has independent vesicular Pr (Pr) and recovery time constant (τrec). Bottom, Parameters from the best fit. The low-Pr pool (Pool 2) has a faster recovery time constant and a larger initial size. D, Top, Comparison between the experimental data (Exp, open circle) and predictions from single-pool (Single-pool, red cross) versus two-pool (Two-pool, red solid circles) depletion model. Bottom, the relative releases from each pool predicted by the two-pool depletion model during repetitive stimulation. Red represents high-Pr pool. Black represents low-Pr pool. The high-Pr pool contributes most of the release during fast depression, and the low-Pr pool contributes most of the release during steady state or slow depression.
To model this two-vesicle-pool hypothesis, we assumed that the properties of each pool (i.e., Pr and recovery time constant) are independent of one other and both pools are activated simultaneously upon stimulation. We set the recovery time constant of one pool to 5.5 s to accord with the measured recovery time constant from depression (Kuo and Trussell, 2011), but let all other parameters be optimized during the fitting procedure. The model was then fit to the averaged population data shown in Figure 2D, which contains responses to a 10 Hz → 200 Hz → 200 Hz train stimuli, with a 15 s gap between the first and second 200 Hz trains. Two pools of vesicles with a 10-fold difference in release probabilities gave the best fit (high-Pr: 0.44; low-Pr: 0.04), and accounted for initial and steady-state depression well throughout the complex pattern of stimulus trains. It should be noted that the two 200 Hz trains used here are expected to probe distinct presynaptic conditions, as the first occurs during steady-state depression and should deplete only the low-Pr pool, whereas the second occurs at quiescent state and should deplete two pools differentially. We found the best-fit parameters from this sequence describes the data better (with smaller sum of square error of the residuals) than fitting the model to two frequencies only (i.e., a 10 Hz → 200 Hz sequence with or without 15 s gap in between), although the latter also give similar estimates (a small high-Pr pool with Pr ∼0.46 and recovery time constant 5.5 s, and a large low-Pr pool with Pr <0.10 and recovery time constant around several hundred milliseconds; data not shown). Thus, our fitting result suggests that the synapse utilizes vesicles with two distinct release probabilities.
The two-pool model also predicts that, as the number of stimuli increases, vesicles from the low-Pr pool contributed more to the total release (Fig. 2D). How do the properties of each pool account for such a trend during repetitive stimulation? From the best-fit parameters (Fig. 2C), the size of the low-Pr pool was twice that of the high-Pr pool, but its Pr was only 10% of the high-Pr pool (0.04 vs 0.44). The release at the beginning of the train was therefore dominated by the high-Pr pool (Fig. 2D, bottom panel). However, the high-Pr pool was depleted rapidly due to its slow recovery time constant (5.5 s), and the ensuing release was mostly contributed by the low-Pr pool (Fig. 2D, bottom panel). The fast recovery rate of the low-Pr pool (recovery time constant ∼130 ms) sustains the release during steady-state depression at 10 Hz and only gets depleted upon stimulating at 200 Hz. Because lack of activity-dependent increase in Pr in the parameters, this depletion model cannot predict the small facilitation during high-frequency stimulation after the synapse is depressed. However, this phase was a minor part of the synaptic response, and the model still described well the majority of short-term depression at the cartwheel synapse.
Ca2+-dependent recovery does not sustain transmission during depression
The other possible mechanism that slows pool depletion rate during repetitive stimulation and could potentially explain our results is activity-dependent enhancement of vesicle replenishment rate (Dittman and Regehr, 1998; Wang and Kaczmarek, 1998; Weis et al., 1999). While models incorporating such activity-dependent recovery mechanisms were also effective (modeling not shown), we sought experimental evidence to confirm whether they were justified at this synapse. Accelerated vesicle recovery is often Ca2+-dependent (Dittman and Regehr, 1998; Wang and Kaczmarek, 1998; Sakaba and Neher, 2001b). Indeed, at cartwheel synapses, there is accelerated recovery from synaptic depression after long 200 Hz trains (Fig. 3A). Such speeding of recovery was not observed when the Ca2+ chelator EGTA (1 mm) was included in the presynaptic recording pipette, showing that recovery was Ca2+-dependent (Fig. 3A,B; recovery fraction in control: 0.36 ± 0.05, n = 5; in 1 mm EGTA: 0.13 ± 0.01, n = 6; p = 0.003, unpaired t test). However, only long (20-pulse) but not short (3-pulse) high-frequency stimulation could induce such acceleration of recovery (Fig. 3A,B; recovery fraction after 3-pulse 200 Hz stimulation: 0.18 ± 0.02, n = 5; p = 0.01 when compared with 20-pulse stimulation in control, paired t test). Importantly, neither the rate nor the extent of depression changed in the presence of 1 mm EGTA at either 10 Hz or 200 Hz (Fig. 3C; p > 0.05, unpaired t test for every stimulus number). Similar results were obtained with cartwheel cells loaded with 10 mm EGTA, while 5 mm BAPTA sharply decreased release (data not shown). We therefore conclude that, although there is Ca2+-dependent acceleration of pool replenishment at the cartwheel synapse, it requires massive Ca2+ influx and may not play a role in sustaining the release during steady-state depression. However, it may nevertheless be that some untested patterns of activity could still reveal a contribution of Ca2+-dependent recovery in sustaining transmission, requiring further investigation.
Figure 3.
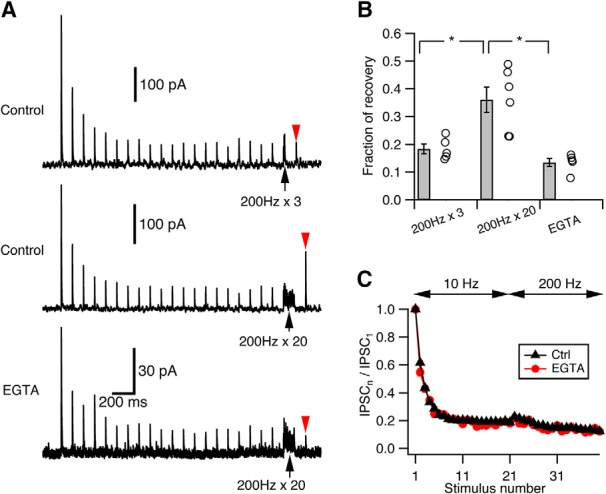
Ca2+-dependent recovery does not contribute to steady-state transmission. A, Example traces illustrating Ca2+-dependent recovery at cartwheel synapses. Top, Train of 3 pulse stimuli at 200 Hz (black arrow) did not enhance recovery (red arrowhead) from synaptic depression. Middle, Train of 20 pulse stimuli at 200 Hz (black arrow) did enhance recovery (red arrowhead) from synaptic depression. Bottom, When 1 mm EGTA was included in the presynaptic recording pipette, the 20 pulse stimuli at 200 Hz (black arrow) could no longer enhance the recovery (red arrowhead) from depression. Traces are averaged from at least 15 trials. Top, Middle, From the same cell. Recovery was tested 100 ms after the end of train stimulation. B, Summary of the recovery from depression under the three conditions shown in A. Recovery was measured as the fraction of the peak amplitude of the IPSC1. Recovery from 200 Hz × 3 stimuli: 0.18 ± 0.02, n = 5; recovery from 200 Hz × 20 stimuli: 0.36 ± 0.05, n = 5; recovery from 200 Hz × 20 stimuli in 1 mm EGTA: 0.13 ± 0.01, n = 6. Recovery from 200 Hz × 20 is significantly larger than that from 200 Hz × 3 (*p = 0.01, paired t test) or that in 1 mm EGTA (*p = 0.003, unpaired t test). C, Kinetics of synaptic depression in response to a 10 Hz → 200 Hz stimulation when 1 mm EGTA was included in the presynaptic pipette (red, n = 5) is not significantly different from control (black, n = 15). p > 0.05 (for every stimulus number, unpaired t test).
Low-Pr pool dominates release during spontaneous activity
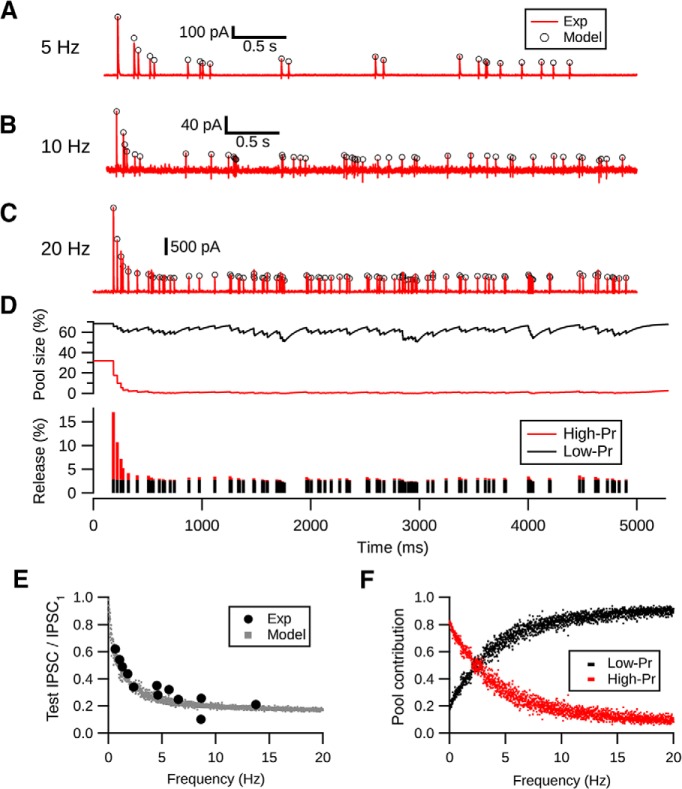
We next tested whether the two-pool depletion model would predict responses to spontaneous spiking, which contains much more irregular patterns of interstimulus intervals. Spontaneous spiking frequency of cartwheel cells ranges from 0 to 30 Hz in vivo (Parham and Kim, 1995; Ma and Brenowitz, 2012). To mimic cartwheel cell spontaneous spiking pattern, we constructed a stimulation paradigm consisting of Poisson spike train with mean frequencies centered at 5, 10, and 20 Hz. We then applied these spike trains to the presynaptic cell in paired cartwheel-fusiform cell recordings. Of the 5 pairs tested, we found that the two-pool model was able to predict synaptic responses well, with fractional error of 6.5 ± 3.7% (Fig. 4A–D). Moreover, the model showed that there is a frequency-dependent depression of the steady-state response during spontaneous firing, which corresponded well with the experimental data observed in the current and a previous study (Kuo and Trussell, 2011) (Fig. 4E).
Figure 4.
Two-pool depletion model predicts frequency-dependent synaptic depression at cartwheel cell synapse. A–C, Random (Poisson) evoked responses (red) centered at 5, 10, and 20 Hz are predicted by the two-pool depletion model (open circles). Each trace is from a different connection. C, Middle, Time course of the change in pool size during Poisson stimulation at 20 Hz. The low-Pr pool (black) has a faster recovery rate compared with the high-Pr pool (red); therefore, the depression is caused by the depletion of the high-Pr pool. D, Relative number of vesicles released from each pool during each stimuli. Low-Pr pool sustains the release after the synapse is depressed. E, Two-pool depletion model predicts the frequency-dependent depression evoked by spontaneous spiking. Solid circles represent data from Kuo and Trussell (2011). Gray dots represent predictions of the steady-state response of Poisson stimulation-evoked responses at various frequencies by the two-pool model. F, Two-pool depletion model shows that the low-Pr pool contributes most of the release during steady-state depression when the average firing frequency is >3 Hz.
How do the contributions of each pool vary as the spontaneous spike frequency changes? To explore this question, we estimated the relative proportions of vesicles released from high- and low-Pr pools during steady-state depression at different spiking frequencies. As shown in Figure 4F, when spontaneous spiking frequency goes above 2.5 Hz, the low-Pr pool is expected to dominate the release compared with the high-Pr pool. This shift is due to the slow recovery rate of the high-Pr pool and the large size of the low-Pr pool, which can be observed in the time course of change of the pool size during 20 Hz stimulation in Figure 4D. In conclusion, high-Pr and low-Pr vesicles contribute differentially to release under low versus high-frequency spontaneous spike conditions.
Small convergence ratio in the cartwheel-fusiform circuit
Our results suggest that inhibition from single cartwheel cells is reduced to ∼20% of its original strength once the cells' average spontaneous firing rate increases from 0 to >5 Hz. Therefore, as the spontaneous firing rate of cartwheel cells increases, the size of the cartwheel cell population needed to provide effective inhibition onto a fusiform cell must increase. Connected cartwheel-fusiform cell pairs share common spontaneous IPSCs, indicating that there are at least two cartwheel cells converging onto the same fusiform cell (Roberts and Trussell, 2010). Is the size of convergent circuit large enough to provide effective inhibition during high-frequency spontaneous firing, despite synaptic depression? We explored this possibility by using optogenetics to selectively activate cartwheel cells. Cartwheel cells express glycine transporter 2 (GlyT2) (Apostolides and Trussell, 2013), allowing us to use a GlyT2-Cre;Ai32 mouse line to drive channelrhodopsin expression in cartwheel cells (see Materials and Methods).
We first tested whether the expression of ChR2(H134R)-EYFP driven by GlyT2-Cre is sufficient to activate cartwheel cells. Immunostaining for EYFP showed that ChR2 was most densely expressed on DCN molecular layer spiny neurons, which exhibit the morphological characteristics of cartwheel cells (Wouterlood and Mugnaini, 1984) (Fig. 5A). In agreement with this observation, cell-attached recordings of cartwheel cells showed that brief pulses of blue light (0.5 ms duration) could evoke spiking (Fig. 5B). On some occasions, they would fire more than one spike, consistent with their tendency to generate spike bursts (Bender et al., 2012) (Fig. 5B). Moreover, firing probability increased with light intensity, indicating that more cartwheel cells could be recruited with stronger light pulses (Fig. 5C).
Figure 5.
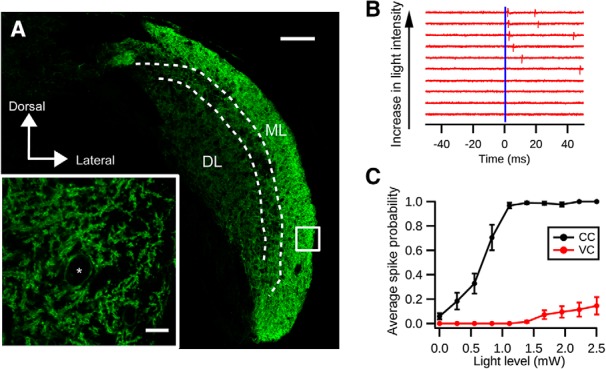
Optogenetic activation of cartwheel cells. A, Immunolabeling of ChR2-EYFP in a coronal section of DCN from a GlyT2-Cre;Ai32 animal. Strong expression of ChR2-EYFP is seen in the DCN molecular layer (ML), where cartwheel cells are located. The deep layer (DL) shows less dense expression of ChR2-EYFP. Scale bar, 100 μm. Inset, Single focal plane image of the white selection. There is strong labeling of ChR2-EYFP in spiny dendrites characteristic of cartwheel cells. *Possible cartwheel cell soma. Scale bar, 10 μm. B, Cartwheel cell spikes with blue light flash. Example traces of a cell-attached recording from a cartwheel cell in response to blue light of different intensities. Blue bar represents the onset of the light stimulation (duration: 0.5 ms). Each red vertical stroke represents an action potential. The spike probability and response latency decrease with increasing light intensity. C, Population averages of spike probability (the chance of generating a spike within 10 ms after the light stimulation) from cartwheel cells (CC, black, n = 9) and vertical cells (VC, red, n = 13). Only 3 of 13 vertical cells respond to light stimulation stronger than 1.5 mW; and even with 2.5 mW blue light stimulation, the spike probability is low (0.15 ± 0.07).
We next examined the specificity of ChR2(H134R)-EYFP expression in the DCN because two other types of fusiform-cell-targeting interneurons, vertical cells and stellate cells, may also express ChR2 driven by GlyT2-Cre. Because stellate cell synapses are predominantly GABAergic (Apostolides and Trussell, 2014) while cartwheel synapses are mainly glycinergic, for ChR2 experiments we included GABAA receptor blocker SR-95531 (5 μm) in the bath to prevent contributions from stellate cells. There was dim fluorescence in the DCN deep layer, suggestive of ChR2 expression in glycinergic vertical cells (Fig. 4A). Indeed, cell-attached recordings revealed that vertical cells could be activated by sustained blue light stimulation (duration: 100 ms, intensity: ∼1 mW; data not shown). However, only 3 of 13 vertical cells tested fired spikes in response to brief (0.5 ms) light pulse stimulation, and they required higher light intensity compared with cartwheel cells (Fig. 5B,C; vertical cells: >1.4 mW). Because the unitary conductance of a vertical-fusiform synapse is 10% that of a cartwheel-fusiform synapse (Kuo et al., 2012), we reasoned that optically evoked IPSCs (oIPSCs) in fusiform cells are mostly from cartwheel cells.
We used two approaches to estimate the convergence ratio (i.e., the number of cartwheel cells contacting a fusiform cell). The first was to divide the maximum light-evoked conductance over average unitary conductance of the cartwheel synapse measured with paired recordings (Person and Raman, 2012b). Because of light scattering, cells in the deeper layers of the slice are presumably exposed to weaker light stimulation compared with cells on the surface. We thus decided to use strong light stimulation (3.5 mW) to recruit potentially all cartwheel cell inputs to the recorded fusiform cells despite the risk that it might activate some vertical cell inputs. We noticed that the responses in fusiform cells to 10 Hz light pulse stimulation only exhibited moderate synaptic depression (10th IPSC/ first IPSC = 0.5 ± 0.1, Fig. 5A; compared with 0.2 in paired recordings, Fig. 1D), so it is likely that some cartwheel synapses were already depressed by spontaneous spiking. The maximal evoked synaptic conductance measured under this condition would therefore be underestimated. To silence the spontaneous activity and relieve synaptic depression, we applied 10 μm noradrenaline to the bath (Kuo and Trussell, 2011). Consistent with previous findings, the peak of the first oIPSC increased to ∼2.5 times of its initial size and the train stimulation evoked more robust synaptic depression after noradrenaline application (Fig. 6A–C). Indeed, the depression triggered by light pulses in noradrenaline was similar in magnitude to that seen with paired recordings (Fig. 6B), indicating that exocytosis triggered by channelrhodopsin and electrical stimulation are similar. Moreover, IPSCs triggered by channelrhodopsin were completely blocked by TTX (0.5 μm, data not shown). Such similarity in depression kinetics also suggests that the contributions from other GlyT2-expressing neurons to oIPSCs (e.g., vertical cells) are minor. The maximum evoked conductance measured in the presence of noradrenaline ranged from 57.4 to 327.1 nS in the 11 fusiform cells tested (average: 138.5 ± 28.3 nS; Fig. 6D). Dividing those over the population average of the unitary conductance from connected cartwheel-fusiform pairs (40.0 ± 17.3 nS, n = 6), we obtained a ratio from 1.4 to 8.2, giving an average of 3.5 ± 0.7 cartwheel cells converging onto a fusiform cell (Fig. 6G). To address the concern that the neurons' projections are cut during brain slicing, we performed these measurements in slices of two different thicknesses (260 μm vs 360 μm) and did not see a significant difference (260 μm: 2.9 ± 0.3, n = 5; 360 μm: 3.9 ± 1.3, n = 6; p = 0.66, Mann–Whitney test). Therefore, the data were pooled together (Fig. 6G).
Given the wide range of unitary conductance of cartwheel-fusiform cell connections, the number of inputs estimated above might be biased because this approach assumes that each individual unitary conductance should be close to the population average. We therefore took another approach by examining how many increments are revealed in the peak optically evoked IPSC amplitudes as we gradually increased the light stimulation intensity, which presumably would recruit increasing numbers of cartwheel cells (Fig. 6E,F). Each step resolved by this method should represent one cartwheel cell's input. To reduce quantal fluctuation upon repeated trials, 4 mm Ca2+ was included in the bath. During the course of recording, it is possible that cartwheel synapses were depressed during some but not all trials due to the irregular pattern of spontaneous firing. This would complicate the interpretation of each “step” as individual cartwheel inputs. We therefore applied a train of 10 light stimuli before each test light pulse to predepress inputs. The number of increments of evoked currents were then determined by K-means cluster analysis (see Materials and Methods; Fig. 6E,F) (Ferragamo et al., 1998; Cao and Oertel, 2010). The number obtained by this method is consistent with that obtained from the maximum conductance over unitary conductance described above: there were on average 3.3 ± 0.2 inputs to the 12 fusiform cells recorded (Fig. 6G; p = 0.60, compared with maximum-over-unitary conductance method, t test; p = 0.34, Mann–Whitney test). Together, our results indicate that the convergence ratio of cartwheel cells is small, consisting of ∼3–4 cartwheel cells targeting a single fusiform cell.
Size of effective convergence increases with spontaneous spiking rate
The rather small size of the convergent circuit formed by cartwheel cells raises the question of whether a given cartwheel cell can provide effective inhibition during high spontaneous spiking rate (i.e., when the synapses are depressed). To answer this, we induced wide-field ChR2 stimulation to elevate firing frequency of the entire cartwheel cell population.
We first tested whether the number of cartwheel cells required to inhibit a postsynaptic fusiform cell (i.e., the effective convergence ratio) increases with spontaneous firing frequency. Action potentials were evoked in a fusiform cell by injecting an EPSC-like waveform while simultaneously varying blue light pulse intensity to recruit inhibition from different numbers of cartwheel cells. The amplitude of the EPSC-like current (400–500 pA) was sufficient to trigger spikes in all trials and was consistent with previous estimates for securely suprathreshold parallel-fiber-evoked EPSCs (Roberts and Trussell, 2010). The inhibition induced in this way would increase with light intensity as cartwheel cells are recruited and fully prevent fusiform cell from firing when the light reaches a critical level (Fig. 7A). After repeating this protocol for 10–15 trials, a “light-inhibition” curve for the fusiform spike probability against different light intensities was constructed, and an “IC50” value for the amount of light that inhibits 50% of the spike generation was obtained from a sigmoidal fit to the data (Fig. 7B). The same protocol was then applied to the cell again, except this time a train of 5 light pulses was delivered 250 ms before current injection to increase cartwheel cell population spiking rate and cause depression. The amount of light just sufficient to inhibit fusiform cell spiking under control condition no longer inhibited spiking, indicating that the light train depressed cartwheel synapses. However, with stronger light intensity, the recruited inhibition could once again effectively prevent spiking in the fusiform cell (Fig. 7A). This was reflected in a rightward shift in the curve and an increase in IC50 in the spike probability-light intensity plot (Fig. 7B). This rightward shift was observed in all 7 fusiform cells tested (Fig. 7C) (control IC50: 0.55 ± 0.05 mW vs depression IC50: 1.15 ± 0.11 mW; p = 0.001, paired t test). Therefore, despite the powerful synaptic depression induced by spontaneous spiking, recruitment of multiple inputs enabled effective inhibition to the postsynaptic principal cell.
Low-Pr pool is critical for effective inhibition in a small convergent circuit
The fact that such a small convergent circuit can provide effective inhibition despite strong synaptic depression was rather surprising. Because our synaptic depression model suggests that low-Pr vesicles dominate the release during high-frequency spontaneous spiking (Fig. 4), it seems that they are critical to setting the limiting number of cartwheel cells required for inhibition. We therefore used the model to quantify the effect of different pools of vesicles on functional convergence during various spontaneous spiking frequencies (Fig. 8A,B). We assume an “inhibition threshold” such that any IPSC larger than the threshold would inhibit fusiform cell spiking. We posited 50% depression as the maximum depression tolerable for effective inhibition by a single cartwheel cell, given that a single undepressed cartwheel cell is capable of inhibiting fusiform cell firing (Roberts and Trussell, 2010). The number of effective inputs can thus be estimated by dividing the threshold over the inhibition strength at different depression levels (Fig. 8A,B). The effective number of cartwheel inputs estimated using this method approximately matched the experimentally estimated convergence (∼3 cartwheel cells), supporting the idea that cartwheel-fusiform circuit can provide effective inhibition in a small convergent diagram. In addition, the number of effective inputs was much larger if the synapse only used the high-Pr pool (30 cells vs 3 cells) (Fig. 8B). This was due to a much more profound frequency-dependent depression when the synapses lacked low-Pr vesicles (Fig. 8A). Hence, the functional size of a convergent neural circuit is defined by the properties of its synaptic vesicles.
Figure 8.
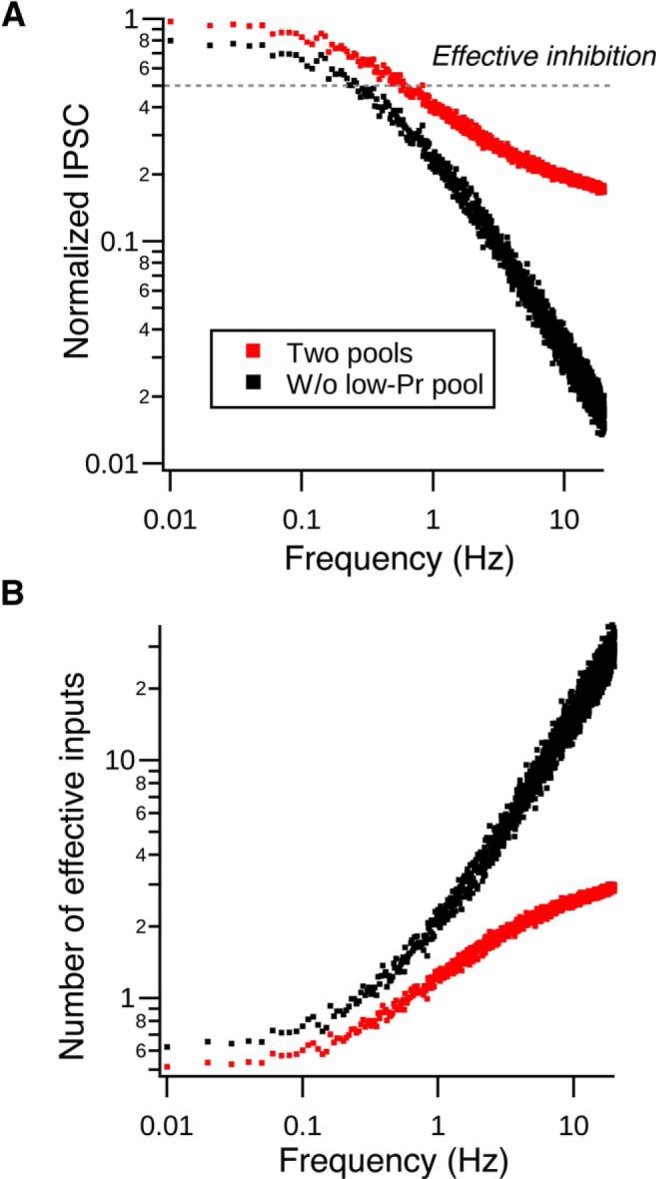
Vesicular release probabilities define effective convergence. A, Normalized peak IPSC amplitude decreases as the spontaneous spiking frequency increases in single cartwheel cells. Red dots are generated by the two-pool depletion model. Black dots are generated by the same model but lacking the low-Pr pool. Gray dotted line indicates the assumed effective inhibition strength needed to inhibit a fusiform cell from spiking (50% of maximum IPSC). B, Number of effective inputs predicted by the model when two pools are used (red dots) or only when the model lacks the low-Pr pool (black dots). The effective number is derived by dividing the effective inhibition strength (0.5) by each dot in A. When the synapse lacks the low-Pr pool, it requires a much larger number of inputs to effectively inhibit fusiform cell spiking compared with when both pools are present. For example, when cartwheel cells spontaneously fire at 10 Hz, it only requires 2–3 cells to provide effective inhibition when the two pools are present at the synapse. The effective convergence ratio increases to ∼30 cartwheel cells when the synapse lacks the low-Pr pool.
Discussion
Although short-term synaptic depression and modulation of neuronal spontaneous firing have been described in numerous brain regions, it remains unclear how their interaction impacts functional neural circuit connectivity. We characterized a dynamic relationship between spontaneous firing rate, synaptic depression, and the effective convergence of an interneuron circuit. Because of activity-dependent synaptic depression, synaptic strength from cartwheel interneurons is weakened by increased spontaneous firing. Thus, the number of cartwheel cells needed to effectively inhibit fusiform cells increases with its spontaneous firing rate. Interestingly, analysis of the synaptic depression kinetics suggests that the type of vesicles used by the synapse is critical for the effective size of the circuit. Because low-Pr vesicles with fast recovery rate prevent cartwheel synapse from complete depression at high spontaneous firing rate, effective inhibition can be performed in a relatively small circuit. Only three to four cartwheel cells are estimated to converge onto a single fusiform cell, and these are sufficient to provide effective inhibition when synapses are depressed by spontaneous firing. The interplay between spontaneous firing rate, synaptic depression, and vesicle recruitment therefore determines the size of the convergent circuit that can effectively influence postsynaptic spiking.
Vesicle pool dynamics and synaptic depression
In this study, we suggest that vesicle depletion mediates synaptic depression at the cartwheel cell synapse. In addition to vesicle depletion, several other mechanisms have been proposed to contribute to short-term synaptic depression, including reduced Ca2+ influx at the presynaptic nerve terminal (Xu and Wu, 2005; Catterall and Few, 2008), postsynaptic receptor desensitization (Trussell et al., 1993; Brenowitz and Trussell, 2001), or saturation. The former seems unlikely because peak amplitudes of action-potential-induced Ca2+ transients at cartwheel cell boutons summate linearly in response to a train of high-frequency action potentials (Roberts et al., 2008; Bender and Trussell, 2009). Regarding receptor desensitization, because synaptic responses evoked by cartwheel cells are mainly glycinergic (Golding and Oertel, 1997; Roberts et al., 2008; Apostolides and Trussell, 2013) and glycine receptors show slow desensitization kinetics (∼30% decline in response to 1 s, 1 mm glycine application) (Harty and Manis, 1998), receptor desensitization should contribute little to such fast synaptic depression. Furthermore, we found a negative correlation between paired-pulse ratio and the peak amplitude of the first IPSC, indicating a presynaptic mechanism that mediates short-term plasticity (Debanne et al., 1996; Regehr, 2012) (Fig. 1E). Thus, we conclude that vesicle depletion is likely to be the major mechanism contributing to the depression.
We propose that the synaptic depression at cartwheel synapse arises by depletion of two pools of vesicles: a high-Pr, slow recovery pool that contributes mainly to the IPSCs in the initial phase of the depression; and a low-Pr, fast recovery pool that sustains release during steady-state activity. Here, our definition of “pool” refers to the “readily releasable pool,” vesicles immediately available upon neural stimulation (Rizzoli and Betz, 2005). Although we were not able to directly clamp or measure capacitance from inhibitory boutons, and thus directly measure vesicle pool dynamics, such measurements have been made at large nerve terminals, particularly the calyx of Held. Interestingly, although the calyx and the cartwheel bouton differ greatly in size and transmitter content, our two-pool depletion model for cartwheel synapse shares many similarities with that proposed for the calyx of Held. First, vesicle depletion also leads to synaptic depression at the calyx of Held, and deconvolution analysis of vesicle depletion kinetics in response to prolonged voltage steps in the calyx revealed that the readily releasable pool consists of a fast- and slow-releasing component, which corresponds to a high-Pr and low-Pr pool in response to short-pulse stimulation (Sakaba and Neher, 2001a). Second, the recovery rate of the fast-releasing pool at the calyx of Held synapse is much slower than that of the slow-releasing pool (Sakaba and Neher, 2001b). Third, although the calyx exhibits Ca2+-dependent acceleration of recovery (Wang and Kaczmarek, 1998), introducing Ca2+-chelator did not change the steady-state level of depression (Weis et al., 1999) and a two-pool vesicle model with distinct release probabilities predicts frequency-dependent depression better than a single-pool model with Ca2+-dependent recovery (Trommershäuser et al., 2003). Finally, synaptic facilitation at the calyx can be revealed by high-frequency stimulation after the synapse is predepressed, suggesting low-Pr vesicles mediating the release at depressed state (Müller et al., 2010). In addition to the calyx, studies at other synapses also propose that the vesicular Pr decreases as the number of stimuli increases, thereby sustaining the release during steady-state depression (Betz, 1970; Saviane and Silver, 2006; McElvain et al., 2015). Thus, our two-pool depletion model for transmission at the cartwheel cell glycinergic synapse may be generalizable to other synapses. A recent study proposes that depression and steady-state release involve distinct release sites for the two phases of the response, based on statistical arguments (Wen et al., 2016). We cannot, however, distinguish between models in which the two pools represent distinct populations acting in parallel or a single population in different states of priming (Neher, 2015).
Small effective size of a convergent circuit
In this study, we estimated that 3–4 cartwheel cells converge onto a single fusiform cell, using two different physiological approaches. This value should in principle be an underestimate because some inputs might be lost during our slicing procedure. However, our results corroborate a recent anatomical study using serial EM reconstruction in hamster DCN, which suggested a low convergence ratio (3–4) based on numbers of somatic boutons on fusiform cells joined by a common axon (Salloum et al., 2014). Moreover, our estimate is similar to an anatomically determined convergence ratio (4.07) in rat DCN based on cell counts in EM (Wouterlood and Mugnaini, 1984). Despite such a small degree of convergence, synchronous activation of these inputs was sufficient to inhibit fusiform cell spiking even when synapses were maximally depressed by high frequency of spontaneous firing. Combined with the previous finding that a single cartwheel cell at rest (i.e., without spontaneous spiking) can effectively inhibit fusiform cell spiking (Roberts and Trussell, 2010), inhibition of fusiform cells is maintained across the full range of spontaneous spike rates using 1–4 inhibitory cells. Such small effective size of convergent circuits has been observed in other brain regions. Cerebellar Purkinje cells, which share genetic, morphological, biochemical, and biophysical similarities with cartwheel cells (Berrebi and Mugnaini, 1991; Oertel and Young, 2004), also converge onto target cerebellar nuclear cells (Person and Raman, 2012a). Interestingly, although the estimated Purkinje-to-nuclear convergence ratio is an order of magnitude larger than that of the cartwheel-fusiform cell circuit (∼30–40 vs 3–4), synchronous activation of only two Purkinje cells is able to entrain spike timing in the target nuclear cell (Person and Raman, 2012b). In the ventral cochlear nucleus, as few as 2 suprathreshold auditory nerve fibers can reduce spike jitter by 40% in the target bushy cells (Xu-Friedman and Regehr, 2005). Similar to cartwheel cell synapses, the examples mentioned above also display spontaneous activity- and frequency-dependent synaptic depression (Telgkamp and Raman, 2002; Xu-Friedman and Regehr, 2005), and so the effective convergence in those circuits might also vary with their background spontaneous firing rates. Nevertheless, these findings suggest that a small effective size of convergent circuits is probably common in the brain.
Implications for sensory processing in DCN
This study provides a possible mechanism for cartwheel interneurons to regulate multisensory integration in DCN via functional connectivity reconfiguration. When the spontaneous firing rate in cartwheel cells is slow, activation of single cartwheel cells is sufficient to inhibit fusiform cell spiking. Conversely, when cartwheel cell spontaneous firing rate is high, only synchronous activation of multiple cartwheel cells will effectively inhibit a fusiform cell. Because cartwheel cells converging onto the same fusiform cell likely do not share the same sets of parallel fiber inputs (Roberts and Trussell, 2010), recruitment of different numbers of cartwheel cells may require activation of distinct sets of parallel fibers and potentially distinct sets of sensory signals. Spontaneous spiking in cartwheel cells can be regulated by a variety of neuromodulators (Bender et al., 2010; Kuo and Trussell, 2011), presumably released during different behavioral states of the animal (Lee and Dan, 2012). One scenario is that specific sets of parallel fibers can effectively inhibit fusiform cell spiking only under certain behavioral states; in this way, the neuromodulators can enhance the salience of a specific sensory signal carried by parallel fibers. For example, sparse parallel fiber activation might effectively inhibit fusiform cells only when noradrenaline is released in vigilant states, during which cartwheel cells are relieved from depression (Berridge and Waterhouse, 2003; Kuo and Trussell, 2011). An alternative view is that the shift of inhibition from multiple to single convergent cartwheel cells through neuromodulation increases the impact of the multisensory pathway versus the auditory (cartwheel cell independent) pathway in shaping fusiform cell firing. In either scenario, neuromodulator-dependent shifts in the significance of a given interneuron's activity show that the convergence ratio in neural circuits can, from a functional standpoint, be a “tunable” parameter, and that the balance of different vesicle pools at individual nerve terminals provides the link between patterns of spikes activity and the effective level of synaptic convergence.
Footnotes
This work was supported by National Institutes of Health Grants NS028901 and DC004450 to L.O.T., and N.L. Tartar Trust Fellowship to H.-W.L. We thank members of the L.O.T. laboratory for helpful discussions; Drs. Erwin Neher, Sam Young, Dan Yaeger, and Tomohiko Irie for critical comments on the manuscript; Dr. Carol Borges-Merjane for help with immunostaining experiments; and Michael Bateschell and Ruby Larisch for help with mouse colony management. Floxed-ChR2(H134R)-EYFP breeder mice were kindly provided by the Westbrook laboratory at the Vollum Institute.
The authors declare no competing financial interests.
References
- Apostolides PF, Trussell LO. Rapid, activity-independent turnover of vesicular transmitter content at a mixed glycine/GABA synapse. J Neurosci. 2013;33:4768–4781. doi: 10.1523/JNEUROSCI.5555-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Apostolides PF, Trussell LO. Chemical synaptic transmission onto superficial stellate cells of the mouse dorsal cochlear nucleus. J Neurophysiol. 2014;111:1812–1822. doi: 10.1152/jn.00821.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bender KJ, Trussell LO. Axon initial segment Ca2+ channels influence action potential generation and timing. Neuron. 2009;61:259–271. doi: 10.1016/j.neuron.2008.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bender KJ, Ford CP, Trussell LO. Dopaminergic modulation of axon initial segment calcium channels regulates action potential initiation. Neuron. 2010;68:500–511. doi: 10.1016/j.neuron.2010.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bender KJ, Uebele VN, Renger JJ, Trussell LO. Control of firing patterns through modulation of axon initial segment T-type calcium channels. J Physiol. 2012;590:109–118. doi: 10.1113/jphysiol.2011.218768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berrebi AS, Mugnaini E. Distribution and targets of the cartwheel cell axon in the dorsal cochlear nucleus of the guinea pig. Anat Embryol (Berl) 1991;183:427–454. doi: 10.1007/BF00186433. [DOI] [PubMed] [Google Scholar]
- Berridge CW, Waterhouse BD. The locus coeruleus–noradrenergic system: modulation of behavioral state and state-dependent cognitive processes. Brain Res Rev. 2003;42:33–84. doi: 10.1016/S0165-0173(03)00143-7. [DOI] [PubMed] [Google Scholar]
- Betz WJ. Depression of transmitter release at the neuromuscular junction of the frog. J Physiol. 1970;206:629–644. doi: 10.1113/jphysiol.1970.sp009034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borst JG. The low synaptic release probability in vivo. Trends Neurosci. 2010;33:259–266. doi: 10.1016/j.tins.2010.03.003. [DOI] [PubMed] [Google Scholar]
- Brenowitz S, Trussell LO. Minimizing synaptic depression by control of release probability. J Neurosci. 2001;21:1857–1867. doi: 10.1523/JNEUROSCI.21-06-01857.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao XJ, Oertel D. Auditory nerve fibers excite targets through synapses that vary in convergence, strength, and short-term plasticity. J Neurophysiol. 2010;104:2308–2320. doi: 10.1152/jn.00451.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catterall WA, Few AP. Calcium channel regulation and presynaptic plasticity. Neuron. 2008;59:882–901. doi: 10.1016/j.neuron.2008.09.005. [DOI] [PubMed] [Google Scholar]
- Chabrol FP, Arenz A, Wiechert MT, Margrie TW, DiGregorio DA. Synaptic diversity enables temporal coding of coincident multisensory inputs in single neurons. Nat Neurosci. 2015;18:718–727. doi: 10.1038/nn.3974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook DL, Schwindt PC, Grande LA, Spain WJ. Synaptic depression in the localization of sound. Nature. 2003;421:66–70. doi: 10.1038/nature01248. [DOI] [PubMed] [Google Scholar]
- Davis KA, Young ED. Granule cell activation of complex-spiking neurons in dorsal cochlear nucleus. J Neurosci Off J Soc Neurosci. 1997;17:6798–6806. doi: 10.1523/JNEUROSCI.17-17-06798.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis KA, Miller RL, Young ED. Effects of somatosensory and parallel-fiber stimulation on neurons in dorsal cochlear nucleus. J Neurophysiol. 1996;76:3012–3024. doi: 10.1152/jn.1996.76.5.3012. [DOI] [PubMed] [Google Scholar]
- Debanne D, Guérineau NC, Gähwiler BH, Thompson SM. Paired-pulse facilitation and depression at unitary synapses in rat hippocampus: quantal fluctuation affects subsequent release. J Physiol. 1996;491:163–176. doi: 10.1113/jphysiol.1996.sp021204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dittman JS, Regehr WG. Calcium dependence and recovery kinetics of presynaptic depression at the climbing fiber to Purkinje cell synapse. J Neurosci. 1998;18:6147–6162. doi: 10.1523/JNEUROSCI.18-16-06147.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do MT, Bean BP. Subthreshold sodium currents and pacemaking of subthalamic neurons: modulation by slow inactivation. Neuron. 2003;39:109–120. doi: 10.1016/S0896-6273(03)00360-X. [DOI] [PubMed] [Google Scholar]
- Elmqvist D, Quastel DM. A quantitative study of end-plate potentials in isolated human muscle. J Physiol. 1965;178:505–529. doi: 10.1113/jphysiol.1965.sp007639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferragamo MJ, Golding NL, Oertel D. Synaptic inputs to stellate cells in the ventral cochlear nucleus. J Neurophysiol. 1998;79:51–63. doi: 10.1152/jn.1998.79.1.51. [DOI] [PubMed] [Google Scholar]
- Golding NL, Oertel D. Physiological identification of the targets of cartwheel cells in the dorsal cochlear nucleus. J Neurophysiol. 1997;78:248–260. doi: 10.1152/jn.1997.78.1.248. [DOI] [PubMed] [Google Scholar]
- Groh A, de Kock CP, Wimmer VC, Sakmann B, Kuner T. Driver or coincidence detector: modal switch of a corticothalamic giant synapse controlled by spontaneous activity and short-term depression. J Neurosci. 2008;28:9652–9663. doi: 10.1523/JNEUROSCI.1554-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harty TP, Manis PB. Kinetic analysis of glycine receptor currents in ventral cochlear nucleus. J Neurophysiol. 1998;79:1891–1901. doi: 10.1152/jn.1998.79.4.1891. [DOI] [PubMed] [Google Scholar]
- Häusser M, Raman IM, Otis T, Smith SL, Nelson A, du Lac S, Loewenstein Y, Mahon S, Pennartz C, Cohen I, Yarom Y. The beat goes on: spontaneous firing in mammalian neuronal microcircuits. J Neurosci. 2004;24:9215–9219. doi: 10.1523/JNEUROSCI.3375-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermann J, Pecka M, von Gersdorff H, Grothe B, Klug A. Synaptic transmission at the calyx of Held under in vivo-like activity levels. J Neurophysiol. 2007;98:807–820. doi: 10.1152/jn.00355.2007. [DOI] [PubMed] [Google Scholar]
- Kanold PO, Davis KA, Young ED. Somatosensory context alters auditory responses in the cochlear nucleus. J Neurophysiol. 2011;105:1063–1070. doi: 10.1152/jn.00807.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y, Trussell LO. Ion channels generating complex spikes in cartwheel cells of the dorsal cochlear nucleus. J Neurophysiol. 2007;97:1705–1725. doi: 10.1152/jn.00536.2006. [DOI] [PubMed] [Google Scholar]
- Kim Y, Trussell LO. Negative shift in the glycine reversal potential mediated by a Ca2+- and pH-dependent mechanism in interneurons. J Neurosci. 2009;29:11495–11510. doi: 10.1523/JNEUROSCI.1086-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koehler SD, Pradhan S, Manis PB, Shore SE. Somatosensory inputs modify auditory spike timing in dorsal cochlear nucleus principal cells. Eur J Neurosci. 2011;33:409–420. doi: 10.1111/j.1460-9568.2010.07547.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuba H, Koyano K, Ohmori H. Synaptic depression improves coincidence detection in the nucleus laminaris in brainstem slices of the chick embryo. Eur J Neurosci. 2002;15:984–990. doi: 10.1046/j.1460-9568.2002.01933.x. [DOI] [PubMed] [Google Scholar]
- Kuo SP, Trussell LO. Spontaneous spiking and synaptic depression underlie noradrenergic control of feed-forward inhibition. Neuron. 2011;71:306–318. doi: 10.1016/j.neuron.2011.05.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo SP, Lu HW, Trussell LO. Intrinsic and synaptic properties of vertical cells of the mouse dorsal cochlear nucleus. J Neurophysiol. 2012;108:1186–1198. doi: 10.1152/jn.00778.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Dan Y. Neuromodulation of brain states. Neuron. 2012;76:209–222. doi: 10.1016/j.neuron.2012.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu T, Trussell LO. Inhibitory transmission mediated by asynchronous transmitter release. Neuron. 2000;26:683–694. doi: 10.1016/S0896-6273(00)81204-0. [DOI] [PubMed] [Google Scholar]
- Ma WL, Brenowitz SD. Single-neuron recordings from unanesthetized mouse dorsal cochlear nucleus. J Neurophysiol. 2012;107:824–835. doi: 10.1152/jn.00427.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mancilla JG, Manis PB. Two distinct types of inhibition mediated by cartwheel cells in the dorsal cochlear nucleus. J Neurophysiol. 2009;102:1287–1295. doi: 10.1152/jn.91272.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McElvain LE, Faulstich M, Jeanne JM, Moore JD, du Lac S. Implementation of linear sensory signaling via multiple coordinated mechanisms at central vestibular nerve synapses. Neuron. 2015;85:1132–1144. doi: 10.1016/j.neuron.2015.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller M, Goutman JD, Kochubey O, Schneggenburger R. Interaction between facilitation and depression at a large CNS synapse reveals mechanisms of short-term plasticity. J Neurosci. 2010;30:2007–2016. doi: 10.1523/JNEUROSCI.4378-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neher E. Merits and limitations of vesicle pool models in view of heterogeneous populations of synaptic vesicles. Neuron. 2015;87:1131–1142. doi: 10.1016/j.neuron.2015.08.038. [DOI] [PubMed] [Google Scholar]
- Oertel D, Young ED. What's a cerebellar circuit doing in the auditory system? Trends Neurosci. 2004;27:104–110. doi: 10.1016/j.tins.2003.12.001. [DOI] [PubMed] [Google Scholar]
- Owen SF, Tuncdemir SN, Bader PL, Tirko NN, Fishell G, Tsien RW. Oxytocin enhances hippocampal spike transmission by modulating fast-spiking interneurons. Nature. 2013;500:458–462. doi: 10.1038/nature12330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parham K, Kim DO. Spontaneous and sound-evoked discharge characteristics of complex-spiking neurons in the dorsal cochlear nucleus of the unanesthetized decerebrate cat. J Neurophysiol. 1995;73:550–561. doi: 10.1152/jn.1995.73.2.550. [DOI] [PubMed] [Google Scholar]
- Person AL, Raman IM. Synchrony and neural coding in cerebellar circuits. Front Neural Circuits. 2012a;6:97. doi: 10.3389/fncir.2012.00097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Person AL, Raman IM. Purkinje neuron synchrony elicits time-locked spiking in the cerebellar nuclei. Nature. 2012b;481:502–505. doi: 10.1038/nature10732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Portfors CV, Roberts PD. Temporal and frequency characteristics of cartwheel cells in the dorsal cochlear nucleus of the awake mouse. J Neurophysiol. 2007;98:744–756. doi: 10.1152/jn.01356.2006. [DOI] [PubMed] [Google Scholar]
- Regehr WG. Short-term presynaptic plasticity. Cold Spring Harb Perspect Biol. 2012;4:a005702. doi: 10.1101/cshperspect.a005702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rizzoli SO, Betz WJ. Synaptic vesicle pools. Nat Rev Neurosci. 2005;6:57–69. doi: 10.1038/nrn1583. [DOI] [PubMed] [Google Scholar]
- Roberts MT, Trussell LO. Molecular layer inhibitory interneurons provide feedforward and lateral inhibition in the dorsal cochlear nucleus. J Neurophysiol. 2010;104:2462–2473. doi: 10.1152/jn.00312.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts MT, Bender KJ, Trussell LO. Fidelity of complex spike-mediated synaptic transmission between inhibitory interneurons. J Neurosci. 2008;28:9440–9450. doi: 10.1523/JNEUROSCI.2226-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubio ME, Juiz JM. Differential distribution of synaptic endings containing glutamate, glycine, and GABA in the rat dorsal cochlear nucleus. J Comp Neurol. 2004;477:253–272. doi: 10.1002/cne.20248. [DOI] [PubMed] [Google Scholar]
- Sakaba T, Neher E. Quantitative relationship between transmitter release and calcium current at the calyx of Held synapse. J Neurosci. 2001a;21:462–476. doi: 10.1523/JNEUROSCI.21-02-00462.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakaba T, Neher E. Calmodulin mediates rapid recruitment of fast-releasing synaptic vesicles at a calyx-type synapse. Neuron. 2001b;32:1119–1131. doi: 10.1016/S0896-6273(01)00543-8. [DOI] [PubMed] [Google Scholar]
- Salloum RH, Chen G, Velet L, Manzoor NF, Elkin R, Kidd GJ, Coughlin J, Yurosko C, Bou-Anak S, Azadi S, Gohlsch S, Schneider H, Kaltenbach JA. Mapping and morphometric analysis of synapses and spines on fusiform cells in the dorsal cochlear nucleus. Front Syst Neurosci. 2014;8:167. doi: 10.3389/fnsys.2014.00167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saviane C, Silver RA. Fast vesicle reloading and a large pool sustain high bandwidth transmission at a central synapse. Nature. 2006;439:983–987. doi: 10.1038/nature04509. [DOI] [PubMed] [Google Scholar]
- Schneggenburger R, Meyer AC, Neher E. Released fraction and total size of a pool of immediately available transmitter quanta at a calyx synapse. Neuron. 1999;23:399–409. doi: 10.1016/S0896-6273(00)80789-8. [DOI] [PubMed] [Google Scholar]
- Shore SE. Multisensory integration in the dorsal cochlear nucleus: unit responses to acoustic and trigeminal ganglion stimulation. Eur J Neurosci. 2005;21:3334–3348. doi: 10.1111/j.1460-9568.2005.04142.x. [DOI] [PubMed] [Google Scholar]
- Telgkamp P, Raman IM. Depression of inhibitory synaptic transmission between Purkinje cells and neurons of the cerebellar nuclei. J Neurosci. 2002;22:8447–8457. doi: 10.1523/JNEUROSCI.22-19-08447.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thanawala MS, Regehr WG. Presynaptic calcium influx controls neurotransmitter release in part by regulating the effective size of the readily releasable pool. J Neurosci. 2013;33:4625–4633. doi: 10.1523/JNEUROSCI.4031-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson SM, Gähwiler BH. Activity-dependent disinhibition: I. Repetitive stimulation reduces IPSP driving force and conductance in the hippocampus in vitro. J Neurophysiol. 1989;61:501–511. doi: 10.1152/jn.1989.61.3.501. [DOI] [PubMed] [Google Scholar]
- Trommershäuser J, Schneggenburger R, Zippelius A, Neher E. Heterogeneous presynaptic release probabilities: functional relevance for short-term plasticity. Biophys J. 2003;84:1563–1579. doi: 10.1016/S0006-3495(03)74967-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trussell LO, Zhang S, Raman IM. Desensitization of AMPA receptors upon multiquantal neurotransmitter release. Neuron. 1993;10:1185–1196. doi: 10.1016/0896-6273(93)90066-Z. [DOI] [PubMed] [Google Scholar]
- Wang LY, Kaczmarek LK. High-frequency firing helps replenish the readily releasable pool of synaptic vesicles. Nature. 1998;394:384–388. doi: 10.1038/28645. [DOI] [PubMed] [Google Scholar]
- Weis S, Schneggenburger R, Neher E. Properties of a model of Ca(++)-dependent vesicle pool dynamics and short term synaptic depression. Biophys J. 1999;77:2418–2429. doi: 10.1016/S0006-3495(99)77079-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen H, McGinley MJ, Mandel G, Brehm P. Nonequivalent release sites govern synaptic depression. Proc Natl Acad Sci U S A. 2016;113:E378–E386. doi: 10.1073/pnas.1523671113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wouterlood FG, Mugnaini E. Cartwheel neurons of the dorsal cochlear nucleus: a Golgi-electron microscopic study in rat. J Comp Neurol. 1984;227:136–157. doi: 10.1002/cne.902270114. [DOI] [PubMed] [Google Scholar]
- Xu J, Wu LG. The decrease in the presynaptic calcium current is a major cause of short-term depression at a calyx-type synapse. Neuron. 2005;46:633–645. doi: 10.1016/j.neuron.2005.03.024. [DOI] [PubMed] [Google Scholar]
- Xu-Friedman MA, Regehr WG. Dynamic-clamp analysis of the effects of convergence on spike timing: II. Few synaptic inputs. J Neurophysiol. 2005;94:2526–2534. doi: 10.1152/jn.01308.2004. [DOI] [PubMed] [Google Scholar]
- Yang H, Xu-Friedman MA. Skipped-stimulus approach reveals that short-term plasticity dominates synaptic strength during ongoing activity. J Neurosci. 2015;35:8297–8307. doi: 10.1523/JNEUROSCI.4299-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young ED, Nelken I, Conley RA. Somatosensory effects on neurons in dorsal cochlear nucleus. J Neurophysiol. 1995;73:743–765. doi: 10.1152/jn.1995.73.2.743. [DOI] [PubMed] [Google Scholar]
- Zucker RS, Regehr WG. Short-term synaptic plasticity. Annu Rev Physiol. 2002;64:355–405. doi: 10.1146/annurev.physiol.64.092501.114547. [DOI] [PubMed] [Google Scholar]