Stable topological insulators achieved using high energy electron beams

Abstract

Topological insulators are potentially transformative quantum solids with metallic surface states which have Dirac band structure and are immune to disorder. Ubiquitous charged bulk defects, however, pull the Fermi energy into the bulk bands, denying access to surface charge transport. Here we demonstrate that irradiation with swift (∼2.5 MeV energy) electron beams allows to compensate these defects, bring the Fermi level back into the bulk gap and reach the charge neutrality point (CNP). Controlling the beam fluence, we tune bulk conductivity from p- (hole-like) to n-type (electron-like), crossing the Dirac point and back, while preserving the Dirac energy dispersion. The CNP conductance has a two-dimensional character on the order of ten conductance quanta and reveals, both in Bi₂Te₃ and Bi₂Se₃, the presence of only two quantum channels corresponding to two topological surfaces. The intrinsic quantum transport of the topological states is accessible disregarding the bulk size.

Defects in solids may introduce additional charges that influence the overall charge transport behaviour. Here, Zhao et al. use swift electron beams to compensate charge defects, which effectively tune Bi₂Te₃ and Bi₂Se₃ from p-type to n-type while preserving their topological properties.

Unconventional quantum matter can be easily hidden within the rich existing library of condensed matter and to recognize it often novel concepts have to be invoked. It also takes a profound understanding of the real material constraints that can prevent the unconventional properties from being detected. Three-dimensional (3D) topological insulators are a spectacular example of this¹—narrow-band semiconductors, well known for their high performance as thermoelectrics², they were discovered to support unusual gapless robust two-dimensional (2D) surface states that are fully spin-polarized with Dirac-type linear electronic energy-momentum dispersion³,⁴, which makes them protected against backscattering by disorder³,⁴,⁵,⁶. These materials have narrow bulk gaps (∼200–300 meV) and have charge carriers donated by intrinsic crystalline lattice defects such as vacancies and antisites⁷. As a result, the conduction through the bulk and its intermixing with surface channels is what largely denies direct access to surface charge transport required for the implementation in spin-based nanoelectronics⁸ or fault-tolerant topological quantum computing⁴.

Extensive attempts to reduce the contribution of bulk carriers, involving techniques such as nanostructured synthesis/growth⁹,¹⁰, chemical doping¹¹ or compositional tuning¹², have relied on electrostatic gating of micro- or nanostructures comprising tens of nanometre thin films¹³ or similarly thin exfoliated crystals¹⁴ to gain less ambiguous access to the surface states. Here we demonstrate that bulk conductivity in topological insulators (TIs) can be decreased by orders of magnitude to charge neutrality point on a large (depth) scale by the controlled use of electron beams, which for energies below ∼3 MeV are known to produce a well-defined, stable and uniform spread of Frenkel (vacancy-interstitial) pairs¹⁵ within their penetration range of hundreds of micrometres. The combined effect of these pairs is to compensate for the intrinsic charged defects responsible for the conductivity of the bulk while crystal lattice integrity is maintained and, as we demonstrate by angularly resolved photoemission spectroscopy (ARPES), the topological Dirac surface states remain robust. Stable surface conduction channels are achieved when a sufficient irradiation dose is followed by the optimally engineered annealing protocol, thereby resolving one of the key limitations of bulk TIs.

Results

Compensating bulk carriers using electron beams

Under exposure to light particles such as electrons, the production of vacancy-interstitial point defects¹⁶ in solids known as Frenkel pairs is well established. The pair formation has an energy threshold which scales with atomic weight—it is high for heavy Bi and is lower for lighter Te and Se, and the effective cross-section σ for pair creation on different sublattices in materials containing these elements depends on the projectile energy (Fig. 1a,b and Supplementary Figs 1,2). This defines a pair-production window: below these thresholds, the given sublattice becomes immune to irradiation, whereas at energies above ∼3 MeV, clustering and even nuclear reactions¹⁷ may occur. The process of Frenkel pair formation is straightforward and can be well controlled. The charge is primarily delivered by introduced vacancies, since at room temperature interstitials do not contribute owing to their much lower (compared with vacancies) migration barriers. For electron beam energies above ∼1.5 MeV, the effective cross-section σ on a Bi sublattice is the highest and we will show that donor type defects on this sublattice do prevail. For energies below Bi threshold (∼1.2 MeV), the creation of Frenkel pairs will be mostly on Se or Te sublattices and, correspondingly, by tuning electron beam energy a different mix of donor/acceptor defects and a net acceptor charge doping can be expected.

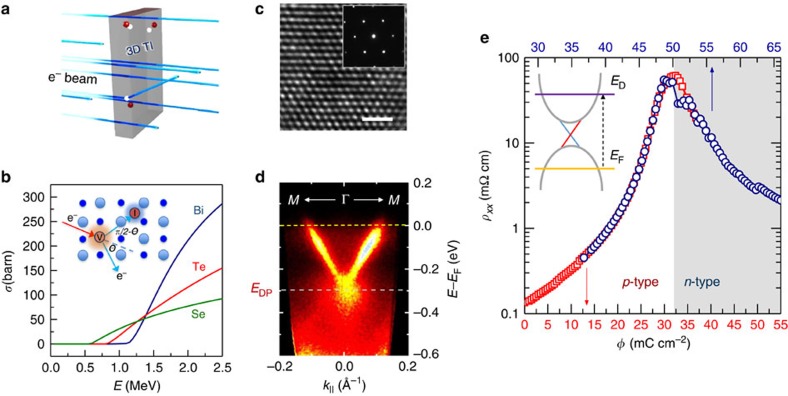
Figure 1. Tuning bulk conductivity of topological materials by swift particle irradiation.

(a) Energetic electron beams can penetrate solids to a depth of many tens of micrometres. Electron irradiation affects the bulk but not the robust topological surfaces. (b) Impinging electrons induce formation of Frenkel vacancy-interstitial pairs (inset), which act to compensate the intrinsic bulk defects. Main panel: calculated crosssections σ for Frenkel pair production in Bi, Te and Se sublattices as a function of electron energy E, assuming displacement energy¹⁶ ∼25 eV. Energy thresholds, E_th, in σ are set by atomic weight; choosing 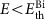or 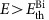allows to tune Fermi level in both p- and n-type TIs. (c) Transmission electron microscopy image of Bi₂Te₃ with electron dose ϕ=1 C cm⁻²; the atomic displacements of ∼1 per 5,000 are not seen. Scale bar, 1 nm. (d) ARPES spectrum taken at 130 K (see ‘Methods' section) of a Bi₂Te₃ crystal after irradiation with high electron dose of 1.7 C cm⁻². The irradiated sample becomes n-type, with Dirac point at E_DP=−290(10) meV relative to the Fermi level E_F (just below the bottom of the bulk conduction band). It demonstrates electronic robustness of Dirac spectrum against electron irradiation. (e) Resistivity of p-type Bi₂Te₃ irradiated with 2.5 MeV electrons versus dose ϕ (red squares) measured in situ at 20 K shows about three orders of magnitude increase at the charge neutrality point (CNP) where the conduction is converted from p- to n-type, moving the Fermi level E_F across the Dirac point (see cartoon). Cycling to room temperature reverses the process, which can be recovered by further irradiation (blue circles) and stabilized. The conversion from n- to p-type is obtained in a material such as Pb-based TI, where vacancies on the Pb sites are known to be of acceptor type.

Generally, crystal growth of tetradymite crystals such as Bi₂Te₃ and Bi₂Se₃ results in equilibrium defect configurations comprising vacancies and antisites on both sublattices⁷,¹⁸. The net free charge balance that delivers carriers to bulk conduction or valence bands from these defects can be varied by growth conditions or doping¹¹. In undoped Bi₂Se₃, where Se vacancies are presumed to dominate, the net conduction is by electron carriers or n-type. In Bi₂Te₃, where antisites are prevalent¹⁹ the conductivity is usually p-type, namely by hole carriers, although by varying stoichiometry it has been grown of either conductivity type. Without a priori knowledge of the net donor or acceptor flavour of the pairs on different sublattices, we have chosen first to irradiate p-type topological materials Bi₂Te₃ and Ca-doped¹¹ Bi₂Se₃ with 2.5 MeV electron beams that create Frenkel pairs on all sublattices according to σ(E), shown in Fig. 1b and Supplementary Fig. 2. Our results demonstrate that in the above-mentioned Bi-based TIs at this energy, the net flavour is of donor type. It is also important to note that even for relatively high (≳1 C cm⁻²) electron irradiation doses, the lattice parameters remain unchanged (see Supplementary Fig. 3).

Ambipolar conduction tuned by irradiation dose

Longitudinal resistivity ρ_xx of the initially p-type Bi₂Te₃ measured at 20 K in situ in the irradiation chamber (see ‘Methods' section) as a function of irradiation dose is shown in Fig. 1e. Most immediately notable features in the figure are a nearly three orders of magnitude resistivity increase to a maximum 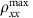and the observed ambipolar conduction as a function of irradiation dose with well-distinguished p (hole) and n (electron) conduction regions. The resistivity maximum 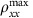(the conductivity minimum 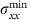) is at the charge neutrality point where conduction is converted from p- to n-type, as determined from Hall resistivity (see Fig. 2). The same type conversion is observed in Ca-doped Bi₂Se₃ (Supplementary Fig. 4a and Supplementary Note 1), which is also p-type¹¹. As long as the terminal irradiation dose ϕ is relatively low, below ∼0.1 C cm⁻², ρ_xx(ϕ) traces its shape upon temperature cycling to room temperature and back to 20 K, with 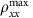reproduced by the next irradiation cycle. Here it is apparent that the value of ϕ_max at the charge neutrality point is not universal; it depends on the starting free carrier concentration n_b but can be straightforwardly scaled using universal slope 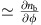of quasi-linear variation of n_b versus dose (Fig. 2a and Supplementary Figs 4b and 5).

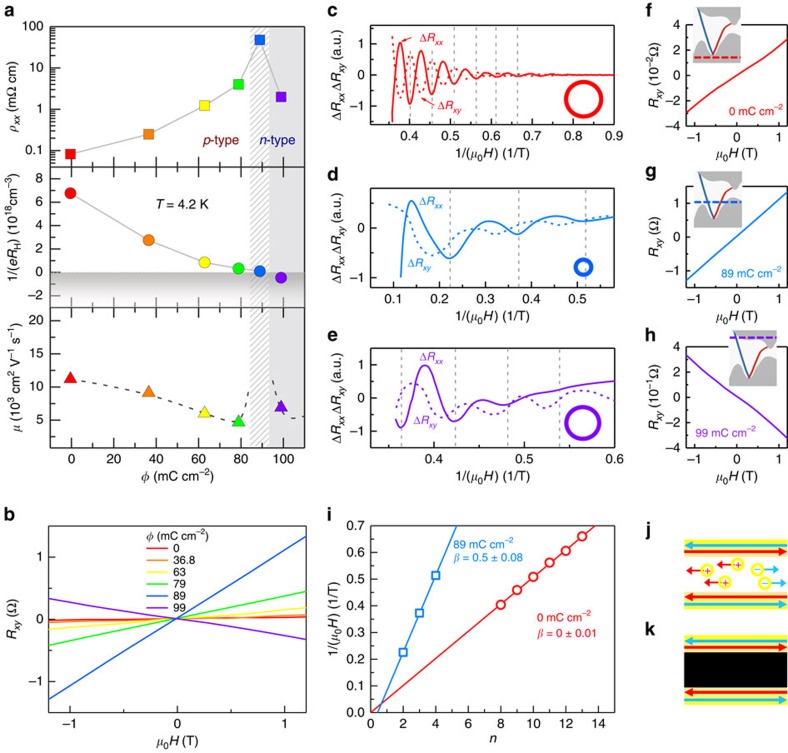
Figure 2. Transport and quantum oscillations across charge neutrality point.

(a) Longitudinal resistivity ρ_xx of Bi₂Te₃ crystals irradiated to different terminal doses and measured at 4.2 K shows three orders of magnitude increase at CNP where the bulk is converted from p- to n-type, as indicated by the sign change of the slope dR_xy/dH of Hall resistance R_xy shown in b. Inverse Hall coefficient 1/eR_H ≃−n_b gives an estimate of net carrier density n_b as a function of dose. At CNP R_H changes sign. Mobility just above CNP appears higher than just below, with the expected trend of μ at CNP indicated by dash. Outside the immediate vicinity of CNP, effective carrier mobilities μ estimated from 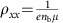in the Drude model are not much affected by the irradiation process, confirming that scattering events by Frenkel-pair point defects are scarce and the main effect is charge compensation. Shubnikov-de Haas (SdH) quantum oscillations of ΔR_xx and ΔR_xy in Bi₂Te₃ with magnetic field applied along the c axis: (c) before e-beam exposure, (d) irradiated to a dose 89 mC cm⁻² and (e) to a dose 99 mC cm⁻². The corresponding sizes of Fermi surfaces obtained from SdH (Supplementary Table 1) are cartooned as circles. (f–h) Low-field R_xy for the samples in (c–e). The Fermi level (dashed line) is moving from the bulk valence band (BVB) in f to the bulk conduction band (BCB) in h as illustrated in outsets by the cartoons of calculated⁵ Bi₂Te₃ band structure. (i) The Landau level index plot versus field minima in the SdH oscillations in c (red) and d (blue) yields an estimate of Berry phase 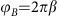, see text. (j,k) Cartoons of a TI with conducting bulk before irradiation (j) and after, with ideally only topological surfaces conducting (k).

Longitudinal and Hall resistivities across CNP

Ex situ measured resistivities of Bi₂Te₃ crystals irradiated to different terminal doses and taken to room temperature before the chill-down to 4.2 K are in full correspondence with the in situ results. Figure 2a shows three orders of magnitude increase in ρ_xx to the maximum, 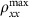, at ϕ_max≈90 mC cm⁻² higher than the in situ ϕ_max (Fig. 1e) likely owing in part to some defect migration (mostly interstitials¹⁶) above 100 K. The p- to n-type conversion is clearly seen in Hall resistance R_xy (Fig. 2b,f–h) flipping its slope dR_xy/dH and Hall coefficient 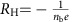changing sign in the conversion region. Near CNP, the net residual bulk carrier density n_b=n_D−n_A is very low (n_D and n_A are concentrations of donors and acceptors, respectively). In this region, local charge fluctuations can be very large creating inhomogeneity akin to a network of puddle-like p–n junctions that nonlinearly screen random potential on long length scales²⁰ and a simple estimate of n_b is no longer appropriate¹⁴. Mobilities in our crystals are significantly higher (μ≅7,000–11,000 cm² V⁻¹ s⁻¹, see Supplementary Table 1) than a commonly observed ≲1,000 cm² V⁻¹ s⁻¹ range¹⁴ near the CNP region.

Shubnikov–de Haas oscillations and Berry phase

The change in net carrier density induced by irradiation is reflected in the observed Shubnikov–de Haas (SdH) quantum oscillations (Fig. 2c–e) of sheet and Hall resistances, ΔR_xx and ΔR_xy, from which an estimate of the Fermi surface size can be obtained (Supplementary Table 1). The Fermi vector in pristine crystals k_F≈0.025 Å⁻¹ is consistently larger than after irradiation and, for example, the dose ϕ≅89 mC cm⁻² that tunes the crystal close to CNP results in k_F≈0.014 Å⁻¹. The corresponding net carrier densities are n_b=5.06 × 10¹⁷ cm⁻³ and n_b≃1.08 × 10¹⁷ cm⁻³, respectively. At higher irradiation dose ϕ≅99 mC cm⁻², with k_F≈0.022 Å⁻¹ Fermi surface size becomes comparable to the pristine material. A comparison of these numbers with carrier densities obtained independently from Hall data (Supplementary Table 1) reveals a good agreement between the two techniques near CNP but about an order of magnitude higher estimate of n_b by the latter²¹ well outside the CNP region. Berry phase 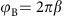can be estimated from SdH oscillations using a semiclassical description²² 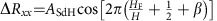, where A_SdH is the oscillation amplitude, H_F is the frequency in 1/H and β is the Berry factor. Near CNP, the obtained Berry factor is β=0.5±0.06 as expected for the topological Dirac particles, while outside the CNP region, a trivial value of β≃0 is obtained (Fig. 2i).

Nonequilibrium defect compensation at low irradiation dose

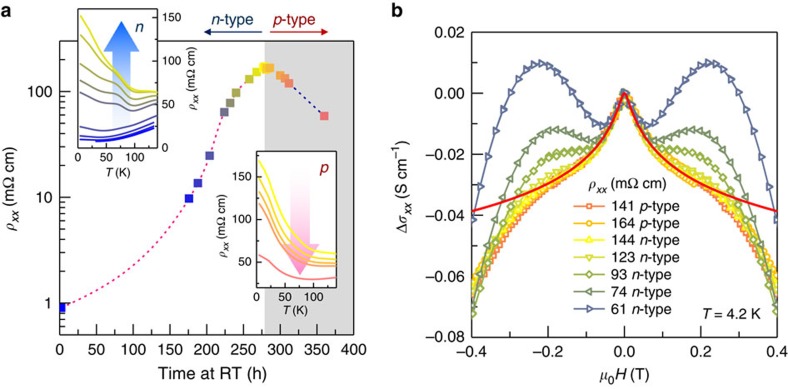
The stability of net carrier density crucially depends on the terminal irradiation dose. First, we illustrate that for low terminal electron doses (ϕ≲0.1 C cm⁻²), the resistivity is not stable as it evolves from the n-region after irradiation through CNP back into the p-region. The experiment was to simply change the dwelling time at room temperature to allow for vacancies to diffuse. The result is the reverse conversion (Fig. 3a) from metallic-like resistivity on the n-side just after irradiation, through insulating resistivity at CNP (after nearly 250 h at room temperature) and back to a weakly semiconducting-like resistivity on the p-side. As the system evolves across CNP, a weak antilocalization quantum interference correction²³ to classical magnetoresistance (MR) emerges in the non-equilibrated conversion region (Fig. 3b), with a complex MR structure and nonlinear Hall resistivity (see Supplementary Fig. 6), likely reflecting a presence of two carrier types. From isochronal annealing experiments (Supplementary Fig. 7 and Supplementary Note 2), we estimate energy barriers controlling defect migration to be ∼0.8 eV corresponding to ∼9,000 K, in line with literature values for vacancy migration in solids¹⁶. We conclude that at low terminal doses while defect migration is sluggish, the equilibrium is not attained.

Figure 3. Time evolution of charge transport across charge neutrality point in Bi₂Te₃ after low-dose exposure.

(a) Evolution of longitudinal resistivity ρ_xx measured at 4.2 K after cycling to room temperature (RT) for a crystal irradiated with dose ϕ=90 mC cm⁻². Each RT dwell time is coded with a different colour. Resistivity is seen to cross charge neutrality point (CNP) in reverse from n-type back to p-type. It is consistent with slow migration (hundreds of hours at RT) of vacancies (in accord with ∼0.8 eV migration barriers, see text) and shows that CNP can be reached by designing a suitable thermal protocol. Insets show ρ_xx(T) for n-type region (upper left) and p-type region (lower right). (b) Change in magnetoconductance (MC) at different RT dwell times; here MC evolves from a quadratic field dependence of a typical bulk metal at short RT dwell times, through a complex region dominated by the charge-inhomogeneous bulk, to a weak antilocalization (WAL) region showing the characteristic low-field cusp near CNP. Here the data were normalized to the value at zero field. A fit to 2D localization theory²⁶ is shown as red line, see text.

Achieving stability at CNP with high irradiation dose

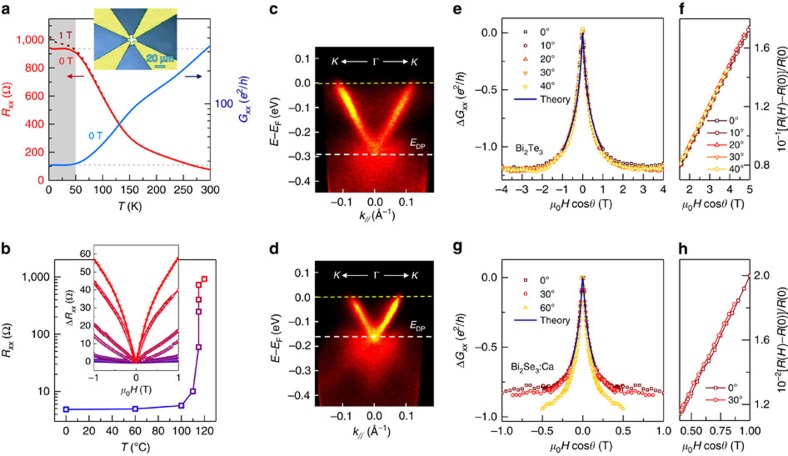
Next we demonstrate that stability can be controlled and optimized in a reverse conversion process by the annealing protocol when the terminal electron dose is sufficiently high. This is the key part of the material modification process by electron irradiation; without it surface transport via electron irradiation could not be obtained²⁴. We demonstrate this for the samples exposed to the dose 10 times higher, ϕ=1 C cm⁻². Figure 4a shows temperature dependence of sheet resistance R_xx and conductance G_xx of Bi₂Te₃ tuned back to CNP through a thermal protocol shown in Fig. 4b, where it remained for months of testing (Supplementary Figs 8,9 and Supplementary Note 3). As clearly seen in ARPES (Fig. 4c,d and Supplementary Fig. 10), under this annealing protocol Dirac dispersion remains preserved. The effect of tuning conduction from the irradiation-induced n-type (Fig. 4c) back towards CNP (Fig. 4d) is a relative shift of the Fermi level toward the Dirac point, consistent with transport data and with the calculated band structure⁵ of Bi₂Te₃ (see cartoons in Fig. 2f–h).

Figure 4. Stable charge neutrality point and 2D conductance in e-beam irradiated topological materials.

(a) Sheet resistance R_xx versus temperature of Bi₂Te₃ crystal at the charge neutrality point (red line) exhibits a plateau at low temperatures—a thumbprint of 2D surface conduction, see right panels in e and f). We note that in Bi₂Te₃, CNP and Dirac point do not coincide, with the Dirac point situated within a valley in the bulk valence bands⁵, and 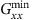is expected to reflect that²³. Magnetic field breaks time reversal symmetry and gaps Dirac bands, resulting in localizing behaviour shown as dash. Inset: optical image of the crystal showing van der Pauw contact configuration used. (b) Annealing protocol with time steps Δt=30 min implemented to tune Bi₂Te₃ crystal with dose 1 C cm⁻² back to stable CNP. Inset: magnetoresistance at 1.9 K after each annealing step, with colours matched to indicate different annealing temperatures. (c,d) ARPES spectra of a Bi₂Te₃ crystal irradiated with electron dose of 1.7 C cm⁻² taken along Γ−K direction in the Brillouin zone. (c) Before annealing, the irradiated sample is n-type, with Dirac point at E_DP∼−290(10) meV relative to the Fermi level E_F. (d) After annealing at 120 °C, Dirac point upshifts to a binding energy of E_DP∼−160(10) meV. The same shift is seen for the scans along Γ−M. (e) WAL low-field quantum interference correction to the linear-in-field magnetotransport ((f), also see text) at CNP in a Bi₂Te₃ crystal at 1.9 K with its characteristic low-field cusp. The 2D character of WAL is evident in its scaling with transverse field H_‖=Hcosθ, where θ is the tilt angle of the field measured from sample's c axis. A fit to 2D localization (HLN) theory²⁶ (solid line) confirms that the contribution is only from two surfaces and yields a dephasing field 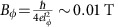. (f) Linear magnetoresistance at CNP shows 2D scaling with H_‖. (g) WAL contribution at CNP in a Bi₂Se₃:Ca(0.09%) crystal at 1.9 K also scales with H_‖. At high fields outside the cusp, the scaling is seen to fail for θ≳60°. A fit to HLN theory (solid line) again confirms the contribution only from two surfaces and yields a smaller dephasing field B_ϕ∼0.004 T (corresponding to dephasing length l_ϕ∼220 nm). (h) Linear magnetoresistance at CNP also scales with H_‖.

R_xx(T) increases exponentially as the temperature decreases, turning below ∼200 K into variable range hopping (Supplementary Fig. 11 and Supplementary Note 4). This bulk behaviour is cut off at low temperatures when the contribution from the surface becomes comparable and a temperature-independent surface transport with minimum conductance¹⁴ 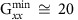e²/h reveals its quantum nature. The 2D character of this region is witnessed by MR that depends only on the transverse component of magnetic field H_‖=Hcosθ (Fig. 4e–h). Unlike the quadratic-in-field MR of a conventional metal, the large (≳10%) magnetoresistance at CNP (Fig. 4a) is found to be linear in field (Fig. 4f,h).

The topological protection of the surface states near CNP can be tested in at least three ways. One, by breaking time reversal symmetry (TRS) which should gap out Dirac states. Another, by the appearance of topological Berry phase⁴ of π (see Fig. 2i). And yet another, by detecting 2D weak antilocalization (WAL) of Dirac particles travelling through time-reversed paths²³ associated with this Berry phase. Figure 4a shows that applying TRS-breaking magnetic field indeed causes R_xx(T) at the lowest temperatures to upturn, showing localizing behaviour consistent with opening of the Dirac gap (see, for example, ref. 25). From this, we conclude that near CNP, even with the complex Bi₂Te₃ band structure, topological conduction channels dominate.

Stable 2D quantum transport at CNP

As we approach CNP, WAL quantum correction to classical conductivity emerges at low magnetic fields as a characteristic positive magnetoresistance cusp²³ (inset in Fig. 4b). In close proximity to CNP, the corresponding cusp in negative magnetoconductance scales with the transverse field H_‖=Hcosθ (Fig. 4e,g), confirming its 2D character. In this case, the number n_Q of quantum conduction channels contributing to WAL can be estimated from 2D localization theory²⁶

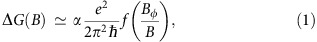where ΔG(B) is the low-field quantum correction to 2D magnetoconductance, coefficient α=n_Q/2 equals to 1/2 for a single 2D channel, 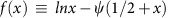, 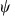is the digamma function, and field 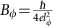is related to the dephasing length l_ϕ of interfering electron paths. In Bi₂Te₃ at CNP, the fit (in Fig. 4e) yields α≃1.26±0.1 corresponding to n_Q∼2, smaller than 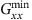. The obtained value of ∼2 is quite remarkable since ‘universality' of n_Q has been questioned²⁷ given a likely formation of subsurface 2D electron gas states of bulk origin. In Bi₂Se₃, where the Dirac point is expected to coincide with CNP, the fit similarly yields α≃1.12±0.1 (Fig. 4g), corresponding to two 2D quantum channels we associate with two independent topological surfaces.

Finally, we remark that using thermal protocol illustrated in Fig. 4b, we found that once CNP is reached, the system remains there for months on cycling, which was the duration of our experiments. This robustness suggests that at higher electron doses, vacancies are likely correlated; for example, di-vacancies can form¹⁶,²⁸ and it is known that point-defect complexes can be stabilized²⁹ in systems with multiple sublattices. With the choice of electron beam energy and terminal electron dose controlling the stability of pairs, and with a suitably designed thermal tuning to charge neutrality, the high-energy electron irradiation offers a path to large scale access to topological states.

Methods

Crystal growth and structural characterization

The standard Bridgman-Stockbarger technique employing a vertical pull through the temperature gradient was used to grow single crystals of Bi₂Te₃ and Ca(0.09%)-doped Bi₂Se₃. X-ray diffraction of crystals was performed in a Panalytical diffractometer using Cu Kα (λ=1.5405 Å) line from Philips high intensity ceramic sealed tube (3 kW) X-ray source with a Soller slit (0.04 rad) incident and diffracted beam optics. Transmission electron microscopy was performed at Evans Analytical Group.

Angularly resolved photoemission spectroscopy

ARPES measurements were performed on the FemtoARPES setup³⁰ using a Ti:sapphire laser operated at 0.25 MHz repetition rate. The specimens were probed with the fourth harmonic (at 6.26 eV), with an overall spectral resolution better than 30 meV. The data were taken along Γ-M and Γ-K directions. We found no substantial differences for measurements performed on several cleaved surfaces.

Electron irradiation

Electron irradiations were carried out in NEC Pelletron-type electrostatic accelerator in Laboratoire de Physique des Solides at École Polytechnique, Palaiseau, configured with a low-temperature target maintained at ∼20 K in a chamber filled with liquid hydrogen fed from a close-cycle refrigerator. All irradiations were performed with samples kept at 20 K, below the mobility threshold of the interstitials which tend to be more mobile than vacancies¹⁶—this ensured the stability of all charges introduced by the irradiation process. It also allowed us to evaluate thermal migration of interstitials during the annealing process. The size of the 2.5 MeV electron beam spot was reduced to 5 mm by a circular diaphragm aperture, with uniformity of the beam current ensured with a constant beam sweep in x and y-directions at two non-commensurate frequencies. Careful calibration of the beam current density, typically of 2 μA on a 0.2 cm² surface, was performed by periodic introduction of a Faraday cage between the diaphragm and the sample chamber and the measurement of current collected on the control metallic sample. Beam current densities, limited to 10 μC cm⁻² s⁻¹ by the cooling rate, allowed modifications of carrier concentration on the order of 10²⁰ cm⁻³.

Transport measurements

The system was set up for in situ transport measurements that could be monitored as a function of electron dose in real time. Crystals used in the irradiation experiments were typically 15 μm thick with spark-weld electrical contacts placed in van der Pauw contact configuration. Ex situ transport and Shubnikov–de Haas oscillations measurements were performed in Quantum Design Physical Property Measurement System equipped with 14 T magnet. In ex situ measurements, when samples were exfoliated to thicknesses of 200 nm and below, lithographically designed contacts with Ti/Au metallurgy were used (see Fig. 4a). Annealing experiments up to 200 °C (such as shown in Fig. 4b and Supplementary Note 2) were performed in a box furnace in flowing nitrogen.

Additional information

How to cite this article: Zhao, L. et al. Stable topological insulators achieved using high energy electron beams. Nat. Commun. 7:10957 doi: 10.1038/ncomms10957 (2016).

Supplementary Material

Supplementary Information

Supplementary Figures 1-11, Supplementary Table 1, Supplementary Notes 1-4 and Supplementary References