Abstract
An important goal in characterizing human color vision is to order color percepts in a way that captures their similarities and differences. This has resulted in the continuing evolution of “uniform color spaces,” in which the distances within the space represent the perceptual differences between the stimuli. While these metrics are now very successful in predicting how color percepts are scaled, they do so in largely empirical, ad hoc ways, with limited reference to actual mechanisms of color vision. In this article our aim is to instead begin with general and plausible assumptions about color coding, and then develop a model of color appearance that explicitly incorporates them. We show that many of the features of empirically-defined color order systems (such as those of Munsell, Pantone, NCS, and others) as well as many of the basic phenomena of color perception, emerge naturally from fairly simple principles of color information encoding in the visual system and how it can be optimized for the spectral characteristics of the environment.
I. INTRODUCTION
The field of color vision encompasses a diverse range of questions and has spawned a number of sub-disciplines. One involves colorimetry –“the branch of color science concerned… with specifying numerically the color of a physically defined visual stimulus” [1] in terms of color matches (basic colorimetry) and color appearance correlates (advanced colorimetry). The latter has involved developing a number of formal algorithms for specifying the basic structure of color appearance. Such algorithms have obvious practical value for gauging the perceptual consequences of colors in different conditions or applications, e.g. when images are rendered on different devices. However, they have largely been designed only by describing empirical measurements of color discrimination or similarity ratings, and not by asking what causes color appearances to be as they are. That is, while the values are useful from an engineering perspective, they are based on a nested series of multi-parameter functions, for which the parameters have been adjusted to make the overall calculation fit known data, but wherein a number of the mathematical sub-features lack a clear rationale or plausible neural mechanisms.
A second line of color research has focused on understanding the actual mechanisms of color coding. This has provided deep insights into how information about the spectral characteristics of light is represented and transformed along the visual pathway, and the neural substrate of these mechanisms. This approach has also helped to elucidate computational principles that likely guided the evolutionary development of color vision. However, these approaches have generally not aimed to generate formal quantitative predictions for color metrics.
In the present work, our aim is to bridge the conceptual gap between these two important goals in color science - one focused on understanding the mechanisms and design principles underlying the neural encoding of color information, and the other focused on developing systems for quantifying and predicting the structure and characteristics of color appearance. Specifically, our aim is to illustrate how a quantitative model of color appearance – with predictive power approaching typical uniform color metrics - can be derived from reasonable and general assumptions about color coding, rather than purely empirical data fitting. Our model is thus in contrast to the many color metrics for which predictive performance is often the main goal at the cost of clarity and transparency of possible underlying explanatory physiological, neural or cognitive mechanisms related to human color perception.
With these thoughts in mind, we begin by discussing the specific behavior we hope to explain - the perceptual organization of surface colors (specifically, colors as perceived within a uniform flat neutral background or context, as opposed to isolated or “aperture” colors). These are usually described by three perceptual attributes: hue (e.g. red vs. green), chroma (pure vs. diluted), and lightness (light vs. dark). The fact that this representation has three key attributes follows plausibly (though not necessarily) from the fact that, as the color normal human eye scans the visible environment, light is sensed by three different types of cone photoreceptors in the retina. It is also widely assumed that these subjective attributes of color arise from combining cone signals by subtraction (opponency) or addition (non-opponency). This two-stage model (of an initial representation based on the three cone types, followed by combining the cones signals within color-opponent mechanisms) explains, in general terms, both the basic color matching characteristics of color vision and also the basic phenomena of color appearance.
However, at a finer level, the characteristics of color appearance remain complex. A wide variety of techniques and studies have been used to describe the relationships involved. Often these approaches arrange surface colors in terms of their perceived similarities and differences. Thus two shades of blue fall closer together than a blue and yellow. Ideally such systems provide what subjects perceive to be an approximately “uniform color space,” in which the distances between any two points represent approximately equivalent perceptual differences. Here we will focus on the Munsell Color System [2] which, while not the most accurate, is possibly the most well-known perceptual color ordering systems, with other examples being the line element models of Helmholtz and Schrodinger [3] and numerous improvements over the years leading to what many feel is the most accurate prediction tool today, the CIECAMO2 system [4] of the International Commission on Illumination (CIE).
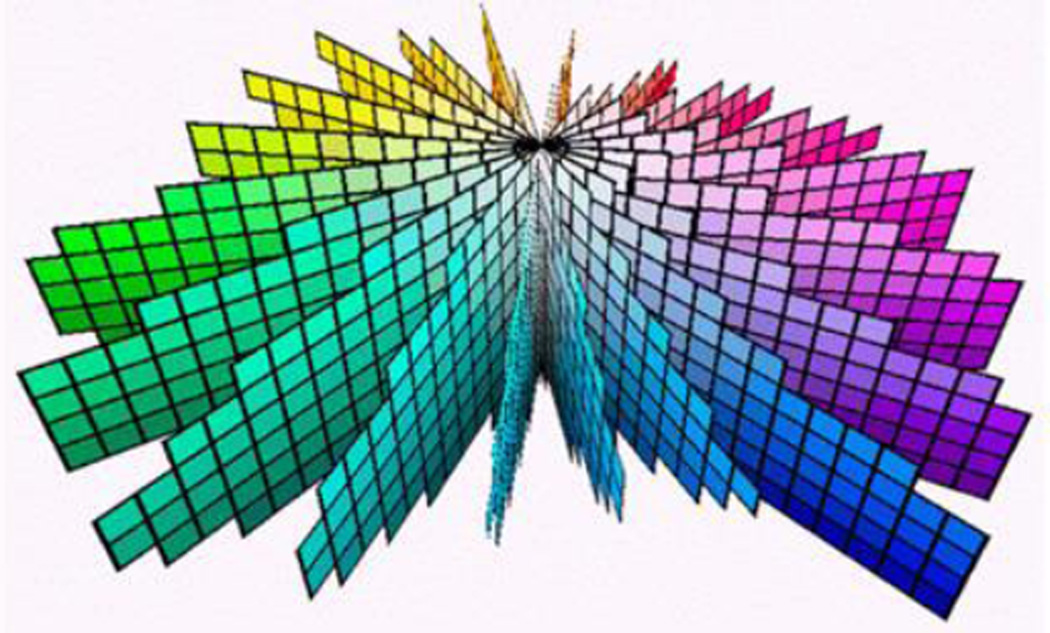
The Munsell Color System [5] was developed through careful studies of classification of colored surfaces carried out by Albert H. Munsell in the early part of the 20th Century, based on the reported observations of numerous human subjects. This system organizes color samples into a three dimensional configuration, as depicted [6] in Fig. 1.
Fig. 1.
The Munsell Color System.
The system is organized into levels of equal perceived lightness (the vertical, axial direction), quantified by a number called Value (V) notionally ranging from V=0 (black) to V=10 (white). It is also organized into planar groupings of equal hue, in which radial distance from the center represents increasing intensity of color, represented by a number called Chroma (C) ranging from zero (gray) to a maximum value that depends on the Hue and Value. The planes of equal Hue are organized in equal perceived spacing in the circumferential direction, and can be defined by a labeling scheme or simply the angle, to identify a specific Hue, H. As with many other color appearance systems, the Munsell chart was organized to have the distance between two samples correspond on average to subjects’ perception of the “size” of the appearance difference between them. Finally, note that the appearance of the samples depends critically on the background, and is normally relative to a neutral gray, which is the context we assume here.
People with normal color vision find such classification systems intuitively clear and meaningful and therefore may not realize they present a fascinating and important characteristic of human color vision – the fact that the arrangement appears sensible and appropriate for essentially everyone with normal color vision. But, what actually are hue, value, and chroma? More generally, what is the connection between the H, V, C coordinates of the Munsell system, and the photoreceptor responses that can be calculated from the spectral power distributions (SPDs) of the reflected light that reaches the eye from each of the various surfaces in a scene? (Recognizing that these reflected light SPDs are the products of the incident illumination SPD and the spectral reflectance functions of the various surfaces.) One might have expected the answer to this question to be simple, but it is not! Actually, understanding this connection has been a goal of modern color metrics for some time, one that has previously been achieved through empirical approaches [7, 8, 9] that are significantly more complex than the method described here, and are much less clearly connected to the underlying physiology of color vision.
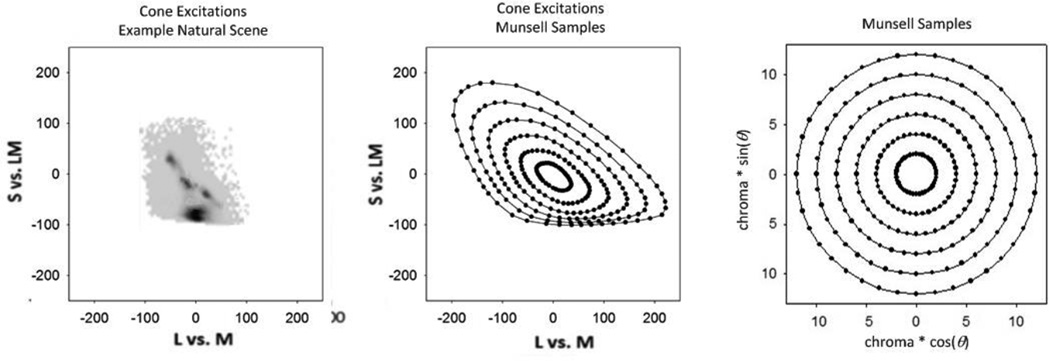
The challenge of this problem of connecting the H, V, C values to cone stimulations [10] is partially illustrated in Fig. 2. The figure’s rightmost panel shows a set of stimuli within the Munsell system, chosen to have equal chroma and lightness and spanning the circle of hues in equal intervals. As mentioned previously, this is a system in which the color differences portrayed are perceived by observers to be approximately perceptually uniform. However, the figure’s middle panel shows these stimuli plotted instead in terms of their corresponding cone photon absorption rates, using a variant of a standard diagram which plots the relative excitations of the cones to different spectra of the same luminance [11]. In terms of the cone absorption rates, the previously uniform set of stimuli is now strongly distorted – stretched along some axes and compressed along others. Moreover, the distortion pattern itself depends, in a complicated way, upon the SPD of the background. The challenge, then, is to identify the transformations that convert the cone photon absorption rates into perceptually meaningful (uniform) differences. As we have noted, in developing uniform color spaces, these connections have been predominantly empirical and rather complex. Thus while they successfully describe color appearance, they provide little insight into the underlying processes or evolutionary factors driving the visual representation of color, because there is little correspondence between the mathematical operations and the actual physiology, nor is there any explanation for how those calculations could be accurately emulated in the nervous system.
Fig. 2.
Cone photon absorption rates for objects in a set of natural scene and of uniform Munsell samples.
As a specific example, consider one of the most sophisticated instantiations of the family of CIE uniform spaces: CIECAM02 [12], which estimates the color differences with a basic set of 14 equation groups involving 39 constant numerical parameters. As with most other models, these include nonlinear calculations resulting from the need to “compress” responses or “adapt” them according to the reference background, but without considering the actual basis or rationale for these adjustments. Moreover, many of the calculations in CIECAM02 involve complex polynomial expressions without any explanation for how such relationships could be emulated physiologically. Further, the many constant numerical parameters were selected to produce a reasonable match to observational data, but without any explanation for how such “tuning” might actually occur within the vision system. Thus, while CIECAM02 and its predecessors are very useful engineering tools, they provide little insight into color appearance (in the same way that the CIE 1931 chromaticity diagram provides an industry standard for color specification yet completely obscures the underlying basis of color matching and trichromacy).
Here, we show that a more explanatory description of color appearance is afforded by starting with some simple assumptions about sensory coding. Again, this is an area that also has an extensive, though more recent, history. A general principle emerging from this approach is that it would have been evolutionarily advantageous for sensory systems to evolve so as to optimize the efficiency of representation of the characteristics of an organism’s environment. Much of this work has drawn from information theory and arguments for coding efficiency, to identify how the limited dynamic range of neural responses should be allocated to carry the most information about the stimulus [13,14,15,16]. This includes adjusting individual neuron response functions based upon the frequency distribution of past stimulation values in order to equalize the information content associated with each response level [17,18], and adjusting the responses across neurons so that they are similar but independent (which maximizes the amount of useful information carried by each neuron) [19,20]. Resource limitations may be an especially critical factor at early stages of the visual system, where the raw image must be compressed into a small number of channels, each restricted to a limited range of levels. As one example, the optic nerve consists of between 770,000 and 1,700,000 nerve fibers [21], transmitting somewhat less than 10,000,000 bits of information per second [22], but this must be used to carry the information arising from over 100,000,000 photoreceptors [23]. Clearly, then, this encoding must be optimized to preserve information about the image [24].
Coding efficiency also requires that the system be optimized for the specific characteristics of the stimulus environment, and be adaptable to changes in the environment [25]. The left panel of Fig. 2 shows the distribution of cone excitations from a sample of a natural outdoor setting [26]. Note that this environmental distribution is somewhat similar to the cone excitations of the Munsell samples, which appear perceptually uniform. This suggests that part of the mapping of the cones to color sensations is very much a mapping from the world, and indeed one could directly try to predict perceptually uniform color spaces from the non-uniform color statistics of natural images [27, 28].
However, our goal is to illustrate how this mapping could be realized by feasible steps in color coding. For this reason, we focus on plausible simple sequential computations for implementing the transformation. We attempt to explain how each step can feasibly adjust its performance parameters in response to the statistical distribution of recent signals from the preceding stage. Admittedly, many of the neural processes underlying color perception remain poorly understood, and many of the mathematical transformations we present do not have uniquely defined neural correlates or might be instantiated in very different ways. Thus our model is not intended to imply the actual physiological basis for color metrics. Instead, the primary focus of the paper is to demonstrate what steps we might expect from fairly simple and general principles, and how close those steps come to emulating the content of empirically defined color metrics.
II. KEY COMPONENTS OF THE MODEL
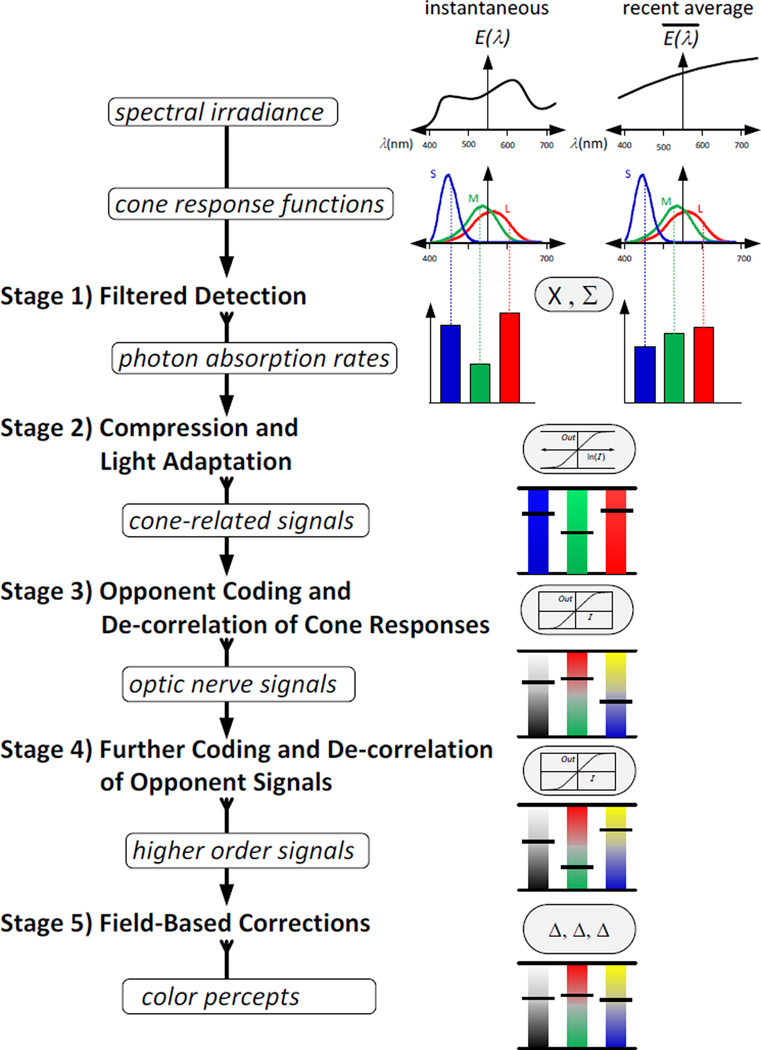
With this background, we will begin with a brief overview of a model consisting of five sequential functional stages. Each stage receives input information and produces a transformation that is input to the next stage. The input for stage one is light entering the eye. The output for stage five is the perception of surface color. Within each stage there is a simple, mathematically describable, transform function that contains one or more numerical parameters that “tune” its performance, and – where possible – we point to the potential mechanisms or principles underlying why this transformation may have evolved and how the parameters may be automatically adjusted over time. One type of “plausible tuning algorithm” would be to slowly adjust a parameter over time in order to achieve and maintain a uniform statistical distribution of recent output values.
Fig. 3 depicts these stages as a flow chart. (We emphasize that these stages are not exhaustive and, for example, do not include many known contextual effects or how color interacts with other attributes such as form or motion. However they are intended to characterize the properties of color appearance as embodied by most color metrics.) Importantly, the figure shows two corresponding tracks. The left track describes putative processing stages and potential neural sites. The right track describes the mathematical models for these stages presented in this paper. Each stage is a function, with operating parameters, and a method for optimizing those parameters. Before exploring those mathematical relationships in detail, we will first briefly summarize the transformations at each of the five stages:
- Stage 1. Filtered Detection
-
◦Modeled process:The input to Stage 1 is the time-history of the SPD of the light incident at a given small region of the retina. This is sampled by the trichromatic cone mosaic, with output corresponding to values representing the cone photon absorption rates in the three classes of cones. For modeling surface colors we consider two of these outputs. The first is the instantaneous rate corresponding to the stimulus, and the second is a recent time average rate, representing the presumed response to the background due to sampling different regions with saccades.
-
◦Mathematical representation:The corresponding input is the SPD of light reflecting to the eye from a test object and also the average SPD of the scene. The filtering and detection of the incident light is simulated by multiplying each SPD with the corneal spectral sensitivities (cone fundamentals) of each of the three cone types and integrating them to determine the test and background “cone photon absorption rates”.
-
◦
- Stage 2. Compression and Light Adaptation
-
◦Modeled process:The model transformed cone signals are assumed to follow a compressive nonlinearity such that responses have greater sensitivity around the mean cone photon absorption rate and smoothly asymptote at very low or high levels. The response is adapted for the recent mean by a gain control that adjusts to the recent history of stimulation.
-
◦Mathematical representation:The proposed mathematical form for the response is the application of a sigmoidal transform function to a logarithmic response function. This requires two parameters: (1) A gain parameter which must be adjusted as a compromise between too low a gain, which reduces the signal to noise ratio, and too high a gain which increases information loss through output saturation; (2) An offset parameter that reduces the difference between the degree of output clipping at the low end and at the high end, thus optimizing information transfer.
-
◦
- Stage 3, Opponent Coding and De-correlation of Cone Responses,.
-
◦Modeled process:Following conventional color models, the model transformed cone signals are combined within three post-receptoral mechanisms. These help to remove the redundancies in the information carried by the different cones by recoding into channels that respond to the sum or differences of the model transformed cone signals. The summing channel is “non-opponent” and forms a mechanism sensitive to achromatic variations. The other two are “opponent” and difference the model transformed cone signals to represent information about the chromatic properties if the stimulus. Within each, the signals are gain-controlled to match the range of inputs so that, over time, the statistical distribution of output values is similar across the three mechanisms.
-
◦Mathematical representation:In the model shown here there are three numerical coefficients that affect the calculation of each of the two color difference signals, and they are assumed to be tuned to the stimulus history. The proposed method is to slowly adjust those parameters in order to ensure that, over long times, (1) achromatic stimuli produce neutral color signals; (2) the average of the output values are also neutral, and (3) the r.m.s. output signal, relative to the neutral point, has a nominally specified value (e.g. 1), for optimal information transfer.
-
◦
- Stage 4. De-correlation of Opponent Signals.
-
◦Modeled process:The previous stage decodes the model transformed cone signals into 3 mechanisms with sensitivities corresponding to the “cardinal” luminance and chromatic dimensions that have been postulated for early post-receptoral color coding. Stage 4 involves a subsequent rotation and scaling of the model chromatic signals, and is included because the responses of the cardinal mechanisms are often correlated for natural color distributions. Specifically, this stage is included to adjust to the “blue-yellow” bias in natural scenes, as illustrated in Figure 1. We note that stages 3 and 4 could be implemented with a single transformation. However, there is evidence to suggest that these adjustments occur at different stages in the visual system [29]. Moreover, if they were combined into a single transformation, there would be no simple mechanism for adaptively tuning those parameters over time in order to achieve and maintain accurate color perception.
-
◦Mathematical representation:The equations at stage 4 apply a rotation and rescaling of the mechanism sensitivities. As in Stage 3 the control parameters are determined in a simple way to optimize the statistical distribution of the output values.
-
◦
- Stage 5. Field-based corrections.
-
◦Modeled process:To successfully predict appearance, color appearance models must include additional “chromatic adaptation” factors that normalize the model values to allow gray and white surfaces to be correctly perceived as uncolored under a range of differently-colored illumination conditions. A wide variety of mechanisms contribute to this “color-constancy” correction.
-
◦Mathematical representation:The mathematical treatment of this stage is simply the global application of an additive correction to the two color signals, to ensure that a neutral gray surface appears approximately colorless. Additionally, in order to express the resultant color appearance information in terms of the scaling used within the Munsell system, three arbitrary scaling parameters are applied in order to express the model output in terms of the Munsell ranges of Value and Chroma, and with the correct zero point for Hue.
-
◦
Fig. 3.
Stages of information processing in color vision.
In the following, we elaborate and provide quantitative details for each of these stages.
A. Stage 1: Filtered Detection
Stage 1 involves the absorption of visible light photons by the cone opsin molecules in the light-sensitive cone cells in the retina. The intensity of light incident on the eye is generally a function of the viewing direction, r̂, and the wavelength λ. It is called the spectral radiance distribution, (and more commonly the spectral power distribution or SPD), and is expressed as Leλ(λ, r̂), in units of W/sr·m3. (Although these are the correct units, it is more common outside of the physics literature to use the units W/nm·sr·m2.)
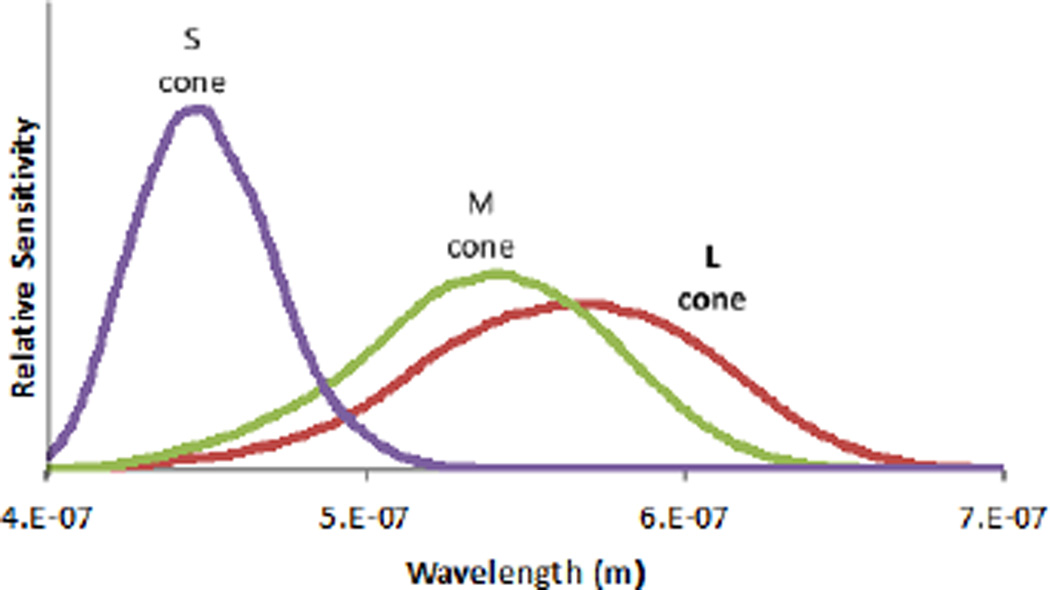
There are three different kinds of cone cells in the retina of the normal human trichromat, which differ in the photopigments they contain and thus in their relative spectral sensitivity as a function of wavelength. Because of absorptions in the lens, ocular media, macular pigment and the retina itself, the pigment absorption spectra are typically less relevant than the corneal spectral sensitivities derived from psychophysical color matching functions. These functions, often referred to as cone fundamentals, are typically labeled L(λ), M(λ) and S(λ), (based on the words long, medium, short describing the relative wavelength of peak absorption). The model described in this paper uses the CIE 10° 2006 cone fundamentals30. The equal-area-normalized cone fundamentals are depicted in Fig. 4. For the purposes of this paper, the normalization is arbitrary because it does not affect the final calculation.
Fig. 4.
The three retinal cone cell spectral sensitivity functions.
Using these three relative response functions, we then define three -cone photon absorption rates as follows:
| (1a) |
| (1b) |
| (1c) |
(Note that in each of these equations, the cone fundamental spectral sensitivity functions appear in both the numerator and the denominator, so the normalization factors for them cancel.) The units of L(r̂), M(r̂), S(r̂) are cd/m2. According to this measure, an SPD with uniform spectral radiance distribution and a photometric luminance Lν of 1 cd/m2 will have that same numerical value, 1, for each of L(r̂), M(r̂), S(r̂). For a general, non-uniform spectral radiance distribution Leλ(λ), the values L(r̂), M(r̂), S(r̂) will usually differ from one another, providing the basic information available for color. and also fundamentally limiting that information. Specifically, the output of each cone is a function of its rate of photon absorption - no information is provided about the wavelength distribution of the absorbed photons, a fundamental constraint known as the “principle of univariance [31]. Thus color information can only be obtained by comparing the outputs of the three cone types.
B. Stage 2. Compression and Light Adaptation
While photon absorption is an approximately linear process (at least up to an intensity that causes photopigment bleaching to become significant), it is important to realize that as a whole the visual system is highly nonlinear. For example, it is well known that in vision, as well as most areas of perception, the ratio of intensities of two stimuli is a better predictor of the perceived difference between them than is their intensity difference [32]. Nonlinearities of this kind are important given the large intensity range over which color vision must operate. People can see color over roughly a million-fold range of luminance values ranging from that of moonlit snow to sunlight shimmering on a lake. Over this entire range, it is desirable to be sensitive to small relative changes of intensity. This has the advantage that a given object can appear much the same when viewed under very different lighting conditions (because when the light intensity changes, it is the ratios of reflected light signals that remain constant).
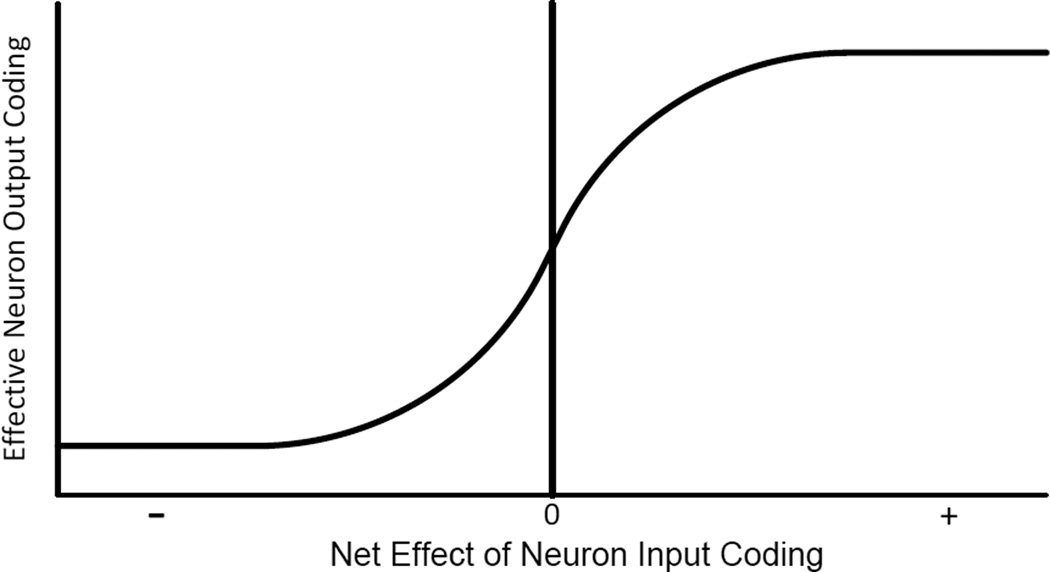
A further important role of nonlinearity in neural processing relates to the fact that neurons have a quite limited ratio of dynamic range to noise. Typically a graph of neuron’s output as a function of stimulus level has a “sigmoidal” shape, as sketched roughly in Fig. 5. There may be a central region that is fairly linear, but the response then approaches asymptotes at both input value extremes.
Fig. 5.
Schematic model of how a neuron output signal depends on the net effect of its input signals
A recognized rationale for this sigmoidal shape is that it provides maximum useful information when the frequency distribution of input values has the form of the ubiquitous normal (or Gaussian) distribution [33]. In this case, which we will use here for simplicity, the ideal mathematical form shown in Fig. 5 is known as the error function, erf(x), which is twice the cumulative probability of a Gaussian distribution, where × is measured from its center in units of standard deviation. Its lower limit, as x approaches −∞, is −1; its upper limit, as x approaches ∞, is 1, and for small values of x, the function is approximately . Many consider the error function to be a very simple, meaningful and useful sigmoidal function. (However, as with many other stages of the model we note that the assumption of a Gaussian distribution, while common, is an idealization that may not be perfectly realized in real systems.)
A further issue is that the world itself varies, and thus neural responses must adapt to adjust to these changes. For example, the narrow dynamic range of the system cannot represent the enormous range of light levels we encounter during the course of a day, and like a camera, must instead be continuously adjusted or centered on the much more limited range of contrasts that occur at a given moment [34]. Similarly for color vision, there is an ongoing need to adjust the operating parameters at each stage, guided by the frequency distribution of fairly recent previous signals, in order to optimize the transfer of information. This tuning adjusts not only to the mean stimulus but also to its variance or contrast, and could potentially also adjust to other moments of the stimulus distributions and thus adjust the shape of the transfer functions. Moreover, these adjustments can occur over many timescales, with some integrating over long intervals (of days, months or years) while in other cases, the time constants may range from seconds to milliseconds [35, 36, 37, 38, 39].
For the purpose of including these adaptation effects, we must now consider the initial encoding of color in more detail. To do so, we need to define certain key components that determine the reference frame or context for judging a color. Recall that Eqs. (1a, 1b, 1c) defined the color information for a given SPD as L(r̂), M(r̂), S(r̂), with the dependence on r̂ indicating that in a typical environment these vary with the viewing direction. We must now be more specific about viewing directions. For the rest of this paper we will use three different triads of color information, as follows:
Lt, Mt, St will denote the L(r̂), M(r̂), S(r̂) values for a test surface in the direction r̂t
Lf, Mf, Sf will denote the L(r̂), M(r̂), S(r̂) values averaged over the current visual field
Lo, Mo, So will denote the L(r̂), M(r̂), S(r̂) values of a very long-term average over many scenes/fields.
Overall, the situation can be summarized approximately as follows: The apparent color of a “test” surface depends on the Lt, Mt, St values for the light reflecting from it, and also depends on Lf, Mf, Sf, and likely also on Lo, Mo, So. Thus, we seek to understand the process by which these 9 values produce the observed color experience denoted by the three values, H, V, C, of the Munsell system.
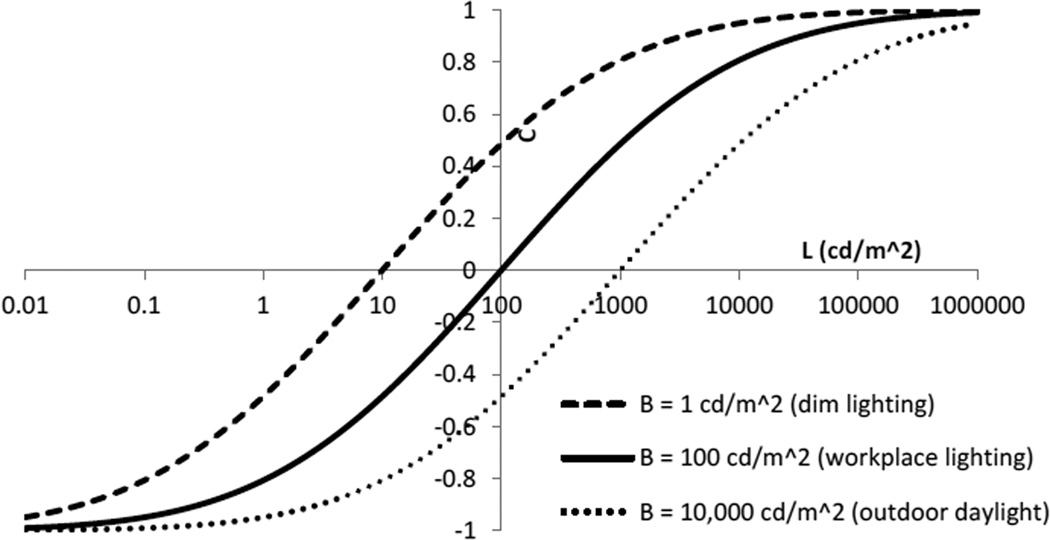
Next, we model the nonlinearity in the cone response. The model response is depicted in Fig. 6. In this plot, the vertical axis has arbitrary scaling. In many measurements of cone responses to light, this form of response is observed, although it is usually described by a different function, known as the Naka-Rushton [40] equation, of the form 2In/(1 + In) −1. The equation we use here is essentially equivalent numerically, but the form we use was selected because it is conceptually simpler, and because it represents the sequential application of two simple functional relationships that have a clear computational utility as described in this paper. In contrast, there is no known physiological mechanism for emulating the fractional powers within the Naka-Rushton equation. The response function shown in Fig. 6 is approximately log-linear in a central portion of its range, which corresponds to about two orders of magnitude of luminance. The range is centered by adaptation according to the average recently experienced (i.e. “ambient or background”) light level. For example, the dashed curve in Fig. 6 shows the response when the ambient luminance level is dim (1 cd/m2) and conversely the dotted curve shows the opposite situation in response to much brighter outdoor daylight (10,000 cd/m2).
Fig. 6.
Model values (arbitrary scaling) representing a cone output vs. logarithm of intensity, based on a truncated logarithm function of the form Output=erf(0.26ln(I/(100cd/m2 B)^.5)), where I is the intensity and B is the logarithmically averaged recent intensity, both in cd/m2
To quantitatively model the response, we’ll need to introduce two constants:
Cc a cone contrast factor, which determines the steepness of the slope of the cone response function;
Cf a cone feedback factor, which is the coefficient for the automatic gain control based on a cone’s time-averaged signal;
For the three cones, we will denote the resultant model transformed cone signals as:
| (2a) |
| (2b) |
| (2c) |
In this model, the constants Cc, Cf, and Lo, Mo, So could potentially be determined by evolution and could be fixed for any individual. On the other hand, it is possible that Lo, Mo, So could be determined by the very long term exposure of individuals to light. As depicted by the values shown in Figure 11, we have set the Lo, Mo, So to be the values that would be obtained for a gray 20% reflective surface illuminated by mid-morning or mid-afternoon sunny daylight, with a luminance of 5000 cd/m2 and a color temperature of 5500K. The results depend only weakly on this choice and were selected as a reasonable proxy for an average viewing condition.
Fig. 11.
Concise compilation of the equations of the 5 stages of the model, with the constants used to produce the results in Figure 10. The only physiologically relevant parameters that were adjusted for that purpose are those in equation (2). The others arise from the statistical approach described here. For the purposes of the data shown in Figure 10, the Munsell samples were assumed to be illuminated with CIE Illuminant C with and uniform illuminance that causes a white surface to have a luminance of 400 cd/m2.
It should be noted that these Eqs. (2a, 2b, 2c), contain division operations, yet there is no known simple way for neurons to directly carry out a division operation, and it would seem even more improbable within a single cone cell. However, it does appear that cone cells have the ability to emulate the calculation of Eqs. (2a, 2b, 2c). Potentially this could involve a combination of an intrinsic logarithmic response with various time-averaged feedback mechanisms [41]. (Some might find the idea of physically emulating the mathematical logarithm function daunting. However chemical systems can do this. For example, in the common pH meter, a simple cell produces an electrical potential difference directly related to pH, which is proportional to the logarithm of the concentration of H+ ions. In general, exponential relationships are commonplace in chemical dynamics, and so therefore are their inverse, logarithmic relationships.)
If the frequency distribution of the logarithm of intensity is the common Gaussian distribution, then applying the error function to the logarithm of intensity, as depicted in Fig. 6, will convert to a uniform frequency distribution of output values. For this reason, we have used the error function applied to the logarithm as the model for the sigmoidal cone response function. For subsequent processing signals, for which a logarithmic transform is not relevant, we could simply use the error function to represent a sigmoidal input/output response. In reality, at least with surface samples and the light intensities studied in this paper, there is little or no computational benefit from using the sigmoidal form in the remaining stages.
C. Stage 3. Opponent Coding and De-correlation of Cone Responses
To summarize, L’, M’, S’ are the model transformed cone signals in response to the current color sample and its background. This recoding is a tremendous improvement over the raw L, M, S excitations for the light itself, thanks to the automatic gain control and logarithmic compression. Nevertheless these signals remain poorly suited for efficiently representing color.
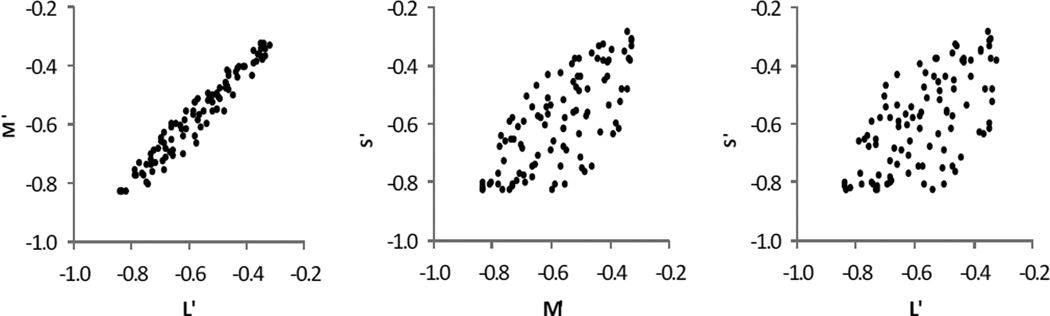
The difficulty is shown in Fig. 7, where pairs of the values for L’, M’, S’ are plotted for 99 colored surfaces that were selected from a large data base of real samples, by means of a Monte Carlo procedure guided by criteria assuring a set of samples that are very uniformly distributed from several perspectives [42]. As can be seen, there is considerable correlation between these three signals, especially between the L’ and M’ signals [43]. This arises from the fact that there is considerable overlap of the spectral sensitivities of the cones. It is well known that it is computationally inefficient to transport highly correlated signals [44] – and thus it would be evolutionarily advantageous to develop a simple arrangement for combining cone responses in a way that reduces this problem, providing the conversion itself is simple. This is thought to be a major rationale for converting the model transformed cone signals into a color- opponent representation [45].
Fig. 7.
These graphs plots of pairs of L’, M’, S’ for 100 randomly selected points in color space, showing they are highly correlated.
Thus, in Stage 3, the L’, M’, S’ independent model transformed cone signals are combined to produce three different output signals [46]. In the actual retina this is initiated within the various neural connections from the receptors to horizontal and bipolar cells in the retina, where emulation of the linear combination processing is quite feasible because neurons can have both excitatory and inhibitory inputs. A wide variety of distinct cell types with different spectral sensitivities have been identified in the primate retina, and how these might contribute to various aspects of color perception remains uncertain [47, 48], but the general transformation of the independent cone signals into non-opponent or opponent mechanisms is well established.
For our model, the first step of Stage 3 is to recode the model transformed cone signals into channels that separately carry the achromatic and chromatic content of the stimulus as follows:
| (3a) |
| (3b) |
| (3c) |
Note that partial decorrelation occurs because the channels now respond to the sums or differences of the model transformed cone signals (effectively realigning the axes of the mechanisms in Fig. 7 so that they lie along the positive or negative diagonals). The first value, λ* is a signal-related to the lightness of the stimulus. The value α corresponds to a reddish vs. blue-green opponent color axis (red is positive, blue-green negative) and is based on comparing the L’ and M’ model transformed cone signals. The value β relates to a yellow-green vs. purple opponent color axis and is based on comparing L’ and M’ model transformed cone signals to S’ model transformed cone signals. (Here these terms are simply a notation for labeling the content described mathematically in the relevant equations. They do not represent precisely defined color dimensions at this stage. Furthermore, the sign for α and for β is arbitrary and here we have simply used the most common convention. The visual system in fact includes cell types encoding both polarities e.g. in “on” and “off” cells for luminance. The polarity of the b channel is such that “yellow-green” is positive in order to be consistent with the polarity of many color spaces, However, we should note that this is opposite to the polarity depicted in the diagram shown in Fig. 1, and is also at odds with the preponderance of S-cone “on” cells found in the retina [49].)
The specific combinations shown maybe considered, by some, to be simple and appropriate for another reason: Most mammals have only two cone types - an S and a single longer wave cone type. Among mammals three-cone vision is largely exclusive to old world primates, and arose from an evolutionarily recent (40 Mya) duplication of the long-wave pigment gene. For this reason the two opponent dimensions have been described as the ancient (S vs. LM) and modern (L vs. M) subsystems of human color vision [50].
The second step of Stage 3 again involves the overall shape and scaling of each mechanism’s response. The opponent calculation for both α and β requires considerably more gain than the λ* channel since, as noted, the difference signals they measure are much smaller because of the overlapping L(λ), M(λ), (and to a lesser extent) S(λ) sensitivity functions. Further, we again assume that it may be desirable for the signal transformation at this point to have its output functional form adjusted parametrically in order to yield a statistically uniform distribution of output values. We have not found a sigmoidal transfer function to be essential at this point, but we have found some advantage for fitting the Munsell system in allowing a different gain for positive outputs than for negative outputs, as depicted in equations 3d and 3e., although the potential mechanisms for achieving this affect and adjusting its performance are uncertain.
| (3d) |
| (3e) |
In this amplification stage, the expectation is that the four constants represent parameters that would adapt over time in response to stimuli [51], so that on average the mean value for both α ’ and β ’ would be 0 and their standard deviation would be an arbitrary constant of 1. In our model, we carry out that calculation by evaluating a’ and b’ for the previously mentioned set of 99 uniformly distributed reflectance spectra and adjusting the constants in Eqs. 3d and 3e as just described.
Fig. 8 shows the same stimulus set as that for Fig. 7, but now replotted in terms of the partially de-correlated and scaled opponent mechanisms β’ vs. α’, β’ vs. λ*, and α’ vs. λ*.
Fig. 8.
Improved distribution of model values for transmission from the model retina to the model brain.
As noted above, for ordinary surfaces at typical light levels, it does not appear necessary to incorporate a sigmoidal character in the output of Eqs. 3d & 3e. However for highly saturated brightly illuminated stimuli, it is possible that some color distortion might arise from saturation. For intense narrow band LEDs and lasers, the distortion of hues could become apparent. Hue distortions of this type are observed in what is called the Bezold-Brücke effect [52], and it is possible that a non-linearity could be feasibly incorporated to help predict this effect.
D. Stage 4. De-correlation of Opponent Signals
As previously mentioned, the initial opponent stage significantly reduces correlation between the model transformed cone signals, but the opponent signals themselves may still have remaining correlations depending on the choice of axes. In fact, the left hand plot in Fig. 8 reveals a positive correlation between the α’ and β’ responses, because the signals vary more along the positive diagonal (a yellowish-bluish axis that is also prevalent in many natural scenes but reflects co-varying signals in the L vs. M and S vs. LM cardinal mechanisms [53]). This residual correlation could be removed by an additional subtractive stage, which applies a differential gain in the ±45° directions, as depicted in Eqs. 4a & 4b, and as anticipated in previous observational studies [54, 55]:
| (4a) |
| (4b) |
Unlike Stage 3, we found little value in a different gain for positive input values vs. negative ones, and so there are just two constants which are to be determined, as in Stage 3, by adjustment to achieve a standard deviation of 1 for the distribution of α ” and β ” values found for the previously mentioned set of 99 uniformly distributed reflectance samples. It should also be noted that this is another case wherein the underlying neural mechanisms may take a very different form. There is considerable evidence for - and also some against - the idea that at cortical levels the cardinal mechanisms are transformed into multiple “high-order” mechanisms tuned to different directions in color space [56, 57, 58]. The advantage of these multiple mechanisms is not immediately obvious from the perspective of efficient coding (since they are redundant with the information already carried by the three cardinal axes). However, this “multiple channels” code could allow the visual system to use a population code for hue, in the same way that it appears to represent other dimensions such as spatial orientation. In this case the implementation would not involve decorrelation but rather adjustments of the relative gains within each mechanism. In either case, the critical point is that the mechanisms are adjusted so that the distribution of responses is made approximately spherical [59].
(As an aside, it is important to ask whether the additional parameters in Stage 4 are actually adding value by significantly reducing the r.m.s. difference between the model-predicted H, V, C values and the actual Munsell values. This is an important consideration because generally, when striving to reduce r.m.s error between experimental data and a model fit, merely adding extra parameters, even if they have no meaning, will often slightly improve the fit if the parameters are carefully selected by means of an optimization algorithm. In this case, there are two reasons to believe these added parameters do have meaning. First, the added parameters were not adjusted by an optimization process to reduce the fitting error, so that fact that the fit was significantly improved strongly suggests the added parameters are an improvement to the model. Second, there are standard statistical tests to determine the fit improvement that would be expected purely from adding free, but meaningless parameters to a model. To check this, we used the well-known Akaike [60] approach to statistical model selection, which provides what is called the Akaike Information Criterion (AIC), which depends on the number of data points and the fit improvement obtained by adding new parameters. We found these additional parameters significantly increase the AIC score, indicating they likely provide improved understanding. That is, the small increase in the overall number of parameters (effectively from 5 to 8), reduces the residual square error of the fit to less than 50% of its original value based on the 5 parameters. This improvement is far greater than one would expect from added parameters that did not significantly refine the model.)
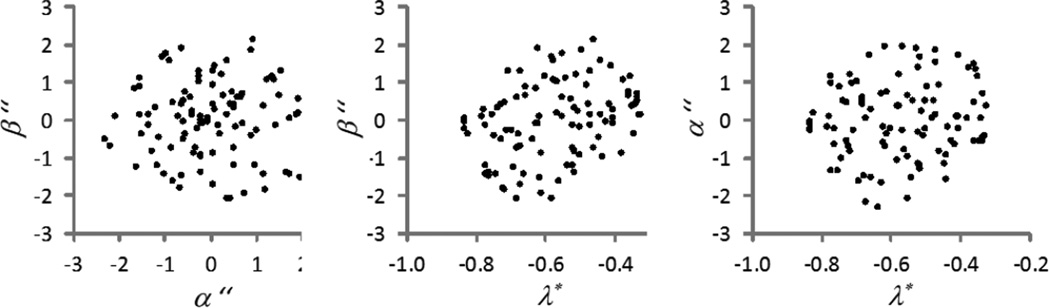
As evidence of the beneficial overall effect of this higher-order decorrelation, the same stimulus set as in Fig. 8 is again replotted as pairs of values β” vs. α”, β” vs. λ*, and α” vs. λ* in Fig. 9, which shows that the distribution is fairly uniform.
Fig. 9.
Improved output distribution after secondary encoding of the color signals received in the brain from the optic nerve.
E. Stage 5. Field based corrections
There are necessarily many additional subtle and elaborate processes that adjust color percepts according to sophisticated inferences about the stimulus, but they are likely not required for the primary goal of this paper - to compare the output of the model with the organization of color experience implied by the Munsell system.
To make this comparison, we first need to scale the output values to match the arbitrary scaling range of the Munsell color system. This consists of an arbitrary rotation of angle θ, and arbitrary linear scaling to give values the correct range for the Munsell system equivalents of λ*, α” and β”, here termed , αint, βint (with the subscript standing for intermediate.) The scaling equations are as follows:
| (5a) |
| (5b) |
| (5b) |
Note that in Eq. (5a) the value one simply corresponds to the fact that the lowest possible value for L*, based on the error function, is −1, which corresponds to ideal black, for which the Munsell value is zero. The last step is the problem of color constancy - separating the color of the surface from the color of the lighting. A certain amount of chromatic adaptation has already occurred as a result of the time-averaged adaptation that was introduced in Stage 2. (Indeed if the coefficient Cf were to be set to −1, all color shift arising from the illuminant color would, over time, be suppressed as this adaptation took place.) However, it is observed that this does not happen – color adaptation is not total, so the observer is able to know, weakly, the color and intensity of the ambient illumination. Another observation is that people are able to discount an illuminant immediately, in the sense that a piece of paper looks white, almost instantly, after the illuminant color has shifted [61], (whereas adaptation is typically defined as a process that takes time). This instantaneous constancy requires spatial comparisons (e.g. the paper may not look white if it is seen in isolation), and can be quite sophisticated, taking into account the relative changes across surfaces and spatial variations in the intensity and color of the illuminant [62, 63, 64].
For the purpose of comparing to the Munsell color set, it is sufficient to use a very simple white-balance procedure, in which the color shift (caused by changing the illuminant), for a neutral gray 20% reflective surface is evaluated. These evaluated shifts for the a and b channels are respectively labeled Δac, Δbc. Using these shifts, the Cartesian output values for comparison to the Munsell color set are as follows:
| (5d) |
| (5e) |
| (5f) |
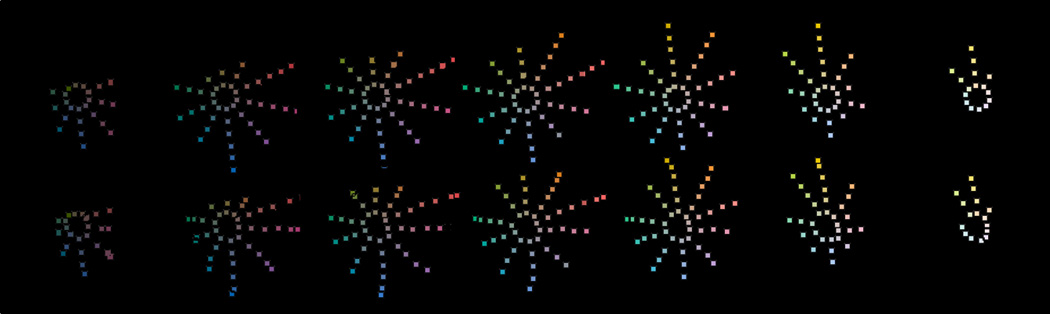
Fig. 10 shows that these five mathematical stages do a rather good job of modeling the perceptual experiences portrayed in the Munsell Color System. The top row depicts the arrangement of Munsell colors, for each of the 10 principal Munsell hues, with seven plots, one for each of the Munsell values ranging from 3 to 9. These are by definition placed in the regular arrays shown. The bottom row depicts the output of the model presented here. Ideally the patterns in the bottom row would perfectly match those in the top and the fit is actually fairly good: The RMS error between the Munsell values and the model values is about ½ unit in each direction, which is likely similar to the experimental error that is intrinsic to the Munsell system.
Fig. 10.
The top row consists of 7 separate plots of sets of Munsell samples for successively increasing Value from 3, at the left, to 9, at the right. For each plot, the polar angle represents the Munsell Hue, depicting 10 Principle Munsell Hues, and the radial distance represents the Chroma, in increments of 2 Munsell units. By definition, this is a regular geometrical arrangement. The bottom row shows the corresponding plots for the output values generated by Eqs. (5d, 5e, 5f). In converting from Cartesian to Polar coordinates, the Hue angle θ is determined by tan(θ)=(βout/(αout) and the Chroma is equal to . If the fit were perfect the patterns of the bottom row plots would perfectly match those of the top plots. The colors of the points shown are approximately the Munsell color corresponding to each plotted point.
Figure 11 concisely summarizes the equations from the five stages described above, including the numerical values used for the parameters in the model.
Another characteristic of this model is that it also demonstrates several well-known observations that have long been attributed to non-linear aspects of the color vision system. They include the Hunt Effect whereby surfaces appear less colorful at low light levels, the Abney effect, in which dilution of monochromatic light by white light produces hue shifts, and several others, which will be interesting areas for further study with this model.
III. Conclusions
The purpose of this paper has been to illustrate how the seemingly complex and unexplained characteristics of a popular approximately uniform color appearance system can be approached from fairly straightforward and plausible ideas about color coding in the visual system. We have done this by means of a simple computational approach that fulfills the standard scientific modeling objectives of simplicity, accuracy, integrability, and correspondence, as well as plausibility from the perspectives of evolution, organismal development, and sensory adaptation. The quantitative expressions for each of the five stages are intentionally simple and undoubtedly imperfect, but nevertheless they describe the observable phenomena of color appearance metrics with reasonable accuracy. It is hoped the model’s simplicity will be valuable pedagogically and perhaps stimulate new avenues of color perception research. As well, some may find it more satisfying to use the simple equations of this model for calculating anticipated color perception experiences. The results will not differ significantly from those of already-available (but much more complex and less intuitive) calculation tools, but we hope the new-found simplicity will result in deeper understanding, and, perhaps, new insights.
Acknowledgments
We thank Marty Banks, Jim Larimer and Ed Pugh for thoughtful conversations that helped lead to this work.
Funding. Postdoctoral Fellowship of the Research Foundation Flanders (FWO) (12B4916N) (KS); National Eye Institute EY-10834 (MW); Natural Sciences and Engineering Research Council Canada NSERC EQPEQ 423559-12 (LW).
References
- 1.Wyszecki G. Current developments in colorimetry. Proceedings of AIC Color. 1973;73:21–51. [Google Scholar]
- 2.Kuehni RG, Schwarz A. Color Ordered: A Survey of Color Systems from Antiquity to the Present. USA: Oxford University Press; 2007. [Google Scholar]
- 3.Schrödinger E. Grundlinien einer Theorie der Farbenmetrik im Tagessehen (Outline of a theory of colour measurement for daylight vision) Annalen der Physik. 1920;4(63):397–456. 481–520. [Google Scholar]
- 4.Fairchild MD. Color Appearance Models, 3rd Ed. Wiley-IS&T, Chichester, UK (2013)colour appearance model. Col. Res. Appl. 2006;31(4):320–330. [Google Scholar]
- 5. [accessed 2015 September 27]; Web site: http://munsell.com/ [Google Scholar]
- 6. [accessed May 31, 2015]; http://www.codeproject.com/Articles/7751/Use-Direct-D-To-Fly-Through-the-Munsell-Color-So. [Google Scholar]
- 7. Ibid 4. [Google Scholar]
- 8.D'Andrade RG, Romney AK. A quantitative model for transforming reflectance spectra into the Munsell color space using cone sensitivity functions and opponent process weights. Proceedings of the National Academy of Sciences. 2003;100(10):6281–6286. doi: 10.1073/pnas.1031827100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Centore P. An Open-Source Inversion Algorithm for the Munsell Renotation. Color Research and Application. 2012;37(6):455–464. [Google Scholar]
- 10.McDermott KC, Webster MA. Uniform color spaces and natural image statistics. JOSA A. 2012;29(2):A182–A187. doi: 10.1364/JOSAA.29.00A182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.MacLeod DI, Boynton RM. Chromaticity diagram showing cone excitation by stimuli of equal luminance. JOSA. 1979;69(8):1183–1186. doi: 10.1364/josa.69.001183. [DOI] [PubMed] [Google Scholar]
- 12.Luo MR, Cui G, Li C. Uniform colour spaces based on CIECAM02 colour appearance model. Col. Res. Appl. 2006;31(4):320–330. [Google Scholar]
- 13.Barlow HB. Possible principles underlying the transformations of sensory messages. In: Rosenblith WA, editor. Sensory Communication. The MIT Press; 1961. pp. 217–234. [Google Scholar]
- 14.van der Twer T, MacLeod DIA. Optimal nonlinear codes for the perception of natural colours. Network: Computation in Neural Systems. 2001;12(3):395–407. [PubMed] [Google Scholar]
- 15.Shannon CE, Weaver W. The mathematical theory of communication. Urbana University of Illinois Press; 1949. [Google Scholar]
- 16.Zhaoping Li. Understanding vision: theory, models, and data. Oxford University Press; 2014. [Google Scholar]
- 17.Laughlin S. A simple coding procedure enhances a neuron's information capacity. Zeitschrift für Naturforschung C. 1981;36(9):910–912. [PubMed] [Google Scholar]
- 18.MacLeod DIA, van der Twer T. Optimal nonlinear codes for the perception of natural colours. Network: Computation in Neural Systems. 2001;12(3):395–407. [PubMed] [Google Scholar]
- 19.Buchsbaum G, Gottschalk A. Trichromacy, opponent colours coding and optimum colour information transmission in the retina. Proceedings of the Royal Society of London B: Biological Sciences. 1983;220(1218):89–113. doi: 10.1098/rspb.1983.0090. [DOI] [PubMed] [Google Scholar]
- 20.Atick JJ. Could information theory provide an ecological theory of sensory processing? Network: Computation in neural systems. 1992;3(2):213–251. doi: 10.3109/0954898X.2011.638888. [DOI] [PubMed] [Google Scholar]
- 21.Jonas JB, Schmidt AM, Müller-Bergh JA, Schlötzer-Schrehardt UM, Naumann GO. Human optic nerve fiber count and optic disc size. Investigative Ophthalmology & Visual Science. 1992;33(6) [PubMed] [Google Scholar]
- 22.Kristin K, McLean J, Segev R, Freed MA, Berry MJ, II, Balasubramanian V, Sterling P. How Much the Eye Tells the Brain. Current Biology. 2006;16(14):1428–1434. doi: 10.1016/j.cub.2006.05.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Curcio CA, Sloan KR, Kalina RE, Hendrickson AE. Human photoreceptor topography. The Journal of Comparative Neurology. 1990;292:497–523. doi: 10.1002/cne.902920402. [DOI] [PubMed] [Google Scholar]
- 24.Srinivasan MV, Laughlin SB, Dubs A, et al. Predictive coding: a fresh view of inhibition in the retina. Proceedings of the Royal Society of London B: Biological Sciences. 1982;216(1205):427–459. doi: 10.1098/rspb.1982.0085. [DOI] [PubMed] [Google Scholar]
- 25.Simoncelli P, Olshausen BA. Natural image statistics and neural representation. Annual review of neuroscience. 2001;24(1):1193–1216. doi: 10.1146/annurev.neuro.24.1.1193. [DOI] [PubMed] [Google Scholar]
- 26. Ibid 10. [Google Scholar]
- 27.Long F, Yang Z, Purves D. Spectral statistics in natural scenes predict hue, saturation, and brightness. Proceedings of the National Academy of Sciences. 2006;103(15):6013–6018. doi: 10.1073/pnas.0600890103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Ibid 10. [Google Scholar]
- 29.Krauskopf J, Williams DR, Mandler MB, Brown AM. Higher order color mechanisms. Vision research. 1986;26(1):23–32. doi: 10.1016/0042-6989(86)90068-4. [DOI] [PubMed] [Google Scholar]
- 30.CIE. Fundamental Chromaticity Diagram with Physiological Axes - Part I. Vienna: CIE; 2006. [Google Scholar]
- 31.Naka KL, Rushton WAH. S-potentials from colour units in the retina of fish (Cyprinidae) The Journal of Physiology. 1966;185(3):536–555. doi: 10.1113/jphysiol.1966.sp008001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ratliff F. On Mach's contributions to the analysis of sensations. Springer; 1970. [Google Scholar]
- 33.Laughlin SB. A simple coding procedure enhances a neuron’s information capacity. Z. Naturforsch. 1981;36:910–912. [PubMed] [Google Scholar]
- 34.Rieke F, Rudd ME. The challenges natural images pose for visual adaptation. Neuron. 2009;64(5):605–616. doi: 10.1016/j.neuron.2009.11.028. [DOI] [PubMed] [Google Scholar]
- 35.Neitz J, Carroll J, Yamauchi Y, Neitz M, Williams DR. Color Perception Is Mediated by a Plastic Neural Mechanism that Is Adjustable in Adults. Neuron. 2002;35:783–792. doi: 10.1016/s0896-6273(02)00818-8. [DOI] [PubMed] [Google Scholar]
- 36.Jarsky T, Cembrowski M, Logan SM, Kath WL, Riecke H, Demb JB, Singer JH. A Synaptic Mechanism for Retinal Adaptation to Luminance and Contrast. The Journal of Neuroscience. 2011;31(30):11003–11015. doi: 10.1523/JNEUROSCI.2631-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wark B, Fairhall A, Rieke F. Timescales of inference in visual adaptation. Neuron. 2009;61(5):750–761. doi: 10.1016/j.neuron.2009.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Baccus SA, Meister M. Fast and slow contrast adaptation in retinal circuitry. Neuron. 2002;36(5):909–919. doi: 10.1016/s0896-6273(02)01050-4. [DOI] [PubMed] [Google Scholar]
- 39.Webster MA. Visual Adaptation. Annual Review of Vision Science,1(1) 2015 doi: 10.1146/annurev-vision-082114-035509. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Ibid 23. [Google Scholar]
- 41.Tranchina D, Peskin CS. Light adaptation in the turtle retina: embedding a parametric family of linear models in a single nonlinear model. Visual Neuroscience. 1988;1(04):339–348. doi: 10.1017/s0952523800004119. [DOI] [PubMed] [Google Scholar]
- 42.Aurelien D, Fini PT, Houser KW, Ohno Y, Royer MP, Smet K, Wei M, Whitehead L. Development of the IES method for evaluating the color rendition of light sources. Optics Express. 2015;23(12):15888–15906. doi: 10.1364/OE.23.015888. [DOI] [PubMed] [Google Scholar]
- 43.Ruderman DL, Cronin TW, Chiao CC. Statistics of cone responses to natural images: Implications for visual coding. JOSA A. 1998;15(8):2036–2045. [Google Scholar]
- 44. Ibid 17. [Google Scholar]
- 45. Ibid. [Google Scholar]
- 46. Ibid. [Google Scholar]
- 47.Lee BB. Color coding in the primate visual pathway: a historical view. JOSA A. 2014;31(4):A103–A112. doi: 10.1364/JOSAA.31.00A103. [DOI] [PubMed] [Google Scholar]
- 48.Dacey DM, Lee BB. The ‘blue-on’ opponent pathway in primate retina originates from a distinct bistratified ganglion cell type. Nature. 1994;367:731–735. doi: 10.1038/367731a0. [DOI] [PubMed] [Google Scholar]
- 49. Ibid. [Google Scholar]
- 50.Mollon JD. Tho'she kneel'd in that place where they grew. The uses and origins of primate colour vision. Journal of Experimental Biology. 1989;146(1):21–38. doi: 10.1242/jeb.146.1.21. [DOI] [PubMed] [Google Scholar]
- 51.McDermott KC, Webster MA. Uniform color spaces and natural image statistics. JOSA A. 2012;29(2):A182–A187. doi: 10.1364/JOSAA.29.00A182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wyszecki G, Stiles WS. Color science: concepts and methods, quantitative data and formulae, Section 5.9: Abbney and Bezold-Brücke effects. 2nd. John Wiley and Sons; 2000. p. 420. [Google Scholar]
- 53.Webster MA, Mizokami Y, Webster SM. Seasonal variations in the color statistics of natural images. Network: Computation in neural systems. 2007;18(3):213–233. doi: 10.1080/09548980701654405. [DOI] [PubMed] [Google Scholar]
- 54.Webster MA, Mollon JD. The Influence of Contrast Adaptation on Color Appearance. Vision Res. 1994;34(I5):1993–2020. doi: 10.1016/0042-6989(94)90028-0. [DOI] [PubMed] [Google Scholar]
- 55.Atick JJ, Li A, Redlich AN. What Does Post-Adaptation Color Appearance Reveal About Cortical Color Representation? Vision Res. 1993;33(1):123–129. doi: 10.1016/0042-6989(93)90065-5. [DOI] [PubMed] [Google Scholar]
- 56.Eskew RT. Higher order color mechanisms: A critical review. Vision research. 2009;49(22):2686–2704. doi: 10.1016/j.visres.2009.07.005. [DOI] [PubMed] [Google Scholar]
- 57.Krauskopf J, Williams JDR, Mandler MB, Brown AM. Higher order color mechanisms. Vision research. 1986;26(1):23–32. doi: 10.1016/0042-6989(86)90068-4. [DOI] [PubMed] [Google Scholar]
- 58.Horwitz GD, Hass CA. Nonlinear analysis of macaque V1 color tuning reveals cardinal directions for cortical color processing. Nature neuroscience. 2012;15(6):913–919. doi: 10.1038/nn.3105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Ibid. [Google Scholar]
- 60.Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control. 1974;19(6):716–723. [Google Scholar]
- 61.Foster DH, Nascimento SMC. Relational colour constancy from invariant cone-excitation ratios. Proceedings of the Royal Society of London. Series B: Biological Sciences. 1994;257(1349):115–121. doi: 10.1098/rspb.1994.0103. [DOI] [PubMed] [Google Scholar]
- 62.Kingdom FA. Lightness, brightness and transparency: a quarter century of new ideas, captivating demonstrations and unrelenting controversy. Vision Research. 2011;51(7):652–673. doi: 10.1016/j.visres.2010.09.012. [DOI] [PubMed] [Google Scholar]
- 63.Anderson B. The perceptual organzation of depth, lightness, color, and opacity. In: Werner John S, Chalupa Leo M., editors. The New Visual Neurosciences. Cambridge: MIT Press; 2014. pp. 653–664. [Google Scholar]
- 64.Brainard DH, Radonjić A. Color constancy. In: Werner JS, Chalupa LM, editors. The New Visual Neurosciences. Cambridge, MA: MIT Press; 2014. pp. 545–556. [Google Scholar]