Densely-packed ZnTPPs Monolayer on the Rutile TiO₂(110)-(1×1) Surface: Adsorption Behavior and Energy Level Alignment

Abstract

The adsorption of a densely packed Zinc(II) tetraphenylporphyrin monolayer on a rutile TiO₂(110)-(1×1) surface has been studied using a combination of experimental and theoretical methods, aimed at analyzing the relation between adsorption behavior and barrier height formation. The adsorption configuration of ZnTPP was determined from scanning tunnel microscopy (STM) imaging, density functional theory (DFT) calculations and STM image simulation. The corresponding energy alignment was experimentally determined from X-ray and UV-photoemission spectroscopies and inverse photoemission spectroscopy. These results were found in good agreement with an appropriately corrected DFT model, pointing to the importance of local bonding and intermolecular interactions in the establishment of barrier heights.

1. INTRODUCTION

Porphyrins, and in particular metalloporphyrins, have attracted significant attention over the past few years, due to their proven viability in supramolecular chemistry in order to develop hierarchical nanoarchitectures,^1-2 in gas-sensing processes,^3-6 in nanoelectronics⁷ or as efficient nanocatalysts,^8-12 with the possibility of using their metal active sites as supports for metallic nanoparticles.¹³

Owing to their strong light absorption properties, interfaces between metalloporphyrins and wide band gap semiconductors have also been natural candidate systems for photovoltaic and photochemical applications. ^14-19 For such applications, the efficiency of photoexcited charge transfer processes depends on the relative energy alignment of the molecular orbitals involved in the light absorption (typically HOMO-LUMO transitions) with respect to the band edges of the surface onto which they are adsorbed. Molecule-substrate energy level alignment at interfaces cannot be readily predicted using, for example, the individual properties of the molecule and of the surface^20-22, as, upon contact, complex charge rearrangement occurs, leading to the creation of an interface dipole.

Although recent progress has led to a better understanding of energy level alignment at the interface between organics and transition-metal oxides films²³, a detailed and comprehensive study of energy alignment at a model organic molecule/oxide semiconductor interface is missing. In particular, experimental evidence indicates that important effects arise at organic/oxides interfaces, as a result of a space charge layer in the oxide or from the strength of the interface chemistry. ^24-27

To date, experimental energy alignment studies of porphyrin derivatives on TiO₂ have been limited to solution sensitized films or single crystal surfaces where molecular adsorbates are covalently bound to the surface via carboxylic acid anchor groups. These methods, although representative of real-life devices, can obscure the intrinsic properties of the molecule/oxide interface owing to disorder arising from multiple bonding geometries and from exposure to the ambient, as well as charge exchange associated with the carboxylic acid anchor groups. ^{16, 28-29}

In this work, we have performed a combined experimental and theoretical study of a paradigmatic model interface: a zinc tetraphenylporphyrin (ZnTPP) monolayer deposited via sublimation onto a well-characterized TiO₂(110) surface in a controlled UHV environment. The result is a well-ordered ZnTPP/TiO₂(110) interface that is highly suited for study using a joint experimental-theoretical approach. The geometry, relative on-surface orientation, periodicity, and registry of the ZnTPP molecular array with the TiO₂(110) substrate have been studied using scanning tunnel microscopy (STM) and a detailed adsorption model has been proposed, based on a density functional theory (DFT) energy minimization approach and supported by simulations of the STM images. Moreover, the energy level alignment has been determined experimentally using a combination of x-ray photoemission, UV-photoemission and inverse photoemission spectroscopies (XPS, UPS, and IPS, respectively). The nature of the charge rearrangement at the interface has been explored using a DFT approach introducing appropriate corrections. Excellent agreement between experiment and theory, in both the geometric structure and the energy level alignment, is found for this system at monolayer coverage. The calculated interface dipole for a different ZnTPP-monolayer, taking for each ZnTPP-molecule the geometry of an isolated molecule interacting with the oxide, differs substantially from the experimental findings, illustrating the importance of intermolecular effects in establishing the ZnTPP-geometry and the interface dipole of the molecular monolayer.

2. METHODS

Surface preparation

The rutile TiO₂(110) sample was a commercially produced single-crystal from MTI corporation, cut to within 0.5° of the (110) plane. The surface was degassed and prepared in an ultrahigh vacuum using several cycles of 1 keV Ar⁺ ion sputtering (while maintaining a maximum sample current of 2 μA) and annealing in UHV at 600°C. The cleanliness of the surface was checked using XPS, and the surface termination was assessed either by low energy electron diffraction (LEED) or STM.

ZnTPP molecules [Frontier Scientific >95% purity] were deposited by way of sublimation deposition in the same UHV environment using a thoroughly degassed Knudsen cell held between 250 and 280°C. The deposition rate was measured using a quartz crystal monitor.

Scanning tunnel microscopy

The STM measurements were performed in a UHV environment at pressures better than 5 × 10⁻¹⁰ Torr with an Omicron variable temperature STM unit. The chamber was also equipped with XPS and LEED. The images presented here were obtained in constant-current mode with the sample at room temperature. Images were processed using the WSxM 5.0 develop 6.4 software.³⁰ Error bars for the STM measurements, due to a combination of noise and drift during imaging, are estimated to ± 0.2 Å for heights, ± 0.2 Å for lateral distances, and ~3° for angles.

Spectroscopic methods

X-ray and ultraviolet photoemission spectroscopy, as well as inverse photoemission spectroscopy measurements, were performed in a single UHV experimental system described elsewhere. ²⁹ In UPS and XPS, the kinetic energy distribution of electrons ejected by excitation from monoenergetic photons reflects the density of occupied states in the system. In IPS, a monoenergetic beam of electrons is directed to the sample and a small fraction undergoes optical decay emitting photons. The resulting photon energy distribution reflects the density of unoccupied states in a manner that is highly complementary to UPS. Core levels were probed using X-ray photoemission spectroscopy excited by non-monochromatized Al Kα radiation, and the valence band electronic states were examined using He II (40.8 eV) excited ultraviolet photoemission spectroscopy. In both cases, electron energy distributions were measured using a cylindrical mirror analyzer.

The conduction band spectra were obtained from inverse photoemission spectroscopy, performed using a grating spectrometer with a primary electron energy of 20.3 eV. The overall energy resolution for the UPS and IPS spectra is estimated to be better than 0.3 and 0.6 eV, respectively. The energy scales of the UPS and IPS spectra were calibrated using the measured position of the Fermi level of a gold sample in contact with the oxide sample.

For both the clean and ZnTPP-covered surfaces, the secondary electrons cutoff has been measured on biased samples using a He I radiation (21.1 eV) so as to determine the electron affinity, given by EA = hν – W – Egap, where hν is the photon source energy, W the total width of the spectra, and Egap is the experimentally measured gap of the oxide surface (i.e., the energy difference between the valence band maximum [VBM] measured by UPS and the conduction band minimum [CBM] measured by IPS) or the molecular gap (i.e., the energy difference between the HOMO centroid measured by UPS and the LUMO centroid measured by IPS).

Theoretical methods

In order to investigate in detail the structural and electronic properties of the ZnTPP/TiO₂(110) interface we have used two complementary DFT simulation packages: i) the accurate plane-wave code Quantum Espresso,³¹ that we have used for the determination of the complex interface atomic geometries; and ii) the efficient local-orbital code Fireball,^32-35 used to analyze the interface electronic properties after introducing appropriate correlation effects on the electronic levels of the organic molecule (see below), as well as for the simulation of the theoretical STM images.

In the calculations carried out using the plane-wave Quantum Espresso code³¹ the atomic geometries have been fully relaxed by means of DFT calculations by including dispersion forces within the DFT+D approach³⁶ in a supercell approximation. For this purpose, we have used the revised version of the generalized gradient corrected approximation of Perdew, Burke, and Ernzerhof (rPBE), ³⁷ and an empirical R⁻⁶ correction to add dispersive (van der Waals) forces to conventional DFT functionals by means of Grimmés prescription³⁶ – see details in previous literature^{36, 38}–. On the other hand, in the Fireball code we use a local-orbital formulation in such a way that self-consistency is implemented on the orbital occupation numbers^{32, 39}, which were calculated using the orthonormal Löwdin orbitals. ^32-35 The advantage of using this local-orbital code is that we can introduce appropriately in its implementation some corrections in the calculations (see equations 1 and 2) that provide an improved description of the electronic structure of the organic/oxide interface (in particular, the organic energy gap, see below). In these calculations we have used a basis set of optimized sp³d⁵ numerical atomic orbitals (NAOs)⁴⁰ for C, N, Ti and Zn, sp³s*p³* for O and s for H, with cut-off radii (in a.u.): s = 4.0, p = 4.5 and d = 5.4 (C); s = 3.6, p = 4.1 and d = 5.2 (N); s = 6.2, p = 6.7, d = 5.7 (Ti); s = 4.5, p = 5.7, d = 3.7 (Zn); s = s* = 3.4, p = p* = 3.8 (O); and s = 4.1 (H). This is the same basis set as used in previous studies involving TCNQ interfaces.²⁵ In our calculations we have used the Local Density Approximation (LDA) functional³³ and the ion-electron interaction has been modelled by means of norm-conserving scalar-relativistic pseudo-potentials.⁴¹

As mentioned above, the organic/oxide interface electronic properties are analyzed introducing some corrections in our local-orbital DFT calculations. These corrections are required due to the following limitations of standard DFT functionals (e.g. LDA, GGA): (a) the Kohn-Sham energy levels yield transport gaps for the organic molecules that are usually too small; ^{21, 42-43} and (b) the initial relative level alignment between the oxide and the organic materials is not correctly described even in well converged LDA (or GGA) calculations.^44-47 Following up previous publications,^48-50 we have introduced two operators to amend these problems. With the following scissor operator:

$$O^{\mathit{scissor}}={\Sigma }_{\left(\mu \nu \right)}\left\{\left(\frac{U}{2}\right)\mid \mu \rangle \langle \mu \mid -\left(\frac{U}{2}\right)\mid \nu \rangle \langle \nu \mid \right\},$$ (1)

|μ〉 (|ν〉) being the empty (occupied) molecular orbitals of the isolated molecule (with the actual geometry of the molecule on the surface), we open the LDA-energy gap, E_g^LDA, to E_g^LDA+U, where U is fixed to yield the experimental energy gap of 3.9 eV (see below). Additionally, the following shift operator,

$$O^{\mathit{shift}}={\Sigma }_{\left(\mu \nu \right)}\left\{\left(\epsilon \right)(\mid \mu \rangle \langle \mu \mid +\mid \nu \rangle \langle \nu \mid )\right\},$$ (2)

introduces a rigid shift, ε, of the molecular levels; ε is fixed to yield the appropriate initial alignment between the oxide and the organic energy levels. These corrections are introduced in the local-orbital Hamiltonian, and the interface electronic structure is then obtained by means of a self-consistent DFT calculation using the interface atomic geometry obtained with the QUANTUM ESPRESSO code.

Finally, theoretical STM calculations have been also performed for the densely-packed ZnTPP/TiO₂(110) interface considered in this study, and compared with the experimental evidence. In order to obtain accurate STM images and tunneling currents, we used an efficient STM theoretical simulation technique that includes a detailed description of the electronic properties of both the tip and the sample. Using this technique, based on a combination of a Keldysh Green’s function formalism and local orbital DFT,^51-53 we split the system into sample and tip, where the sample here is the ZnTPP/TiO₂(110) system. In these calculations we have used a W-tip formed by 5 atoms (one of them in the apex) attached to an extended W(100)-crystal. Within this approach, in the tunneling regime at low temperature, the STM current is given by: ^51-53

$$I=\frac{4\pi e^2}{ħ}{\int }_{E_F}^{E_F+e{V}_s}d\omega Tr\left[T_{ts}{\rho }_{ss}\right(\omega \left)T_{st}{\rho }_{tt}\right(\omega -eV\left)\right],$$ (3)

where V_s is the surface voltage, ρ_tt and ρ_ss are the density of states (DOS) matrices – in the local orbital basis – associated with the tip and sample, whilst T_ts and T_st are the local orbital Hamiltonian matrices coupling tip and sample (see Refs. ^51-53 for further details).

3. RESULTS AND DISCUSSION

Adsorption geometry

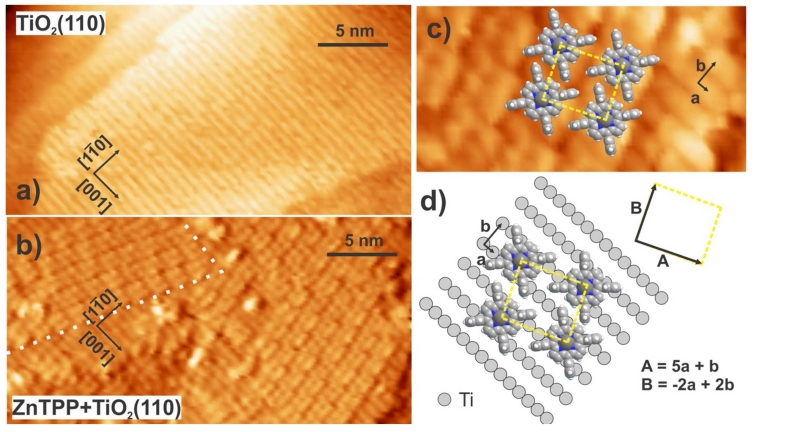
When cut along the (110) plane, rutile TiO₂ crystals expose a surface with two-fold symmetry, comprised of alternated O and Ti rows running along the [001] crystallographic direction. STM images of the clean and ZnTPP-covered TiO₂(110) surface, measured by tunneling into the unoccupied states (+2V), are shown Figure 1. Figure 1a) is an STM image of the clean surface. Although the O rows are protruding above the plane containing the first exposed Ti atoms, the latter appear as bright rows in STM images obtained at this bias owing to the unoccupied Ti 3d states of the conduction band, and the former as darker lines between those rows. ⁵⁴ A detailed analysis of Figure 1a) gives a measured row separation of 6.3 ± 0.2 Å, which is in good agreement with the value of 6.5 Å expected based on the bulk lattice parameters.

Figure 1.

STM images of a) a clean TiO₂(110) surface before and b) after ZnTPP adsorption. Both images were taken at V_s=+2V, and are thus mapping unoccupied states. c) A zoomed-in area of b) that contains both a ZnTPP-covered region and a clean surface region, allowing the determination of the molecular adsorption scheme shown in d).

Studies of ZnTPP molecule deposited by sublimation onto single crystal surfaces in ultrahigh vacuum have used two different methods to achieve monolayer coverage: (i) molecular deposition with increasing exposure until the surface is fully covered by a monolayer of molecules, or (ii) deposition of a molecular multilayer followed by low temperature (150 to 200°C) annealing to desorb weakly bound molecules and leave a monolayer on the surface.^55-57 Recently, method i has been used to study adsorption of a ZnTPP derivative on TiO₂(110) and led to a somewhat disordered monolayer with no clear evidence of preferred adsorption sites.⁵⁸ In the study described here, we have chosen method ii: desorption of a multilayer at room temperature followed by annealing at 150°C. An STM image of a surface prepared in this way is shown in Figure 1b). This method of preparation leads to large terraces that are nearly completely covered by ordered molecular features. The molecular array is comprised of a rectangular lattice with measured dimensions of 16.3 Å × 14.3 Å. Fig 1c) is a close-up of the lower right corner of Figure 1b) showing adjacent regions with and without ZnTPP molecules. The smaller repeating unit, which is composed of four bright lobes arranged in a square configuration, is characteristic of ZnTPP and associated with the four mesophenyls of the molecule. The center of ZnTPP typically appears as a depression owing to the absence of unoccupied Zn states at this bias. ^{16, 57}

Using the adjacent clean and molecule-covered regions of the surface, the registry of the molecular array with respect to the surface lattice of the substrate can be determined. Extrapolating the oxygen rows in Figure 1c) towards the molecule-covered area shows that the Zn center of each molecule, as well as opposite pyrroles of the porphyrin macrocycle, lie along an oxygen row. As a result, the phenyls are aligned with the Ti rows adjacent to the oxygen row on which the molecule is centered. While it is not possible to determine the precise location of the ZnTPP molecules along the oxygen row, it is clear that the primitive vectors of the molecular lattice (A and B) are not aligned with those of the underlying surface (a and b). Figure 1d) shows an adsorption geometry that is consistent with the STM images of Figures. 1b) and 1c). For simplicity, only the Ti rows are represented here. Using a notation where a is the unit vector along the [001] direction with a Ti—Ti distance of 3 Å and b the unit vector in the [$1\stackrel{‒}{1}0$] direction with a Ti—Ti distance between two rows of 6.5 Å, the ZnTPP lattice vectors A and B can be expressed in terms of the substrate lattice vectors as A = 5a+b and B = −2a+2b. Additionally, Figure 1b) shows that two different domains are visible on the surface, indicating that the ZnTPP molecules can organize themselves in two equivalent ways, which are reflected about a $1\stackrel{‒}{1}0$ mirror plane.

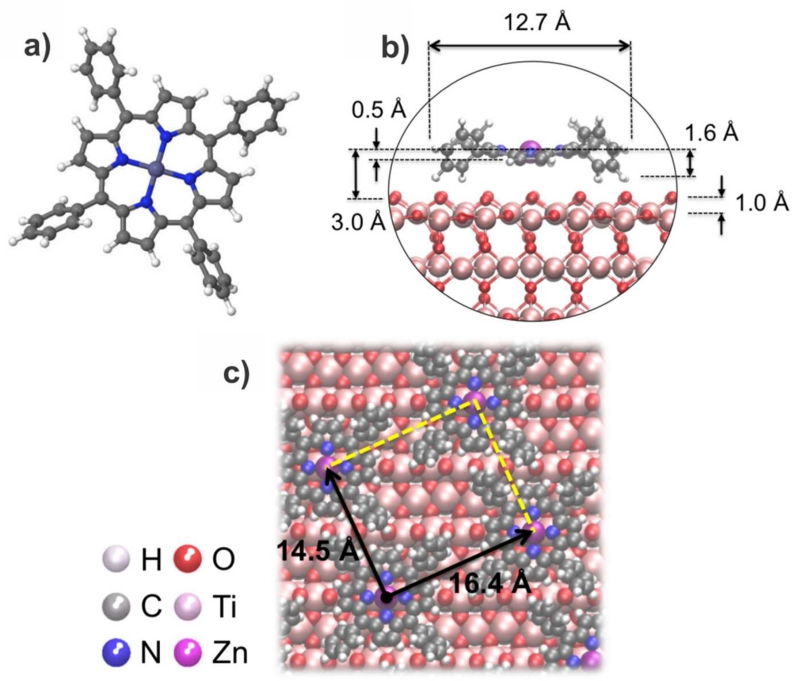
The overlayer geometry deduced from our STM measurements is both confirmed and refined by our theoretical calculations. Using the Quantum Espresso code as described in section II, we find that the lowest energy configuration corresponds to a geometry in which the central Zn atom is placed 3.0 Å directly above an oxygen atom of the O row, as shown Figure 2b). In this model geometry the ZnTPP molecules form a monolayer with one molecule per unit cell with dimensions 16.4 Å × 14.5 Å (see Figure 2c)), quite close to the experimentally measured values. For reference, the calculated geometry of the gas phase ZnTPP molecule is shown Figure 2a). We should stress that in our calculations the final molecule geometry depends crucially on the repulsive interaction between the mesophenyl rings of adjacent molecules; calculations for an isolated molecule on the oxide surface yield a distinct molecular conformation and, if this geometry is used in the monolayer case, we obtain a smaller charge transfer to the oxide. We will see later that accounting for the adsorption geometry of the full monolayer is critical for obtaining the correct energy alignment at the interface. Upon adsorption, the ZnTPP molecules become distorted as shown in Figure 2c). The ZnTPP porphyrin ring is adsorbed at a distance of 2.5-3.0 Å above the TiO₂(110) O-row, with the mesophenyl rings keeping a rotation with respect to the flat ZnTPP molecular skeleton similar to the one found for the gas-phase geometry. In particular, the mesophenyl rings of the molecule rotate by an angle between 2.5° and 6.5° with respect to the gas-phase geometry, so that those rings form an angle of 50±2° with the flat porphyrin molecular skeleton, instead of 54.5° in the gas phase; these rotations enable some of the H atoms of the mesophenyl rings to form weak bonds with the O atoms of the surface, such that the H-O distances are between 2.2 and 2.4 Å.

Figure 2.

Surface geometry for the densely-packed ZnTTP/TiO₂(110) interface. a) Gas-phase molecule; b) Geometry of the molecule on TiO₂(110); c) Close packed geometry of the ZnTPP monolayer.

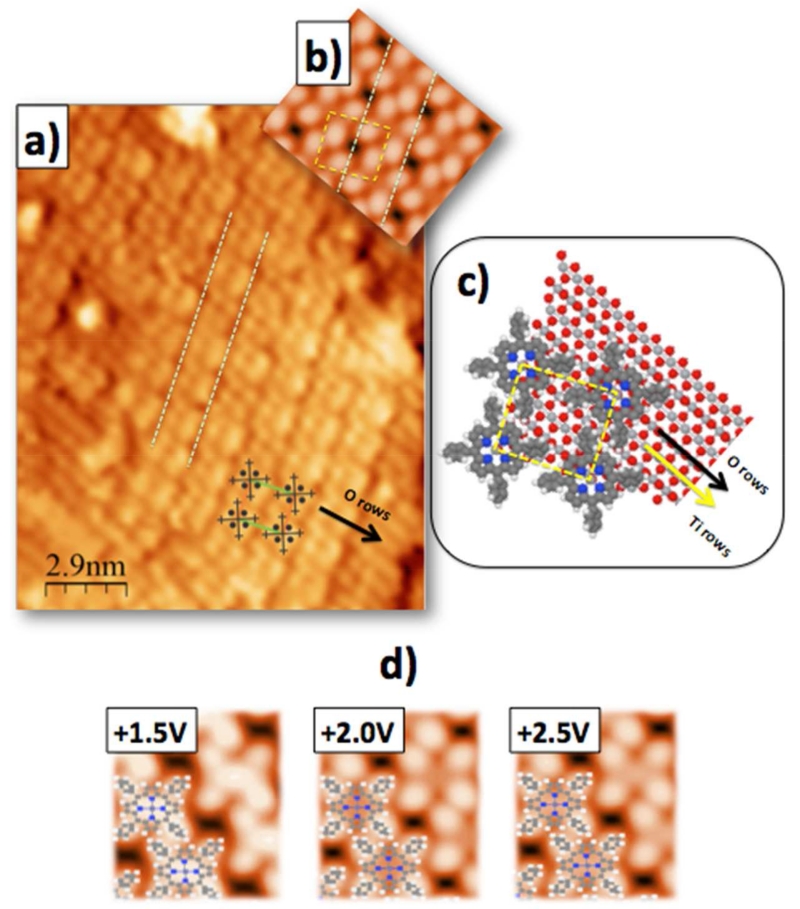
Using this relaxed geometry summarized in Figure 2, we have also calculated the theoretical STM image for the ZnTPP monolayer on TiO₂(110), using a combination of a Green’s function formalism and local-orbital DFT, as described in section II. Figure 3a) is reported the experimental STM image measured at V_s=+2V. Figure 3b) shows the theoretical STM image for a tunneling bias of V_s=+2.0 V, and Figure 3d) shows a series of computed STM images for V_s= +1.5, +2.0 and +2.5 V, respectively. For comparison, the adsorption geometry of the ZnTPPs on the TiO₂(110) surface is also reported in Figure 3c). For simplicity, the details of the corrections introduced in the local-orbital DFT electronic structure calculation (equations 1 and 2) are discussed in the next section, although the corrections to the energy alignment are taken into account in these images. At these tunneling conditions, the mesophenyls appear as bright lobes arranged in a square, while the central Zn atom is not contributing to the image, in good agreement with the experimental STM image. Notice that in the STM image of Figure 3b), two out of four mesophenyl rings show, due to their rotation, some non-negligible overlap with the corresponding mesophenyls of neighbouring molecules. This suggests the possibility of probing different surface geometries depending on the alternative rotation of those ZnTPP-mesophenyls.

Figure 3.

Comparison between a) experimental and b) simulated STM images at V_s=+2.0 V for the ZnTPP/TiO₂(110) interface model represented in c). For comparison, d) shows a series of computed STM images for V_s= +1.5, +2.0 and +2.5 V, respectively.

The good agreement between the experimentally determined molecular bonding geometry and that found by a density functional theory (DFT) energy minimization approach combined with simulations of the STM images strongly suggests that this theoretical interface geometry is an appropriate structural model for our combined theoretical and experimental analysis of the interface electronic structure and energy level alignment.

Energy alignment

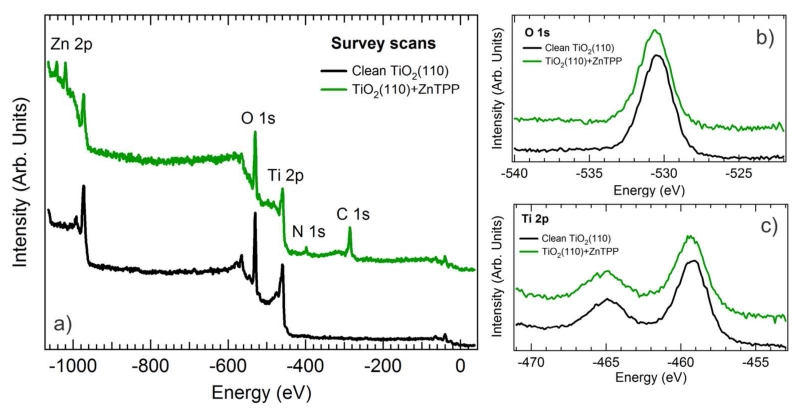
In order to fully characterize the energy alignment of the TiO₂(110)/ZnTPP monolayer interface, XPS, UPS, and IPS spectra of the core levels, valence band and conduction band, respectively, were measured before and after the ZnTPP monolayer was established. A survey scan of the TiO₂(110) surface before and after molecular deposition is shown in Figure 4a). The XPS spectrum of the clean surface (black curve) indicates the presence of only Ti 2p and O 1s core levels, whereas, the spectrum after ZnTPP monolayer formation (green curve) contains peaks associated with the Zn 2p, C 1s and N 1s core levels. Figures 4b) and 4c) contain high resolution O 1s and Ti 2p core level spectra. The absence of any appreciable shift in these core levels after ZnTPP deposition indicates that adsorption of this molecule does not induce band bending which suggests that there is relatively little charge transfer between the surface and the ZnTPP overlayer.²⁵ This is not surprising given that the molecule is weakly bound to the TiO₂ surface.

Figure 4.

a) XPS survey scans measured on the clean TiO₂(110) surface and covered with a monolayer of ZnTPP molecules. No band bending was observed upon ZnTPP adsorption as observed from b) the O 1s and c) Ti 2p core levels of the TiO₂ substrate before and after ZnTPP monolayer formation.

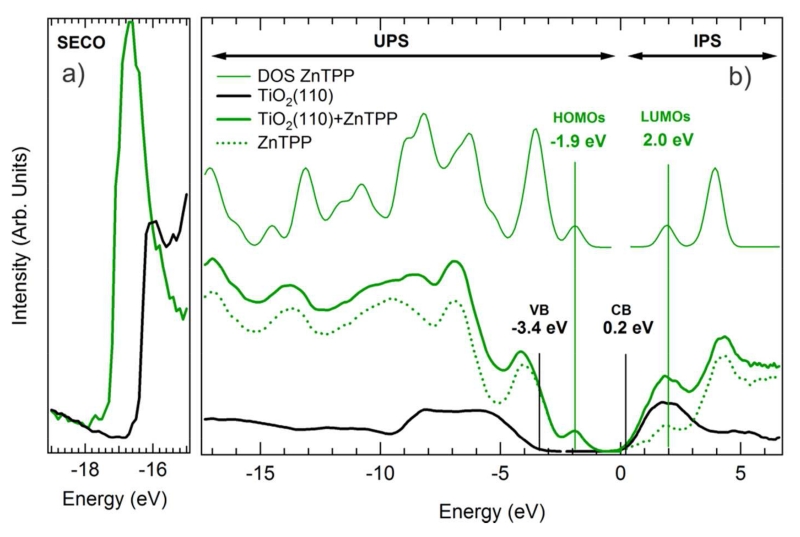
UPS spectra of the valence band and secondary electron cutoff (SECO), as well as IPS spectra of the conduction band region for the clean TiO₂(110) and ZnTPP monolayer covered surfaces are shown in Figure 5. All spectra have been referenced to a common Fermi level set at 0 eV, so that occupied states occur at negative energy and unoccupied states at positive energy. The VB and CB of clean TiO₂(110) (black curve) shown in Figure 5b) are characteristic of that surface. The VB is mainly composed of O 2p states with a sharp high-energy edge that when extrapolated yields a valence band maximum at −3.4 eV. The CB possesses strong Ti 3d features, whose edge when extrapolated puts the conduction band minimum at 0.2 eV. Thus the band gap measured on this TiO₂(110) surface is 3.6 eV, consistent with that reported in the literature. ^{16, 28-29} As expected, the TiO₂(110) surface appears strongly n-doped with the Fermi energy near the conduction band minimum. The electron affinity of the pristine surface is estimated to be 4.6 eV, based on the SECO edge of Figure 5a).

Figure 5.

a) Secondary electron cut off (SECO), b) UPS and IPS spectra of the clean (heavy black curve) and ZnTPP-covered (heavy green curve) TiO₂(110) surface. The difference spectrum (dotted green curve) is to be compared to the calculated DOS (thin green curve).

The spectra of Figure 5b) that were obtained from the ZnTPP monolayer-covered TiO₂(110) surface (thick green curve) exhibit strong molecular features both in the occupied and unoccupied states. By subtracting appropriately scaled UPS and IPS spectra of the clean surface from the spectra of the ZnTPP-covered surface, features associated with the molecular layer can be isolated. The background-subtracted curves, representing the molecular contribution to the spectra, are shown as the green dotted lines in Figure 5b). This experimentally measured electronic structure can be directly compared to the DOS calculated (GAMESS-US⁵⁹, B3LYP^60-62, 6-31G*⁶³ adjusted to fit the experimental HOMO-LUMO gap) for a ZnTPP gas phase molecule shown on top of Figure 5b) as a thin green line.

It is clear that there is a good correspondence between the measured occupied and unoccupied states and the calculated ZnTPP molecule electronic structure. In particular, molecular states that are found in the TiO₂(110) band gap region around −1.9 eV, can be attributed to the ZnTPP highest occupied molecular orbitals (HOMOs), while the first unoccupied states measured around 2 eV in IPS correspond to the ZnTPPs lowest unoccupied molecular orbitals (LUMOs). Additionally, both the theoretical and experimental curves exhibit strong mesophenyl-related features in both the occupied and unoccupied states, centered at −3.0 eV and 4.0 eV, respectively. The good agreement between the difference spectra and the molecular calculation provides further evidence that there is relatively little charge transfer between the surface and the molecular layer. ²⁵ Finally, using the SECO measured on the ZnTPP monolayer shown in Figure 5a), an effective electron affinity of 1.9 eV is calculated for the ZnTPP monolayer. These results are very similar to those found in earlier studies of TiO₂(110) surfaces sensitized with ZnTPP derivatives in solution.^{16, 28-29}

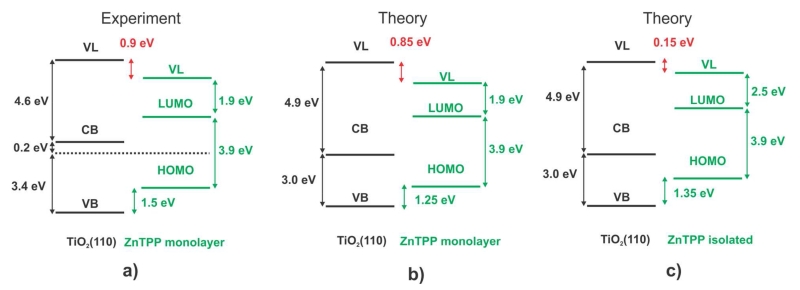
Figure 6a) shows the full energy diagram for the monolayer ZnTPP/TiO₂(110) system that is drawn from the experimental measurements. The shift in the VLs of the clean and ZnTPP-covered TiO₂(110) surfaces indicates that there is an interface dipole of 0.9 eV.

Figure 6.

Energy alignment-Comparison: a) Experiment for a monolayer, b) theory for the ZnTPP monolayer and c) theory for a ZnTPP monolayer with the molecular adsorption geometry corresponding to an isolated ZnTPP molecule on TiO₂(110) (see text).

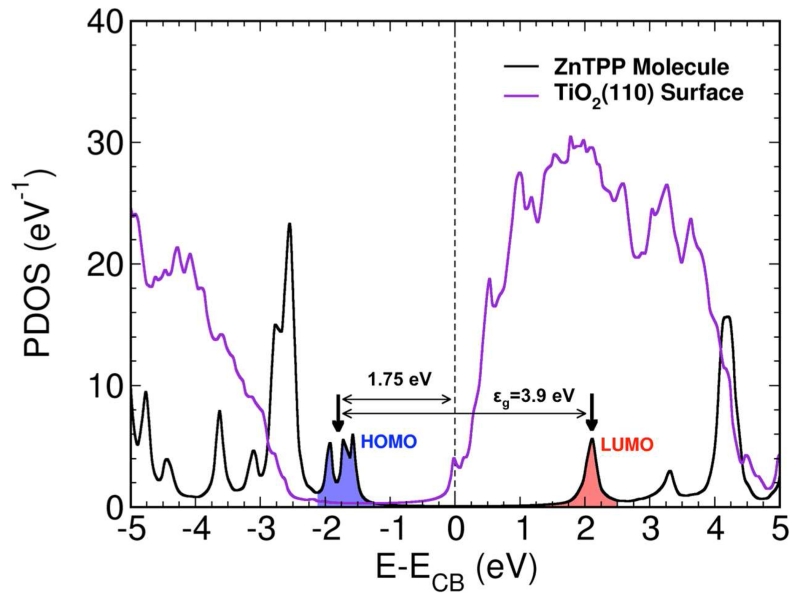
We have analyzed theoretically the interface energy level alignment by means of the local-orbital (FIREBALL) DFT code using the geometry provided by our plane-waves (QUANTUM ESPRESSO) DFT calculations (see Figure 2). As mentioned above, in our local-orbital Hamiltonian we have introduced the scissor and shift operators with the values U and ε chosen to yield initially the values of the molecular levels as shown by the experimental data of Figure 6a). In particular, the HOMO/LUMO energy gap for the (deformed) organic molecule is set to 3.9 eV, using the scissor operator; also, the initial affinity level is set to 1.9 eV (energy difference from the LUMO level to the initial vacuum level), using the shift operator. Figure 6b) shows the final position for the different energy levels at the organic/oxide interface (i.e. after self-consistency) and Figure 7 shows our calculated DOS projected on the molecule and on the oxide orbitals. We should mention that our LDA-calculations for TiO₂ yield an energy gap for the oxide of 3.0 eV, instead of the 3.6 eV measured experimentally; we have minimized the effects of this energy difference, assuming that the CB and VB edges of the oxide are 4.9 eV and 7.9 eV, respectively, instead of 4.6 eV and 8.2 eV. From Figure 7, we see that the HOMO level (taken as an average of the different levels of the HOMO broken symmetry) is located around 1.25 eV above the oxide valence band edge, while the LUMO level is 2.15 eV above the oxide conduction band edge. This indicates, as shown in Figure 6b), that in our calculations the interface dipole is around 0.85 eV in excellent agreement with the experimental evidence (0.9 eV, see Figure 6a). This dipole is mostly due to the electron charge transfer from the molecule to the oxide, which we find to be around 0.28 electrons per molecule. The electron transfer alone yields an interface dipole of around 0.8 eV. An additional 0.05 eV is associated with the intrinsic dipole of the slightly deformed molecule. It is also worth mentioning that, in the calculated DOS shown in Figure 7, the occupied and unoccupied mesophenyl-related states already mentioned above (see Figure 5) are found around −3 and 4 eV, respectively, in reasonable agreement with the results shown in that figure.

Figure 7.

DOS projected on the molecule and oxide orbitals.

As a final note we point out that, in performing these theoretical calculations, it was important to consider full monolayer coverage in order to accurately represent the experiments. When calculations were performed for the case of an isolated ZnTPP molecule on the TiO₂(110) surface, it was found that the ZnTPP molecule acquired a saddle-shaped porphyrin ring and rotated mesophenyls: an adsorption geometry similar to the one obtained for ZnTPP embedded in a monolayer. However, the molecule-surface distance is significantly larger for the isolated molecule case: the zinc-terminal oxygen distance is found to be 3.9 Å, which is 0.9 Å larger than the same distance calculated for the monolayer. This has non-negligible effects on the energy alignment at the interface. The calculated energy alignment for a monolayer, taking for each molecule the geometry of the isolated case, is shown in Figure 6c). Although the HOMO and LUMO positions are not markedly different from the ones calculated for the monolayer, the interface dipole is reduced by 0.7 eV to a value 0.15 eV. This change is the result of less charge transfer from the molecule to the oxide, a consequence of the larger molecule-surface separation. In other words, the repulsive interaction between the mesophenyl rings of adjacent molecules stabilizes a densely-packed monolayer with a reduced molecule-surface distance, resulting in greater molecule-to-surface charge transfer and a larger interface dipole.

4. CONCLUSION

The adsorption geometry and the energy level alignment of a ZnTPP monolayer on the rutile TiO₂(110) surface, a model weakly bound organic monolayer/oxide semiconductor interface, has been studied using a combination of STM, XPS, UPS, IPS and DFT calculations.

It is found that for the ZnTPP monolayer obtained by desorption of a multilayer grown on a TiO₂(110) surface, ZnTPPs forms a dense and highly-ordered array in registry with the underlying TiO₂(110) surface. In particular, each ZnTPP molecule is centered on top of an oxygen atom of a bridging oxygen row and that the molecule is distorted upon adsorption. In this configuration, rotated phenyls accommodate weak hydrogen bonds to the surface oxygen atoms.

Theoretical exploration indicates that the energy alignment of the ZnTPP molecular levels with respect to the TiO₂(110) band edges is highly sensitive to the molecular coverage and subsequent adsorption configurations. Only a densely packed monolayer model, accounting for molecular distortions and molecules-molecules interactions, led to the correct interface dipole. These results point to the fact that it is crucial for organic/oxide interfaces, even for weakly bonded adsorbates, to properly take into account the short- and long-range interactions of the system as whole.