A roadmap to multifactor dimensionality reduction methods

Abstract

Complex diseases are defined to be determined by multiple genetic and environmental factors alone as well as in interactions. To analyze interactions in genetic data, many statistical methods have been suggested, with most of them relying on statistical regression models. Given the known limitations of classical methods, approaches from the machine-learning community have also become attractive. From this latter family, a fast-growing collection of methods emerged that are based on the Multifactor Dimensionality Reduction (MDR) approach. Since its first introduction, MDR has enjoyed great popularity in applications and has been extended and modified multiple times. Based on a literature search, we here provide a systematic and comprehensive overview of these suggested methods. The methods are described in detail, and the availability of implementations is listed. Most recent approaches offer to deal with large-scale data sets and rare variants, which is why we expect these methods to even gain in popularity.

Introduction

In analyzing the susceptibility to complex traits, it is assumed that many genetic factors play a role simultaneously. In addition, it is highly likely that these factors do not only act independently but also interact with each other as well as with environmental factors. It therefore does not come as a surprise that a great number of statistical methods have been suggested to analyze gene–gene interactions in either candidate or genome-wide association studies, and an overview has been given by Cordell [1]. The greater part of these methods relies on traditional regression models. However, these may be problematic in the situation of nonlinear effects as well as in high-dimensional settings, so that approaches from the machine-learning community may become attractive. From this latter family, a fast-growing collection of methods emerged that are based on the Multifactor Dimensionality Reduction (MDR) approach.

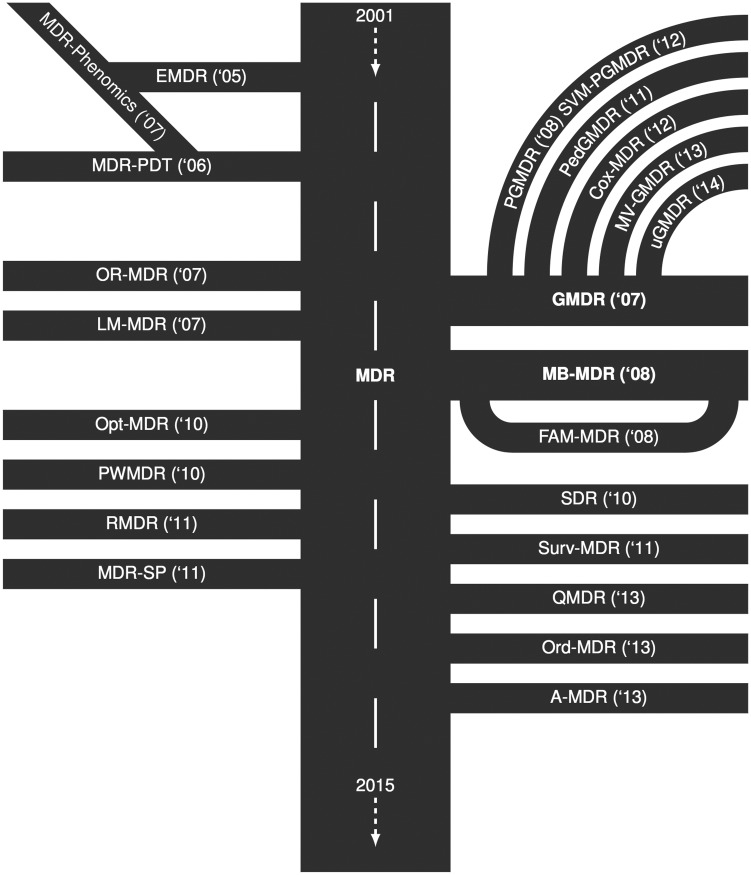
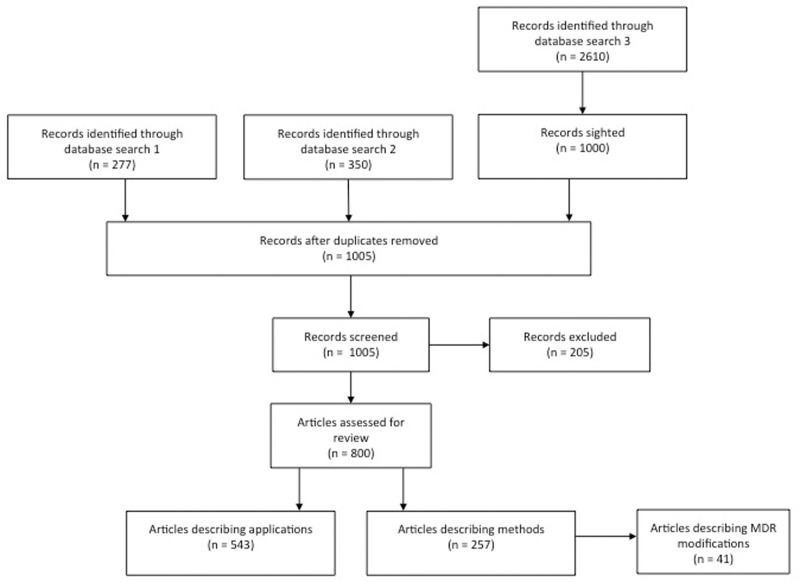
Since its first introduction in 2001 [2], MDR has enjoyed great popularity. From then on, a vast amount of extensions and modifications were suggested and applied building on the general idea, and a chronological overview is shown in the roadmap (Figure 1). For the purpose of this article, we searched two databases (PubMed and Google scholar) between 6 February 2014 and 24 February 2014 as outlined in Figure 2. From this, 800 relevant entries were identified, of which 543 pertained to applications, whereas the remainder presented methods’ descriptions. Of the latter, we selected all 41 relevant articles introducing MDR or extensions thereof, and the aim of this review now is to provide a comprehensive overview of these approaches.

Figure 1.

Roadmap of Multifactor Dimensionality Reduction (MDR) showing the temporal development of MDR and MDR-based approaches. Abbreviations and further explanations are provided in the text and tables.

Figure 2.

Flow diagram depicting details of the literature search. Database search 1: 6 February 2014 in PubMed (www.ncbi.nlm.nih.gov/pubmed) for [(‘multifactor dimensionality reduction’ OR ‘MDR’) AND genetic AND interaction], limited to Humans; Database search 2: 7 February 2014 in PubMed (www.ncbi.nlm.nih.gov/pubmed) for [‘multifactor dimensionality reduction’ genetic], limited to Humans; Database search 3: 24 February 2014 in Google scholar (scholar.google.de/) for [‘multifactor dimensionality reduction’ genetic].

Throughout, the focus is on the methods themselves. Although important for practical purposes, articles that describe software implementations only are not covered. However, if possible, the availability of software or programming code will be listed in Table 1. We also refrain from providing a direct application of the methods, but applications in the literature will be mentioned for reference. Finally, direct comparisons of MDR methods with traditional or other machine learning approaches will not be included; for these, we refer to the literature [58–61].

Table 1.

Overview of named MDR-based methods

Name	Description	Data structure	Cov	Pheno	Small sample sizesa	Applications
Multifactor Dimensionality Reduction (MDR) [2]	Reduce dimensionality of multi-locus information by pooling multi-locus genotypes into high-risk and low-risk groups	U	No/yes, depends on implementation (see Table 2)	D	No	Numerous phenotypes, see refs. [2, 3–11]
Classification of cells into risk groups
Generalized MDR (GMDR) [12]	Flexible framework by using GLMs	U	Yes	D, Q	No	Numerous phenotypes, see refs. [4, 12–33]
Pedigree-based GMDR (PGMDR) [34]	Transformation of family data into matched case-control data	F	Yes	D, Q	No	Nicotine dependence [34]
Support-Vector-Machine-based PGMDR (SVM-PGMDR) [35]	Use of SVMs instead of GLMs	F	Yes	D, Q	Yes	Alcohol dependence [35]
Unified GMDR (UGMDR) [36]	Simultaneous handling of families and unrelateds	U and F	Yes	D, Q	No	Nicotine dependence [36]
Cox-based MDR (Cox-MDR) [37]	Transformation of survival time into dichotomous attribute using martingale residuals	U	Yes	S	No	Leukemia [37]
Multivariate GMDR (MV-GMDR) [38]	Multivariate modeling using generalized estimating equations	U	Yes	D, Q, MV	No	Blood pressure [38]
Robust MDR (RMDR) [39]	Handling of sparse/empty cells using ‘unknown risk’ class	U	No	D	Yes	Bladder cancer [39]
Log-linear-based MDR (LM-MDR) [40]	Improved factor combination by log-linear models and re-classification of risk	U	No	D	Yes	Alzheimer's disease [40]
Odds-ratio-based MDR (OR-MDR) [41]	OR instead of naïve Bayes classifier to classify its risk	U	No	D	Yes	Chronic Fatigue Syndrome [41]
Optimal MDR (Opt-MDR) [42]	Data driven instead of fixed threshold; $P$-values approximated by generalized EVD instead of permutation test	U	No	D	No
MDR for Stratified Populations (MDR-SP) [43]	Accounting for population stratification by using principal components; significance estimation by generalized EVD	U	No	D	No
Pair-wise MDR (PW-MDR) [44]	Handling of sparse/empty cells by reducing contingency tables to all possible two-dimensional interactions	U	No	D	Yes	Kidney transplant [44]
Evaluation of the classification result
Extended MDR (EMDR) [45]	Evaluation of final model by ${\chi }^2$ statistic; consideration of different permutation strategies	U	No	D	No
Different phenotypes or data structures
Survival Dimensionality Reduction (SDR) [46]	Classification based on differences between cell and whole population survival estimates; IBS to evaluate models	U	No	S	No	Rheumatoid arthritis [46]
Survival MDR (Surv-MDR) [47]	Log-rank test to classify cells; squared log-rank statistic to evaluate models	U	No	S	No	Bladder cancer [47]
Quantitative MDR (QMDR) [48]	Handling of quantitative phenotypes by comparing cell with overall mean; $t$-test to evaluate models	U	No	Q	No	Renal and Vascular End-Stage Disease [48]
Ordinal MDR (Ord-MDR) [49]	Handling of phenotypes with >2 classes by assigning each cell to most likely phenotypic class	U	No	O	No	Obesity [49]
MDR with Pedigree Disequilibrium Test (MDR-PDT) [50]	Handling of extended pedigrees using pedigree disequilibrium test	F	No	D	No	Alzheimer’s disease [50]
MDR with Phenomic Analysis (MDR-Phenomics) [51]	Handling of trios by comparing number of times genotype is transmitted versus not transmitted to affected child; analysis of variance model to assesses effect of PC	F	No	D	No	Autism [51]
Aggregated MDR (A-MDR) [52]	Defining significant models using threshold maximizing area under ROC curve; aggregated risk score based on all significant models	U	No	D	No	Juvenile idiopathic arthritis [52]
Model-based MDR (MB-MDR) [53]	Test of each cell versus all others using association test statistic; association test statistic comparing pooled high-risk and pooled low-risk cells to evaluate models	U	No	D, Q, S	No	Bladder cancer [53, 54], Crohn’s disease [55, 56], blood pressure [57]

Cov = Covariate adjustment possible, Pheno = Possible phenotypes with D = Dichotomous, Q = Quantitative, S = Survival, MV = Multivariate, O = Ordinal.

Data structures: F = Family based, U = Unrelated samples.

^aBasically, MDR-based methods are designed for small sample sizes, but some methods provide special approaches to deal with sparse or empty cells, typically arising when analyzing very small sample sizes.

In the first section, the original MDR method will be described. Different modifications or extensions to that focus on different aspects of the original approach; hence, they will be grouped accordingly and presented in the following sections. Distinctive characteristics and implementations are listed in Tables 1 and 2.

Table 2.

Implementations of MDR-based methods

Method	Ref	Implementation	URL	Consist/Sig	Cov
MDR	[62, 63]	Java	www.epistasis.org/software.html	k-fold CV	Yes
	[64]	R	Available upon request, contact authors	k-fold CV, bootstrapping	No
	[65, 66]	Java	sourceforge.net/projects/mdr/files/mdrpt/	k-fold CV, permutation	No
	[67, 68]	R	cran.r-project.org/web/packages/MDR/index.html	k-fold CV, 3WS, permutation	No
	[69]	C++/CUDA	sourceforge.net/projects/mdr/files/mdrgpu/	k-fold CV, permutation	No
	[70]	C++	ritchielab.psu.edu/software/mdr-download	k-fold CV, permutation	No
GMDR	[12]	Java	www.medicine.virginia.edu/clinical/departments/psychiatry/sections/neurobiologicalstudies/genomics/gmdr-software-request	k-fold CV	Yes
PGMDR	[34]	Java	www.medicine.virginia.edu/clinical/departments/psychiatry/sections/neurobiologicalstudies/genomics/pgmdr-software-request	k-fold CV	Yes
SVM-GMDR	[35]	MATLAB	Available upon request, contact authors	k-fold CV, permutation	Yes
RMDR	[39]	Java	www.epistasis.org/software.html	k-fold CV, permutation	Yes
OR-MDR	[41]	R	Available upon request, contact authors	k-fold CV, bootstrapping	No
Opt-MDR	[42]	C++	home.ustc.edu.cn/∼zhanghan/ocp/ocp.html	GEVD	No
SDR	[46]	Python	sourceforge.net/projects/sdrproject/	k-fold CV, permutation	No
Surv-MDR	[47]	R	Available upon request, contact authors	k-fold CV, permutation	Yes
QMDR	[48]	Java	www.epistasis.org/software.html	k-fold CV, permutation	Yes
Ord-MDR	[49]	C++	Available upon request, contact authors	k-fold CV, permutation	No
MDR-PDT	[50]	C++	ritchielab.psu.edu/software/mdr-download	k-fold CV, permutation	No
MB-MDR	[55, 71, 72]	C++	www.statgen.ulg.ac.be/software.html	Permutation	No
	[73]	R	cran.r-project.org/web/packages/mbmdr/index.html	Permutation	Yes
	[74]	R	www.statgen.ulg.ac.be/software.html	Permutation	Yes

Ref = Reference, Cov = Covariate adjustment possible, Consist/Sig = Strategies used to determine the consistency or significance of model.

The original MDR method

Method

Multifactor dimensionality reduction

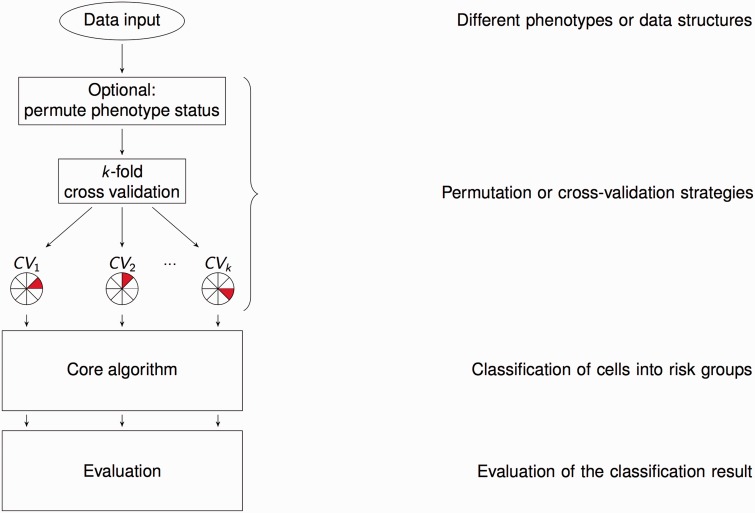
The original MDR method was first described by Ritchie et al. [2] for case-control data, and the overall workflow is shown in Figure 3 (left-hand side). The main idea is to reduce the dimensionality of multi-locus information by pooling multi-locus genotypes into high-risk and low-risk groups, thus reducing to a one-dimensional variable. Cross-validation (CV) and permutation testing is used to assess its ability to classify and predict disease status. For CV, the data are split into $k$ roughly equally sized parts. The MDR models are developed for each of the possible $\raisebox{1ex}{$k-1$}\!\left/ \!\raisebox{-1ex}{$k$}\right.$ of individuals (training sets) and are used on each remaining $1/k$ of individuals (testing sets) to make predictions about the disease status.

Figure 3.

Overview of the original MDR algorithm as described in [2] on the left with categories of extensions or modifications on the right. The first stage is data input, and extensions to the original MDR method dealing with other phenotypes or data structures are presented in the section ‘Different phenotypes or data structures’. The second stage comprises CV and permutation loops, and approaches addressing this stage are given in section ‘Permutation and cross-validation strategies’. The following stages encompass the core algorithm (see Figure 4 for details), which classifies the multifactor combinations into risk groups, and the evaluation of this classification (see Figure 5 for details). Methods, extensions and approaches mainly addressing these stages are described in sections ‘Classification of cells into risk groups’ and ‘Evaluation of the classification result’, respectively.

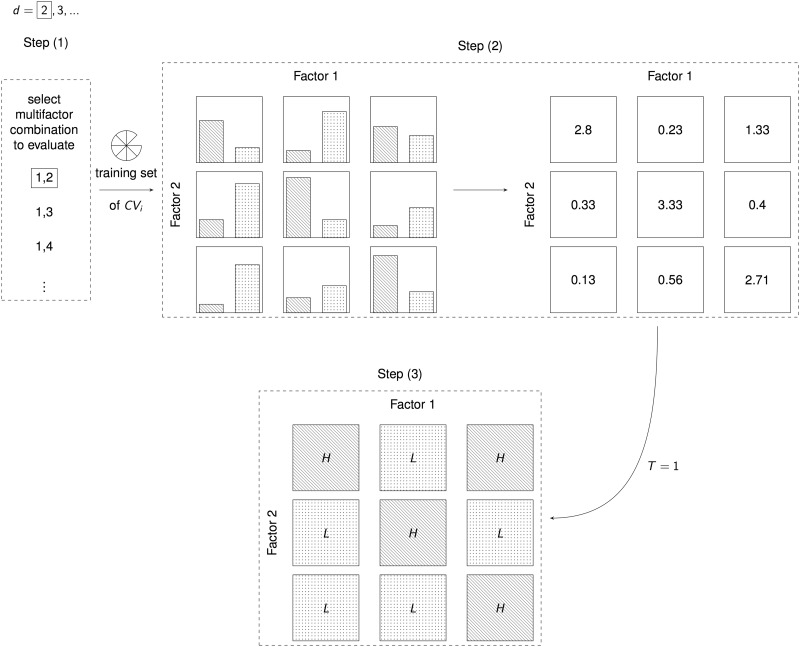
Three steps can describe the core algorithm (Figure 4):

1. Select $d$ factors, genetic or discrete environmental, with $l_i, i=1,\dots ,d$, levels from $N$ factors in total;

2. within the current training set, represent the selected factors in $d$-dimensional space and estimate the case ($n_1$) to control ($n_0$) ratio $r_j=\frac{n_{1_j}}{n_{0_j}}$ in each cell $c_j, j=1,\dots ,\prod _{i=1}^d{l}_i$; and

3. label $c_j$ as high risk ($H$), if $r_j$ exceeds some threshold $T$ (e.g. $T=1$ for balanced data sets) or as low risk otherwise.

Figure 4.

The MDR core algorithm as described in [2]. The following steps are executed for every number of factors ($d$). (1) From the exhaustive list of all possible $d$-factor combinations select one. (2) Represent the selected factors in $d$-dimensional space and estimate the cases to controls ratio in the training set. (3) A cell is labeled as high risk ($H$) if the ratio exceeds some threshold ($T$) or as low risk otherwise.

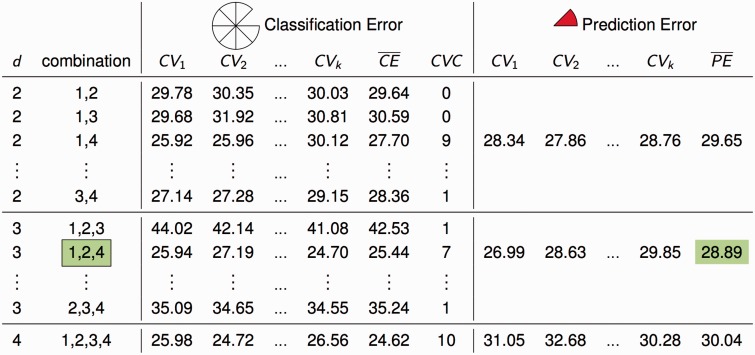
These three steps are performed in all CV training sets for each of all possible $d$-factor combinations. The models developed by the core algorithm are evaluated by CV consistency ($CVC$), classification error ($CE$) and prediction error ($PE$) (Figure 5). For each $d=1,\dots ,N$, a single model, i.e. combination, that minimizes the average classification error ($\overline{CE}$) across the CEs in the CV training sets on this level is selected. Here, $CE$ is defined as the proportion of misclassified individuals in the training set. The number of training sets in which a specific model has the lowest $CE$ determines the $CVC$. This results in a list of best models, one for each value of $d$. Among these best classification models, the one that minimizes the average prediction error ($\overline{PE}$) across the PEs in the CV testing sets is selected as final model. Analogous to the definition of the $CE$, the $PE$ is defined as the proportion of misclassified individuals in the testing set. The $CVC$ is used to determine statistical significance by a Monte Carlo permutation strategy.

Figure 5.

Evaluation of cell classification as described in [2]. The accuracy of every $d$-model, i.e. $d$-factor combination, is assessed in terms of classification error (CE), cross-validation consistency ($CVC$) and prediction error (PE). Among all $d$-models the single model with lowest average CE is selected, yielding a set of best models for each $d$. Among these best models the one minimizing the average PE is selected as final model. To determine statistical significance, the observed $CVC$ is compared to the empirical distribution of $CVC$ under the null hypothesis of no interaction derived by random permutations of the phenotypes.

The original method described by Ritchie et al. [2] needs a balanced data set, i.e. same number of cases and controls, with no missing values in any factor. To overcome the latter limitation, Hahn et al. [75] proposed to add an additional level for missing data to each factor.

The problem of imbalanced data sets is addressed by Velez et al. [62]. They evaluated three methods to prevent MDR from emphasizing patterns that are relevant for the larger set: (1) over-sampling, i.e. resampling the smaller set with replacement; (2) under-sampling, i.e. randomly removing samples from the larger set; and (3) balanced accuracy (BA) with and without an adjusted threshold. Here, the accuracy of a factor combination is not evaluated by $(1-CE)$ but by the BA as $(sensitivity+specifity)/2$, so that errors in both classes receive equal weight regardless of their size. The adjusted threshold $T_{adj}$ is the ratio between cases and controls in the complete data set. Based on their results, using the BA together with the adjusted threshold is recommended.

Extensions and modifications of the original MDR

In the following sections, we will describe the different groups of MDR-based approaches as outlined in Figure 3 (right-hand side). In the first group of extensions, the core is a different approach to classify multifactor categories into risk groups (step 3 of the above algorithm). This group comprises, among others, the generalized MDR (GMDR) approach. In another group of methods, the evaluation of this classification result is modified. The focus of the third group is on alternatives to the original permutation or CV strategies. The fourth group consists of approaches that were suggested to accommodate different phenotypes or data structures. Finally, the model-based MDR (MB-MDR) is a conceptually different approach incorporating modifications to all of the described steps simultaneously; thus, MB-MDR framework is presented as the final group.

It should be noted that many of the approaches do not tackle one single issue and thus could find themselves in more than one group. To simplify the presentation, however, we aimed at identifying the core modification of every approach and grouping the methods accordingly.

Classification of cells into risk groups

The GMDR framework

Generalized MDR

As Lou et al. [12] note, the original MDR method has two drawbacks. First, one cannot adjust for covariates; second, only dichotomous phenotypes can be analyzed. They therefore propose a GMDR framework, which offers adjustment for covariates, coherent handling for both dichotomous and continuous phenotypes and applicability to a variety of population-based study designs. The original MDR can be viewed as a special case within this framework.

The workflow of GMDR is identical to that of MDR, but instead of using the ratio of cases to controls to label each cell and assess $CE$ and $PE$, a score is calculated for every individual as follows: Given a generalized linear model (GLM) $l\left({\mu }_i\right)=\alpha +{\mathit{x}}_i^T\beta +\hspace{0.17em}{\mathit{z}}_i^T\gamma +{\mathit{x}}_i^T\otimes {\mathit{z}}_i^T\delta$ with an appropriate link function $l$, where ${\mathit{x}}_i^T$ codes the interaction effects of interest (8 degrees of freedom in case of a 2-order interaction and bi-allelic SNPs), ${\mathit{z}}_i^T$ codes the covariates and ${\mathit{x}}_i^T\otimes {\mathit{z}}_i^T$ codes the interaction between the interaction effects of interest and covariates. Then, the residual score of each individual $i$ can be calculated by $S_i=y_i-l^{-1}(\widehat{{\mu }_i})$, where $\widehat{{\mu }_i}$ is the estimated phenotype using the maximum likelihood estimations $\widehat{\alpha }$ and $\widehat{\gamma }$ under the null hypothesis of no interaction effects ($\beta =\delta =0).$

Within each cell, the average score of all individuals with the respective factor combination is calculated and the cell is labeled as high risk if the average score exceeds some threshold $T$, low risk otherwise. Significance is evaluated by permutation.

Given a balanced case-control data set without any covariates and setting $T=0$, GMDR is equivalent to MDR.

There are several extensions within the suggested framework, enabling the application of GMDR to family-based study designs, survival data and multivariate phenotypes by implementing different models for the score per individual.

Pedigree-based GMDR

In the first extension, the pedigree-based GMDR (PGMDR) by Lou et al. [34], the score statistic ${\mathit{s}}_{ij}=t_{ij}\left({\mathit{g}}_{ij}-{\overline{\mathit{g}}}_{ij}\right)$ uses both the genotypes of non-founders $j$ (${\mathit{g}}_{ij}$) and those of their ‘pseudo non-transmitted sibs’, i.e. a virtual individual with the corresponding non-transmitted genotypes (${\overline{\mathit{g}}}_{ij}$) of family $i$. In other words, PGMDR transforms family data into a matched case-control data. If transmitted and non-transmitted genotypes are the same, the individual is uninformative and the score ${\mathit{s}}_{ij}$ is $0$, otherwise the transmitted and non-transmitted contribute $t_{ij}$ and $-t_{ij}$ to the corresponding components of ${\mathit{s}}_{ij}$. To allow for covariate adjustment or other coding of the phenotype, $t_{ij}$ can be based on a GLM as in GMDR. Under the null hypotheses of no association, transmitted and non-transmitted genotypes are equally frequently transmitted so that ${\mathit{s}}_{ij}=0$. As in GMDR, if the average score statistics per cell exceed some threshold $T$, it is labeled as high risk.

Obviously, creating a ‘pseudo non-transmitted sib’ doubles the sample size resulting in higher computational and memory burden. Therefore, Chen et al. [76] proposed a second version of PGMDR, which calculates the score statistic ${\mathit{s}}_{ij}$ on the observed samples only. The non-transmitted pseudo-samples contribute to construct the genotypic distribution under the null hypothesis. Simulations show that the second version of PGMDR is similar to the first one in terms of power for dichotomous traits and advantageous over the first one for continuous traits.

Support vector machine PGMDR

To improve performance when the number of available samples is small, Fang and Chiu [35] replaced the GLM in PGMDR by a support vector machine (SVM) to estimate the phenotype per individual. The score per cell in SVM-PGMDR is based on genotypes transmitted and non-transmitted to offspring in trios, and the difference of genotype combinations in discordant sib pairs is compared with a specified threshold to determine the risk label.

Unified GMDR

The unified GMDR (UGMDR), proposed by Chen et al. [36], offers simultaneous handling of both family and unrelated data. They use the unrelated samples and unrelated founders to infer the population structure of the entire sample by principal component analysis. The top components and possibly other covariates are used to adjust the phenotype of interest by fitting a GLM. The adjusted phenotype is then used as score for unrelated subjects including the founders, i.e. $s_{ij}={\tilde{y}}_{ij}$. For offspring, the score is multiplied with the contrasted genotype as in PGMDR, i.e. $s_{ij}={\tilde{y}}_{ij}\left({\mathit{g}}_{ij}-{\overline{\mathit{g}}}_{ij}\right)$. The scores per cell are averaged and compared with $T$, which is in this case defined as the mean score of the complete sample. The cell is labeled as high risk if the average score of the cell is above the mean score, as low risk otherwise.

Cox-MDR

In another line of extending GMDR, survival data can be analyzed with Cox-MDR [37]. The continuous survival time is transformed into a dichotomous attribute by considering the martingale residual from a Cox null model with no gene–gene or gene–environment interaction effects but covariate effects. Then the martingale residuals reflect the association of these interaction effects on the hazard rate. Individuals with a positive martingale residual are classified as cases, those with a negative one as controls. The multifactor cells are labeled depending on the sum of martingale residuals with corresponding factor combination. Cells with a positive sum are labeled as high risk, others as low risk.

Multivariate GMDR

Finally, multivariate phenotypes can be assessed by multivariate GMDR (MV-GMDR), proposed by Choi and Park [38]. In this approach, a generalized estimating equation is used to estimate the parameters and residual score vectors of a multivariate GLM under the null hypothesis of no gene–gene or gene–environment interaction effects but accounting for covariate effects. Aggregation of the elements of the score vector gives a prediction score per individual. The sum over all prediction scores of individuals with a certain factor combination compared with a threshold $T$ determines the label of each multifactor cell.

Further approaches

In addition to the GMDR, other methods were suggested that handle limitations of the original MDR to classify multifactor cells into high and low risk under certain circumstances.

Robust MDR

The Robust MDR extension (RMDR), proposed by Gui et al. [39], addresses the situation with sparse or even empty cells and those with a case-control ratio equal or close to $T$. These conditions result in a BA near $0.5$ in these cells, negatively influencing the overall fitting. The solution proposed is the introduction of a third risk group, called ‘unknown risk’, which is excluded from the BA calculation of the single model. Fisher’s exact test is used to assign each cell to a corresponding risk group: If the $P$-value is greater than $\alpha$, it is labeled as ‘unknown risk’. Otherwise, the cell is labeled as high risk or low risk depending on the relative number of cases and controls in the cell. Leaving out samples in the cells of unknown risk may lead to a biased BA, so the authors propose to adjust the BA by the ratio of samples in the high- and low-risk groups to the total sample size. The other aspects of the original MDR method remain unchanged.

Log-linear model MDR

Another approach to deal with empty or sparse cells is proposed by Lee et al. [40] and called log-linear models MDR (LM-MDR). Their modification uses LM to reclassify the cells of the best combination of factors, obtained as in the classical MDR. All possible parsimonious LM are fit and compared by the goodness-of-fit test statistic. The expected number of cases and controls per cell are provided by maximum likelihood estimates of the selected LM. The final classification of cells into high and low risk is based on these expected numbers. The original MDR is a special case of LM-MDR if the saturated LM is selected as fallback if no parsimonious LM fits the data sufficient.

Odds ratio MDR

The naïve Bayes classifier used by the original MDR method is replaced in the work of Chung et al. [41] by the odds ratio (OR) of each multi-locus genotype to classify the corresponding cell as high or low risk. Accordingly, their method is called Odds Ratio MDR (OR-MDR). Their approach addresses three drawbacks of the original MDR method. First, the original MDR method is prone to false classifications if the ratio of cases to controls is similar to that in the entire data set or the number of samples in a cell is small. Second, the binary classification of the original MDR method drops information about how well low or high risk is characterized. From this follows, third, that it is not possible to identify genotype combinations with the highest or lowest risk, which might be of interest in practical applications. The authors propose to estimate the OR of each cell by ${\widehat{\theta }}_j=\frac{\raisebox{1ex}{$n_{1_j}$}\!\left/ \!\raisebox{-1ex}{$n_1$}\right.}{\raisebox{1ex}{$n_{0_j}$}\!\left/ \!\raisebox{-1ex}{$n_0$}\right.}$. If ${\widehat{\theta }}_j$ exceeds a threshold $T$, the corresponding cell is labeled as high risk, otherwise as low risk. If $T=1$, MDR is a special case of OR-MDR. Based on ${\widehat{\theta }}_j$, the multi-locus genotypes can be ordered from highest to lowest OR. Additionally, cell-specific confidence intervals for ${\widehat{\theta }}_j$ can be approximated either by usual asymptotic methods or by bootstrapping, hence giving evidence for a truly low- or high-risk factor combination. Significance of a model still can be assessed by a permutation strategy based on $CVC$.

Optimal MDR

Another approach, called optimal MDR (Opt-MDR), was proposed by Hua et al. [42]. Their method uses a data-driven instead of a fixed threshold to collapse the factor combinations. This threshold is chosen to maximize the ${\chi }^2$ values among all possible $2\times 2$ (case-control$\times$high-low risk) tables for each factor combination. The exhaustive search for the maximum ${\chi }^2$ values can be done efficiently by sorting factor combinations according to the ascending risk ratio and collapsing successive ones only. This reduces the search space from $2^{\prod _{i=1}^d{l}_i-1}$ possible $2\times 2$ tables to $\prod _{i=1}^d{l}_i-1$. In addition, the $CVC$ permutation-based estimation of the $P$-value is replaced by an approximated $P$-value from a generalized extreme value distribution (EVD), similar to an approach by Pattin et al. [65] described later.

MDR stratified populations

Significance estimation by generalized EVD is also used by Niu et al. [43] in their approach to control for population stratification in case-control and continuous traits, namely, MDR for stratified populations (MDR-SP). MDR-SP uses a set of unlinked markers to calculate the principal components that are considered as the genetic background of samples. Based on the first $K$ principal components, the residuals of the trait value ($y_i^{*}$) and genotype ($x_{ij}^{*}$) of the samples are calculated by linear regression, thus adjusting for population stratification. Thus, the adjustment in MDR-SP is used in each multi-locus cell. Then the test statistic $T_j^2$ per cell is the correlation between the adjusted trait value and genotype. If $T_j^2>0$, the corresponding cell is labeled as high risk, or as low risk otherwise. Based on this labeling, the trait value for each sample is predicted (${\widehat{y}}_i$) for every sample. The training error, defined as $\sum _{i in training data set}{\left({\widehat{y}}_i-y_i^{*}\right)}^2/\sum _{i in training data set}{\left(y_i^{*}\right)}^2$, is used to identify the best $d$-marker model; specifically, the model with the smallest average $PE$, defined as $\sum _{i in testing data set}{\left({\widehat{y}}_i-y_i^{*}\right)}^2/\sum _{i in testing data set}{(y_i^{*})}^2$ in CV, is selected as final model with its average $PE$ as test statistic.

Pair-wise MDR

In high-dimensional ($d>2)$ contingency tables, the original MDR method suffers in the scenario of sparse cells that are not classifiable. The pair-wise MDR (PWMDR) proposed by He et al. [44] models the interaction between $d$ factors by $(\begin{array}{c}d\\ 2\end{array})$ two-dimensional interactions. The cells in every two-dimensional contingency table are labeled as high or low risk depending on the case-control ratio. For every sample, a cumulative risk score is calculated as number of high-risk cells minus number of low-risk cells over all two-dimensional contingency tables. Under the null hypothesis of no association between the selected SNPs and the trait, a symmetric distribution of cumulative risk scores around zero is expected in cases as well as in controls. In case of an interaction effect, the distribution in cases will tend toward positive cumulative risk scores, whereas it will tend toward negative cumulative risk scores in controls. Hence, a sample is classified as a case if it has a positive cumulative risk score and as a control if it has a negative cumulative risk score. Based on this classification, the training and $PE$ can be calculated in CV. The statistical significance of a model can be assessed by a permutation strategy based on the $PE$.

Evaluation of the classification result

One essential part of the original MDR is the evaluation of factor combinations regarding the correct classification of cases and controls into high- and low-risk groups, respectively. For each model, a $2\times 2$ contingency table (also called confusion matrix), summarizing the true negatives (TN), true positives (TP), false negatives (FN) and false positives (FP), can be created. As mentioned before, the power of MDR can be improved by implementing the BA instead of raw accuracy, if dealing with imbalanced data sets.

In the study of Bush et al. [77], 10 different measures for classification were compared with the standard CE used in the original MDR method. They encompass precision-based and receiver operating characteristics (ROC)-based measures (F-measure, geometric mean of sensitivity and precision, geometric mean of sensitivity and specificity, Euclidean distance from an ideal classification in ROC space), diagnostic testing measures (Youden Index, Predictive Summary Index), statistical measures (Pearson’s χ² goodness-of-fit statistic, likelihood-ratio test) and information theoretic measures (Normalized Mutual Information, Normalized Mutual Information Transpose). Based on simulated balanced data sets of 40 different penetrance functions in terms of number of disease loci (2–5 loci), heritability (0.5–3%) and minor allele frequency (MAF) (0.2 and 0.4), they assessed the power of the different measures. Their results show that Normalized Mutual Information (NMI) and likelihood-ratio test (LR) outperform the standard CE and the other measures in most of the evaluated situations. Both of these measures take into account the sensitivity and specificity of an MDR model, thus should not be susceptible to class imbalance. Out of these two measures, NMI is easier to interpret, as its values range from 0 (genotype and disease status independent) to 1 (genotype completely determines disease status). $P$-values can be calculated from the empirical distributions of the measures obtained from permuted data.

Namkung et al. [78] take up these results and compare BA, NMI and LR with a weighted BA (wBA) and several measures for ordinal association. The wBA, inspired by OR-MDR [41], incorporates weights based on the ORs per multi-locus genotype: $w_j={\left|\log {\widehat{\theta }}_j\right|}^{\alpha }, {\widehat{\theta }}_j=\frac{\raisebox{1ex}{$n_{1_j}$}\!\left/ \!\raisebox{-1ex}{$n_{0_j}$}\right.}{\raisebox{1ex}{$n_1$}\!\left/ \!\raisebox{-1ex}{$n_0$}\right.}$. The number of cases and controls in each cell $c_j$ is adjusted by the respective weight, and the BA is calculated using these adjusted numbers. Adding a small constant should prevent practical problems of infinite and zero weights. In this way, the effect of a multi-locus genotype on disease susceptibility is captured. Measures for ordinal association are based on the assumption that good classifiers produce more TN and TP than FN and FP, thus resulting in a stronger positive monotonic trend association. The possible combinations of TN and TP (FN and FP) define the concordant (discordant) pairs, and the $\gamma$-measure estimates the difference between the probability of concordance and the probability of discordance: $\gamma =\frac{TP·TN-FP·FN}{TP·TN+FP·FN}$. The other measures assessed in their study, Kandal’s ${\tau }_b$, Kandal’s ${\tau }_c$ and Somers’ $d$, are variants of the $\gamma$-measure, adjusting the effects of tied pairs or table size. Comparisons of all these measures on a simulated data sets regarding power show that ${\tau }_c$ has similar power to BA, Somers’ $d$ and $\gamma$ perform worse and wBA, ${\tau }_c$, NMI and LR improve MDR performance over all simulated scenarios. The improvement is larger in scenarios with small sample sizes, larger numbers of SNPs or with small causal effects. Among these measures, wBA outperforms all others.

Two other measures are proposed by Fisher et al. [79]. Their metrics do not incorporate the contingency table but use the fraction of cases and controls in each cell of a model directly. Their Variance Metric (VM) for a model is defined as ${\sum }_{j=1}^{{\prod }_{i=1}^d{l}_i}\raisebox{1ex}{$n_j$}\!\left/ \!\raisebox{-1ex}{$n$}\right.{(\raisebox{1ex}{$n_{j_1}$}\!\left/ \!\raisebox{-1ex}{$n_j$}\right.-\raisebox{1ex}{$n_1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.)}^2$, measuring the difference in case fractions between cell level and sample level weighted by the fraction of individuals in the respective cell. For the Fisher Metric (FM), a Fisher’s exact test is applied per cell on $\left(\begin{array}{cc}{n}_{j_1}& n_1-n_{j_1}\\ n_{j_0}& n_0-n_{j_0}\end{array}\right)$, yielding a $P$-value $p_j$, which reflects how unusual each cell is. For a model, these probabilities are combined as ${\sum }_{j=1}^{{\prod }_{i=1}^d{l}_i}-2\log p_j$. The higher both metrics are the more likely it is that a corresponding model represents an underlying biological phenomenon. Comparisons of these two measures with BA and NMI on simulated data sets also used in [62] show that in most situations VM and FM perform significantly better.

Most applications of MDR are realized in a retrospective design. Thus, cases are overrepresented and controls are underrepresented compared with the true population, resulting in an artificially high prevalence. This raises the question whether the MDR estimates of error are biased or are truly appropriate for prediction of the disease status given a genotype. Winham and Motsinger-Reif [64] argue that this approach is appropriate to retain high power for model selection, but prospective prediction of disease gets more challenging the further the estimated prevalence of disease is away from 50% (as in a balanced case-control study). The authors recommend using a post hoc prospective estimator for prediction. They propose two post hoc prospective estimators, one estimating the error from bootstrap resampling ($C{E}_{boot}$), the other one by adjusting the original error estimate by a reasonably accurate estimate for population prevalence ${\widehat{p}}_D$($C{E}_{adj}$). For $C{E}_{boot}$, $N$ bootstrap resamples of the same size as the original data set are created by randomly sampling cases at rate ${\widehat{p}}_D$ and controls at rate $1-{\widehat{p}}_D$. For each bootstrap sample the previously determined final model is reevaluated, defining high-risk cells with sample prevalence greater than ${\hat{p}}_D$, with $C{E}_{boo{t}_i}=\frac{1}{n}\left(\text{FP}+\text{FN}\right), i=1,\dots ,N$. The final estimate of $C{E}_{boot}$is the average over all $C{E}_{boo{t}_i}$. The adjusted original error estimate is calculated as $C{E}_{adj}=\frac{1}{n}(\frac{1-{\widehat{p}}_D}{\raisebox{1ex}{$n_0$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}·\text{FP}+\frac{{\widehat{p}}_D}{\raisebox{1ex}{$n_1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}·\text{FN})$. A simulation study shows that both $C{E}_{boot}$ and $C{E}_{adj}$ have lower prospective bias than the original $CE$, but $C{E}_{adj}$ has an extremely high variance for the additive model. Hence, the authors recommend the use of $C{E}_{boot}$ over $C{E}_{adj}$.

Extended MDR

The extended MDR (EMDR), proposed by Mei et al. [45], evaluates the final model not only by the $PE$ but additionally by the ${\chi }^2$ statistic measuring the association between risk label and disease status. Furthermore, they evaluated three different permutation procedures for estimation of $P$-values and using 10-fold CV or no CV. The fixed permutation test considers the final model only and recalculates the PE and the ${\chi }^2$ statistic for this specific model only in the permuted data sets to derive the empirical distribution of those measures. The non-fixed permutation test takes all possible models of the same number of factors as the selected final model into account, thus producing a separate null distribution for each $d$-level of interaction. The third permutation test is the standard method used in the original MDR (omnibus permutation), creating a single null distribution from the best model of each randomized data set. They found that 10-fold CV and no CV are fairly consistent in identifying the best multi-locus model, contradicting the results of Motsinger and Ritchie [63] (see below), and that the non-fixed permutation test is a good trade-off between the liberal fixed permutation test and conservative omnibus permutation.

Alternatives to original permutation or CV

The non-fixed and omnibus permutation tests described above as part of the EMDR [45] were further investigated in a comprehensive simulation study by Motsinger [80]. She assumes that the final goal of an MDR analysis is hypothesis generation. Under this assumption, her results show that assigning significance levels to the models of each level $d$ based on the omnibus permutation strategy is preferred to the non-fixed permutation, because FP are controlled without limiting power.

Because the permutation testing is computationally expensive, it is unfeasible for large-scale screens for disease associations. Therefore, Pattin et al. [65] compared 1000-fold omnibus permutation test with hypothesis testing using an EVD. The accuracy of the final best model selected by MDR is a maximum value, so extreme value theory might be applicable. They used 28 000 functional and 28 000 null data sets consisting of 20 SNPs and 2000 functional and 2000 null data sets consisting of 1000 SNPs based on 70 different penetrance function models of a pair of functional SNPs to estimate type I error frequencies and power of both 1000-fold permutation test and EVD-based test. Additionally, to capture more realistic correlation patterns and other complexities, pseudo-artificial data sets with a single functional factor, a two-locus interaction model and a mixture of both were created. Based on these simulated data sets, the authors verified the EVD assumption of independent and identically distributed (IID) observations with quantile–quantile plots. Despite the fact that all their data sets do not violate the IID assumption, they note that this might be a problem for other real data and refer to more robust extensions to the EVD. Parameter estimation for the EVD was realized with 20-, 10- and 5-fold permutation testing. Their results show that using an EVD generated from 20 permutations is an adequate alternative to omnibus permutation testing, so that the required computational time thus can be reduced importantly.

One major drawback of the omnibus permutation strategy used by MDR is its inability to differentiate between models capturing nonlinear interactions, main effects or both interactions and main effects. Greene et al. [66] proposed a new explicit test of epistasis that provides a $P$-value for the nonlinear interaction of a model only. Grouping the samples by their case-control status and randomizing the genotypes of each SNP within each group accomplishes this. Their simulation study, similar to that by Pattin et al. [65], shows that this approach preserves the power of the omnibus permutation test and has a reasonable type I error frequency. One disadvantage of their approach is the additional computational burden resulting from permuting not only the class labels but all genotypes.

The internal validation of a model based on CV is computationally expensive. The original description of MDR recommended a 10-fold CV, but Motsinger and Ritchie [63] analyzed the impact of eliminated or reduced CV. They found that eliminating CV made the final model selection impossible. However, a reduction to 5-fold CV reduces the runtime without losing power.

The proposed method of Winham et al. [67] uses a three-way split (3WS) of the data. One piece is used as a training set for model building, one as a testing set for refining the models identified in the first set and the third is used for validation of the selected models by obtaining prediction estimates. In detail, the top $x$ models for each $d$ in terms of BA are identified in the training set. In the testing set, these top models are ranked again in terms of BA and the single best model for each $d$ is selected. These best models are finally evaluated in the validation set, and the one maximizing the BA (predictive ability) is chosen as the final model. Because the BA increases for larger $d$, MDR using 3WS as internal validation tends to over-fitting, which is alleviated by using $CVC$ and choosing the parsimonious model in case of equal $CVC$ and $PE$ in the original MDR. The authors propose to address this problem by using a post hoc pruning process after the identification of the final model with 3WS. In their study, they use backward model selection with logistic regression. Using an extensive simulation design, Winham et al. [67] assessed the impact of different split proportions, values of $x$ and selection criteria for backward model selection on conservative and liberal power. Conservative power is described as the ability to discard false-positive loci while retaining true associated loci, whereas liberal power is the ability to identify models containing the true disease loci regardless of FP. The results of the simulation study show that a proportion of 2:2:1 of the split maximizes the liberal power, and both power measures are maximized using x = #loci. Conservative power using post hoc pruning was maximized using the Bayesian information criterion (BIC) as selection criteria and not significantly different from 5-fold CV. It is important to note that the choice of selection criteria is rather arbitrary and depends on the specific goals of a study. Using MDR as a screening tool, accepting FP and minimizing FN prefers 3WS without pruning. Using MDR 3WS for hypothesis testing favors pruning with backward selection and BIC, yielding equivalent results to MDR at lower computational costs. The computation time using 3WS is approximately five time less than using 5-fold CV. Pruning with backward selection and a $P$-value threshold between $0.01$ and $0.001$ as selection criteria balances between liberal and conservative power.

As a side effect of their simulation study, the assumptions that 5-fold CV is sufficient rather than 10-fold CV and addition of nuisance loci do not affect the power of MDR are validated. MDR performs poorly in case of genetic heterogeneity [81, 82], and using 3WS MDR performs even worse as Gory et al. [83] note in their study. If genetic heterogeneity is suspected, using MDR with CV is recommended at the expense of computation time.

Different phenotypes or data structures

In its original form, MDR was described for dichotomous traits only. Some extensions to different phenotypes have already been described above under the GMDR framework but several extensions on the basis of the original MDR have been proposed additionally.

Survival Dimensionality Reduction

For right-censored lifetime data, Beretta et al. [46] proposed the Survival Dimensionality Reduction (SDR). Their method replaces the classification and evaluation steps of the original MDR method. Classification into high- and low-risk cells is based on differences between cell survival estimates and whole population survival estimates. If the averaged (geometric mean) normalized time-point differences are smaller than $1$, the cell is labeled as high risk, otherwise as low risk. To measure the accuracy of a model, the integrated Brier score (IBS) is used. During CV, for each $d$ the IBS is calculated in each training set, and the model with the lowest IBS on average is selected. The testing sets are merged to obtain one larger data set for validation. In this meta-data set, the IBS is calculated for each prior selected best model, and the model with the lowest meta-IBS is selected final model. Statistical significance of the meta-IBS score of the final model can be calculated via permutation. Simulation studies show that SDR has reasonable power to detect nonlinear interaction effects.

Surv-MDR

A second method for censored survival data, called Surv-MDR [47], uses a log-rank test to classify the cells of a multifactor combination. The log-rank test statistic comparing the survival time between samples with and without the specific factor combination is calculated for every cell. If the statistic is positive, the cell is labeled as high risk, otherwise as low risk. As for SDR, BA cannot be used to assess the quality of a model. Instead, the square of the log-rank statistic is used to choose the best model in training sets and validation sets during CV. Statistical significance of the final model can be calculated via permutation. Simulations showed that the power to identify interaction effects with Cox-MDR and Surv-MDR greatly depends on the effect size of additional covariates. Cox-MDR is able to recover power by adjusting for covariates, whereas Surv-MDR lacks such an option [37].

Quantitative MDR

Quantitative phenotypes can be analyzed with the extension quantitative MDR (QMDR) [48]. For cell classification, the mean of each cell is calculated and compared with the overall mean in the complete data set. If the cell mean is greater than the overall mean, the corresponding genotype is considered as high risk and as low risk otherwise. Clearly, BA cannot be used to assess the relation between the pooled risk classes and the phenotype. Instead, both risk classes are compared using a $t$-test and the test statistic is used as a score in training and testing sets during CV. This assumes that the phenotypic data follows a normal distribution. A permutation strategy can be incorporated to yield $P$-values for final models. Their simulations show a comparable performance but less computational time than for GMDR. They also hypothesize that the null distribution of their scores follows a normal distribution with mean 0, thus an empirical null distribution could be used to estimate the $P$-values, reducing the computational burden from permutation testing.

Ord-MDR

A natural generalization of the original MDR is provided by Kim et al. [49] for ordinal phenotypes with $l$ classes, called Ord-MDR. Each cell $c_j$ is assigned to the phenotypic class that maximizes $\raisebox{1ex}{$n_l{}_j$}\!\left/ \!\raisebox{-1ex}{$n_l$}\right.$, where $n_l$ is the overall number of samples in class $l$ and $n_l{}_j$ is the number of samples in class $l$ in cell $j$. Classification can be evaluated using an ordinal association measure, such as Kendall’s ${\tau }_b.$

Additionally, Kim et al. [49] generalize the $CVC$ to report multiple causal factor combinations. The measure ${\text{GCVC}}^K$ counts how many times a certain model has been among the top $K$ models in the CV data sets according to the evaluation measure. Based on ${\text{GCVC}}^K$, multiple putative causal models of the same order can be reported, e.g. ${\text{GCVC}}^K>0$ or the 100 models with largest ${\text{GCVC}}^K.$

MDR with pedigree disequilibrium test

Although MDR is originally designed to identify interaction effects in case-control data, the use of family data is possible to a limited extent by selecting a single matched pair from each family. To profit from extended informative pedigrees, MDR was merged with the genotype pedigree disequilibrium test (PDT) [84] to form the MDR-PDT [50]. The genotype-PDT statistic is calculated for each multifactor cell and compared with a threshold, e.g. 0, for all possible $d$-factor combinations. If the test statistic is greater than this threshold, the corresponding multifactor combination is classified as high risk and as low risk otherwise. After pooling the two classes, the genotype-PDT statistic is again computed for the high-risk class, resulting in the MDR-PDT statistic. For each level of $d$, the maximum MDR-PDT statistic is selected and its significance assessed by a permutation test (non-fixed). In discordant sib ships with no parental data, affection status is permuted within families to maintain correlations between sib ships. In families with parental genotypes, transmitted and non-transmitted pairs of alleles are permuted for affected offspring with parents.

Edwards et al. [85] included a CV strategy to MDR-PDT. In contrast to case-control data, it is not straightforward to split data from independent pedigrees of various structures and sizes evenly. For each pedigree in the data set, the maximum information available is calculated as sum over the number of all possible combinations of discordant sib pairs and transmitted/non-transmitted pairs in that pedigree’s sib ships. Then the pedigrees are randomly distributed into as many parts as required for CV, and the maximum information is summed up in each part. If the variance of the sums over all parts does not exceed a certain threshold, the split is repeated or the number of parts is changed. As the MDR-PDT statistic is not comparable across levels of $d$, $PE$ or matched OR is used in the testing sets of CV as prediction performance measure, where the matched OR is the ratio of discordant sib pairs and transmitted/non-transmitted pairs correctly classified to those who are incorrectly classified. An omnibus permutation test based on $CVC$ is performed to assess significance of the final selected model.

MDR-Phenomics

An extension for the analysis of triads incorporating discrete phenotypic covariates (PC) is MDR-Phenomics [51]. This method uses two procedures, the MDR and phenomic analysis. In the MDR procedure, multi-locus combinations compare the number of times a genotype is transmitted to an affected child with the number of times the genotype is not transmitted. If this ratio exceeds the threshold $\text{T}=1.0$, the combination is classified as high risk, or as low risk otherwise. After classification, the goodness-of-fit test statistic, called $\text{C}$ statistic, is calculated, testing the association between transmitted/non-transmitted and high-risk/low-risk genotypes. The phenomic analysis procedure aims to assess the effect of PC on this association. For this, the strength of association between transmitted/non-transmitted and high-risk/low-risk genotypes in the different PC levels is compared using an analysis of variance model, resulting in an $\text{F}$ statistic. The final MDR-Phenomics statistic for each multi-locus model is the product of the $\text{C}$ and $\text{F}$ statistics, and significance is assessed by a non-fixed permutation test.

Aggregated MDR

The original MDR method does not account for the accumulated effects from multiple interaction effects, due to selection of only one optimal model during CV. The Aggregated Multifactor Dimensionality Reduction (A-MDR), proposed by Dai et al. [52], makes use of all significant interaction effects to build a gene network and to compute an aggregated risk score for prediction. Cells $c_j$ in each model are classified either as high risk if $\raisebox{1ex}{$n_{1_j}$}\!\left/ \!\raisebox{-1ex}{$n_j$}\right.$ exceeds $\raisebox{1ex}{$n_1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.$ or as low risk otherwise. Based on this classification, three measures to assess each model are proposed: predisposing OR ($O{R}_p$), predisposing relative risk ($R{R}_p$) and predisposing ${\chi }^2$(${\chi }_p^2$), which are adjusted versions of the usual statistics. The unadjusted versions are biased, as the risk classes are conditioned on the classifier. Let $x=$ OR, relative risk or χ², then OR_p, RR_p or χ²_p$=x/F_0^{-1}(F\left(x\right))$. Here, $F_0(x)$ is estimated by a permutation of the phenotype, and $F\left(x\right)$ is estimated by resampling a subset of samples. Using the permutation and resampling data, $P$-values and confidence intervals can be estimated. Instead of a fixed $\alpha =0.05$, the authors propose to select an $\widehat{\alpha }\le 0.05$ that maximizes the area under a ROC curve (AUC). For each $\widehat{\alpha }$, the models with a $P$-value less than $\widehat{\alpha }$ are selected. For each sample, the number of high-risk classes among these selected models is counted to obtain an aggregated risk score. It is assumed that cases will have a higher risk score than controls. Based on the aggregated risk scores a ROC curve is constructed, and the AUC can be determined. Once the final $\hat{\alpha }$ is fixed, the corresponding models are used to define the ‘epistasis enriched gene network’ as adequate representation of the underlying gene interactions of a complex disease and the ‘epistasis enriched risk score’ as a diagnostic test for the disease. A considerable side effect of this method is that it has a large gain in power in case of genetic heterogeneity as simulations show.

The MB-MDR framework

Model-based MDR

MB-MDR was first introduced by Calle et al. [53] while addressing some major drawbacks of MDR, including that important interactions could be missed by pooling too many multi-locus genotype cells together and that MDR could not adjust for main effects or for confounding factors. All available data are used to label each multi-locus genotype cell. The way MB-MDR carries out the labeling conceptually differs from MDR, in that each cell is tested versus all others using appropriate association test statistics, depending on the nature of the trait measurement (e.g. binary, continuous, survival). Model selection is not based on CV-based criteria but on an association test statistic (i.e. final MB-MDR test statistics) that compares pooled high-risk with pooled low-risk cells. Finally, permutation-based strategies are used on MB-MDR’s final test statistic.

Initially, MB-MDR used Wald-based association tests, three labels were introduced (High, Low, O: not H, nor L), and the raw Wald $P$-values for individuals at high risk (resp. low risk) were adjusted for the number of multi-locus genotype cells in a risk pool. MB-MDR, in this initial form, was first applied to real-life data by Calle et al. [54], who illustrated the importance of using a flexible definition of risk cells when looking for gene-gene interactions using SNP panels. Indeed, forcing every subject to be either at high or low risk for a binary trait, based on a particular multi-locus genotype may introduce unnecessary bias and is not appropriate when not enough subjects have the multi-locus genotype combination under investigation or when there is simply no evidence for increased/decreased risk. Relying on MAF-dependent or simulation-based null distributions, as well as having 2 $P$-values per multi-locus, is not convenient either. Therefore, since 2009, the use of only one final MB-MDR test statistic is advocated: e.g. the maximum of two Wald tests, one comparing high-risk individuals versus the rest, and one comparing low risk individuals versus the rest.

Since 2010, several enhancements have been made to the MB-MDR methodology [74, 86]. Key enhancements are that Wald tests were replaced by more stable score tests. Moreover, a final MB-MDR test value was obtained via multiple options that allow flexible treatment of O-labeled individuals [71]. In addition, significance assessment was coupled to multiple testing correction (e.g. Westfall and Young’s step-down MaxT [55]). Extensive simulations have shown a general outperformance of the method compared with MDR-based approaches in a variety of settings, in particular those involving genetic heterogeneity, phenocopy, or lower allele frequencies (e.g. [71, 72]). The modular built-up of the MB-MDR software makes it an easy tool to be applied to univariate (e.g., binary, continuous, censored) and multivariate traits (work in progress). It can be used with (mixtures of) unrelated and related individuals [74]. When exhaustively screening for two-way interactions with 10 000 SNPs and 1000 individuals, the recent MaxT implementation based on permutation-based gamma distributions, was shown to give a 300-fold time efficiency compared to earlier implementations [55]. This makes it possible to perform a genome-wide exhaustive screening, hereby removing one of the major remaining concerns related to its practical utility.

Recently, the MB-MDR framework was extended to analyze genomic regions of interest [87]. Examples of such regions include genes (i.e., sets of SNPs mapped to the same gene) or functional sets derived from DNA-seq experiments. The extension consists of first clustering subjects according to similar region-specific profiles. Hence, whereas in classic MB-MDR a SNP is the unit of analysis, now a region is a unit of analysis with number of levels determined by the number of clusters identified by the clustering algorithm. When applied as a tool to associate gene-based collections of rare and common variants to a complex disease trait obtained from synthetic GAW17 data, MB-MDR for rare variants belonged to the most powerful rare variants tools considered, among those that were able to control type I error.

Discussion and conclusions

When analyzing interaction effects in candidate genes on complex diseases, procedures based on MDR have become the most popular approaches over the past decade. Considering the variety of extensions and modifications, this does not come as a surprise, since there is almost one method for every taste. More recent extensions have focused on the analysis of rare variants [87] and large-scale data sets, which becomes feasible through more efficient implementations [55] as well as alternative estimations of $P$-values using computationally less expensive permutation schemes or EVDs [42, 65]. We therefore expect this line of methods to even gain in popularity. The challenge rather is to select a suitable software tool, because the various versions differ with regard to their applicability, performance and computational burden, depending on the kind of data set at hand, as well as to come up with optimal parameter settings. Ideally, different flavors of a method are encapsulated within a single software tool. MBMDR is one such tool that has made important attempts into that direction (accommodating different study designs and data types within a single framework). Some guidance to select the most suitable implementation for a particular interaction analysis setting is provided in Tables 1 and 2.

Even though there is a wealth of MDR-based methods, a number of issues have not yet been resolved. For instance, one open question is how to best adjust an MDR-based interaction screening for confounding by common genetic ancestry. It has been reported before that MDR-based methods lead to increased type I error rates in the presence of structured populations [43]. Similar observations were made regarding MB-MDR [55]. In principle, one may select an MDR method that allows for the use of covariates and then incorporate principal components adjusting for population stratification. However, this may not be adequate, since these components are typically selected based on linear SNP patterns between individuals. It remains to be investigated to what extent non-linear SNP patterns contribute to population strata that may confound a SNP-based interaction analysis. Also, a confounding factor for one SNP-pair may not be a confounding factor for another SNP-pair. A further issue is that, from a given MDR-based result, it is often difficult to disentangle main and interaction effects. In MB-MDR there is a clear option to adjust the interaction screening for lower-order effects or not, and hence to perform a global multi-locus test or a specific test for interactions. Once a statistically relevant higher-order interaction is obtained, the interpretation remains difficult. This in part due to the fact that most MDR-based methods adopt a SNP-centric view rather than a gene-centric view. Gene-based replication overcomes the interpretation difficulties that interaction analyses with tagSNPs involve [88]. Only a limited number of set-based MDR methods exist to date.

In conclusion, current large-scale genetic projects aim at collecting information from large cohorts and combining genetic, epigenetic and clinical data. Scrutinizing these data sets for complex interactions requires sophisticated statistical tools, and our overview on MDR-based approaches has shown that a variety of different flavors exists from which users may select a suitable one.

Key Points

• For the analysis of gene–gene interactions, MDR has enjoyed great popularity in applications. Focusing on different aspects of the original algorithm, multiple modifications and extensions have been suggested that are reviewed here.

• Most recent approaches offer to deal with large-scale data sets and rare variants, which is why we expect these methods to even gain in popularity.

Funding

This work was supported by the German Federal Ministry of Education and Research for IRK (BMBF, grant # 01ZX1313J). The research by JMJ and KvS was in part funded by the Fonds de la Recherche Scientifique (F.N.R.S.), in particular “Integrated complex traits epistasis kit” (Convention n° 2.4609.11).

Biographies

Damian Gola is a PhD student in Medical Biometry and Statistics at the Universität zu Lübeck, Germany. He is under the supervision of Inke R. König.

Jestinah M. Mahachie John was a researcher at the BIO3 group of Kristel van Steen at the University of Liège (Belgium). She has made significant methodological contributions to enhance epistasis-screening tools.

Kristel van Steen is an Associate Professor in bioinformatics/statistical genetics at the University of Liège and Director of the GIGA-R thematic unit of Systems Biology and Chemical Biology in Liège (Belgium). Her interest lies in methodological developments related to interactome and integrated analyses.

Inke R. König is Professor for Medical Biometry and Statistics at the Universität zu Lübeck, Germany. She is interested in genetic and clinical epidemiology and published over 190 refereed papers.