Abstract
Matching wavefront correctors and wavefront sensors by minimizing the condition number and mean wavefront variance is proposed. The particular cases of two continuous-sheet deformable mirrors and a Shack-Hartmann wavefront sensor with square packing geometry are studied in the presence of photon noise, background noise and electronics noise. Optimal number of lenslets across each actuator are obtained for both deformable mirrors, and a simple experimental procedure for optimal alignment is described. The results show that high-performance adaptive optics can be achieved even with low cost off-the-shelf Shack-Hartmann arrays with lenslet spacing that do not necessarily match those of the wavefront correcting elements.
1. Introduction
The design or selection of a wavefront corrector for an adaptive optics (AO) system is based on the spatial and temporal characteristics of the aberrations to be compensated for [1, 2]. Once the wavefront corrector is selected, a matching wavefront sensor should be designed. The matching can be achieved by minimizing the condition number of the AO response matrix and the noise propagation coefficient of the AO control matrix, provided the noise in all sensing elements is equal and uncorrelated [3–7]. The former is not always a valid hypothesis. For example, in Shack-Hartmann (SH) wavefront sensors, the lenslets over the pupil boundaries will collect a smaller average number of photons than the ones inside the pupil.
In this work, the use of the condition number and mean wavefront variance to design a wavefront sensor matching a given wavefront corrector is proposed, to account for noise differences across the wavefront sensor signals. The method is illustrated by studying the matching of two commercially available deformable mirrors (DMs) and SH wavefront sensors, all with square packing geometries. Results are presented for different sources of noise, namely, photon noise, background noise and readout noise. No a priori knowledge of the aberrations to be compensated for is assumed. The results show that, surprisingly, SH sensors with non-matching geometries can achieve comparable performances to matching ones, and that for the two DMs studied there is an optimal single range of number of SH lenslets across each actuator. It is also shown that experimental minimization of the mean variance error can be used as a practical alignment method.
2. Theory
Let us begin by assuming an AO system described by the linear equation
| (1) |
where x is a vector formed by nc wavefront corrector driving signals, s is a vector formed by ns wavefront sensor signals, and A is the response matrix of the system. Using the singular value decomposition (SVD), the response matrix can be conveniently represented as the product of three matrices [8],
| (2) |
where T denotes transpose. The matrix VT, of dimensions nc × nc, is a change of basis in the wavefront corrector space, from the driving signals to a set of orthonormal modes. These modes also depend on the wavefront, and are usually referred to as system modes. The matrix U has dimensions ns × nc and translates from the system modes to the wavefront sensor space. Finally, Λ is a diagonal matrix with null or positive elements λi, the singular values. Each singular value can be thought of as the gain of a system mode. The ratio of the maximum to the minimum singular values is defined as the condition number. A low condition number is desirable, as it indicates that the AO system modes are balanced [5–7], and more importantly, lead to more stable closed-loop performance, as explained below.
The linear spatial control of an AO system is described by an equation of the form,
| (3) |
with B being the spatial control matrix and g the gain. A common spatial control matrix is the Moore-Penrose pseudoinverse [8] of A, which provides the wavefront corrector signals that minimize the norm of the vector formed by the wavefront sensor signals. Using the SVD, the pseudoinverse can be calculated as
| (4) |
where Λ−1 is simply Λ with the non-null singular values replaced with their reciprocals. Because of the reciprocal relation, noise in the modes that have low singular values will produce large control signals, potentially leading to unstable closed-loop wavefront correction. These modes can be filtered by replacing their associated singular value reciprocals with zeros. This makes the closed-loop performance more stable, due to the decrease in noise sensitivity. However, the filtering also decreases the number of aberrations that the system can correct for. It is therefore desirable to design the AO system with a low condition number, both for stable performance and good wavefront correction.
The spatial control matrix B is a modal wavefront reconstructor that estimates the wavefront in term of wavefront corrector modes. Using error propagation analysis assuming uncorrelated noise between wavefront sensor signals (σj), one gets that the mean error E in the wavefront estimation [10], is
| (5) |
where Bij are the elements of the spatial control matrix and Apupil is the pupil area. If the wavefront corrector signals form an orthonormal basis, then E is the wavefront root-mean-squared (RMS) error in the wavefront corrector space.
Finally, it is worth noting that when the noise σ is equal for all sensing elements (e.g. shear interferometer) and the spatial control matrix is either the pseudoinverse or its filtered version, Eq. 5 can be rewritten in terms of the singular values of the response matrix as
| (6) |
by using the properties of the SVD matrices. This formula is more computationally efficient to implement. Using the linear algebra software LAPACK [9], calculation of the singular values to implement Eq. 6 is approximately four times faster than calculating the pseudoinverse to implement Eq. 5. This was tested using Matlab 7 (MathWorks, USA) and the results are consistent with the LAPACK documentation.
3. Method
Typically, when designing a SH wavefront sensor for a given wavefront corrector, only a handful of highly symmetric matching geometries are considered [6]. In this work, the performance of a square packing SH lenslet array is studied by exploring the parameter space defined by the number of SH lenslets across each DM actuator, orientation and lateral displacement with respect to the DM. The method can be applied to any other regular SH array or DM packing geometry, such as hexagonal.
The first DM studied is a Mirao 52 (ImagineEyes, France) with 52 actuators arranged over an 8 by 8 square grid with three actuators missing on each corner. The influence functions used for modeling the DM response were gaussian surfaces, obtained by least square fitting experimental data obtained using a GPI interferometer (Zygo, USA). The value of the influence functions at neighboring actuators is approximately 60% of its peak value. The second DM is a Multi-DM (Boston Micromachines, USA), with 120 actuators arranged over a 12×12 square grid with 6 actuators missing on each corner. The value of the influence functions at neighboring actuators was taken as 26%, based on data provided by the manufacturer.
The response matrix of the AO system was calculated assuming that the SH lenslet array has 100% fill factor, and that each SH signal is proportional to the average wavefront over the lenslet. Only lenslets with more than half their area contained within the pupil were considered, in order to exclude SH signals with low signal. To increase calculation speed, reduce memory requirements and keep errors to a minimum when estimating the average wavefront slope over each lenslet, we took advantage of the DM surface being continuous. The average wavefront slope in the x-direction over the lenslet Ω is by definition
| (7) |
In most practical cases Ω is convex and its boundary can be separated into two curves, 𝒞max and 𝒞min, defined by the extreme points of the curve along the y-dimension (A and B), as shown in figure 1. Then, performing the integration in the x-coordinate yields
| (8) |
where (xmax,y) and (xmin,y) run along 𝒞max and 𝒞min respectively. Therefore, the evaluation of the mean wavefront slope over the pupil only requires evaluation of the wavefront at the lenslet boundaries, as opposed to wavefront gradients over the lenslet area, greatly reducing the computing time and errors. In addition to this, most lenslet’s boundaries are shared by two lenslets, thus only half the wavefront evaluations are required. The same reasoning was applied for calculating the wavefront slope along the y-direction.
Fig. 1.
Geometry used for the calculation of the mean wavefront over a lenslet, which does not need to be hexagonal. The mean wavefront over the lenslet area Ω is calculated as the integral of the difference of the wavefront values over the curves 𝒞max and 𝒞min.
Three different noise sources will be considered separately: photon (shot) noise, background noise and electronics (e.g. readout and dark current) noise. Most practical cases can be described by a combination of these, which if they are uncorrelated can be simply combined by taking the square root of the addition of their variances. The amplitudes of the three sources of noise for a SH sensor using a center-of-mass algorithm, verify the following relationships [11],
| (9) |
| (10) |
| (11) |
where NT and ND are the FWHM of the real and the diffraction-limited SH spot in pixel units, is the total number of pixels used in the center-of-mass intensity calculation, σe is the RMS number of noise electrons per pixel per frame, and nph and nbg are the number of detected photons and background photons per lenslet per frame, respectively.
Let us now assume a SH sensor with diffraction limited spots, programmed with an iterative center of mass algorithm that reduces the number of pixels used in each iteration until the area used for calculation is comparable to the diffraction limited spot size. Then, for a fixed wavelength and a constant uniform photon flux over the pupil of the SH, the noise for each SH lenslet can be taken to the more convenient form
| (12) |
| (13) |
| (14) |
where Alenslet is the lenslet area within the pupil.
A range of lenslet sizes relative to the DMs actuators was investigated by calculating first the AO response matrix taking advantage of Eq. 8, and then the associated condition number and mean wavefront errors. Three mean wavefront errors were calculated for each SH configuration, assuming the presence of only one source of noise for each, using the formulas 12–14. These calculations were repeated for each lenslet size, covering the parameter space with a uniform rectangular grid. The sampling interval along the lenslet size and displacement dimensions was one hundredths of the pupil radius, and 3 degrees along the orientation dimension.
4. Results and discussion
4.1. Optimal Shack-Hartmann lenslet size
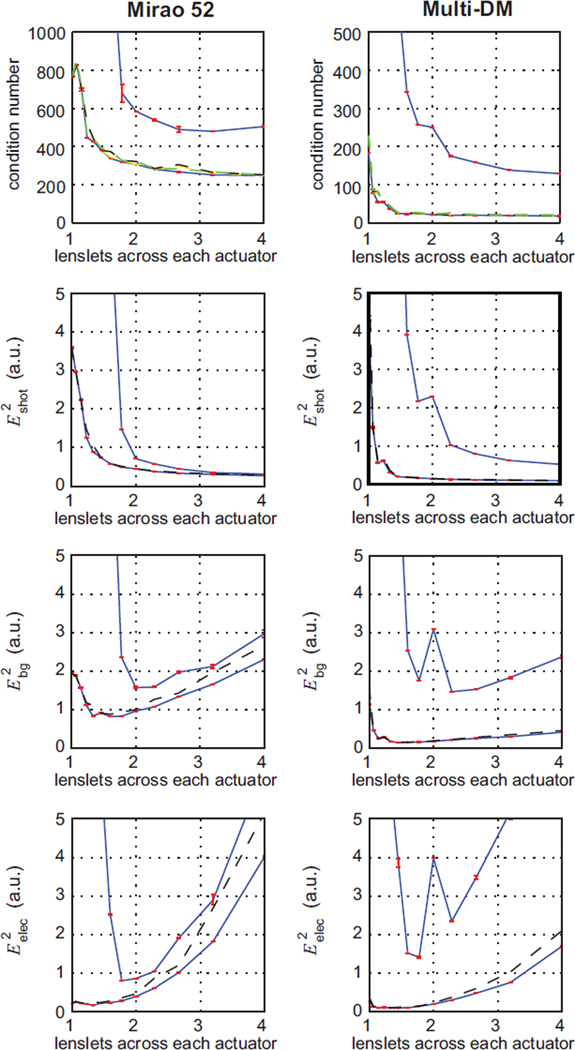
The results for the Mirao 52 and the Multi-DM are presented on the left and right columns of figure 2, respectively. The blue solid curves indicate the maximum and minimum values the condition number and the wavefront variance (E2) take over the range of number of lenslets across each DM actuator. The hardly visible vertical error bars (in red) were calculated as the difference between the peak (minimum or maximum) value and its nearest calculated value for the same lenslet size.
Fig. 2.
Condition number and E2 plots for AO systems using a square packing SH and a Mirao 52 or a Multi-DM. The areas between the blue solid lines comprise the range of values for all possible SH orientations and alignment with respect to the DMs. The dashed curve in the condition number plots correspond to the configurations that produce the lowest E2 for all three sources of noise, and the dashed curve in the E2 plots to the configurations with lowest condition number.
One of the most noticeable features in the top six plots is that a one-actuator-to-one-lenslet configuration performs very poorly as indicated by the large condition numbers and wavefront variances. In particular, this is valid for Fried’s geometry [10], where the lenslet corners coincide with the actuators centers. Even in an AO where the dominant source of noise is electronics noise, the large condition number values might significantly degrade the AO stability. A surprising result illustrated by the plots, is the smooth variation of the condition number and the wavefront variance with lenslet size. This shows that not only very symmetrical configurations can perform well, but also off-the-shelf SH arrays that might not exactly match the actuator spacing can be used without sacrificing performance.
Interestingly, as the number of lenslets across each actuator is increased, a region with low condition numbers is reached in both mirrors. These low condition numbers can be achieved even for poorly oriented and laterally aligned systems, although good alignment is still desirable. This can be explained by noticing that a low number of lenslets per actuator, say one, can be aligned so that the lenslet center is over the actuator center, thus having minimum signal from all lenslets. By having more lenslets, the possibility of having such poor sensing configuration becomes impossible, as shown by the sharp decay of the top blue curves around 1.5 lenslets per actuator for both DMs. It is also worth observing the much lower condition numbers achievable by the Multi-DM, approximately one order of magnitude lower than the Mirao 52.
The shot noise-limited plot shows that as the number of lenslets increases, the wavefront variance tends to a constant value. This is explained by noticing that the variance of the shot noise error is inversely proportional to the lenslet area (Eq. 12) and the area of the lenslets decreases linearly with the total number of lenslet over the pupil. These two factors balance each other. The background noise on the other hand, has a stronger dependence on the lenslet area, and thus produces wavefront variances curves (third row) with a minimum. The wavefront variance in an electronics noise-dominated SH shows an even more pronounced increase with the number of lenslets across each actuator. It turns out that for the DMs studied here, the position of the curves minima remain very close to those of the background noise-limited case.
Based on these plots, it is reasonable to define the optimal range of lenslets across each DM actuator as the range that minimizes all three sources of noise and the condition number simultaneously. Defined in this way, the optimal range for the Mirao 52 is between 1.5 and 2.0 lenslets per actuator and between 1.4 and 1.8 for the Multi-DM. This range might change if a priori knowledge of the aberrations to be corrected for, is incorporated in the control matrix or if other noise sources are considered.
4.2. Optimal Shack-Hartmann array alignment
When the SH array is incorporated to the AO system, it has to be correctly oriented and positioned relative to the DM for optimal AO performance. Here, the word optimal has the same meaning as above: minimal noise impact on wavefront variance and minimal condition number. The orientation can be adjusted by direct observation of the SH spot pattern when actuating a row or a column of DM actuators. The lateral positioning, however, is not so trivial, although it can be achieved without any additional optical setup or tool, as explained next.
First, an estimation of the noise sources amplitudes must be obtained (e.g. σshot, σbg, σelec). The illuminated area of the lenslet required to calculate the noise amplitudes (Eqs. 12=14) can be directly estimated from the SH image, as proportional to the light intensity detected in the area of the detector associated to each SH lenslet (e.g. by summing all the pixel values or taking the peak intensity). Second, the response matrix of the system should be experimentally obtained for the initial SH array position. Then, using this matrix, the associated control matrix is calculated and fed into equation 5. Now, the SH array is moved to a new position and the procedure repeated until satisfactorily low wavefront variances and condition numbers are reached.
It might appear that minimizing both the condition number and the wavefront variance simultaneously might not be possible. However, this does not seem to be the case for the two DMs studied here, as illustrated by the plots in figure 2. The dashed curves in the wavefront variance plots correspond to the wavefront variance from the configurations with minimal condition number. In some cases, minimizing the condition number also minimize the wavefront variance, as for both shot noise related curves. Minimizing the wavefront variances on the other hand, always minimizes the condition number, as indicated by the dashed overlapping curves in the condition number plots. Therefore, for these two DMs, the optimal alignment can be experimentally found by searching for minimum wavefront variance.
5. Conclusions
The matching of wavefront correctors and wavefront sensors by minimizing the condition number and mean wavefront variance was proposed and demonstrated in the presence of different noise sources for two commercially available deformable mirrors. Optimal ranges of numbers of SH lenslets across each DM actuator were obtained for both DMs, and a simple experimental procedure for optimal alignment was described. The lenslet size ranges obtained are valid for most current AO applications: astronomical AO using electron-multiplied CCDs, which is a shot noise limited application; ophthalmic AO which is limited by the background noise due to intraocular scattering; and low cost AO with CMOS sensors, which is limited by electronics noise. The results show that high-performance AO can be achieved even with low cost off-the-shelf SH arrays with lenslet spacing that do not necessarily match those of the wavefront correcting elements.
Acknowledgments
This research was supported by the NIH grant BRP-EY014375 and the NSF-CfAO grant AST-9876783. I would like to thank Ramkumar Sabesan and Geunyoung Yoon, for useful discussions and the experimental measurements of the Mirao 52 deformable mirror influence functions. I am also grateful to the reviewers for their suggestions, which greatly improved the manuscript.
References and links
- 1.Paterson Carl, Munro Ian, Dainty JC. A low cost adaptive optics system using a membrane mirror. Opt. Express. 2000;6:175–185. doi: 10.1364/oe.6.000175. http://www.opticsinfobase.org/abstract.cfm?URI=oe-6-9-175. [DOI] [PubMed] [Google Scholar]
- 2.Dalimier Eugenie, Dainty Chris. Comparative analysis of deformable mirrors for ocular adaptive optics. Opt. Express. 2005;13:4275–4285. doi: 10.1364/opex.13.004275. http://www.opticsinfobase.org/abstract.cfm?URI=oe-13-11-4275. [DOI] [PubMed] [Google Scholar]
- 3.Ragazzoni Roberto, Farinato J. Sensitivity of a pyramidic wave front sensor in closed loop adaptive optics. J. Mod. Opt. 1996;43:289–293. [Google Scholar]
- 4.Dubra Alfredo, Paterson Carl, Dainty J. Christopher. Wave-front reconstruction from shear phase maps by use of the discrete Fourier transform. Appl. Opt. 2004;43:1108–1113. doi: 10.1364/ao.43.001108. [DOI] [PubMed] [Google Scholar]
- 5.Furber Mark E. Optimal design of wavefront sensors for adaptive optical systems: part 1, controlability and observability analysis. Opt. Eng. 1997;36:1843–1855. [Google Scholar]
- 6.Jiang Wenhan, Zhang Yudong, Xian Hao, Guan Chunlin, Ling Ning. A wavefront correction system for inertial confinement fusion. Proc. of the Second International Workshop on Adaptive Optics for Industry and Medicine. 2000:8–15. [Google Scholar]
- 7.Paterson Carl, Dainty JC. Hybrid curvature and gradient wave-front sensor. Opt. Lett. 2000;25:1687–1689. doi: 10.1364/ol.25.001687. [DOI] [PubMed] [Google Scholar]
- 8.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical recipes in C: The art of scientific computing. 2nd. Cambridge, United Kingdom: Cambridge University Press; 1992. [Google Scholar]
- 9.Anderson E, Bai Z, Bischof C, Blackford S, Demmel J, Dongarra J, Du Croz J, Greenbaum A, Hammarling S, McKenney A, Sorensen D. LAPACK Users’ Guide. third. Philadelphia, PA: Society for Industrial and Applied Mathematics; 1999. [Google Scholar]
- 10.Southwell WH. Wave-front estimation from wave-front slope measurements. J. Opt. Soc. Am. 1980;70:998–1006. [Google Scholar]
- 11.Rousset Gérard. Wave-front sensors. In: Roddier Francǫis., editor. Adaptive optics in Astronomy. Cambridge, U.K.: Cambridge University Press; pp. 91–130. [Google Scholar]