What Is Moving in Hybrid Halide Perovskite Solar Cells?

Conspectus

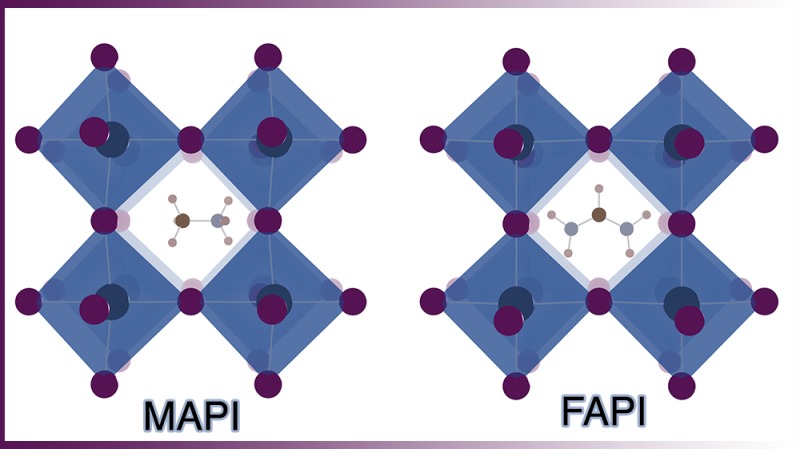
Organic–inorganic semiconductors, which adopt the perovskite crystal structure, have perturbed the landscape of contemporary photovoltaics research. High-efficiency solar cells can be produced with solution-processed active layers. The materials are earth abundant, and the simple processing required suggests that high-throughput and low-cost manufacture at scale should be possible.

While these materials bear considerable similarity to traditional inorganic semiconductors, there are notable differences in their optoelectronic behavior. A key distinction of these materials is that they are physically soft, leading to considerable thermally activated motion.

In this Account, we discuss the internal motion of methylammonium lead iodide (CH₃NH₃PbI₃) and formamidinium lead iodide ([CH(NH₂)₂]PbI₃), covering: (i) molecular rotation-libration in the cuboctahedral cavity; (ii) drift and diffusion of large electron and hole polarons; (iii) transport of charged ionic defects. These processes give rise to a range of properties that are unconventional for photovoltaic materials, including frequency-dependent permittivity, low electron–hole recombination rates, and current–voltage hysteresis. Multiscale simulations, drawing from electronic structure, ab initio molecular dynamic and Monte Carlo computational techniques, have been combined with neutron diffraction measurements, quasi-elastic neutron scattering, and ultrafast vibrational spectroscopy to qualify the nature and time scales of the motions. Electron and hole motion occurs on a femtosecond time scale. Molecular libration is a sub-picosecond process. Molecular rotations occur with a time constant of several picoseconds depending on the cation. Recent experimental evidence and theoretical models for simultaneous electron and ion transport in these materials has been presented, suggesting they are mixed-mode conductors with similarities to fast-ion conducting metal oxide perovskites developed for battery and fuel cell applications. We expound on the implications of these effects for the photovoltaic action.

The temporal behavior displayed by hybrid perovskites introduces a sensitivity in materials characterization to the time and length scale of the measurement, as well as the history of each sample. It also poses significant challenges for accurate materials modeling and device simulations. There are large differences between the average and local crystal structures, and the nature of charge transport is too complex to be described by common one-dimensional drift-diffusion models. Herein, we critically discuss the atomistic origin of the dynamic processes and the associated chemical disorder intrinsic to crystalline hybrid perovskite semiconductors.

1. Introduction

Methylammonium lead iodide was first reported in the cubic perovskite crystal structure in 1978.¹ The first solar cell was published in 2009,² with high-efficiency (≥10%) cells since 2012. There have been many detailed discussions and reviews on the development, progress, and limitations of this technology. The focus of this Account is the dynamic behavior of hybrid organic–inorganic perovskites, which has been linked to the performance, degradation, and unusual physics of these materials and their associated devices. Our principal concern is the atomistic origin of these processes, and their description by first-principle and multiscale materials modeling. For brevity, we refer to the methylammonium compound CH₃NH₃PbI₃ as MAPI and the formamidinium compound [CH(NH₂)₂]PbI₃ as FAPI.

2. Molecular Motion

Weber first reported MAPI in the cubic perovskite crystal structure (O_h symmetry),¹ which may be surprising considering the anisotropy of the molecular building block (CH₃NH₃⁺ is of C_3v symmetry). However, as early as 1985, it was understood that these molecules were orientationally disordered in the crystal, giving rise to an effective higher lattice symmetry on average.³ In 1987, Poglitsch and Weber linked this dynamic disorder to the temperature and frequency dependence of the complex permittivity.⁴ Despite being crystalline solids, the dielectric response of these materials has one component that is akin to a polar liquid due to the rotational freedom of the dipolar molecules.⁵ For MAPI, at 300 K, the contribution of CH₃NH₃⁺ rotations to the static dielectric response can be estimated as ∼ 9, as will be discussed below.

Early work on the characterization of the crystal structure identified three phases of MAPI: orthorhombic, tetragonal, and cubic Bravais lattices in order of increasing temperature.⁶ While the position of Bragg peaks in X-ray diffraction can distinguish between the three phases, the peak intensities arising from CH₃NH₃⁺ relative to PbI₃^– are too weak to assign accurate molecular orientations. The recent application of high-resolution powder neutron diffraction (with a more even distribution of scattering cross-section between light and heavy atoms) has provided a quantitative description of the temperature dependent average structures (summarized in Figure 1).⁷ At high temperatures, the structure of MAPI can be represented by the cubic space group Pm3̅m, whereas below ca. 327 K it is better described by the tetragonal space group I4/mcm. The cubic-tetragonal transition is second order (Ehrenfest classification) and continuous over 165–327 K. This transition is linked to the anisotropy of the molecular disorder, as well as inorganic octahedral deformation and tilting, which changes from predominately two dimensions (tetragonal) to three dimensions (cubic). The energy balance between the phases can be affected by epitaxial or uniaxial strain. At 165 K, there is a first-order transition to the orthorhombic Pnma phase, with associated discontinuities in the observable physical properties. The transition entropy suggests an ordering of the molecular species,⁸ and a full powder neutron solution shows columnar antiferroelectric ordering (head-to-tail arrangement of the CH₃NH₃⁺ cations in 1D channels).⁷ It is possible that other low-temperature orderings can form with different epitaxial strain, temperature quench regimes, applied electric fields, and sample processing.

Figure 1.

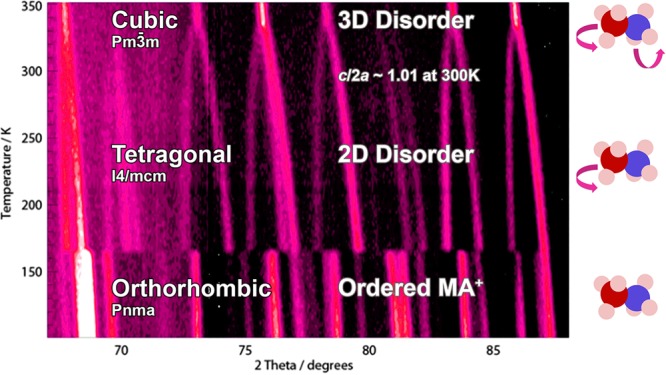
Temperature-dependent (100–352 K) powder neutron-diffraction pattern of CH₃NH₃PbI₃. From ref (7). Adapted by permission of the RSC. The space groups of the average crystals structures are shown with a schematic of the extent of disorder in the CH₃NH₃⁺ sublattice.

For FAPI, analysis of powder neutron diffraction has assigned a room temperature space group of Pm3̅m, which is isostructural to the high-temperature MAPI structure.⁹ Faulted or twinned phases at the nanoscale can appear as hexagonal to single-crystal diffraction methods, which explains the earlier assignment of a hexagonal space group.¹⁰ A distinction of FAPI is that the corner-sharing perovskite structure (black color) is in competition with a face-sharing δ phase (yellow color);¹⁰ this is also the case for CsSnI₃.^11,12 In contrast to MAPI, knowledge of the low temperature phase behavior of FAPI is currently lacking.

A point to consider regarding structural characterization by diffraction, which is particularly relevant to perovskite structured materials, is that standard techniques probe only the average crystal structure. The intensities of Bragg peaks are related to the average positions of single atoms within the unit cell. The relative positions of atoms (e.g., bond lengths and angles) requires higher-order correlation functions. These can be accessed through using X-ray or neutron total scattering techniques. Disordered crystalline materials display large atomic displacement parameters. This is the case for both MAPI and FAPI at room temperature.^7,9 The material is continuously distorting through this average position as a function of time; the thermal vibrations are large relative to the interatomic spacings.

We have attempted to address the issue of molecular motion using three scales of materials modeling: (i) static lattice, (ii) molecular dynamic, and (iii) Monte Carlo approaches, which we will now address in turn.

Static Lattice

The standard approach in density functional theory calculations of solids is to first minimize all forces on the system by structural relaxation. In the absence of temperature, the size and shape of the crystallographic unit cell is relaxed with respect to the quantum mechanical forces. This should include all internal degrees of freedom. It is for this “equilibrium” athermal crystal structure that the electronic structure is calculated, and so the total energy and other properties are extracted.

As a starting point we assessed the total energy difference of different molecular orientations within a single “quasi-cubic” unit cell of MAPI.¹³ We note that any electronic structure calculation on such unit cells implicitly assumes that the methylammonium molecules are arranged into an infinite ferroelectric domain; although, it should be noted that there is no long-range electric field created with the standard “tinfoil” boundary conditions. We found that the energy difference between the low index ⟨100⟩ (cube face), ⟨110⟩ (cube edge), and ⟨111⟩ (cube diagonal) orientations of the CH₃NH₃⁺ ions are similar (within 15 meV) with small barriers between them (<40 meV), but with the facial ⟨100⟩ orientation being preferred. Even from this static description, one can envisage molecular orientational disorder driven by thermal energy (k_bT = 26 meV at 300 K).

Molecular Dynamics

The most simple method to incorporate temperature into first-principles simulations is through molecular dynamics (MD). The forces on the ions are calculated quantum-mechanically but the ion velocities are classical and integrated numerically with Newton’s laws of motion to positions. Finite temperature is maintained by rescaling ion motion against a thermostat. Such simulations should display the full range of anharmonic behavior, but due to finite computational resources, rare events are undersampled.

Renderings of our MD simulations¹⁴ on supercells of MAPI and FAPI are available online.^15,16 Without any deep analysis of the trajectories, it is clear to an observer that the molecules are rotationally mobile at room temperature, with a time scale of motion on the order of picoseconds. A more detailed statistical treatment gives time constants of 3 ps (MA)¹⁷ and 2 ps (FA)⁹ for molecular reorientations at 300 K.

There are a range of complex motions displayed, involving relative twisting of the head and tail groups, libration of a molecular in a single orientation, and the rotation of molecules between orientations. The results support and expand upon the picture obtained using static lattice techniques: a statistical analysis¹⁴ reveals the extent of the disorder as well as the preference for facial ⟨100⟩ orientations that are also evident in neutron diffraction measurements.^7,9

A surprising result from the MD simulations is that the PbI₆ octahedra are far from ideal, even for a cubic lattice. While the “average” structure may appear cubic the local structure is distorted significantly. Pb–I–Pb bond angles of 180° would be expected for an ideal network, while values of 165–172° are found in the relaxed cubic structure.¹⁸ Pb(II) is a prototype “lone pair” cation with a ground-state electronic configuration of 5d¹⁰6s²6p⁰. In a centrosymmetric coordination environment, on-site sp hybridization is forbidden by group theory; however, local distortions allow for hybridization that can result in electronic stabilization. In effect, these systems display a dynamic second-order Jahn–Teller instability,¹⁹ in addition to displacive instabilities associated with rigid titling of the octahedra. These displacive motions are particularly important as the electronic bands at the gap relevant for device operation are hybridized Pb and I atomic orbitals, and will be directly affected by such distortion. These predictions are supported by measurements of the local structure of CH₃NH₃SnBr₃ by X-ray scattering that indicated lone pair distortions.²⁰

A limitation with ab initio molecular dynamics simulations is that they are restricted to small simulation cells, which include a limited set of phonon wavevectors. A subtlety of pervoskite molecular dynamics is that the expansions should be even in the number of octahedra, to avoid falsely constraining the simulation by preventing zigzag tilts through the periodic boundaries. The development of an analytical interatomic potential model can provide access to much larger simulation cells and integration times, and hence describe temporal correlations over larger areas.

Monte Carlo

In order to simulate disordered materials on a scale relevant to photovoltaic devices, we constructed a model Hamiltonian that describes the intermolecular dipole interactions and solved for the temperature dependent equilibrium structure using on-lattice Monte Carlo (MC).¹⁴ Since our original report, the Starrynight codes have been generalized to three-dimensional boundary conditions¹⁷ and to include defect structures.²¹ We note that the as-parametrized model considers rotating molecular dipoles, but these can be considered an effective dipole of the unit cell including local lattice distortions, which is also applicable to model fully inorganic perovskites. By universality arguments, systems described with the same symmetry and form of Hamiltonian should have identical transitions and equilibrium behavior.

The strength of the methylammonium dipole moment is comparable to the electric polarization calculated for simple models of the room temperature tetragonal phase.²² A molecular dipole of 2.2 D ≈ 3 μC cm^–2 is predicted from quantum chemistry; by calculating the torque generated around the center of mass due to an applied electric field, the magnitude of the dipole is rotation and position invariant even for a charged molecule. For formamidinium, the value is reduced to 0.2 D; however, the smaller molecular dipole can be compensated by larger structural distortions in the solid-state owing to the steric effect of the additional amine group.

The general behavior obtained from the MC simulations is easy to follow: ordering of molecular dipoles at low T minimizes the total energy of the system by maximizing the dipole–dipole interactions, while disorder at high T is driven by configurational entropy. The electrostatic potential resulting from dipole alignment suggests that electrons and holes may be segregated by this structure. This hypothesis has been subsequently confirmed by direct electronic structure calculation²³ and applied in a device model.²⁴

The molecular motion discussed above has been supported by recent quasi-elastic neutron scattering (QENS) investigations.^17,25 This technique is particularly sensitive to the motion of hydrogen atoms due to the high incoherent neutron-scattering cross-section of hydrogen nuclei. To get sufficient signal, over 10 g of material was required for these studies, relying on bulk synthesis procedures which may not be representative of the active material (thin film) in devices. Analysis in one of these studies²⁵ suggests that only ca. 20% of the molecules were fully rotationally active in the time scale of the measurement (200 ps), which could be explained by the presence of ordered domains.

Ultrafast pump–probe vibrational spectroscopy applied to device-relevant films offers a direct realspace measurement of methylammonium motion within MAPI: a fast libration (“wobbling in a cone”) motion at 300 fs, and a slower rotation (reoriention) with a 3 ps signature.²⁶ Here the decay of the polarization anisotropy within the 10 ps measurement window indicates that 80% of the molecules were rotationally active during this time, and that any ordered domains must therefore be continuously interconverting.²⁶ The time constant for reorientation in FAPI is calculated as 2 ps at 300 K,⁹ with no direct measurements available at this time. The associated frequency range for molecular rotations of 0.3–0.5 THz overlaps with the low end of the vibrational spectrum, associated with distortions of the octahedral cage.

In order to further understand the device behavior, we need to understand the nature and motion of electrical carriers.

3. Electron and Hole Transport

There has been significant debate concerning the nature of photogenerated electron–hole pairs in MAPI: free carriers or excitons? It is now clear that the small effective mass of the electron and hole combined with the large static dielectric constant result in long-time scale exciton binding energies, E_B ≪ k_bT at operating temperatures.²⁷⁻²⁹ The situation can be different in lower dimensional perovskite networks where exciton binding is enhanced.

The exciton is a quasi-particle—a bound state of an electron polaron and a hole polaron. The long-term energetic stability of these particles is dependent upon the dielectric function. The most simple effective mass approximation takes the static dielectric constant (ϵ₀), giving a binding energy 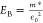, where m* represents the reduced carrier mass. Due to the frequency dependence of this dielectric function (i.e., the range of response times of the lattice and molecular motion), excitons may be instantaneously stable yet decay away on the time scales of the dielectric response with E_B ∼ 6 meV at 300 K.²⁹ The differing time scales of the dielectric response lead to non-hydrogenic energy levels of the bound exciton.²⁸

The calculated high-frequency (optical) dielectric constant of 5 increases to 24 when the harmonic phonon response of the lattice is included.²⁷ The additional molecular rotational contribution can further increase the static dielectric constant to 33 (assuming an unhindered dipolar liquid at 300 K). These values represent a bulk response and exclude any effects from space charges or conductivity.

An early dielectric study⁵ shows the strong frequency dependence (and therefore response time) of the permittivity above 165 K, which can fitted with a Kirkwood–Fröhlich model for a dipolar liquid, indicating the increasing hindrance of motion (and thus slower response time, greater dielectric response) of the methylammonium ions upon cooling toward the 165 K transition. In the pristine low temperature phase, the molecules are fixed and the dielectric response is limited to the electronic and ionic components with E_B ∼ 16 meV.²⁹ The dielectric response will have less frequency spread, and more normal excitonic behavior will be recovered, with the potential for long-lived excitons in the orthorhombic perovskite phase.

As with any semiconductor, variation in the photophysics and electrical transport properties reported in the literature can be related to sample variation (stoichiometry, surface, morphology, point and extended defect structures). Solution processed materials are particularly susceptible to such variation. Care must be taken not to draw general conclusions from a single experiment or data source on the hybrid perovskites. Some recent reports have used high-quality single crystals whose properties should be more transferable.

Hall effect measurements suggest intrinsic dark carrier mobilities of 8–66 cm² V^–1 s^–1.^10,30 This is comparable to other solution-processed semiconductors.³¹ The field-effect mobility is much smaller, 10^–2–10^–4 cm² V^–1 s^–1.³² These figures are relatively low considering the high dispersion and well-defined bands in the electronic structure of MAPI. CdTe, which has a similar band structure to MAPI, displays an electron mobility exceeding 1000 cm² V^–1 s^–1 at low temperature. High performance photovoltaics do not directly require high mobility active materials, rather a sufficient mobility to extract photogenerated charges before recombination.

Much more remarkable are the minority-carrier diffusion lengths which exceed 1 μm.³³ This value is large for a direct band gap semiconductor, particularly one which is solution processed (and therefore structurally defective). The value is comparable to high-quality vacuum processed CdTe. This long carrier diffusion length, being larger than the film thickness necessary to absorb the full solar spectrum, makes MAPI and FAPI such high-performance photovoltaic materials.

From temperature-dependent transport measurements, the dominant carrier scattering mechanism has been attributed to acoustic phonons.^34,35 From studying the time constants of transient recombination, monoexponential (suggesting a monomolecular process) electron–hole recombination is dominant under normal (sunlight, low fluence) operating conditions, while biexponential recombination (suggesting a bimolecular process) is a better match to higher light intensities.³⁶ The data can be fitted with moderate bulk and interface trap densities, but more importantly they suggest the existence of an internal mechanism that suppresses direct electron–hole interactions.

There are two likely causes of the non-Langevin recombination: (i) the local structure of molecular dipoles and octahedra distortions (leading to an inhomogeneity of the electrostatic potential) separates electron and holes in real space; (ii) the relativistic splitting of the conduction band (a Rashba–Dresselhaus effect³⁷ driven by the internal crystal field) results in separation of electrons and holes in reciprocal space. Polarized domains have been observed from piezoforce microscopy.³⁸ Both effects, illustrated in Figure 2, could contribute to the long minority-carrier lifetimes and deserve more detailed attention from theory, computation, and experiment.

Figure 2.

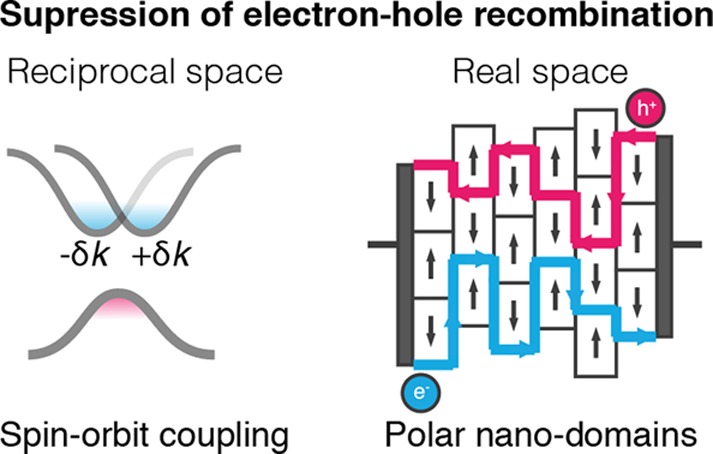
Bimolecular electron–hole recombination rates in hybrid perovskites are anomalously low. Two mechanisms are illustrated: (i) Relativistic splitting of the band edge states suppresses electron–hole recombination at the valence and conduction band edges due to momentum selection rules. The band edges are separated in reciprocal space. (ii) Fluctuations in electrostatic potential caused by molecular arrangements/octahedral distortion could cause electrons and holes to separate as proposed in ref (39). The band edges are separated in real space. These are two models that could reduce recombination rates.

A critical question is the spatial extent of the electron and hole carriers in comparison to local molecular order, as this affects both mechanisms discussed above. Within the large-polaron theory of Fröhlich we previously estimated a coupling constant (α) of 1.2.¹⁴ However, this was based on an estimate for the longitudinal optical phonon frequency of 9 THz, while phonon calculations⁴⁰ have revealed a lower lying optical mode at 2.25 THz, which increases α to 2.4. We can therefore revise our estimate of the effective electron and hole radius to ∼4 unit cells and the associated phonon-drag increase in the bare carrier effective mass to 40%.

4. Drift and Diffusion of Ions

Ion transport in inorganic perovskites is well established, with large anion vacancy diffusion coefficients. The activation energy in CsPbCl₃ was measured to be 0.29 eV (0.69 eV including the vacancy formation energy) with a diffusion coefficient of 2.66 × 10^–3 cm² s^–1.⁴¹

In methylammonium lead iodide, we have shown that the Schottky defect formation energy (the energy required to form a stoichiometric amount of isolated charged vacancies) is low (0.14 eV per defect); in Kröger–Vink notation:

1

Even for a stoichiometric material, there is a thermodynamic driving force for the formation of a high concentration of vacant lattice sites independent of the growth conditions.⁴² The enthalpic cost of defect formation (0.14 eV per defect) is offset by the gain in configurational entropy of the system to an extent beyond the dilute defect limit. Fortunately, these defects do not result in deep electronic states in the band gap, and thus Shockley–Read–Hall type nonradiative recombination is avoided.

A reservoir of available charged point defects in the lattice could support a significant ionic current, as evidenced in impedance spectroscopy of MAPI.⁴³ However, further to the presence of defects, the mobility of each species depends on the activation energy for solid-state diffusion (ΔH^diff), with a hopping rate given by

2

where ν represents an effective frequency of the diffusing species in the direction of the saddle point.

The transport of ions and electrons can be approximated as two separate processes owing to the difference in time constants (see Table 1), with the total current density being a sum of the ionic and electron partial current density:

3

However, the two processes are invariably coupled. Considering a material placed under an applied voltage with ion blocking electrodes, j_ionic = 0 under steady-state conditions. After the current is turned on ions and electrons will flow, but the ions will gradually cease to be available for transport. The initial equilibration of the ionic distribution relies on the solid-state diffusion pathways discussed above, which are activated processes that are slow and can give rise to a temporal change in the current–voltage behavior before equilibrium is reached. Electromigration of ions due to momentum transfer from the photovoltaic current in an operating solar cell can also occur, while ion leakage into the electron and hole contacts is also a possibility. Ion transport can now be considered the most likely origin of the slow component of the reported hybrid perovskite current–voltage “hysteresis”⁴⁴ and the reversible photocurrents.⁴⁵

Table 1. Summary of Dynamic Processes and Estimates of Their Associated Time Constants in CH₃NH₃PbI₃.

process	microscopic origin	time scale	frequency	diffusion coefficient
lattice vibrations	vibrational entropy	10 fs to 1 ps	1–100 THz
molecular libration	vibrational entropy	0.5 ps	2 THz
molecular rotation	rotational entropy	3 ps	0.3 THz
electron transport	drift and diffusion	∼1 fs	∼1000 THz	10–6 cm2 s–1
hole transport	drift and diffusion	∼1 fs	∼1000 THz	10–6 cm2 s–1
ion transport	drift and diffusion	∼1 ps	∼1 THz	10–12 cm2 s–1

The measured frequency-dependent permittivity of a hybrid perovskite film is compared with the outer-yellow skin of a banana in Figure 3. Both samples show a rapidly increasing dielectric response with decreasing frequency of the applied electric field. The banana is a good ionic conductor, and an example of a lossy dielectric composite, that shows an apparent hysteresis in current–voltage measurements at low-frequencies in the regime where charging and discharging processes at the electrode interfaces are dominant.⁴⁶ The similarity with the response of CH₃NH₃PbI₃ is notable, with the added complication of contributions from electronic carriers whose concentration are influenced by the light intensity.⁴⁷

Figure 3.

Comparison of the frequency-dependent dielectric response of a banana (Adapted from ref (46) with permission by IoP, Copyright 2008) and CH₃NH₃PbI₃ (Adapted with permission from ref (47). Copyright 2014 American Chemical Society.). Broadband spectra of (a) real and (b) imaginary dielectric permittivity and (c) conductivity of a banana skin at room temperature. The (d) real and (e) imaginary permittivity of a CH₃NH₃PbI₃ thin film under dark and 1 sun illumination conditions. The free carrier concentration is increased with above band gap illumination.

Planar photovoltaic devices will have a build up in electric field (space charge region) from ion accumulation apply evenly across the charge carriers. In contrast, mesoporous devices will still offer diffusive extraction pathways. Rates of ion diffusion will be strongly affected by material stoichiometry (defect concentration and self-healing ability) and material composition (diffusion along grain boundaries and interfaces). This combination of factors may have led to the large variation in reports of hysteresis time constants and the “hysteresis-free” devices.⁴⁸

The microscopic origin of ion transport is currently controversial with recent proposals of dominant: (a) proton diffusion;⁴⁹ (b) methylammonium diffusion;⁵⁰ (c) iodide diffusion.^51,52 While the observable response is most likely a combination of several processes, the three key factors that determine the contribution of individual ions are the concentration, activation energy, and attempt frequency (eq 2). Given the structural disorder of these materials discussed previously, the hybrid perovskites are expected to exhibit nonideal diffusion behavior due to the complex kinetics associated with a range of local coordination environments and migration pathways. Unlike electron transport with electrons and hole wave functions delocalized over many unit cells, ion transport is dependent on and more sensitive to the local structure.

Concerning proton diffusion, free H⁺ ions are unlikely to present in abundance since methylammonium is a weak acid. The reaction CH₃NH₃⁺ ⇌ CH₃NH₂ + H⁺ has an equilibrium constant K_a of ∼4 × 10^–11 at 300 K. Taking into account the density of MAPI, this would correspond to a nominal H⁺ concentration of 10¹¹ cm^–3, which may be affected by the preparatory conditions (e.g., humidity) and reactions with iodine but nonetheless is minor compared to the other defects present.

There should be an adequate supply of charged Pb²⁺, I^– and CH₃NH₃⁺ vacancies with predicted concentrations of 10¹⁷–10²⁰cm^–3 within the assumption of thermal equilibrium and noninteracting defects.⁴² Due to the orientational disorder of the molecular cations, long-range diffusion of CH₃NH₃⁺ should be slower with transport between successive cages being a relatively complex process, thus lowering the attempt frequency. The effective frequency should be largest for the iodide ions, as diffusion consists of short jumps over small distances, which is aided by the high polarizability and large thermal displacements for anions in a perovskite lattice. There is evidence of fast vacancy-mediated anion diffusion in inorganic halide perovskites with a low activation energy, and thus we consider this to be the dominant process in MAPI and FAPI. Further evidence is provided by the rapid anion exchange process between the chloride, bromide and iodide perovskites, which itself is an exceptional phenomenon. A cation exchange process has also recently been observed between MAPI and FAPI,⁵³ which is slower than anion exchange and hence consistent with anion diffusion being a faster process.

5. Conclusions

The time scales of the various processes discussed in this Account are summarized in Table 1. There is still much work to do concerning correlated movements, including the formation of ordered molecular domains, the nature of electron and hole polarons, and the true coupling between electronic and ionic charge carriers. Our discussion has largely focused on what is moving in CH₃NH₃PbI₃, but we have also shown that comparable behavior is apparent in [CH(NH₂)₂]PbI₃. It is expected that other hybrid perovskites will behave similarly, but there will be differences, for example, due to different molecular size, shape, and/or polarization. In particular, the high-performance mixture of (MA)_1–x(FA)_xPbI_3–3xBr_3x could exhibit additional dynamic processes relating to the cation and anion distributions on their respective sublattices. Inorganic perovskites would be expected to exhibit many of these phenomena, with the exception of molecular rotations, and hence could provide a platform to investigation dynamic disorder with one less degree of freedom. While halide perovskites may be relatively simple to synthesize, they still pose great challenges for a rigorous fundamental understanding.

Biographies

Jarvist Moore Frost is presently a Research Associate at the Department of Chemistry at the University of Bath. He was awarded his PhD in Physics at Imperial College London under the supervision of Prof. Jenny Nelson FRS on the simulation of bulk heterojunction solar cells. For research on perovskite solar cells, he received the 2014 young researcher prize from the UK SUPERSOLAR Hub. Jarvist maintains an interest in statistical physics, multiscale simulation techniques, and bicycles.

Aron Walsh holds the Chair of Materials Theory in the Centre for Sustainable Chemical Technologies at the University of Bath, and is dual professor with the Global E³ Institute at Yonsei University. He was awarded his BA and PhD from Trinity College Dublin (Ireland), completed a postdoctoral position at the National Renewable Energy Laboratory (USA), and held a Marie Curie fellowship at University College London (UK). Aron maintains an interest in atomistic processes at the interface of solid-state chemistry and physics, and existential Japanese cinema.

The authors declare no competing financial interest.

Special Issue

Published as part of the Accounts of Chemical Research special issue “Lead Halide Perovskites for Solar Energy Conversion”.