Joint torques in a freely walking insect reveal distinct functions of leg joints in propulsion and posture control

Abstract

Determining the mechanical output of limb joints is critical for understanding the control of complex motor behaviours such as walking. In the case of insect walking, the neural infrastructure for single-joint control is well described. However, a detailed description of the motor output in form of time-varying joint torques is lacking. Here, we determine joint torques in the stick insect to identify leg joint function in the control of body height and propulsion. Torques were determined by measuring whole-body kinematics and ground reaction forces in freely walking animals. We demonstrate that despite strong differences in morphology and posture, stick insects show a functional division of joints similar to other insect model systems. Propulsion was generated by strong depression torques about the coxa–trochanter joint, not by retraction or flexion/extension torques. Torques about the respective thorax–coxa and femur–tibia joints were often directed opposite to fore–aft forces and joint movements. This suggests a posture-dependent mechanism that counteracts collapse of the leg under body load and directs the resultant force vector such that strong depression torques can control both body height and propulsion. Our findings parallel propulsive mechanisms described in other walking, jumping and flying insects, and challenge current control models of insect walking.

1. Introduction

Understanding the control of complex motor behaviours such as walking requires an understanding of the mechanical output during unrestrained locomotion. In the case of walking, the integrated actions of the nervous, muscular and skeletal systems are reflected in net torques about the leg joints. Joint torques are thus a critical measure in the study of motor control [1].

Joint torques in walking are well described in humans [1] and a number of other vertebrates (e.g. [2–6]). However, similarly detailed descriptions of joint torques in invertebrates are lacking, in part because their relatively small legs complicate the measures required for inverse dynamics calculations. This is unfortunate, because detailed knowledge exists about the neural mechanisms of movement generation in invertebrates. In insects, much of the neural infrastructure driving the basic rhythmic motor activity of leg joints has been studied, including modulatory influences of sensory feedback (for reviews, see [7,8]). Moreover, the control potential of muscles and skeletal structures has been demonstrated (e.g. [9–12]). Although ground reaction forces have been measured in several insect species, including crickets [13], cockroaches [14], ants [15] and stick insects [16], to date, no study has resolved both the magnitude and timing of joint torques in detail, let alone their variability during unrestrained locomotion. Therefore, our view of how the joints of an insect leg interact to control propulsion and body height in walking largely depends on kinematic findings. Although kinematic analysis has yielded much insight into spatial [17] and temporal [18] patterns of coordination in locomotion, it cannot reveal the functional contributions of single leg joints to a movement [1]. This is because in a mechanically coupled system, a given joint movement could be produced by multiple patterns of joint torques.

To unravel the relative contributions of single leg joints to the overall body dynamics, we choose to study the stick insect (Carausius morosus; figure 1a). Next to the cockroach, the stick insect is a major model system for walking control in invertebrates [19] and biomimetic hexapod robots [20]. The slow and adaptive joint movements of its unspecialized walking legs rely heavily upon sensory feedback, making them ideal candidates to study the sensory control of legged locomotion. Methodologically, the relatively long and sprawled legs facilitate ground reaction force measurements [16] and whole-body motion capture in locomotion [21]. Here, we exploit these benefits to estimate the torque of all of its leg joints in unrestrained level walking. Our objectives are (i) to attribute functions to each leg joint in propulsion and body weight support, (ii) to test whether these functions reflect distinctly different leg postures in cockroaches and stick insects, and (iii) to identify potential commonalities of walking control and the control of other forms of locomotion, jumping in particular.

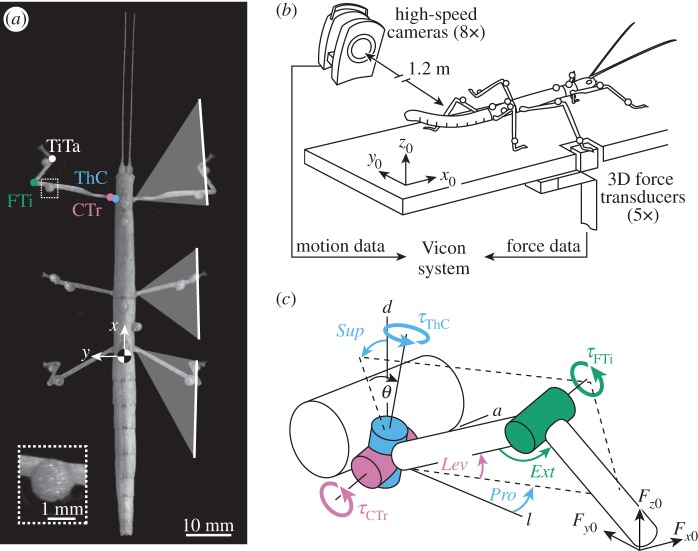
Figure 1.

(a) The stick insect C. morosus with motion-capture markers. Motion of each leg is driven by three main joints: the thorax–coxa (ThC, blue) and the coxa–trochanter (CTr, purple) joint, which together act as the ‘hip’, and the femur–tibia (FTi, green) joint, which acts as the ‘knee’. Also shown is the tibia–tarsus (Ti Ta, white). White lines indicate average movement ranges of legs. (b) Whole-body motion capture was integrated with ground reaction force measurements of single legs as animals walked freely along a horizontal walkway (one of eight Vicon cameras and one of five force transducers are shown). (c) Rigid link model of a leg used for joint torque calculations. The ThC joint is slanted relative to the vertical body axis (θ = 30°). Positive torques (τ) about this joint supinate (Sup) and protract (Pro) the leg. Positive torques about the CTr and FTi joint lift the femur (Lev) and extend the tibia (Ext) within the leg plane (dashed lines), respectively. a, anterior; l, lateral; d, dorsal.

When judging on leg posture and kinematics alone, the function of individual leg joints appear to be very different among species and forms of locomotion. For example, the stick insect holds its legs out to the side of the body and moves its leg joints within an almost vertically oriented leg plane (figure 1a), similar to sprawled-posture vertebrates [5,6]. This is different from the cockroach, where the hind legs move in a plane that is nearly horizontal [22], and different from the locust, where the specialized jumping legs are held upright, but parallel to the body [23]. In light of these differences, the leg joints of the stick insect are expected to control propulsion and body height quite differently. Here, we show that this is not the case, and that joint torques in stick insect legs suggest a functional division of joints for propulsion and posture control similar to that seen in other animals and other forms of locomotion.

2. Material and methods

We used 12 adult, female C. morosus reared in a laboratory colony (body mass: 0.8 ± 0.1 g, mean ± s.d; body length head to tail: approx. 75 mm; figure 1a). Animals walked along a horizontal walkway (40 × 500 mm) and, during successful trials, stepped onto one of five integrated miniature force transducers with their right hind, middle or front leg (figure 1b). To determine joint torques, motion and force data were combined in a three-dimensional rigid link model of the leg (figure 1c).

(a). Motion capture

Body and leg motions were captured and reconstructed as described in [21]. In brief, we used a marker-based motion-capture system, comprising eight infrared high-speed cameras (Vicon MX10 with T10 cameras, controlled by software Nexus v. 1.4.1; Vicon, Oxford, UK). The system automatically tracked the positions of lightweight retro-reflective markers (diameter: 1.5 mm; mass: 4 mg) at 200 Hz. Camera lenses had a focal length of 25 mm and were approximately 1.2 m away from the set-up. The resulting spatial accuracy of three-dimensional marker trajectories was approximately 0.1 mm. One marker was attached to each femur (mass: approx. 9 mg) and tibia (mass: approx. 4 mg), three to the metathorax and one to the meso- and prothorax (figure 1a). Note that the additional mass of the leg markers did not affect torque calculations (electronic supplementary material, figure S1). The kinematic model was obtained by direct analytical calculations from segment dimensions and positions of all markers on the segments, which were measured from high-resolution photographs (approx. 0.02 mm per pixel). As the Vicon system recorded marker trajectories only, we used an additional digital video camera (Basler A602fc, Ahrensburg, Germany) to record a complementary, synchronized side view of the walkway at 50 Hz for visual validation of the kinematic analysis.

Marker coordinates were post-processed in Matlab (The MathWorks, Natick, MA, USA). Time courses were low-pass filtered using a zero-lag, fourth-order Butterworth filter with a cut-off frequency of 20 Hz. Kinematic calculations were based on a main kinematic chain for the thoracic segments and a kinematic side chain for each leg as described in [21]. We defined a body-fixed coordinate system [x, y, z] based on the three markers on the metathorax. It originated in the insect's centre of mass (CoM) at the metathoracic–abdominal joint. The axes of the coordinate system were defined such that x points towards the head (fore–aft), y towards the left body side (medio-lateral) and z upwards (dorsoventral) (figure 1a).

(b). Force measurements

Single leg ground reaction forces were recorded at 1000 Hz with a resolution of approximately 0.05 mN, using strain-gauge-based force transducers [24]. Each transducer detected normal and horizontal forces along the three axes of the global coordinate system [x₀, y₀, z₀]. The axes of this coordinate system were defined relative to the walkway (figure 1b). Forces along each axis were measured by two strain gauges, one attached to the front and another to the backside of a thin spring steel strip. To measure forces along all axes, three strips were connected perpendicularly to each other. The uppermost strip was oriented parallel to the ground. It carried a piece of balsa wood (5 × 5 mm contact area), which served as a firm foothold for the tarsus during walking (figure 1b). With a stiffness more than 20 mN mm⁻¹ in each direction, the force transducers were considered hard ground. Signals from the strain gauges were amplified, A/D converted, fed into the Vicon system for synchronization, and post-processed in Matlab.

Time courses of forces were expressed in mN based on calibration data for each transducer. Calibration data were obtained prior to experimentation by applying known loads in the range of ±30 mN along x₀, y₀ and z₀. The relation between force and output voltage was linear in all directions. All time courses were low-pass filtered with a fourth-order, zero-lag Butterworth filter with cut-off frequencies of either 12.5 or 25 Hz, which were chosen based on fast Fourier transforms of the raw force signals. Signal drift within a single stance phase (approx. 700 ms) was negligible. Filtered data were corrected for a possible offset in each trial, based on a 200 ms time window prior to the touchdown of the leg. Due to the mechanical arrangement of the steel strips, there was a constant 50% crosstalk between forces measured along x₀ and z₀, which could be corrected by subtraction. Touchdown and lift-off events for each step were determined manually based on the normal force component. To combine motion and force data for torque calculations (below), data were normalized to the duration of the respective stance phase, using cubic spline interpolation. In the Results section, forces are expressed as action (not reaction) forces in body-fixed coordinates [x, y, z].

(c). Rigid link model for torque calculations

In stick insects, motion of each leg is driven by three joints (figure 1a): the thorax–coxa (ThC) joint and the coxa–trochanter (CTr) joint, which together act as the ‘hip’, and the femur–tibia (FTi) joint, which acts as the ‘knee’. Torques about these joints were determined from a three-dimensional rigid link model with 3 d.f. (figure 1c). The CTr and FTi joints are approximated as hinges with 1 d.f. each. They provide elevation–depression and extension–flexion of the leg, respectively. Both joints move in the same plane, the leg plane (dashed line in figure 1c). The ThC joint has actually 3 d.f., similar to a ball-and-socket joint. However, most of the movement around this joint is described by the coupled protraction–retraction and supination–pronation of the leg plane [25]. The ThC joint axis can thus be modelled as a single slanted axis (i.e. 1 d.f.). The tibia–tarsus (TiTa) joint was used as an estimate of the foot contacting the ground, because motion-capture markers cannot be placed on the tarsus without restraining movements. Owing to the short length of the coxa (approx. 1.5 mm) and associated difficulties in measuring its orientation accurately within the leg plane, we applied two further model simplifications. First, the ThC joint was considered slanted with respect to the vertical body axis by θ = 30° (see also [25]). Second, the CTr joint was considered to be directly connected to the thorax, such that, with regard to leg depression, the torques about the ThC and CTr joints were lumped together. These model simplifications were justified and did not affect the conclusions reached in this study (electronic supplementary material, figures S2–S4).

Torques about the leg joints (τ = [τ_ThC, τ_CTr, τ_FTi]) were calculated as external torques, assuming quasi-static dynamics. Torques due to gravity and inertia were negligible (electronic supplementary material, figure S1). We combined the orientations and positions of the joints (manipulator Jacobian J) with the three-dimensional force vector 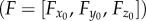measured at the foot according to [26],

2.1

2.2

where a is the rotational axis of a joint and p its position in global coordinates. Note that p_CTr = p_ThC in our model. Positive torques about the slanted ThC joint protract (angle Pro) and supinate (angle Sup) the leg. Positive torques about the CTr and FTi joint lift the femur (angle Lev) and extend the tibia (angle Ext), respectively (figure 1c). To illustrate whether or not a joint rotated in the direction of the applied torque, we calculated each joint's mechanical power as the dot product of the joint's net torque and its angular velocity. To obtain a single angular velocity for the ThC joint (instead of two for Pro and Sup), we took the first derivative of the angle describing the rotation of the leg plane around the slanted ThC joint axis.

(d). Statistical analysis

In the Results section, we first infer the contributions of individual leg joints to propulsion and body weight support from grand mean time courses (mean of animal means). Individuals contributed at least 17 steps to an animal mean. Grand means of hind, middle and front legs were calculated from N = 9, N = 10 and N = 6 animal means, respectively.

To assess whether the shape of the grand mean was representative of the more variable single steps, we calculated the minimum accumulated cost (c) between single-step (s) and grand mean (m) time courses of torques. Unlike a simple point-by-point comparison, which results in large differences if two time series have the same shape but are shifted in time, the minimum accumulated cost allows for temporal variation by ‘synchronizing’ the time series (figure 5a, inset). It therefore represents a meaningful measure of time course similarity. The accumulated cost was calculated using dynamic programming according to [27],

2.3

where d is the Euclidian distance between the value of s at time i (i = 1, 2, … , 100% stance) and the value of m at time j (j = 1, 2, … , 100% stance), and min is the minimum of cumulative distances of adjacent time points. To compare across joints and legs, the accumulated cost was normalized to the peak-to-peak amplitude of the respective grand mean, resulting in the variability index shown in figure 5a. In calculating the accumulated cost, repeated measures of an animal were treated as independent observations and pooled across animals. Sample sizes for right hind, middle and front legs were n = 429, n = 270 and n = 142 steps, respectively. Statistical tests were performed using Matlab and R (R Core Team, www.R-project.com).

Figure 5.

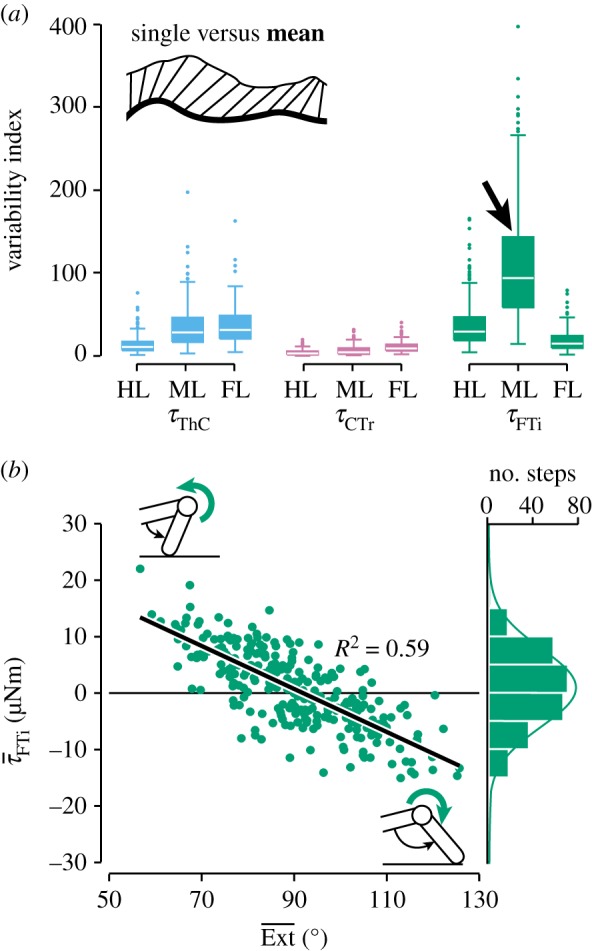
Joint torque variability in level walking. (a) The variability (dissimilarity between single-step and grand mean time courses) was particularly high at the middle leg's FTi joint (arrow). HL, hind leg (n = 429 steps from N = 9 animals); ML, middle leg (n = 270 steps from N = 10 animals); FL, front leg (n = 142 steps from N = 6 animals). (b) At the middle leg's FTi joint, torque magnitudes were negatively correlated with the net extension of the tibia.

3. Results

To study the functions of insect leg joints during free walking, we determined joint torques in the legs of stick insects. Animals walked along a horizontal walkway (figure 1b) at an intermediate forward velocity of 42 ± 10 mm s⁻¹ (mean ± s.d.; n = 841 stance phases from N = 12 animals, pooled across legs). Typically, four legs were in ground contact at any time. Average stance and swing phase durations were 697 ± 190 ms and 254 ± 89 ms, respectively. The average stride frequency was 1.1 ± 0.2 strides s⁻¹.

We will focus on the two major motor tasks in this walking situation: body weight support and propulsion. The control of medio-lateral balance is discussed in electronic supplementary material, S2.

(a). Body weight support

We hypothesized that torques about the CTr joint support the body weight, because this joint depresses the leg. We therefore expected the time courses of CTr torques to positively correlate with the time courses of the vertical leg forces.

The magnitude of vertical forces differed greatly between hind and middle legs, which moved close to the body's CoM, and front legs (see also [16]). Peak forces in hind legs (−4.2 ± 0.6 mN, grand mean ± s.d. of animal means, N = 9) and middle legs (−4.8 ± 0.6 mN, N = 10) supported about 50% body weight each (figures 2 and 3b). In contrast, peak forces in front legs (−1.6 ± 0.4 mN, N = 6) supported only about 20% body weight (figure 4b). As expected, the time courses of vertical forces and CTr torques correlated strongly for both grand means and per-animal means (table 1; p < 0.001 each). CTr torques were directed towards leg depression throughout the stance phase (τ_CTr < 0; figures 2–4c). Peak torques in hind legs (−57.7 ± 6.6 µNm) and middle legs (−54.0 ± 8.8 µNm) were similarly high, and much stronger than in front legs (−22.7 ± 6.0 µNm). These results corroborate the kinematic prediction that torques about the CTr joint are critical for body weight support.

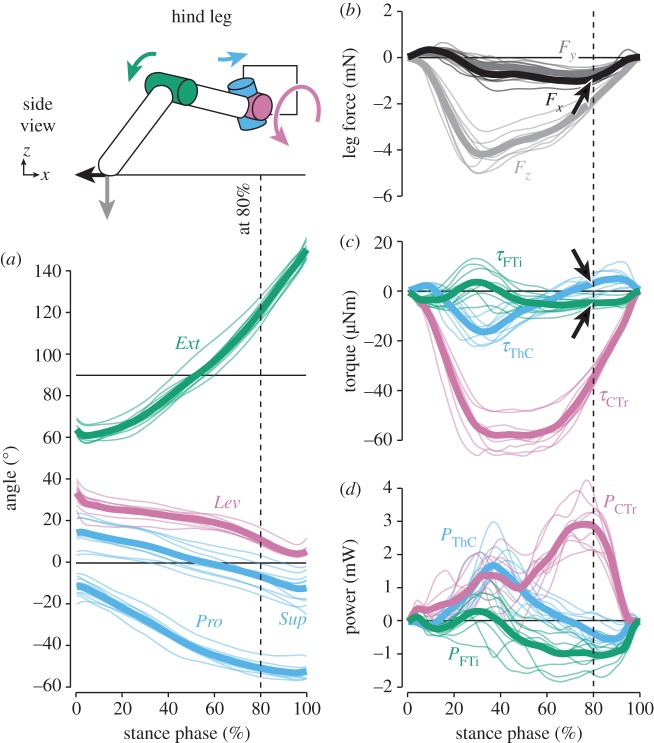
Figure 2.

Kinematics and dynamics of hind legs. Thin lines represent means of individual animals (N = 9), thick lines the grand mean. The schematic illustrates the kinematics and dynamics of the leg at 80% of the stance phase, when the propulsive force was highest (arrow in (b)). Torques about the ThC and FTi joints counteracted the movement of the leg segments at this time (arrows in (c)). See electronic supplementary material, video S1, for an animation.

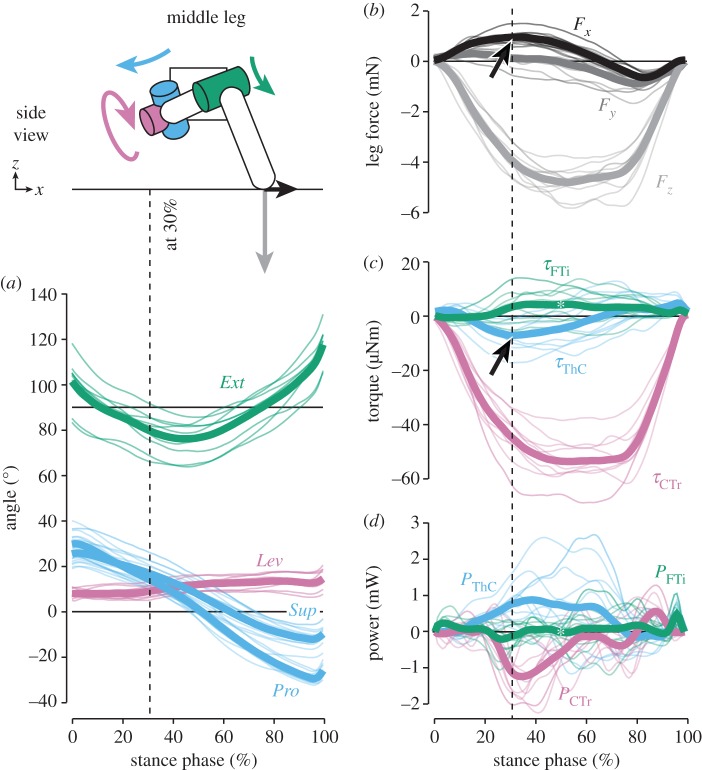
Figure 3.

Kinematics and dynamics of middle legs. Thin lines represent means of individual animals (N = 10), thick lines the grand mean. The schematic illustrates the kinematics and dynamics of the leg at 30% of the stance phase, when the braking force was highest (arrow in (b)). Torques about the ThC joint counteracted the fore–aft force at this time (arrow in (c)). Asterisks in (c,d) point out the variability at the FTi joint, with time courses of opposing signs largely cancelling each other out in the grand mean. See electronic supplementary material, video S2, for an animation.

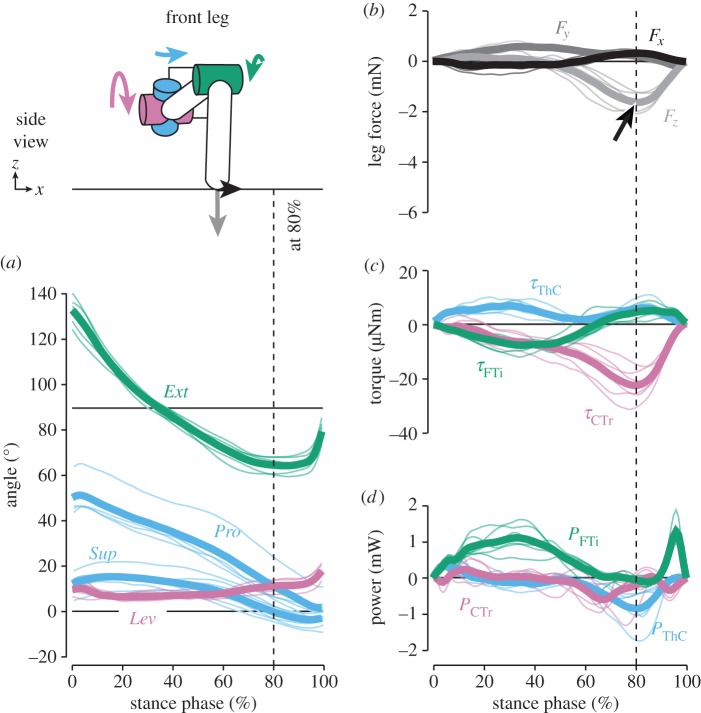
Figure 4.

Kinematics and dynamics of front legs. Thin lines represent means of individual animals (N = 6), thick lines the grand mean. The schematic illustrates the kinematics and dynamics of the leg at 80% of the stance phase, when the vertical force was highest. The arrow in (b) marks the relatively weak contribution to body weight support compared with hind and middle legs. Note that in some steps, small positive vertical forces in the first half of stance resulted from the body being pulled forwards. See electronic supplementary material, video S3, for an animation.

Table 1.

Correlations between time courses of joint torques and leg forces (grand means). The superscripts following the p-values denote the number of individuals with the same correlation result (positive, negative or no correlation) as the grand means. See electronic supplementary material, table S2, for a summary of all correlations.

	hind leg		middle leg		front leg
	r-value	p-value	r-value	p-value	r-value	p-value
τThC versus Fx	0.19	0.06(4/9)	−0.90	<0.001(10/10)	−0.14	0.17(1/6)
τCTr versus Fz	0.96	<0.001(9/9)	1.00	<0.001(10/10)	0.93	<0.001(6/6)
τFTi versus Fx	0.28	<0.01(6/9)	0.07	0.47(2/10)	0.91	<0.001(6/6)

(b). Propulsion

We hypothesized that the proximal ThC joint and the distal FTi joint control propulsion, because all legs were substantially retracted and flexed/extended about these joints (angles Pro and Sup; figures 2–4a). We therefore expected the time courses of ThC and FTi torques to positively correlate with the time courses of the fore–aft leg forces. Unexpectedly, correlations were generally weak (table 1).

In hind legs, fore–aft forces were directed backwards to propel the body until the end of the stance phase (F_x < 0; figure 2b; see also [16]). Torques about the ThC joint, however, only initially pointed towards retraction (τ_ThC < 0; figure 2c). ThC torques peaked at approximately 30% of the stance phase (−16.3 ± 4.1 µNm), but were small or even switched towards protraction when propulsive forces were highest (figure 2c, arrow). Accordingly, the mechanical power at the ThC joint peaked at approximately 30% of the stance phase and declined to zero thereafter (figure 2d). Although the leg was extended throughout the stance phase (Ext increased to 150°), torques about the FTi joint pointed towards flexion during the second half (τ_FTi < 0; figure 2c, arrow). Accordingly, the mechanical power was negative during this time. Torques about the ThC and FTi joints therefore correlated only weakly with the fore–aft forces of the leg. At the CTr joint, on the other hand, the mechanical power peaked at the time of maximum propulsive force (approx. 80% stance phase; figure 2d). These results suggest that propulsive fore–aft forces in hind legs resulted to a large extent from strong CTr torques pressing down the extended leg and, in turn, extending the tibia (see also electronic supplementary material, video S1).

In middle legs, fore–aft forces were mainly directed forwards (F_x > 0) to decelerate the body, and switched to backward-directed propulsive forces (F_x < 0) only near the end of the stance phase (figure 3b; see also [16]). Torques about the ThC joint, however, first pointed towards retraction, then towards protraction—opposite to the fore–aft forces measured on the ground (figure 3c, arrow). Time courses of ThC torques were in fact strongly negatively correlated with the fore–aft forces for both grand means and per-animal means (table 1; p < 0.001 each). The time point at which the ThC torque switched from net retraction to net protraction could be predicted by the time point at which the leg plane switched from supination to pronation (linear regression on per-animal means; d.f. = 8, p < 0.001, R² = 0.77). Notably, torques about the FTi joint were highly variable (see below). The variability can be seen in figure 3c (asterisk), where the grand mean shows only a small net extension torque because animal means of opposing signs largely cancelled each other out. Therefore, the correlation between time courses of FTi torques and fore–aft forces was weak (table 1). Unexpectedly, fore–aft forces resulted again to a large extent from CTr torques. Strong depression torques concurrently reduced propulsion at the beginning of stance when the leg plane was supinated (Sup > 0) and increased propulsion late in stance when the leg plane was pronated (Sup < 0) (see also electronic supplementary material, video S2). Accordingly, the time point at which the fore–aft force switched from pointing forwards to pointing backwards could be predicted by the time point at which the leg plane switched from supination to pronation (linear regression on per-animal means; d.f. = 8, p < 0.01, R² = 0.65).

These results suggest that depression torques about the CTr joint of hind and middle legs were critical for generating propulsion, in addition to supporting the body weight. Contrary to kinematic predictions, torques about the ThC and FTi joints contributed relatively little to propulsion in these legs and were often directed opposite to the movement of the leg segments. Only the relatively small propulsive forces of front legs were generated by torques about the FTi joint (figure 4; electronic supplementary material, video S3). Torques towards flexion (τ_FTi < 0) ‘pulled’ the animal forwards in the first half of the stance phase when the leg moved more in parallel to the long body axis. Correlations between time courses of FTi torques and fore–aft forces were significant in all animals (table 1; p < 0.001).

(c). Joint-specific variability

Torques about the middle leg's FTi joint appeared to be more variable than at any other joint. To analyse this observation statistically and compare across joints and legs, we assessed the variability of joint torques by comparing the shape of the grand mean time course to the time courses of single steps (see Material and methods). The resulting variability index differed significantly among joints (ANOVA for steps pooled across animals; F_8,2514 = 403.25, p < 0.001) and was indeed highest for the middle leg's FTi joint (figure 5a, arrow; Tukey's HSD tests at the 0.05 level of significance). Torques about this joint varied considerably from step to step, spanning a large continuum from net flexion to net extension (figure 5b, histogram). Opposite time courses of torques were measured at the middle leg FTi joints of all animals, but did not occur at any of the other leg joints. A large part of the variability could be accounted for by step-to-step variations in the orientation of the tibia within the leg plane. For each step, we averaged the FTi torque and the extension angle across each stance phase to give the net torque magnitude and the net tibia orientation. Torques tended to counteract a deviation from an angle of 90° relative to the femur (Ext = 90°), which is the neutral posture of the tibia (figure 5b). That is, high torques towards flexion (τ_FTi < 0) tended to occur when the tibia was strongly extended (Ext > 90°) and, vice versa, high torques towards extension (τ_FTi > 0) tended to occur when the tibia was strongly flexed (Ext < 90°). A linear regression on steps pooled across animals was significant (d.f. = 268, p < 0.001, R² = 0.59; figure 5b), as were the 10 per-animal regressions (p < 0.01 each).

In contrast to the FTi joint of the middle leg, the variability of torques about the other leg joints was related to smaller variations in timing and magnitude, such that the grand means captured the general shape of the time course. Linear correlations between torque magnitudes and any one postural parameter or walking speed were weak at these joints (data not shown). Smaller variations probably resulted from cumulative effects, which may include variable activation dynamics of insect muscle [28], variable stance phase durations of the other legs, and other causes.

4. Discussion

We have determined complete time courses of joint torques in all legs of freely walking stick insects with a precision and resolution that was previously available only in vertebrate experiments. We found that the leg joints contributed differently to propulsion and body weight support (figures 2–4), and that some joint torques were highly flexible (figure 5).

(a). Unexpected joint functions in walking stick insects

Unexpectedly, walking stick insects generated propulsive forces mainly by the same action that also supported body weight against gravity: depression of their hind and middle leg femora. Owing to the pronation of the leg plane with regard to the vertical, hind legs could accelerate the body by CTr torques that depressed the femur and, in turn, extended the tibia (figure 2). Similarly, middle legs decelerated or accelerated the body by CTr torques whenever the leg plane was supinated or pronated, respectively (figure 3). These mechanisms were not directly predicted from kinematics, because all legs are retracted and flexed/extended around the ThC and FTi joints in the direction expected for propulsion. Instead, ThC and FTi torques were often directed opposite to the movement of the leg segments or the fore–aft forces measured on the ground. Albeit counterintuitive at first sight, these torque patterns can be explained by a posture-dependent mechanism that counteracts gravity-induced collapse of the leg under body load. For example, further extension of a highly extended leg is counteracted by a flexion torque, as seen in hind and middle legs (figures 2c and 5b). Similarly, further supination of an already supinated middle leg is counteracted by a retraction torque (figure 3c). The requirement for torques counteracting the effects of gravity is similar in sprawled-postured vertebrates that lift their body above the ground [5,6]. Upright/sagittal postures like those of humans typically require extension torques to counteract gravity-induced flexion of the leg joints [29].

(b). Common principles in locomotion control: power and steering units

Although details of stick insect joint torques might reflect specializations to meet the animal's distinct morphology and posture, the mechanism of controlling propulsion by means of femoral depression probably reflects a more common principle in locomotion.

Cockroaches, for example, move their hind legs in a plane that is more horizontal than vertical [22], very different from stick insects. In this posture, depression of the femur results not only in a downward but also a rearward push, which generates thrust. Accordingly, activity patterns of the cockroach depressor trochanteris muscle were interpreted in control of both body weight support and propulsion [30,31]. Our measurements predict a similar role for the depressor muscle in the stick insect. Despite substantial differences in leg posture and kinematics, the two major model systems in insect walking appear to control propulsion more similarly than previously thought.

At a more conceptual level, the ThC and FTi joints serve the leg to maintain a particular pushing direction, thus ‘steering’ the power provided by the CTr joint to control walking. An analogous functional division into ‘power’ and ‘steering’ joints has been found in the control of insect escape jumps [32,33]. Locusts, for example, power their jumps with torques about the FTi joint and steer by controlling jump elevation with the ThC joint [32]. Froghoppers power their jumps with torques about the CTr joint and steer by controlling jump azimuth with the FTi joint [33]. In a similar vein, large indirect flight power muscles of most insects provide the mechanical energy required for flapping the wings, while smaller steering muscles determine its transformation into lift and drag by adjusting the stroke plane and the wing's angle of attack [34,35]. Our findings provide the prospect that such a control strategy is also common in walking insects with distinctly different leg posture and kinematics. Note that this does not necessarily imply a total functional separation into power and steering units. Insect flight power muscles, for example, can modulate steering as well [36,37]. And in the case of stick insect walking, the anatomically complex ThC joint could assist the CTr joint in body support and depression-driven propulsion if it was modelled with more than 1 d.f. (see electronic supplementary material, S1).

(c). Implications of joint torques for models of walking control

Current models of sensory control of insect walking incorporate both behaviour-derived mechanisms [20] and physiological mechanisms inferred from reduced preparations [8]. While these models replicate basic joint kinematics [38], some control aspects may have to be revised to account for the joint torques in free walking.

One aspect concerns the timing of step phase transitions. Our data suggest that load signals from the CTr joint might be more suitable in this regard than proprioceptive signals from the other leg joints, and from the FTi joint [7] in particular. This is because CTr joint torques were comparatively high and invariable (see low step-to-step variability in figure 5a). High torques are a consequence of the horizontal posture of the trochantero-femur, being nearly orthogonal to the resultant ground reaction force vector. This situation is very similar to that in sprawled-postured vertebrates [5,6]. From a mechanical perspective, high CTr torques and associated high strains in the trochantero-femur may seem undesirable. Fast-running cockroaches, for example, appear to minimize the total amount of torques produced by the leg joints [14]. From a control perspective, on the other hand, strong and reliable changes in CTr torques may facilitate the control of stance by means of local load sensors. Indeed, strain sensors in the form of campaniform sensilla are highly concentrated near the CTr joint and are known to provide reinforcing excitatory input to the motor neurons of the depressor muscle [39]. A strong decrease in torques could cause a sudden drop in this excitatory input and terminate the stance phase in a reliable manner.

Another aspect concerns the timing and magnitude of torque generation at the ThC and FTi joints. In current control models, joint torques are generated assuming distinct states of antagonistic neural activity [8,38]. These states of activity are thought to reflect joint kinematics, in that for example leg retraction and extension are generated by retraction and extension torques. Our data challenge this assumption, because the need to counteract gravity-induced collapse of a leg under load also requires torques counteracting a joint's movement (figures 2, 3 and 5). Generating these flexible, posture-dependent torques might in turn require a more flexible activation of motor neural networks than currently envisaged, possibly even co-activation.

In revising current models of walking control, it will thus be helpful to understand how torques are related to antagonistic muscle activity at the joints, and how torques are shaped by passive forces from muscles [11] and skeletal structures [12]. As joint torques represent the net effect of active and passive forces [1], future studies will need to combine inverse dynamics with electromyographic recordings in freely walking insects to reveal the relationship between motor input and motor output at the joints.

Data accessibility

Data deposited in Dryad: http://dx.doi.org/10.5061/dryad.md17d.

Authors' contributions

C.J.D. and J.S. conceived the study; C.J.D. performed experiments and analysed results; C.J.D., V.D. and J.S. interpreted results; C.J.D. drafted the manuscript; C.J.D., V.D. and J.S. revised the manuscript and gave final approval for publication.

Competing interests

The authors declare no competing interests.

Funding

This work was supported by Large-Scale Project 4 (EICCI) of the Cluster of Excellence Cognitive Interaction Technology ‘CITEC’ (EXC 277) funded by the German Research Foundation (DFG).