Investigation of grid performance using simple image quality tests

Abstract

Antiscatter grids improve the X-ray image contrast at a cost of patient radiation doses. The choice of appropriate grid or its removal requires a good knowledge of grid characteristics, especially for pediatric digital imaging. The aim of this work is to understand the relation between grid performance parameters and some numerical image quality metrics for digital radiological examinations. The grid parameters such as bucky factor (BF), selectivity (Σ), Contrast improvement factor (CIF), and signal-to-noise improvement factor (SIF) were determined following the measurements of primary, scatter, and total radiations with a digital fluoroscopic system for the thicknesses of 5, 10, 15, 20, and 25 cm polymethyl methacrylate blocks at the tube voltages of 70, 90, and 120 kVp. Image contrast for low- and high-contrast objects and high-contrast spatial resolution were measured with simple phantoms using the same scatter thicknesses and tube voltages. BF and SIF values were also calculated from the images obtained with and without grids. The correlation coefficients between BF values obtained using two approaches (grid parameters and image quality metrics) were in good agreement. Proposed approach provides a quick and practical way of estimating grid performance for different digital fluoroscopic examinations.

Introduction

Grids are important tools of the detection part of the X-ray systems for the effective rejection of scattered X-rays and image quality improves at a cost of increased patient dose with their use.

In conventional radiology, the grids are selected according to the type of procedure considering the patient dose image quality optimization. Once a specific grid is installed in an X-ray system, it is permanently used for all the clinical procedures undertaking in this system and is rarely changed. Although the removal of the grid is recommended for some cases, especially for the fluoroscopic pediatric examinations, it is not frequently done in the routine work because of practical limitations.[1]

The situation is different for digital radiology and fluoroscopy. Adjustment of image contrast in these systems gives the user an option to remove the grid when the patient radiation dose becomes critical. Some predictions can be made for patient dose image quality optimization from the grid parameters for some adult patient examinations, but this becomes more difficult for pediatric patients because of their thinner body parts and higher radiation sensitivities. It is also not easy to define a range of patient thickness where removal of grid is suggested.

In digital radiology and fluoroscopy, flexibility of using different type of grids in one system or making the examinations without any grid require better understanding of the grid parameters by the users.

Grid manufacturers specify their products with grid pattern, focus range, grid ratio, strip density, cover, and inter-space materials. The performance characteristics of grids are given by some other parameters. Following the measurements of transmissions of primary, scatter, and total radiation, the primary transmission (T_p), scatter transmission (T_s), and total transmission (T_t) radiation factors are calculated and bucky factor (BF), contrast improvement factor (CIF), selectivity (Σ), and signal-to-noise improvement factors (SIF_GP) are determined from these factors. However, performance of a specific grid for a particular examination cannot be predicted from these data alone. Evaluation of grid specifications may assist the users to have a relative idea about the patient dose-image quality optimization for the selection of a specific grid. Although manufacturers make recommendations for the appropriate grids to be used for the clinical applications, it is the responsibility of users to select the optimum grid for their specific clinical procedure and to implement the examination with or without grid in the case of pediatric examinations.

The aim of this work is to understand the relation between grid performance parameters and some numerical image quality metrics for digital fluoroscopic examinations. We also investigated if any information can be obtained from the use of these metrics regarding the prediction of grid efficiency, especially for pediatric examinations. For this purpose, grid parameters were measured together with some image quality metrics for different acquisition geometries. To find the grid parameters, primary, scatter, and total radiation were measured using four grids with different grid ratios, strip densities, and cover materials for various scatter thicknesses and tube voltages, using the acquisition geometries suggested by International Electrotechnical Commission (IEC) and grid parameters mentioned above were calculated.[2] In the second part of work, the images of low- and high-contrast phantoms were obtained with and without grids using similar acquisition geometries and exposure parameters. The numerical image quality metrics such as contrast, signal-to-noise ratio (SNR), high-contrast spatial resolution (HCSR), and SIF_IQ were determined. These results were evaluated to determine the relation between grid parameters and image quality metrics. In addition, the variation of grid parameters as a function of scatter thicknesses and tube voltage were investigated. Patient thickness ranges that can be examined with or without grid for pediatric examinations are also suggested.

Materials and Methods

A prototype digital fluoroscopy unit dedicated for research and training purposes was used in this study. The system is equipped with an amorphous silicon flat panel of 24.5 cm × 29.5 cm detector (Varian PacScan 2520V, Varian Medical System, USA) with a detector pitch of 124 µm. All exposure readings were acquired with RadCal 20 × 6–6 (MDH-Radcal Monrovia CA, USA) 6cc ion chamber. Focus to chamber distance of 115 cm was kept constant for all the measurements. The X-ray tube voltage was set to 70, 90, and 120 kVp. Half-value layer was measured as 3.1 mm Al at 80 kVp. Fluoroscopic exposures rates were adjusted for each beam quality by adjusting the tube mA only. Polymethyl methacrylate (PMMA) blocks of dimensions 25 cm × 25 cm × 5 cm were used to build thicknesses of 5 cm, 10 cm, 15 cm, 20 cm, and 25 cm to simulate different projection of adult and pediatric patients. Reproducibility of X-ray exposure and accuracy of the kVp settings were checked routinely and were found to be <2%. The response function of the detector was measured for each beam quality and linearity of image pixel value with detector air kerma was confirmed.[3] Detector offset and gain corrections were made whenever the beam quality and the grid were changed.

Measurement and calculation of some grid parameters

In the initial part of this work, some of the grid parameters such as primary transmission (T_p), the scatter transmission (T_s), and total transmission (T_t) factors were measured for 12 grids. Among those, four grids with different ratios, strip densities, and cover materials were selected for the remaining part of this work [Table 1] and those giving close performance to the selected ones were excluded. Acquisition geometries defined in IEC standard were used with minor modifications.[2] Instead of using a single scatter thickness, measurements were repeated for the PMMA thicknesses of 5 cm, 10 cm, 15 cm, 20 cm, and 25 cm at tube voltages of 70 kVp, 90 kVp, and 120 kVp. The dose rate at the entrance of the phantoms was within 55–1350 µGy/sec range.

Table 1.

Properties of the grids used in the study

For the measurement of the primary radiation, the geometry shown in Figure 1 was used. PMMA blocks were placed next to the X-ray port to reduce the scatter radiation by the air gap as much as possible. The outside of the detector field was covered with a lead collimator except for a 10 mm diameter opening so that the primary photons entered perpendicularly to the flat panel detector. Exposures were made with and without grid using the same tube currents and T_P values were calculated from the mean value of pixels in the region of interests (ROI) selected on the respective images. This geometry was carefully aligned for each exposure to use the same detector region. The primary transmission factor is expressed by the following equation:

Figure 1.

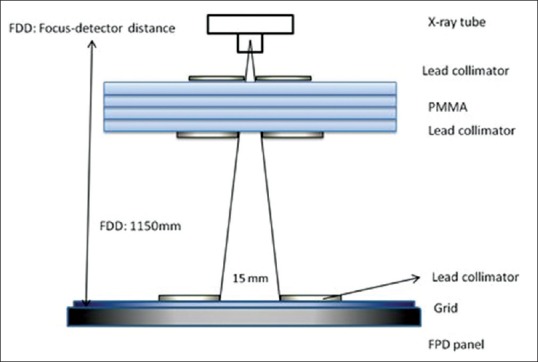
Configuration used for the measurement of primary radiation

T_p = P⁺/P⁻ (1)

where P+ and P− represent the mean ROI pixel values for grid and nongrid measurements, respectively.

Figure 2 shows the configuration for the measurement of scatter transmission, T_s. PMMA blocks were placed adjacent to the detector surface and primary radiation was stopped with a lead plate with diameter of 30 mm and 4 mm thickness. Measurements were obtained from a circular ROI with 10 mm diameter at the center of the image. The scatter transmission factor is calculated from the ratio of mean pixel contents with and without grid as;

Figure 2.

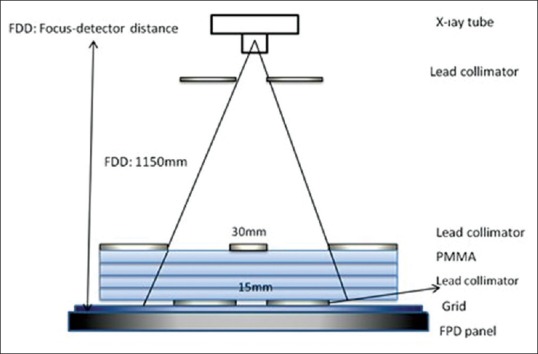
Configuration used for the measurement of scatter radiation. The same configuration is used to measure the total radiation after the removal of 30 mm lead collimator

T_s = S⁺/S⁻ (2)

The beam stop was removed for the measurement of total transmission radiation (primary plus scatter) and total transmission factor was calculated similarly from the mean pixel values obtained from images with grid (T⁺) and without grid (T⁻):

T_t = T⁺/T⁻ (3)

Next, the BF_GP, Σ, CIF, and SIF_GP were calculated as follows;

The BF is defined as the factor by which the patient exposure is increased when a grid is used and is given by the following equation

BF_GP = 1/T_t (4)

The selectivity is defined as the ratio of the primary transmission to the scatter transmission of the grid showing the ability of a grid to remove scatter and is calculated as

Σ = T_p/T_s (5)

The main task of the grid is to improve the image contrast by preventing the scattered radiation reaching the detector and the effectiveness of the grid in improving image contrast is given by the CIF:

CIF = T_p/T_t (6)

The ratio of SNR values obtained from images with and without grid is defined as the SNR improvement factor, and SIF is commonly used as an indication of grid performance in digital imaging.[4,5] A SIF value of higher than one indicates improvement of image quality with the use of grid. It is calculated from the following equation:[4]

SIF_GP = T_p/T_t^0.5 (7)

Image quality measurements

In the second part of this work, image quality measurements were made using low-contrast (LCD4, Leeds test objects, 2000) and HCSR (Hüttner type 18) phantoms. The low-contrast phantom consists of a series of 11.1 mm diameter discs with different object contrasts. The Hüttner phantom used for HCSR measurements consists of groups of square wave patterns of spatial frequency varying from 0.5 to 5.0 cycles/mm. The low-contrast phantom was positioned at the surface of the PMMA block facing the X-ray tube for the measurement of minimum detectable contrast (MDC) and the Hüttner phantom was placed at its center with a 45° orientation. MDC and highest perceptible spatial frequencies in terms of Lp/mm were determined qualitatively obtaining the mean score of three observers. A small cupper disk with a diameter of 2 cm and 0.64 mm thickness was also fitted adjacent of Hüttner phantom for contrast and SNR measurements. PMMA blocks were placed next to the detector leaving a small gap from the detector cover for the positioning of the grids. Measurements were carried out with and without grids using a subset of thicknesses, tube voltages, and mA stations. X-ray beam was collimated to the border of PMMA blocks. The following numerical parameters were evaluated for the performance evaluation of grids;

The contrast (C) was calculated from the mean pixel values measured from the ROIs placed within the border of the Cu disk image (N_l) and background region (N_BG).

C = (N_l – N_BG)/N_BG(8)

The SNR was determined using the same ROIs defined above;

SNR = (N_l – N_BG)/(N_l + N_BG)^0.5 (9)

HCSR was calculated from the Hüttner image;

HCSR = SD₁ – SD₂ (10)

where SD₁ is the standard deviation of the pixel values in an ROI selected inside the Group 7 and SD₂ is the standard deviation for the pixel values in the ROI selected in the background of the phantom image.[6]

BF was calculated from the ratio of pixel contents measured from the images taken without (N_BG⁻) and with grids (N_BG⁺), since the similar exposure parameters were used for these image pairs.

BF_IQ = N_BG⁻/N_BG⁺ (11)

Finally, SIF_IQ were calculated from SNR measurements using images obtained with and without grids.

SIF = SNR⁺/SNR⁻ (12)

Results

All the measurements were made with and without grid by changing the thickness of PMMA blocks and repeating measurements for each kVp settings and then, by changing the kVp at each thickness.

Table 2 presents the measured and calculated metrics of four grids for different PMMA thicknesses (5, 10, 20, and 25 cm). These measurements were repeated at 70 kVp, 90 kVp, and 120 kVp. T_p, T_s, and T_t of all grids decreased with increasing grid ratio due to the reduction of solid angle given by the space between lead strips.

Table 2.

Measured and the calculated grid parameters

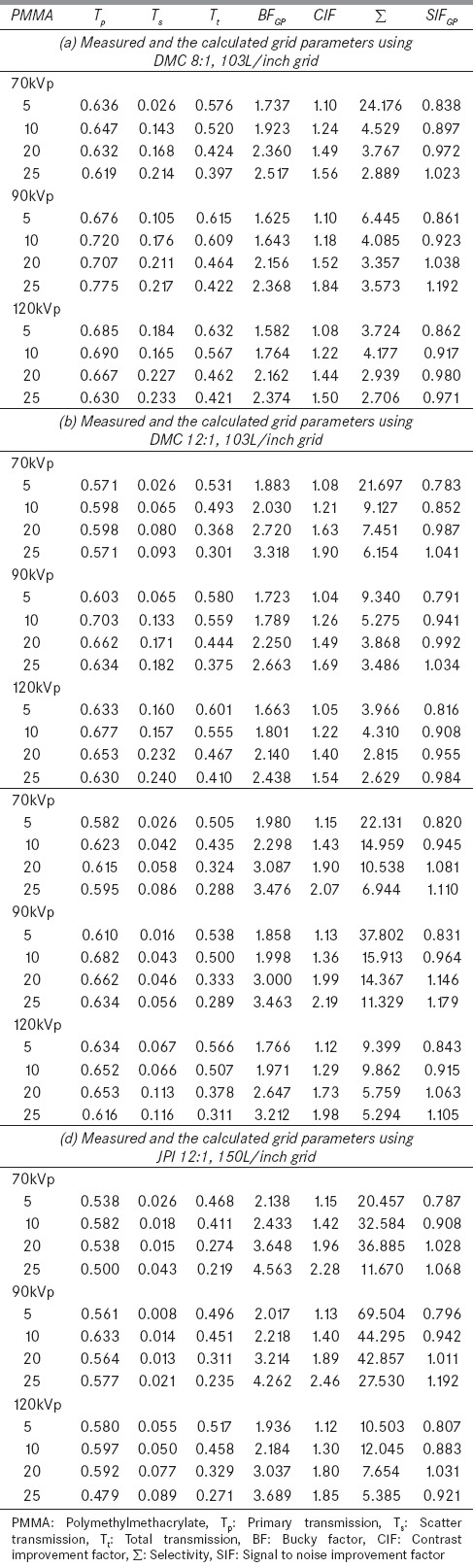
T_p did not change with the scatter thickness for any of the grids at any tube voltage except for a drop that was observed for the JPI 12.1 grid. Slightly higher T_P values of some grids were observed for 90 kVp for the blocks thicker than 5 cm.

T_s values of carbon cover grids slightly increase with increasing PMMA thickness and the rate of increase with thickness reduced with kVp. The increase in T_s for aluminum (Al) cover grids was lower and did not change with grid ratio. The increase in T_s with kVp was more obvious, similar for each thickness for all the grids with the exception of 5 cm scatter thickness.

A linear decrease in T_t with scatter thickness was observed for all the grids at each kVp. The increase of T_t with kVp was saturated for some grids after 90 kVp and the increase slightly continued for others, reflecting the kVp variation of T_p and T_s.

The T_p, T_s, and T_t values of grids with Al cover were lower than those found for carbon cover grids due to their higher attenuation of X-rays. Table 2 also gives the BF_GP, Σ, CIF, and SIF_GP results. The variation of BF_GP with PMMA thickness and kVp followed the reciprocal of T_t as expected. Σ and CIF also showed consistent behavior with their definitions; CIF increased and Σ decreased with thickness for each kVp setting and their variation with tube voltage followed the variations of T_p, T_s, and T_t. In general, our results were in agreement with the reported values.[7,8,9,10,11,12]

SIF_GP values increased with thicknesses for each kVp setting for all the grids and slightly higher values were observed at 90 kVp for the larger thicknesses of Al cover grids. SIF_GP values were less than one for all the grids for 5 cm and 10 cm thicknesses at all kVp settings. SIF_GP values were very close to one for the majority of the grids even for 20 cm thickness, but were higher than one for 25 cm thickness. In general, SIF_GP values of A1 cover grids were higher than those for carbon cover grids.

Table 3 shows C, SNR, BF_IQ, HCSR, MDC, SIF_IQ, and Lp/mm results measured from the phantom images of PMMA blocks at three different kVps.

Table 3.

Measured and the calculated image quality parameters

C decreased linearly with scatter thickness for all the grids, but with a slower rate at higher kVp images. Contrast reduces with the tube voltage at each scatter thickness, but with a lower rate in comparison to reduction with thicknesses. The rate of decrease was the lowest for nongrid case.

The SNR decreased linearly with thickness at 70 kVp. For 90 kVp and 120 kVp, however, SNR drops sharply between 5 cm and 10 cm thicknesses and reduces with a much slower rate after 10 cm thickness. SNR values of different grids were quite close to each other, even to the SNR of images obtained without grid. SNR decreased linearly with the tube voltage for the blocks thicker than 5 cm, but with a slower rate with increasing thickness. For 5 cm thickness, SNR increased with kVp for all the grids and SNR of nongrid images were slightly higher. This is because the improvement of SNR with beam quality is more dominant than its degradation due to the low scatter effect of 5 cm block.

Variation of HCSR with PMMA thickness and tube voltage shows a similar behavior with the variation of SNR. The improvement of HCSR with the use of grids was also more obvious than the improvement of SNR.

The contrast, SNR, and HCSR of Al covered grids were better than the carbon covered grids probably due to their very low scatter transmission factors. However, the BF of these grids was remarkably higher because of their poor transmission factor for primary radiation.

BFs were also calculated from the ratio of pixel contents in the ROIs selected at the uniform part of the phantom images taken without and with grid, since the same exposure parameters (kVp, mA, etc.) were used for the collection of these images. Variation of BFs with block thicknesses and kVp were similar to those found from the T_t measurements. High values were observed for the Al cover grids.

SIF_IQ values were less than one for all the grids at each kVp for the thicknesses of 5 cm and 10 cm and slightly higher than one for 15 cm thickness for carbon-covered grids. Higher SIF_IQ values were found almost for all the grids for the thicknesses of 20 and 25 cm indicating the increasing function of the grid with thicknesses.

SIF_IQ values are calculated from SNR measurements. Image noise is signal dependent, i.e., it is different in the areas of high and low attenuation and this affects SNR calculations.[13] We noticed some fluctuations in SNR measurements when very low or very high objects were used in these measurements. Cupper thicknesses in the range of 0.2-1.0 mm provide adequate SNR measurements.

Discussion

In this work, two sets of measurements using similar scatter thicknesses and beam qualities were carried out for the assessment of grid and image quality parameters. Good agreement has been found between the two sets of parameters that may help to better understand the influence of grid characteristics on image quality.

This work is not aiming to suggest the substitution of grid parameters with the image quality indexes for the specification of grid characteristics, because, the image quality results are not only effected from the grid, but also from the object contrast of the image quality phantom and selected exposure geometry.

BF is one of the most important parameters for the grid since it gives the multiplicative factor for the amount of radiation that reaches the patient. BF_GP, measured from grid parameters, and BF_IQ, calculated using image quality phantoms, showed similar variations for different thicknesses and tube voltages. The mean of correlation coefficients between the two BF values for different thicknesses were 96.7, 92.5, and 92.7 at each kVp set, and were 94.5, 80, 86, 91, and 87 for different kVps at each thickness. However, the BFs found from image quality measurements were higher than the BFs calculated from T_t because the scatter is higher in phantom images taken without grid. The range of these BFs was larger than the BFs from T_t measurements, and this range increases as a function of thicknesses. The BFs found from image quality tests should not be an indication of the grid specification, but could be treated as a factor giving the relative radiation dose differences among the grids and the variation of grid response when used with different thicknesses of scatter and tube voltage.

The responses of each grid to the variations of scatter thicknesses and kVp were quite similar for the image quality parameters (C, HCSR, and SNR) and grid characteristic of CIF and Σ. The distinctions of grids from each other were better reflected by the contrast and HCSR in comparison to SNR information. Since the task of the grid is to reduce the effect of scatter as much as possible, the image contrast may be accepted as a good metric for grid performance indication. Regarding to the grid parameters CIF and Σ, probably the Σ is the preferable quantity in this respect, since the contrast is manipulated by the user in digital imaging. Although it was possible to discriminate carbon and Al cover grids from each other, neither image contrast nor Σ gave some distinct results related to the grid ratios, probably due to the use of grids with closer grid ratios in this work. However, considerable fluctuations were observed on Σ due to the very low photon statistic in the scatter fraction measurement geometry.

There is a general consensus in the literature to remove the grids for the radiographic and fluoroscopic examinations of infants and younger children. Some publications make a general advice without giving any body size,[1,14,15] whereas some suggest the removal of grid up to 12–15 cm thicknesses.[16,17,18] There are also some reports in the literature suggesting the removal of grid even for some adult examinations for digital radiography.[19,20]

The SIF_IQ values found from image quality measurement suggest the removal of the grid for 5 cm and 10 cm block thicknesses regardless of the grid type and tube voltage, and this recommendation even holds for 15 cm thickness. This is well-confirmed by the SIF_GP values found from grid characteristics. Grids could be removed up to scatter thickness of 20 cm at some tube voltages for carbon cover grids. In the case of Al cover grids, however, removal of grid cannot be tolerated for 20 cm and 25 cm thicknesses.

In general, the removal of grid around 15–20 cm is debatable and depends on the type of grid and also tube voltage, and could be evaluated in terms of BF and image contrast. For example, in case of carbon cover grid with 8:1 ratio, SIF_IQ is higher than one for 15 cm thickness at all the kVp settings. MDC is 0.42 for all kVp, but at a cost of BF_IQ of 3.2, 2.9, and 2.6. If we again take the MDC value of 0.42 as a base line value, for the grid with the ratio of 12:1, the grid can be removed for thicknesses < 15 cm for 70 kVp providing almost four times less the dose. This issue is more critique for Al cover grids due to their high BFs; removal of grid can be suggested for 15 cm thickness at the tube voltage of 70 kVp for 10:1 ratio grid and probably for 12:1 ratio grid with the BFs of 5.3 and 6.0, respectively.

Both SIF_GP and SIF_IQ increased with thickness and their correlation was quite good for all the grids in the cases of 70 and 90 kVp with mean correlation coefficients of 92.5 and 90.2, but degraded to 76.5 for 120 kVp. However, SIF_GP did not change with kVp.

If we compare the SIF_GP with the SIF_IQ, higher values were noticed for the latter. This is because the effect of scatter is more pronounced for image quality measurements which cause the grid to be more efficient.

Grid manufacturers specify the physical characteristics of their products according to the measurement protocols recommended by IEC; a single size water phantom (30 cm × 30 cm × 20 cm) and a tube voltage of 80 kVp were suggested in this protocol. The grid parameters such as BF, Σ, SNR, and CIF, however, all change with kVp and also with the thickness of the scatter. If there is a need for optimum grid selection for a specific examination or concern about grid removal, user may implement simple image quality tests to assess the image contrast, BF, and SIF. Although results are affected from the object contrast, they can be used as an indication of grid efficiency. Our results also show that investigating the variation of grid characteristics with scatter thickness and tube voltage may help users to predict the performance of their grids for different clinical cases.

Conclusion

The performance of the Al covered grids was better than the carbon-covered grids regarding to image quality. However, the BF of these grids was significantly higher due to the poor transmission factor for primary radiation. The SIF calculated from image quality measurements suggests the removal of the grid for 5–15 cm block thicknesses regardless of grid type.

Financial support and sponsorship

Nil.

Conflicts of interest

There are no conflicts of interest.