Abstract
Modern treatment planning systems provide accurate dosimetry in heterogeneous media (such as a patient' body) with the help of tissue characterization based on computed tomography (CT) number. However, CT number depends on the type of scanner, tube voltage, field of view (FOV), reconstruction algorithm including artifact reduction and processing filters. The impact of these parameters on CT to electron density (ED) conversion had been subject of investigation for treatment planning in various clinical situations. This is usually performed with a tissue characterization phantom with various density plugs acquired with different tube voltages (kilovoltage peak), FOV reconstruction and different scanners to generate CT number to ED tables. This article provides an overview of inhomogeneity correction in the context of CT scanning and a new evaluation tool, difference volume dose-volume histogram (DVH), dV-DVH. It has been concluded that scanner and CT parameters are important for tissue characterizations, but changes in ED are minimal and only pronounced for higher density materials. For lungs, changes in CT number are minimal among scanners and CT parameters. Dosimetric differences for lung and prostate cases are usually insignificant (<2%) in three-dimensional conformal radiation therapy and < 5% for intensity-modulated radiation therapy (IMRT) with CT parameters. It could be concluded that CT number variability is dependent on acquisition parameters, but its dosimetric impact is pronounced only in high-density media and possibly in IMRT. In view of such small dosimetric changes in low-density medium, the acquisition of additional CT data for financially difficult clinics and countries may not be warranted.
Keywords: Computed tomography artifact, computed tomography number, electron density, treatment planning
Introduction
Treatment planning systems (TPS) have evolved from using actual data to analytical approaches derived from pencil beams.[1] The older generations of TPS provided dosimetry exclusively in water (without inhomogeneity correction) based on regular fields[2] and Clarkson integration[3] for irregular fields for patient treatment. However, a patient’s body is not homogenous and not water equivalent. Rather, it is complex and heterogeneous with natural variation in tissues such as lung, cartilage, bone, and implanted high-density and high-atomic number (Z) materials such as dental fillings, pacemakers, and prostheses.
Attempts have been made to provide correction factors for lung inhomogeneity, beginning with Batho.[4] McDonald et al.[5] provided a comprehensive set of tables for lung correction with respect to energy, field size, and depth. The equivalent tissue-air ratio was introduced to correct for inhomogeneities;[6,7] this was followed by power law.[8,9] Use of computed tomography (CT) data did not start until the introduction of the generalized equation based on CT pixel-by-pixel correction.[10] Various other algorithms[11,12,13,14,15] have been proposed over time including algorithm based on electron transport.[16] A detailed evolution of the inhomogeneity correction and its impact on patient care has been provided by AAPM Report 85.[17]
Inhomogeneity corrections were also debated as clinicians were reluctant to use them without clinical outcome data.[17,18,19,20,21,22,23] However, inhomogeneity correction has become an essential part of treatment planning in modern therapy and is required for intensity-modulated radiation therapy (IMRT).[24] Recent advances in dose calculation using advanced algorithms based on Monte Carlo modeling such as pencil beam, convolution/superposition, and collapsed cone have facilitated improved dosimetry and dose calculation accuracies.[17,25,26,27] However, advanced dose algorithms require electron density (ED) from CT data to account for the effects of inhomogeneity rather than physical density scaling as was advocated by the older algorithms such as equivalent path length (EPL).[28] To correlate the CT numbers in a patient’s CT study with the corresponding ED values, a CT number – ED calibration curve should be determined. The CT number of any voxel is given as below which is represented in Hounsfield units (HU):
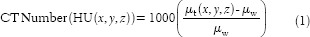
Where x, y, z is the coordinate of a voxel, µt and µw are the linear attenuation coefficients of tissue in a voxel (x, y, z) and water, respectively. CT number is a quantity and HU is a unit; however, these terms are interchangeably used. By definition, HU is 0 for water and −1000 for air at standard temperature and pressure. It is obvious that CT number depends on the attenuation property of a medium, and it should be dependent on beam energy, density, and atomic number.[29] It follows that the CT number of a given tissue is not constant. Rather, it depends on tube voltage (kilovoltage peak [kVp]), field of view (FOV), scattering conditions, and vendor-specific CT reconstruction algorithms.
The tissue characterization in terms of CT number and ED calibration used in TPS have been proposed by several investigators[30,31] using a commercial phantom. The calibration curve (CT-ED) is stored in the database of the TPS for dose calculation purposes. The CT-ED curve and its impact on dosimetry has been documented in the context of older dose calculation algorithms to be 1.3%, 0.8%, 0.5% for Co-60, 6 MV and 21 MV beam, respectively, and was independent of either EPL or power law calculation.[32] Morgan et al.[33] used advanced TPS and quantified the dosimetric impact very similar to data previously presented by Jones et al.[34,35] for variation in lung density and field size.
The selection of CT-scanner and technical consideration for TPS has been provided by Cao et al.[36] Each CT scanner manufacturer optimizes CT images based on the selection of body section to be imaged; however, different techniques may be used depending on the scan protocol. Since the selection of technique on a CT scanner may provide the same tissue with a different CT number, the treatment planner must know the impact of such changes. The variation of CT numbers due to different scanning parameters has been noted by many investigators,[37,38,39] and some studies have been performed to investigate its dosimetric effect by using inhomogeneous cubic or anthropomorphic phantoms.[40,41] Most of these studies evaluated the absolute doses per monitor unit (MU) to a single point (such as isocenter or a reference dose point) without consideration of dose coverage to targets and critical organs. The impact of kilovoltage setting for low-Z inhomogeneity for a scanner has also been reported to be insignificant clinically,[42] however variability among different CT scanners studies has been limited. Recently Zurl et al.[43] compared CT parameters and showed that variation up to 20% in HU could be noted; however the impact on dose is limited to only 1.5%. Thus, effect of CT number for photon and electron beam Monte Carlo calculations has been noted to be different and needs attention.[44] Ebert et al.[45] provided variability of CT number from a GE scanner at various kV settings and tube currents. It was shown that tube current (mAs) does not a play role and only kV provides variation in CT number.
The objective of this review article is to evaluate the variation of CT numbers of different scanning parameters such as tube voltage (kVp), and physical and reconstruction FOV on several commercial scanners and compare it with other publications. The dosimetric impact of different CT number - ED calibration from different scanners is also evaluated for clinical cases with emphasis on dose coverage to tumor targets and its impact to critical organs. Conclusions are then made if such CT data are needed within the limit of dosimetric accuracy for radiotherapy centers and countries where additional scan could be a financial hardship to the patients.
Computed Tomography Number to Electron Density Calibration
To revisit CT number-ED calibration, a tissue characterization phantom (RMI, Gammex, Middleton, WI, USA) was used to evaluate under different scanning conditions. The phantom consists of a solid water disk approximating the size of an average pelvis that contains interchangeable rods made of various tissue equivalent materials. The physical density (g/cm3) ranges from 0.3 (LN-300 lung) to 1.84 (cortical bone), and the corresponding ED relative to water varies from 0.292 to 1.707. The RMI CT-phantom is commonly used in radiotherapy clinics in the United States. The quality assurance in the manufacturing of these tissue-equivalent plugs is very precise (<1% variation), which was verified among five phantoms.[46] The phantom was placed in the center of a CT gantry by careful alignment with lasers and scanned with different imaging protocols using various tube voltages (80–140 kVp) on each scanner. Two reconstruction fields of view (33 cm and 48 cm) were chosen to reconstruct the images with a 512 × 512 matrix with 5 mm slice thickness contiguously. After image reconstruction, a circular region of interest (ROI) of 1.5 cm diameter was placed on each density plug and the mean CT numbers of the ROIs were recorded. To minimize the effect of image artifacts and beam hardening, multiple CT scans of the phantom were acquired with different combinations of insert position and the resultant mean CT numbers were averaged. The same process was repeated on several scanners including wide bore (85 cm) and small bore (72 cm) Philips PQ5000 scanners (Philips HealthCare, Andover, MA, USA) and a Somatom 4 scanner (Siemens Medical Solutions, Malvern, PA, USA). The CT number - ED table was generated in each configuration as described by Constantinou et al.[30] The resultant CT number - ED conversions were compared between different scanners, reconstructed FOV, and tube voltages.
Dosimetric Impact of Computed Tomography Number to Electron Density Calibration
The CT number - ED calibration tables were imported into the Eclipse TPS (Varian Medical Systems, Palo Alto, CA, USA) and were used to investigate its impact on dose calculations. Under institutional review board exempt status, two typical cases (lung and prostate) were chosen in this study. Treatment planning was performed using the analytical anisotropic algorithm that provides superior inhomogeneity correction as reported by many investigators.[47,48,49] To investigate the dosimetric impact in low-density tissues, three-dimensional (3D) conformal as well as IMRT plans were generated to achieve optimum coverage of a representative tumor lesion centrally located in the right lung of a patient for both 6 and 15 MV X-rays. In each plan, a different CT number - ED calibration table for a given tube voltage (80 kVp–140 kVp) was used for inhomogeneity correction. The remaining parameters, for example, beam arrangements, and MU were kept the same. The difference in dose coverage of the planning target volume (PTV) and organs at risk (OAR) (lung and heart) were compared by evaluating the dose-volume histograms (DVHs). In the second case, the CT study of a prostate cancer patient was chosen so that some beams passed through the hip with high-density bone compared to the soft tissue. A 3D treatment plan using 4-field box technique was generated as well as a 7-field IMRT plan. The dose differences in PTV and OAR (rectum, bladder, and femoral heads) with various ED tables were evaluated. For comparison in both cases and techniques, 3D conformal radiation therapy (3DCRT) and IMRT, the MU calculated for the 140 kVp CT scan for optimum coverage of the PTV was used for calculation in other CT scans with different kVp setting. Again, the planning parameters, for example, beam arrangements, fields, and MU were kept the same. For clinical evaluation of treatment plans, a new concept based on volume difference from DVH (dV-DVH) is introduced to provide to compare competing DVHs when the differences among the DVHs are negligible. The dV-DVH of a structure is a plot of the difference between the volume of the structure covered by a given dose and a reference volume at the same dose. The dV-DVH magnifies the subtle difference between DVHs that are closed to each other. This proposed concept dV-DVH provides a better evaluation tools for plan comparisons where DVHs have small differences and are not differentiated. The clinical implication of dV-DVH is yet to be realized as we believe this is the 1st time that the concept of dV-DVH is introduced in treatment planning.
Outcome of Computed Tomography Number to Electron Density Calibration
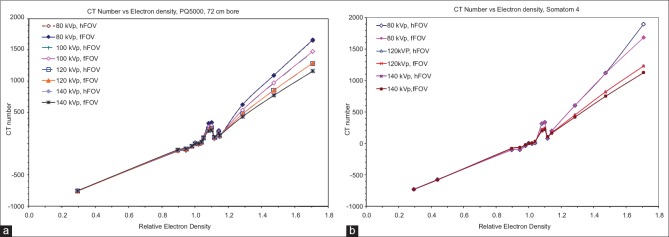
CT number versus relative ED for different tube voltages and reconstructed FOVs were plotted for a Philips PQ5000 and a Siemens Somatom 4 scanner in Figure 1a and b, respectively. The discontinuity (bump) at around density 1.1 is typical of RMI phantom and has been noted by other investigators.[42,46] This is probably due to the artifact in the plug that has different chemical compositions but same physical density. The differences in CT numbers versus tube voltages are minimal in the density region from 0.3 (lung) to 1.0 (water). This discrepancy becomes significant for high-density materials and can reach up to 43% for cortical bone (1668 HU at 80 kVp vs. 1167 at 140 kVp) with a trend that higher kVp yields a lower CT number. This is probably due to the increase in photoelectric attenuation for lower photon energies which lead to higher CT number. Full- and half-FOV reconstructions have little effect on the CT numbers of all materials for both scanners; the only exception was the 11% difference (1869.4 HU vs. 1686.4 HU) for cortical bone at 80 kVp for the Somatom 4 CT.
Figure 1.
Computed tomography number versus tube voltage for a Philips PQ5000 (a) and Somatom 4 scanner (b). For both scanners, data are shown with full (f) and half (h) field of view. Note that the computed tomography number is relatively unaffected for low-density materials for both kilovoltage peak and field of view
The illustration in Figure 2 compares the CT number to relative ED calibration curves of the two CT scanner vendors for the same FOV. Significant differences in CT number were observed for high-density tissues between the two scanners. Lower kVp tends to have larger discrepancy between scanners with the maximum difference of 15% at 80 kVp. The CT number to ED calibration curves for the Philips PQ5000 scanner with different gantry apertures (72 cm and 85 cm) are compared as shown in Figure 3. Again at low density, there is no difference in CT numbers. However, large differences are noted at higher densities especially for bone. The maximum difference in CT number was 10% occurring at 80 kVp for cortical bone.
Figure 2.
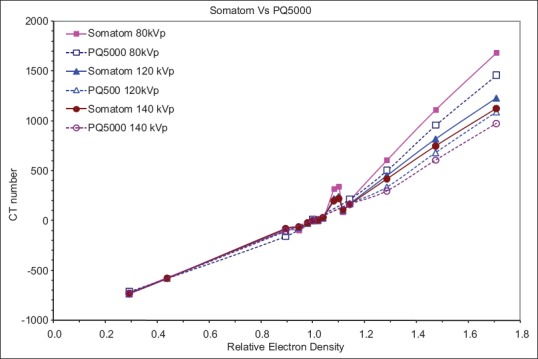
Comparison of computed tomography number from two different manufacturers (Philips and Siemens) with same scan aperture and reconstructed field of view. Note significant changes in computed tomography number for bone with two scanners
Figure 3.
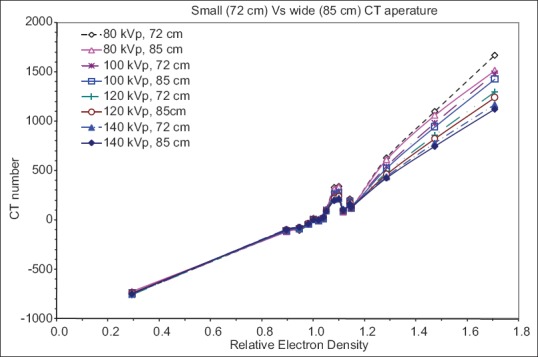
Comparison of computed tomography number for Philips PQ5000 with different apertures (72 cm and 85 cm). There is a very little difference in computed tomography number between two scanners
Dosimetric Impact in Clinical Cases
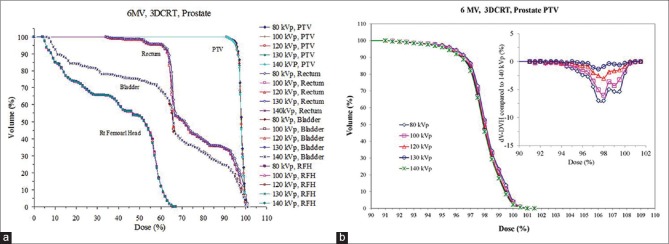
The dosimetric impact of ED variation was revisited to evaluated two clinically relevant cases (lung and prostate). For the lung case, the differences between 3DCRT and IMRT were minimal for PTV coverage for all ED tables. Figure 4 shows the DVHs for the 3DCRT plans with 6 MV beams. It can be seen that for a given structure (PTV or OAR), the DVHs are practically indistinguishable for all CT number to ED curves obtained with different kVp. Similar findings were also observed for 15 MV beam (not shown). For the IMRT plans, the small differences among the various plans are probably due to the plan optimization process. Overall, the differences in DVHs caused by different CT number to ED calibrations were negligible (<1%) for all 4 plans (6 MV and 15 MV and 3DCRT and IMRT). This is probably because the CT number variation of lung tissue for different tube voltages has been shown to be minimal [Figures 1 and 2]. To better examine and quantify the small deviation in DVHs, the PTV volume coverage of all the ED calibrations was compared to that of 140 kVp. The differences in the range of dose levels (90–110%) were minimal. For both the 6 MV and 15 MV plans, the calibration of 80 kVp led to the largest deviation from that of 140 kVp with less volume coverage. This might be caused by high-density material presented in the paths of the beams. Nevertheless, the maximum difference was only 1.1% for both plans and can be considered as clinically insignificant. Similarly, no significant difference was found for DVHs of critical organs such as spinal cord, heart, and right lung as shown in Figure 4.
Figure 4.
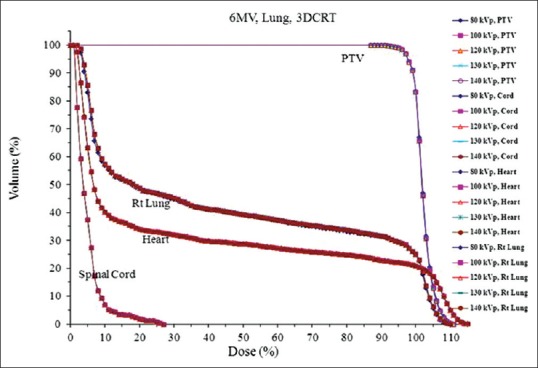
Dose-volume histograms of planning target volume, spinal cord, heart and lung of a tumor lesion centrally located in the right lung calculated using computed tomography number to electron density calibrations of different tube voltages (80–140 kVp)
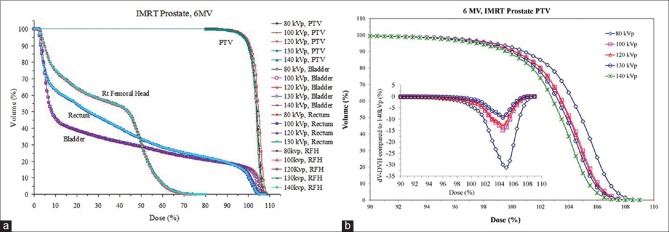
Compared with the lung case, the DVHs for the prostate PTV demonstrated a slightly larger difference between different tube voltage calibrations as shown in Figure 5a and b and Figure 6a and b for 3DCRT and IMRT, respectively. The dV-DVH concept was introduced to magnify the effect of differences in DVH which is shown in the insets [Figures 5b and 6b] whereas differences in DVH seem to be small. For both 6 MV and 15 MV plans, lower kVp calibration tends to result in less volume coverage for dose range from 95% to 100% of the prescription dose. The largest differences were −9.6% for 6 MV and −8.3% for 15 MV fields, respectively, both occurred at the 97.5% of dose prescription in 3DCRT. This dose deviation can be mainly caused by the presence of large bony structures around prostate and the considerable variation of CT number - ED versus tube voltage of high-density materials as demonstrated in Figures 1 and 2. With regard to critical organs such as rectum and bladder, the tube voltage caused very small variation in dose distribution as shown in Figures 5 and 6.
Figure 5.
(a) Comparison of dose-volume histogram for a prostate three-dimensional conformal radiation therapy with various electron densities associated with tube voltages (80–140 kVp) and (b) magnified view of dose-volume histogram for planning target volume only. Also note the plot of dV-dose-volume histogram in inset providing useful information where dose-volume histogram cannot be easily differentiated
Figure 6.
(a) Comparison of dose-volume histogram for a prostate intensity-modulated radiation therapy with various electron densities associated with tube voltages (80–140 kVp) and (b) magnified view of dose-volume histogram for planning target volume only. Also note the plot of dV-dose-volume histogram in inset providing useful information where dose-volume histograms cannot be easily differentiated
The differences are slightly higher in IMRT plans as shown in Figure 6b compared to Figure 5b for the 3DCRT. Some of these differences are inherent to IMRT optimization where an exact solution is not achievable and variability in inter- and intra-institution and planner are significant.[50] The differences in 3DCRT and IMRT for the prostate case are <2% and <5%, respectively, based on analysis of dV-DVH as shown in Figures 5b and 6b.
Discussion
Two types of curves CT number versus ED and ED versus CT numbers are shown in various references.[31,32,40,42,45] However, CT number versus ED curve is better suited as ED is unknown variable which should be evaluated based on scanners derived CT number. We reevaluated and quantified the variation of CT number - ED calibration between different vendors, tube voltages, and FOVs and its impact on radiation treatment planning and dose calculation as shown by other investigators.[32,40,42] After scanning an ED calibration phantom using the same scanning parameters on six different scanners, Constantinou et al.[30] observed more than 200 HU difference in cortical bone between different scanner vendors. By analysis of published data for a number of scanners, Thomas[32] showed that there was no great difference in the relationship between CT number to relative ED for low-density materials between the different manufacturers and calibration techniques. These are confirmed in this study. For high-density materials, considerable differences between data sets from different machines and measurement techniques were observed. Analytic calculation based on effective depth showed that changes in inhomogeneity correction factors were less than 1.5% for a 10% change in CT number. In a similar study, CT number was found to be stable with respect to different acquisition parameters, except for the tube voltage setting that can lead to errors of about 300 HU for high-density materials.[40] The authors also investigated the dosimetric impact using a simplified anthropomorphic phantom with a single bone embedded in a tissue equivalent material and found around 2% maximum error. Guan et al.[41] investigated the dosimetric impact of different CT number - ED curves for full lung plus three typical bone sites under single beam irradiation. The dose per MU was found to be 2% higher for 80 kV than that of 130 kV at a depth just beyond bone for high-density bones. For low-density bones and lung, the difference is only 1% or less for different kV. A recent study by Zurl et al.[43] indicated that even though the CT number variation can be significant, its dosimetric impact is limited to only 1.5% concluded from study based on 28 real patients. Compared with the above studies, we observed similar variation in CT number among different scanners. The tube voltage was found to be the most influential factor, whereas other scanner parameters have minimal effect. We also found that CT number deviations are minimal for low-density materials but become significant for high-density materials. Instead of comparing single point dose or MU/Gy in simplified phantoms, we investigated the impact on dose-volume coverage in real patient plans. We found very small differences for PTV coverage in lung, but relatively higher difference for the prostate case as evaluated using dV-DVH.
As demonstrated in our study, high-density materials may have a large effect on the accuracy of CT number and dose calculation. In additional to bones, contrast agents and metal implants are two high-density materials that are commonly present in patient CT scans. The influence of CT contrast agents on dose calculation had been investigated by Ramm et al.[51] A typical bolus of 3 cm3 and CT number of 1400 HU was found to cause overdose of up to 7.4% and 5.4% for 6 MV and 25 MV photon beams, respectively. It was suggested that contrast agents with CT number lower than 500 HU and volume less than 5 cm in diameter will not cause significant changes (<1–3%) in dose calculation. The situation of metal implant is more complex because it not only causes saturation of the CT number in the metal implant itself, but also generates significant artifacts that affect the accuracy of CT numbers of other materials. It is unfortunate that none of the scanners can provide artifact-free CT data as well as none of the TPS can give accurate dose distribution with high-Z materials.[52,53,54,55,56,57,58,59,60] In view of such findings, along with the guideline of dosimetric considerations for patients with hip prostheses as provided in AAPM TG 63 report,[56] it is prudent to eliminate beams passing through metals to reduce dosimetric error.
One of the biggest drawbacks in TPS is the estimation of actual CT number which is marred by the artifact. Artifact reduction algorithms are an active area of research in diagnostic imaging for the interpretation on images as well as dosimetry in radiation therapy. These algorithms have limited success as shown in various references.[28,53,59,61,62,63,64,65,66,67,68,69,70,71,72,73,74] An extended CT-scale calibration to 16 bit has been proposed which has been shown with limited success in the prediction of electron densities of metal inserts.[61,75] Some TPS provide ad-hoc corrections by inserting electron/physical density up to Z = 22 (4.5 g/cm3) for titanium, however prosthesis such as steel, molybdenum, chromium, and various other alloys are still beyond reach of most TPS. Monte Carlo-based TPS which are on the horizon might prove to be useful in such situations.
For most of the studies reported so far, the dosimetric impact of different CT number to ED conversion was mainly focused on photon beams. The variability in CT number could be large but its impact on dose in low-density medium or for thorax and pelvic malignancies are limited (<2%). In addition, most scanners provide very similar CT numbers, as shown by Cheng et al.[46] The influence of scanning parameters on CT number and corresponding dosimetric impact on dose calculation for electron and proton beams require further investigation which has not been discussed here due to range and stopping power issues.[76]
Summary
Based on previously published papers and revisiting this issue from a separate angle, it is concluded that the variation of CT number versus scanning parameters and CT scanner vendors is different. CT numbers for the same material from different CT scanners are expected to be variable. However, for low-density media, CT number changes are minimal with scanners and X-ray energies but deviations could be significant for high-density materials. A higher tube voltage gives lower CT number, while other parameters such as reconstruction FOV and scanner aperture have little effect on CT number. For low-density tissues, inhomogeneity correction can be successfully (±2%) applied with a single CT - ED table for 120–140 kVp. Larger variation in dose coverage was observed for high-density tissues between different tube voltages. Thus, it may be advisable to perform more strict calibrations corresponding to tube energy especially when IMRT is used. The dV-DVH is a simple and useful tool for dosimetric comparison as it enhances graphically the small differences between the DVHs that are superimposed on each other. Validity of acquiring different CT data for planning should be evaluated based on necessity and actual gain in dosimetry especially for poor patients, centers, and countries.
Financial support and sponsorship
Nil.
Conflicts of interest
There are no conflicts of interest.
Acknowledgment
We are greatly thankful to Dr. James McDonough of University of Pennsylvania, Philadelphia, USA, and Mr. Rajinder Singh of St. Vincent Medical Center, Los Angeles, USA, for some of the CT data presented in this manuscript.
References
- 1.Ahnesjö A, Saxner M, Trepp A. A pencil beam model for photon dose calculation. Med Phys. 1992;19:263–73. doi: 10.1118/1.596856. [DOI] [PubMed] [Google Scholar]
- 2.Day MJ. A note on the calculation of dose in X-ray fields. Br J Radiol. 1950;23:368–9. doi: 10.1259/0007-1285-23-270-368. [DOI] [PubMed] [Google Scholar]
- 3.Clarkson JR. A note on depth doses in fields of irregular shape. Br J Radiol. 1941;14:265–8. [Google Scholar]
- 4.Batho HF. Lung corrections in cobalt 60 beam therapy. J Can Assoc Radiol. 1964;15:79–83. [PubMed] [Google Scholar]
- 5.McDonald SC, Keller BE, Rubin P. Method for calculating dose when lung tissue lies in the treatment field. Med Phys. 1976;3:210–6. doi: 10.1118/1.594234. [DOI] [PubMed] [Google Scholar]
- 6.Sontag MR, Cunningham JR. The equivalent tissue-air ratio method for making absorbed dose calculations in a heterogeneous medium. Radiology. 1978;129:787–94. doi: 10.1148/129.3.787. [DOI] [PubMed] [Google Scholar]
- 7.Sontag MR, Cunningham JR. Corrections to absorbed dose calculations for tissue inhomogeneities. Med Phys. 1977;4:431–6. doi: 10.1118/1.594329. [DOI] [PubMed] [Google Scholar]
- 8.Wong JW, Henkelman RM. Reconsideration of the power-law (Batho) equation for inhomogeneity corrections. Med Phys. 1982;9:521–30. doi: 10.1118/1.595098. [DOI] [PubMed] [Google Scholar]
- 9.Young ME, Kornelsen RO. Dose corrections for low-density tissue inhomogeneities and air channels for 10-MV X rays. Med Phys. 1983;10:450–5. doi: 10.1118/1.595392. [DOI] [PubMed] [Google Scholar]
- 10.Wong JW, Henkelman RM. A new approach to CT pixel-based photon dose calculations in heterogeneous media. Med Phys. 1983;10:199–208. doi: 10.1118/1.595294. [DOI] [PubMed] [Google Scholar]
- 11.Tatcher M, Palti S. Evaluation of density correction algorithms for photon-beam dose calculations. Radiology. 1981;141:201–5. doi: 10.1148/radiology.141.1.7291526. [DOI] [PubMed] [Google Scholar]
- 12.Tang WL, Khan FM, Gerbi BJ. Validity of lung correction algorithms. Med Phys. 1986;13:683–6. doi: 10.1118/1.595830. [DOI] [PubMed] [Google Scholar]
- 13.Rice RK, Mijnheer BJ, Chin LM. Benchmark measurements for lung dose corrections for X-ray beams. Int J Radiat Oncol Biol Phys. 1988;15:399–409. doi: 10.1016/s0360-3016(98)90022-0. [DOI] [PubMed] [Google Scholar]
- 14.el-Khatib EE, Evans M, Pla M, Cunningham JR. Evaluation of lung dose correction methods for photon irradiations of thorax phantoms. Int J Radiat Oncol Biol Phys. 1989;17:871–8. doi: 10.1016/0360-3016(89)90081-3. [DOI] [PubMed] [Google Scholar]
- 15.Yu CX, Wong JW. Implementation of the ETAR method for 3D inhomogeneity correction using FFT. Med Phys. 1993;20:627–32. doi: 10.1118/1.597010. [DOI] [PubMed] [Google Scholar]
- 16.Mackie TR, el-Khatib E, Battista J, Scrimger J, Van Dyk J, Cunningham JR. Lung dose corrections for 6- and 15-MV X rays. Med Phys. 1985;12:327–32. doi: 10.1118/1.595691. [DOI] [PubMed] [Google Scholar]
- 17.Papanikolaou N, Battista JJ, Boyer AL, Kappas C, Klein EE, Mackie TR, et al. Madison, WI: AAPM; 2004. Tissue Inhomogeneity Correction for Megavoltage Photon Beams: Report of the Task Group No.65 of the Radiation Therapy Committee of the American Association of Physicist in Medicine, AAPM Report No 85. [Google Scholar]
- 18.Orton CG, Mondalek PM, Spicka JT, Herron DS, Andres LI. Lung corrections in photon beam treatment planning: Are we ready? Int J Radiat Oncol Biol Phys. 1984;10:2191–9. doi: 10.1016/0360-3016(84)90223-2. [DOI] [PubMed] [Google Scholar]
- 19.Mijnheer BJ, Heukelom S, Lanson JH, van Battum LJ, van Bree NA, van Tienhoven G. Should inhomogeneity corrections be applied during treatment planning of tangential breast irradiation? Radiother Oncol. 1991;22:239–44. doi: 10.1016/0167-8140(91)90156-b. [DOI] [PubMed] [Google Scholar]
- 20.McKenna WG, Yeakel K, Klink A, Fraass BA, van de Geijn J, Glatstein E, et al. Is correction for lung density in radiotherapy treatment planning necessary? Int J Radiat Oncol Biol Phys. 1987;13:273–8. doi: 10.1016/0360-3016(87)90139-8. [DOI] [PubMed] [Google Scholar]
- 21.Chin LM, Cheng CW, Siddon RL, Rice RK, Mijnheer BJ, Harris JR. Three-dimensional photon dose distributions with and without lung corrections for tangential breast intact treatments. Int J Radiat Oncol Biol Phys. 1989;17:1327–35. doi: 10.1016/0360-3016(89)90545-2. [DOI] [PubMed] [Google Scholar]
- 22.Jayaraman S, Johnston SA, Sabina SA, Baker AS, Asbell SO. Variation of lung density corrections in a typical patient population. Med Dosim. 1989;14:179–84. doi: 10.1016/0958-3947(89)90205-7. [DOI] [PubMed] [Google Scholar]
- 23.Farraday LA, Doswell GT. Treatment planning for the breast patient: With or without lung correction? Med Dosim. 1992;17:1–9. doi: 10.1016/0958-3947(92)90002-w. [DOI] [PubMed] [Google Scholar]
- 24.Al-Hallaq HA, Reft CS, Roeske JC. The dosimetric effects of tissue heterogeneities in intensity-modulated radiation therapy (IMRT) of the head and neck. Phys Med Biol. 2006;51:1145–56. doi: 10.1088/0031-9155/51/5/007. [DOI] [PubMed] [Google Scholar]
- 25.Ahnesjö A, Weber L, Murman A, Saxner M, Thorslund I, Traneus E. Beam modeling and verification of a photon beam multisource model. Med Phys. 2005;32:1722–37. doi: 10.1118/1.1898485. [DOI] [PubMed] [Google Scholar]
- 26.Dvorak P, Stock M, Kroupa B, Bogner J, Georg D. Analysis of the dose calculation accuracy for IMRT in lung: A 2D approach. Acta Oncol. 2007;46:928–36. doi: 10.1080/02841860701253052. [DOI] [PubMed] [Google Scholar]
- 27.Knöös T, Ceberg C, Weber L, Nilsson P. The dosimetric verification of a pencil beam based treatment planning system. Phys Med Biol. 1994;39:1609–28. doi: 10.1088/0031-9155/39/10/007. [DOI] [PubMed] [Google Scholar]
- 28.Seco J, Evans PM. Assessing the effect of electron density in photon dose calculations. Med Phys. 2006;33:540–52. doi: 10.1118/1.2161407. [DOI] [PubMed] [Google Scholar]
- 29.Watanabe Y. Derivation of linear attenuation coefficients from CT numbers for low-energy photons. Phys Med Biol. 1999;44:2201–11. doi: 10.1088/0031-9155/44/9/308. [DOI] [PubMed] [Google Scholar]
- 30.Constantinou C, Harrington JC, DeWerd LA. An electron density calibration phantom for CT-based treatment planning computers. Med Phys. 1992;19:325–7. doi: 10.1118/1.596862. [DOI] [PubMed] [Google Scholar]
- 31.Saw CB, Loper A, Komanduri K, Combine T, Huq S, Scicutella C. Determination of CT-to-density conversion relationship for image-based treatment planning systems. Med Dosim. 2005;30:145–8. doi: 10.1016/j.meddos.2005.05.001. [DOI] [PubMed] [Google Scholar]
- 32.Thomas SJ. Relative electron density calibration of CT scanners for radiotherapy treatment planning. Br J Radiol. 1999;72:781–6. doi: 10.1259/bjr.72.860.10624344. [DOI] [PubMed] [Google Scholar]
- 33.Morgan AM, Knöös T, McNee SG, Evans CJ, Thwaites DI. Clinical implications of the implementation of advanced treatment planning algorithms for thoracic treatments. Radiother Oncol. 2008;86:48–54. doi: 10.1016/j.radonc.2007.11.033. [DOI] [PubMed] [Google Scholar]
- 34.Jones AO, Das IJ. Comparison of inhomogeneity correction algorithms in small photon fields. Med Phys. 2005;32:766–76. doi: 10.1118/1.1861154. [DOI] [PubMed] [Google Scholar]
- 35.Jones AO, Das IJ, Jones FL., Jr A Monte Carlo study of IMRT beamlets in inhomogeneous media. Med Phys. 2003;30:296–300. doi: 10.1118/1.1539040. [DOI] [PubMed] [Google Scholar]
- 36.Cao M, Das IJ, Mahesh M. Technical factors for consideration in selecting a 4-D CT simulator. J Am Coll Radiol. 2012;9:444–6. doi: 10.1016/j.jacr.2012.02.023. [DOI] [PubMed] [Google Scholar]
- 37.Groell R, Rienmueller R, Schaffler GJ, Portugaller HR, Graif E, Willfurth P. CT number variations due to different image acquisition and reconstruction parameters: A thorax phantom study. Comput Med Imaging Graph. 2000;24:53–8. doi: 10.1016/s0895-6111(99)00043-9. [DOI] [PubMed] [Google Scholar]
- 38.Kilby W, Sage J, Rabett V. Tolerance levels for quality assurance of electron density values generated from CT in radiotherapy treatment planning. Phys Med Biol. 2002;47:1485–92. doi: 10.1088/0031-9155/47/9/304. [DOI] [PubMed] [Google Scholar]
- 39.Millner MR, McDavid WD, Waggener RG, Dennis MJ, Payne WH, Sank VJ. Extraction of information from CT scans at different energies. Med Phys. 1979;6:70–1. doi: 10.1118/1.594555. [DOI] [PubMed] [Google Scholar]
- 40.Cozzi L, Fogliata A, Buffa F, Bieri S. Dosimetric impact of computed tomography calibration on a commercial treatment planning system for external radiation therapy. Radiother Oncol. 1998;48:335–8. doi: 10.1016/s0167-8140(98)00072-3. [DOI] [PubMed] [Google Scholar]
- 41.Guan H, Yin FF, Kim JH. Accuracy of inhomogeneity correction in photon radiotherapy from CT scans with different settings. Phys Med Biol. 2002;47:N223–31. doi: 10.1088/0031-9155/47/17/402. [DOI] [PubMed] [Google Scholar]
- 42.Kendall RL, Gifford KA, Kirsner SM. The impact of peak-kilovoltage settings on heterogeneity-corrected photon-beam treatment plans. Radiother Oncol. 2006;81:206–8. doi: 10.1016/j.radonc.2006.10.005. [DOI] [PubMed] [Google Scholar]
- 43.Zurl B, Tiefling R, Winkler P, Kindl P, Kapp KS. Hounsfield units variations: Impact on CT-density based conversion tables and their effects on dose distribution. Strahlenther Onkol. 2014;190:88–93. doi: 10.1007/s00066-013-0464-5. [DOI] [PubMed] [Google Scholar]
- 44.Verhaegen F, Devic S. Sensitivity study for CT image use in Monte Carlo treatment planning. Phys Med Biol. 2005;50:937–46. doi: 10.1088/0031-9155/50/5/016. [DOI] [PubMed] [Google Scholar]
- 45.Ebert MA, Lambert J, Greer PB. CT-ED conversion on a GE Lightspeed-RT scanner: Influence of scanner settings. Australas Phys Eng Sci Med. 2008;31:154–9. doi: 10.1007/BF03178591. [DOI] [PubMed] [Google Scholar]
- 46.Cheng CW, Zhao L, Wolanski M, Zhao Q, James J, Dikeman K, et al. Comparison of tissue characterization curves for different CT scanners: Implication in proton therapy treatment planning. Transl Cancer Res. 2012;1:236–46. [Google Scholar]
- 47.Fogliata A, Nicolini G, Vanetti E, Clivio A, Cozzi L. Dosimetric validation of the anisotropic analytical algorithm for photon dose calculation: Fundamental characterization in water. Phys Med Biol. 2006;51:1421–38. doi: 10.1088/0031-9155/51/6/004. [DOI] [PubMed] [Google Scholar]
- 48.Van Esch A, Tillikainen L, Pyykkonen J, Tenhunen M, Helminen H, Siljamäki S, et al. Testing of the analytical anisotropic algorithm for photon dose calculation. Med Phys. 2006;33:4130–48. doi: 10.1118/1.2358333. [DOI] [PubMed] [Google Scholar]
- 49.Akino Y, Das IJ, Cardenes HR, Desrosiers CM. Correlation between target volume and electron transport effects affecting heterogeneity corrections in stereotactic body radiotherapy for lung cancer. J Radiat Res. 2014;55:754–60. doi: 10.1093/jrr/rrt231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Das IJ, Cheng CW, Chopra KL, Mitra RK, Srivastava SP, Glatstein E. Intensity-modulated radiation therapy dose prescription, recording and delivery: Patterns of variability among institutions and planning systems. J Natl Cancer Inst. 2008;100:300–7. doi: 10.1093/jnci/djn020. [DOI] [PubMed] [Google Scholar]
- 51.Ramm U, Damrau M, Mose S, Manegold KH, Rahl CG, Böttcher HD. Influence of CT contrast agents on dose calculations in a 3D treatment planning system. Phys Med Biol. 2001;46:2631–5. doi: 10.1088/0031-9155/46/10/308. [DOI] [PubMed] [Google Scholar]
- 52.Erlanson M, Franzén L, Henriksson R, Littbrand B, Löfroth PO. Planning of radiotherapy for patients with hip prosthesis. Int J Radiat Oncol Biol Phys. 1991;20:1093–8. doi: 10.1016/0360-3016(91)90210-u. [DOI] [PubMed] [Google Scholar]
- 53.Hilgers G, Nuver T, Minken A. The CT number accuracy of a novel commercial metal artifact reduction algorithm for large orthopedic implants. J Appl Clin Med Phys. 2014;15:4597. doi: 10.1120/jacmp.v15i1.4597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Keall PJ, Siebers JV, Jeraj R, Mohan R. Radiotherapy dose calculations in the presence of hip prostheses. Med Dosim. 2003;28:107–12. doi: 10.1016/S0958-3947(02)00245-5. [DOI] [PubMed] [Google Scholar]
- 55.Keall PJ, Chock LB, Jeraj R, Siebers JV, Mohan R. Image reconstruction and the effect on dose calculation for hip prostheses. Med Dosim. 2003;28:113–7. doi: 10.1016/S0958-3947(02)00246-7. [DOI] [PubMed] [Google Scholar]
- 56.Reft C, Alecu R, Das IJ, Gerbi BJ, Keall P, Lief E, et al. Dosimetric considerations for patients with HIP prostheses undergoing pelvic irradiation. Report of the AAPM Radiation Therapy Committee Task Group 63. Med Phys. 2003;30:1162–82. doi: 10.1118/1.1565113. [DOI] [PubMed] [Google Scholar]
- 57.Su A, Reft C, Rash C, Price J, Jani AB. A case study of radiotherapy planning for a bilateral metal hip prosthesis prostate cancer patient. Med Dosim. 2005;30:169–75. doi: 10.1016/j.meddos.2005.06.001. [DOI] [PubMed] [Google Scholar]
- 58.Kung JH, Reft H, Jackson W, Abdalla I. Intensity-modulated radiotherapy for a prostate patient with a metal prosthesis. Med Dosim. 2001;26:305–8. doi: 10.1016/s0958-3947(01)00079-6. [DOI] [PubMed] [Google Scholar]
- 59.Lewis M, Reid K, Toms AP. Reducing the effects of metal artefact using high keV monoenergetic reconstruction of dual energy CT (DECT) in hip replacements. Skeletal Radiol. 2013;42:275–82. doi: 10.1007/s00256-012-1458-6. [DOI] [PubMed] [Google Scholar]
- 60.Ding GX, Yu CW. A study on beams passing through hip prosthesis for pelvic radiation treatment. Int J Radiat Oncol Biol Phys. 2001;51:1167–75. doi: 10.1016/s0360-3016(01)02592-5. [DOI] [PubMed] [Google Scholar]
- 61.Glide-Hurst C, Chen D, Zhong H, Chetty IJ. Changes realized from extended bit-depth and metal artifact reduction in CT. Med Phys. 2013;40:061711. doi: 10.1118/1.4805102. [DOI] [PubMed] [Google Scholar]
- 62.Kassim I, Joosten H, Barnhoorn JC, Heijmen BJ, Dirkx ML. Implications of artefacts reduction in the planning CT originating from implanted fiducial markers. Med Dosim. 2011;36:119–25. doi: 10.1016/j.meddos.2010.02.002. [DOI] [PubMed] [Google Scholar]
- 63.Kwon H, Kim KS, Chun YM, Wu HG, Carlson JN, Park JM, et al. , Evaluation of a commercial orthopaedic metal artefact reduction tool in radiation therapy of patients with head and neck cancer. Br J Radiol. 2015;88:20140536. doi: 10.1259/bjr.20140536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Paudel MR, Mackenzie M, Fallone BG, Rathee S. Evaluation of normalized metal artifact reduction (NMAR) in kVCT using MVCT prior images for radiotherapy treatment planning. Med Phys. 2013;40:081701. doi: 10.1118/1.4812416. [DOI] [PubMed] [Google Scholar]
- 65.Robertson DD, Yuan J, Wang G, Vannier MW. Total hip prosthesis metal-artifact suppression using iterative deblurring reconstruction. J Comput Assist Tomogr. 1997;21:293–8. doi: 10.1097/00004728-199703000-00024. [DOI] [PubMed] [Google Scholar]
- 66.Toftegaard J, Fledelius W, Seghers D, Huber M, Brehm M, Worm ES, et al. Moving metal artifact reduction in cone-beam CT scans with implanted cylindrical gold markers. Med Phys. 2014;41:121710. doi: 10.1118/1.4901553. [DOI] [PubMed] [Google Scholar]
- 67.Wang G, Snyder DL, O’Sullivan JA, Vannier MW. Iterative deblurring for CT metal artifact reduction. IEEE Trans Med Imaging. 1996;15:657–64. doi: 10.1109/42.538943. [DOI] [PubMed] [Google Scholar]
- 68.Glover GH, Pelc NJ. An algorithm for the reduction of metal clip artifacts in CT reconstructions. Med Phys. 1981;8:799–807. doi: 10.1118/1.595032. [DOI] [PubMed] [Google Scholar]
- 69.Bal M, Spies L. Metal artifact reduction in CT using tissue-class modeling and adaptive prefiltering. Med Phys. 2006;33:2852–9. doi: 10.1118/1.2218062. [DOI] [PubMed] [Google Scholar]
- 70.Wei J, Chen L, Sandison GA, Liang Y, Xu LX. X-ray CT high-density artefact suppression in the presence of bones. Phys Med Biol. 2004;49:5407–18. doi: 10.1088/0031-9155/49/24/001. [DOI] [PubMed] [Google Scholar]
- 71.Andersson KM, Ahnesjö A, Vallhagen Dahlgren C. Evaluation of a metal artifact reduction algorithm in CT studies used for proton radiotherapy treatment planning. J Appl Clin Med Phys. 2014;15:4857. doi: 10.1120/jacmp.v15i5.4857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Baissalov R, Sandison GA, Donnelly BJ, Saliken JC, McKinnon JG, Muldrew K, et al. Suppression of high-density artefacts in X-ray CT images using temporal digital subtraction with application to cryotherapy. Phys Med Biol. 2000;45:N53–9. doi: 10.1088/0031-9155/45/5/404. [DOI] [PubMed] [Google Scholar]
- 73.Li H, Noel C, Chen H, Harold Li H, Low D, Moore K, et al. Clinical evaluation of a commercial orthopedic metal artifact reduction tool for CT simulations in radiation therapy. Med Phys. 2012;39:7507–17. doi: 10.1118/1.4762814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Yazdi M, Gingras L, Beaulieu L. An adaptive approach to metal artifact reduction in helical computed tomography for radiation therapy treatment planning: Experimental and clinical studies. Int J Radiat Oncol Biol Phys. 2005;62:1224–31. doi: 10.1016/j.ijrobp.2005.02.052. [DOI] [PubMed] [Google Scholar]
- 75.Coolens C, Childs PJ. Calibration of CT Hounsfield units for radiotherapy treatment planning of patients with metallic hip prostheses: The use of the extended CT-scale. Phys Med Biol. 2003;48:1591–603. doi: 10.1088/0031-9155/48/11/308. [DOI] [PubMed] [Google Scholar]
- 76.Das IJ, Paganetti H. Madison, WI: Medical Physics Publishing; 2015. Principles and Practice of Proton Beam Therapy. [Google Scholar]