Volume and Value of Big Healthcare Data

Abstract

Modern scientific inquiries require significant data-driven evidence and trans-disciplinary expertise to extract valuable information and gain actionable knowledge about natural processes. Effective evidence-based decisions require collection, processing and interpretation of vast amounts of complex data. The Moore's and Kryder's laws of exponential increase of computational power and information storage, respectively, dictate the need rapid trans-disciplinary advances, technological innovation and effective mechanisms for managing and interrogating Big Healthcare Data. In this article, we review important aspects of Big Data analytics and discuss important questions like: What are the challenges and opportunities associated with this biomedical, social, and healthcare data avalanche? Are there innovative statistical computing strategies to represent, model, analyze and interpret Big heterogeneous data? We present the foundation of a new compressive big data analytics (CBDA) framework for representation, modeling and inference of large, complex and heterogeneous datasets. Finally, we consider specific directions likely to impact the process of extracting information from Big healthcare data, translating that information to knowledge, and deriving appropriate actions.

In 1798, Henry Cavendish estimated the mean density of the Earth by studying the attraction of 2-inch diameter pendulous balls to larger 10-inch diameter ones and comparing that to the Earth's gravitational pull [1]. Just like many scientists before him, he used less than 30 observations to provide a robust estimate of a parameter of great interest, in this case, the mean density of the Earth (5.483±0.1904 g/cm³). Nowadays, using modern physics techniques, we know that the Earth's real mean density is 5.513 g/cm³, which is within Cavendish’ margin of error, but requires powerful instruments, millions of observations, and advanced data analytics to compute.

Big Data vs. Big Hardware

It is accepted that all contemporary scientific claims need to be supported by significant evidence, allow independent verification and agree with other scientific principles. In many cases, this translates into collecting, processing and interpreting vast amounts of heterogeneous and complementary observations (data) that are transformed into quantitative or qualitative information ultimately leading to new knowledge. The Moore's and Kryder's laws of exponential increase of computational power (transistors) and information storage, respectively [2], are driven by rapid trans-disciplinary advances, technological innovation and the intrinsic quest for more efficient, dynamic and improved human experiences. For instance, the size and complexity of healthcare, biomedical and social research information collected by scientists in academia, government, insurance agencies and industry doubles every 12-14 months [3]. By the end of 2014, about 1 in 2 people across the Globe will have Internet access and collectively humankind (7.4 billion people) may store more than 10²³ bytes (100 Zettabytes) of data.

Consider the following two examples of exponential increase of the size and complexity of neuroimaging and genetics data, Table 1. These rates accurately reflect the increase of computational power (Moore's law), however they are expected to significantly underestimate the actual rate of increase of data acquisition (as only limited resources exist to catalogue the plethora of biomedical imaging and genomics data collection) [2].

Table 1.

Increase of Data Volume and Complexity relative to Computational Power.

Neuroimaging (annually)		Genomics (BP/Yr)		Moore's Law (transistor counts)	Bandwidth (Edholm's Law)	Years
Size	Complexity	Size	Complexity
200 GB	1	10 MB	1	1×105	105	1985-1989
1 TB	2	100 MB	2	1×106	106	1990-1994
50 TB	5	10 GB	3	5×106	108	1995-1999
250 TB	6	1TB	4	1×107	109	2000-2004
1 PB	7	30TB	5	8×106	1010	2005-2009
5 PB	8	1 PB	7	1×109	1011	2010-2014
10+ PB	9	20+ PB	8	1×1011	1013	2015-2019 (estimated)

MB (megabyte) = 10⁶, GB (gigabyte) = 10⁹, TB (terabyte) = 10¹², PB (petabyte) = 10¹⁵, BP=base pairs Complexity = measure of data heterogeneity (e.g., new imaging data acquisition modalities or sequence coverage depth; complexity of 5 indicates a 5-fold increase of the data diversity over 1985)

Neuroimaging Genetics

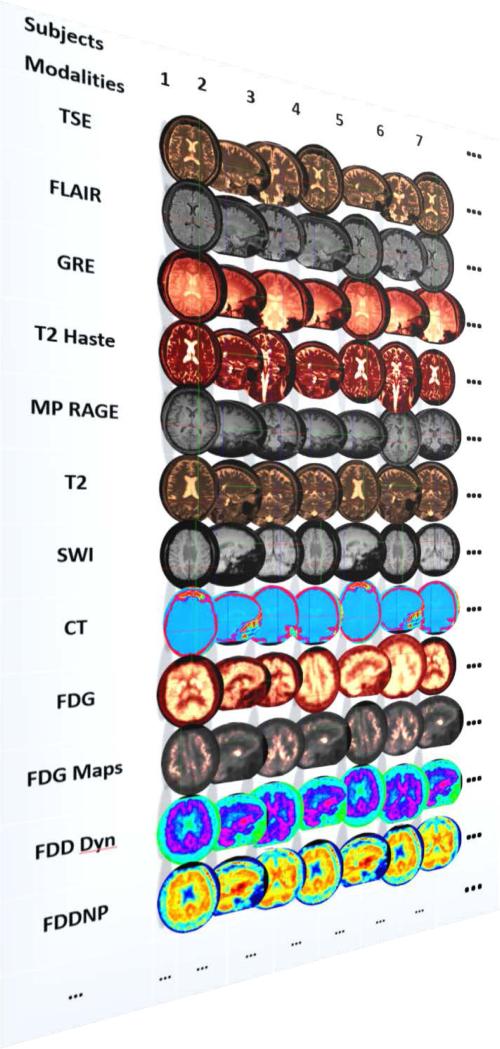
Figure 1 demonstrates the increase of data complexity and heterogeneity as new neuroimaging modalities, acquisition protocols, enhanced resolution and technological advances provide rapid and increasing amount of information (albeit not necessarily completely orthogonal to other modalities). In addition to the imaging data, most contemporary brain mapping studies include complex meta-data (e.g., subject demographics, study characteristics), clinical information (e.g., cognitive scores, health assessments), genetics data (e.g., single nucleotide polymorphisms, genotypes), biological specimens (e.g., tissue samples, blood tests), meta-data, and other auxiliary observations [4, 5]. Clearly there are four categories of challenges that arise in such studies. First is the significant complexity of the available information, beyond data size and source heterogeneity. Second, the efficient representation of the data, which needs to facilitate handling incompleteness and sampling incongruence in space, time and measurement. Third, the data modeling is complicated by various paradigm and biological constrains, difficulties with algorithmic optimization, and computing limitations. Forth, the ultimate scientific inference requires high-throughput, expeditive and adaptive joint processing, analysis and visualization, which are extremely difficult in Big Data explorations using all the available information, as opposed to relying on a smaller and cleaner sample of homologous elements.

Figure 1.

The expansion of new multi-channel imaging modalities in brain-mapping studies illustrates the rapid increase of data complexity. Image modality abbreviations: TSE=turbo spin echo; FLAIR=Fluid-attenuated inversion recovery (magnetic resonance imaging, MRI, pulse sequence); GRE=gradient-echo imaging; T2 Haste=T2-weighted half-Fourier acquisition single-shot turbo spin-echo; MP RAGE=magnetization-prepared rapid gradient-echo imaging; T2=spin-spin relaxation image magnetization allowing decay before measuring the MR signal by changing the echo time (TE); SWI=Susceptibility weighted imaging; CT=computed tomography; FDG=fluorodeoxyglucose positron emission tomography (PET) imaging; FDG Maps=(various) derived volumetric statistical maps; FDD Dyn=dynamic Frequency Domain Decomposition; FDDNP=2-(1-{6-[(2-[fluorine-18]fluoroethyl)(methyl)amino]-2-naphthyl}-ethylidene)malononitrile. The heterogeneity of these data is used to illustrate the data size, complexity, multiple scales, and source diversity of only one component of contemporary neurodegenerative studies – neuroimaging data.

Big Data Characteristics

Big healthcare data refers to complex datasets that have some unique characteristics, beyond their large size, that both facilitate and convolute the process of extraction of actionable knowledge about an observable phenomenon. Typically, Big healthcare data include heterogeneous, multi-spectral, incomplete and imprecise observations (e.g., diagnosis, demographics, treatment, prevention of disease, illness, injury, and physical and mental impairments) derived from different sources using incongruent sampling.

There are two important characteristics of Big healthcare data – their energy and life-span. Energy encapsulates the holistic information content included in the data, which, because of its size, may often represent a significant portion of the joint distribution of the underlying healthcare process. That is, the instance of Big biomedical data may resemble extremely closely the unknown distribution of the clinical phenomenon of interest. This facilitates accurate exploration of the clinical state of patients or cohorts purely by empirically observed information, rather than by analytical or parametric models, which may be associated with specific assumptions limiting their applications.

As an example, consider a fusion of US healthcare, economics and demographic data collected by the Centers for Medicare & Medicaid Services (CMS), Bureau of Labor Statistics (BLS) and the Census Bureau. An instance mashing these heterogeneous and complex data (for 2012) is aggregated and distributed by the SOCR Data Dashboard (http://socr.umich.edu/HTML5/Dashboard) [6]. The energy of the integrated data archive is more than the sum of the information content contained within each database individually. The potential to explore multivariate associations across the aggregated dataset make it more useful for both within discipline explorations, e.g., healthcare expenditures (CMS) may be affected by employment statistics (BLS), as well as across discipline studies, e.g., impact of race (Census) on physician reimbursement rates (CMS) accounting for labor force participation (BLS). Such mashed datasets poses many of the core Big Data characteristics, e.g., multiple source heterogeneities, high-dimensionality, large size, incongruences of sampling rates, and incompleteness.

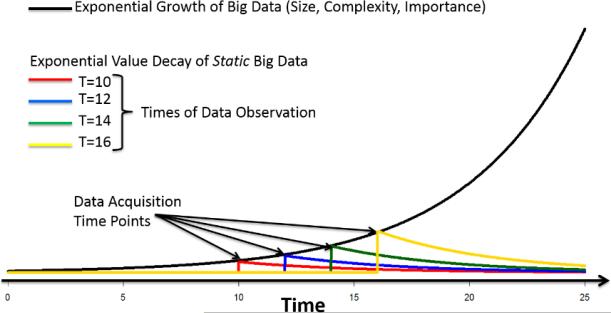
Much like the observed exponential increase of the size and complexity of Big healthcare data, its life-span, in terms of its value past time of acquisition, also follows an exponential model. However, the lifespan and value of healthcare data rapidly decay at an exponential rate – this is known as information devaluation, see Figure 2. For instance, the power of the aggregated CMS, BLS and Census data archive rapidly decays as the relevance of the data to influence bio-social decision making (political, healthcare, demographic, economic, etc.) diminishes significantly over time. Although the 2012 statistics may be useful to predict 2015 Medicare spending, relative to the changing population demographics and the state of the economy (e.g., unemployment, inflation), the most significant predictors would be the (observed or predicted) population size, healthcare costs and medical procedures reimbursement rates observed in years 2013-2017. Thus, rapid acquisition, aggregation, processing and democratization of data is critical to fully utilize their potential power, extract useful information, and derive actionable knowledge.

Figure 2.

Parallels between the growth in size and decay in value of large heterogeneous datasets. The horizontal axis represents time, whereas the vertical axis shows the value of data. As we acquire more data at an ever faster rate, its size and value exponentially increase (black curve). The color curves indicate the exponential decay of the value of data from the point of its fixation (becoming static).

Big Data Analytics

There is currently no established analytical foundation for systematic representation of Big Data that facilitates the handling of data complexities and at the same time enables joint modeling, information extraction, high-throughput and adaptive scientific inference. One idea is to explore the core principles of distribution-free and model-agnostic methods for scientific inference. Classical examples of these include non-parametric techniques that enable data-driven decision making, without making specific assumptions about the process distribution, and calculation or estimation of statistics as functions on a sample independent of parameter specifications [7, 8]. In these cases, scientific inference does not depend on fitting parametrized distributions but rather on ordering, comparing, ranking or stratifying statistics derived from the observed data [9]. Modern classification, prediction, and machine-learning inference approaches differ from model-based parametric methods by their underlying assumptions and the number of parameters that need to be estimated to generate the framework supporting the decision making process, data analytics, and inference. Model-based techniques have a fixed number of parameters and postulate explicitly their probability distributions, whereas non-parametric methods relax the a priori beliefs of the parameter distributions and allow varying number of parameters, relative to the amount of training data [10, 11]. Bayesian inference plays a pivotal role in contemporary machine learning, data mining, supervised and unsupervised classification, and clustering [12-14]. The following example illustrates the importance of employing Bayesian principles in Big Data inference. Suppose a patient visits a primary care clinic and is seen by a male provider not wearing a badge or other insignia. Using only this information, to address the clinician appropriately, the patient is trying to figure out if he is more likely to be a doctor or a nurse (assuming these are the only options in this clinical setting). As a male provider, traditional stereotypes may suggest that he is more likely to be a doctor than a nurse. However, a deeper inspection shows exactly the opposite – the odds are that the male provider is a nurse. Why? Let's denote F = Female, D = (primary care) Doctor, and N = Nurse. We can use Bayesian rule [15] to compute the odds likelihood ratio, $\frac{P(N\mid M)}{P(D\mid M)}$, which represents the data-driven evidence about the enigmatic credentials of the (male) healthcare provider:

$$\underset{\begin{array}{c}\hfill oddslikelihood\hfill \\ \hfill ratio\hfill \end{array}}{\underbrace{\frac{P(N\mid M)}{P(D\mid M)}}}=\frac{\frac{P(M\mid N)\times P\left(N\right)}{P\left(M\right)}}{\frac{P(M\mid D)\times P\left(D\right)}{P\left(M\right)}}=\underset{likelihoodratio}{\underbrace{\frac{P(M\mid N)}{P(M\mid D)}}}\times \underset{baserate}{\underbrace{\frac{P\left(N\right)}{P\left(D\right)}}}=\frac{\frac{1}{13}}{\frac{2}{3}}\times \frac{\frac{4,500,000}{US}}{\frac{435,000}{US}}=\frac{3}{26}\times 10.3=1.2.$$

Here, we use the current (2015) estimates of primary care physicians (435K in the US), practicing nurses (4.5M in the US), and the reported gender distributions in the 2 professions (F:M ratios are 1:2 for physicians and 12:1 for nurses), according to the Kaiser Family Foundation ¹. An odds likelihood ratio bigger than 1 illustrates that there is higher chance the (male) healthcare provider is a nurse, rather than a physician, dispelling an initial stereotypic vision of females and males as predominantly nurses and physicians, respectively.

In general, understanding the underlying processes and extracting valuable information from complex heterogeneous data requires distribution-free techniques, as the real probability distributions of multivariate, incomplete, incongruent and large datasets may be out of reach. Joint distribution models for the complete datasets may be impractical, incomplete or inconsistent. Conditional or marginal probability distributions may be available for some variables or well-delineated strata of the data. As many classical statistical methods make assumptions about data distributions, the results from such analyses are valid only when these assumptions are approximately satisfied. For example, bivariate Pearson's correlation assumes normally distributed variables and no significant outliers, whereas Spearman's correlation trades off sensitivity with the need for parametric assumptions, and employs distribution-free rank-ordering, to quantify the strength of bivariate correlation. Typically, distribution-free inference is not completely parameter free. Albeit there may not be distribution model parameters to be estimated, there are still parameters that need to be determined using the training data that can subsequently be used to classify prospective data, predict process behavior, forecast trends or identify associations in testing data [16].

Compressive Sensing Motivation

Another approach to Big Data representation and analytics is Compressive Big Data Analytics (CBDA), which borrows some of the compelling ideas for representation, reconstruction, recovery and data denoising recently developed for compressive sensing [17, 18]. In compressive sensing, a sparse (incomplete) data is observed and one looks for a high-fidelity estimation of the complete dataset. Sparse data (or signals) can be described as observations with a small support, i.e., small magnitude according to the zero-norm. Let's define the nested sets

$$S_k=\{x:{\Vert x\Vert }_o\stackrel{\mathrm{def}}{=}\mid supp\left(x\right)\mid \le k\},$$

where the data x, as a vector or tensor, has at most k non-trivial elements. Note that if x, z ∈ S_k, then

$$x+z\in S_{2k}\supseteq S_k.$$

If Φ_n×n = (φ₁, φ₂, φ_3, ... ,φ_n) represents an orthonormal basis, the data may be expressed as x = Φc, where c_i = 〈x, φ_i〉, i.e., c = Φ^Tx, and ∥c∥_o ≤ k. Even if x is not strictly sparse, its representation c is sparse. For each dataset, we can assess and quantify the error of approximating x by an optimal estimate x̂ ∈ S_k by computing

$${\sigma }_k{\left(x\right)}_p={\min }_{\widehat{x}\in S_k}{\Vert x-\widehat{x}\Vert }_p.$$

In compressive sensing, if x ∈ Rⁿ, and we have a data stream generating m linear measurements, we can represently = Ax, where A_m×n is a dimensionality reducing matrix (m << n), i.e., A_m×n:Rⁿ → R^m. The null space of A is N(A) = {z ∈ Rⁿ: Az = 0 ∈ R^m} and A uniquely represents all x ∈ S_k ⇔ N(A) contains no vectors in S_2k. The spark of a matrix A represents the smallest number of columns of A that are linearly dependent. If A_m×n is a random matrix whose entires are independent and identically distributed, then spark(A) = m + 1, with probability 1. Taking this a step further, if the entries of A are chosen according to a sub-Gaussian distribution, then with high probability, for each k, there exists δ_2k ∈ (0,1) such that

$$(1-{\delta }_{2k}){\Vert x\Vert }_2^2\le {\Vert Ax\Vert }_2^2\le (1+{\delta }_{2k}){\Vert x\Vert }_2^2,$$ (1)

for all x ∈ S_2k [19]. When we know that the original signal is sparse, to reconstruct x given the observed measurements y, we can solve the optimization problem:

$$\widehat{x}=\arg {\min }_{z:Az=y}{\Vert z\Vert }_0.$$

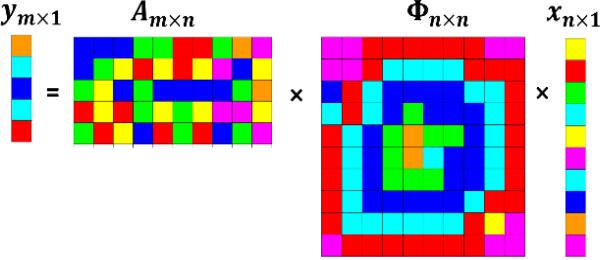
Linear programming may be used to solve this optimization problem if we replace the zero-norm by its more tractable convex approximation, the l₁-norm, x̂ = arg min_z:Az=y∥z∥₁. Given that A_m×n has the above property (1) and ${\delta }_{2k}<\sqrt{2}-1$, if we observe y = Ax, then the solution x̂ satisfies ${\Vert \widehat{x}-x\Vert }_2\le C_0\frac{{\sigma }_k{\left(x\right)}_1}{\sqrt{k}}$. Thus, in compressive sensing applications, if x ∈ S_k and A satisfies condition (1), we can recover any k-sparse signal x exactly (as σ_k(x)₁ = 0) using only O(k log(n/k)) observations, since $m=O\left(\frac{k\log (n∕k)}{{\delta }_{2k}^2}\right)$. Finally, if A_m×n is random (e.g., chosen according to a Gaussian distribution) and Φ_n×n is an orthonormal basis, then A_m×n × Φ_n×n will also have a Gaussian distribution, and if m is large, A′ = A × Φ will also satisfy condition (1) with high probability. Image acquisition in the Fourier domain (e.g., magnetic resonance imaging) presents a motivational example illustrating the components of the model (Y_m×1 = A_m×n × Φ_n×n × X_n×1) [20, 21], Figure 3.

Figure 3.

Schematic representation of the unobservable (x) and observable (y) data, and the corresponding orthonormal basis (Φ) and random sampling matrix (A), describing the compressive sensing reconstruction of x using sparse observations y.

Compressive Big Data Analytics (CBDA)

To develop a similar foundation for Compressive Big Data Analytics, one may start by iteratively generating random (sub)samples from the Big Data collection. Using classical techniques we can obtain model-based or non-parametric inference based on the sample. Next, likelihood estimates (e.g., probability values quantifying effects, relations, sizes) can be obtained and the process can continue iteratively. This amounts to repeating the (re)sampling and inference steps many times (with or without using the results of previous iterations as priors for subsequent steps). Finally, bootstrapping techniques may be employed to quantify joint probabilities, estimate likelihoods, predict associations, identify trends, forecast future outcomes, or assess accuracy of findings. The goals of compressive sensing and compressive big data analytics are somewhat different. The former aims to obtain a stochastic estimate of a complete dataset using sparsely sampled incomplete observations. The latter attempts to obtain a quantitative joint inference characterizing likelihoods, tendencies, prognoses, or relationships. However, a common objective of both problem formulations is the optimality (e.g., reliability, consistency) of their corresponding estimates.

As an example, suppose we represent (observed) Big Data as a large matrix Y ∈ R^n×t, where n=sample size (instances) and t = elements (e.g., time, space, measurements, etc.) To formulate the problem in an analytical framework, let's assume L ∈ R^n×t is a low rank matrix representing the mean or background data features, D ∈ R^n×m is a (known or unknown) design or dictionary matrix, S ∈ R^m×t is a sparse parameter matrix with small support (supp(S) << m × t), E ∈ R^n×t denote the model error term, and Λ_Ω(·) be a sampling operator generating incomplete data over the indexing pairs of instances and data elements $\Omega \subseteq \{1,2,\dots ,n\}\times \{1,2,\dots ,t\}$. In this generalized model setting, the problem formulation involves estimation of L, S (and D, if it is unknown), according to this model representation [22]:

$${\Lambda }_{\Omega }\left(Y\right)={\Lambda }_{\Omega }(L+DS+E).$$ (2)

Having quick, reliable and efficient estimates of L, S and D would allow us to make inference, compute likelihoods (e.g., p-values), predict trends, forecast outcomes, and adapt the model to obtain revised inference using new data. When D is known, the model in equation (2) is jointly convex for L and S, and there exist iterative solvers based on sub-gradient recursion (e.g., alternating direction method of multipliers) [23]. However, in practice, the size of Big Datasets presents significant computational problems, related to slow algorithm convergence, for estimating these components that are critical for the final study inference. One strategy for tackling this optimization problem is to use a random Gaussian sub-sampling matrix A_m×n (much like in the compressive sensing protocol) to reduce the rank of the observed data (Y_m×l, where (m, l) ∈ Ω) and then solve the minimization using least squares. This partitioning of the difficult general problem into smaller chunks has several advantages. It reduces the hardware and computational burden, enables algorithmic parallelization of the global solution, and ensures feasibility of the analytical results. Because of the stochastic nature of the index sampling, this approach may have desirable analytical properties like predictable asymptotic behavior, limited error bounds, estimates’ optimality and consistency characteristics. One can design an algorithm that searches and keeps only the most informative data elements by requiring that the derived estimates represent optimal approximations to y within a specific sampling index subspace $\left\{(m,l)\right\}\subseteq \Omega$. It would be interesting to investigate if CBDA inference estimates can be shown to obey error bounds similar to the upper bound results of point imbedding's in high-dimensions (e.g., Johnson-Lindenstrauss lemma [24]) or the compressive sensing restricted isometry property. The Johnson-Lindenstrauss lemma guarantees that for any 0 < ε 1, a set of points ${\left\{P_k\right\}}_1^K\in R^n$ can be linearly embedded $(\Psi :R^n\to R^{n^{\prime }})$ into ${\{\Psi \left(P_k\right)={P_k}^{\prime }\}}_1^K\in R^{n^{\prime }}$, for all $n^{\prime }\ge 4\left(\frac{\ln \left(K\right)}{\frac{{ϵ}^2}{2}-\frac{{ϵ}^3}{3}}\right)$, almost preserving their pairwise distances, i.e., $(1-ϵ){\Vert P_i-P_j\Vert }_2^2\le {\Vert {P_i}^{\prime }-{P_j}^{\prime }\Vert }_2^2\le (1+ϵ){\Vert P_i-P_j\Vert }_2^2$. The restricted isometry property ensures that if ${\delta }_{2k}<\sqrt{2}-1$ and the estimate x̂ = arg min_z:Az=y∥z∥₁, where A_m×n satisfies property (1), then the data reconstruction is reasonable, i.e., ${\Vert \widehat{x}-x\Vert }_2\le C_0\frac{{\sigma }_k{\left(x\right)}_1}{\sqrt{k}}$. Ideally, we can develop iterative space-partitioning CBDA algorithms that either converge to a fix pointor or generate estimates that are close to their corresponding inferential parameters.

The CBDA approach may provide a scalable solution addressing some of the Big Data management and analytics challenges. Random CBDA sampling may be conducted on the data-element level, not only the case level, and the sampled values may not be necessarily homologous across all data elements (e.g., high-throughput random sampling from cases and variables within cases). An alternative approach may be to use Bayesian methods to investigate the theoretical properties (e.g., asymptotics as sample sizes increase where the data has sparse conditions) of model-free inference entirely based on the complete dataset without any parametric or model-dependent restrictions.

Discussion

Big healthcare data is not a panacea and its promises may not be fully realized without significant R&D investments, broad commitment to open-science, and enormous technological advances. An information-theoretic interpretation of Gödel's incompleteness principle [25] suggests the intrinsic limitations of information derived from Big healthcare data. Healthcare data cannot be consistent and complete at the same time. In other words, any computational inference, or decision making, based on Big healthcare data would be expected to either be reliable within a restricted domain (e.g., time, space) or be more broadly applicable (e.g., cohort or population studies) but less consistent; certainly not both. This dichotomy is also supported by our general scientific experience where statistical inference on small or large sample sizes depends on corresponding large or small variances of parameter estimations, respectively. Yet, in the case of enormous samples, the estimation accuracy is inversely proportional to the sample-size of the data, due to lack of control and expected violations of core parametric assumptions. For example, from a statistical perspective exploring genetic association of Autism, a complete census surveying the entire population would be desirable. However, such study would be impractical because of the enormous amount of time and resources necessary to compile the data, complete the information extraction, ensure data reliability and consistency, prior to taking an appropriate action. Using classical data analytics, these problems may be exacerbated by the unavoidable errors expected to creep in due to lack of control, uniformity and technological reliability for interrogating huge samples. The end result may diminish the value of the acquired health data and negatively impact the resulting scientific inference. Big healthcare data analytics aim to address some of these holistic information-processing challenges and provide rapid and effective estimation and prediction based on dynamic and heterogeneous data.

Collectively, US industry and government organizations are spending over $200B annually to provide open access to Cloud resources (storage, computing, social networking, etc.) The services-oriented Cloud is a very decentralized, rapidly evolving and powerful infrastructure engineered to manage Big Data, including human health data. Such data can be mined, processed and interrogated to extract specific human traits, biological dynamics and social interaction information, which ultimately may lead to tremendous benefits (social, biomedical, financial, environmental, or political).

Decisively, there are specific directions that could significantly impact the process of extracting information from Big healthcare data, translating that information to knowledge, and deriving appropriate actions: (1) enforce open-science principles in healthcare research; (2) engage and actively participate (e.g., fund) in non-traditional high-risk/high-potential-impact studies; (3) adapt to rapid, agile and continuous development, testing, redesign, productization and utilization of data, tools, services and architecture; (4) redesign the healthcare data science curricula (from high-school to doctoral level training). Big healthcare data is incredibly powerful, but its Achilles heel is time. Its value is in the moment and its importance decreases exponentially with time, which makes critically important the rapid response and concerted effort to process collected clinical information.

Information hoarding (e.g., neighboring health care systems unwilling to share clinical data about patients they have in common, health insurers unwilling to reveal providers’ reimbursement rates, computational scientist limiting access to powerful new resources, etc.) only expedites the decay in value of many interesting Big healthcare datasets. Collaborative distribution of such information, paired with significant institutional commitment to open data science, holds a great potential to democratize the information universe and radically change our understanding of disease cause, comorbidity, progression and ultimately cure. There are two ways to deal with the influx of significant disruptive technologies – (passive) reactive response or proactive action. Government institutions and regulators, funding agencies, and organizations involved in generating, aggregating, processing, analyzing, interpreting, managing or managing large, incongruent, heterogeneous and complex data may choose to lead the wave or follow the wake of the Big healthcare data revolution.

Future innovations in Big healthcare data analytics are most likely going to come from disparate resources, small-group initiatives, open-source/open-science community and truly trans-disciplinary interactions, less so from Big-Business, Big-Academy, or Big-Government. We need a concerted effort and efficient funding mechanisms to harness the ingenuity of the broader community using large-number of smaller-budget, rapid-development, high-risk, and product-oriented health research projects. In the era of Big healthcare data analytics, continuous-development, rapid agile prototyping, and experience-based (evidence-based) redesign represent the new innovation paradigm covering basic science, computational modeling, applied research and all aspects of system complexity studies.

In the 21^st century to achieve the same scientific impact, matching the reliability and the precision of the prediction that Cavendish did in the 18^th century, it will require a monumental community effort using massive and complex information perhaps on the order of 2²³ bytes, instead of just 23 observations like the ones used by Cavendish to estimate so accurately the mean density of the Earth.