SUMMARY
Postsynaptic responses in many CNS neurons are typically small and variable, often making it difficult to distinguish physiologically relevant signals from background noise. To extract salient information, neurons are thought to integrate multiple synaptic inputs and/or selectively amplify specific synaptic activation patterns. Here, we present evidence for a third strategy: directionally selective ganglion cells (DSGCs) in the mouse retina multiplicatively scale visual signals via a mechanism that requires both nonlinear NMDA receptor (NMDAR) conductances in DSGC dendrites and directionally tuned inhibition provided by the upstream retinal circuitry. Postsynaptic multiplication enables DSGCs to discriminate visual motion more accurately in noisy visual conditions without compromising directional tuning. These findings demonstrate a novel role for NMDARs in synaptic processing and provide new insights into how synaptic and network features interact to accomplish physiologically relevant neural computations.
INTRODUCTION
Computations in the brain require the combined properties of synapses, neurons and circuitry. When individual synapses exhibit high variability, as in most networks, neurons must employ mechanisms to increase signal fidelity. One common strategy is to reduce the impact of a single synaptic activation on postsynaptic firing, so that a neuron’s output reflects the integrated ‘vote’ of numerous synaptic inputs. An alternative strategy is to amplify signals close to their origin to reduce the impact of noisy elements within the postsynaptic cell and surrounding circuitry. Various mechanisms can amplify postsynaptic responses, including postsynaptic receptors (Branco et al., 2010; Lavzin et al., 2012; Polsky et al., 2004; Smith et al., 2013), dendritic spines (Harnett et al., 2012) and active dendritic conductances (London and Hausser, 2005; Major et al., 2013; Mel, 1993) . While the potential benefits of synaptic amplification are clear, its precise roles in physiological computations have been more difficult to identify. Without a clearly defined computational context, it is also difficult to identify and measure the relevant change in neural performance due to different synaptic processing schemes. Here, we identify the characteristics and underlying mechanisms of synaptic scaling in DSGCs of mouse retina, as well as the computational role of this scaling in early visual processing.
DSGCs respond preferentially to visual stimuli moving in a particular direction across the retina (Barlow and Hill, 1963; Figure 1A,B). Synaptic inputs to DSGCs comprise GABAergic inhibition and cholinergic excitation from SACs (Briggman et al., 2011; Lee et al., 2010; Wei et al., 2010; Yonehara et al., 2010) and glutamatergic input, predominantly from bipolar cells (Lee et al., 2014), that is received postsynaptically by AMPA receptors (AMPARs) and NMDARs (Lee et al., 2010; Stafford et al., 2014; Tjepkes and Amthor, 2000; Weng et al., 2005). Direction selectivity (DS) computation originates in starburst amacrine cell (SAC) dendrites, which respond preferably to stimuli moving from the cell body towards the dendritic tips (Euler et al., 2002). SAC dendrites preferentially contact DSGCs tuned to the opposite direction (Briggman et al., 2011), so that GABAergic inhibitory input from SACs is larger in response to motion in the DSGC’s non-preferred (null) direction (Fried et al., 2002; Lee et al., 2010; Vaney et al., 2012). SACs may therefore supply the “shunting” inhibition postulated to enable multiplicative interactions between excitatory and inhibitory inputs in DSGCs (Torre and Poggio, 1978).
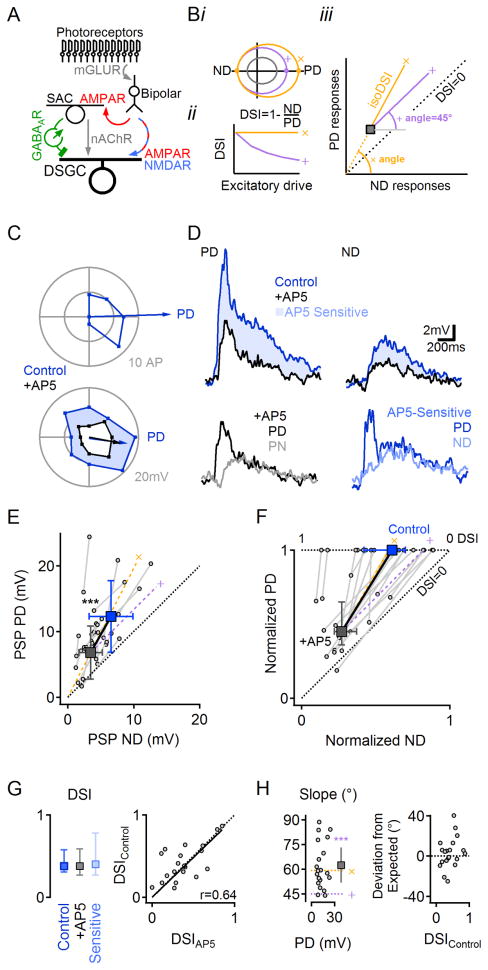
Figure 1. NMDAR perform multiplicative scaling of synaptic inputs in DSGCs.
(A) Retinal DS network schematic. For simplicity, only the ON pathway is shown. Visual information is conveyed from photoreceptors through bipolar cells to DSGCs by glutamatergic inputs that are not DS. DS is computed first in SACs, which provide inhibitory GABAergic and excitatory cholinergic drive to DSGCs.
(B) Impact of additive (purple, ’+’) vs. multiplicative (yellow, ‘x’) excitatory scaling of baseline responses(grey). i, Additive scaling increases the responses by a constant in all directions of stimulation, whereas multiplication scales the responses in different directions proportionally. ii, Multiplicative, but not additive scaling, preserves DS. iii, On a PD vs. ND plot, additive scaling follows a 45° angle line (right), whereas multiplicative scaling follows a line that connects the unscaled responses to the origin.
(C) Polar plot of suprathreshold (top) and subthreshold (bottom) responses in a DSGC to a leading edge of a bright bar moving across the retina in eight directions. This DSGC had a preference for rightward motion (retinal orientation in recording chamber was not preserved relative to in situ anatomy). See Figure S1 for a detailed analysis of postsynaptic currents and suprathreshold DS responses.
(D) Top, PD and ND PSPs from the same cell before and after NMDAR blockade by AP5. Bottom, the AP5-insensitive (black, left) and -sensitive (blue, right, shaded top) components of the PD PSP are larger compared to ND.
(E) Summarized PSP amplitudes in control (blue) and AP5 (black; n=19). Squares, mean (±SD) of the dataset. Gray lines and circles show average responses from individual cells. Yellow (‘x’) and purple (‘+’) dashed lines indicate theoretical multiplicative and additive scaling of responses in AP5. See Figure S2 for discussion on the conditions suitable for multiplicative scaling analysis.
(F) The data in (E) normalized by the control PD response in each DSGC.
(G) Left, DSI values (median ±quartile) in control conditions are similar to the DSI of AP5-insensitive and -sensitive components of the PSP. Right, DSI from individual cells correlate before and after NMDAR blockade by AP5 (p=0.53, n=19). DSI values were preserved for different stimulus contrast levels and NMDAR subunit compositions (Figures S3, S4).
(H) Left, the slope of NMDAR scaling, calculated from (E) does not depend on PSP amplitude. The mean slope (±confidence interval of 99.9%; square) follows the expected multiplicative trend (‘x’, yellow), and is significantly different from addition (‘+’, purple, p<0.001, z-test). Circles indicate slopes of individual cells vs. PD PSP for each cell (n=19). Right, the difference between the observed and the expected multiplicative slopes does not depend on the degree of DS (p=0.4).
By contrast, the computational contributions of the excitatory inputs to DSGCs remain undetermined: Although acetylcholine (ACh) is also released from SACs, ACh receptor activation in DSGCs is not strongly tuned to any direction (Lee et al., 2010; Vaney et al., 2012; Yonehara et al., 2010), but see (Pei et al., 2015), and recent reports indicate that bipolar cells transmit directionally untuned glutamatergic signals to DSGCs (Chen et al., 2014; Park et al., 2014; Yonehara et al., 2013). Both nicotinic ACh receptor (nAChR) and NMDAR-mediated signals contribute significantly to light-evoked responses in DSGCs, but neither are required to compute DS (Kittila and Massey, 1997; Lee et al., 2010; Tjepkes and Amthor, 2000; Weng et al., 2005). Due to their dual dependence on postsynaptic voltage and presynaptic activity, NMDAR conductances may confer unique computational capabilities to synapses (Major et al., 2013; Mel, 1993) and have been shown to underlie nonlinear dendritic signaling (Branco et al., 2010; Lavzin et al., 2012; Smith et al., 2013), but a specific role for NMDARs in DS has not been shown.
Here, we show that NMDAR-mediated synaptic inputs to DSGCs increase postsynaptic responses to motion in the preferred and null directions (PD and ND, respectively) by the same proportion, a multiplicative operation that requires both the voltage-dependent NMDAR conductance and directionally tuned inhibition and enhances DS signaling in response to noisy visual stimuli. Numerical simulations reproduce the experimental results and suggest that NMDAR-mediated inputs offset the reduction in driving force on excitatory conductances so that excitatory postsynaptic current remains proportional to synaptic input over a wide range of postsynaptic potentials, enabling shunting inhibition to act in a precisely divisive manner. Taken together, these results show how specific synaptic properties and circuit features combine to accomplish an essential computation early in the visual pathway.
RESULTS
NMDARs multiplicatively scale the synaptic drive to DSGCs
To examine roles for NMDARs in DS signaling, we imaged and recorded in isolated mouse retina from DSGCs expressing GFP under control of the D4 dopamine receptor promoter (Huberman et al., 2009). Action potentials (APs) elicited by bars of light moving across the retina were recorded with a somatic patch electrode in the cell-attached configuration to determine PD and ND (Figure 1C, top, Figure S1A,B). The degree of DS was quantified as the DS Index (DSI; See Experimental Procedures; Figure 1Bii). To examine synaptic integration without the nonlinearity of AP generation, we obtained whole-cell recordings from DSGCs, blocked voltage-gated sodium channels with extracellular TTX or intracellular QX-314, and recorded light-evoked postsynaptic potentials (PSPs; Figure 1C, bottom, D). PSPs exhibited significant DS (p=0.0002 between PD and ND, paired t-test, n=19; Figure 1D–F). The PD and ND observed in PSP recordings corresponded closely to those exhibited by APs in the same cells (e.g., Figure 1C), although the DSI of PSPs was lower than that of AP responses (p<10−8, Wilcoxon signed rank test for paired data, n=33, Figure S1C). Consistent with previous reports (Fried et al., 2002; Taylor and Vaney, 2002), inhibitory inputs to DSGCs, recorded under whole-cell voltage clamp, were larger in response to ND stimulation (Figures S1D–G).
Because bipolar signals to DSGCs are not directionally tuned (Park et al., 2014; Yonehara et al., 2013), glutamatergic input might increase the PSP amplitude by the same amount in all directions (i.e., additively; Figure 1Bi, ‘+’). Instead, the NMDAR-mediated component of the PSP was larger in response to PD stimulation (PD = 5.8±3.1mV, ND = 3.3±2.8mV; n=19; p=0.001, paired t-test; Figure 1D, bottom right). On average, NMDAR blockade reduced PD and ND PSPs by a similar fraction, indicating that NMDAR scaling was proportional to the underlying (non-NMDAR-mediated) PSP, i.e., multiplicative (Figure 1Biii, ‘×’; Figures 1E,F and S2). The distinction between additive and multiplicative scaling is especially relevant for DS signaling, because only multiplicative scaling preserves the PD:ND ratio and, therefore, consistent DS (Figure 1Bii). Accordingly, NMDAR and non-NMDAR-mediated PSP components exhibited indistinguishable DS compared to each other or control (Figure 1G, p>0.5, Wilcoxon signed rank test with Bonferroni correction). As another way to distinguish additive vs. multiplicative scaling by NMDARs, we measured the angle of the line connecting the PD vs. ND points in control and AP5 for each cell (Figure 1H). Additive scaling by NMDARs would be indicated by a line at a 45° angle relative to the x-axis, whereas multiplicative scaling would follow a line that passes from the origin through the PD vs. ND point in the presence of AP5. This line, representing a consistent PD:ND response ratio (“isoDSI”, Figure 1Biii), forms an angle equal to tan−1(PD responseAP5/ND responseAP5). The slopes derived from the PSP data in Figure 1E ranged from ~45°, indicating additive scaling in some cells, to nearly 90°, suggesting that, in other cells, NMDARs contributed to PD responses almost exclusively (Figure 1H, left). Most cells, however, exhibited slopes close to that expected for multiplication (Figure 1H, right); accordingly, slopes measured from the entire data set were not significantly different from those predicting multiplicative scaling (measured: 62.5±14.2°, expected: 59.4±10.7°, p=0.4; paired t-test, n=19). Further experiments showed that NMDAR multiplication occurred over a range of contrast levels (Figure S3) and was robust to developmental changes in NMDAR subunit composition (Figure S4).
Synaptic multiplication is mediated by postsynaptic NMDARs
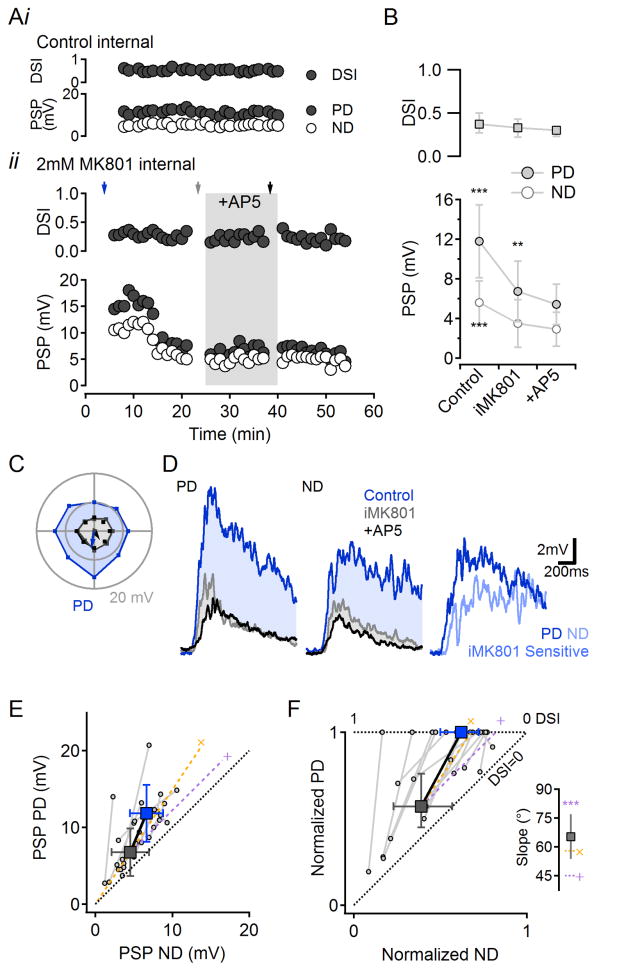
Our interpretation of these results presumes that NMDAR antagonists act primarily on postsynaptic NMDARs in DSGCs. To test whether bath-applied AP5 affects DS circuitry presynaptic to recorded DSGCs, we patched and filled DSGCs with internal solution containing MK801 (iMK801, 2mM; Figure 2) to block NMDARs only in the patched cell (Berretta and Jones, 1996). The tip of the electrode was filled with MK801-free internal solution to introduce a delay between commencement of whole-cell recording and dialysis of the cell with iMK801. iMK801 significantly reduced light evoked PSPs (p<0.001, n=15, Figure 2A,B). As with AP5, PD and ND responses were reduced proportionally and the calculated DSI was not affected (Figure 2B–F). The reduction in PSP amplitude was not due to non-specific rundown of light responses, as PSP amplitudes remained constant in DSGCs filled with a control internal (e.g., Figure 2A, top, n=4). Following iMK801 dialysis, subsequent blockade of all NMDARs in the tissue with bath-applied AP5 reduced PD PSPs only slightly (16±17% reduction, p=0.01, n=15; Figure 2A,B) and did not affect light-evoked EPSCs (8±12% reduction, p=0.25, n=6; Figure S5), indicating that the multiplicative scaling is mediated predominantly by postsynaptic NMDARs in the recorded DSGC. Accordingly, bath-applied AP5 did not affect light-evoked PSPs in SACs (Figure S6), or, in the presence of iMK801, IPSCs recorded in DSGCs (Figure S5), consistent with previous reports in rabbit that SACs receive little NMDAR-mediated synaptic input (Kittila and Massey, 1997; Linn and Massey, 1991).
Figure 2. Synaptic multiplication in DSGCs is mediated by postsynaptic NMDARs.
(A) i, With normal intracellular solution, PSP amplitude and DSI remained stable over time. Responses shown from a single cell; similar results observed in 4 cells. ii, When MK801 (iMK801, 2mM) was included in the patch solution, PSPs became smaller but DSI was preserved. Subsequent application of AP5 exerted small effects, indicating that iMK801 blocked most of the NMDARs on the cell. The tip of the electrode was filled with MK801-free solution to introduce a delay between “break-in” and iMK801 action, enabling “control” responses to be recorded. See also Figure S5 for effects of iMK801 on voltage-clamped EPSCs and IPSCs.
(B) Summarized effects of iMK801 and subsequent bath AP5 application on DSI (median ±quartile), top, and PD:ND PSP amplitudes (mean ±SD), bottom (n=15 cells).**p<0.01,***p<0.001 vs. corresponding AP5 values, ANOVA followed by multiple comparison Tukey test.
(C) Directional tuning of subthreshold responses from the cell in (Aii) recorded at times marked by the arrows (in Aii) for control (blue), iMK801 (grey) and bath AP5 (black).
(D) Example PSPs evoked by visual stimulation in PD (left) and ND (middle). Same cell as (C) and (A) (bottom). Right, the iMK801-sensitive component of the response was larger in response to PD stimuli.
(E) Summary of PSP PD vs. ND responses in control (blue) and iMK801 (grey) conditions from 15 cells. Filled squares, population averages (mean ±SD). Gray lines and circles show average responses from individual cells. Yellow (‘x’) and purple (‘+’) dashed lines indicate theoretical multiplicative and additive scaling of iMK801 responses.
(F) The data in (E) normalized to the control PD response. The average amplification with postsynaptic NMDARs follows a multiplicative trend. Inset, The mean slope of the scaling is as predicted for multiplication and is significantly different from addition (p<0.001). Error bars, confidence interval of 99.9%.
See also Figure S6 for experimental evidence that AP5 does not affect SAC responses in the DS signaling pathway.
Numerical simulations suggest that NMDAR multiplication depends on DS circuitry
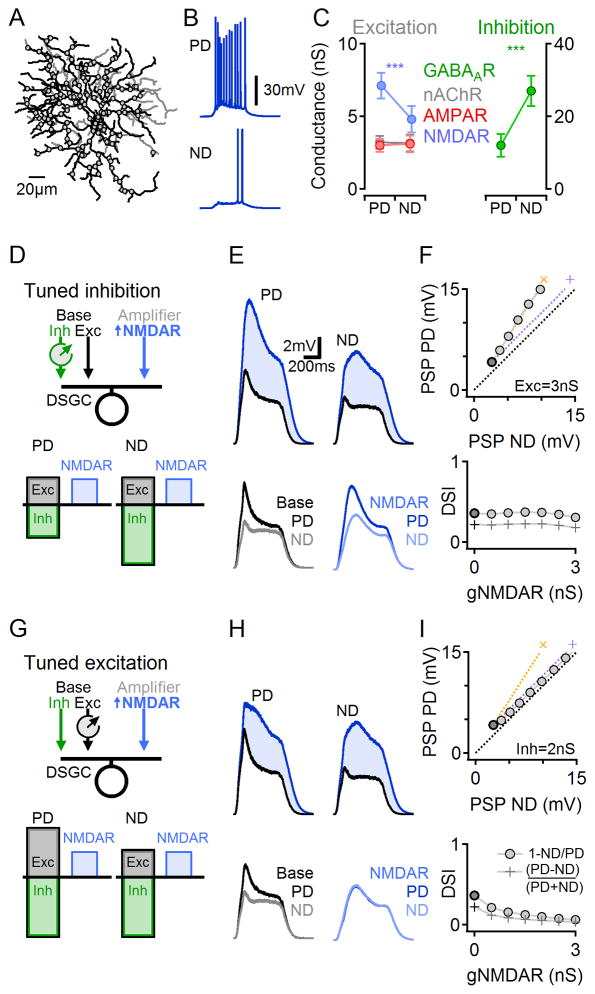
To explore the mechanisms of subthreshold multiplication, we constructed a morphologically and biophysically realistic mathematical model of a DSGC (Experimental Procedures; Figure 3). Glutamatergic (NMDAR and AMPAR mediated), GABAergic and cholinergic synaptic inputs were distributed homogeneously over the entire DSGC dendritic tree (Jeon et al., 2002) and DS was implemented by directionally tuning the inhibitory drive (Figures 3A–C). We then varied the strength of the NMDAR inputs (to mimic application of AP5) and measured the effects on simulated PD and ND responses (Figure 3D). In agreement with our experimental results with AP5, simulated PSPs exhibited postsynaptic multiplication and consistent DS over a range of NMDAR input strengths (Figure 3E,F).
Figure 3. Numerical simulations of DS signaling.
(A) The morphology (ON dendrites in black, OFF dendrites in gray) and synaptic locations (circles) on the reconstructed DSGC. Synaptic input was modeled only on the ON dendrites. Each synaptic location included ‘SAC’-mediated GABAAR and nicotinic AChR inputs and ‘bipolar cell’-mediated AMPAR and NMDAR inputs. Inhibitory input was set to be stronger in response to ND stimuli.
(B) Example simulated AP responses to PD (top) and ND (bottom) stimuli.
(C) Simulated synaptic conductances in response to PD and ND stimuli. Although glutamate release was not directionally tuned, the NMDAR conductance became functionally tuned due to its dependence on the postsynaptic membrane potential.
(D–F) Simulated responses with DS tuned inhibitory inputs.
(D) Schematic of inhibitory DS circuit configuration.
(E) Simulated PSPs, as in Figure 1D. Blue, gNMDAR=2.5nS; black, gNMDAR=0nS.
(F) PD vs. ND PSP amplitudes (top) and DSI (bottom) for increasing NMDAR conductance values. Baseline responses (zero NMDAR conductance, equivalent to the effect of AP5) are marked in black. The simulation replicated experimental results of multiplicative scaling (‘x’, yellow).
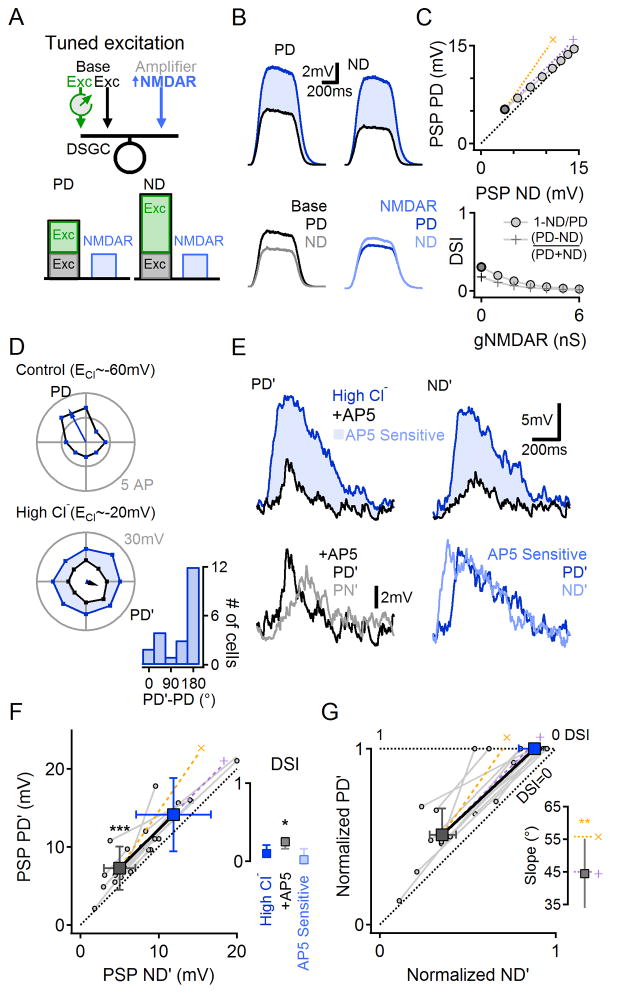
(G–I) Similar to (D–F) for a tuned excitation DS scheme.
(G) Schematic for tuned excitation simulation. Cholinergic presynaptic excitatory drive was larger in response to PD stimuli; inhibitory and glutamatergic drives were directionally untuned. See also Figure S8 for an explanation of the difference between synaptic scaling in tuned excitation and tuned inhibition systems.
Interestingly, in an alternative DS circuitry scenario in which (non-NMDAR) excitation but not inhibition was directionally tuned, the model predicted that NMDAR inputs would increase synaptic potentials in an additive manner (Figure 3G–I). This result held over the entire range of model parameters tested, even when the non-NMDAR (baseline) PSP waveforms were virtually identical between tuned excitation and inhibition simulations (compare black traces in Figure 3E and H).
NMDARs scale additively when directionally tuned input is excitatory
To test the model’s prediction that NMDARs would scale PSPs additively when excitatory input was directionally tuned, we took advantage of the fact that synaptic inhibition in DSGCs depends on the chloride reversal potential (ECl). We dialyzed patched DSGCs with internal solution containing 65mM chloride, thereby moving ECl to ~-20mV and making the GABAergic drive excitatory (Figure 4). The model predicted that this specific circuit arrangement–with directionally tuned (Erev=−20mV) and untuned (Erev=0mV) excitation and no inhibition–would cause NMDARs to scale additively (Figure 4A–C, similar to Figure 3G–I). Because GABAergic input is larger in response to ND stimulation, in most (15/20) cells dialysis with 65mM chloride solution reversed DS tuning to a new PD (PD’) compared to control DS (measured in the cell-attached configuration prior to whole-cell recording; Figure 4D;(Taylor et al., 2000). The difference between PD’ and ND’ responses, though significant (14.1±4.7 vs. 11.9±4.8 mV, p=0.003, n=12, paired t-test), was smaller than in physiological ECl conditions, consistent with the model predictions (Figure 4B,C). Blocking NMDARs significantly reduced PSPs evoked by PD’ and ND’ stimuli (Figure 4D,E, n=12, p<0.001, paired t-test). Unlike in control ECl conditions (Figure 1D), however, the NMDAR-mediated component of the PSP was similar in response to PD’ and ND’ stimulation (Figure 4E, bottom right), a directionally untuned signal contributing additive, rather than multiplicative, scaling (Figure 4F,G; slope = 45.5±3.7° (mean ± SD), n=12, p=0.01 vs. the expected multiplicative slope, paired t-test, Figure 4G, inset). Accordingly, NMDAR input reduced the mean DSI (Figure 4F, inset, n=12, p=0.03, Wilcoxon signed rank test with Bonferroni correction), as predicted by the model (Figure 4C).
Figure 4. NMDARs-mediated scaling is additive when excitation is directionally tuned.
(A) Schematic of numerical simulation (similar to that shown in Figure 3) of a DSGC receiving directionally tuned excitatory GABAergic drive (Erev=−20mV), untuned excitatory glutamatergic/cholinergic drive (Erev=0mV) and no inhibition.
(B) Simulated responses, as in Figure 3E,H.
(C) As in Figure 3F,I. Simulated NMDAR conductance scaled PSPs additively (top), leading to decreased DSI (bottom).
(D–E) Experiments in which GABAergic input was rendered excitatory by elevating intracellular [Cl−].
(D) Top, Suprathreshold directional tuning (cell-attached, i.e., native Cl−i). Bottom, Subthreshold tuning from the same cell after dialysis with high-Cl− intracellular solution (blue). Black, following bath application of AP5. Inset, the shift in PD’ with high-Cl− internal relative to PD measured in the cell- attached configuration.
(E) Top, PSPs in response to PD’ and ND’ stimuli. Bottom, AP5-insensitive (black, left) and -sensitive (blue, right) components. The AP5-sensitive component was not directionally tuned.
(F) PD’ vs. ND’ PSP amplitudes from 12 cells before and after bath application of AP5. Population mean (±SD, squares) follow the predicted additive scaling (‘+’, purple). Inset, Median (±quartile) DSI after intracellular dialysis with elevated chloride solution, and the AP5-insensitive (+AP5) and AP5-sensitive components of the PSP.
(G) Data in (F) normalized to the control PD response in the corresponding DSGC. Inset, Slopes of NMDAR-mediated scaling were significantly different from the multiplicative prediction (**p<0.01, z-test) and similar to the expected additive scaling. See also Figure S8 for further explanation about why tuned excitation leads to additive scaling.
Voltage-dependent NMDAR conductance is required for multiplicative scaling
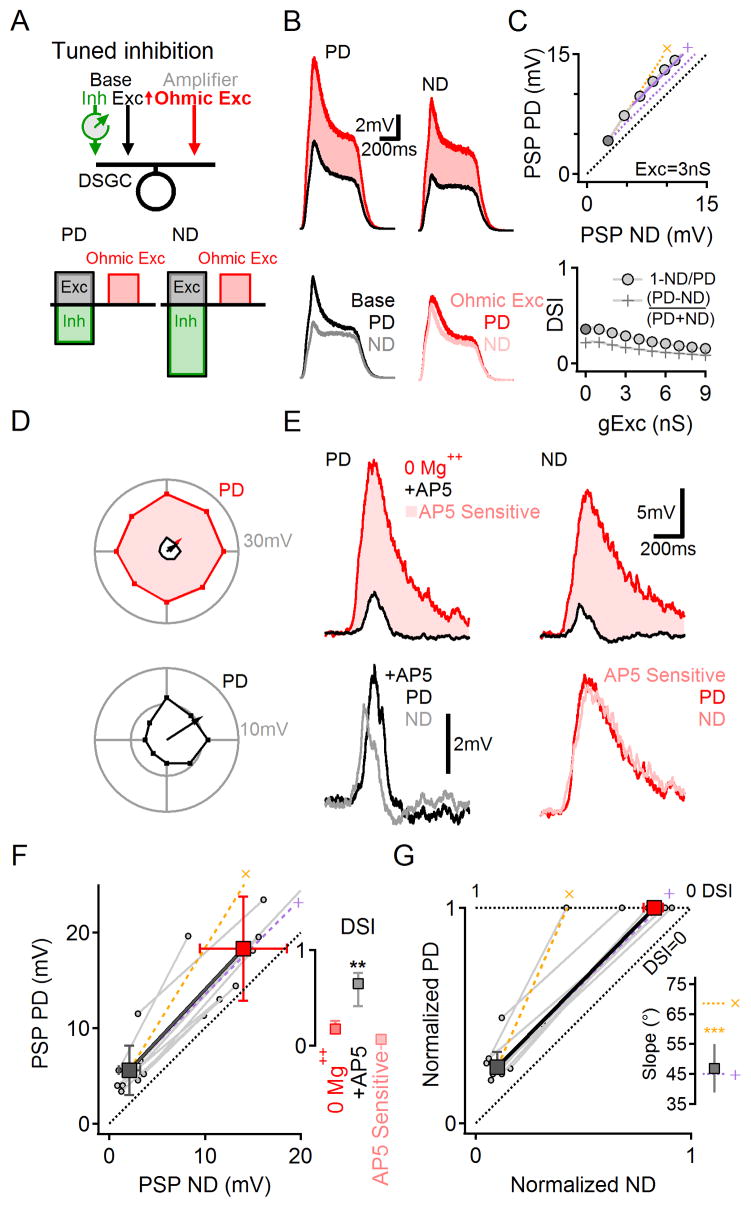
The results presented in Figure 4 indicate that directionally tuned inhibition is required for NMDAR multiplication. Our simulations suggested that tuned inhibition makes the NMDAR conductance smaller in response to ND stimulation (Figure 3C), presumably because the larger inhibitory shunt reduces postsynaptic depolarization and reinforces Mg++ block of the NMDAR channel (Mayer et al., 1984; Nowak et al., 1984; Tjepkes and Amthor, 2000). Accordingly, when the simulated NMDAR conductance was rendered voltage-independent, synaptic scaling became additive (Figures 5A–C, S7). To test this prediction experimentally, we removed Mg++ from the extracellular solution (Nowak et al., 1984; Tjepkes and Amthor, 2000). In close agreement with the simulation, light responses in 0 Mg++ solution exhibited reduced DSI (Figure 5D–F; (Tjepkes and Amthor, 2000)), although PD and ND responses remained significantly different (n=8, p=0.01, paired t-test; Figure 5F). The AP5-sensitive, NMDAR-mediated component of the PSP was similar in response to PD and ND stimuli, indicating additive scaling (Figure 5D–G, Slopes of 45.5±5.3° (mean ± SD), n=8, p<0.001 vs. the expected multiplicative trend, paired t-test, Figure 5G, inset).
Figure 5. Voltage dependent NMDARs are required for multiplicative scaling.
(A) Schematic of numerical simulation (similar to that shown in Figure 3) of a DSGC receiving base excitation and (tuned) inhibition plus synaptic scaling via an Ohmic (voltage-independent) excitatory synaptic conductance.
(B) Simulated responses, in response to PD and ND stimuli, with and without Ohmic excitatory scaling.
(C) Simulated Ohmic conductance scaled PSPs additively (top), leading to decreased DSI (bottom). This effect did not depend on the time course of the scaled conductance (Figure S7).
(D–E) Experiment in which voltage-dependence of NMDAR conductance was reduced by removing extracellular Mg++.
(D) Top, Example of directional tuning in 0 Mg++ ACSF (red) and in the presence of AP5 (black). Bottom, responses in AP5 enlarged.
(E) Top, PSPs in response to PD and ND stimuli in 0 Mg++ solution (red) and in the presence of AP5 (black). Bottom, AP5-insensitive (black, left) and -sensitive (red, right) components. The AP5-sensitive component was not directionally tuned. See Figures S5, S6 for evidence that removing extracellular Mg++ exerts minimal effects on the presynaptic DS circuitry.
(F) PD vs. ND PSP amplitudes in 0 Mg++ solution before and after bath application of AP5 (n=8). Population mean (±SD, squares) follow the predicted additive scaling (‘+’, purple). Inset, Median (±quartile) DSI in 0 Mg++ solution, and the AP5-insensitive (+AP5) and AP5-sensitive components of the PSP.
(G) Data in (F) normalized to the control PD response in the corresponding DSGC. Inset, Slopes of NMDAR-mediated scaling were significantly different from the multiplicative prediction (***p=0.0006, paired t-test) and similar to the expected additive scaling. See also Figure S8 for further explanation about why ohmic excitation scales PSPs additively.
Control experiments indicated that removing extracellular Mg++ exerted little effect on DS signaling presynaptic to DSGCs (see also (Nowak et al., 1984; Tjepkes and Amthor, 2000)): 1) In DSGCs dialyzed with iMK801 to block NMDARs only in the recorded cell, light-evoked EPSCs and IPSCs were similar in the absence and presence of extracellular Mg++ (Figure S5); 2) Light responses in SACs were not affected by extracellular Mg++ concentration (Figure S6; see also (Kittila and Massey, 1997; Linn and Massey, 1991)).
Mechanisms underlying multiplicative and additive synaptic scaling in DSGCs
A simple, single-compartment model provides a conceptual framework for understanding NMDAR-mediated synaptic scaling in different scenarios (Figure S8). First, consider an excitatory synaptic input that behaves as an “ideal” current source, i.e., one that produces the same current regardless of the postsynaptic potential (Figure S8Ai,ii). In this case, the PSP is directly proportional to the excitatory conductance; shunting inhibition, which is larger during ND stimulation, decreases the input resistance of the postsynaptic membrane and reduces the PSP by the same fraction at all stimulation levels, perfect division that produces consistent DSI (Figure S8Aiii,iv). By contrast, the current produced by an AMPAR or nAChR-mediated synaptic conductance decreases as the membrane potential nears the excitatory reversal potential (0 mV; Figure S8Bi,ii), creating a subproportional relationship between PSP amplitude and synaptic conductance (Figure S8Biii). As shunting inhibition reduces the PSP amplitude, it simultaneously increases the driving force on the excitatory conductance such that the fractional reduction of larger PSPs by the shunt is decreased, leading to lower DSI (Figure S8Biv). These effects of decreased driving force can be offset by the voltage-dependent NMDAR conductance, which increases with depolarization over the physiological membrane potential range, causing the total excitatory synaptic drive to behave more like an ideal current source (Diamond and Copenhagen, 1993); Figure S8Ci,ii) and enabling DSI to remain consistent over a larger response range (Figure S8Ciii,iv).
When DS is mediated by directionally tuned, Ohmic excitatory input (Figure S8Di,ii), the PD excitatory conductance decreases the input resistance of the cell, making it harder for other excitatory conductances to depolarize the cell during a PD response. Even an ideal current is unable to amplify responses effectively in this scenario (Figure S8Diii,iv). In theory, the NMDAR conductance could benefit from larger PD PSPs due to tuned excitation (Figure S8Ei,ii). In practice, however, the reduced input resistance and smaller driving force during PD responses makes the scaling by NMDARs similar to that by an ideal current, i.e. approximately additive (Figure S8Eiii,iv).
NMDARs enhance accuracy of DS signaling in noisy visual conditions
Our findings suggest that DSGC NMDARs and the DS network exhibit features that promote multiplicative interactions between synaptic inputs. Nonetheless, we and others observed that blocking NMDARs does not reduce the DSI of average responses to noiseless visual stimuli (Figures 1, S1; (Kittila and Massey, 1997; Tjepkes and Amthor, 2000). In a complex visual world, however, DS computations must be robust to changes in visual features of the moving object and surrounding environment, i.e., visual noise. By acting as a logical AND gate between presynaptic and postsynaptic activation, NMDAR-mediated multiplication might amplify correlated excitatory inputs (Schnupp and King, 2001) and thereby enable DSGCs to distinguish visual motion from a noisy background.
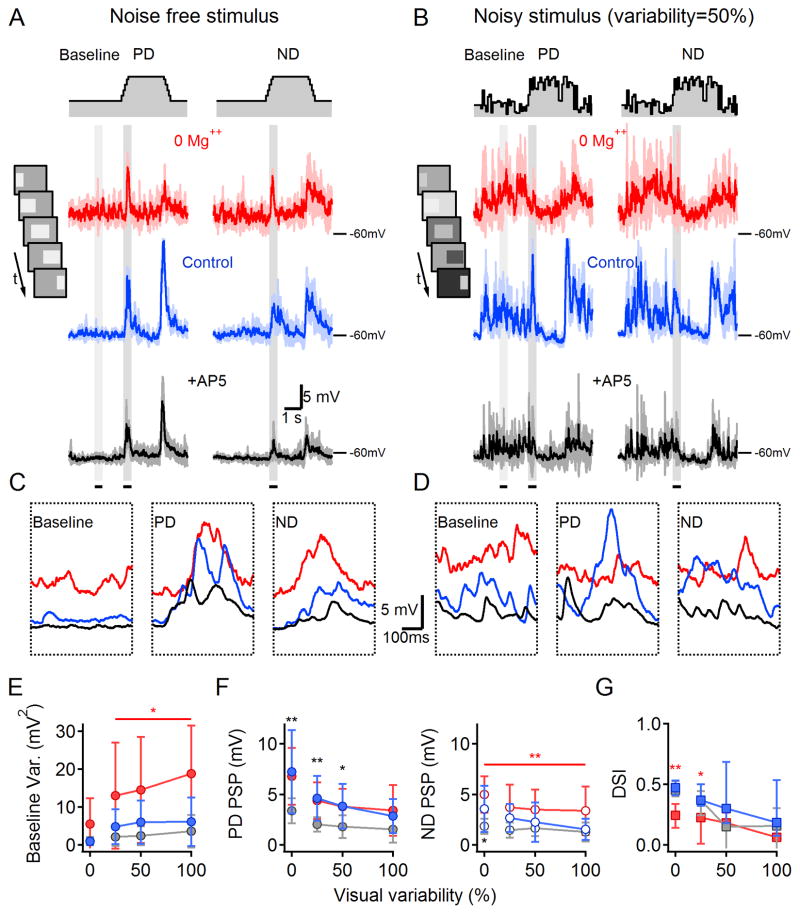
To test this idea, we examined the impact of NMDARs on DS signaling in response to noisy visual stimuli (Figure 6A–D). The stimulus was identical to that used previously except that the background and bar luminances were varied independently every 50 ms to add visual noise without introducing any directional biases that might complicate the interpretation of DS network responses (see Experimental Procedures). In these experiments, PSPs were recorded from DSGCs first in Mg++ free solution, then in the presence of Mg++ and finally following bath application of AP5. Removing Mg++ increased baseline membrane potential fluctuations, especially during a noisy background (Figure 6E). PD PSP amplitudes were not larger in Mg++-free solution (n=12 cells, p=0.8, paired t-test; Figure 6F), however, possibly due to the relatively depolarized resting membrane potential in 0 Mg++ (+3.4±3.6mV compared to control, Figure 6C,D) that may have slightly reduced the driving force and occluded small increases in PSP amplitude. In agreement with our previous observations, ND PSPs were consistently larger in 0 Mg++ in all noise conditions (Figure 6F, right), leading to reduced DS (Figure 6G). AP5 significantly reduced PD PSPs evoked by noisy stimuli (Figure 6F), indicating that NMDARs contribute to DSGC signaling in noisy visual conditions, but, as in the noise-free condition, AP5 did not change the DSI (Figure 6G).
Figure 6. DSGC responses to noisy visual stimulation.
(A) PSPs (solid: mean, shaded: SD, n=4 repetitions) recorded from a DSGC in response to noise-free PD (left) and ND (right) stimulation in 0 Mg++ ACSF (‘0 Mg++’, red), after addition of 1mM Mg++ (‘Control’, blue) and subsequent bath application of 50 μm AP5 (+AP5, black). Color scheme applies to the entire figure. Top, schematic time course of noise-free illumination. Inset, Schematized movie frames of the standard stimulation protocol, consisting of a bright bar moving across the display.
(B) As in (A) for noisy stimulation conditions in which the luminance of the background and stimulus (bar) changed independently between frames with similar mean levels as (A) and SD of 50% of the mean.
(C–D) Expanded view of average responses in (A) and (B) during the 500-ms epochs indicated by the gray regions in (A) and (B).
(E) The variance of the membrane potential (mean ±SD) during the baseline period increased with variability of the background luminance.
(F) PSP amplitudes (mean ±SD) elicited by PD (left) and ND (right) stimuli decreased (relative to baseline) as visual noise increased.
(G) DSI (median ± quartile) was reduced by visual noise in all conditions. Statistical analysis in (E–G) was conducted within individual noise levels and color coded as in (A,*p<0.05,**p<0.01 vs. other conditions, n=12, paired t-test with Bonferroni correction).
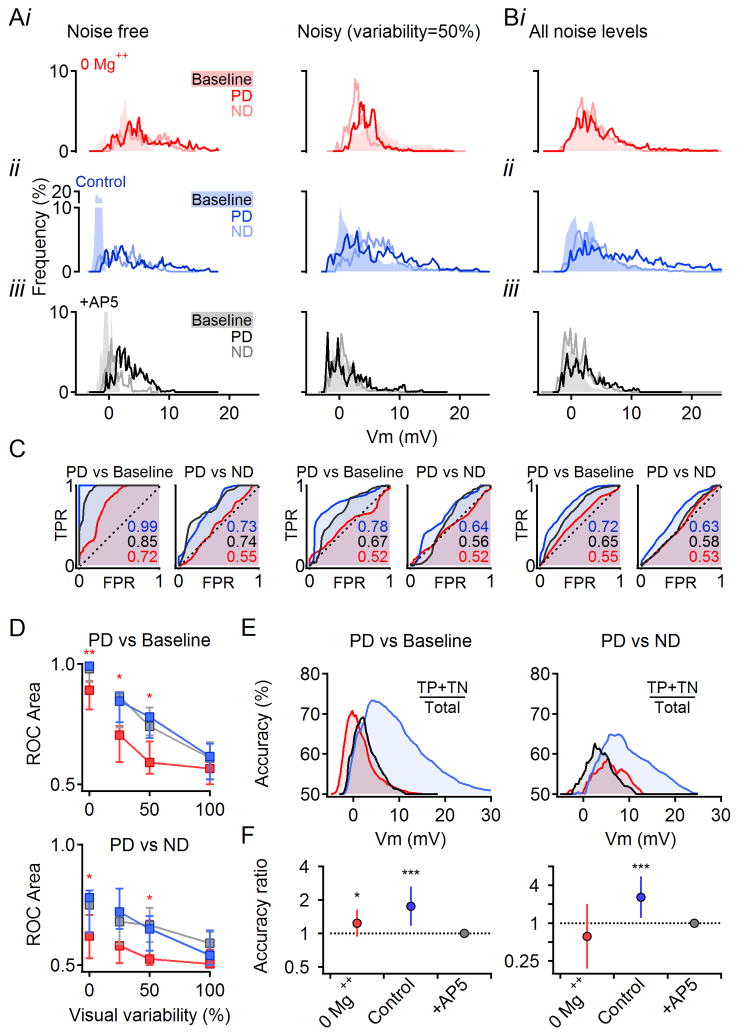
To determine how well DSGCs distinguish salient signals (i.e., PD stimulation) from background noise, we applied the receiver operating characteristic (ROC) classification test to PSPs evoked by motion stimuli under various noise levels (Figure 7A,B; membrane potential values acquired during periods indicated by gray regions in Figure 6A,B). The ROC curve (Figure 7C) was produced by plotting true vs. false positive rates (TPR and FPR respectively) derived from a distribution of membrane potentials. For two identical distributions, TPR = FPR and the ROC curve follows a diagonal line and has an area under the curve (AUC) of 0.5, indicating that discrimination between the distributions is no better than chance. For two non-overlapping distributions that can be perfectly distinguished from each other, the ROC curve reaches the top left corner and AUC = 1. ROC analysis indicated that, in noise-free stimulation conditions, visual signals were distinguished from background activity almost perfectly in control conditions and with NMDARs blocked (median AUC = 0.99 and 0.98 respectively, Figure 7C,D). In 0 Mg++ solution however, the discrimination was significantly reduced to 0.83 (Figure 7C; p=0.008, n=12, Wilcoxon Signed Rank Test with Bonferroni correction), mainly due to the broader distribution of the baseline responses (Figure 7Ai). ROC discrimination fell sharply with increasing noise (Figure 7B–D). Discrimination remained significantly lower in Mg++-free solution up to 50% stimulus variability, beyond which discrimination in all conditions approached chance levels (Figure 7D).
Figure 7. Multiplicative scaling improves subthreshold signal fidelity in noisy visual conditions.
(A) All-points histograms of membrane potentials from the same cell in Figure 6A–D in response to noise-free and noisy visual stimuli. Data collected during baseline (shaded) and responses (PD and ND, solid lines) during the periods indicated in gray in Figure 6A. Color scheme as in Figure 6.
(B) Histograms of membrane potentials from the cell in (A) pooled across all visual noise levels.
(C) ROC analysis of discrimination between signal (PD responses) and baseline or ND histograms shown in (A) and (B). TPR, true positive rate; FPR, false positive rate (see Experimental Procedures). For indistinguishable distributions, the ROC follows the unity line and has an area under the curve of 0.5. For non-overlapping distributions, the ROC reaches the left top corner and has an area under the curve of 1.
(D) Median (± quartile) area under the ROC curve for PD vs. baseline histograms (top) and PD vs. ND (bottom) as a function of the visual noise (*p<0.05,**p<0.01 between 0 Mg++ and other conditions within individual noise levels, n=12, Wilcoxon Signed Rank Test with Bonferroni correction).
(E) Accuracy of discrimination between the PD and baseline (left) and PD and ND (right) at all noise levels (data from B) as a function of the membrane potential (see Experimental Procedures).
(F) Summarized accuracy analysis for discrimination between PD and baseline (left) and PD vs. ND (right) responses recorded at all noise levels (n=12 cells). The area under the accuracy curve in 0 Mg++ and control solutions was normalized to the area in AP5. The resulting accuracy ratio (mean, error bars-99% confidence intervals) is shown on a logarithmic axis (*p<0.05,***p<0.001 different from unity, z-test with Bonferroni correction).
ROC curves are normalized and so do not indicate how signal classification varies as a function of discrimination threshold. Neurons adapt their AP threshold for different reasons (Fontaine et al., 2014), so accurate classification should, ideally, occur over a range of thresholds. We therefore calculated classification accuracy–the percentage of the correctly classified responses (i.e., true positives and true negatives)–at each possible discrimination threshold (Figure 7E). To examine accuracy in all visual conditions, we pooled data in response to all four visual variability levels. Although the maximum accuracy was similar in control and AP5, as predicted by the ROC results, accuracy was higher in control over a broader range of membrane potentials. Accordingly, the area under the accuracy curve was significantly larger in control compared to the AP5 condition (Figure 7F, left). This effect was not simply because PSPs are larger in control: Accuracy was significantly lower in 0 Mg++ (Figure 7E,F, left), even though PD PSP amplitudes in 0 Mg++ were similar to those in control solutions (Figures 6F, 7Ai).
To determine whether NMDARs also increase the accuracy of motion discrimination, we applied the same analysis to PD vs. ND PSPs pooled across all stimulus noise levels (Figure 7C–F). ROC analysis indicated that motion discrimination was reduced in 0 Mg++ conditions (Figure 7C,D), and that accuracy was significantly increased in control over NMDAR-blocked conditions (Figure 7E,F, right). Taken together, these results indicate that voltage-dependent NMDAR conductances enhance accurate detection of visual signals in DSGCs.
NMDAR multiplication improves fidelity of suprathreshold DS signaling in DSGCs
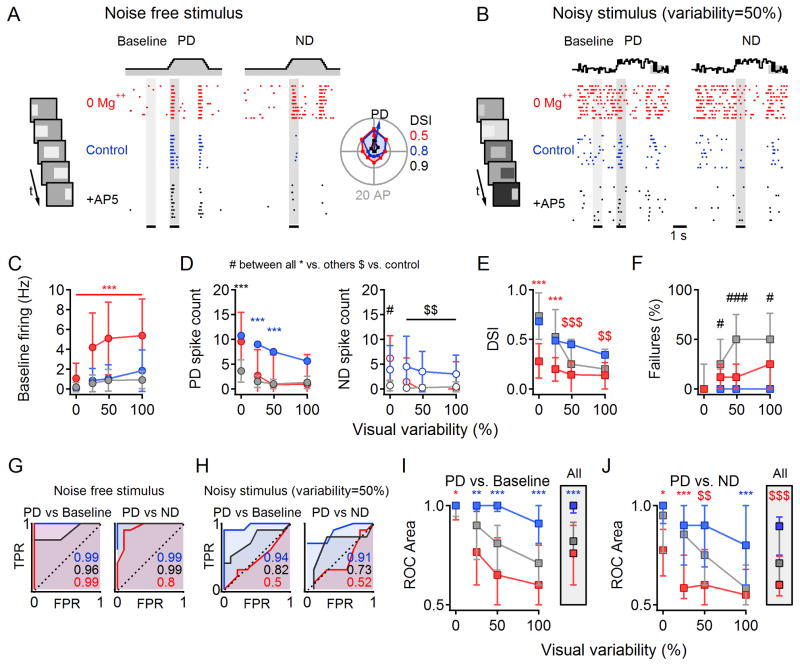
We next tested whether NMDARs improve discrimination of visually evoked AP responses, recorded in the cell-attached configuration with Nav channels active, in Mg++ free solution (n=34 cells), in physiological Mg++, (n=25 cells) and in the presence of AP5 (n=21 cells), Figure 8A,B).
Figure 8. Multiplicative scaling improves output fidelity in noisy visual conditions.
(A) Raster plot of spikes in one DSGC (n=10 repetitions) in response to PD (left) and ND (right) stimuli in 0 Mg++ ACSF (‘0 Mg++’, red), after addition of 1mM Mg++ (‘Control’, blue) and subsequent addition of 50 μm AP5 (‘+AP5’, black). Color scheme applies to the entire figure. Top, schematic time course of noise-free illumination. Inset, left, Schematized movie frames of the standard visual stimulation protocol. Inset, right, DS tuning of responses. Calculated DSI values indicated color coded by the condition.
(B) As in (A) for noisy stimulation conditions in which the luminance of the background and stimulus (bar) changed independently between frames with similar mean levels as (A) and SD of 50% of the mean.
(C) Baseline firing rate as a function of visual noise. Here and below statistical analysis was conducted within individual noise levels with ANOVA followed by multiple comparison Tukey test. Statistical significance color coded as in (A).*p<0.05,**p<0.01,***p<0.001 vs. other conditions, #p<0.05,###p<0.001 between all conditions, $$p<0.01,$$$p<0.001 vs. control).
(D) Average spike count (± SD) during PD (left) and ND (right) stimulation.
(E) DSI (median ±quartile) is reduced by noise in all conditions, but the reduction is more pronounced in 0 Mg++.
(F) Failure rate (the percentage of trials with PD firing below baseline firing level).
(G) ROC analysis of responses in (A) at times indicated by the grey regions.
(H) As in (G) for the data shown in (B).
(I) Median (±quartile) area under ROC plots for PD vs. baseline histograms as a function of visual noise. Inset, Area under ROC for responses averaged over all noise levels.
(J) As in (I) for PD vs. ND responses.
Similar to our subthreshold results, the baseline firing in 0 Mg++ was elevated compared to control (Figure 8A,C) and, although PD responses were not affected (p=0.3, Figure 8A,D left), ND responses were increased (p=0.04; Figure 8A,D right), leading to reduced DSI (p<0.001 vs. control and AP5, ANOVA with multiple comparison Tukey test; Figure 8A,E), in agreement with previous results in rabbit DSGCs (Tjepkes and Amthor, 2000). Increasing visual stimulus noise degraded DS signaling in all three conditions, but to a significantly different extent. Noisy background luminance increased baseline firing most prominently in 0 Mg++ conditions (Figure 8B,C), masking responses to motion stimuli (Figure 8B,D) and reducing DSI even further (Figure 8E).
These results demonstrate that, although the AP threshold nonlinearity enhances DS in DSGCs (Figures 1, S1), the fidelity of AP output signals is influenced by subthreshold synaptic responses. Given that the DSI of AP responses was unaffected by bath application of AP5 (Figure 8E), however, the question remains why NMDAR-mediated multiplication is useful. To a first approximation, the primary effect of NMDAR blockade was on signal fidelity: AP5 significantly reduced the number of APs evoked by both background illumination and motion stimuli (Figure 8C,D), to an extent that a significant fraction of PD stimuli failed to elicit APs in DSGCs (“Failures”, Figure 8F), thereby essentially blinding DSGCs to visual stimuli.
Other benefits of multiplicative NMDAR scaling became apparent when AP responses were subjected to ROC analysis. Consistent with PSP results (Figure 7), in noise-free conditions, PD stimuli were discriminated from background almost perfectly in all conditions (Figure 8G), but as stimulus variability increased the control responses significantly outperformed those in the AP5 and 0 Mg++ conditions (Figure 8H,I). Because of the larger amplitude of ND response, the discrimination between PD and ND was significantly reduced in 0 Mg++ condition (Figure 8J, p=0.02, ANOVA with multiple comparison Tukey test). Accordingly, the averaged PD stimulus discrimination over all visual conditions was significantly better under control conditions (Figure 8I and J ‘All’).
DISCUSSION
Soon after making the first recordings from DSGCs, Barlow and colleagues recognized that the retina could, in principle, compute DS via any of several possible synaptic and circuit configurations (Barlow and Levick, 1965). Here, we have shown that a network arrangement providing directionally tuned inhibition to DSGCs, the scenario initially favored by Barlow (Barlow and Levick, 1965) and subsequently confirmed by numerous groups (Fried et al., 2002; Lee et al., 2010; Vaney et al., 2012), enables NMDARs on DSGC dendrites to increase light responses proportionally, thereby increasing signal fidelity without compromising DS tuning. This multiplication requires the voltage-dependent NMDAR conductance in order to operate over a sufficiently broad membrane potential range. Although it remains unclear how neurons in higher visual areas interpret DS signals originating in the retina, any metric or downstream detector of DS ought to benefit from the multiplicative scaling provided by DSGCs. In addition to increasing the absolute amplitude of DS signals, multiplication enhances signal discrimination and the accuracy of DS signaling (Figures 6–8).
Comparison with other multiplication mechanisms
Suprathreshold multiplication, in which the spike rate scales as a product of division or multiplication between synaptic inputs, has been reported in several systems (Fox and Daw, 1992; Gabbiani et al., 2002; Mitchell and Silver, 2003; Pena and Konishi, 2001; Prescott and De Koninck, 2003; Priebe and Ferster, 2012; Rothman et al., 2009; Silver, 2010; Wilson et al., 2012). Theoretical analysis shows that a steep, almost exponential, relationship between PSP amplitude and firing rate enables many neurons to transform an additive change in PSP amplitudes into a multiplicative change in the number of APs (Haider and McCormick, 2009; Murphy and Miller, 2003; Silver, 2010). Consistent with a prominent role for APs in DS signaling fidelity, we found that DSGC AP responses exhibited significantly greater DSI than did subthreshold PSPs (Figure S1C). The suprathreshold rectification provided by APs cannot, however, compensate for suboptimal synaptic DS computation: when NMDAR scaling was modified to be additive (by removing extracellular Mg++), DSI was reduced significantly for both PSP and AP responses (Figures 5, 6, and 8). These results indicate that NMDAR-mediated multiplication of subthreshold responses significantly influences suprathreshold DS signaling.
In many neurons, supralinear synaptic amplification by voltage-dependent NMDAR conductances depends on the location and timing of active synaptic inputs, the strength of activation and the background excitatory and especially inhibitory input levels (Branco and Hausser, 2011; Jadi et al., 2012; Major et al., 2008; Makara and Magee, 2013; Polsky et al., 2004). The multiplication mechanism that we describe in DSGCs requires directionally tuned inhibition: when directional input was rendered excitatory, NMDAR scaling became additive (Figure 4). Other than this specific requirement, which is fulfilled by the DS circuitry, multiplication in DSGCs appeared quite robust, persisting over a range of developmental ages and visual stimulus strength/variability (Figures 6, S3 and S4). Our simulations further suggested that multiplication is robust to broad changes in dendritic geometry, stimulation parameters, ratios and relative locations of excitatory and inhibitory synaptic inputs and the voltage dependence of NMDAR blockade by Mg++ (data not shown).
Comparison with other mechanisms of DS
Although tuned inhibition appears to be a consistent feature of DS computation (Briggman et al., 2011; Fried et al., 2002; Lee et al., 2010; Vaney et al., 2012), additional mechanisms to enhance DS signaling may vary between different species and DSGC subtypes. DSGCs in rabbit retina generate dendritic sodium spikes that significantly sharpen DS tuning (Oesch et al., 2005; Sivyer and Williams, 2013), and a different DSGC subtype in mouse employs both dendritic spikes and gap junction-mediated interconnectivity to synchronize and temporally advance the timing of DS signaling (Trenholm et al., 2014; Trenholm et al., 2013). We did not detect dendritic spikes in DRD4 DSGCs (data not shown), and our computer simulations did not require regenerative dendritic events to replicate experimentally recorded PSP and (somatic) AP responses and DSI values, suggesting that passive PSP propagation to the soma is sufficient to generate reliable DS detection in these DSGCs. As both dendritic and somatic spikes depend largely on postsynaptic depolarization, synaptic integration dynamics ought to influence both types of spikes similarly. We would expect, therefore, that postsynaptic multiplicative amplification would also enhance the fidelity of DS signaling in cells that produce dendritic spikes. In that case, the location of synaptic integration would shift from the soma to dendritic segments, but the rules governing synaptic input transformation to spike would likely remain similar.
Most DSGCs are symmetric about their dendritic field, although some DSGC subtypes exhibit elongated dendritic arbors that are skewed toward their PD. This morphological feature has been shown to expand the range of DS computation, probably by taking advantage of increased summation when inputs arrive onto proximal dendrites prior to the distal dendritic tips (Trenholm et al., 2011), reminiscent of latencies in transmission between thalamic neurons and DS neurons in primary visual cortex (Saul and Humphrey, 1992). Interestingly, cortical direction and orientation selectivity computation do not appear to require differentially tuned excitation and inhibition, as both excitatory and inhibitory inputs are larger in response to PD stimuli (Anderson et al., 2000; Murphy and Miller, 2003; Priebe and Ferster, 2008; Tan et al., 2011). The cortex, therefore, employs what is mainly a tuned excitation DS computation scheme. Our experiments suggest that multiplicative synaptic integration in DSGCs is abolished when directionally tuned GABAergic input is made excitatory (Figure 4), but we were unable to test the effects of directionally tuning glutamatergic input and, therefore, NMDAR activation. In the cortex, directionally tuned NMDAR activation may give rise to dendritic NMDA spikes specifically in response to PD stimulation and therefore contribute to DS signaling (Lavzin et al., 2012; Smith et al., 2013). In the retina, tuned excitation may be impractical, as it would presumably require many additional bipolar cell types or directional feedback inhibition onto highly compartmentalized bipolar cell terminals (Vaney et al., 2012). Tuned inhibition may therefore represent the best feasible strategy to produce robustly tuned signals in DSGCs.
DSGC motion discrimination and downstream DS signaling
What can single DSGC responses teach us about how visual motion is encoded downstream in the visual system? In the mammalian retina, preferred directions of ON-OFF DSGCs are aligned with the four cardinal axes (Oyster and Barlow, 1967), and downstream neurons may receive input from DSGCs with different PD orientations (Marshel et al., 2012). A postsynaptic network could therefore directly compare responses from neighboring DSGCs that are oriented to different angles to obtain a direction profile of stimulus. The ROC analysis provides a mathematical framework for estimating the accuracy of such comparisons.
Our results show that in the absence of visual noise there is little computational benefit to NMDAR-mediated multiplicative scaling, as both the DSI and ROC separation were similar in the presence and absence of NMDARs (Figures 6–8). With increasing visual noise, however, a clear distinction between the two conditions became evident, as the responses to stimuli in the absence of functioning NMDARs were overwhelmed by background noise (Figures 6–8). This decrease in signal fidelity upon NMDAR blockade was not simply due to a reduced excitatory drive, as increasing the number of APs with a non-multiplicative excitatory input (with Mg++ free extracellular solution) did not reverse the negative effects of visual noise on spiking responses and reduced DSI in all visual conditions (Figure 8).
EXPERIMENTAL PROCEDURES
See Supplemental Experimental Procedures for details. The significance level is 0.05 in all analyses unless noted otherwise.
Recording procedures
All animal procedures were conducted in accordance with NIH guidelines, as approved by the NINDS Animal Care and Use Committee. Retinas were isolated from eGFP-DRD4/Chat-Cre/TdTomato (RRID:MMRRC_000231-UNC) mice (postnatal days 14 70). All subsequent procedures and recordings were performed in Ames media or artificial cerebrospinal fluid equilibrated with 95% O2/5% CO2. Recordings were performed in ambient light levels to reduce rod-pathway activation. All experiments were performed at ~35 °C. Cells were identified by their GFP expression using a Zeiss LSM-510 multiphoton microscope.
Visual stimulation
Light stimuli were generated with a 405-nm LED collimated and masked by a LCD display controlled by the acquisition software and focused through the microscope condenser to illuminate the tissue at the focal plane of the photoreceptors. Visual stimuli consisted of bright bars moving at 1 mm/sec along the long axis in 8 different directions.
Simulations
Multicompartmental numerical simulations were performed in the NEURON simulation environment using morphology of one reconstructed DSGC. The cell was stimulated by a network of 282 presynaptic cells, releasing simulated vesicles based on the presynaptic membrane potential. DS tuning was simulated by a stronger (inhibitory and/or excitatory, based on the examined conditions) synaptic conductance in response to a moving ‘light’ bar.
Supplementary Material
Acknowledgments
We thank Ms. Hua Tian for mouse husbandry and genotyping support, Drs. Nelson Spruston, Mark Stopfer, Nitin Gupta, Nicholas Oesch and Rowland Taylor and his lab members and for discussions, and Drs. Kevin Briggman, Wei Li, and Nicholas Oesch for comments on the manuscript. The authors declare no competing financial interests. This work was supported by the NINDS Intramural Research Program (NS003145).
Footnotes
AUTHOR CONTRIBUTIONS
Conceptualization, A.P.P. and J.S.D.; Methodology, A.P.P. and J.S.D.; Software, A.P.P.; Validation, A.P.P and J.S.D.; Formal Analysis, A.P.P.; Investigation, A.P.P.; Resources, A.P.P. and J.S.D.; Data Curation, A.P.P.; Writing–Original Draft, A.P.P.; Writing Review & Editing, J.S.D. and A.P.P.; Visualization, A.P.P.; Supervision, J.S.D.; Project Administration, A.P.P. and J.S.D.; Funding Acquisition, J.S.D.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson JS, Carandini M, Ferster D. Orientation tuning of input conductance, excitation, and inhibition in cat primary visual cortex. Journal of neurophysiology. 2000;84:909–926. doi: 10.1152/jn.2000.84.2.909. [DOI] [PubMed] [Google Scholar]
- Barlow HB, Hill RM. Selective sensitivity to direction of movement in ganglion cells of the rabbit retina. Science (New York, NY. 1963;139:412–414. doi: 10.1126/science.139.3553.412. [DOI] [PubMed] [Google Scholar]
- Barlow HB, Levick WR. The mechanism of directionally selective units in rabbit's retina. The Journal of physiology. 1965;178:477–504. doi: 10.1113/jphysiol.1965.sp007638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berretta N, Jones RS. Tonic facilitation of glutamate release by presynaptic N-methyl-D-aspartate autoreceptors in the entorhinal cortex. Neuroscience. 1996;75:339–344. doi: 10.1016/0306-4522(96)00301-6. [DOI] [PubMed] [Google Scholar]
- Branco T, Clark BA, Hausser M. Dendritic discrimination of temporal input sequences in cortical neurons. Science. 2010;329:1671–1675. doi: 10.1126/science.1189664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Branco T, Hausser M. Synaptic integration gradients in single cortical pyramidal cell dendrites. Neuron. 2011;69:885–892. doi: 10.1016/j.neuron.2011.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggman KL, Helmstaedter M, Denk W. Wiring specificity in the direction-selectivity circuit of the retina. Nature. 2011;471:183–188. doi: 10.1038/nature09818. [DOI] [PubMed] [Google Scholar]
- Chen M, Lee S, Park SJ, Looger LL, Zhou ZJ. Receptive field properties of bipolar cell axon terminals in the direction-selective sublaminas of the mouse retina. Journal of neurophysiology. 2014 doi: 10.1152/jn.00283.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diamond JS, Copenhagen DR. The contribution of NMDA and non-NMDA receptors to the light-evoked input-output characteristics of retinal ganglion cells. Neuron. 1993;11:725–738. doi: 10.1016/0896-6273(93)90082-3. [DOI] [PubMed] [Google Scholar]
- Euler T, Detwiler PB, Denk W. Directionally selective calcium signals in dendrites of starburst amacrine cells. Nature. 2002;418:845–852. doi: 10.1038/nature00931. [DOI] [PubMed] [Google Scholar]
- Fontaine B, Pena JL, Brette R. Spike-threshold adaptation predicted by membrane potential dynamics in vivo. PLoS computational biology. 2014;10:e1003560. doi: 10.1371/journal.pcbi.1003560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox K, Daw N. A Model for the Action of NMDA Conductances in the Visual Cortex. Neural computation. 1992;4:59–83. [Google Scholar]
- Fried SI, Munch TA, Werblin FS. Mechanisms and circuitry underlying directional selectivity in the retina. Nature. 2002;420:411–414. doi: 10.1038/nature01179. [DOI] [PubMed] [Google Scholar]
- Gabbiani F, Krapp HG, Koch C, Laurent G. Multiplicative computation in a visual neuron sensitive to looming. Nature. 2002;420:320–324. doi: 10.1038/nature01190. [DOI] [PubMed] [Google Scholar]
- Haider B, McCormick DA. Rapid neocortical dynamics: cellular and network mechanisms. Neuron. 2009;62:171–189. doi: 10.1016/j.neuron.2009.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harnett MT, Makara JK, Spruston N, Kath WL, Magee JC. Synaptic amplification by dendritic spines enhances input cooperativity. Nature. 2012;491:599–602. doi: 10.1038/nature11554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huberman AD, Wei W, Elstrott J, Stafford BK, Feller MB, Barres BA. Genetic identification of an On-Off direction-selective retinal ganglion cell subtype reveals a layer-specific subcortical map of posterior motion. Neuron. 2009;62:327–334. doi: 10.1016/j.neuron.2009.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jadi M, Polsky A, Schiller J, Mel BW. Location-dependent effects of inhibition on local spiking in pyramidal neuron dendrites. PLoS computational biology. 2012;8:e1002550. doi: 10.1371/journal.pcbi.1002550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeon CJ, Kong JH, Strettoi E, Rockhill R, Stasheff SF, Masland RH. Pattern of synaptic excitation and inhibition upon direction-selective retinal ganglion cells. The Journal of comparative neurology. 2002;449:195–205. doi: 10.1002/cne.10288. [DOI] [PubMed] [Google Scholar]
- Kittila CA, Massey SC. Pharmacology of directionally selective ganglion cells in the rabbit retina. Journal of neurophysiology. 1997;77:675–689. doi: 10.1152/jn.1997.77.2.675. [DOI] [PubMed] [Google Scholar]
- Lavzin M, Rapoport S, Polsky A, Garion L, Schiller J. Nonlinear dendritic processing determines angular tuning of barrel cortex neurons in vivo. Nature. 2012;490:397–401. doi: 10.1038/nature11451. [DOI] [PubMed] [Google Scholar]
- Lee S, Chen L, Chen M, Ye M, Seal RP, Zhou ZJ. An Unconventional Glutamatergic Circuit in the Retina Formed by vGluT3 Amacrine Cells. Neuron. 2014;84:708–715. doi: 10.1016/j.neuron.2014.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S, Kim K, Zhou ZJ. Role of ACh-GABA Cotransmission in Detecting Image Motion and Motion Direction. Neuron. 2010;68:1159–1172. doi: 10.1016/j.neuron.2010.11.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linn DM, Massey SC. Acetylcholine release from the rabbit retina mediated by NMDA receptors. J Neurosci. 1991;11:123–133. doi: 10.1523/JNEUROSCI.11-01-00123.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- London M, Hausser M. Dendritic computation. Annual review of neuroscience. 2005;28:503–532. doi: 10.1146/annurev.neuro.28.061604.135703. [DOI] [PubMed] [Google Scholar]
- Major G, Larkum ME, Schiller J. Active properties of neocortical pyramidal neuron dendrites. Annual review of neuroscience. 2013;36:1–24. doi: 10.1146/annurev-neuro-062111-150343. [DOI] [PubMed] [Google Scholar]
- Major G, Polsky A, Denk W, Schiller J, Tank DW. Spatiotemporally graded NMDA spike/plateau potentials in basal dendrites of neocortical pyramidal neurons. Journal of neurophysiology. 2008;99:2584–2601. doi: 10.1152/jn.00011.2008. [DOI] [PubMed] [Google Scholar]
- Makara JK, Magee JC. Variable dendritic integration in hippocampal CA3 pyramidal neurons. Neuron. 2013;80:1438–1450. doi: 10.1016/j.neuron.2013.10.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshel JH, Kaye AP, Nauhaus I, Callaway EM. Anterior-posterior direction opponency in the superficial mouse lateral geniculate nucleus. Neuron. 2012;76:713–720. doi: 10.1016/j.neuron.2012.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayer ML, Westbrook GL, Guthrie PB. Voltage-dependent block by Mg2+ of NMDA responses in spinal cord neurones. Nature. 1984;309:261–263. doi: 10.1038/309261a0. [DOI] [PubMed] [Google Scholar]
- Mel BW. Synaptic integration in an excitable dendritic tree. Journal of neurophysiology. 1993;70:1086–1101. doi: 10.1152/jn.1993.70.3.1086. [DOI] [PubMed] [Google Scholar]
- Mitchell SJ, Silver RA. Shunting inhibition modulates neuronal gain during synaptic excitation. Neuron. 2003;38:433–445. doi: 10.1016/s0896-6273(03)00200-9. [DOI] [PubMed] [Google Scholar]
- Murphy BK, Miller KD. Multiplicative gain changes are induced by excitation or inhibition alone. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2003;23:10040–10051. doi: 10.1523/JNEUROSCI.23-31-10040.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowak L, Bregestovski P, Ascher P, Herbet A, Prochiantz A. Magnesium gates glutamate-activated channels in mouse central neurones. Nature. 1984;307:462–465. doi: 10.1038/307462a0. [DOI] [PubMed] [Google Scholar]
- Oesch N, Euler T, Taylor WR. Direction-selective dendritic action potentials in rabbit retina. Neuron. 2005;47:739–750. doi: 10.1016/j.neuron.2005.06.036. [DOI] [PubMed] [Google Scholar]
- Oyster CW, Barlow HB. Direction-selective units in rabbit retina: distribution of preferred directions. Science (New York, NY. 1967;155:841–842. doi: 10.1126/science.155.3764.841. [DOI] [PubMed] [Google Scholar]
- Park SJ, Kim IJ, Looger LL, Demb JB, Borghuis BG. Excitatory synaptic inputs to mouse on-off direction-selective retinal ganglion cells lack direction tuning. J Neurosci. 2014;34:3976–3981. doi: 10.1523/JNEUROSCI.5017-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pei Z, Chen Q, Koren D, Giammarinaro B, Acaron Ledesma H, Wei W. Conditional Knock-Out of Vesicular GABA Transporter Gene from Starburst Amacrine Cells Reveals the Contributions of Multiple Synaptic Mechanisms Underlying Direction Selectivity in the Retina. J Neurosci. 2015;35:13219–13232. doi: 10.1523/JNEUROSCI.0933-15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pena JL, Konishi M. Auditory spatial receptive fields created by multiplication. Science. 2001;292:249–252. doi: 10.1126/science.1059201. [DOI] [PubMed] [Google Scholar]
- Polsky A, Mel BW, Schiller J. Computational subunits in thin dendrites of pyramidal cells. Nature neuroscience. 2004;7:621–627. doi: 10.1038/nn1253. [DOI] [PubMed] [Google Scholar]
- Prescott SA, De Koninck Y. Gain control of firing rate by shunting inhibition: roles of synaptic noise and dendritic saturation. Proceedings of the National Academy of Sciences of the United States of America. 2003;100:2076–2081. doi: 10.1073/pnas.0337591100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe NJ, Ferster D. Inhibition, spike threshold, and stimulus selectivity in primary visual cortex. Neuron. 2008;57:482–497. doi: 10.1016/j.neuron.2008.02.005. [DOI] [PubMed] [Google Scholar]
- Priebe NJ, Ferster D. Mechanisms of neuronal computation in mammalian visual cortex. Neuron. 2012;75:194–208. doi: 10.1016/j.neuron.2012.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothman JS, Cathala L, Steuber V, Silver RA. Synaptic depression enables neuronal gain control. Nature. 2009;457:1015–1018. doi: 10.1038/nature07604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saul AB, Humphrey AL. Evidence of input from lagged cells in the lateral geniculate nucleus to simple cells in cortical area 17 of the cat. Journal of neurophysiology. 1992;68:1190–1208. doi: 10.1152/jn.1992.68.4.1190. [DOI] [PubMed] [Google Scholar]
- Schnupp JW, King AJ. Neural processing: the logic of multiplication in single neurons. Current biology : CB. 2001;11:R640–642. doi: 10.1016/s0960-9822(01)00381-5. [DOI] [PubMed] [Google Scholar]
- Silver RA. Neuronal arithmetic. Nature reviews Neuroscience. 2010;11:474–489. doi: 10.1038/nrn2864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sivyer B, Williams SR. Direction selectivity is computed by active dendritic integration in retinal ganglion cells. Nature neuroscience. 2013;16:1848–1856. doi: 10.1038/nn.3565. [DOI] [PubMed] [Google Scholar]
- Smith SL, Smith IT, Branco T, Hausser M. Dendritic spikes enhance stimulus selectivity in cortical neurons in vivo. Nature. 2013;503:115–120. doi: 10.1038/nature12600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stafford BK, Park SJ, Wong KY, Demb JB. Developmental Changes in NMDA Receptor Subunit Composition at ON and OFF Bipolar Cell Synapses onto Direction-Selective Retinal Ganglion Cells. J Neurosci. 2014;34:1942–1948. doi: 10.1523/JNEUROSCI.4461-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan AY, Brown BD, Scholl B, Mohanty D, Priebe NJ. Orientation selectivity of synaptic input to neurons in mouse and cat primary visual cortex. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2011;31:12339–12350. doi: 10.1523/JNEUROSCI.2039-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor WR, He S, Levick WR, Vaney DI. Dendritic computation of direction selectivity by retinal ganglion cells. Science (New York, NY. 2000;289:2347–2350. doi: 10.1126/science.289.5488.2347. [DOI] [PubMed] [Google Scholar]
- Taylor WR, Vaney DI. Diverse synaptic mechanisms generate direction selectivity in the rabbit retina. J Neurosci. 2002;22:7712–7720. doi: 10.1523/JNEUROSCI.22-17-07712.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tjepkes DS, Amthor FR. The role of NMDA channels in rabbit retinal directional selectivity. Visual neuroscience. 2000;17:291–302. doi: 10.1017/s0952523800172128. [DOI] [PubMed] [Google Scholar]
- Trenholm S, Johnson K, Li X, Smith RG, Awatramani GB. Parallel mechanisms encode direction in the retina. Neuron. 2011;71:683–694. doi: 10.1016/j.neuron.2011.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trenholm S, McLaughlin AJ, Schwab DJ, Turner MH, Smith RG, Rieke F, Awatramani GB. Nonlinear dendritic integration of electrical and chemical synaptic inputs drives fine-scale correlations. Nature neuroscience. 2014;17:1759–1766. doi: 10.1038/nn.3851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trenholm S, Schwab DJ, Balasubramanian V, Awatramani GB. Lag normalization in an electrically coupled neural network. Nature neuroscience. 2013;16:154–156. doi: 10.1038/nn.3308. [DOI] [PubMed] [Google Scholar]
- Vaney DI, Sivyer B, Taylor WR. Direction selectivity in the retina: symmetry and asymmetry in structure and function. Nature reviews. 2012;13:194–208. doi: 10.1038/nrn3165. [DOI] [PubMed] [Google Scholar]
- Wei W, Hamby AM, Zhou K, Feller MB. Development of asymmetric inhibition underlying direction selectivity in the retina. Nature. 2010 doi: 10.1038/nature09600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weng S, Sun W, He S. Identification of ON-OFF direction-selective ganglion cells in the mouse retina. The Journal of physiology. 2005;562:915–923. doi: 10.1113/jphysiol.2004.076695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson NR, Runyan CA, Wang FL, Sur M. Division and subtraction by distinct cortical inhibitory networks in vivo. Nature. 2012;488:343–348. doi: 10.1038/nature11347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yonehara K, Balint K, Noda M, Nagel G, Bamberg E, Roska B. Spatially asymmetric reorganization of inhibition establishes a motion-sensitive circuit. Nature. 2010 doi: 10.1038/nature09711. [DOI] [PubMed] [Google Scholar]
- Yonehara K, Farrow K, Ghanem A, Hillier D, Balint K, Teixeira M, Juttner J, Noda M, Neve RL, Conzelmann KK, Roska B. The first stage of cardinal direction selectivity is localized to the dendrites of retinal ganglion cells. Neuron. 2013;79:1078–1085. doi: 10.1016/j.neuron.2013.08.005. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.