Human insulin dynamics in women: a physiologically based model

Abstract

Currently available models of insulin dynamics are mostly based on the classical compartmental structure and, thus, their physiological utility is limited. In this work, we describe the development of a physiologically based model and its application to data from 154 patients who underwent an insulin-modified intravenous glucose tolerance test (IM-IVGTT). To determine the time profile of endogenous insulin delivery without using C-peptide data and to evaluate the transcapillary transport of insulin, the hepatosplanchnic, renal, and peripheral beds were incorporated into the circulatory model as separate subsystems. Physiologically reasonable population mean estimates were obtained for all estimated model parameters, including plasma volume, interstitial volume of the peripheral circulation (mainly skeletal muscle), uptake clearance into the interstitial space, hepatic and renal clearance, as well as total insulin delivery into plasma. The results indicate that, at a population level, the proposed physiologically based model provides a useful description of insulin disposition, which allows for the assessment of muscle insulin uptake.

insulin administration continues to be an important therapy in treating patients with Type 1 and also Type 2 diabetes mellitus. Some newer classes of pharmacotherapies, moreover, act by stimulating endogenous insulin secretion, including incretin analogs and DPP-4 inhibitors (20). Thus, a more complete understanding of the pathophysiology of insulin dynamics may lead to improved management of diabetes in patients treated with insulin or with therapies that promote endogenous insulin release.

Insulin disposition in humans has been studied previously, using compartmental analysis to quantify the kinetics of insulin's distribution and elimination (see Ref. 6 for a review). Although such compartment models for insulin dynamics are useful for describing plasma insulin concentration-time profiles (e.g., following intravenous, subcutaneous, and inhaled insulin administration), a drawback of the reported one- (15), two- (23), and three- (27) compartment mammillary models, including time-varying (21) and nonlinear models (16), is that the model compartments have little anatomical and physiological correspondence. As a consequence, the model and its parameters cannot be readily interpreted in terms of fundamental transport mechanisms, which underlie the distribution and elimination of insulin. For example, previously reported compartment models do not provide information on the dynamics of insulin uptake by skeletal muscle tissue, yet such information is valuable since muscle uptake of insulin is the rate-limiting step in insulin-stimulated muscle glucose uptake (1, 3). Moreover, the mechanism of this transport process remains unclear (2, 18). These compartment models, furthermore, do not readily allow for prediction of insulin dynamics in patient populations with liver, cardiovascular, kidney, and other relevant diseases, and, as such, provide limited ability to reflect changes in insulin disposition in disease progression.

To address the aforementioned limitations of current models of insulin dynamics, we have developed a physiologically based pharmacokinetic (PBPK) model for insulin disposition using plasma glucose and insulin time course data from patients who underwent a frequently sampled insulin modified-intravenous glucose tolerance test (IM-IVGTT) to determine β-cell function and insulin sensitivity (11, 29, 32, 37). The specific aims of the study were to use the insulin concentration data from the IM-IVGTT test obtained in healthy females and in women at risk for developing diabetes to construct a physiologically based circulatory model of insulin dynamics in humans that will serve as a tool to allow evaluation of the uptake of insulin into the skeletal muscle, as well as the estimation of both hepatic and renal clearance of insulin.

MATERIALS AND METHODS

Participants and study design.

Women who previously exhibited gestational diabetes (that is, those who are at risk for developing diabetes) and women who had normal pregnancies were recruited from the outpatient department of the University Clinic of Vienna. The details of the clinical study, including the ethical committee's approvals, have been reported elsewhere (37). A total of 120 patients who previously exhibited gestational diabetes and 34 women who had normal pregnancy had complete data and were used in the analysis reported herein. The anthropometric characteristics of these 154 women are as follows: body weight: 73 ± 16 kg; body mass index: 27 ± 6 kg/m²; age: 33 ± 5 yr (means and SD). All women underwent IM-IVGTT 8 to 10 wk postpartum. After a 10- to 12-h overnight fast, bolus doses of glucose (0.3 g/kg) and insulin (0.3 U/kg in 1 min) were given at time 0 and 20 min, respectively. Insulin was measured in samples taken immediately before glucose ingestion and at 0, 3, 4, 5, 6, 8, 10, 14, 19, 22, 27, 30, 35, 40, 50, 70, 100, 140, and 180 min after glucose injection. Blood was rapidly centrifuged, and insulin was determined in plasma by commercially available radioimmunoassay (Serono Diagnostics, Freiburg, FRG) providing an interassay coefficient of variation of 5%.

Model.

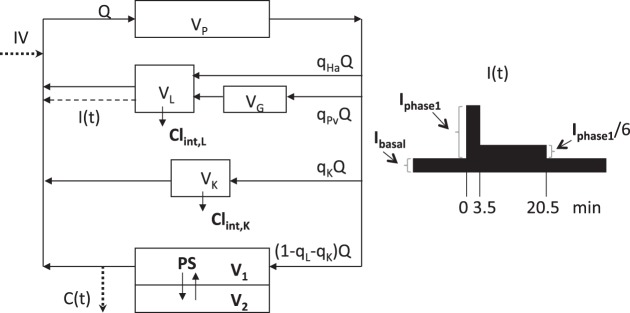
The structure of the PBPK model used in this study is depicted in Fig. 1. It represents the simplest possible model for analyzing the following processes governing insulin's dynamics: uptake into the interstitial space, pancreatic secretion, hepatic extraction, and renal elimination. The model consists of subsystems representing the pulmonary (distribution volume V_P) and systemic circulation, with the latter separated into the splanchnic circulation, the kidneys (V_K), and the rest of the systemic circulation as three parallel subsystems. The splanchnic circulation is formed by the liver (V_L), together with the gastrointestinal tract, including the spleen and pancreas (V_G) arranged in series. In the peripheral circulation (mainly skeletal muscle), permeation through the capillary wall, from the plasma compartment (V₁) to the interstitial space (V₂), is determined by the permeability-surface product (PS). Cardiac plasma output is denoted by Q. The parameters q_L and q_K indicate the fractions of blood flow to the liver and kidney, while q_Ha and q_Pv represent hepatic artery and portal vein blood flow (all parameters defined in Table 1). The posthepatic delivery rate of insulin, I(t), consists of a constant basal rate, I_basal, and the response due to glucose injection. For the time course of the latter, a specific pattern has been assumed a priori as depicted in Fig. 1. It is a simplified form of I(t) profiles reported in the literature (10, 19) and consists of a suprabasal phase 1 (peak) rate lasting 3.5 min (I_phase1) followed by a reduced phase 2 rate lasting 17 min (I_phase1/6). On the basis of a well-mixed organ model, the intrinsic clearances CL_int,L and CL_int,K account for hepatic extraction (metabolism) and renal elimination of insulin. The complete set of equations describing the model shown in Fig. 1 is provided in the appendix. Since all patients were in a fasted state when the IM-IVGTT was initiated, the model was assumed to be in steady state prior to glucose administration (see appendix for further details).

Fig. 1.

Schematic structure of the circulatory model of insulin dynamics, with exogenous input [glucose, 0.3 g/kg as a bolus dose at time 0 and insulin infusion (0.3 U/kg in 1 min) at 20 min] and endogenous posthepatic delivery rate of insulin, I(t). C(t) denotes the sampled insulin concentration. Subsystems include the pulmonary and splanchnic circulation kidneys, and the rest of the systemic circulation (mainly skeletal muscle). Model parameters are described in Table 1. (Bold letters denote those parameters estimated in the population analysis.) The posthepatic delivery rate of insulin, I(t), is shown in the inset on the right. It consists of the basal delivery rate, I_basal, plus the assumed pattern of glucose-induced delivery consisting of a peak rate, I_phase1, followed by a reduced rate, I_phase1/6.

Table 1.

Parameters used in the model

	Symbol, Unit	Source
Estimated parameters
Muscle plasma volume	V1, ml/kg
Muscle interstitial volume	V2, ml/kg
Permeability-surface product	PS, ml/min
Intrinsic hepatic clearance	CLint,L, ml/min
Intrinsic renal clearance	CLint,K, ml/min
Basal delivery rate	Ibasal, mU/min
Peak delivery rate	Iphase1, mU/min
Derived parameters
Hepatic clearance	CLhep, ml/min	Eq. 1
Renal clearance	CLren, ml/min
Hepatic extraction	Ehep, %	Eq. 2
Total insulin delivery	TID, U	Eq. 3
Total insulin secretion	TIS, U	Eq. 4
Parameters derived from fixed ratios
Lung plasma volumea	VP	V1·1.1
Gut plasma volumeb	VG	V1·0.34
Liver plasma volumec	VL	V1·0.17
Kidney plasma volumed	VK	V1·0.05
Cardiac plasma outpute	Q	4000·(BW/70)0.71
Flow fraction to hepatic arteryf	qH,a	Q·0.08
Flow fraction to portal vein	qPv	Q·0.20
Flow fraction to kidney	qK	Q·0.17

^aRef. 35;

^bRefs. 17, 12;

^cRefs. 17, 12;

^dRefs. 17, 25;

^eRef. 7;

^fRef. 36; ^gRef. 36; ^hRef. 36. BW, body weight.

To select the most parsimonious model of insulin distribution in the peripheral circulation, the two-compartment tissue model was compared with both simpler and more complex models. The alternate models included a one-compartment (flow-limited) distribution model and a model with a saturable (Michaelis-Menten) uptake process and lymphatic back-transport from the interstitial space to the venous pool. We have neglected extraction since it was not possible to estimate separately insulin clearance by the kidney and the rest of the peripheral circulation. Non-flow-limited models for the other organs and tissues were not supported by the experimental data of the IM-IVGTT study used in the current work.

Parameter estimation and statistical analysis.

The insulin concentration-time data from all patients were analyzed simultaneously using a hierarchical, population modeling approach, which allows information from individual patients to collectively inform the model estimation. The hierarchical modeling analysis yields estimates of the population mean and interpatient variability for those estimated parameters of the tested models, as well as their precision as percent relative standard error (%RSE). Furthermore, estimates of the individual subject parameters are available. The hierarchical analysis was accomplished via maximum likelihood estimation using the expectation-maximization algorithm (or MLEM) in the ADAPT (version 5) software for pharmacokinetic/pharmacodynamic system analysis (8). Estimated model parameters were assumed to follow a multivariate log-normal distribution, and the error associated with measured insulin was assumed to be normally distributed with SD dependent on insulin (additive and proportional error terms). Model selection for insulin distribution was based on the resulting values of the Akaike Information Criterion (AIC) for the tested models (as implemented in Ref. 8), as well as on the plausibility of estimated model parameters.

The model parameters V₁, V₂, PS, CL_int,L, and CL_int,K, as well as I_basal and I_phase1, were estimated using the data, while the parameters V_P, V_G, V_L, and V_K were determined based on V₁ and Q, q_K, q_Ha, and q_Pv were fixed (Table 1). Volumes were estimated as a fraction of body weight (BW), and cardiac plasma output was estimated as a power function of BW.

Other relevant quantities were derived from the estimated and fixed model parameters. For the one-compartment liver model (see Fig. 1), the hepatic clearance was obtained as follows (q_L = q_Ha + q_Pv):

$$C{L}_{hep}=\frac{q_{L}QC{L}_{\mathrm{int},L}}{q_{L}Q+C{L}_{\mathrm{int},L}}$$ (1)

An analogous formula (one-compartment organ model) was used to calculate renal clearance, CL_ren, and thus, the total clearance of insulin is given by the sum of CL_hep + CL_ren. From Eq. 1 the hepatic extraction ratio (E_hep) of insulin was obtained as

$$E_{hep}=\frac{{CL}_{\mathrm{int},L}}{qLQ+{CL}_{\mathrm{int},L}}$$ (2)

The total insulin delivery (TID), i.e., the total amount of insulin delivered after hepatic degradation, was calculated from the estimated delivery rate of insulin above basal as follows:

$$TID={\displaystyle {\int }_0^{20.5}I\left(t\right)dt-{\displaystyle {\int }_0^{20.5}{I}_{phase1}dt}}$$ (3)

On the basis of Eqs. 2 and 3 and the total insulin secretion (TIS) was calculated as

$$TIS=TID/\left(1-E_{hep}\right)$$ (4)

Multiple-comparison inference was performed using the nonparametric Kruskal-Wallis test.

RESULTS

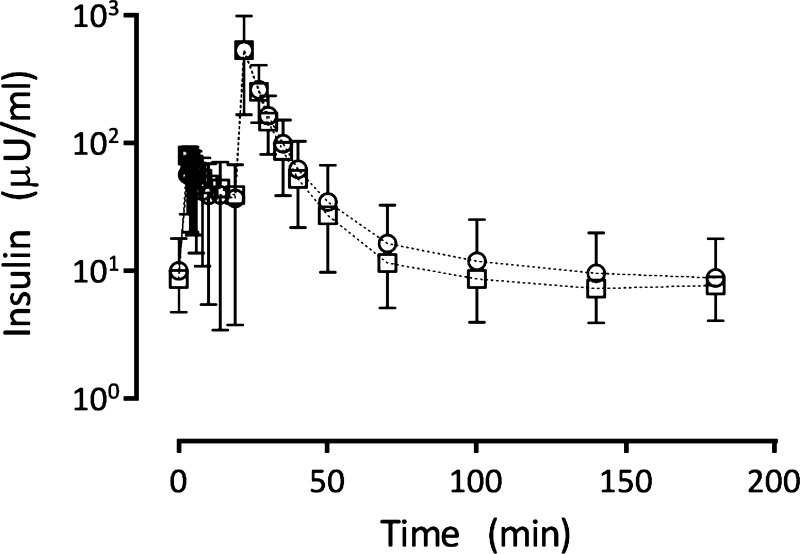
Figure 2 shows insulin plasma concentration (means and SD) for all patients from each group. The mean insulin concentration time curves for the women who previously exhibited gestational diabetes and control groups were largely superimposable. Moreover, separate modeling analyses based on data from each group resulted in no significant differences in estimated model parameters (results not shown). Thus, the data from both groups were combined in the final model development, and subsequent analysis is presented below.

Fig. 2.

Measured insulin plasma concentration data (means ± SD) for the 120 patients at risk for developing diabetes (○) and the 34 control subjects (□).

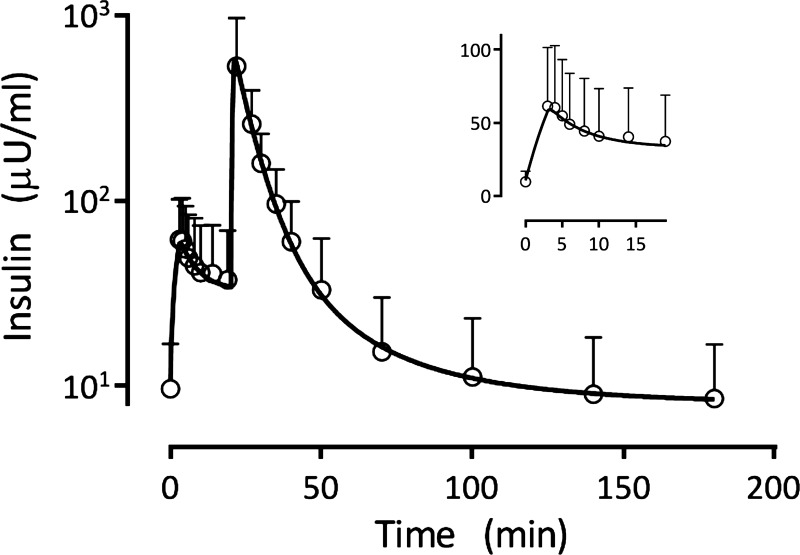
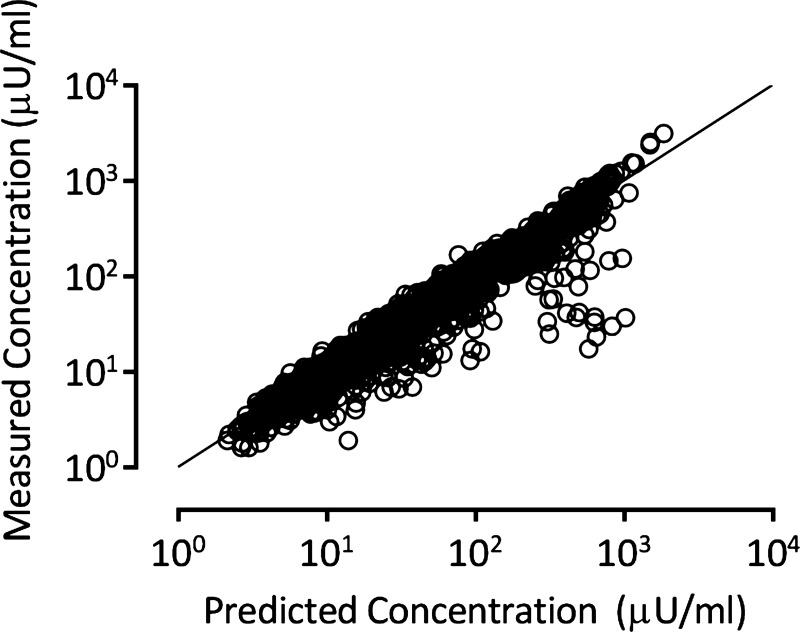
The insulin concentration time profile predicted on the basis of each patient's model parameters (conditional mean estimates, derived and fixed) were averaged and are shown in Fig. 3 together with the mean and standard deviation of the measured insulin. The inset in Fig. 3 more clearly shows the ability of the population model to also describe the dynamics of insulin following glucose administration and prior to insulin injections. A composite graph showing a plot of the measured plasma insulin concentrations in all 154 patients vs. the corresponding patient model predictions (2,926 values in total) demonstrates the goodness-of-fit obtained with the model (Fig. 4). Although some model overprediction is noted, the coefficient of determination for the regression line is r² = 0.83 (P < 0.0001), indicating that the model fits the data with good fidelity over this wide range of plasma insulin values. Replacing the two-compartment tissue model by a one-compartment model (instantaneous distribution of insulin into the interstitial space) led to an increase in AIC (23,946 vs. 23,493). No decrease in AIC was achieved by incorporating either a saturable uptake or lymphatic back-transport process into the model.

Fig. 3.

Average of the 154 individual subject model predicted insulin concentration time curves, together with the measured plasma insulin values (means ± SD). The inset shows the same information from the time of glucose administration prior to insulin administration, with the ordinate shown on a linear scale.

Fig. 4.

Goodness-of-fit plot showing the individual subject predicted vs. observed plasma insulin concentrations. The solid line represents the line of identity.

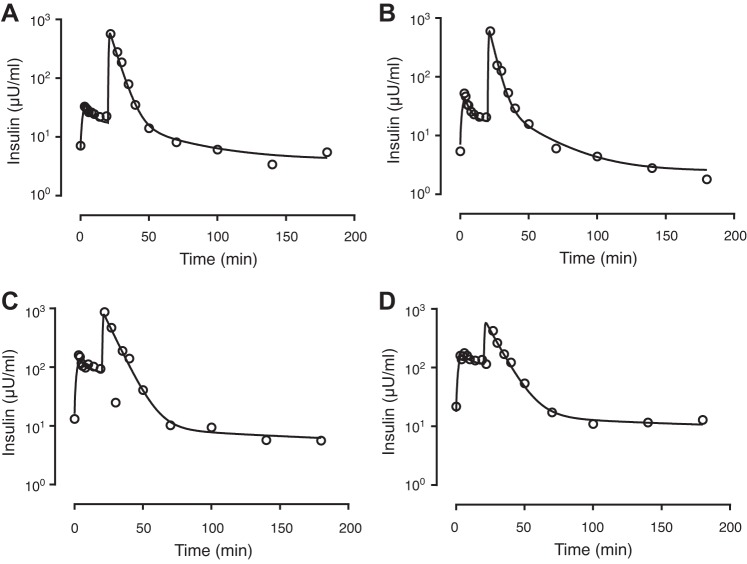
Table 2 lists the estimated population mean estimates for V₁, V₂, PS, CL_int,L, CL_int,K, I_basal, and I_phase1, together with their intersubject variability, obtained using the model shown in Fig. 1 (percent relative standard errors, %RSE, shown for each estimate). The table also shows the resulting values of the derived quantities, including the hepatic clearance (CL_hep), renal clearance (CL_ren), hepatic extraction ratio (E_hep, %), total insulin delivery (TID), and total insulin secretion (TIS), calculated based on the definitions presented in the materials and methods. A renal extraction ratio of 0.22 corresponds to a BW of 70 kg, as determined using the value of renal flow in Table 1 and renal clearance in Table 2. As an example, Fig. 5 shows observed insulin concentrations together with model predictions (based on individual parameter estimates) for four selected patients with different insulin delivery rates. The subjects in Fig. 5, A and B, had lower values of total insulin delivery (0.26 U and 0.27 U) relative to the mean population estimate (0.40 U). The subject in Fig. 5C had a TID (0.89 U) closer to the population mean, while the subject in Fig. 5D had a considerably larger TID of 2.0 U. Despite this greater than seven-fold difference in TID between these subjects, insulin dispositions as assessed by the total clearance varied over less than a twofold range (303 ml/min for the subject in Fig. 5C vs. 477 ml/min for the subject in Fig. 5D).

Table 2.

Population parameter estimates for the model of insulin distribution, elimination and secretion dynamics in patients undergoing an intravenous glucose tolerance test

Model Parameter	Symbol, Unit	Mean (%RSE)	Interpatient CV% (%RSE)
Muscle blood volumea	V1, ml/kg	19.1 (6)	49 (9)
Muscle interstitial volumea	V2, ml/kg	24.9 (17)	81 (22)
Permeability-surface product	PS, ml/min	75.8 (13)	64 (21)
Intrinsic hepatic clearance	CLint,L, ml/min	571 (22)	67 (27)
Intrinsic renal clearance	CLint,K, ml/min	171 (51)	65 (53)
Basal delivery rate	Ibasal, mU/min	2.93 (10)	80 (9)
Peak delivery rate	Iphase1, mU/min	61.2 (8)	73 (10)
Hepatic clearanceb	CLhep, ml/min	363	42
Renal clearanceb	CLren, ml/min	141	54
Hepatic extractionb	Ehep, %	46	36
Total insulin deliveryb	TID, U	0.397	73
Total insulin secretionb	TIS, U	0.730	85

^aThese volumes include muscle and all other tissues with the exception of the hepatosplanchnic organs and kidneys.

^bThe equations for these derived parameters are presented in materials and methods.

Fig. 5.

Examples of individual predictions for four selected patients. The estimated total insulin delivery, TID (U), for each patient is as follows: 0.26 U (A), 0.27 U (B), 0.89 U (C), and 2.0 U (D).

DISCUSSION

To our knowledge, this is the first physiologically based circulatory model of insulin dynamics developed to describe insulin disposition following IM-IVGTT in humans. In addition to the exogenous insulin infusion from the IM-IVGTT protocol, the model accounts for the resulting endogenous posthepatic secretion of insulin (i.e., the basal level and the response to glucose stimulation) and divides the systemic system into three lumped subsystems: hepatosplanchnic, renal, and the remainder (largely skeletal muscle). The latter was modeled by a vascular space compartment and an interstitial space compartment with permeation controlled by the permeability surface area parameter (PS), which assumes that insulin uptake is mainly determined by skeletal muscle. The model allows for estimation of hepatic insulin clearance and extraction, and an estimate of renal insulin clearance through the kidney subsystem was included in the model.

The IM-IVGTT study upon which the current modeling analysis is based was designed to evaluate insulin sensitivity and was not designed explicitly with the goal of modeling insulin disposition. However, by using prior information for certain model parameters (Table 1), exploiting the information in the measured insulin data from both the glucose and insulin administration portions of the IM-IVGTT protocol, and using a population modeling approach guided by prior information about liver and renal insulin clearance, we obtained reliable values for the estimated model parameters. Following the glucose dose of the IM-IVGTT protocol, the plasma insulin measurements provide information about the endogenous insulin secretion despite the simplified form of the pancreatic insulin release profile assumed. The large insulin dose given at 20 min provides considerable information about the phases of insulin disposition, especially muscle distribution parameters in the earlier phases of the disposition profile, along with total clearance from the later disposition phase. To investigate the reliability of the estimated skeletal muscle distribution parameters of the model (both population mean and intersubject variability), the population analysis was also performed with intrinsic insulin renal clearance fixed at 171 ml/min (the estimated value shown in Table 2) and at 243 ml/min (corresponding to a total renal clearance of 200 ml/min). The resulting estimates for the skeletal muscle distribution parameters of the model (both population mean and intersubject variability) were largely unchanged, regardless of the value used for the fixed intrinsic renal clearance, providing some support for the reliability of the of the skeletal muscle distribution model.

Insulin clearance and hepatic extraction.

Hepatic extraction of insulin is an important contributor to its peripheral concentration, given that the liver filters ∼50% (5, 6) of the secreted hormone before it reaches the systemic circulation. This process, however, is often ignored in metabolic studies involving the evaluation of insulin secretion and delivery to the periphery circulation, where it acts on glucose uptake. By using the model introduced here, we show that it is possible to reflect the hepatic handling of insulin and quantify its contribution to the available systemic insulin concentration. The population estimates obtained from the population analysis of our circulatory model have been assessed by comparing them with directly measured quantities. The model-based estimates of hepatic and renal clearance were 363 and 141 ml/min, respectively, similar to the corresponding values of 320–400 and 200 ml/min reported in humans (14, 33). This holds true also for the ratio of hepatic to peripheral clearance (28), assuming that renal extraction is the main contribution to the latter. The estimated mean hepatic extraction ratio of 46% is in accordance with values reported previously for humans (5, 6). The estimated total clearance, CL_hep+CL_ren, of 504 ml/min is somewhat lower than that of 716 ml/min reported in a pharmacokinetic study (23), which could be attributed to different subject populations and experiment designs. Note that the estimated parameter CL_int,L is independent of blood flow; CL_hep is a derived parameter that is dependent on hepatic blood flow (Eq. 1).

Muscle distribution.

The estimate of insulin distribution volume V₁ of 19.1 ml/kg is higher than the typical value of muscle blood volume reported for humans 12 ml/kg (17), but this is not unexpected in that V₁ in the model includes not only skeletal muscle blood volume but also that of other tissues of distribution. The V₂ estimate of 24.9 ml/kg obtained in the modeling analysis is smaller than the muscle interstitial volume of 39 ml/kg reported by Bonadonna et al. (4) and may be due to the endogenous insulin level leading to a less well-defined terminal insulin disposition phase. For the transendothelial insulin transport into the interstitial space, a permeability-surface product (or uptake clearance) of 75.8 ml/min was estimated (PS in the model), compared with a value of 105 ml/min measured directly in human skeletal muscle using microdialysis (13). A different model was used by Pretty et al. (24) to calculate uptake rate constants from arterial and interstitial insulin concentration data taken from various sources in the literature. Our results are also within the range of PS values (11 and 91 ml/min) reported in (24). Our results do not suggest a saturable uptake of insulin, which is in agreement with some findings (3, 26), but not with others (16). Finally, the modeling results do not include the lymphatic back transport pathway, but this may be a consequence of the relatively short time course of this IM-IVGTT protocol during which any contribution of lymphatic transport to plasma insulin would be minimal.

Pancreatic secretion and systemic delivery.

Even though a simplified piecewise constant shape of insulin delivery rate assumed in the present work, the resulting estimates of the underlying biphasic insulin secretion rates were within the range of values reported previously for the same dose of glucose (0.3 g/kg) in humans. The model estimate of the maximum rate of insulin delivery (I_phase1, first peak in Fig. 1) was 61.2 mU/min, which is within the wide range of 43–181 mU/min reported by Ferrannini and Pilo (10), but higher than that of 12 mU/min estimated by Tura et al. (31). The estimated basal delivery rate (I_basal in Fig. 1) was 2.98 mU/min, which is lower than 7 mU/min reported by Polonsky et al. (22) and somewhat higher than the value of 0.95 mU/min reported by Tura et al. (31). Note that the calculation of insulin secretion (Eq. 4) is based on the assumption that insulin clearance is not saturated, as required by Eq. 2.

The objective of the work reported herein was to develop a PBPK model of insulin dynamics. To achieve this aim, given the clinical study design, it was necessary to assume both a time-constant hepatic extraction and a piecewise constant pattern of insulin delivery, as has been used previously (e.g., Ref. 34). The simplified model used for insulin release, while appropriate for the patient population under study, would not be applicable more broadly as part of a complete IM-IVGTT model for other populations or study designs. Despite these limitations, the resulting overall PBPK model includes parameters representing the physiological properties that determine insulin disposition. We note that other model-based approaches, such as those based on an empirical description of insulin disposition and C-peptide data allow the estimation of the time dependence of extraction and the pattern of insulin secretion (30, 31). Insulin release profiles so obtained, could then be incorporated into the PBPK model for insulin disposition reported in this work.

In conclusion, the physiologically based model of insulin dynamics presented describes the IM-IVGTT insulin data obtained in this population of patients with reasonable fidelity. As a consequence of the model's physiological basis, it can be used to predict alterations in insulin dynamics that might be expected in diabetic complications involving cardiovascular system, as well as the liver and kidneys. Thus, the model provides a framework for incorporating disease progression into predictions of insulin dynamics that may further inform insulin-based treatment of diabetes. Moreover, independent estimates of the model's physiological parameters in individual subjects (e.g., noninvasive estimates of cardiac output) can be used to improve the model's subject-specific predictive ability.

GRANTS

This article was funded by the National Institutes of Health Grant P41-EB001978 to D. Z. D'Argenio.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: M.W., G.P., and D.Z.D. analyzed data; M.W., A.T., G.P., and D.Z.D. interpreted results of experiments; M.W. and D.Z.D. prepared figures; M.W., G.P., and D.Z.D. drafted manuscript; M.W., A.T., A.K.-W., G.P., and D.Z.D. edited and revised manuscript; M.W., A.T., A.K.-W., G.P., and D.Z.D. approved final version of manuscript; A.K.-W. conception and design of research; A.K.-W. performed experiments.

Appendix

The following equations define the circulatory model as shown in Fig. 1. The symbol A_i is the insulin amount in compartment i, IV(t) is the insulin infusion rate and C(t) denotes the measured concentration. The definitions of the other symbols are provided in the text. As described in materials and methods, they have been implemented using the ADAPT software (8). Model assumptions are provided in the materials and methods, and these include a simplified, two-phase form of I(t), nonflow limited distribution in skeletal muscle, flow-limited update in all other organs/tissues, and first-order liver and renal clearances.

$$\begin{array}{cc}\frac{d{A}_p}{dt}=IV\left(t\right)+I\left(t\right)+q_{L}Q\frac{A_L}{V_L}+q_{K}Q\frac{A_K}{V_K}+\left(1-q_L-q_K\right)Q\frac{A_1}{V_1}-Q\frac{A_P}{V_P},\hfill & A_P\left(0\right)=0\hfill \\ \frac{d{A}_G}{dt}=q_{PV}Q\left(\frac{A_P}{V_P}-\frac{A_G}{V_G}\right),\hfill & A_G\left(0\right)=0\hfill \\ \frac{d{A}_L}{dt}=q_{Ha}Q\frac{A_P}{V_P}+q_{Pv}Q\frac{A_G}{V_G}-q_{L}Q\frac{A_L}{V_L}-C{l}_{\mathrm{int},L}\frac{A_L}{V_L},\hfill & A_L\left(0\right)=0\hfill \\ \frac{d{A}_K}{dt}=q_{K}Q\left(\frac{A_P}{V_P}-\frac{A_K}{V_K}\right)-C{l}_{\mathrm{int},K}\frac{A_K}{V_K},\hfill & A_K\left(0\right)=0\hfill \\ \frac{d{A}_1}{dt}=\left(1-q_L-q_K\right)Q\left(\frac{A_P}{V_P}-\frac{A_1}{V_1}\right)+PS\left(\frac{A_2}{V_2}-\frac{A_1}{V_1}\right),\hfill & A_1\left(0\right)=0\hfill \\ \frac{d{A}_2}{dt}=PS\left(\frac{A_1}{V_1}-\frac{A_2}{V_2}\right),\hfill & A_2\left(0\right)=0\hfill \\ C\left(t\right)=\frac{A_1}{V_1}\hfill & \hfill \end{array}$$

The form of IV(t) in the first equation above is depicted in Fig. 1. A run-in period is incorporated in IV(t) for simulations to allow the estimated basal delivery rate (I_basal) to produce the corresponding non-zero basal values of insulin in all tissues prior to the start of the IM-IVGTT protocol (t = 0 in Fig. 1).