The abundance of ²⁸Si³²S, ²⁹Si³²S, ²⁸Si³⁴S, and ³⁰Si³²S in the inner layers of the envelope of IRC+10216

Abstract

We present high spectral resolution mid-IR observations of SiS towards the C-rich AGB star IRC+10216 carried out with the Texas Echelon-cross-Echelle Spectrograph mounted on the NASA Infrared Telescope Facility. We have identified 204 ro-vibrational lines of ²⁸Si³²S, 26 of ²⁹Si³²S, 20 of ²⁸Si³⁴S, and 15 of ³⁰Si³²S in the frequency range 720 – 790 cm⁻¹. These lines belong to bands v = 1 – 0, 2 – 1, 3 – 2, 4–3, and 5–4, and involve rotational levels with J_low ≲ 90. About 30 per cent of these lines are unblended or weakly blended and can be partially or entirely fitted with a code developed to model the mid-IR emission of a spherically symmetric circumstellar envelope composed of expanding gas and dust. The observed lines trace the envelope at distances to the star ≲ 35R_⋆(≃ 0″.7). The fits are compatible with an expansion velocity of 1+2.5(r/R_⋆ −1) km s⁻¹ between 1 and 5R_⋆, 11 km s⁻¹ between 5 and 20R_⋆, and 14.5 km s⁻¹ outwards. The derived abundance profile of ²⁸Si³²S with respect to H₂ is 4.9 × 10⁻⁶ between the stellar photosphere and 5R_⋆, decreasing linearly down to 1.6 × 10⁻⁶ at 20R_⋆ and to 1.3 × 10⁻⁶ at 50R_⋆. ²⁸Si³²S seems to be rotationally under LTE in the region of the envelope probed with our observations and vibrationally out of LTE in most of it. There is a red-shifted emission excess in the ²⁸Si³²S lines of band v = 1 – 0 that cannot be found in the lines of bands v = 2 – 1, 3 – 2, 4 – 3, and 5 – 4. This excess could be explained by an enhancement of the vibrational temperature around 20R_⋆ behind the star. The derived isotopic ratios ²⁸Si/²⁹Si, and ³²S/³⁴S are 17 and 14, compatible with previous estimates.

1 INTRODUCTION

IRC+10216 (CW Leo) is the closest asymptotic giant branch (AGB) star to Earth (≃ 120 pc; Groenewegen et al. 2012). During the last decades this star was usually considered as an isolated star with an effective temperature of ≃ 2300 K (Ridgway & Keady 1988) and surrounded by an optically thick C-rich circumstellar envelope (CSE) composed of molecular gas and dust, which results from the ejection of stellar material at a rate ≃ 1 – 5 × 10⁻⁵ (e.g., Knapp & Morris 1985; Cernicharo et al. 1996; Schöier & Olofsson 2001; De Beck et al. 2012). Although there were indirect evidences suggesting that it could be actually a binary system (Mauron & Huggins 1999, 2000; Fong et al. 2013; Decin et al. 2011, 2014; Cernicharo et al. 2015a,c), Kim et al. (2014) recently reported the discovery of what could be a faint companion of the AGB star responsible of the ejected matter.

More than 80 molecular species have been detected in its CSE (e.g., Kawaguchi et al. 1995; Cernicharo et al. 2000; He et al. 2008; Patel et al. 2011). Although most of them form in the outer envelope, the so-called parent molecules (e.g., CO, C₂H₂, HCN, SiS, SiO, CS, SiC₂, Si₂C) are formed in warm and dense shells near the stellar photosphere (Keady & Ridgway 1993; Boyle et al. 1994; Cernicharo et al. 2010, 2015b), where strong dynamical mechanisms probably exist (Hinkle et al. 1982; Bowen 1988) and an active chemistry has been inferred (Willacy & Cherchneff 1998; Agúndez & Cernicharo 2006; Cherchneff 2006). The dust formation and the subsequent gas acceleration involved in the development of the envelope (e.g., Gilman 1972; Morris 1987; Bowen 1988; Fonfría et al. 2008) are supposed to be intimately related to the refractory nature and abundance of the parent molecules, in particular to C- and Si-bearing species such as SiS, SiC₂, and Si₂C (Cernicharo et al. 2015b). These molecules are believed to be highly depleted due to dust throughout the first 20 – 30R_⋆ outwards from the stellar photosphere (Turner 1987; Bieging & Nguyen-Quang-Rieu 1989; Bieging & Tafalla 1993; Boyle et al. 1994; Lucas et al. 1995; Agúndez et al. 2012; Fonfría et al. 2014).

The emission of SiS has been analysed in the mid-infrared (Boyle et al. 1994), the submillimetre (Patel et al. 2009, 2011; Decin et al. 2010, 2014), and the millimetre frequency ranges (Morris 1975; Henkel et al. 1983, 1985; Turner 1987; Kahane et al. 1988, 2000; Bieging & Nguyen-Quang-Rieu 1989; Carlström et al. 1990; Bieging & Tafalla 1993; Lucas et al. 1995; Lucas 1997; Cernicharo et al. 2000, 2014; Fonfría Expósito et al. 2006; Schöier et al. 2007; Agúndez et al. 2012; Fonfría et al. 2014; Velilla Prieto et al. 2015). Its abundance throughout the middle and outer envelope is reasonably well estimated (≃ (1–2)×10⁻⁶ outwards from ≃ 10–15R_⋆ ≃ 0.2–0.3 arcsec) but its value in the innermost envelope is still controversial due to discrepancies of up to one order of magnitude between the results of several works.

The main goal of the current work is to derive a reliable SiS abundance profile for the innermost envelope of IRC+10216 in order to settle the controversy through the analysis of high spectral resolution molecular observations in the mid-IR, which has been proven as a powerful method to probe the region close to the central star (Keady et al. 1988; Keady & Ridgway 1993; Boyle et al. 1994; Fonfría et al. 2008).

In this Paper we present the identification of 265 lines of the vibrational bands v = 1 – 0, 2 – 1, 3 – 2, 4 – 3, and 5 – 4 of the silicon sulphide isotopologues ²⁸Si³²S, ²⁹Si³²S, ²⁸Si³⁴S, and ³⁰Si³²S observed with high-spectral resolution (≃ 3 – 4 km s⁻¹) towards IRC+10216. About 30 per cent of them have enough quality to be properly fitted and analysed. The observing procedure is included in Section 2. Comments on the fitting process of the molecular lines can be found in Section 3. The description of the observed SiS lines, the results of the fitting procedure, and their analysis are addressed in Section 4. Finally, a brief summary of the current work and our conclusions can be found in Section 5.

2 OBSERVATIONS

We observed IRC+10216 with the Texas Echelon-cross-Echelle Spectrograph (TEXES; Lacy et al. 2002) at the NASA Infrared Telescope Facility (IRTF) on 2002 Dec 12. We used the TEXES high resolution echelon grating with a first order grating as the cross-disperser. In this mode, a single setting covered a spectral range of ≃ 0.25 μm. The entire range (11.6 – 13.9 μm) was covered with 10 separate settings. We nodded IRC+10216 off the slit for sky subtraction. The weather was good enough during the observations that the median background level measured in the off positions showed no significant variations. We used a black body-sky difference spectrum to correct for the atmosphere. The data were reduced with the standard TEXES pipeline (Lacy et al. 2002). We normalised each spectrum by removing the baseline with a polynomial fit. The rms of the random noise is ≃ 0.15 per cent of the continuum emission.

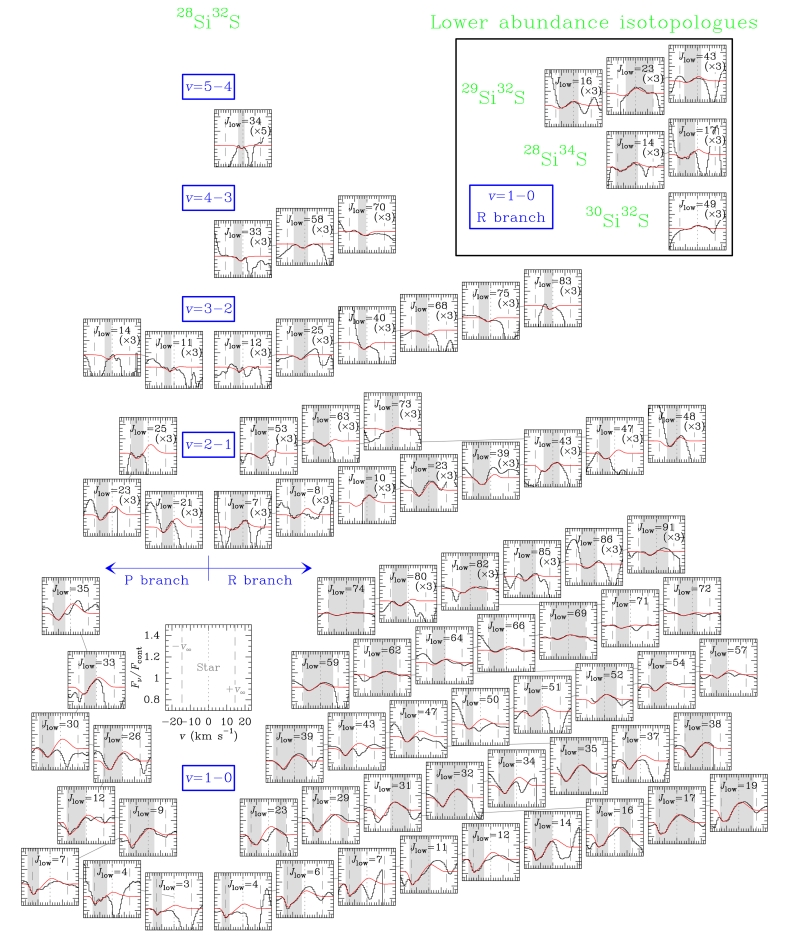
Although most of the lines in the spectrum are produced by C₂H₂, HCN, and their main isotopologues (Fonfría et al. 2008), we have identified 204 lines of ²⁸Si³²S, 26 of ²⁹Si³²S, 20 of ²⁸Si³⁴S, and 15 of ³⁰Si³²S in the frequency range between 720 to 790 cm⁻¹. A hundred and fifteen of the ²⁸Si³²S lines belong to band v = 1 – 0, 54 to band v = 2 – 1, 13 to band v = 3–2, 16 of band v = 4–3, and 6 of band v = 5–4. Seventy three of them are unblended or partially blended and can be fitted (Fig. 1). The identified lines of ²⁹Si³²S, ²⁸Si³⁴S, and ³⁰Si³²S pertain to band v = 1 – 0. Three, two, and one of them, respectively, are unblended or partially blended and can be reasonably fitted. The lines of bands involving vibrational states with higher energy are below the detection limit. No lines of the other SiS isotopologues, which are at least 100 times less abundant than ²⁸Si³²S (e.g., Kahane et al. 2000; Cernicharo et al. 2000), have been detected in our spectrum.

Figure 1.

²⁸Si³²S, ²⁹Si³²S, ²⁸Si³⁴S, and ³⁰Si³²S lines in the observed spectrum (black histogram). Most of the lines surrounding those of the SiS isotopologues belong to C₂H₂, HCN, and their isotopologues (Fonfría et al. 2008). The synthetic spectrum is plotted in red. The abscissa axis represents the Doppler velocity (v = V_LSR – v_sys, v_sys = −26.5 km s⁻¹; Cernicharo et al. 2000; He et al. 2008; Patel et al. 2011). The vertical dark grey dotted and dashed lines indicate the velocity of the star (0 km s⁻¹) and the maximum and minimum gas expansion velocity projected on to the line-of-sight (+v_∞ and −v_∞), respectively (v_∞ = 14.5 km s⁻¹). The frequency range shaded in light grey in every inset indicates the part of the lines used in the fits. The intensity of some lines with respect to the baseline was multiplied by 3 and 5 to improve their visibility (it is indicated at the upper right corner of the corresponding insets as ×3 or ×5).

We have used the low spectral resolution ISO/SWS observations carried out on 1996 May 31 (Cernicharo et al. 1999) to determine the properties of the dusty envelope. We estimate the uncertainty of these observations due to noise and the calibration process in ≃ 10 per cent.

3 MODEL OF ENVELOPE AND FITTING PROCEDURE

The observed SiS lines were fitted and analysed with the aid of the code developed by Fonfría et al. (2008), which solves numerically the radiation transfer equation of a spherically symmetric envelope composed of gas and dust in radial expansion. It was successfully used to analyse the mid-IR spectra of C₂H₂, HCN, C₄H₂, and C₆H₂ at 8 and 13 μm towards IRC+10216 and the protoplanetary nebula CRL618 (Fonfría et al. 2008, 2011). The code does not solve the statistical equilibrium equations, which would require a very large amount of CPU time to determine the population of all the ro-vibrational levels involved in the calculations. Instead, it makes use of rotational and vibrational temperature profiles provided by the user. The code solves the radiation transfer equation and produces the spectrum of the envelope convolved with a given Gaussian beam. The new 3D version of this code, presented in Fonfría et al. (2014), allowed us to calculate as well the emission of a simple asymmetrical envelope. A deeper insight on how this code works in its 1D and 3D versions and its benchmarking can be found in Fonfría et al. (2008) and Fonfría et al. (2014).

3.1 Adopted envelope model and spectroscopic constants

In order to analyse the SiS lines identified in the observed spectrum, we adopted the model of envelope composed of several concentric shells with a constant expansion velocity derived by Fonfría et al. (2008) from the analysis of the mid-IR spectra of C₂H₂ and HCN, which are produced in the same region of the envelope of IRC+10216 that the observed SiS lines trace. Despite the fact that some authors used a different model with a more continuous expansion velocity profile (e.g., Schöier et al. 2006b; Decin et al. 2010, 2014; De Beck et al. 2012), the adopted model seems to be more suitable to describe the inner layers of the envelope (Keady et al. 1988; Keady & Ridgway 1993; Boyle et al. 1994; Fonfría et al. 2008, 2014; Cernicharo et al. 2011, 2013; Agúndez et al. 2012; Daniel et al. 2012). With the aim of supporting our choice, we briefly discuss about the quality of the fits using the selected velocity profile and that recently derived by Decin et al. (2014) in Appendix A. Thus, we assumed that the CSE is divided into three Regions (I, II, and III) separated by two acceleration shells located at 5 and 20R_⋆, which were initially 0.5R_⋆ thick each (Table 1). The gas expansion velocity, v_exp, is initially assumed to be 5, 11, and 14.5 km s⁻¹ in Regions I, II, and III, respectively. In order to improve the expansion velocity field close to the star, different thicks of the inner acceleration shell (ending at 5R_⋆) and expansion velocities in Region I were tried. The mass conservation results in a gas density profile following very approximately the law ∞ $r^{-2}{v}_{\exp }^{-1}$, since a negligible amount of the total ejected mass (≲ 0.25 per cent) is locked in the dust grains (De Beck et al. 2012; Decin et al. 2014). We assumed that there is no atomic H in gas phase (Knapp & Bowers 1983; Glassgold 1996; Agúndez & Cernicharo 2006). The line width at the stellar surface is assumed to be 5 km s⁻¹, decreasing to the terminal value of 1 km s⁻¹ at 5R_⋆ following the power-law ∝ 1/r (e.g., Huggins & Healy 1986; Keady et al. 1988; Schöier et al. 2006a; Agúndez et al. 2012). This line width profile is compatible with the turbulent velocity ≳ 3 km s⁻¹ suggested by Keady et al. (1988) and Monnier et al. (2000) and the line width of ≃ 5 – 8 km s⁻¹ inferred from the vibrational excited lines of SiS, CS, and HCN observed in the mm and sub-mm wavelength ranges by Patel et al. (2009, 2011) and Cernicharo et al. (2011), which are supposed to be formed in the inner layers of the envelope. The kinetic temperature was adopted to follow the profile derived from the analysis of the CO emission by De Beck et al. (2012), i.e., T_k ∝ r^−0.58 between the stellar surface and 9R_⋆, ∝ r^−0.4 from 9R_⋆ to 65R_⋆, and ∝ r^−1.2 outwards. The rotational and vibrational temperature profiles were assumed to follow r^−γ, a dependence on the distance to the star tightly related to the cooling process of the envelope (McKee et al. 1982; Doty & Leung 1997). γ can be different for each region and for the rotational and vibrational temperatures. γ cannot be determined for both the rotational and vibrational temperatures in Region III due to the low sensitivity of the model to the emission coming from that zone. Thus, we adopted γ = 0.55 and 1.0, respectively (Fonfría et al. 2008; Agúndez et al. 2012). We assumed SiS is in rotational LTE at the stellar photosphere. No dust was considered to exist in Region I. Throughout the rest of the envelope, we adopted dust grains composed of 95 per cent of amorphous carbon (AC) and 5 per cent SiC, with a size of 0.1 μm, and a density of 2.5 g cm⁻³ (Fonfría et al. 2008).

Table 1.

Stellar and envelope parameters involved in the fits

Parameter	Units	Value	Error	Ref.
D	pc	123	—	2
α ⋆	arcsec	0.02	—	3
R ⋆	cm	3.7 × 1013	—
Ṁ	M☉ yr−1	2.1 × 10−5	—	4
T ⋆	K	2330	—	3
xHe		0.2	—	5
R in	R ⋆	5	—	4
R out	R ⋆	20	—	4
vexp (1R⋆ ≤ r < Rin)*	km s−1	1 + 2.5(r/R⋆ − 1)	—	1
vexp (Rin ≤ r < Rout)	km s−1	11.0	—	4
vexp (r ≥ Rout)	km s−1	14.5	—	4
Tk(1R⋆ ≤ r < 9R⋆)	K	T⋆(R⋆/r)0.58	—	6
Tk(9R⋆ ≤ r < 65R⋆)	K	T⋆(9R⋆/r)0.40	—	6
Tk(r ≥ 65R⋆)	K	T⋆(65R⋆/r)1.2	—	6
Δv(1R⋆ ≤ r < Rin)	km s−1	5(R⋆/r)	—	7
Δv(r ≥ Rin)	km s−1	1	—	8
f AC	per cent	95	—	4
f siC	per cent	5	—	4
τdust (11 μm)		0.70	+0.11/ −0.09	1
Tdust(Rin)	K	825	+130/ −160	1
γ dust		0.39	+0.04/ −0.06	1

D: distance to the star; α_⋆: angular stellar radius; R_⋆: linear stellar radius; Ṁ : mass-loss rate; T_⋆: stellar effective temperature; ^xHe: abundance of He; R_in and R_out: positions of the inner and outer acceleration shells; v_exp: gas expansion velocity; T_k: gas kinetic temperature; Δ_v: line width; fX: fraction of dust grains composed of material X, i.e., amorphous carbon (AC) or silicon carbon (SiC); τ_dust: dust optical depth along the line-of-sight; T_dust: temperature of dust grains; γ_dust: exponent of the decreasing dust temperature power-law. The parameters for which no uncertainty has been provided (−) were assumed as fixed throughout the whole fitting process. *The fit to the observed SiS lines was better with this expansion velocity field in Region I and it was assumed during the whole fitting process (see Section 4.1.1). References: (1) This work (2) Groenewegen et al. (2012) (3) Ridgway & Keady (1988) (4) Fonfría et al. (2008) (5) Cox (2000) (6) De Beck et al. (2012) (7) Agúndez et al. (2012) (8) Huggins & Healy (1986).

The rest frequencies of the observed lines and the energy of the vibrational states involved in the calculations (v ≤ 9; E_vib ≲ 9400 K) were taken from the MADEX code (Cernicharo et al. 2012) and the fits presented by Velilla Prieto et al. (2015). The optical constants needed to calculate the opacity of the dust grains were taken from Rouleau & Martin (1991) for amorphous carbon and from Mutschke et al. (1999) for SiC.

3.2 Fitting procedure

The fitting procedure is based on the minimisation of the reduced χ² function defined as

$${\chi }_{\mathrm{red}}^2=\frac{1}{n-p}\sum _{i=1}^n\frac{1}{{\sigma }_i^2}{\left[{\left(\frac{F_{\nu }}{F_{\mathrm{cont}}}\right)}_{\mathrm{obs},i}-{\left(\frac{F_{\nu }}{F_{\mathrm{cont}}}\right)}_{\mathrm{synth},i}\right]}^2,$$ (1)

where n and p are the number of frequency channels and of parameters involved in the fitting process, (F_ν/F_cont)_obs and (F_ν/F_cont)_synth are the flux normalised to the continuum for the synthetic and observed spectra, respectively, and σ_i is the uncertainty of the observed normalised flux for each channel. In this work, σ_i was considered equal to the noise rms for all the frequency channels. We assumed a number of physical parameters related to the envelope model as fixed during the fitting process (gas expansion velocity field, H₂ density, kinetic temperature, or line width, among others; see Tables 1 and 2). The parameters related to ²⁸Si³²S derived from the fits were the abundance with respect to H₂, the vibrational temperature at the stellar photosphere, and the rotational and vibrational temperatures at the inner and outer acceleration shells. The ²⁸Si/²⁹Si, ²⁸Si/³⁰Si, and ³²S/³⁴S isotopic ratios were estimated from the lines of ²⁹Si³²S, ²⁹Si³²S, and ²⁸Si³⁴S as scaling factors of the abundance profile of ²⁸Si³²S (Section 4.2). The fits to the lines of the SiS isotopologues were performed assuming the rotational and vibrational temperatures derived from the fits to the lines of ²⁸Si³²S. Several other parameters related to the dust component of the envelope, such as the dust optical depth or the temperature of the dust grains, were left as free parameters in order to fit the continuum and kept fixed when the SiS lines were fitted. The fits were carried out using all the observed lines from each isotopologue simultaneously. A number of observed SiS lines were slightly offset along the frequency and normalised flux level axes to get the best fit. These offsets in the normalised flux level axis are included to remove artefacts introduced during the baseline removal or due to blends with other lines coming from IRC+10216 or weak telluric lines. The offsets in the frequency axis are always smaller than the spectral resolution of the observations (≃ 3 – 4 km s⁻¹) but larger than typical with TEXES observations. The offsets have larger amplitude, although still generally less than 2 km s⁻¹, toward higher frequencies. The line list we used is based on experimental measurements and has small errors in our spectral range (≲ 0.5 km s⁻¹), as expected for a simple molecule like SiS. We see slightly small amplitude frequency offsets when we looked at the atmospheric features, suggesting that the determination of the frequency scale is less precise at higher frequencies for these data.

Table 2.

Parameters involved in the fits of ²⁸Si³²S lines

Parameter	Units	Value	Error	Ref.
x(1R⋆ ≤ r < Rin)	×10−6	4.9	+0.8/ − 0.6	1
x(r = Rout)	×10−6	1.6	+0.3/ − 0.3	1
x(r ≥ 50R⋆)	×10−6	1.3	—	2
Trot (R⋆)	K	2330	—
Trot (Rin)	K	860	+130/ − 120	1
Trot (Rout)	K	400	+70/ − 40	1
γ rot		0.55	—	2
Tvib,v = 1-0(R⋆)	K	1560	+140/ − 120	1
Tvib,v=1-0(Rin)	K	613	+11/ − 11	1
Tvib,v = 1-0(Rout)	K	227	+12/ − 12	1
Tvib,v = 2-1(R⋆)	K	1290	+130/ − 80	1
Tvib,v = 2-1(Rin)	K	490	+18/ − 10	1
Tvib,v = 2-1(Rout)	K	190	+60/ − 70	1
Tvib,v = 3-2(R⋆)	K	760	+80/ − 100	1
Tvib,v = 3-2(Rin)	K	418	+20/ − 20	1
Tvib,v = 3-2(Rout)	K	153*	—	1
Tvib,v=4-3(R⋆)	K	550	+220/ − 230	1
Tvib,v = 4-3(Rin)	K	313*	—	1
Tvib,v=4-3(Rout)	K	117*	—	1
Tvib,v=5-4(R⋆)	K	312†		1
Tvib,v = 5-4(Rin)	K	224*	—	1
Tvib,v = 5-4(Rout)	K	80*	—	1
γ vib		1.0	—	3

x: abundance relative to H₂; T_rot: rotational temperature; γ_rot: exponent of the rotational temperature power-law outwards from R_out; T_vib: vibrational temperature; γ_vib: exponent of the vibrational temperature power-law outwards from R_out for all the vibrational bands. T_rot and T_vib are ∞ r^−γ, where γ depends on the Region of the CSE and the temperature. The parameters for which no uncertainty has been provided (−) were assumed as fixed throughout the whole fitting process. *Linearly extrapolated from the vibrational temperature of other bands at the same position in the envelope. †This parameter is free but the fitted lines are too weak to derive a reliable error. References: (1) This work (2) Agúndez et al. (2012) (3) Fonfría et al. (2008).

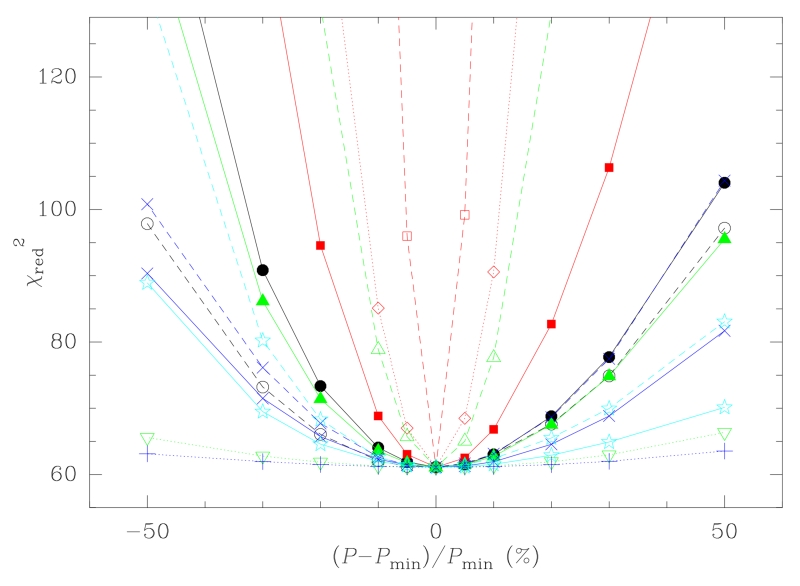
The model was sensitive to changes in most of the parameters related to SiS at distances ≲ 35R_⋆ and to dust up to ≃ 400R_⋆. The uncertainties of the free parameters (Tables 1 and 2) were calculated by varying them until the the difference between the observed and the computed synthetic spectrum was larger than the detection limit of 3σ in each channel. This conservative decision directly affects the derived uncertainties, which could be overestimated. During this process, all free parameters were varied at the same time to account for any possible influence between them that could substantially affect the derived uncertainties. These errors reflected the sensitivity of the model to each parameter, as can be seen in the shape of the ${\chi }_{\mathrm{red}}^2$ function (Fig. 2), which shows the largest curvature around its minimum (best fit) for the most influential parameters on the model (e.g., the vibrational temperature of bands v = 1 – 0 and 2 – 1 at the end of the inner acceleration shell, R_in). The minimum ${\chi }_{\mathrm{red}}^2$ achieved during the best fit is ≃ 60. This large value is mostly related to contamination of the SiS lines by other features in the frequency intervals used to calculate the ${\chi }_{\mathrm{red}}^2$ function. Although these differences do not severely affect the global minimisation process due to the large number of lines involved, they increase the minimum value of ${\chi }_{\mathrm{red}}^2$. This value could be diminished by modifying the frequency interval where the ${\chi }_{\mathrm{red}}^2$ function is calculated for each line to remove what seems a contamination after the end of the fitting process, but this choice could compromise the objectivity of the minimisation procedure and was discarded.

Figure 2.

Dependence of the ${\chi }_{\mathrm{red}}^2$ function around its minimum (${\chi }_{\mathrm{red},\min }^2$ ≃ 60.8) on a given free parameter P . P_min is the value of the parameter P derived from the best fit. The parameter x(R_⋆ ≤ r ≤ R_in) is plotted in solid black (●), x(r = R_out) in dashed black (○), T_rot(R_in) in solid cyan (*), T_rot(R_out) in dashed cyan (*), T_{vib,v = 1 – 0}(R_⋆) in solid red (■), T_{vib,v = 1 – 0}(R_in) in dashed red (□), T_{vib,v = 1 – 0}(R_out) in dotted red (⋄), T_{vib,v = 2 – 1}(R_⋆) in solid green (▲), T_{vib,v = 2 – 1}(R_in) in dashed green (△), T_{vib,v = 2 – 1}(R_out) in dotted green (▽), T_{vib,v = 3 – 2}(R_⋆) in solid blue (×), T_{vib,v = 3 – 2}(R_in) in dashed blue (×), and T_{vib,v = 4 – 3}(R_⋆) in dotted blue (+). See the caption of Tables 1 and 2 for the definitions of these parameters.

4 RESULTS AND ANALYSIS

4.1 ²⁸Si³²S

Most of the observed lines in bands v = 1–0 and 2–1 show shapes compatible with P-Cygni profiles (Fig. 1). The emission component cannot be clearly recognised in the profiles of the lines of band v = 3–2, although this fact can be consequence of strong overlaps with close lines. This component is insignificant in the profiles of the lines of bands v = 4 – 3 and 5–4. The lines of band v = 1–0 display typical absorption depths of 10 – 20 per cent of the continuum emission while the lines of bands v = 2 – 1, 3 – 2, 4 – 3, and 5 – 4 are weaker with absorption depths smaller than 5, 2.5, 1.3, and 0.7 per cent of the continuum, respectively. The maximum absorption for all the lines occurs at velocities between −14.3 and −4.5 km s⁻¹. The absorption component of the lines of band v = 1 – 0 with J_low ≲ 12 and ≳ 23 show main contributions peaking at ≃ −13.5 and −9 km s⁻¹ in average, respectively. The absorption component of these lines have widths of ≃ 7 km s⁻¹, even for the lines involving ro-vibrational levels with the highest energies. The absorption of the lines with 12 ≲ J_low ≲ 23 show both absorption contributions (at −13.5 and −9 km s⁻¹) and, consequently, the largest absorption widths (≃ 9 – 10 km s⁻¹). A width of 7 km s⁻¹ is also found in the absorption components of the lines of band v = 2 – 1, which display their maximum between −10 and −5 km s⁻¹. The absorption of the lines of bands v = 3 – 2, 4 – 3, and 5 – 4 show smaller widths of ≃ 2.5 – 6.5 km s⁻¹, peaking between −6 and −4 km s⁻¹.

The velocity of the maximum absorption and the shape of the absorption component of the lines are consequences of the expansion velocity of the emitting gas. The width of the absorption components can be produced by expansion velocity gradients, line broadening due to turbulence, the varying thermal line width due to the large temperature gradient, and the different directions along what the absorbing gas expands (more important for the gas close to the star). Thus, the absorption of the low excitation lines is mostly formed far from the star where the gas is colder and it expands at large velocities. The high excitation lines require warm gas and/or an efficient radiative pumping mechanism, conditions that are fulfilled close to the star. Hence, the absorption of the observed high excitation lines indicate that the gas in the innermost envelope expands at low velocities. The observed medium excitation lines, mostly produced between the regions where the low and high excitation lines are formed, display large absorption widths which suggest the existence of an expansion velocity gradient due to the absorption of gas at different velocities. The detailed analysis of the absorption components of the observed lines performed in the current work suggests that the actual expansion velocity profile and our choice (Section 3.1) are essentially compatible but it can be improved close to the star.

4.1.1 Improving the gas expansion velocity field

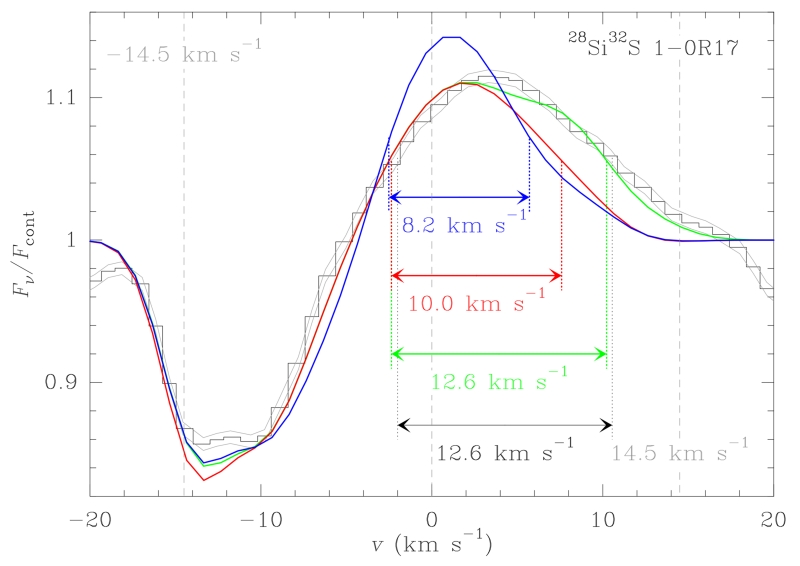
The part of the synthetic SiS line profiles arising from the gas in Regions II and III is in a reasonably good agreement with the observations. These calculations assumed the expansion velocity field initially considered in our model (Section 3.1). Although a constant gas expansion velocity of 5 km s⁻¹ can be adopted as the average velocity in Region I (1R_⋆ ≤ r < 5R_⋆), a linear dependence between the stellar atmosphere and 5R_⋆ ranging from 1 to 11 km s⁻¹, i.e., v_exp(1R_⋆ ≤ r < 5R_⋆) = 1 + 2.5(r/R_⋆ − 1) km s⁻¹, describes better the emission component of the ²⁸Si³²S lines of bands v = 1–0 and 2–1 (Fig. 3). This velocity gradient gives rise to a wider emission component of the low excitation lines, although it is worth noting that the observed lines of band v = 1 – 0 with J ≲ 40 show a red-shifted emission excess with respect to the synthetic lines that is not accounted by the improved expansion velocity field (see Figs. 1 and 3, and Section 4.1.4 for a discussion about this topic). Lines of bands v = 3 – 2, 4 – 3, and 5 – 4 are reasonably well reproduced with both expansion velocity fields since these lines are formed close to the photosphere (Agúndez et al. 2012; Velilla Prieto et al. 2015), where the expansion velocity is expected to be low.

Figure 3.

Comparison between the observed ²⁸Si³²S line 1 – 0R(17) (black histogram) and the synthetic line calculated with three different models depending on the expansion velocity field in Region I (blue and red), and on the symmetry of the envelope (green). All these lines have been taken from the best global fit to the observations. The line in blue has been calculated with a constant expansion velocity of 5 km s⁻¹ in Region I. The line in red is produced by a spherical symmetric envelope with a gas expansion velocity of 1+2.5(r/R_⋆ −1) between 1R_⋆ and 5R_⋆ (Region I). The line in green is the synthetic line calculated assuming the envelope model of the red line but with an asymmetric vibrational temperature distribution (see Section 4.1.4). The curves in grey depart 3σ from the observations, where σ is the rms of the noise of the spectrum (≃ 0.15 per cent of the continuum). The widths included in the Figure stand for the FWHM of the emission component of the profiles.

Hence, we used the improved expansion velocity field with the gradient in Region I in our fits.

4.1.2 ²⁸Si³²S abundance with respect to H₂

The best fit to the whole set of lines derived assuming the envelope model presented above was achieved with a constant ²⁸Si³²S abundance with respect to H₂ by number of 4.9 × 10⁻⁶ in Region I followed by a linear decrease in Region II down to 1.6 × 10⁻⁶ at the outer acceleration shell, and a further decrease outwards down to 1.3 × 10⁻⁶ at 50R_⋆. The ²⁸Si³²S abundance beyond the outer acceleration shell is compatible with the results by Boyle et al. (1994), Schöier et al. (2007), and Agúndez et al. (2012) within a factor of 2 and with the results by Decin et al. (2010) within up to a factor of 3, a disagreement smaller than the uncertainty they estimated for their own results (Table 3). However, our ²⁸Si³²S abundance is about 10 and 4 times smaller in Region I than the results by Boyle et al. (1994) and Schöier et al. (2007), respectively. The large discrepancy of one order of magnitude found between our derived abundance in Region I and that proposed by Boyle et al. (1994) is due to significant differences in the spectra. In the spectrum presented by Boyle et al. (1994) only the blue-shifted part of the lines, corresponding to the absorption depths, were totally covered during the observations while the emission components were largely (but not completely) missed. The emission component of most of the lines they observed was probably blended with telluric lines or features of other molecules existing in the envelope of IRC+10216. In addition, it is usually difficult to determine the baseline in spectral regions with many molecular lines, such as the region containing SiS (see figs. 1-6 in Fonfría et al. 2008). Thus, the line profiles were assumed to display no emission resulting in lines with absorption components deeper than they actually were due to the remnants of the emission components. The modelling of these lines required an exceedingly low vibrational temperature and a significant increase of the estimated ²⁸Si³²S abundance in Region I and part of Region II compared to the actual profile. Schöier et al. (2007) derived the abundance by fitting previous observations acquired with BIMA by Bieging & Tafalla (1993). These observations seem not to be affected by any instrumental effect suggesting that the disagreement between our results and those by Schöier et al. (2007) may be produced by an actual variation in the ²⁸Si³²S emission. Such variation would not be related to the stellar pulsation phase, known to influence the emission of several molecules (Carlström et al. 1990; Cernicharo et al. 2014), since both observations were carried out close to maximum light (see Table 3; Monnier et al. 1998). The abundances proposed by Bieging & Nguyen-Quang-Rieu (1989) and Decin et al. (2010), although based on observations acquired near maximum light, are affected by large errors that prevent us from deriving reliable conclusions about the time evolution. Therefore, the observed variation in the ²⁸Si³²S abundance could be the consequence of a larger time-scale change in the mass-loss rate (Cernicharo et al. 2015a,c) or the gas phase chemistry close to the star, considering that our observations were acquired about 14 yr after the observations taken by Bieging & Tafalla (1993), and the ejected gas is expected to spend about 10 – 15 yr travelling across Region I.

Table 3.

Abundance of ²⁸Si³²S relative to H₂

R ⋆	R in	R out	≥ 50R⋆	Error	IR Phase	Ref.
4.9	4.9	1.6	1.3	*	0.08	1
3.0	3.0	2.4	1.3	1.5 – 2.0	Multiepoch	2
4.0	4.0	4.0	4.0	4	0.04	3
19	17	1.7	1.7	2–3	0.05 – 0.24	4
51	33	2.5	≤ 0.9	2	0.5	5
7.5	7.5	7.5	7.5	2 – 3	0.09 – 0.29	6

The abundances are multiplied by 10⁻⁶. Their errors are provided as multiplicative/dividing factors. The pulsation phase was calculated following the analysis of the infrared light curves performed by Monnier et al. (1998). *See Table 2. (1) This work (2) Agúndez et al. (2012) (3) Decin et al. (2010) (4) Schöier et al. (2007) (5) Boyle et al. (1994) (6) Bieging & Nguyen-Quang-Rieu (1989)

The 28Si³²S abundance with respect to H₂ calculated with chemical models under thermodynamical equilibrium (TE) is larger than ≃ 10⁻⁵ in Region I (Willacy & Cherchneff 1998; Agúndez & Cernicharo 2006), i.e., a factor of 2 larger than our results. The TE and chemical kinetic models give constant abundances in most of Region I and beyond, meaning that gas-phase chemical reactions involving SiS are only expected to play an important role in the vicinity of the star (e.g., Agúndez & Cernicharo 2006). Hence, the large decrease in the SiS abundance outwards from the inner acceleration zone is probably due to depletion on to dust grains, as was suggested previously (Turner 1987; Bieging & Nguyen-Quang-Rieu 1989; Bieging & Tafalla 1993; Boyle et al. 1994; Schöier et al. 2007; Agúndez et al. 2012).

4.1.3 Rotational and vibrational temperatures

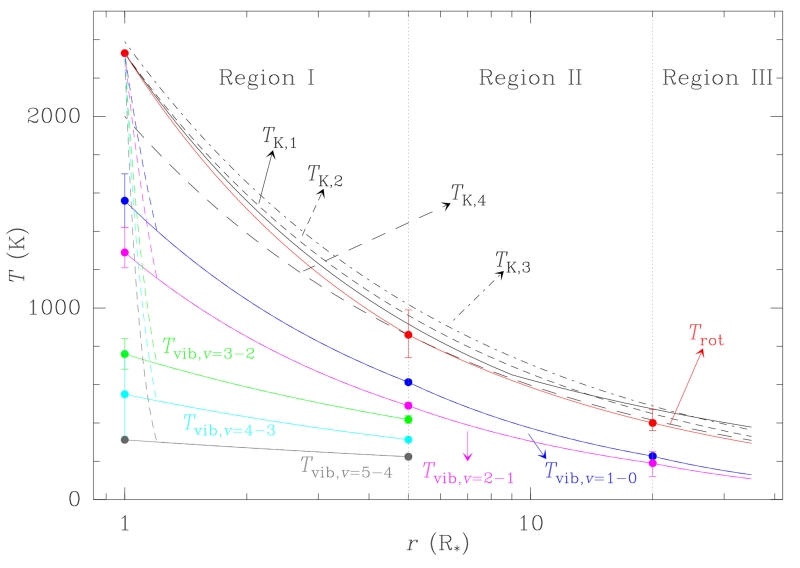
The rotational temperature profile in the ground vibrational state derived from our fits throughout the dust formation zone (1R_⋆ ≤ r ≲ 30R_⋆; e.g., Fonfría et al. 2008; Decin et al. 2010) are similar to the kinetic temperature proposed in previous works within the estimated uncertainties (Fig. 4), demonstrating that the ²⁸Si³²S molecules in the vibrational ground state is under rotational LTE throughout the first ≃ 35R_⋆ of the envelope. Moreover, our results suggest that the rotational temperature for the vibrational states v = 1 to 5 can be assumed to be the same for the vibrational ground state in the region of the envelope where these vibrational states are significantly populated, i.e., at distances to the star ≲ 10R_⋆.

Figure 4.

Kinetic, rotational, and vibrational temperatures of ²⁸Si³²S from the stellar photosphere up to 35R_⋆. The kinetic temperatures, T_k, derived in previous works (references 1, 2, 3, and 4) are plotted in solid, short dashed, dashed-dot, and long dashed, black lines. The rotational temperature, T_rot, derived in the frame of the current work is plotted in solid red. The vibrational temperatures, T_vib, derived from ro-vibrational bands v = 1 – 0, 2 – 1, 3 – 2, 4 – 3, and 5 – 4 are plotted in blue, magenta, green, cyan, and grey solid lines, respectively. The dashed lines in these colours represent possible dependences of the vibrational temperatures on the distance to the star between the stellar photosphere and ≃ 1.2R_⋆, where Cernicharo et al. (2013) propose a larger gas density than we assume in the current work. T_vib,v = 3 – 2, T_vib,v = 4 – 3, and T_vib,v = 5 – 4 are only plotted up to 5R_⋆ because the lines of these bands are mostly formed in Region I and no information on larger distances to the star can be retrieved from them. References: (1) De Beck et al. (2012) (2) Agúndez et al. (2012) (3) Schöier et al. (2007) (4) Boyle et al. (1994)

The vibrational temperatures derived from bands v = 1 – 0, 2 – 1, 3 – 2, 4 – 3, and 5 – 4 are significantly smaller than the kinetic temperature (Fig. 4), which indicates that ²⁸Si³²S is vibrationally out of LTE and its vibrational states are, mainly, radiatively populated. Using the gas density profile presented in Section 3.1, we estimate the gas density at the stellar photosphere, n_gas(R_⋆), to be ≃ 4.2×10¹⁰ cm⁻³. The critical density, n_crit, at this position can be estimated with the A-Einstein coefficients of the observed ²⁸Si³²S ro-vibrational transitions, which range from 0.8 to 6.2 s⁻¹ (the MADEX code; Cernicharo et al. 2012; Velilla Prieto et al. 2015), and the de-excitation ro-vibrational state-to-state collisional rates discussed in Velilla Prieto et al. (2015), where the calculations performed by Toboła et al. (2008) for the colliding pair ²⁸Si³²S:He were improved and extrapolated to high ro-vibrational levels. As far as we know, there is no data in the literature about ro-vibrational transitions due to collisional processes between ²⁸Si³²S and H₂. Thus, we assume that the collisional rates are the same for H₂ and for He, and that these rates, calculated for a kinetic temperature ranging between 300 and 1500 K, can be extrapolated up to ≃ 2300 K following the power-law $T_{\mathrm{k}}^{1∕2}$. We estimate that the maximum ²⁸Si³²S ro-vibrational collisional rates ranged from 1.8 × 10⁻¹³ to 1.5 × 10⁻¹² cm³ s⁻¹ for the transitions of bands v = 1 – 0 to 5 – 4. Hence, n_crit ≳ 4 × 10¹² cm⁻³ at the stellar photosphere, two orders of magnitude larger than the estimated gas density. However, the analysis of the HNC emission performed by Cernicharo et al. (2013) is compatible with an H₂ density very close to the star larger than 10¹² – 10¹³ cm⁻³ as a consequence of the matter levitation due to the stellar pulsation (Bowen 1988; Willacy & Cherchneff 1998; Agúndez & Cernicharo 2006; Agúndez et al. 2012; Cherchneff 2006), being similar or exceeding the estimated critical density (n_gas(R_⋆) ≳ n_crit). Thus, the vibrational excitation would be dominated by collisions and ²⁸Si³²S might be vibrationally under or close to LTE in the vicinity of the stellar photosphere, meaning that the vibrational temperatures at this position we derive in the current work are significantly constrained by the power law consider to prevail throughout Region I and should be assumed as lower limits. In this case, a more realistic approach would include a new Region adjoining the photosphere of less than 1R_⋆ thick (e.g., an extension of the photosphere), where the dependence of the vibrational temperature with the distance to the star would be much steeper than in the rest of Region I (Fig. 4). The larger flatness in Region I showed by T_{vib,v = 3 – 2}, T_{vib,v = 4 – 3}, and T_{vib,v = 5 – 4} in comparison to the vibrational temperature derived from bands v = 1 – 0 and 2 – 1 are probably related to the lack of reliable information about the emission component of the lines of bands v = 3 – 2, 4 – 3, and 5 – 4. Thus, the vibrational temperature for these bands could be steeper than our best fit suggests throughout Region I, as the results by Velilla Prieto et al. (2015) indicate. On the other hand, the decrease experienced by the vibrational temperature in Region I when the vibrational quantum number v increases (T_{vib,v = 1 – 0}(R_⋆) compared to T_{vib,v = 2 – 1}(R_⋆), T_{vib,v = 3 – 2}(R_⋆), and so on) derived from our fits seems to be significant, as the uncertainties suggest (Table 2). This variation is probably caused by the different A-Einstein coefficients of the ro-vibrational transitions of bands v = 1 – 0 to 5–4, that are about v_up times larger than for band 1–0.

4.1.4 The red-shifted emission excess

The observed lines of the v = 1 – 0 band with J_low ≲ 40 show a red-shifted emission excess at Doppler velocities of ≳ 6 – 10 km s⁻¹ with respect to the lines derived from the best fit. The affected lines involve ro-vibrational levels with energies below 700 K, suggesting that the emitting gas is located further than ≃ 15R_⋆ from the star. This scenario is compatible with the lack of an emission excess in higher excitation lines, which are mostly produced closer to the star than ≃ 10R_⋆. A similar red-shifted emission excess was already reported by Fonfría et al. (2008) in the ro-vibrational lines of C₂H₂ and HCN. Interferometer observations carried out with HPBW ≃ 0.25 – 0.35 arcsec of the lines Si³⁴S(v = 0, J = 15–14), H¹³CN(v = 0, J = 3–2), and SiO(v = 0, J = 6 – 5) (Shinnaga et al. 2009; Fonfría et al. 2014) also showed red-shifted emission excesses probably produced in the dust formation zone (1R_⋆ ≤ r ≲ 30R_⋆; e.g., Fonfría et al. 2008; Decin et al. 2010), the same region where the ro-vibrational lines presented and analysed in the current work and by Fonfría et al. (2008) are formed.

A spherically symmetric envelope model cannot reproduce the red-shifted emission excess and the absorption component of many lines at the same time. Since these absorption components highly constrain the possible structure, the expansion velocity field, and the physical and chemical conditions prevailing throughout the envelope, other models should be invoked to explain the observations. As most of the emission component of the SiS lines of the v = 1 – 0 band comes from the rear part of the envelope close to the star while the absorption component is formed in front of the star, the red-shifted emission excess could be modelled assuming an asymmetric SiS abundance and/or vibrational temperature distributions. This asymmetry could be a consequence of (1) gas expanding at velocities higher than expected in the surroundings of the stellar photosphere through, e.g., the existence of an outflow behind the star (Fonfría et al. 2014), (2) the influence of the companion on the ejected matter by the AGB star by its orbital movement (Cernicharo et al. 2015a,c), or (3) an anisotropic mass loss from the AGB star.

A simple 2D envelope model can be proposed and its molecular emission calculated with our code (Fonfría et al. 2014) in order to show the feasibility of an asymmetric emission. In this model, we defined a conical region behind the star with its axis parallel to the line-of-sight, its vertex matching up with the centre of the star, and an aperture of 120°, where the SiS abundance and the vibrational temperature for band v = 1 – 0 could be different than in the rest of the envelope. These magnitudes could only depend on the distance to the star in both regions. The aperture was chosen to modify the part of the emission component of the lines of the v = 1 – 0 band where the excess was found. The initial physical and chemical conditions were those derived from the best fit assuming the spherically symmetric envelope (Tables 1 and 2). In the best fit adopting the asymmetric model (see Fig. 3), the vibrational temperature of the v = 1 – 0 band in the conical region behind the star was incremented from ≃ 230 up to ≃ 300 K at the outer acceleration shell (located at 20R_⋆), following the law ∝ r^−0.45 outwards. The variation of the SiS abundance in the conical region derived from the fitting process was negligible. This 2D envelope model did not introduce any significant modification in the synthetic lines of bands v = 2 – 1, 3 – 2, 4 – 3, and 5 – 4 compared to the results of the spherically symmetric envelope model.

4.2 Isotopic ratios

The observed lines of ²⁹Si³²S, ²⁸Si³⁴S, and ³⁰Si³²S belong to band v = 1 – 0 and show shapes compatible with P-Cygni profiles (Fig. 1). These lines are weak, with differences between the maximum emission and absorption of about three to four times σ for lines with J_low ≲ 50. Most of the lines in the observed frequency range are blended with C₂H₂, HCN, and ²⁸Si³²S lines. Only a handful of lines over the detection limit are sufficiently isolated and can be conveniently fitted (Fig. 1). The lines of ²⁹Si³²S and ²⁸Si³⁴S were strong enough to derive the isotopic ratios ²⁸Si/²⁹Si and ³²S/³⁴S with a relatively good accuracy of ≃ 30 and 40 per cent, respectively (Table 4). The fit to the only ³⁰Si³²S line suitable to be analysed gave an isotopic ratio ²⁸Si/³⁰Si of 39 with an error of 60 per cent. The lack of available lines and the large uncertainty prevent us to derive reliable conclusions about this isotopic ratio.

Table 4.

Isotopic ratios in the innermost envelope

Ratio	Value	Error	Reference
28Si/29Si	17	+5/ − 4	1
	18	+2/ − 2	2
	8.2	+1.7/ − 1.7	3
	15.1	+0.7/ − 0.7	4
	17.2	+1.1/ − 1.1	5
	> 15.4	−	6
32S/34S	14	+6/ − 4	1
	22.0	+2.5/ − 2.5	2
	30	+8/ − 8	3
	19.6	+1.3/ − 1.3	4
	18.9	+1.3/ − 1.3	5
	21.8	+2.6/ − 2.6	6

(1) This work (2) Agúndez et al. (2012) (3) Patel et al. (2011) (4) Patel et al. (2009) (5) He et al. (2008) (6) Kahane et al. (2000) and Cernicharo et al. (2000). The isotopic ratios by Patel et al. (2011) presented here were calculated by assuming as reliable the isotopic ratios derived from optically thin lines that do not show extended emission when possible (see table 6 of this reference).

The ratios ²⁸Si/²⁹Si and ³²S/³⁴S are compatible with previous estimates derived from observations carried out in the mm wavelength range (Table 4). These observations mostly recovered the long scale emission of the envelope that comes from layers composed of matter expelled more than ≃ 800 yr ago (Cernicharo et al. 2015c), while our observations traced gas recently ejected. Hence, no significant changes in the nucleosynthesis of the most abundant Si and S isotopes are expected to have happened during the last 1000 yr.

5 CONCLUSIONS

In this paper, we have presented high spectral resolution observations in the mid-IR range (≃ 12.5 – 14.0 μm) towards the AGB star IRC+10216. Two hundred and four lines coming from band v = 1 – 0, 2 – 1, 3 – 2, 4 – 3, and 5 – 4 of ²⁸Si³²S, 26 from v = 1 – 0 of ²⁹Si³²S, 20 from v = 1 – 0 of ²⁸Si³⁴S, and 15 from v = 1 – 0 of ³⁰Si³²S have been identified in the observed spectrum. About 30 per cent of the total set of detected lines are unblended or partially blended and could be fitted and analysed. We have found that:

• the quality of the fits is higher by assuming that the gas expansion velocity profile grows linearly from the photosphere up to 5R_⋆ following the dependence v_exp(1R_⋆ ≤ r < 5R_⋆) = 1 + 2.5(r/R_⋆ − 1) km s⁻¹ compared to the fits based on a constant velocity of 5 km s⁻¹. Our fits support the expansion velocity profile proposed by Fonfría et al. (2008) outwards from 5R_⋆, i.e., v_exp(5R_⋆ ≤ r < 20R_⋆) = 11 km s⁻¹ and v_exp(r ≥ 20R_⋆) = 14.5 km s⁻¹.

• The abundance of ²⁸Si³²S is 4.9×10⁻⁶ between the stellar photosphere and the inner acceleration shell (located at 5R_⋆) and decreases linearly down to 1.6 × 10⁻⁶ at the outer acceleration shell (at 20R_⋆). The observed lines are compatible with an abundance of 1.3 × 10⁻⁶ at 50R_⋆. The decrease in the abundance beyond the inner acceleration shell is probably explained by the depletion of SiS on to the dust grains due to its refractory nature and the lack of gas-phase chemical reactions expected to be enabled in this region of the CSE.

• ²⁸Si³²S is vibrationally out of LTE in most of the envelope. The vibrational temperature for the vibrational ground state is 1560(R_⋆/r)^0.58 K between the stellar surface and the inner acceleration shell (Region I) and 613(R_⋆/r)^0.72 K up to the outer acceleration shell (Region II). For the v = 1 vibrational state, the relation is 1290(R_⋆/r)^0.60 K in Region I and 490(R_⋆/r)^0.68 K in Region II. Beyond the outer acceleration shell, the vibrational temperature for these states is compatible with an exponent of −1. For v = 2, 3, and 4, the vibrational temperature is compatible with 760(R_⋆/r)^0.37, 550(R_⋆/r)^0.35, and 312(R_⋆/r)^0.20 K in Region I, respectively.

• ²⁸Si³²S can be assumed to be rotationally under LTE with a rotational temperature of 2330(R_⋆/r)^0.62 K between the stellar photosphere and the inner acceleration shell and 860(R_⋆/r)^0.55 K outwards.

• There is a red-shifted emission excess at large velocities in the ²⁸Si³²S lines of bands v = 1 – 0 and 2 – 1 not noticed in the lines of bands v = 3 – 2, 4 – 3, and 5 – 4. This excess can be explained by an asymmetry of the vibrational temperature distribution for what the gas behind the star shows a higher excitation around ≃ 20R_⋆ that mostly affects the lines of band v = 1 – 0.

• The isotopic ratios ²⁸Si/²⁹Si and ³²S/³⁴S derived from our observations are 17 and 14, respectively. These ratios, referred to matter in the vicinity of the star, are compatible with the previously proposed values for outer shells of the envelope.

APPENDIX A: GAS EXPANSION VELOCITY FIELD

In order to fit the observed lines, we initially chose the expansion velocity profile derived by Fonfría et al. (2008) from the analysis of several hundreds of C₂H₂ and HCN lines in the mid-IR. During the current work we slightly modified this velocity profile to improve the quality of the fits to the SiS lines proving that the velocity profile derived by Fonfría et al. (2008) is essentially compatible with the actual profile. However, Decin et al. (2014) has recently published a new profile based on the analysis of high angular resolution observations (HPBW ≃ 0.33 arcsec) carried out with ALMA in the submillimetre wavelength range. In this new profile, the gas expands at 2 – 3 km s⁻¹ between the stellar surface and 5.6R_⋆ and grows linearly up to 11R_⋆, where it reaches the terminal expansion velocity (profile 1; not shown). These authors also proposed a more complex profile compatible with their observations where the expansion velocity is 8 km s⁻¹ between 8 and 10R_⋆ (profile 2; not shown).

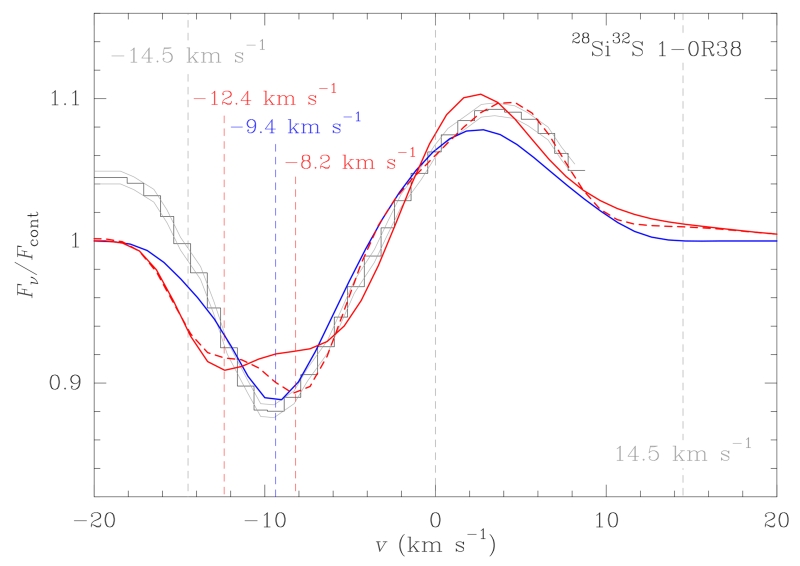
We tried to fit our observations with these new velocity profiles finding that it is not possible to get better fits than that the obtained with the profile derived in the current work (Section 4.1.1). The largest deviations of the synthetic from the observed lines appear in the lines of the ro-vibrational band v = 1 – 0 with J_low ranging from 30 to 50 (Fig. A1). The maximum absorption of these lines occurs between −10 and −9 km s⁻¹. Assuming a spherically symmetric expanding envelope, the maximum absorption is produced in front of the star by the shells of the envelope located at distances to it smaller than ≃ 15 – 20R_⋆ and where the overlapping fraction between the molecular absorption of contiguous shells is maximum. A gradient in the expansion velocity field would diminish this fraction and, consequently, the optical depth, making the absorption less prominent. This diminishing could be balanced with a larger molecular abundance but it would also affect the shape of the whole absorption component. Adopting a continuous abundance profile described by its linearly connected values at 1, 5.6, and 11R_⋆ for the profile 1 and at 1, 5.6, 8, 10, and 11R_⋆ for the profile 2, the best fits cannot properly reproduce the absorption component of the observed lines (Fig. A1). Both profiles produce absorptions for the lines of band v = 1 – 0 with J_low = 30 – 50 comprising two velocity contributions approximately at −13 and between −9 and −7 km s⁻¹, which are produced by the gas expanding at the terminal velocity and at 7–9 km s⁻¹, respectively. However, the minima of the absorption components of the observed lines are between both contributions. The main characteristics of the absorption component of the observed lines are better explained with the expansion velocity field derived in the current work.

Figure A1.

Comparison between the observed ²⁸Si³²S line 1 – 0R(38) (black histogram) and the synthetic lines calculated with the expansion velocity profiles of Decin et al. (2014) (profile 1 and profile 2 in the text in solid and dashed red lines, respectively) and the current work (blue solid line). The synthetic lines are derived from the best fits to the observed lines of band v = 1 – 0. The curves in grey depart 3σ from the observations, where σ is the rms of the noise of the spectrum (≃ 0.15 per cent of the continuum).