BCL::SAXS: GPU Accelerated Debye Method for computation of Small Angle X Ray Scattering Profiles

Abstract

Small angle X-ray scattering (SAXS) is an experimental technique used for structural characterization of macromolecules in solution. Here, we introduce BCL::SAXS – an algorithm designed to replicate SAXS profiles from rigid protein models at different levels of detail. We first show our derivation of BCL::SAXS and compare our results with the experimental scattering profile of Hen Egg White Lysozyme. Using this protein we show how to generate SAXS profiles representing: 1) complete models, 2) models with approximated side chain coordinates, and 3) models with approximated side chain and loop region coordinates. We evaluated the ability of SAXS profiles to identify a correct protein topology from a non-redundant benchmark set of proteins. We find that complete SAXS profiles can be used to identify the correct protein by receiver operating characteristic (ROC) analysis with an area under the curve (AUC) > 99%. We show how our approximation of loop coordinates between secondary structure elements improves protein recognition by SAXS for protein models without loop regions and side chains. Agreement with SAXS data is a necessary but not sufficient condition for structure determination. We conclude that experimental SAXS data can be used as a filter to exclude protein models with large structural differences from the native.

Introduction

Protein structure determination remains a major challenge in the field of structural biology¹. While X-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy can provide high resolution structures, these techniques can be limited by size², high flexibility³, and membrane environment³. Computational de novo protein structure prediction methods have been developed, but are limited by the vast conformational search space that needs to be searched when no template structure is available⁴. To overcome these experimental and computational limitations, hybrid methods – i.e. the combination of multiple techniques – can be utilized to gain structural insights of proteins^5-7.

SAXS offers an alternative to traditional structure determination techniques

Small angle X-ray scattering (SAXS) is an experimental structural characterization method for rapid analysis of biological macromolecules in solution^8-12. During data acquisition in SAXS, macromolecules move freely in solution while a beam of X-Rays with constant wavelength λ irradiate the sample. At the point of interaction between X-Rays and electrons in the sample, both elastic and inelastic scattering occur. This work considers the case of elastic scattering by electrons. The intensity of the scattered X-Rays captured on the detector is proportional to the Fourier Transform of a pairwise distance function ρ(r) that gives the probability of finding two atoms a certain distance apart. This distance function is weighted by the excess scattering density of the respective scattering volume compared to the solvent. For a more comprehensive review of SAXS theory we recommend several reviews^8,9,13-16. SAXS profiles are reported by intensity (I) as a function of momentum transfer vector (q). Large interatomic distances contribute to the intensity profile at small q, while short interatomic distances contribute to the intensity at large q. Several parameters can be extracted directly from the scattering profile including: the molecular mass (MM), radius of gyration (R_g), hydrated particle volume (V_p) and maximum particle diameter (D_max). The state of the protein (folded vs. unfolded) can be observed from the Kratky representation of the scattering data plotting q vs. q²I(q). The scattering profile can be transformed into the pairwise distance density function which is a histogram of distances between pairs of points in a particle. This shape information has been used for the validation of structural models^17,18.

Use of SAXS experimental data in computation

The experimental SAXS profile has been used to filter a set of proposed models by comparing the computed SAXS profile of each model with the experimental data^5,19. Furthermore, the experimental profile has been incorporated into an energy function for protein folding to obtain a model consistent with experimental data²⁰. More recently SAXS has been used to identify and model protein flexibility from an ensemble set of conformers²¹. In this approach a large library of initial conformers are given as input. After a sufficient library of conformers has been found, the experimental SAXS data are used to ascertain which combination of conformers optimally fit the data. In this case, the scattering intensity (I) is represented by a linear combination of the selected conformers. The crucial step in this analysis is computation of a SAXS profile from a proposed protein model.

Protein Structure Prediction

De novo protein structure prediction methods have two major components – a sampling algorithm and a scoring function. During the sampling phase, the protein model is perturbed. The protein is then scored, using a scoring function designed to identify native-like topologies. This process is iterated in order to minimize the scoring function. The challenge in this process is sampling the large conformational space of a protein densely enough so that one model approaches the native conformation. To be time-efficient, the protein model is often simplified to remove conformational degrees of freedom (coarse grained sampling) and the scoring function is therefore rapid but inaccurate. Sampling for larger proteins is further complicated by non-local contacts, amino acids in contact in Euclidean space (< 8Å), that are far apart in sequence (> 12 residues). As the number of non-local contacts increase, the accuracy of de novo protein structure prediction methods drastically decreases.²² Atomic detail is added in a later stage of the protocol and the model is rescored / optimized with a higher accuracy scoring function. The accuracy necessary to identify the correct topology by its superior energy at this stage is a RMSD value of approximately 2Å when compared with the native structure.

BCL::Fold is designed to address the sampling bottleneck

BCL::Fold is a protein structure prediction method that rapidly assembles secondary structure elements (SSEs) into topologies.^23,24 This approach provides a means to focus sampling on long range contacts between amino acid pairs. To begin, a pool of predicted SSEs is generated from an input FASTA sequence of amino acids. SSEs are randomly selected from the pool and assembled using a Monte Carlo Metropolis (MCM) assembly protocol to produce a coarse grained representation of the protein without side chain atoms and loop region residues. During assembly the model is evaluated using a consensus knowledge-based scoring function. This process is repeated 10,000 to 100,000 times. The underlying hypothesis of BCL::Fold is that the interactions between SSEs determine the majority of the protein core and give rise to its thermodynamic stability. Once the models have been generated, they are clustered by RMSD100 into N cluster centers. The medoid from each cluster center is selected for loop construction and side chain addition using Rosetta²⁵ to produce a set of proposed conformations for a given protein sequence in the absence of experimental data.

BCL::SAXS is a GPU accelerated Debye implementation for profile reconstruction

The use of experimental SAXS profiles during the construction of protein models with BCL::Fold would provide additional constraints on the sampling space of a given protein sequence. To incorporate experimental SAXS restraints into BCL::Fold, we must first develop a method to compare experimental SAXS profiles with profiles generated from protein models produced by BCL::Fold, i.e. missing loop region and side chain residues.

Here we describe our newly developed algorithm BCL::SAXS. It computes complete SAXS scattering profiles for complete protein models and an approximate scattering profile for protein models that consist of secondary structure elements only as used in BCL::Fold^23,24,26,27. The main methods to calculate a SAXS scattering profile from atomic coordinates are spherical harmonics with multipole expansion, Monte Carlo methods, and the Debye formula^28-31. Multipole expansion methods have been shown to be highly accurate, but difficult to modify for incomplete protein models. The Debye formula is easy to modify, but comes with a high computational cost. Ultimately we want to compare SAXS Profiles generated from BCL::Fold models^23,24 – i.e. protein structure that lack loops and side chains – with experimental SAXS profiles. To facilitate this, we chose to use the Debye formula, implement approximations for missing loops and side chain atoms, and address the computational cost with graphical processing unit (GPU) acceleration.

Overall approach

In BCL::SAXS inter-atomic pairwise distances are computed explicitly for each heavy atom using the Debye formula for atomic scatterers³². It models the hydration layer based on the solvent accessible surface area of each atom. To maximize the fit to experimental data BCL::SAXS optimizes the hydration layer density and the excluded volume of the protein. We accelerated the algorithm performance by using graphical processing unit (GPU) parallel threads. We demonstrate the discriminatory power of SAXS at three different abstraction levels consistent with the BCL::Fold folding protocol²³: 1) complete protein models, 2) protein models with approximated side chain coordinates, 3) protein models with approximated side chain coordinates and approximated loop regions. We quantify the performance of the protocol from a set of 455 proteins with SAXS profiles computed in silico and experimental data from Hen Egg White Lysozyme. Furthermore, our work introduces a new approximation of the coordinates of residues in loop regions for crude protein models missing these residues. BCL::SAXS is available to the scientific community via the BCL::Commons user interface (www.meilerb.org). It is free for academic use.

Materials and Methods

To accurately determine the SAXS profile from the atomic coordinates of full atom protein models we utilized several key equations – the Debye formula for atomic scatterers and three equations to calculate the form factors^28,29,32-35. The form factors are continuous functions of the magnitude of the momentum transfer vector $\overrightarrow{q}$. Using the Euclidean atomic coordinates from structures stored in the protein data bank (PDB)³⁶, scattering profiles are reconstructed. The following equations, starting with the Debye formula, depict the method:

$$\mathrm{I}\left(\mathrm{q}\right)=\sum _{\mathrm{i}=1}^{\mathrm{M}}\sum _{\mathrm{j}=1}^{\mathrm{M}}{\mathrm{F}}_{\mathrm{i}}\left(\mathrm{q}\right){\mathrm{F}}_{\mathrm{j}}\left(\mathrm{q}\right)\frac{\sin \left({\mathrm{qr}}_{\mathrm{ij}}\right)}{{\mathrm{qr}}_{\mathrm{ij}}}$$ (1)

where the intensity, I(q) is a function of the magnitude of the momentum transfer vector $\overrightarrow{q}$. It is given by $\mid \overrightarrow{q}\mid =\left(4\pi \sin \theta \right)∕\lambda$, where θ is given by a scattering angle of 2θ, and λ is the wavelength of the incident beam. F_i(q) and F_j(q) are the atomic form factors and r_ij is the pairwise Euclidean distance between atom i and atom j. M is the number of atoms in the protein and the summations run over all atoms. To calculate the form factors, we subtracted the displaced solvent contribution from the form factor in vacuo and added the contribution of the hydration layer:

$${\mathrm{F}}_{\mathrm{i}}\left(\mathrm{q}\right)={\mathrm{f}}_{\mathrm{v},\mathrm{i}}\left(\mathrm{q}\right)-{\mathrm{c}}_1{\mathrm{f}}_{\mathrm{s},\mathrm{i}}\left(\mathrm{q}\right)+{\mathrm{c}}_2{\mathrm{S}}_{\mathrm{i}}{\mathrm{f}}_{\mathrm{w},\mathrm{i}}\left(\mathrm{q}\right)$$ (2)

where f_v,i(q) is the atomic form factor in vacuo, f_s,i(q) is the form factor of the hypothetical atom that represents the displaced solvent³⁰, and f_w,i(q) is the contribution from the hydration layer. S_i is the solvent accessible surface area of the given atom. C₁ is used to modify the total excluded volume of the atoms and C₂ is used to modify the water density in the hydration shell. The atomic form factor in vacuo approximation is based on the combination of relativistic Dirac-Slater wave functions and numerical Hartree-Fock wave functions^33,34,37,38. These Hartree-Fock scattering factors were previously computed from q = 0 to q = 1.5 at intervals of 0.01Å^{−1M 39}. For convenience, these scattering factors were previously fit to the 5-gaussian (Cromer-Mann) analytic function:

$${\mathrm{f}}_{\mathrm{v},\mathrm{i}}\left(\mathrm{q}\right)=\sum _{\mathrm{i}=1}^4{\mathrm{a}}_{\mathrm{i}}\cdot {\mathrm{e}}^{-{\mathrm{b}}_{\mathrm{i}}{\left(\frac{\mathrm{q}}{4\pi }\right)}^2}+\mathrm{c}$$ (3)

where a, b, and c are the constants for each atom, and q is the momentum transfer vector. This approximation is only valid with a q range from 0 to 2.0Å^33,34,37 which is sufficient for SAXS scattering experiments where the valid scattering angle range is from 0 to ≈ 0.33Å^8,9. For larger scattering angles, a 6-gaussian approximation must be used which is valid from 0 to ≈ 6.0 ų⁸. The displaced solvent scattering f_s,i(q) was approximated by V_i³⁰, the excluded solvent volume V displaced by atom i:

$${\mathrm{f}}_{\mathrm{s},\mathrm{i}}\left(\mathrm{q}\right)={\mathrm{q}}_{\mathrm{s}}{\mathrm{V}}_{\mathrm{i}}{\mathrm{e}}^{\frac{-{\mathrm{q}}^2{\mathrm{V}}_{\mathrm{i}}^{2∕3}}{4\pi }}$$ (4)

where q_s is the solvent density of 0.334e Å^{−3 35}. The combination of these equations yields a SAXS scattering profile from rigid body data stored in a pdb file.

GPU Parallel processing to accelerate algorithm

The pairwise nature of the Debye formula has a computational cost of O(N²) for each value of q evaluated, where N represents the number of atoms contained in the protein. This high computational cost and time requirement has precluded the use of the direct calculation of SAXS profiles using the Debye formula during folding simulations. To circumvent this computational limitation, alternative approaches for this calculation including multipole expansion methods for spherical harmonics³⁰ and approximation of the individual form factors have been developed²⁹. In contrast, to directly compute the SAXS profile using the Debye formula we leverage here the parallel architecture of graphical processing unit (GPU) threads using OpenCL and computed SAXS profiles directly.

GPU Implementations of the Debye Formula for SAXS Profile Reconstruction

In 2013, Antonov et al. showed how to use GPU acceleration to evaluate SAXS profiles in a Markov Chain Monte Carlo framework⁴⁰. From a protein structure created in silico, they reconstructed the SAXS profile using the Debye formula and GPU Acceleration. To address the O(N²) complexity of the Debye formula they created a coarse grain representation of the protein model with a one or two-body “dummy atom” approximation for each residue. The two body representation required the development of 21 form factors to represent each new atom type – one for Alanine, one for Glycine, one for the Backbone, and 18 for the remaining side chains. These form factors were derived using a Monte Carlo simulation of a set of 297 high resolution crystal structures from the Protein Data Bank (PDB)²⁹. This algorithm was benchmarked on problem sizes ranging from 64 to 8192 scattering bodies. The speed up ranges from 16× to 394×. A protein represented by 1888 bodies with 51 discrete q values took 2408 ms on a central processing unit (CPU) and 9 ms with GPU acceleration.

BCL::SAXS GPU Implementations of the Debye Formula for SAXS Profile Reconstruction

To build upon the previous work we parameterize the excluded volume and hydration shell in the form factor calculation and operate on individual atoms. For full atom representations of proteins we can account for deviations in electron density and hydration shell thickness. The Debye formula can be visualized as an N×N square matrix of N-atom rows by N-atom columns where N is the number of atoms in the protein. The pairwise Euclidean distances are calculated for each entry in the matrix with the diagonal represented by zeros. Pairwise distance calculations in a matrix form are an ideal calculation type for GPU acceleration because each GPU thread can calculate a single Euclidean distance with the only limitation being memory. To address memory requirements, the algorithm was restructured to have each thread calculate a Debye partial sum for a current atom i:

$${\mathrm{I}}_{\mathrm{partial}}={\mathrm{F}}_{\mathrm{i}}\left(\mathrm{q}\right)\sum _{\mathrm{j}=1}^{\mathrm{M}}{\mathrm{F}}_{\mathrm{j}}\left(\mathrm{q}\right)\frac{\sin \left({\mathrm{qr}}_{\mathrm{ij}}\right)}{{\mathrm{qr}}_{\mathrm{ij}}}$$ (5)

This technique enables the application of this accelerated algorithm to very large multimeric systems in excess of 90,000 atoms with the current GPU memory constraints while leveraging device shared memory in a tiling technique. The result of this partial sum is a matrix of q rows by N-atom columns where q is the momentum transfer vector and N is the total number of atoms. These partial sums are then summed across each column to completion for each q using a GPU reduction sum kernel to arrive at the desired q number of sums.

Generation of SAXS scattering profile from atomic coordinates with CRYSOL

To measure the time the algorithm takes on different types of GPUs, experimental scattering curves were approximated from high resolution protein structures in the PDB using the program CRYSOL³⁰. This program computes the scattering profile using spherical harmonics and multipole expansion for fast calculation of the spherically averaged scattering profile.

Approximate SAXS scattering profiles for protein models without side chain and loop regions

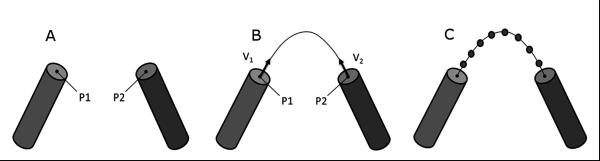
To approximate the side chain regions of a given amino acid, the form factors for the atoms with missing side chain coordinates were added to the C_β position of the respective amino acid. This approach is analogous to how the form factors for hydrogen are folded into their respective heavy atom in CRYSOL³⁰. The loop regions were approximated by removing atomic coordinate data between secondary structure elements (SSEs) and computing a path from the c-terminus of the first SSE to the n-terminus of the second SSE. The amino acid residues in the loop regions were placed at points along the path (figure 1). While crude, this approach is much more rapid than actual construction of loops.

Figure 1. Construction of curvilinear path and placement of residues in region between two SSEs.

(A) Protein model with two α-helical structures, p₁ and p₂. (B) Approximated path with unit vectors v₁ and v₂ pointing in the helical direction of SSE₁ and the helical direction of SSE₂ (C) Residues placed equidistant along the curvilinear path between SSEs.

Vector calculations to approximate the loop path between two secondary structure elements

P₁ represents the C_β position vector of the last residue in the N-terminal SSE, while P₂ represents the C_β position vector of the first residue in the C-terminal SSE.

$$\overrightarrow{{\mathrm{P}}_{1,\mathrm{n}}}=\{{\mathrm{x}}_1,{\mathrm{y}}_1,{\mathrm{z}}_1\}$$ (6)

$$\overrightarrow{{\mathrm{P}}_{2,\mathrm{c}}}=\{{\mathrm{x}}_1,{\mathrm{y}}_1,{\mathrm{z}}_1\}$$ (7)

CP₁ represents the center position vector of the last residue in the N-terminal SSE, while CP₂ represents the center position vector of the first residue on the C-terminal SSE.

$$\overrightarrow{{\mathrm{CP}}_{1,\mathrm{n}}}=\{{\mathrm{x}}_2,{\mathrm{y}}_2,{\mathrm{z}}_2\}$$ (8)

$$\overrightarrow{{\mathrm{CP}}_{2,\mathrm{c}}}=\{{\mathrm{x}}_2,{\mathrm{y}}_2,{\mathrm{z}}_2\}$$ (9)

We computed a vector pointing in the same orientation of the SSE by subtracting the C_β position of the center of the SSE from P₁ and P₂.

$$\overrightarrow{{\mathrm{V}}_{\mathrm{n}}}=\overrightarrow{{\mathrm{P}}_{\mathrm{n}}}-\overrightarrow{{\mathrm{CP}}_{\mathrm{n}}}$$ (10)

where n is the index of the point. The direction of the vectors V₁ and V₂ were computed by dividing them by their magnitude.

$$\overrightarrow{{\mathrm{D}}_{\mathrm{n}}}=\frac{\overrightarrow{{\mathrm{V}}_{\mathrm{n}}}}{\sqrt{{\mathrm{V}}_{\mathrm{nx}}^2+{\mathrm{V}}_{\mathrm{ny}}^2+{\mathrm{V}}_{\mathrm{nz}}^2}}$$ (11)

The scalar distance (D_sse) between two SSEs was computed by subtracting P₂ from P₁ and then taking the norm of the resulting vector. The percentage to move from P₁ toward P₂ at each step (L) along path (S) was computed by dividing one by one more than the number of amino acids in the loop region.

$$L=\frac{1}{N_{aa}+1}$$ (12)

The predicted Euclidean loop length (P) was computed by multiplying the number of amino acids by the C_α − C_α spacing of 3.2 Å. The 3.2 Å term is the average distance between amino acids in the coil region of a protein. It was computed by averaging the C_α distance between residues in the engrailed homeodomain (pdb id: 1ENH)⁴¹.

$$\mathrm{P}={\mathrm{N}}_{\mathrm{aa}}\times 3.2\mathrm{Å}$$ (13)

Pathway Calculations for Loop approximation

The path length (S) between two SSEs was approximated as a curve starting in the direction of SSE₁ and ending in the direction of SSE₂. The curve calculation consists of a linear, parabolic, and a directional component. The linear component is given by:

$$\overrightarrow{\mathrm{l}\left(\mathrm{L}\right)}=(1-\mathrm{L}){\overrightarrow{\mathrm{P}}}_1+\mathrm{L}{\overrightarrow{\mathrm{P}}}_2$$ (14)

where L is the percentage between [0, 1]. When L=0, the equation reduces to the Euclidean vector coordinates of the starting point. When L=1, the equation reduces to the Euclidean vector coordinates of the end point. The parabolic component is given by:

$$\mathrm{p}\left(\mathrm{L}\right)=\mathrm{N}\times \mathrm{L}(1-\mathrm{L})$$ (15)

where N is a normalization factor to size the height of the parabola and control parabolic path length. The directional component is given by:

$$\overrightarrow{\mathrm{d}\left(\mathrm{L}\right)}=[(1-\mathrm{L})\overrightarrow{{\mathrm{d}}_1}+\mathrm{L}\overrightarrow{{\mathrm{d}}_2}]$$ (16)

where d₁ and d₂ are unit directional vectors pointing in the direction of SSE₁ and SSE₂ respectively. The complete parabolic approximation function is:

$$\overrightarrow{\mathrm{P}\left(\mathrm{L}\right)}=(1-\mathrm{L})\overrightarrow{{\mathrm{P}}_1}+\mathrm{L}\overrightarrow{{\mathrm{P}}_2}+\mathrm{NL}(1-\mathrm{L})\times [(1-\mathrm{L})\overrightarrow{{\mathrm{d}}_1}+\mathrm{L}\overrightarrow{{\mathrm{d}}_2}]$$ (17)

Normalization Factor and Path Length Calculations

The normalization factor (N) controls the height of the curve and corresponding path length. To calculate N for a given loop region we divided the curve in half and approximated the arc to be the hypotenuse of a right triangle. The base of the triangle was the Euclidean distance between the SSEs divided by two (Figure 2). With these approximations, the normalization factor (N) is given by the Pythagorean Theorem:

$$\mathrm{N}=\frac{1}{2}\sqrt{{\mathrm{P}}^2-{\mathrm{D}}_{\mathrm{sse}}^2}$$ (18)

Where N is the normalization factor, P is the predicted loop length, and D_sse is the Euclidean distance between P₁ and P₂.

Figure 2. Depiction of the parabolic height approximation method.

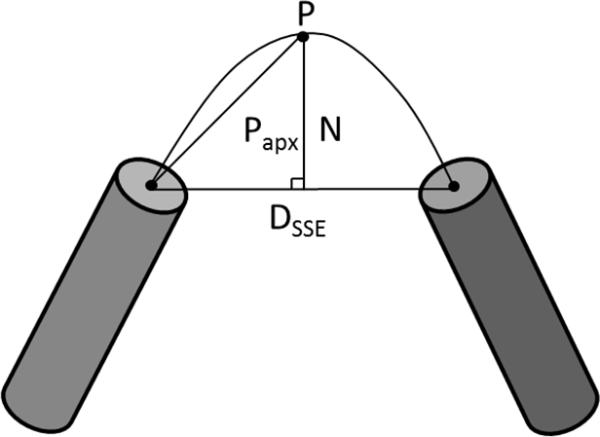
D_sse is the Euclidean distance between SSEs, P_apx is the estimated length of the hypotenuse side of a right triangle. N is the normalization factor and controls the height of the parabola.

Model quality was assessed by the χ agreement between the calculated and experimental SAXS curves

To compare the scattering profiles, we first normalized the experimental and calculated scattering intensities to be between (0, 1]. To magnify the effects of small distances, (higher q values), the scattering intensities (I) for both data sets were converted to a log₁₀ scale. To account for concentration differences in experimental data, the calculated curve was multiplied by a scaling weight (c) that minimizes the χ score^28,30.

$$\mathrm{c}=\left[{\sum }_{\mathrm{k}=1}^{\mathrm{Q}}\frac{{\mathrm{I}}_{\mathrm{cal}}\left({\mathrm{q}}_{\mathrm{k}}\right)\cdot {\mathrm{I}}_{\exp }\left({\mathrm{q}}_{\mathrm{k}}\right)}{{\sigma }_{\exp }^2\left({\mathrm{q}}_{\mathrm{k}}\right)}\right]{\left[\sum _{\mathrm{k}=1}^{\mathrm{Q}}\frac{{\mathrm{I}}_{\mathrm{m}}^2\left({\mathrm{q}}_{\mathrm{k}}\right)}{{\sigma }_{\exp }^2\left({\mathrm{q}}_{\mathrm{k}}\right)}\right]}^{-1}$$ (19)

where I_cal is the intensity of the calculated curve, I_exp is the intensity of the experimental curve, σ is the experimental error and q is the momentum transfer vector. Using cubic splines, the derivative of the intensities for both data sets were computed. Similar to other approaches to modeling proteins from a SAXS scattering profile^11,42,43, we score a model based on the χ score between the experimental profile and the profile computed by our algorithm BCL::SAXS.

$$\chi =\sqrt{\frac{1}{\mathrm{Q}}\sum _{\mathrm{i}=1}^{\mathrm{q}}{\left(\frac{{\mathrm{I}}_{\exp }\left({\mathrm{q}}_{\mathrm{i}}\right)-{\mathrm{cI}}_{\mathrm{cal}}\left({\mathrm{q}}_{\mathrm{i}}\right)}{\sigma \left({\mathrm{q}}_{\mathrm{i}}\right)}\right)}^2}$$ (20)

where Q is the number of entries in the data set and σ is the experimental error of the measured profile. In cases where no experimental error is provided it is simulated. We compute the χ score from different states of the experimental and calculated scattering profiles. The first state on the absolute scale is to compute the χ score right after the initial profile reconstruction with the Debye formula and scaling. The second state is to compute the χ score after converting the both experimental and computed data to the log₁₀ scale. The third state is to compute the χ score after taking the derivative of the log₁₀ representation of the experimental and calculated curves.

For complete models, we identify the optimal χ values by optimizing combinations of the excluded volume parameter, C₁ and the hydration layer parameter, C₂ inside a boundary (0.8 ≤ C₁ ≤ 1.2 and 0 ≤ C₂ ≤ 4.0). Using these parameters we compute the scaling parameter c that minimizes χ for each C₁, C₂ combination.

Results

To illustrate the use of BCL::SAXS, we show the results using hen egg white lysozyme (PDB ID: 6LYZ, molecular weight 14 kDa). The X-Ray scattering results for this protein were obtained from an open access database, BIOISIS, containing experimental SAXS data for hen egg white lysozyme (BIOSIS ID: LYSOZP). The SAXS profile for this protein was collected at the SIBYLS Beamline ASL BL12.3.1 and the experimental setup has been previously described⁴⁴. To account for uncertainty in the PDB definitions of secondary structure of 6LYZ, we added additional SSEs by taking the consensus prediction of the secondary structure server 2Struc⁴⁵. This meta server runs secondary structure prediction using the Dictionary of Secondary Structure of Proteins (DSSP)⁴⁶, DSSPcont⁴⁷, Stride⁴⁸, P-SEA⁴⁹, PALSSE⁵⁰, STICK⁵¹, KAKSI⁵², and TM-Align⁵³. The final SSE definitions used for analysis are shown in Table 1. The final model with loop approximations is shown in figure 3.

TABLE I.

SSE Definitions for Hen Egg White Lysozyme

Type	SSE Number	Start Residue	Sequence Location	End Residue	Sequence Location
Helix	1	ARG	5	HIS	15
Helix	2	LEU	25	SER	36
Helix	3	CYS	80	LEU	84
Helix	4	ILE	88	ASP	101
Helix	5	VAL	109	CYS	115
Helix	6	ASP	119	ARG	125
Strand	1	LYS	1	PHE	3
Strand	2	PHE	38	THR	40
Strand	3	ALA	42	ASN	46
Strand	4	SER	50	GLY	54
Strand	5	GLN	57	SER	60

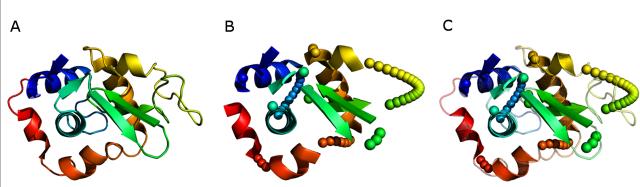
Figure 3. Depiction of Hen Egg White Lysozyme PDBid:6lyz.

(A) The crystal structure of Lysozyme with the n-terminal region colored blue and the c terminal region colored red. (B) Depiction of the native structure with the loop regions removed and approximated by pseudo atoms along the curvilinear path between SSEs. (C) Overlay of the native and approximated version of Hen Egg White Lysozyme.

The SAXS comparison derivative χ score

When comparing SAXS profiles between two distinct proteins, the common method is to use the χ formula previously shown.^28,30,54 However, when computing a SAXS profile for models with approximate the side chain atoms and loop regions, we observe a systematic upward shift from the original I(q) profile (Figure 4A). This shift between the experimental and approximated profiles increases the rate of false positive identification by SAXS scores (Figure 5). We observe also that minima and maxima of the I(q) profile are less affected. Therefore, by comparing the derivative of the profiles, we take the shape of the SAXS profile into account which decreases the rate of false positive identification by SAXS score.

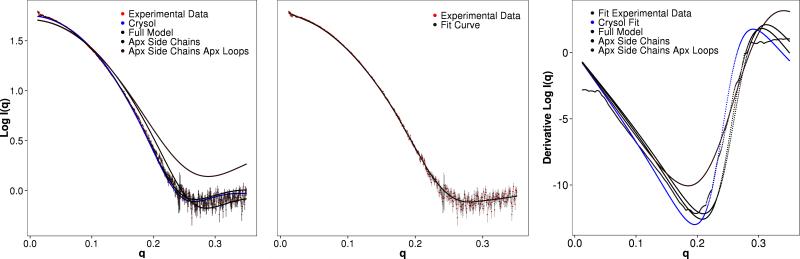
Figure 4. Depiction of the Experimental SAXS profile for Hen Egg White Lysozyme and SAXS profiles computed with BCL::SAXS for different protein states.

Panel A represents the fit on a log10 scale with Experimental data being the SAXS profile or Hen Egg White lysozyme, Crysol is the curve generated through Crysol from 6lyz and fit to the experimental data. Full Model is the curve generated through BCL::SAXS from 6lyz. Apx Side Chains is the curve generated through BCL::SAXS using Backbone atoms only and summing the form factors for all side chain atoms at the Cβ coordinate of the residue. Apx Side Chains Apx Loops is the curve generated through BCL::SAXS using loop approximation and side chain approximation. Panel B shows the locally weighted scatterplot smoothing (LOESS) of the experimental SAXS data points. Panel C shows the fit of previous data types from panel A using the derivative of the log10 profiles.

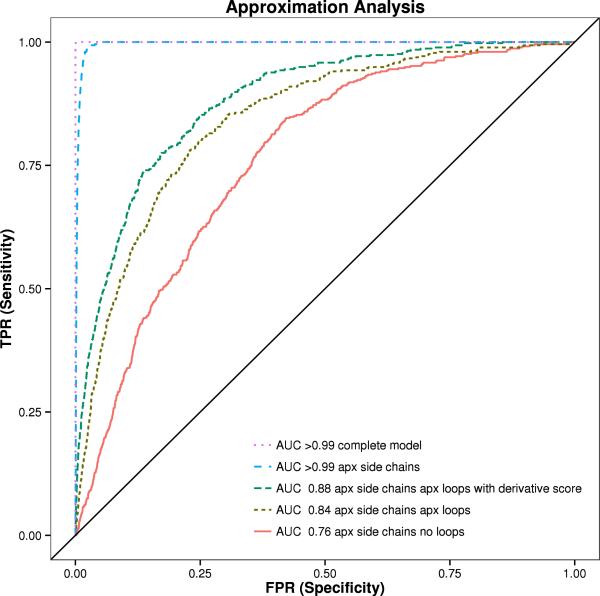
Figure 5. ROC Analysis of 455 proteins from Pisces dataset in different states.

The area under the curve (AUC) is shown with BCL::SAXS profiles generated for complete protein models (orange), models with approximated side chains (purple), approximated side chains and with loop approximation method (blue), approximated side chains without loop approximation method (red), and the derivative of the approximated side chains with the loop approximation method (green). The standard χ score was used to compare the profiles for all plots except for green, where the derivative χ score was used.

For this derivative comparison, a curve was fit through the experimental data points using locally weighted scatterplot smoothing (LOESS)^55,56 using a span of 0.2 and a polynomial degree of 1 in R. The span variable determines how much of the data is used to fit each local polynomial. A large span produces the smoothest function while the smaller the span, the closer the regression will conform to the data. Splines were used to numerically differentiate the fit profile. The derivative results and scores are shown in figure 4 and table 2. To measure the similarity between an experimental SAXS profile and complete protein models, we use the standard χ score. By using this score, we can easily compare our method with other established methods in the field such as CRYSOL. The user can specify what metric to use during analysis.

Table II.

Chi Scores comparing experimental SAXS data for Hen Egg White Lysozyme with profiles generated from the crystal structure (6LYZ) for CRYSOL and BCL::SAXS.

Type	Log10 χ	Derivative χ
Crysol	2.81	0.96
BCL::SAXS Full Model	2.32	1.01
BCL::SAXS Apx Side Chains	9.16	1.17
BCL::SAXS Apx Side Chains and Loops	19.83	1.25

Non-redundant dataset for protein discrimination benchmark

To determine how well the SAXS score can distinguish protein folds from each other, we evaluated a representative subset of 455 proteins with a 20% identify cutoff, 1.6 Å resolution cutoff, and 0.25 R-factor cutoff from the PICES databank^57,58. These proteins can be formed into a 455 × 455 matrix (207,025 pairings) where the diagonal represents a protein paired with itself (a true positive) and the off diagonal elements represents a protein paired with a different protein. Using scattering profiles generated through CRYSOL, we computed the difference between the native protein and the test protein for each pairing. If the minimum SAXS score for a given protein was on the diagonal for the i^th row and j^th column, then we correctly identified the protein from all other candidate proteins and classified that as a true positive. If the minimum SAXS score was not on the diagonal, we classified it as a false positive. Using receiver operating characteristic (ROC) curves, we plotted the false positive rate on the x-axis and the true positive rate on the y-axis.

The area under the curve (AUC) for complete protein models is > 99%. When side chains are removed, the AUC remains > 99%. The AUC for proteins without side chains and loop regions is 76%. When loop regions are approximated, the AUC is 84%. The derivative score improves the AUC to 88%. See figure 5. There were 207,025 total pairing evaluated in this experiment. In all but three cases the lowest SAXS score was the native protein when using complete protein models for analysis. For proteins 1YOZA and 3I31A the native was ranked second, while for protein 3L42A the native was ranked third.

Structural Similarity of proteins with similar SAXS scores

To determine if protein models with similar SAXS scores were similar in protein structure, MAMMOTH⁵⁹ was used to rank structural similarity between two proteins. See figure 6. The 455 × 455 matrix was used to score the structural similarity of a pair of proteins. The diagonal represents self-paired proteins. The higher the Z-score, the more similar the two structures are. A Z-score below four indicates that two proteins are structurally different. In the SAXS analysis, a lower SAXS score indicates the scattering profiles of two proteins are very similar. In this analysis, a high Z-Score and a low SAXS score indicate that proteins identified by SAXS as similar are structurally similar. Figure 6 panel A depicts 3H5L chain A (molecular weight 44.92 kDA) paired with a copy of itself. As expected the SAXS similarity score is very low and the Z-score is high. Interestingly, panel B depicts 1N1F chain A (molecular weight 18.35 kDA) paired with 2GPE chain A (molecular weight 5.95 kDA). Although there is a difference of 12.4 kDA, the SAXS score indicates that the proteins are similar. Figure 6 shows that structurally similar proteins (high Mammoth Z-score) always have a low SAXS score (bottom left corner). However, while structurally dissimilar proteins (low Mammoth Z-score) tend to have increased SAXS scores, the observed range of SAXS scores widens. As expected, structurally different proteins can appear similar in a SAXS experiment if their overall shape is similar.

Figure 6. Structural MAMMOTH Z-score vs. SAXS profile similarity score of 455 proteins from Pisces dataset.

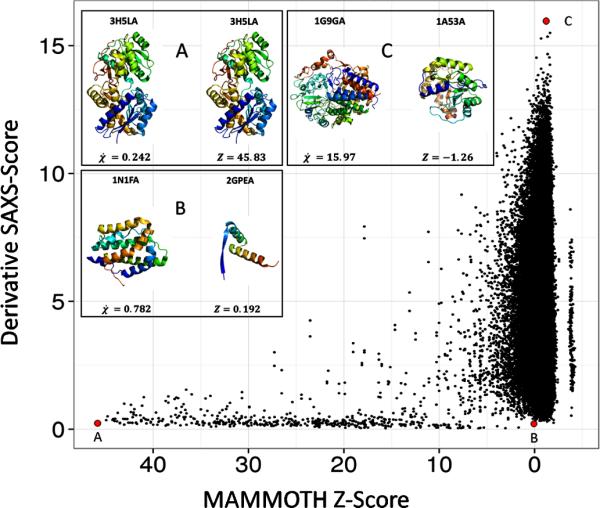
All 455 proteins were scored by structural similarity to each other with self-pairing receiving the highest z-score (x-axis). SAXS profiles for all 455 proteins were generated and the χ score between all scores was computed (y-axis). Panels A, B, and C correlate with their respective red dot. Panel A depicts 3H5LA paired with itself. Panel B depicts 1N1FA paired with 2GPEA. Panel C depicts 1G9GA paired with 1A53A. The derivative χ score was used to compare the 455 SAXS profiles.

SAXS Degeneracy in the scattering profile

During elastic scattering, energy is conserved between incident X-Rays that scatter by interactions with electrons in the target sample. The magnitude of the wave vector $\overrightarrow{\mathrm{k}}$ for both the incident and scattered wave is given by 2π / λ. The change in wave-vector is only in direction and the difference between $\overrightarrow{{\mathrm{k}}_1}$ and $\overrightarrow{{\mathrm{k}}_{\mathrm{f}}}$ is given by $\overrightarrow{\mathrm{q}}$ – the momentum transfer vector. The X-ray scattering amplitude at $\overrightarrow{\mathrm{q}}$ by a particle at position $\overrightarrow{{\mathrm{r}}_{\mathrm{j}}}$ is given by:

$${\mathrm{A}}_{\mathrm{j}}\left(\overrightarrow{\mathrm{q}}\right)=\mathrm{f}\left(\mathrm{q}\right){\mathrm{e}}^{(\mathrm{i}\overrightarrow{\mathrm{q}}\cdot {\overrightarrow{\mathrm{r}}}_{\mathrm{j}})}$$ (21)

where f is the form factor for the atom j at a magnitude for q given by 4πsinθ / λ. The form factor decreases from a maximum at q = 0. At this q value, the form factor is equivalent to the atomic number Z of the atom. Hence, atoms with higher Z are stronger scatterers. The amplitude for an ensemble of particles is a summation of the amplitudes of all particles:

$$\mathrm{A}\left(\overrightarrow{\mathrm{q}}\right)=\sum _{\mathrm{j}=1}^{\mathrm{n}}\mathrm{f}\left(\mathrm{q}\right){\mathrm{e}}^{(\mathrm{i}\overrightarrow{\mathrm{q}}\cdot {\overrightarrow{\mathrm{r}}}_{\mathrm{j}})}$$ (22)

The scattering intensity is given by the amplitude multiplied by its complex conjugate $\mathrm{A}{\left(\overrightarrow{\mathrm{q}}\right)}^{\ast }$:

$$\mathrm{I}\left(\overrightarrow{\mathrm{q}}\right)=\mathrm{A}\left(\overrightarrow{\mathrm{q}}\right)\mathrm{A}{\left(\overrightarrow{\mathrm{q}}\right)}^{\ast }$$ (23)

The observed scattering pattern is not the complex amplitude function. It is the modulus squared of the amplitude function. Most of the structural information obtained from X-ray scattering experiments reside in the phase of the wave-function. This phase information is stored in the imaginary part of the amplitude function and is lost when multiplied by the complex conjugate. This loss of phase information results in a loss of structural uniqueness. Furthermore the effect is compounded because during a SAXS experiment samples are free to rotate. The observed I(q) function is therefore also an average over possible orientations. The loss of orientation and phase information results in the degeneracy in the scatting profile (multiple structures yielding similar SAXS profiles) as observed in figure 6.

To show the relation between the molecular weight of the compared proteins and the similarity of the SAXS profiles, we calculated molecular weights for all 455 proteins in the PISCES data set used in the MAMMTOH analysis. We then combined the molecular weight difference with the derivative SAXS score to generate a density plot (Figure 7). As expected, we observe that for proteins of similar molecular weight a range of SAXS similarity scores χ are possible from very similar to dissimilar determined solely by the similarity in overall shape. As the difference in molecular weight increases, the minimum SAXS similarity scores χ increases also, i.e. structures with large molecular weight differences do not have similar SAXS profiles, even if the overall shape is similar.

Figure7. The SAXS similarity scores χ in relation to molecular weight difference.

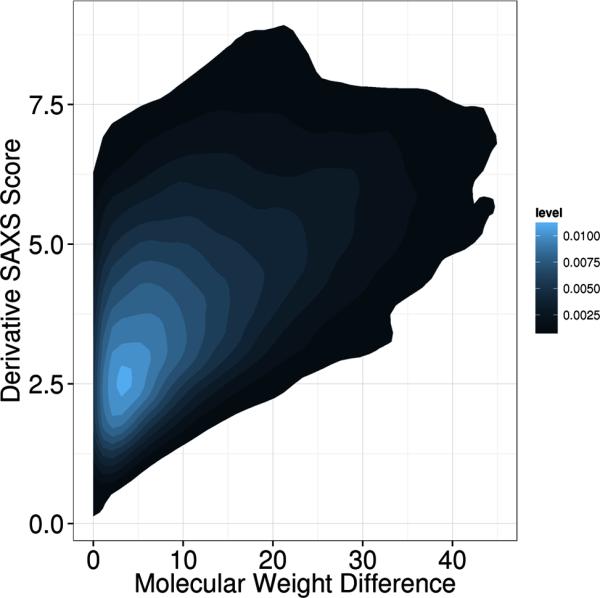
Molecular weights for all 455 proteins from the PISCES data set were calculated. The absolute value of the difference in weight between two proteins was computed for all pairs. The density plot depicts the difference in molecular weight on the x-axis and the derivative SAXS similarity score χ on the y-axis.

Scoring BCL::Models with SAXS

BCL::Fold was run to generate 10,000 protein models of 3FRR. These models were only comprised of secondary structure elements. Using the side chain and loop region approximations, BCL::SAXS was used to construct SAXS profiles for all 10,000 models generated by BCL::Fold. (Figure 8) From this figure, we observe that the correct topology has a very low SAXS score. We note that model C has a lower SAXS score (1.43) than model B (1.71) although model B has a much lower RMSD100 score (7.72) than model C (16.29). This behavior is expected because SAXS cannot distinguish topologies that fit inside the overall SAXS envelope. Agreement with by SAXS score is a necessary condition for correct protein identification, but not sufficient to uniquely identify the correct model. However, because of this, the SAXS score can be used as a filter to remove models that score above a threshold.

Figure 8. Filtering models produced by BCL::Fold by SAXS score.

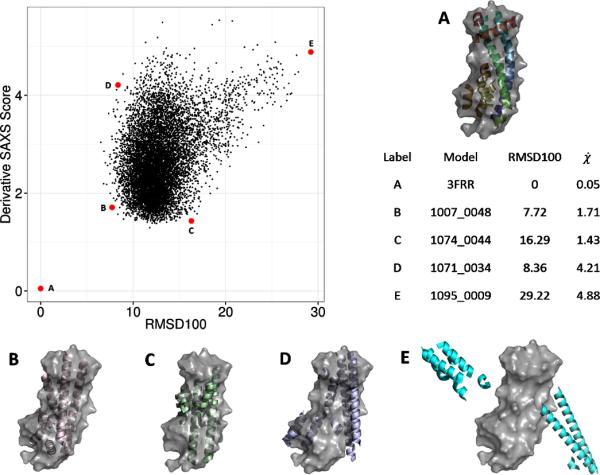
BCL::SAXS was used to score 10,000 protein confirmations of 3FRRA generated by BCL::Fold. In each case the surface of the native confirmations is shown in gray. Each black dot represents one model. The red dots labeled with A,B,C,D,E show examples of different conformations sampled by BLC::Fold and their respective scores. The derivative χ score was used to compare the 10,000 BCL models with the native structure.

GPU Algorithm Yields Orders of Magnitude Speed Improvements

The GPU accelerated Debye calculation was benchmarked on several protein systems from the PDB with sizes ranging from 1,800 atoms to 92,000 atoms. The benchmark was performed on several devices ranging from low-end workstation class GPUs (Quadro 600) to high-end consumer grade GPUs (GTX680). See Table 3. The speed was determined by measuring the time in seconds from the start of the Debye formula to the SAXS profile return from the Debye formula. The Maximum Speed up is the maximum of the ratio of the CPU time in seconds divided by the GPU time in seconds.

Table III.

Timing results of GPU vs. CPU benchmarks. All timings are reported in seconds. Crysol reported timings to the nearest second. The first two measurements were not accurate and have been omitted.

PDB	Atoms	BCL::SAXS	Crysol	Quadro 600 $225	GTX470 $325	GTX480 $325	GTX580 $550	GTX680 $1000	C1060 $1300	Maximum Speedup
		CPU $1300
1O26_A	1832	3.6	-	0.1	0.07	0.07	0.07	0.07	0.09	51×
1WA5_C	7543	65	-	1	0.31	0.28	0.27	0.20	0.37	325×
1NR1	23217	624	2	9.3	2	1.9	1.8	1.2	2.7	520×
1ZUM	43243	2300	5	30	4.9	4.1	3.9	2.4	6.5	958×
1VSZ	91846	15365	10	132	19.8	16.9	15.8	9.0	26.3	1707×

Discussion

We have demonstrated how to compute SAXS profiles from atomic coordinates. In our approach for complete protein models we did not make approximations to the Debye formula, rather we used GPU acceleration to handle the double summation of all atoms and used the Hartree-Fock scattering factors directly. For proteins of sizes ranging from 1832 atoms to 91,846 atoms we find, as expected, that without GPU acceleration, the O(N²) computational cost of the Debye formula results in a significant slow-down when compared to the O(q²D²N) algorithm implemented in CRYSOL (Table III). The magnitude of the momentum transfer vector is given by q and D is the max dimension of the macromolecule. With GPU acceleration computation times are comparable. The GPU card that gave the best performance was GTX680.

In order to compare experimental scattering profiles with approximated profiles we computed the first derivative of the profiles and then computed the similarity score ($\stackrel{.}{\chi }$), between the derivatives of the SAXS profiles. This enabled us to reduce the amount of false positives obtained during our analysis and improve the accuracy in structure identification using SAXS profiles from 84% to 88%. BCL::SAXS was >99% accurate in picking the native protein from a set of other proteins when using complete proteins from the PDB and using the standard χ comparison score. With the side chains approximated, BCL::SAXS remained >99% accurate in picking the native protein from a set of other proteins. With the loop regions removed, the accuracy dropped from >99% to 76%. This result shows that loop regions play an important role in defining overall protein shape. Using our loop approximation algorithm and the derivative of the χ score, the accuracy increased to 88%. This result shows that having an approximate estimate of a protein location can have significant impact on the accuracy of SAXS scattering profiles generated from rigid bodies.

The MAMMOTH analysis shows that proteins with very similar z-scores (structurally similar proteins) also have a low SAXS $\stackrel{.}{\chi }$ score. Importantly, the analysis shows that very similar structures do not have high SAXS scores. In the middle range of the analysis, we observe that SAXS scores are degenerate. Different structures can have similar SAXS scores. This degeneracy is inherently due to the spherical averaging of atoms in the SAXS data collection process. Because of this degeneracy SAXS cannot be used exclusively to predict protein structure.

Conclusion

We explored the idea of approximating the SAXS score for protein models without side chain and loop coordinates by placing dummy atoms along a path between secondary structure elements. The SAXS profile can be used to distinguish different proteins from each other, but cannot be used exclusively to distinguish different permutations of the same topology. However, the SAXS profile can be used as a filter to exclude protein models that are very different from the native from further analysis as a filter.