Abstract
Water, an important constituent in bone, resides in different compartments in bone matrix and may impose significant effects on its bulk mechanical properties. However, a clear understanding of the mechanistic role of water in toughening bone is yet to emerge. To address this issue, this study used a progressive loading protocol, coupled with measurements of in situ mineral and collagen fibril deformations using synchrotron X-ray diffraction techniques. Using this unique approach, the contribution of water to the ultrastructural behavior of bone was examined by testing bone specimens in different loading modes (tension and compression) and hydration states (wet and dehydrated). The effect of water on the mechanical behavior of mineral and collagen phases at the ultrastructural level was loading-mode dependent and correlated with the bulk behavior of bone. Tensile loading elicited a transitional drop followed by an increase in load bearing by the mineral phase at the ultrastructural level, which was correlated with a strain hardening behavior of bone at the bulk level. Compression loading caused a continuous loss of load bearing by the mineral phase, which was reflected at the bulk level as a strain softening behavior. In addition, viscous strain relaxation and pre-strain reduction were observed in the mineral phase in the presence of water. Taken together, the results of this study suggest that water dictates the bulk behavior of bone by altering the interaction between mineral crystals and their surrounding matrix.
Keywords: Bone, Synchrotron X-ray scattering, Toughness, Mineral, Collagen
INTRODUCTION
Bone fragility fracture is a major concern in the healthcare of the elderly and post-menopausal patients due to its severe consequences of morbidity and even mortality and the associated high healthcare costs. For effective treatments of such fractures, it necessitates a clear understanding of the underlying mechanisms, pertaining to changes in material and structural properties of the tissue.
Bone is a highly hierarchical composite made of proteins (mostly type I collagen and a small volume of non-collagenous proteins) and minerals (highly substituted carbonated apatite crystals), with water filling the bone matrix spaces at all hierarchies (Horch, et al., 2012, Nyman, et al., 2008). At the ultrastructural level, bone is a nano-composite of mineralized collagen fibrils that are formed by collagen triple helices in a staggered arrangement, with minerals permeated in the gap regions of the fibrils and in the spaces between the fibrils (Prostak and Lees, 1996). The mechanical behavior of the mineralized collagen fibrils and the hydroxyapatite (HA) crystals has been deemed to play a critical role in toughening the tissue at ultrastructural levels (Burr, 2002, Currey, 1984, Gupta, et al., 2006, Wang, et al., 2001).
Different toughening mechanisms acting at different hierarchical levels are considered for greater energy dissipation in bone (Nalla, et al., 2004, Zimmermann, et al., 2011), such as crack bridging and crack deflections at microscopic levels (Nalla, et al., 2004, Zimmermann, et al., 2011), and mineral-collagen interfacial debonding and intrafibrillar plasticity through sliding at ultrastructural levels (Gupta, et al., 2013, Hoo, et al., 2011, Luo, et al., 2011, Siegmund, et al., 2008). Researchers have also postulated that some macromolecules may act as a glue between mineralized collagen fibrils (Fantner, et al., 2005, Thompson, et al., 2001). For instance, previous evidence shows that some non-collagenous proteins (e.g. osteopontin) may play a role in bone toughness by binding mineral crystals at the collagen gap regions (Lai, et al., 2014, Nikel, et al., 2013, Poundarik, et al., 2012).
Water, as another important constituent in bone, resides in three different compartments in bone matrix (Wilson, et al., 2006) and may impose significant effects on the bulk mechanical properties of bone. Acting as a plasticizer, water makes bone tougher, but more compliant and weaker (Broz, et al., 1993, Nyman, et al., 2006). A recent study revealed that water molecules that are present in small gap regions (presumably < 0.4 nm) play a dominant role in the mechanical behavior of bone (Samuel, et al., 2014). Nonetheless, a clear understanding of the mechanistic role of water is yet to emerge.
Moreover, it is well known that tension and compression elicit different failure modes in bone (Arthur Moore and Gibson, 2002, Fazzalari, et al., 1998). In tension, patches of extensive diffuse damage in the extracellular matrix were observed, whereas in compression, “cross-hatch” microdamage or shear bands indicating a shear-dominated failure mode were observed (Fazzalari, et al., 1998, Reilly and Currey, 2000). Thus, it is also necessary to understand the role of water in influencing the mechanical behavior in different loading modes.
This study was intended to determine the effect of water on the in situ deformation of bone constituents (i.e. mineral crystals and collagen fibrils) under tension and compression loading modes. To address this issue, we used a progressive loading protocol, coupled with measurements of in situ mineral and collagen fibril deformations using synchrotron X-ray diffraction techniques. Using this unique approach, the contribution of water to the ultrastructural behavior of bone in tension and compression was determined by testing wet and dehydrated bone specimens, respectively.
MATERIALS & METHODS
Specimen preparation
Six male human cadaveric femurs (N=6) were collected from the National Disease Research Initiatives (NDRI, Philadelphia, PA). Two cylindrical compression specimens (Φ3.0mm×5.0mm) were cored out from the anterior quadrant of the mid-diaphysis of each femur. In addition, two dog-bone-shaped tension specimens (2mm×2mm cross section, 8 mm gauge) were machined from the same anatomic aspect using a CNC machine. To determine the effects of dehydration on the in situ deformation of mineral and collagen fibrils, the specimens from each donor were divided into dry and control groups. The specimens in dry groups were dehydrated at 70°C temperature and 25 in Hg vacuum for 8 hours. Dehydration at 70°C was found sufficient to remove mobile and bound water from the tissue (Nyman et al., 2006), without causing significant loss to the bulk mechanical properties (Samuel, Sinha, Zhao, & Wang, 2014). The structural water was not considered in this study since the water is part of the mineral lattice and can be removed only at 200-400°C (LeGeros, Bonel, & Legros, 1978), which may completely denature the collagen phase. The control specimens were stored in gauze soaked with phosphate buffered saline (PBS) at −20°C prior to mechanical testing.
Experimental setup
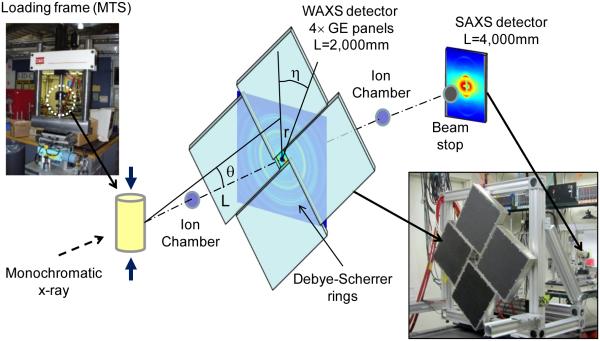
Mechanical testing of bone specimens were conducted concurrently with X-ray scattering measurements at the 1-ID beam line, Advanced Photon Source, Argonne National Laboratory (Fig. 1). An MTS servo hydraulic load frame (MTS 858) was used for loading the specimens in tension and compression. A force transducer attached to the load frame was used to record the load and then to calculate the stress applied to the specimens. An extensometer was used to record the elongation of the gage region, which was then used to calculate the externally applied strains. The control specimens were kept hydrated by continuously dripping phosphate buffered saline (PBS) solution onto the specimens. A strip of absorbent paper was wrapped around the test area of the specimen to ensure that a layer of water was trapped on the surface of bone throughout the duration of the test. The drip rate was adjusted to ensure the specimen was not allowed to dehydrate. A monochromatic X-ray beam with a cross section of 100μm×100μm was incident at the specimen center. Four GE area detector panels were used to record WAXS diffraction patterns, and arranged to include a center hole through which the SAXS signal could propagate and be simultaneously collected with a Bruker 6500 CCD further downstream. No radiation damage to the specimens was expected since the total radiation dosage in the test duration was several orders of magnitude below the threshold dosage (20-60 kGy) that could induce tissue damage (Singhal, Deymier-Black, Almer, & Dunand, 2011).
Fig. 1.
Schematic of the X-ray diffraction experimental setup: The diffraction angle (θ) was measured based on the radius (r) of the diffraction (Debye) ring and the distance of the sensor panel to the specimen (L), which was employed to determine the lattice spacing using the Bragg’s equation.
Mechanical Testing Protocol
To determine the progressive change in mechanical properties of bone at both the bulk and ultrastructural levels, a unique loading protocol developed in our laboratory was used (Wang and Nyman, 2007). This protocol included multiple loading cycles, each of which consisted of a sequence of load-dwell-unload-dwell-reload stages. The test specimen was loaded to failure in a series of incremental strains applied during each cycle in both tension and compression. In each cycle, the specimen was first loaded in displacement control to a specified strain level following which the specimen was allowed to stress relax for a period of 150 seconds at a constant external strain in displacement control. Following stress-relaxation, the specimen was unloaded to a baseline load of 5.0N and relaxed for another 150 seconds at the baseline load in load control mode. The loading cycle were repeated until specimen failure. The relaxation times were determined experimentally to allow sufficient relaxation in the specimen.
Internal strain measurements using synchrotron X-ray diffraction
The lattice spacing of mineral and collagen fibrils in bone during loading was measured using a modified Bragg’s equation:
| (1) |
where, k is a constant with value 12.39, EB is the incident beam energy measured in keV; 2θ is the angle between the transmitted beam and the diffracted beam. Wide-angle X-ray scattering (WAXS) and small-angle X-ray scattering (SAXS) images were recorded to measure the lattice spacing in mineral crystallites (d spacing) and collagen fibrils (D period), respectively.
Diffracted x-rays from polycrystals (e.g. HA crystallites in bone) form concentric diffraction cones known as Debye cones (Fig. 1). Debye cones when projected onto an area detector form concentric circles depicting the diffraction from all lattice planes in the crystallites that fulfill the diffraction condition as described by the Bragg’s law. The d spacing was measured by calculating the 2θ angle using a relation tan2θ = r/L, where r is the radius of the Debye ring and L is the distance from the bone specimen to the detector measured using a Cerium oxide calibrant. Changes in d spacing were calculated by measuring the distortion of the Debye ring. The in situ strain of mineral and collagen fibrils was then assessed using the following equation:
| (2) |
where, dη0 and dη are the d spacing prior to and after loading, respectively, and η denotes the azimuth angle, along which the normal of 002 lattice planes in the crystals and the longitudinal axis of the collagen fibrils are aligned with the loading axis (η=90°).
Estimation of internal stress of the mineral and collagen phase
The internal stress of the mineral phase along the loading axis was estimated using the longitudinal and transverse strains measured from the 002 lattice plane deformation in these directions. In this study, the average transverse strains εxx and εzz were assumed equal based on the axisymmetric properties along the longitudinal axis of bone. X-ray elastic constants were calculated using a Kröner-Eshelby model to determine the average elastic properties of polycrystals using the elastic constants of Hydroxyapatite (HAP) single crystals by Stock et al (Almer and Stock, 2005). X-ray elastic compliances were reported to be S1=−2.27×10−6MPa−1, S2/2=10.2×10−6MPa−1 in the same study. Using the compliance values, the stress along the loading direction σyy was calculated as:
| (3) |
In addition, the axial modulus estimated from in-silico models of mineralized collagen fibrils (Hambli and Barkaoui, 2012, Siegmund, et al., 2008) was used to approximate stresses in the mineralized fibrils aligned in the longitudinal axis of bone.
Determination of pre-strain status in the mineral phase
In this study, the d-spacing of 002 planes in the mineral phase was measured using X-ray diffraction on deproteinized/dehydrated bone powders and intact bone specimens, respectively, prior to loading. Deproteinization was used to remove the pre-strains in the mineral phase by the surrounding organic matrix and dehydration was conducted to avoid potential hydration induced strains. The bone powder was used to estimate the d-spacing of the mineral phase under no pre-strain, whereas the intact bone specimens were used to determine the initial pre-strain status of the mineral phase. In the absence of pre-strain, the d-spacing of the longitudinally (dL) and transversely (dT) oriented 002 planes in mineral crystals should be identical. However, dL and dT would be different when the mineral phase is pre-strained. In this study, therefore, we used the following measure (ζ) to assess changes in the pre-strain status of the mineral phase after unloading in each cycle during the progressive loading scheme,
| (4) |
where, ζ was defined as pre-strain reduction index. The value of ζ varies from zero to unity, with a value of one indicating the pre-strain level in the unloaded specimen and zero indicating a complete removal of pre-strain.
Determination of time-dependent strain relaxation
Previous studies (Dong, et al., 2011) reported that the internal strain of the mineral phase exhibited time-dependent changes after bulk yielding, which concurred with the stress relaxation of bulk specimens during the dwell period before the unloading step in each loading cycle. In this study, we measured changes in the internal strain (Δε) of both mineral and collagen phases during the bulk stress relaxation (dwelling) stage in each load cycle. In-situ strain relaxation of both the mineral and collagen phases during bulk stress relaxation of the specimen in each load cycle, was measured by loading the specimens to a predetermined macroscopic strain and allowing to relax at the fixed strain level. The difference in strain of both mineral and collagen phases at the beginning and end of bulk stress relaxation was recorded as the magnitude of strain relaxation. This measurement was intended to determine the effect of water on the viscoelastic response of bone at the ultrastructural level.
Statistical analysis
Two-way ANOVA was performed to determine the effect of loading modes and dehydration on the bulk and in situ mechanical properties of bone. In addition, multiple comparisons were implemented to detect significant differences between groups. Moreover, regressions were performed to determine the correlation between any two parameters. The statistical significance was considered only if p < 0.05.
RESULTS
Bulk mechanical behavior
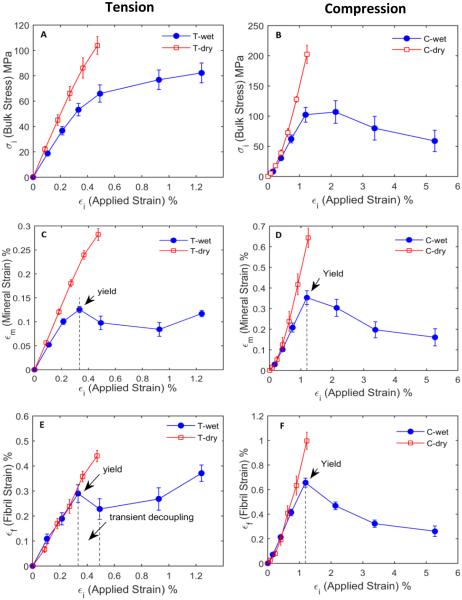
Significant differences (p<0.05) were observed in the bulk mechanical properties of bone between wet and dry specimens in different loading modes (compression vs. tension) (Fig. 2A, 2B). Dry bone specimens were stronger and stiffer than wet bone specimens (Table 1) and showed little post-yield deformation (p<0.05). On the other hand, wet bone specimens exhibited appreciable plastic deformation and failed at much higher strain levels (p<0.05). In addition, considerable differences in mechanical behavior of bone were also observed between tension and compression, showing that the post-yield behavior of wet bone specimens demonstrated a strain hardening effect in tension, but a strain softening effect in compression. Moreover, wet bone specimens showed a greater failure strain in compression than in tension (Table 1).
Fig. 2.
Bulk and ultrastructural behavior of bone under different conditions: stress-strain curve of bone under wet and dry conditions in tension (A) and in compression (B); bulk vs. internal strain of the mineral phase of bone in tension (C) and in compression (D); and bulk vs. internal strain of the collagen phase in bone, in tension (E) and in compression (F), respectively. Not all load cycles have been shown for compression wet specimens as the measured properties saturate beyond ~5% applied strain.
Table 1.
Bulk mechanical properties of bone under wet and dry conditions in tension and compression
| Tension | Compression | |||
|---|---|---|---|---|
| Wet (n=5) | Dry (n=5) | Wet (n=6) | Dry (n=6) | |
| Elastic Modulus (GPa) | 18.6 ± 1.2 | 24.8 ± 0.7 | 11.2 ± 1.3 | 17.7 ± 3.4 |
| Ultimate Strength (MPa) | 87.6 ± 6.4* | 127 ± 3.4* | 106.8 ± 18.8 | 245 ± 31.5* |
| Failure Strain (%) | 1.3 ± 0.3* | 0.6 ± 0.02* | 16.4 ± 0.91* | 1.50 ± 0.40* |
| Toughness (MJ/m3) | 0.9 ± 0.4 | 0.4 ± 0.02 | 11.3 ± 0.45 | 1.75 ± 0.70 |
Note: The values shown are mean ± standard deviation. Statistically significant difference (p < 0.05) was observed across Wet and Dry groups in both tension and compression loading modes for each mechanical property.
The ultimate strength and failure strain values under tension and compression are not always consistent with the plot shown in Fig. 2. This is due to the fact that the specimens were loaded to failure after completion of a prescribed number of load cycles. The plots in fig. 2 show only the maximum applied strain/stress in each load cycle since X-ray data was recorded only within a load cycle, whereas the ultimate strength data comes from a final loading stage at the end of a predetermined number of cyclic loadings.
Internal vs. bulk strains
By plotting the mineral and collagen strains against the bulk tissue strain (Fig. 2C, D, E, F), it was observed that the collagen strain was smaller compared to the bulk tissue strain, but greater than the mineral strain, irrespective of different loading modes and hydration status. In the elastic region, the collagen and mineral phases in the wet bone specimens deformed at 88% and 38% of the bulk tissue strain in tension and 55% and 30% in compression, respectively. In dry specimens, the collagen and mineral strains increased to 94% and 60% of the bulk strain in tension and 76% and 50% in compression, respectively. These ratios were not fully consistent with those reported in the previous studies (Gupta, et al., 2006). We speculate that such differences might arise due to differences in the experimental setups such as specimen types and hydration states.
In addition, dry bone specimens exhibited that the mineral and collagen strains were almost linearly proportional to the bulk strain until failure. However, wet bone specimens demonstrated remarkably different post-yield behaviors of the collagen and mineral phases between tension and compression. In tension, both the mineral and collagen strains dropped at the onset of yielding and then gradually increased with increasing bulk strains, whereas in compression the mineral and collagen strains continuously decreased after yielding until failure (Fig. 2C, D, E, F). This important observation suggests that there exist two distinct underlying deformation mechanisms at the ultrastructural level in bone, depending on the loading mode.
Load bearing by the mineral and collagen phases
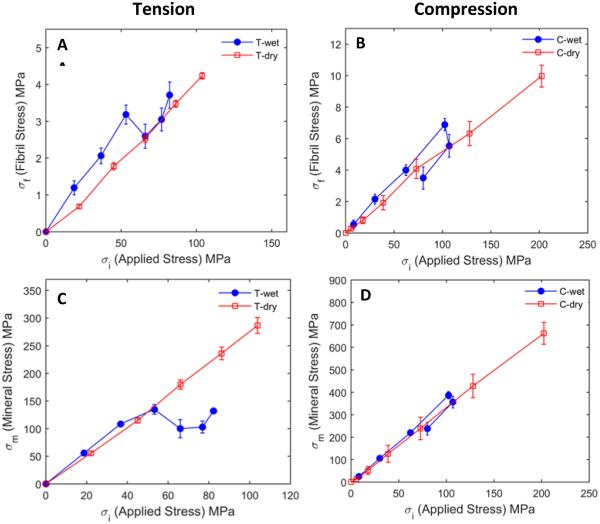
The internal stress of the 002 lattice plane in the mineral phase along the loading axis was estimated in the linear elastic region using the Kröner-Eshelby model. The estimated internal stress in the mineral phase carried a considerably higher stress than the nominal macroscopic stress applied to the bulk tissue, indicating that there is a high degree of stress concentration in the mineral phase prior to bulk yielding (Fig. 3C, 3D).
Fig. 3.
Mineral and collagen fibril stresses vs. the macroscopic stress under wet and dry conditions in tension (A & C) and compression (B & D). The contribution of the collagen phase to load bearing of bone is minimal compared to the mineral phase. Both mineral and collagen stresses showed a linear relationship with the bulk stress under dry condition for both loading modes. Under the hydrated condition, mineral stress increased prior to yield, dropped at the yield point and gradually increased thereafter in tension, but had almost a linear relationship with the bulk strain in compression. Mineral strain values were much higher than those of bulk stress, indicating a remarkable stress concentration in the mineral phase. The mineral stress was estimated using the Kröner-Eshelby model.
Immediately after yielding, the mineral phase exhibited a transient reduction in stress with respect to bulk stress, followed by a gradual increase in stress under tension in wet condition (Fig. 3A, 3B). Upon dehydration, the stress drop disappeared. On the other hand, load transferred to the mineral phase in compression exhibited a linear relationship with the bulk strain both before and after yielding and in wet and dehydrated states. In addition, no post-yield stress drop in the mineral phase was observed as seen in tension.
The stress transfer to the mineral phase was highly dependent on the hydration state of bone. Mineral crystals experienced much larger stresses in dry state (~650MPa in compression, ~300MPa in tension) than in wet state (~400MPa in compression, ~150MPa in tension). These results indicate a water-mediated load transfer phenomenon in bone under both tensile and compressive loading. The contribution of the collagen phase to the load bearing of bone was very limited (~10MPa in compression and ~4.5MPa in tension for dry and ~7.0MPa in compression, ~4.0MPa in tension for wet specimens, respectively), only about two orders of magnitude less than that of the mineral phase (Fig. 3), thus implying that the role of the collagen phase in load bearing is negligible compared to the mineral phase.
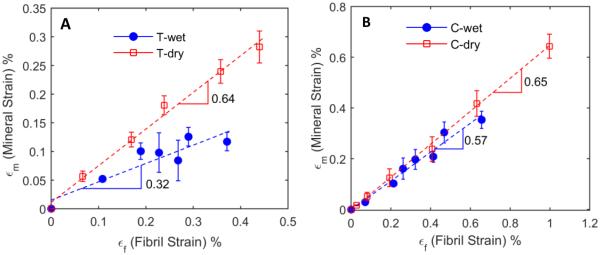
Strain ratio between mineral crystals and collagen fibrils
The relationship between the mineral to collagen strains was linearly proportional in both wet and dehydrated states and in both tension and compression (Fig. 4). Dry bone specimens exhibited a higher strain ratio (i.e. greater slope) between the mineral and collagen phases in both tension and compression (0.64 and 0,65, respectively), suggesting that in the absence of water, mineral crystals and collagen fibrils deform in a more concerted manner (Fig. 4), irrespective of loading modes. Upon hydration, the bone specimens showed a much less strain ratio (0.32) between the mineral and collagen phases in tension than that (0.57) in compression.
Fig. 4.
Strain in the mineral phase plotted against the collagen fibril strain in tension (A) and compression (B). Slope obtained by a linear fit quantifies the degree of cooperation between the mineral and collagen fibril deformation. In compression, no considerable changes in cooperation between the mineral and collagen deformation was observed between dry (0.65) and wet (0.57) specimens in compression. However, in tension the degree of deformation cooperation remarkably decreased (0.32) under wet condition, whereas the degree of cooperation between the mineral and collagen deformation was comparable with that in compression (0.64) if bone is dehydrated.
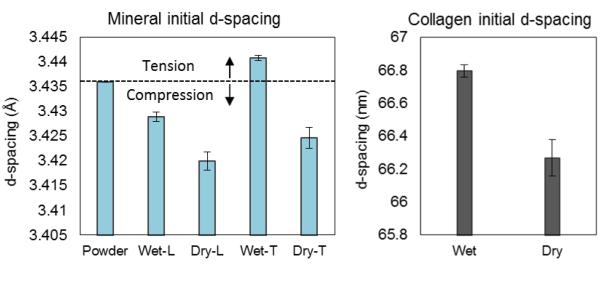
Changes in pre-strain status
In order to estimate the pre-strain status in the mineral phase, the d-spacing of 002 planes in the mineral phase under the pre-strain free condition was determined using a deproteinized, dehydrated and powdered bone sample. Compared to the reference d-spacing, wet specimens demonstrated a reduction in d-spacing of 002 planes in the longitudinal direction, while an increase in the transverse plane, indicating that the mineral crystals were compressively pre-strained along the longitudinal axis of bone (Fig. 5). However, dry specimens exhibited a different pre-strain condition in the mineral phase, in which the 002 planes were under compression in both longitudinal and transverse directions, with the d-spacing in the longitudinal direction being slightly smaller than in the transverse direction. In addition, the collagen phase was also considerably contracted under dry condition (Fig. 5B).
Fig. 5.
Initial d-spacing of specimens in the unloaded state: The d-spacing value of bone powder represented the d-spacing of bone crystals without any pre-straining. The contraction of d-spacing in longitudinal and the extension in transverse direction of wet specimens indicated compressive pre-straining in the mineral phase along the longitudinal direction of bone. Dry specimens exhibited contraction in the mineral phase in both transverse and longitudinal directions, indicating a biaxial shrinkage in the matrix surrounding the mineral crystals. Collagen fibrils also exhibited shrinkage in the longitudinal direction by dehydration.
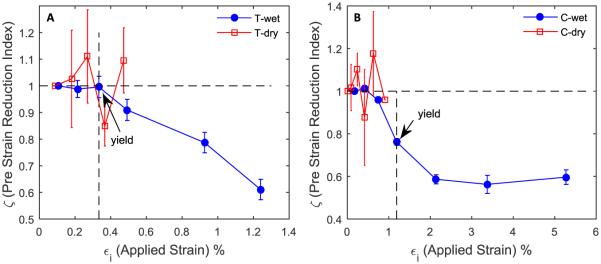
Moreover, the pre-strain reduction index (ζ) continuously decreased with applied bulk strain for wet bone specimens in both tension and compression (Fig. 6), indicating a progressively decreasing pre-strain after yielding in both loading modes. In contrast, very limited pre-strain reduction was observed in dehydrated bone specimens in both loading modes. In addition, the pre-strain reduction saturated under compression with increasing applied strain. These observations suggest that the hydration status of bone matrix is pertinent to the pre-strain in the tissue induced by the surrounding constraints to the mineral crystals and the pre-strain may vary with increasing deformation of bulk tissues.
Fig. 6.
Pre-strain reduction in wet vs. dry bone in tension (A) and in compression (B): Pre-strain reduction index (ζ) varies from one to zero, one indicating the original pre-strained state of the mineral phase and zero indicating a complete removal of pre-strain. Dry specimens exhibited no reduction in pre-strain, whereas wet specimens showed significant reduction in pre-strain. In compression, the pre-strain reduction index saturated at bulk strains higher than 2%.
Viscoelastic relaxation of mineral crystals
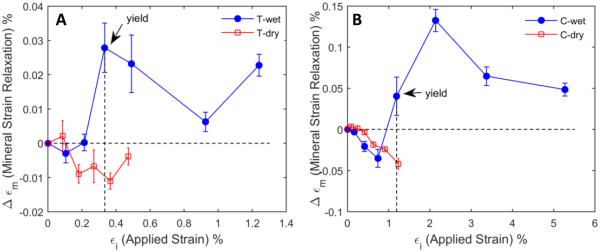
The time-dependent relaxation in the mineral strain was greatly influenced by the hydration state of the specimen, showing that such viscoelastic strain relaxation occurred immediately after yielding on wet bone specimens, irrespective of the loading modes, whereas such strain relaxation was very limited in dry bone specimens (Fig. 7). In addition, the time dependent changes in the mineral strain were most significant at yielding but soon saturated.
Fig. 7.
Viscous strain relaxation in the mineral phase (Δεm) vs. bulk strain (εi) during the dwelling period of each loading cycle for wet and dry specimens in tension (A) and compression (B): The mineral strain relaxation is the magnitude of strain difference between the mineral strain at the onset of dwelling for bulk stress relaxation and the mineral strain at the end of dwelling. Dry specimens did not show considerable viscous strain relaxation, whereas wet specimens exhibited significant viscous strain relaxation after yielding in both loading modes.
DISCUSSIONS
It has been well known that the toughness of bone is considerably influenced by its hydration state, with the absence of water making bone behave in a brittle manner (Nyman, et al., 2006, Samuel, et al., 2014). Among the three forms of water in bone, removal of bound water was shown to have a dominant effect on bone toughness and strength (Nyman, et al., 2008, Wilson, et al., 2006). A recent study reveals that water molecules in very small gap regions (<4Å in size) impose the greatest influence on bone toughness (Samuel, et al., 2014), thus suggesting that the effect of hydration status on bone toughness is most likely originated from the ultrastructural level. However, little is known about how water interacts with bone constituents at the ultrastructural level and how those interactions would consequently influence the bulk mechanical properties of bulk bone tissues. This study provides direct experimental evidence that water dictates the post-yield deformation of bone by influencing the nanomechanics of bone at ultrastructural levels.
First, this study indicates that the influence of hydration status on the ultrastructural mechanical behavior of bone is loading-mode dependent. In compression, the mineral and collagen strains and stresses in wet bone exhibit a continuous decrease after yielding, which underlies the strain softening behavior observed at the bulk tissue level (Fig. 2B, 2D, 2F). Different from compression, the load bearing by the mineral and collagen phases in tension is no longer linearly proportional to the bulk load applied to bone (Fig. 2A, C, & E), exhibiting a partial decrease in load bearing immediately after yielding followed by an increase in load bearing (Fig. 3). Upon removal of water, however, the ultrastructural strain and stress in both mineral and collagen phases become linearly proportional to those of bulk tissue irrespective of loading modes. Taken together, the above results suggest that: (1) The bulk mechanical behavior of bone is coincident with the ultrastructural mechanical behavior of the mineral and collagen phases; (2) the ultrastructural mechanical behavior is significantly affected by the hydration status; (3) the underlying mechanics that dictate the effect of water on the ultrastructural mechanical behavior of bone is loading–mode dependent; and (4) water appears to play a significant role in reducing the load bearing by individual bone constituents (i.e. mineral crystals and collagen fibrils).
Another interesting observation of this study is that the ultrastructural deformation of the mineral and collagen phases of wet bone does not fully conform to the bulk deformation in tension (Fig. 2A, 2C, & 2E, Fig. 3A & 3C). The decrease in both mineral and collagen strains observed in this study after yield and a recovery/increase at higher applied strains does not exactly match with the continuous strain hardening behavior at the bulk level of bone. This could be an indicator of failure in the primary load bearing phase and the subsequent transfer of externally applied load to a secondary load bearing component in bone, as often seen in engineering composite materials. Since the fundamental building block of human bone is lamellae, which is actually a composite material of mineralized collagen fibrils embedded in an extrafibrillar matrix (Gupta, et al., 2013, Nair, et al., 2014, Nikel, et al., 2013), it is possible that the load transfer may occur between the two ultrastructural compartments of bone. Since this is out of the scope of our study, we leave this interesting topic for future investigations.
As to the relationship in deformation between the mineral and collagen phases in bone, the mineral strain always maintains a linear relationship with the collagen strain irrespective of the loading modes and hydration conditions, thus indicating a consistent conformation in the ultrastructural deformation between the mineral and collagen phases, even though the strain ratio (i.e. the slope of curves) varies with different hydration conditions. For instance, hydration lessens the mineral to fibril strain ratio (i.e. reduced slopes) mainly in tension (Fig. 4). In contrast, such differences diminish by dehydration in both tension and compression loading modes (0.64 vs. 0.69). These results suggest that a relative sliding between the mineral and collagen phases may occur in tension in the presence of water.
Next, it is interesting to note that in the post yield deformation the ultrastructural deformation of the mineral and collagen phases are less than and not linearly proportional to the bulk deformation (strain) of bone (Fig. 2). Thus, additional mechanisms at the ultrastructural level become necessary to accommodate the mismatch in deformation between the ultrastructural and bulk levels. It is well known that there exists a large mismatch in stiffness between the mineral and collagen phases (i.e. elastic modulus of hydroxyapatite crystals~150GPa vs. elastic modulus of collagen fibrils~ 1-5GPa). From a composite mechanics perspective, such huge mismatch in stiffness would necessitate a shear-dominated load transfer through the interface between the two phases in order to balance the local differences in the mineral and collagen strains. When external load exceeds the capacity of the interface to transfer the load, failure would occur along the interfaces, causing permanent damage (inelastic deformation) to the tissue. Presumably, either intrafibrillar sliding between the mineral crystals and collagen molecules (Nair, et al., 2014) or intergranular sliding in the extrafibrillar matrix (Tai, et al., 2006) may contribute to the inelastic deformation of bone at bulk levels.
This study also provided some intriguing evidence that may give some insights into the underlying mechanism of the ultrastructural origins of bulk post-yield behavior of bone. As shown in Figs. 6 & 7, changes in the pre-strain and time-dependent strain relaxation in the mineral phase were coincident with bulk yielding of bone. Since these measurements, to a large extent, represent changes in the local environment around the mineral phase, useful information may be obtained from the results to decipher the underlying mechanism of yielding and post-yield behavior of bone at ultrastructural levels.
In hydrated condition, the mineral phase in bone is subjected to an approximately uniaxial pre-strain, which is compressive along the longitudinal axis while tensile along the transverse directions (Fig. 5). Upon yielding, the pre-strain in the mineral phase begins to relax with increasing applied strain in both tensile and compressive loading modes (Fig. 6). Speculated by other researchers, the pre-strain in mineral phase may be originated due to functional adaptations under load during bone remodeling or due to non-uniformities in the mechanical environment around the mineral crystals (Tadano and Yamada, 2014). Thus, the initial pre-strain in the mineral crystals is most likely imposed through the matrix surrounding the crystals. It could be logically inferred that any damage to the surrounding matrix that causes a reduced confinement of the mineral phase would result in a reduction in pre-strain. Removal of water from bone matrix results in a hydrostatically compressive pre-strain to the mineral phase. A recent study reported dehydration induced longitudinal compression in both mineral and collagen phases (Bertinetti et al., 2015), which is consistent with the results from this study. No appreciable reduction in pre-strain is observed until bone failure in dehydrated specimens (Figs. 5 & 6). It is not surprising because dehydrated bone fails at very small strain levels even before any pre-strain reduction could be induced.
The time-dependent relaxation of mineral strain in wet bone has been reported in the previous studies (Dong, et al., 2011). The results of this study indicate that such a time-dependent relaxation occurs only in hydrated condition and after bone yields (Fig. 7). More interestingly, collagen fibrils in bone do not exhibit such strain relaxation response irrespective of loading modes and hydration status. Considering that the mineral crystals themselves are not expected to deform viscoelastically, the viscous response of the mineral phase must be originated from the interaction between the mineral crystals and the surrounding matrix. Although the underlying mechanism is still unclear, two possible scenarios may be considered. First, the viscous strain relaxation in mineral crystals may be induced through the interface between mineral crystals and collagen molecules in mineralized collagen fibrils of bone (Gupta, et al., 2013). Second, the organic interface between the mineral crystals in the extrafibrillar matrix of bone (Lai, et al., 2014, Nair, et al., 2014) may be viscous in nature, thus causing the mineral phase to respond with viscoelastic behavior. In either case, the presence of water in bone matrix is indispensable for sustaining the viscous behavior of bone.
The above key findings indicate that although water mediates the stress/strain transfer between bone constituents, the deformation characteristics of bone constituents under tension and compression are different. Such differences can be hardly explained using the current shear dominated strain transfer models (Gupta, et al., 2013), which are often used in mechanics of composite materials. Thus, it is necessary to have a more comprehensive model to capture the ultrastructural deformation of bone constituents under different loading modes.
There are some limitations in this study. First, the bulk properties of bone were measured using a progressive loading scheme. Thus, these measured properties may be different from those obtained from conventional monotonic loading tests since the measurements in the progressive loading test do not reflect viscous and damage-induced effects that can be caught in monotonic loading tests. Second, the internal stress of the mineral and collagen phases was estimated using very simple elastic models. Also, the elastic modulus value used for mineral phase (150GPa) was that of pure hydroxyapatite whereas the mineral in bone is highly carbonated apatite (100-120GPa). Thus, these stress data could be used only for the purpose of qualitative comparisons. Third, due to the loss of specimens during the experiments the sample size is slightly smaller in tension groups (n=5) than in compression groups (n=6). Fourth, we have not considered the effects of fluid flow mechanisms of poroelasticity, which is relevant to the bulk mechanical behavior of bone (Cowin, 1999). Finally, the dehydration treatment can only remove mobile and bound water, while leaving the structural water intact in bone. Thus, this study focuses only on the combined effect of mobile and bound water in bone.
CONCLUSIONS
The results of this study indicate that water plays a critical role in altering the ultrastructural mechanical behavior of bone, which is coincident with the bulk mechanical behavior of bone. The water-mediated changes in the ultrastructural behavior of bone include: (1) reduction in the mineral and collagen strains after yielding; (2) reduction in the mineral-collagen strain ratio; (3) reduction in pre-strain of the mineral phase; and (4) induction of viscous response to the mineral phase. In addition, the effect of water on the ultrastructural behavior of bone is loading-mode dependent, corresponding to the strain hardening behavior in tension and strain softening behavior in compression at the bulk tissue level. Taken together, it is postulated that water may alter the properties of the matrix surrounding the mineral crystals in bone, thus leading to changes in mechanical behavior of bone at the ultrastructural levels.
ACKNOWLEDGEMENTS
Research reported in this publication was partially supported by the National Institute of Arthritis and Musculoskeletal and Skin Diseases of the National Institutes of Health (NIAMS/NIH) under Award Number AR055955 and a NSF grant (CMMI-1266390). The content is solely the responsibility of the authors and does not necessarily represent the official views of NIH and NSF. Use of the Advanced Photon Source is supported by the U.S. Department of Energy, Office of Science, under the U.S. Department of Energy contract DE-AC02-06CH11357.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Almer JD, Stock SR. Internal strains and stresses measured in cortical bone via high-energy X-ray diffraction. Journal of Structural Biology. 2005;1:14–27. doi: 10.1016/j.jsb.2005.08.003. [DOI] [PubMed] [Google Scholar]
- Arthur Moore TL, Gibson LJ. Microdamage accumulation in bovine trabecular bone in uniaxial compression. J Biomech Eng. 2002;1:63–71. doi: 10.1115/1.1428745. [DOI] [PubMed] [Google Scholar]
- Broz JJ, Simske SJ, Greenberg AR, Luttges MW. Effects of rehydration state on the flexural properties of whole mouse long bones. Journal of biomechanical engineering. 1993;4A:447–449. doi: 10.1115/1.2895510. [DOI] [PubMed] [Google Scholar]
- Bertinetti L, Masic A, Schuetz R, Barbetta A, Seidt B, Wagermaier W, Fratzl P. Osmotically driven tensile stress in collagen-based mineralized tissues. Journal of the Mechanical Behavior of Biomedical Materials. 2015;52:14–21. doi: 10.1016/j.jmbbm.2015.03.010. [DOI] [PubMed] [Google Scholar]
- Burr DB. Bone material properties and mineral matrix contributions to fracture risk or age in women and men. Journal of musculoskeletal & neuronal interactions. 2002;3:201–204. [PubMed] [Google Scholar]
- Cowin SC. Bone poroelasticity. Journal of Biomechanics. 1999;32(3):217–238. doi: 10.1016/s0021-9290(98)00161-4. [DOI] [PubMed] [Google Scholar]
- Currey JD. Effects of differences in mineralization on the mechanical properties of bone. Philosophical transactions of the Royal Society of London Series B, Biological sciences. 1984;1121:509–518. doi: 10.1098/rstb.1984.0042. [DOI] [PubMed] [Google Scholar]
- Dong XN, Almer JD, Wang X. Post-yield nanomechanics of human cortical bone in compression using synchrotron X-ray scattering techniques. Journal of biomechanics. 2011;4:676–682. doi: 10.1016/j.jbiomech.2010.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fantner GE, Hassenkam T, Kindt JH, Weaver JC, Birkedal H, Pechenik L, Cutroni JA, Cidade GAG, Stucky GD, Morse DE, Hansma PK. Sacrificial bonds and hidden length dissipate energy as mineralized fibrils separate during bone fracture. Nature materials. 2005;8:612–616. doi: 10.1038/nmat1428. [DOI] [PubMed] [Google Scholar]
- Fazzalari NL, Forwood MR, Manthey BA, Smith K, Kolesik P. Three-dimensional confocal images of microdamage in cancellous bone. Bone. 1998;4:373–378. doi: 10.1016/s8756-3282(98)00111-2. [DOI] [PubMed] [Google Scholar]
- Gupta HS, Krauss S, Kerschnitzki M, Karunaratne A, Dunlop JWC, Barber AH, Boesecke P, Funari SS, Fratzl P. Intrafibrillar plasticity through mineral/collagen sliding is the dominant mechanism for the extreme toughness of antler bone. Journal of the mechanical behavior of biomedical materials. 2013:366–382. doi: 10.1016/j.jmbbm.2013.03.020. [DOI] [PubMed] [Google Scholar]
- Gupta HS, Seto J, Wagermaier W, Zaslansky P, Boesecke P, Fratzl P. Cooperative deformation of mineral and collagen in bone at the nanoscale. Proceedings of the National Academy of Sciences of the United States of America. 2006;47:17741–17746. doi: 10.1073/pnas.0604237103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hambli R, Barkaoui A. Physically based 3D finite element model of a single mineralized collagen microfibril. Journal of Theoretical Biology. 2012:28–41. doi: 10.1016/j.jtbi.2012.02.007. [DOI] [PubMed] [Google Scholar]
- Hoo RP, Fratzl P, Daniels JE, Dunlop JWC, Honkimaki V, Hoffman M. Cooperation of length scales and orientations in the deformation of bovine bone. Acta Biomaterialia. 2011;7:2943–2951. doi: 10.1016/j.actbio.2011.02.017. [DOI] [PubMed] [Google Scholar]
- Horch RA, Gochberg DF, Nyman JS, Does MD. Clinically compatible MRI strategies for discriminating bound and pore water in cortical bone. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2012;6:1774–1784. doi: 10.1002/mrm.24186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai ZB, Wang M, Yan C, Oloyede A. Molecular dynamics simulation of mechanical behavior of osteopontin-hydroxyapatite interfaces. Journal of the mechanical behavior of biomedical materials. 2014:12–20. doi: 10.1016/j.jmbbm.2014.04.002. [DOI] [PubMed] [Google Scholar]
- LeGeros RZ, Bonel G, Legros R. Types of “H2O” in human enamel and in precipitated apatites. Calcified Tissue Research. 1978;26(2):111–118. doi: 10.1007/BF02013245. [DOI] [PubMed] [Google Scholar]
- Luo Q, Nakade R, Dong X, Rong Q, Wang X. Effect of mineral-collagen interfacial behavior on the microdamage progression in bone using a probabilistic cohesive finite element model. Journal of the mechanical behavior of biomedical materials. 2011;7:943–952. doi: 10.1016/j.jmbbm.2011.02.003. [DOI] [PubMed] [Google Scholar]
- Nair AK, Gautieri A, Buehler MJ. Role of intrafibrillar collagen mineralization in defining the compressive properties of nascent bone. Biomacromolecules. 2014;7:2494–2500. doi: 10.1021/bm5003416. [DOI] [PubMed] [Google Scholar]
- Nalla RK, Kruzic JJ, Ritchie RO. On the origin of the toughness of mineralized tissue: microcracking or crack bridging? Bone. 2004;5:790–798. doi: 10.1016/j.bone.2004.02.001. [DOI] [PubMed] [Google Scholar]
- Nikel O, Laurencin D, McCallum SA, Gundberg CM, Vashishth D. NMR investigation of the role of osteocalcin and osteopontin at the organic-inorganic interface in bone. Langmuir : the ACS journal of surfaces and colloids. 2013;45:13873–13882. doi: 10.1021/la403203w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nyman JS, Ni Q, Nicolella DP, Wang X. Measurements of mobile and bound water by nuclear magnetic resonance correlate with mechanical properties of bone. Bone. 2008;1:193–199. doi: 10.1016/j.bone.2007.09.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nyman JS, Roy A, Shen X, Acuna RL, Tyler JH, Wang X. The influence of water removal on the strength and toughness of cortical bone. Journal of biomechanics. 2006;5:931–938. doi: 10.1016/j.jbiomech.2005.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poundarik AA, Diab T, Sroga GE, Ural A, Boskey AL, Gundberg CM, Vashishth D. Dilatational band formation in bone. Proceedings of the National Academy of Sciences of the United States of America. 2012;47:19178–19183. doi: 10.1073/pnas.1201513109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prostak KS, Lees S. Visualization of crystal-matrix structure. In situ demineralization of mineralized turkey leg tendon and bone. Calcified tissue international. 1996;6:474–479. doi: 10.1007/BF00369213. [DOI] [PubMed] [Google Scholar]
- Reilly GC, Currey JD. The effects of damage and microcracking on the impact strength of bone. J Biomech. 2000;3:337–343. doi: 10.1016/s0021-9290(99)00167-0. [DOI] [PubMed] [Google Scholar]
- Samuel J, Sinha D, Zhao JC-G, Wang X. Water residing in small ultrastructural spaces plays a critical role in the mechanical behavior of bone. Bone. 2014:199–206. doi: 10.1016/j.bone.2013.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegmund T, Allen MR, Burr DB. Failure of mineralized collagen fibrils: modeling the role of collagen cross-linking. Journal of biomechanics. 2008;7:1427–1435. doi: 10.1016/j.jbiomech.2008.02.017. [DOI] [PubMed] [Google Scholar]
- Singhal A, Deymier-Black AC, Almer JD, Dunand DC. Effect of high-energy X-ray doses on bone elastic properties and residual strains. Journal of the Mechanical Behavior of Biomedical Materials. 2011;4(8):1774–1786. doi: 10.1016/j.jmbbm.2011.05.035. [DOI] [PubMed] [Google Scholar]
- Tai K, Ulm F-J, Ortiz C. Nanogranular origins of the strength of bone. Nano letters. 2006;11:2520–2525. doi: 10.1021/nl061877k. [DOI] [PubMed] [Google Scholar]
- Tadano S, Yamada S. Residual Stress and Structural Anisotropy of Cortical Bone. Mechanics of Biological Systems and Materials. 2014;4:117–122. [Google Scholar]
- Thompson JB, Kindt JH, Drake B, Hansma HG, Morse DE, Hansma PK. Bone indentation recovery time correlates with bond reforming time. Nature. 2001;6865:773–776. doi: 10.1038/414773a. [DOI] [PubMed] [Google Scholar]
- Wang X, Bank RA, TeKoppele JM, Agrawal CM. The role of collagen in determining bone mechanical properties. J Orthop Res. 2001;6:1021–1026. doi: 10.1016/S0736-0266(01)00047-X. [DOI] [PubMed] [Google Scholar]
- Wang X, Nyman JS. A novel approach to assess post-yield energy dissipation of bone in tension. Journal of biomechanics. 2007;3:674–677. doi: 10.1016/j.jbiomech.2006.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson EE, Awonusi A, Morris MD, Kohn DH, Tecklenburg MM, Beck LW. Three structural roles for water in bone observed by solid-state NMR. Biophys J. 2006;10:3722–3731. doi: 10.1529/biophysj.105.070243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson EE, Awonusi A, Morris MD, Kohn DH, Tecklenburg MMJ, Beck LW. Three structural roles for water in bone observed by solid-state NMR. Biophysical journal. 2006;10:3722–3731. doi: 10.1529/biophysj.105.070243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmermann EA, Schaible E, Bale H, Barth HD, Tang SY, Reichert P, Busse B, Alliston T, Ager JW, 3rd, Ritchie RO. Age-related changes in the plasticity and toughness of human cortical bone at multiple length scales. Proceedings of the National Academy of Sciences of the United States of America. 2011;35:14416–14421. doi: 10.1073/pnas.1107966108. [DOI] [PMC free article] [PubMed] [Google Scholar]