Abstract
As the indispensable role of natural microbial communities in many aspects of life on Earth is uncovered, the bottom-up engineering of synthetic microbial consortia with novel functions is becoming an attractive alternative to engineering single-species systems. Here, we summarize recent work on synthetic microbial communities with a particular emphasis on open challenges and opportunities in environmental sustainability and human health. We next provide a critical overview of mathematical approaches, ranging from phenomenological to mechanistic, which can be used to decipher the principles that govern the function, dynamics and evolution of microbial ecosystems. Finally, we present our outlook on key aspects of microbial ecosystems and synthetic ecology that require further developments, including the need for more efficient algorithms and a better integration of empirical methods and model-driven analysis, the importance of improving gene function annotation, and the value of a standardized library of well-characterized organisms to be used as building blocks of synthetic communities.
Keywords: Microbial communities, Synthetic Biology, Systems Biology, Metabolic network modeling, Metabolic engineering
Graphical Abstract
Introduction
Synthetic ecology of microbes is concerned with the design, construction and understanding of engineered microbial consortia 1. It is a young, fast-developing research area, clearly distinct from synthetic biology, though related to it in a number of ways. Why would one want to engineer new microbial communities? How would engineered communities differ from natural ones? And how could one hope to design a community with desired properties, other than by tinkering with their intracellular circuits, or by mixing different species, based on experience and intuition? Here, we delve into these questions by discussing several examples of prior work in this area, and by presenting an overview of the growing landscape of mathematical approaches aimed at understanding the function, dynamics and evolution of microbial ecosystems, and at enabling the rational design of new microbial consortia.
The idea of designing microbial consortia is inspired by the ubiquitous presence of microbial communities on our planet, and the key role that these communities play in many aspects of human life. Microbial communities are implicated in biogeochemical cycles 2 and human health 3, and have been enlisted for a wide array of biotechnological applications, ranging from the ancient arts of brewing and cheese-making 4 to recent efforts towards the overproduction of biofuels and chemicals 5; 6 and wastewater treatment 7; 8. Engineering novel microbial communities may involve inducing the coexistence of unusual combinations of wild-type organisms, or constructing ecosystems of genetically modified species, thus creating a continuum of possible strategies between synthetic biology and ecology.
One of the appeals of synthetic ecology is that it may enable us to perform novel tasks by understanding and embracing – rather than avoiding - properties that are inherent in the natural microbial world, such as diversity, competition for resources, division of labor and obligate interdependence. A community of organisms may perform tasks that no individual species could possibly perform on its own (i.e., from a functional perspective, a community is more than the simple sum of its parts 9). Moreover, relative to monocultures, engineered communities may achieve increased stability and resilience 10. The emergence of community-level properties is a result of interactions among different species. Inter-species interactions are one of the primary factors shaping the structure, function and dynamics of microbial communities and are believed to play a key role in the emergence of biodiversity 11; 12. Interactions among species can be mediated by a complex web of diffusible chemical signaling molecules and/or metabolites 13; 14; 15 or by direct contact with neighboring microorganisms 16; 17; 18. These interactions can be obligatory or non-obligatory, beneficial or deleterious.
Beneficial interactions often involve cases where one or more species feed on products of other community members 19; 20; 21. In obligatory cooperative (i.e., syntrophic) interactions, individual species cannot survive in absence of their partners. For example, in a cross-feeding interaction, both species could secrete nutrients essential for the growth of their partner 22; 23; 24. Alternatively, one species could rely on the waste product of the other while maintaining a favorable thermodynamic condition in return 25; 26; 27; 28. For example, in the absence of a suitable electron acceptor, methanogens can provide thermodynamically favorable growth condition for sulfate-reducing bacteria by scavenging hydrogen in the environment while using the fermentation by-products (e.g., acetate, formate) produced by sulfate-reducers 27; 28. Whether obligatory beneficial interactions are abundant in natural communities is still an open question, potentially relevant for understanding unculturability of the vast majority of microorganisms in the laboratory in monocultures 29. A common hypothesis is that unculturability of many species is due to their dependence on other microbial species for nutrients or growth factors 30.
Negative interactions are ubiquitous in nature. In addition to the competition for the same limiting resource, these interactions include growth inhibition effects of signaling molecules like bacteriocins, and active killing through a wide range of antibiotic mechanisms 31; 32; 33. Moreover, community dynamics can be heavily affected by parasitic interactions (e.g., between bacteria and their bacteriophage) 34; 35 where the parasite benefits while the host is negatively affected.
A broad spectrum of applications have driven the desire to build new communities, ranging from the conceptual challenge of characterizing small synthetic systems as a gateway towards understanding the more complex natural ones to the interest in achieving a specific biotechnological task (e.g., treatment of human diseases, overproduction of biochemicals and bioremediation of contaminated environments). Here, we first review some examples of such efforts and next focus on how mathematical modeling can complement these empirical efforts to better understand ecological principles underpinning the function and dynamics of microbial communities. We also present an overview of the existing challenges and future perspectives in synthetic ecology with a particular focus on the role of mathematical modeling.
Using synthetic ecology to understand natural microbial communities
Natural microbial communities often contain tens to thousands of microbial species 36. This makes it challenging to experimentally characterize the identity of community members, their function and interactions. A bottom-up approach to address these limitations is to design synthetic microbial consortia that could serve as simplified models of their natural counterparts, while affording enhanced tractability and controllability. These synthetic systems would allow one to explore a number of key ecological and evolutionary questions such as the impact of interactions and environmental factors on the emergence, evolution and maintenance of coexistence. Synthetic microbial consortia can be established by co-culturing wild-type species in a growth medium similar to their natural habitat, or they can be constructed by using targeted genetic perturbations or design of environmental conditions that induce new interspecies interactions (e.g., through metabolic exchange, antibiotic secretion, or quorum sensing) (see Fig. 1). Here, we review some examples of such efforts.
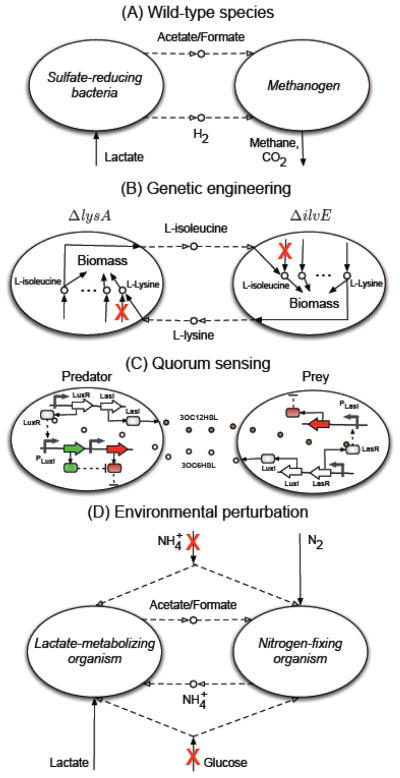
Fig. 1.
Examples of various mechanisms for establishing a synthetic microbial community. Dashed and solid arrows in (A), (B) and (D) denote interspecies metabolite exchanges and the measurable uptake/export of metabolites by community, respectively. (A) Co-culturing wild-type species under conditions resembling naturally occurring environments. An example is the association between sulfate-reducing bacteria and methanogens. Here a sulfate-reducing bacterium utilizes lactate as the sole carbon source and produces acetate/formate, which is used by a methanogen that is incapable of using lactate. The methanogen bacteria scavenge hydrogen in return thereby providing a thermodynamically favorable condition for the growth of sulfate-reducing bacteria 25; 28. (B) Using genetically engineered species to induce metabolite exchanges. An example is the association between two (or more) mutant strains where each strain relies on its partner for the essential amino acid it cannot produce on its own 22; 23. (C) Using synthetic genetic circuits to induce interactions through quorum sensing. Generally, each species may produce a signaling molecule that activates or represses the transcription of one (or more) gene(s) in another species. The example shown here is a predator-prey system 48, where empty and filled circles represent signaling molecules 3OC6HSL and 3OC12HSL (synthesized by LuxI and LasI), respectively, solid arrow denote protein production, dashed arrows represent activation and inhibition/killing. At low density of the prey, the predators die due to the constitutive expression of a killer protein (shown by red). At high concentration of the prey, 3OC6HSL activates LuxR in predators, which in turn induces the expression of antidote gene (shown by green) thereby rescuing the predators. At the same time, 3OC12HSL (produced by predators) activates LasR in preys, which induces the expression of a killer protein. (D) Using environmental perturbations. Here, we show a hypothetical example, where each microorganism can grow on its own in the presence of glucose and ammonium. However, in the absence of these two compounds they rely on each other for the carbon and nitrogen source as only one can fix nitrogen and only one can metabolize lactate. The potential for such interactions between Desulfovibrio vulgaris and Methanococcus maripaludis has been reported using computational modeling 56.
Artificial consortia with wild-type species grown in a medium resembling their natural habitat have been established to gain a deeper understanding of the community properties. An example is co-culturing methanogens and sulfate-reducing bacteria to better understand methane production and mutualistic interactions in subsurface anaerobic environments as noted earlier 25; 27; 28. They have been also used to elucidate the biodiversity-function and biodiversity-stability relationships in natural microbial communities 37; 38; 39; 40. For example, Von Canstein et al 37 found that increasing the diversity of microbial species in a biofilm improves the mercury removal efficiency in a changing environment. Assessing the stability of synthetic bacterial communities of different diversities (ranging from one to 12 members) showed that the biomass of more diverse communities are stabilized against (i.e., less affected by) abiotic perturbations such as addition of heavy metals, NaCl and warming 40. While the majority of studies focused on the impact of richness (the number of species), Wittebolle et al 41 examined the impact of initial community evenness (relative abundance of species) using eighteen different denitrifying bacterial species from four different phyla and microbial microcosms. This study demonstrated that the initial evenness is a key determinant of the functional stability of the community.
For cases where establishing a consortium is not possible with wild-type species, a common strategy is to implement defined genetic perturbations, which can create new inter-species interactions through metabolite exchange or antibiotic production 22; 23; 42; 43; 44; 45; 46; 47. For example, by using 14 knockout strains of Escherichia coli, each lacking a gene responsible for the production of an essential amino acid, Mee et al 23 constructed communities of increased complexity (from two- to 14-member) in order to assess the impact of synthetic cross-talk between the mutants on population dynamics and stability (see Fig. 1B). In another study, Harcombe 43 used a synthetic two-species system composed of Salmonella enterica and an Escherichia coli mutant unable to synthesize an essential amino acid to elucidate the mechanisms and evolutionary origins of cooperation between unrelated species. This study concluded that cooperation can evolve under two conditions, namely the presence of a preexisting reciprocation mechanism and the preferential availability of reciprocation to cooperative phenotypes.
Using synthetic genetic circuits to induce new interactions through quorum sensing has been also widely used to establish synthetic microbial communities 48; 49; 50; 51; 52; 53; 54. For example, in order to assess experimentally the relation between the parameters of Hamilton’s rule (a mathematical model for the emergence and maintenance of cooperation 55) and the quantities that govern the behavior of a microbial ecosystem, Chuang et al 50 engineered two producer and non-producer populations of E. coli, where producers synthesize the growth-enhancing Rhl autoinducer molecule as the common good. This autoinducer activates the expression of an antibiotic resistance gene in both producers and non-producers. This study showed that the nonlinearity of the growth benefit as a function of the common good tends to limit the predictive accuracy of the Hamilton’s rule 50. In another study, a population-driven synthetic quorum sensing switch was engineered to enable the dispersal of a second cell type into an existing colonizer biofilm, the subsequent formation of a robust two-species biofilm and finally the displacement of the initial colonizers 53. Rather than using genetic circuits that modulate gene expression in independent cells through quorum sensing, Chen et al 54 recently took a different strategy by constructing a dual feedback oscillator genetic circuit distributed across two nonisogenic populations of E. coli. The consortium consists of an “activator” and a “repressor” E. coli strain, each implementing half of a dual-relaxation oscillator and communicating through two orthogonal signaling molecules. Emergent population-level oscillations were observed only when the two organisms are cultured together 54.
In addition to genetic perturbations, it is known that appropriate design of environmental conditions can induce or significantly alter the dynamics and stability of microbial interactions 56; 57; 58. For example, by using a microfluidic device controlling the spatial structure and chemical communication Kim et al 59 reported the realization of a stable syntrophic consortium of three different species of wild-type soil bacteria, where each species performs a unique function essential for the survival of the entire community. In another study, Zuroff et al 57 showed that by fine tuning the oxygen transport rate a stabilized mutualism between the obligate anaerobic Clostridium phytofermentans and yeast can be established in which yeast protects C. phytofermentans from oxygen inhibition in return for soluble carbohydrates released from the degradation of lignocellulosic material. Another study reported on the impact of antibiotic levels as a key environmental factor in shaping a wide range of synthetic interactions including extinction, mutualism and commensalism between two E. coli populations 58.
Applications of synthetic ecology in biomedicine, metabolic engineering and environmental sciences
The construction of synthetic microbial communities has been pursued for a number of practical applications including human health, the production of chemicals, bioenergy, foods and drugs, and the mitigation of harmful human-induced environmental damage. These efforts have been so far mostly driven by experience and intuition, and by knowledge of the metabolic capabilities and environmental interactions of different organisms. In the following, we briefly review some of these application areas.
Human health and disease
Microbial communities that live on or within our body have a marked, though still poorly understood, effect on the physiology and health of the human host and seem to reliably perform crucial tasks for us. For example, the human gut microbiota enable the breakdown of otherwise indigestible polysaccharides and are essential for the development and homeostasis of the immune system in the gut and for resistance against pathogenic bacteria 60; 61. Specific shifts in taxonomic composition (states of “dysbiosis”) of the human microbiota are known to be associated with an increasing number of diseases 3. Previous studies have reported strong associations between the composition of the gut microbiota and several complex diseases such as obesity and atherosclerosis, diabetes and inflammatory bowel disease 62; 63; 64; 65; 66; 67. On the other hand, diet, environment and age are also known to influence the composition and structure of the gut microbiota 64; 68; 69. Similarly to the gut, the oral cavity is the home for one of the most complex microbial communities in the human body, forming highly structured biofilms in the form of dental plaques 70; 71. These communities are responsible for two major categories of diseases including dental caries (tooth decay) and periodontitis (inflammatory and infectious gum disease) 9; 72; 73; 74.
While there is a flourishing industry proposing ways to enhance the health-promoting effects of certain human-associated microbes, the systematic validated use of synthetic microbial communities to cure disease is still at the very early stages of investigation, with a recognized large potential impact 75. For example, the recent advent of gut-on-a-chip technology 76 lays the foundation to construct such synthetic communities in order to facilitate the study of intestinal physiology, digestive diseases and drug development. Another area where synthetic ecology can contribute is constructing synthetic microbial consortia helping to shift an imbalanced microbiota in the human body to the healthy state. A classical example is treating Clostridium difficile infection by using fecal microbiota transplant, where fecal bacteria from a healthy individual are transplanted into a recipient with C. difficile infection. This method has been reported to be more effective than using antibiotics (see 77 for a review). An alternative to using natural communities from healthy individuals could be to design efficient synthetic consortia for the targeted treatment of a wide of range of other microbiota-associated diseases.
Consortia-based cell factories
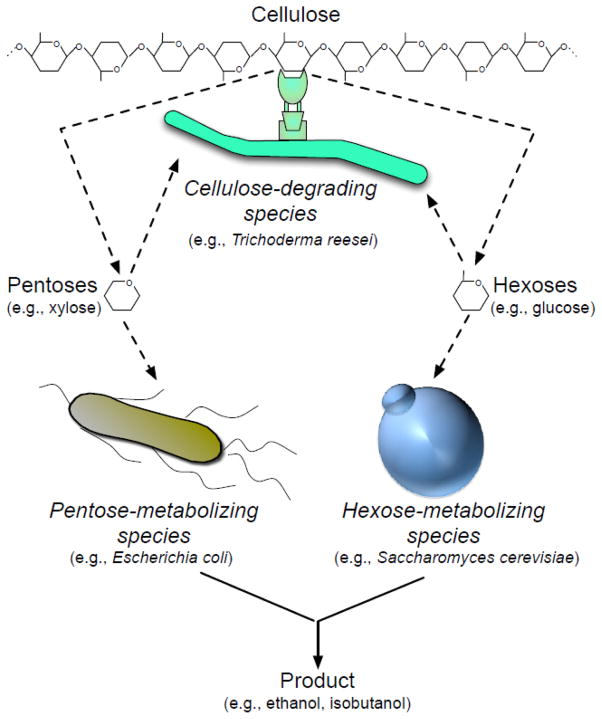
Recent advances in synthetic biology have allowed researchers to engineer single-species microbial cell factories for the enhanced production of chemicals and energy 78; 79; 80. However, the efficient microbial conversion of complex biological feedstock to desired products typically requires multiple different functionalities. This poses a challenge in engineering monocultures as optimizing a single species for one trait usually comes at the expense of other traits due to the existence of tradeoffs in the performance limits of different functional traits 6; 81; 82. These difficulties have attracted researchers to the challenge of designing synthetic consortia-based microbial cell factories with task-specialized species. This “division of labor” would allow the community as a whole to perform multiple functions (e.g., utilizing multiple resources) in parallel or serially thereby leading to enhanced productivity and stability 6; 10. Another advantage of using consortia-based cell factories is its inherent compartmentalization, which facilitates the decrease in cross-reactions and side products 5. An example of a complex overproduction task that can be addressed using multi-species microbial cell factories is the conversion of lignocellulosic biomass to biofuels, which involves the hydrolysis of lignocellulose to soluble sugars and subsequently the conversion of these sugars to biofuels or any other product of interest. There is no known microorganism capable of performing all these tasks. A possible solution is to construct a synthetic consortium composed of a lingnocellulose degrader and another microorganism to ferment the released sugars to the products of interest (see Fig. 2 and Table 1). An example of such approach, among others 57; 83; 84; 85; 86, is a synthetic consortia composed of the fungus Trichoderma reesei secreting cellulase to hydrolyze lignocellulosic feedstock into soluble saccharides and Escherichia coli, which converts these saccharides into the products of interest such as isobutanol 87.
Fig. 2.
Consortia-based conversion of lignocellulosic feedstock to biofuels by division of labor. One organism is proficient in the degradation of lignocellulosic feedstock into soluble sugars (e.g., Trichoderma reese and Clostridium cellulolyticum), one in metabolizing pentoses (e.g., Escherichia coli) and the other in metabolizing hexoses (e.g., Saccharomyces cerevisiae). See also Table 1.
Table 1.
Examples of consortia-based cell factories to produce biofuel from lignocellulosic material.
| (Ligno)cellulose- degrading species | Pentose fermenting species | Hexose fermenting species | Product(s) | Reference |
|---|---|---|---|---|
| Trichoderma reesei | Escherichia coli | Escherichia coli | Isobutanol. | Minty et al 87 |
| Trichoderma reese | Scheffersomyces stipitis | Saccharomyces cerevisiae, | Ethanol | Brethauer et al 83 |
| Clostridium thermocellum | Clostridium beijerinckii | Clostridium beijerinckii | Acetone, butanol and ethanol | Wen et al 244 |
| Clostridium themocellum and Clostridium thermolacticum | Clostridium thermolacticum | Clostridium themocellum | Ethanol | Xu and Tschirner 85 |
| Clostridium thermocellum | Thermoanaerobacter strains (X514 and 39E) | Thermoanaerobacter strains (X514 and 39E) | Ethanol | He et al 86 |
| Clostridium phytofermentans | - | Candida molischiana or Saccharomyces cerevisiae cdt-1 | Ethanol | Zuroff et al 57 |
Another challenge in the conversion of lignocellulosic biomass to biofuels is that there is no microorganism that can ferment all pentoses and hexoses produced from the hydrolysis of cellulose. Wild-type microorganisms either use these sugars sequentially (e.g., first glucose and then xylose) or are in principle incapable of utilizing pentoses (such as Saccharomyces cerevisiae). A possible resolution of this issue for the latter is using synthetic biology techniques to “knock in” the genes enabling the degradation of otherwise non-degradable sugars, e.g., introducing the genes of xylose consumption pathways into S. cerevisiae 88. However, these approaches suffer from the preferential use of sugars, which leads to a decreased productivity 89; 90. A recently pursued alternative strategy to avoid all these limitations is the design of synthetic consortia where each strain exclusively uses only one sugar 91; 92; 93; 94. For example, Xia et al 94 reported the engineering of a consortium composed of three substrate-selective E. coli mutants each capable of metabolizing only glucose, xylose or arabinose by removing the genes responsible for the metabolism of the other two sugars. This consortium was capable of simultaneously consuming the mixture of all three sugars. In another study, both steps of lignocellulose degradation and the conversion of mixture of sugars to a product of interest were integrated by using a co-culture consisting of Clostridium themocellum and Clostridium thermolacticum85. While both species have multiple de-polymerization enzymes enabling them to degrade different forms of cellulose, the former is efficient in catabolizing glucose and the latter is proficient in pentose degradation. This allowed the enhanced production of ethanol from cellulose by the co-culture of both species 85.
Another common limitation associated with using synthetic biology techniques to assemble novel metabolic pathways converting a desired feedstock to a product of interest is that different parts of these typically long pathways often require specialized environments or compartments for optimal operation. A recent study proposed the resolution of this issue by a division of labor strategy where the long conversion pathway is divided among multiple community members 95. In this study, the synthetic pathway for the production of precursors of anti-cancer drug paclitaxel was divided into two modules one expressed in S. cerevisiae and the other in E. coli. Neither of these two organisms can produce the paclitaxel precursors on their own, however, each provides the best host environment for part of the pathway they are harboring. The stable co-culture established by mutualistic interactions between these two organisms (where taxadiene, a metabolic intermediate produced by E. coli, is used and functionalized by yeast) enabled the enhanced production of a number of different paclitaxel precursors 95. A few other studies took a similar strategy to achieve higher production yields of products of interest using two genetically modified strains of E. coli 96; 97. For example, Saini et al 96 reported on the enhanced production yield of n-butanol from glucose upon the distribution of the n-butanol production pathway across two different E. coli strains, one producing butyrate from glucose and the other producing n-butanol from butyrate.
Microbial consortia for environmental applications
The importance of using microbial communities for the bioremediation of contaminated environments has been known for years as these environments contain a mixture of multiple different organic wastes and metals, which cannot be degraded and/or removed by a single microorganism. Synthetic microbial consortia have been used as an alternative to naturally occurring communities to improve and accelerate the biodegradation of pollutants 98; 99; 100; 101; 102. For example, a co-culture of a genetically engineered Escherichia coli and a wild-type Ochrobactrum sp. was established in a laboratory-scale bioreactor to degrade methyl parathion, a highly toxic pesticide commonly used for agriculture crop protection 100. The engineered E. coli strain overproduces methyl parathion hydrolase converting methyl parathion into p-nitrophenol, which is a toxic intermediate and serves as the sole carbon, nitrogen and energy source for and degraded by Ochrobactrum sp. More recently a synthetic consortium composed of three fungal strains Aspergillus lentulus, Aspergillus terreus and Rhizopus oryzae for the simultaneous removal of multiple metals and dyes was reported 103. Even though the detailed mechanism of inter-species interactions was not explored in this study, it was shown that these fungal species stably work in concert by distribution of tasks among different specialized members, where Aspergillus lentulus removes Cu2+ and Acid Blue 161, Aspergillus terreus removes Cr6+ and Rhizopus oryzae removes Pigment Orange 34. This synthetic community was reported to be more efficient in the removal of these metals and dyes compared to their monoculture counterparts 103.
Bioelectrochemical systems such as microbial fuel cells have been used to simultaneously degrade complex organic matter in contaminated environments and to produce electric power, chemicals and biofuels 104; 105. Syntrophic microbial consortia are widely used in microbial fuel cells, where multiple fermentative bacteria degrade a mixture of complex organic pollutants and exoelectrogenic microorganisms (typically Geobacter species) rapidly convert fermentation intermediates into electrical current or chemicals/biofuels thereby eliminating their feedback inhibition on fermentative bacteria 106. Synthetic microbial consortia have been used to design more efficient microbial fuel cells 107; 108; 109; 110; 111; 112; 113. A notable example is the study by Venkataraman et al 110, which demonstrated that a mutualistic co-culture of Pseudomonas aeruginosa and Enterobacter aerogenes in a bioelectrochemical system leads to up to 14-fold increase in electric power generation compared to either of the monocultures. The mutualistic interactions are mediated by 2,3-butanediol, which is a by-product of glucose fermentation by E. aerogenes and is subsequently used by P. aeruginosa. The increased current production was attributed to the removal of fermentation by-product by P. aeruginosa as well as the enhanced production of pyocyanin (electron shuttles) by P. aeruginosa 110. A more recent study addressed the issue that butyrate, which is an anaerobic fermentation by-product is not directly used by Geobacter sulfurreducens in anode. A synthetic consortium composed of two different but complementary mixed cultures was designed for the anode to overcome this issue, where one oxidizes butyrate to acetate and the other (enriched in Geobacter species) produces electric current by the consumption of acetate 112. This synthetic community led to an enhanced production of electric current that outperformed the previous naturally derived communities.
Mathematical modeling and computational analysis of microbial communities
Despite the growing availability of high-throughput experimental data (especially metagenomic sequences) for a diverse range of complex natural microbial communities, the full characterization and understanding of these communities is still a challenging task. This is partly due to the fact that it is very difficult, if not impossible, to measure the extent and direction of inter-species interactions (a key determinant of community’s function and dynamics 11; 12) even using the state-of-the-art experimental techniques. Furthermore, engineering synthetic consortia to perform sophisticated tasks for application areas reviewed above requires searching through a complex web of organisms and interactions in time and space, which can no longer be achieved by empirical tinkering. The development of efficient computational techniques and/or mathematical modeling tools can address some of these questions and shed light onto the experimentally inaccessible aspects of microbial communities. These models are critical in addressing a variety of ecologically and evolutionary relevant questions such as quantifying the impact of inter-species interactions and environmental factors on the emergence of cooperation, coexistence of cooperators and cheaters and the evolutionary fate of the communities. More importantly, they can play a critical role in the rational design of synthetic consortia for desired applications. In the following, we review some of the most common techniques for modeling microbial communities.
Ecological based modeling
Ecological theories of inter-species interactions
Two important models from theoretical ecology that have been successfully employed to analyze inter-species microbial interactions are resource ratio theory (RRT) and the maximum power principle (MPP). RRT models the competition between two or more species for a limiting resource based on the assumption that the outcome of competition is determined by the ratio of supply rates of the limiting nutrient(s) 114. RRT has been primarily used to model competition 115; 116; 117; 118, but has been extended to account for cooperative interactions as well 119.
MPP is another interesting model, which relies on the assumption that all biological systems are coordinated to increase power (i.e., metabolic rate) whenever constraints allow 120; 121. By comparing model predictions with experimental observations, DeLong 122 showed that MPP can successfully predict various outcomes of competition in two-species microcosm communities. In particular, it was concluded that in the case of competitive exclusion the winning species uses more power (i.e., it acquires and uses more energy and thus reproduces faster) than the losing species. In the case of coexistence, either the community-level power exceeds that of individual species in isolation, or the power that a species can attain within the community is higher than what could be reached in isolation 123.
In addition to RRT and MPP, a number of other ecological models and theories have been proposed recently, which have a great potential for modeling microbial interactions 124; 125; 126. An example of such a theory, which offers a new perspective on the emergence and evolution of costly cooperation in microbial communities is the Black Queen Hypothesis (BQH) 125. It posits that cooperation among species may emerge due to purely selfish traits. The most important assumption of BQH is that some costly microbial functions are often leaky, such that the resulting public goods can be used by other species. It further hypothesizes that since these functions are costly and thus undesirable, adaptive loss of the corresponding genes may happen in some species. This inevitably turns some community members to “helpers” and the rest to “beneficiaries” and builds an obligatory association between helpers and beneficiaries. The “black queens” here refers to these costly functions that most species strive to avoid, analogous to the queen of spades in the game Hearts 125. This theory has the potential to devise a possible evolutionary path for the emergence of cross-feeding, whereby leakiness and gene loss may be followed by the evolution of costly cooperative traits in beneficiaries to maximize the production of the vital by-product by the helpers 126. Recently, Oliveira et al 127 examined the evolution of cross-feeding based on BQH by developing a ecoevolutionary model that accounts for multiple secretions by each species, which can be exchanged among genotypes. They concluded that the evolution of cooperative exchanges reduces the community productivity relative to an autonomous strain performing all vital functions it needs, and that this type of cooperative behavior evolves only under specific demographic regimes characterized by intermediate genetic mixing 127.
Population dynamic models
A traditional way of modeling the dynamics of microbial communities rooted in theoretical ecology is the use of coupled differential equations describing the temporal evolution of microbial species abundances. The most widely-used such model is the Lotka–Volterra (LV) model, originally developed for modeling predator-prey dynamics, and later generalized to model combinations of competitive and cooperative interactions 128; 129. The LV equations can, in general, be written as follows 128:
| (1) |
where Nk is the abundance of species k, K denotes the total number of species, rk is the intrinsic net growth (i.e., growth minus decay) rate and bkk denotes the interaction coefficients (or strengths) measuring the effect of one individual in population k′ on the growth of one individual in population k, which can assume a negative, zero or positive value denoting a negative, neutral, or positive interaction, respectively. In this form, the LV model takes into account the impact of the presence or absence of other species implicitly through the interaction coefficient, but cannot capture explicitly indirect interactions through e.g., metabolite exchange or quorum sensing 130. In an attempt towards addressing this limitation, a recent study proposed to include in LV models the explicit dynamics of exchanged metabolites in a one-way mutualistic interaction where one species grows on the waste product of another species 131. Generalized LV models (Equation 1) have been used to model bacteria-bacteriophage interactions 132; 133; 134 as well as microbial interactions in the gut 135; 136 and in a cheese microbial community 137. For example, Fisher and Mehta 135 used sparse linear regression to infer interaction coefficients in a discrete LV model of microbial dynamics using species abundance data for the gut microbiota of two individuals. In another effort, the generalized LV models were extended further to account for the impact of time-dependent external perturbations 136. After using linear regression to infer interaction coefficients, this extended model was used to computationally assess the impact of infection by pathogens and antibiotic administration on the dynamics and stability of the mouse gut microbiota. It is worth noting that in addition to LV models, various other ODE-based models have been used to describe the dynamics of interacting microbial populations in different settings 23; 87; 138; 139; 140; 141.
Spatial modeling
Except for laboratory setups, most natural microbial communities display highly complex spatial structure. As a result, community interactions and abundances vary not only with time but also with space due to the heterogeneity of their habitat, the existence of natural gradients (e.g. different amounts of oxygen penetrating through a biofilm), and self-organization properties of the microbes themselves. For example, a given resource may be differentially available to a given species in different spatial locations, thus affecting significantly the function, stability, dynamics and evolution of the entire ecosystem. In this case, instead of ODEs, the dynamics of the system is best captured by partial deferential equation (PDE) models. The most widely-used PDE model is the reaction-diffusion equation, which determines the density of each species at different time points and different locations in space due to diffusion and population dynamics 142; 143:
| (2) |
where Ck is the concentration (or density) of species k at time t in location (x, y, z), Dk is the diffusion coefficient of species k in the medium (measuring dispersal rate), and rk denotes growth or decline in population k due to population dynamics, which can be determined at a given point (x, y, z) in space by using any population dynamic model described in the previous section. Note that the first term in the right-hand side of Equation (2) determines dispersal due to diffusion. This equation is thus reduced to population dynamic models (based on ODEs) for a homogeneous environment. This same equation can be used to model the spatio-temporal variations in the concentration of shared compounds in a microbial community in which case the term rk stands for the net production rate of a compound k by different members of the community.
This class of PDE-based models and their extensions/simplifications have been used in conjunction with population-based models to study a variety of ecological phenomena related to spatial effects such as range expansion and diffusion-based spatial patterning 144; 145,146; 147; 148; 149. For example, by using a one-dimensional reaction-diffusion equation, Datta et al 146 successfully modeled the wave front profiles observed in a range expansion experiment involving populations of cooperator and cheater yeast strains. They also used a similar reaction-diffusion equation to model the spreading of cooperator and defector alleles and to analytically derive the velocity of defectors invading a spatially extended population of cooperators 146. In a subsequent related study, a spatial model of a mixed population of cooperators and defectors coupling changes in both population density and allele frequencies was developed and it was shown that cooperators are favored at the edge of an expanding population, and under certain conditions, they can spread into new territories faster than they are invaded by defectors 146. More recently, a reaction-diffusion model was used to construct a model of cross-feeding mutualism that explicitly accounts for the production, consumption and diffusion of public goods 149. Interestingly, this study showed that while species migration improves mutualism and stabilizes coexistence, cooperation is lost beyond a critical diffusivity of public goods. Furthermore, for the case of unequal diffusivity of public goods, the species with slower-diffusing public goods will dominate the co-culture and destroy cooperation by driving the other species to extinction.
Game theoretical models
The complex balancing of benefits and costs associated with inter-species interactions in microbial communities can also be effectively addressed by using game theory and evolutionary game theory approaches 45; 87; 150; 151; 152; 153; 154; 155 (see also 156 and 157 for comprehensive reviews). Game theory is a general mathematical framework to model strategic interactions among a number of agents (players) where the payoff of each agent (i.e., how happy each agent is) is not only a function of its own strategy (action) but also a function of other players’ strategies.
The payoffs are mathematically represented as a (multi-dimensional) matrix whose entries represent the payoff of each player for a given strategy profile. This payoff matrix is used to determine the equilibrium of the system, a state where no player has any incentive to deviate from its current strategy given all other players’ strategies, because no change in strategy would increase the player’s payoff. In evolutionary game theory, the payoff of each player depends not only on the action of other payers but also on their relative abundances. This payoff is then used to determine the reproductive fitness of each player. The most popular way of modeling the reproduction dynamics of mixed interacting populations in evolutionary game theory is using the replicator’s equation 158:
| (3) |
| (4) |
| (5) |
Here, x = [x1, x2, …, xK]T represents the composition of the community with xk being the relative abundance (frequency) of species K, fK (x) is the fitness of species k, ϕ(x) denotes the average fitness of the community and akk′ represents the payoff of species k confronting species k′ (extracted from the payoff matrix of the game). According to Equation (3), the frequency of species k increases, decreases or remains constant, based on whether its fitness is greater than, less than or equal to the average fitness, respectively. Even though this model does not explicitly capture the emergence of new phenotypes due to mutation, it is usually used to assess whether a pre-specified mutated phenotype can invade an existing phenotype. It has been shown that the replicator equation for a game with K strategies can be transformed into the generalized LV model with K − 1 species 158. This alludes to a fundamental link between evolutionary game theory and theoretical ecology.
A prominent example of modeling microbial interactions using game theory is the work by Gore et al 45. They experimentally assessed and modeled the outcome of interactions between a wild-type cooperator strain of Saccharomyces cerevisiae, which produces the invertase enzyme to hydrolyze sucrose and convert it to glucose and fructose, and a cheater mutant strain of S. cerevisiae, which benefits from the sugars resulted from sucrose hydrolysis but does not endure the cost of producing invertase. In this work, instead of assuming that fitness is a linear function of the relative abundance of species (see Equation 4), experimental data were used to formulate a fitness function that depends nonlinearly on the relative abundance of both species, and on the production cost of invertase. This nonlinear model could explain the experimentally observed coexistence between cheaters and cooperators, which is the reminiscent of a classical game theory scenario, termed the snowdrift game. In another study, the dynamics of a game between two bacterial species competing for a limiting resource in a fluctuating environment was captured by an extension of the LV model that allows switching from one species (strategy) to another 151. Each species was assumed to take either of the two strategies constant (environment-insensitive) growth and susceptible (environment-dependent) growth. This analysis showed that the constant growth strategies always outcompete or evenly match with its competing strategy. Despite the limitations associated with quantifying the payoffs in biological systems, game theory and evolutionary game theory remain an attractive mathematical tool to model microbial interactions. For example, they can be used to assess whether an engineered microbial consortium for a desired biotechnological application can be invaded by cheaters, or to determine the range of environmental conditions where cheaters are dominated by or coexist with cooperators (e.g., see 159).
It is worth noting that game theory/evolutionary game theory models were also extended to capture the impact of spatial structure by assuming that game players are located on the vertices of a non-complete graph and preferentially interact only with their neighbors 158. This approach was recently used to investigate the emergence and fate of cooperation in “diffusible public good dilemmas” in microbial communities 160. In this model, both colony geometry and public good diffusion are described by graphs and it was found that cooperation is favored when public goods decay and diffuse slowly and when colonies are flatter 160.
Individual-based modeling
Individual-based (also known as agent-based) models (IbMs) explicitly treat each individual cell as a discrete independent entity that interacts with other individuals and with its continuous environment. These models allow the introduction of individual variability (e.g., in growth rates, substrate uptake and secretions rates, cell mass, cell volume, etc.). This modeling formalism is a bottom-up approach where the dynamics and function of the whole system is governed by that of individual cells in their pursuit of optimal fitness 161. While the biomass spreading is modeled using the discrete individual-based approach (where cells are modeled as spheres spreading only when they get too close to each other), changes in concentration of soluble substrates in the continuous environment can be modeled using reaction-diffusion equations. Therefore, in contrast to previously described PDE models, here reaction-diffusion models are used only to follow the dynamics of the shared compounds rather than microbial biomass. The discrete and continuous models are then integrated numerically using the so-called “hybrid Eulerian–Lagrangian approach” 162.
These models have been employed extensively to analyze microbial interactions 163; 164; 165; 166; 167; 168; 169. For example, Nadell et al 165 used a two-dimensional individual-based model to uncover how cooperative and cheater cells can spontaneously segregate from each other in space as the size of a biofilm colony expands. This spatial segregation allows cooperative cells to preferentially interact with other cooperative cells thereby avoiding exploitation by cheaters and favoring the evolution cooperation. This same modeling framework was used in a later study 167 to assess how addition of a new species to a biofilm microbial community will affect the evolution of cooperation. Momeni et al 168 also used an individual-based model to systematically explore how different types of ecological interactions affecting the fitness of species can lead to distinct patterning in three-dimensional communities grown from two fluorescently-marked populations of cells initially distributed randomly on top of a surface. This model predicted that interactions benefiting at least one population could allow initially disparate partner ratios to converge over time. Furthermore, it revealed that strongly cooperative cells are inter-mixed by forming patches successively accumulating on top of each other.
Genome-scale metabolic network modeling
All the modeling approaches described so far aim at predicting the dynamics of microbial communities based on the description of the abundance of different species and on a crude description of how each species affects other species. Interaction terms, described for example as a matrix in Equation 1 or Equation 4, constitute a simplified abstraction of inter-species interactions driven by the complex network of molecular processes that take place within individual cells. Mathematical modeling of intracellular networks is a growing research area, and one of the pillars of systems biology. The question is whether and how one can build a bridge between systems biology and microbial ecology in order to study ecosystem-level function and dynamics by modeling the detailed wiring present within each cell.
A major progress in this direction has been made possible, in the last decade, by the rapid advances in the construction of genome-scale stoichiometric-based models of metabolism. Each model consists of a compilation of all biochemical reactions occurring in an organism derived from its annotated genome. These models also typically contain a fictitious reaction (referred to as biomass reaction) whose reactants are precursors essential for cellular growth and whose stoichiometric coefficients correspond to the relative contributions of these precursors to the cell’s dry biomass. The flux of this reaction is considered to be an indicative of cell’s growth capacity. Genome-scale stoichiometric models of metabolism are now available for a wide variety of organisms, ranging from bacteria to archaea and plants 170; 171; 172; 173.
Flux Balance Analysis (FBA) 174 is a mathematical modeling approach that utilizes these stoichiometric models to analyze how cells allocate environmentally available resources for homeostasis and reproduction. It is capable of making quantitative predictions of intracellular reaction fluxes, the export and secretion rates of metabolites and the cell’s growth rate under the pseudo steady-state without requiring any kinetic parameters. Toward this end, a core assumption in FBA is that metabolic fluxes in the cell are close to a predictable optimum (e.g., maximum biomass production) describing a state achieved by the cell through evolutionary adaptation (e.g., adaptation toward maximum growth). This optimality criterion is formulated as a linear programming problem (for a single-species system):
| (6) |
| (7) |
where I and J denote the set of metabolites and reactions in the network, Sij is the stoichiometric coefficient of metabolite i in reaction j (an entry of the stoichiometric matrix), LBj and UBj are lower and upper bounds on the flux of reaction j, respectively, vj denotes the flux of a reaction j serving as optimization variables and vbiomass is biomass production flux. Constraint (6) represents steady-state mass balance for each metabolite in the network and Constraints (7) impose lower and upper bounds for each reaction flux. In addition to the maximization of biomass flux, other studies have explored alternative objective functions 175 or the sampling of all flux values irrespective of any optimality principle 176. FBA has been experimentally tested for several systems, and successfully used for model-driven biological discovery as well as for a variety of biomedical and biotechnological applications (see 177; 178; 179; 180 for comprehensive reviews).
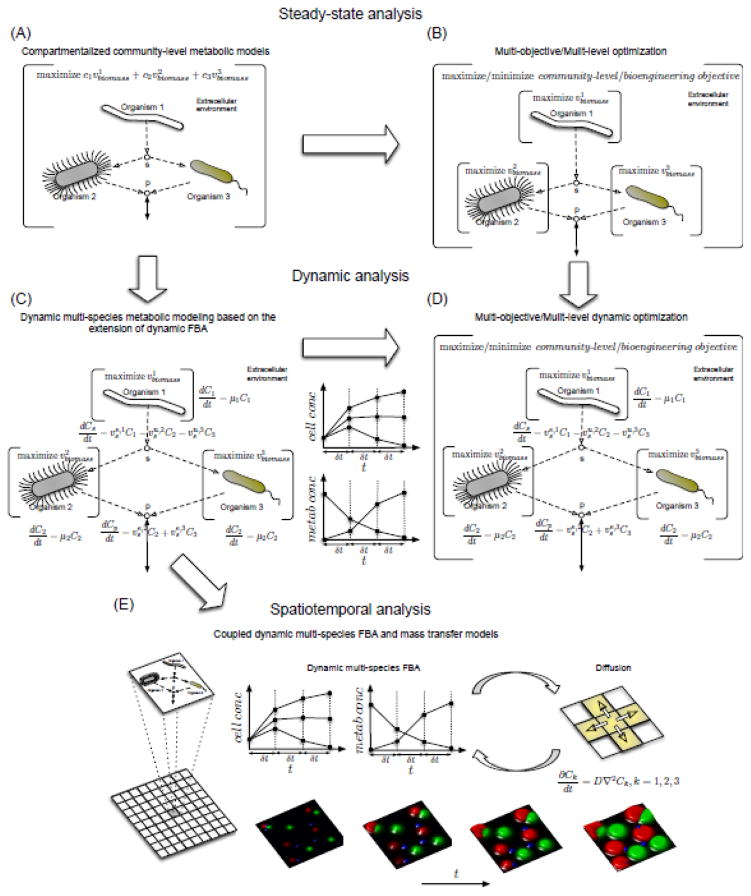
The ability to model the metabolism of an organism at genome-scale paved the way for an unprecedented opportunity to transition from phenomenological modeling (e.g. LV equations) to mechanistic modeling of microbial communities at genome-scale resolution. This enabled researchers to ask many questions that could not be directly addressed using other modeling approaches: Can one infer, instead of assuming, inter-species interaction networks from intracellular metabolic networks (see Fig. 3)? Can one predict whether compounds secreted by one organism could be used by a different organism? Can these metabolic interactions lead to an overall efficient resource utilization? How often do cross-feeding or competition arise? These questions spurred the development of metabolic models for simple multi-species microbial systems. These models evolved from steady-state analysis to dynamic and spatiotemporal analysis of microbial communities (see Table 2 and Fig. 4).
Fig. 3.
Metabolic modeling of microbial communities provides an opportunity to infer, rather than assuming, inter-species interactions network from the intracellular metabolic networks of community members.
Table 2.
A summary of various categories of community modeling approaches using genome-scale metabolic models.
| Modeling formalism | Modeling condition | Type of optimization problem | Reference |
|---|---|---|---|
| Compartmentalized community- level metabolic models based on FBA | Steady-state | Linear programming | Stolyar et al 181, Shoaie et al 184, Heinken and Thiele 186, Bordbar et al 187, Klitgord and Segre 56, Gomes de Oliveira Dal’Molin et al 189, Bizukojc et al 190, Merino et al 191, Nagarajan et al 192 |
| Compartmentalized community- level metabolic models based on MOMA | Steady-state | Quadratic programming | Wintermute and Silver 22 |
| (De-)Compartmentalized community-level metabolic models based on elementary mode analysis | Steady-state | NA | Taffs et al 195, |
| Analysis of metabolic model- derived metrics quantifying the degree of cooperation and/or competition | Steady-state | NA | Zelezniak et al 196, Kreimer et al 197, Levy et al 198; 200, Borenstein and Feldman 199 |
| Community FBA based on the balanced growth of microorganisms | Steady-state | Linear/Nonlinear programming | Khandelwal et al 194 |
| Multi-level and multi-objective modeling | Steady-state | Nonlinear programming | Zomorrodi and Maranas 201, El-Semman et al 202 |
| Dynamic multi-species metabolic modeling based on the extension of dynamic FBA 211 for single species | Dynamic | Linear programming | Zhuang et al 203, Salimi et al 204, Hanly and Henson 206; 207,209, Tzamali et al 208, Chiu et al 212 |
| Multi-level and multi-objective dynamic metabolic modeling | Dynamic | Nonlinear programming | Zomorrodi et al 214 |
| Direct integration of community-level dynamic FBA and diffusion models | Spatiotemporal | Linear programming | Harcombe et al 215, Cole et al 216 |
Fig. 4.
Evolution of the metabolic modeling of microbial communities from steady-state to dynamic to spatio-temporal analysis. Brackets represent an optimization problem, empty circles represent shared metabolites (labeled as s and p), dashed arrows represent inter-species metabolic extracellular interactions (metabolite exchanges) and solid arrows denote the uptake and export of metabolites. (A) Steady-state analysis using compartmentalized community-level metabolic models with the objective function being a weighted sum of biomass fluxes of community members 181. (B) Steady-state analysis using a multi-objective and multi-level optimization procedure (a nested optimization problem, where some of the constraints are another optimization problem referred to as inner-level problems 180). Here, a separate FBA problem is defined for each community member serving as inner-level optimization problems and capturing species-level fitness criteria. These FBA problems are integrated by using constraints in the outer-level problem representing metabolite exchanges among community members. The objective function of the outer-level problem captures a community-level fitness criterion (e.g., maximization of the total community biomass) or a desired community-level bioengineering objective (e.g., the overproduction of a desired compound) 201. (C) Dynamic analysis by using the dynamic multi-species metabolic modeling 203 based on an extension of dynamic FBA for single species 211. Here, biomass and shared metabolite concentrations are dynamically updated using a finite difference approximation of the conservation of mass equations. A separate FBA problem is solved for each species at each time point to determine their growth rate. (D) Dynamic analysis using a dynamic multi-level and multi-objective optimization procedure that combines procedures in (B) and (C) 214. Here, species-level FBA problems are coupled with a community-level or a desired bioengineering objective function using the conservation of mass equations. (E) Spatio-temporal analysis by the direct coupling of dynamic metabolic analysis in (C) and diffusion models 215.
Steady-state models
Metabolic modeling of microbial communities was pioneered by Stolyar and colleagues 181 who reconstructed a stoichiometric metabolic model of a simple mutualistic microbial community consisting of Desulfovibrio vulgaris and Methanococcus maripaludis. This analysis treated a multi-species community analogously to multi-compartment metabolic models of eukaryotes, such as Saccharomyces cerevisiae 182; 183. In these eukaryotes models, multiple organelles are modeled by defining suitably labeled compartment-specific metabolites and reactions, and adding transport reactions across compartments, as dictated by the knowledge of diffusion or transporters. In a community-level model, members can be similarly treated as compartments embedded in a meta-compartment that represents the shared environment. Formally, the stoichiometric matrices of individual species can be combined with each other in a larger block matrix, to construct a community-level stoichiometric matrix. One subtle aspect of implementing FBA simulations for a microbial community based on this compartment-based stoichiometry is the identification of an appropriate objective function. In the Desulfovibrio-Methanococcus model, the widely-employed FBA objective of biomass maximization was replaced with the maximization of a weighted sum of the biomass production fluxes for the community members (see Figure 4A). This community-level FBA problem can then be formulated as follows:
| (8) |
| (9) |
| (10) |
where all basic parameters and variables are analogous to those defined for the single-species FBA problem (Equations 6–7), except for the additional superscript label k, which denotes the community member k to which they belong. In addition, wk is a pre-specified weight for the biomass flux of each community member in the objective function, Ishared is the set of shared metabolites, and Kexport, i and Kuptake, i are the sets of community members exporting and uptaking a shared metabolite i, respectively. Moreover, the variable vEX_i(e) represents the community’s net exchange rate of shared metabolite i with the surrounding environment (a positive value implies export while a negative value implies uptake). Constraints (8) and (9) are similar to Constraints (6) and (7), respectively, for community member k and Constraint (10) represents a steady-state balance on the shared metabolite i in the extracellular compartment, where it is produced by some community members and is consumed by some others.
This compartment-based approach and its variants were used in many subsequent community metabolic modeling studies, ranging from the study of the gut microbiota 184; 185; 186 and interactions between multiple tissues in human and plants 187; 188; 189 to the overproduction of chemicals 190 and the study of a variety of other synthetic and natural multi-species systems 22; 56; 191,192. For example, Heinken and Thiele 186 constructed a metabolic model of pairwise interactions between 11 representative microorganisms in the gut, in conjunction with a metabolic model of human small intestinal enterocytes subject to three different diets. Here, the host and microbes interact through a compartment simulating the intestinal lumen serving as a pool for nutrients derived from the diet and enterocytes. This study suggests the presence of species-specific commensal, parasitic, mutualistic, or competitive interactions among these microbes. In another effort, as a step toward modeling a whole plant system a multi-tissue model consisting of six different tissues related to root, stem and leaf were reconstructed 189. This model was utilized to probe the division of labor between the source and sink tissues assuming that all tissues work in concert for plant growth by minimizing energy usage (photon capture) as the objective function. Nonlinear objective functions to model microbial communities have been also explored by extension of the minimization of metabolic adjustment (MOMA) framework 193 to model synthetic crosstalk between pairs of auxotrophic E. coli mutants 22. On another front, this multi-compartment approach was used to show computationally that it is in principle possible to induce a cross-feeding interaction between two microbial species by cultivating them in an appropriately designed medium 56. The search for such syntrophy-inducing media used a mixed-integer linear optimization approach to minimize the number of exchanged metabolites under the constraint that the biomass production by each species must be greater than a pre-specified threshold. Conceptually, this study illustrated the possibility of engineering interactions and communities by tweaking the environment rather than manipulating the genomes of the organisms. Other studies pursued an extension of FBA that directly accounts for species abundances based on the concept of balanced growth of microorganisms (community FBA) 194, or stoichiometric-based metabolic modeling of microbial communities independent of an optimality assumption, such as elementary mode analysis 195 or the analysis of (topological-based) metrics quantifying the degree of inter-species competitive/cooperative metabolic interactions 196; 197; 198; 199; 200.
One of the delicate issues, both conceptually and technically, in handling stoichiometric FBA-based models of communities is the interplay and trade-offs between individual organisms’ objectives and potential ecosystem-level ones. An approach explicitly designed to address this interplay, and to aid in the development of engineered communities capable of defined tasks is the multi-level multi-objective optimization method, OptCom 201. This is a nested optimization problem where some of the constraints are another optimization problem (referred to as inner-level problems) 180. OptCom couples distinct FBA problems for each community member (as inner problems with potentially conflicting objective functions), with a community-level objective function (as the outer-level objective). Species-specific inner problems are linked together through the inter-species interaction constraints in the outer problem that express the metabolite exchange among community members (i.e., Equation 10). The objective function of the outer-level problem is to optimize a community-level fitness function (see Figure 4B). Even though a universal community-level objective function is hard to identify, maximization of the entire community biomass has been used as a first approximation, assuming that the whole community works as a “super-organism” striving to maximize its growth 201. Alternatively, one can impose a desired bioengineering objective for the outer-level problem (such as the overall production of a given compound) to provide guidance on what type of interactions are needed to achieve this goal. OptCom was used to examine the addition of a new member to an existing community representative of those in subsurface anaerobic environments 201 and to model interactions between Bifidobacterium adolescentis and Faecalibacterium prausnitzii in the gut microbiota 202. It is worth noting that due to the fact that it relies on a multi-level optimization framework, OptCom is computationally more costly than the conventional single-level FBA formulations. Therefore, it is most appropriate for cases where different species- and community-level objective functions are sought. Furthermore, OptCom is not a suitable modeling framework for purely competitive microbial communities as a community-level objective function is biologically irrelevant for such systems.
Dynamic models
The FBA-based community-level approaches described above, while useful for several applications, have some inherent limitations, due to the nature of FBA. These limitations include the lack of explicit temporal scales, the incapacity to predict microbial species abundances as well as the need to define a priori a community-level objective function. Interestingly, a lot of these issues are naturally resolved by extending steady-state genome-scale methods to approaches that explicitly model the dynamics of microbial growth and of environmental metabolites 203; 204; 205; 206; 207; 208; 209. These methods (see 210 for a review) are mostly based on the extension of dynamic FBA (dFBA) 211 for single-species systems (see Figure 4C). As a first attempt in this direction Zhuang et al 203 proposed Dynamic Multi-species Metabolic Modeling (DMMM) framework, where cell densities are updated similarly to dFBA, while shared metabolite concentrations evolve by taking into account all species producing or consuming each shared metabolite:
| (11) |
| (12) |
Here, Ck and Ci denote the density of species k (g/l) and the concentration of shared metabolite i (mmol.gDW−1.h−1)), respectively and μk (h−1) is the specific growth rate of species k. Constraint (11) represents the exponential growth phase and Constraint (12) expresses the conservation of mass for the shared metabolite i in the extracellular space. These differential equations are discretized using a finite differences method, in which the specific growth rate μk for species k at each time point is determined by solving the corresponding FBA problem. Notably, in the solution of each FBA problem, uptake limits for the shared metabolites are determined by using kinetic expressions (such as Monod kinetics), which estimate the uptake flux upper bound as a function of the extracellular concentration of that metabolite.
DMMM was used to model competition between Geobacter sulfurreducens and Rhodoferax ferrireducensin in natural and manually perturbed anoxic subsurface environments 203 and a co-culture of Clostridium acetobutylicum and Clostridium cellulolyticum for consolidated bioprocessing of lignocellulosic material 204. An extension of the DMMM framework 203 was also developed to identify the optimal acetate and Fe(III) addition rates for the effective uranium reduction by controlling the relative abundance of Geobacter sulfurreducens and sulfate-reducing bacteria 205. In addition to addressing environmental issues, these approaches have been used for exploring possible ways to increase the production of chemicals and biofuels 206; 207; 209; 212. For example, a multi-species dFBA framework was combined with flux variability analysis (FVA) 213 to identify the biosynthetic capacity of a large number of synthetic two-species communities consisting of over 100 microbial species, where the co-culture enables the production of metabolites that cannot be produced by mono-cultures in the same growth medium 212. The dynamic nature of this analysis revealed two phases where new biosynthetic capabilities emerge: One as soon as the organisms are introduced into the same medium and the other toward the end of the growth period in a nutrient-depleted growth medium.
In line with these advances in dynamic analysis tools, an extension of the OptCom procedure 201, termed d-OptCom (dynamic OptCom), was proposed for the dynamic multi-objective metabolic modeling of microbial communities 214 (see Figure 4D). Here, time-dependent conservation of mass for the biomass of community members and shared metabolites (Equations 11 and 12) as well as kinetic expressions determining the uptake rate of shared metabolites are included as new constraints in the outer-level problem. While, similarly to OptCom, the inner-level optimization problems are species-specific FBA problems subject to uptake rates determined by the outer problem, maximization of the total community biomass concentration was used as the outer-level objective function (instead of maximizing the sum of biomass fluxes in OptCom). d-OptCom was used to model the dynamics and biomass composition of synthetic two-species consortia composed of two cross-feeding E. coli mutants and that of a uranium-reducing community comprised of Geobacter sulfurreducens, Rhodoferax ferrireducens, and Shewanella oneidensis 214. Notably, the use of community-level objective function allowed for the emergence of costly cooperation in the former case study, which cannot be captured by DMMM-like approaches. Nevertheless, in cases where a community-level objective is biologically irrelevant (e.g., for a pure competitive ecosystems) or uncertain, DMMM-like approaches are preferred since they have lower computational cost and they allow the whole community’s function and dynamics to emerge solely from the selfish behavior (i.e., growth maximization) of its constituent species.
Spatio-temporal models
As noted earlier, in addition to temporal variability, microbial communities generally display high spatial heterogeneity, due both the inhomogenous nature of the surrounding environment, and the locality of interactions between different microbes in the absence of vigorous mixing. By adding a spatial component to the community-level dynamic FBA concept described above, it is possible to explicitly model inter-species interactions in structured environments, such us layered biofilms, or colonies on a Petri dish. The development of such an integrated platform was the goal of a recent modeling framework termed COMETS (Computation Of Microbial Ecosystems in Time and Space) 215. The COMETS framework directly couples community-level dFBA with diffusion models to enable the spatio-temporal analysis of microbial communities using genome-scale metabolic models 215 (see Figure 4E). A heterogeneous environment is approximated by a spatially structured lattice. Each point in this lattice may contain an arbitrary number of species and different concentrations of shared metabolites. Simulations consist of two fundamental steps including (i) cellular growth and metabolite secretion/production at each lattice point modeled by a multi-species dFBA framework similar to DMMM 203 and (ii) a finite difference approximation of the shared metabolites and biomass diffusion in the lattice. COMETS predictions were tested experimentally for two-species and three-species synthetic consortia involving E. coli, Salmonella enterica and Methylobacterium extorquens. COMETS enabled the study of how pairs of cross-feeding colonies may be affected by the interposition of a third colony in between them, highlighting the complex dependency of inter-species interactions on spatial organization. A modeling strategy similar to COMETS was used to model the emergence of acetate cross-feeding sub-populations in colonies of E. coli growing on an agar plate 216.
Current challenges in modeling microbial communities
A long-standing challenge in the model-driven analysis of microbial communities is the increase in demand for computational resources for complex and/or large-scale microbial communities. For example, such problems arise for individual-based models, where one typically deals with a considerably large number of individual cells, as well as for FBA-based methods, in which it may need to handle a large number of community members whose genome-scale metabolic models could contain of the order of a thousand reactions and metabolites. These issues become even more prohibitive if spatial heterogeneity is taken into account, especially in two- or three-dimensional discretized space. Due to these limitations both IbM and FBA studies that include spatial heterogeneity have been so far applied to small-scale (from micrometers to centimeters) environments 163; 215; 217. In addition to more powerful computers and more efficient core algorithms, these issues can be addressed by reducing the complexity of the problem in a number of ways. For IbMs, for example, a proposed solution has been to work with “super-individuals”, which are representatives of a large number of individuals with similar traits 218. This approach, however, weakens the intrinsic advantage of IbMs, which is to capture variability at the individual cell level 162.
Similarly to super-individuals, one can reduce the number of necessary genome-scale metabolic models in a complex microbial community by using the concept of “a functional guild”. A guild is a group of organisms that use the same class of environmental resources in the same manner 219. Instead of considering all species in a community one could work with a few representative guilds without the significant loss of accuracy. This strategy has been used before in metabolic modeling of microbial communities from Octopus and Mushroom Springs in Yellowstone National Park 195; 201. Alternatively, it may prove useful to build and employ, for example, genus-level models containing all or most abundant metabolic reactions from their member species.
A possible strategy to address high computational demands for modeling large-scale heterogeneous environments is creating a “look-up” table. This table contains precomputed solutions for a computationally manageable list of combinations of environmentally-relevant cell and nutrients distributions in space (e.g. a matrix of possible values for nitrogen and carbon source concentrations in the medium). This approach has been pursued for single-species FBA simulations in a large heterogeneous environments 220 but can be easily extended to both multi-species FBA simulations or IbMs. In this way, instead of directly solving a FBA problem for each species at each time and grid point, the required reaction fluxes are updated simply by interpolating within this loop-up table. Future developments could use combinations of pre-computed solution tables and new calculations, as dictated by environmental conditions.
As a complementary strategy to reduce the computing time, one can invest in the development of efficient high-performance numerical and computational methods that can alleviate the CPU demand of synthetic ecology algorithms. An example of progress in this direction has been recently reported through the development of a software tool termed Biocellion 221 for the individual-based modeling of large communities containing millions to billions of cells. By utilizing efficient numerical and parallelization techniques, it was possible to reduce the required CPU time for a case study on pattern formation in microbial communities 168 from a week to a few hours 221.
In addition to computational complexity, the development of stoichiometric-based algorithms for synthetic ecology needs to address a number of other challenges. Some of these challenges are rooted in our limited capacity to translate genomes and metagenomes into complete and accurate lists of functions for individual species in a community. Despite the availability of automated metabolic model reconstruction pipelines such as MetaFlux 222, ModelSeed 171 and the RAVEN toolbox223, all these algorithms can only partially compensate for the lack of knowledge of gene function. These algorithms provide only first-draft reconstructions, whose conversion to a computationally reliable model still requires extensive and time-consuming manual curation. New algorithms, e.g. using likelihood-based gene annotation and gap filling 224 can alleviate to some extent the need for manual curation, but they do not fully resolve the need for manual curation. A major leap towards resolving this problem at its root may result from coordinating big community endeavors for the prediction and experimental validation of individual gene functions, as pioneered for example by the COMBREX consortium 225.
More broadly, the granularity at which taxonomy should be represented in stoichiometric metabolic models constitutes a technically and conceptually fascinating question. Brought to the extreme, one could ask whether it is possible to build community-level stoichiometric models as “soups of enzymes” irrespective of the knowledge of what reaction is performed by what species, similar to previously proposed models of biosphere-level metabolism 226; 227 (also see 195). One of the advantages of this approach would be the possibility of building community-level models straight from metagenomic sequencing data. Such metagenomic-based metabolic models could indeed conveniently capture the entire repertoire of functions of the community as a whole. However, the lack of metabolite and reaction compartmentalization in these models could lead to significant complications or predictions errors, for example due to the disruption of membrane gradient-mediated processes 228.
Conclusions and future perspectives
The emergence of synthetic ecology has provided an attractive alternative to engineering single-species systems for a wide variety of tasks ranging from the discovery of key ecological features of natural microbial communities to the targeted design of synthetic consortia for biotechnological and biomedical applications. While several examples of promising small synthetic ecosystems have demonstrated the feasibility of this approach, the most exciting opportunities of synthetic ecology require coping, in a more systematic way, with the complexity of microbial systems, and in particular with a hierarchy of nested networks, from those within microbes to those between them. Predictive mathematical modeling approaches can play a key role in addressing these challenges: they can help decipher how inter-species interactions in natural microbial communities govern community dynamics and evolution, and they can translate harvested knowledge into methods for the design of new communities with desired properties. The successful development of these predictive tools will require both revisiting existing modeling approaches to cope with the inherent complexity of microbial ecosystems, and inventing new ones.
When combined with engineering principles, these modeling approaches have a great potential in complementing experimental efforts (by reducing or prioritizing costly experiments) to address a number of current challenges in biotechnology, and biomedicine. The most immediate application is the rational design of microbial communities capable of performing a desired task. This brings to the forefront the need to develop efficient “computational consortia design” algorithms similar to strain design algorithms for single-species systems, which have been successfully applied to bioenergy and metabolic engineering applications (see 180 for a review of these tools). For example, as mentioned before, mathematical modeling tools such as OptCom 201 and d-OptCom 214 can be easily re-purposed/adjusted for engineering applications by mathematically describing the desired engineering objective as the outer-level objective function, while the inner-level problems simulate species-specific fitness criteria as before. There are also several ways of incorporating engineering interventions in these and other similar frameworks. For example, one can use binary variables to determine whether a gene in a specific community member must be knocked out or whether a community member or a nutrient in the growth medium should be removed or if a new one should be added, to optimize the desired engineering objective 56; 201; 214. Moreover, new computational approaches, combining ideas from synthetic biology, metabolic engineering and ecosystem-level modeling could enable the concurrent design of environments and strains to achieve a desired behavior. At a finer scale, taking into account the interplay between multiple biological processes contributing to the ecological behavior of a community member can enhance the predictive power and the scope of modeling frameworks. For instance, recent advances in whole-cell modeling 229 and integrated metabolic-expression (ME) models 230 have enabled capturing several ecologically relevant biological processes that are not addressed by stoichiometric-based metabolic models such as gene expression, regulation and signal transduction. Although the current studies using these models have focused on individual species so far 231; 232, it is likely that these models will play a crucial role in constructing more predictive models of microbial communities.
Another important aspect for which modeling can play a key role in guiding the design of synthetic communities is the assessment of synthetic consortia stability. Similarly to engineered single species, instability is a major problem associated with engineered consortia, either based on wild-type or on genetically modified strains. Many existing consortia design strategies rely on the assumption that interactions among community members are fixed. However, patterns of inter-species interactions can be significantly modulated by environmental changes, and can change during the course of evolutionary adaptation 233. Thus, understanding processes that may guarantee stability and resilience in presence of these changes would require taking explicitly into account the volatility and context-dependence of interactions. Knowledge from the large body of evolutionary and ecological theory literature dedicated to addressing the problem of stability and the evolutionary fate of inter-species interactions in communities (e.g., 234; 235; 236; 237) could be used to inform computational consortia design tools to arrive at evolutionary stable communities. The importance of this integration has been recognized before 238 but has not been realized so far. Given that natural microbial communities are generally stable and robust to perturbations, some studies suggest the use of a top-down approach to address the stability issue. This was achieved by using artificial selection to sequentially screen a natural microbial community and arrive at a refined community capable of efficiently and stably performing the desired function 239; 240. For example, this approach was used to select for an efficient 3-chloroaniline degrading community 240. The promise of artificial selection was also shown by using individual-based modeling in a later study 241.
Even though both bottom-up and top-down approaches use different formalisms and assumptions, a synergy between these two could have great potential and applications. For example, a community obtained through sequential screening or laboratory evolution experiments could be later scrutinized to reveal its key species and interactions. Moreover, in analogy to a process referred to as “refactoring” in synthetic biology 242, one could build a more tractable, standardized and simplified version of such a community. Refactoring a microbial community would entail redesigning a screened natural community from the bottom up by systematically eliminating undesired and poorly understood organisms and interactions, and replacing them with well-characterized ones. A refactored community could achieve the same functionality of the original one, but with enhanced stability and tractability. Thus, similar to the standardization of biological parts (biobricks) for synthetic biology 243, we envision that the field of synthetic ecology may similarly benefit from a registry of standard “ecological parts”. This registry would catalogue well-characterized ecological parts such as microorganisms and small ecological modules (motifs) with defined functions, inputs/outputs, interaction properties and, ideally, evolutionary characteristics. Such a registry would facilitate the experimental construction of increasingly complex consortia and could be complemented with new modeling tools to identify the required building blocks and the ecological circuit connectivity that bring about a desired function.
Highlights.
Synthetic microbial consortia are implicated in environmental sustainability and biomedicine
Mathematical models are an essential tool for the rational design of synthetic ecosystems
A main goal is to infer community outputs and interactions based on genomes
Faster computation, data/model integration and standardization needed for progress
Acknowledgments
This work was supported by the Office of Science (BER), U.S. Department of Energy grant DE-SC0012627, by NIH grants 5R01GM089978, 5R01GM103502 and 5R01DE024468, by NSF grant 1457695 and by Defense Advanced Research Projects Agency Biological Technologies Office (BTO), Program: Biological Robustness In Complex Settings (BRICS), Purchase Request No. HR0011515303, Program Code: TRS-0 Issued by DARPA/CMO under Contract No. HR0011-15-C-0091.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Dunham MJ. Synthetic ecology: a model system for cooperation. Proc Natl Acad Sci U S A. 2007;104:1741–2. doi: 10.1073/pnas.0611067104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Follows MJ, Dutkiewicz S, Grant S, Chisholm SW. Emergent biogeography of microbial communities in a model ocean. Science. 2007;315:1843–6. doi: 10.1126/science.1138544. [DOI] [PubMed] [Google Scholar]
- 3.Cho I, Blaser MJ. The human microbiome: at the interface of health and disease. Nat Rev Genet. 2012;13:260–70. doi: 10.1038/nrg3182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wolfe BE, Dutton RJ. Fermented foods as experimentally tractable microbial ecosystems. Cell. 2015;161:49–55. doi: 10.1016/j.cell.2015.02.034. [DOI] [PubMed] [Google Scholar]
- 5.Shong J, Jimenez Diaz MR, Collins CH. Towards synthetic microbial consortia for bioprocessing. Curr Opin Biotechnol. 2012;23:798–802. doi: 10.1016/j.copbio.2012.02.001. [DOI] [PubMed] [Google Scholar]
- 6.Bernstein HC, Carlson RP. Microbial Consortia Engineering for Cellular Factories: in vitro to in silico systems. Comput Struct Biotechnol J. 2012;3:e201210017. doi: 10.5936/csbj.201210017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Daims H, Taylor MW, Wagner M. Wastewater treatment: a model system for microbial ecology. Trends Biotechnol. 2006;24:483–9. doi: 10.1016/j.tibtech.2006.09.002. [DOI] [PubMed] [Google Scholar]
- 8.Gude V. A New Perspective on Microbiome and Resource Management in Wastewater Systems. J Biotechnol Biomater. 2015:5. [Google Scholar]
- 9.Kuramitsu HK, He X, Lux R, Anderson MH, Shi W. Interspecies interactions within oral microbial communities. Microbiol Mol Biol Rev. 2007;71:653–70. doi: 10.1128/MMBR.00024-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Briones A, Raskin L. Diversity and dynamics of microbial communities in engineered environments and their implications for process stability. Curr Opin Biotechnol. 2003;14:270–6. doi: 10.1016/s0958-1669(03)00065-x. [DOI] [PubMed] [Google Scholar]
- 11.Little AE, Robinson CJ, Peterson SB, Raffa KF, Handelsman J. Rules of engagement: interspecies interactions that regulate microbial communities. Annu Rev Microbiol. 2008;62:375–401. doi: 10.1146/annurev.micro.030608.101423. [DOI] [PubMed] [Google Scholar]
- 12.Haruta S, Kato S, Yamamoto K, Igarashi Y. Intertwined interspecies relationships: approaches to untangle the microbial network. Environ Microbiol. 2009;11:2963–9. doi: 10.1111/j.1462-2920.2009.01956.x. [DOI] [PubMed] [Google Scholar]
- 13.Ryan RP, Dow JM. Diffusible signals and interspecies communication in bacteria. Microbiology. 2008;154:1845–58. doi: 10.1099/mic.0.2008/017871-0. [DOI] [PubMed] [Google Scholar]
- 14.Keller L, Surette MG. Communication in bacteria: an ecological and evolutionary perspective. Nat Rev Microbiol. 2006;4:249–58. doi: 10.1038/nrmicro1383. [DOI] [PubMed] [Google Scholar]
- 15.Faust K, Raes J. Microbial interactions: from networks to models. Nat Rev Microbiol. 2012;10:538–50. doi: 10.1038/nrmicro2832. [DOI] [PubMed] [Google Scholar]
- 16.Dubey GP, Ben-Yehuda S. Intercellular nanotubes mediate bacterial communication. Cell. 2011;144:590–600. doi: 10.1016/j.cell.2011.01.015. [DOI] [PubMed] [Google Scholar]
- 17.Benomar S, Ranava D, Cárdenas ML, Trably E, Rafrafi Y, Ducret A, Hamelin J, Lojou E, Steyer JP, Giudici-Orticoni MT. Nutritional stress induces exchange of cell material and energetic coupling between bacterial species. Nat Commun. 2015;6:6283. doi: 10.1038/ncomms7283. [DOI] [PubMed] [Google Scholar]
- 18.Pande S, Shitut S, Freund L, Westermann M, Bertels F, Colesie C, Bischofs IB, Kost C. Metabolic cross-feeding via intercellular nanotubes among bacteria. Nat Commun. 2015;6:6238. doi: 10.1038/ncomms7238. [DOI] [PubMed] [Google Scholar]
- 19.Prokopenko MG, Hirst MB, De Brabandere L, Lawrence DJ, Berelson WM, Granger J, Chang BX, Dawson S, Crane EJ, Chong L, Thamdrup B, Townsend-Small A, Sigman DM. Nitrogen losses in anoxic marine sediments driven by Thioploca-anammox bacterial consortia. Nature. 2013;500:194–8. doi: 10.1038/nature12365. [DOI] [PubMed] [Google Scholar]
- 20.Elias S, Banin E. Multi-species biofilms: living with friendly neighbors. FEMS Microbiol Rev. 2012;36:990–1004. doi: 10.1111/j.1574-6976.2012.00325.x. [DOI] [PubMed] [Google Scholar]
- 21.Seth EC, Taga ME. Nutrient cross-feeding in the microbial world. Front Microbiol. 2014;5:350. doi: 10.3389/fmicb.2014.00350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wintermute EH, Silver PA. Emergent cooperation in microbial metabolism. Mol Syst Biol. 2010;6:407. doi: 10.1038/msb.2010.66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mee MT, Collins JJ, Church GM, Wang HH. Syntrophic exchange in synthetic microbial communities. Proc Natl Acad Sci U S A. 2014;111:E2149–56. doi: 10.1073/pnas.1405641111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pande S, Merker H, Bohl K, Reichelt M, Schuster S, de Figueiredo LF, Kaleta C, Kost C. Fitness and stability of obligate cross-feeding interactions that emerge upon gene loss in bacteria. ISME J. 2014;8:953–62. doi: 10.1038/ismej.2013.211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.McInerney MJ, Bryant MP. Anaerobic Degradation of Lactate by Syntrophic Associations of Methanosarcina barkeri and Desulfovibrio Species and Effect of H(2) on Acetate Degradation. Appl Environ Microbiol. 1981;41:346–54. doi: 10.1128/aem.41.2.346-354.1981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pak K, Bartha R. Mercury methylation by interspecies hydrogen and acetate transfer between sulfidogens and methanogens. Appl Environ Microbiol. 1998;64:1987–90. doi: 10.1128/aem.64.6.1987-1990.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Traore AS, Fardeau ML, Hatchikian CE, Le Gall J, Belaich JP. Energetics of Growth of a Defined Mixed Culture of Desulfovibrio vulgaris and Methanosarcina barkeri: Interspecies Hydrogen Transfer in Batch and Continuous Cultures. Appl Environ Microbiol. 1983;46:1152–6. doi: 10.1128/aem.46.5.1152-1156.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schink B. Energetics of syntrophic cooperation in methanogenic degradation. Microbiol Mol Biol Rev. 1997;61:262–80. doi: 10.1128/mmbr.61.2.262-280.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kaeberlein T, Lewis K, Epstein SS. Isolating “uncultivable” microorganisms in pure culture in a simulated natural environment. Science. 2002;296:1127–9. doi: 10.1126/science.1070633. [DOI] [PubMed] [Google Scholar]
- 30.D’Onofrio A, Crawford JM, Stewart EJ, Witt K, Gavrish E, Epstein S, Clardy J, Lewis K. Siderophores from neighboring organisms promote the growth of uncultured bacteria. Chem Biol. 2010;17:254–64. doi: 10.1016/j.chembiol.2010.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hibbing ME, Fuqua C, Parsek MR, Peterson SB. Bacterial competition: surviving and thriving in the microbial jungle. Nat Rev Microbiol. 2010;8:15–25. doi: 10.1038/nrmicro2259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Koeppel AF, Wu M. Species matter: the role of competition in the assembly of congeneric bacteria. ISME J. 2014;8:531–40. doi: 10.1038/ismej.2013.180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Riley MA, Wertz JE. Bacteriocins: evolution, ecology, and application. Annu Rev Microbiol. 2002;56:117–37. doi: 10.1146/annurev.micro.56.012302.161024. [DOI] [PubMed] [Google Scholar]
- 34.Sieber M, Robb M, Forde SE, Gudelj I. Dispersal network structure and infection mechanism shape diversity in a coevolutionary bacteria-phage system. ISME J. 2014;8:504–14. doi: 10.1038/ismej.2013.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Samson JE, Magadán AH, Sabri M, Moineau S. Revenge of the phages: defeating bacterial defences. Nat Rev Microbiol. 2013;11:675–87. doi: 10.1038/nrmicro3096. [DOI] [PubMed] [Google Scholar]
- 36.Curtis TP, Sloan WT, Scannell JW. Estimating prokaryotic diversity and its limits. Proc Natl Acad Sci U S A. 2002;99:10494–9. doi: 10.1073/pnas.142680199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Von Canstein H, Kelly S, Li Y, Wagner-Döbler I. Species diversity improves the efficiency of mercury-reducing biofilms under changing environmental conditions. Appl Environ Microbiol. 2002;68:2829–37. doi: 10.1128/AEM.68.6.2829-2837.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kassen R, Buckling A, Bell G, Rainey PB. Diversity peaks at intermediate productivity in a laboratory microcosm. Nature. 2000;406:508–12. doi: 10.1038/35020060. [DOI] [PubMed] [Google Scholar]
- 39.Bell T, Newman JA, Silverman BW, Turner SL, Lilley AK. The contribution of species richness and composition to bacterial services. Nature. 2005;436:1157–60. doi: 10.1038/nature03891. [DOI] [PubMed] [Google Scholar]
- 40.Awasthi A, Singh M, Soni SK, Singh R, Kalra A. Biodiversity acts as insurance of productivity of bacterial communities under abiotic perturbations. ISME J. 2014;8:2445–52. doi: 10.1038/ismej.2014.91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wittebolle L, Marzorati M, Clement L, Balloi A, Daffonchio D, Heylen K, De Vos P, Verstraete W, Boon N. Initial community evenness favours functionality under selective stress. Nature. 2009;458:623–6. doi: 10.1038/nature07840. [DOI] [PubMed] [Google Scholar]
- 42.Waite AJ, Shou W. Adaptation to a new environment allows cooperators to purge cheaters stochastically. Proc Natl Acad Sci U S A. 2012;109:19079–86. doi: 10.1073/pnas.1210190109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Harcombe W. Novel cooperation experimentally evolved between species. Evolution. 2010;64:2166–72. doi: 10.1111/j.1558-5646.2010.00959.x. [DOI] [PubMed] [Google Scholar]
- 44.Kubo I, Hosoda K, Suzuki S, Yamamoto K, Kihara K, Mori K, Yomo T. Construction of bacteria-eukaryote synthetic mutualism. Biosystems. 2013;113:66–71. doi: 10.1016/j.biosystems.2013.05.006. [DOI] [PubMed] [Google Scholar]
- 45.Gore J, Youk H, van Oudenaarden A. Snowdrift game dynamics and facultative cheating in yeast. Nature. 2009;459:253–6. doi: 10.1038/nature07921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Shou W, Ram S, Vilar JM. Synthetic cooperation in engineered yeast populations. Proc Natl Acad Sci U S A. 2007;104:1877–82. doi: 10.1073/pnas.0610575104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kerr B, Riley MA, Feldman MW, Bohannan BJ. Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors. Nature. 2002;418:171–4. doi: 10.1038/nature00823. [DOI] [PubMed] [Google Scholar]
- 48.Balagaddé FK, Song H, Ozaki J, Collins CH, Barnet M, Arnold FH, Quake SR, You L. A synthetic Escherichia coli predator-prey ecosystem. Mol Syst Biol. 2008;4:187. doi: 10.1038/msb.2008.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Chuang JS, Rivoire O, Leibler S. Simpson’s paradox in a synthetic microbial system. Science. 2009;323:272–5. doi: 10.1126/science.1166739. [DOI] [PubMed] [Google Scholar]
- 50.Chuang JS, Rivoire O, Leibler S. Cooperation and Hamilton’s rule in a simple synthetic microbial system. Mol Syst Biol. 2010;6:398. doi: 10.1038/msb.2010.57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Saeidi N, Wong CK, Lo TM, Nguyen HX, Ling H, Leong SS, Poh CL, Chang MW. Engineering microbes to sense and eradicate Pseudomonas aeruginosa, a human pathogen. Mol Syst Biol. 2011;7:521. doi: 10.1038/msb.2011.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Weber W, Daoud-El Baba M, Fussenegger M. Synthetic ecosystems based on airborne inter- and intrakingdom communication. Proc Natl Acad Sci U S A. 2007;104:10435–40. doi: 10.1073/pnas.0701382104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hong SH, Hegde M, Kim J, Wang X, Jayaraman A, Wood TK. Synthetic quorum-sensing circuit to control consortial biofilm formation and dispersal in a microfluidic device. Nat Commun. 2012;3:613. doi: 10.1038/ncomms1616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chen Y, Kim J, Hirning A, Josić K, Bennett M. Emergent genetic oscillations in a synthetic microbial consortium. Sceience. 2015:349. doi: 10.1126/science.aaa3794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hamilton WD. The genetical evolution of social behaviour. I. J Theor Biol. 1964;7:1–16. doi: 10.1016/0022-5193(64)90038-4. [DOI] [PubMed] [Google Scholar]
- 56.Klitgord N, Segrè D. Environments that induce synthetic microbial ecosystems. PLoS Comput Biol. 2010;6:e1001002. doi: 10.1371/journal.pcbi.1001002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Zuroff TR, Xiques SB, Curtis WR. Consortia-mediated bioprocessing of cellulose to ethanol with a symbiotic Clostridium phytofermentans/yeast co-culture. Biotechnol Biofuels. 2013;6:59. doi: 10.1186/1754-6834-6-59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Hu B, Du J, Zou RY, Yuan YJ. An environment-sensitive synthetic microbial ecosystem. PLoS One. 2010;5:e10619. doi: 10.1371/journal.pone.0010619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kim HJ, Boedicker JQ, Choi JW, Ismagilov RF. Defined spatial structure stabilizes a synthetic multispecies bacterial community. Proc Natl Acad Sci U S A. 2008;105:18188–93. doi: 10.1073/pnas.0807935105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Sommer F, Bäckhed F. The gut microbiota--masters of host development and physiology. Nat Rev Microbiol. 2013;11:227–38. doi: 10.1038/nrmicro2974. [DOI] [PubMed] [Google Scholar]
- 61.Tremaroli V, Bäckhed F. Functional interactions between the gut microbiota and host metabolism. Nature. 2012;489:242–9. doi: 10.1038/nature11552. [DOI] [PubMed] [Google Scholar]
- 62.Ley RE. Obesity and the human microbiome. Curr Opin Gastroenterol. 2010;26:5–11. doi: 10.1097/MOG.0b013e328333d751. [DOI] [PubMed] [Google Scholar]
- 63.Karlsson FH, Fåk F, Nookaew I, Tremaroli V, Fagerberg B, Petranovic D, Bäckhed F, Nielsen J. Symptomatic atherosclerosis is associated with an altered gut metagenome. Nat Commun. 2012;3:1245. doi: 10.1038/ncomms2266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Karlsson F, Tremaroli V, Nielsen J, Bäckhed F. Assessing the human gut microbiota in metabolic diseases. Diabetes. 2013;62:3341–9. doi: 10.2337/db13-0844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Musso G, Gambino R, Cassader M. Interactions between gut microbiota and host metabolism predisposing to obesity and diabetes. Annu Rev Med. 2011;62:361–80. doi: 10.1146/annurev-med-012510-175505. [DOI] [PubMed] [Google Scholar]
- 66.Bakhtiar SM, LeBlanc JG, Salvucci E, Ali A, Martin R, Langella P, Chatel JM, Miyoshi A, Bermúdez-Humarán LG, Azevedo V. Implications of the human microbiome in inflammatory bowel diseases. FEMS Microbiol Lett. 2013;342:10–7. doi: 10.1111/1574-6968.12111. [DOI] [PubMed] [Google Scholar]
- 67.Missaghi B, Barkema HW, Madsen KL, Ghosh S. Perturbation of the human microbiome as a contributor to inflammatory bowel disease. Pathogens. 2014;3:510–27. doi: 10.3390/pathogens3030510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Biagi E, Nylund L, Candela M, Ostan R, Bucci L, Pini E, Nikkïla J, Monti D, Satokari R, Franceschi C, Brigidi P, De Vos W. Through ageing, and beyond: gut microbiota and inflammatory status in seniors and centenarians. PLoS One. 2010;5:e10667. doi: 10.1371/journal.pone.0010667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Flint HJ. The impact of nutrition on the human microbiome. Nutr Rev. 2012;70(Suppl 1):S10–3. doi: 10.1111/j.1753-4887.2012.00499.x. [DOI] [PubMed] [Google Scholar]
- 70.Kolenbrander PE. Oral microbial communities: biofilms, interactions, and genetic systems. Annu Rev Microbiol. 2000;54:413–37. doi: 10.1146/annurev.micro.54.1.413. [DOI] [PubMed] [Google Scholar]
- 71.Dewhirst FE, Chen T, Izard J, Paster BJ, Tanner AC, Yu WH, Lakshmanan A, Wade WG. The human oral microbiome. J Bacteriol. 2010;192:5002–17. doi: 10.1128/JB.00542-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Nishihara T, Koseki T. Microbial etiology of periodontitis. Periodontol 2000. 2004;36:14–26. doi: 10.1111/j.1600-0757.2004.03671.x. [DOI] [PubMed] [Google Scholar]
- 73.Jenkinson HF, Lamont RJ. Oral microbial communities in sickness and in health. Trends Microbiol. 2005;13:589–95. doi: 10.1016/j.tim.2005.09.006. [DOI] [PubMed] [Google Scholar]
- 74.Galimanas V, Hall MW, Singh N, Lynch MD, Goldberg M, Tenenbaum H, Cvitkovitch DG, Neufeld JD, Senadheera DB. Bacterial community composition of chronic periodontitis and novel oral sampling sites for detecting disease indicators. Microbiome. 2014;2:32. doi: 10.1186/2049-2618-2-32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Waldor MK, Tyson G, Borenstein E, Ochman H, Moeller A, Finlay BB, Kong HH, Gordon JI, Nelson KE, Dabbagh K, Smith H. Where next for microbiome research? PLoS Biol. 2015;13:e1002050. doi: 10.1371/journal.pbio.1002050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Kim HJ, Ingber DE. Gut-on-a-Chip microenvironment induces human intestinal cells to undergo villus differentiation. Integr Biol (Camb) 2013;5:1130–40. doi: 10.1039/c3ib40126j. [DOI] [PubMed] [Google Scholar]
- 77.Burke KE, Lamont JT. Fecal transplantation for recurrent Clostridium difficile infection in older adults: a review. J Am Geriatr Soc. 2013;61:1394–8. doi: 10.1111/jgs.12378. [DOI] [PubMed] [Google Scholar]
- 78.Prather KL, Martin CH. De novo biosynthetic pathways: rational design of microbial chemical factories. Curr Opin Biotechnol. 2008;19:468–74. doi: 10.1016/j.copbio.2008.07.009. [DOI] [PubMed] [Google Scholar]
- 79.Yadav VG, De Mey M, Lim CG, Ajikumar PK, Stephanopoulos G. The future of metabolic engineering and synthetic biology: towards a systematic practice. Metab Eng. 2012;14:233–41. doi: 10.1016/j.ymben.2012.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Nielsen J, Keasling JD. Synergies between synthetic biology and metabolic engineering. Nat Biotechnol. 2011;29:693–5. doi: 10.1038/nbt.1937. [DOI] [PubMed] [Google Scholar]
- 81.Byrne D, Dumitriu A, Segrè D. Comparative multi-goal tradeoffs in systems engineering of microbial metabolism. BMC Syst Biol. 2012;6:127. doi: 10.1186/1752-0509-6-127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Goel A, Wortel MT, Molenaar D, Teusink B. Metabolic shifts: a fitness perspective for microbial cell factories. Biotechnol Lett. 2012;34:2147–60. doi: 10.1007/s10529-012-1038-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Brethauer S, Studer MH. Consolidated bioprocessing of lignocellulose by a microbial consortium. Energy & Environmental Science. 2014;7:1446–1453. [Google Scholar]
- 84.Salehi Jouzani G, Taherzadeh M. Advances in consolidated bioprocessing systems for bioethanol and butanol production from biomass: a comprehensive review. Biofuel Research Journal. 2015;5:152–195. [Google Scholar]
- 85.Xu L, Tschirner U. Improved ethanol production from various carbohydrates through anaerobic thermophilic co-culture. Bioresour Technol. 2011;102:10065–71. doi: 10.1016/j.biortech.2011.08.067. [DOI] [PubMed] [Google Scholar]
- 86.He Q, Hemme CL, Jiang H, He Z, Zhou J. Mechanisms of enhanced cellulosic bioethanol fermentation by co-cultivation of Clostridium and Thermoanaerobacter spp. Bioresour Technol. 2011;102:9586–92. doi: 10.1016/j.biortech.2011.07.098. [DOI] [PubMed] [Google Scholar]
- 87.Minty JJ, Singer ME, Scholz SA, Bae CH, Ahn JH, Foster CE, Liao JC, Lin XN. Design and characterization of synthetic fungal-bacterial consortia for direct production of isobutanol from cellulosic biomass. Proc Natl Acad Sci U S A. 2013;110:14592–7. doi: 10.1073/pnas.1218447110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Ho NW, Chen Z, Brainard AP. Genetically engineered Saccharomyces yeast capable of effective cofermentation of glucose and xylose. Appl Environ Microbiol. 1998;64:1852–9. doi: 10.1128/aem.64.5.1852-1859.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Sedlak M, Edenberg HJ, Ho NWY. DNA microarray analysis of the expression of the genes encoding the major enzymes in ethanol production during glucose and xylose co-fermentation by metabolically engineered Saccharomyces yeast. Enzyme and Microbial Technology. 2003;33:19–28. [Google Scholar]
- 90.Chandrakant P, Bisaria V. imultaneous bioconversion of glucose and xylose to ethanol by Saccharomyces cerevisiae in the presence of xylose isomerase. Applied Microbiology and Biotechnology. 2000;53:301–309. doi: 10.1007/s002530050025. [DOI] [PubMed] [Google Scholar]
- 91.Eiteman MA, Lee SA, Altman E. A co-fermentation strategy to consume sugar mixtures effectively. J Biol Eng. 2008;2:3. doi: 10.1186/1754-1611-2-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Eiteman MA, Lee SA, Altman R, Altman E. A substrate-selective co-fermentation strategy with Escherichia coli produces lactate by simultaneously consuming xylose and glucose. Biotechnol Bioeng. 2009;102:822–7. doi: 10.1002/bit.22103. [DOI] [PubMed] [Google Scholar]
- 93.Unrean P, Srienc F. Continuous production of ethanol from hexoses and pentoses using immobilized mixed cultures of Escherichia coli strains. J Biotechnol. 2010;150:215–23. doi: 10.1016/j.jbiotec.2010.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Xia T, Eiteman MA, Altman E. Simultaneous utilization of glucose, xylose and arabinose in the presence of acetate by a consortium of Escherichia coli strains. Microb Cell Fact. 2012;11:77. doi: 10.1186/1475-2859-11-77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Zhou K, Qiao K, Edgar S, Stephanopoulos G. Distributing a metabolic pathway among a microbial consortium enhances production of natural products. Nat Biotechnol. 2015;33:377–83. doi: 10.1038/nbt.3095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Saini M, Hong Chen M, Chiang CJ, Chao YP. Potential production platform of n-butanol in Escherichia coli. Metab Eng. 2015;27:76–82. doi: 10.1016/j.ymben.2014.11.001. [DOI] [PubMed] [Google Scholar]
- 97.Zhang H, Pereira B, Li Z, Stephanopoulos G. Engineering Escherichia coli coculture systems for the production of biochemical products. Proc Natl Acad Sci U S A. 2015;112:8266–71. doi: 10.1073/pnas.1506781112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Cowan SE, Gilbert E, Liepmann D, Keasling JD. Commensal interactions in a dual-species biofilm exposed to mixed organic compounds. Appl Environ Microbiol. 2000;66:4481–5. doi: 10.1128/aem.66.10.4481-4485.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Dejonghe W, Berteloot E, Goris J, Boon N, Crul K, Maertens S, Höfte M, De Vos P, Verstraete W, Top EM. Synergistic degradation of linuron by a bacterial consortium and isolation of a single linuron-degrading variovorax strain. Appl Environ Microbiol. 2003;69:1532–41. doi: 10.1128/AEM.69.3.1532-1541.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Li L, Yang C, Lan W, Xie S, Qiao C, Liu J. Removal of methyl parathion from artificial off-gas using a bioreactor containing a constructed microbial consortium. Environ Sci Technol. 2008;42:2136–41. doi: 10.1021/es702631x. [DOI] [PubMed] [Google Scholar]
- 101.Zhang H, Yang C, Li C, Li L, Zhao Q, Qiao C. Functional assembly of a microbial consortium with autofluorescent and mineralizing activity for the biodegradation of organophosphates. J Agric Food Chem. 2008;56:7897–902. doi: 10.1021/jf801684g. [DOI] [PubMed] [Google Scholar]
- 102.Kurade MB, Waghmode TR, Jadhav MU, Jeon BH, Govindwar SP. Bacterial-yeast consortium as an effective biocatalyst for biodegradation of sulphonated azo dye Reactive Red 198. Rsc Advances. 2015;5:23046–23056. [Google Scholar]
- 103.Mishra A, Malik A. Novel fungal consortium for bioremediation of metals and dyes from mixed waste stream. Bioresour Technol. 2014;171:217–26. doi: 10.1016/j.biortech.2014.08.047. [DOI] [PubMed] [Google Scholar]
- 104.Rabaey K, Rozendal RA. Microbial electrosynthesis - revisiting the electrical route for microbial production. Nat Rev Microbiol. 2010;8:706–16. doi: 10.1038/nrmicro2422. [DOI] [PubMed] [Google Scholar]
- 105.Lovley DR, Nevin KP. Electrobiocommodities: powering microbial production of fuels and commodity chemicals from carbon dioxide with electricity. Curr Opin Biotechnol. 2013;24:385–90. doi: 10.1016/j.copbio.2013.02.012. [DOI] [PubMed] [Google Scholar]
- 106.Kiely PD, Regan JM, Logan BE. The electric picnic: synergistic requirements for exoelectrogenic microbial communities. Curr Opin Biotechnol. 2011;22:378–85. doi: 10.1016/j.copbio.2011.03.003. [DOI] [PubMed] [Google Scholar]
- 107.Qu Y, Feng Y, Wang X, Logan BE. Use of a coculture to enable current production by geobacter sulfurreducens. Appl Environ Microbiol. 2012;78:3484–7. doi: 10.1128/AEM.00073-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Bourdakos N, Marsili E, Mahadevan R. A defined co-culture of Geobacter sulfurreducens and Escherichia coli in a membrane-less microbial fuel cell. Biotechnol Bioeng. 2014;111:709–18. doi: 10.1002/bit.25137. [DOI] [PubMed] [Google Scholar]
- 109.Badalamenti JP, Torres CI, Krajmalnik-Brown R. Coupling dark metabolism to electricity generation using photosynthetic cocultures. Biotechnol Bioeng. 2014;111:223–31. doi: 10.1002/bit.25011. [DOI] [PubMed] [Google Scholar]
- 110.Venkataraman A, Rosenbaum MA, Perkins SD, Werner JJ, Angenent LT. Metabolite-based mutualism between Pseudomonas aeruginosa PA14 and Enterobacter aerogenes enhances current generation in bioelectrochemical systems. Energy & Environmental Science. 2011;4:4550–4559. [Google Scholar]
- 111.Rosenbaum MA, Bar HY, Beg QK, Segrè D, Booth J, Cotta MA, Angenent LT. Shewanella oneidensis in a lactate-fed pure-culture and a glucose-fed co-culture with Lactococcus lactis with an electrode as electron acceptor. Bioresour Technol. 2011;102:2623–8. doi: 10.1016/j.biortech.2010.10.033. [DOI] [PubMed] [Google Scholar]
- 112.Miceli JF, Garcia-Pena I, Parameswaran P, Torres CI, Krajmalnik-Brown R. Combining microbial cultures for efficient production of electricity from butyrate in a microbial electrochemical cell. Bioresource Technology. 2014;169:169–174. doi: 10.1016/j.biortech.2014.06.090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Liu Y, Deng DD, Lan XJ. A Highly Efficient Mixed-culture Biofilm as Anodic Catalyst and Insights into Its Enhancement through Electrochemistry by Comparison with G. sulfurreducens. Electrochimica Acta. 2015;155:327–334. [Google Scholar]
- 114.Miller TE, Burns JH, Munguia P, Walters EL, Kneitel JM, Richards PM, Mouquet N, Buckley HL. A critical review of twenty years’ use of the resource-ratio theory. Am Nat. 2005;165:439–48. doi: 10.1086/428681. [DOI] [PubMed] [Google Scholar]
- 115.Smith VH. Effects of resource supplies on the structure and function of microbial communities. Antonie Van Leeuwenhoek. 2002;81:99–106. doi: 10.1023/a:1020533727307. [DOI] [PubMed] [Google Scholar]
- 116.Cherif M, Loreau M. Stoichiometric constraints on resource use, competitive interactions, and elemental cycling in microbial decomposers. Am Nat. 2007;169:709–24. doi: 10.1086/516844. [DOI] [PubMed] [Google Scholar]
- 117.Brauer VS, Stomp M, Huisman J. The nutrient-load hypothesis: patterns of resource limitation and community structure driven by competition for nutrients and light. Am Nat. 2012;179:721–40. doi: 10.1086/665650. [DOI] [PubMed] [Google Scholar]
- 118.Bellucci M, Ofiţeru ID, Beneduce L, Graham DW, Head IM, Curtis TP. A preliminary and qualitative study of resource ratio theory to nitrifying lab-scale bioreactors. Microb Biotechnol. 2015;8:590–603. doi: 10.1111/1751-7915.12284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.de Mazancourt C, Schwartz MW. A resource ratio theory of cooperation. Ecol Lett. 2010;13:349–59. doi: 10.1111/j.1461-0248.2009.01431.x. [DOI] [PubMed] [Google Scholar]
- 120.Lotka AJ. Contribution to the Energetics of Evolution. Proc Natl Acad Sci U S A. 1922;8:147–51. doi: 10.1073/pnas.8.6.147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Sciubba E. What did Lotka really say? A critical reassessment of the “maximum power principle”. Ecological Modelling. 2011;222:1347–1353. [Google Scholar]
- 122.DeLong JP. The maximum power principle predicts the outcomes of two-species competition experiments. Oikos. 2008;117:1329–1336. [Google Scholar]
- 123.Falkowski PG, Fenchel T, Delong EF. The microbial engines that drive Earth’s biogeochemical cycles. Science. 2008;320:1034–9. doi: 10.1126/science.1153213. [DOI] [PubMed] [Google Scholar]
- 124.Lafferty KD, DeLeo G, Briggs CJ, Dobson AP, Gross T, Kuris AM. ECOLOGICAL THEORY. A general consumer-resource population model. Science. 2015;349:854–7. doi: 10.1126/science.aaa6224. [DOI] [PubMed] [Google Scholar]
- 125.Morris JJ, Lenski RE, Zinser ER. The Black Queen Hypothesis: evolution of dependencies through adaptive gene loss. MBio. 2012:3. doi: 10.1128/mBio.00036-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Sachs JL, Hollowell AC. The origins of cooperative bacterial communities. MBio. 2012:3. doi: 10.1128/mBio.00099-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Oliveira NM, Niehus R, Foster KR. Evolutionary limits to cooperation in microbial communities. Proc Natl Acad Sci U S A. 2014;111:17941–6. doi: 10.1073/pnas.1412673111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Hofbauer J, Sigmund K. Evolutionary games and population dynamics. Cambridge University Press; Cambridge, U.K. ; New York: 1998. [Google Scholar]
- 129.Wangersky PJ. LOTKA-VOLTERRA POPULATION MODELS. Annual Review of Ecology and Systematics. 1978;9:189–218. [Google Scholar]
- 130.Song H, Cannon W, Beliaev A, Konopka A. Mathematical Modeling of Microbial Community Dynamics: A Methodological Review. Processes. 2014;2:711–752. [Google Scholar]
- 131.Estrela S, Trisos CH, Brown SP. From metabolism to ecology: cross-feeding interactions shape the balance between polymicrobial conflict and mutualism. Am Nat. 2012;180:566–76. doi: 10.1086/667887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Santos SB, Carvalho C, Azeredo J, Ferreira EC. Population dynamics of a Salmonella lytic phage and its host: implications of the host bacterial growth rate in modelling. PLoS One. 2014;9:e102507. doi: 10.1371/journal.pone.0102507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Lenski R. Advances in Microbial Ecology. Springer; US: 1988. Dynamics of Interactions between Bacteria and Virulent Bacteriophage; pp. 1–44. [Google Scholar]
- 134.Hoffmann KH, Rodriguez-Brito B, Breitbart M, Bangor D, Angly F, Felts B, Nulton J, Rohwer F, Salamon P. Power law rank-abundance models for marine phage communities. FEMS Microbiol Lett. 2007;273:224–8. doi: 10.1111/j.1574-6968.2007.00790.x. [DOI] [PubMed] [Google Scholar]
- 135.Fisher CK, Mehta P. Identifying keystone species in the human gut microbiome from metagenomic timeseries using sparse linear regression. PLoS One. 2014;9:e102451. doi: 10.1371/journal.pone.0102451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Stein RR, Bucci V, Toussaint NC, Buffie CG, Rätsch G, Pamer EG, Sander C, Xavier JB. Ecological modeling from time-series inference: insight into dynamics and stability of intestinal microbiota. PLoS Comput Biol. 2013;9:e1003388. doi: 10.1371/journal.pcbi.1003388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Mounier J, Monnet C, Vallaeys T, Arditi R, Sarthou AS, Hélias A, Irlinger F. Microbial interactions within a cheese microbial community. Appl Environ Microbiol. 2008;74:172–81. doi: 10.1128/AEM.01338-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Bull JJ, Harcombe WR. Population dynamics constrain the cooperative evolution of cross-feeding. PLoS One. 2009;4:e4115. doi: 10.1371/journal.pone.0004115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Kerner A, Park J, Williams A, Lin XN. A programmable Escherichia coli consortium via tunable symbiosis. PLoS One. 2012;7:e34032. doi: 10.1371/journal.pone.0034032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Weitz JS, Hartman H, Levin SA. Coevolutionary arms races between bacteria and bacteriophage. Proc Natl Acad Sci U S A. 2005;102:9535–40. doi: 10.1073/pnas.0504062102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Harvey E, Heys J, Gedeon T. Quantifying the effects of the division of labor in metabolic pathways. J Theor Biol. 2014;360:222–42. doi: 10.1016/j.jtbi.2014.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Cantrell RS, Cosner C. Spatial ecology via reaction-diffusion equations. J. Wiley; Chichester, England; Hoboken, NJ: 2003. Wiley series in mathematical and computational biology. [Google Scholar]
- 143.Cosner C. Tutorials in Mathematical Biosciences IV. Springer; Berlin Heidelberg: 2008. Reaction–Diffusion Equations and Ecological Modeling; pp. 77–115. [Google Scholar]
- 144.Holmes EE, Lewis MA, Banks JE, Veit RR. PARTIAL-DIFFERENTIAL EQUATIONS IN ECOLOGY - SPATIAL INTERACTIONS AND POPULATION-DYNAMICS. Ecology. 1994;75:17–29. [Google Scholar]
- 145.Murray FRSJ. Interdisciplinary Applied Mathematics. Springer; New York: 2003. Mathematical Biology II: Spatial Models and Biomedical Applications. [Google Scholar]
- 146.Datta MS, Korolev KS, Cvijovic I, Dudley C, Gore J. Range expansion promotes cooperation in an experimental microbial metapopulation. Proc Natl Acad Sci U S A. 2013;110:7354–9. doi: 10.1073/pnas.1217517110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Korolev KS. The fate of cooperation during range expansions. PLoS Comput Biol. 2013;9:e1002994. doi: 10.1371/journal.pcbi.1002994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Müller MJ, Neugeboren BI, Nelson DR, Murray AW. Genetic drift opposes mutualism during spatial population expansion. Proc Natl Acad Sci U S A. 2014;111:1037–42. doi: 10.1073/pnas.1313285111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Menon R, Korolev KS. Public Good Diffusion Limits Microbial Mutualism. Physical Review Letters. 2015:114. doi: 10.1103/PhysRevLett.114.168102. [DOI] [PubMed] [Google Scholar]
- 150.Madeo D, Comolli LR, Mocenni C. Emergence of microbial networks as response to hostile environments. Front Microbiol. 2014;5:407. doi: 10.3389/fmicb.2014.00407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Mao J, Blanchard AE, Lu T. Slow and steady wins the race: a bacterial exploitative competition strategy in fluctuating environments. ACS Synth Biol. 2015;4:240–8. doi: 10.1021/sb4002008. [DOI] [PubMed] [Google Scholar]
- 152.Schuster S, Kreft JU, Schroeter A, Pfeiffer T. Use of game-theoretical methods in biochemistry and biophysics. J Biol Phys. 2008;34:1–17. doi: 10.1007/s10867-008-9101-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Lambert G, Vyawahare S, Austin RH. Bacteria and game theory: the rise and fall of cooperation in spatially heterogeneous environments. Interface Focus. 2014;4:20140029. doi: 10.1098/rsfs.2014.0029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Wang Z, Goldenfeld N. Theory of cooperation in a micro-organismal snowdrift game. Phys Rev E Stat Nonlin Soft Matter Phys. 2011;84:020902. doi: 10.1103/PhysRevE.84.020902. [DOI] [PubMed] [Google Scholar]
- 155.Hol FJ, Galajda P, Nagy K, Woolthuis RG, Dekker C, Keymer JE. Spatial structure facilitates cooperation in a social dilemma: empirical evidence from a bacterial community. PLoS One. 2013;8:e77042. doi: 10.1371/journal.pone.0077042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156.Hummert S, Bohl K, Basanta D, Deutsch A, Werner S, Theissen G, Schroeter A, Schuster S. Evolutionary game theory: cells as players. Mol Biosyst. 2014;10:3044–65. doi: 10.1039/c3mb70602h. [DOI] [PubMed] [Google Scholar]
- 157.Frey E. Evolutionary game theory: Theoretical concepts and applications to microbial communities. Physica a-Statistical Mechanics and Its Applications. 2010;389:4265–4298. [Google Scholar]
- 158.Nowak MA. Evolutionary dynamics : exploring the equations of life. Belknap Press of Harvard University Press; Cambridge, Mass: 2006. [Google Scholar]
- 159.Schuster S, Kreft JU, Brenner N, Wessely F, Theissen G, Ruppin E, Schroeter A. Cooperation and cheating in microbial exoenzyme production--theoretical analysis for biotechnological applications. Biotechnol J. 2010;5:751–8. doi: 10.1002/biot.200900303. [DOI] [PubMed] [Google Scholar]
- 160.Allen B, Gore J, Nowak MA. Spatial dilemmas of diffusible public goods. Elife. 2013;2:e01169. doi: 10.7554/eLife.01169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Ferrer J, Prats C, López D. Individual-based modelling: an essential tool for microbiology. J Biol Phys. 2008;34:19–37. doi: 10.1007/s10867-008-9082-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Hellweger FL, Bucci V. A bunch of tiny individuals-Individual-based modeling for microbes. Ecological Modelling. 2009;220:8–22. [Google Scholar]
- 163.Lardon LA, Merkey BV, Martins S, Dötsch A, Picioreanu C, Kreft JU, Smets BF. iDynoMiCS: next-generation individual-based modelling of biofilms. Environ Microbiol. 2011;13:2416–34. doi: 10.1111/j.1462-2920.2011.02414.x. [DOI] [PubMed] [Google Scholar]
- 164.Kreft JU. Biofilms promote altruism. Microbiology. 2004;150:2751–60. doi: 10.1099/mic.0.26829-0. [DOI] [PubMed] [Google Scholar]
- 165.Nadell CD, Foster KR, Xavier JB. Emergence of spatial structure in cell groups and the evolution of cooperation. PLoS Comput Biol. 2010;6:e1000716. doi: 10.1371/journal.pcbi.1000716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Estrela S, Brown SP. Metabolic and demographic feedbacks shape the emergent spatial structure and function of microbial communities. PLoS Comput Biol. 2013;9:e1003398. doi: 10.1371/journal.pcbi.1003398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Mitri S, Xavier JB, Foster KR. Social evolution in multispecies biofilms. Proc Natl Acad Sci U S A. 2011;108(Suppl 2):10839–46. doi: 10.1073/pnas.1100292108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Momeni B, Brileya KA, Fields MW, Shou W. Strong inter-population cooperation leads to partner intermixing in microbial communities. Elife. 2013;2:e00230. doi: 10.7554/eLife.00230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Ghosh P, Mondal J, Ben-Jacob E, Levine H. Mechanically-driven phase separation in a growing bacterial colony. Proc Natl Acad Sci U S A. 2015;112:E2166–73. doi: 10.1073/pnas.1504948112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170.Feist AM, Herrgård MJ, Thiele I, Reed JL, Palsson B. Reconstruction of biochemical networks in microorganisms. Nat Rev Microbiol. 2009;7:129–43. doi: 10.1038/nrmicro1949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Henry CS, DeJongh M, Best AA, Frybarger PM, Linsay B, Stevens RL. High-throughput generation, optimization and analysis of genome-scale metabolic models. Nat Biotechnol. 2010;28:977–82. doi: 10.1038/nbt.1672. [DOI] [PubMed] [Google Scholar]
- 172.Saha R, Suthers PF, Maranas CD. Zea mays iRS1563: a comprehensive genome-scale metabolic reconstruction of maize metabolism. PLoS One. 2011;6:e21784. doi: 10.1371/journal.pone.0021784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Feist AM, Scholten JC, Palsson B, Brockman FJ, Ideker T. Modeling methanogenesis with a genome-scale metabolic reconstruction of Methanosarcina barkeri. Mol Syst Biol. 2006;2 doi: 10.1038/msb4100046. 2006 0004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 174.Orth JD, Thiele I, Palsson B. What is flux balance analysis? Nat Biotechnol. 2010;28:245–8. doi: 10.1038/nbt.1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175.Schuetz R, Kuepfer L, Sauer U. Systematic evaluation of objective functions for predicting intracellular fluxes in Escherichia coli. Mol Syst Biol. 2007;3:119. doi: 10.1038/msb4100162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176.Schellenberger J, Palsson BO. Use of Randomized Sampling for Analysis of Metabolic Networks. Journal of Biological Chemistry. 2009;284:5457–5461. doi: 10.1074/jbc.R800048200. [DOI] [PubMed] [Google Scholar]
- 177.Bordbar A, Monk JM, King ZA, Palsson BO. Constraint-based models predict metabolic and associated cellular functions. Nat Rev Genet. 2014;15:107–20. doi: 10.1038/nrg3643. [DOI] [PubMed] [Google Scholar]
- 178.McCloskey D, Palsson B, Feist AM. Basic and applied uses of genome-scale metabolic network reconstructions of Escherichia coli. Mol Syst Biol. 2013;9:661. doi: 10.1038/msb.2013.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179.O’Brien EJ, Monk JM, Palsson BO. Using Genome-scale Models to Predict Biological Capabilities. Cell. 2015;161:971–87. doi: 10.1016/j.cell.2015.05.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 180.Zomorrodi AR, Suthers PF, Ranganathan S, Maranas CD. Mathematical optimization applications in metabolic networks. Metab Eng. 2012;14:672–86. doi: 10.1016/j.ymben.2012.09.005. [DOI] [PubMed] [Google Scholar]
- 181.Stolyar S, Van Dien S, Hillesland KL, Pinel N, Lie TJ, Leigh JA, Stahl DA. Metabolic modeling of a mutualistic microbial community. Mol Syst Biol. 2007;3:92. doi: 10.1038/msb4100131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 182.Duarte NC, Herrgård MJ, Palsson B. Reconstruction and validation of Saccharomyces cerevisiae iND750, a fully compartmentalized genome-scale metabolic model. Genome Res. 2004;14:1298–309. doi: 10.1101/gr.2250904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 183.Aung HW, Henry SA, Walker LP. Revising the Representation of Fatty Acid, Glycerolipid, and Glycerophospholipid Metabolism in the Consensus Model of Yeast Metabolism. Ind Biotechnol (New Rochelle N Y) 2013;9:215–228. doi: 10.1089/ind.2013.0013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 184.Shoaie S, Karlsson F, Mardinoglu A, Nookaew I, Bordel S, Nielsen J. Understanding the interactions between bacteria in the human gut through metabolic modeling. Sci Rep. 2013;3:2532. doi: 10.1038/srep02532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185.Shoaie S, Nielsen J. Elucidating the interactions between the human gut microbiota and its host through metabolic modeling. Front Genet. 2014;5:86. doi: 10.3389/fgene.2014.00086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186.Heinken A, Thiele I. Anoxic conditions promote species-specific mutualism between gut microbes in silico. Appl Environ Microbiol. 2015 doi: 10.1128/AEM.00101-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 187.Bordbar A, Feist AM, Usaite-Black R, Woodcock J, Palsson BO, Famili I. A multi-tissue type genome-scale metabolic network for analysis of whole-body systems physiology. BMC Syst Biol. 2011;5:180. doi: 10.1186/1752-0509-5-180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 188.Thiele I, Heinken A, Fleming RM. A systems biology approach to studying the role of microbes in human health. Curr Opin Biotechnol. 2013;24:4–12. doi: 10.1016/j.copbio.2012.10.001. [DOI] [PubMed] [Google Scholar]
- 189.Gomes de Oliveira Dal’Molin C, Quek LE, Saa PA, Nielsen LK. A multi-tissue genome-scale metabolic modeling framework for the analysis of whole plant systems. Front Plant Sci. 2015;6:4. doi: 10.3389/fpls.2015.00004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 190.Bizukojc M, Dietz D, Sun J, Zeng AP. Metabolic modelling of syntrophic-like growth of a 1,3-propanediol producer, Clostridium butyricum, and a methanogenic archeon, Methanosarcina mazei, under anaerobic conditions. Bioprocess Biosyst Eng. 2010;33:507–23. doi: 10.1007/s00449-009-0359-0. [DOI] [PubMed] [Google Scholar]
- 191.Merino MP, Andrews BA, Asenjo JA. Stoichiometric model and flux balance analysis for a mixed culture of Leptospirillum ferriphilum and Ferroplasma acidiphilum. Biotechnol Prog. 2015;31:307–15. doi: 10.1002/btpr.2028. [DOI] [PubMed] [Google Scholar]
- 192.Nagarajan H, Embree M, Rotaru AE, Shrestha PM, Feist AM, Palsson B, Lovley DR, Zengler K. Characterization and modelling of interspecies electron transfer mechanisms and microbial community dynamics of a syntrophic association. Nat Commun. 2013;4:2809. doi: 10.1038/ncomms3809. [DOI] [PubMed] [Google Scholar]
- 193.Segrè D, Vitkup D, Church GM. Analysis of optimality in natural and perturbed metabolic networks. Proc Natl Acad Sci U S A. 2002;99:15112–7. doi: 10.1073/pnas.232349399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 194.Khandelwal RA, Olivier BG, Röling WF, Teusink B, Bruggeman FJ. Community flux balance analysis for microbial consortia at balanced growth. PLoS One. 2013;8:e64567. doi: 10.1371/journal.pone.0064567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 195.Taffs R, Aston JE, Brileya K, Jay Z, Klatt CG, McGlynn S, Mallette N, Montross S, Gerlach R, Inskeep WP, Ward DM, Carlson RP. In silico approaches to study mass and energy flows in microbial consortia: a syntrophic case study. BMC Syst Biol. 2009;3:114. doi: 10.1186/1752-0509-3-114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 196.Zelezniak A, Andrejev S, Ponomarova O, Mende DR, Bork P, Patil KR. Metabolic dependencies drive species co-occurrence in diverse microbial communities. Proc Natl Acad Sci U S A. 2015;112:6449–54. doi: 10.1073/pnas.1421834112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 197.Kreimer A, Doron-Faigenboim A, Borenstein E, Freilich S. NetCmpt: a network-based tool for calculating the metabolic competition between bacterial species. Bioinformatics. 2012;28:2195–7. doi: 10.1093/bioinformatics/bts323. [DOI] [PubMed] [Google Scholar]
- 198.Levy R, Borenstein E. Metabolic modeling of species interaction in the human microbiome elucidates community-level assembly rules. Proc Natl Acad Sci U S A. 2013;110:12804–9. doi: 10.1073/pnas.1300926110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 199.Borenstein E, Feldman MW. Topological signatures of species interactions in metabolic networks. J Comput Biol. 2009;16:191–200. doi: 10.1089/cmb.2008.06TT. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 200.Levy R, Carr R, Kreimer A, Freilich S, Borenstein E. NetCooperate: a network-based tool for inferring host-microbe and microbe-microbe cooperation. BMC Bioinformatics. 2015;16:164. doi: 10.1186/s12859-015-0588-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 201.Zomorrodi AR, Maranas CD. OptCom: a multi-level optimization framework for the metabolic modeling and analysis of microbial communities. PLoS Comput Biol. 2012;8:e1002363. doi: 10.1371/journal.pcbi.1002363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202.El-Semman IE, Karlsson FH, Shoaie S, Nookaew I, Soliman TH, Nielsen J. Genome-scale metabolic reconstructions of Bifidobacterium adolescentis L2-32 and Faecalibacterium prausnitzii A2-165 and their interaction. BMC Syst Biol. 2014;8:41. doi: 10.1186/1752-0509-8-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 203.Zhuang K, Izallalen M, Mouser P, Richter H, Risso C, Mahadevan R, Lovley DR. Genome-scale dynamic modeling of the competition between Rhodoferax and Geobacter in anoxic subsurface environments. ISME J. 2011;5:305–16. doi: 10.1038/ismej.2010.117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 204.Salimi F, Zhuang K, Mahadevan R. Genome-scale metabolic modeling of a clostridial co-culture for consolidated bioprocessing. Biotechnol J. 2010;5:726–38. doi: 10.1002/biot.201000159. [DOI] [PubMed] [Google Scholar]
- 205.Zhuang K, Ma E, Lovley DR, Mahadevan R. The design of long-term effective uranium bioremediation strategy using a community metabolic model. Biotechnol Bioeng. 2012;109:2475–83. doi: 10.1002/bit.24528. [DOI] [PubMed] [Google Scholar]
- 206.Hanly TJ, Henson MA. Dynamic flux balance modeling of microbial co-cultures for efficient batch fermentation of glucose and xylose mixtures. Biotechnol Bioeng. 2011;108:376–85. doi: 10.1002/bit.22954. [DOI] [PubMed] [Google Scholar]
- 207.Hanly TJ, Henson MA. Dynamic metabolic modeling of a microaerobic yeast co-culture: predicting and optimizing ethanol production from glucose/xylose mixtures. Biotechnol Biofuels. 2013;6:44. doi: 10.1186/1754-6834-6-44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 208.Tzamali E, Poirazi P, Tollis IG, Reczko M. A computational exploration of bacterial metabolic diversity identifying metabolic interactions and growth-efficient strain communities. BMC Syst Biol. 2011;5:167. doi: 10.1186/1752-0509-5-167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 209.Hanly TJ, Henson MA. Dynamic model-based analysis of furfural and HMF detoxification by pure and mixed batch cultures of S. cerevisiae and S. stipitis. Biotechnol Bioeng. 2014;111:272–84. doi: 10.1002/bit.25101. [DOI] [PubMed] [Google Scholar]
- 210.Henson MA, Hanly TJ. Dynamic flux balance analysis for synthetic microbial communities. IET Syst Biol. 2014;8:214–29. doi: 10.1049/iet-syb.2013.0021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 211.Mahadevan R, Edwards JS, Doyle FJ. Dynamic flux balance analysis of diauxic growth in Escherichia coli. Biophys J. 2002;83:1331–40. doi: 10.1016/S0006-3495(02)73903-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 212.Chiu HC, Levy R, Borenstein E. Emergent biosynthetic capacity in simple microbial communities. PLoS Comput Biol. 2014;10:e1003695. doi: 10.1371/journal.pcbi.1003695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 213.Mahadevan R, Schilling CH. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab Eng. 2003;5:264–76. doi: 10.1016/j.ymben.2003.09.002. [DOI] [PubMed] [Google Scholar]
- 214.Zomorrodi AR, Islam MM, Maranas CD. d-OptCom: Dynamic multi-level and multi-objective metabolic modeling of microbial communities. ACS Synth Biol. 2014;3:247–57. doi: 10.1021/sb4001307. [DOI] [PubMed] [Google Scholar]
- 215.Harcombe WR, Riehl WJ, Dukovski I, Granger BR, Betts A, Lang AH, Bonilla G, Kar A, Leiby N, Mehta P, Marx CJ, Segrè D. Metabolic resource allocation in individual microbes determines ecosystem interactions and spatial dynamics. Cell Rep. 2014;7:1104–15. doi: 10.1016/j.celrep.2014.03.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 216.Cole JA, Kohler L, Hedhli J, Luthey-Schulten Z. Spatially-resolved metabolic cooperativity within dense bacterial colonies. BMC Syst Biol. 2015;9:15. doi: 10.1186/s12918-015-0155-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 217.Knutson CE, Werth CJ, Valocchi AJ. Pore-scale simulation of biomass growth along the transverse mixing zone of a model two-dimensional porous medium. Water Resources Research. 2005:41. [Google Scholar]
- 218.Scheffer M, Baveco JM, Deangelis DL, Rose KA, Vannes EH. SUPER-INDIVIDUALS A SIMPLE SOLUTION FOR MODELING LARGE POPULATIONS ON AN INDIVIDUAL BASIS. Ecological Modelling. 1995;80:161–170. [Google Scholar]
- 219.Begon M, Townsend CR, Harper JL. Ecology : from individuals to ecosystems. 4. Blackwell Pub; Malden, MA ; Oxford: 2005. [Google Scholar]
- 220.Scheibe TD, Mahadevan R, Fang Y, Garg S, Long PE, Lovley DR. Coupling a genome-scale metabolic model with a reactive transport model to describe in situ uranium bioremediation. Microb Biotechnol. 2009;2:274–86. doi: 10.1111/j.1751-7915.2009.00087.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 221.Kang S, Kahan S, Momeni B. Simulating microbial community patterning using Biocellion. Methods Mol Biol. 2014;1151:233–53. doi: 10.1007/978-1-4939-0554-6_16. [DOI] [PubMed] [Google Scholar]
- 222.Latendresse M, Krummenacker M, Trupp M, Karp PD. Construction and completion of flux balance models from pathway databases. Bioinformatics. 2012;28:388–96. doi: 10.1093/bioinformatics/btr681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 223.Agren R, Liu L, Shoaie S, Vongsangnak W, Nookaew I, Nielsen J. The RAVEN toolbox and its use for generating a genome-scale metabolic model for Penicillium chrysogenum. PLoS Comput Biol. 2013;9:e1002980. doi: 10.1371/journal.pcbi.1002980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 224.Benedict MN, Mundy MB, Henry CS, Chia N, Price ND. Likelihood-based gene annotations for gap filling and quality assessment in genome-scale metabolic models. PLoS Comput Biol. 2014;10:e1003882. doi: 10.1371/journal.pcbi.1003882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 225.Roberts RJ, Chang YC, Hu Z, Rachlin JN, Anton BP, Pokrzywa RM, Choi HP, Faller LL, Guleria J, Housman G, Klitgord N, Mazumdar V, McGettrick MG, Osmani L, Swaminathan R, Tao KR, Letovsky S, Vitkup D, Segrè D, Salzberg SL, Delisi C, Steffen M, Kasif S. COMBREX: a project to accelerate the functional annotation of prokaryotic genomes. Nucleic Acids Res. 2011;39:D11–4. doi: 10.1093/nar/gkq1168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 226.Raymond J, Segrè D. The effect of oxygen on biochemical networks and the evolution of complex life. Science. 2006;311:1764–7. doi: 10.1126/science.1118439. [DOI] [PubMed] [Google Scholar]
- 227.Ebenhöh O, Handorf T, Heinrich R. Structural analysis of expanding metabolic networks. Genome Inform. 2004;15:35–45. [PubMed] [Google Scholar]
- 228.Klitgord N, Segrè D. The importance of compartmentalization in metabolic flux models: yeast as an ecosystem of organelles. Genome Inform. 2010;22:41–55. [PubMed] [Google Scholar]
- 229.Karr JR, Sanghvi JC, Macklin DN, Gutschow MV, Jacobs JM, Bolival B, Assad-Garcia N, Glass JI, Covert MW. A whole-cell computational model predicts phenotype from genotype. Cell. 2012;150:389–401. doi: 10.1016/j.cell.2012.05.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 230.Lerman JA, Hyduke DR, Latif H, Portnoy VA, Lewis NE, Orth JD, Schrimpe-Rutledge AC, Smith RD, Adkins JN, Zengler K, Palsson BO. In silico method for modelling metabolism and gene product expression at genome scale. Nat Commun. 2012;3:929. doi: 10.1038/ncomms1928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 231.Purcell O, Jain B, Karr JR, Covert MW, Lu TK. Towards a whole-cell modeling approach for synthetic biology. Chaos. 2013;23:025112. doi: 10.1063/1.4811182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 232.O’Brien EJ, Lerman JA, Chang RL, Hyduke DR, Palsson B. Genome-scale models of metabolism and gene expression extend and refine growth phenotype prediction. Mol Syst Biol. 2013;9:693. doi: 10.1038/msb.2013.52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 233.Escalante AE, Rebolleda-Gómez M, Benítez M, Travisano M. Ecological perspectives on synthetic biology: insights from microbial population biology. Front Microbiol. 2015;6:143. doi: 10.3389/fmicb.2015.00143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 234.Ives AR. PREDICTING THE RESPONSE OF POPULATIONS TO ENVIRONMENTAL-CHANGE. Ecology. 1995;76:926–941. [Google Scholar]
- 235.Mueller LD, Joshi A. Monographs in population biology. Princeton University Press; Princeton, N.J: 2000. Stability in model populations. [Google Scholar]
- 236.Nowak MA, Sasaki A, Taylor C, Fudenberg D. Emergence of cooperation and evolutionary stability in finite populations. Nature. 2004;428:646–50. doi: 10.1038/nature02414. [DOI] [PubMed] [Google Scholar]
- 237.Borrelli JJ, Allesina S, Amarasekare P, Arditi R, Chase I, Damuth J, Holt RD, Logofet DO, Novak M, Rohr RP, Rossberg AG, Spencer M, Tran JK, Ginzburg LR. Selection on stability across ecological scales. Trends Ecol Evol. 2015;30:417–25. doi: 10.1016/j.tree.2015.05.001. [DOI] [PubMed] [Google Scholar]
- 238.Goldman RP, Brown SP. Making sense of microbial consortia using ecology and evolution. Trends Biotechnol. 2009;27:3–4. doi: 10.1016/j.tibtech.2008.10.003. author reply 4. [DOI] [PubMed] [Google Scholar]
- 239.Swenson W, Wilson DS, Elias R. Artificial ecosystem selection. Proc Natl Acad Sci U S A. 2000;97:9110–4. doi: 10.1073/pnas.150237597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 240.Swenson W, Arendt J, Wilson DS. Artificial selection of microbial ecosystems for 3-chloroaniline biodegradation. Environ Microbiol. 2000;2:564–71. doi: 10.1046/j.1462-2920.2000.00140.x. [DOI] [PubMed] [Google Scholar]
- 241.Williams HT, Lenton TM. Artificial selection of simulated microbial ecosystems. Proc Natl Acad Sci U S A. 2007;104:8918–23. doi: 10.1073/pnas.0610038104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 242.Temme K, Zhao D, Voigt CA. Refactoring the nitrogen fixation gene cluster from Klebsiella oxytoca. Proc Natl Acad Sci U S A. 2012;109:7085–90. doi: 10.1073/pnas.1120788109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 243.MIT. Registry of Standard Biological Parts. 2003. [Google Scholar]
- 244.Wen ZQ, Wu MB, Lin YJ, Yang LR, Lin JP, Cen PL. A novel strategy for sequential co-culture of Clostridium thermocellum and Clostridium bezjerinckii to produce solvents from alkali extracted corn cobs. Process Biochemistry. 2014;49:1941–1949. [Google Scholar]