Invited Review Article: Pump-probe microscopy

Abstract

Multiphoton microscopy has rapidly gained popularity in biomedical imaging and materials science because of its ability to provide three-dimensional images at high spatial and temporal resolution even in optically scattering environments. Currently the majority of commercial and home-built devices are based on two-photon fluorescence and harmonic generation contrast. These two contrast mechanisms are relatively easy to measure but can access only a limited range of endogenous targets. Recent developments in fast laser pulse generation, pulse shaping, and detection technology have made accessible a wide range of optical contrasts that utilize multiple pulses of different colors. Molecular excitation with multiple pulses offers a large number of adjustable parameters. For example, in two-pulse pump-probe microscopy, one can vary the wavelength of each excitation pulse, the detection wavelength, the timing between the excitation pulses, and the detection gating window after excitation. Such a large parameter space can provide much greater molecular specificity than existing single-color techniques and allow for structural and functional imaging without the need for exogenous dyes and labels, which might interfere with the system under study. In this review, we provide a tutorial overview, covering principles of pump-probe microscopy and experimental setup, challenges associated with signal detection and data processing, and an overview of applications.

I. INTRODUCTION

Pump-probe microscopy is a specific implementation of a general approach, the use of nonlinear optical processes to improve molecular specificity, resolution, and penetration depth. Nonlinear optical processes such as frequency doubling began to be extensively explored shortly after the invention of the laser.¹ Many such processes provide intrinsic molecular contrast; for example, two-photon absorption (TPA) requires a resonance match to a transition at twice the laser frequency. However, these effects scale as the second (or higher) power of the laser intensity, and observable signatures are much smaller than with conventional, linear effects even with an amplified laser system. In some cases, these effects can only be measured through minute changes imprinted on the excitation fields, in which case, the detection is highly complicated by the intrinsic pulse-to-pulse amplitude instability of most amplified systems. As a result, for the first several decades of exploration of nonlinear effects, the vast majority of the work was done with peak powers that would be fine for crystals or even solutions, but clearly unacceptable for biological tissue; in addition, the low repetition rate of such systems (typically about 1 kHz) precluded acquiring a spatially resolved image in a reasonable amount of time.

Thus, the introduction of two-photon excited fluorescence (TPF) microscopy,² using the relatively low peak powers of a modelocked laser system, represented a major step forward. Two-photon microscopy is common in biology laboratories today, with several systems commercially available. Nonlinear laser scanning optical microscopy has advanced dramatically over the last decade and has become a commonplace in dedicated biological, biomedical, and materials science research labs.^3–8 It permits much deeper high-resolution tissue imaging than does conventional microscopy because the excitation photons (mostly in the near-infrared) are less strongly scattered than visible light and the induced fluorescence (proportional to intensity squared) is largely generated at the un-scattered light focus. In general, this method produces light which is shorter in wavelength than the excitation light, easily separable from the strong laser beams. In favorable cases, two-photon fluorescence microscopy achieves a penetration depth up to 1 mm in scattering tissue.

However, this approach has several fundamental limitations. The most obvious one is that the target has to fluoresce (few endogenous targets do). Another challenge is that tissue markers that do fluoresce in the visible and near-infrared tend to have absorption and fluorescence spectra that are very broad and unstructured. This lack of distinguishing features reduces specificity, at least in comparison to other spectroscopic methods such as magnetic resonance or vibrational spectroscopy. Melanin, the skin’s protective pigment, exemplifies both challenges; it has a low fluorescence quantum yield (in the order of 10⁻³) and has broad absorption and emission lines (in addition, melanin can even reabsorb fluorescence throughout the UV and visible). For these reasons, pigmented lesions are a very difficult target for conventional TPF microscopy (in Sec. IV, we will describe more elaborate measurement techniques that analyze fluorescence dynamics for added pigment contrast). Because of these limitations, most conventional TPF applications use extrinsic fluorophores, which for clinical applications are limited by toxicity issues.⁹

A major focus of recent work has been the development of methods to detect molecular signatures which do not generate light of a different color.¹⁰ TPA can exist in molecules which do not fluoresce (or fluoresce very weakly), such as melanins or hemoglobins.^11–13 Self-phase modulation (SPM, resulting in self-induced index of refraction changes at high peak power) can even exist for samples which do not absorb^10,14–17 and can offer additional functional contrast in tissue; for example, the nonlinear refractive index differences in intracellular environments¹⁸ or changes with neuronal firing.¹⁶ The challenge is that at the powers we would typically be willing to apply to biological samples (milliwatts), only about one photon in a million is lost to TPA; far more are lost to scattering or linear absorption, and hence those present a strong background. The fundamental solution has been to use either femtosecond pulse shaping^10,19,20 or pulse train modulation¹¹ to separate nonlinear signals from the linear background. Pump-probe microscopy is one of these methods; over the last few years, it has become clear that carefully controlled modulation of a train of “pump” laser pulses, coupled with clean detection of that modulation frequency on a train of time-delayed “probe” laser pulses, can provide distinctive signatures even between molecules with very similar linear absorption spectra. This is because the dynamics of the population excited by the pump laser (and the corresponding hole in the ground state population) evolves under many different, complex processes on a femtosecond to picosecond timescale. Certain aspects of the excited state population dynamics can be analyzed by recording fluorescence lifetimes (assuming fluorescence is present), but the richer parameter space of pump-probe microscopy offers advantages in specificity. The earliest femtosecond pump-probe imaging experiment used photographic plates to record photo-induced melting and evaporation of silicon on timescales of 100 fs–600 ps.²¹ Today, high quality images can be obtained with simple detection of transmitted or scattered light, with very modest power dissipation (less average power than a laser pointer), in a short time (many frames per second), and with high enough sensitivity to image specific endogenous tissue markers. Pump-probe microscopy has been the subject of two recent reviews^22,23 that have a considerable amount of detail on material science and nanomaterials applications. In this review, we will frame pump-probe microscopy in the broader context of nonlinear optical microscopy and provide more detail on signal-to-noise ratio considerations, data analysis techniques, and applications in biology and art conservation.

II. THE PUMP-PROBE MICROSCOPE

A. Overview of optical nonlinearities

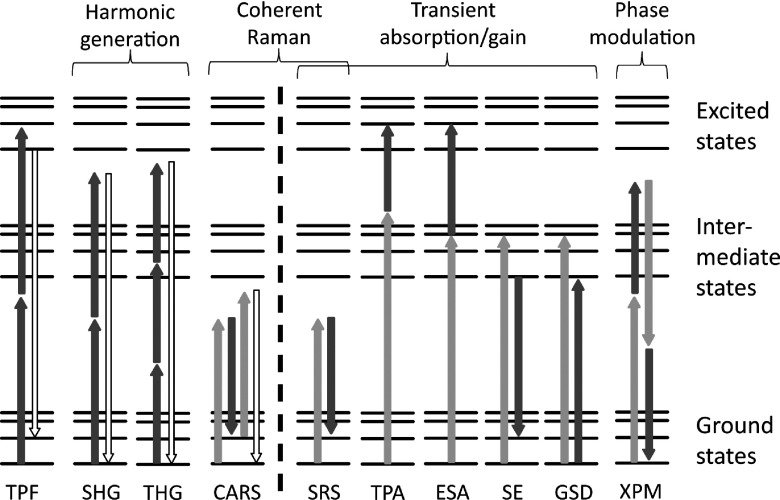
Figure 1 illustrates a variety of optical interactions that proved useful for gaining contrast in microscopy. These processes are well known to optical physicists (much less so to microscopists) and some of them even serve as showcases for the conventional series expansion of nonlinear polarization in optical textbooks^24,25 (second-harmonic generation (SHG) and third-harmonic generation (THG) exemplify second- and third-order susceptibility terms, respectively). Some contrast types in Fig. 1 can be directly associated with a corresponding term in this expansion (e.g., two-photon absorption, two-photon fluorescence, coherent Raman, and cross-phase modulation (XPM) are all associated with third-order susceptibilities), while others (e.g., those processes involving appreciable population transfer) are best described using different approaches.²⁵ For the purpose of this review, we simply consider an interaction to be nonlinear if the observable signal depends on the illumination intensity with a power that is higher than linear, irrespective of the underlying order of the susceptibility.

FIG. 1.

Nonlinear optical interactions available for multiphoton image contrast. On the left side of the dashed line are conventional contrast mechanisms: two-photon-excited fluorescence (TPF), second-harmonic generation (SHG), third-harmonic generation (THG), and coherent anti-Stokes Raman scattering (CARS). On the right are additional contrasts accessible with pump-probe microscopy: stimulated Raman scattering (SRS), two-photon absorption (TPA, degenerate or non-degenerate), excited-state absorption (ESA), stimulated emission (SE), ground state depletion (GSD), and cross-phase modulation (XPM).

The concept of pump-probe is very general and can be applied to a variety of nonlinear interactions. For this reason, we first briefly review the general properties of nonlinear microscopy and provide references to established modalities. Many of the expressions quantifying the properties of conventional nonlinear microscopy (such as achievable resolution and penetration depth) can also be applied to pump-probe microscopy. We then focus on aspects unique to pump-probe, such as modulation detection methods and specialized synchronized, multi-color pulse sources.

B. Nonlinear laser scanning optical microscopy

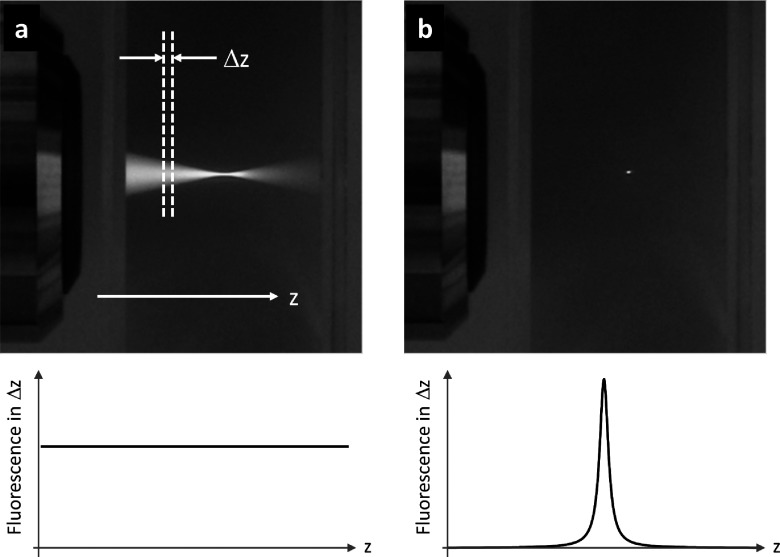
Nonlinear laser scanning optical microscopy has advanced dramatically over the last decade and has become a commonplace in dedicated biological, biomedical, and materials science research labs.^3–8 Nonlinear microscopy has distinct advantages over linear microscopy (such as confocal fluorescence) for three-dimensional imaging, especially in highly scattering media such as biological tissue. In order to understand why this is so, consider a laser beam focused by a microscope objective into a thick homogeneous specimen, uniformly labeled with a fluorophore (see Fig. 2).

FIG. 2.

Top: fluorescence generated in Rhodamine excited by (a) continuous wave UV light and (b) short near-IR pulses. Bottom: integrated fluorescence from a thin slice of thickness Δz for (a) linear excitation and (b) nonlinear excitation.

In the linear regime, the incident light can excite the fluorophore via a one-photon transition, and the emitted fluorescence from any thin plane (perpendicular to the beam propagation) is proportional to the product of light intensity and the cross-sectional area of the beam. The intensity is highest at the focal plane, but in the out-of-focus planes, the reduced intensity is compensated by increased cross-sectional area. So the in-focus and out-of-focus planes each produce an equal amount of fluorescence, resulting in a loss of depth information. Depth information can be recovered with the use of numerical deconvolution techniques²⁶ or a confocal pinhole to reject the out-of-focus light²⁷ (optical coherence tomography uses interferometry to recover depth information, but it does not work with incoherent fluorescence emission). These methods work well in clear and moderately scattering samples, but strong scattering reduces the effectiveness of the pinhole and reduces image contrast at large depths.

Nonlinear microscopy is less susceptible to image degradation caused by scattering. In nonlinear microscopy, the generated signal scales non-linearly with power; for example, in the case of two-photon-excited fluorescence, the signal scales quadratically with excitation power. The advantage of such a nonlinear process is that signal generation occurs predominantly where the intensity is highest, i.e., at the focus, and provides almost complete suppression of signal from surrounding out-of-focus regions without the need for a pinhole or numerical deconvolution. In scattering media, deflected light is generally too weak to generate significant nonlinear signal (it is surface contribution, rather than scattered light, that ultimately limits the achievable imaging depth²⁸). The spatial localization of the excitation (as opposed to localization in the detection, as in confocal microscopy) makes nonlinear microscopy less susceptible to light scattering. In addition, multiphoton-excited fluorescence uses several low-energy (long-wavelength) photons instead of a single high-energy (short-wavelength) photon to excite a molecule, which benefits from the reduced attenuation of longer excitation wavelengths in tissue. As a result, nonlinear microscopy achieves much greater imaging depths than scanning confocal microscopy^28,29 at a comparable spatial resolution.^30,31 For example, over a millimeter of depth penetration has recently been achieved in three-photon excited fluorescence imaging of labelled vasculature and neurons in a mouse brain.³²

The range of light-matter interactions that can be used to generate image contrast in nonlinear microscopy is quite diverse, as illustrated in Figure 1. The most widely used nonlinear contrast types, shown on the left, are based on the interactions most easily measured: TPF,² SHG,^33,34 THG,^35,36 Coherent anti-Stokes Raman scattering (CARS^37,38), and four-wave mixing.^39,40 Each of these interactions generates a new color, which is readily separated from scattered excitation light using a colored glass or dielectric filter and detected with a photomultiplier. However, few materials or endogenous targets in tissue provide such convenient contrast.

The nonlinear light-matter interactions in the right of Fig. 1 could substantially broaden the range of available targets. However, these interactions do not generate new colors and therefore require more sophisticated measurement techniques. “Pump-probe imaging” is one such technique, which imposes a modulation on one of the incident pulse trains (the pump) so that the nonlinear signal of interest appears as a modulation in the other pulse train (the probe). This modulation transfer, from the pump onto the probe, can be detected with a lock-in amplifier with high sensitivity. An important consideration is to choose a modulation frequency in an uncongested band of the radio-frequency spectrum of the probe pulse train (typically >1 MHz, away from the low-frequency laser noise).

Because multiple photons are involved, there is a larger parameter space that can be utilized for generation of molecular contrast. In linear microscopy, users may tune the excitation wavelength, detection wavelength, and time delay between excitation and detection (e.g., in coherence tomography and fluorescence lifetime experiments), essentially limiting the parameter space to three dimensions in which to separate molecular components. For two-photon interactions, one can vary the wavelength of each excitation pulse, the detection wavelength, the timing between the excitation pulses, and the detection gating window, resulting in a five-dimensional parameter space. Here we focus primarily on wavelength and relative timing, but adding polarization directions of the excitation and detected light fields further increases the available parameter space. Hence, nonlinear contrast mechanisms provide more opportunities for molecular specificity, e.g., in biological tissue without the need for exogenous dyes and labels, which might interfere with the system under study. The focus of this review is on techniques and applications that take advantage of the dependence on time delay between the pump and probe pulse to provide contrast between molecules that have otherwise indistinguishable optical properties.

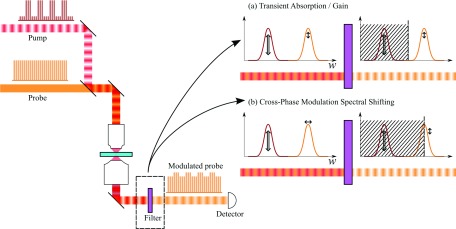
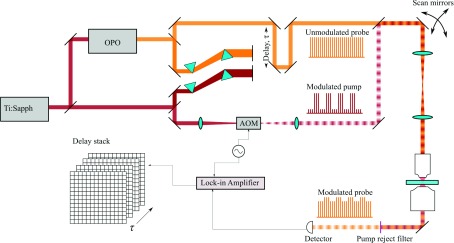
Multiphoton microscopes commonly employ short-pulse laser sources (typically ∼100 fs, though Raman-based CARS/stimulated Raman scattering (SRS) microscopes employ narrower bandwidth ∼1-2 ps pulses to achieve higher spectral resolution). Several user-friendly and well-engineered commercial multiphoton systems are on the market; but for the do-it-yourselfers, there are instructions available (at all levels of performance and complexity) for system construction from scratch^41–43 or starting from a commercial confocal system.⁴⁴ In addition, control software is freely accessible (such as MPScope⁴⁵ or ScanImage⁴⁶). Because two-photon fluorescence and harmonic generation utilize similar laser sources and detection strategies, pump-probe microscopy lends itself to implementation in a multimodal approach.^47–50 For a recent review specifically addressing multimodality in nonlinear microscopy, see Ref. 51. Adding pump-probe contrast to an existing multiphoton microscope is a matter of generating a second, time-synchronized pulse train, modulating one of the beams, and adding lock-in detection to one of the imaging channels (see Fig. 3).

FIG. 3.

Pump-probe schematic. An intensity-modulated pump and non-modulated probe are combined and passed through a laser scanning microscope. The collected light is filtered before detection by one of two schemes. (a) For transient absorption/gain processes that imprint an amplitude modulation on the probe, the filter only needs to reject the pump before detection. (b) For phase modulation processes that shift the probe optical spectrum, a filter that cuts off part of the probe spectrum converts the spectral shift into an amplitude modulation (XPMSS).

C. Transient absorption/gain processes

In transient absorption or gain processes, a molecule couples two or more light fields to cause a loss or gain in one or more of these fields. To measure such nonlinear interactions, the probe is measured in the presence and absence of interactions with the pump in the focal spot and the relative change is recorded. A convenient way to achieve this comparison is to rapidly modulate the pump and analyze the induced change in the probe with a lock-in amplifier. Figure 3(a) illustrates this process. Practically, there must be some means of rejecting the modulated pump field before the detector, which would overwhelm the lock-in amplifier. Most commonly, pump rejection is done chromatically, leveraging differences in pump and probe wavelength, but differences in direction or polarization can also be used. Pump rejection is straightforward in detecting transmitted light, but can be more challenging when detecting backscatter.⁵²

The majority of optical interactions shown on the right in Fig. 1 are transient absorption or gain processes. In SRS, the interference of two pulses can coherently drive a molecular vibration if the frequency difference between the pulses coincides with the vibrational frequency of the molecule. In SRS, the higher-energy (shorter wavelength) pulse experiences a loss, while the lower-energy (longer wavelength) pulse experiences a gain. In TPA, a molecular transition occurs by simultaneous absorption of two photons. Absorption can occur with two photons from one beam (degenerate TPA) or with one photon from each beam (non-degenerate TPA, also sometimes referred to as sum-frequency absorption or SFA). Note that in this review, we consider only the non-degenerate version of TPA, which lends itself more naturally to measurement with pump-probe techniques. TPA is the first step in two-photon fluorescence, but TPA allows for the detection of molecules that do not fluoresce appreciably (e.g., those that relax via non-radiative processes). Both SRS and TPA involve virtual states and require the pulses to be overlapped in time. The remaining transient absorption/gain processes in Fig. 1 involve a real intermediate state, whose evolution can be probed on the timescale of femtoseconds to picoseconds by scanning the time delay between the pump and probe pulses. In excited state absorption (ESA), a photon from one pulse is absorbed, exciting the molecule from the ground to an intermediate state. This process can increase absorptivity of the second pulse, which can excite the molecule to an even higher energy state. In stimulated emission (SE), the second pulse can stimulate the emission of a photon after higher states have been populated by the first pulse. This process leads to a decreased attenuation of the second pulse (this pulse experiences gain). In ground state depletion (GSD or ground state bleach), the first pulse excites molecules, thereby reducing population in the ground state. The second pulse, inducing transitions from the ground to other excited states, therefore encounters fewer molecules in the ground state and as a consequence also experiences decreased attenuation. Both SE and GSD have been successfully utilized to obtain super-resolution images via stimulated emission depletion and ground state depletion microscopy (see Ref. 53 for a review of these and other super-resolution techniques). The enhanced spatial resolution in these techniques relies on the highly nonlinear light-molecule interaction, which effectively changes the linear, diffraction-limited point spread function to one that can exhibit much sharper features. In this review, we focus on intensity levels that are low enough to only generate signals that are “weakly” nonlinear (i.e., proportional to the product of pump and probe intensities).

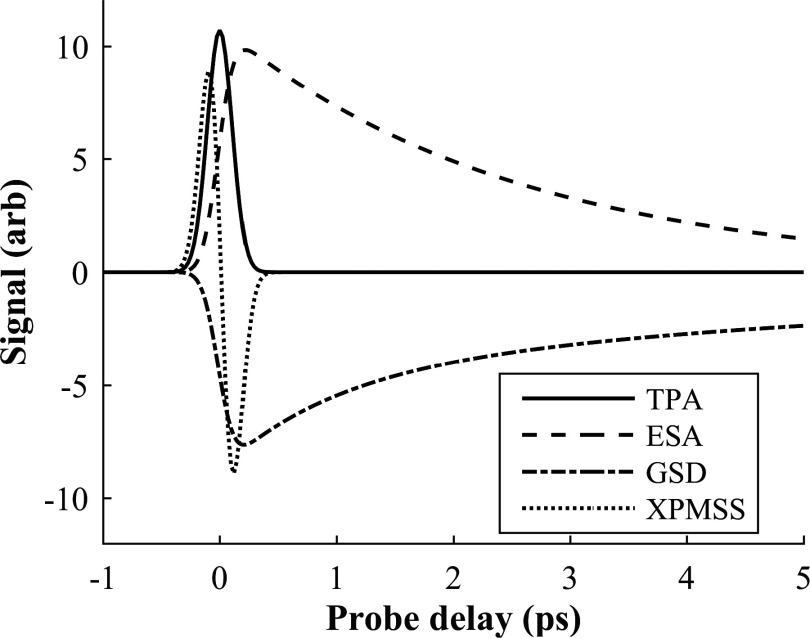
Transient absorption and gain processes can be distinguished from each other by observing whether the probe signal increases or decreases in the presence of the pump. In a lock-in amplifier referenced to the pump modulation, absorption and gain processes are 180° out of phase. Therefore, processes that increase probe absorption in the presence of the pump (TPA, ESA) lead to a lock-in signal that is opposite in sign from processes that decrease absorption (SE, GSD). SRS can have either sign, depending on whether the lower- or higher-energy pulses are used as the probe. In the following, we assign positive signals to increased probe absorption, consistent with the transient absorption literature. Furthermore, varying the temporal delay between pump and probe pulses (here by varying the optical path length of one of the beams) can record excited-state relaxation dynamics, thus providing additional molecular specificity. Figure 4 illustrates typical temporal dynamics for some of the nonlinear processes.

FIG. 4.

Typical time traces for various nonlinear interactions (two-photon absorption, excited-state absorption, ground state depletion, and cross-phase modulation spectral shifting [XPMSS, discussed below]).

D. Phase modulation processes

While nonlinear optical interactions can change the amplitude of light fields via transient absorption and gain processes, a variety of effects can alter their phases. The phase of light, though more difficult to measure than the intensity, is of prime importance in visualizing transparent, unlabeled specimens. Linear techniques such as phase microscopy or differential interference microscopy⁵⁴ have made a dramatic impact on biological microscopy, but these are primarily applicable to thin samples without appreciable scattering. Depth-resolved phase-sensitive techniques are being developed (e.g., phase-sensitive optical coherence tomography⁵⁵ measures the accumulated phase in the light path relative to a reference surface and oblique back-illumination microscopy⁵⁶ uses backscattered light to effectively create a gradient illumination) that offer refractive index contrast in thick media in epi-mode. Extending phase contrast to the nonlinear optical domain would directly take advantage of the optical sectioning properties of nonlinear microscopy and also offer the possibility to map localized phase information in thick, scattering samples.

This may be possible through SPM and XPM interactions. SPM is a nonlinear process that modulates the refractive index by an amount proportional to the instantaneous pulse intensity (n = n_o + n₂I), most commonly due to Kerr nonlinearities.²⁵ SPM is sensitive to a wide range of material properties, such as resonant and non-resonant electronic or molecular reorientation effects, causing common transparent solvents to differ by more than two orders of magnitude in SPM coefficients.⁵⁷ Other transient phase modulation processes with femtosecond to picosecond dynamics are impulsive stimulated Raman⁵⁸ and Brillouin scattering.⁵⁹

Though SPM is routinely measured through the Z-scan technique,^60,61 it proves quite difficult to extract in an imaging environment because of scattering. Early micro-spectroscopic experiments in single cells relied on the detection of pump-induced polarization changes⁶² and more recent measurement methods based on spectral pulse re-shaping were experimentally complex.^14,15,17 A promising and convenient way to improve sensitivity is to measure XPM, the dual-color version of SPM. By simple modifications to a pump-probe microscope, one can leverage XPM contrast to provide nonlinear phase information that is complementary to transient absorption/gain. XPM between two pulses manifests itself as a phase change in the probe beam as a function of the temporally varying pump intensity.⁶³ These phase changes can be measured by interferometry, as long as a stable reference pulse can be mixed with the probe at the detector.⁶⁴ One way to accomplish this is to generate a collinear, time-delayed copy of the probe with a birefringent crystal, to serve as a reference.^65,66 This approach has been used to measure transient changes in refractive index in gold nanoparticles, in a slow stage-scanning microscope,⁶⁷ but has not been successfully demonstrated yet in a fast beam-scanning microscope. In addition, the use of polarization to separate probe and reference pulses is likely to present difficulties in thick, optically scattering specimens. An alternative is to measure temporal phase modulations by their effects on the optical spectrum on the probe, which is shifted in opposite directions, depending on whether the probe pulse is temporally aligned with the rising or falling edge of the pump pulse (when pump and probe pulses are temporally aligned, the probe spectrum is not shifted but merely symmetrically broadened). This spectral shift can be converted into a detectable amplitude change by passing the probe through a spectral filter that rejects the low- (or high-) frequency half of the spectrum.⁶⁸ This principle is illustrated in Fig. 3(b). This “cross-phase modulation spectral shifting” (XPMSS) method encodes the nonlinear phase signature in the spectral domain and hence is able to extract phase contrast even in cases where linear techniques are made impossible by scattering. More recently, a pump-probe spectral interferometry technique has been developed that utilizes several phase-shifted copies of the probe pulse created by a femtosecond pulse shaper.¹⁸ This method was used to image structure in onion epithelial cells by analyzing reorientation dynamics of water, which is affected by the water’s microenvironment.

E. Experimental setup of a pump-probe microscope

Femtosecond time-resolved pump-probe techniques have been used for decades in spectroscopy, but only recent advances in laser technology have resulted in synchronized, dual-color sources that are fast and stable enough to allow imaging at low power and reasonable frame rates. In the description of the experimental setup (and the example applications), we limit our discussion to instruments that resolve temporal dynamics of optically induced transients by scanning the delay between pump and probe pulses. Hence we exclude SRS, which generally operates with picosecond rate laser sources, but instead refer the reader to recent reviews^69–72 on this subject. Figure 5 shows a schematic of a typical high temporal resolution pump-probe microscope, whose components we will describe below.

FIG. 5.

Schematic of a typical experimental pump-probe microscopy setup. A portion of the output of an ultrafast oscillator laser source (e.g., Ti:sapphire) is split to pump an optical parametric oscillator (OPO) to generate a synchronized pulse train at a different wavelength. Prism compressors on both beams pre-compensate for dispersion in the setup. The pump is modulated with an acousto-optic modulator (AOM), typically at >1 MHz, and combined with the unmodulated probe by a dichroic mirror. A delay line introduces a computer-controllable pump-probe delay τ. The scan mirrors (galvanometers) are imaged onto the back focal plane of the microscope objective, and the focal spot is raster-scanned through the sample to build up an image. After collecting transmitted light with a condenser, the pump is rejected by a chromatic filter, and the probe is detected with an amplified photodiode. This signal is analyzed with a lock-in amplifier which is synchronized to the pump modulation. Image stacks are constructed by acquiring frames at different pump-probe time delays.

1. Pulse source and synchronization

A variety of laser sources have been used to drive pump-probe microscopy. These have in common some means of generating distinct, separable pump and probe pulses, with pulse duration and pulse-to-pulse timing error less than the transient dynamics timescales under study. By far, the most common approach is to start with a Ti:sapphire oscillator (∼80 MHz repetition rate) and generate a second pulse train at a wavelength distinct from the fundamental by either SHG or with an optical parametric oscillator (OPO), as indicated in Fig. 5. Use of periodically poled crystals of variable period allows for color conversion over a wide wavelength range in an OPO (e.g., Coherent Mira-OPO) or even with a single pass through a crystal.⁷³ Very efficient color conversion has also recently been demonstrated in photonic crystal fibers⁷⁴ making use of soliton self-frequency shifts (to longer wavelengths) or dispersive waves (to shorter wavelengths), though the achievable colors are limited by specific fiber and pulse parameters. Where pump and probe wavelengths must be independently tunable across the visible wavelengths, a single Ti:sapphire oscillator can drive two OPOs.⁷⁵ For measuring picosecond dynamics, electronically synchronized Ti:sapphire oscillators have been employed;^76,77 sub-femtosecond synchronization is possible,⁷⁸ but has not been used for pump-probe imaging. Amplified pulse sources have also been used. These allow users to trade repetition rate for higher peak intensity to drive nonlinear processes for wavelength conversion. In the 100–250 kHz, μJ pulse energy regime, optical parametric amplifiers (OPAs) have been used to supply tunable-wavelength pump and probe pulses.^79–81 In the 1–5 kHz, mJ pulse energy regime, bulk supercontinuum generation has been used to provide broadband probe pulses without the complexity of an OPO or OPA.^82,83 Though these amplified systems must be attenuated to prevent damaging the sample in raster-scan imaging applications, they provide plenty of overhead for wide-field imaging with “smart pixel” array detectors, in which each pixel performs lock-in detection in parallel.⁸⁴ Recently, alternatives to the standard Ti:sapphire workhorse have found their way into transient absorption microscopy, including ultrafast fiber lasers,^85–87 high repetition rate (1 MHz) amplified systems,⁸⁸ and even modulated continuous-wave laser diodes.⁸⁹

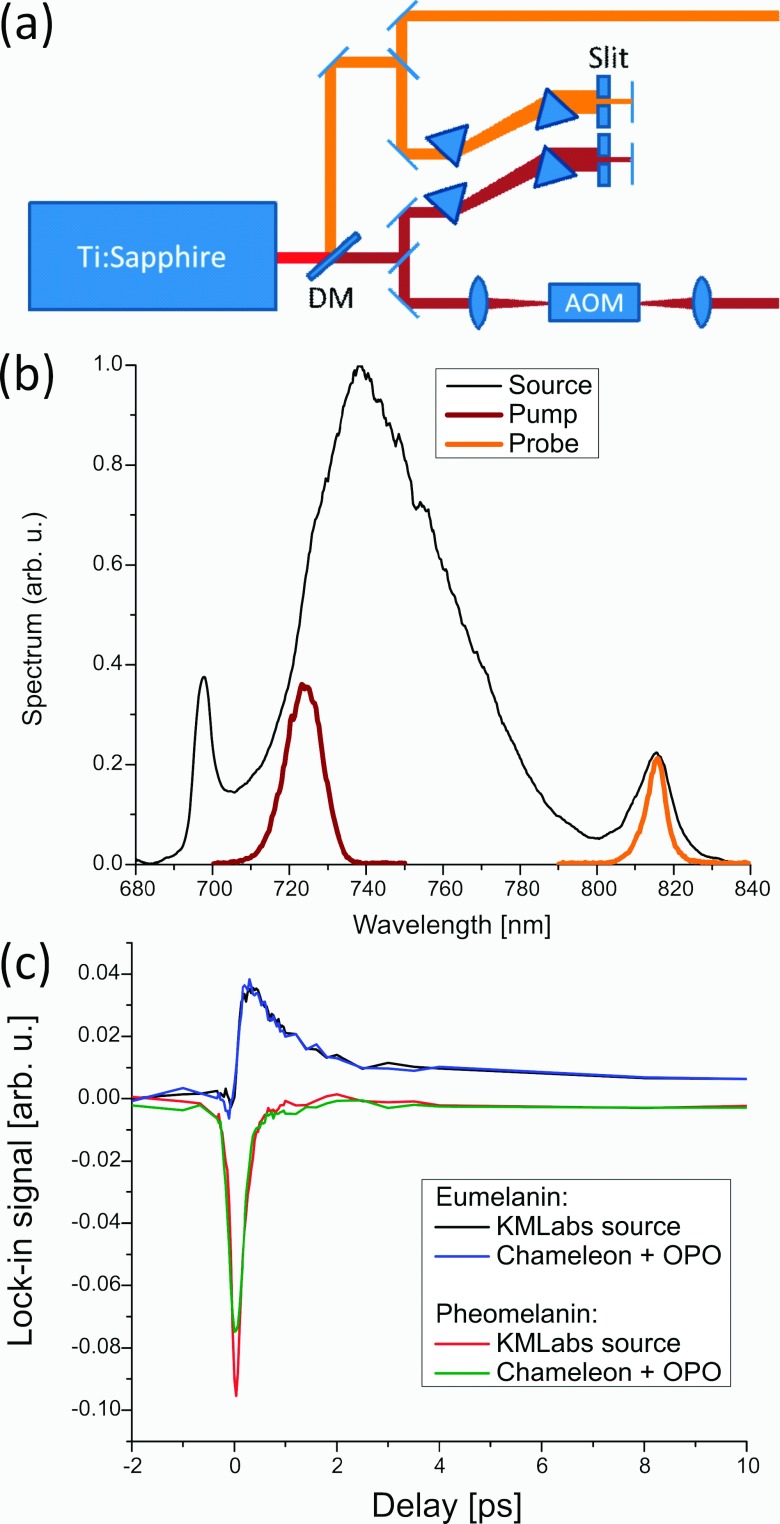
Another convenient option to obtain synchronized pump and probe pulse trains is to select two spectral regions from a broadband pulse source. Two picosecond pulse trains with a spectral separation of a few tens of nm have been demonstrated for coherent Raman spectroscopy,⁹⁰ but with modern Ti:sapphire oscillators a much broader range of the gain bandwidth is accessible. Figure 6 shows an example where pulse trains optimized for imaging of melanins (pump at 720 nm, probe at 815 nm) were extracted from a commercial broadband oscillator (Griffin-5, KM Labs). The initial color separation occurs at the dichroic beam splitter and the following prism pairs serve as both wavelength selectors and dispersion compensators. Because pulse shaping optics and high power microscope objectives can exhibit substantial chromatic dispersion, temporal pre-compensation of the source with prism pairs, grating pairs, or chirped mirrors is required for optimum contrast. Figure 6(c) compares pump-probe delay traces of two melanin samples (natural eumelanin and synthetic pheomelanin) acquired with a broadband single-box source versus an oscillator/OPO combination. The traces are similar and transient absorption images under similar imaging conditions are virtually indistinguishable. The one-box system has the advantages of lower cost, smaller footprint, and turn-key operation, but is obviously limited in the achievable wavelength range. A much broader wavelength range for pump and probe can be achieved with ultra-broadband sources such as a fiber-generated supercontinuum;⁹¹ however, due to the highly nonlinear nature of the continuum generation, the relatively poor amplitude stability can be problematic.

FIG. 6.

(a) Schematic of the use of a single broadband laser source. (b) Pump and probe spectra selected from the laser output spectrum. (c) Comparison of pump-probe delay traces in melanin samples for a broadband laser source and an oscillator/OPO combination.

One of the most critical features of a pump-probe microscope is the ability to reject pump light from the detector. In systems with chromatic separation between pump and probe, the pump is rejected before the detector by a colored glass or dielectric filter or by a grating monochromator. Pump and probe can also be separated based on orthogonal polarization in samples where there is negligible scattering⁹² or by a spatial offset of pump and probe beams⁸⁰ (although this approach cannot make full use of the objective numerical aperture and suffers reduced spatial resolution).

Acquiring images with molecular contrast requires that the time dependence of the pump-probe signals can be mapped in order to measure molecular relaxation dynamics. Fine and arbitrary control of the inter-pulse delay (typically with a time resolution smaller that the pulse cross-correlation width) can be achieved via a computer-controlled delay line in one of the arms. The required precision and range of mechanical travel are determined by the time scale of the population dynamics of interest. For slow dynamics, where the ground state repopulation time occupies a significant fraction of the laser repetition period, a pair of asynchronous laser sources suffices: the pump-probe delay is rapidly scanned at the difference frequency of the sources. This technique, known as asynchronous optical pulse scanning (ASOPS), has been demonstrated with stimulated emission imaging.⁹³ But for fast dynamics that decay in a few picoseconds, the majority of the ASOPS scanning time would be wasted recording zero signal. In case the desired time delay exceeds the repetition time of the laser source, dynamics can be extracted by measuring phase shifts of the amplitude modulation as a function of modulation frequency—a frequency-domain method commonly employed to measure long fluorescence lifetimes.⁹⁴ If only slow dynamics need to be resolved, pulse synchronization requirements are greatly relaxed or can in certain cases be eliminated entirely by using a continuous-wave probe.⁹⁵ Slow dynamics can then still be recovered through the phase angle output of the lock-in or by spread-spectrum modulation,⁹⁶ but information on fast dynamics cannot be retrieved.

2. Temporal shaping and spatial beam delivery

The pump-probe microscope relies on the detection of amplitude modulation that is transferred from an externally modulated pump to the initially un-modulated probe pulse train. The frequency of modulation should be chosen high enough to avoid dominant laser noise and away from regions of spurious noise sources—a typical range is several to several tens of MHz. Such high-frequency modulations exceed the capabilities of mechanical shutters or choppers, but are easily accomplished with acousto- or electro-optic modulators. The use of such high-frequency modulation can achieve sensitivity down to ΔT/T ≈ 10⁻⁷ (see Ref. 97), compared with the typical ΔT/T ≈ 10⁻⁴ reported for low-frequency (kHz) modulation.⁹⁸ In addition, high-frequency modulation requires a high repetition laser source, which also improves the signal-to-noise ratio in virtue of averaging many more measurements per pixel dwell time, i.e., $SNR\propto \sqrt{m}$, where m is the number of laser shots per pixel. For example, given the same pulse energy and duration at the focal plane, measurements with an 80 MHz oscillator will have an improvement over a 1 kHz source by a factor of about 280. One drawback of high repetition-rate pulse trains, however, is that long-lived processes cannot fully relax between subsequent pulses; for this reason, some experiments have employed pulse pickers to reduce repetition rate from an 80 MHz Ti:sapphire oscillator down to a few MHz (for example, Refs. 97, 99, and 100).

After modulation and temporal adjustment, the pump and probe beams are spatially overlapped with a dichroic mirror and directed towards the microscope. The spatial profile and divergence of the two beams need to be matched to achieve good focal overlap in the sample. Spatial overlap between pump and probe beams can also be raster-scanned, to measure spatial extents and propagation of the pump excitation.^97,101,102 In addition, counter-propagating pump and probe beams have been used.¹⁰³

To achieve focal scanning in the microscope, several options exist, ranging from home-built systems and microscope kits to complete, commercial microscope system (for example, the authors have successfully equipped a Zeiss LSM510 for pump-probe contrast). For home-built systems, care must be taken to avoid excessive chromatic aberrations, which would degrade focal overlap when scanning a wide field of view. Lateral scanning (X-Y) is generally performed with scanning mirrors and axial scanning (Z) with a movable objective, but XYZ sample scanning can also be employed (albeit at a reduced scanning speed). For suitable objectives, we refer the reader to the multiphoton microscopy literature (e.g., Refs. 104 and 105).

3. Detection

A variety of detectors have been used for pump-probe imaging, including photodiodes, amplified photodiodes, avalanche photodiodes (APDs), and photomultiplier tubes (PMTs). Balanced detectors have also been employed to cancel noise from probe amplitude fluctuations (for example, Refs. 68, 81, 100, and 106). The probe beam can be detected in transmission or in backscatter- (epi-) mode. Transmission experiments are most appropriate for highly transparent samples and samples that exhibit little scattering. For very thick samples (for example in deep tissue imaging), very little to no light is transmitted and epi-detection is required. In this case, probe light that is scattered after passing through the focal spot carries the transferred modulation. In a typical imaging experiment, only as little as one part per million of the pump modulation might be transferred to the probe; therefore, a careful rejection of pump light is required. For the detection of transient absorption/gain with well-separated colors for pump and probe, a chromatic edge filter can reject the pump while passing the probe. In case the pump and probe are of different polarizations, polarizers can offer a means of separation. If a selective pump filter cannot be used (e.g., if the color or polarization separation is too small for efficient pump rejection), a dual-frequency modulation is an option.¹⁰⁷ In this scheme, both pump and probe beams are amplitude-modulated, but at different modulation frequencies. The nonlinear nature of the pump-probe interaction results in a mixing of the two modulation frequencies and in detectable frequency components at the sum- and difference-frequency.

For cross-phase modulation contrast through XPMSS, a part (generally the lower- or higher-frequency half) of the probe spectrum is rejected, in addition to the rejection of the pump beam, to convert the small XPM-induced probe frequency shifts into measureable amplitude fluctuations on the detector. Since the photodiode output is filtered by the lock-in amplifier at the pump modulation reference frequency, only pump-induced spectral shifts are observed. Optionally, a balanced photodiode illuminated with the two halves of the probe spectrum can be used to suppress transient absorption/gain interactions that do not shift the probe spectrum but still introduce a change in probe amplitude.

Laser scanning of the excitation beams in pump-probe microscopy currently limits achievable frame rates. Parallel acquisition through multiple foci¹⁰⁸ or ultimately wide field illumination could speed up acquisition but would require parallel detection electronics. Tuned filters¹⁰⁹ could be parallelized at moderate cost, but would not provide phase sensitive detection (e.g., for the separation of transient loss from gain processes). An array of lock-in amplifiers would be prohibitively expensive, even with lower-cost custom designs.⁵² Recently a CCD capable of in-pixel demodulation has been shown to detect pump-probe signals in imaging,⁸⁴ albeit only at low modulation frequencies.

4. Signal and noise considerations

Here, we detail the various contributions to the detected photocurrent, for the sake of pointing out the various noise contributions and strategies for improving signal to noise ratio (SNR). For the sake of discussion, we restrict ourselves to processes that scale with the product of pump and probe intensities. The photocurrent signal of interest, J_pp, is the convolution of the nonlinear optical response R with the cross-correlation of pump and probe intensity envelopes I_pu and I_pr, multiplied by the overall detection responsivity r_d (which accounts for sample transmissivity and the detection optics collection efficiency).

$${\displaystyle J_{\text{pp}}=r_{\text{d}}R\otimes \left(I_{\text{pu}}*I_{\text{pr}}\right)=r{I}_{0,\text{pu}}{I}_{0,\text{pr}}{R}^{\prime },}$$

where I₀ is the peak pulse intensity, and $R^{\prime }=R\otimes \left(I_{\text{pu}}*I_{\text{pr}}\right)/\left(I_{0,\text{pu}}{I}_{0,\text{pr}}\right)$ is the optical response convolved with the pump-probe cross-correlation. Typically, the pump-probe signal is extremely small, compared to the probe background, e.g., $J_{\text{pp}}\sim 10^{-5}\times {\overline{J}}_{\text{pr}}$, where ${\overline{J}}_{\text{pr}}$ is the average DC photocurrent measured from the probe in the absence of pump-probe interactions. If we assume an 800 nm probe beam with 1 mW average power incident on a silicon photodiode, this amounts to J_pp ∼5 nA.

The total detected photocurrent contains a number of undesirable noise contributions added to the signal of interest, such as electronic noise J_e, shot noise J_shot, and relative intensity noise on the probe beam, J_RIN,pr,

$${\displaystyle J=J_{\text{pp}}+{\overline{J}}_{\text{pr}}+J_{\text{RIN,pr}}+J_{\text{shot}}+J_{\text{e}}.}$$

By far, the most detrimental is relative intensity noise on the probe beam. The typical specification for a Ti:sapphire modelocked laser is ∼0.15% relative intensity noise, which is a factor of 150 greater than the typical pump-probe signal. Relative intensity noise is frequency-dependent; it falls off rapidly above 300 kHz¹¹⁰ and is negligible above 1 MHz. Therefore, probe intensity noise is effectively rejected by modulating the pump beam at f_m > 1 MHz and filtering the detector output with a lock-in amplifier. As for electronic noise, the typical RF lock-in amplifier has a 50 Ω input impedance and an input noise figure of 5 nV/√Hz. Considering a detection bandwidth of 20 kHz (50 μs pixel dwell time, fast enough for ∼3 s/frame at 256 × 256 pixels), this noise figure amounts to 14 nA, which is a factor of 2 or 3 times greater than the typical pump-probe signal. Therefore an amplified photodiode is often required to boost the signal above the lock-in noise floor. In addition, the signal of interest is not much greater than the shot noise. Again, considering a detection bandwidth of 20 kHz, the shot noise RMS current (i.e., the standard deviation of J_shot) is ${\sigma }_{\text{shot}}=\sqrt{2q{J}_{\text{pr}}\mathrm{\Delta }f}=1.8\text{nA}$. It is important to note that RF modulation and lock-in detection do not mitigate all 1/f noise sources.¹¹¹ Additive noise sources are rejected, but multiplicative noise sources are not. The pump-probe signal itself will contain a contribution from both pump and probe intensity noises I_RIN,

$${\displaystyle J_{\text{pp}}=r_d{\overline{I}}_{0,\text{pu}}\left(1+I_{\mathit{RIN},\text{pu}}\right){\overline{I}}_{0,\text{pr}}\left(1+I_{\mathit{RIN},\text{pr}}\right)R^{\prime }\approx r_d{\overline{I}}_{0,\text{pu}}{\overline{I}}_{0,\text{pr}}{R}^{\prime }\left(1+I_{\mathit{RIN},\text{pu}}+I_{\mathit{RIN},\text{pr}}\right).}$$

Under most scenarios, these multiplicative relative intensity noise contributions are far less significant than the other noise sources. But in scenarios where multiplicative noise is important, decreasing Δf (by scanning slower and averaging longer at each pixel) will not help, because of the 1/f character of laser intensity noise. In these situations, rapid scanning and averaging successive frames will mitigate 1/f noise much more effectively.¹¹² Fast scanning is also advantageous in samples where the primary damage concern is thermal (i.e., in highly absorbing pigments such as melanin), as it exposes each pixel for a shorter amount of time and allows a cooling period between repeated measurements.

III. PRINCIPLES OF DATA AND IMAGE ANALYSES FOR PUMP-PROBE MICROSCOPY

Once a delay stack is acquired (see Fig. 5), the data must be processed to produce an image with molecular contrast. The problem is similar to that of analyzing hyperspectral images, in that the goal is to produce a spatial map of each of the underlying molecular species. Many well-developed algorithms exist for handling hyperspectral stacks,¹¹³ but their adaptation to pump-probe data is not always straightforward. Processing is challenging due to the pump-probe signals’ multi-exponential and bipolar (positive and negative) nature¹¹⁴ and the fact that multi-exponentials do not comprise an orthogonal function basis set. Further complications arise due to the fact that subtle changes in the samples’ chemical environment can have a significant impact on the pump-probe ultrafast photodynamic response. For example, the presence of metals such as iron in melanin¹¹⁵ or unknown minerals in historical art pigments^116,117 can significantly change the measured signal. Therefore, in order to identify these (often, unexpected) changes, it is important to analyze the data without the use of a priori information. In this section, we review the methods that have been implemented for pump-probe microscopy to identify and differentiate between various pigmented molecules and to quantify their relative concentration.

The data collected, x, for each pixel in the image can be represented as the sum over all molecular species’ ultrafast photodynamic response, at a given pump-probe time delay τ, multiplied by their concentration,

$${\displaystyle x\left(\tau \right)=\sum _{i=1}^m{a}_i\left(\tau \right)c_i,}$$ (1)

where a_i is the temporal response of the ith molecule and c_i is its concentration. This can be expanded to include all pixels and all acquired pump-probe time-delays using matrix notation,

$${\displaystyle {\mathbf{X}}_{(t\times p)}^T={\mathbf{A}}_{(t\times m)}{\mathit{c}}_{(m\times p)},}$$ (2)

where p denotes the number of pixels, t the number of pump-probe time delays, and m the number of molecular species. (We use the transpose of the data matrix, ${\mathbf{X}}_{(t\times p)}^T$, for consistency with the analysis that follows.) If all the independent pigmented molecules present in the sample are known, along with their photodynamic response—that is, if A is known—this overdetermined set of linear equations can be solved for the unknown concentration, c, via matrix inversion. However, it is often difficult to fully characterize A. Consequently, if an unexpected molecule were present and/or if the response of a known molecule were to change due to its environment, without properly accounting for it in A, then this operation will yield erroneous results. This problem is known as overfitting and it can have a profound impact on the quantitative molecular images. For example, the response of hemoglobin and eumelanin has some similarities,^118,119 thus, if the two species are not explicitly accounted for, hemoglobin can be assigned as eumelanin, which is highly undesirable for melanoma diagnosis.

A. Principal component analysis

Principal component analysis (PCA) is commonly used in hyperspectral analysis and was one of the first methods used to characterize pump-probe images without the use of a priori information. PCA provides a description of the data in terms of orthonormal vectors derived from the data itself. The analysis can be thought as the singular value decomposition (SVD) of the data matrix, X, and/or as an eigenvalue decomposition of the data covariance matrix, X^TX/(p − 1). To understand the advantages and disadvantages of this method, first consider the singular value decomposition of X,

$${\displaystyle {\mathbf{X}}_{(p\times t)}={\mathbf{U}}_{(p\times p)}{\mathbf{\Sigma }}_{(p\times t)}{{\mathbf{V}}^T}_{(t\times t)},}$$ (3)

where U and V are unitary matrices (i.e., U^TU = 1), known as left-singular vectors and right-singular vectors, respectively, and Σ is a diagonal matrix corresponding to the singular values of X. Then, the covariance matrix of the data matrix (assuming zero mean and ignoring scaling factors) can be described as

$${\displaystyle {\mathbf{X}}^T\mathbf{X}={\left(\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^T\right)}^T\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^T=\mathbf{U}{\mathbf{\Sigma }}^2{\mathbf{V}}^T.}$$ (4)

For more details and rigorous mathematical derivations, we refer the readers to Refs. 120 and 121. For the purpose of this review, it is sufficient to state that the principal components (PCs) of the data are given by the columns of V, which are equal to the eigenvectors of the covariance matrix (Eq. (4)). This relationship is important because (1) SVD algorithms are computationally inexpensive and (2) it provides an intuitive mathematical/geometrical interpretation of the analysis: because PCA organizes the PCs by decreasing variance, the first PC is a vector pointing towards the direction of highest variance. The second component is orthogonal to the first and points towards the direction of the second highest variance, etc. This is a useful property since the first few PCs describe the most important features of the data, while the latter PCs primarily describe noise components in the signal. It is also worth noting that the ith eigenvalue of the covariance matrix, ${\mathbf{\Sigma }}_{ii}^2/(p-1)$, gives the variance captured by the ith PC.

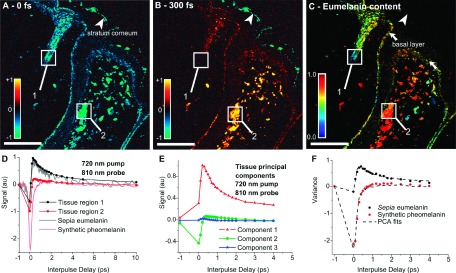
To illustrate this procedure, PCA was applied to 32 pigmented, unstained, thin cutaneous lesions of various pathological diagnoses (specifically, benign dermal nevi, compound nevi, dysplastic nevi, melanoma in situ, invasive primary melanoma, pigmented basal cell carcinoma, and seborrheic keratoses).¹²² Representative spectra, with 21 pump-probe time delays, from 137 hand-selected regions were used to determine the PCs (t = 21 and p = 137). The first three PCs (scaled by their variance) are shown in Fig. 7(e), where the first two PCs account for more than 98% of the variance. Further, the components show good agreement with the signals obtained from melanin standards: synthetic pheomelanin closely resembles PC 2, and sepia eumelanin from cuttlefish ink can be obtained using a combination of PCs 1 and 2 (see Fig. 7(d)).

FIG. 7.

Summary of PCA processing.¹²² (a) and (b) show the raw data, X, at two pump-probe time delays, τ = 0 fs and τ = 300 fs. (d) Spectra from two representative regions, along with that of sepia eumelanin and synthetic pheomelanin. (e) First three PCs, V_{(t x m′=3)}, resulting from 137 representative spectra drawn from 32 cutaneous samples. (c) Estimate of the relative melanin concentration (fractional eumelanin, (c′_m=1 + c′_m=2)/c′_m=1). (f) Spectra from the same regions as (d) along with the fits using the PCs. Reproduced from Matthews et al., Sci. Transl. Med. 3, 71ra15 (2011). Published by the American Association for the Advancement of Science.

A purely mathematical interpretation of the data can be obtained using the projections of the data onto the PCs (known as the scores, Z),

$${\displaystyle {\mathbf{Z}}_{(p\times m^{\prime })}={\mathbf{X}}_{(p\times t)}{\mathbf{V}}_{(t\times m^{\prime })},}$$ (5)

where V is truncated to m′ PCs (in this case m′ = 2). This process yields m′ images, each corresponding to the scores (or projections) of the PCs, which allows some interpretation (albeit mathematical) of the data without use of a priori information. This process also has the advantage of reducing noise since Z is derived from the PCs that possess the most variance.

An important limitation of principal component analysis is that if the underlying number of unique chemical species (referred to as “endmembers” in the hyperspectral image analysis literature) is unknown, it may not be inferred from the number of principal components accounting for the majority of the variance in a dataset. In other words, if m′ = 2 PCs capture 99% of the variance in the data, there could be m > 2 molecular species present. It is often possible to qualitatively reconstruct a set of n endmembers with fewer than n principal components. In addition, the principal components do not have to reflect the properties of the actual endmembers. The reason for this ambiguity is that PCA extracts orthogonal components, whereas the multi-exponential signal recorded in pump-probe measurements tends to be highly non-orthogonal.

To quantify the data in terms of physical properties of the sample (i.e., relative molecular concentration), a priori information is required: First, the temporal response of all molecular species present in the sample, described by A, needs to be mapped onto the space spanned by the PCs,

$${\displaystyle {\mathbf{M}}_{(m\times m^{\prime })}={{\mathbf{A}}^T}_{(m\times t)}{\mathbf{V}}_{(t\times m^{\prime })}.}$$ (6)

This mapping can then be used to transform the projected data (scores) onto the physical model,

$${\displaystyle {\mathbf{c}}_{(p\times m)}^{\prime }={\mathbf{Z}}_{(p\times m^{\prime })}{{\mathbf{M}}^T}_{(m^{\prime }\times m)},}$$ (7)

where c′ is an estimate of the concentration matrix, c^T. This process was applied to estimate the relative eumelanin content shown in Fig. 7(c). Unfortunately, these final steps (which are part of any projection-based method) are fraught with the same limitations as directly inverting the linear system in Eq. (2), since A must be known.

B. Phasor analysis

Similar challenges have been encountered in Fluorescent Lifetime Imaging Microscopy (FLIM), which contains unipolar (i.e., non-negative), multi-exponential signals. In FLIM, signals are typically quantified by fitting the exponential response to a predetermined number of decay rates or by using more sophisticated inverse Laplace transforms.^123,124 However, such methods can be computationally expensive and require signals with a high signal to noise ratio, which is often not available in pump-probe microscopy, particularly for in vivo applications.^119,125 An alternative approach, named phasor analysis, has emerged as a simple, yet powerful tool for differentiating between various fluorophores and mixtures thereof.¹²⁴ We have recently adapted this method for pump-probe microscopy and have shown that it is a robust and convenient method for analyzing pigments’ ultra-fast dynamics.¹¹⁴

In phasor analysis, signals are decomposed into their Fourier transform’s real and imaginary parts, g and s, respectively, at a given frequency, ω,

$${\displaystyle g\left(\omega \right)=\frac{\int I\left(t\right)cos\left(\omega t\right)\text{d}t}{\int \left|I\left(t\right)\right|\text{d}t},}$$ (8)

$${\displaystyle s\left(\omega \right)=\frac{\int I\left(t\right)sin\left(\omega t\right)\text{d}t}{\int \left|I\left(t\right)\right|\text{d}t}.}$$ (9)

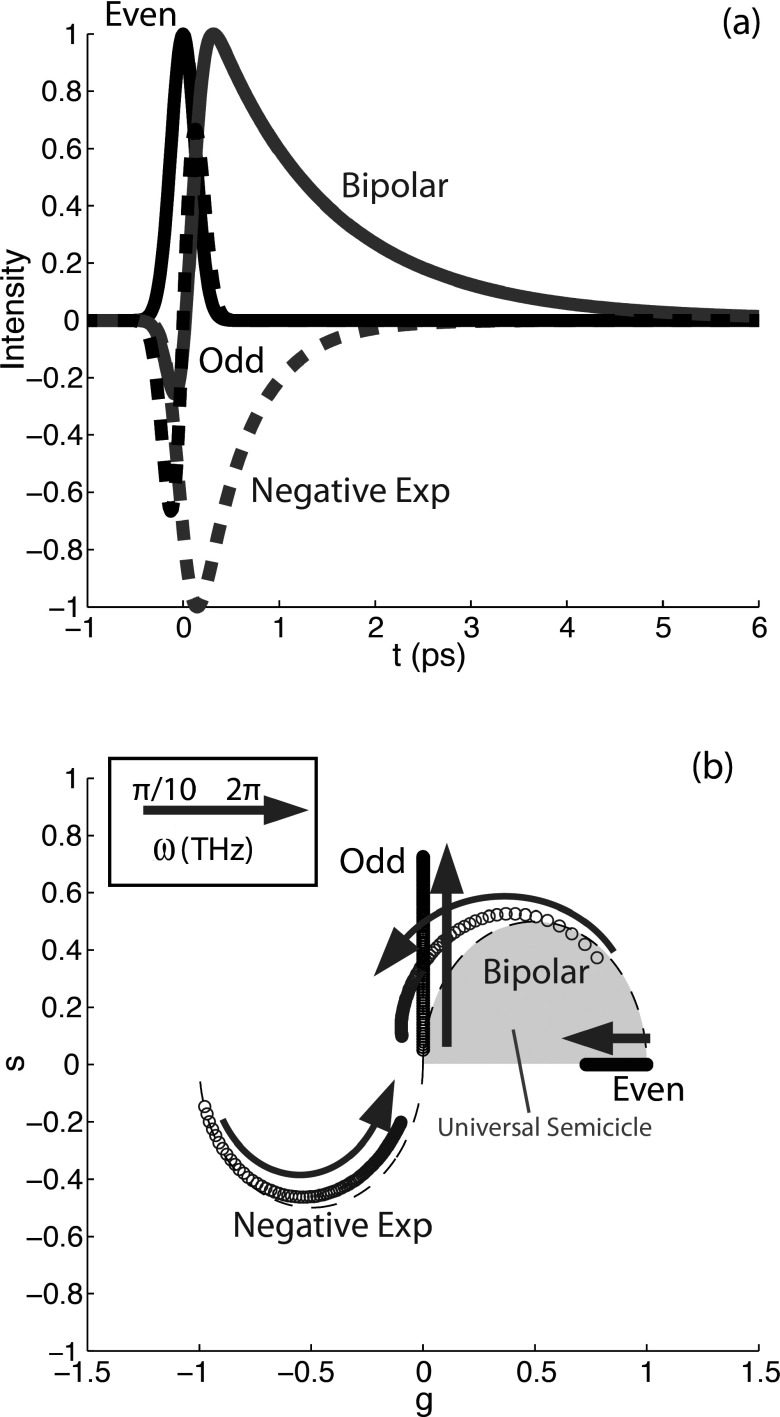
The two components are then plotted against one another (see Fig. 8). Note that the parameters are normalized by the absolute value of the temporal response, I(t); thus the phasors are always bounded by a well-defined area and the mapping is independent of signal intensity. For FLIM, where the signals are always positive exponentials, the phasors are bounded by an area known as the universal semicircle, which lies on the first quadrant of phasor space (see gray shaded area indicated in Fig. 8(b)). In our case, the photodynamic behavior can take on more functional forms and thus the transformation of pump-probe signals can span the entire unit circle. Figure 8 shows some examples of typical pump-probe dynamics and their mapping to phasor space as a function of the analysis frequency. It should be noted that this transformation is sensitive to offsets (baseline) on the measured signals. In practice, the baseline for each pixel is estimated by examining the recorded signal at t < 0, when the pump arrives after the probe. For noisy data, this estimate can be improved by making a reduced-rank approximation of the image stack (reconstructing the stack from the first few PCs).

FIG. 8.

(a) Simulated ultrafast pump-probe photodynamics: Even function (solid black line) represents an instantaneous response such as TPA. Odd function (dashed black line) may result from XPM. Unipolar, negative exponential curve (dashed gray line) may result from SRS or GSD. The bipolar signal (solid gray line) is a combination of lines 1-3, and it resembles the eumelanin dynamics. (b) Corresponding phasors at different frequencies ranging from ω = 0.01π to 2π THz. Each point is an increment of 0.01π THz. Adapted with permission from Robles et al., Opt. Express 20, 17082 (2012). Copyright 2012 Optical Society of America.

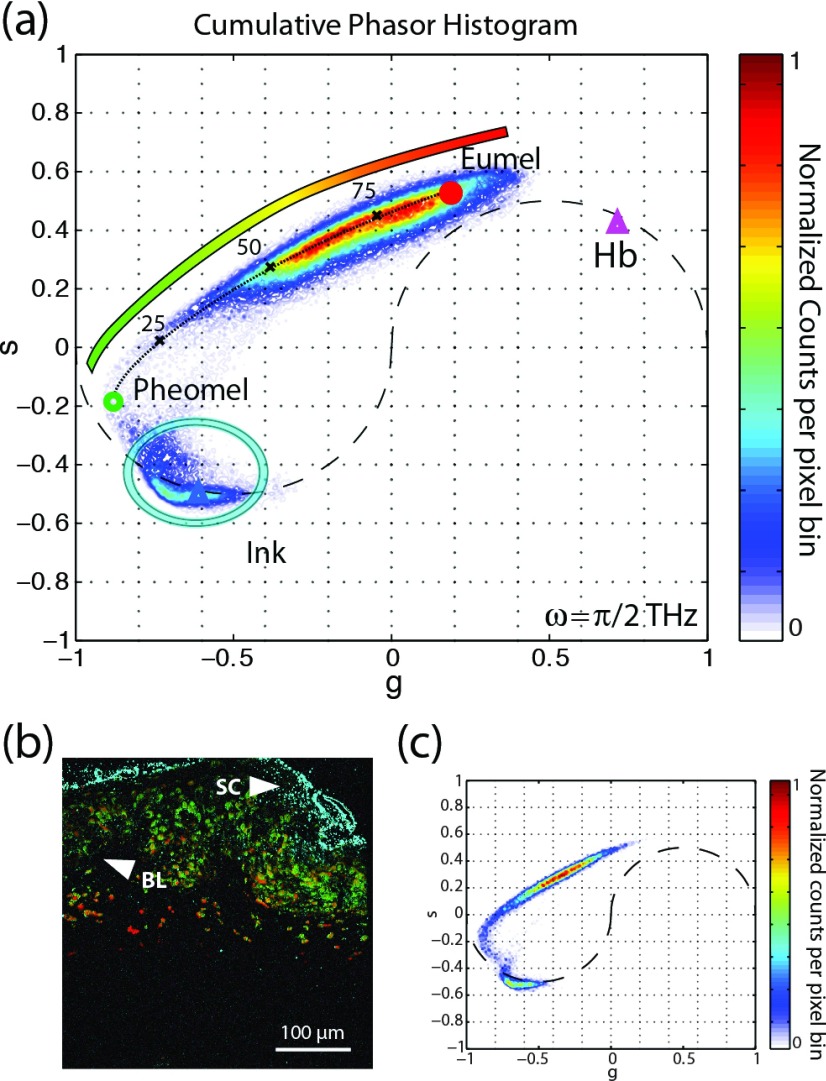
Phasor analysis was applied to the same data set as previously discussed for PCA. Here, all images were used to construct a two-dimensional histogram of the phasors. The results are shown in Fig. 9(a), which also shows reference phasors from sepia eumelanin (red dot), synthetic pheomelanin (green dot), hemoglobin (purple triangle), and surgical ink (blue triangle). The clusters in the cumulative histogram overlap with the reference for each species. This information may be used for qualitative analysis by assigning a particular color to a given location in phasor-space. As the inset of Fig. 9(a) illustrates, we choose the false-color mapping for melanins to vary from red to green, hemoglobin is assigned as purple, and surgical ink as cyan. Figure 9(b) shows a representative pump-probe image with colorimetric molecular contrast achieved via phasor analysis, along with its corresponding phasor histogram (Fig. 9(c)).

FIG. 9.

(a) Cumulative histogram phasor plot of 42 cutaneous samples. The figure also shows the phasors of standard references of eumelanin (red dot), pheomelanin (green circle), hemoglobin (purple triangle), and surgical ink (blue triangle). The color bar within the figure denotes the color schema used for the image in (b). (b) Representative pump-probe image with colorimetric contrast derived from phasor analysis. (c) Phasor histogram of a representative image in (b). Adapted with permission from Robles et al., Opt. Express 20, 17082 (2012). Copyright 2012 Optical Society of America.

More recent work has produced a hybrid approach, which takes a geometrical representation of PCA to display the data in a similar manner to phasor analysis.¹²⁶ This process takes the top 3 PCs, which in most cases are enough to capture most of the data variance, to produce a three-dimensional space. Then, by describing this space in spherical coordinates, the azimuth and elevation angles contain all the spectral (biochemical) information of interest, while the radius describes the concentration. A two dimensional cumulative histogram of the angles provides an intuitive format to view the spectral information, similar to phasor analysis but it avoids nonlinearities (i.e., curved paths) and permits a quantitative analysis.

IV. APPLICATIONS OF PUMP-PROBE MICROSCOPY

Development of high-sensitivity pump-probe imaging techniques has initially focused on transient absorption in nanomaterials.^107,127 Increased speed and sensitivity have since enabled applications of these techniques in biomedical engineering where multiphoton absorption,^10,12,128 ground state depletion,⁹⁵ stimulated emission,⁷⁵ and SRS¹²⁹ contrast were demonstrated. In Secs. IV A–IV C, we will provide examples in the fields of materials science, biomedicine, and art conservation. In these examples, we again limit ourselves to processes that utilize the high temporal resolution of ultrafast modelocked laser pulses (on the order of tens to hundreds of femtoseconds).

A. Materials characterization

Because transient absorption provides details not only on electronic energy levels but also on the population dynamics within them, it has been used extensively for characterization of a wide range of nanomaterials such as the following: nanostructures such as quantum wells,¹³⁰ silver nanocubes,¹³¹ and nanowires of various materials;^{100–102,132–134} bulk and patterned semiconductors,^{84,92,103,106} polymer blends, and organic semiconductor films;^{80,82,83,135,136} topological insulators;¹³⁷ graphene,^98,138–143 and carbon nanotubes;^76,144,145 and most recently, perovskites.^81,97 For excellent review papers on transient absorption microscopy in materials sciences, we refer the reader to Refs. 4, 22, and 23 and hence provide only a few example applications.

Some of these nanostructured materials, e.g., graphene, have exceptionally large susceptibilities, yet very weak fluorescence, and are therefore ideal targets for pump-probe spectroscopic studies. Bulk femtosecond transient absorption spectroscopy has also been utilized to explore ground and excited state dynamics of nanoparticles such as single-walled carbon nanotubes, thereby shedding much light on their photophysical properties: the role of triplet states;¹⁴⁶ the influence of environmental factors such as solvent dielectrics;¹⁴⁷ and the creation, diffusion, and the decay of single or multiple excitons within a single carbon nanotube.^148,149

However, bulk spectroscopic studies (without the high spatial resolution of a microscope) of ensembles of nanomaterials average over inherent variations present within the sample. Extended materials, such as graphene, are rarely uniform, exhibiting spatial heterogeneity in thickness, structure, alignment, and coupling to their substrate on varying length scales, depending on the growth conditions. For individual nanoparticles, differences in their size, aggregation states, and local environment can drastically affect their transient absorption properties. In the case of carbon nanotubes, results can be most reliably interpreted when data are acquired on tubes of a uniform type and size (this can be achieved, for example, by separation with gradient ultra-centrifugation¹⁵⁰). However, not all materials can be cleanly separated—multi-walled carbon nanotubes defy such separation procedures because of their complexity and heterogeneity in structure.

Pump-probe microscopy can provide a wide range of dynamical properties on a microscopic scale. In extended materials, pump-probe imaging can map out variations within the material or changes in coupling to the environment and substrate. For example, femtosecond transient absorption microscopy has been successfully used to study local variations of charge carrier dynamics in graphene¹⁵¹ and graphene oxide.¹⁴³ Pump-probe imaging also provides the ability to isolate individual nanoparticles and therefore avoids averaging over an ensemble of particles. For example, single particle measurements make it possible to directly separate damping from ensemble dephasing of coherent vibrational oscillations.⁶⁷ The earliest far-field microscopic pump-probe studies of nanoparticles measured electron dynamics by observing changes in amplitude¹⁵² of scattered probe light. Pump-induced phase changes were measured with a differential interference contrast technique¹⁵³ and by interferometry with a time-delayed reference pulse.⁶⁷ However, polarization and interferometric detection are experimentally challenging, and the easier (now-conventional) modulation transfer technique soon started to take hold.¹²⁷

An example application in nanomaterials that takes explicit advantage of the high spatial information afforded by imaging is the study of surface plasmon-polariton propagation. An optical excitation that is localized to the end of a nanowire propagates, but emits only at discontinuities. This transport can be directly observed by spatially decoupled pump-probe microscopy, where the pump is fixed at one location, but the probe is raster-scanned. Such a setup has been used to study plasmon excitations in gold nanowires.¹³⁴ Even higher spatial resolution can be achieved by near-field imaging techniques. Coupling pump and probe beams into a scanning near-field optical microscope (SNOM), sub-wavelength (and sub-particle) resolution has been obtained. For example, near-field pump-probe microscopy was used to map electron dynamics in individual gold nanorods.¹⁰⁷

B. Biological imaging

In this section, we focus on time-resolved femtosecond pump-probe microscopy (other reviews cover stimulated Raman in detail⁷⁰). The first biological application, in 1995, imaged stimulated emission of a dye-labelled cell in vitro.⁹³ By recording the signal as a function of probe delay, this provided a method of detecting fluorescence lifetime without the need for high-speed detectors. The technique was later extended to a polarization-resolved method,¹⁵⁴ again using exogenous dyes and labels. Xie’s group advanced stimulated emission targets to endogenous chromophores,⁷⁵ and this was found to allow visualization of chromophores that, due to nonradiative relaxation, do not produce any measurable spontaneous fluorescence.

Molecular imaging of complex molecules, such as melanins, broadened pump-probe imaging to include ground state depletion and excited state absorption.¹²⁸ Melanins are complex biopolymers that are synthesized from the oxidation of tyrosine and are broadly classified into two chemically distinct classes: the brown/black eumelanin, composed of dihydroxyindole subunits, and the yellow/red pheomelanin, composed of benzothiazine subunits.¹⁵⁵ Eumelanin and pheomelanin have broad linear optical absorption spectra that lack distinguishing features. Therefore, state-of-the art methods to quantify melanin chemistry in biological tissue rely on high-performance liquid chromatography analysis of oxidative degradation products,¹⁵⁶ which requires large amounts of material and destroys the specimen in the process.

Microscopic information on the melanin distribution can be obtained using fluorescence dynamics. Despite the low fluorescence quantum yield, several studies have use fluorescence lifetime imaging contrast to map melanin in tissue with high spatial resolution^157–159 and even differentiate eumelanin and pheomelanin.¹⁶⁰ Pump-probe imaging, owing to its high-dimensional parameter space, provides a vastly different transient response from the two melanins¹⁶¹ even though they have similar linear spectra. The pump-probe response of melanin is much like a spectral hole burning measurement, in which intense ground state bleaching (negative pump-probe signal) is observed for λ_pu and λ_pr close to one another. The key feature with melanins is that when λ_pu and λ_pr are tuned away from one another, ground state bleaching gives way to excited state absorption (positive pump-probe signal). The point at which the response changes sign depends on a number of factors, such as the width of the absorption bands of the underlying chromophores within the heterogeneous ensemble and the availability of dipole-allowed excited state transitions. Thus we can find a wavelength combination at which two types of melanins have opposite-signed response (see Fig. 10). This has enabled the study of pigment chemistry on microscopic scales where bulk analysis would destroy the spatial information, such as sub-cellular melanin distributions,¹⁶² and in rare materials where chemical analysis would destroy the specimen, such as in fossils.¹⁶³ Other factors that influence the pump-probe response of melanin include metal ion content¹⁶³ and aggregation state,¹¹⁵ some examples of which are also shown in Fig. 10.

FIG. 10.

(a) Eumelanin and pheomelanin, compared with pigments in biopsied human tissue.¹²² (b) Response to chemical oxidation¹¹⁵ and (c) molecular weight.¹¹⁵ (a) Reproduced from Mathews et al., Sci. Transl. Med. 3, 71ra15 (2011). Published by the American Association for the Advancement of Science; (b) and (c) reproduced from Simpson et al., J. Phys. Chem. A 118, 993 (2014). Copyright 2014 American Chemical Society.

Our recent focus has been to use this technique to study pigmented lesions and melanoma. At present, identifying and removing early-stage melanoma before it has the chance to metastasize require an accurate diagnosis by examining stained biopsy sections under a microscope for certain histopathologic criteria.¹⁶⁴ But several studies have demonstrated that making consistent, accurate diagnoses of early-stage melanoma is extremely challenging.^165,166 This difficulty can be explained in part because nearly all of the histopathologic criteria used to identify melanoma are also common to benign pigmented lesions¹⁶⁴ and also because, in spite of the vast knowledge of biomolecular factors associated with melanoma, the exact sequence by which a melanocyte progresses from normal to malignant remains unclear.¹⁶⁷ Hence there is a need for more biomarkers to aid pathologists.¹⁶⁸ One readily available means of assessing melanocyte behavior is to assess pigment chemistry with pump-probe microscopy. In biopsy sections, we have found differences in pigment expression between “pre-malignant” dysplastic nevi and invasive melanoma.¹²² Also, we have used pump-probe contrast in vivo to visualize pigmented cells in mouse models of melanoma.¹²⁵ Employed in vivo, pump-probe microscopy therefore enables the capture of dynamics and time-course of pigment chemistry and progression in the early stages of malignancy, of which traditional histology can only provide a snapshot.

Melanin imaging exemplifies the key advantage of time-resolved pump-probe microscopy: its ability to derive high-contrast pump-probe signatures to differentiate chromophores that have otherwise nearly indistinguishable linear optical properties. Hemoglobin is another target that has been imaged with pump-probe microscopy, and oxygenation can be determined by exchanging pump and probe wavelengths,¹⁶⁹ as shown in Figs. 11(b) and 11(c). As pump-probe microscopes with broader wavelength ranges become available, more biological pigments may be targeted.

FIG. 11.

(a) Molecular contrast in a biopsy section of malignant melanoma¹⁶² and (b) and (c) hemoglobin image (mouse ear) at different pump-probe wavelengths.¹⁶⁹ Red arrow: artery; blue arrows: veins. (a) Reproduced from Simpson et al., J. Invest. Dermatol. 133, 1822 (2013). Published by Elsevier; (b) and (c) reproduced from Fu et al., J. Biomed. Opt. 13, 040503 (2008). Copyright 2008 Society of Photo-Optical Instrumentation Engineers.

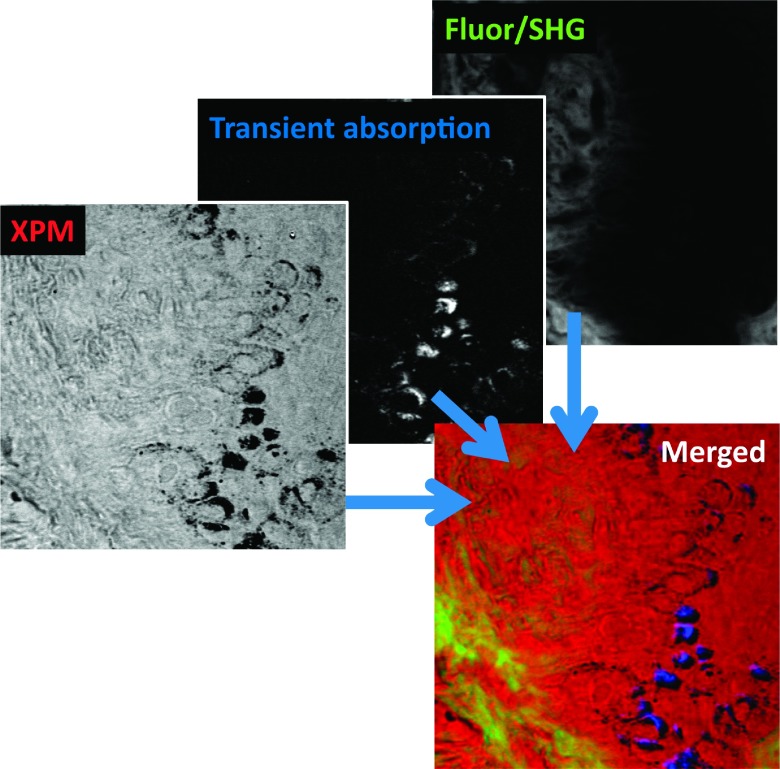
Because pump-probe detection readily integrates with other modalities, the pigment-specific pump-probe images can be placed within the context of the morphology of the surrounding tissue.¹⁷⁰ Such morphological images could be acquired, for example, with conventional SHG or fluorescence contrast. The nonlinear refractive index (e.g., measured through XMPSS) can provide additional contrast to gain a more comprehensive picture of unstained tissue⁶⁸ (Fig. 12).

FIG. 12.

Images of the dermo-epidermal junction in a melanoma biopsy.⁶⁸ Shown are XPMSS, transient absorption (tuned to visualize melanin), and combined multiphoton autofluorescence and SHG. The merged image shows the comprehensive contrast through multimodal multiphoton imaging. Adapted with permission from Wilson et al., Biomed. Opt. Express 3, 854 (2012). Copyright 2012 Optical Society of America.

Pump-probe imaging is well suited to study endogenous targets in tissue, but it can also be applied to exogenous contrasts—in pre-clinical studies, a large number of injected or expressed agents are in routine use (very few optical contrast agents are approved for human use). Transient absorption imaging has been used to generate non-fluorescent contrast in biological tissue from several types of nanostructures, including semiconducting and metallic single-walled carbon nanotubes,^77,171 nanodiamonds,⁸⁵ gold nanorods,⁸⁶ and graphene and graphene oxide.¹⁷²

C. Art imaging

Despite their apparent differences, paintings and biological tissue have many things in common from an optical microscopy standpoint: both are very heterogeneous and very strongly scattering materials that contain a variety of absorbing pigments one would like to identify and map. While in biomedicine, nonlinear optical microscopy is routinely used to image tissue structure and pigment distribution at high resolution, applications in art conservation science are sparse. Yet, many stages of art characterization, authentication, preservation, and conservation are in need of additional tools to assess structural information at a microscopic level, along with chemical composition. Such methods could help identify individual pigments and/or pigment mixtures, their three-dimensional layering structure, and method of application. Ideally, an artwork microscope should combine high resolution with a large field of view in the lateral and depth dimension, preferably all the way to the support structure (such as the canvas). Most importantly, however, it should not damage the artwork under study. Pump-probe microscopy has the potential to fulfill these conditions. In many instances, it may save a conservator from resorting to the invasive gold standard of removing a small chip of paint sample for pigment mapping (much like the practice of using tissue biopsies to diagnose a disease).

The reason conventional nonlinear microscopy has not been extensively employed in art imaging is the lack of suitable contrast. TPF has been utilized to reconstruct faded inscriptions on a historic amphora,¹⁷³ but few pigments fluoresce—and therefore TPF microscopy has limited applicability. Layer thickness of transparent glaze and varnishes have been measured by harmonic generation,¹⁷⁴ but the symmetry constraints of harmonic generation severely restrict the range of possible targets. CARS imaging has recently been investigated for paint identification and imaging,¹⁷⁵ but small Raman cross sections, combined with a large contaminating non-resonant background, pose severe technical challenges.

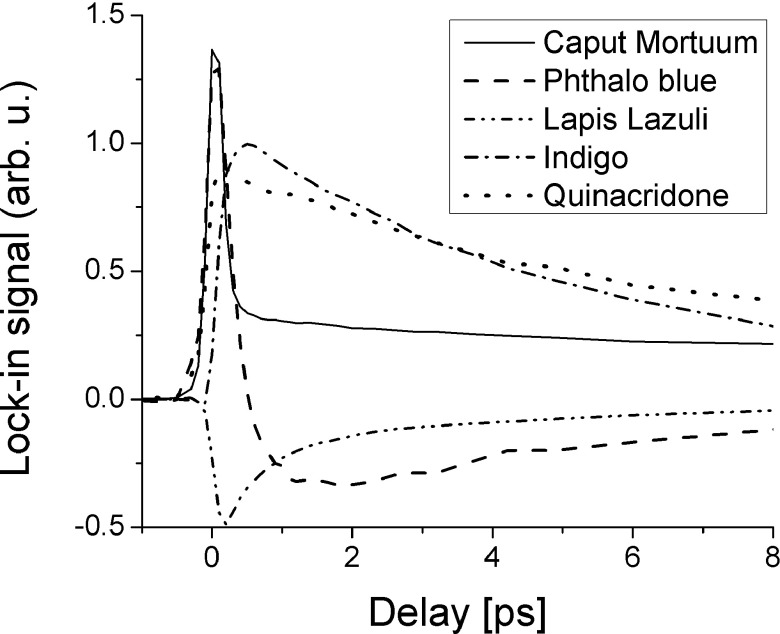
In contrast, pump-probe microscopy has found an almost ideal application area in art imaging. The artists’ palette consists of pigments with a vast variety of spectral absorption properties, which is the largest determining factor for a pigment’s color. However, the spectral features (such as absorption lines or bands) are broad, thus identification of a specific pigment in a mixture is often difficult. Nonlinear optical effects can provide much richer and molecule-specific signatures: pigments whose linear absorption characteristics are very similar might still exhibit a nonlinear transient loss/gain spectrum that differs dramatically. Both the energy structure (such as electronic excited states and the vibrational sub-structure) and the population dynamics (the redistribution between these states) imprint on the pump-probe response. Figure 13 shows pump-probe responses for a selection of pigments, all performed at a single wavelength combination (here 720 nm pump/810 nm probe). The responses illustrate the variety of photodynamics, offering a rich parameter space for pigment specific mapping. In some of the pigments, one can observe a variation in pump-probe dynamics even though the pigments are of the same visual color. For example, we studied a selection of samples of lapis lazuli, a historical mineral pigment prized (very highly) for its rich blue color and compared it to lapis’ synthetic analogue, ultramarine blue. Variations in the dynamics within and between the natural lapis samples were observed (the multi-exponential decay times differ markedly),¹¹⁷ as well as between the natural and synthetic pigments.

FIG. 13.

Transient absorption traces of mineral, inorganic, and organic pigments.

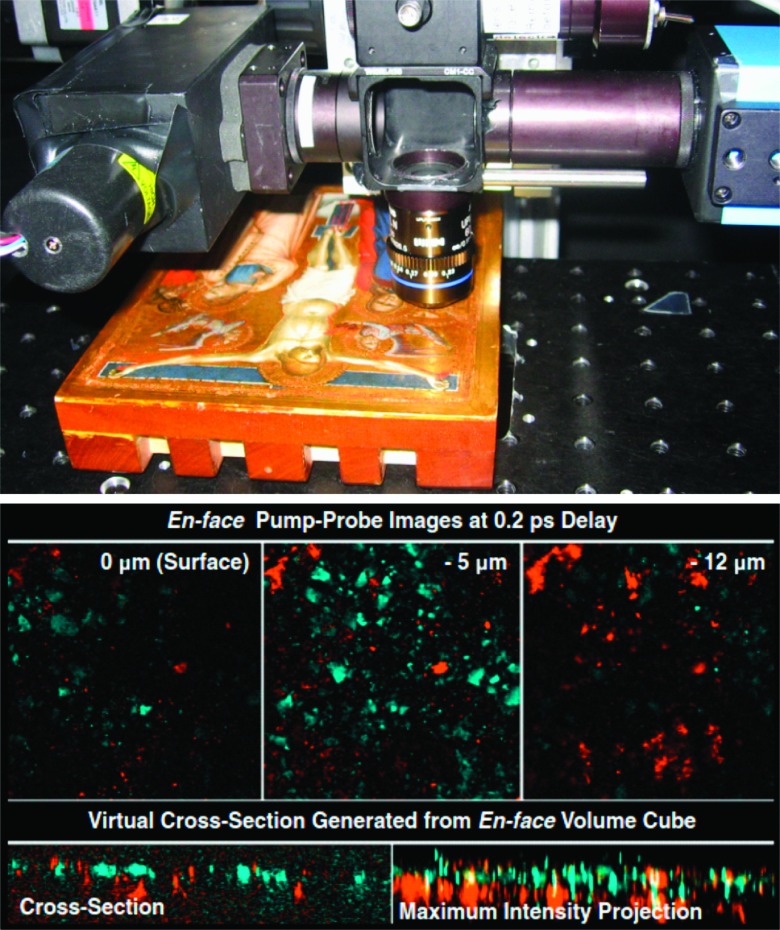
Figure 14 illustrates the 3-d imaging capability of pump-robe microscopy in historical artwork.¹¹⁶ Volume image stacks were acquired from Puccio Capanna’s 14th century Renaissance masterpiece The Crucifixion. A pump-probe volume dataset was taken with a fixed 200-fs delay in the angel’s robe (pump/probe wavelengths were 710/810 nm, total power was 1.5 mW). The images from this set have been false-colored according to the signal at this delay: cyan for negative signal (corresponding to lapis lazuli) and orange for positive (iron oxide/mordant and gold; with only a single delay, these three materials cannot be separated). A virtual cross section extracted from the volume data is also shown in this figure. It shows a positive component mixed within the lapis lazuli layer (most likely iron oxide) with another positive component underneath (most likely gold and possibly underlying mordant found in microscopic cracks in the gold layer). Further improvements in imaging speed and achievable wavelength range, combined with the enhanced analysis tool described earlier, could substantially enhance the amount of information that conservators can non-invasively extract from paintings.

FIG. 14.

Pump-probe in historic artwork.¹¹⁶ Left: the painting was imaged in the region of the angel’s robe with a wavelength combination of 720/810 nm. Right: false-color coded en face images (top, each image is 185 × 185 μm), a virtual cross section, and a maximum intensity projection (bottom, dimensions are 185 × 50 μm). Adapted from Villafana et al., Proc. Natl. Acad. Sci. U. S. A. 111, 1708 (2014). Copyright 2014 National Academy of Sciences of the United States of America.

V. CONCLUSIONS AND OUTLOOK

As the preceding examples show, the most remarkable feature of pump-probe microscopy is the contrast enhancement: linear absorption spectra are almost always broad and featureless, but pump-probe signals are often rich functions of pump wavelength, probe wavelength, and inter-pulse delay. This provides opportunities to extract molecular information which is often inaccessible by other techniques.

Probably the biggest current limitation is that the most common approach to pump-probe microscopy relies on relatively complex laser systems, which need to produce two or more different, stable, and well-synchronized trains of ultrashort (∼100–200 fs) laser pulses. However, this complexity arises mostly because of the desire to explore a wide parameter space in the initial experiments. For example, since delivered powers are typically about 1 mW and modern modelocked titanium-sapphire lasers routinely provide several watts, short-pulse lasers can be spectrally filtered to provide both pulse trains if both wavelengths are within the Ti:sapphire bandwidth. More generally, advances in stable continuum generation and fiber laser sources, driven by other applications, make it certain that cheaper, even portable pump-probe systems can be developed.

Once the laser sources are established, the additional changes required for the conversion of a conventional multi-photon to a pump-probe microscope are fairly moderate (on the detection side, it could be as simple as an optical blocking filter for the pump color and an electronic lock-in amplifier). The microscope core, such as the scan engine and light delivery to the sample, often does not need to be modified. Most multiphoton systems are already designed to operate with widely tunable laser sources and the optics can likely handle multiple colors. Developments in multiphoton imaging, such as high scanning speeds for video rate imaging, remote light delivery for ultralight (e.g., rodent-wearable) scan heads, and adaptive optics techniques for ultra-deep imaging, therefore are also directly applicable to pump-probe microscopy. Pump-probe contrast and conventional multiphoton contrast can naturally be combined into the same microscope and together they provide complimentary information on a wide range of exogenous and endogenous targets.