Falsification Testing of Instrumental Variables Methods for Comparative Effectiveness Research

Abstract

Objectives

To demonstrate how falsification tests can be used to evaluate instrumental variables methods applicable to a wide variety of comparative effectiveness research questions.

Study Design

Brief conceptual review of instrumental variables and falsification testing principles and techniques accompanied by an empirical application. Sample STATA code related to the empirical application is provided in the Appendix.

Empirical Application

Comparative long‐term risks of sulfonylureas and thiazolidinediones for management of type 2 diabetes. Outcomes include mortality and hospitalization for an ambulatory care–sensitive condition. Prescribing pattern variations are used as instrumental variables.

Conclusions

Falsification testing is an easily computed and powerful way to evaluate the validity of the key assumption underlying instrumental variables analysis. If falsification tests are used, instrumental variables techniques can help answer a multitude of important clinical questions.

Falsification testing is an old idea that has great potential as a method for evaluating the internal validity of comparative effectiveness research (CER) studies. Though rarely identified as such, falsification tests are familiar to most researchers, as they are a routine, almost automatic component of reporting of randomized controlled trial (RCT) results. Falsification testing of observational studies requires more planning in advance, but it is not much more difficult to perform than for RCTs. Given the growing importance of observational studies and instrumental variables methods in CER, falsification testing can play a vital role in improving the reliability and impact of this research.

To understand falsification testing, consider the table of sample means of the explanatory variables by treatment and control group included in most reporting of RCT results. What purpose does this serve? Our expectation is that the sample means will not be significantly different between groups because group assignment was intended to be random. Random assignment is the “identifying assumption” of RCTs because randomization permits us to infer causal effects of treatment. If the sample means differ by group, the identifying assumption has been falsified and we have reason to doubt the internal validity of the trial. That is, a table of means by group is a falsification test of an RCT's central assumption.

As I will show, similar falsification tests can be implemented for observational studies, which are becoming an increasingly important source of clinical evidence. Wider adoption of electronic medical records and substantial new investments ($3 billion in research and infrastructure between 2013 and 2019) by the Patient‐Centered Outcomes Research Institute (PCORI) (Krumholz and Selby 2012) are increasing capacity to conduct observational, comparative effectiveness, and patient‐centered outcomes research. A recent analysis of responses to the National Ambulatory Medical Care Survey showed that the percentage of all physicians who had adopted a basic electronic medical record increased from 25.8 percent in 2010 to 38.2 percent in 2012 (Hsiao et al. 2013a). These rapid changes in technology and research resources raise the prospect of large observational studies based on clinical data with vastly richer detail than what has been available in the past from administrative or claims‐based records.

This emerging “big data” environment holds promise to extend the reach of clinical and health services research to include the study of rare events, heterogeneous treatment effects, long‐term outcomes, and other topics that are difficult or impossible to study with RCTs (Selby et al. 2012; Krumholz 2014). RCTs typically involve numbers of subjects in the hundreds, limiting comparisons to a few treatment options, and making patient subgroup comparisons difficult or impossible. In addition, external validity is constrained by recruitment that frequently excludes the most complex or severely ill patients as well as treatment that is conducted in academic medical centers with research staff supplementing clinical staff. In contrast, observational studies can efficiently exploit electronic medical records and administrative databases containing information on tens or hundreds of thousands of patients of all types, treated in a wide variety of clinical settings and followed up for many years.

Despite these advantages, a key challenge facing observational CER is evaluating the validity of causal inference made with observational data (National Research Council 2013; PCORI Methodology Committee 2013; Velentgas et al. 2013). This is a topic that has generated controversy for hundreds of years (Dowd 2011). Recently, however, important technical strides have been made in design and analytic methods to increase the internal validity of observational studies despite a lack of purposeful, explicit randomization. Depending on the source and strength of treatment variation in observational studies, different statistical methods may be appropriate. For example, if the study is small enough that it is practical to collect data on every potentially confounding variable, propensity score methods can ensure balance of observed variables between treatment and comparison groups, revealing the causal effect of treatment. On the other hand, if the study is too large for practical collection of important variables that might be unavailable in clinical or administrative data, risk‐adjusted or propensity score estimates are likely to be biased and quasi‐experimental methods like instrumental variables (IV) probably will be more appropriate (Pizer 2009).1

This article reviews the fundamental concepts underlying IV estimation and falsification testing, and then demonstrates the steps involved using a specific example comparing the long‐term risks associated with alternative oral medications used to manage type 2 diabetes (Prentice et al. 2014). Sample STATA code to implement these steps is provided in the Appendix SA1.

Fundamental Concepts

What Is IV?

To understand how instrumental variables methods work, it is helpful to start by returning again to why causal inference is valid in an RCT. As illustrated in Figure 1A, participants in an RCT are assigned randomly between treatment and control groups. Because this sorting is accomplished by a mechanism (flip of a coin) that is uncorrelated with any patient or provider characteristics, we expect the mean values of all variables (whether observed or not) to be the same in both groups. Furthermore, because the coin flip has no direct effect on the outcome, any mean difference observed at the end of the trial must be due to treatment itself (Pizer 2009).

Figure 1.

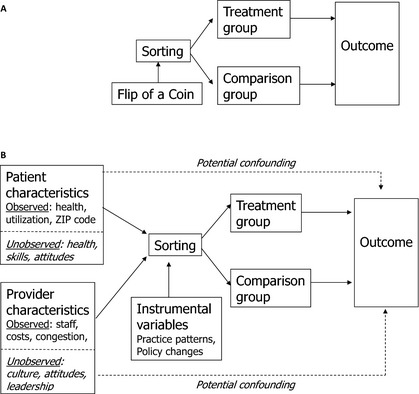
(A) Causal Inference in a Randomized Controlled Trial. (B) Causal Inference in an Observational Study

Source: Adapted from Pizer (2009).

Causal inference in observational studies is more complex, as illustrated in Figure 1B. Sorting into treatment and comparison groups is not determined by one, random factor; instead, numerous patient and provider characteristics, both observed and unobserved, can play a role. Many of these variables may also directly affect the outcome, resulting in potential confounding (illustrated by the dotted lines in the Figure). For example, sicker patients are more likely to choose more aggressive treatments, leading unadjusted comparisons to suggest that aggressive treatments are associated with poor outcomes (Pizer 2009).

The standard method of reducing this confounding is to try to control for individual characteristics that might affect outcome risk, using a regression model to statistically adjust for between‐group differences in risk factors (Iezzoni 1997). Propensity score matching or weighting is a variant on this approach, whereby propensity scores are calculated using a long list of variables (including interactions and transformations) that might be related to the outcome (D'Agostino 1998; Rubin 2007; Garrido et al. 2014). Members of the treatment group are typically matched by propensity score with members of the comparison group through a process ensuring that observable characteristics are balanced between groups.

Unfortunately, neither standard risk adjustment nor propensity score methods can ensure that unobserved patient and provider characteristics will be balanced or adjusted for in the analysis. In Figure 1B, one such unobservable confounder is level of self‐care skill. Patients with more skills may seek more aggressive treatment, having more confidence that they will be able to manage any additional complexity that may be involved. Because such patients are likely to have better outcomes than those with less well developed skills, failing to adjust for unobserved skill differences could lead to an erroneous finding of a beneficial treatment effect.

An IV approach potentially can solve this problem. Imagine a situation where the flip of a coin does not exclusively determine assignment to treatment like it does in an RCT, but it has a strong influence on part of the population. An IV model statistically isolates the component of variation in treatment that can be traced back to the coin flip and then examines differences in outcomes that are due to that component alone, separated from observed and unobserved potential confounders (Pizer 2009). This is like finding a little RCT inside a lot of observational data.

Of course, coin flips like this are rarely found in real data, so the researcher must find another variable (an instrument) that has the experimental properties of the coin flip: it must be strongly related to sorting into treatment, and it must not be related to the outcome, except through its effect on treatment.2 The first property (instrument strength) is illustrated in Figure 1B by the solid arrow connecting the IV to sorting. The second property, known as the exclusion restriction, is illustrated in the Figure by the lack of any arrow connecting the IV directly to the outcome.

IV models in CER are implemented and tested by translating the diagram in Figure 1B into two equations for estimation. The first explains variation in treatment as a function of patient characteristics, provider characteristics, instrumental variables, and unobserved factors (denoted by u). The second explains variation in outcomes as a function of patient characteristics, provider characteristics, receipt of treatment, and unobserved factors (denoted by v), some of which might be the same as in the first equation.

$$\text{Treatment}=\mathrm{f}(\text{patient characteristics, provider characteristics, IV})+u$$ (1)

$$\text{Outcome}=\mathrm{g}(\text{patient characteristics, provider characteristics, Treatment})+v$$ (2)

These equations can be estimated simultaneously or sequentially, but naively estimating the outcome equation (2) without accounting for the treatment equation (1) will lead to bias if there are unobservable factors that influence both treatment and outcomes. For example, if the unobserved confounder is the patient's self‐care skill, as mentioned above, naïve estimation of equation (2) will falsely attribute some of the effect of self‐care skill to the treatment. An IV model could solve this problem by isolating for analysis the component of treatment variation that is due to the instrument and eliminating the component that is due to individual characteristics like self‐care skill.3

Should IV Be Used for CER?

The use of IV methods in health research has been growing rapidly. Garabedian et al. (2014) performed a systematic search for comparative effectiveness studies relying on IV. They found 187 studies published between 1992 and 2011, with the frequency of publication increasing rapidly from fewer than two per year before 1998 to 34 in 2011 alone (Garabedian et al. 2014). They also found that geographic, facility‐level, or provider‐level practice pattern differences were used as the IV in fully 46 percent of these studies. Practice pattern instruments can be easily constructed and applied to an enormous variety of CER questions, so it is vital to be able to evaluate the validity of this approach.

The increasing popularity of IV among comparative effectiveness researchers is leading to intensifying debate in the literature about the strengths and weaknesses of the approach, with different authors reaching seemingly conflicting conclusions. For example, Garabedian et al. (2014) conclude, “Although no observational method can completely eliminate confounding, we recommend against treating instrumental variable analysis as a solution to the inherent biases in observational CER studies.” In contrast, Glymour, Tchetgen, and Robins (2012) conclude, “Given that it will often be nearly free to conduct IV analyses with secondary data, they may prove extremely valuable in many research areas … [however if IV] is uncritically adopted into the epidemiologic toolbox, without aggressive evaluations of the validity of the design in each case, it may generate a host of false or misleading findings.” Although these authors seem to be pointing in different directions, they agree that IV methods can go badly wrong. To assess the potential of IV for CER, it is clearly necessary to understand the potential pitfalls.

How Can IV Go Wrong?

There are two principal threats to the internal validity of IV estimates. First, if the instrument is not strongly enough related to sorting into treatment, IV estimates will be highly imprecise and can be biased, a problem known as “weak instruments” (Bound, Jaeger, and Baker 1995). Second, IV estimates can be biased or misleading because the exclusion restriction is invalid. The exclusion restriction is violated if the IV is correlated with the outcome through some pathway other than treatment. For example, if practice patterns for the treatment in question are related to diffusion of new knowledge, receipt of the treatment may be correlated with receipt of other services that are sensitive to new knowledge and also have effects on the outcome. In this case, the IV estimate would falsely attribute some of the beneficial effects of other treatment improvements to the treatment under study.

IV estimates can be misleading even if the instrument is strong and the exclusion restriction is valid. This can occur because IV estimates measure outcome differences that can be attributed to treatment variations caused by the instrument. If the instrument only affects a small subpopulation, the IV estimates may not be generalizable to a larger population. In other words, the IV estimate measures a local average treatment effect (LATE) (Imbens and Angrist 1994; Harris and Remler 1998).4 This issue is analogous to the external validity problem faced by RCTs (Imbens and Angrist 1994).

How Can IV Be Tested?

Instrument strength is directly observable in the treatment equation, so testing is straightforward (Stock and Yogo 2005). In contrast, the exclusion restriction is impossible to prove empirically and is often left to theoretical argument and subject matter expertise (Grootendorst 2007; Rassen et al. 2009; Swanson and Hernán 2013; Garabedian et al. 2014). Naturally, this reduces confidence in IV methods (Swanson and Hernán 2013). Falsification tests can be particularly useful for IV because they help evaluate the validity of the exclusion restriction, thereby identifying cases where the instrument is confounded and strengthening confidence in cases where no evidence of confounding is revealed.

The idea of falsification testing dates back at least to Popper (1959), but it has been the subject of more attention recently in health outcomes research because of the increasing opportunities for observational studies discussed above (Glymour, Tchetgen, and Robins 2012; Prasad and Jena 2013; Garabedian et al. 2014). Although falsification tests in general can take many forms, there are two particularly useful strategies for testing the exclusion restriction in IV CER studies: (1) investigating an alternative outcome that ought not to be affected by the treatment under study but would be affected by potential confounders that might be correlated with the proposed IV; and (2) investigating an alternative population that again ought not to be affected by the treatment but would be affected by potential confounders.

For example, consider a study comparing stroke outcomes among patients receiving alternative anticoagulation therapies for atrial fibrillation (depicted in panel A of Figure 2). Garabedian et al. (2014) argued that practice pattern IV studies are often vulnerable to bias because they fail to control for one or more of the following patient characteristics: race, education, income, age, insurance status, health status, and health behaviors. For example, if health behaviors are correlated with anticoagulant prescribing patterns and the outcomes under study, this could indeed be a problem. However, patients without atrial fibrillation but who have carotid artery disease are also at elevated risk for stroke and should not be treated with anticoagulants. If anticoagulant prescribing patterns are unrelated to stroke outcomes for carotid disease patients, then it is less likely that confounding health behaviors are correlated with anticoagulant prescribing patterns (panel B of Figure 2). Instead of using an alternative population (those with carotid disease), another option would be to choose an alternative outcome that should not be affected by the treatment but would be affected by health behaviors (e.g., incident lung cancer).

Figure 2.

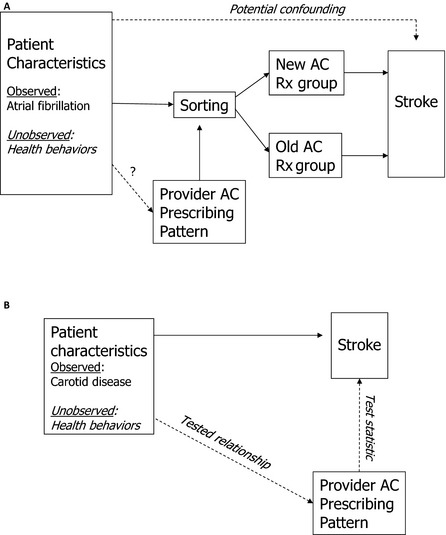
(A) Study of Alternative Anticoagulation Therapies for Patients with Atrial Fibrillation. (B) Falsification Test Using Population with Carotid Disease

AC, anticoagulant. Provider characteristics omitted for simplicity.

More formally, an ideal falsification test for the exclusion restriction would estimate an alternative specification for equation (2) that excludes treatment but includes the practice pattern IV.

$$\text{Outcome}=\mathrm{g}(\text{patient characteristics, provider characteristics, IV})+v$$ (3)

This equation is estimated for an alternative population or an alternative outcome, selected to be as close as possible to the outcomes and populations of interest without being subject to the treatment under study. If the IV has no significant estimated effect on the outcome in equation (3), then the exclusion restriction is not rejected. Note that multiple tests are possible for the same application, so prespecification is valuable to avoid selective reporting (Prasad and Jena 2013).

Conducting and Testing a Real IV Analysis

To make the above conceptual discussion more concrete, consider a recent analysis conducted by Prentice et al. (2014). The investigators set out to compare the effects on long‐term outcomes of two classes of oral medications used as second‐line agents to control type 2 diabetes: sulfonylureas (SU), like glyburide and glipizide, and thiazolidinediones (TZD), like rosiglitazone and pioglitazone. SUs are well‐established, inexpensive, and often used as first‐ and second‐line agents in diabetes treatment (Alexander et al. 2008; Bognar et al. 2013). SU use increases the risk for hypoglycemia, and concerns about their potential association with cardiovascular disease have been present since the 1970s (Groop 1992). Several recent studies have reported an increased risk of cardiovascular disease and death among patients who started on an SU compared to metformin (MET) as an initial treatment of diabetes (Roumie et al. 2012; O'Riordan 2013). TZDs have also been associated with adverse events, including cardiovascular outcomes (MI and CHF), osteoporosis, and bladder cancer (Nissen and Wolski 2007; Bennett et al. 2011; Hsiao et al. 2013a). To compare the effectiveness and risks of these two medication classes, Prentice and colleagues applied a practice pattern IV technique to a large administrative database combining data elements from the Veterans Health Administration (VHA) and Medicare.

The outcomes chosen for study were readily computable from the administrative data and included all‐cause mortality, hospital admission (VHA or Medicare) for any of 13 ambulatory care–sensitive conditions (ACSC) as defined by the Agency for Healthcare Research and Quality (AHRQ 2001, 2013) and AMI or stroke. The VA Vital Status File, which determines the date of death from VA, Medicare, and Social Security Administration data, was used to determine all‐cause mortality (Arnold et al. 2006). ACSC hospitalizations are hypothesized to be preventable with high‐quality outpatient care and include several diabetes and cardiovascular complications such as uncontrolled diabetes, short‐ and long‐term complications of diabetes, or congestive heart failure (AHRQ 2001, 2013). AMI definitions were based on Petersen et al. (1999) and Kyota et al. (2004), and stroke definitions were based on Reker et al. (2002). Due to the overall scarcity of the stroke and AMI outcomes in the data, models that predicted these outcomes separately were unstable. Consequently, AMI and stroke were combined into one outcome. The modeled outcome was the amount of time between the initiation date of SU or TZD and the earliest date of any of the three outcomes, censoring on the date an individual started a third drug or the end of the study period.

Step One: Choose and Specify IV

When considering a quasi‐experimental design, it is vital to identify a source of variation in treatment that is arbitrary or random with respect to potentially confounding variables. This source of variation could be a policy change or boundary (as in interrupted time series or regression discontinuity), or it could be practice variation or program location5 (as in many IV studies). In Figure 1B, the source of arbitrary or random variation in treatment that is only related to the outcome through its effect on treatment is labeled the instrumental variable. The choice and specification of the IV should be determined through consideration of institutional factors and the causal diagram in Figure 1B.

The VHA is the largest integrated health care system in the United States serving over 8.3 million patients each year and spending nearly 4 billion dollars on prescriptions in 2009 (US GAO 2010; VHA 2014). There is significant physician‐prescribing practice variation (Gellad et al. 2010, 2012) and VHA patients are assigned to their primary care physicians by variable and often arbitrary methods (Doyle, Ewer, and Wagner 2010; Prentice et al. 2015). Consequently, provider‐level prescribing variation is unlikely to be related to the observable or unobservable patient characteristics shown in Figure 1B and identified by Garabedian and colleagues. This is a promising start for a potential instrument.

Prentice and colleagues defined treatment as initiating either SU or TZD as a second hypoglycemic agent after experience with metformin, noting that most patients who initiated one or the other remained on it 2 years later (Prentice et al. 2014). They defined their instrument as the proportion of second‐line agent prescriptions (SU or TZD) written for SU by each provider (for all of their patients) during the year prior to the patient's initiation date for their second‐line agent (Prentice et al. 2014). Providers and patients were paired based on that initiation date to minimize confounding that could occur if patients later switched providers. If a provider had <10 patient‐level second‐line agent prescriptions during the prior year (70 percent of the time), the rate at the community‐based outpatient clinic (CBOC) or VHA medical center (VAMC) where the provider practiced was used.

To check whether this instrument was random with respect to patient characteristics, Prentice and colleagues performed a simple falsification test by comparing sample means between SU and TZD initiators (columns 1 and 2 of Table 1), and then between those paired with high versus low SU prescribers (columns 3 and 4 of Table 1). Although there were some notable differences by initiation group—for example, SU initiators were more likely to have baseline HbA1c >9—these differences were no longer evident when patients were grouped by provider‐prescribing pattern (Table 1), indicating that the first falsification test did not reject the proposed instrument.6

Table 1.

Selected Sample Means or Percentages for Patients Starting Sulfonylureas (SU) or Thiazolidinediones (TZD) as Second Agent and Patients Assigned to Above‐ and Below‐Median SU‐Prescribing Providers

Demographics	Individual Treatment		Provider SU Prescribing
	Start SU (n = 73,726)	Start TZD (n = 7,210)	Top 50% SUa (n = 40,483)	Bottom 50% SUa (n = 40,453)
Age (years), mean	69.1b	70.1	69.2	69.2
Male	98	98	98	98
White	88	89	90	87
Diabetes management
HbA1c ≥9	9	5	8	8
Retinopathy complications	14	16	14	14
Nephropathy complications	10	12	10	10
Neuropathy complications	19	22	20	19
Cerebrovascular complications	13	14	13	13
Cardiovascular complications (some)	24	28	25	25
Cardiovascular complications (severe)	26	23	25	25
Peripheral vascular complications	14	16	14	14
Metabolic complications	1	1	1	1
Cardiovascular comorbidities
BMI obese	41	39	41	41
Congestive heart failure	13	12	13	13
Cardiac arrhythmias	21	21	21	21
Valvular disease	10	11	9	10
Hypertension	84	84	84	84
Pulmonary circulatory disorder	1	1	1	1
Chronic pulmonary disease	23	21	24	23
Provider process quality variables
Provider % HbA1c >9 in baseline period, mean	10	10	10	10
Provider BP % >140 or >90 in baseline period, mean	41	42	41	41
Provider LDL % >100 in baseline period, mean	38	40	38	38
Outcomes
ACSC hospitalization	18	13	18	17
All‐cause mortality	10	7	10	9
Stroke or AMI	5	4	5	5

^aThese two columns show descriptive statistics of patients assigned to providers who prescribe SU below and above the sample median.

^bFor ease of presentation, percentages are presented unless otherwise noted.

Source. Excerpted from Prentice et al. (2014, table 2).

Step Two: Choose and Specify Control Variables

Once an IV has been chosen, consider other potential confounders that might be correlated with the IV as well as the outcome. In the practice pattern example, patient characteristics are not expected to be correlated with the IV for institutional reasons, and Table 1 demonstrates that this appears to be true in the data. In contrast, as shown in Figure 1B, provider and facility characteristics like the quality of care delivered might be correlated with practice patterns and might also affect the outcome. If possible, this danger can be mitigated by including provider and facility quality measures as control variables in the outcome equation. Although they are less likely to be instrument confounders, it is a good idea to include patient characteristics as control variables as well because they will improve the precision of estimates (if they are related to the outcome).

Prentice and colleagues specified three process quality measures to control for potentially confounding provider and facility characteristics: percent of HbA_1c labs >9 percent (ACCORD 2008; Turner, Holman, and Cull 1998), percent of blood pressure readings >140/90 mmHg (The State of Health Care Quality 2011), and percent of LDL cholesterol labs >100 mg/dL (NCQA 2011). These variables were computed at the same provider, CBOC or VAMC level and time periods as the IV prescribing rate. Sample means for these variables are shown in Table 1, which also demonstrates that the IV appears to balance these factors as well.7

Step Three: Choose Falsification Sample and Outcomes

Once the IV and control variables have been specified, it is tempting to proceed with the study, but a little more advance planning is essential to support falsification testing. If the instrument is valid, it should affect the outcome only through treatment. Therefore, it should have no effect on outcomes that are not in the treatment pathway. Such outcomes could be the result of unrelated disease processes affecting the study population, or they could be study outcomes experienced by those not subject to the study treatment. In either case, investigators will usually have to specify the necessary data when the study protocol is submitted for funding consideration and human subjects protection review. An ideal falsification sample would not be exposed to the study treatment, but it would be exposed to all of the potential confounders that might be correlated with the instrument and the outcome, like provider‐ or facility‐level quality of care.

In the diabetes study, Prentice and colleagues specified two populations for falsification testing that were closely related to the study population but not subject to treatment by SU or TZD (Prentice et al. 2014). First, they selected all individuals who received a new prescription of MET and followed them for 1 year. They assumed these patients were being treated with MET as their first‐line agent and their disease had not progressed to the point of needing a second‐line agent in that time period. Consequently, the SU prescribing rate should not affect the outcomes for these individuals. They used provider SU prescribing rates to predict all‐cause mortality, ACSC hospitalization, and stroke or AMI controlling for all the demographics, comorbidities and process quality variables. As no individuals in this population were on SU, no treatment equation was estimated and the falsification test was performed by including the instrument in an alternative specification of the outcome equation.

Using the same analyses, the second falsification test used a sample of individuals who initiated insulin after MET and took no other diabetes drugs during the study period. Again, the conceptual model indicated that SU prescribing rates should not affect the outcomes for these individuals if there were no important instrument‐outcome confounders. An appealing feature of this pair of falsification tests is that the falsification populations bracket the study population in terms of disease severity, with MET‐only patients the least severe and insulin patients the most severe. If the falsification tests support the exclusion restriction, it is difficult to imagine why it would fail only among those with moderate disease.

Step Four: Estimate IV Model

Linear IV models can be estimated easily in most statistical packages, but health outcomes of interest are often more appropriately estimated by nonlinear methods like logistic regression or survival models. Nonlinear IV models can also be estimated, but methods often involve specialized programming, making implementation more difficult. Two‐stage residual inclusion is a widely applicable and easily implemented approach that does not involve specialized programming beyond the use of standard commands in a statistical package like STATA (Terza, Basu, and Rathouz 2008; Pizer 2009). The first‐stage treatment equation (1) is estimated by logistic or probit regression, and the first‐stage residual is calculated as uhat = Treatment − fhat (patient characteristics, provider characteristics, IV), where fhat(.) is the estimated function f(.) and gives the predicted probability of treatment. The second‐stage outcome equation (4) is estimated next, after including the estimated residual, uhat, as a covariate along with the original treatment variable. This additional variable controls for possible correlation between unobservable factors affecting treatment (u) and unobservable factors affecting the outcome (v).8

$$\text{Outcome}=\mathrm{g}(\text{patient characteristics, provider characteristics, Treatment, uhat})+v$$ (4)

The first‐stage residual term, uhat, is an estimated quantity, but statistical software will not automatically account for the increased uncertainty that implies, so standard errors for estimates from equation (4) must be recalculated by bootstrapping (Efron 1970).

In the diabetes study, Prentice et al. (2014) used a probit model to estimate their treatment equation and Cox models including the first‐stage residual to estimate their outcome equations. The strength of their practice pattern IV is demonstrated by the size and precision of its estimated effect in the treatment equation (Table 2). The IV estimates of treatment effects are expressed as hazard ratios in Table 3, indicating that SU prescribing significantly increased the risk of mortality and ACSC hospitalization relative to TZD prescribing, but did not have a significant effect on the risk of stroke or heart attack. As SUs are widely used and considered safe while TZDs are used less frequently and typically considered more risky, these are surprising and potentially important results.

Table 2.

Selected First‐Stage Probit Results: Receiving Sulfonylureas (SU) Compared to Thiazolidinediones (TZD) (n = 80,936)

	Coefficient	P < |t|	95% Confidence Interval
Instrument
Provider prescribing history	2.215	0.000	2.098–2.332

Model also includes baseline demographics, Elixhauser comorbidities, Young severity index, HbA_1c, BMI, microalbumin, serum creatinine, provider quality controls, Veterans Affairs Medical Center fixed effects, and year effects that are not shown.

Source. Excerpted from Prentice et al. (2014, table 3).

Table 3.

Second‐Stage Cox Proportional Hazard Models: Effect of Sulfonylureas (SU) on Mortality, Ambulatory Care–Sensitive Condition (ACSC) Hospitalization, and Cardiovascular Outcomes (n = 80,936)

	Hazard Ratio	P < |t|	95% Confidence Interval
All‐cause mortality	1.50	0.014	1.09–2.09
ACSC hospitalization	1.68	<0.001	1.31–2.15
Stroke or heart attack	1.15	0.457	0.80–1.66

Models include baseline demographics, Elixhauser comorbidities, Young severity index, HbA_1c, BMI, microalbumin, serum creatinine, provider quality controls, year fixed effects, and Veterans Affairs Medical Center random effects.

Source. Excerpted from Prentice et al. (2014, table 4).

Step Five: Compute Falsification Test

The falsification tests specified above can be computed by estimating equation (3) with either the falsification sample and the study outcomes or with the study sample and the falsification outcomes. The exclusion restriction is rejected if the IV in equation (3) has a statistically significant effect on the outcome. No bootstrapping is necessary because none of the covariates in equation (3) are estimated. Although presenting multiple falsification tests is better than only one, it is not possible to prove conclusively that there is no confounding. As with other aspects of analytic design, specification of falsification tests at the proposal stage of a project helps to allay concerns that investigators might be presenting only the results that support their design.

In the diabetes study, Prentice and colleagues found no significant effects of the IV on any of the outcomes in either falsification sample (Table 4). These results are consistent with validity of the IV and improve confidence in the IV estimates, but it is always possible that a different test specification or a larger sample could detect a problem.

Table 4.

Falsification Test: Effect of Sulfonylureas (SU) Prescribing Rate on Mortality, Ambulatory Care–Sensitive Condition (ACSC) Hospitalization, and Cardiovascular Outcomes

	Hazard Ratio	P < |t|	95% Confidence Interval
MET only sample (n = 76,860)
All‐cause mortality	1.30	0.115	0.94–1.79
ACSC hospitalization	1.23	0.149	0.93–1.62
Stroke or heart attack	1.11	0.657	0.70–1.77
MET and insulin sample (n = 4,015)
Mortality	1.30	0.427	0.68–2.52
ACSC hospitalizationa	0.81	0.425	0.47–1.37

Models include baseline demographics, Elixhauser comorbidities, Young severity index, HbA_1c, BMI, microalbumin, serum creatinine, provider quality controls, year fixed effects, and Veterans Affairs Medical Center random effects.

^aThe stroke and heart attack model did not converge in the MET and insulin sample due to small sample sizes.

Source. Excerpted from Prentice et al. (2014, table 5).

It is also possible that an instrument that is not rejected for one population will be rejected for another, closely related population. Bartel, Chan, and Kim (2014) use day of the week admitted to the hospital as an instrument for length of stay when measuring the effect of length of stay on rehospitalization and other outcomes for patients with heart failure. For institutional or personal preference reasons, patients admitted on Monday or Tuesday tend to have shorter lengths of stay than those admitted on Thursday or Friday (who are more likely to stay over the weekend). Bartel, Chan, and Kim tabulate patient characteristics by their instrument to try to falsify the assumption that admission day is uncorrelated with observed and unobserved health status, and they find that the instrument is not rejected for patients with the most severe disease, but it is rejected for less severe cases. This makes sense because severe cases might have to respond to symptoms immediately, making admission day effectively random, but less severe cases might choose their admission day with a desired length of stay in mind. The investigators appropriately proceed to use the instrument only for the population supported by the falsification test (Bartel, Chan, and Kim 2014).9

Conclusion

Falsification testing is a fundamental scientific tool that is particularly useful when considering an instrumental variables approach to an observational study. With proper advance planning, falsification tests can be easily applied to potential instruments, with the results either rejecting the instruments or increasing confidence in them. Causal inference from an instrumental variables observational study will never be as strong as it could be from a well‐executed randomized clinical trial, but, if testing supports the strength and validity of the instruments, these studies can shed light on a multitude of important clinical questions that would otherwise be too confounded to investigate with other observational study designs.

Supporting information

Appendix SA1: Annotated STATA Code.