Room-temperature local ferromagnetism and its nanoscale expansion in the ferromagnetic semiconductor Ge_1–xFe_x

Abstract

We investigate the local electronic structure and magnetic properties of the group-IV-based ferromagnetic semiconductor, Ge_1−xFe_x (GeFe), using soft X-ray magnetic circular dichroism. Our results show that the doped Fe 3d electrons are strongly hybridized with the Ge 4p states, and have a large orbital magnetic moment relative to the spin magnetic moment; i.e., m_orb/m_spin ≈ 0.1. We find that nanoscale local ferromagnetic regions, which are formed through ferromagnetic exchange interactions in the high-Fe-content regions of the GeFe films, exist even at room temperature, well above the Curie temperature of 20–100 K. We observe the intriguing nanoscale expansion of the local ferromagnetic regions with decreasing temperature, followed by a transition of the entire film into a ferromagnetic state at the Curie temperature.

A major issue that must be addressed for the realization of semiconductor spintronic devices is to achieve room-temperature ferromagnetism in ferromagnetic semiconductors (FMSs) based on the widely used III–V and group-IV materials. In Ga_1−xMn_xAs (GaMnAs), which is the most intensively studied FMS, the highest Curie temperature (T_C) ever reported is 200 K¹. In GaMnAs, T_C is limited by the presence of interstitial Mn atoms, which are antiferromagnetically coupled to the substitutional Mn atoms². Recently, however, the group-IV-based FMS, Ge_1–xFe_x (GeFe), has been reported to exhibit several attractive features³,⁴,⁵. It can be grown epitaxially on Si and Ge substrates without the formation of intermetallic precipitates, and is therefore compatible with mature Si process technology. Unlike GaMnAs, in GeFe, interstitial Fe atoms do not lead to a decrease in T_C⁶, and T_C can be easily increased to above 200 K by thermal annealing⁷. Furthermore, T_C does not depend on the carrier concentration, and thus T_C and resistivity can be controlled separately⁸, which is a unique feature that is only observed in GeFe and is a considerable advantage in overcoming the conductivity mismatch problem between ferromagnetic metals and semiconductors in spin-injection devices. Despite these attractive features, a detailed microscopic understanding of the ferromagnetism in GeFe, which is vitally important for room-temperature applications, is lacking. Here, we investigate the local electronic and magnetic properties of GeFe using X-ray absorption spectroscopy (XAS) and X-ray magnetic circular dichroism (XMCD), which are powerful techniques for element-specific detection of local electronic states and magnetic moments⁹,¹⁰,¹¹,¹²,¹³. We find that nanoscale local ferromagnetic regions remain in the GeFe films even at room temperature, i.e., well above T_C; it follows that GeFe potentially has strong ferromagnetism, which persists even at room temperature. Furthermore, we observe the intriguing feature that ferromagnetic regions, which are formed above T_C via the ferromagnetic exchange interaction in high-Fe concentration regions of the films, develop and expand as the temperature decreases, and that all of them coalesce at temperatures below T_C. Such a nanoscale expansion of the ferromagnetic regions is a key feature in understanding materials that exhibit single-phase ferromagnetism despite the inhomogeneous distribution of magnetic atoms in the film⁶,⁷,¹⁴,¹⁵.

Results and Discussion

Basic properties of our GeFe films

We carried out XMCD measurements on two samples (labeled A and B) consisting of a 120-nm-thick Ge_0.935Fe_0.065 layer grown on a Ge(001) substrate by low-temperature molecular beam epitaxy (LT-MBE) [Fig. 1(a,b)] (see Methods). The Ge_0.935Fe_0.065 layer of sample A was grown at 160 °C, whereas that of sample B was grown at 240 °C. These samples are the same as those studied in ref. 6. From the Arrott plots of the H dependence of the magnetic circular dichroism (MCD) measured with visible light with a photon energy of 2.3 eV (corresponding to the L-point energy gap of bulk Ge), we found T_C = 20 K and 100 K for samples A and B, respectively. Detailed crystallographic analyses, including in situ reflection high-energy electron diffraction (RHEED), high-resolution transmission electron microscopy (TEM), spatially resolved transmission-electron diffraction (TED) combined with energy-dispersive X-ray spectroscopy (EDX) and X-ray diffraction (XRD), showed that the GeFe films have a diamond-type single-crystal structure without any ferromagnetic precipitates and with nanoscale spatial Fe concentration fluctuations of 4–7% (sample A) and 3–10% (sample B)⁶. We found that T_C is higher when the fluctuations in the Fe concentration are larger⁶. In addition, channeling Rutherford backscattering (c-RBS) and channeling particle-induced X-ray emission (c-PIXE) measurements showed that ~85% (~15%) of the doped Fe atoms exist at the substitutional (tetrahedral interstitial) sites in both samples A and B, and that the interstitial Fe concentration is not related to T_C⁶. This also indicates that there are no ferromagnetic precipitates with different crystal structures in our films.

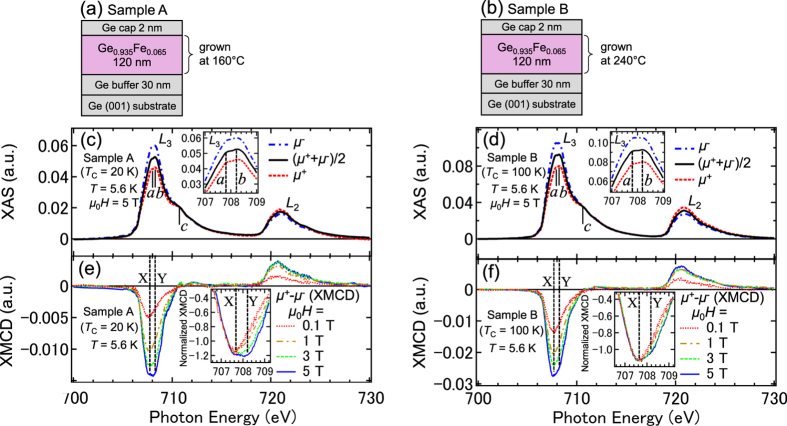
Figure 1. Sample structures, XAS spectra and XMCD spectra.

(a,b) Schematic structures of sample A (a) and sample B (b). (c,d) XAS spectra of μ⁻, μ⁺ and (μ⁺ + μ⁻)/2 at the L₂ (~721 eV) and L₃ (~708 eV) absorption edges of Fe for sample A (c) and sample B (d) measured at 5.6 K with μ₀H = 5 T applied perpendicular to the film surface. The insets show a magnified plot of the spectra at the Fe L₃ edge. (e,f) XMCD (=μ⁺ − μ⁻) spectra at the L₂ and L₃ absorption edges of Fe for sample A (e) and sample B (f) measured at 5.6 K with various H applied perpendicular to the film surface. The insets show a magnified plot of the spectra at the Fe L₃ edge, in which the XMCD data are normalized to 707.3 eV.

XAS and XMCD measurements

We measured the Fe L_2,3-edge XAS spectra [μ⁺, μ⁻ and (μ⁺ + μ⁻)/2] of samples A [Fig. 1(c)] and B [Fig. 1(d)] at 5.6 K with μ₀H = 5 T applied perpendicular to the film surface. Here, μ⁺ and μ⁻ refer to the absorption coefficients for photon helicity parallel and antiparallel to the Fe 3d majority spin direction, respectively. In both films, three peaks a, b and c are observed at the Fe L₃ edge in the XAS spectra [see also the insets in Fig. 1(c,d)]. We found that the small peak c was suppressed by etching the surface with dilute HF, indicating that this peak, which can be assigned to the Fe³⁺ state, originates from a small quantity of surface Fe oxide¹⁶, which remains even after surface cleaning. Meanwhile, peaks a and b are assigned to the Fe atoms in GeFe. Peaks a and b can be assigned to the Fe²⁺ state¹⁷,¹⁸.

We measured the Fe L_2,3-edge XMCD (=μ⁺ − μ⁻) spectra of samples A [Fig. 1(e)] and B [Fig. 1(f)] at 5.6 K with various H applied perpendicular to the film surface. Here, we discuss the XMCD intensities at 707.66 eV (X) and 708.2 eV (Y), which correspond to the photon energies of peaks a and b in the XAS spectra, respectively. When normalized to 707.3 eV, the XMCD spectra with various H differ, and the intensity at X grows faster than that at Y as H increases, as shown in the insets of Fig. 1(e,f). As shown in Fig. 1(c,d), the shapes of the XAS spectra at the Fe L₃ edge are similar between samples A and B, which have almost the same interstitial Fe concentrations (i.e., 15% of the total Fe content⁶); therefore, we can assign the XMCD intensity at X to the substitutional Fe atoms and the paramagnetic component of the XMCD intensity at Y to the interstitial Fe atoms. We do not observe fine structures due to multiplet splitting at the Fe L₃ edge in both samples, which would be observed if the 3d electrons were localized and were not strongly hybridized with other orbitals¹⁹. These observations indicate that the Fe 3d electrons are strongly hybridized with the Ge 4p states²⁰.

Determination and analyses of the orbital and spin magnetic moments

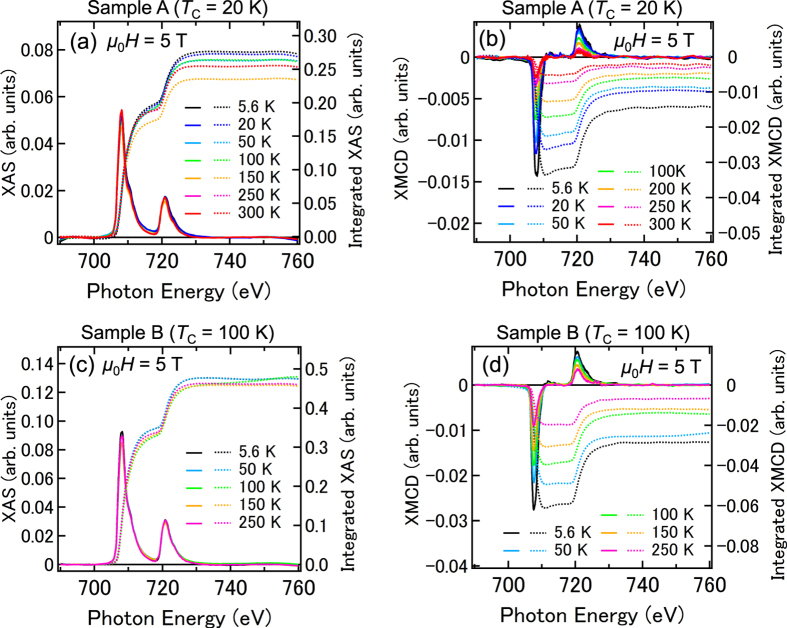
We determine the orbital magnetic moment, m_orb, and the spin magnetic moment, m_spin, the orbital magnetic moment relative to the spin magnetic moment, m_orb/m_spin, and the total magnetic moment, M = m_spin + m_orb, of the substitutional Fe atoms in accordance with the well-established procedure using the XMCD sum rules²¹,²²,²³,²⁴,²⁵. Figure 2(a) shows the XAS spectra (solid curves) and the XAS signals integrated from 690 eV (dashed curves) of sample A. Figure 2(b) shows the XMCD spectra (solid curves) and the XMCD signals integrated from 690 eV (dashed curves) of sample A. Here, the measurements were carried out with a magnetic field μ₀H = 5 T applied perpendicular to the film surface at various temperatures. Figure 2(c,d) shows the same data measured for sample B. For the XMCD sum-rules analyses, we define r, p and q as the following equations at each temperature.

Figure 2. Integrated XAS and XMCD spectra.

(a,c) XAS [=(μ⁺ + μ⁻)/2] spectra (solid curves) and the XAS signals integrated from 690 eV (dashed curves) of sample A (a) and sample B (c). (b,d) XMCD (=μ⁺ − μ⁻) spectra (solid curves) and the XMCD signals integrated from 690 eV (dashed curves) of sample A (b) and sample B (d). These measurements were carried out with a magnetic field μ₀H = 5 T applied perpendicular to the film surface at 5.6 K (black curves), 20 K (blue curves), 50 K (light blue curves), 100 K (green curves), 150 K (orange curves), 250 K (pink curves), and 300 K (red curves).

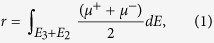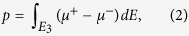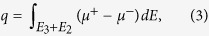where E₃ (690–718 eV) and E₂ (718–760 eV) represent the integration energy ranges for the L₃ and L₂ absorption edges, respectively. Here, E represents the incident photon energy. We can obtain m_spin and m_orb of substitutional Fe atoms using the XMCD sum rules, which are expressed as follows:

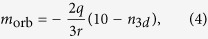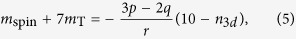where n_3d and m_T are the number of 3d electrons on the Fe atom and the expectation value of the intra-atomic magnetic dipole operator, respectively. We neglect m_T because it is negligibly small for Fe atoms at the T_d symmetry site²⁴. By dividing equation (4) by equation (5), m_orb/m_spin is expressed by

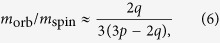Thus, we can obtain m_orb/m_spin directly from the XMCD spectra without any assumptions.

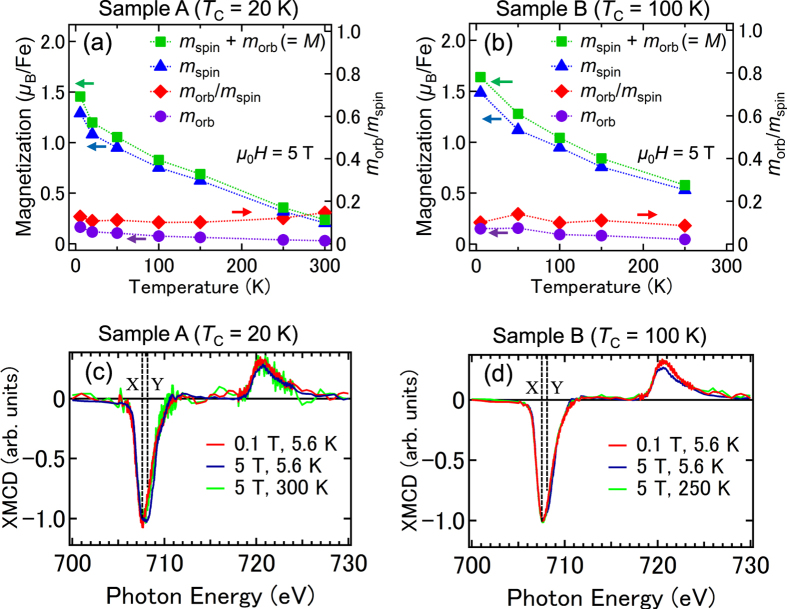
By the above calculations with equations (2), (3) and (6) using the temperature dependence of XMCD spectra shown in Fig. 2, we obtained the temperature dependence of m_orb/m_spin of substitutional Fe atoms as shown in Fig. 3(a,b). For sample A, m_orb/m_spin = 0.12 ± 0.02, and for sample B, m_orb/m_spin = 0.11 ± 0.03, both of which are positive and larger than that of bulk Fe (where m_orb/m_spin ~ 0.043¹⁹); the orbital angular momentum in GeFe is not quenched. The observation that the spin and orbital angular momentum are parallel suggests that the Fe 3d shell is more than half filled. This implies that the Fe atoms are in the 2⁺ state rather than in the 3⁺ state, in which the Fe 3d shell is half-filled and the orbital angular momentum vanishes. This result is consistent with the peak positions of the XAS spectra (see Fig. 1(c,d)). The large m_orb is a characteristic property of GeFe, and excludes the possibility of the existence of ferromagnetic Fe metal precipitates in our films.

Figure 3. Temperature dependence of m_spin + m_orb, m_spin, m_orb and m_orb/m_spin, and the normalized XMCD spectra with different magnetic fields and temperatures.

(a,b) The temperature dependence of m_spin + m_orb, m_spin, m_orb, and m_orb/m_spin for sample A (a) and sample B (b) with an applied magnetic field of μ₀H = 5 T. (c,d) XMCD spectra of samples A (c) and B (d) normalized to 707.3 eV measured at 5.6 and 300 K with magnetic fields of 0.1 and 5 T applied perpendicular to the film surface.

We describe the derivation of m_spin and m_orb using equations (4) and (5). Figure 3(c,d) shows the XMCD spectra of samples A (c) and B (d) normalized to 707.3 eV measured at 5.6 and 300 K with magnetic fields of 0.1 and 5 T applied perpendicular to the film surface. In both films, all the line shapes of the XMCD spectra are almost the same, which means that the paramagnetic component observed at Y in Fig. 1(e,f) is negligibly small in comparison with the entire XMCD spectra and almost all XMCD intensities are composed of the absorptions by the substitutional Fe atoms observed at X in Fig. 1(e,f). This result means that the integrated values of the XMCD spectra p [equation (2)] and q [equation (3)] can be attributed only to the substitutional Fe atoms. Meanwhile, because the XAS signals have both contributions of the substitutional and interstitial Fe atoms, we reduced the integrated XAS intensity r [equation (1)] to 85% of its raw value (85% is the approximate ratio of the substitutional Fe atoms to that of the total Fe atoms in both samples A and B⁶) when using the XMCD sum rules. We note that this assumption, that each substitutional Fe atom and each interstitial Fe atom contribute equally to the integrated XAS intensity [r value (equation (1))], does not affect our main conclusions in this paper (see Supplementary Discussion S1). We took n_3d to be 6 and the correction factor for m_spin to be 0.88²⁵ for Fe²⁺ in equations (4) and (5). By the above calculations using the temperature dependence of XAS and XMCD spectra shown in Fig. 2, we obtained the temperature dependence of m_spin, m_orb and m_spin + m_orb (=M) of substitutional Fe atoms shown in Fig. 3(a,b). The M values obtained by the XMCD measurements are 1.00 μ_B/Fe for sample A and 1.43 μ_B/Fe for sample B when a magnetic field μ₀H = 1 T is applied perpendicular to the film surface at 5.6 K. The magnetizations measured by superconducting quantum interference device (SQUID) under the same condition at 5 K are 0.7 μ_B/Fe for sample A and 1.3 μ_B/Fe for sample B⁶. These values are close to those obtained by XMCD. The slight differences may originate from the unavoidable inaccuracy of the subtracting procedure of the large diamagnetic response of the substrate in the SQUID measurements. We see that both m_spin and m_orb (and therefore the total magnetic moment M = m_spin + m_orb) are larger in sample B (T_C = 100 K) than in sample A (T_C = 20 K) over the entire temperature region when μ₀H = 5 T.

Figure 4 shows the H dependence of the XMCD intensity at energy X and a temperature of 5.6 K, the MCD intensity measured with visible light of 2.3 eV at 5 K, and the magnetization measured using a SQUID at 5 K for sample B. The shapes of these curves show excellent agreement with each other; it follows that the spin splitting of the valence band composed of the Ge 4p orbitals is induced by the Fe 3d magnetic moment, which originates from the substitutional Fe atoms, through the p–d hybridization. The MCD hysteresis curve did not depend on the sweeping speed of the magnetic field unlike superparamagnetic materials with spin blocking [see Supplementary Discussion S2 ²⁶,²⁷]. This result supports our understanding that the GeFe films are ferromagnetic below T_C.

Figure 4. Magnetic field dependence of the normalized XMCD, MCD and magnetization.

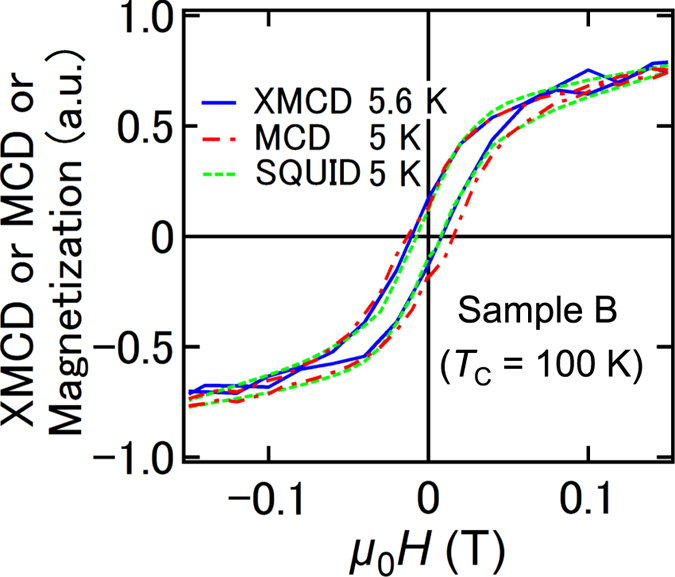
The H dependence of the XMCD intensity at X shown in Fig. 1 (707.66 eV) at 5.6 K, the MCD intensity at 5 K with a photon energy of 2.3 eV corresponding to the L-point energy gap of bulk Ge, and the magnetization measured using a SQUID at 5 K for sample B.

Room-temperature local ferromagnetism and the nanoscale expansion of the local ferromagnetic regions in the GeFe films

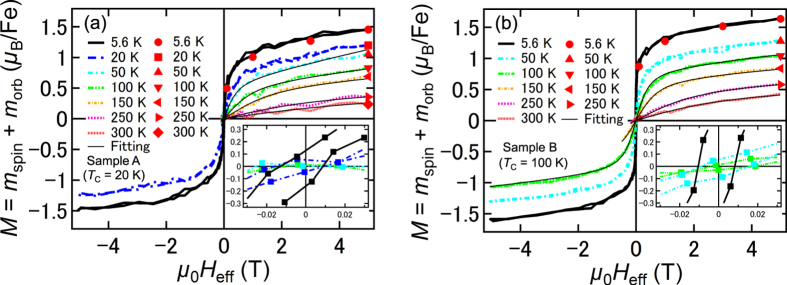
Figure 5(a,b) shows the effective magnetic-field (H_eff) dependence of the XMCD intensity measured at X for samples A (a) and B (b) at various temperatures. Here, M is also plotted (filled red symbols), and μ₀H_eff is obtained by subtracting the product of M and the density of the substitutional Fe atoms from μ₀H to eliminate the influence of the demagnetization field (see Supplementary Discussion S3). The insets show clear hysteresis below T_C in both samples. The XMCD–H_eff curves show large curvature above T_C in both samples [see the main panels of Fig. 5(a,b)], indicating that part of the film is superparamagnetic (SPM) above T_C. It indicates that local ferromagnetic regions form in nanoscale high-Fe concentration regions at temperatures above T_C, and thus M can be described by

Figure 5. Effective magnetic field dependence of the total magnetic moment.

(a,b) The dependence of the XMCD intensity measured at X on the effective magnetic field H_eff for sample A (a) and sample B (b) at various temperatures. The total magnetization (M = m_spin + m_orb) obtained using the XMCD sum rules is also plotted (filled red symbols). We scaled the vertical axis of the XMCD intensity so that it represents M at each temperature. In all measurements, H was applied perpendicular to the film surface.

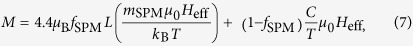where f_SPM and m_SPM are fitting parameters expressing the fraction of SPM substitutional Fe atoms and the magnetic moment per local ferromagnetic region, respectively. Also, C is the Curie constant per substitutional Fe atom, and L is the Langevin function. Here, 4.4 μ_B is the ideal saturated value of M; i.e., M = m_spin + (m_orb/m_spin) ×m_spin, where m_spin = 4 μ_B (for Fe²⁺) and m_orb/m_spin ≈ 0.1 [Fig. 3(a,b)] when all the substitutional Fe atoms are magnetically active. Here, the Curie constant per substitutional Fe atom is obtained using the following equations:

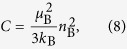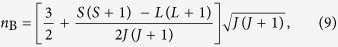where μ_B, k_B, n_B, S, L and J represent the Bohr magneton, the Boltzmann constant, the effective Bohr magneton number, the spin angular momentum, the orbital angular momentum and the total angular momentum, respectively. Here, S = 2 (for Fe²⁺), and L = 0.4 (L = 2 S × m_orb/m_spin, where m_orb/m_spin ≈ 0.1 as shown in Fig. 3(a,b)), and J = 2.4 (=L + S because the spin and orbital angular momenta of a substitutional Fe atom are parallel) in equation (9). Thus, n_B is estimated to be 5.24. The first and second terms in equation (7) correspond to the SPM and paramagnetic components, respectively. In Fig. 5(a,b), the thin black solid curves correspond to the best fit obtained with equation (7). For sample B, the M–H_eff curves at temperatures in the range 100–300 K are well reproduced by equation (7), which indicates that the ferromagnetic – SPM transition occurs at T_C = 100 K. With sample A, the M–H_eff curves at temperatures above T_C (i.e., T ≥ 20 K) are well reproduced by equation (7), except for T = 20 K, which is probably due to the onset of ferromagnetism. These good fits up to room temperature indicate that ferromagnetic interactions within the nanoscale high-Fe concentration regions remain at room temperature in both samples.

Here, we estimate the ratios of the substitutional ferromagnetic, paramagnetic, and magnetically inactive Fe atoms to the total number of substitutional Fe atoms at 5.6 K in samples A and B. In this discussion, we only consider substitutional Fe atoms. The obtained results are summarized in Table 1. At 5.6 K, in principle, the H_eff dependence of M (=m_spin + m_orb) of one substitutional paramagnetic Fe atom is expressed by the Langevin function. Thus, theoretically, the H_eff dependence of M of one substitutional paramagnetic Fe atom at 5.6 K is obtained by substituting 4.4 μ_B, 1 and 5.6 K in m_SPM, f_SPM and T of equation (7), respectively (Fig. 6). Here, the experimental M–H_eff curves at 5.6 K shown in Fig. 5(a,b) can be approximately expressed by the sum of the square hysteresis curve originating from substitutional ferromagnetic Fe atoms and the Langevin function originating from substitutional paramagnetic Fe atoms. From the high-field magnetic susceptibility 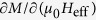(μ_B/T per Fe) of the M–H_eff curve, we can estimate the fraction of the substitutional paramagnetic Fe atoms. We approximated by the slope of the M–H_eff line from 4 T to 5 T. In this way, from Fig. 6, the theoretical value is estimated to be 0.33 μ_B/T per one substitutional paramagnetic Fe (slope of the black dashed line in Fig. 6). As shown in Fig. 5(a,b), the experimental values at 5.6 K in samples A and B are 0.08 μ_B/T and 0.06 μ_B/T, respectively; it follows that the ratios of the substitutional paramagnetic Fe atoms to the total number of substitutional Fe atoms are ~24% (=0.08/0.33) in sample A and ~18% (=0.06/0.33) in sample B. Next, we estimate the fraction of substitutional ferromagnetic Fe atoms. The extrapolated M value from the high magnetic field region to H_eff = 0 in Fig. 5(a,b) is 1.1 μ_B per Fe atom in sample A, and 1.3 μ_B per Fe atom in sample B at 5.6 K. Because the M–H_eff curve of the substitutional paramagnetic Fe atoms is expressed by the Langevin function at this temperature as mentioned above, these extrapolated M values include a contribution of the substitutional paramagnetic Fe atoms, which is estimated by a linear extrapolation of M to H_eff = 0 in the M–H_eff curve of the substitutional paramagnetic Fe atoms. In Fig. 6, for one substitutional paramagnetic Fe atom, it is 1.1 μ_B per Fe. Thus, the contribution of the substitutional paramagnetic Fe atoms to the extrapolated M value is experimentally ~0.26 μ_B (=1.1 μ_B × 0.24) per Fe for sample A and ~0.20 μ_B (=1.1 μ_B × 0.18) per Fe for sample B. These results suggest that only ~19% [=(1.1 − 0.26)/4.4] and ~25% [=(1.3 − 0.20)/4.4] of the substitutional Fe atoms are ferromagnetic in samples A and B, respectively. This result means that 57% (=100 − 24 − 19 for sample A and 100 − 18 − 25 for sample B) of the substitutional Fe atoms do not contribute to the total magnetization. We think that some fraction of these substitutional magnetically inactive Fe atoms couple antiferromagnetically. This is also supported by the weak spin-glass behaviour observed in GeFe at very low temperatures⁷.

Table 1. Ratios of the substitutional ferromagnetic, paramagnetic, and magnetically inactive Fe atoms to the total number of substitutional Fe atoms at 5.6 K in samples A and B.

Sample	Ferromagnetic	Paramagnetic	Inactive
A	19%	24%	57%
B	25%	18%	57%

Figure 6. Effective magnetic-field dependence of the total magnetization M(=m_spin + m_orb) per one substitutional paramagnetic Fe at 5.6 K obtained using equation (7).

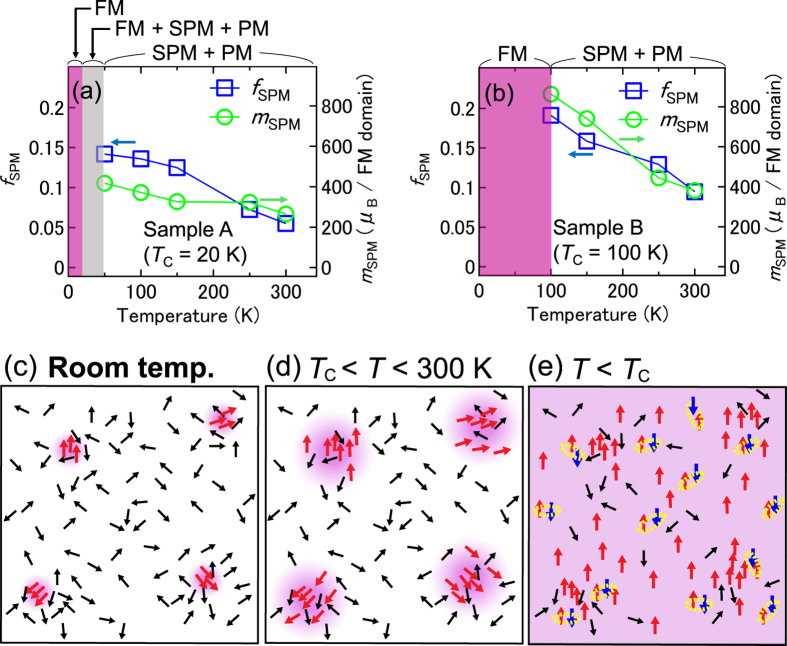
We see a similar trend in the temperature dependence of the fitting parameters f_SPM and m_SPM in both films; i.e., f_SPM and m_SPM both increase with decreasing temperature (Fig. 7(a,b)). This result implies that the ferromagnetic regions, which form only in the nanoscale high-Fe concentration regions at room temperature [Fig. 7(c)], expand toward lower Fe concentration regions with decreasing temperature [Fig. 7(d)], and finally the entire film becomes ferromagnetic at T_C [Fig. 7(e)]. This appears to be a characteristic feature of materials that exhibit single-phase ferromagnetism, despite the inhomogeneous distribution of magnetic atoms in the film⁶,⁷. As shown in Fig. 7(a,b), f_SPM and m_SPM are larger in sample B than in sample A, which can be attributed to the difference in spatial fluctuations of the Fe concentration, which are 4–7% in sample A and 3–10% in sample B⁶. The larger the nonuniformity of the Fe distribution is, the larger each local ferromagnetic region, f_SPM, and m_SPM become, and the local ferromagnetic regions can be more easily connected magnetically, resulting in a higher T_C.

Figure 7. Nanoscale expansion process of the local ferromagnetic regions.

(a,b) The temperature dependence of the best-fit parameters f_SPM and m_SPM obtained for sample A (a) and sample B (b). The red, grey, and white areas indicate ferromagnetic (FM), FM + SPM + paramagnetic (PM), and SPM + PM regions, respectively. (c–e) Schematic diagrams showing the most likely picture of the magnetic states in the Ge_0.935Fe_0.065 films with zero magnetic field at room temperature (i.e., T = 300 K) (c), T_C < T < 300 K (d) and T < T_C (e). The small black, red and blue arrows correspond to the magnetic moments of the paramagnetic, ferromagnetic, and antiferromagnetically coupled substitutional Fe atoms, respectively. The red areas indicate ferromagnetic regions. Antiferromagnetically coupled Fe atoms are thought to exist all over the film at temperatures below T_C.

Summary

We have investigated the local electronic structure and magnetic properties of the doped Fe atoms in the Ge_0.935Fe_0.065 films, which have a diamond-type single-crystal structure without any ferromagnetic precipitates and with nanoscale spatial Fe concentration fluctuations, using XAS and XMCD. The Fe atoms appear in the 2⁺ state, with the 3d electrons strongly hybridized with the 4p electrons in Ge; this results in a delocalized 3d nature and long-range ferromagnetic ordering, leading to the excellent agreement between the H dependence of magnetization, MCD and XMCD. Using the XMCD sum rules, we obtained the M–H_eff curves, which can be explained by the coexistence of SPM and paramagnetic properties at temperatures above T_C. The fitting results clearly show that the local ferromagnetic regions, which exist at room temperature, expand with decreasing temperature, leading to a ferromagnetic transition of the entire system at T_C. The nonuniformity of the Fe concentration seems to play a crucial role for the formation of the ferromagnetic regions, and our results indicate that strong ferromagnetism is inherent to GeFe, and persists at room temperature. Such a nanoscale expansion of the ferromagnetic regions is a key feature in understanding materials that exhibit single-phase ferromagnetism (i.e., where the film is free from any ferromagnetic precipitates) despite the inhomogeneous distribution of magnetic atoms in the film⁶,⁷,¹⁴,¹⁵.

Methods

Sample preparation

The Ge_0.935Fe_0.065 thin films were grown on Ge(001) substrates by LT-MBE. The growth process is described as follows. After the Ge(001) substrate was chemically cleaned and its surface was hydrogen-terminated by buffered HF solution, it was introduced in the MBE growth chamber through an oil-free load-lock system. After degassing the substrate at 400 °C for 30 minutes and successive thermal cleaning at 900 °C for 15 min, we grew a 30-nm-thick Ge buffer layer at 200 °C, which was followed by the growth of a 120-nm-thick Ge_0.935Fe_0.065 layer at T_S = 160 (sample A) or 240 °C (sample B). After that, we grew a 2-nm-thick Ge capping layer at 200 °C to avoid the surface oxidation of the GeFe layer. The in situ RHEED was used to check the crystallinity and morphology of the surface during the growth. The diffraction pattern of the Ge_0.0935Fe_0.065 showed intense and sharp 2 × 2 streaks with no extra spots, which indicate a 2-dimensional growth mode and exhibit a diamond-type single-crystal structure. To remove the oxidized surface layer, the samples were briefly etched in dilute hydrofluoric acid (HF) prior to loading into the XAS (XMCD) vacuum chamber.

XAS and XMCD measurements

We performed XAS and XMCD measurements at the soft X-ray beamline BL23SU of SPring-8 with a twin-helical undulator of in-vacuum type²⁸. The monochromator resolution was E/ΔE > 10000. The XAS and XMCD spectra were obtained by reversing photon helicity at each energy point and were recorded in the total-electron-yield mode. The XMCD spectra were taken both for positive and negative applied magnetic fields and were averaged in order to eliminate experimental artifacts. Backgrounds of the XAS spectra at the Fe L_2,3-edge were assumed to be hyperbolic tangent functions.

Additional Information

How to cite this article: Wakabayashi, Y. K. et al. Room-temperature local ferromagnetism and its nanoscale growth in the ferromagnetic semiconductor Ge_1–xFe_x. Sci. Rep. 6, 23295; doi: 10.1038/srep23295 (2016).