Resilience to major life stressors is not as common as thought

Abstract

We attempted to replicate findings that “most people are resilient” following three events: spousal loss, divorce, and unemployment. We applied growth mixture models to the same longitudinal data set that has previously been used to assert that resilience is ubiquitous. When using identical model specifications as in prior studies, we found that resilient trajectories were most common, but the number of trajectories identified was different. When we relaxed the assumptions that (a) all classes have similar variability in levels of post-adversity adjustment and (b) there is no variability in changes within classes (as in prior studies), we found that a resilience class was least common. Methodologically, our results demonstrate how findings on trajectories of change following major life stressors vary substantially depending on statistical model specifications. Conceptually, they underscore the errors inherent in any categorical statements about “rates of resilience” among individuals confronted with major life stressors. Pragmatically, they underscore the dangers in recommending against prophylactic interventions -- based on one method of analyzing longitudinal data -- for individuals who have experienced major life stressors.

Recognizing the importance of replicating major findings in psychology (Ledgerwood, 2014), our focus is on recurrent claims about resilience, a construct representing the maintenance of positive adaptation despite significant adversity (Luthar, Cicchetti, & Becker, 2000; Masten, 2001). Well over six decades ago, this construct appeared in the developmental literature, as researchers recognized unexpectedly positive adjustment among children facing major life adversities and sought to discern what contributed to their apparent resilience (see Luthar, 2006 for a review). Around the turn of the 21^st century, the term resilience began to appear more in the literature on adults as well (see Bonanno, Mancini, & Westphal, 2011; Zautra et al., 2008).

Specifically, we seek to replicate prior reports that among adults, resilience -- operationalized as stable healthy levels of well-being, and the absence of negative outcomes during or following potentially harmful circumstances -- is the prototypical trajectory following exposure to potentially traumatic events (e.g., Seery, Holamn, & Silver, 2010). In a prolific body of work involving samples facing diverse traumas ranging from bereavement and spinal cord injury to terrorist attacks and natural disasters, Bonanno and colleagues have reported that resilience is the most common response following significant negative life events (Bonanno et al., 2011; Bonanno & Diminich, 2013). Rates of resilience were reportedly 68% after a heart attack (Galatzer-Levy & Bonanno, 2014); 72% after the onset of chronic pain (Zhu, Galatzer-Levy, & Bonanno, 2014); 74% after cancer diagnosis (Burton, Galatzer-Levy, & Bonanno, in press); 61% following a mass shooting on college campus (Orcutt et al., 2014); and 85% after deployment to military service (Bonanno et al., 2012).

Conclusions based on such high rates of resilience have led some to go beyond deriving implications for scientific research and theory, to recommendations on the (lack of) need for interventions for people exposed to traumas. For example, it has been suggested that in the aftermath of events such as 9/11 or natural disasters, “widespread prophylactic interventions” are not just unnecessary but even harmful (Bonanno et al., 2011). Among the arguments supporting this suggestion are those on “risk-management” (Adams, 1995), which suggests that when risk is reduced in their environments, people respond with behaviors that increase the chance of injury (as air bags in cars can promote more risky driving behaviors). Thus, among people exposed to major life stressors, any interventions designed to promote resilience could lead some “to overestimate their own coping ability or to underestimate the level of distress they might experience in response to a potential psychological hazard such as combat” (Bonanno et al., 2011; p. 527).

Rates of resilience: Variations based on data analytic models?

Previously noted assertions that resilience is common in the face of potentially traumatic events have primarily been derived from trajectories identified via growth mixture modeling (GMM; see Bonanno & Diminich, 2013), an approach that identifies discrete trajectories of change in a given variable in the population under study (Muthén & Muthén, 2000). GMM contrasts with growth curve (or multilevel) modeling where the sample as a whole is assumed to show a particular trajectory over time (e.g., a college graduating class will show linear growth in income through their 50’s), with the allowance that within this overall trajectory, individuals can vary in exactly where they start (intercept) and in their change over time (slope; see Bollen & Curran, 2006; Singer & Willett, 2003). In GMM, by contrast, the aim is to move beyond describing one overall trajectory of change over time, instead allowing for the possible existence of distinct sub-groups within the data (e.g., a graduating class sub-group shows linear increases in income, one shows plateaus in early years while pursing graduate studies, and one levels off in later years due to early retirement). Once these sub-groups or distinct growth curves are identified, trajectories of longitudinal change across and within them can be allowed to vary in their levels (intercept) and rate of change over time (slope; for discussion, see Ram & Grimm, 2009). The underlying claim has been that although final trajectory models are somewhat affected by theory (Feldman, Masyn, & Conger, 2009; Muthén, 2004), compared with traditional approaches, GMM analyses come “closest to allowing the data to speak for itself independent of a priori theoretical assumptions” (Bonanno & Diminich, 2013, p 383).

Contrasting with the latter declaration, others have emphasized that sub-groups derived from GMM must be interpreted with great caution (Chassin, Sher, Hussong, & Curran, 2013; Nagin & Tremblay, 2005; Sher et al., 2011). GMM is an exploratory approach, with sub-group determination conducted in a post-hoc manner and findings varying substantially depending on model specifications; accordingly, extreme circumspection must be used when implementing these models and interpreting the results (see Grimm & Ram, 2009; Ram & Grimm, 2009). To illustrate, Bauer and Curran (2003) demonstrated that non-normality in the outcome variable can lead to the conclusion that multiple latent classes underlie the data even though the data are from a single population.

Concerns such as these suggest the value of replication analyses on estimated “rates of resilience” in prior research, and accordingly, we re-examined rates reported in the German Socio-Economic Panel study. In previous publications, GMM was applied to three potentially traumatic events within this data set: spousal loss, divorce, and unemployment, with 58.7%, 71.8%, and 69.0% of individuals reportedly in the resilient trajectory (showing stable high scores on life satisfaction before and after each event), respectively (see Galatzer-Levy, Bonanno, & Mancini, 2010; Mancini, Bonanno, & Clark, 2011).

In replication GMM analyses within this paper, our aim is to demonstrate that changes in two central a priori assumptions can lead to substantively different conclusions regarding both the number of classes or sub-groups identified over time, and the distribution of people across these classes or sub-groups (that is, the proportion of people showing resilient trajectories versus others). Toward this end, we employed three different data analytic strategies; specific differences between these and analyses in prior publications are depicted in Figure 1, with two hypothetical sub-groups, labeled “resilient” and “recovery” shown for illustrative purposes.

Figure 1.

Graphical illustration of the assumptions used while examining changes in life satisfaction in relation to adverse events. Thick solid lines represent average slopes of the Resilient (red) and Recovery (blue) trajectories; regular solid lines represent confidence intervals around the trajectories; dotted lines represent hypothetical participants within a trajectory. In Part A (as in prior published analyses), the variance in level for the Resilient and Recovery classes is constrained to be equal; the confidence intervals span a similar distance (+/− 2 points here); and the variance in the rate of change is set to 0 in each class. In Part B, by contrast, there is variability in levels of life satisfaction between groups; their confidence intervals differ (illustrated here as Resilient: +/− 1.5 points; Recovery +/− 2.5 points); and there is variability in rates of change (slopes) between different participants in a class.

In the first of our replications, using the authors’ descriptions in previous publications on resilience rates, we ran exactly the same statistical models underlying the findings on all three events, i.e., spousal loss, divorce, and unemployment (Galatzer-Levy et al., 2010; Mancini et al., 2011). In these models, the variance for levels of life satisfaction was estimated, whereas the variance for rate of change in life satisfaction was constrained to 0. In other words, individuals within a given sub-group were allowed to differ from one another in their precise levels of life satisfaction, but all individuals within that sub-group showed exactly the same trajectory of change.

This is illustrated in Figure 1A, with four hypothetical participants, a and b in the resilient trajectory, both showing stable good functioning over time, and c and d showing recovery with dips in functioning around the time of the event, followed by improvements. Note that the variability in all possible scores is assumed to be the same in the resilient and recovery trajectories. In other words, as shown in this hypothetical example, all people in both sub-groups would fall within +2 and −2 points from mean scores of their whole sub-group (Figure 1A). Note also that a and b show exactly the same trajectory or slope over time (a generally flat line), as do c and d (a shallow “V” with stability in years before and years after the event).

In our second set of replications, we used the same approach as in prior studies with one difference: trajectories were allowed to differ in the amount of variance around the mean growth curve. Thus, we allowed for the possibility that people in the resilient trajectory, overall, might show less fluctuation around the subgroup’s mean scores over time (in keeping with their overall personal stability over time), whereas those in the recovery trajectory might show greater variability above and below their group’s mean over time. This is illustrated by the confidence intervals being the same (CI=2 in Figure 1A) within models in prior publications, as opposed to having different values in our analyses (shown in Figure 1B as CI=1.5 for “resilient” and 2.5 for recovery, for illustrative purposes).

In the third set of analyses, we allowed for individuals to vary in level and rate of change not just between groups but also within sub-groups. As shown in Figure 1A, previously published analyses stipulated that Persons a and b (and all others in the Resilient trajectory) would show stable scores over time, whereas Persons c and d (and all others in the Recovery trajectory) would show only differences in levels, but parallel dips in life satisfaction around the time of the event. By contrast, as shown in Figure 1B, we allowed for the possibility that some individuals in the Resilient trajectory could be stable across all years (like Person a) but others may have hit a low point well before the event, rising to high levels at the time of the event (e.g., Person b showed substantial declines in life satisfaction between years −3 to year −1). Similarly, our analyses allowed for the possibility that within the Recovery class in Figure 1B, person d might take longer to recover from the event (until year 3), whereas Person c bounced back more quickly (year 1).

The modeling decisions represented in Figure 1B were guided by conceptual considerations that although two individuals may both belong to the Resilient or Recovery subgroup, their path towards resilience or recovery can differ from one another. In addition to conceptual considerations, these modeling decisions were guided by previous research showing large between-person differences in both levels and rates of change in relation to adverse life events (Lucas et al., 2003, 2004). Events such as divorce or spousal loss, for example, can be preceded by years of difficulties such as marital strife or increasing disability (Sbarra, Hasselmo, & Bourassa, 2015). Thus, it is plausible that among individuals with stable high life satisfaction after divorce or spousal loss, for some, the worst times were much before the event so that the suffering leading up to the event was more traumatic than the event itself.

The Present Study

Given the prominence of the construct of resilience in research and substantial associated implications for social policies (i.e., suggestions that post-trauma interventions should be eschewed), our goal was to replicate prior findings that resilience is the modal response to spousal loss, divorce, and unemployment. Using the same longitudinal data set as in prior studies, we conducted three sets of analyses: (1) exactly the same as those in earlier publications, (2) similar to prior analyses but allowing for estimation of variance in adjustment before and after the events, and (3) allowing also for variation among individuals within each of the trajectories.

Method

We examined our research questions using data from 28 annual waves (1984 – 2011) of the German Socio-Economic Panel (SOEP) study. Comprehensive information about the design, participants, variables, and assessment procedures in the study is reported in Wagner et al. (2007). A brief overview of details relevant to the present analysis is given below.

Participants and Procedure

The SOEP is a nationally representative annual panel study of private households and their inhabitants initiated in 1984 and covers ~50,000 residents of former West and East Germany, including immigrants and resident foreigners. Potential participants were randomly selected from a set of randomly selected locations in Germany where all family members older than 16 years of age within each household were eligible for participation. Relatively high initial response rates (60 – 70%) and low longitudinal attrition (3 – 10%) provide for an overall sample that is representative of the population living in private households. Data were primarily collected via face-to-face interviews and self-administered mail questionnaires.

For the present study, we included participants who experienced spousal loss, divorce, or unemployment, using updated data over 28 years (1984 – 2011) as opposed to 20 years (1984 – 2003) in the studies that we attempt to replicate (Galatzer-Levy et al., 2010; Mancini et al., 2011). As expected with the passage of eight additional years, percentages of participants experiencing the events were somewhat higher in the present analyses versus previous work (rendering greater statistical power): 464 vs. 1,214 for spousal loss; 629 vs. 1,579 for divorce; and 774 vs. 2,461 for unemployment.

Measures

Life satisfaction

Participants’ reported on their life satisfaction annually, answering the question “How satisfied are you with your life, all things considered?” using a 0 (totally unsatisfied) to 10 (totally satisfied) rating scale. This item has been used widely in psychological research (see Lucas et al., 2003, 2004; for measurement properties, see Cheung & Lucas, 2015; Fujita & Diener, 2005; Lucas & Donnellan, 2012).

Spousal loss

Spousal loss was determined by responses to the question “Has your family situation changed since the beginning of year X (e.g., 2002)?” in the category “spouse/partner has died.” Timing of spousal loss was defined as the year the participant reported their spouse/partner died. Following Mancini and colleagues (2011), we excluded participants who were above the age of 75 at the wave of the reported spousal loss. Participants were, on average, 61 years of age at the wave of reported spousal loss (SD = 11.09, range 25 – 75), had attained, on average, 10.87 years of education (SD = 2.17, range 7 – 18), 74% were women, and, on average, provided 8.40 life satisfaction observations (SD = 2.66, range 1 – 11).

Divorce

Divorce was determined by responses to the question “Has your family situation changed since the beginning of year X (e.g., 2002)?” in the category “divorce.” Timing of divorce was defined as the year the participant reported their divorce. Following Mancini and colleagues (2011), we excluded participants who were above the age of 75 at the wave of the reported divorce. Participants were, on average, 39.49 years of age at the wave of the reported divorce (SD = 9.10, range 21 – 75), had attained, on average, 12.06 years of education (SD = 2.50, range 7 – 18), 55% were women, and, on average, provided 8.19 life satisfaction observations (SD = 2.53, range 1 – 11).

Unemployment

At each wave, participants reported their labor force status. As in previous work we are replicating (Galatzer-Levy et al., 2010), unemployment onset was defined as the wave at which participants who in the previous 3 waves reported being in full-time employment and in the following wave reported being registered as unemployed, were between the ages of 21 and 60 at the time of their reported unemployment, and participated in the study for at minimum, four years following unemployment. Participants were, on average, 42.38 years of age at the wave of reported unemployment (SD = 12.36, range 21 – 60), had attained, on average, 11.19 years of education (SD = 2.25, range 7 – 18), 44% were women, and, on average, provided 9.59 life satisfaction observations (SD = 1.65, range 1 – 11).

Statistical Analysis

We used GMM to examine whether there were distinct classes of individuals in how life satisfaction changed in relation to spousal loss, divorce, and unemployment. GMM is a combination of the latent growth curve and mixture models and has the ability to simultaneously estimate trajectories of change and infer sub-groups of individuals with distinct multivariate normal distributions (for discussion, see Grimm & Ram, 2009; Muthén, 2004; Ram & Grimm, 2009). GMM allows researchers to investigate whether the population under study consists of discrete sub-groups of individuals, each with different change trajectories. As a preliminary step, a longitudinal model of change needs to be established to allow for GMM to subsequently attempt to identify sub-groups or classes underlying the sample. To do so, each individual’s time series must be re-aligned to onset of the specific event (i.e, wave of reported spousal loss, divorce, or unemployment in this case).

In all GMM analyses conducted for this report, we used all observations between 5 years prior to and 5 years following the event (i.e., participants could have provided up to 11 observations). This was done to increase statistical power (i.e., more observations) and have a long enough time interval to track change before and after the event (see Diallo & Morin, in press; Lucas et al., 2003, 2004). In sections that follow, we describe the specific sets of longitudinal models that we applied to the data.

Replication: Part 1

As in analyses by Mancini and colleagues (2011), we examined longitudinal models of change for spousal loss and divorce in which we estimated (a) a level (intercept) parameter representing average life satisfaction, and (b) a latent basis slope factor to examine changes in life satisfaction. Importantly, we note that as in the original analyses, subgroups were allowed to vary in initial levels (intercept) and individuals’ variance within their respective groups was modeled to be equal between the sub-groups and the variance in the rate of change over time (slope) was constrained to 0. Please see Figure S1 in Online Supplemental Materials for specific model set-up.

For unemployment, we followed procedures by Galatzer-Levy and colleagues (2010), where a three-slope piecewise longitudinal model of change was estimated. The three slopes were estimated to examine the different components of change in life satisfaction in relation to unemployment – change in the years leading up to the event (years −5 to −2), surrounding the event (year −1 to 1) and change in the years after the event (years 1 to 5). This model was estimated to attempt to examine the various stages through which life satisfaction has the potential to change in relation to unemployment. As indicated above, we note that variance in initial level of life satisfaction was estimated, whereas the variance for all the slopes (across subgroups identified) was constrained to be 0. Please see Figure S2 in Online Supplemental Materials for specific model set-up.

Replication: Part 2

In a second set of analyses, we used the same longitudinal models of change described in Part 1, but we estimated the variance in the latent slope factor for spousal loss and divorce, and for the three slopes for unemployment and their covariances; this is in contrast to setting the slope variance and covariances to 0. Thus, we allowed for (a) variability in the change trajectories within each sub-group or class, and also allowed classes to differ (b) in the amount of variation around the mean of life satisfaction, and (c) in rate of change in life satisfaction. This allowed for the possibility, for example that individuals within the stable, well-adjusted resilient trajectory could differ in their rate of change over time, as they might have shown less variability in adjustment across time than did people in trajectories that struggled considerably at different points in time (confidence intervals of 1.5 versus 2, shown in the examples in Figure 1B). Please see Figures S3 and S4 in Online Supplemental Materials for specific model set-up.

Replication: Part 3

Based on previous research showing that changes in life satisfaction in relation to aversive life events is a multi-phase process, we estimated a multi-phase longitudinal model of change (see Infurna, Gerstorf, & Ram, 2013; Lucas et al., 2003, 2004) considering two phases in addition to pre-event levels: pre-event change and post-event change. First, we allowed for variations in individuals’ life satisfaction levels prior to the event (pre-event level) as well as in the amount of change in life satisfaction preceding the event (year −5 to year 0; pre-event change). Also, allowed to vary was the total amount of change in life satisfaction following the event (year 0 to year 5; post-event change). We estimated separate latent factors for pre- and post-event change (as opposed to estimating linear and quadratic change), so that we could get separate estimates for the total amount of change that transpired in the years leading up to and following the event -- as shown by the varying slopes of Participants a versus b in the resilient sub-group, and of c versus d in the Recovery sub-group, in Figure 1B -- following recommendations in previous research (see Lucas et al., 2003, 2004; Infurna & Wiest, 2015).

For each latent factor, a mean and variance parameter was estimated. The factor means describe the extent of change (i.e., population-mean level change), and the variance indicates the extent of between-person differences in the individual trajectories around the mean trajectory. We estimated the variance for level, and pre-event change, and post-event change, allowing the means and variances to vary within and between groups. Please see Figure S5 in Online Supplemental Materials for specific model set-up.

Steps for model fitting

Our analyses proceeded in several steps. First, we fit the baseline model for each of the three parts for our analyses to identify a univariate single-class growth model. Next, we estimated a series of GMMs with 2 through 5 classes to determine the number of distinct classes and the nature of their differences.

To select the best fitting model within each of our three sets of analyses, we used multiple fit statistics, including information criteria (e.g., Bayesian Information Criterion – better fitting models have a lower Bayesian Information Criterion [BIC]; see Nylund, Asparouhov, & Muthén, 2007), entropy (values above .7 indicate more distinct classes and that individuals are grouped into classes that describe their functional configuration well), approximate likelihood ratio tests (LRTs) that compare the relative fit of models to similarly structured models with one fewer class, and interpretation of the class parameters (see Ram & Grimm, 2009). After selecting the best fitting model, we plotted the model implied trajectories with the 95% confidence interval to further determine the extent to which each of the classes are in fact distinct from one another. All models were estimated using MPlus (see Muthén & Muthén, 1998–2012), with incomplete data accommodated using full information maximum likelihood.

Results

Our results are divided into three sections, based on the three models described in the preceding section, and in the Introduction.

Replication: Part 1

Spousal Loss

The top section of Table 1 shows results from a series of models using the same specifications as in prior publications (Mancini et al., 2011), allowing for 1 to 5 classes to be estimated in the data examining change in life satisfaction in relation to spousal loss. Based on the BIC, entropy, and the two LRTs, we determined that the 3-class model provided the most parsimonious fit to the data; this is in contrast to findings of Mancini et al. (2011), which indicated that a 4-class model was optimal. Despite the BIC being lower for the 4-class solution in our analyses (Table 1), the LRTs both determined that the 4-class solution did not fit significantly better than the 3-class solution. The three classes were not evenly distributed and the parameter estimates for each of the three groups are shown in the top section of Table 2.

Table 1.

Model Fit Statistics for Growth Mixture Models Determining Number of Classes for How Life Satisfaction Changes in Relation to Spousal Loss, Divorce, and Unemployment: Replication Part A.

	1-Class	2-Class	3-Class	4-Class	5-Class
Spousal Loss
Sample size
Nc = 1	1,214	349.00	245.40	231.70	36.30
Nc = 2		865.00	907.00	862.85	323.59
Nc = 3			61.60	62.99	559.33
Nc = 4				56.46	45.20
Nc = 5					249.58
Fit statistics
# of free parameters	13	16	19	22	25
BIC	39,517	39,331	39,279	39,276	39,285
ABIC	39,476	39,280	39,219	39,207	39,205
Entropy		0.509	0.677	0.690	0.598
Vuong-Lo-Mendell-Rubin LRT		0.0029	0.0420	0.1183	0.2751
Lo-Mendell-Rubin Adjusted LRT		0.0036	0.0472	0.1263	0.2871
Divorce
Sample size
Nc = 1	1,579	243.43	160.64	109.60	11.04
Nc = 2		1,335.57	1,183.95	1,156.49	177.17
Nc = 3			234.42	190.25	1,108.46
Nc = 4				122.66	106.83
Nc = 5					175.50
Fit statistics
# of free parameters	13	16	19	22	25
BIC	49,976	49,742	49,681	49,651	49,658
ABIC	49,935	49,691	49,621	49,582	49,579
Entropy		0.703	0.709	0.717	0.733
Vuong-Lo-Mendell-Rubin LRT		0.0150	0.1296	0.6618	0.5382
Lo-Mendell-Rubin Adjusted LRT		0.0176	0.1409	0.6675	0.5442
Unemployment
Sample size
Nc = 1	2,461	2,008.16	1,982.12	198.25	1,803.55
Nc = 2		452.84	108.61	116.23	247.99
Nc = 3			370.26	240.23	112.23
Nc = 4				1,906.30	128.45
Nc = 5					168.78
Fit statistics
# of free parameters	6	11	16	21	26
BIC	89,826	89,157	89,008	88,853	88,753
ABIC	89,807	89,122	88,957	88,786	88,671
Entropy		0.691	0.771	0.765	0.752
Vuong-Lo-Mendell-Rubin LRT		0.0000	0.0232	0.4400	0.0140
Lo-Mendell-Rubin Adjusted LRT		0.0000	0.0251	0.4458	0.0149

Note. Spousal Loss. In the 1-class model, the CFI was 0.849 and the RMSEA was 0.091.

Divorce. In the 1-class model, the CFI was 0.856 and the RMSEA was 0.086.

Unemployment. In the 1-class model, the CFI was 0.836 and the RMSEA was 0.092.

Table 2.

Fixed and Random Effects for Change in Life Satisfaction in Relation to Spousal Loss in the Classes Illustrated in Figure 2.

	Resilient	Recovery	Improvement
Replication: Part 1 (A)
Sample size	245.40	907.00	61.60
Average probability of class membership	0.77	0.87	0.80
Factor means
Level	7.69* (0.17)	7.05* (0.09)	3.94* (0.47)
Slope	−1.25* (0.27)	−0.23* (0.07)	0.89* (0.27)
Variances
Level	1.62* (0.10)	1.62* (0.10)	1.62* (0.10)
Slope	0	0	0
Covariance between level and slope	0	0	0
Residual	1.98* (0.06)	1.98* (0.06)	1.98* (0.06)
Replication: Part 2 (B)
Sample size	325.07	653.10	235.83
Average probability of class membership	0.79	0.77	0.82
Factor means
Level	7.62* (0.18)	6.93* (0.12)	6.14* (0.31)
Slope	−0.21* (0.06)	−0.46* (0.09)	−0.30* (0.11)
Variances
Level	1.84* (0.35)	1.57* (0.23)	2.71* (0.60)
Slope	0.11* (0.05)	0.27* (0.11)	0.33 (0.17)
Covariance between level and slope	−0.52* (0.26)	−0.28* (0.10)	−0.52* (0.26)
Residual	0.59* (0.06)	1.78* (0.27)	4.48* (0.59)
Replication: Part 3 (C)
Sample size	574.88	639.12
Average probability of class membership	0.85	0.89
Factor means
Level	7.31* (0.10)	6.77* (0.08)
Pre-event slope	−0.99* (0.12)	−1.61* (0.11)
Post-event slope	0.81* (0.12)	1.36* (0.09)
Variances
Level	1.88* (0.17)	2.26* (0.22)
Pre-event slope	2.10* (0.37)	3.33* (0.49)
Post-event slope	1.25* (0.34)	1.99* (0.45)
Covariance between level and pre-event slope	−0.71* (0.14)	−1.50* (0.27)
Covariance between level and post-event slope	0.40* (0.13)	0.32 (0.23)
Covariance between pre- and post-event slope	−1.28* (0.32)	−1.64* (0.41)
Residual	0.72* (0.05)	2.77* (0.45)

Note. Replication: Part 1. Parameter estimates for latent basis slope factor: 0, 0.10, 0.27, 0.48, 1.73, 3.16, 2.07, 1.44, 1.23, 1.02, 1 for the time interval −5 years to 5 years in relation to spousal loss.

Replication: Part 2. Parameter estimates for latent basis slope factor: 0, 0.02, 0.16, 0.34, 1.34, 3.26, 1.93, 1.47, 1.13, 0.97, 1 for the time interval −5 years to 5 years in relation to spousal loss.

Replication: Part 3. Parameter estimates for pre-event slope latent basis slope factor: 0, 0.00, 0.04, 0.10, 0.37, 1, 1, 1, 1, 1, 1 for the time interval −5 years to 5 years in relation to spousal loss. Parameter estimates for post-event slope latent basis slope factor: 0, 0, 0, 0, 0, 0, 0.64, 0.83, 0.94, 0.98, 1 for the time interval −5 years to 5 years in relation to spousal loss.

^*p < .05

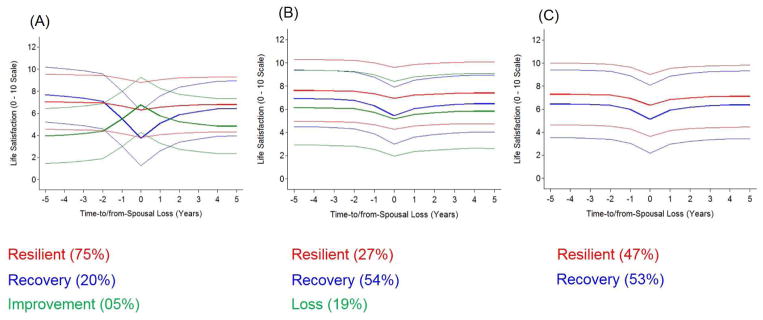
Figure 2A graphically illustrates the three classes, along with their 95% confidence intervals. We found that the Resilient sub-group was the largest (as did Mancini et al., 2011), with 75% of the population likely to belong to this sub-group. The second largest group (Recovery; 20%) showed substantial declines in life satisfaction in the years surrounding spousal loss, followed by a return to almost previous levels of life satisfaction in the years thereafter. The third group, Improvers (5%), showed increases in life satisfaction in the years leading up to spousal loss. Note that the confidence intervals indicate that there was substantial overlap in the three groups, indicating that these trajectories may not be as distinct from one another as previously thought.

Figure 2.

Graphical illustration of changes in life satisfaction in relation to spousal loss for our three statistical models of analysis. (A) Exactly the same as in prior publications; (B) allowing for trajectories to differ in variance around their own mean curves; (C) also allowing for variance within trajectories. The thick solid line indicates the model implied change for each class and the solid lines are the 95% confidence intervals for each class.

Divorce

The middle section of Table 1 shows our results from a series of models testing whether 1 through 5 classes underlie the population for changes in life satisfaction in relation to divorce. Based on the BIC, entropy, and LRTs, we determined that the 2-class solution provided the best fit to the data; again, this is in contrast with the Mancini et al (2011) finding that a 3-class solution was optimal. Although the BIC value was lower in the 3-, 4-, and 5-class solutions, the LRTs had p-values greater than .05, suggesting that each additional class did not significantly improve model fit.

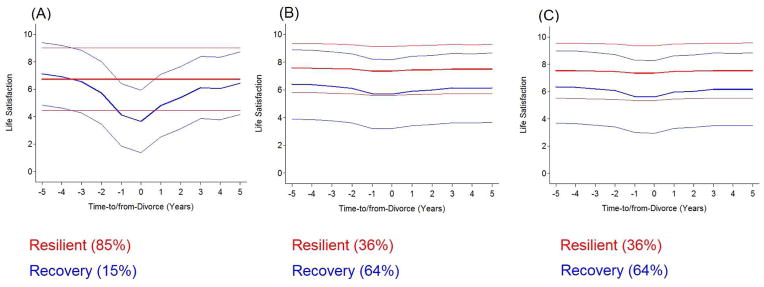
The top section in Table 3 shows the parameter estimates for the 2-class solution and Figure 3A graphically illustrates the 2-classes with their 95% confidence intervals. Again, the largest group displayed a stable, high trajectory of life satisfaction indicative of resilience (85%), whereas the second group was much smaller (15%) and showed substantial declines in the years leading up to and surrounding divorce, with improvements in the years thereafter (Recovery). And again, the confidence intervals indicate substantial overlap in the two classes.

Table 3.

Fixed and Random Effects for Change in Life Satisfaction in Relation to Divorce in the Classes Illustrated in Figure 3.

	Resilient	Recovery
Replication: Part 1 (A)
Sample size	1,335.59	243.41
Average probability of class membership	0.81	0.93
Factor means
Level	6.74* (0.05)	7.11* (0.17)
Slope	0.00 (0.02)	−0.67* (0.28)
Variances
Level	1.36* (0.08)	1.36* (0.08)
Slope	0	0
Covariance between level and slope	0	0
Residual	2.13* (0.05)	2.13* (0.05)
Replication: Part 2 (B)
Sample size	569.96	1,009.04
Average probability of class membership	0.87	0.93
Factor means
Level	7.58* (0.12)	6.39* (0.08)
Slope	−0.08* (0.03)	−0.25* (0.13)
Variances
Level	0.82* (0.21)	1.63* (0.19)
Slope	0.11 (0.13)	0.28 (0.32)
Covariance between level and slope	−0.12 (0.13)	−0.32 (0.25)
Residual	0.66* (0.07)	2.88* (0.14)
Replication: Part 3 (C)
Sample size	570.97	1,008.03
Average probability of class membership	0.87	0.93
Factor means
Level	7.53* (0.10)	6.34* (0.08)
Pre-event slope	−0.18 (0.09)	−0.74* (0.10)
Post-event slope	0.20* (0.07)	0.57* (0.09)
Variances
Level	1.07* (0.15)	1.84* (0.18)
Pre-event slope	1.00* (0.19)	2.48* (0.42)
Post-event slope	0.71* (0.14)	2.00* (0.31)
Covariance between level and pre-event slope	−0.47* (0.12)	−1.03* (0.23)
Covariance between level and post-event slope	−0.10 (0.08)	0.01 (0.16)
Covariance between pre- and post-event slope	−0.43* (0.14)	−1.20* (0.30)
Residual	0.59* (0.05)	2.60* (0.12)

Note. Replication: Part 1. Parameter estimates for latent basis slope factor: 0, 0.31, 0.84, 2.07, 4.46, 5.19, 3.43, 2.58, 1.47, 1.60, 1 for the time interval −5 years to 5 years in relation to divorce.

Replication: Part 2. Parameter estimates for latent basis slope factor: 0, 0.09, 0.53, 1.13, 2.77, 2.85, 1.94, 1.64, 1.07, 1.15, 1 for the time interval −5 years to 5 years in relation to divorce.

Replication: Part 3. Parameter estimates for pre-event slope latent basis slope factor: 0, 0.04, 0.19, 0.37, 0.94, 1, 1, 1, 1, 1, 1 for the time interval −5 years to 5 years in relation to divorce. Parameter estimates for post-event slope latent basis slope factor: 0, 0, 0, 0, 0, 0, 0.63, 0.76, 0.96, 0.97, 1 for the time interval −5 years to 5 years in relation to divorce.

^*p < .05

Figure 3.

Graphical illustration of changes in life satisfaction in relation to divorce for our three statistical models of analysis. (A) Exactly the same as in prior publications; (B) allowing for trajectories to differ in variance around their own mean curves; (C) also allowing for variance within trajectories. The thick solid line indicates the model implied change for each class and the solid lines are the 95% confidence intervals for each class.

Unemployment

The bottom part of Table 1 displays the results from the GMM analyses that allowed for 1 through 5 classes to be estimated for unemployment. The 3-class solution provided the most parsimonious fit to the data based on the BIC, entropy, LRTs, and interpretation of classes. Yet again, these findings contrast with those of Galatzer-Levy et al. (2010) indicating that a 4-class solution provided the most parsimonious fit. Compared to the 3-class solution, the BIC was lower for the 4- and 5-class solutions, but the LRTs indicated that increasing the number of classes did not significantly improve model fit and did not provide classes that were meaningfully different from one another in their trajectory of change. The top section of Table 4 displays the parameter estimates for the three classes.

Table 4.

Fixed and Random Effects for Change in Life Satisfaction in Relation to Unemployment in the Classes Illustrated in Figure 4.

	Resilient	Recovery	Improvement
Replication: Part 1 (A)
Sample size	1,982.12	370.61	108.61
Average probability of class membership	0.90	0.82	0.80
Factor means
Level	6.45* (0.06)	6.30* (0.18)	5.91* (0.57)
Slope 1	−0.13* (0.02)	−0.22 (0.05)	0.58* (0.16)
Slope 2	−0.02 (0.02)	−1.15* (0.11)	0.22 (0.18)
Slope 3	0.07* (0.02)	0.18* (0.07)	0.18 (0.16)
Variances
Level	1.41* (0.06)	1.41* (0.06)	1.41* (0.06)
Slope 1	0	0	0
Slope 2	0	0	0
Slope 3	0	0	0
Covariance between level and slope 1	0	0	0
Covariance between level and slope 2	0	0	0
Covariance between level and slope 3	0	0	0
Covariance between slope 1 and slope 2	0	0	0
Covariance between slope 1 and slope 3	0	0	0
Covariance between slope 2 and slope 2	0	0	0
Residual	1.90* (0.04)	1.90* (0.04)	1.90* (0.04)
Replication: Part 2 (B)
Sample size	1,147.16	1,313.84
Average probability of class membership	0.91	0.87
Factor means
Level	6.97** (0.06)	5.91* (0.06)
Slope 1	−0.06* (0.01)	−0.15* (0.02)
Slope 2	−0.10* (0.02)	−0.24* (0.03)
Slope 3	0.06* (0.01)	0.12* (0.02)
Variances
Level	1.25* (0.10)	1.89* (0.14)
Slope 1	0.02* (0.01)	0.10* (0.02)
Slope 2	0.11* (0.03)	0.39* (0.06)
Slope 3	0.03* (0.01)	0.10* (0.02)
Covariance between level and slope 1	0.04* (0.02)	0.17* (0.04)
Covariance between level and slope 2	−0.03 (0.03)	−0.25* (0.07)
Covariance between level and slope 3	−0.07* (0.02)	−0.13* (0.04)
Covariance between slope 1 and slope 2	−0.01 (0.004)	−0.04* (0.01)
Covariance between slope 1 and slope 3	0.003 (0.01)	−0.03 (0.02)
Covariance between slope 2 and slope 2	−0.02* (0.01)	−0.05* (0.03)
Residual	0.75* (0.04)	2.64* (0.10)
Replication: Part 3 (C)
Sample size	1,159.21	1,301.79
Average probability of class membership	0.88	0.91
Factor means
Level	7.23* (0.05)	6.35* (0.07)
Pre-event slope	−0.71* (0.07)	−1.14* (0.08)
Post-event slope	0.49* (0.07)	0.56* (0.08)
Variances
Level	1.19* (0.08)	1.70* (0.11)
Pre-event slope	1.08* (0.17)	2.04* (0.27)
Post-event slope	0.88* (0.16)	1.82* (0.32)
Covariance between level and pre-event slope	−0.17* (0.07)	−0.50* (0.15)
Covariance between level and post-event slope	−0.09 (0.07)	−0.31* (0.13)
Covariance between pre- and post-event slope	−0.72* (0.15)	−0.95* (0.24)
Residual	0.72* (0.04)	2.66* (0.11)

Note. Replication: Part 1. Factor loadings for slope 1: −4, −3, −2, −1, 0, 0, 0, 0, 0, 0, 0 for the time interval −5 years to 5 years in relation to unemployment. Factor loadings for slope 2: 0, 0, 0, 0, 0, 1, 2, 2, 2, 2, 2 for the time interval −5 years to 5 years in relation to unemployment. Factor loadings for slope 3: 0, 0, 0, 0, 0, 0, 0, 1, 2, 3, 4 for the time interval −5 years to 5 years in relation to unemployment.

Replication: Part 2. Factor loadings for slope 1: 4, −3, −2, −1, 0, 0, 0, 0, 0, 0, 0 for the time interval −5 years to 5 years in relation to unemployment. Factor loadings for slope 2: 0, 0, 0, 0, 0, 1, 2, 2, 2, 2, 2 for the time interval −5 years to 5 years in relation to unemployment. Factor loadings for slope 3: 0, 0, 0, 0, 0, 0, 0, 1, 2, 3, 4 for the time interval −5 years to 5 years in relation to unemployment.

Replication: Part 3. Parameter estimates for pre-event slope latent basis slope factor: 0, 0.04, 0.05, 0.16, 0.30, 1, 1, 1, 1, 1, 1 for the time interval −5 years to 5 years in relation to unemployment. Parameter estimates for post-event slope latent basis slope factor: 0, 0, 0, 0, 0, 0, 0.61, 0.81, 0.93, 0.96, 1 for the time interval −5 years to 5 years in relation to unemployment.

Figure 4A graphically illustrates the 3-classes, with a stable, high trajectory of life satisfaction again being most common (Resilient; 81%), followed by two smaller classes of equal size that show Recovery (15%) and improvements after job loss (04%). As in both prior analyses, there was substantial overlap in the three classes, indicating that these trajectories may not be as distinct from one another as previously thought.

Figure 4.

Graphical illustration of changes in life satisfaction in relation to unemployment for our three statistical models of analysis. (A) Exactly the same as in prior publications; (B) allowing for trajectories to differ in variance around their own mean curves; (C) also allowing for variance within trajectories. The thick solid line indicates the model implied change for each class and the solid lines are the 95% confidence intervals for each class.

Replication: Part 2

We use the longitudinal model described under “Replication: Part 2” under Statistical Analyses in the Methods section for models reported on in this section. The major difference in the models described here versus the previous section was that the variance in slopes were estimated (as were covariances), and levels and slope variances were allowed to differ between the different trajectories.

Spousal Loss

The top section of Table 5 shows results from a series of models that allowed for 1 through 5 classes fit to the data for spousal loss. Based on the model fit statistics, the 1-class solution provided the best fit to the data. Due to the low entropy values (at .644 and below) across the 2 through 5-class solutions, we interpret this as the GMM procedures conveying that there may not be more than one distinct sub-group in the sample.

Table 5.

Model Fit Statistics for Growth Mixture Models Determining Number of Classes for How Life Satisfaction Changes in Relation to Spousal Loss, Divorce, and Unemployment: Replication Part 2.

	1-Class	2-Class	3-Class	4-Class	5-Class
Spousal Loss
Sample size
Nc = 1	1,214	582.58	653.10	657.35	613.19
Nc = 2		631.42	235.83	273.60	39.29
Nc = 3			325.07	24.01	194.09
Nc = 4				259.03	138.48
Nc = 5					228.96
Fit statistics
# of free parameters	15	22	29	36	39
BIC	39,292	38,490	38,423	38,419	38,438
ABIC	39,244	38,420	38,331	38,305	38,314
Entropy		0.574	0.537	0.644	0.588
Vuong-Lo-Mendell-Rubin LRT		0.0000	0.0054	0.1473	0.0050
Lo-Mendell-Rubin Adjusted LRT		0.0000	0.0059	0.1517	0.0055
Divorce
Sample size
Nc = 1	1,579	569.95	747.43	301.47	196.51
Nc = 2		1,009.05	531.61	610.95	586.40
Nc = 3			299.97	187.09	304.34
Nc = 4				479.49	3.17
Nc = 5					488.58
Fit statistics
# of free parameters	15	22	29	36	40
BIC	49,788	48,486	48,288	48,274	48,291
ABIC	49,741	48,416	48,196	48,160	48,164
Entropy		0.693	0.599	0.560	0.623
Vuong-Lo-Mendell-Rubin LRT		0.0000	0.0026	0.2080	0.4254
Lo-Mendell-Rubin Adjusted LRT		0.0000	0.0028	0.2139	0.4293
Unemployment
Sample size
Nc = 1	2,461	1,313.84	1,330.19	502.14	793.61
Nc = 2		1,147.16	730.15	301.61	482.20
Nc = 3			400.66	710.30	132.76
Nc = 4				946.95	408.48
Nc = 5					643.96
Fit statistics
# of free parameters	15	31	46	55	58
BIC	88,949	86,888	86,636	86,602	86,602
ABIC	88,901	86,789	86,490	86,427	86,418
Entropy		0.646	0.623	0.553	0.543
Vuong-Lo-Mendell-Rubin LRT		0.0000	0.0007	0.1945	0.0386
Lo-Mendell-Rubin Adjusted LRT		0.0000	0.0007	0.1969	0.0393

Note. Spousal Loss. In the 1-class model, the CFI was 0.863 and the RMSEA was 0.088. In the 5-class solution, in the 2^nd class, the variance for intercept and slope factor (and its covariance) were set to 0 due to a correlation greater than +/−1 when allowing them to be freely estimated.

Divorce. In the 1-class model, the CFI was 0.879 and the RMSEA was 0.073. In the 5-class model, the variance for level and the latent basis slope factor (and the covariance) was set to 0 in the 4th class due to a correlation greater than +/−1 when allowing them to be freely estimated.

Unemployment. In the 1-class model, the CFI was 0.940 and the RMSEA was 0.060. In the 3-class solution, in the 3rd class, the covariance between the pre-event and post-event slopes was set to 0 due to a correlation greater than +/−1 when allowing them to be freely estimated. In the 4-class solution, the variance for the first slope factor (and its covariances) was set to 0 for the 2nd and 4th class due to a correlation greater than +/−1 when allowing them to be freely estimated. In the 5-class solution, the covariances were all set to 0 for each group due to a correlation greater than +/−1 when allowing them to be freely estimated.

To compare the solutions with those in previously published analyses (Figure 2A), however, we examined the data estimates for the 3-class solution. The middle section of Table 2 provides the parameter estimates for these 3-classes. In the 3-class solution (see Figure 2B), only 27% of the sample was likely to belong to a resilient trajectory characterized by stable, high levels of life satisfaction. This is in sharp contrast to what we found earlier, with 75% of people likely to be in a resilient trajectory in relation to spousal loss. As shown in Figure 2B, furthermore, the three trajectories differed in both levels and slopes, with the resilient trajectory showing the least amount of variability in change.

Divorce

The middle section of Table 5 shows results from a series of GMM analyses that estimated 1 through 5 classes for the divorce data. We determined that the 2-class solution provided the most parsimonious fit to the data. Although the BIC was lower for the 3-class solution and the LRTs were both significant, the entropy value for the 2-class solution was substantially higher (0.693 versus 0.599), indicating that the classes were more distinct from one another in the 2-class solution compared to the 3-class solution. The middle section of Table 3 shows the parameter estimates for the two classes and Figure 3B graphically illustrates the two classes. The Resilient trajectory was only comprised of 36% of the sample, whereas the Recovery group consisted of 64% of the sample. This finding is in contrast to the previous (Part A) results documenting that 85% of participants were resilient to divorce.

Unemployment

The bottom section of Table 5 shows results from a series of GMM analyses examining whether 1 through 5 classes best represent how life satisfaction changed in relation to unemployment. We determined that the 2-class solution provided the most parsimonious fit to the data. Although, the BIC was lower for the 3-class solution, the entropy value was lower in the 3-class solution and the 3-class solution did not provide classes that were meaningfully different from one another in their trajectory of change (two classes displayed similar trajectories to that of recovery). The bottom section of Table 4 provides parameter estimates for each group and Figure 4B graphically illustrates the two class solution, with 47% of the sample belonging to a Resilient trajectory that maintains relatively stable with high levels of life satisfaction despite unemployment, whereas 53% were likely to experience a sharp decline in life satisfaction in the year surrounding job loss, followed by sustained lower levels in the years thereafter. We note that given the low entropy value and the considerable overlap shown in Part B in Figure 3 between the two classes, we recognize that the 2-class solution may be difficult to replicate and there may only be a single class of individuals that vary in their intercept and slope values, but follow the same overall trajectory of change.

Replication: Part 3

We use the longitudinal model described under “Replication: Part 3” in the Methods section for results in this section. Similar to before, we estimated a series of models that estimated 1 through 5 classes that allowed the factor means and variances to differ not just between sub-groups, but also, now, among individuals within each of the sub-groups.

Spousal loss

The top section of Table 6 shows findings pertaining to spousal loss and model fit statistics from a series of models with 1 through 5 classes. It should be noted that the model fit statistics in Table 6 suggest that a 1-class solution might actually represent the best model. When going from a 1-class to 2-class solution, we observed a decline in the BIC, but the entropy values (0.603 and below) indicated that having more than 1-class did not lead to classes that could be distinguished. Furthermore, the 95% confidence intervals showed a great of overlap across classes, and the classes followed a similar mean trajectory, which further suggests that a 1-class solution provided the best representation of the data.

Table 6.

Model Fit Statistics for Growth Mixture Models Determining Number of Classes for How Life Satisfaction Changes in Relation to Spousal Loss, Divorce, and Unemployment: Replication Part 3.

	1-Class	2-Class	3-Class	4-Class	5-Class
Spousal Loss
Sample size
Nc = 1	1,214	574.88	399.33	371.88	380.13
Nc = 2		639.12	690.15	206.10	277.04
Nc = 3			124.51	305.60	110.15
Nc = 4				330.42	304.12
Nc = 5					142.56
Fit statistics
# of free parameters	18	29	38	39	46
BIC	39,054	38,273	38,221	38,294	38,266
ABIC	38,997	38,181	38,100	38,170	38,119
Entropy		0.581	0.603	0.529	0.564
Vuong-Lo-Mendell-Rubin LRT		0.0000	0.0123	0.2214	0.1181
Lo-Mendell-Rubin Adjusted LRT		0.0000	0.0129	0.2255	0.1214
Divorce
Sample size
Nc = 1	1,579	570.97	522.99	441.39	371.76
Nc = 2		1,008.03	306.51	317.45	74.03
Nc = 3			749.50	601.01	310.66
Nc = 4				219.14	560.53
Nc = 5					262.03
Fit statistics
# of free parameters	18	29	40	51	53
BIC	49,481	48,204	48,056	48,051	48,053
ABIC	49,424	48,112	47,929	47,889	47,884
Entropy		0.699	0.592	0.551	0.560
Vuong-Lo-Mendell-Rubin LRT		0.0000	0.0000	0.1327	0.0047
Lo-Mendell-Rubin Adjusted LRT		0.0000	0.0000	0.1361	0.0051
Unemployment
Sample size
Nc = 1	2,461	1,301.79	433.09	432.12	185.77
Nc = 2		1,159.21	1,319.00	788.36	978.54
Nc = 3			708.91	364.93	674.46
Nc = 4				875.60	282.97
Nc = 5					339.26
Fit statistics
# of free parameters	18	29	40	48	54
BIC	88,623	86,475	86,178	86,141	86,117
ABIC	88,566	86383	86,060	85,989	85,945
Entropy		0.648	0.616	0.591	0.589
Vuong-Lo-Mendell-Rubin LRT		0.0000	0.0000	0.2995	0.0054
Lo-Mendell-Rubin Adjusted LRT		0.0000	0.0001	0.3029	0.0059

Note. Spousal Loss. In the 1-class model, the CFI was 0.923 and the RMSEA was 0.068. In the 3-class solution, the covariance for intercept-pre-event slope and intercept-post-event slope was set to 0 due to a correlation greater than +/−1 when allowing them to be freely estimated. In the 4-class solution, the covariances for each class were set to 0 due to correlations being greater than +/−1 when allowing them to be freely estimated. In the 5-class solution, the covariances for each class were set to 0 and in the 3^rd class, the intercept variance was set to 0 due to correlations being greater than +/−1 when allowing them to be freely estimated.

Divorce. In the 1-class model, the CFI was 0.954 and the RMSEA was 0.046. In the 5-class solution, in the 1^st class the post-event variance and the covariance for intercept-post-event slope and pre-event slope and post-event slope were set to 0 and in the 2^nd class, all of the variances and covariances were set to 0 due to a correlation greater than +/−1 when allowing them to be freely estimated.

Unemployment. In the 1-class model, the CFI was 0.978 and the RMSEA was 0.037. In the 4-class solution, in the 1^st class, the variance for the post-event slope and the intercept-post-event slope and pre-event slope and post-event slope were set to 0 due to a correlation greater than +/−1 when allowing them to be freely estimated. In the 4-class solution, in the 3^rd class, the variance in pre-event and post-event slope and their covariances were set to 0 due to a correlation greater than +/−1 when they were freely estimated.

Acknowledging these factors, once again, we examined the 2-class solution to allow comparability to previously published models (Figure 2A). The bottom section of Table 2 provides parameter estimates for the two class solution. Figure 2C graphically illustrates the 2-class solution for changes in life satisfaction in relation to spousal loss, with 36% and 64% of participants in the Resilient and Recovery sub-groups. We observed that the variance in level and rates of change were smaller in the resilient class as compared to the recovery class (see parameter estimates at the bottom of Table 2), providing further evidence that allowing the variance in level and rates of change to differ between classes is appropriate.

Divorce

Based on the model fit statistics shown in the middle section of Table 6, the 2-class solution provided the best model for the data for changes in life satisfaction in relation to divorce. Figure 3C graphically illustrates the 2-class solution with the 95% confidence intervals. Similar to our analyses in Replication: Part 2, 36% of the sample had the likelihood of being resilient – defined as maintaining high, stable levels of life satisfaction. Conversely, 64% of the sample was likely to experience strong declines in life satisfaction in the year surrounding divorce and a slow recovery in the years thereafter. Again, the parameter estimates for the 2-classes are shown in the bottom of Table 3 and show that there is more variability in level and rates of change (pre-event and post-event slope) in life satisfaction in the Recovery sub-group, compared to the Resilient sub-group.

Unemployment

The model fit statistics shown in the bottom section of Table 6 indicate that a 2-class solution was optimal for these data. When comparing the 2-class and 3-class solutions, the entropy value was lower in the 3-class solution and two classes displayed similar trajectories to that of recovery. Figure 4C graphically illustrates the 2-class solution with the 95% confidence intervals. In contrast to our findings in Replication: Part 1, only 48% were resilient, compared to 52% belonging to the Recovery class. Parameter estimates for these two groups are shown in the bottom of Table 4; yet again, the variance in level and rates of change (pre-event and post-event slope) differed between the classes, with the resilient trajectory showing the smallest.

Discussion

In trying to replicate prior findings on “rates of resilience” surrounding spousal loss, divorce, and unemployment, our analyses showed very different results from findings previously published. When applying exactly the same model specifications, we found that the resilient trajectory was most common, but that the number of trajectories differed for all three events examined. In a second set of analyses in which we relaxed the stringent assumptions applied in prior reports, we consistently found that resilience represented the least common trajectory. Finally, when we estimated a multi-phase longitudinal model of change, we found, at most, two trajectories in all cases.

Rates of resilience: Replication using prior model specifications

Applying exactly the same model specifications as in previously published findings, our own results differed from previous reports in indicating that the optimal solutions were three versus four classes respectively for life satisfaction in relation to spousal loss, two versus three classes for divorce, and three versus four classes for unemployment. It is unclear why the findings consistently differed across all life adversities. One possibility is that we used updated data, examined change in the 11 years surrounding the event as opposed to nine or eight, and had a larger participant pool across the events.¹ Furthermore, the model fit statistics (e.g., BIC, entropy, and LRTs) were not included in the Mancini et al. (2011) report, making it unclear as to what the defining criteria were when deciding on the 4-class solution for spousal loss and 3-class solution for divorce.

Most importantly, when we followed conceptual considerations that paths towards resilience can differ across persons within a given sub-group – removing the strict assumptions applied in earlier publications -- the resilient trajectories were much smaller. In previous analyses and our own, respectively, rates of resilience were 59% versus 47% for spousal loss, 72% versus 36% for divorce, and 69% versus 48% for unemployment. The substantial disparity in trajectory sizes reflects major conceptual differences in assumptions underlying analyses (as illustratively depicted in Figures 1A and 1B): We allowed for the possibility that (a) individuals could differ in life satisfaction not just after the events but also before them, and (b) within any given class, constituent members could vary in adjustment over time, rather than showing exactly the same change process or slope across time (see Lucas et al., 2003, 2004).²

It should be noted that the relatively low rates of resilience in our own results are consistent with studies published by different research laboratories. In examining adjustment in relation to disability onset, for example, Infurna and Wiest (2015) found that 15% of participants displayed a resilient trajectory with life satisfaction as the outcome, whereas with self-rated health as the outcome, there was no resilient trajectory at all. Similarly, when examining resilience to unemployment across three indicators of subjective well-being, the proportion of people in the Resilient class substantially differed (life satisfaction: 61%; negative affect: 48%; positive affect: 20%; Infurna, Wiest, & Luthar, 2015). The absence of a resilient trajectory was also reported in research following exposure to personal sexual assault (Steenkamp et al., 2012).

From a scientific perspective, our findings underscore the need to re-examine not only conclusions that resilience is the modal response to adversity, but also that it is distinct from recovery (Bonanno et al., 2011; Bonanno & Diminich, 2013). Developmental scholars have argued that the pattern called recovery – with time-limited dips in functioning just around the occurrence of the event -- is, in itself, a form of resilience or “doing well” despite adversity (Luthar & Brown, 2007; Rutter, 2013; Masten & Narayan, 2012; Zautra et al., 2008). Supporting these contentions are findings, within this study, that the resilient and recovery trajectories each fell well within the 95% confidence intervals of the other across all life events, suggesting, in fact, that they are not necessarily distinct.

Inasmuch as our findings demonstrate that a priori choices regarding GMM model specification can significantly affect the size of sub-groups called resilient, they underscore the need for further replication research exploring issues examined here. GMM is a constrained exploratory data-driven method (Bauer & Curran, 2003; Grimm & Ram, 2009; Ram & Grimm, 2009), so that there remains significant possibility for confirmation biases if researchers impose the same model assumptions across multiple data sets. Any results based on a single sample and a single measure cannot possibly be treated as establishing, with any veracity, actual population “rates of resilience”. Thus, studies across multiple studies, constructs, and research laboratories are needed to establish confidence in the generalizability of particular published results (Grimm & Ram, 2009).

We also note, importantly, that our findings should by no means be viewed as a call to discourage researchers from using GMM in examining resilience; to the contrary, we hope that they will spur further efforts to use GMM approaches in studies of resilience. GMM does have significant advantages in comparison to other methods of analyzing longitudinal data in the capacity to illuminate whether (or not) the population under study consists of discrete sub-groups of individuals that are distinct from one another. Thus, there is much value in further applications of this approach, but with careful, deliberate consideration of the degree to which assumptions imposed on data might affect the number of classes identified in relation to particular adversities, and the proportion of people that belong to each class.

Rates of resilience: Differences based on domain

There is another critical conceptual reason to question previous assertions that resilience (stable good functioning) is typical, and that there is always variability across adjustment domains. In developmental science, it has long been recognized that following exposure to significant stressors, children can excel in some areas while struggling considerably in others (Luthar, Crossman, & Small, 2015), so that it is entirely inappropriate to confer “diagnoses of resilience” (Rutter, 2012). To illustrate, among stress-exposed youth who are rated as very well adjusted by friends or teachers, many experience high levels of covert distress such as depressive or anxiety symptoms (Luthar, 1991). Similarly, among adults, it is entirely plausible that some bereaved individuals will revert to earlier global life satisfaction levels, but they may still experience other difficulties such as symptoms of depression or physical health problems (e.g., Werner, 2012) rendering suspect any global labels of resilience.

Considered collectively, these factors underscore the inadvisability of any declarations on “rates of resilience” based on a single measure, as in this study and in the prior (widely cited) studies that we sought to replicate. ³ As Almedom and Glandon (2007) have correctly argued, labels of resilience must necessitate more than a single item of adults’ life satisfaction ratings, or the absence of PTSD symptoms among affected individuals. Others, similarly, have noted that it is critical to “consider a wider range of outcomes, including not only PTSD but substance abuse, depression, anger and violence, interpersonal and role functioning, behavioral and developmental disturbances, and physical health“ (Watson, Brymer & Bonanno, 2011, p. 490).

The need for careful consideration of these issues goes well beyond scientific opinions; they have enormous implications for social policy. Findings that resilience is “typical” have engendered suggestions that “Resilience-building interventions may be ineffective and perhaps even harmful” (Bonanno et al., 2011 p. 529; see also Bonanno, Brewin, Kaniasty, & La Greca, 2010). Such declarations can have the unfortunate and serious consequence of leading policy makers to decide against providing resources for those individuals who do, in fact, suffer considerably in the wake of serious adversities, such as natural disasters or serious community violence (Jayawickreme & Blackie, 2014).

Based on both conceptual factors (the necessarily limited breadth of adjustment domains measured in a particular study) and the serious implications for social policy (withholding of resources for those deeply affected), therefore, we would strenuously argue against any declarations, in future research, on how many people are resilient. Instead, we believe that it will be much more productive to focus scientific efforts on trying to learn from those who do function relatively well in the face of adversities, and harness what is learned toward expediently helping those who falter (see Schoenbaum et al., 2014). As discussed by Masten and Narayan (2012), interventions for young people in the context of disaster have been shown to be effective when a resilience perspective is utilized, with the timing and amount of help, as well as specific strategies used, are appropriate for the particular risk group targeted (see also Almedom & Glandon, 2007).

In the ultimate analysis, it is quite plausible that time does, in fact heal – for most people and given long enough periods of time; but this by no means obviates the need for psychologists to consider carefully the needs of those who suffer considerably in the wake of serious adversities. Stated differently, over a period spanning years or decades, most divorced or bereaved individuals probably do “regress to their (own) lifetime levels” of adaptation on global measures of life satisfaction (Diener, Lucas, & Scollon, 2006; Lucas, 2007); this by no means renders trivial, or unworthy of scientific attention, the high levels of (diverse) symptoms, and/or problems in critical areas of everyday functioning, that can deeply affect the lives of many in the aftermath of major life stressors.

Summary

In conclusion, there is a critical need for more replication analyses of data underlying claims that resilience is common. Given the major implications for theory and science on this construct as well as public policy, it would be useful if different research laboratories (cf. Maner, 2014) were to reexamine “rates of resilience” in longitudinal data sets. The critical question is, will stable, healthy functioning before and after the event be typical even after allowing for variability in adjustment preceding events such as divorce or spousal loss; margins of error in rates of resilience or recovery; and consideration of outcomes other than self-reported adjustment on a single measure? Such replication efforts are critical to establish if there is – as our findings indicate – the need to temper statements that analyses of one sample represent “population-based estimates” that two thirds of people are resilient after heart attacks (Galatzer-Levy & Bonanno, 2014), or that 85% of soldiers deployed to Iraq and Afghanistan are resilient and do not need any interventions after prolonged trauma exposure (see Bonanno et al., 2012). Given the enormous implications for informing societal and policy decisions, resilience researchers must hold themselves to the highest standards of scientific responsibility, ensuring circumspection in conclusions drawn based on particular data sets, measures, and analyses.