What Strains the Anterior Cruciate Ligament During a Pivot Landing?

Abstract

Background

The relative contributions of an axial tibial torque and frontal plane moment to anterior cruciate ligament (ACL) strain during pivot landings are unknown.

Hypothesis

The peak normalized relative strain in the anteromedial (AM) bundle of the ACL is affected by the direction of the axial tibial torque but not by the direction of the frontal plane moment applied concurrently during a simulated jump landing.

Study Design

Controlled and descriptive laboratory studies.

Methods

Fifteen adult male knees with pretensioned knee muscle-tendon unit forces were loaded under a simulated pivot landing test. Compression, flexion moment, internal or external tibial torque, and knee varus or valgus moment were simultaneously applied to the distal tibia while recording the 3D knee loads and tibiofemoral kinematics. The AM-ACL relative strain was measured using a 3-mm differential variable reluctance transducer. The results were analyzed using nonparametric Wilcoxon signed–rank tests. A 3D dynamic biomechanical knee model was developed using ADAMS and validated to help interpret the experimental results.

Results

The mean (SD) peak AM-ACL relative strain was 192% greater (P <.001) under the internal tibial torque combined with a knee varus or valgus moment (7.0% [3.9%] and 7.0% [4.1%], respectively) than under external tibial torque with the same moments (2.4% [2.5%] and 2.4% [3.2%], respectively). The knee valgus moment augmented the AM-ACL strain due to the slope of the tibial plateau inducing mechanical coupling (ie, internal tibial rotation and knee valgus moment); this augmentation occurred before medial knee joint space opening.

Conclusion

An internal tibial torque combined with a knee valgus moment is the worst-case ACL loading condition. However, it is the internal tibial torque that primarily causes large ACL strain.

Clinical Relevance

Limiting the maximum coefficient of friction between the shoe and playing surface should limit the peak internal tibial torque that can be applied to the knee during jump landings, thereby reducing peak ACL strain and the risk for noncontact injury.

More than 250,000 anterior cruciate ligament (ACL) injuries occur each year in the United States.¹³ Eighty percent of patients who sustain an ACL tear exhibit a concomitant impaction injury to the articular cartilage, and greater than 50% have meniscal tears.^2,4,9,51,55 Anterior cruciate ligament ruptures also increase the risk for developing degenerative joint disease over time.²² Clearly, better insights into ACL injury mechanisms might improve current ACL injury prevention programs. According to recent systematic reviews,^43,45 noncontact ACL injuries are most likely to occur when landing on a slightly flexed knee that is loaded by moments in 3 orthogonal planes. An internally directed tibial torque and/or knee valgus moment, combined with a quadriceps muscle contraction to resist the flexion moment, appears to be particularly detrimental to the ACL. However, it remains unclear how multiplanar moments interact to increase ACL strain.

Previous in vivo and in vitro studies have consistently reported that an internal tibial rotation increases ACL strain more than an external tibial rotation with or without a quadriceps muscle force.^1,11,26,36 It is known that an internal tibial rotation induces a coupled anterior tibial translation relative to the femur, thereby increasing ACL strain.¹⁸ On the other hand, post hoc injury video analyses have reported that ACL injuries occurred under both internal and external tibial rotation, often combined with a knee valgus angulation.³⁷ As discussed in the next paragraph, it appears that the role of axial tibial rotation in ACL injury mechanisms has not drawn as much attention as that of the knee valgus loading.⁴³

Over the past decade, knee valgus loading has been identified as the primary mechanism for noncontact ACL injury, and thus many ACL injury prevention programs have focused on reducing valgus loading to the knee during jump landings.^15,16,21,34 This is primarily because the knee often appears to pass through a valgus posture on videotapes of athletes who are landing and/or pivoting as they sustain an ACL injury (eg, Figure 1D in Olsen et al 2004).³⁷ Some in vitro studies have demonstrated that a knee valgus moment increases ACL tension^2,26 and strain.⁵⁸ However, Fleming et al¹¹ reported relatively constant ACL strain values over a range of valgus moments tested under both weightbearing and nonweightbearing conditions. So, these results are not equivocal.

It has been theorized that a knee valgus moment increases ACL strain while the medial knee joint opening occurs.⁴² If it were true that a knee valgus moment typically causes the noncontact ACL injury by inducing medial joint opening, then concomitant medial collateral ligament (MCL) injuries would be seen frequently with noncontact ACL tears because the MCL is known to be the primary restraint to a knee valgus loading. In addition, Yasuda et al⁶⁰ demonstrated that the maximum elongation of the MCL occurs before that of the ACL near full extension during a lateral impact loading. Combined ACL-MCL injuries are relatively rare (ie, 4%–27% of total ACL injuries).^19,30 Furthermore, in 80% of acute ACL injuries, lateral femoral condyle and posterolateral tibial plateau bone bruises are observed.^12,17,51,57 These bone bruise patterns suggest that large knee valgus moments, anterior tibial subluxation, or internal tibial torque may be involved in ACL injury under high compressive joint force loading.^33,50,51,57 Unfortunately, it is not known which is the most common form of loading during ACL injury.

During in vivo activities, the knee is commonly subjected to a combination of forces and moments in the sagittal, frontal, and transverse planes. It has been shown that the ACL tension produced by combining 2 loading conditions cannot simply be estimated by superposing the ACL tensions produced by each loading condition individually.²⁵ Hence, we investigated the effect on ACL strain of combined frontal plane and transverse plane knee moments in the presence of simulated muscle forces during a realistic landing. We tested the primary hypothesis in vitro that the normalized peak anteromedial (AM) bundle–ACL relative strain would be affected by the direction of the axial tibial torque but not by the direction of the frontal plane moment when applied concurrently. Insights could guide future interventions aimed at reducing the risk for ACL injury. Recently, it has been speculated that a greater lateral tibial slope, compared with a medial tibial slope, causes a more posterior translation of the lateral than medial femoral condyle, thereby causing internal tibial rotation during a valgus loading.^23,52 Thus, to better understand the biomechanical factors increasing ACL strain and to help interpret our experimental results, we also developed, validated, and then used a simple biomechanical model of the knee in silico.

METHODS

Specimen Procurement and Preparation

Fifteen fresh-frozen cadaveric limbs (mean [SD] age, 70.4 (2.9) years; mean [SD] body weight, 839.4 [113.0] N; 9 males) were acquired from the University of Michigan Anatomical Donations Program. All lower extremities were visually checked for scars, indication of surgery, malalignments, or deformities. Before specimen procurement, the bone was exposed by dissection 8 inches proximal and distal to the knee joint line, and frontal plane digital images of axially compressed and fully extended legs were taken to determine the natural frontal plane limb alignment. Then, following the methods of Withrow et al,^58,59 the lower extremities were cut 8 inches proximal and distal to the knee joint to standardize specimen length. Specimens were then dissected, leaving the ligamentous knee structures and the tendons of quadriceps, medial and lateral hamstring, and medial and lateral gastrocnemius muscles intact. Each end of the specimen was potted using polymethylmethacrylate. The frontal plane alignment of the knees was reproduced based on the above frontal plane digital images. The dissected specimens were frozen at −20°C until needed and thawed at room temperature for 12 hours before testing commenced. During the testing, saline solution was regularly sprayed to prevent soft tissue dehydration.

Knee Testing Apparatus

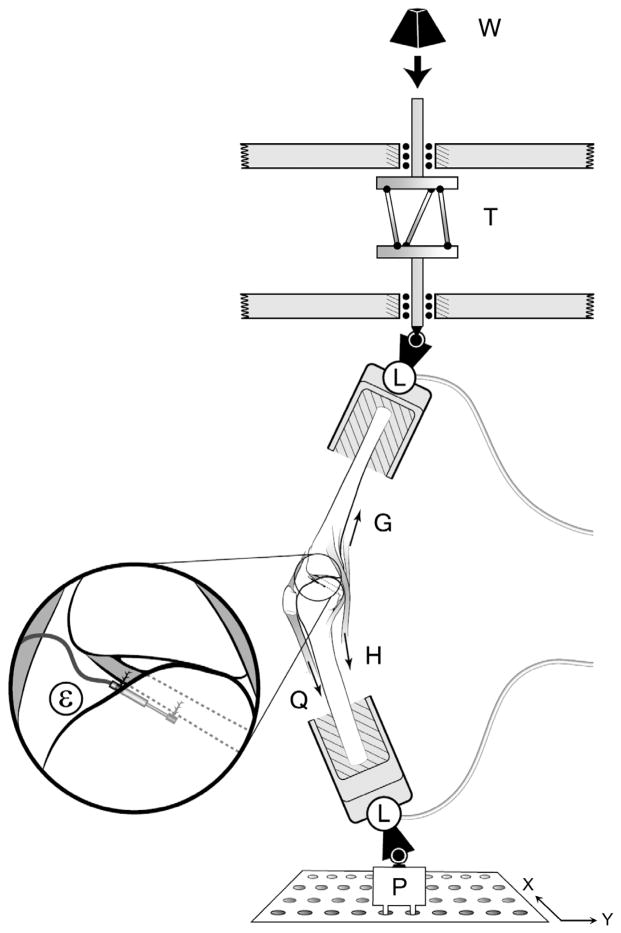
The modified Withrow et al^35,36,58,59 testing apparatus was used to simulate the position of a single extremity as it strikes the ground while landing on 1 leg during a jump or pivot maneuver. The simulated quadriceps muscle was represented by elastic structures (ie, 2-mm woven nylon cord; tensile stiffness, ~2 kN/cm) pretensioned to 180 N. The same elastic structures were used to represent the medial and lateral hamstring and gastrocnemius muscles, initially pretensioned to 70 N each. Each simulated muscle-tendon unit was connected from the femur or tibia to the relevant tendons via liquid nitrogen cryo-clamps through the anatomic lines-of-action, thereby representing its in vivo dynamic resistance to sudden stretch (Figure 1). In all trials, the initial knee flexion angle was maintained at 15°. A jump landing ground-reaction force was simulated by dropping a weight onto the distal tibia of an inverted knee generating a 2*BW (ie, BW is each donor’s postmortem body weight) impulsive force. A customized shock absorber (ACE Controls Inc, Farmington, Michigan) was interposed between the drop weight and the distal end of the tibia to shape the ground-reaction force so as to peak at 50 to 60 msec (see Appendix 1, available with the online article and at http://ajs.sagepub.com/supplemental/).^35,36 The weight drop was initiated in a standardized manner via a quick-release mechanism to mimick impulsive ground-reaction forces typically seen in a jump landing.^5,28,31,54 In a new departure from the original Withrow apparatus, a custom torsional transformer was added and mounted in series with the distal tibia (see T in Figure 1). The weight of the torsional transformer was equilibrated through the use of a constant force spring. The torsional transformer was designed to transform the linear momentum of the drop weight into the combination of an axial compressive force and an impulsive axial torque component at impact. The torsional transformer consisted of 2 circular plates and 3 inclined palls connecting 2 plates, where the top plate can only translate vertically, whereas the bottom plate can both translate vertically and rotate. The angle of the palls to the vertical was adjustable and preset to give the desired gain between the applied compressive force and the rotational torque delivered to the specimen. The peak axial torque was adjusted to reach a nominal value between 20 and 30 N·m.⁴⁸ For the baseline loading condition, the specimen was oriented such that the impulsive compressive force initially acted ~3 cm posterior to the knee in the sagittal plane. For varus or valgus loading condition, the bottom of the knee construct (P in Figure 1) was translated medially or laterally (ie, ±x direction in Figure 1) so that the knee specimen was initially adducted or abducted with the impulsive compressive force inclined at 7° to the sagittal plane, respectively.

Figure 1.

Schematic diagram of the test apparatus showing how a weight (W) dropped from a fixed height onto the torsional transformer device (T) applied impulsive compression and axial torque to the distal tibia of an inverted knee specimen. For the varus or valgus loading condition, the knee specimen was initially adducted or abducted by translating the bottom plate (P) in ±x direction. The two 6 degrees of freedom load cells (L) measured the 3 components of force and moment applied to the knee specimen. Quadriceps (Q), hamstrings (H), and gastrocnemius (G) forces using 1 degree of freedom transducers. A miniature displacement transducer (ε) implanted on the surface of the anteromedial bundle of the ACL measured relative strain. (Reprinted with permission from Oh et al.³⁵)

Two 6 degrees of freedom load cells (AMTI, Watertown, Massachusetts) measured the 3D tibial forces and moments delivered to the knee construct, as well as the 3D femoral reaction forces and moments. A 3-mm differential variable reluctance transducer (DVRT, Microstrain, Burlington, Vermont) was mounted on the AM bundle of the ACL to record ACL relative strain. The anterior knee joint capsule was opened so as to visually identify the AM bundle and its fiber direction. To standardize the location of the DVRT on the AM-ACL, it was placed parallel to the fiber direction at the first quartile of the ACL length measured from the tibial attachment site. Five single degree of freedom load cells (Transducer Techniques, Temecula, California) were connected to the assembly of the cryo-clamp and elastic structure to measure simulated muscle tensions. The impulsive forces and moments, 5 simulated muscle-tendon unit forces, and AM-ACL relative strain data were recorded at 2 kHz using a 16-bit analog-to-digital converter board. Six infrared-emitting diodes, 3 each rigidly mounted to the femur and tibia, respectively, via a mounting plate and bone screws, were tracked with use of an Optotrak Certus system (Northern Digital Inc, Waterloo, Canada) recording tibiofemoral kinematics¹⁴ at 400 Hz with an accuracy of up to 0.1 mm and resolution of 0.01 mm.

Testing Protocol

Forty trials were completed for each specimen (Table 1). During the first 5 preconditioning trials, the height of the weight drop was varied to find the drop height such that it best simulated a 2*BW impulsive ground-reaction force for the baseline loading condition (ie, BASE1 and BASE2). That drop height was then maintained throughout all trials to apply the same kinetic energy to the knee specimens. After the preconditioning trials, 6 blocks were run on each specimen in a BASE1 – A – B – C – D –BASE2 repeated-measures design. The baseline loading condition (ie, BASE1 and BASE2) was designed to simulate a drop landing in which the impulsive ground-reaction force provides the compressive force on the knee joint and induces the knee flexion, thereby causing sudden stretch of the quadriceps muscle-tendon equivalent. That stretch of the quadriceps muscle-tendon equivalent resulted in the posterior femoral displacement relative to the tibia (ie, anterior tibial translation relative to femur), thereby increasing the ACL strain. For the first experimental blocks (A), either a knee valgus or varus moment, combined with internal or external tibial torque, was added to the baseline loading condition in a randomized manner. Then, the direction of the frontal plane moment was reversed for the blocks B and D, whereas the direction of the axial tibial torque was reversed for the blocks C and D. The first trial for each loading block was considered as a preconditioning trial, and the last 5 trials were used to perform the statistical analysis.

TABLE 1.

Repeated-Measures Experiment Protocol Proceeded From Trial Block in Top Row to Bottom Row^a

Protocol	Loading Direction	Trials
BASE1	Compression + flexion moment	5
Internal tibial torque + knee varus moment*	Compression + flexion moment + internal tibial torque + varus moment	6
Internal tibial torque + knee valgus moment*	Compression + flexion moment + internal tibial torque + valgus moment	6
External tibial torque + knee varus moment*	Compression + flexion moment + external tibial torque + varus moment	6
External tibial torque + knee valgus moment*	Compression + flexion moment + external tibial torque + valgus moment	6
BASE2	Compression + flexion moment	6

^aThe order of the 4 blocks of experimental trials (marked by an asterisk) interposed between the 2 baseline trial blocks (BASE1 and BASE2) was randomized. See text for details.

AM-ACL Relative Strain

The initial length of the DVRT was defined as the length of the DVRT in the initial 15° preimpact static posture under the simulated muscle forces because it is problematic to find the unloaded zero strain state.¹⁰ The change in DVRT length from this initial length, divided by the initial length, was used to calculate the “relative” strain in the AM region of the ACL under the impulsive loading.

Statistical Analysis

The peak AM-ACL relative strain for each individual trial was normalized by the mean peak AM-ACL relative strain of both baseline loading conditions (ie, BASE1 and BASE2). This was done for the last 5 individual trials of each testing block. Then, the 5 normalized peak AM-ACL relative strain values were averaged to find a representative strain value for the corresponding loading condition. A nonparametric Wilcoxon signed–rank test was used to test the hypothesis. An alpha level of .05 was chosen for the level of significance.

3D Dynamic Knee Model

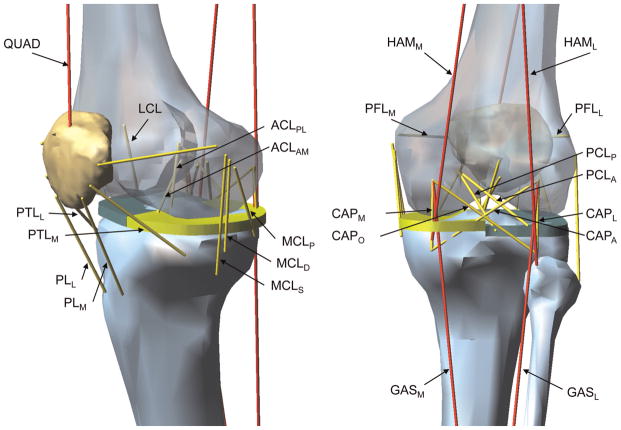
A 3-dimensional lower limb model was constructed to better interpret the experimental results and further investigate how the frontal plane moments and axial tibial torques interact to affect the ACL strain under a simulated landing. The knee model was designed to replicate the knee loading and response in the in vitro testing apparatus. The segmented femur, tibia, fibula, and patella were obtained from the visible human male data set⁵⁶ and imported into a dynamic simulation software (MD Adams R3, MSC.Software Inc, Santa Ana, California). As shown in Figure 1, using 2 universal joints, the proximal end of the femur and the distal end of the tibia were connected to the base frame and a cylinder rod that allows vertical motion and axial rotation, respectively. Thus, the knee joint was fully unconstrained (ie, 6 degrees of freedom). As introduced earlier, to consider the effect of the medial and lateral tibial posterior slopes on the interaction between an axial tibial torque and frontal plane moment, 2 flat plates were placed to the proximal end of the tibia. According to the report by McLean et al,²⁷ the medial and lateral posterior tibial slopes were set to be 5.5° and 8.5°, respectively. The contact forces between the femur and 2 tibial plateaus and the femur and patella were defined using the penalty methods implemented in the ADAMS software. In addition, to detect the medial or lateral joint space opening, the contact forces between the medial and lateral femoral condyles and tibial plateaus were monitored. Viscoelastic behavior of the 10 ligaments and 4 anterior and 4 posterior knee joint capsule structures was modeled using Kelvin-Voigt elements consisting of a bilinear elastic spring^29,44,46,47 and a viscous damper in parallel (Figure 2 and Appendix 2, available online).

Figure 2.

Schematic of the knee model showing muscles and ligaments: quadriceps, medial and lateral hamstrings, and medial and lateral gastrocnemius muscles (QUAD, HAM_M, HAM_L, GAS_M, and GAS_L, respectively); the anteromedial and posterolateral bundles of the anterior cruciate ligament (ACL_AM and ACL_PL, respectively); the anterior and posterior bundles of the posterior cruciate ligament (PCL_A and PCL_P, respectively); the lateral collateral ligament and the superficial, deep, and posterior medial collateral ligament (LCL, MCL_S, MCL_D, and MCL_P, respectively); the medial and lateral patellofemoral ligament and the medial and lateral patellotibial ligament for the anterior knee capsule (PFL_M, PFL_L, PTL_M, and PTL_L, respectively); the medial, lateral, oblique popliteal, and arcuate popliteal fiber for the posterior knee capsule (CAP_M, CAP_L, CAP_O, and CAP_A, respectively); and the medial and lateral patellar ligament (PL_M and PL_L, respectively).

An individual baseline trial showing representative behaviors of the knee specimens tested was found, and that impulsive compressive force was applied to the distal tibia as an input to drive the knee model simulation. To validate the model simulation, the resultant quadriceps muscle forces, knee flexion angle, and AM-ACL relative strain profiles were quantitatively compared with the corresponding profiles obtained from the experiment by evaluating Pearson correlation coefficients from the time when the impact was initiated and to when 80 msec had elapsed. Because the peak AM-ACL relative strain occurred at a mean ± SD of 71 ± 7 msec in the experiment (Appendix 1, available online), the model validation was focused on better replicating the knee joint behaviors over the first 80 msec. After the validation test (Appendix 3, available online), parametric studies were performed to investigate how the theoretical representation of the medial and lateral tibial plateau would affect the AM-ACL strain, MCL and lateral collateral ligament (LCL) strain, internal-external tibial rotation, and knee varus-valgus angulation when the axial tibial torque and frontal plane moment measured from the experiment were added to the validated baseline loading condition individually and concurrently (Table 2).

TABLE 2.

Loading Conditions for Parametric Studies

Study	Loading Condition
1	Compression + flexion moment + axial tibial torques (−50 N·m ~ 50 N·m)a
2	Compression + flexion moment + frontal plane moments (−150 N·m ~ 150 N·m)b
3	Compression + flexion moment + internal tibial torque (20 N·m) + frontal plane moments (−150 N·m ~ 150 N·m)b
4	Compression + flexion moment + external tibial torque (−20 N·m) + frontal plane moments (−150 N·m ~ 150 N·m)b

^aPositive value represents internal tibial torque.

^bPositive value represents knee abduction moment.

RESULTS

Effect of Interaction Between Frontal Plane Moments and Axial Tibial Torques on AM-ACL Relative Strain

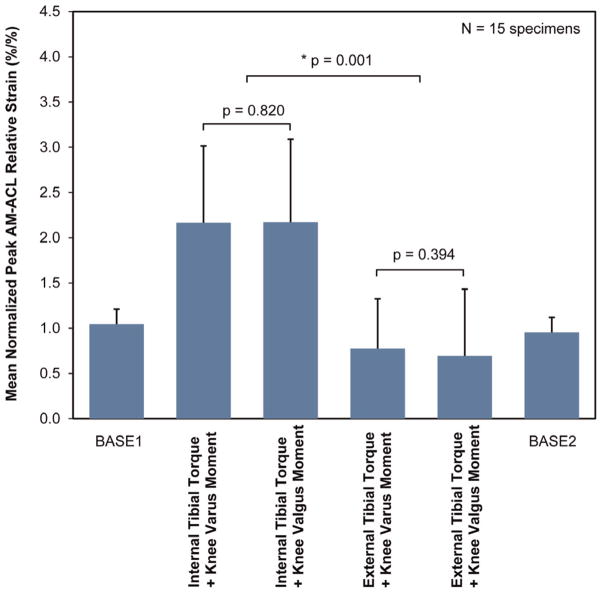
The experimental results support the primary hypothesis: the normalized peak AM-ACL relative strain under the internal tibial torque was significantly greater than the corresponding values under the external tibial torque regardless of the direction of the frontal plane moment (Figure 3). The mean peak AM-ACL relative strain under the internal tibial torque combined with the knee valgus or varus moment (7.0% ± 4.1% and 7.0% ± 3.9%, respectively) was 192% greater than the corresponding values under external tibial torque combined with the knee valgus or varus moment (2.4% ± 3.2% and 2.4% ± 2.5%, respectively). There was no difference between the 2 baseline loading conditions, thereby confirming the knee specimens were not damaged during the testing (P = .460) (Figure 3). The input force, input moments, and primary and secondary outcome measurements for each loading condition are summarized in Table 3. Sample time course data from a single representative specimen and trial are shown in Appendix 1 (available online).

Figure 3.

Mean (SD, represented by error bars) normalized peak AM-ACL relative strain values under each loading condition. The asterisk indicates a significant difference. Regardless of the direction of the frontal plane moment, the mean normalized peak AM-ACL relative strain was greater under the internal tibial torque than under the external tibial torque. ACL, anterior cruciate ligament; AM, anteromedial bundle.

TABLE 3.

Mean (±SD) Value for the Input Force and Moments and the Primary and Secondary Outcome Measurements by Test Block (N = 15 specimens)^a

	BASE1	Internal Tibial Torque + Varus Moment	Internal Tibial Torque + Valgus Moment	External Tibial Torque + Varus Moment	External Tibial Torque + Valgus Moment	BASE2
Input force
Impulsive compressive force, N	1457 ± 131	871 ± 89	844 ± 88	1113 ± 114	1121 ± 121	1429 ± 136
Input moments
Axial tibial torque,b N·m		27.0 ± 4.5	26.0 ± 3.4	−25.5 ± 6.0	−24.5 ± 6.3
Frontal plane moment,c N·m		−44.2 ± 4.5	42.8 ± 4.5	−56.5 ± 5.8	60.0 ± 6.2
Primary outcome
AM-ACL relative strain, %	3.8 ± 2.8	7.0 ± 3.9	7.0 ± 4.1	2.4 ± 2.5	2.4 ± 3.2	3.4 ± 2.7
Secondary outcomes
Quadriceps force, N	772 ± 133	806 ± 135	918 ± 159	835 ± 190	726 ± 150	753 ± 133
Knee flexion angle, deg	4.4 ± 1.1	5.2 ± 1.0	6.1 ± 1.0	2.6 ± 1.1	1.9 ± 1.0	4.1 ± 1.0
Anterior tibial translation, mm	1.6 ± 0.7	4.4 ± 1.6	4.5 ± 1.7	1.0 ± 0.9	1.0 ± 0.9	1.6 ± 0.6
Axial tibial rotation,b deg	2.7 ± 1.1	13.5 ± 2.6	13.3 ± 2.2	−15.3 ± 3.6	−15.0 ± 4.2	2.4 ± 0.8
Frontal plane angle,b deg	0.9 ± 0.5	2.2 ± 1.3	2.6 ± 1.5	−3.1 ± 1.6	−3.0 ± 1.5	0.8 ± 0.5

^aACL, anterior cruciate ligament; AM, anteromedial bundle; BASE1 and BASE2, 2 baseline trial blocks.

^bPositive value represents internal tibial torque or rotation.

^cPositive value represents knee valgus moment or angle.

Effect of Model-Predicted Interaction Between Frontal Plane Moments and Axial Tibial Torques on AM-ACL Relative Strain

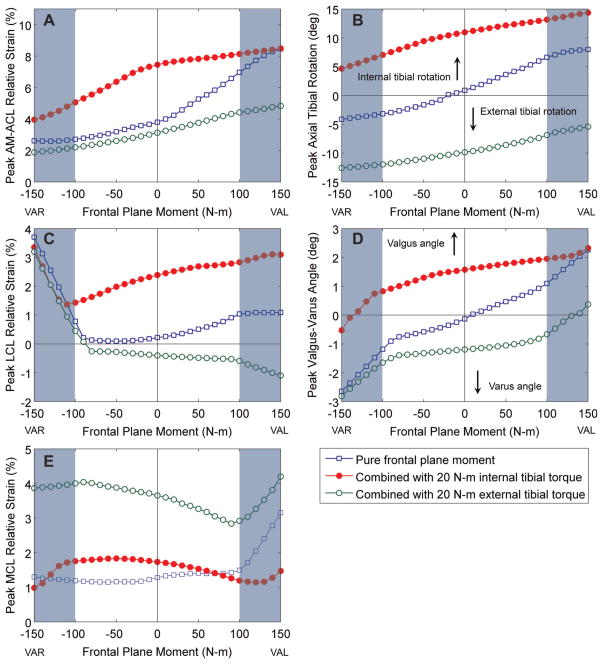
The model AM-ACL relative strain increased when the frontal plane moment was combined with a 20 N·m internal tibial torque (Figure 4). As the knee valgus moment was increased, the model AM-ACL relative strain tended to increase, whereas the AM-ACL strain decreased as the varus moment increased. A knee valgus and varus moment resulted in coupled internal and external tibial rotations, respectively. A medial or lateral knee joint opening only occurred when the knee varus or valgus moment exceeded approximately ±100 N·m, respectively. The model LCL or MCL relative strain increased markedly when the lateral or medial joint opening occurred.

Figure 4.

Model-predicted effect of the frontal plane moment on the peak AM-ACL relative strain, peak LCL and MCL relative strain, peak axial tibial rotation, and peak knee valgus-varus angle. The positive frontal plane moment values represent the knee valgus moment (VAL), whereas the negative frontal plane moment values represent the knee varus moment (VAR). The shaded area indicates the range of the frontal plane moment where the medial or lateral joint opening occurred. ACL, anterior cruciate ligament bundle; AM, anteromedial bundle; LCL, lateral collateral ligament; MCL, medial collateral ligament. insights into AM-ACL behavior under the different loading conditions.

DISCUSSION

This study was designed to investigate the effect of axial tibial torque combined with a knee varus or valgus moment on peak AM-ACL relative strain under dynamic loading conditions simulating a realistic pivot landing.^41,48 As the baseline loading condition, each cadaveric knee, with its static transknee muscle forces holding it slightly flexed, was tested with an impulsive compressive force of 2 times body weight and a standardized resultant flexion moment. Then, in the experimental trials, an impulsive axial tibial torque combined with a frontal plane moment was added so as to investigate the relative effect of the combined loading on the AM-ACL relative strain. In addition, to better interpret the experimental results, and to further investigate the effect of the combined loading on ACL strain, the 3D dynamic knee model was built and validated by replicating the in vitro experiment. Our in vitro study reports a new finding that peak AM-ACL strain was most sensitive to the direction of axial tibial torque but less sensitive to the direction of the frontal plane moment. The knee model simulation clearly showed similar behavior in that a knee valgus moment increases the ACL strain by generating a coupled internal tibial rotation before medial joint space opening can occur.

Relative Insensitivity of ACL Strain to Frontal Plane Moments

The experimental results show that the direction of the frontal plane moment did not significantly affect peak AM-ACL relative strain when the axial tibial torque was simultaneously applied. The model simulation results support these experimental findings. Over the range of the frontal plane moments applied in the in vitro experiment (ie, ±50 N·m), the change in the AM-ACL strain predicted by the model simulation was less than 1.5%, which is less than the SD of the AM-ACL relative strain measured (cf, Table 3 vs Figure 4A). On the contrary, the model simulation corroborated the findings of Withrow et al⁵⁸ that the AM-ACL strain significantly increased when the knee valgus moment was solely combined with the impulsive compressive force and flexion moment, in the absence of axial tibial torque (pure frontal plane moment in Figure 4A). It is worth noting that although a knee valgus moment contributes to an increased ACL strain, the model simulation suggests that the knee valgus moment would have to be 3 times as large as the internal tibial torque required to cause ~8.5% AM-ACL relative strain (cf, Figure 4A vs Appendix 4A, available online). Overall, the results from both our in vitro experiment and model simulation suggest that knee valgus loading has a second order of effect on ACL strain. This can be explained by the inherent mechanical coupling between internal tibial rotation and knee valgus angulation as discussed in the next paragraph.

The Role of Mechanical Coupling Between Valgus Loading and Internal Tibial Rotation

Mechanical coupling between internal tibial rotation and knee abduction has been observed in many previous studies.^38,39 Recently, Simon et al⁴⁹ provided a clear insight into the coupled motion: A steeper posterior slope of the lateral tibial plateau, compared with the medial tibial plateau, causes the lateral femoral condyle to slide posteriorly off the tibial plateau more than the medial femoral condyle does under an axial compressive force; this increases the internal tibial rotation. Taking this one step further, we can expect that the knee valgus angle should also increase during the same motion (please see Appendix 5, available online). This concept is supported by an in vivo study by McLean et al,²⁷ who found that during a dynamic single-leg land-and-cut task, both the peak knee valgus angle and peak internal tibial rotation were significantly correlated to the ratio between the medial and lateral tibial slope, where the ratio was dominated by the lateral tibial slope. In our in vitro experiment, the insensitivity of the peak AM-ACL strain to the frontal plane moments could be because the internal tibial rotation that resulted from the applied internal tibial torque predominated compared with the increased or decreased internal tibial rotation caused by the applied knee valgus or varus moment, respectively. Furthermore, considering that femoral condylar liftoff would not occur until the frontal plane moment exceeds a certain threshold and that the threshold would increase as transknee forces increase,²⁴ our results help explain how isolated ACL injuries can occur without MCL injuries (Figure 4). Our study suggests that an internal tibial rotation induced by an internal tibial torque plays a primary role in increasing the ACL strain and that a knee valgus moment increases the ACL strain by augmenting internal tibial rotation until a medial joint opening occurs (please see Appendix 5, available online).

Study Limitations

This study has several limitations. First, to limit the number of test cycles undergone by each specimen, we only conducted tests at 1 initial knee flexion angle (15°). But this angle was chosen because Li et al²⁰ reported ACL strain to be highest with the knee in 15° of flexion. A second limitation is that only a single set of muscle-tendon pretensions was tested. Following our previous studies,^35,36,58,59 the pretension values of the muscle-tendon units were chosen to achieve a static equilibrium state maintaining 15° knee flexion angle before the impact. A third limitation was that we tested male knee specimens, so our results cannot be generalized to females. Although it is known that the female ACL would rupture in response to relatively smaller external loads compared with the male ACL,³² we do not expect the qualitative results would change had we used female specimens. Other limitations include the fact that we could not measure absolute strain in the ACL but instead relied on relative strain.^58,59 None of these limitations alters the qualitative results that we found.

Finally, a number of standard assumptions and simplifications had to be made to develop the simulation model. Because the knee model was not subject specific, the effect of knee morphological variations is not known. The bilinear viscoelastic soft tissue behaviors for ligament and muscle-tendon units were adapted from the literature. The initial strains for the MCL, LCL, and joint capsular fibers were set close to zero when the knee joint was loaded at 15° flexion before impact. Despite these assumptions, we believe that knee model simulations provide valuable

Clinical Relevance

Basic biomechanical principles inform us that the maximum internal tibial torque that can be applied to the knee is limited by the coefficient of friction between shoe and playing surface. The higher that coefficient, the larger the torque can be. It is known that higher shoe-playing surface friction is associated with a greater risk of ACL injury.^6–8,40 Neuromuscular injury prevention programs are helpful in reducing the risk that dangerous maneuvers are used during play. However, the neuromuscular delay needed to volitionally develop a higher level of transknee forces⁵³ may render such responses too slow to protect the knee during the first phase of a pivot landing. Then, the magnitude of internal tibial torque will directly depend on the lateral foot-ground reaction shear force that arises from shoe-surface friction, especially given the low moment of inertia of the shank about its long axis and the mechanical coupling due to tibial slopes. Therefore, in sports associated with ACL injuries, one might consider limiting the magnitude of the dynamic coefficient of friction between shoe and playing surface for athletes of a given age and gender.