Alignment of sources and detectors on breast surface for noncontact diffuse correlation tomography of breast tumors

Abstract

Noncontact diffuse correlation tomography (ncDCT) is an emerging technology for 3D imaging of deep tissue blood flow distribution without distorting hemodynamic properties. To adapt the ncDCT for imaging in vivo breast tumors, we designed a motorized ncDCT probe to scan over the breast surface. A computer-aided design (CAD)-based approach was proposed to create solid volume mesh from arbitrary breast surface obtained by a commercial 3D camera. The sources and detectors of ncDCT were aligned on the breast surface through ray tracing to mimic the ncDCT scanning with CAD software. The generated breast volume mesh along with the boundary data of ncDCT at the aligned source and detector pairs were used for finite-element-method-based flow image reconstruction. We evaluated the accuracy of source alignments on mannequin and human breasts; largest alignment errors were less than 10% in both tangential and radial directions of scanning. The impact of alignment errors (assigned 10%) on the tumor reconstruction was estimated using computer simulations. The deviations of simulated tumor location and blood flow contrast resulted from the alignment errors were 0.77 mm (less than the node distance of 1 mm) and 1%, respectively, which result in minor impact on flow image reconstruction. Finally, a case study on a human breast tumor was conducted and a tumor-to-normal flow contrast was reconstructed, demonstrating the feasibility of ncDCT in clinical application.

1. Introduction

The altered tissue hemodynamics and metabolism in tumor pathogenesis have been well documented. It has been noted that the autonomic growth and spread of malignant tumors are partially dependent on increased angiogenesis arising from the increased metabolic demand [1–3]. Previous studies in breast cancer reported that hypermetabolism and increased angiogenesis were linked to increased blood flow, total hemoglobin concentration, and tissue metabolism [4–10]. For example, positron emission tomography showed significant tumor-to-normal tissue blood flow contrasts in breasts up to fivefold higher [4]. In carcinomas compared to benign lesions, flow velocities in large arteries adjacent to tumors acquired by Doppler ultrasound were significantly higher by up to threefold [9]. Thus, the functional imaging of tumor hemodynamics/metabolism is an exciting new strategy and provides a more finely grained and individualized understanding of cancer pathophysiology and treatment [11,12].

Near-infrared (NIR) diffuse optical spectroscopy/tomography (DOS/DOT) is a noninvasive, portable, and relatively inexpensive tool for functional imaging of deep tumor oxygenation [6–8,13–15]. NIR diffuse correlation spectroscopy/tomography (DCS/DCT) has also been developed more recently, which is capable of imaging blood flow distributions in deep tissues [16–23]. Most of these diffuse optical techniques deliver and receive NIR light using optical fibers placed on top of the tissue surface. These contact-based approaches may be disadvantaged for in vivo measurements due to the distortion of tissue hemo-dynamics resulted from the compression of probe contact on soft tissues with irregular boundaries. To overcome this limitation, our laboratory has recently developed a noncontact DCS/DCT (ncDCS/ncDCT) system for three-dimensional (3D) imaging of human tissue blood flow distribution without probe–tissue contact [24–26]. A finite element method (FEM) [27,28] based framework was also established facilitating ncDCT image reconstruction for tissues with arbitrary geometries [26].

This ncDCT system has been tested in tissue-like liquid phantoms with a simple semi-infinite geometry [26]. During the test, a motorized linear stage was employed to carry out ncDCT probe scanning over the flat surface of liquid phantoms. However, when applying the ncDCT system for in vivo investigations, the system must be modified to adapt to complex tissue boundaries. The goal of this study was to adapt the ncDCT system for the use of tumor detection in human breasts. For this purpose, we designed a motorized rotational stage to scan over the breast tissue and used a commercial 3D camera (NextEngine, California, USA) to obtain breast surface geometry. Several challenges exist when inputting the geometrical information to the FEM-based image reconstruction of ncDCT. First, the breast surface contour mesh generated by the 3D camera must be extended to a solid volume mesh to include the tissue volume imaged. Second, because the data from the 3D camera and ncDCT were collected in different coordinate systems, coregistration of the two coordinates is necessary. Finally, the projected sources and detectors of ncDCT (several hundreds of pairs) on the breast surface must be precisely aligned on the surface of solid mesh for the accomplishment of image reconstruction.

Computer-aided design (CAD) is a powerful tool for 2D and 3D solid modeling and coordinate transformation, and has been increasingly applied in the biomedical field [29,30]. The application programming interface (API) has been recently introduced to CAD software (e.g., SolidWorks, Dassault Systemes, Massachusetts, USA), which allows to access and control CAD software easily. In this study, we proposed a CAD-based approach to create the solid volume mesh from the surface contour mesh (generated by a 3D camera), to coregister the data obtained from the 3D camera and ncDCT, and finally to align the sources and detectors of ncDCT on the surface of the solid breast model. We then evaluated the accuracy of source alignment on the breast surface as well as the influence of alignment errors on flow image reconstruction of breast tumor. This approach lays the groundwork of ncDCT for in vivo imaging of spatial blood flow distribution in breast tissues.

2. Methods and Materials

A. Motorized Rotational Probe for ncDCT

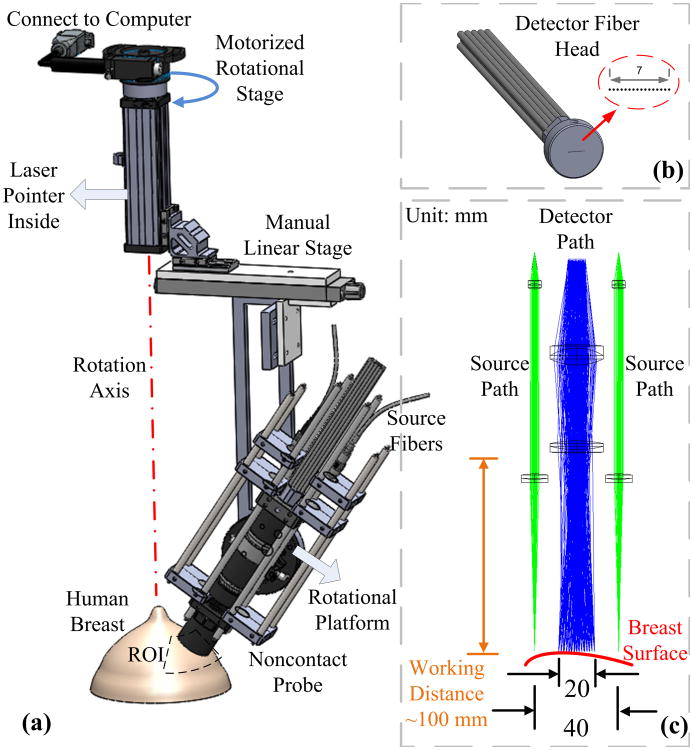
Details about ncDCT can be found elsewhere [26]. Figure 1 shows the rotational probe design of ncDCT for the imaging of tissue blood flow distribution in human breast. Two source fibers (WF200/220/245, CeramOptec, Massachusetts, USA) connected to two long-coherence lasers (785 nm, CrystaLaser, Nevada, USA) were projected alternatively onto the breast surface through achromatic lenses [Fig. 1(c)]. The detector fiber bundle [Fig. 1(b)] consisted of 15 single-mode fibers (SM800-5.6-125, Fibercore, California, USA), which were equally arranged in a 7 mm line to cover a 20 mm range through the magnification of lenses. A long-pass filter with a cutoff wavelength of 750 nm (FEL0750, Thorlabs, New Jersey, USA) was set in the detector path to reduce the influence of ambient light.

Fig. 1.

Schematic diagram of ncDCT rotational scanning system. (a) A motorized rotational stage was used to scan over a representative ROI on the breast. A laser pointer was used to align the rotation axis approximately through the nipple. The relative position between the ncDCT probe and ROI (i.e., working distance, initial step of scanning) can be adjusted manually by the linear stage and the rotational platform. (b) Fifteen single-mode detector fibers were equally arranged in a 7 mm line to cover a 20 mm range through the magnification of lenses. (c) The source and detector fibers were projected on the breast surface using achromatic lenses. Two source paths were attached to the sides of the detector path.

The probe head was adjusted to focus the source and detector fiber tips on the breast surface. Photons emitted from the lasers were injected alternatively through the two source paths into the tissue sample. Photons transported/scattered through the sample were eventually collected through the detection path by a linear detector array of 15 avalanche photodiodes (APDs, Perkin Elmer, Canada). The distance between the two projected sources was 40 mm and the resulting source-detector (S-D) separations were in the span of 10 to 30 mm [Fig. 1(c)]. A multichannel autocorrelator (Correlator.com, New Jersey, USA) took the 15 APD outputs and calculated the light intensity autocorrelation functions to extract blood flow index. A linear stage (5236A16, McMaster-Carr, Illinois, USA) and a custom-made rotational platform were used to manually align the line-shape probe at the initial scanning position of a selected region of interest (ROI) and approximately parallel to the breast tissue surface [Fig. 1(a)]. A motorized rotational stage (CR1-Z7, Thorlabs, New Jersey, USA) was used to drive the ncDCT probe, scanning over the ROI.

B. Scanning Procedure over Breast Tissue Surface

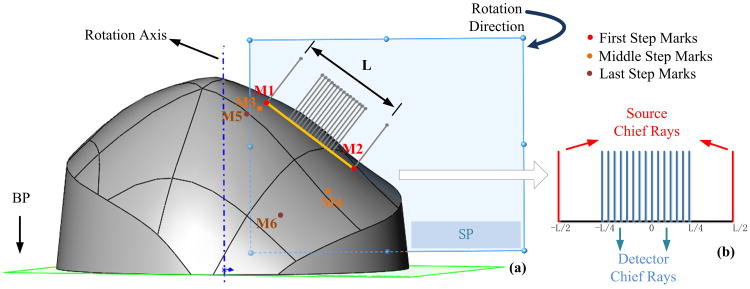
A breast model of a plastic mannequin placed on a bed was first used to explore the feasibility of the scanning protocol over the breast. A laser pointer inside the rotation arm was used to align the rotation axis approximately through the nipple [Fig. 1(a)]. The optical probe was then adjusted to make the two source chief rays approximately perpendicular to the surface of the mannequin breast. The probe scanned 60 deg over a ROI through 21 steps with a 3-deg increment per step. Total scanning time was ∼25 min with 60 s sampling time per step at 1 Hz sampling rate for each DCS laser source. The projected source pairs at the 1st, 11th, and 21st steps, as well as the rotation center, were visually marked on the breast surface using a marker pen.

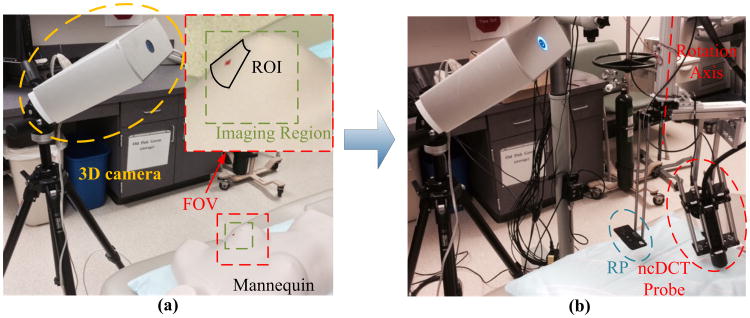
After ncDCT probe scanning, the breast surface with marks was imaged by the 3D camera [Fig. 2(a)]. The camera operated at a working distance of ∼17 in:, and with a field of view (FOV) of 10 in: × 13 in: [see the inset in Fig. 2(a)] and an acquisition time of ∼2 min. The mannequin was then removed from the bed and a small foam pad perpendicular to the rotation axis was attached to the DCS scanner [Fig. 2(b)]. The 3D camera took another image to include the small foam pad as a reference plane (RP), which was used for the coregistration of two coordinate systems: 3D camera and ncDCT. Note that the 3D camera was kept at the exact same position/location when taking the two images [Figs. 2(a) and 2(b)].

Fig. 2.

3D camera to obtain surface images of the breast and reference plane (RP). (a) The breast surface with source marks was imaged by the 3D camera. An “imaging region” (∼5″ × 5″), displayed in the inset, was selected inside the FOV for generating the solid breast model (see Fig. 3). (b) After the mannequin was removed, a small foam pad was attached to the DCS scanner. The 3D camera took another image to include the small foam pad whose surface (RP) was adjusted perpendicularly to the rotation axis. The RP was used for the coregistration of two coordinate systems: 3D camera and ncDCT.

After the feasibility test in the mannequin breast model, we used a similar but simplified protocol to scan over a ROI on a realistic human breast. A 22-year-old female subject who had a fibroadenoma (benign tumor with no evidence of malignancy) in the breast volunteered to participate in this study after written consent in accordance with approval of the Institutional Review Board at the University of Kentucky. The subject lay supine on the bed comfortably and her body was fixed on the bed using soft form pads and pillows to reduce potential body motion artifacts during measurements. The tumor location was determined by ultrasound imaging, and the tumor mass margin along the longitudinal and latitudinal directions was marked on the ultrasound image. The ncDCT probe then scanned 60 deg over a ROI throughout 16 scanning steps with a 4-deg increment per step. This simplified protocol reduced the scanning time to ∼17 min. Consequently, six marks of three source pairs were made at the 1st, 8th, and 16th steps. Following ncDCT scanning, in situ breast tissue optical properties (i.e., reduced scattering coefficient ${\mu }_s^{\prime }$, and absorption coefficient μ_a) were measured at three different locations by a commercial frequency-domain tissue oximeter (Imagent, ISS, Illinois, USA). The averaged ${\mu }_s^{\prime }$ and μ_a over multiple sites were used as initial inputs for flow image reconstruction. Finally, 3D camera scanning procedures were performed identically to those used in the mannequin breast model as described above. The total measurement time in the clinical room was ∼25 min.

C. Solid Modeling of Breast Tissue Volume

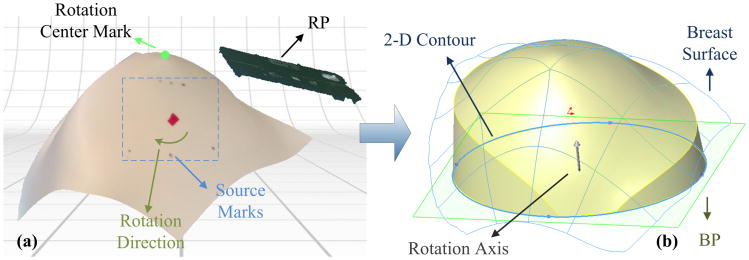
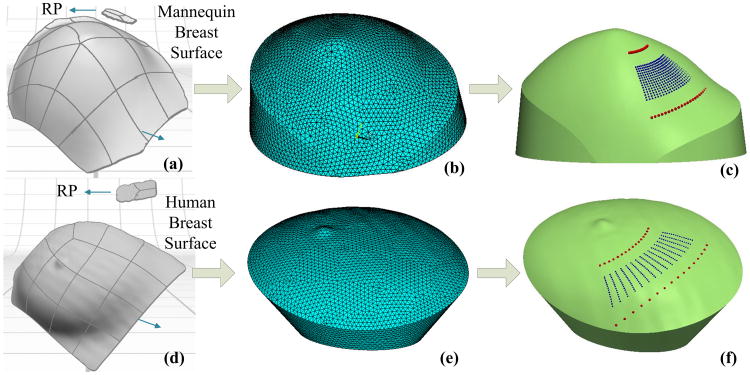
For 3D flow image reconstructions, a solid breast model/mesh including the tissue volumes to be imaged is required. Figure 3 illustrates the procedure to convert the mannequin (or human) breast surface image acquired by the 3D camera to a solid volume model. The 3D camera control software (ScanStudio HD, NextEngine, California, USA) generated a 3D surface mesh with three pairs of source marks and a rotation center mark [Fig. 3(a)]. The RP is also displayed in the figure. A nonuniform rational basis spline (NURBS) continuous surface was extracted by autofitting the nodes of the surface mesh. We then created a bottom plane (BP) parallel to the RP. The distance between the BP and the rotation center point was set as 50 mm. Finally, a solid breast model was generated by extruding a 2D circular contour on the BP along the rotation axis to the breast surface [Fig. 3(b)]. This solid breast model including the marked ROI was eventually used to generate a 3D tissue volume mesh for flow image reconstruction. The volume of the solid breast model was determined by the area of 2D circular contour, the angle of the extruding, and the distance between the BP and the rotation center point. These parameters should be selected individually to ensure photons being diffused sufficiently inside a relatively large tissue volume [31]. On the other hand, the tissue volume should be minimized to reduce the calculation burden for image reconstruction.

Fig. 3.

Procedures converting the acquired breast surface to a solid breast model. (a) The mannequin breast surface with source marks and the reference plane (RP) were integrated into one image. The three pairs of source marks and the rotation center mark can be clearly seen. (b) A bottom plane (BP) parallel to the RP was created and a 3D solid breast model was then generated by extruding the 2D contour on BP along the rotation axis to the 3D breast surface.

D. Coregistration of the Solid Breast Model and ncDCT Coordinate Systems

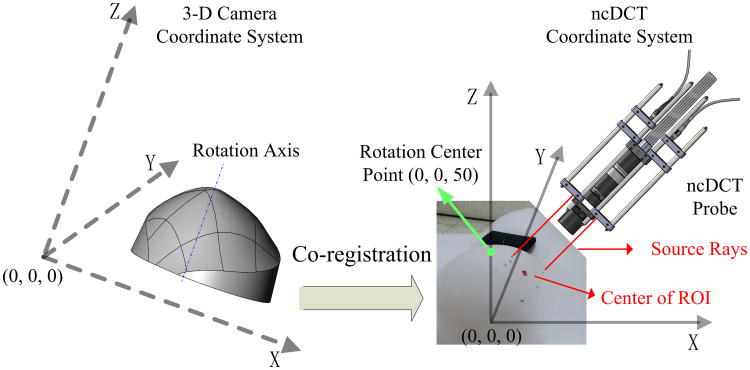
The breast surface imaging and ncDCT scanning were originally implemented in different coordinate systems (Fig. 4). For the coregistration of the two systems, we defined the x–y plane of the ncDCT coordinate system at the BP and z-axis along the rotation axis of the ncDCT. The coordinate of the rotation center was thus at (0, 0, 50 mm). The initial scanning position of the ncDCT linear array was aligned to the ncDCT system by adjusting the two source rays through the source marks made at the first step (see details in Section 2.E). This coregistration procedure allowed us to place the solid breast model into the ncDCT coordinate.

Fig. 4.

Coregistration procedures to place the solid breast model obtained in 3D camera coordinate system (left) into the ncDCT coordinate system (right). The rotation center of the ncDCT probe obtained by the 3D camera (left) was placed at (0, 0, 50 mm) in the ncDCT coordinate system (right).

E. Alignment of Sources and Detectors on the Surface of the Solid Breast Model

For FEM-based ncDCT image reconstructions, sources and detectors must be projected on the breast tissue surface. We employed the CAD method operated by API to define a scanning plane (SP) perpendicular to the BP and passing through the initial pair of source marks [M1 and M2, Fig. 5(a)] and to mimic the probe scanning procedure over the breast surface. Each source or detector path in the SP was simplified as a single chief optical ray [Fig. 5(b)] perpendicular to a crossing straight line (M1 to M2). The two sources were located at −L/2 and L/2 along the crossing line of length L and the 15 detectors spanned in the range of −L/4 to L/4. We then projected the sources and detectors along the chief optical rays onto the surface of the solid breast model. The projected points of intersection on the breast surface represented the aligned sources and detectors at the initial scanning step. The SP with source and detector rays was repeatedly rotated around the rotation axis for projecting sources and detectors at all scanning steps onto the surface of the solid breast model.

Fig. 5.

Alignment of sources and detectors on the surface of the solid breast model. (a) A scanning plane (SP) perpendicular to the BP and crossing the optical rays of sources and detectors was first aligned to pass through the initial pair of source marks (M1 and M2). (b) Each source or detector path was then simplified as a single chief optical ray perpendicular to the straight line connecting the source marks (M1 to M2). The sources and detectors along the chief optical rays were then projected onto the surface of the solid breast model. The SP was next rotated around the rotation axis step-by-step with a 3-deg increment per step for projecting sources and detectors at all scanning steps.

F. Evaluation of Source Alignment Errors

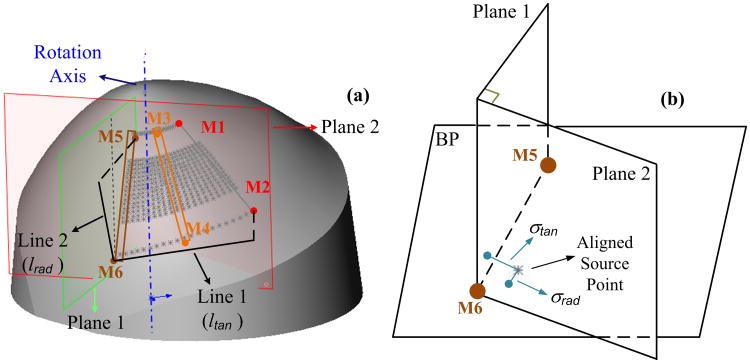
To characterize the alignment errors at different scanning steps, we quantified the distance from the aligned source points to the corresponding source marks. The absolute alignment error (σ: mm) was measured by the distance between the aligned and marked source points. The relative alignment errors were evaluated along the radial (γ_rad) and tangential (γ_tan) directions of the rotation by calculating the ratios of radial and tangential distance deviations (σ_rad and σ_tan) to the measured radial and tangential distances (l_rad and l_tan), respectively:

$${\gamma }_{tan}=\frac{{\sigma }_{tan}}{l_{tan}}\times 100\%;{\gamma }_{\text{rad}}=\frac{{\sigma }_{rad}}{l_{rad}}\times 100\%.$$

Figure 6 demonstrates how to quantify the relative alignment errors at the source mark M6. Briefly, two planes (Plane 1 and Plane 2) were set up to be perpendicular to the BP. Plane 1 crossed the mark pair of M5 and M6 along the radial direction while Plane 2 was crossing M6 and perpendicular to Plane 1 along the tangential direction. σ_tan and σ_rad were the distances from the aligned source (nearby M6) to the two planes, respectively. l_rad and l_tan were the projected distances on the BP from M6 to M5 and from M6 to M2, respectively.

Fig. 6.

Characterization of source alignment errors at different scanning steps. (a) The projected source close to M6 is used for demonstration. Line 1 and Line 2 are perpendicular projections of M6-M2 and M6-M5 on the BP, respectively. The lengths of Line 1 and Line 2 are defined as l_tan and l_rad, respectively. Plane 1 crosses M5 and M6 while Plane 2 crosses M6 and is perpendicular to Plane 1. Both Plane 1 and Plane 2 are perpendicular to the BP. (b) σ_tan and σ_rad are the distances between the aligned and marked source points along tangential and radial directions, respectively, which can be measured by the distances from the aligned source point to the Plane 1 and Plane 2, respectively.

G. FEM-Based Flow Image Reconstruction of ncDCT

Details about the FEM-based forward and inverse solutions of ncDCT for blood flow imaging reconstruction can be found in our recent publications [26]. Briefly, the facilitation of DCT image reconstruction is accomplished through integration into an open software package for FEM-based DOT termed NIRFAST [27,28]. Exploiting the high mathematical similarity of the forward/inverse problems (e.g., boundary condition and mathematical assumptions) between DOT and DCT, we introduce a “dynamic absorption” of correlation with delay time due to dynamic processes of moving scatterers (primarily red blood cells). DCT can then be conceptualized as a modified formulation of DOT, which computes autocorrelation function instead of photon fluence rate. For computer simulations, the autocorrelation function can be generated using multiple delay times (e.g., 60 τ was used in this study) in the forward solution. For imaging reconstruction, the blood flow distribution can be extracted using the measured boundary data at multiple S-D pairs in the inverse solution.

3. Results

A. Solid Models with Aligned Sources and Detectors

The mannequin breast model and the human breast were used to demonstrate the CAD-based approach described earlier. Figures 7(a)–7(c) illustrate the modeling procedures and results obtained from the mannequin breast model. The 3D NURBS surface image [Fig. 7(a)] was transformed to the solid volume mesh by ANSYS (ANSYS, Pennsylvania, USA) with an average node distance of 2 mm [Fig. 7(b)]. The sources and detectors were then aligned on the surface of volume mesh [Fig. 7(c)]. Similarly, Figs. 7(d)–7(f) illustrate the modeling procedures and results obtained from an in vivo human breast. The resulting volume meshes [Figs. 7(c) and 7(f)] with sources and detectors aligned on their surfaces can be input into NIRFAST [27,28] for ncDCT image reconstructions [26].

Fig. 7.

Modeling procedures and results of solid breast meshes with the sources and detectors aligned on the mannequin (upper panel) and human (bottom panel) breasts. The images of mannequin (a) and human (d) breast surfaces and corresponding reference planes were obtained by the 3D camera. The 3D solid breast models were generated by extruding the 2D circular contours on BP along the rotation axis to the breast surfaces. The breast volume meshes [(b) and (e)] were then created from the 3D solid breast models. Finally, the sources and detectors were aligned on the surfaces of solid volume meshes [(c) and (f)].

B. Source Alignment Errors

Table 1 summarizes the measured radial and tangential distances (l_rad and l_tan) at different source marks as well as corresponding absolute and relative alignment errors of the sources on the surfaces of mannequin and human breast. For both cases, the absolute errors (σ) increased with the increase of scanning step, which is expected as the alignment was calibrated on the first pair of source marks (M1 and M2). On average, the absolute error observed in the human breast (σ = 2.64 ± 1.65 mm) was larger than that in the mannequin breast (σ = 0.79 ± 0.50 mm). The mean relative error in the tangential direction (γ_tan = 4.56 ± 2.18%) was larger than that in the radial direction (γ_rad = 2.43 ± 1.17%), indicating the major contribution of tangential errors to the alignment errors. Similarly to the absolute errors, γ_tan increased with the increase of scanning step and its mean value in the human breast (5.63 ± 2.44%) was larger than that in the mannequin breast (3.50 ± 1.48%).

Table 1. Absolute and Relative Alignment Errors between the Projected Sources and the Original Source Marks on the Mannequin and Human Breasts.

Case	Marks	σ(mm)	σtan (mm)	ltan (mm)	γtan(%)	σrad (mm)	lrad (mm)	γrad(%)
Mannequin	M3	1.34	0.23	9.24	2.48	1.06	35.33	3.00
	M4	1.25	0.64	23.87	2.68	0.75		2.12
	M5	1.79	0.84	14.79	5.67	1.04	32.46	3.20
	M6	2.56	1.43	45.03	3.17	1.09		3.35
Human	M3	1.11	0.90	22.38	4.02	0.52	39.20	1.32
	M4	2.28	1.56	39.80	3.92	1.64		4.18
	M5	4.20	3.83	41.96	9.13	0.32	34.61	0.92
	M6	6.26	4.26	78.27	5.44	0.46		1.33

C. Impact of Source and Detector Alignment Errors on Flow Image Reconstruction

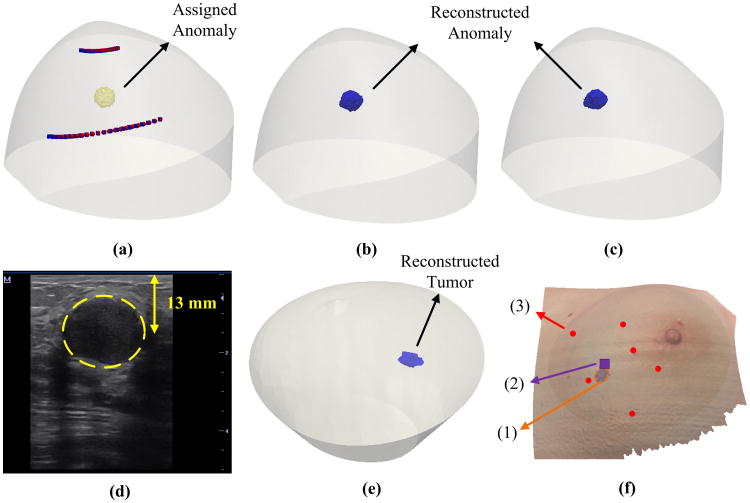
In order to evaluate the impact of alignment errors on imaging reconstruction of blood flow contrast, computer simulations were conducted on the mannequin breast [Fig. 8(a)]. A sphere anomaly with a radius of 5 mm was assigned to be 8 mm beneath the surface of the breast to mimic a breast tumor. A solid mesh was created with 4 mm node distance and was refined to 1 mm node around the known anomaly region (∼20 mm radius) to improve detection resolution while not overwhelmingly increasing the number of nodes. For simplicity, optical properties for both anomaly and background were set throughout the tissue at μ_a = 0.06 cm⁻¹ and ${\mu }_s^{\prime }=6{\text{cm}}^{-1}$. The flow indices for background and anomaly were set as 1 × 10⁻⁸ cm²/s and 5 × 10⁻⁸ cm²/s, respectively, resulting in a relative flow contrast (rBF) of fivefold between the anomaly (tumor) and surrounding nodes (healthy tissues). We then assigned alignment errors of 10% in the rotation angles (i.e., 3.3° instead of 3°) for all sources and detectors at all scanning steps. For example, the source alignment errors at M5 and M6 were: γ_tan = 10.55%; γ_rad = 2.04% and γ_tan = 9.85%; γ_rad = 4.93%, respectively. The levels of these errors are consistent with our experimental results shown in Table 1. The impact of alignment errors on the tumor location and blood flow contrast was evaluated by comparing the reconstructed results with and without alignment errors.

Fig. 8.

Image reconstruction results from computer simulations (upper panel) and the human breast (bottom panel). (a) A breast mesh with an assigned sphere anomaly (radius = 5 mm) at the center of the ROI and 8 mm beneath the surface of the mannequin breast. The red and blue dots represent the sources without and with alignment errors, respectively. The detectors are not shown for clarity. (b) Reconstructed anomaly using the sources and detectors without alignment errors. (c) Reconstructed anomaly using the sources and detectors with assigned alignment errors. (d) Ultrasound image of breast tumor (inside the dashed circle area) in the human subject. (e) Reconstructed human breast tumor using the solid breast mesh with the sources and detectors aligned on the human breast [see Fig. 7(f)]. (f) Comparison of tumor locations determined by ncDCT and ultrasound imaging on x–y plane: (1) the reconstructed tumor is projected on the breast surface, (2) the central location of the tumor determined by the ultrasound probe, and (3) source marks of ncDCT scanning.

Figures 8(b) and 8(c) show the reconstructed anomaly using the sources and detectors without and with alignment errors, respectively. The reconstructed anomaly centers deviated 1.30 mm (without alignment errors) and 2.07 mm (with alignment errors) from the assigned original coordinate [Fig. 8(a)], respectively. The shift of the anomaly central location (0.77 mm) was less than the node distance (1 mm). When using a full width half-maximum (FWHM) threshold to segment the anomaly [32], the mean values of reconstructed flow contrasts were 5.63-fold and 5.68-fold, respectively. Thus, the deviation of average rBF contrasts caused by alignment errors was less than 1%.

D. In Vivo Breast Tumor Reconstruction Using ncDCT

Figure 8(e) shows the reconstructed 3D flow contrast image of tumor inside the patient's breast using the FWHM threshold to segment the tumor. The central depth and dimension of the reconstructed tumor were 9.7 mm and 16.9 mm × 15.5 mm, respectively. The measured μ_a and ${\mu }_s^{\prime }$ of the breast tissue using the Imagent were 0.04 cm⁻¹ and 7.8 cm⁻¹, respectively, which were used as inputs for flow image reconstruction. The peak and averaged tumor-to-normal blood flow contrasts were 16.2-fold and 11.3-fold, respectively. The ultrasound image [Fig. 8(d)] shows a tumor with the dimension of 19.0 mm × 18.3 mm at the central depth of 13.0 mm beneath the breast surface. Figure 8(f) shows the reconstructed tumor projected on the surface of the breast, which agrees with the tumor location on the x–y plane determined by the ultrasound image.

4. Discussion and Conclusions

Most DCT measurements used optical fibers in contact with tissues for photon emission/collection and required tissues to conform to simple boundaries such as a slab. The compression on the tissue may introduce distortions in tissue hemodynamics [33]. An obvious solution to this problem is to place the sources and detectors away from the interface, allowing for the non-contact imaging of arbitrary boundaries. We have recently developed a noncontact DCT system and have demonstrated its feasibility for 3D imaging of flow contrasts in tissue phantoms with a simple flat surface [26]. Our ultimate goal is to translate this ncDCT system from benchtop to clinics for imaging of in vivo tissues with complex geometries such as human breasts. This paper reports a critical step toward the translation of the ncDCT system for in vivo imaging of breast tumors.

Currently, a variety of methods exist for obtaining irregular tissue geometries. Previous studies for DOT have used magnetic resonance imaging (MRI) [28,34,35] and computer tomography (CT) [36] to obtain solid volume meshes for imaging reconstruction. Hybrid systems combining DOT and MRI have also been reported recently [37–40]. However, the high cost, large instrumentation, and poor mobility of MRI or CT are major limiting factors for their frequent use in clinic. Only a few studies used 3D cameras to generate tissue surface geometries for DOT. For example, Dehghani et al. employed a 3D camera to scan over human breast surface before placing the source and detector fibers on its surface [41]. Obvious deformation of breast tissues was observed after placing the optical fibers for the contact DOT measurements. Previous fluorescence tomography studies in small animals (mouse or rat) used a 3D camera or CCD camera to acquire animal surface geometry, where the animals were either fixed in a small chamber [42,43] or rotated over 360 deg [44,45]. However, translation of these methods from small animals to humans is not straightforward since many constraining factors associated with human subjects must be considered, such as safety, flexibility, and comfort.

Our study utilized a 3D camera to obtain the surface geometry of the breast. The 3D camera can be placed at the bedside close to the subject, which makes the operation flexible in clinical rooms. The fully noncontact measurements by both 3D camera and ncDCT guarantee subject safety and comfort. The CAD-based approach with API allows us to convert the 3D surface profile to the 3D solid model, coregister the two coordinate systems (i.e., 3D camera and ncDCT), and align automatically the sources and detectors of ncDCT on the surface of the solid breast model.

Most of previous studies used a software such as Netgen [28], iso2mesh [46], or Matlab [43] to generate a volume mesh from the surface mesh obtained by a 3D camera [47] or CCD [44]. The source and detector locations on the surface of volume mesh were determined by ray tracing on the individual surface mesh nodes. Therefore, the accuracy of S-D alignment depended on the distance and distribution of surface mesh nodes. By contrast, we aligned the sources and detectors directly on the continuous surface (NURBS), which was extracted by autofitting the nodes of the surface mesh using CAD tools (see Section 2.C). Therefore, our alignment did not rely on the surface nodes. Furthermore, the CAD-based alignment method used in this study mimicked the same scanning procedure of the ncDCT probe, thus providing an easy way to assess the performances of scanning and alignment.

The accuracy of S-D alignment on the breast model is critical as it affects the accuracy of flow image reconstruction. Note that for simplicity the alignment accuracies in this study were characterized based only on the representative sources marked at the initial, middle, and final steps. We observed in this study that maximal alignment errors over scanning steps were less than 10%; i.e., 5.67% (mannequin) and 9.13% (human) in the tangential direction, and 3.35% (mannequin) and 4.18% (human) in the radial direction (Table 1). On average, the relative errors in the tangential direction were larger than those in the radial direction for both mannequin and human breasts, and the tangential errors increased with the increase of scanning step. These are expected since any imprecision of mechanically rotational scanning by the ncDCT probe should result in larger tangential errors along the rotation direction compared to the radial errors. Furthermore, the tangential errors may be accumulated with the increase of scanning step. By contrast, the radial errors are generally not accumulative as the length of the rigid scanning arm is fixed. In addition, perpendicularity between the rotation axis and the breast surface may also affect the alignment accuracy. The mechanical scanning errors can be reduced by using a high-precision motorized stage and the non-perpendicularity may be corrected by using an intelligent system to adjust the scanning axis based on a dynamic scanning of breast surface geometry.

It is also not surprising that the tangential errors observed in the human breast are larger than those found in the mannequin breast because some influencing factors may not be well controlled in human subjects, such as the irregular shape of a real breast as well as a subject's breathing or moving during the ncDCT measurement. However, the total averaging time of 60 s for blood flow measurement at each scanning step has greatly reduced the influence of a subject's breathing. To reduce potential motion artifacts resulted from body motion, we can re-mark source positions immediately after the body motion occurs and use difference marks for the alignment. Integration of all marked source positions for the alignment can increase the alignment accuracy, which will be the subject of our future work.

Computer simulations are commonly used to evaluate the performance of an imaging system. In this study, the impact of alignment errors on image reconstruction was determined by quantifying the deviations of central location and flow contrast of the assigned tumor inside the breast. The deviation of the reconstructed anomaly location (0.77 mm) resulting from the alignment errors was found to be smaller than the mesh node distance (1 mm) and the deviation of reconstructed flow contrast due to the alignment errors was less than 1%. Thus, the impacts of alignment errors on flow image reconstruction are ignorable.

The results from the patient with tumor demonstrate the feasibility of ncDCT in clinical use. The average tumor-to-normal blood flow contrast of 11.3-fold observed in this study is comparable to previously reported flow contrasts of 2- to 10-fold in breast tumors detected by DCS [10,48], noticing that tumor blood flow contrasts quantified by DCS may be underestimated due to the partial volume effect. In addition, the potential cross talk between μ_a, ${\mu }_s^{\prime }$, and blood flow may also result in overestimation or underestimation of blood flow contrasts [49]. When assuming homogeneous μ_a and ${\mu }_s^{\prime }$, over the entire breast, the realistic heterogeneous μ_a and ${\mu }_s^{\prime }$, over the tumor can generate errors in tumor blood flow contrast. To overcome this limitation, a separate DOT instrument enabling 3D imaging of μ_a and ${\mu }_s^{\prime }$, distributions in the breast is needed [50,51].

The reconstructed tumor central depth of 9.7 mm is slightly shorter than the ultrasound finding (13.0 mm). This is likely due to the deep location of the tumor, which is slightly beyond the sensitive depth of diffuse light detected by our current ncDCT system. Based on photon diffuse theory, the penetration depth of diffuse light is ∼1/2 of the S-D separation [49]. The largest S-D separation of current ncDCT is 30 mm, allowing for a penetration depth up to ∼15 mm. It is thus not surprising that the reconstruction errors increased as the tumor (dimension based on ultrasound image: 19.0 mm × 18.3 mm) center was located at a depth of 13 mm. In addition, noises from clinical measurements may also contribute to the reconstruction errors. For the verification, we conducted computer simulations with the same size/location of a spherical anomaly (diameter = 18 mm) as the human tumor and similar level of measurement noises. We observed that the reconstructed anomaly was located at ∼10.9 mm beneath the breast surface with a diameter of 15.1 mm (data are not shown), which fairly agreed with our in vivo measurement results (i.e., tumor central depth = 9.7 mm and dimension = 16.9 mm × 15.5 mm).

The focus of this study was to develop a CAD-based approach to align the sources and detectors of ncDCT on the surface of breast volume mesh for blood flow image reconstruction. We evaluated the accuracy of the source alignments using computer simulations and on a plastic mannequin and an in vivo human breast. Although we reported only one in vivo human case in this paper as an example, more simulations and in vivo imaging results from human breasts have been recently published by our group [52].

Theoretically, ultrasound imaging is not a part of ncDCT setup. However, given that fact that our ncDCT is the first optical imaging system providing 3D blood flow contrast distributions in breast tumors, we do need to compare our results with other standard imaging modalities (such as ultrasound photography) for validation. Also, ultrasound imaging of breast tumors helps us to determine the region of interest for ncDCT scanning. In addition, a priori knowledge of tumor location and volume can improve flow contrast reconstruction [52], which will be the subject of our future work.

In conclusion, we have developed a motorized rotational probe for ncDCT imaging of breast tissues and a CAD-based approach for the alignment of sources and detectors on the surface of solid breast models. The generated breast volume mesh along with the boundary data collected from the aligned sources and detectors can be used for FEM-based flow image reconstruction. The results indicate that relative source alignment errors on both mannequin and human breasts are less than 10% throughout all scanning steps, which result in minor impact on flow image reconstruction. The recovery of in vivo breast tumor demonstrates the feasibility of ncDCT for clinical applications. Furthermore, the ncDCT system has the potential to be used for the imaging of deep blood flow distributions in a variety of soft or vulnerable tissues (e.g., breast tumor, pressure ulcer, burned tissue).