Spectral gap optimization of order parameters for sampling complex molecular systems

Significance

Molecular-dynamics (MD) simulations have become a versatile tool for exploration of complex molecular systems. However, they are limited in the timescales that can be reached. Thus, over the years, a suite of enhanced-sampling algorithms have been proposed that assist MD to transcend the timescale limitation, with diverse applications across physical and life sciences. A continuing grand challenge in the success of many such sampling methods pertains to a judicious choice of order parameters. In this work, we propose a new method for designing order parameters that minimizes the role played by human intuition and makes the progress significantly more automated than before. We expect this algorithm to be of great use in furthering the success of enhanced sampling.

Abstract

In modern-day simulations of many-body systems, much of the computational complexity is shifted to the identification of slowly changing molecular order parameters called collective variables (CVs) or reaction coordinates. A vast array of enhanced-sampling methods are based on the identification and biasing of these low-dimensional order parameters, whose fluctuations are important in driving rare events of interest. Here, we describe a new algorithm for finding optimal low-dimensional CVs for use in enhanced-sampling biasing methods like umbrella sampling, metadynamics, and related methods, when limited prior static and dynamic information is known about the system, and a much larger set of candidate CVs is specified. The algorithm involves estimating the best combination of these candidate CVs, as quantified by a maximum path entropy estimate of the spectral gap for dynamics viewed as a function of that CV. The algorithm is called spectral gap optimization of order parameters (SGOOP). Through multiple practical examples, we show how this postprocessing procedure can lead to optimization of CV and several orders of magnitude improvement in the convergence of the free energy calculated through metadynamics, essentially giving the ability to extract useful information even from unsuccessful metadynamics runs.

With the advent of increasingly accurate force fields and powerful computers, molecular-dynamics (MD) simulations have become a ubiquitous tool for studying the static and dynamic properties of systems across disciplines. However, most realistic systems of interest are characterized by deep, multiple free-energy basins separated by high barriers. The timescales associated with escaping such barriers can be formidably high compared with what is accessible with straightforward MD even with the most powerful computing resources. Thus, to accurately characterize such landscapes with atomistic simulations, a large number of enhanced-sampling schemes have become popular, starting with the pioneering works of Torrie, Valleau, Bennett, and others (1–13). Many of these schemes involve probing the probability distribution along selected low-dimensional collective variables (CVs), either through a static preexisting bias or through a bias constructed on-the-fly, that enhances the sampling of hard-to-access but important regions in the configuration space.

The quality, reliability, and usefulness of the sampled distribution is in the end deeply dependent on the quality of the chosen CV. Specifically, one key assumption inherent in several enhanced-sampling methods is that of timescale separation (14): for efficient and accurate sampling, the chosen CV should encode all of the relevant slow dynamics in the system, and any dynamics not captured by the CV should be relatively fast. For most practical applications, there are a large number of possible CVs that could be chosen, and it is not at all obvious how to construct the best low-dimensional CV or CVs for biasing from these various possible options. Success in enhanced-sampling simulations has traditionally relied on an apt use of physical intuition to construct such low-dimensional CVs. Identification of good low-dimensional CVs is in fact useful not just for enhanced-sampling simulations such as umbrella sampling and metadynamics but also for distributed computing techniques like Markov state models (MSMs) (15), allowing one to significantly improve the quality and reliability of the constructed kinetic models. Last but not the least, having an optimal low-dimensional CV can also help in the building of Brownian dynamics-type models (16, 17). Indeed, given the importance of this problem, there exists a range of methods that have been proposed to solve it (18–25).

In this communication, we report a new and computationally efficient algorithm for designing good low-dimensional slow CVs. We suggest that the best CV is one with the maximum separation of timescales between visible slow and hidden fast processes (14, 26). This timescale separation is calculated as the spectral gap between the slow and fast eigenvalues of the transition probability matrix (see Theory for a rigorous definition and implementation of the spectral gap as used in this work). The method is named spectral gap optimization of order parameters (SGOOP). Note that, in this work, henceforth we refer to the best CV in the singular, without loss of any generality in the treatment. The notion of such a timescale separation and spectral gap is at the core of not just enhanced-sampling methods but also coarse-grained, multiscale, MSM, and projection operator methods (15, 27–29).

Our algorithm involves learning the best linear or nonlinear combination of given candidate CVs, as quantified by a maximum path entropy (30) estimate of the spectral gap for the dynamics of that CV. The input to the algorithm is any available information about the static and dynamic properties of the system, accumulated through (i) a biased simulation performed along a suboptimal trial CV, possibly (but not necessarily) complemented by (ii) short bursts of unbiased MD runs, or (iii) by knowledge of experimental observables. Any type of biased simulation could be used in i, as long as it allows projecting the stationary probability density estimate on generic CVs without having to repeat the simulation. Metadynamics (31) provides this functionality in a straightforward manner, and hence it is our method of choice here. Given this information, we use the principle of maximum caliber (30) to set up an unbiased master equation for the dynamics of various trial CVs. Through a simple postprocessing optimization procedure, we then find the CV with the maximal spectral gap of the associated transfer matrix. For instance, this optimization can be performed through a simulated annealing approach that maximizes the spectral gap by performing a robust global search in the space of trial CVs.

Through three practical examples, we show how our postprocessing procedure can lead to better choices of CVs, and to several orders of magnitude improvement in the convergence of the free energy calculated through the popular enhanced-sampling technique metadynamics. Furthermore, the algorithm is generally applicable irrespective of the number of stable basins. Our algorithm essentially provides the much needed ability to extract useful information about relevant CVs even from unsuccessful metadynamics runs. In addition to use in free-energy sampling methods, the optimized CV can then also be used in other methods that provide kinetic rate constants (32, 33). We expect this algorithm to be of widespread use in designing CVs for biasing during enhanced-sampling simulations, making the process significantly more automatic and far less reliant on human intuition.

Theory

Let us consider a molecular system with N atoms at temperature T. We assume there exists a large number d of available order parameters with $1\ll d\ll N$, collectively referred to as $\left\{\mathrm{\Theta }\right\}$, such that the dynamics in this d-dimensional space is Markovian. These could be intermolecular distances (18), torsional angles, solvation states, nucleus size/shape (34), bond order parameters (35), etc. The identification of such order parameters poses another complicated problem, but as routinely done in other methods aimed at optimizing CVs (15, 18, 24), we assume such order parameters are a priori known.

There are several available biasing techniques that can sample the probability distribution of the space $\left\{\mathrm{\Theta }\right\}$, and even calculate the rate constants for escape from stable states in this space (32). All of these techniques are feasible only for a very small number of CVs whose number is much smaller than d—typically one to three. These are the order parameters whose fluctuations are deemed to be most important for the system or process being studied, and by building a fixed or time-dependent bias of these CVs, one should be able to determine the true unbiased probability distribution of the full space $\left\{\mathrm{\Theta }\right\}$. However, how does one decide what is an optimal low-dimensional subset or combination of the available order parameters? This dimensionality reduction is of central importance to methods such as umbrella sampling, metadynamics, and others, the answer to which decides the speed of convergence of the biased simulation, or if it will even ever converge within practically useful simulation times.

The key idea in the current work is to perform enhanced sampling (e.g., metadynamics) with a choice of trial CVs, complemented by information gathered from short bursts of unbiased MD simulations and experimental observables when available, to iteratively improve the CVs. The maximum caliber framework (30, 36, 37), which is a dynamical generalization of the hugely popular maximum entropy framework (38), provides a method for accomplishing this, which is now used in fields as diverse as biology, signal processing, and image reconstruction. In this, given certain information about the system at hand, one builds a model that is consistent with our ignorance of unknown or missing information. The maximum caliber approach (30) is a generalization of this approach to dynamics, with similar underlying ideas.

We start by choosing a trial CV given by $f\left\{\mathrm{\Theta }\right\}$, where f maps the space $\left\{\mathrm{\Theta }\right\}$ onto a lower-dimensional space. The space along this trial CV $f\left\{\mathrm{\Theta }\right\}$ is then discretized in grids labeled n. This CV could be multidimensional, with n then indexing the multidimensional grids. Let $p_n\left(t\right)$ denote the instantaneous probability of the system being found in grid n. For the sake of clarity, we assume that f is a linear combination of $\left\{\mathrm{\Theta }\right\}$, i.e., $f=c_1{\mathrm{\Theta }}_1+c_2{\mathrm{\Theta }}_2+\dots +c_d{\mathrm{\Theta }}_d$. The treatment developed here applies to nonlinear combinations as well, which we show in the examples. Then, for a fixed $\Delta t$, we write a master equation:

$$\frac{\mathrm{\Delta }{p}_n\left(t\right)}{\mathrm{\Delta }t}={\Sigma }_m{k}_{mn}{p}_m\left(t\right)-{\Sigma }_m{k}_{nm}{p}_n\left(t\right)\equiv {\Sigma }_m{\mathbf{K}}_{nm}{p}_m\left(t\right),$$ [1]

where $k_{nm}$ is the rate of transition from grid n to m per unit time (39). The matrix $\mathbf{K}$, where ${\mathbf{K}}_{nm}=k_{mn}$, is the entirety of all these rates. If the dynamics of $f\left\{\mathrm{\Theta }\right\}$ is Markovian, then the matrix $\mathbf{\Omega }$ of transition probabilities is given for small $\Delta t$ by the following:

$$\mathbf{\Omega }=\text{exp}\left(\mathbf{K}\mathrm{\Delta }t\right)\approx \mathbf{I}+\mathbf{K}\mathrm{\Delta }t,$$ [2]

and should not depend on the value of $\mathrm{\Delta }t$ used in Eq. 1. This provides a self-consistency check of whether or not the CV so generated is Markovian. Similar to $\mathbf{K}$, the matrix $\mathrm{\Omega }$ has terms ${\mathbf{\Omega }}_{nm}={\omega }_{mn}$, where ${\omega }_{ab}=k_{ab}\mathrm{\Delta }t$ for $a\ne b$ and the normalization ${\Sigma }_b{\omega }_{ab}=1$ is satisfied. In the maximum caliber approach, one uses all available stationary state and dynamical information to construct probabilities of micropaths. Instead of defining the entropy as a function of microstate probabilities as in information theory and statistical thermodynamics (38), one now defines an entropy S as a functional of the probabilities of micropaths, which is essentially a path integral. For the Markovian process of Eq. 1 (40):

$$S=-{\Sigma }_{ab}{p}_a{\omega }_{ab}\log {\omega }_{ab}.$$ [3]

Note that ${\omega }_{ab}$ are not rate constants but transition probabilities of a Markov model that is discrete in both space and time. Path ensemble averages of time-dependent quantities $A_{ab}$ can now be calculated as follows (30), where the subscripts a,b denote grid indices:

$$\langle A\rangle ={\Sigma }_{ab}{p}_a{\omega }_{ab}{A}_{ab}.$$ [4]

The path entropy of Eq. 3 incremented by quantities accounting for constraints placed by our knowledge of observables $\langle A^n\rangle$, where n runs over the number of known observables, and some other constraints such as detailed balance, is collectively called caliber (30). As derived for instance in ref. 37, maximizing the caliber is then equivalent to being least committal about missing dynamic and static information, with the end result being that one obtains a relation between the grid-to-grid rates and the stationary probabilities as follows:

$${\omega }_{ab}=\sqrt{\frac{p_b}{p_a}}{e}^{-{\Sigma }_i{\rho }_i{A}_{ab}^i}.$$ [5]

Here, i runs over the number of available dynamical pieces of information, and ${\rho }_i$ is the Lagrange multiplier for the associated constraint. As a special case, consider when the only observable at hand is the mean number of transitions $\langle N\rangle$ in observation interval $\mathrm{\Delta }t$ over the entire gridded CV (37). $\langle N\rangle$ would be a measure of the total number of jumps in the time $\mathrm{\Delta }t$ between any two points on the gridded CV. In this case, the above equation takes a particularly simple and useful form:

$${\omega }_{ab}=\sqrt{\frac{p_b}{p_a}}{e}^{-\rho }.$$ [6]

Eqs. 5 and 6 are the two central equations in this work upon which the estimation of the spectral gap of the dynamics is based. Interestingly, an equation similar to Eq. 6 has been previously derived by Bicout and Szabo by assuming a constant position-dependent diffusivity (41).

Spectral Gap.

Our method involves calculating for various trial CVs the spectral gap of the associated transition probability matrix $\mathbf{\Omega }$. Let $\left\{\lambda \right\}$ denote the set of eigenvalues of $\mathbf{\Omega }$, with ${\lambda }_0\equiv 1>{\lambda }_1\ge {\lambda }_2\dots$. The size of this set depends on the discretization interval of the trial CV f—for the purposes of improving CVs, we found very little sensitivity to the details of the discretization. The spectral gap is then defined as ${\lambda }_s-{\lambda }_{s+1}$, where s is the number of barriers apparent from the free-energy estimate projected on the CV at hand, that are higher than a user-defined threshold (typically $\mathrm{\gtrsim }\hspace{0.17em}{k}_{B}T$). Estimating the Lagrange multiplier is computationally expensive, so a first estimate for maximizing the spectral gap is performed using Eq. 6 where the Lagrange multiplier ρ need not be computed, because it sets only the overall timescale but does not influence the spectral gap. Also note that, in the limit of small $\mathrm{\Delta }t$, the matrix $\mathbf{\Omega }$ will be diagonally dominated (42), and to estimate the spectral gap one needs only an accurate estimate of relative local free energies.

There is a wide scope for creativity in choosing the dynamic observables to be used to constrain the caliber for calculating the spectral gap. For instance, one could consider the average number of transitions per unit time not on the entire grid as we do here, but separately in different parts of the configuration space. One could even include experimental observables such as correlation functions from scattering experiments. More static or dynamical information (41, 43–47) simply introduces additional Lagrange multipliers and can be treated through Eq. 5. This can be done if the intention is to calculate an accurate kinetic model with correct estimates of the dominant eigenvalues and not just the spectral gap. For detailed balance to be satisfied through Eq. 5, the observable must be symmetric or be symmetrized on the grid, i.e., $A_{ab}=A_{ba}$.

Algorithm.

We are now in a position to describe the actual algorithm. It comprises the following two steps in a sequential manner, and can be improved by iterating:

• i)Perform metadynamics along a trial CV $f=c_1{\mathrm{\Theta }}_1+c_2{\mathrm{\Theta }}_2+\dots +c_d{\mathrm{\Theta }}_d$ to get a crude estimate of the stationary density.
• ii)As postprocessing, perform optimization in the space of mixing coefficients $\left\{c_1,c_2\dots c_d\right\}$ to identify the CV with the maximal spectral gap. The reweighting functionality (31) of metadynamics allows projection of free-energy estimates on different CVs with minimal computational effort, and is used to calculate the $\mathbf{\Omega }$ matrix through Eq. 6 (see ref. 31 and Supporting Information for a summary of reweighting in metadynamics). We elaborate on the optimization procedure details in the next section (Illustrative Examples).

The optimization procedure gives the best CV as the one with highest spectral gap, given the information at hand. As in any maximum entropy framework (38), the better the quality of this information, the more accurate will be the spectral gap. However, even with very poor quality information, as we show in the examples, the algorithm still leads to significant improvements in the CV. Furthermore, whether or not the CV is Markovian can also be checked by repeating step ii for different time intervals $\mathrm{\Delta }t$ of observation and determining whether the spectral gap is independent of the value of $\mathrm{\Delta }t$.

It is natural to compare our approach with MSM. The similarity between these two approaches begins and ends with the construction of the master equation Eq. 1. A MSM builds this equation by constructing extensive unbiased simulations and attempts to obtain all relevant eigenvalues. Ours is a maximum path entropy-based approach that uses biased and unbiased simulations to obtain the difference between the slow and fast eigenvalues rather than the exact spectrum of eigenvalues.

Illustrative Examples

Model 2D Landscapes: The De Leon–Berne Potential.

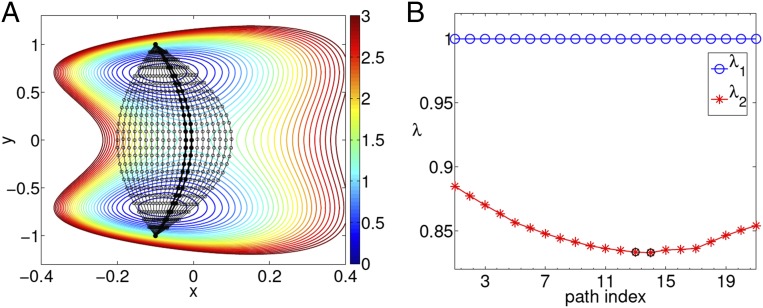
The first illustrative example for SGOOP is a model two-state potential introduced by De Leon and Berne (48). To sample this landscape at temperature $k_{\mathrm{B}}T=0.1$, we perform metadynamics with path CVs, a class of widely used CVs that can capture nonlocal and nonlinear fluctuations (see Supporting Information and ref. 49 for details). Path CVs require specification of a series of landmarks between two points in configuration space, where the landmarks can be described in terms of generic order parameters. Fluctuations in the system can then be enhanced in the direction along and perpendicular to these landmarks, leading to efficient exploration of the space. In Fig. 1A, we show the 2D potential along with several possible path CVs imposed on it. We first perform a short trial metadynamics run biasing the y coordinate. By postprocessing this, we generate the spectral gaps for various paths using Eq. 6 (Fig. 1B). By comparing Fig. 1A against Fig. 1B, it is clear how the path with maximum spectral gap is the minimum energy pathway passing through the saddle point. In this case, although this result could have simply been obtained through nudged elastic band-type calculations (50), the point is to use this example to develop intuition for the method. Also note that moving around the best path to others that are a bit distant from it, does not lead to much change in the spectral gap. This is consistent with the observation that, in several enhanced-sampling methods such as metadynamics or umbrella sampling (3, 7, 8), the CV need not be precisely the true reaction coordinate, as long as it has a sufficient overlap with it (49, 51).

Fig. 1.

In A, we provide the 2D De Leon–Berne potential (48) with several candidate path CVs imposed on it. Black circles denote the corresponding landmarks (49). See Supporting Information for further details of path CVs. In B, the corresponding eigenvalues ${\lambda }_1$ and ${\lambda }_2$ (i.e., excluding the stationary eigenvalue ${\lambda }_0$) are shown for each of these paths. As per the spectral gap given here by ${\lambda }_1-{\lambda }_2$, we identify two possible good paths marked with black circles in B and correspondingly with thicker black lines in A. Energy is in absolute units and $k_{\mathrm{B}}T=0.1$.

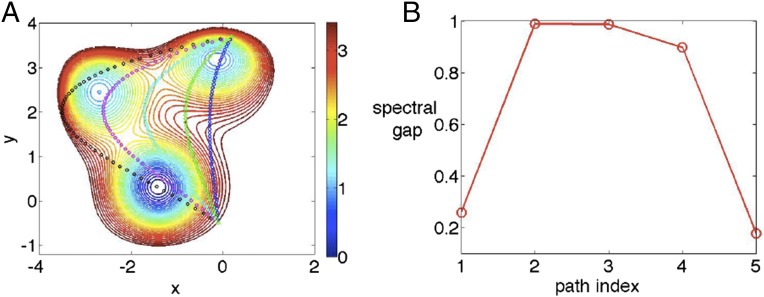
In Supporting Information, we provide a similar analysis on another 2D model potential but with three states (Fig. S1). The conclusions are similar.

Fig. S1.

(A) Three-state potential with five trial path CVs imposed on it, and (B) corresponding spectral gaps. Energies are in absolute units and simulation temperature was $k_{\mathrm{B}}T=0.15$. In both figures, paths are to be counted in the same order, and the second and third paths counting from the left have the maximal spectral gaps. These can be seen to be roughly the minimum energy pathways.

Five-Residue Peptide.

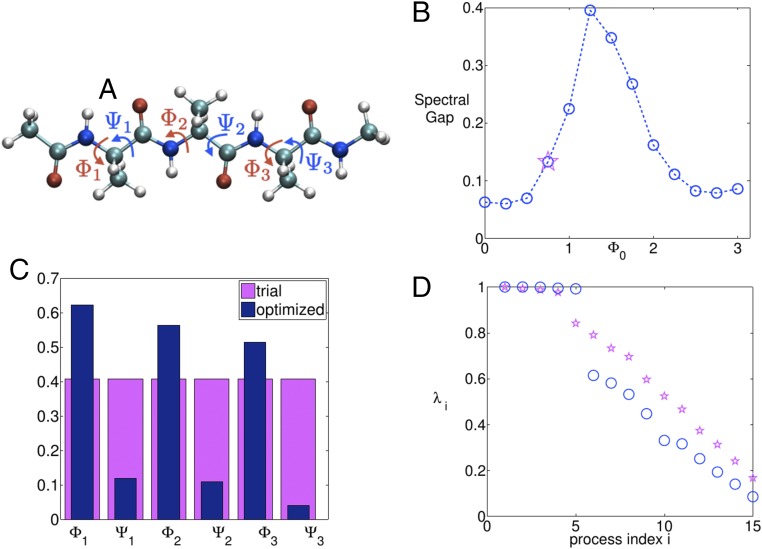
Now, we move to a more complex system, which has also been considered as a test case for new enhanced-sampling methods (52) to establish their usefulness. This is the five-residue peptide Ace–Ala₃–Nme in vacuum (Fig. 2A), where there are six possibly relevant dihedral torsion angles. Here, we ask the question: what is the best possible 1D linear combination of these six dihedrals that we could bias but still maximally enhance exploration of the 6D space comprising all of the dihedrals?

Fig. 2.

(A) The five-residue peptide studied in this work. The six dihedral angles are marked. (B) The output of the simulated annealing algorithm run separately for different ${\theta }_0$ values (blue circles). The starting value with the trial choice of CV is marked with a magenta-colored star. (C) The trial (magenta) and optimized (blue) mixing coefficients $\left\{c\right\}$ for the six dihedrals. (D) The spectrum of eigenvalues for dynamics projected on the trial (magenta) and optimized (blue) CVs. A distinct improvement can be seen in the spectral gap. Process index i refers to the ith index in the transition matrix.

In this problem, for periodicity-related numerical reasons, we bias a reference cosine defined by cos($\theta -{\theta }_0$), where θ is one of the six dihedral angles, and ${\theta }_0$ is some reference value whose optimal choice we do not know a priori. Through our algorithm we then seek to identify:

• i)The best choice of mixing coefficients $\left\{c\right\}$ to use in trial CV $f=c_1{\Phi }_1^{\prime }+c_2{\Psi }_1^{\prime }+c_3{\Phi }_2^{\prime }+c_4{\Psi }_2^{\prime }+c_5{\Phi }_3^{\prime }+c_6{\Psi }_3^{\prime }$, where we keep the Euclidean norm of $\left\{c\right\}$= 1, and for any angle θ the prime denotes the transformation $\theta \mapsto 0.5+\cos \left(\theta -{\theta }_0\right)$;
• ii)The best choice of ${\theta }_0$, kept same for all six dihedrals.

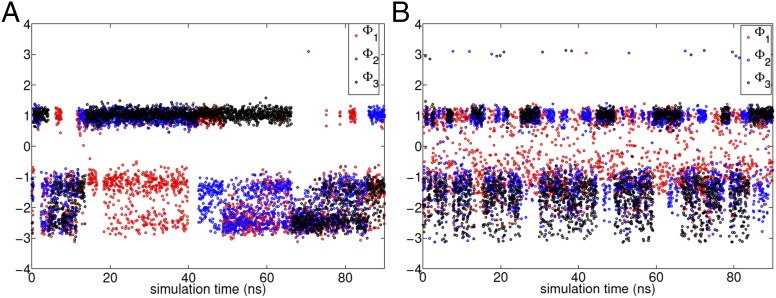
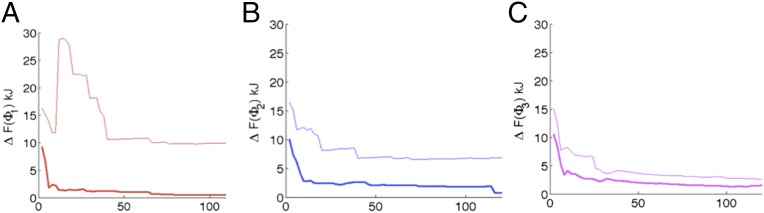
We start with the trial CV where all members of $\left\{c\right\}$ are the same subject to Euclidean norm of $\left\{c\right\}$= 1, and an arbitrary choice of ${\theta }_0=0.75$ radians is taken. A short metadynamics run is performed biasing this trial CV. See Supporting Information for details of the metadynamics and MD parameters (53–55), and Fig. 3A for the metadynamics trajectory used for spectral gap optimization. Based on the free-energy estimate generated from this run, a simulated annealing procedure is performed in the space $\left\{c\right\}$ for various ${\theta }_0$ values. Starting from the spectral gap estimated using Eq. 6 for the trial CV, this involves executing Metropolis moves in the $\left\{c\right\}$ space with an attempt to find the global maxima of the spectral gap. In Fig. 2, B–D, respectively, we show how the spectral gap is increased by the simulated annealing procedure, and the corresponding best estimate of $\left\{c,{\theta }_0\right\}$. The algorithm suggests the minimal role of the angles ${\Psi }_1,{\Psi }_2,{\Psi }_3$ as can be seen through their relatively low weights (52) (Fig. 2C). The spectrum of eigenvalues for dynamics projected on the trial (magenta) and optimized (blue) CVs, along with respective spectral gaps is provided in Fig. 2D. Fig. 3, A and B, shows the metadynamics trajectories for the three dihedral angles ${\Phi }_1,{\Phi }_2,{\Phi }_3$, with the trial and the optimized CVs, respectively. A very pronounced improvement in the quality of sampling can be seen. Fig. 4 A–C shows the rate of convergence of the error of the estimated free energy (31) with respect to reference values from other approaches (52), through metadynamics runs performed with each of the trial and optimized CVs, respectively. The error metric is the same as in refs. 52 and 56, and is calculated for all points within 25 kJ of the global minimum in the respective 1D free energy. The behavior is robust with respect to the choice of this threshold value. As can be seen, the optimized CV, even though it was obtained on the basis of a very poorly converged and short (20-ns) metadynamics run, leads to several orders of magnitudes improvement in the rate at which the free energies converge. Interestingly, iterating the algorithm with the improved 1D CV did not lead to much improvement in the sampling, reflecting that the optimized coefficients $\left\{c\right\}$ are close to the best that can be achieved with a 1D CV for this problem.

Fig. 3.

A and B show trajectories obtained from metadynamics biasing the trial CV and the optimized CV, respectively. The first 20 ns of the trajectory shown in A was used to generate the optimized CV for B. A very pronounced improvement in the enhancement of sampling can be seen with the optimized CV.

Fig. 4.

Errors in the 1D free energies for three dihedrals in kilojoules calculated with respect to respective reference free energies (52, 61, 62) using the error metric from ref. 56. Thin and thick lines denote values using the trial and optimized CVs, respectively. A, B, and C denote error in the free energies for the dihedrals Φ₁, Φ₂, and Φ₃, respectively.

Discussion

To conclude, we have introduced a new approach named SGOOP for improving the choice of low-dimensional CVs for biasing in enhanced sampling in complex systems. This is accomplished through the use of a maximum caliber-based approach, where we build kinetic models for different CVs. For each CV, we separate out the slow motions that involve crossing barriers, from hidden or orthogonal motions. Through a spectral gap maximization, we make the orthogonal fluctuations as fast as possible, compared with the slow motions apparent in the CV. The algorithm is iterative in spirit and attempts to learn how to improve CVs based on available stationary and dynamic data. We also provide several proof-of-concept practical examples to establish the potential usefulness of the method. For model 2D potentials, the algorithm was shown to yield the minimum energy pathway. For a small peptide, we found very significant improvement in determining the best 1D CV from six possible functions with no ad hoc or intuition-based tuning. Future work will use this algorithm to treat a range of problems, especially involving protein–ligand unbinding. For instance, the displacement of water molecules and protein flexibility are often slowly varying order parameters in unbinding (33, 51, 57, 58), but do we really need to bias one or both of these for the purpose of sampling? Another issue to be considered in future work is whether we can use these optimized CVs to obtain reliable dynamical information from metadynamics (25, 32), including the very important off-rate for ligand unbinding (51, 59).

One central limitation of this algorithm is having to specify possibly a large number of order parameters that may be important. However, for many physical problems, one does have a sense of which order parameters could be at work, and this is where we expect this algorithm to be of tremendous use. Another obvious limitation is with systems devoid of a timescale separation (60)—for example, in glassy systems where there is an effectively continuous spectrum of eigenvalues with no discernible timescale separation. However, the dynamics of many complex and real-world molecular systems does thankfully show a timescale separation between few relevant slow modes and remaining fast ones (62), and we expect our algorithm to be of help in unraveling the thermodynamics and dynamics in such systems.

Metadynamics

Here, we briefly describe metadynamics and the related concepts that are used in the present work.

Reweighting.

The reweighting operation in metadynamics is central to this work, as it allows projecting probability densities on arbitrary collective variables (CVs) without having to repeat the simulation. A more detailed discussion can be found in ref. 31. In metadynamics, one constructs a time-dependent bias V (s,t) as a function of some low-dimensional CV s (R), where R denotes the configurational coordinates. At time t, the biased probability distribution for $\mathbf{R}$ can then be written as follows:

$$P\left(\mathbf{R},t\right)=\frac{e^{-\beta \left[U\left(\mathbf{R}\right)+V\left(\mathbf{s}\left(\mathbf{R}\right),t\right)\right]}}{{\displaystyle \int d\mathbf{R}\hspace{0.17em}{e}^{-\beta \left[U\left(\mathbf{R}\right)+V\left(\mathbf{s}\left(\mathbf{R}\right),t\right)\right]}}},$$ [S1]

where $U\left(\mathbf{R}\right)$ is the potential energy of the system (31). This in turn can be rewritten as follows:

$$P\left(\mathbf{R},t\right)=P_0\left(\mathbf{R}\right)\hspace{0.17em}{e}^{-\beta \left[V\left(\mathbf{s}\left(\mathbf{R}\right),t\right)-c\left(t\right)\right]},$$ [S2]

where $P_0\left(\mathbf{R}\right)$ is the unbiased Boltzmann probability density and the function $c\left(t\right)$ is defined as follows:

$$c\left(t\right)=\frac{1}{\beta }\log \frac{{\displaystyle \int ds{e}^{-\beta F\left(s\right)}}}{{\displaystyle \int ds{e}^{-\beta \left(F\left(s\right)+V\left(s,t\right)\right)}}}.$$ [S3]

β is the inverse of the temperature multiplied by the Boltzmann constant $k_{\mathrm{B}}$. The time-dependent function $c\left(t\right)$ is an estimator for the reversible work done by the bias. As shown in ref. (31), it can be calculated by substituting the running estimate of $F\left(s\right)$ (31) into Eq. S3 as follows:

$$c\left(t\right)=\frac{1}{\beta }\text{log}\frac{{\displaystyle \int d\mathbf{s}\exp \left[\frac{\gamma }{\gamma -1}\beta V\left(\mathbf{s},t\right)\right]}}{{\displaystyle \int d\mathbf{s}\exp \left[\frac{1}{\gamma -1}\beta V\left(\mathbf{s},t\right)\right]}}.$$ [S4]

Here, γ is the bias factor in well-tempered metadynamics that modulates the decay of hill height each time a point is revisited (8). Using Eq. S4 in Eq. S2, we can then easily calculate the distribution of any generic observable $O\left(\mathbf{R}\right)$ over the unbiased ensemble from the metadynamics trajectory through the following:

$${\langle O\left(\mathbf{R}\right)\rangle }_0=\langle O\left(\mathbf{R}\right)e^{\beta \left[V\left(\mathbf{s}\left(\mathbf{R}\right),t\right)-c\left(t\right)\right]}\rangle .$$ [S5]

Path CVs.

In the path CV framework (2, 49), one assumes that initial and final states A and B are known. One then specifies a series of landmarks between these two points, which can be described in terms of generic order parameters in some high-dimensional space R. This series of landmarks then denotes a trial path connecting the initial and final states in the space R, which we call ${\mathbf{S}}_0\left(t\right)$. Two variables s and z are then introduced, defined as follows, that, for a given series of landmarks, respectively denote distances along and perpendicular to the trial path:

$$s\left(\mathbf{R}\right)=\underset{\lambda \to \infty }{\text{lim}}\frac{{\displaystyle {\int }_0^{1}dt\hspace{0.17em}t\hspace{0.17em}{e}^{-\lambda {\Vert \mathbf{S}\left(\mathbf{R}\right)-{\mathbf{S}}_0\left(t\right)\Vert }^2}}}{{\displaystyle {\int }_0^{1}dt\hspace{0.17em}{e}^{-\lambda {\Vert \mathbf{S}\left(\mathbf{R}\right)-{\mathbf{S}}_0\left(t\right)\Vert }^2}}},$$ [S6]

$$z\left(\mathbf{R}\right)=\underset{\lambda \to \infty }{\text{lim}}\left(-\frac{1}{\lambda }\text{log}{\displaystyle {\int }_0^{1}dt\hspace{0.17em}{e}^{-\lambda {\Vert \mathbf{S}\left(\mathbf{R}\right)-{\mathbf{S}}_0\left(t\right)\Vert }^2}}\right).$$ [S7]

In practice, the paths are discretized (i.e., a finite number of landmarks are chosen), and λ is taken as the inverse distance between points in the path (49).

Simulation Setup for Metadynamics Calculations

All peptide simulations are performed with the GROMACS 4.5.4 MD package (54), patched with the PLUMED 2.2 plugin (53). The production runs were NVT (constant number, volume, temperature) with a temperature of 300 K implemented with the stochastic velocity rescaling thermostat (55). An integration time step of 2 fs was used for all runs. The model potentials were simulated in an in-house code.

For De Leon–Berne potential (main text), Gaussian hills were added every 50,000 integration time steps, with a starting height of 0.1 $k_{\mathrm{B}}T$, width of 0.1 unit, and tempering factor (8) of 6.

For the five-residue peptide (main text), Gaussian hills were added every 400 integration time steps, with a starting height of 1.7 kJ/mol, width of 0.03 units, and tempering factor (8) of 15.

For the three-state potential (SGOOP Optimization Details), Gaussian hills were added every 50,000 integration time steps, with a starting height of 0.4 $k_{\mathrm{B}}T$, width of 0.2 unit, and tempering factor (8) of 15.

SGOOP Optimization Details

For the model potentials, the maximum spectral gap was ascertained by tabulation against candidate CVs. For the peptide, simulated annealing was performed with negative of the spectral gap as the objective function. A starting temperature of 2.5 units was used for the Metropolis moves, with a geometric cooling schedule, where at each step the temperature was reduce by a factor of 0.995.

SGOOP on a 2D Three-State Potential

Similar to the De Leon–Berne potential described in the main text, we tested SGOOP as a proof of principle on another 2D potential but with three states at temperature $k_{\mathrm{B}}T=0.15$. This potential can be seen in Fig. S1A, along with five candidate path CVs imposed on it (49). The functional form of this potential is given by the following:

$$V\left(x,y\right)=-3.0e^{-{\left(x+2.8\right)}^2-{\left(y-2.5\right)}^2}-3.7e^{-{\left(x+0.1\right)}^2-{\left(y-3.5\right)}^2}-3.7e^{-{\left(x+1.4\right)}^2-{\left(y-0.3\right)}^2}+0.005\left({\left(x+1\right)}^6+{\left(y-1\right)}^6\right).$$

We first perform short trial metadynamics run biasing the y coordinate. By applying SGOOP, we obtain spectrum of eigenvalues corresponding to trial paths, and the corresponding spectral gaps (Fig. S1B). As can be seen, the maximal spectral gap so obtained is approximately for the minimum energy pathways on this landscape filtering out the bad paths.